DeepMind с помощью ИИ ускорила умножение матриц
06.10.2022 Богдан Каминский
#DeepMind#Искусственный Интеллект
Лаборатория DeepMind использовала ИИ AlphaZero для решения фундаментальной математической задачи в информатике и побила рекорд, установленный более 50 лет назад. Об этом пишет Technology Review.
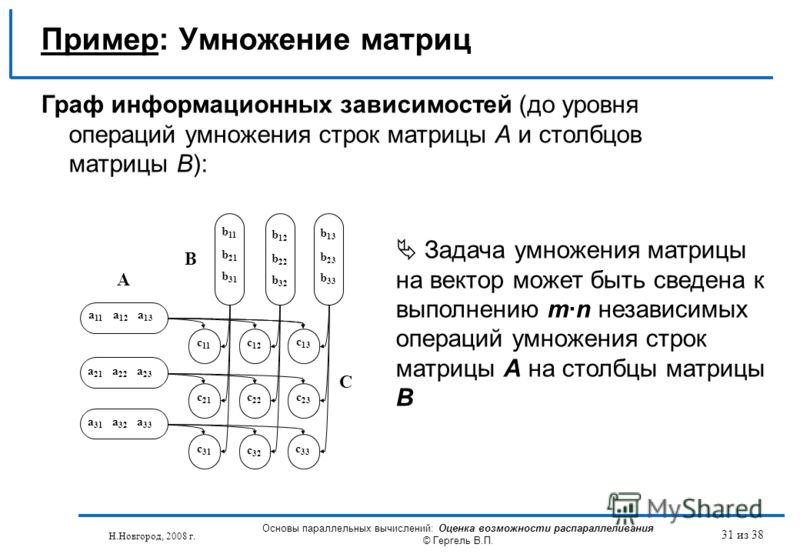
Речь идет об умножении матриц. Это важнейший тип вычислений, лежащий в основе различных приложений, от отображения изображений на экране до моделирования сложных физических процессов.
Несмотря на широкое распространение метода, он все еще недостаточно изучен. Матрица — это сетка чисел, которая может представлять собой что угодно. Базовая техника перемножений двух таких объектов преподается в средней школе.
Однако все усложняется при попытке найти более быстрый метод решения задачи. По словам ученых, вариантов перемножения двух матриц может быть больше, чем атомов во Вселенной.
«Количество возможных действий почти бесконечно», — сказал инженер DeepMind Томас Хьюберт.
Подход исследователей заключается в превращении задания в своего рода настольную игру под названием TensorGame. Доска представляет собой задачу на умножение, а каждый ход направлен на ее решение. Таким образом, серия предпринятых действий к конечной цели представляет собой алгоритм.
Затем ученые обучили играть в эту игру новую версию AlphaZero, названную AlphaTensor. Аналогично шахматам или Го искусственный интеллект изучал лучшие серии шагов при умножении матриц. За победу с минимальным количеством ходов AlphaTensor получал вознаграждение.
«Мы превратили это в игру — наш любимый вид фреймворка», — сказал Хьюберт.
Главный результат исследователей состоит в ускорении решения данной задачи. Например, базовый школьный метод умножения матриц четыре на четыре состоит из 64 шагов. Самый быстрый способ решения задачи в 1969 году открыл немецкий математик Фолькер Штрассен: он состоит из 49 ходов.
По словам исследователей, система DeepMind превосходит лучшие существующие алгоритмы для более чем 70 различных размеров матриц. Их впечатлило количество различных правильных алгоритмов, которые нашел AlphaTensor для каждой задачи.
«Удивительно, что существует по меньшей мере 14 000 способов умножения матриц четыре на четыре», — говорит Хусейн Фаузи, научный сотрудник DeepMind.
После поиска самых быстрых алгоритмов в теории команда использовала AlphaTensor для поиска алгоритмов на графических процессорах Nvidia V100 и Google TPU. Согласно результатам тестирования, программа нашла верные решения на 10-20% быстрее, чем при помощи стандартных методов на аналогичных чипах.
По словам исследователей, это также имеет фундаментальное значение для самого машинного обучения. Ускорение вычисления может оказать большое влияние на тысячи повседневных компьютерных задач, сократив расходы и сэкономив энергию.
В будущем DeepMind планирует использовать AlphaTensor для поиска других типов алгоритмов.
Напомним, в июле ИИ-лаборатория заявила, что системе AlphaFold предсказала структуры более 200 млн белков. Это почти все известные науке соединения, обнаруженные в растениях, бактериях и животных.
В мае DeepMind представила визуальную языковую модель с 80 млрд параметров.
Подписывайтесь на новости ForkLog в Telegram: ForkLog AI — все новости из мира ИИ!
Нашли ошибку в тексте? Выделите ее и нажмите CTRL+ENTER
| Comments: | ||||||||||||||||||||||||||||||||||||||||||||||||
Ни разу сейчас не математик, но как вот твердо запомнил в курсе линейной алгебры чисто визуальную картинку — столбец правой матрицы взлетает, поворачивается на 90 градусов и «сопрягается» поэлементно со строками левой матрицы, так до сих пор ее и помню (а много чего другого из линейной алгебры знал, да давно забыл). Но это конечно никто такой картинке не учил, сама она сформировалась в попытке визуализировать определение с торчащими во все сторооны индексами до состояния, в котором операцию умножения можно более-менее быстро сделать вручную… Вроде бы усвоению дальнейшего материала это особо не мешало. Как раз возможность быстро визуально представлять процесс умножения позволяла как-то осмысленно воспринимать все последующее. Представить визуально альтернативный вариант я вроде могу, но мне от этого определенно становится плохо…
А я кстати всегда представляю наоборот — строка левой матрицы падает вправо, поворачивается на 90 градусов и совпадает с столбцом правой…
А как этому можно обучить вместо нормального умножения матриц? Ведь умножать по его методу невозможно, не записывая промежуточные результаты, в то время как обычное умножение требует O(1) оперативной памяти. В дополнение к обычному умножению, чтобы лучше что-то объяснить — возможно.
А почему это важно, есть или нет промежуточные результаты? Если нам нравится, можем именно так определить умножение, а если его выполнять вручную, все равно в итоге будет то же кол-во умножений и сложений. Промежуточные матрицы надо записывать, но зато записывать их очень просто, их столбцы это просто масштабированные столбцы первой матрицы. (без темы) — (Анонимно) Развернуть
Нео вращается в своей Матрице…
Почему русские не смогли самостоятельно додуматься даже как матрицы перемножать, пользуются изобретениями американцев.
А до понятия матрицы русские самостоятельно додумались? 😉
Задумался, не даст ли это более эффективной компьютерной реализации с использованием векторных инструкций, например. Но кажется, всё-таки нет
Впервые вижу такой подход. Я всегда считал, что умножение матриц – это Заодно вспомнилось (в основном из-за нечётких выражений «строки умножить на столбцы» и «столбцы умножить на строки»): довольно регулярно, когда говоришь студентам, что если умножаешь матрицу A (слева) на столбец, состоящий из единиц (справа), то результат является суммой столбцов матрицы A — то кто-нибудь «поправляет»: нет, суммой строчек (и это не ошибка, а небрежное обращение с математическим текстом). Edited at 2020-05-13 21:26 (UTC)
Про матрицы, боюсь, получится, как с объяснением деления в израильском учебнике математики, которое взрывает мозг, на мой взгляд. Для того, чтобы разделить 40 на 5, надо найти, сколько раз число 5 «умещается» в 40. Вроде, правильно, но как-то абсолютно наизнанку и не понятно.
Для меня самым большим сюрпризом в израильской школьной математике было то, что разложение квадратного двучлена, угаданное по теореме-Виета-наоборот, предшествует формуле решения квадратного уравнения — или, по сути дела, является первым изучаемым методом решения квадратных уравнений. (без темы) — (Анонимно) Развернуть (без темы) — (Анонимно) Развернуть (без темы) — (Анонимно) Развернуть
поправьте ссылку на статью: sci-hub.im
Хорошо, но у меня открываются обе. Вы в России?
Хмм.
Нет, матрица на матрицу — это суперпозиция операторов, вторичный, да не совсем такой. (без темы) — (Анонимно) Развернуть
Все это хорошо, но не если умножать в голове.
This is very interesting, I need to think it through.
This makes it clear that image of matrix multiplication is the span of columns, among other things.
Определение нам вроде бы давали стандартное, но то, что умножение матриц можно представить в виде как строки на столбцы, так и столбцы на строки — это точно объяснялось подробно. И точно использовалась потом в доказательствах. Не помню уже точно каких фактов, но наверняка чего-то связанным с транспонированием. Edited at 2020-05-14 03:39 (UTC)
| ||||||||||||||||||||||||||||||||||||||||||||||||
Вот и ответ, почему у Крылова ничего не получилось — глуповат народ.
Какое-то время назад я наткнулся на подобное в «настоящей» математической статье: там упоминалась «циклическая перестановка строчек матрицы», но автор имел в виду, что одна и то же циклическая перестановка происходит в каждой строчке – для меня это, конечно, «циклическая перестановка столбцов».
2 — 7x + 10 = 0. Чтобы его решить, надо угадать два числа, сумма которых 7, а произведение 10…
Матрица — оператор, отображающий вектор в вектор. Вектор — это таки столбец. i-тая строка матрицы — покоординатные предписания, с каким весом мариновать координаты вектора, чтобы получить i-тую координату результата преобразования. Матрица на матрицу — это вторичный конструкт, оператор просто применяется поочередно к набору векторов.
k — сумма не более чем min(n,k) отображение ранга 1; стоит дать такую задачку на семинаре и ее обсудить. Но вот прямо строить вокруг этого все изложение выглядит неестественным.
Но тут боюсь соврать, не помню.Полное руководство для начинающих по умножению матриц для науки о данных с помощью Python Numpy | by GreekDataGuy
Изучите умножение матриц для машинного обучения, следуя примерам Python
Линейная алгебра является основой машинного обучения от логистической регрессии до глубоких нейронных сетей.
Если вы какое-то время занимаетесь наукой о данных, но не понимаете математики, стоящей за этим, лучше всего начать с умножения матриц. Это доступно, практично и знакомит вас с математическими объектами машинного обучения: скалярами, векторами и матрицами.
Ах да, и Нампи гуляет по парку.
К концу этой статьи вы получите практическое представление об умножении матриц.
Здесь мы будем сравнивать матрицы со скалярами.
Матрица представляет собой двумерный массив, в котором каждый элемент массива имеет 2 индекса. Например, [[1, 2], [3, 4]] — это матрица, а индекс 1 равен (0,0).
Мы можем доказать это, используя Python и Numpy.
импортировать numpy как npA = [[1, 2],
[3, 4]]np.array(A) [0,0]
=> 1
Говоря о форме матриц, мы говорим «строки x столбцы». Мы бы сказали, что 1-я матрица ниже имеет форму 2×2, а 2-я имеет форму 3×2.
[[1, 2],
[3, 4]][[10, 20],
[11, 21],
[12, 22]]
Напротив, скаляр — это просто число , как число 5 .
Простая форма умножения матриц называется скалярным умножением , умножением скаляра на матрицу.
Скалярное умножение обычно выполняется легко. Каждое значение во входной матрице умножается на скаляр, и выход имеет ту же форму, что и входная матрица.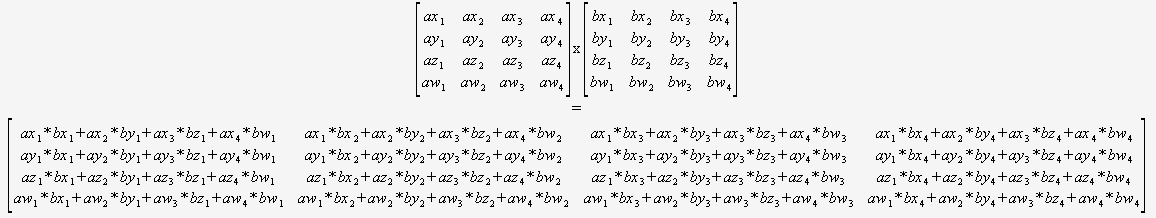
Давайте сделаем приведенный выше пример, но с Python Numpy.
a = 7
B = [[1,2],
[3,4]]np.dot(a,B)=> array([[ 7, 14],
=> [21, 28]] )
Еще один пример скалярного умножения. На этот раз скаляр, умножающий матрицу 3×1.
И в Numpy.
a = 4
B = [[1],[2],[3]]np.dot(a,B)=> array([[ 4],
=> [ 8],
=> [12]])
Порядок не имеет значения при скалярном умножении. «скаляр х матрица» и «матрица х скаляр» дают один и тот же результат. Но не так при умножении 2-х матриц .
Теперь самое интересное. Умножьте 2D-матрицу на 2D-матрицу.
Следует помнить несколько вещей.
- Заказ имеет значение сейчас.
AB != BA - Матрицы можно перемножать, если количество столбцов в первой равно количеству строк во второй
- Умножение — это скалярное произведение строк и столбцов. Строки 1-й матрицы со столбцами 2-й
Пример 1
На изображении выше 19 в индексе (0,0) полученной матрицы является скалярным произведением 1-й строки 1-й матрицы и 1-й столбец 2-й матрицы .
Давайте воспроизведем результат в Python.
A = [[1,2],
[3,4]]B = [[5,6],
[7,8]]np.dot(A,B)=> array([[19, 22],
=> [43, 50]])
И давайте докопаемся до сути порядка. Попробуйте np.dot(A,B) , а затем попробуйте np.dot(B,A) .
np.dot(A,B)
=> массив([[19, 22],
=> [43, 50]])np.dot(B,A)
=> массив([[23, 34 ],
=> [31, 46]])
Теперь обратите внимание, как отличается вывод! Вы найдете тот же результат, вычислив его на бумаге (как бы неинтуитивно это ни было, если вы не знакомы с матрицами).
Пример 2
Теперь умножим матрицу 2×3 на матрицу 3×2.
И в Python с Numpy.
A = [[1,2,3],
[4,5,6]]B = [[10,11],
[20,21],
[30,31]]np.dot(A ,B)=> array([[140, 146],
=> [320, 335]])
Пример 3
Последний пример. Умножьте 1×5 на матрицу 5×1.
Обратите внимание, что все вычисления, которые мы здесь делаем, просто возвращают одну ячейку в выходной матрице.
И снова на Python.
А = [[1,2,3,4,5]]В = [[10],
[20],
[30],
[40],
[50]]np.dot(A,B)=> array([[550]])
Это охватывает 3 уникальных случая умножения матриц и должно дать вам общее представление о том, как это работает. Я показал все расчеты на каждом шаге диаграмм, чтобы вам было легко следовать им.
Умножение матриц (и линейная алгебра) является основой для глубокого обучения и машинного обучения.
Хотя вам не нужно, чтобы он подключался и работал со Sklearn, мысленное представление о том, как это работает, поможет вам понять его модели. И с этим пониманием приходит повышенная эффективность в настройке и настройке этих моделей для повышения производительности.
Как умножать матрицы? С Примерами
Умножение матриц является одной из фундаментальных, но продвинутых концепций матриц. Вы должны быть осторожны при умножении матриц. Это не так просто, как кажется. Вы должны хорошо знать все основные понятия, такие как, что такое матрица, строки и столбцы в матрице, как представлять матрицу и как умножать матрицы.
Снова в школу: Матрицы — это группы чисел, переменных, символов или выражений в прямоугольной таблице с различным количеством строк и столбцов. Это прямоугольные массивы с различными операциями, такими как сложение, умножение и транспонирование. Элементами матрицы являются числа или элементы, составляющие матрицу. Горизонтальные элементы матриц — это строки, а вертикальные — столбцы.
Вы можете изобразить количество строк и столбцов с помощью переменных. Например, пусть количество строк в матрице K равно «m», а количество столбцов — «n». Таким образом, мы можем представить матрицу K как [K] m x n . Матрица представлена в квадратных скобках «[]» с произведением ее строк и столбцов в нижнем индексе.
До 1812 года человечеству не было известно умножение матриц. Филипп Мари Бине, французский математик, изобрел умножение матриц в 1812 году для описания линейных карт с матрицами. Он обнаружил, что умножение матриц является бинарной операцией.
Две матрицы перемножаются, образуя одну матрицу.
Далее в этой статье вы узнаете правила и основные принципы умножения матриц.
Формула умножения матрицы
Пример матриксной формулы
Take A и B — две матрицы,
A = [A11 A12 ⋯ A1N
A21 A22 ⋯ A2N
………………………………………………….
Am1 Am2 ⋯Amn],
B=[B11 B12 ⋯B1n
B21 B22 ⋯B2n
………….
BM1 BM2 ⋯ BMN]
Матрикс C = AB обозначена
C = [C11C12 …… .C1C
C21C22 …… .C2C
…91919191919191919191919191919191919. Ca1Ca2…….Cac]
Элемент матрицы C, где C — произведение матрицы A X B.
Элемент матрицы C, где C — произведение матрицы A X B.
Cxy=Ax1By1+….+AxbBby=∑k=1bAxkBky
Для x = 1…… a и y = 1…….c
Правила умножения матриц- Если число столбцов в A равно количество строк в B, то определяется произведение A и B.
- Нет необходимости определять BA, если определен AB.
- И AB, и BA определены, если A и B — квадратные матрицы одного порядка.
- Не требуется, чтобы AB равнялся BA, если определены оба AB и BA.
- Не требуется, чтобы одна из матриц была нулевой матрицей, если произведение двух матриц является нулевой матрицей.
- В математике операция умножения матриц имеет некоторые специфические характеристики. Эти характеристики перечислены ниже.
- Некоммутативность: когда две матрицы A и B перемножаются, AB BA означает, что умножение матриц некоммутативно.
- Распределяемость: Если A, B и C совместимы, свойство распределения можно использовать при умножении матриц, т. е. A (B + C) = AB + BC.
- Произведение со скаляром: Если перемножить матрицы A и B, результатом будет AB, тогда c(AB) = (cA)B = A(Bc), где c — скаляр.
- Транспонирование: формула (AB)T = BTAT, где T означает транспонирование, может использоваться для выражения транспонирования произведения матриц A и B.
- Комплексное сопряжение: (AB)* = B *A*, если A и B являются сложными элементами.
- Умножение матриц ассоциативно. Если произведения (AB)C и A(BC) трех матриц A, B и C определены, то (AB)C = A. (BC).
- Определитель: Сумма определителей каждой отдельной матрицы равна определителю произведения матриц. Например, Det (AB) = Det A Det B.
Во введении к этой статье вы прочитали, что умножение матриц — это бинарная операция. Это означает, что всякий раз, когда вы находите произведение двух или более матриц, ответом является единственная матрица, следующая за исходными матрицами. Для перемножения двух матриц проверяется их совместимость. Это означает, что две матрицы должны следовать набору правил для умножения.
Эти параметры совместимости описаны ниже:
- Значение количества столбцов в матрице один должно быть равно значению количества строк в матрице 2.
- Если вышеуказанное условие не удовлетворяет, матрицы нельзя умножить.
- Если матрицы являются квадратными матрицами одного порядка, их можно умножать друг на друга.
- Квадратную матрицу 2 x 2 нельзя умножить на квадратную матрицу 3 x 3. Ее можно умножить на другую квадратную матрицу 2 x 2.
Давайте рассмотрим пример, чтобы лучше понять это:
Пример 1: Предположим, у нас есть две матрицы, K и L. Порядок матриц задан как m x n и n x o соответственно. Выяснить, можно ли перемножать матрицы?
Решение: Дано
Матрица 1 = [ K ] m x n
Матрица 2 = [ L ] n x o
Мы видим, что количество столбцов в матрице равно количеству строк K матрица L. Следовательно, две матрицы можно перемножить.
Результирующая матрица: Матрица, полученная путем умножения двух матриц, является результирующей матрицей. Эта матрица может быть представлена как:
- Имя матрицы в квадратных скобках
- Произведение количества строк матрицы 1 на количество столбцов матрицы два в порядке.
Снова обратимся к приведенному выше примеру:
Мы знаем, что K и L совместимы с умножением. Таким образом, результирующая матрица, скажем, D, будет = [D] m x o , где m = количество строк матрицы один, а o = количество столбцов матрицы 2.
Пример 2: Матрица [ K ] 2 x 4 умножается на матрицу [ X ] 4 х 2 . Если [ Y ] результирующая матрица, то каков порядок Y.
Решение: Нам дано
Матрица 1 = [ K ] 2 x 4
Матрица 2 = [ X ] 4 x 2
Поскольку количество столбцов матрицы K равно количеству строк матрицы X, K и X можно перемножить. Следовательно,
Матрица Y = [ Y ] 2 x 2
Порядок матрицы Y равен 2 x 2. Y — квадратная матрица.
Ориентация двух матриц также является решающим фактором для определения произведения матриц. Если есть две матрицы, K и L, то чтобы найти произведение K и L, вы должны сначала написать матрицу K, а затем написать матрицу L.
Если вы запишете матрицу L перед матрицей K, вы получите совершенно другую матрицу . Коммутативный закон не применяется при умножении матриц. Это означает, что KL ≠ LK.
Теперь, когда мы разобрались с правилами умножения двух матриц, давайте научимся умножать матрицы.
Как умножать матрицы?Давайте изучим пошаговую процедуру умножения двух матриц. Поначалу это может показаться вам запутанным, но когда вы освоитесь, перемножать матрицы так же просто, как намазать маслом свой тост.
Шаг 1: Проверьте совместимость предоставленных матриц. Если они несовместимы, оставьте умножение.
Шаг 2: Возьмите первую строку матрицы 1 и умножьте ее на первый столбец матрицы 2. Затем умножьте первую строку матрицы 1 на 2-й столбец матрицы 2. Теперь умножьте первую строку матрицы 1 на 3-й столбец матрицы 2 и так далее. Полученные из них значения заполнят первую строку матрицы продукта.
Шаг 3: Теперь возьмите вторую строку матрицы 1 и умножьте ее на первый столбец матрицы 2 и выполните те же шаги, что и для 2.
Это заполнит вторую строку матрицы произведения.
Шаг 4: Продолжайте эти шаги, выполняя каждую строку, пока не будет получена матрица произведения.
Под умножением строк и столбцов мы подразумеваем, что элементы, присутствующие в этих строках и столбцах, будут умножены. Не забудьте умножить соответствующие элементы, а затем добавить продукты, чтобы найти элемент матрицы продукта.
Если вы не уверены в шагах, посмотрите на пример пошагового решения ниже:
Пример: Найдите произведение матриц, приведенных ниже:
K = и L =
Решение:
Шаг 1: Матрица K имеет порядок 1 x 4, а матрица L имеет порядок 4 x 2. Поскольку количество столбцов матрицы K соответствует количеству строк матрицы L, поэтому матрицы совместимы для умножения. Полученная матрица имеет порядок 1 x 2.
Шаг 2: Поскольку K имеет только 1 строку, умножьте ее на первый столбец матрицы L следующим образом: (2 x 4) + (4 x 5) + (1 x 4) + (7 x 3) = 51.
Обратите внимание, как 1-й элемент строки умножается на 1-й элемент столбца 1, аналогично 2-му, 3-му и 4-му. Затем они складываются вместе, чтобы получить результирующий матричный элемент.
Шаг 3: Теперь аналогичным образом умножьте 1-ю строку на второй столбец матрицы L. Результат будет (2 x 3) + (4 x 2) + (1 x 9) + (7 x 6) = 65. .
Шаг 4: Разместите результат в матрице продуктов. Предположим, что [ X ] — результирующая матрица; следовательно, X = [51 65].
Мы только что научились перемножать две матрицы. В следующем разделе вы узнаете, как решить квадратную матрицу (2 x 2).
Мы только что научились перемножать две матрицы. В следующем разделе вы узнаете, как решить квадратную матрицу (2 x 2).
Как умножить матрицу 2 x 2 Для умножения матриц 2 x 2 вы должны хорошо знать шаги, описанные в предыдущем разделе. Поскольку мы перемножаем 2 квадратные матрицы одного порядка, нам не нужно проверять совместимость в этом случае.
Помните, что матрица произведения также будет иметь тот же порядок, что и квадратная матрица. Давайте решим пример, чтобы понять, как умножить матрицу 2 x 2.
Пример: Умножить квадратную матрицу на
A = и B =
Шаг 1: Умножаем первую строку матрицы A на первый столбец матрицы B. Получаем (2 x 1) + (9 x 3) = 29. Теперь умножаем первую строку матрицы A со вторым столбцом матрицы B. Получаем (2 x -4) + (9 x 7) = -8 + 63 = 55.
Шаг 2: Повторим шаг 1, но изменим строку матрица A. Первый и второй столбцы матрицы B будут умножены на строку 2 матрицы A. Результатом будет
(3 x 1) + (-7 x 3) = 3 – 21 = -18, и (3 x -4) + (-7 х 7) = -12 – 49= -61
Шаг 3: Разместите результаты правильно
.
Следовательно, результирующая матрица C =
Точно так же вы можете решать квадратные матрицы, такие как 3 x 3, 4 x 4 и так далее.
Часто задаваемые вопросы
Q1.
Что такое умножение матриц?Ответ: Процесс умножения двух матриц для получения результата в виде одной матрицы известен как умножение матриц. Используется такой вид бинарной операции.
Q2. Как умножить две заданные матрицы?
Ответ: Чтобы перемножить две матрицы, мы должны сначала определить, совпадают ли количество строк в первой матрице и количество столбцов во второй матрице. Элементы столбца и строк первой матрицы теперь должны быть умножены друг на друга и сложены. Здесь мы должны сделать скалярное произведение столбцов и строк.
Q3. Что получится в результате умножения матрицы (2×3) на матрицу (3×3)?
Ответ: Единственная матрица, полученная путем перемножения матриц (2×3) и (33), — это матрица (2×3).
Q4. Как умножить матрицу 3×3?
Ответ: Первый элемент получается сложением всех строк и столбцов первой и второй матриц. Аналогичным образом умножьте и сложите компоненты двух матриц по столбцам и по строкам, чтобы получить элементы произведения двух матриц 3 × 3.