Решить неравенство 2 x 1 x 4: Решите неравенство 2^x>=4 (2 в степени х больше или равно 4)

02.03.23 Простейшие показательные неравенства — презентация онлайн

Похожие презентации:

Показательные неравенства

Показательные неравенства

Показательные неравенства

Показательные неравенства, их типы и методы решения

Функции и последовательности

Показательные неравенства, их типы и методы решения

Основные функции и их графики

Мультимедийное пособие «Функция»

Свойства последовательности. Функция

Функции. Различные способы задания функции

02.03.23
Простейшие
показательные
неравенства
Показательные
неравенства
Определение
Простейшие
неравенства
Решение неравенств
Определение
Показательные неравенства –
это неравенства, в которых
неизвестное содержится в
показателе степени.
Примеры:
х
3 ≤ 9;
х
х+1
2 +5⋅ 2 >11
Виды неравенств
Линейное нер-во
2х+7>0
-8х+4<0
Квадратное нер-
во
х^2-4х+3>0
Простейшие
показательные
неравенства – это
неравенства вида:
x
b
x
b
a >a
x
b
a <a
a ≥a
x
b
a ≤a
где a > 0, a 1, b – любое число.
При решении простейших
неравенств используют свойства
возрастания или убывания
показательной функции.
a > a |} ⇔x > b a > a | } ⇔ x < b
x
b
x
b
a >1
a
x2
a
x1
0<
a<
1
a
x2
a
x1
x1
a <a
x 1< x 2
x2
x2
x2
x1
x1
x1
y=a
x
a <a
x 1> x 2
x2
Какие из перечисленных функций являются
возрастающими, а какие убывающими?
1¿ y=5
x
возрастающая , т. к .5>1
x убывающая ,т.к .0<0,5<1
2¿ y=0,5
x
возрастающая , т.к .10>1
3¿ y=10
x возрастающая , т. к . π >1
4¿ y=π
Какие из функций являются
возрастающими, а какие убывающими?

()
2
5¿ y=
3
x
6¿ y=49
2
убывающая , т. к . 0< <1
3
−x
1
1
убывающая , т. к . 49 = и 0< <1
49
49
−1
При а>1 функция возрастает
a
x
a
x
x0
a a a
x
x0
x a x0
x
x0
При 0<а<1 функция убывает
x
x
x
x
a
a x0 a
a
0
x
a a
x0
x0
0
x a
x0
x0
Решения показательных
неравенств:
1. 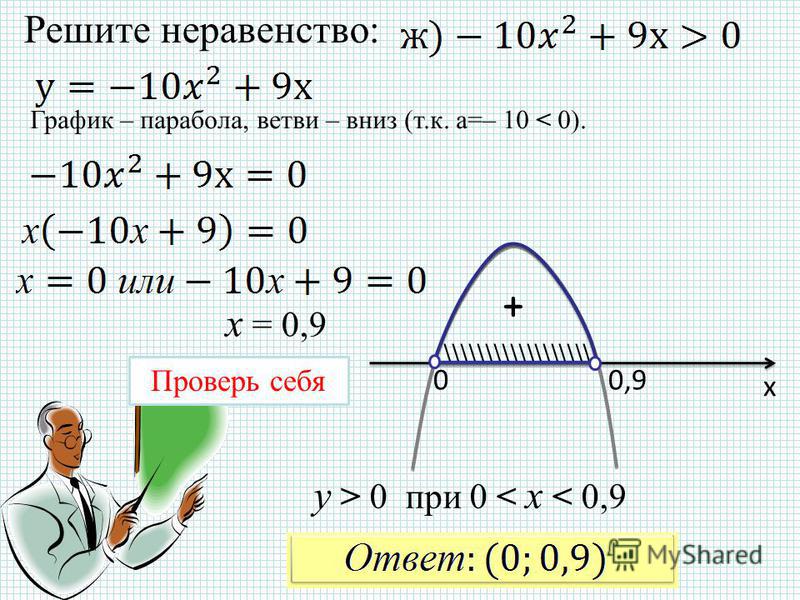Способ Уравнивание оснований правой
и левой части
Решите неравенство:
x
3 >81
x
4
3 >3
x
т . к. 3>1 , то функция y=3 возрастающая
x >4
x0
Решите неравенство:
()()
x
1x
1
0 ≥
2
2
3
2
()
x
1
1
т .к.0< <1 ,то функция y=
убывающая
2
2
3
x≤
2
x∈¿
Решите неравенство:
3x 1
2 ≥ ;
2
3x
−1
2 ≥2 ;
т . к. основание 2 >1 , тофункция возрастающая
3 x≥ −1;
1
x ≥− ;
3
x∈¿
Показательные неравенства
Простейшие показательные неравенства
Неравенства, решаемые вынесением за
скобки степени с меньшим показателем
Неравенства, решаемые введение новой
переменной
Простейшие
показательные неравенства
х
1¿. 3 >9 ⇔ 3 x > 32 ⇔ x >2
Ответ: х >2 .
2¿.
()
х
1 1
> ⇔
2 4
Ответ: х < 2 .
() ()
x
1
1
>
2
2
2
⇔ x <2
Решение показательных неравенств
Способ 2: Вынесение за скобки степени с
меньшим показателем
х− 3 1
х
3 + ⋅ 3 >10
3
3
х− 3
3
3
1 3
(1+ ⋅ 3 )>10
3
х− 3
х− 3
(1+9)>10
⋅ 10>10 : 10
х− 3
>1
х− 3
0
3
3
3 > 1, то
>3
х − 3>0
х >3 .
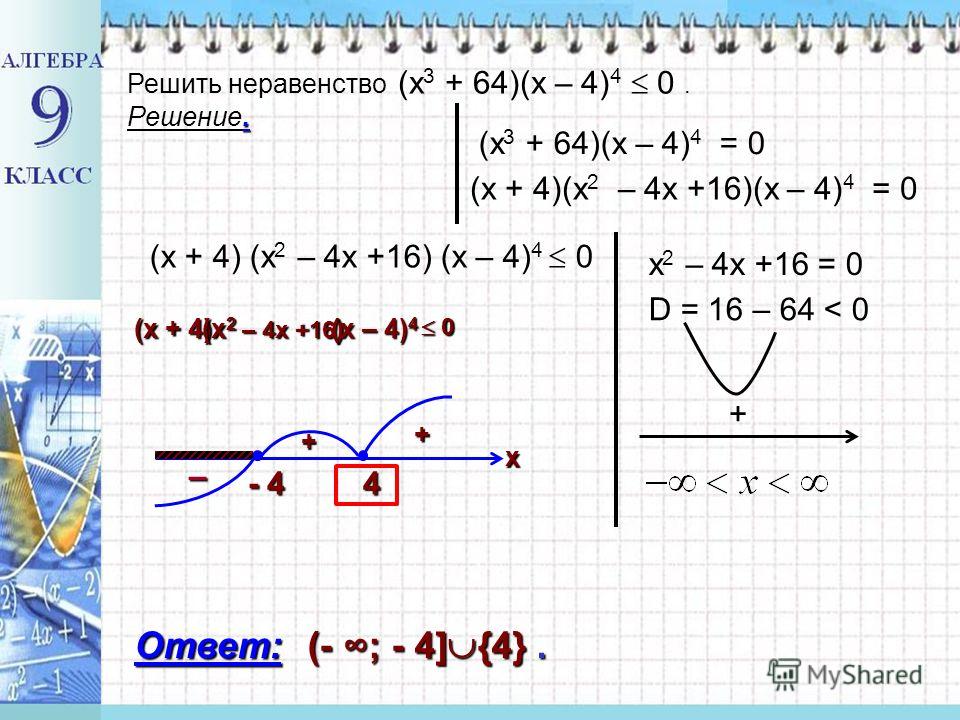
Ответ: х >3
Решение показательных неравенств
Способ 3: введение новой переменной
х
х
9 −10 ⋅ 3 <−9
2х
х
3 −10 ⋅ 3 +9 <0
х
3 =t (t>0)
(t − 9) ( t − 1) <0
1<t <9
2
t − 10 t+9< 0
D=102 − 4 ⋅ 9=100 −36=64=82
10+8 18
t 1=
= =9
2
2
10 −8 2
t 2=
= =1
2
2
x
1<3 < 9
х
0
3 <3 ; 3 >3 ;
х
2
х <2
3>1, то
х >0 .
Ответ: х < 2. х>0
Показательные неравенства в ЕГЭ(профиль)
ТИП 14 Решите неравенство:
1)
11)
21)
31)
2)
12)
22)
32)
3)
13)
23)
33)
4)
14)
24)
34)
5)
15)
25)
35)
6)
16)
26)
36)
7)
17)
27)
37)
8)
18)
28)
38)
9)
19)
29)
39)
10)
20)
30)
40)
Показательные неравенства в ЕГЭ(база)
ТИП 17 Найдите корень уравнения
1)
8)
2)
9)
3)
4)
5)
6)
7)
Домашняя работа
п. 6.4 изучить стр.173 (учебник 10 класс)
Выполнить задания ЕГЭ на решение
простейших логарифмических уравнений
тип 5 (профиль (13 прототипов)) или тип
17(база (9 прототипов))

English     Русский Правила

3-8 9 Оценить квадратный корень из 12 10 Оценить квадратный корень из 20 11 Оценить квадратный корень из 50 94 18 Оценить квадратный корень из 45 19 Оценить квадратный корень из 32 20 Оценить квадратный корень из 18 92

4.

7 Решение линейных неравенств | Уравнения и неравенства

Предыдущий 4.6 Буквенные уравнения

Следующий 4.8 Краткое содержание главы

4.7 Решение линейных неравенств (EMA3H)

Линейное неравенство похоже на линейное уравнение в том, что наибольший показатель степени переменной равен \(\текст 1}\). Ниже приведены примеры линейных неравенств.

\начать{выравнивать*} 2х+2&\ле 1\ \frac{2 — x}{3x + 1} & \ge 2 \\ \frac{4}{3}x — 6 & < 7x + 2 \конец{выравнивание*}

Методы, используемые для решения линейных неравенств, аналогичны тем, которые используются для решения линейных уравнений. Единственный разница возникает, когда есть умножение или деление, которое включает знак минус. Например, мы знайте, что \(8>6\). Если обе части неравенства разделить на \(-\text{2}\), то получим \(-4>-3\), что неверно. Следовательно, знак неравенства необходимо поменять местами, что дает \(-4<-3\).

Чтобы сравнить неравенство с нормальным уравнением, мы сначала решим уравнение.

Решите \(2x + 2 = 1\):

\начать{выравнивать*} 2х+2&=1\ 2х & = 1 — 2 \ 2х&=-1\ х & = -\фракция{1}{2} \конец{выравнивание*}

Если мы представим этот ответ на числовой прямой, мы получим:

Теперь найдем \(x\) в неравенстве \(2x + 2 \le 1\):

\начать{выравнивать*} 2х+2&\ле 1\ 2x&\le 1 — 2\ 2х&\ле-1\ х & \ le — \ гидроразрыва {1} {2} \конец{выравнивание*}

Если мы представим этот ответ на числовой прямой, мы получим:

Мы видим, что для уравнения существует только одно значение \(х\), при котором уравнение верно. Однако, для неравенства существует диапазон значений, для которых неравенство верно. Это главное отличие между уравнением и неравенством.

Помните: когда мы делим или умножаем обе части неравенства на отрицательное число, направление изменения неравенства. Например, если \(x<1\), то \(-x>

-1\). Также обратите внимание, что мы не можем разделить или умножить на переменную.

Следующее видео знакомит с линейными неравенствами.

Видео: 2FGH

Интервальное обозначение (EMA3J)

Примеры:

\(\влево(4;12\вправо)\)	Круглые скобки означают, что номер не включен. В этот интервал входят все действительные числа больше, но не равны \(\text{4}\) и меньше, но не равны \(\текст{12}\).
\(\влево(-\infty ;-1\вправо)\)	Круглые скобки всегда используются для положительной и отрицательной бесконечности. Этот интервал включает все действительные числа меньше, но не равны \(-\text{1}\).
\(\влево[1;13\вправо)\)	Квадратная скобка означает, что число включено. В этот интервал входят все действительные числа больше или равные \(\text{1}\) и меньше, но не равные \(\текст{13}\).

Важно отметить, что это обозначение может использоваться только для представления интервала действительных чисел.

Мы представим приведенный выше ответ в интервальной записи как \(\left(-\infty ; -\frac{1}{2}\right]\)

Рабочий пример 17: Решение линейных неравенств

Найдите \(r\):

\[6 — г > 2\]

Представьте ответ на числовой прямой и в интервальной записи.

Переставить и решить для \(r\)

\начать{выравнивать*} -r & > 2 — 6 \\ -r & > -4 \end{выравнивание*}

Умножить на \(-\text{1}\) и поменять знак неравенства

\[г < 4\]

Представьте ответ в числовой строке

Представить ответ в интервальной нотации

\[\влево(-\infty ; 4\вправо)\]

Рабочий пример 18: Решение линейных неравенств

Найдите \(q\):

\[4q + 3 < 2(q + 3)\]

Представьте ответ на числовой прямой и в интервальной записи.

Развернуть скобу

\начать{выравнивать*} 4q + 3 & < 2(q + 3) \\ 4q + 3 & < 2q + 6 \end{выравнивание*}

Переставить и решить для \(q\)

\начать{выравнивать*} 4q + 3 & < 2q + 6 \\ 4q - 2q & < 6 - 3 \\ 2q & < 3 \end{выравнивание*}

Разделить обе стороны на \(\text{2}\)

\начать{выравнивать*} 2q & < 3 \\ д & < \ гидроразрыва {3} {2} \end{выравнивание*}

Представьте ответ в числовой строке

Представить ответ в интервальной нотации

\(\left(-\infty ; \frac{3}{2}\right)\)

температура текст

Рабочий пример 19: Решение сложных линейных неравенств

Найдите \(x\):

\[5 \le x + 3 < 8\]

Представьте ответ на числовой прямой и в интервальной записи.

Вычесть \(\text{3}\) из всех частей неравенства

\[\begin{массив}{ccccc} 5 — 3 &\le&x + 3 — 3 &< & 8 - 3 \\ 2 & \le & x & < & 5 \конец{массив}\]

Представьте ответ в числовой строке

Представить ответ в интервальной нотации

\(\влево[2 ; 5\вправо)\)

температура текст

Учебник Упражнение 4.6

\(x < -1 \text{ и } x \ge 6 ; x \in \mathbb{R}\)

\(3 < x < 6 ; x \in \mathbb{R}\)

\(x \neq 3 ; x \neq 6 ; x \in \mathbb{R}\)

\(x > -10 ; x \in \mathbb{R}\)

\(3x + 4 > 5x + 8\)

\начать{выравнивать*} 3х+4&>5х+8\ 3х — 5х & > 8 — 4\ -2х > 4\ 2х<-4\ х < -2 \конец{выравнивание*}

Представлено на числовой прямой:

В интервальной записи: \((-\infty; -2)\)

\(3(x — 1) — 2 \le 6x + 4\)

\начать{выравнивать*} 3(х — 1) — 2 & \le 6x + 4 \\ 3х — 5 и \ле 6х + 4\ 3х — 6х &\ле 4+5\ -3х\ле 9\ х \ge -\frac{9}{3} \\ х \ гэ -3 \конец{выравнивание*}

Представлено на числовой прямой:

В интервальной записи: \([-3; \infty)\)

\(\dfrac{x — 7}{3} > \dfrac{2x — 3}{2} \)

\начать{выравнивать*} \frac{x — 7}{3} & > \frac{2x — 3}{2} \\ 2(х — 7) & > 3(2х — 3) \\ 2х — 14 > 6х — 9\ -4х > 5\ х < -\фракция{5}{4} \конец{выравнивание*}

Представлено на числовой прямой:

В интервальной записи: \((-\infty; -\frac{5}{4})\)

\(-4(x — 1) < x + 2\)

\начать{выравнивать*} -4 (х — 1) & < х + 2 \\ -4x + 4 & < х + 2 \\ -5х < -2\ х > \ гидроразрыва {2} {5} \конец{выравнивание*}

Представлено на числовой прямой:

В интервальной записи: \((\frac{2}{5}; \infty)\)

\(\dfrac{1}{2}x + \dfrac{1} {3}(x — 1) \ge \dfrac{5}{6}x — \dfrac{1}{3}\)

\начать{выравнивать*} \frac{1}{2}x + \frac{1}{3}(x — 1) & \ge \frac{5}{6}x — \frac{1}{3} \\ \frac{1}{2}x + \frac{1}{3}x — \frac{1}{3} & \ge \frac{5}{6}x — \frac{1}{3} \ \ \frac{1}{2}x + \frac{1}{3}x — \frac{5}{6}x & \ge \frac{1}{3} — \frac{1}{3} \ \ \frac{3}{6}x + \frac{2}{6}x — \frac{5}{6}x & \ge 0 \\ 0x\ge 0 \конец{выравнивание*}

Неравенство верно для всех действительных значений \(x\).

\(-2 \le x — 1 < 3\)

\[\begin{массив}{ccccc} -2 & \le & x — 1 & < & 3 \\ -1 & \le & x & < & 4 \конец{массив}\]

Представлено на числовой прямой:

В интервальной записи: \([-1; 4)\)

\(-5 < 2x - 3 \le 7\)

\[\begin{массив}{ccccc} -5&<&2x - 3&\le&7\ -2 & < & 2x & \le & 10 \\ -1 & < & х & \ле & 5 \конец{массив}\]

Представлено на числовой прямой:

В интервальной записи: \((-1; 5]\)

\(7(3x + 2) — 5(2x — 3) > 7\)

\начать{выравнивать*} 7 (3x + 2) — 5 (2x — 3) & > 7 \\ 21х + 14 — 10х + 15 и > 7\ 11х&>-22\ х & > -2 \конец{выравнивание*}

Представлено на числовой прямой:

В интервальной записи: \((-2; \infty)\)

\(\dfrac{5x — 1}{-6} \ge \dfrac{1 — 2x}{3}\)

\начать{выравнивать*} \frac{5x — 1}{-6} & \ge \frac{1 — 2x}{3} \\ 5x — 1 & \ge -2(1 — 2x) \\ 5x — 1 & \ge -2 + 4x \ 5x — 4x & \ge -1\ х & \ ge -1 \конец{выравнивание*}

Представлено на числовой прямой:

В интервальной записи: \([-1; \infty)\)

\(3 \le 4 — x \le 16\)

\[\begin{массив}{ccccc} 3&\ле&4 — х&\ле&16\ -1&\le&-x&\le&12\ 1 & \ge & x & \ge & -12 \конец{массив}\]

Представлено на числовой прямой:

В интервальной записи: \([1; 12]\)

\(\dfrac{-7y}{3} — 5 > -7\)

\начать{выравнивать*} \frac{-7y}{3} — 5 & > -7 \\ -7у — 15 и > -21\ -7у&>-6\ у & < \ гидроразрыва {6} {7} \конец{выравнивание*}

Представлено на числовой прямой:

В интервальной записи: \((-\infty;\frac{6}{7})\)

\(1 \le 1 — 2y < 9\)

\[\begin{массив}{ccccc} 1&\le&1 — 2у&<&9\ 0&\le&-2y&<&8\ 0 & \ge & y & > & -4 \\ -4 & < & у & \ле & 0 \конец{массив}\]

Представлено на числовой прямой:

В интервальной записи: \((-4;0]\)

\(-2 < \dfrac{x - 1}{-3} < 7\)

\[\begin{массив}{ccccc} -2 & < & \dfrac{x - 1}{-3} & < & 7 \\ 6&>&х-1&>&-21\ 7&>&х&>&-20\ -20 & < & х & < & 7 \конец{массив}\]

Представлено на числовой прямой:

В интервальной записи: \((-20;7)\)

\(2x -1 < 3(x+11)\)

\begin{align*} 2 х -1 &< 3(х +11) \\ 2 х -1 &< 3 х +33 \\ 2 х -3 х &< 33 +1 \ -1 х &< 34\ \поэтому х &> -34 \end{выравнивание*}

\[\left(-34;\infty\right)\]

\(x -1 < -4(x-6)\)

\begin{align*} х-1 &<-4(х-6) \\ х -1 &< -4 х +24 \\ х +4 х &< 24 +1 \\ 5 х &< 25\ \поэтому х &< 5 \end{align*}

\[\left(-\infty;5\right)\]

\(\dfrac{x-1}{8} \leq \dfrac{2(x-2)}{3}\)

\начать{выравнивать*} \frac{x-1}{8} &\leq \frac{2(x-2)}{3} \\ 3(х-1) &\leq 16(х-2) \\ 3x-3 &\leq 16x-32\ 3x -16x &\leq -32 +3\ -13x &\leq -29\ \поэтому х &\geq\frac{29}{13} \конец{выравнивание*}

\(\; x \in \left[ \frac{29}{13} ;\infty\right)\).

\(\dfrac{x+2}{4} \leq \dfrac{-2(x-4)}{7}\)

\начать{выравнивать*} \frac{x+2}{4} &\leq \frac{-2(x-4)}{7} \\ 7(х+2) &\leq -8(х-4) \\ 7x+14 &\leq -8x+32 \\ 7x +8x &\leq 32 -14\ 15x &\leq 18\\ \поэтому х &\leq\frac{6}{5} \конец{выравнивание*}

\(\; x \in \left(-\infty; \frac{6}{5} \right]\).

\(\dfrac{1}{5}x — \dfrac{5}{ 4}(x+2) > \dfrac{1}{4}x + 3\)

\begin{align*} \frac{1}{5}x — \frac{5}{4}(x+2) &> \frac{1}{4}x +3 \\ 4x — 25(x+2) &> 5x +60 \\ 4х — 25х-50 &> 5х +60\ 4х — 25 х -5х &> 60 + 50\\ -26x &> 110\\ \следовательно, x &< -\frac{55}{13} \end{выравнивание*}

Интервал: \[\left(-\infty;-\frac{55}{13}\right)\]

\(\dfrac{1}{5}x — \dfrac{2}{5}(x+3) \geq \dfrac{4}{2}x +3\)

\begin{align*} \frac{1}{5}x — \frac{2}{5}(x+3) &\geq \frac{4}{2}x +3 \\ 2x — 4(x+3) &\geq 20x +30 \\ 2x — 4x-12 &\geq 20x+30\ 2x — 4 x -20x &\geq 30 + 12\\ -22x &\geq 42\\ \поэтому x &\leq -\frac{21}{11} \end{выравнивание*}

Интервал: \[\left(-\infty;-\frac{21}{11}\right]\]

\(4x +3 < -3 \quad\text{or}\quad 4x +3 > 5\)

Решите неравенство: \[\begin{массив}{rclcrcl} 4x +3 &<& -3 &\text{or}& 4x +3 &>& 5 \\ 4x &<& -3-3 &\text{or}& 4x &>& 5-3 \\ х &<& \frac{-3-3}{4} &\text{or}& x &>& \frac{5-3}{4} \\ x &<& - \frac{3}{2} &\text{or}& x &>& \frac{1}{2} \\ \конец{массив}\]

\[\left(-\infty; — \frac{3}{2}\right) \cup \left(\frac{1}{2}; \infty\right)\]

\(4 \ ge -6x -6 \ge -3\)

Решите неравенство: \[\begin{массив}{rcccl} 4 &\ge&-6x -6 &\ge&-3 \\ 4+6 &\ge& -6x &\ge& -3+6 \\ \frac{4+6}{-6} &\le& x &\le& \frac{-3+6}{-6} \\ — \frac{5}{3} &\le& x &\le& — \frac{1}{2} \\ \конец{массив}\]

\[\left[- \frac{5}{3}; — \frac{1}{2}\right]\]

\(6b — 3 > b + 2 , ~b \in \mathbb{Z}\)

\начать{выравнивать*} 6b — 3 > b + 2 , ~b \in \mathbb{Z}\\ 5б > 5\ б > 1 \конец{выравнивание*}

\(3a — 1 < 4a + 6 , ~a \in \mathbb{N}\)

\начать{выравнивать*} 3а — 1 < 4а + 6\ -а < 7\ а > -7 \конец{выравнивание*}

Однако нам говорят, что \(a \in \mathbb{N}\) и, следовательно, \(a > 0\).