Матрица правило треугольников: Правило треугольников онлайн

Правило треугольника

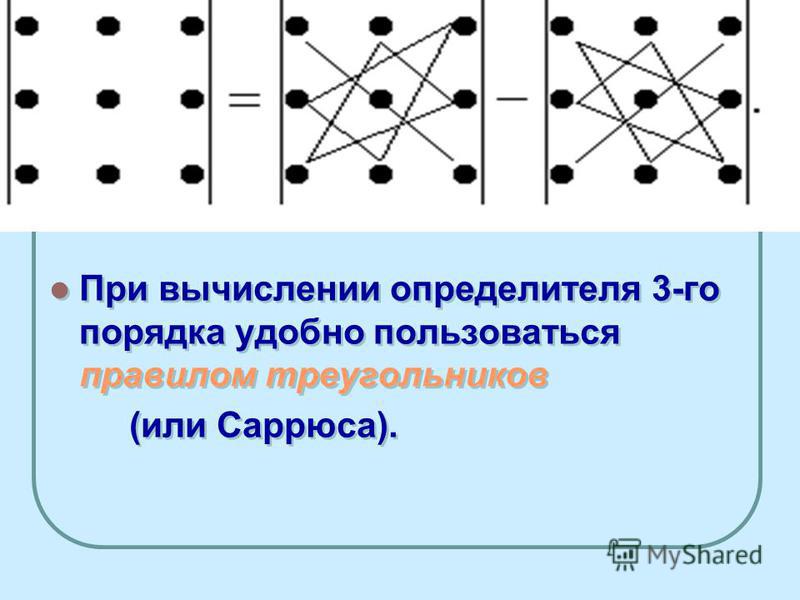
Правило Саррюса

Справа от определителя дописывают первых два столбца и произведения элементов на главной диагонали и на диагоналях, ей параллельных, берут со знаком «плюс»; а произведения элементов побочной диагонали и диагоналей, ей параллельных, со знаком «минус»:

Разложение определителя по строке или столбцу

Определитель равен сумме произведений элементов строки определителя на их алгебраические дополнения. Обычно выбирают ту строку/столбец, в которой/ом есть нули. Строку или столбец, по которой/ому ведется разложение, будет обозначать стрелкой.

16) Свойства определителей

1.   (определитель не меняется при транспонировании вокруг главной диагонали).

2. Если одна из строк определителя состоит из нулей, определитель равен нулю.

3. От перестановки двух строк определитель меняет лишь знак.

4. Определитель, содержащий две одинаковые строки, равен нулю.

5. Если все элементы некоторой строки определителя умножить на число  , определитель умножится на  .

6. Определитель, содержащий две пропорциональные строки, равен нулю.

7. Если все элементы  -й строки определителя представлены в виде суммы  , то определитель равен сумме двух определителей, у которых все строки, кроме  -й, такие же, как в исходном определителе, а  -я строка в одном определителе состоит из  , а в другом — из  .

Определение 3.  -я строка определителя называется линейной комбинацией остальных его строк, если  такие, что, умножая -ю строку на  , а затем складывая все строки, кроме  -й, получаем  -ю строку.

8. Если одна из строк определителя является линейной комбинацией остальных его строк, определитель равен нулю.

9. Определитель не изменится, если к элементам одной его строки прибавить соответствующие элементы другой, умноженные на одно и то же число.

17) Минором некоторого элемента a

ijназывается определитель , полученный из данного, путем вычеркивания i строки и j столбца, на пересечении которых находится выбранный элемент.

; ; и т.д.

Алгебраическим дополнением элемента a_ij называется его минор, взятый со знаком +, если сумма i+j — число четное; и со знаком – если сумма нечетная.

1 8) Определителем n-го порядка называют выражение вида

n-строк

m-столбцов

Разложение определителя по строке или столбцу

Определитель равен сумме произведений элементов строки определителя на их алгебраические дополнения. Обычно выбирают ту строку/столбец, в которой/ом есть нули. Строку или столбец, по которой/ому ведется разложение, будет обозначать стрелкой.

Пример:

Для разложения выгоднее всего выбирать ту строку или столбец, которые содержат более всего нулей. Естественно, что в данном случае имеет смысл раскладывать по третьей строке.

19) Матрицей называется таблица чисел, состоящая из m строк и n столбцов.

Элементом матрицы называется содержимое ее клетки.

Элементы матрицы обычно обозначают малыми буквами латинского алфавита с двумя индексами, где первый индекс – номер строки, а второй – номер столбца, где элемент расположен, например  – элемент, расположенный на пересечении i-й строки и j-го столбца.

Матрицы называются равными, если они имеют одинаковую размерность и их элементы, стоящие на одинаковых местах, равны.

20) Виды матриц

1. Если число строк матрицы совпадает с числом ее столбцов, т.е. m = n, то матрица

   называется квадратной порядка n, а в противном случае прямоугольной.

2.  Квадратная матрица называется диагональной, если все ее элементы, стоящие вне главной диагонали, равны нулю.

3. Диагональная матрица, у которой все элементы равны единице, называется единичной

4. Матрица, все элементы которой равны нулю, называется нулевой.

5. Матрица, содержащая в себе лишь один столбец (строку) называется вектор столбцом (вектор строкой)

6. Квадратная матрица называется треугольной, если все её элементы, расположенные по одну сторону диагонали, равны нулю.

21) Основные операции над матрицами и их свойства. (сумма, разность, произведение матрицы на число).

1. Суммой двух матриц A и B одинаковой размерности mxn называется матрица C=A+B т ой же размерности m_xn, элементы которой сij = aij + bij, для i=1,2,…,m; j=1,2,…,n (т.е. матрицы складываются поэлементно)

Свойства операции сложения матриц.

Для любых матриц А,В,С одного размера выполняются равенства:

1) А + В = В + А (коммутативность),

2) (А + В) + С = А + (В + С) = А + В + С ( ассоциативность)

3) Для матриц данного порядка существует нейтральный элемент по сложению, которым является нулевая матрица.

То есть, справедливо свойство А+О=А.

4)Для ненулевой матрицы А данного порядка существует матрица (–А), их суммой является нулевая матрица: А+(-А)=О.

2. Разность двух матриц одинаковой размерности определяется через следующие операции: A – B = A + (1)*B

3. Умножение матрицы на число. Произведением матрицы A на число , называется матрица B A , элементы которой bij aij для i=1, 2, …, m; j= 1,2,…, n.

Следствие: общий множитель всех элементов матрицы можно выносить за знак матрицы.

Свойства операции произведение матрицы на число

1) (Дистрибутивность умножения относительно сложения)

2) (дистрибутивность)

3) (ассоциативность)

4) Нейтральным числом по умножению на произвольную матрицу А является единица, то есть,  .

22) Произведением двух матриц А и В называется матрица С, элемент которой, находящийся на пересечении i-й строки и j-го столбца, равен сумме произведений элементов i-й строки матрицы А на соответствующие (по порядку) элементы j-го столбца матрицы В.

Произведение двух матриц АВ имеет смысл только в том случае, когда число столбцов матрицы А совпадает с числом строк матрицы В 

Пример:

.

Вычисляем элементы матрицы C = AB.

Найденное произведение матриц: 

Определители. Линейная алгебра 2 — презентация онлайн

Похожие презентации:

Определители. Свойства определителей и методы их вычисления

Линейная алгебра. Определители. (Лекция 2)

Определители. Свойства определителей

Определители. Свойства определителей

Матрицы и определители

Матрицы, определители. Обратная матрица. Ранг матрицы. Системы линейных уравнений элементы векторной алгебры

Матрицы и определители

Матрицы и определители

Линейная алгебра. Матрицы

Матрицы и определители

1. § 2. Определители

Каждой квадратной м. А можно поставить в
соответствие число, которое называется
ее определителем и обозначается det A, A
или символом Δ.
Определитель матрицы второго порядка
a11 a12 вычисляется по правилу:
A
a21 a22
A
a11 a12
a21 a22
a11a22 a12a21

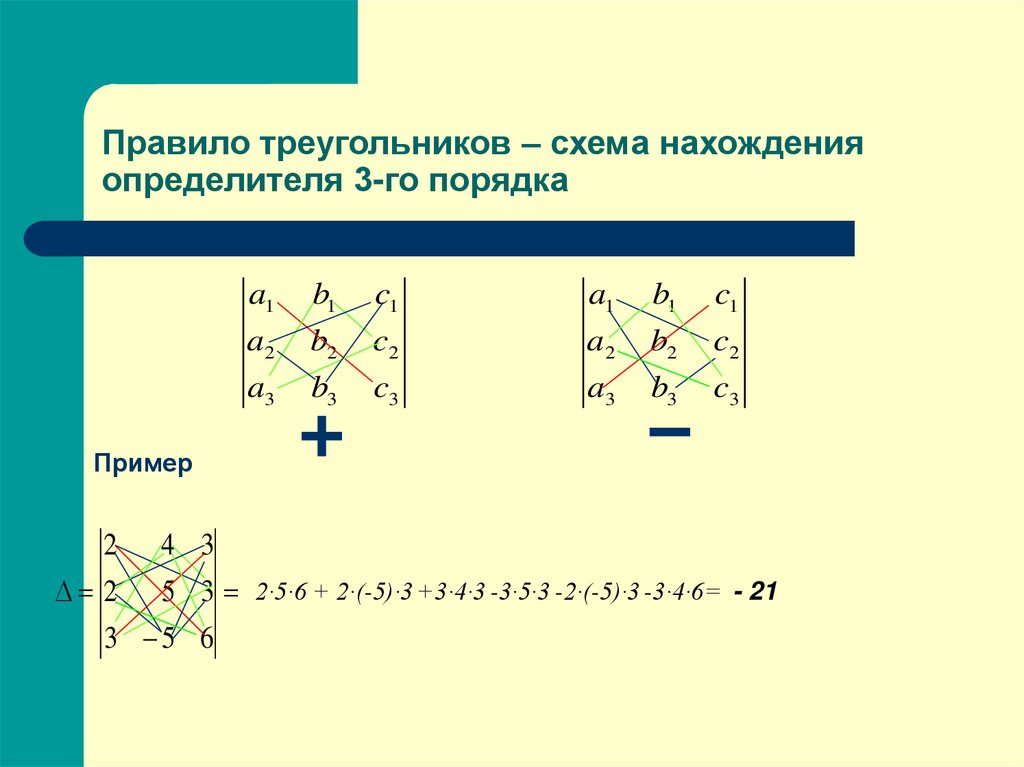
2. Вычисление определителей третьего порядка (правило треугольников и правило Саррюса)

Определитель квадратной матрицы 3-го порядка
a11
A a21
a
31
a12
a22
a32
a13
a23
a33
вычисляется по правилу треугольников:
a11 a12
a13
A a21 a22 a23 a11a22a33 a12a23a31 a13a21a32
a31 a32 a33
a31a22a13 a32a11a23 a 33a21a12 .

3. Правило Саррюса (модифицированное правило треугольников)

+
a11
a 21
a 31
—
+
+
a 12 a 13 a11 a 12
a 22 a 23 a 21 a 22 =
a 32 a 33 a 31 a 32
—
a11a22a33 a12a23a31 a13a21a32
a13a22a31 a11a23a32 a12a21a33

4. Свойства определителей матриц

1. Определитель не меняется при
транспонировании матрицы.
2. Если в определителе поменять местами
две строки (два столбца), то
определитель меняет знак.
3. Если все элементы одной строки
(столбца) определителя
пропорциональны (в частности, равны)
соответствующим элементам другой
строки (столбца), то он равен нулю.
4. Если в определителе строка (столбец)
состоит из нулей, то определитель равен
нулю.
5. Общий множитель у элементов какой-либо
строки (столбца) можно вынести за знак
определителя.
6. Определитель не изменится, если ко всем
элементам одной строки (столбца)
прибавить соответствующие элементы
другой строки (столбца), умноженные на
одно и то же число.
7. Определитель диагональной и треугольной
(верхней или нижней) матриц равен
произведению диагональных элементов.
8. Определитель произведения квадратных матриц
равен произведению их определителей: A B A B
9. Если всякий элемент любой строки (столбца)
представляет собой сумму двух слагаемых, то
определитель равен сумме двух определителей,
в первом из которых в соответствующей строке
(столбце) оставлены первые слагаемые, а во
втором – вторые.

7. Минор и алгебраическое дополнение

Опр 1. Минором
M ij элемента
aij
определителя n-порядка называется
определитель (n-1) порядка, полученный
вычеркиванием i- строки и j – столбца из
исходного определителя.
Опр. 2. Алгебраическим дополнением Ai j
элемента a i j определителя n – порядка наз.
число, вычисляемое по правилу:
Aij 1
i j
M ij

8. Теорема разложения

Определитель n-го порядка равен сумме
произведений элементов любой его
строки (или столбца) и
соответствующих им алгебраических
дополнений
n
A aij Aij ai1 Ai1 ai 2 Ai 2 … ain Ain
j 1
(разложение по i-строке)
i 1, n
n
A aij Aij a1 j A1 j a2 j A2 j … anj Anj
i 1
(разложение по j-столбцу)
j 1, n

English     Русский Правила

Треугольная матрица

Марко Табога, доктор философии

Говорят, что квадратная матрица быть:

Треугольные матрицы часто появляются в линейной алгебре и в теории линейный системы.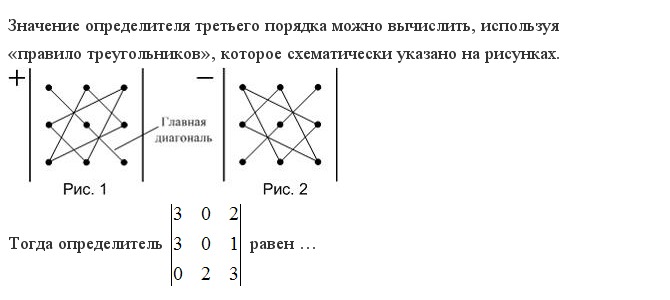

Поэтому стоит подробно изучить их свойства, что мы делаем ниже.

Содержание

1. Определение

2. Примеры

3. Транспонирование треугольной матрицы треугольной

4. Продуктом двух треугольных матриц является треугольная

5. Треугольная матрица подводима, если его диагональные входные записи являются Nearlo

6. .

Определение

Далее следуют формальные определения.

Определение А матрица является нижнетреугольным тогда и только тогда, когда когда бы ни .

Помните, что главная диагональ квадратная матрица это множество всех записей, индексы строк и столбцов которых совпадают, это набор

Следовательно, в нижней треугольной матрице все элементы выше основного диагональные (т. е. те, у которых индекс столбца больше, чем индекс строки ) равны нулю.

Определение А матрица является верхнетреугольным тогда и только тогда, когда когда бы ни .

Таким образом, в верхнетреугольной матрице все элементы ниже главной диагонали (т. е. те, чей индекс столбца меньше, чем индекс строки ) равны нулю.

Примеры

Ниже приведены некоторые примеры треугольных матриц.

Пример Рассмотрим матрица элементы на главной диагонали все записи выше главной диагонали ноль: Следовательно, матрица нижняя треугольная.

Пример Определите матрица элементы на главной диагонали все записи ниже главной диагонали ноль: Следовательно, матрица верхнетреугольная.

В следующих разделах сообщается о ряде свойств, которым удовлетворяют треугольные матрицы.

Транспонирование треугольной матрицы является треугольным

Предложение Транспонирование нижней треугольной матрицы является верхней треугольной.

Доказательство

Предположим, что является нижним треугольным, так что когда бы ни . По определению, элементы транспонирования удовлетворятьПоэтому, когда бы ни . Следовательно, имеет верхнюю треугольную форму.

Предложение Транспонирование верхней треугольной матрицы является нижней треугольной.

Пруф

Аналогично предыдущему.

Произведение двух треугольных матриц треугольное

Предложение Произведение двух нижних треугольных матриц является нижним треугольным.

Доказательство

Предположим, что а также два нижние треугольные матрицы. Нам нужно доказать что всякий раз . Но когда , у нас есть это где: в ногу мы использовали тот факт, что потому что ; в ногу мы использовали тот факт, что потому что .

Предложение Произведение двух верхнетреугольных матриц верхнетреугольно.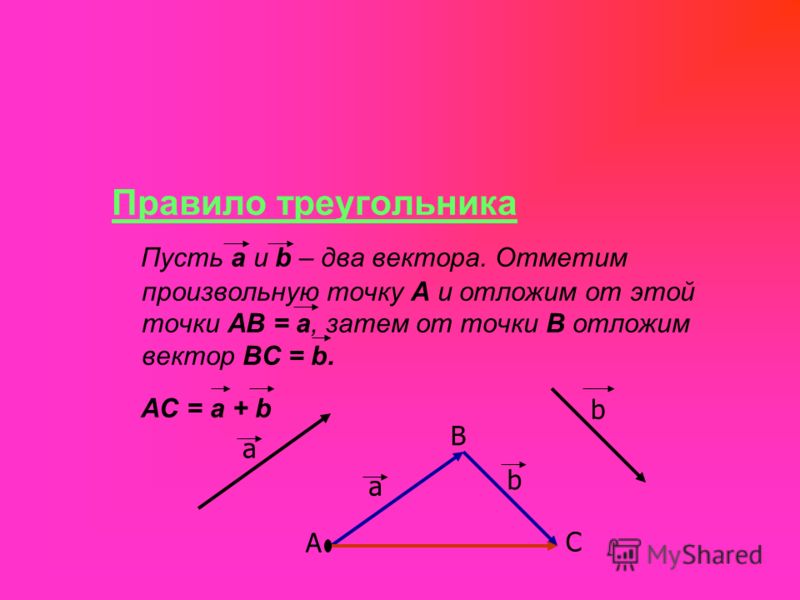

Доказательство

Доказательство аналогично предыдущему.

Треугольная матрица обратима, если ее диагональ записи не равны нулю

Предложение Треугольная матрица (верхняя или нижняя) обратимы тогда и только тогда, когда все элементы на его главной диагонали отличны от нуля.

Доказательство

Сначала докажем часть «только если». Предположим, нижняя треугольная матрица имеет нулевую запись на главной диагонали в строке , что есть, учтите в подматрица образован первым ряды . -й столбец равен нулю, потому что , и все столбцы справа от него равны нулю, потому что нижний треугольный. Затем, имеет не более ненулевые столбцы. Как следствие, он имеет не более линейно независимый столбцы. Таким образом, его столбец ранга самое большее . Поскольку ранг строки и ранг столбца совпадают, это означает, что имеет не более линейно независимые строки. Как следствие, ряды не являются линейно независимыми. Но ряды также ряды . Поэтому ряды не являются линейно независимыми, не является полноранговым и необратимым. Подводя итог, мы доказали, что если на главной диагонали есть нулевая запись , тогда не является обратимым. Как следствие, обратим, только если на главной диагонали нет нулевых элементов. Мы сейчас необходимо доказать «если часть» (если нет нулевых записей на основной диагонали, то обратим). Будем доказывать от противного. Если необратима, то его строки не являются линейно независимыми и одна из них (допустим, это -й строка) может быть записана как линейная сочетание другого строки: если есть другие строки ниже , с индексами , то их коэффициенты в линейной комбинации должны быть равны нулю. Особенно, должен быть равен нулю, потому что -й строка является единственной, имеющей ненулевую запись в -й колонка и имеет нулевую запись в -й столбец. Следовательно, By тот же жетон, должен быть равен нулю, потому что -й строка — единственная в линейной комбинации, имеющая ненулевую запись в -й колонка и имеет нулевую запись в -й столбец. Таким образом, мы повторяем это рассуждение, пока не придем к выводу, что В качестве а следствие, но это невозможно, потому что имеет ненулевую запись в -й колонка и все имеют нулевые записи в этом столбце. Таким образом, мы доказали от противного что если все диагональные элементы отличны от нуля, то нет строки можно записать как линейную комбинацию остальных. Как следствие, строки линейно независимы и обратим. Теперь мы доказали предложение для нижних треугольных матрицы. Доказательство для верхнетреугольных матриц аналогично (заменить столбцы со строками).

Обратная треугольная матрица является треугольной

Утверждение Если нижний (верхний) треугольный матрица обратим, то обратный ему нижний (верхний) треугольный. Кроме того, каждый вход по главной диагонали равен обратной величине соответствующего элемента на главной диагонали , что для .

Доказательство

Пусть быть нижняя треугольная матрица. Обозначим через в столбцы . По определению, обратное удовлетворяетгде это единичная матрица. Столбцы являются векторы на стандартной основе. -й вектор стандартного базиса имеет все элементы равные нулю, кроме -й, что равно . По результатам, представленным в лекции о матрица произведения и линейные комбинации, столбцы удовлетворять для . Это система уравнений, которую можно записать какПримечание что константы в правой части равны нулю во всех уравнениях, кроме -й. С обратим, его диагональные элементы () не равны нулю. С , первое уравнение имеет решение . Подставив это решение во второе уравнение, получим (потому что ). Затем решаем третье уравнение и так далее, пока не придем к -й уравнение, где впервые найдено ненулевое решение . Таким образом, элементы вектор-столбца над -й ряд все нулевые. Но это -й столбец и утверждение справедливо для всех . Как следствие, все записи индекс строки которого меньше индекса столбца, равны нулю. Другими словами, нижний треугольный. Доказательство для верхнетреугольных матриц аналогично.

Треугольные матрицы и ступенчатая форма

В этом разделе исследуется связь между треугольными матрицами и матрицами в эшелонированной форме.

Предложение Если верхняя треугольная матрица обратима, то она находится в рядно-эшелонная форма.

Доказательство

Помните, что матрица находится в строке ступенчатая форма тогда и только тогда, когда 1) все ее ненулевые строки имеют стержень (т.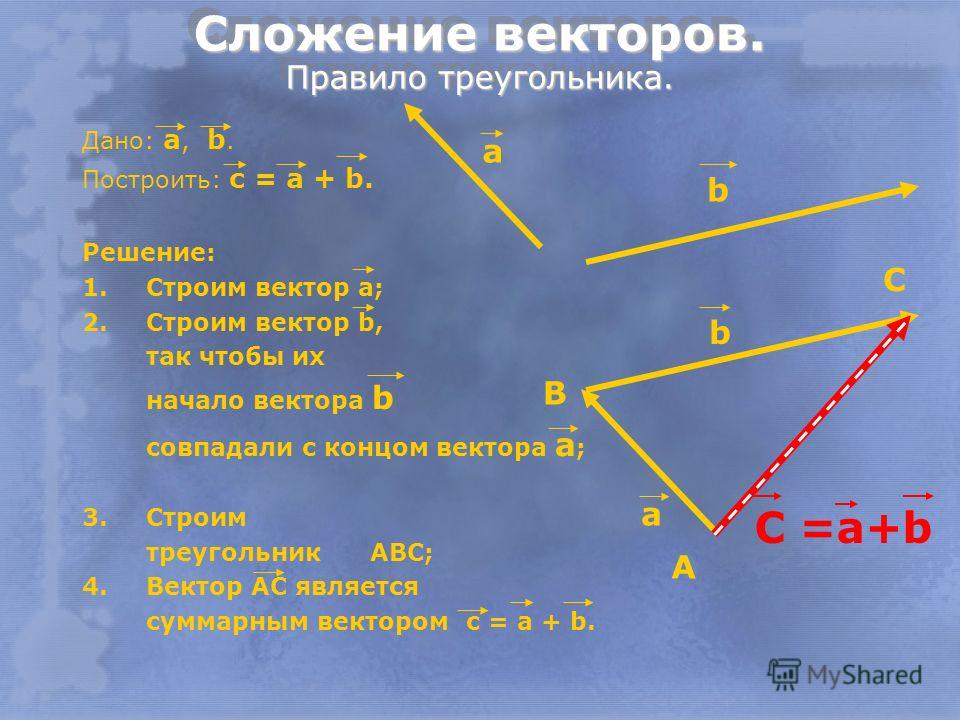 е. ненулевая запись такая, что все записи слева и ниже от нее равны ноль) и 2) все его нулевые строки расположены ниже ненулевых строк. Предполагать является обратимой верхней треугольной матрицей. Затем, не имеет нулевых строк, так как все его диагональные элементы отличны от нуля. Более того, каждый ряд содержит диагональную запись, которая является опорной, поскольку не равна нулю и имеет только нули под ним и слева от него. Следовательно, находится в форме эшелона строки.

Предложение Если нижняя треугольная матрица обратима, то она находится в эшелон колонны форма.

Доказательство

Это прямое следствие предыдущее предложение. Нам просто нужно использовать факты, что: 1) транспонирование верхняя треугольная матрица является нижней треугольной; 2) транспонирование матрицы в форме эшелона строки находится в форме эшелона столбца.

Предложение Если квадратная матрица имеет форму эшелона строк, то она является верхнетреугольной.

Доказательство

Пусть — квадратная матрица в форме эшелона строк. Просканируйте ряды сверху вниз в поисках точек опоры. Вы найдете сводную точку в каждой строке пока не доберетесь до нулевых строк. Каждая точка поворота, которую вы найдете, находится ниже и правее. предыдущего. Таким образом, опорные точки всегда находятся справа от основной. диагональ. Входы слева от опорных точек должны быть нулевыми. Следовательно, fortiori элементы слева от главной диагонали равны нулю. Следовательно, имеет верхнюю треугольную форму.

Предложение Если квадратная матрица имеет эшелонированную форму столбцов, то она является нижней треугольной.

Доказательство

Это прямое следствие предыдущее предложение. Нам просто нужно использовать тот факт, что транспонирование матрица в форме эшелона строк находится в форме эшелона столбцов, а транспонирование верхняя треугольная матрица является нижней треугольной.

Как цитировать

Пожалуйста, указывайте как:

Taboga, Marco (2021). «Треугольная матрица», Лекции по матричной алгебре. https://www.statlect.com/matrix-алгебра/треугольная-матрица.

матрицы — Как найти углы треугольников, заданных матрицей?

Задавать вопрос

спросил 4 года, 7 месяцев назад

Изменено 4 года, 7 месяцев назад

Просмотрено 302 раза

$\begingroup$

Предположим, у нас есть треугольник $ABC$, вершины которого определяются следующей матрицей: $$\begin{vmatrix} А_х&А_у&1\\ B_x&B_y&1\\ C_x&C_y&1\\ \end{vmatrix}= \begin{vmatrix} 3&3&1\\ 0&0&1\\ 5&0&1\\ \end{vmatrix}$$

Можно ли найти углы треугольника, используя только информацию из матрицы? Под этим я подразумеваю, что мы не рисуем треугольник.