Свойства определителей:
20.Какая подстановка называется четной?
Подстановка называется чётной если при всех записях подстановки чётности верхней и нижней строк (перестановок) – совпадают.
Например, тождественная подстановка( ) будет чётной:
21.Какая подстановка называется нечетной?
Подстановка называется нечётной если при всех записях подстановки чётности верхней и нижней строк (т.е. перестановок) – противоположны.
22.Сформулируйте определение определителя матрицы
Определителем (детерминантом) квадратной матрицы n–го порядка называют
число, равное алгебраической сумме всех возможных произведений элементов этой матрицы, взятых по одному из каждой строки и каждого столбца; при этом знак, с которым произведение входит в сумму определяется по правилу:
Сомножители в каждом произведении записываются в порядке следования строк, тогда номера столбцов образуют перестановки. Если перестановка четная, то произведение берется со знаком «+», а если нечётная – то со знаком «-».
Произведение элементов матрицы (слагаемые, из которых состоит сумма) называется
членом определителя.
! Элементы матрицы при этом могут быть также и комплексными числами!
НАПРИМЕР, при n=6 произведение а21а13а62а34а46а55 является членом
определителя, так как в него входит точно по одному элементу из каждой строки и из каждого столбца.
Подстановка, составленная из его индексов будет:
В ней 4 инверсии в верхней строке и 2 в нижней. Общее число инверсий 6, то есть подстановка чётная. Значит, этот член определителя входит в сумму со знаком «+».
1.При транспонировании матрицы её определитель не меняется.
2.Если поменять местами две строки или два столбца определителя, то определитель изменит знак, а по абсолютной величине не изменится.
3.Пусть C = AB где A и B квадратные матрицы. Тогда det C = detA ∙ detB .
4.Если все элементы одной строки (столбца) равны нулю, то и определитель равен нулю.
5.Определитель с двумя одинаковыми строками (столбцами) равен 0.
6.Определитель с двумя пропорциональными строками или столбцами равен 0.
7.Определитель треугольной матрицы равен произведению диагональных элементов.
8.Определитель диагональной матрицы равен произведению диагональных элементов.
9.Если все элементы строки (столбца) умножить на одно и то же число, то определитель умножится на это число.
10.Если каждый элемент некоторой строки (столбца) определителя представлен в виде суммы двух слагаемых, то определитель равен сумме двух определителей, у которых все строки (столбцы) кроме данной, прежние, а в данной строке (столбце) в первом определителе стоят первые, а во втором — вторые слагаемые.
11.Теорема Якоби: Если к элементам некоторого столбца определителя прибавить соответствующие элементы другого столбца, умноженные на произвольный множитель λ, то величина определителя не изменится.
23.Сформулируйте определение минора Мij матрицы А
Определение. Минор Mij элемента aij матрицы An×n – это определитель матрицы,
полученной из матрицы A вычёркиванием i-й строки и j-го столбца (т. е. строки и столбца, на пересечении которых находится элемент aij).
е. строки и столбца, на пересечении которых находится элемент aij).
ПРИМЕР: Для того, чтобы составить M32, вычеркнем из некой матрицы A третью
строку и второй столбец (именно на пересечении третьей строки и второго столбца расположен элемент A32). Получим новую матрицу, определитель которой и есть минор M32:
24. Сформулируйте определение алгебраического дополнения Аij матрицы А
Алгебраическое дополнение Aij элемента aij матрицы An×n это число, которое | |
находится по формуле: |
|
Aij=(−1)i+j Mij, где Mij – минор элемента aij. | |
ПРИМЕР: найти | алгебраическое дополнение A12: |
| |
Определитель матрицы равен сумме произведений элементов строки
определителя на их алгебраические дополнения.
Это позволяет упростить вычисление определителя матриц больших порядков сведя к вычислению определителей более низкого порядка (миноров).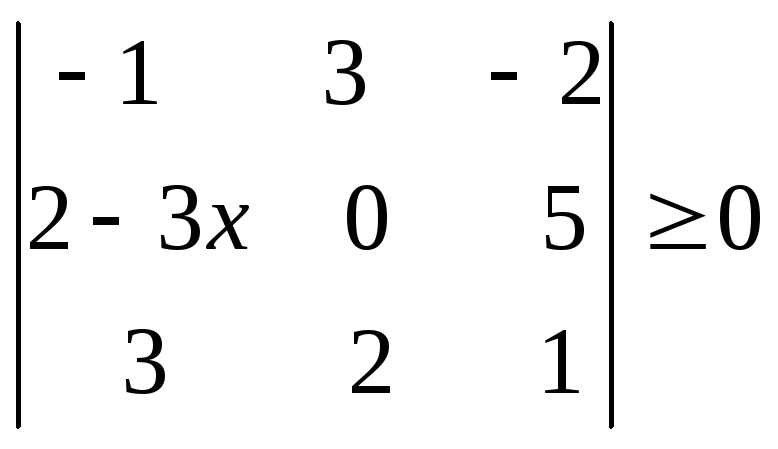 При этом обычно выбирают ту строку/столбец, где есть нули.
При этом обычно выбирают ту строку/столбец, где есть нули.
25.Как изменится определитель матрицы, если 2 его строки умножить на 2?
Если все элементы строки (столбца) умножить на одно и то же число, то
определитель умножится на это число.
Следовательно, если две строки умножить на 2, то определитель умножится на 4.
26.Чему равен определитель матрицы, имеющий два одинаковых столбца?
Определитель равен нулю, если он имеет два одинаковых столбца (или две
одинаковые строки).
Это следует из свойства смены знака определителя при перемене двух строк местами (в данном случае одинаковых). Т.к. строки одинаковы, то и определители обеих матриц должны быть одинаковы, но при этом, знак определителя должен меняться.
То есть , , откуда .
27.Как изменится определитель, если у матрицы поменять местами 2 строки?
Если две строки определителя поменять местами, то определитель сменит знак.
ДОКАЗАТЕЛЬСТВО: Действительно, если взять любой член некоего определителя, то в новом определителе номера 2-х строк поменяются местами, а номера
столбцов останутся прежними.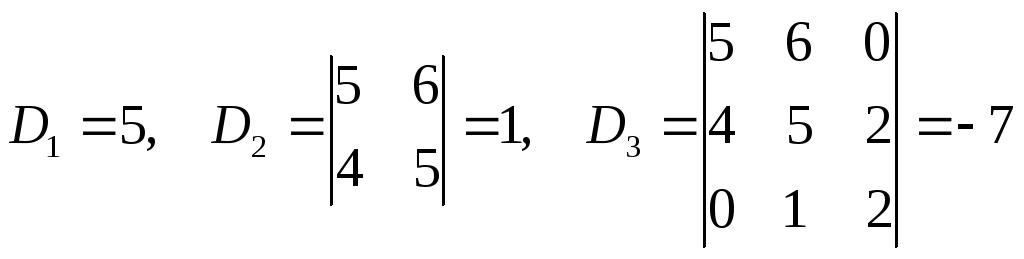 Следовательно, в новом определителе это же самое произведение (член определителя) будет входить с другим знаком, так как в номерах строк произошла одна транспозиция, а номера столбцов не изменились, то верхняя и нижняя строки подстановки, составленной из номеров строк и столбцов этих элементов будут иметь противоположные чётности. Итак, все члены данного определителя изменили знак, следовательно, и сам определитель изменил знак.
Следовательно, в новом определителе это же самое произведение (член определителя) будет входить с другим знаком, так как в номерах строк произошла одна транспозиция, а номера столбцов не изменились, то верхняя и нижняя строки подстановки, составленной из номеров строк и столбцов этих элементов будут иметь противоположные чётности. Итак, все члены данного определителя изменили знак, следовательно, и сам определитель изменил знак.
28.Чему равен определитель треугольной матрицы?
Определитель треугольной матрицы (верхней или нижней) равен произведению
её диагональных элементов (то есть элементов, стоящих на главной диагонали)
29.Чему равен определитель диагональной матрицы?
Определитель диагональной матрицы равен произведению её диагональных
элементов (то есть элементов, стоящих на главной диагонали)
! Ведь диагональная матрица является одновременно и верхней, и нижней треугольной.
30.Сформулируйте критерии равенства нулю определителя
1)Если все элементы строки (или столбца) определителя равны нулю, то
определитель равен нулю.
2) Определитель равен нулю, если он имеет две одинаковые строки (или столбца).
Это следует из свойства смены знака определителя при перемене двух строк местами (в данном случае одинаковых). Т.к. строки одинаковы, то и определители обеих матриц должны быть одинаковы, но при этом, знак определителя должен меняться.
То есть , , откуда .
3) Если две строки определителя пропорциональны, то определитель равен нулю. Т.к. если все элементы какой-нибудь строки определителя имеют общий множитель,
то его можно вынести за знак определителя и мы приходим к пункту 2) – равным строкам.
НЕОБХОДИМОЕ и ДОСТАТОЧНОЕ условие равенства определителя нулю:
Для равенства определителя нулю необходимо и достаточно, чтобы его строки (столбцы) были линейно зависимыми *.
*то есть если какая-то из строк (столбцов) может быть представлена в виде
линейной комбинации других строк (столбцов).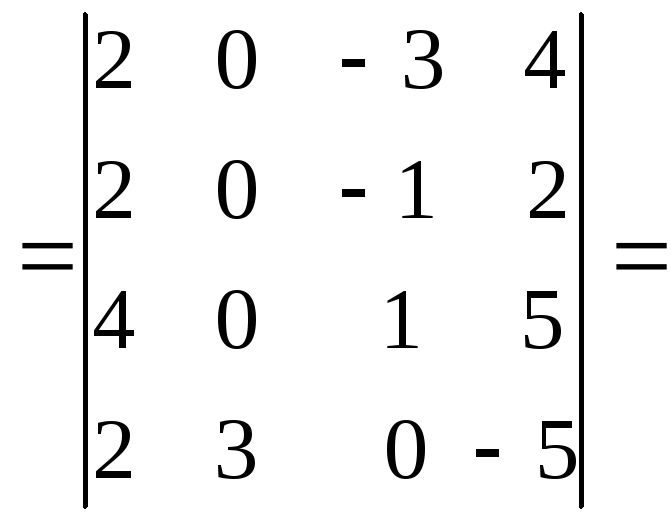
31.Запишите формулу для вычисления обратной матрицы
Определение. Обратная матрица A−1 — матрица, произведение которой на
исходную матрицу A равно единичной матрице E того же порядка:
A·A-1 = A-1·A = E
Обратная матрица A−1 существует тогда и только тогда, когда исходная матрица A – невырожденная. Если обратная матрица A−1 существует, то она единственная.
! Невырожденная матрица – матрица, определитель которой не равен нулю. Соответственно, вырожденная матрица – та, у которой определитель равен нулю.
Обратную матрицу А-1 можно найти по следующей формуле:
A-1 = | 1 | ÃT |
det(A) |
где det(A) — определитель матрицы А, Ã – матрица алгебраических дополнений соответствующих элементов матрицы А или союзная матрица.
Таким образом, чтобы найти обратную матрицу A−1, требуется:
1. Найти определитель матрицы A и убедиться, что он не равн нулю, т.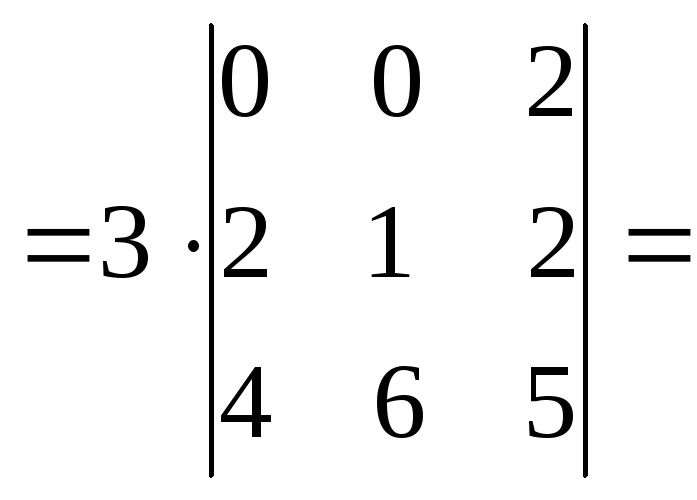 е. что
е. что
матрица А – невырожденная.
2. Составить алгебраические дополнения Aij каждого элемента матрицы A и
записать союзную матрицу из найденных алгебраических дополнений.
3.Записать транспонированную союзную матрицу
4.Записать обратную матрицу с учетом, что в формуле выше союзная матрица является транспонированной.
Свойства обратной матрицы
det(A-1) = 1det(A) (A·B)-1 = A-1·B-1 (A-1)T = (AT)-1
A-1
(kA)-1 = k
(A-1)-1 = A
32.А и В – матрицы. Чему равно (АВ)-1
(A·B)-1 = A-1·B-1
33.А – матрица. Чему равен (detA)-1
Определитель обратной матрицы всегда равен определителю исходной матрицы в минус первой степени (если конечно он не равен нулю).
Следовательно (detA)-1 равен определителю обратной матрицы А-1 det(A-1)
34.Дано матричное уравнение АХ=В. Чему равен Х?
Если A·X = B, То X = A-1·B.
Важно учитывать некомутативность произведения матриц!
35.Дано матричное уравнение ХА=В. Чему равен Х?
Если X·A = B,
То X = B· A-1.
Важно учитывать некомутативность произведения матриц!
36.А – матрица и detA=2. Чему равен det(AT) det(AT)= detA=2
37.А – матрица и detA=2. Чему равен det(A-1)
Определитель обратной матрицы всегда равен определителю матрицы в минус первой степени (если конечно он не равен нулю)
Следовательно det(A-1) = (detA)-1= 2-1=1/2
38.Способы вычисления определителя
1.Определитель матрицы разложением по строкам и столбцам через миноры.
2.Определитель матрицы методом треугольников
3.Определитель матрицы методом понижения порядка
4.Определитель методом приведения к треугольному виду (методом Гаусса)
5.Определитель матрицы методом декомпозиции
39.Способы построения обратной матрицы
1.Метод Алгебраических Дополнений (Союзной Матрицы)
2.Метод Гаусса (исключения неизвестных )
3.Нахождение обратной матрицы методом линейных преобразований
По сути метод линейных преобразований — это тот же метод алгебраических преобразований
(союзной матрицы), но с другой формой записи.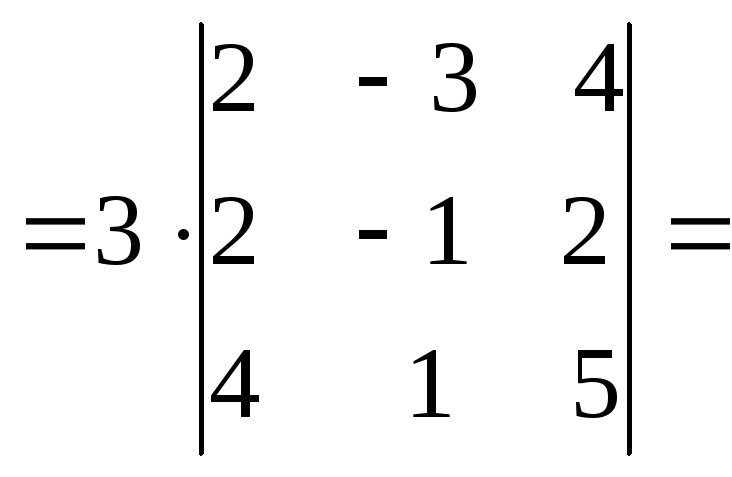
|
|
| Результат вычисления матричного выражения является матрицей. |
| ||||
| ВАЖНО: |
| ||||||
| При |
| обычных | расчётах | справедлив | алгебраический | приоритет: | сначала |
учитываются скобки, | затем выполняется возведение в степень/извлечение | корней, | ||||||
потом умножение/деление и в последнюю очередь – сложение/вычитание. |
|
| ||||||
Матричные выражения устроены аналогично, плюс некоторые специфические матричные операции: транспонирование и нахождение обратной матрицы.
Внимание! операция транспонирования имеет более высокий приоритет, чем умножение. Нахождение обратной матрицы также имеет приоритет перед умножением.
Нахождение обратной матрицы также имеет приоритет перед умножением.
ПРИМЕР Рассмотрим матричное выражение ,
где – некоторые матрицы. В данном матричном выражении три слагаемых и операции сложения/вычитания выполняются в последнюю очередь.
В первом слагаемом сначала нужно транспонировать матрицу «Бэ»: , потом выполнить умножение и внести «двойку» в полученную матрицу.
Скобки, как и в числовых выражениях, меняют порядок действий: – тут сначала выполняется умножение АВ, потом полученная матрица транспонируется и умножается на 2.
Во втором слагаемом (CD)-1 в первую очередь выполняется матричное умножение CD, и обратная матрица находится уже от произведения. Если скобки убрать: CD-1, то сначала необходимо найти обратную матрицу D-1, а затем перемножить матрицы: C на D-1.
С третьим слагаемым всё очевидно: возводим матрицу в куб и затем вносим «пятёрку» в полученную матрицу.
ГДЕ ИСПОЛЬЗУЮТСЯ МАТРИЦЫ В ЖИЗНИ (зачем они нужны)
Системы линейных уравнений — матрица коэффициентов
Таблица умножения по сути — произведение матриц (1,2,3,4,5,6,7,8,9)ТX(1,2,3,4,5,6,7,8,9) Файл bmp — это матрица цветов пикселей
Все вращения в классической механике описываются матрицами. Напряжения и сдвиги тож. Также матрица — это числовая запись многомерного вектора и их использование в
Напряжения и сдвиги тож. Также матрица — это числовая запись многомерного вектора и их использование в
конкретном случае зависит исключительно от того, можно ли исследуемый процесс представить в виде вектора:
Диэлектрическая и магнитная проницаемости в анизотропных средах — матрицы (тензоры). Тензор инерции, тензор энергии-импульса, тензор э/м поля — несут два индекса = матрицы.
Совместная диффузия нескольких веществ задается матрицей коэффициентов диффузии. В ОТО без тензоров никак. И квантовая механика тоже может быть записана в матричной
форме, правда, там матрицы специфические…
С.В.РЕЗНИЧЕНКООПРЕДЕЛИТЕЛИАНАЛ ИЧЕСКАЯ ГЕОМЕТРИЯ В ПРИМЕРАХ И ЗАДАЧАХ
РАЗДЕЛ http://old2. МАТРИЦЫ.pskgu. .ru/ebooks/rezsw..htmlСИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ Глава 2. Определители (детерминанты) квадратных матриц
§1. Перестановки и подстановки
§2. Определение детерминанта (определителя) порядка n
Если некоторый столбец (или строка) состоит из нулей, то определитель равен 0.
 — Студопедия
— СтудопедияПоделись
Задания для самостоятельной работы
1. . Найти .
2. . Найти .
3. . Найти .
4. . Можно ли данные матрицы сложить, умножить?
5. Найти линейную комбинацию матриц 2А+3В, где
. Ответ:
6. Дано . Найти произведение АВ и ВА.
Ответ: ; ВА – не существует.
7. Найти произведение матриц ААТ и АТА.
Ответ: , .
8. Вычислить определители данных матриц.
а) б)
в) г)
9. Вычислить определители:
а) б) в)
Ответ: а) -3; б) 2; в) 63.
10. № 586 — № 593, № 596, № 597. [6]
11. № 1204, № 1211- № 1216, №1252-1255. [5]
Рекомендуемая литература: [7] стр. 16-22, [4] стр. 60-64.
ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 2
Тема: Обратная матрица. Матричный метод решения систем линейных алгебраических уравнений.
Краткие сведения из теории и примеры решения задач.
Обратная матрица
Пусть А квадратная матрица n–го порядка.
Квадратная матрица А называется невырожденной, если ее определитель не равен нулю (Δ≠0). В противном случае (Δ=0) матрица называется вырожденной.
Присоединенной матрицей к матрице А, называется матрица
, где Аij – алгебраическое дополнение элемента аijданной матрицы А.
А* получается транспонированием матрицы, составленной из алгебраических дополнений Аij к элементам аij(А*=(Аij)Т).
Квадратная матрицаА-1называется обратной по отношению к матрице А того же порядка, если выполняется условие АА-1 = А-1А = Е.
Обратная матрица определяется по формуле .
Алгоритм вычисления элементов обратной матрицы А-1 таков:
1.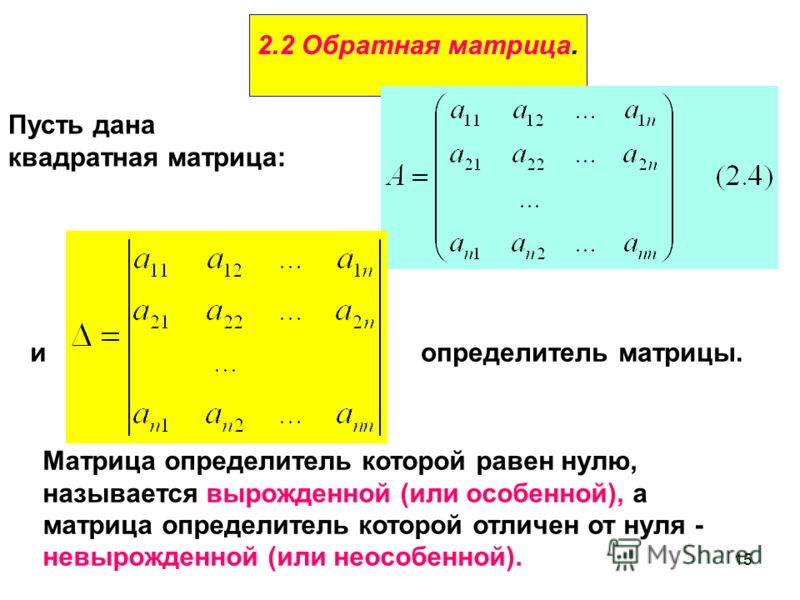 Вычисляем определитель матрицы А, ΔА≠0.
Вычисляем определитель матрицы А, ΔА≠0.
2. Вычисляем алгебраическое дополнение к каждому элементу матрицы А.
3. Составляем матрицу из алгебраических дополнений (Аij).
4. Транспонировав полученную матрицу, получаем присоединенную матрицу А*=(Аij)Т.
5. Все элементы матрицы А*делим на величину определителя матрицы А.
Пример. Найти матрицу, обратную заданной матрице А:
;
Вычислим алгебраические дополнения:
Составляем присоединенную матрицу и находим обратную:
; .
Проверку правильности нахождения обратной матрицы легко выполнить, учитывая, что произведение исходной матрицы на обратную дает единичную матрицу, т.е. АА-1 = А-1А = Е.
Проверка:
Замечание. Нахождение обратной матрицы второго порядка (и только второго порядка) можно выполнить следующим простым способом:
1) найти определитель исходной матрицы А;
2) в исходной матрице А поменять местами элементы, стоящие на главной диагонали, изменить знаки на противоположные у элементов побочной диагонали, т. е. получить присоединенную матрицу.
е. получить присоединенную матрицу.
3) Разделить элементы присоединенной матрицы на величину определителя.
Например, если , то и .
линейная алгебра — Доказательство определителя = 0
Вот еще два условия.
(D) Найдите $n — 1$ таких векторов (размером $N$ каждый), что $n$ строк или столбцов вашей матрицы являются линейными комбинациями этих векторов.
Это более общий вариант, чем (B), потому что, если вы знаете (B), вы можете выбрать все эти строки или столбцы, кроме одной, в качестве векторов. Однако (B) не является более общим, чем (D), потому что для перехода от (D) к (B) нужно инвертировать матрицу размера $n$, где $n$ может достигать $N$, что так же сложно, как сначала вычислить исходный определитель.
Если $ n = N $, это условие на самом деле говорит, что матрица имеет нулевой определитель, если она является произведением матрицы $ N \times (N-1) $ на матрицу $ (N-1) \times N $. { N-1} $. Пусть $A$ — матрица $N \times N$, элементом которой $a_{i,j}$ является скалярное произведение $\langle \mathbf{u}_i|\mathbf{v}_j\rangle $. Мы хотим доказать, что $ \det A = 0 $.
{ N-1} $. Пусть $A$ — матрица $N \times N$, элементом которой $a_{i,j}$ является скалярное произведение $\langle \mathbf{u}_i|\mathbf{v}_j\rangle $. Мы хотим доказать, что $ \det A = 0 $.
Самый простой способ доказать это — использовать условие (D). Возьмем базис $ (\mathbf{e}_1, \dots, \mathbf{e}_{N-1}) $ векторного пространства и запишем векторы в этом базисе как $ \mathbf{u}_i = \sum_k u_{i,k} \mathbf{e}_k $ и $ \mathbf{v}_j = \sum_k v_{j,k} \mathbf{e}_k $. Общий элемент матрицы может быть записан как $ a_{i,j} = \langle\mathbf{u}_i|\mathbf{v}_j\rangle = \sum_k u_{i,k} v_{j,k} $. Это означает, что любая строка $ \mathbf{a}_i = (a_{i,1}, \dots, a_{i,N}) $ является линейной комбинацией векторов $ \mathbf{w}_1, \dots, \mathbf{w}_{N-1} $, где $ \mathbf{w}_k = (v_{1,k}, \dots, v_{N,k}) $, а именно $ \mathbf{a}_i = u_{i,1} \mathbf{w}_1 + \dots u_{i,N-1} \mathbf{w}_{N-1} $.
Аналогичным образом можно использовать условие (B). Для этого нужно сначала найти линейную зависимость среди векторов $\mathbf{u}_1, \dots, \mathbf{u}_N $. Такая зависимость должна существовать, потому что это $N$ векторы в $N-1$ мерном пространстве. Предположим, что $ \mathbf{0} = \lambda_1 \mathbf{u}_1 + \dots + \lambda_N \mathbf{u}_N $, где не все коэффициенты равны нулю. Теперь $ \sum_i \lambda_i a_{i,j} = \sum_i \langle\mathbf{u}_i|\mathbf{v}_j\rangle = $ $ \bigl\langle \bigl(sum_i\mathbf{u}_i\ bigr)\bigm|\mathbf{v}_j\rangle = \langle\mathbf{0}|\mathbf{v}_j\rangle = 0 $, что означает, что строки матрицы линейно зависимы. 9j \prod_i u_{i,k_i} v_{j_i,k_i} $$
Такая зависимость должна существовать, потому что это $N$ векторы в $N-1$ мерном пространстве. Предположим, что $ \mathbf{0} = \lambda_1 \mathbf{u}_1 + \dots + \lambda_N \mathbf{u}_N $, где не все коэффициенты равны нулю. Теперь $ \sum_i \lambda_i a_{i,j} = \sum_i \langle\mathbf{u}_i|\mathbf{v}_j\rangle = $ $ \bigl\langle \bigl(sum_i\mathbf{u}_i\ bigr)\bigm|\mathbf{v}_j\rangle = \langle\mathbf{0}|\mathbf{v}_j\rangle = 0 $, что означает, что строки матрицы линейно зависимы. 9j \prod_i u_{i,k_i} v_{j_i,k_i} $$
где $ j : (\{1\dots N\} \to \{1\dots N\}) $ перебирает все перестановки и $ k : (\{1\dots N\} \to \{1\dots N-1\}) $ по всем последовательностям.
Любой такой вектор $k$ должен иметь повторение, потому что диапазон меньше домена. Пусть, таким образом, $k_r = k_s$, где $r
Обновление: отредактированы формулы в доказательстве с использованием (D), так как ранее я сделал ошибку.
Матрица имеет полный ранг тогда и только тогда, когда ее определитель отличен от 0
Зависимости:
- Поле
- Ранг матрицы
- Определитель после операции элементарной строки
- Поле является областью целостности
- Квадратная матрица полного ранга в RREF является единичной матрицей.
- Определитель верхней треугольной матрицы
Пусть $A$ — матрица размером $n$ на $n$ над полем. {n+i} 0 |B[-n, -i]|
= 0 \]
Следовательно, $\operatorname{rank}(A) \neq n \Rightarrow |B| = 0$.
{n+i} 0 |B[-n, -i]|
= 0 \]
Следовательно, $\operatorname{rank}(A) \neq n \Rightarrow |B| = 0$.
Следовательно, $\operatorname{rank}(A) = n \iff |B| \neq 0 \ тогда и только тогда, когда |A| \neq 0$.
Зависимость для:
- Каждая комплексная матрица имеет собственное значение
- Характеристический многочлен матрицы
- Определитель произведения есть произведение определителей
Информация:
- Глубина: 9
- Количество транзитивных зависимостей: 45
Переходные зависимости:
- /линейная-алгебра/векторные-пространства/условие-для-подпространства
- /линейная-алгебра/матрицы/гаусс-джордан-алго
- /множества-и-отношения/эквивалентность-отношение
- Группа
- Звенеть
- Полиномиальный
- Интегральный домен
- Сравнение коэффициентов многочлена с непересекающимися переменными
- 0х = 0 = х0
- Поле
- Векторное пространство
- Линейная независимость
- Охватывать
- Поле является областью целостности
- полукольцо
- Матрица
- Укладка
- Система линейных уравнений
- Произведение сложенных матриц
- Умножение матриц ассоциативно
- Уменьшенная форма эшелона строк (RREF)
- Подматрица
- определитель
- Определитель верхней треугольной матрицы
- Замена двух последних строк матрицы инвертирует ее определитель.

- Матрицы над полем образуют векторное пространство
- Пространство строки
- Элементарная операция строки
- Определитель после операции элементарной строки
- Каждая элементарная операция строки имеет уникальную обратную
- Эквивалентность строк матриц
- Матрицы, эквивалентные строкам, имеют одинаковое пространство строк.
- RREF уникален
- Единичная матрица
- Обратная матрица
- Инверсия продукта
- Элементарная операция со строками — предварительное умножение матриц.



