Умножение отрицательных и положительных чисел. Умножение отрицательных чисел: правило, примеры
В этой статье мы рассмотрим деление положительных чисел на отрицательные и наоборот. Дадим подробный разбор правила деления чисел с разными знаками, а также приведем примеры.
Правило деления чисел с разными знаками
Правило для целых чисел с разными знаками, полученное в статье о делении целых чисел, справедливо также для рациональных и действительных чисел. Приведем более общую формулировку этого правила.
Правило деления чисел с разными знаками
При делении положительного числа на отрицательное и наоборот нужно модуль делимого разделить на модуль делителя, а результат записать со знаком минус.
В буквенном виде это выглядит так:
a ÷ — b = — a ÷ b
A ÷ b = — a ÷ b .
Результатом деления чисел с разными знаками всегда является отрицательное число. Рассмотренное правило, по сути, сводит деление чисел с разными знаками к делению положительных чисел, так как модули делимого и делителя являются положительными.
Еще одна эквивалентная математическая формулировка данного правила имеет вид:
a ÷ b = a · b — 1
Чтобы разделить числа a и b , имеющие разные знаки, нужно число a умножить на число, обратное числу b , то есть b — 1 . Данная формулировка применима на множестве рациональных и действительных чисел, она позволяет перейти от деления к умножению.
Рассмотрим теперь, как применять описанную выше теорию на практике.
Как делить числа с разными знаками? Примеры
Ниже мы рассмотрим несколько характерных примеров.
Пример 1. Как делить числа с разными знаками?
Разделим — 35 на 7 .
Сначала запишем модули делимого и делителя:
35 = 35 , 7 = 7 .
Теперь разделим модули:
35 7 = 35 7 = 5 .
Допишем перед результатом знак минус и получим ответ:
Теперь воспользуемся другой формулировкой правила и вычислим число, обратное 7 .
Теперь проведем умножение:
35 · 1 7 = — — 35 · 1 7 = — 35 7 = — 5 .
Пример 2. Как делить числа с разными знаками?
Если мы делим дробные числа с рациональными знаками, делимое и делитель нужно представить в виде обыкновенных дробей.
Пример 3. Как делить числа с разными знаками?
Разделим смешанное число — 3 3 22 на десятичную дробь 0 , (23) .
Модули делимого и делителя соответственно равны 3 3 22 и 0 , (23) . Переводя 3 3 22 в обыкновенную дробь, получаем:
3 3 22 = 3 · 22 + 3 22 = 69 22 .
Делитель также представим в виде обыкновенной дроби:
0 , (23) = 0 , 23 + 0 , 0023 + 0 , 000023 = 0 , 23 1 — 0 , 01 = 0 , 23 0 , 99 = 23 99 .
Теперь делим обыкновенные дроби, выполняем сокращения и получаем результат:
69 22 ÷ 23 99 = — 69 22 · 99 23 = — 3 2 · 9 1 = — 27 2 = — 13 1 2 .
В заключение рассмотрим случай, когда делимое и делитель являются иррациональными числами и записываются в виде корней, логарифмов, степеней и т.д.
В такой ситуации частное записывается в виде числового выражения, которое по возможности упрощается. При необходимости вычисляется его приближенное значение с необходимой точностью.
Пример 4. Как делить числа с разными знаками?
Разделим числа 5 7 и — 2 3 .
По правилу деления чисел с разными знаками, запишем равенство:
5 7 ÷ — 2 3 = — 5 7 ÷ — 2 3 = — 5 7 ÷ 2 3 = — 5 7 · 2 3 .
Избавимся от иррациональности в знаменателе и получим окончательный ответ:
5 7 · 2 3 = — 5 · 4 3 14 .
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
В данной статье дадим определение деления отрицательного числа на отрицательное, сформулируем и обоснуем правило, приведем примеры деления отрицательных чисел и разберем ход их решения.
Деление отрицательных чисел. Правило
Напомним, в чем суть операции деления. Данное действие представляет собой нахождение неизвестного множителя по известному произведению и известному другому множителю. Число с называется частным от деления чисел a и b , если верно произведение c · b = a . При этом, a ÷ b = c .
Правило деления отрицательных чисел
Частное ои деления одного отрицательного числа на другое отрицательное число равно частному от деления модулей этих чисел.
Пусть a и b — отрицательные числа. Тогда
a ÷ b = a ÷ b .
Данное правило сводит деление двух отрицательных чисел к делению положительных чисел. Оно справедливо не только для целых чисел, но также для рациональных и действительных чисел. Результат деления отрицательного числа на отрицательное есть всегда положительное число.
Приведем еще одну формулировку данного правила, подходящую для рациональных и действительных чисел. Она дается с помощью взаимно-обратных чисел и гласит: для деления отрицательного числа a на число undefined умножить на число b — 1 , обратное числу b .
a ÷ b = a · b — 1 .
Это же правило, сводящее деление к умножению, можно применять также и для деления чисел с разными знаками.
Равенство a ÷ b = a · b — 1 можно доказать, используя свойство умножения действительных чисел и определение взаимно обратных чисел. Запишем равенства:
a · b — 1 · b = a · b — 1 · b = a · 1 = a .
В силу определения операции деления, данное равенство доказывает, что есть частное от деления числа на число b.
Перейдем к рассмотрению примеров.
Начнем с простых случаяв, переходя к более сложным.
Пример 1. Как делить отрицательные числа
Разделим — 18 на — 3 .
Модули делителя и делимого соответственно равны 3 и 18 . Запишем:
18 ÷ — 3 = — 18 ÷ — 3 = 18 ÷ 3 = 6 .
Пример 2. Как делить отрицательные числа
Разделим — 5 на — 2 .
Аналогично, записываем по правилу:
5 ÷ — 2 = — 5 ÷ — 2 = 5 ÷ 2 = 5 2 = 2 1 2 .
Такой же результат получится, если использовать вторую формурировку правила с обратным числом.
5 ÷ — 2 = — 5 · — 1 2 = 5 · 1 2 = 5 2 = 2 1 2 .
Деля дробные рациональные числа удобнее всего представлять их в виде обыкновенных дробей. Однако, можно делить и конечные десятичные дроби.
Пример 3. Как делить отрицательные числа
Разделим — 0 , 004 на — 0 , 25 .
Сначала записываем модули этих чисел: 0 , 004 и 0 , 25 .
Теперь можно выбрать один из двух способов:
- Разделить десятичные дроби столбиком.
- Перейти к обыкновенным дробям и выполнить деление.
Разберем оба способа.
1. Выполняя деление десятичных дробей столбиком, перенесем запятую на две цифры вправо.
Ответ: — 0 , 004 ÷ 0 , 25 = 0 , 016
2. Теперь приведем решение с переводом десятичных дробей в обыкновенные.
0 , 004 = 4 1000 ; 0 , 25 = 25 100 0 , 004 ÷ 0 , 25 = 4 1000 ÷ 25 100 = 4 1000 · 100 25 = 4 250 = 0 , 016
Полученные результаты совпадают.
В заключение отметим, что если делимое и делитель являются иррациональными числами и задаются в виже корней, степеней, логарифмов и т.д., результат деления записывается в виде числового выражения, приблизительное значение которого вычисляется в случае необходимости.
Пример 4. Как делить отрицательные числа
Вычислим частное от деления чисел — 0 , 5 и — 5 .
0 , 5 ÷ — 5 = — 0 , 5 ÷ — 5 = 0 , 5 ÷ 5 = 1 2 · 1 5 = 1 2 5 = 5 10 .
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
На этом уроке мы повторим правила сложения положительных и отрицательных чисел.
Также научимся умножать числа с разными знаками и узнаем правила знаков для умножения. Рассмотрим примеры умножения положительных и отрицательных чисел.
Свойство умножения на ноль остается верным и в случае отрицательных чисел. Ноль умножить на любое число — будет ноль.
Список литературы
- Виленкин Н.Я., Жохов В.И., Чесноков А.С., Шварцбурд С.И. Математика 6. — М.: Мнемозина, 2012.
- Мерзляк А.Г., Полонский В.В., Якир М.С. Математика 6 класс. — Гимназия. 2006.
- Депман И.Я., Виленкин Н.Я. За страницами учебника математики. — М.: Просвещение, 1989.
- Рурукин А.Н., Чайковский И.В. Задания по курсу математика 5-6 класс. — М.: ЗШ МИФИ, 2011.
- Рурукин А.Н., Сочилов С.В., Чайковский К.Г. Математика 5-6. Пособие для учащихся 6-х классов заочной школы МИФИ. — М.: ЗШ МИФИ, 2011.
- Шеврин Л.Н., Гейн А.Г., Коряков И.О., Волков М.В. Математика: Учебник-собеседник для 5-6 классов средней школы. — М.: Просвещение, Библиотека учителя математики, 1989.
Домашнее задание
- Интернет-портал Mnemonica.ru ().
- Интернет-портал Youtube.com ().
- Интернет-портал School-assistant.ru ().
Задача 1. Точка движется по прямой слева направо со скоростью 4 дм. в секунду и в настоящий момент проходит через точку A. Где будет находиться движущаяся точка по прошествии 5 секунд?
Нетрудно сообразить, что точка будет находиться на 20 дм. вправо от A. Запишем решение этой задачи относительными числами. Для этого условимся в следующих знакоположениях:
1) скорость вправо будем обозначать знаком +, а влево знаком –, 2) расстояние движущейся точки от A вправо будем обозначать знаком + и влево знаком –, 3) промежуток времени после настоящего момента знаком + и до настоящего момента знаком –. В нашей задаче даны, след., такие числа: скорость = + 4 дм. в секунду, время = + 5 секунд и получилось, как сообразили арифметически, число + 20 дм., выражающее расстояние движущейся точки от A через 5 секунд.
По смыслу задачи мы видим, что она относится к умножению. Поэтому решение задачи удобно записать:
(+ 4) ∙ (+ 5) = + 20.
Задача 2. Точка движется по прямой слева направо со скоростью по 4 дм. в секунду и в настоящий момент проходит через точку A. Где находилась эта точка 5 секунд назад?
Ответ ясен: точка находилась влево от A на расстоянии 20 дм.
Решение удобно, согласно условиям относительно знаков, и, имея в виду, что смысл задачи не изменился, записать так:
(+ 4) ∙ (– 5) = – 20.
Задача 3. Точка движется по прямой справа налево со скоростью 4 дм. в секунду и в настоящий момент проходит через точку A. Где будет находиться движущаяся точка спустя 5 секунд?
Ответ ясен: на 20 дм. слева от A. Поэтому, согласно тем же условиям относительно знаков, мы можем записать решение этой задачи так:
(– 4) ∙ (+ 5) = – 20.
Задача 4. Точка движется по прямой справа налево со скоростью по 4 дм. в секунду и в настоящий момент проходит через точку A.
Ответ ясен: на расстоянии 20 дм. справа от A. Поэтому решение этой задачи следует записать так:
(– 4) ∙ (– 5) = + 20.
Рассмотренные задачи указывают, как следует распространить действие умножения на относительные числа. Мы имеем в задачах 4 случая умножения чисел со всевозможными комбинациями знаков:
1) (+ 4) ∙ (+ 5) = + 20;
2) (+ 4) ∙ (– 5) = – 20;
3) (– 4) ∙ (+ 5) = – 20;
4) (– 4) ∙ (– 5) = + 20.
Во всех четырех случаях абсолютные величины данных чисел следует перемножить, у произведения приходится ставить знак + тогда, когда у множителей одинаковые знаки (1-й и 4-й случаи) и знак –, когда у множителей разные знаки (случаи 2-й и 3-й).
Отсюда же видим, что от перестановки множимого и множителя произведение не изменяется.
Упражнения.
Выполним один пример на вычисление, где входят и сложение и вычитание и умножение.
Чтобы не спутать порядка действий, обратим внимание на формулу
Здесь написана сумма произведений двух пар чисел: надо, следовательно, сперва число a умножить на число b, потом число c умножить на число d и затем полученные произведения сложить.
Также в формуле
надо сперва число b умножить на c и затем полученное произведение вычесть из a.
Если бы требовалось произведение чисел a и b сложить с c и полученную сумму умножить на d, то следовало бы написать: (ab + c)d (сравнить с формулой ab + cd).
Если бы надо было разность чисел a и b умножить на c, то написали бы (a – b)c (сравнить с формулой a – bc).
Поэтому установим вообще, что если порядок действий не обозначен скобками, то надо сначала выполнить умножение, а потом уже сложение или вычитание.
Приступаем к вычислению нашего выражения: выполним сначала сложения, написанные внутри всех маленьких скобок, получим:
Теперь надо выполнить умножение внутри квадратных скобок и затем из вычтем полученное произведение:
Теперь выполним действия внутри витых скобок: сначала умножение и потом вычитание:
Теперь останется выполнить умножение и вычитание:
16. Произведение нескольких множителей. Пусть требуется найти
(–5) ∙ (+4) ∙ (–2) ∙ (–3) ∙ (+7) ∙ (–1) ∙ (+5).
Здесь надо первое число умножить на второе, полученное произведение на 3-е и т. д. Не трудно на основании предыдущего установить, что абсолютные величины всех чисел надо между собою перемножить.
Если бы все множители были положительны, то на основании предыдущего найдем, что и у произведения надо написать знак +. Если бы какой-либо один множитель был отрицателен
напр., (+2) ∙ (+3) ∙ (+4) ∙ (–1) ∙ (+5) ∙ (+6),
то произведение всех предшествующих ему множителей дало бы знак + (в нашем примере (+2) ∙ (+3) ∙ (+4) = +24, от умножения полученного произведения на отрицательное число (в нашем примере +24 умножить на –1) получили бы у нового произведения знак –; умножив его на следующий положительный множитель (в нашем примере –24 на +5), получим опять отрицательное число; так как все остальные множители предполагаются положительными, то знак у произведения более изменяться не может.
Если бы было два отрицательных множителя, то, рассуждая, как выше, нашли бы, что сначала, пока не дошил до первого отрицательного множителя, произведение было бы положительно, от умножения его на первый отрицательный множитель новое произведение получилось бы отрицательным и таковы бы оно и оставалось до тех пор, пока не дойдем до второго отрицательного множителя; тогда от умножения отрицательного числа на отрицательно новое произведение получилось бы положительным, которое таким останется и в дальнейшем, если остальные множители положительны.
Если бы был еще третий отрицательный множитель, то полученное положительно произведение от умножения его на этот третий отрицательный множитель сделалось бы отрицательным; оно таковым бы и осталось, если остальные множители были все положительны. Но если есть еще четвертый отрицательный множитель, то от умножения на него произведение сделается положительным. Рассуждая так же, найдем, что вообще:
Чтобы узнать знак произведения нескольких множителей, надо посмотреть, сколько среди этих множителей отрицательных: если их вовсе нет, или если их четное число, то произведение положительно: если же отрицательных множителей нечетное число, то произведение отрицательно.
Итак, теперь мы легко узнаем, что
(–5) ∙ (+4) ∙ (–2) ∙ (–3) ∙ (+7) ∙ (–1) ∙ (+5) = +4200.
(+3) ∙ (–2) ∙ (+7) ∙ (+3) ∙ (–5) ∙ (–1) = –630.
Теперь нетрудно видеть, что знак произведения, а также и его абсолютная величина, не зависят от порядка множителей.
Удобно, когда имеем дело с дробными числами, находить произведение сразу:
Удобно это потому, то не приходится делать бесполезных умножений, так как предварительно полученное дробное выражение сокращается, сколько возможно.
Урок по математике в 6 классе «Умножение положительных и отрицательных чисел», по учебнику Зубарева И. И. | План-конспект урока по алгебре (6 класс) на тему:
Тема урока: Умножение положительных и отрицательных чисел.
Цели урока:
Организовать совместную деятельность, нацеленную на предметный результат: вывести правила умножения положительных и отрицательных чисел;
Создать условия для развития умений ϲᴩавнивать, выявлять закономерности, обобщать, учить думать, высказывать свое мнение;
Воспитывать трудолюбие, аккуратность, умение работать коллективно.
Ход урока:
Организационный момент. Приветствие учеников. Проверка домашнего задания. Отмечаю отсутствующих.
Учитель: Проводится фронтальная устная работа.
- Какую большую тему мы изучаем? (Положительные и отрицательные числа.)
- Какие действия над положительными и отрицательными мы уже знаем?
- Как сложить два отрицательных числа?
- Как сложить два числа с разными знаками?
На доске записаны примеры вычислите: слайд 2
12-16=-4 -7-(-7)=0
-2,1 +3=0,9 -5+(-3)=-8
3 +(-0,5)=2,5 -4-2=-6
-11+8=-3 3-(-1)=4
5∙ 3=15 (-5)∙ 3=-
(-5)∙ (-3)= 5∙ (-3)
Ребята, а все примеры мы можем решить? Нет.
А почему?
Тогда какая задача нашего сегодняшнего урока, что бы вы хотели узнать? (как умножить положительные и отрицательные числа) .
Итак, тема нашего урока: «Умножение положительных и отрицательных
чисел».
Слайд 3.Открываем тетради и записываем число- 12.11 Классная работа. Умножение положительных и отрицательных чисел.
Мы с вами умеем умножать положительные числа. Правильно? Да.
Пусть у нас есть 5 ∙ 3. Мы знаем , что 5 ∙ 3 =15 с одной стороны, а с другой-
5 ∙ 3= 5 + 5 + 5 = 15..
Слайд 5. Оба числа положительные.
5∙ 3 = 15.
Значит, при умножении положительного числа на положительное число есть положительное число. Модули перемножаются.
А что мы ещё знаем? Нуль умножить на любое число есть число нуль.
При умножении любого числа на один есть то же самое число
А знаем ли мы законы умножения? Да.
Давайте вспомним их: Слайд 4
1. Переместительный: а∙в = в∙а.
2. Сочетательный: а∙ (в∙с) = (а∙в)с.
Изучение нового материала, работа с версиями детей, сравнение лично полученного результата с научным.
Проведем небольшой математический эксперимент. А теперь рассмотрим, где первый множитель отрицательное число, а второй натуральное число: ( -5) ∙ 3. Как умножить эти числа? Кто догадался? Правильно, умножение заменим сложение6.
(– 5) · 3 = (– 5) + (– 5) + (– 5) = – (5 + 5 + 5) = – 15.
Значит, что (-5)*3=(-15). Слайд 6.
Какой вывод можно сделать? Значит, при умножении отрицательного числа на положительное число получается число отрицательное.
А если мы поменяем числа местами, что будет? Зная переместительный закон умножения, можно сказать: при умножении положительного числа на отрицательное число получается число отрицательное. 3 случай. Слайд7.
А если вместо 5 взять 1, то что получится? Правильно, (-1) ∙ 3 = -3. Значит,
при умножении любого числа на (-1) получается число, ему противоположное: (-1) ∙ а = а ∙ (-1) = — а.
А теперь рассмотрим пример ( 4 случай), где два числа отрицательные (-5)*(-3) и нам надо найти их произведение.
Давайте подумаем, как мы можем записать -5 через произведение? Правильно: отрицательный множитель можно заменить произведением (-1) на положительное число, а затем применить сочетательный закон умножения:
(-5)*(-3)=((-1)*5)*(-3)=(-1)*(5*(-3))=- 1▪(-15)=15
Историческая справка.
Еще XVIII в. великий русский ученый, математик и механик Леонард Эйлер объяснил это правило умножения отрицательных чисел.
Он объяснял так: произведение (-5)*(-3) не может быть равно (-15) и его нельзя заменить на сумму. Однако оно должно быть связано как-то с числом 15. Остается одна возможность (-5)*(-3)=15. Т. К. 3 и (-3) – противоположные числа, то противоположное -15 есть число 15. Слайд 8.
А теперь давайте сформулируем правило умножения двух отрицательных чисел: при умножении двух отрицательных чисел получается положительное число, модуль которого равен произведению модулей множителей.
5. Первичное закрепление нового материала.
– Исходя из выше сказанного, мы с вами получили правила умножения положительных и отрицательных чисел.
Кто может сформулировать правила?
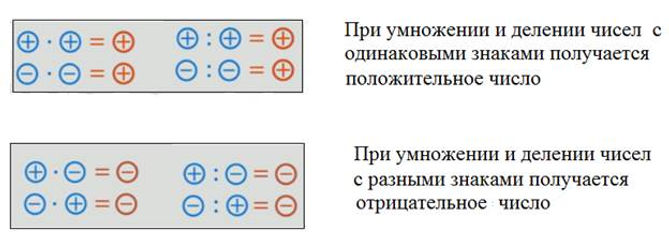
Выводы: 1) Произведение двух чисел одного знака положительно, а произведение двух чисел с разными знаками отрицательно;
2) Чтобы найти модуль произведения, нужно ᴨеᴩеᴍножить модули сомножителей.
– Откройте учебник стр. 83 , прочитайте правила, ϲᴩавните их с теми, которые мы вывели сами, сделайте вывод, как умножить два отрицательных числа, как умножить два числа с разными знаками:
1. Установить какие знаки имеют множители.
2. Установить знак результата.
3. Найти модуль произведения.
Запомните правила знаков для произведения очень просто. Коротко их формируют так: «плюс на плюс даёт плюс», «Минус на плюс дает минус», «Плюс на минус дает минус». «Минус на минус дает плюс».
Для того чтобы хорошо запомнить, посмотрите на эту таблицу (Правило знаков). Слайд 9.
«+» * «+» = «+» «+» * «–» = «–»
«–» * «–» = «+» «–» * «+» = «–»
Закрепление
1.
Найдите значение числового выражения, применяя правила: слайд 10
7∙ (-6) = — 42
-8 ∙( -4) = 32
-1 ∙1,1 = — 1,1
-1,34 ∙0 = 0
2. Найди ошибку (устно): слайд 11
А) – 3∙ (-6) = — 18 г) -24∙ (-0,5) = -12
Б) 5 ∙ (-0,4) = 2 д) -10 ∙ (-10) = 100
В) 6∙ (-1,2) = — 7,2 е) -10 ∙34 = — 3,4
Работа с учебником № 370 (2 ученика выходят к доске)
а) (- 6) * (- 3) = 18 в) – 5 * (- 0,7)= 3,5
б) (- 0,8) * (- 9) = 7,2 г) – 2 * (- 1, 6) = 3,2
Решить № 372(а — г) ( 2 ученика выходят к доске)
а) (- 15) * 6 = — 90 в) (- 2,7)* (- 0,3) = 0,81
б)7,8* (-4 )= — 31,2 г) (- 8) * (- 21) = 168
Повторяем правила на умножение положительных и отрицательных чисел.
Физкультминутка. Вы, ребята, все устали. Слайд 12
Много думали, считали.
Отдохнуть уже пора!
Физминутка тут – “Ура!”
7. Самостоятельная работа слайд 13.
Проверяем ответы. Поднимите руки те, кто сделал без ошибок. Молодцы! За урок получаете пятёрки.
А теперь те, кто допустил одну ошибку. Опустите руки. Две ошибки. Ребята , вам ещё надо поработать над данной темой . Слайд 14.
Итоги урока. Д/з. Рефлекϲᴎя
– А теперь давайте попытаемся понять, что же каждому из нас дал сегодняшний урок. Иʜᴛᴇресно ли вам сегодня было? Чему научились? Что вызвало затруднение?
- Как ᴨеᴩеᴍножить два числа с разными знаками?
- Как ᴨеᴩеᴍножить два отрицательных числа?
- Приведите примеры на каждое правило.
Слайд 15
Домашнее задание: § 12.Выучить правила на страницах 82 и 83
решить № 372 ( д — и), 373(а,в), 385 (а,б)
(Учитель объясняет решение примеров.)
бакалавриат — Как объяснить, что отрицательное число, умноженное на отрицательное число, является положительным числом и что $-(-x)=x$?
Я не буду здесь давать конкретных объяснений, потому что думаю, что это сильно зависит от уровня знаний ученика.
Скорее, я хотел бы подчеркнуть некоторые общие моменты, которые, по моему мнению, учителям полезно иметь в виду при объяснении и мотивировании этих и связанных с ними вопросов, касающихся расширения «систем счисления» (здесь расширение от положительных до отрицательных целых чисел).
Во-первых, часто полезно взглянуть на историю развития этих концепций. Например, нам нужно иметь в наличии отрицательные целые числа, рациональные числа и (мнимые) квадратные числа, чтобы дать единую (единообразную) формулу для решения квадратного уравнения (предыдущие древние решения квадратного уравнения раздвоились на пестрые случаи, потому что они имели чтобы избежать работы с еще не понятыми отрицательными или «мнимыми» или «иррациональными» числами).
Тем не менее, когда у нас есть такие числа, решение квадратного уравнения становится детской игрой, используя простую алгебру, завершая квадрат. Особого внимания к такой алгебре заслуживает тот факт, что используемые арифметические законы (коммутативные, ассоциативные и дистрибутивные законы) верны для все типов задействованных чисел (т.
е. все они коммутативных колец ). Из-за постоянства этих законов, даже если мы можем обходиться дробями, «иррациональными» и «мнимыми» числами, любые результаты, которые мы выводим о «натуральных» целых числах, остаются верными. Это одна из основных причин, по которой мы хотим сохранить эти законы, когда расширяем наши системы счисления. Это позволяет нам давать «универсальные» доказательства, работающие в любом из этих колец. Кроме того, проблемы могут упроститься при переходе к удлинительным кольцам, например. нелинейные задачи могут сводиться к линейным задачам в алгебраических кольцах расширений.
В старые времена (доаксиоматический метод) ограничение сохранения законов арифметики при расширении наших систем счисления иногда называли принципом постоянства, приписываемым Ганкелю или Пикоку. В настоящее время, когда доступен аксиоматический метод, мы просто выражаем его на этом языке, например, мы хотим, чтобы рациональные, квадратичные и комплексные числа были коммутативными кольцами расширений кольца целых чисел.
{\large =\,0}+\color{#0a0}{-a}\, =\, \color{#0a0}{-a} $ $
Это доказательство Закона Знаков использует хорошо известные законы положительных целых чисел (особенно закон распределения ), поэтому, если мы потребуем, чтобы эти законы сохранялись в большей системе положительных целых и отрицательных целых чисел, тогда Закон Знаков является логическим следствием этих основных законов натуральных чисел.
Эти фундаментальные законы «чисел» аксиоматизированы алгебраической структурой, известной как кольцо, и различными ее специализациями. Поскольку приведенное выше доказательство использует только кольцевых законов (в первую очередь распределительный закон ), Закон Знаков действует в каждом кольце, т.е. кольца полиномов, степенные ряды, матрицы, дифференциальные операторы и т. д. На самом деле каждая нетривиальная кольцевая теорема (т. е. та, которая не вырождается в теорему о лежащей в основе аддитивной группе или мультипликативном моноиде) должна использовать дистрибутивный закон, поскольку это единственный закон, который связывает аддитивную и мультипликативную структуры, которые в совокупности образуют кольцевую структуру.
Без дистрибутивного закона кольцо вырождается в множество с двумя совершенно не связанными между собой аддитивной и мультипликативной структурами. Итак, в каком-то смысле распределительный закон — это keystone кольцевой структуры.
2 быстрых шага для умножения отрицательных чисел
Home / 7th Class / 2 быстрых шага для умножения отрицательных чисел
Вот как умножать отрицательные числа умноженный. Возможно, вам придется умножать отрицательные числа на положительное число или умножать отрицательное число на другое отрицательное число. При умножении отрицательных чисел вы можете следовать простой схеме, чтобы получить ответ. Отрицательное, умноженное на положительное, дает отрицательное число. Отрицательное, умноженное на отрицательное, дает положительное число. Вы также можете подсчитать количество отрицательных чисел в выражении. Если общее количество отрицательных чисел четно, то ваш ответ будет положительным. Если общее количество отрицательных чисел нечетное, то ваш ответ будет отрицательным.
Стандарт общего ядра: 7.ns.1
Связанные темы: Добавление отрицательных чисел, вычитание отрицательных чисел, деление отрицательных чисел, порядок работы
Возврат к: , 7 -й класс
Как можно умножить отрицательное число на положительное?
Умножение отрицательных чисел — это математические задачи, связанные с умножением отрицательных чисел. Проблемы могут иметь отрицательное время положительное или отрицательное время отрицательное. Отрицательное число, умноженное на положительное число, дает отрицательное число. Отрицательное число, умноженное на отрицательное число, дает положительное число.
- Когда вы умножаете отрицательное число на положительное, ответ будет равен отрицательному числу.
- Если умножить отрицательное число на отрицательное, ответ будет равен положительному числу.
Посмотрите наше бесплатное видео о том, как умножать отрицательные числа . В этом видео показано, как решить проблемы, описанные в нашей бесплатной рабочей таблице «Умножение отрицательных чисел», которую вы можете получить, отправив свое электронное письмо выше.
Посмотрите бесплатное видео «Умножение отрицательных чисел» на YouTube здесь: Как умножить отрицательные числа. Вы можете получить рабочий лист, использованный в этом видео, бесплатно, нажав на ссылку в описании ниже.
При умножении отрицательных чисел нужно помнить два важных правила. Первое правило заключается в том, что если вы умножаете два числа с одинаковым знаком, ваш ответ будет положительным числом. Если вы делаете положительное, умноженное на положительное, и они имеют одинаковый знак, у обоих есть два положительных значения, которые будут равны положительному числу.
Если вы умножаете отрицательное число на другое отрицательное, чтобы они имели одинаковый знак, это также будет положительное число. Если вы умножаете два числа с противоположными знаками, то ответом будет отрицательное число. Например, вы умножаете отрицательное число на положительное, которое будет отрицательным числом, а если вы делаете положительное число, умноженное на отрицательное, это также будет равняться отрицательному числу.
Просто чтобы дать вам пару быстрых примеров, если мы сделали отрицательное 2, умноженное на отрицательное 3, оба эти числа будут отрицательными. Итак, у них одинаковый знак, потому что они оба отрицательные, а это означает, что наш ответ должен быть положительным числом. В этом случае отрицательное 2 умножить на отрицательное 3 или просто 2 умножить на 3 равно 6, и тогда мы знаем, что отрицательное число, умноженное на отрицательное, дает положительное, потому что они имеют одинаковый знак. Таким образом, ответ на это будет просто положительный 6.
Быстрый пример для противоположных знаков, если мы сделали положительные 5 раз отрицательные 4, это означает, что они имеют противоположные знаки, поэтому они разные. Это положительно, а это отрицательно, и это означает, что наш ответ должен быть отрицательным. Когда мы умножаем их вместе, мы просто умножаем числа 5 на 4, и это дает нам 20, но поскольку они являются противоположными знаками, положительное число умножается на отрицательное число, это дает нам отрицательное значение в качестве окончательного решения. Это было бы отрицательным 20.
Вот и первая задача на нашем листе умножения отрицательных чисел. Вы можете видеть, что эта задача дает нам отрицательное число, умноженное на пять. Теперь первое, что вы можете заметить, это то, что это отрицательное число, и эта пятерка тоже отрицательное число. Мы уже знаем, что два отрицательных значения, умноженное на отрицательное, равно положительному. Это потому, что они имеют один и тот же знак. Итак, все, что вам нужно сделать, это умножить один на пять, а один на пять, очевидно, будет пять, и тогда мы знаем, что наш ответ должен быть положительным, потому что отрицательное, умноженное на отрицательное, дает положительный результат.
Наше окончательное решение будет положительное пять или просто пять.
Переходя к номеру два на листе, чтобы узнать, как умножать отрицательные числа, мы получаем 1, умноженное на минус 8. Теперь у нас есть противоположные знаки, это положительное, а это 8 отрицательное. Мы уже знаем, что положительное на отрицательное противоположно, а это значит, что наш ответ должен быть отрицательным. Если они имеют разные знаки, значит, ваш ответ будет отрицательным. Неважно, положительное время отрицательное или отрицательное время положительное. В этом случае, когда вы умножаете 1 на 8, это дает вам 8, но тогда положительное значение умножается на отрицательное, поэтому ваш ответ должен быть отрицательным. Ваш ответ на это будет отрицательным 8.
Номер три на нашем рабочем листе дает нам отрицательное 4 умноженное на отрицательное 2. Опять же, это отрицательное число, умноженное на другое отрицательное число, и мы знаем, что отрицательное число, умноженное на отрицательное, будет равным положительному.