Решение матрицы правилом треугольника
Компьютеры admin 0 комментариев
Содержание
- 1 Определитель матрицы 3-го порядка: правило треугольника
- 2 Правило Саррюса
- 3 Методы разложения по элементам строки и столбца
- 4 Свойства определителя
- 5 Навигация
- 5.1 Популярные статьи
- 5.2 Облако тегов
Теперь Вам нужно перейти в свою почту и подтвердить отправку отзыва
Обработка информации о пользователях
Мы обрабатываем ваши персональные данные исключительно для:
– организации Вашего участия в мероприятиях и опросах, организованных нами и нашими партнерами;
– коммуникации с вами, когда вы обращаетесь к нам, например, для получения консультационной поддержки.
Определитель (детерминант) матрицы — некоторое число, с которым можно сопоставить любую квадратную матрицу А = ( a i j ) n × n .
|А|, ∆ , det A — символы, которыми обозначают определитель матрицы.
Способ вычисления определителя выбирают в зависимости от порядка матрицы.
Определитель матрицы 2-го порядка вычисляют по формуле:
d e t A = 1 — 2 3 1 = 1 × 1 — 3 × ( — 2 ) = 1 + 6 = 7
Определитель матрицы 3-го порядка: правило треугольника
Чтобы найти определитель матрицы 3-го порядка, необходимо одно из правил:
- правило треугольника;
- правило Саррюса.
Как найти определитель матрицы 3-го порядка по методу треугольника?
а 11 а 12 а 13 а 21 а 22 а 23 а 31 а 32 а 33 = a 11 × a 22 × a 33 + a 31 × a 12 × a 23 + a 21 × a 32 × a 13 — a 31 × a 22 × a 13 — a 21 × a 12 × a 33 — a 11 × a 23 × a 32
А = 1 3 4 0 2 1 1 5 — 1
d e t A = 1 3 4 0 2 1 1 5 — 1 = 1 × 2 × ( — 2 ) + 1 × 3 × 1 + 4 × 0 × 5 — 1 × 2 × 4 — 0 × 3 × ( — 1 ) — 5 × 1 × 1 = ( — 2 ) + 3 + 0 — 8 — 0 — 5 = — 12
Правило Саррюса
Чтобы вычислить определитель по методу Саррюса, необходимо учесть некоторые условия и выполнить следующие действия:
- дописать слева от определителя два первых столбца;
- перемножить элементы, которые расположены на главной диагонали и параллельных ей диагоналях, взяв произведения со знаком «+»;
- перемножить элементы, которые расположены на побочных диагоналях и параллельных им, взяв произведения со знаком «—».

а 11 а 12 а 13 а 21 а 22 а 23 а 31 а 32 а 33 = a 11 × a 22 × a 33 + a 31 × a 12 × a 23 + a 21 × a 32 × a 13 — a 31 × a 22 × a 13 — a 21 × a 12 × a 33 — a 11 × a 23 × a 32
А = 1 3 4 0 2 1 — 2 5 — 1 1 3 0 2 — 2 5 = 1 × 2 × ( — 1 ) + 3 × 1 × ( — 2 ) + 4 × 0 × 5 — 4 × 2 × ( — 2 ) — 1 × 1 × 5 — 3 × 0 × ( — 1 ) = — 2 — 6 + 0 + 16 — 5 — 0 = 3
Методы разложения по элементам строки и столбца
Чтобы вычислить определитель матрицу 4-го порядка, можно воспользоваться одним из 2-х способов:
- разложением по элементам строки;
- разложением по элементам столбца.
Представленные способы определяют вычисление определителя n как вычисление определителя порядка n-1 за счет представления определителя суммой произведений элементов строки (столбца) на их алгебраические дополнения.
Разложение матрицы по элементам строки:
d e t A = a i 1 × A i 1 + a i 2 × A i 2 + . . . + а i n × А i n
Разложение матрицы по элементам столбца:
d e t A = а 1 i × А 1 i + а 2 i × А 2 i + . . . + а n i × А n i
. . + а n i × А n i
Если раскладывать матрицу по элементам строки (столбца), необходимо выбирать строку (столбец), в которой(-ом) есть нули.
А = 0 1 — 1 3 2 1 0 0 — 2 4 5 1 3 2 1 0
- раскладываем по 2-ой строке:
А = 0 1 — 1 3 2 1 0 0 — 2 4 5 1 3 2 1 0 = 2 × ( — 1 ) 3 × 1 — 1 3 — 2 5 1 3 1 0 = — 2 × 1 — 1 3 4 5 1 2 1 0 + 1 × 0 — 1 3 — 2 5 1 3 1 0
- раскладываем по 4-му столбцу:
А = 0 1 — 1 3 2 1 0 0 — 2 4 5 1 3 2 1 0 = 3 × ( — 1 ) 5 × 2 1 0 — 2 4 5 3 2 1 + 1 × ( — 1 ) 7 × 0 1 — 1 2 1 0 3 2 1 = — 3 × 2 1 0 — 2 4 5 3 2 1 — 1 × 0 1 — 1 2 1 0 3 2 1
Свойства определителя
- если преобразовывать столбцы или строки незначительными действиями, то это не влияет на значение определителя;
- если поменять местами строки и столбцы, то знак поменяется на противоположный;
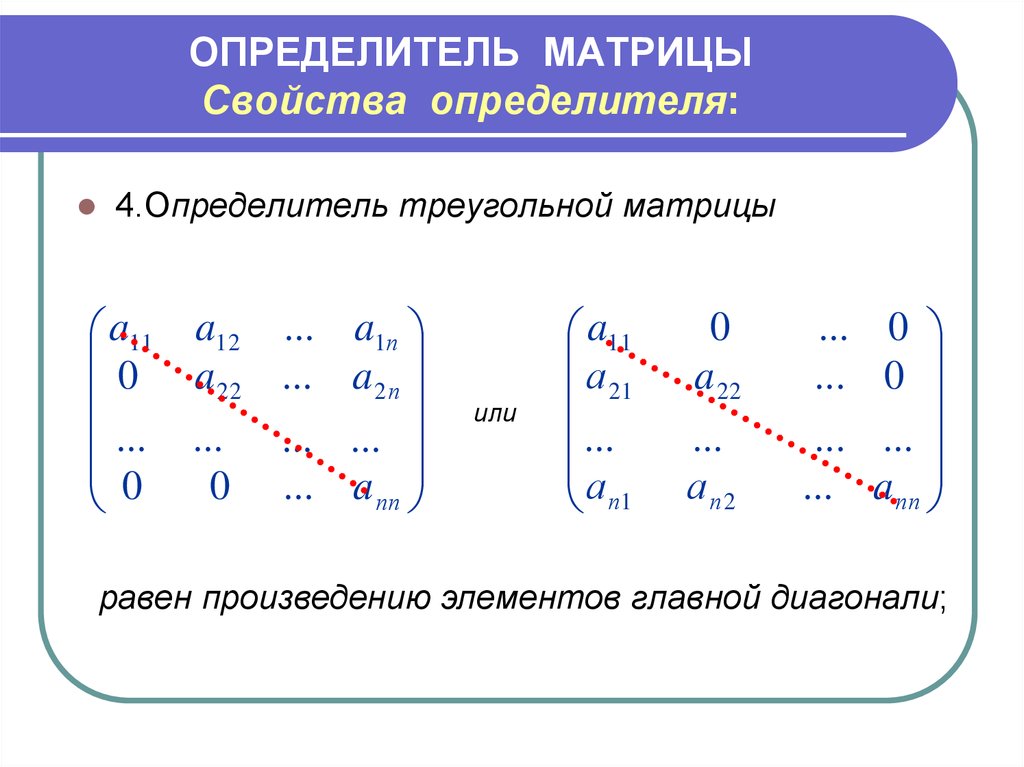
- определитель треугольной матрицы представляет собой произведение элементов, которые расположены на главной диагонали.
Пример 6
А = 1 3 4 0 2 1 0 0 5
d e t А = 1 3 4 0 2 1 0 0 5 = 1 × 5 × 2 = 10
Определитель матрицы, который содержит нулевой столбец, равняется нулю.
Навигация
Популярные статьи
Облако тегов
Найти определитель матрицы третьего порядка
Содержание статьи
1. Правило Саррюса
2. Правило треугольников
3. Использование формулы разложения по строчке
4. Метод Гаусса
Существует несколько способов нахождения определителей матриц третьего порядка. Рассмотрим их подробнее.
Рассмотрим их подробнее.
Перечислим основные способы, используемые для этого:
- Правило Саррюса;
- Правило треугольников;
- Использование специальной формулы для вычисления;
- Использование метода Гаусса или иначе метода перестановок.
Правило Саррюса
Правило Саррюса для вычисления матриц 3-ьего порядка применяется просто: достаточно соответственно рисунку переписать 2 первых столбика справа рядом с матричной таблицей, а затем записать произведения, стоящие по диагоналям со знаками.
Замечание 1
Если диагональ идёт сверху слева вниз направо — то произведение записывается со знаком «+», а если диагональ идёт из правого верхнего угла в нижний левый — то со знаком «-».
Рисунок 1. Формула третьего порядка. Автор24 — интернет-биржа студенческих работ
Пример 1
Дана матричная таблица $A$. Вычислите детерминант с помощью правила Саррюса.
$A = \begin{pmatrix} 0 & 3 & -1 \\ 1 & 4 & 2 \\ 2 & 5 & 3 \\ \end{pmatrix}$
Решение:
Рисунок 2. Вычисление определителя 3 порядка. Автор24 — интернет-биржа студенческих работ
Вычисление определителя 3 порядка. Автор24 — интернет-биржа студенческих работ
$Δ = 0 \cdot 4 \cdot 3 + 3 \cdot 2 \cdot 2 – 1 \cdot 1 \cdot 5 – 3 \cdot 1 \cdot 3 – 0 \cdot 2 \cdot 5 + 1 \cdot 4 \cdot 2 = 0 + 12 – 5 — 9 – 0 + 8 = 6$
Правило треугольников
Это правило немного похоже на предыдущее. Суть его в том, что произведения элементов с главной диагонали и двух треугольников, задействующих все остальные элементы как показано на рисунке, записываются со знаком плюс, а произведения элементов с побочной диагонали и двух синих треугольников — с противоположным.
Рисунок 3. Треугольники. Автор24 — интернет-биржа студенческих работ
Пример 2
Найдите определитель из прошлого задания, используя метод треугольников.
Решение:
Рисунок 4. Наглядный пример как пользоваться. Автор24 — интернет-биржа студенческих работ
$Δ= 0 \cdot 4 3 + 3 \cdot 2 \cdot 2 – 1 \cdot 5 \cdot 1 + 1 \cdot 4 \cdot 2 – 1 \cdot 3 \cdot 3 – 2 \cdot 5 \cdot 0 = 0 + 12 – 5 + 8 – 9 – 0 = 6$
Использование формулы разложения по строчке
$A = \begin{pmatrix} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \\ \end{pmatrix}$
Для матрицы 3 на 3, приведённой выше, определитель можно сосчитать по формуле:
$Δ =\begin{array}{|ccc|} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \\ \end{array}=a_{11} \cdot \begin{array}{|cc|} a_{22} & a_{23} \\ a_{32} & a_{33} \\ \end{array} – a_{12} \cdot \begin{array}{|cc|} a_{11} & a_{13} \\ a_{21} & a_{23} \\ a_{31} & a_{33} \\ \end{array} + a_{13} \cdot \begin{array}{|cc|} a_{11} & a_{12} \\ a_{21} & a_{22} \\ a_{31} & a_{32} \\ \end{array}= a_{11} \cdot a_{22} \cdot a_{33} – a_{12} \cdot a_{23} \cdot a_{31} + a_{13} \cdot a_{21} \cdot a_{32} — a_{13} \cdot a_{22} \cdot a_{31}$.
Пример 3
Разложите определитель матрицы из предыдущих примеров по 1-ой строчке и найдите его.
Решение:
$Δ = 0 \cdot \begin{array}{|cc|} 4 & 2 \\ 5 & 3 \\ \ \end{array} – 3 \cdot \begin{array} {|cc|} 1 & 2 \\ 2 & 3 \\ \ \end{array} + (-1) \cdot \begin{array}{|cc|} 1 & 4 \\ 2 & 5 \\ \ \end{array} = 0 – 3 \cdot (1 \cdot 3 – 2 \cdot 2) + (-1) \cdot (5 – 8) = 0 – 3 \cdot(-1) + (-1) \cdot (-3) = 3 + 3 = 6$
Метод Гаусса
Чтобы вычислить детерминант этим методом, нужно используя разрешённые преобразования получить треугольную матрицу.
Разрешёнными преобразованиями являются сложение и вычитание строчек и столбцов, в то время как при перестановке строчек и столбцов между собой необходимо помнить о смене знака определителя в конце.
После этого нужно перемножить элементы, стоящие на главной диагонали, их произведение и будет определителем.
Пример 4
Примените метод Гаусса для получения детерминанта матрицы из предыдущих примеров.
Решение:
$A = \begin{pmatrix} 0 & 3 & -1 \\ 1 & 4 & 2 \\ 2 & 5 & 3 \\ \end{pmatrix}$
Переставим первую строчку со второй, при этом запомним, что знак детерминанта в конце поменяется:
$\begin{pmatrix} 1 & 4 & 2 \\ 0 & 3 & -1 \\ 2 & 5 & 3 \\ \end{pmatrix}$;
Вычтем из третьей строчки 1-ую, умноженную на 2:
$\begin{pmatrix} 1 & 4 & 2 \\ 0 & 3 & -1 \\ 0 & -3 & -1 \\ \end{pmatrix}$;
Сложим между собой третью строчку со второй:
$\begin{pmatrix} 1 & 4 & 2 \\ 0 & 3 & -1 \\ 0 & 0 & -2 \\ \end{pmatrix}$;
Получили искомый вид матрицы. Теперь можно сосчитать определитель, минус появляется из-за перемены строчек местами:
$Δ=-\begin{pmatrix} 1 & 4 & 2 \\ 0 & 3 & -1 \\ 0 & 0 & -2 \\ \end{pmatrix}= -(1 \cdot 3 \cdot ( — 2) ) = 6 $
Сообщество экспертов Автор24
Автор этой статьи
Дата последнего обновления статьи: 07. 05.2022
05.2022
Нахождение определителя матрицы методом треугольника
Методы вычисления определителей
В общем случае правило вычисления определителей $n$-го порядка является довольно громоздким. Для определителей второго и третьего порядка существуют рациональные способы их вычислений.
Вычисления определителей второго порядка
Чтобы вычислить определитель матрицы
второго порядка, надо от произведения элементов главной диагонали отнять произведение элементов побочной диагонали:
Задание. Вычислить определитель второго порядка $left| begin& \ & endright|$
Решение. $left| begin& \ & endright|=11 cdot 5-(-2) cdot 7=55+14=69$
Методы вычисления определителей третьего порядка
Для вычисления определителей третьего порядка существует такие правила.
Правило треугольника
Схематически это правило можно изобразить следующим образом:
Произведение элементов в первом определителе, которые соединены прямыми, берется со знаком “плюс”; аналогично, для второго определителя – соответствующие произведения берутся со знаком “минус”, т. е.
е.
Задание. Вычислить определитель $left| begin& & \ & & \ & & endright|$ методом треугольников.
Решение. $left| begin& & \ & & \ & & endright|=3 cdot 1 cdot(-2)+4 cdot(-2) cdot(-1)+$
$$+3 cdot 3 cdot 1-(-1) cdot 1 cdot 1-3 cdot(-2) cdot 3-4 cdot 3 cdot(-2)=54$$
Правило Саррюса
Справа от определителя дописывают первых два столбца и произведения элементов на главной диагонали и на диагоналях, ей параллельных, берут со знаком “плюс”; а произведения элементов побочной диагонали и диагоналей, ей параллельных, со знаком “минус”:
Задание. Вычислить определитель $left| begin& & \ & & \ & & endright|$ с помощью правила Саррюса.
Решение.
$$+(-1) cdot 4 cdot(-2)-(-1) cdot 1 cdot 1-3 cdot 3 cdot(-2)-3 cdot 4 cdot(-2)=54$$
Разложение определителя по строке или столбцу
Определитель равен сумме произведений элементов строки определителя на их алгебраические дополнения. Обычно выбирают ту строку/столбец, в которой/ом есть нули. Строку или столбец, по которой/ому ведется разложение, будет обозначать стрелкой.
Обычно выбирают ту строку/столбец, в которой/ом есть нули. Строку или столбец, по которой/ому ведется разложение, будет обозначать стрелкой.
Задание. Разложив по первой строке, вычислить определитель $left| begin& & \ & & \ & & endright|$
Решение. $left| begin& & \ & & \ & & endright| leftarrow=a_ cdot A_+a_ cdot A_+a_ cdot A_=$
Этот метод позволяет вычисление определителя свести к вычислению определителя более низкого порядка.
Задание. Вычислить определитель $left| begin& & \ & & \ & & endright|$
Решение. Выполним следующие преобразования над строками определителя: из второй строки отнимем четыре первых, а из третьей первую строку, умноженную на семь, в результате, согласно свойствам определителя, получим определитель, равный данному.
Определитель равен нулю, так как вторая и третья строки являются пропорциональными.
Для вычисления определителей четвертого порядка и выше применяется либо разложение по строке/столбцу, либо приведение к треугольному виду, либо с помощью теоремы Лапласа.
Разложение определителя по элементам строки или столбца
Задание. Вычислить определитель $left| begin& & & \ & & & \ & & & \ & & & endright|$ , разложив его по элементам какой-то строки или какого-то столбца.
Решение. Предварительно выполним элементарные преобразования над строками определителя, сделав как можно больше нулей либо в строке, либо в столбце. Для этого вначале от первой строки отнимем девять третьих, от второй – пять третьих и от четвертой – три третьих строки, получаем:
Полученный определитель разложим по элементам первого столбца:
Полученный определитель третьего порядка также разложим по элементам строки и столбца, предварительно получив нули, например, в первом столбце. Для этого от первой строки отнимаем две вторые строки, а от третьей – вторую:
$$=4 cdot(2 cdot 8-4 cdot 4)=0$$
Замечание
Последний и предпоследний определители можно было бы и не вычислять, а сразу сделать вывод о том, что они равны нулю, так как содержат пропорциональные строки.
Приведение определителя к треугольному виду
С помощью элементарных преобразований над строками или столбцами определитель приводится к треугольному виду и тогда его значение, согласно свойствам определителя, равно произведению элементов стоящих на главной диагонали.
Задание. Вычислить определитель $Delta=left| begin& & & \ & & & \ & & & \ & & & endright|$ приведением его к треугольному виду.
Решение. Сначала делаем нули в первом столбце под главной диагональю. Все преобразования будет выполнять проще, если элемент $a_$ будет равен 1. Для этого мы поменяем местами первый и второй столбцы определителя, что, согласно свойствам определителя, приведет к тому, что он сменит знак на противоположный:
Далее получим нули в первом столбце, кроме элемента $a_$ , для этого из третьей строки вычтем две первых, а к четвертой строке прибавим первую, будем иметь:
Далее получаем нули во втором столбце на месте элементов, стоящих под главной диагональю. И снова, если диагональный элемент будет равен $pm 1$ , то вычисления будут более простыми. Для этого меняем местами вторую и третью строки (и при этом меняется на противоположный знак определителя):
И снова, если диагональный элемент будет равен $pm 1$ , то вычисления будут более простыми. Для этого меняем местами вторую и третью строки (и при этом меняется на противоположный знак определителя):
Далее делаем нули во втором столбце под главной диагональю, для этого поступаем следующим образом: к третьей строке прибавляем три вторых, а к четвертой – две вторых строки, получаем:
Далее из третьей строки выносим (-10) за определитель и делаем нули в третьем столбце под главной диагональю, а для этого к последней строке прибавляем третью:
Ответ. $Delta=-80$
Теорема Лапласа
Пусть $Delta$ – определитель $n$-го порядка. Выберем в нем произвольные $k$ строк (или столбцов), причем $k leq n-1$ . Тогда сумма произведений всех миноров $k$-го порядка, которые содержатся в выбранных $k$ строках (столбцах), на их алгебраические дополнения равна определителю.
Задание. Используя теорему Лапласа, вычислить определитель $left| begin& & & & \ & & & & \ & & & & \ & & & & \ & & & & endright|$
Решение. Выберем в данном определителе пятого порядка две строки – вторую и третью, тогда получаем (слагаемые, которые равны нулю, опускаем):
Выберем в данном определителе пятого порядка две строки – вторую и третью, тогда получаем (слагаемые, которые равны нулю, опускаем):
В ходе решения задач по высшей математике очень часто возникает необходимость вычислить определитель матрицы. Определитель матрицы фигурирует в линейной алгебре, аналитической геометрии, математическом анализе и других разделах высшей математики. Таким образом, без навыка решения определителей просто не обойтись. Также для самопроверки Вы можете бесплатно скачать калькулятор определителей, он сам по себе не научит решать определители, но очень удобен, поскольку всегда выгодно заранее знать правильный ответ!
Я не буду давать строгое математическое определение определителя, и, вообще, буду стараться минимизировать математическую терминологию, большинству читателей легче от этого не станет. Задача данной статьи – научить Вас решать определители второго, третьего и четвертого порядка. Весь материал изложен в простой и доступной форме, и даже полный (пустой) чайник в высшей математике после внимательного изучения материала сможет правильно решать определители.
Весь материал изложен в простой и доступной форме, и даже полный (пустой) чайник в высшей математике после внимательного изучения материала сможет правильно решать определители.
Определитель можно вычислить только для квадратной матрицы (более подробно см. Действия с матрицами)
На практике чаще всего можно встретить определитель второго порядка, например:
, и определитель третьего порядка, например: .
Определитель четвертого порядка
тоже не антиквариат, и к нему мы подойдём в конце урока.
Надеюсь, всем понятно следующее: Числа внутри определителя живут сами по себе, и ни о каком вычитании речи не идет! Менять местами числа нельзя!
(Как частность, можно осуществлять парные перестановки строк или столбцов определителя со сменой его знака, но часто в этом нет никакой необходимости – см. следующий урок Свойства определителя и понижение его порядка)
Таким образом, если дан какой-либо определитель, то ничего внутри него не трогаем!
Обозначения: Если дана матрица
, то ее определитель обозначают .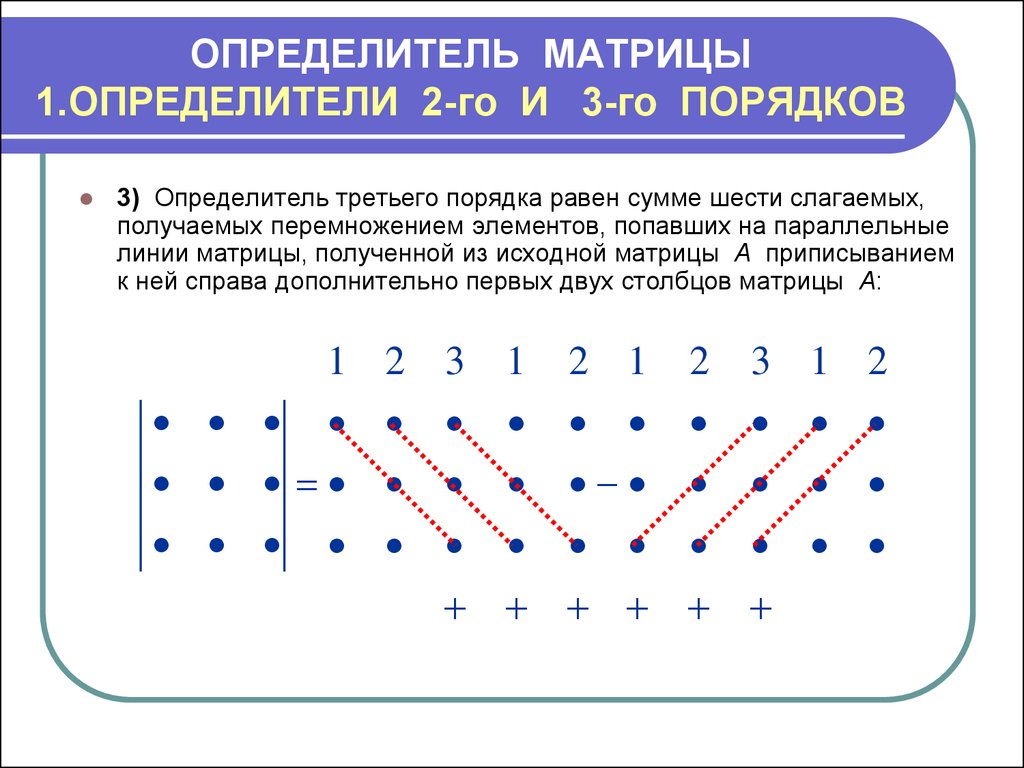 Также очень часто определитель обозначают латинской буквой или греческой .
Также очень часто определитель обозначают латинской буквой или греческой .
1) Что значит решить (найти, раскрыть) определитель? Вычислить определитель – это значит НАЙТИ ЧИСЛО. Знаки вопроса
в вышерассмотренных примерах – это совершенно обыкновенные числа.
2) Теперь осталось разобраться в том, КАК найти это число? Для этого нужно применить определенные правила, формулы и алгоритмы, о чём сейчас и пойдет речь.
Начнем с определителя «два» на «два»:
ЭТО НУЖНО ЗАПОМНИТЬ, по крайне мере на время изучения высшей математики в ВУЗе.
Сразу рассмотрим пример:
Готово. Самое главное, НЕ ЗАПУТАТЬСЯ В ЗНАКАХ.
Определитель матрицы «три на три» можно раскрыть 8 способами, 2 из них простые и 6 – нормальные.
Начнем с двух простых способов
Аналогично определителю «два на два», определитель «три на три» можно раскрыть с помощью формулы:
Формула длинная и допустить ошибку по невнимательности проще простого. Как избежать досадных промахов? Для этого придуман второй способ вычисления определителя, который фактически совпадает с первым. Называется он способом Саррюса или способом «параллельных полосок».
Как избежать досадных промахов? Для этого придуман второй способ вычисления определителя, который фактически совпадает с первым. Называется он способом Саррюса или способом «параллельных полосок».
Суть состоит в том, что справа от определителя приписывают первый и второй столбец и аккуратно карандашом проводят линии:
Множители, находящиеся на «красных» диагоналях входят в формулу со знаком «плюс».
Множители, находящиеся на «синих» диагоналях входят в формулу со знаком минус:
Сравните два решения. Нетрудно заметить, что это ОДНО И ТО ЖЕ, просто во втором случае немного переставлены множители формулы, и, самое главное, вероятность допустить ошибку значительно меньше.
Теперь рассмотрим шесть нормальных способов для вычисления определителя
Почему нормальных? Потому что в подавляющем большинстве случаев определители требуется раскрывать именно так.
Как Вы заметили, у определителя «три на три» три столбца и три строки.
Решить определитель можно, раскрыв его по любой строке или по любому столбцу.
Таким образом, получается 6 способов, при этом во всех случаях используется однотипный алгоритм.
Определитель матрицы равен сумме произведений элементов строки (столбца) на соответствующие алгебраические дополнения. Страшно? Все намного проще, будем использовать ненаучный, но понятный подход, доступный даже для человека, далекого от математики.
В следующем примере будем раскрывать определитель по первой строке.
Для этого нам понадобится матрица знаков:
. Легко заметить, что знаки расположены в шахматном порядке.
Внимание! Матрица знаков – это мое собственное изобретение. Данное понятие не научное, его не нужно использовать в чистовом оформлении заданий, оно лишь помогает Вам понять алгоритм вычисления определителя.
Сначала я приведу полное решение. Снова берем наш подопытный определитель и проводим вычисления:
И главный вопрос: КАК из определителя «три на три» получить вот это вот:
?
Итак, определитель «три на три» сводится к решению трёх маленьких определителей, или как их еще называют, МИНОРОВ. Термин рекомендую запомнить, тем более, он запоминающийся: минор – маленький.
Термин рекомендую запомнить, тем более, он запоминающийся: минор – маленький.
Коль скоро выбран способ разложения определителя по первой строке, очевидно, что всё вращается вокруг неё:
Элементы обычно рассматривают слева направо (или сверху вниз, если был бы выбран столбец)
Поехали, сначала разбираемся с первым элементом строки, то есть с единицей:
1) Из матрицы знаков выписываем соответствующий знак:
2) Затем записываем сам элемент:
3) МЫСЛЕННО вычеркиваем строку и столбец, в котором стоит первый элемент:
Оставшиеся четыре числа и образуют определитель «два на два», который называется МИНОРОМ данного элемента (единицы).
Переходим ко второму элементу строки.
4) Из матрицы знаков выписываем соответствующий знак:
5) Затем записываем второй элемент:
6) МЫСЛЕННО вычеркиваем строку и столбец, в котором стоит второй элемент:
Оставшиеся четыре числа записываем в маленький определитель.
Ну и третий элемент первой строки. Никакой оригинальности:
7) Из матрицы знаков выписываем соответствующий знак:
8) Записываем третий элемент:
9) МЫСЛЕННО вычеркиваем строку и столбец, в котором стоит третий элемент:
Оставшиеся четыре числа записываем в маленький определитель.
Остальные действия не представляют трудностей, поскольку определители «два на два» мы считать уже умеем. НЕ ПУТАЕМСЯ В ЗНАКАХ!
Аналогично определитель можно разложить по любой строке или по любому столбцу. Естественно, во всех шести случаях ответ получается одинаковым.
Определитель «четыре на четыре» можно вычислить, используя этот же алгоритм.
При этом матрица знаков у нас увеличится:
В следующем примере я раскрыл определитель по четвертому столбцу:
А как это получилось, попробуйте разобраться самостоятельно. Дополнительная информация будет позже. Если кто захочет прорешать определитель до конца, правильный ответ: 18. Для тренировки лучше раскрыть определитель по какому-нибудь другому столбцу или другой строке.
Для тренировки лучше раскрыть определитель по какому-нибудь другому столбцу или другой строке.
Потренироваться, раскрыть, провести расчёты – это очень хорошо и полезно. Но сколько времени вы потратите на большой определитель? Нельзя ли как-нибудь быстрее и надёжнее? Предлагаю ознакомиться с эффективными методами вычисления определителей на втором уроке – Свойства определителя. Понижение порядка определителя.
Автор: Емелин Александр
(Переход на главную страницу)
Профессиональная помощь по любому предмету – Zaochnik.com
Вычисление определителя методом сведения к треугольному виду.
Метод сведения определителя к треугольному виду использует те же преобразования, что и метод эффективного понижения порядка. Только при вычислении определителя методом эффективного понижения порядка мы постепенно уменьшаем порядок определителя, а для метода сведения к треугольному виду порядок определителя остаётся неизменным до конца процесса решения. Суть метода сведения к треугольному виду такова: с помощью действий со строками (или столбцами) преобразовать определитель к виду, когда все элементы, лежащие ниже (или выше) главной диагонали равны нулю. Т.е. после преобразований определитель должен принять одну из двух форм (элементы на главной диагонали выделены синим цветом):
Суть метода сведения к треугольному виду такова: с помощью действий со строками (или столбцами) преобразовать определитель к виду, когда все элементы, лежащие ниже (или выше) главной диагонали равны нулю. Т.е. после преобразований определитель должен принять одну из двух форм (элементы на главной диагонали выделены синим цветом):
Хотя разницы и нет, обычно приводят к первому случаю, когда нули расположены под главной диагональю. После преобразований определитель вычисляется простым умножением элементов, расположенных на главной диагонали. Для того, чтобы обнулить требуемые элементы и вычислить определитель, нам пригодятся несколько свойств определителей, которые указаны в теме “Некоторые свойства определителей”. Я запишу ниже несколько свойств, которые нам пригодятся при решении. В примечании после каждого свойства будет указан пример его применения.
- Если поменять местами две строки (столбца) определителя, то знак определителя изменится на противоположный.
Пример применения этого свойства: показатьскрыть
Рассмотрим определитель $left| begin 2 & 5 \ 9 & 4 end right|$. Найдём его значение, используя формулу №1 из темы вычисления определителей второго и третьего порядков:
Найдём его значение, используя формулу №1 из темы вычисления определителей второго и третьего порядков:
$$left| begin 2 & 5 \ 9 & 4 end right|=2cdot 4-5cdot 9=-37.$$
Теперь поменяем местами первую и вторую строки. Получим определитель $left| begin 9 & 4 \ 2 & 5 end right|$. Вычислим полученный определитель: $left| begin 9 & 4 \ 2 & 5 end right|=9cdot 5-4cdot 2=37$. Итак, значение исходного определителя равнялось (-37), а у определителя с изменённым порядком строк значение равно $-(-37)=37$. Знак определителя изменился на противоположный.
Пример применения этого свойства: показатьскрыть
Рассмотрим определитель $left| begin -7 & 10 & 0\ -9 & 21 & 4 \ 2 & -3 & 1 end right|$. Прибавим к элементам второй строки соответствующие элементы третьей строки, умноженные на 5. Записывают это действие так: $r_2+5cdot$. Вторая строка будет изменена, остальные строки останутся без изменений.
$$ left| begin -7 & 10 & 0\ -9 & 21 & 4 \ 2 & -3 & 1 end right| begin phantom\ r_2+5cdot\ phantom end= left| begin -7 & 10 & 0\ -9+5cdot 2 & 21+5cdot (-3) & 4+5cdot 1 \ 2 & -3 & 1 end right|= left| begin -7 & 10 & 0\ 1 & 6 & 9 \ 2 & -3 & 1 end right|. $$
$$
Пример применения этого свойства: показатьскрыть
Рассмотрим определитель $left| begin -7 & 10 \ -9 & 21 end right|$. Заметьте, что все элементы второй строки делятся на 3:
$$left| begin -7 & 10 \ -9 & 21 end right|=left| begin -7 & 10 \ 3cdot(-3) & 3cdot 7 end right|$$
Число 3 и есть общий множитель всех элементов второй строки. Вынесем тройку за знак определителя:
$$ left| begin -7 & 10 \ -9 & 21 end right|=left| begin -7 & 10 \ 3cdot(-3) & 3cdot 7 end right|= 3cdot left| begin -7 & 10 \ -3 & 7 end right| $$
Пример применения этого свойства: показатьскрыть
Буквами $r$ (от слова “row”) станем обозначать строки: $r_1$ – первая строка, $r_2$ – вторая строка и так далее. Буквами $c$ (от слова “column”) станем обозначать столбцы: $c_1$ – первый столбец, $c_2$ – второй столбец и так далее.
Найти определитель $Delta = left|begin -8 & 2 & 9 & 17\ -3 & 1 & 2 & 6\ 13 & -3 & -7 & -26\ 11 & 1 & 23 & 6endright|$.
В принципе, начинать решение можно и не преобразовывая определитель. Однако очень удобно, когда первым элементом первой строки является единица (ну, или (-1) на крайний случай). Единицы есть во втором столбце нашего определителя. Сделаем так, чтобы второй столбец стал первым. Для этого просто поменяем местами первый и второй столбцы, используя свойство (1). Не забываем, что при смене мест двух столбцов перед определителем появится знак “минус”:
$$Delta = left|begin -8 & 2 & 9 & 17\ -3 & 1 & 2 & 6\ 13 & -3 & -7 & -26\ 11 & 1 & 23 & 6endright|=-left|begin 2 & -8 & 9 & 17\ 1 & -3 & 2 & 6\ -3 & 13 & -7 & -26\ 1 & 11 & 23 & 6endright|.$$
Итак, столбцы поменяли, однако единица покамест не вышла на первое место в первой строке, – но это дело поправимое. Поменяем местами первую и вторую строки, при этом перед определителем вновь возникнет знак “минус”. Ну, а так как “минус” на “минус” даёт “плюс”, то получим мы следующее:
$$Delta =-left|begin 2 & -8 & 9 & 17\ 1 & -3 & 2 & 6\ -3 & 13 & -7 & -26\ 1 & 11 & 23 & 6endright|=-left( -left|begin 1 & -3 & 2 & 6\ 2 & -8 & 9 & 17\ -3 & 13 & -7 & -26\ 1 & 11 & 23 & 6endright|right)= left|begin 1 & -3 & 2 & 6\ 2 & -8 & 9 & 17\ -3 & 13 & -7 & -26\ 1 & 11 & 23 & 6endright|. $$
$$
Начнём решение. Нам нужно получить нули под главной диагональю. Для этого придётся осуществить несколько шагов, на которых будем изменять строки нашего определителя. На первом шаге мы должны сделать так, чтобы все элементы первого столбца стали нулями – кроме элемента на главной диагонали, выделенного красным цветом:
$$ left|begin boldred & -3 & 2 & 6\ normgreen & -8 & 9 & 17\ normblue & 13 & -7 & -26\ normpurple & 11 & 23 & 6endright| $$
Преобразования со строками, которые нужно выполнить, чтобы обнулить “серые” элементы, получаются так:
Запись $r_2-2r_1$ означает, что от элементов второй строки вычли соответствующие элементы первой строки, умноженные на два. Полученный результат записали вместо прежней второй строки. Остальные записи расшифровываются аналогично. Согласно свойству (2) значение определителя от таких действий не изменится. Для наглядности я запишу это действие отдельно:
После выполнения всех требуемых операций со строками, мы получим новый определитель. Записывается это так:
Записывается это так:
$$ Delta=left|begin 1 & -3 & 2 & 6\ 2 & -8 & 9 & 17\ -3 & 13 & -7 & -26\ 1 & 11 & 23 & 6endright| begin phantom \ r_2-2r_1 \ r_3+3r_1 \ r_4-r_1 end= left|begin 1 & -3 & 2 & 6\ 0 & -2 & 5 & 5\ 0 & 4 & -1 & -8 \ 0 & 14 & 21 & 0endright|. $$
Перед тем, как мы пойдём дальше, обратим внимание на то, что все элементы четвёртой строки делятся на 7. Согласно свойству (3) число 7 можно вынести за знак определителя:
$$ left|begin 1 & -3 & 2 & 6\ 0 & -2 & 5 & 5\ 0 & 4 & -1 & -8 \ 0 & 14 & 21 & 0endright|=7cdot left|begin 1 & -3 & 2 & 6\ 0 & -2 & 5 & 5\ 0 & 4 & -1 & -8 \ 0 & 2 & 3 & 0endright| $$
Теперь нам нужно обнулить элементы во втором столбце (под главной диагональю). Т.е., обнулению подлежат элементы, выделенные зелёным и синим цветом. Элемент на главной диагонали, который останется без изменений, выделен красным цветом:
$$ left|begin 1 & -3 & 2 & 6\ 0 & boldred & 5 & 5\ 0 & normblue & -1 & -8 \ 0 & normblue & 3 & 0endright| $$
А если бы вместо числа -2 возник ноль? показатьскрыть
Если бы вместо числа -2 получился ноль, мы бы поменяли местами строки или столбцы. Например, вот так:
Например, вот так:
$$ left|begin 1 & -3 & 2 & 6\ 0 & 0 & 5 & 5\ 0 & 4 & -1 & -8 \ 0 & 2 & 3 & 0endright| =[r_2leftrightarrow] =-left|begin 1 & -3 & 2 & 6\ 0 & 2 & 3 & 0\ 0 & 4 & -1 & -8 \ 0 & 0 & 5 & 5 endright| $$
Или же может возникнуть иная ситуация: когда обнулятся все элементы во втором столбце под первой строкой. Вот так:
$$ left|begin 1 & -3 & 2 & 6\ 0 & 0 & 5 & 5\ 0 & 0 & -1 & -8 \ 0 & 0 & 3 & 0endright| $$
В этом случае имеем пропорциональность столбцов, т.е. $c_2=-3c_1$, а это означает, что определитель равен 0.
В принципе, мы можем получить (-1) на месте диагонального “красного элемента”. Для этого достаточно поменять местами второй и третий столбцы, а затем поменять местами вторую и третью строки. Однако в нашем случае этого можно и не делать, так как все “синие элементы” нацело делятся на “красный элемент”, т. е. на (-2). Следовательно, никакой работы с дробями не предвидится. Впрочем, тут дело вкуса: можете попробовать для тренировки продолжить решение, поменяв местами строки и столбцы, чтобы “красным элементом” стала (-1). Выполним такие операции со строками:
е. на (-2). Следовательно, никакой работы с дробями не предвидится. Впрочем, тут дело вкуса: можете попробовать для тренировки продолжить решение, поменяв местами строки и столбцы, чтобы “красным элементом” стала (-1). Выполним такие операции со строками:
Отдельно выписывать действия со строками не станем, так как они полностью аналогичны рассмотренным ранее. Наш определитель станет таким:
$$ Delta=7cdot left|begin 1 & -3 & 2 & 6\ 0 & -2 & 5 & 5\ 0 & 4 & -1 & -8 \ 0 & 2 & 3 & 0endright| begin phantom \ phantom \ r_3+2r_2 \ r_4+r_2end= 7cdot left|begin 1 & -3 & 2 & 6\ 0 & -2 & 5 & 5\ 0 & 0 & 9 & 2 \ 0 & 0 & 8 & 5endright|. $$
Осталось последнее действие. Нужно обнулить элемент 8 под главной диагональю:
$$ left|begin 1 & -3 & 2 & 6\ 0 & -2 & 5 & 5\ 0 & 0 & 9 & 2 \ 0 & 0 & boldred & 5endright| $$
Тут уже придется поработать с дробями. Обычно такой работы стараются избегать – и до этого момента нам это удавалось – но теперь уже деваться некуда:
Обычно такой работы стараются избегать – и до этого момента нам это удавалось – но теперь уже деваться некуда:
$$ Delta = 7cdot left|begin 1 & -3 & 2 & 6\ 0 & -2 & 5 & 5\ 0 & 0 & 9 & 2 \ 0 & 0 & 8 & 5endright| begin phantom \ phantom \ phantom \ r_4-fracr_3 end= 7cdot left|begin 1 & -3 & 2 & 6\ 0 & -2 & 5 & 5\ 0 & 0 & 9 & 2 \ 0 & 0 & 0 & fracendright|. $$
Преобразования окончены. Осталось лишь использовать свойство (4) и переменожить элементы, расположенные на главной диагонали:
$$ Delta=7cdot 1cdot (-2)cdot 9 cdot frac=-406. $$
Ответ получен. Полное решение без пояснений выглядит так:
$$ Delta = left|begin -8 & 2 & 9 & 17\ -3 & 1 & 2 & 6\ 13 & -3 & -7 & -26\ 11 & 1 & 23 & 6endright| =[c_1leftrightarrow] =left|begin 2 & -8 & 9 & 17\ 1 & -3 & 2 & 6\ -3 & 13 & -7 & -26\ 1 & 11 & 23 & 6endright| =[r_1leftrightarrow]=\ =left|begin 1 & -3 & 2 & 6\ 2 & -8 & 9 & 17\ -3 & 13 & -7 & -26\ 1 & 11 & 23 & 6endright| begin phantom \ r_2-2r_1 \ r_3+3r_1 \ r_4-r_1 end= 7cdot left|begin 1 & -3 & 2 & 6\ 0 & -2 & 5 & 5\ 0 & 4 & -1 & -8 \ 0 & 2 & 3 & 0endright| begin phantom \ phantom \ r_3+2r_2 \ r_4+r_2 end=\ =7cdot left|begin 1 & -3 & 2 & 6\ 0 & -2 & 5 & 5\ 0 & 0 & 9 & 2 \ 0 & 0 & 8 & 5endright| begin phantom \ phantom \ phantom \ r_4-fracr_3end =7cdot left|begin 1 & -3 & 2 & 6\ 0 & -2 & 5 & 5\ 0 & 0 & 9 & 2 \ 0 & 0 & 0 & fracendright| =7cdot 1cdot (-2)cdot 9 cdot frac=-406. $$
$$
В принципе, преобразования метода сведения к треугольному виду просты, однако стоит иметь в виду свойства определителей, изложенные соответствующей теме. Например, на каком-то шаге может обнулиться строка или столбец, или же окажется, что некие строки или столбцы пропорциональны. Это будет означать, что рассматриваемый определитель равен 0.
Решение матриц.
Решение матриц – это понятие, которое обобщает все возможные операции, производимые с матрицами. Математическая матрица – таблица элементов. О такой таблице, где m строк и n столбцов, говорят, что это матрица имеет размерность m на n.
Общий вид матрицы:
Для решения матриц необходимо понимать, что такое матрица и знать основные ее параметры. Основные элементы матрицы:
Основные виды матриц:
- Квадратная – такая матрица, где число строк = числу столбцов (m=n).
- Нулевая – где все элементы матрицы = 0.

- Транспонированная матрица — матрица В, которая была получена из исходной матрицы A путем замены строк на столбцы.
- Единичная – все элементы главной диагонали = 1, все остальные = 0.
- Обратная матрица — матрица, при умножении на которую исходная матрица даёт в результате единичную матрицу.
Матрица может быть симметричной относительно главной и побочной диагонали. Т.е., если а12=а21, а13=а31,….а23=а32…. аm-1n=аmn-1, то матрица симметрична относительно главной диагонали. Симметричными могут быть лишь квадратные матрицы.
Далее приведем основные методы решения матриц.
Методы решения матриц.
Почти все методы решения матрицы заключаются в нахождении ее определителя n-го порядка и большинство из них довольно громоздки. Чтобы найти определитель 2го и 3го порядка есть другие, более рациональные способы.
Нахождение определителей 2-го порядка.
Для вычисления определителя матрицы А 2го порядка, необходимо из произведения элементов главной диагонали вычесть произведение элементов побочной диагонали:
Методы нахождения определителей 3го порядка.
Ниже приведены правила для нахождения определителя 3го порядка.
Правило треугольника при решении матриц.
Упрощенно правило треугольника, как одного из методов решения матриц, можно изобразить таким образом:
Другими словами, произведение элементов в первом определителе, которые соединены прямыми, берется со знаком “+”; так же, для 2го определителя – соответствующие произведения берутся со знаком “-“, то есть по такой схеме:
Правило Саррюса при решении матриц.
При решении матриц правилом Саррюса, справа от определителя дописывают первые 2 столбца и произведения соответствующих элементов на главной диагонали и на диагоналях, которые ей параллельны, берут со знаком “+”; а произведения соответствующих элементов побочной диагонали и диагоналей, которые ей параллельны, со знаком “-“:
Разложение определителя по строке или столбцу при решении матриц.
Определитель равен сумме произведений элементов строки определителя на их алгебраические дополнения. Обычно выбирают ту строку/столбец, в которой/ом есть нули. Строку либо столбец, по которой/ому ведется разложение, будут обозначать стрелкой.
Приведение определителя к треугольному виду при решении матриц.
При решении матриц методом приведения определителя к треугольному виду, работают так: с помощью простейших преобразований над строками либо столбцами, определитель становится треугольного вида и тогда его значение, в соответствии со свойствами определителя, будет равно произведению элементов, которые стоят на главной диагонали.
Теорема Лапласа при решении матриц.
Решая матрицы по теореме Лапласа, необходимо знать непосредственно саму теорему. Теорема Лапласа: Пусть Δ – это определитель n-го порядка. Выбираем в нем любые k строк (либо столбцов), при условии k ≤ n – 1. В таком случае сумма произведений всех миноров k-го порядка, содержащихся в выбранных k строках (столбцах), на их алгебраические дополнения будет равна определителю.
Решение обратной матрицы.
Последовательность действий для решения обратной матрицы:
- Понять, квадратная ли данная матрица. В случае отрицательного ответа становится ясно, что обратной матрицы для нее не может быть.
- Понять, квадратная ли данная матрица. В случае отрицательного ответа становится ясно, что обратной матрицы для нее не может быть.
- Вычисляем алгебраические дополнения.
- Составляем союзную (взаимную, присоединённую) матрицу C.
- Составляем обратную матрицу из алгебраических дополнений: все элементы присоединённой матрицы C делим на определитель начальной матрицы. Итоговая матрица будет искомой обратной матрицей относительно заданной.
- Проверяем выполненную работу: умножаем матрицу начальную и полученную матрицы, результатом должна стать единичная матрица.
Решение систем матриц.
Для решения систем матриц наиболее часто используют метод Гаусса.
Метод Гаусса — это стандартный способ решения систем линейных алгебраических уравнений (СЛАУ) и он заключается в том, что последовательно исключаются переменные, т.е., при помощи элементарных изменений систему уравнений доводят до эквивалентной системы треугольного вида и из нее, последовательно, начиная с последних (по номеру), находят каждый элемент системы.
Метод Гаусса является самым универсальным и лучшим инструментом для нахождения решения матриц. Если у системы бесконечное множество решений или система является несовместимой, то ее нельзя решать по правилу Крамера и матричным методом.
Метод Гаусса подразумевает также прямой (приведение расширенной матрицы к ступенчатому виду, т.е. получение нулей под главной диагональю) и обратный (получение нулей над главной диагональю расширенной матрицы) ходы. Прямой ход и есть метод Гаусса, обратный – метод Гаусса-Жордана. Метод Гаусса-Жордана отличается от метода Гаусса лишь последовательностью исключения переменных.
Пример
При \(n=5\) проблема может выглядеть следующим образом:
$$\begin{pmatrix} 2 и 7 и 1 и 8 и 2\\ 0 и 8 и 1 и 8 и 2\\ 0 и 0 и 8 и 4 и 5\\ 0 и 0 и 0 и 9 и 0\\ 0 и 0 и 0 и 0 и 4 \end{pmatrix} \cdot \begin{pmatrix} x_1 \\ x_2 \\ x_3 \\ x_4 \\ x_5 \end{pmatrix} = \begin{pmatrix} 3 \\ 1 \\ 4 \\ 1 \\ 5 \end{pmatrix}$$
Это всего лишь сокращение для:
\begin{align} 2 \cdot x_1 + 7 \cdot x_2 + 1 \cdot x_3 + 8 \cdot x_4 + 2 \cdot x_5 &= 3\\ 8 \cdot x_2 + 1 \cdot x_3 + 8 \cdot x_4 + 2 \cdot x_5 &= 1\\ 8 \cdot x_3 + 4 \cdot x_4 + 5 \cdot x_5 &= 4\\ 9 \cdot x_4 + 0 \cdot x_5 &= 1\\ 4 \cdot x_5 &= 5 \end{align}
Первый шаг: найти $x_5$
Сначала вы видите, что \(x_5 = \frac{5}{4}\). Итак, вы делите \(b\) на текущую строку.
Не делить на 0. Когда вам нужно делить на 0, а b равно 0, эта система имеет бесконечное количество решений. Если вам придется делить на 0, а b не равно 0, то эта система не имеет решения.
Когда вам нужно делить на 0, а b равно 0, эта система имеет бесконечное количество решений. Если вам придется делить на 0, а b не равно 0, то эта система не имеет решения.
Теперь вы замените каждое вхождение \(x_5\) в приведенной выше системе уравнений:
\begin{align} 2 \cdot x_1 + 7 \cdot x_2 + 1 \cdot x_3 + 8 \cdot x_4 + 2 \cdot \frac{5}{4} &= 3\\ 8 \cdot x_2 + 1 \cdot x_3 + 8 \cdot x_4 + 2 \cdot \frac{5}{4} &= 1\\ 8 \cdot x_3 + 4 \cdot x_4 + 5 \cdot \frac{5}{4} &= 4\\ 9\cdot x_4 + 0 \cdot \frac{5}{4} &= 1\\ 4 \cdot \frac{5}{4} &= 5 \end{align}
Теперь вы делаете умножения и удаляете первую тривиальную строку.
\начать{выравнивание} 2 \cdot x_1 + 7 \cdot x_2 + 1 \cdot x_3 + 8 \cdot x_4 + \frac{5}{2} &= 3\\ 8 \cdot x_2 + 1 \cdot x_3 + 8 \cdot x_4 + \frac{5}{2} &= 1\\ 8 \cdot x_3 + 4 \cdot x_4 + \frac{25}{4} &= 4\\ 9\cdot x_4 + 0 &= 1\\ \end{align}
Второй шаг: обновление
Получение постоянных множителей в правой части уравнений:
\begin{align} 2 \cdot x_1 + 7 \cdot x_2 + 1 \cdot x_3 + 8 \cdot x_4 &= \frac{1}{2} \\ 8 \cdot x_2 + 1 \cdot x_3 + 8 \cdot x_4 &= -\frac{3}{2} \\ 8 \cdot x_3 + 4 \cdot x_4 &= -\frac{9}{4}\\ 9 \cdot x_4 &= 1\\ \end{align}
Теперь вы находитесь в той же ситуации, что и на первом шаге. Далее вы будете решать для \(x_4\), затем для \(x_3, x_2\) и, наконец, для \(x_1\).
Далее вы будете решать для \(x_4\), затем для \(x_3, x_2\) и, наконец, для \(x_1\).
Это называется «обратная замена».
Согласно Wolfram|Alpha, решение таково:
$$x = \frac{1}{4608} \cdot \begin{pmatrix}4017\\-1182\\-1552\\512\\5760\end {пматрица} = \begin{pmatrix}\frac{1339}{1536} \\ -\frac{197}{768} \\ -\frac{97}{288} \\ \frac{1}{9} \\ \frac{ 5}{4}\end{pmatrix}$$
Прямой алгоритм Python
Я буду использовать дроби для операций, так как не хочу терять точность при делении.
#!/usr/bin/env Python
# -*- кодировка: utf-8 -*-
defsolveUpperTriangularMatrix(R,b):
# Преобразование R и b в дробь
из дробей импорт дроби
fR, fb = [], []
для x, строка в enumerate(R):
fЛиния = []
для y, el в перечислении (строке):
fLine.append (Дробь (эл))
fR.append(fLine)
для эль в b:
fb.append (Дробь (эл))
# Решение будет здесь
х = [Дробь (0)] * длина (б)
для шага в диапазоне (len(b) - 1, 0 - 1, -1):
если fR[шаг][шаг] == 0:
если fb[шаг] != 0:
вернуть "Нет решения"
еще:
вернуть "Бесконечные решения"
еще:
x[шаг] = fb[шаг] / fR[шаг][шаг]
для строки в диапазоне (шаг - 1, 0 - 1, -1):
fb[строка] -= fR[строка][шаг] * x[шаг]
вернуть х
если __name__ == "__main__":
Р = [
[2, 7, 1, 8, 2],
[0, 8, 1, 8, 2],
[0, 0, 8, 4, 5],
[0, 0, 0, 9, 0],
[0, 0, 0, 0, 4],
]
б = [3, 1, 4, 1, 5]
x = решитьВерхнюю треугольную матрицу (R, b)
печать (х)
# Преобразование x в число с плавающей запятой
х = карта (с плавающей запятой, х)
печать (х)
Улучшенный алгоритм
Как и в случае с унипотентными нижними треугольными матрицами, мы можем работать непосредственно с данным вводом:
#!/usr/bin/env python
# -*- кодировка: utf-8 -*-
defsolveUpperTriangularMatrix(R,b):
# Преобразование R и b в дробь
из дробей импорт дроби
для x, строка в enumerate(R):
для y, el в перечислении (строке):
R[x][y] = Дробь (el)
для x, el в перечислении (b):
b[x] = дробь (el)
# Решение будет здесь
для шага в диапазоне (len(b) - 1, 0 - 1, -1):
если R[шаг][шаг] == 0:
если б[шаг] != 0:
вернуть "Нет решения"
еще:
вернуть "Бесконечные решения"
еще:
b[шаг] = b[шаг] / R[шаг][шаг]
для строки в диапазоне (шаг - 1, 0 - 1, -1):
b[строка] -= R[строка][шаг] * b[шаг]
если __name__ == "__main__":
Р = [
[2, 7, 1, 8, 2],
[0, 8, 1, 8, 2],
[0, 0, 8, 4, 5],
[0, 0, 0, 9, 0],
[0, 0, 0, 0, 4],
]
б = [3, 1, 4, 1, 5]
решитьверхнюю треугольную матрицу (R, b)
печать (б)
Преобразование в дробь
Можно подумать, что преобразование в дробь не обязательно. Но если просто удалить строку с 5 по 16, то получится:
Но если просто удалить строку с 5 по 16, то получится:
[1, 0, -1, 0, 1]
из-за целочисленной арифметики. Когда вы конвертируете ввод в число с плавающей запятой до
передав его в solveUpperTriangularMatrix , вы получите
[0,8717447916666666, -0,25651041666666663, -0,33680555555555556, 0,1111111111111111, 1,25]. 92)\).Пространственная сложность
Обратите внимание, что я пользуюсь системой динамической типизации Python. Я думаю, что трудно увидеть космическую сложность в программах на Python. Но когда вы сделаете то же самое на C++, вы увидите, что вам понадобится место в \(\mathcal{O}(n)\) при преобразовании. Без преобразования вы находитесь в \(\mathcal{O}(1)\).
Думаю, вы можете оставить этот выбор пользователю ваших функций. Когда ему нужны лучшие результаты, он должен вводить данные в виде дроби. Когда он хочет получить результаты быстрее, он должен указать ввод как число с плавающей запятой.
Примечания
В этом алгоритме нам ничего не нужно ниже диагонали.
Включите JavaScript для просмотра комментариев с помощью Disqus.
Линейные системы — основы численных вычислений
Обратимся теперь к центральной проблеме этой главы: даны квадратная матрица \(n\x n\) \(\mathbf{A}\) и \(n\ )-вектор \(\mathbf{b}\), найдите \(n\)-вектор \(\mathbf{x}\) такой, что \(\mathbf{A}\mathbf{x}=\mathbf{b }\). Записав эти уравнения, получим 9{-1}\mathbf{A}) \mathbf{x} = \mathbf{I} \mathbf{x} = \mathbf{х}. \end{split}\]
Если \(\mathbf{A}\) сингулярно, то \(\mathbf{A}\mathbf{x}=\mathbf{b}\) может не иметь решения или бесконечно много решений.
Пример 10
Если мы определим
\[\begin{split}\mathbf{S} = \begin{bmatrix} 0 и 1\\0 и 0 \end{bmatrix},\end{split}\]
, то легко проверить, что для любого действительного значения \(\alpha\) мы имеем
\[\begin{split}\mathbf{S} \begin{bmatrix} \альфа\1 \end{bmatrix} знак равно \begin{bmatrix} 1\0 \end{bmatrix}.\end{split}\]
Следовательно, линейная система \(\mathbf{S}\mathbf{x}=\mathbf{b}\) с \(\mathbf{b}=\begin{bmatrix} 1\\0\end{bmatrix}\ ) имеет бесконечно много решений.
Можно доказать, что для многих других вариантов \(\mathbf{b}\) система не имеет решений.
Не используйте обратную
Обратные матрицы необходимы для математических дискуссий и выводов. Однако, как вы помните из курса линейной алгебры, их не так просто вычислить из элементов исходной матрицы. Хотя это можно сделать численно с помощью компьютера, это почти никогда не делается, потому что, когда цель состоит в том, чтобы решить линейную систему уравнений, обратная не нужна — и процесс ее нахождения медленнее, чем решение исходной задачи.
У Джулии есть команда inv, которая находит обратную матрицу. Но, как показано в разделе Интерполяция населения Китая, для решения линейной системы уравнений следует использовать обратную косую черту (символ
\, не путать с косой чертой/, используемой в веб-адресах).Треугольные системы
Процесс решения особенно легко продемонстрировать для системы с треугольной матрицей. Например, рассмотрим нижнюю треугольную систему
\[\begin{split} \begin{bmatrix} 4 и 0 и 0 и 0 \\ 3 и -1 и 0 и 0 \\ -1 и 0 и 3 и 0 \\ 1 и -1 и -1 и 2 \end{bmatrix} \mathbf{x} = \begin{bmatrix} 8\5\0\1 \end{bmatrix}.
\end{split}\]
В первой строке этой системы просто указано, что \(4x_1=8\), что легко решается как \(x_1=8/4=2\). Теперь во второй строке указано, что \(3x_1-x_2=5\). Поскольку \(x_1\) уже известно, его можно заменить, чтобы найти, что \(x_2 = -(5-3\cdot 2)=1\). Точно так же третья строка дает \(x_3=(0+1\cdot 2)/3 = 2/3\), а последняя строка дает \(x_4=(1-1\cdot 2 + 1\cdot 1 + 1). \cdot 2/3)/2 = 1/3\). Следовательно, решение
\[\begin{split} \mathbf{x} = \begin{bmatrix} 2 \\ 1 \\ 2/3 \\ 1/3 \end{bmatrix}.\end{split}\]
Только что описанный процесс называется прямой заменой. В \(4\times 4\) нижнем треугольном случае \(\mathbf{L}\mathbf{x}=\mathbf{b}\) это приводит к формулам
(27)\[\begin{split }\начать{разделить} x_1 &= \frac{b_1}{L_{11}} \\ x_2 &= \frac{b_2 - L_{21}x_1}{L_{22}} \\ x_3 &= \frac{b_3 - L_{31}x_1 - L_{32}x_2}{L_{33}} \\ x_4 &= \frac{b_4 - L_{41}x_1 - L_{42}x_2 - L_{43}x_3}{L_{44}}. \end{split}:label: forwardsub\end{split}\]
Для верхних треугольных систем \(\mathbf{U}\mathbf{x}=\mathbf{b}\) аналогичный процесс обратной замены начинается с решения для последнего компонента \(x_n=b_n/U_{nn}\ ) и работает в обратном порядке.
Для случая \(4\times 4\) имеем
\[\begin{split} \begin{bmatrix} U_{11} и U_{12} и U_{13} и U_{14} \\ 0 и U_{22} и U_{23} и U_{24} \\ 0 и 0 и U_{33} и U_{34} \\ 0 и 0 и 0 и U_{44} \end{bmatrix} \mathbf{x} = \begin{bmatrix} б_1\б_2\б_3\б_4 \end{bmatrix}.\end{split}\]
Решение системы в обратном порядке, начиная с \(x_4\) и далее в порядке убывания, дает
\[\begin{split}\begin{split} x_4 &= \frac{b_4}{U_{44}} \\ x_3 &= \frac{b_3 - U_{34}x_4}{U_{33}} \\ x_2 &= \frac{b_2 - U_{23}x_3 - U_{24}x_4}{U_{22}} \\ x_1 &= \frac{b_1 - U_{12}x_2 - U_{13}x_3 - U_{14}x_4}{U_{11}}. \end{split}\end{split}\]
Должно быть ясно, что прямая или обратная замена невозможна тогда и только тогда, когда один из диагональных элементов матрицы системы равен нулю. Мы по существу доказали следующую теорему.
Теорема 11 (Треугольная особенность)
Треугольная матрица является особой тогда и только тогда, когда хотя бы один из ее диагональных элементов равен нулю.

Реализация
Рассмотрим, как реализовать последовательный процесс, подразумеваемый уравнением (27). Кажется очевидным, что мы хотим пройтись по элементам \(\mathbf{x}\) по порядку. В каждой итерации этого цикла у нас есть выражение, длина которого зависит от номера итерации. Один из способов сделать это — использовать вложенный цикл:
для i = 1:4 с = 0 для j = 1:i-1 s += L[i,j]*x[j] конец х[я] = (б[я]-с) / L[я,я] конецБолее короткая версия внутреннего цикла по
jпредставляет собой пониманиеs = sum( L[i,j]*x[j] for j=1:i-1 )Однако, когда
iравно 1, диапазон1:i-1пуст, и суммирование не выполняется. Чтобы избежать этого, мы можем обработать этот случай до того, как начнется циклi, и начать этот цикл с 2. Такой подход используется в функции 12.Функция 12 (forwardsub)
Прямая замена для решения линейной системы нижнего треугольника
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 | """ впередсаб(L,b) Решите нижнетреугольную линейную систему с матрицей `L` и правый вектор `b`. |
Реализация обратной замены очень похожа на прямую замену и описана в функции 13.
Функция 13 (backsub)
Обратная замена для решения верхнетреугольной линейной системы
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 | """
задний саб(U,b)
Решите верхнетреугольную линейную систему с матрицей `U` и
правый вектор `b`.
"""
функция backsub(U,b)
n = размер (U, 1)
х = нули (п)
х[n] = b[n]/U[n,n]
для i = n-1:-1:1
s = сумма (U[i,j]*x[j] для j=i+1:n)
х[i] = (b[i] - s) / U[i,i]
конец
вернуть х
конец
|
Пример из раздела «Решение треугольных систем» — это наш первый ключ к пониманию того, что задачи линейных систем могут иметь большие числа обусловленности, что делает неточные решения неизбежными в арифметике с плавающей запятой. Позже в этой главе мы научимся обнаруживать такие проблемы. Однако прежде чем достичь этого, нам нужно обсудить, как решать общие линейные системы, а не только треугольные.
Позже в этой главе мы научимся обнаруживать такие проблемы. Однако прежде чем достичь этого, нам нужно обсудить, как решать общие линейные системы, а не только треугольные.
Упражнения
✍ Найдите правый вектор \(\mathbf{b}\) такой, что система \(\begin{bmatrix} 0&1\\0&0 \end{bmatrix} \mathbf{x}= \mathbf{b}\) не имеет решения.
✍ Решите следующие треугольные системы вручную.
(а) \(\displaystyle \begin{выровнено} -2x_1 &= -4 \\ х_1 - х_2 &= 2 \\ 3x_1 + 2x_2 + x_3 &= 1 \end{выровнено} \qquad\) (б) \(\displaystyle \begin{bmatrix} 4 и 0 и 0 и 0 \\ 1 и -2 и 0 и 0 \\ -1 и 4 и 4 и 0 \\ 2 и -5 и 5 и 1 \end{bmatrix} \mathbf{x} = \begin{bmatrix} -4\1\-3\5 \end{bmatrix}\qquad\) (с) \(\displaystyle \begin{выровнено} 3x_1 + 2x_2 + x_3 &= 1 \\ х_2 - х_3 &= 2 \\ 2 х_3 &= -4 \конец{выровнено}\)
⌨ Используйте forwardsub для решения систем из предыдущей задачи.
 Убедитесь, что решение правильное, вычислив \(\mathbf{L}\mathbf{x}\) и вычитая \(\mathbf{b}\).
Убедитесь, что решение правильное, вычислив \(\mathbf{L}\mathbf{x}\) и вычитая \(\mathbf{b}\).⌨ Используйте backsub для решения следующих систем. Убедитесь, что решение правильное, вычислив \(\mathbf{U}\mathbf{x}\) и вычитая \(\mathbf{b}\).
(а) \(\displaystyle \begin{bmatrix} 3 и 1 и 0 \\ 0 и -1 и -2 \\ 0 и 0 и 3 \\ \end{bmatrix} \mathbf{x} = \begin{bmatrix} 1\1\6 \end{bmatrix}\qquad\) (б) \(\displaystyle \begin{bmatrix} 3 и 1 и 0 и 6 \\ 0 и -1 и -2 и 7 \\ 0 и 0 и 3 и 4 \\ 0 и 0 и 0 и 5 \end{bmatrix} \mathbf{x} = \begin{bmatrix} 4\1\1\5 \end{bmatrix}\)
9{n \times p}\), имеет столбцы \(\mathbf{b}_1,\ldots,\mathbf{b}_p\), то мы можем сразу представить \(p\) линейные системы, написав \(\ mathbf{A} \mathbf{X} = \mathbf{B}\), где \(\mathbf{X}\) равно \(n\times p\). В частности, это уравнение подразумевает \(\mathbf{A} \mathbf{x}_j = \mathbf{b}_j\) для \(j=1,\ldots,p\).⌨ Решение треугольных систем показало решения \(\mathbf{A}\mathbf{x}=\mathbf{b}\), где
\[\begin{split}\mathbf{A} = \begin{bmatrix} 1 & -1 & 0 & \alpha-\beta & \beta \\ 0 & 1 & -1 & 0 & 0 \\ 0 & 0 & 1 & -1 & 0 \\ 0 & 0 & 0 & 1 & -1 \\ 0 & 0 & 0 & 0 & 1 \end{bmatrix}, \quad \mathbf{b} = \begin{bmatrix} \alpha \\ 0 \\ 0 \\ 0 \\ 1 \end{bmatrix}.\end{split}\] 9{12}\), составив таблицу значений \(\beta\) и \(|x_1-1|\).
(a) Измените forwardsub и backsub так, чтобы они решали случай, когда второй ввод равен \(n\x p\) для \(p\ge 1\). {-1}\). Используйте этот факт, чтобы написать функцию
{-1}\). Используйте этот факт, чтобы написать функцию linverse , который использует ваш модифицированный forwardsub для вычисления обратной нижней треугольной матрицы. Проверьте свою функцию как минимум на двух нетривиальных матрицах. (Напоминаем вам, что это всего лишь упражнение; обратные матрицы редко бывают хорошей идеей в числовой практике!)
Треугольная матрица — нижняя и верхняя треугольная матрица, примеры
LearnPracticeDownload
Треугольная матрица — это квадратная матрица, в которой все элементы ниже и/или выше диагонали равны нулю. У нас есть в основном два типа треугольных матриц.
У нас есть в основном два типа треугольных матриц.
- Квадратная матрица, все элементы которой выше главной диагонали равны нулю, называется нижней треугольной матрицей .
- Квадратная матрица, все элементы которой ниже главной диагонали равны нулю, называется верхней треугольной матрицей .
В этой статье давайте рассмотрим различные типы треугольных матриц, включая верхнюю треугольную матрицу и нижнюю треугольную матрицу, их определения и свойства. Мы также решим несколько примеров на основе треугольной матрицы для лучшего понимания концепции.
| 1. | Что такое треугольная матрица? |
| 2. | Типы треугольных матриц |
| 3. | Верхняя треугольная матрица |
| 4. | Нижняя треугольная матрица |
| 5. | Свойства треугольной матрицы |
6. | Часто задаваемые вопросы о треугольной матрице |
Что такое треугольная матрица?
Треугольная матрица — это особый вид квадратной матрицы в наборе матриц. Существует два типа треугольных матриц: нижняя треугольная матрица и верхняя треугольная матрица.
- Квадратная матрица называется нижней треугольной матрицей, если все элементы над ее главной диагональю равны нулю.
- Квадратная матрица называется верхней треугольной матрицей, если все элементы ниже главной диагонали равны нулю.
Ниже приведен пример треугольной матрицы:
\(A = \left[\begin{array}{ccc} 2 & -1 & 3 \\ 0 & 5 & 2\\ 0 & 0 & -2 \end{array}\right]\) (верхний треугольник)
\(B = \left[\begin{array}{ccc} 2 & 0 & 0 \\ 1 & 5 & 0 \\ 1 & -1 & -2 \end{массив}\right]\) (нижний треугольник)
Типы треугольных матриц
Мы изучаем различные типы треугольных матриц. Ниже приведен список некоторых специальных типов треугольных матриц:
- Верхнетреугольная матрица: треугольная матрица называется верхнетреугольной, если все элементы ниже главной диагонали равны нулю.

- Нижняя треугольная матрица: треугольная матрица называется нижней треугольной матрицей, если все элементы выше главной диагонали равны нулю.
- Строго треугольная матрица: треугольная матрица называется строго треугольной, если все элементы главной диагонали равны нулю.
- Строго нижняя треугольная матрица: Нижняя треугольная матрица называется строго нижней треугольной матрицей, если все элементы главной диагонали равны нулю.
- Строго верхнетреугольная матрица: Верхняя треугольная матрица называется строго верхнетреугольной матрицей, если все элементы главной диагонали равны нулю.
- Единичная треугольная матрица: говорят, что треугольная матрица является единичной треугольной матрицей, если все элементы главной диагонали равны 1.
- Единичная нижняя треугольная матрица: нижняя треугольная матрица называется единичной нижней треугольной матрицей, если все элементы главной диагонали равны 1.
- Единичная верхняя треугольная матрица: говорят, что верхняя треугольная матрица является единичной верхней треугольной матрицей, если все элементы главной диагонали равны 1.

В следующих разделах мы в основном исследуем два типа треугольных матриц, а именно верхнюю и нижнюю треугольные матрицы.
Верхняя треугольная матрица
Квадратная матрица размера n × n A = [a ij ] называется верхней треугольной матрицей размера тогда и только тогда, когда a ij = 0 для всех i > j. Это означает, что все элементы ниже главной диагонали квадратной матрицы равны нулю в верхней треугольной матрице. Общее обозначение верхней треугольной матрицы: U = [u ij для i ≤ j, 0 для i > j]. Пример верхней треугольной матрицы приведен ниже:
\(U = \left[\begin{array}{ccc} 6 & 0 & 8 \\ 0 & 10 & -12\\ 0 & 0 & 2 \end {массив}\справа]\)
Нижняя треугольная матрица
Квадратная матрица размера n × n A = [a ij ] называется нижней треугольной матрицей тогда и только тогда, когда a ij = 0 для всех i < j. Это означает, что все элементы выше главной диагонали квадратной матрицы равны нулю в нижней треугольной матрице.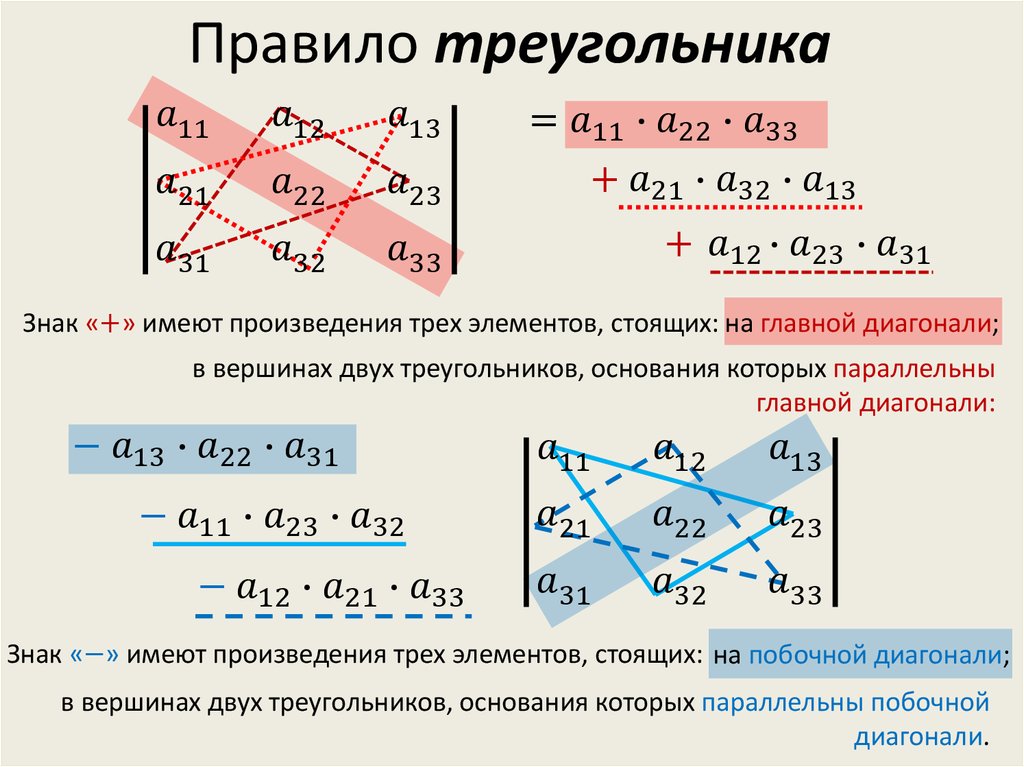 Общее обозначение нижней треугольной матрицы: L = [l ij для i ≥ j, 0 для i < j]. Ниже приведен пример нижней треугольной матрицы:
Общее обозначение нижней треугольной матрицы: L = [l ij для i ≥ j, 0 для i < j]. Ниже приведен пример нижней треугольной матрицы:
\(L = \left[\begin{array}{ccc} -1 & 0 & 0 \\ 0 & -8 & 0 \\ 3 & -4 & 2 \конец{массив}\справа]\)
Свойства треугольной матрицы
Поскольку мы поняли смысл треугольной матрицы, давайте рассмотрим некоторые ее важные свойства. Ниже приведен список свойств треугольной матрицы:
- Транспонирование треугольной матрицы треугольное.
- Транспонирование нижней треугольной матрицы равно n верхней треугольной матрице и наоборот.
- Произведение двух треугольных матриц есть треугольная матрица.
- Треугольная матрица обратима тогда и только тогда, когда все элементы главной диагонали отличны от нуля.
- Произведение двух нижних (верхних) треугольных матриц есть нижняя (верхняя) треугольная матрица.
- Обратная треугольная матрица является треугольной.
- Определитель треугольной матрицы является произведением элементов главной диагонали.

Важные замечания о треугольной матрице
- Обратимая матрица может быть записана как произведение нижней треугольной и верхней треугольной матриц тогда и только тогда, когда ее старшие главные миноры отличны от нуля. Это также известно как разложение LU.
- В матрице есть как верхняя, так и нижняя треугольная, тогда она называется диагональной матрицей.
Темы, связанные с треугольной матрицей
- Калькулятор матриц
- Формула матрицы
Примеры треугольной матрицы
Пример 1: Определите, является ли данная матрица треугольной. Также определите его тип.
\(A = \left[\begin{array}{ccc} -1 & 0 \\ \\ 9& -8 \end{array}\right]\)
Решение:
Элемент над диагональю равен 12 = 0, а под диагональю равен 21 = 9.
Следовательно, данная матрица является нижней треугольной матрицей, так как элемент выше главной диагонали равен нулю.

Ответ: Следовательно, матрица A является нижней треугольной матрицей.
Пример 2: Найдите значения 'a' и 'b' в заданной матрице B такие, что B является строго верхней треугольной матрицей.
\(B = \left[\begin{array}{ccc} 2a & 3 \\ \\ b & 0 \end{array}\right]\)
Решение:
Предположим, что B строго верхняя треугольная матрица, элементы ниже диагонали равны нулю, а элементы главной диагонали равны нулю.
Следовательно, мы должны иметь 2a = 0 и b = 0.
Теперь 2a = 0 ⇒ a = 0
Ответ: Следовательно, a = 0 и b = 0.
Пример 3: Найдите определитель матрицы A = \(\left[\begin{array}{ccc}
2&0&0\
0&а&0\
1 и 4 и б
\end{массив}\right]\).Решение:
Данная матрица является треугольной матрицей (нижней), так как все ее элементы выше диагонали равны нулю.

Следовательно, его определитель есть произведение диагональных элементов.
Итак, det A = (2)(a)(b) = 2ab.
Ответ: 2аб.
перейти к слайдуперейти к слайдуперейти к слайду
Есть вопросы по основным математическим понятиям?
Станьте чемпионом по решению проблем, используя логику, а не правила. Узнайте, почему математика стоит за нашими сертифицированными экспертами.
Часто задаваемые вопросы о треугольной матрице
Что такое треугольная матрица в линейной алгебре?
Треугольная матрица — это особый тип квадратной матрицы в линейной алгебре, элементы которой ниже и выше диагонали имеют форму треугольника. Элементы выше и/или ниже главной диагонали треугольной матрицы равны нулю.
Каковы свойства треугольной матрицы?
Некоторые из важных свойств треугольных матриц:
- Транспонирование треугольной матрицы является треугольным.

- Произведение двух треугольных матриц есть треугольная матрица.
- Определитель треугольной матрицы равен произведению элементов главной диагонали.
Как называется матрица, если она одновременно и верхняя, и нижняя треугольная?
Если матрица одновременно нижнетреугольная и верхнетреугольная, то все ее недиагональные элементы равны нулю. В этом случае она называется диагональной матрицей.
Когда треугольная матрица обратима?
Треугольная матрица (нижняя или верхняя) обратима тогда и только тогда, когда все элементы главной диагонали отличны от нуля.
Что такое верхняя треугольная матрица?
Квадратная матрица размера n × n A = [a ij ] называется верхнетреугольной матрицей тогда и только тогда, когда a ij = 0 для всех i > j. Это означает, что все элементы ниже главной диагонали квадратной матрицы равны нулю в верхней треугольной матрице.
Что такое обратная нижняя треугольная матрица?
Обратная нижняя треугольная матрица также является нижней треугольной матрицей.


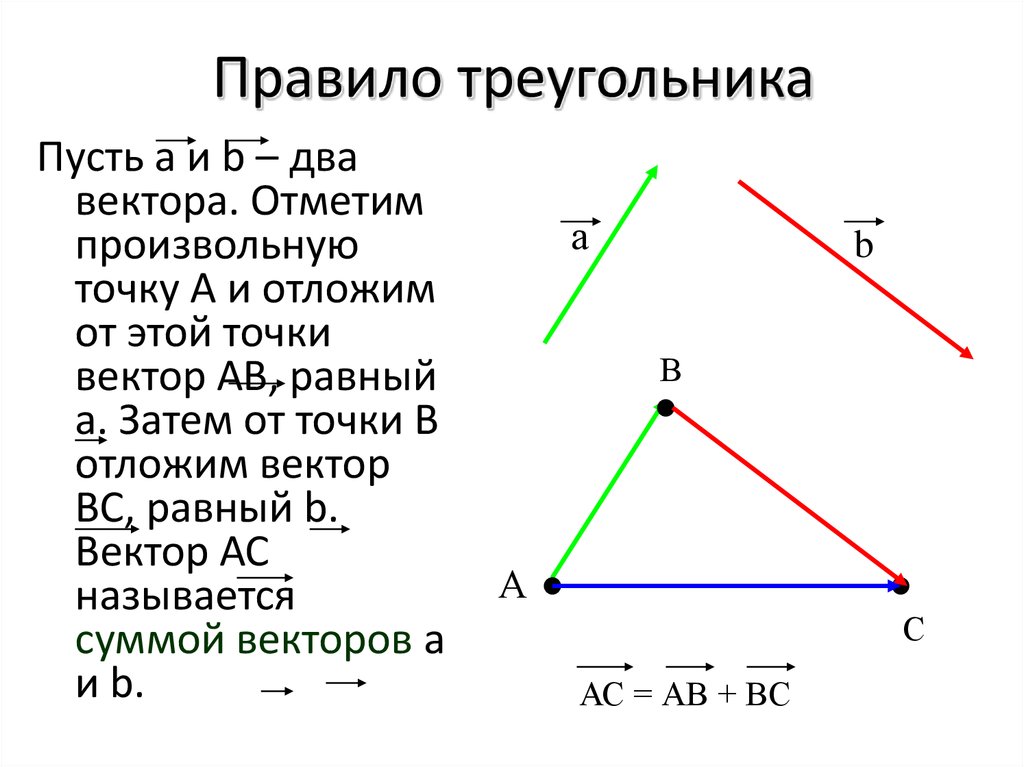

 Можно доказать, что для многих других вариантов \(\mathbf{b}\) система не имеет решений.
Можно доказать, что для многих других вариантов \(\mathbf{b}\) система не имеет решений.  \end{split}\]
\end{split}\]  Для случая \(4\times 4\) имеем
Для случая \(4\times 4\) имеем 
 """
функция forwardsub(L,b)
n = размер (L, 1)
х = нули (п)
х[1] = б[1]/L[1,1]
для я = 2: п
s = сумма (L[i,j]*x[j] для j=1:i-1)
x[i] = (b[i] - s) / L[i,i]
конец
вернуть х
конец
"""
функция forwardsub(L,b)
n = размер (L, 1)
х = нули (п)
х[1] = б[1]/L[1,1]
для я = 2: п
s = сумма (L[i,j]*x[j] для j=1:i-1)
x[i] = (b[i] - s) / L[i,i]
конец
вернуть х
конец
 Убедитесь, что решение правильное, вычислив \(\mathbf{L}\mathbf{x}\) и вычитая \(\mathbf{b}\).
Убедитесь, что решение правильное, вычислив \(\mathbf{L}\mathbf{x}\) и вычитая \(\mathbf{b}\).