Как решить систему линейных уравнений методом Гаусса: принцип, пример
Sign in
Password recovery
Восстановите свой пароль
Ваш адрес электронной почты
MicroExcel.ru Математика Алгебра Метод Гаусса для решения СЛАУ
В данной публикации мы рассмотрим, что такое метод Гаусса, зачем он нужен, и в чем заключается его принцип. Также мы на практическом примере продемонстрируем, как метод можно применить для решения системы линейных уравнений.
- Описание метода Гаусса
- Принцип метода Гаусса
- Пример решения СЛАУ
Описание метода Гаусса
Метод Гаусса – классический способ последовательного исключения переменных, применяемый для решения системы линейных уравнений. Назван так в честь немецкого математика Карла Фридриха Гаусса (1777 – 1885).
Но для начала напомним, что СЛАУ может:
- иметь одно единственное решение;
- иметь бесконечное множество решений;
- быть несовместной, т.
 е. не иметь решений.
е. не иметь решений.
Практическая польза
Метод Гаусса – отличный способ решить СЛАУ, которая включает более трех линейных уравнений, а также систем, не являющихся квадратными.
Принцип метода Гаусса
Метод включает следующие этапы:
- прямой – расширенная матрица, соответствующая системе уравнений, путем элементарных преобразований над строками приводится к верхнему треугольному (ступенчатому) виду, т.е. под главной диагональю должны находиться только элементы, равные нулю.
- обратный – в полученной матрице элементы над главной диагональю также обнуляются (нижний треугольный вид).
Пример решения СЛАУ
Давайте решим систему линейных уравнение ниже, воспользовавшись методом Гаусса.
Решение
1. Для начала представим СЛАУ в виде расширенной матрицы.
2. Теперь наша задача – это обнулить все элементы под главной диагональю. Дальнейшие действия зависят от конкретной матрицы, ниже мы опишем те, что применимы к нашему случаю. Сначала поменяем строки местами, таким образом расположив их первые элементы в порядке возрастания.
Сначала поменяем строки местами, таким образом расположив их первые элементы в порядке возрастания.
3. Вычтем из второй строки удвоенную первую, а из третьей – утроенную первую.
4. Прибавим к третьей строке вторую.
5. Отнимем из первой строки вторую, и одновременно с этим действием разделим третью строку на -10.
6. Первый этап завершен. Теперь нам нужно получить нулевые элементы над главной диагональю. Для этого из первой строки вычтем третью, умноженную на 7, а ко второй прибавим третью, умноженную на 5.
7. Финальная расширенная матрица выглядит следующим образом:
8. Ей соответствует система уравнений:
Ответ: корни СЛАУ: x = 2, y = 3, z = 1.
ЧАЩЕ ВСЕГО ЗАПРАШИВАЮТ
Таблица знаков зодиака
Нахождение площади трапеции: формула и примеры
Нахождение длины окружности: формула и задачи
Римские цифры: таблицы
Таблица синусов
Тригонометрическая функция: Тангенс угла (tg)
Нахождение площади ромба: формула и примеры
Нахождение объема цилиндра: формула и задачи
Тригонометрическая функция: Синус угла (sin)
Геометрическая фигура: треугольник
Нахождение объема шара: формула и задачи
Тригонометрическая функция: Косинус угла (cos)
Нахождение объема конуса: формула и задачи
Таблица сложения чисел
Нахождение площади квадрата: формула и примеры
Что такое тетраэдр: определение, виды, формулы площади и объема
Нахождение объема пирамиды: формула и задачи
Признаки подобия треугольников
Нахождение периметра прямоугольника: формула и задачи
Формула Герона для треугольника
Что такое средняя линия треугольника
Нахождение площади треугольника: формула и примеры
Нахождение площади поверхности конуса: формула и задачи
Что такое прямоугольник: определение, свойства, признаки, формулы
Разность кубов: формула и примеры
Степени натуральных чисел
Нахождение площади правильного шестиугольника: формула и примеры
Тригонометрические значения углов: sin, cos, tg, ctg
Нахождение периметра квадрата: формула и задачи
Теорема Фалеса: формулировка и пример решения задачи
Сумма кубов: формула и примеры
Нахождение объема куба: формула и задачи
Куб разности: формула и примеры
Нахождение площади шарового сегмента
Что такое окружность: определение, свойства, формулы
3.
 2. Метод Гаусса | Электронная библиотека
2. Метод Гаусса | Электронная библиотекаЕстественные науки / Методы вычислений / 3.2. Метод Гаусса
Основная идея метода Гаусса заключается в следующем: по исходной системе линейных уравнений строим другую систему линейных уравнений , имеющую то же решение x, что и первая, но матрица которой является верхней треугольной матрицей. А затем решаем систему линейных уравнений с верхней треугольной матрицей.
Метод Гаусса состоит из двух этапов:
1 Прямой ход метода Гаусса. Прямой ход метода Гаусса заключается в преобразовании исходной системы линейных уравнений к эквивалентной системе линейных уравнений с верхней треугольной матрицей.
2. Обратная подстановка. Обратная подстановка метода Гаусса заключается в решении системы линейных уравнений с верхней треугольной матрицей. При этом компоненты вектора решения находятся в обратном порядке .
С точки зрения операций над матрицами метод Гаусса заключается в разложении исходной матрицы А в произведение двух треугольных матриц: нижней треугольной матрицы , на диагонали которой стоят единицы, и верхней треугольной матрицы с ненулевыми диагональными элементами:
,
, , , , .
.
Другими словами, вместо системы линейных уравнений решается две системы линейных уравнений с треугольными матрицами:
Ly = b,
Ux = y.
Определение. Элементы, расположенные на главной диагонали верхней треугольной матрицы , полученной после выполнения прямого хода метода Гаусса, называют ведущими элементами.
Теорема
Для существования —разложения матрицы А необходимо и достаточно, чтобы у матрицы А все главные миноры были отличны от нуля.
Мы будем рассматривать: метод Гаусса без выбора ведущего элемента, метод Гаусса с частичным выбором ведущего элемента и метод Гаусса с полным выбором ведущего элемента. В методе Гаусса без выбора ведущего элемента исходная матрица A представляется в виде произведения двух треугольных матриц LU.
Следствие. Метод Гаусса без выбора ведущего элемента можно применять в том случае, когда все главные миноры матрицы системы линейных уравнений отличны от нуля.
Пример 1
Рассмотрим матрицу .
Определитель матрицы не равен нулю (det(A)0), но первый главный минор равен нулю, следовательно, -разложение матрицы А невозможно. Система линейных уравнений с этой матрицей имеет единственное решение, но оно не может быть получено методом Гаусса без выбора ведущего элемента.
Пример 2
Решить систему линейных уравнений методом Гаусса без выбора ведущего элемента:
Решение
Прямой ход
М1 = 10, М2 = -1, М3 = -155, где Мi – главные миноры матрицы A. Все главные миноры отличны от нуля, следовательно, можно применять метод Гаусса без выбора ведущего элемента.
Нам необходимо, используя эквивалентные преобразования, получить верхнюю треугольную матрицу.
Вместо необходимо получить ноль. Для этого умножим первое уравнение на такое число, чтобы при сложении этого уравнения со вторым исключилось неизвестное .
Умножим первое уравнение на 0.3 и прибавим ко второму. Умножим первое уравнение на –0.5 и прибавим к третьему. Получим:
Умножим первое уравнение на –0.5 и прибавим к третьему. Получим:
Умножили второе уравнение на 25 и прибавим к третьему. Получим:
Мы получили систему линейных уравнений с верхней треугольной матрицей.
Обратная подстановка
, следовательно, z =1.
, следовательно, .
, следовательно, .
Пример 3
Записать -разложение матрицы А.
Решение
Рассмотрим матрицу А из предыдущего примера. U – верхняя треугольная матрица, полученная в результате прямого хода. L – нижняя треугольная матрица, на главной диагонали которой расположены единицы. Ненулевые элементы матрицы – это множители, используемые на шагах исключения, с противоположным знаком:
; ; ; ;
; .
Проверка:
Ведущие элементы 10, -0.1, 155.
Формулы метода Гаусса
Прямой ход
; .
.
Обратная подстановка
.
.
Нахождение значения определителя матрицы методом Гаусса без выбора ведущего элемента
, следовательно, .
Если Т – треугольная матрица размерности n, то , где tii – диагональные элементы матрицы T.
Определитель треугольной матрицы равен произведению ее элементов, расположенных на главной диагонали.
, .
Определитель матрицы А, у которой все главные миноры отличны от нуля, равен произведению ее ведущих элементов, вычисленных методом Гаусса без выбора ведущего элемента.
Пример 4
Найти значение определителя матрицы.
Решение
Рассмотрим матрицу из примера 2:
Отметим, что если один из главных миноров матрицы А равен нулю, то при попытке решить систему линейных уравнений мы получим деление на ноль (). Это первый недостаток метода Гаусса без выбора ведущего элемента.
Второй недостаток: если какой-либо из ведущих элементов принимает малые значения по модулю, то вычислительный алгоритм метода Гаусса без выбора ведущего элемента становится неустойчивым.
Правило. Если ведущие элементы в методе Гаусса по модулю больше, либо равны 1, то ошибки округления в процессе вычисления подавляются, в противном случае ошибки округления увеличиваются.
Условие устойчивости: .
Сложность метода Гаусса без выбора ведущего элемента
Число арифметических действий, необходимых для реализации метода Гаусса без выбора ведущего элемента пропорционально n3, где n – число линейных уравнений. Записывается это так: , где NA – число арифметических действий. Объем памяти, необходимый для реализации алгоритма, пропорционален – .
Введем понятие невязки или вектора невязки
Определение. Невязкой или вектором невязки называется вектор: , где – вычисленное решение системы линейных уравнений .
Суммирование по Гауссу | Поговорим о науке
Суммарность Гаусса названа в честь Иоганна Карла Фридриха Гаусса. Он был немецким математиком. Гаусс — один из самых влиятельных математических мыслителей в истории. Легенда гласит, что Гаусс придумал новый метод суммирования последовательностей в очень молодом возрасте. Легенда гласит, что его учитель математики попросил класс сложить числа от 1 до 100. Другими словами, учитель хотел, чтобы они сложили 1 + 2 + 3 + 4 + 5… вплоть до 100!
Легенда гласит, что его учитель математики попросил класс сложить числа от 1 до 100. Другими словами, учитель хотел, чтобы они сложили 1 + 2 + 3 + 4 + 5… вплоть до 100!
Учитель предполагал, что это займет у учеников очень много времени. Подумайте, сколько времени вам понадобится, чтобы сложить все числа от 1 до 100 одно за другим. Однако Гаусс ответил 5050 почти сразу.
Эта история может быть не совсем правдой. Но это напоминает нам, что самые младшие ученики иногда открывают новые математические закономерности. Теперь давайте подумаем о шаблоне, который Гаусс использовал для быстрого решения этой проблемы.
Уловка, которую использовал Гаусс для решения этой задачи, заключается в том, что не имеет значения, в каком порядке мы складываем числа. В каком бы порядке мы ни следовали, мы получим один и тот же результат.
Например:
2 + 3 имеет тот же ответ, что и 3 + 2.
Мы можем переставить числа от 1 до 100 хитрым способом. Это может помочь нам добавить их быстрее. Вот простой пример, который покажет вам, как работает эта стратегия группировки.
Это может помочь нам добавить их быстрее. Вот простой пример, который покажет вам, как работает эта стратегия группировки.
Допустим, вы хотите сложить числа от 1 до 10.
1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 = ?
Шаблон, показывающий сложение пар от одного до десяти (© Let’s Talk Science, 2021).
Возможно, вы заметили кое-что странное. Каждая из этих пар в сумме дает 11. Итак, мы можем думать о нашей задаче так:
(1 + 10) + (2 + 9) + (3 + 8) + (4 + 7) + (5 + 6) = ?
(11) + (11) + (11) + (11) + (11) = ?
Поскольку у нас 5 пар, наш ответ:
11 + 11 + 11 + 11 + 11 = 11 x 5 = 55
Что ж, это куда-то идет!
Давайте посмотрим на это по-другому. Вместо того, чтобы выстраивать числа в один ряд. Расставь цифры в два ряда. В первом ряду числа увеличиваются. Во втором ряду числа уменьшаются. От 1 до 10 это будет выглядеть так.
Image — Text Version Числа от 1 до 10 выстроены в порядке возрастания в верхнем ряду. Числа от 10 до 1 выстраиваются в порядке убывания в нижнем ряду.
Числа от 10 до 1 выстраиваются в порядке убывания в нижнем ряду.
Теперь просуммируйте каждый столбец.
Изображение — Версия текстаСумма каждого столбца равна 11.
Сумма всех приведенных выше чисел равна
Мы можем записать это как:
Изображение – Текстовая версияСумма – это количество пар, умноженное на сумму каждой пары, и эта сумма делится на 2. В нашем случае десять умножается на одиннадцать, а затем делится на два. . Это дает окончательную сумму 55.
Мы можем использовать алгебру , чтобы представить этот шаблон. Алгебра использует буквы и другие символы для представления чисел в уравнениях. Мы можем использовать букву n , чтобы представить, сколько чисел в нашем списке. Это самое большое число. В нашем примере n будет равно 10. Количество пар будет равно этому числу, деленному на 2. Вы заметите, что размер пары равен количеству пар плюс 1. Таким образом, мы могли бы написать использовать n для записи
Это самое большое число. В нашем примере n будет равно 10. Количество пар будет равно этому числу, деленному на 2. Вы заметите, что размер пары равен количеству пар плюс 1. Таким образом, мы могли бы написать использовать n для записи
(количество пар) x (сумма каждой пары) = n/2 x (n +1)
Но помните, как и раньше, нам нужна сумма только одной строки, а не обеих. Таким образом, мы делим приведенную выше формулу на 2 и получаем:
Изображение — Версия текстаn вне скобки, за которой следует n плюс один внутри скобки. Это делится на 2.
Можем ли мы сделать то же самое для суммы, которая является нечетным числом, скажем, 67? Попробуйте сами, прежде чем смотреть ответ ниже.
Вопрос:
1 + 2 + 3 + 4 ….. 66 + 67 =?
(Ответ внизу страницы)
Шаблон, показывающий сложение пар от одного до десяти (© Let’s Talk Science, 2021).Реальные приложения
Эта задача является примером нахождения суммы арифметической последовательности .
Нахождение суммы последовательности может помочь людям решить множество реальных задач. Компании находят сумму последовательностей, чтобы оценить затраты или доход. Даже расчет стоимости проезда на такси представляет собой сумму арифметической последовательности. Вы начинаете с базового тарифа. Ваша общая стоимость увеличивается на ту же сумму каждую минуту.
Нахождение суммы последовательности также является распространенным вопросом информатики. Компьютерщики используют для этого метод Гаусса. Вопрос «Отсутствующий номер» — это распространенный вопрос технического собеседования. Для ее решения нужен метод Гаусса. Многие из этих приложений используют сложные на вид формулы.
ОТВЕТ
1 + 2 + 3 + 4……66 + 67 = ?
n = 67, n + 1 = 68
n(n + 1)/2
67 x 68/2
= 2 278
Исключение Гаусса | Колледж Алгебра
Результаты обучения
- Напишите расширенную матрицу для системы уравнений.
- Выполнение операций со строками над расширенной матрицей.
- Используйте исключение Гаусса для решения системы уравнений, представленной в виде расширенной матрицы.
- Интерпретируйте решение системы уравнений, представленной в виде расширенной матрицы.
Карл Фридрих Гаусс жил в конце 18-го и начале 19-го веков, но до сих пор считается одним из самых плодовитых математиков в истории. Его вклад в математику и физику охватывает такие области, как алгебра, теория чисел, анализ, дифференциальная геометрия, астрономия и оптика, среди прочих.
Немецкий математик Карл Фридрих Гаусс (1777–1855).
Впервые мы столкнулись с методом исключения Гаусса в книге «Системы линейных уравнений: две переменные». В этом разделе мы вернемся к этой технике решения систем, на этот раз с использованием матриц.
Операции со строками и расширенная матрица
Матрица может служить средством для представления и решения системы уравнений. Чтобы выразить систему в матричной форме, мы извлекаем коэффициенты переменных и констант, и они становятся элементами матрицы. Мы используем вертикальную линию, чтобы отделить записи коэффициентов от констант, по существу заменяя знаки равенства. Когда система записывается в такой форме, мы называем ее расширенная матрица .
Например, рассмотрим следующую систему уравнений [латекс]2\умножить на 2[/латекс].
[латекс]\begin{array}{l}3x+4y=7\\ 4x — 2y=5\end{array}[/latex]
Мы можем записать эту систему в виде расширенной матрицы:
[латекс ]\left[\begin{array}{rr}\hfill 3& \hfill 4\\ \hfill 4& \hfill -2\end{array}\text{ }|\text{ }\begin{array}{r}\ hfill 7\\ \hfill 5\end{array}\right][/latex]
Мы также можем написать матрицу, содержащую только коэффициенты. Это называется матрица коэффициентов .
Это называется матрица коэффициентов .
[латекс]\влево[\начало{массив}{cc}3& 4\\ 4& -2\конец{массив}\право][/латекс]
Система уравнений три на три , например
[латекс]\begin{array}{l}3x-y-z=0\hfill \\ \text{ }x+y=5\hfill \\ \text{ }2x — 3z=2\hfill \end{array }[/latex]
имеет матрицу коэффициентов
[latex]\left[\begin{array}{rrr}\hfill 3& \hfill -1& \hfill -1\\ \hfill 1& \hfill 1& \hfill 0\ \\hfill 2& \hfill 0& \hfill -3\end{массив}\right][/latex]
и представлен расширенной матрицей
[латекс]\left[\begin{array}{rrr}\hfill 3& \hfill -1& \hfill -1\\ \hfill 1& \hfill 1& \hfill 0\\ \ hfill 2& \hfill 0& \hfill -3\end{массив}\text{ }|\text{ }\begin{array}{r}\hfill 0\\ \hfill 5\\ \hfill 2\end{массив}\ right][/latex]
Обратите внимание, что матрица написана таким образом, что переменные выстраиваются в свои собственные столбцы: x — термины идут в первом столбце, y — термины во втором столбце и z — термины в третьем столбце. Очень важно, чтобы каждое уравнение было записано в стандартной форме [latex]ax+by+cz=d[/latex], чтобы переменные совпадали. Если в уравнении отсутствует переменный член, коэффициент равен 0.
Очень важно, чтобы каждое уравнение было записано в стандартной форме [latex]ax+by+cz=d[/latex], чтобы переменные совпадали. Если в уравнении отсутствует переменный член, коэффициент равен 0.
Как: Для заданной системы уравнений напишите расширенную матрицу столбец.
Пример: Написание расширенной матрицы для системы уравнений
Запишите расширенную матрицу для заданной системы уравнений.
[латекс]\begin{array}{l}\text{ }x+2y-z=3\hfill \\ \text{ }2x-y+2z=6\hfill \\ \text{ }x — 3y +3z=4\hfill \end{array}[/latex]
Показать решение
Попробуйте
Напишите расширенную матрицу данной системы уравнений.
[латекс]\начало{массив}{l}4x — 3y=11\\ 3x+2y=4\конец{массив}[/латекс]
Показать решение
Написание системы уравнений из расширенной матрицы
Мы можем использовать расширенные матрицы для решения систем уравнений, поскольку они упрощают операции, когда системы не перегружены переменными. Однако важно понимать, как переключаться между форматами, чтобы сделать поиск решений более плавным и интуитивно понятным. Здесь мы будем использовать информацию в расширенной матрице, чтобы записать система уравнений в стандартной форме.
Однако важно понимать, как переключаться между форматами, чтобы сделать поиск решений более плавным и интуитивно понятным. Здесь мы будем использовать информацию в расширенной матрице, чтобы записать система уравнений в стандартной форме.
Пример: Запись системы уравнений из расширенной матрицы Форма
Найдите систему уравнений из расширенной матрицы.
[латекс]\left[\begin{array}{rrr}\hfill 1& \hfill -3& \hfill -5\\ \hfill 2& \hfill -5& \hfill -4\\ \hfill -3& \hfill 5& \ hfill 4\end{массив}\text{ }|\text{ }\begin{array}{r}\hfill -2\\ \hfill 5\\ \hfill 6\end{массив}\right][/latex]
Показать решение
Попробуйте
Напишите систему уравнений из дополненной матрицы.
[латекс]\left[\begin{array}{ccc}1& -1& 1\\ 2& -1& 3\\ 0& 1& 1\end{массив}|\begin{массив}{c}5\\ 1\ \ -9\end{массив}\right][/latex]
Показать решение
Операции со строками
Теперь, когда мы можем записывать системы уравнений в расширенной матричной форме, мы рассмотрим различные операции со строками, которые можно выполнять над матрицей, такие как сложение, умножение на константу и перестановка строк.
Выполнение операций со строками над матрицей — это метод, который мы используем для решения системы уравнений. Чтобы решить систему уравнений, мы хотим преобразовать матрицу строк-ступенчатой формы , в которой есть единицы вниз по главной диагонали от верхнего левого угла до нижнего правого угла и нули в каждой позиции ниже как показано на главной диагонали.
[латекс]\begin{array}{c}\text{Форма строки-эшелона}\\ \left[\begin{array}{ccc}1& a& b\\ 0& 1& d\\ 0& 0& 1\end{ массив}\справа]\конец{массив}[/латекс]
Мы используем операции со строками, соответствующие операциям с уравнениями, чтобы получить новую матрицу, эквивалентную строк в более простой форме. Вот рекомендации по получению формы ряд-эшелон.
- В любой ненулевой строке первое ненулевое число равно 1. Оно называется ведущим 1.
- Все строки со всеми нулями помещаются в конец матрицы.
- Любой интерлиньяж 1 находится ниже и правее предыдущего интерлиньяжа 1.

- В любом столбце, содержащем ведущую единицу, во всех остальных позициях столбца стоят нули.
Чтобы решить систему уравнений, мы можем выполнить следующие операции со строками, чтобы преобразовать матрицу коэффициентов в форму ступенчатой строки и выполнить обратную подстановку, чтобы найти решение.
- Поменять местами ряды. (Обозначение: [латекс] {R}_{i}\leftrightarrow {R}_{j}[/латекс] )
- Умножить строку на константу. (Обозначение: [латекс]c{R}_{i}[/латекс] )
- Добавить произведение строки, умноженной на константу, к другой строке. (Обозначение: [латекс]{R}_{i}+c{R}_{j}[/латекс])
Каждая из операций строки соответствует операциям, которые мы уже изучили для решения систем уравнений с тремя переменными. С этими операциями есть несколько ключевых ходов, которые быстро достигнут цели записи матрицы в форме строки-эшелона. Чтобы получить матрицу в форме строки-эшелона для поиска решений, мы используем метод исключения Гаусса, который использует операции со строками для получения 1 в качестве первой записи, чтобы строка 1 могла использоваться для преобразования оставшихся строк.
Общее примечание: Исключение Гаусса
Метод исключения Гаусса относится к стратегии, используемой для получения ступенчато-строковой формы матрицы. Цель состоит в том, чтобы написать матрицу [latex]A[/latex] с номером 1 в качестве записи вниз по главной диагонали и со всеми нулями ниже.
[латекс]A=\left[\begin{array}{rrr}\hfill {a}_{11}& \hfill {a}_{12}& \hfill {a}_{13}\\ \ hfill {a}_{21}& \hfill {a}_{22}& \hfill {a}_{23}\\ \hfill {a}_{31}& \hfill {a}_{32}& \hfill {a}_{33}\end{массив}\right]\stackrel{\text{После исключения Гаусса}}{\to}A=\left[\begin{array}{rrr}\hfill 1& \hfill {b}_{12}& \hfill {b}_{13}\\ \hfill 0& \hfill 1& \hfill {b}_{23}\\ \hfill 0& \hfill 0& \hfill 1\end{массив} \право][/латекс]
Первый шаг стратегии Гаусса включает в себя получение 1 в качестве первой записи, так что строка 1 может использоваться для изменения строк ниже.
Как: Для расширенной матрицы выполнить операции над строками, чтобы получить эшелонированную форму
- Первое уравнение должно иметь старший коэффициент, равный 1.
 Поменяйте строки местами или умножьте на константу, если это необходимо.
Поменяйте строки местами или умножьте на константу, если это необходимо. - Используйте операции со строками, чтобы получить нули в первом столбце после первой записи 1.
- Используйте операции со строками, чтобы получить 1 в строке 2, столбце 2.
- Используйте операции со строками, чтобы получить нули вниз по столбцу 2, под записью 1.
- Используйте операции со строками, чтобы получить 1 в строке 3, столбце 3.
- Продолжайте этот процесс для всех строк, пока не будет 1 в каждом элементе вниз по главной диагонали, а ниже не будут только нули.
- Если какие-либо строки содержат все нули, поместите их внизу.
Пример: выполнение операций над строками над расширенной матрицей 3×3 для получения формы строк-эшелонов
Выполнение операций над строками данной матрицы для получения формы строк-эшелонов.
[латекс]\left[\begin{array}{rrr}\hfill 1& \hfill -3& \hfill 4\\ \hfill 2& \hfill -5& \hfill 6\\ \hfill -3& \hfill 3& \hfill 4 \end{array}\text{ }|\text{ }\begin{array}{r}\hfill 3\\ \hfill 6\\ \hfill 6\end{array}\right][/latex]
Показать Решение
Попробуй
Запиши систему уравнений в ступенчато-строковой форме.
[латекс]\begin{array}{l}\text{ }x — 2y+3z=9\hfill \\ \text{ }-x+3y=-4\hfill \\ 2x — 5y+5z=17 \hfill \end{массив}[/latex]
Показать раствор
[латекс]\left[\begin{array}{ccc}1& -\frac{5}{2}& \frac{5}{2}\\ \text{ }0& 1& 5\\ 0& 0& 1\ end{array}|\begin{array}{c}\frac{17}{2}\\ 9\\ 2\end{array}\right][/latex]
Решение системы методом исключения Гаусса
Мы увидели, как написать систему уравнений с расширенной матрицей , а затем как использовать операции со строками и обратную подстановку для получения эшелонированной формы строк. Теперь мы будем использовать исключение Гаусса в качестве инструмента для решения системы, записанной в виде расширенной матрицы. В нашем первом примере мы покажем вам процесс использования исключения Гаусса в системе двух уравнений с двумя переменными.
Пример: Решение системы 2 X 2 методом исключения Гаусса
Решите данную систему методом исключения Гаусса.
[латекс]\begin{array}{l}2x+3y=6\hfill \\ \text{ }x-y=\frac{1}{2}\hfill \end{array}[/latex]
Показать Решение
Попробуйте
Решите данную систему методом исключения Гаусса.
[латекс]\begin{array}{l}4x+3y=11\hfill \\ \text{ }\text{}\text{}x — 3y=-1\hfill \end{array}[/latex ]
Показать решение
В следующем примере мы будем решать систему двух уравнений с двумя зависимыми переменными. Напомним, что зависимая система имеет бесконечное число решений, и результатом операций со строками над ее расширенной матрицей будет уравнение типа [латекс]0=0[/латекс]. Мы также рассмотрим написание общего решения для зависимой системы.
Пример: Решение зависимой системы
Решите систему уравнений.
[латекс]\begin{array}{l}3x+4y=12\\ 6x+8y=24\end{массив}[/latex]
Показать решение
Теперь мы перейдем к ступенчатой форме, чтобы решить систему линейных уравнений 3 на 3. Общая идея состоит в том, чтобы исключить все переменные, кроме одной, с помощью операций со строками, а затем выполнить обратную замену для решения других переменных.
Общая идея состоит в том, чтобы исключить все переменные, кроме одной, с помощью операций со строками, а затем выполнить обратную замену для решения других переменных.
Пример. Решение системы линейных уравнений с использованием матриц
Решите систему линейных уравнений с помощью матриц.
[латекс]\begin{array}{c}\begin{array}{l}\hfill \\ \hfill \\ x-y+z=8\hfill \end{array}\\ 2x+3y-z =-2\\ 3x — 2y — 9z=9\end{массив}[/latex]
Показать решение
Напомним, что есть три возможных результата для решений линейных систем. В предыдущем примере решение [латекс]\влево(4,-3,1\вправо)[/латекс] представляет точку в трехмерном пространстве. Эта точка представляет собой пересечение трех плоскостей. В следующем примере мы решаем систему, используя операции со строками, и обнаруживаем, что она представляет собой зависимую систему. Зависимая система в 3-х измерениях может быть представлена двумя идентичными плоскостями, как и в 2-х измерениях, где зависимая система представляет собой две идентичные линии.
Пример: Решение зависимой системы 3 x 3
Решите следующую систему линейных уравнений с помощью исключения Гаусса.
[латекс]\begin{массив}{r}\hfill -x — 2y+z=-1\\ \hfill 2x+3y=2\\ \hfill y — 2z=0\end{массив}[/latex ]
Показать решение
Общее решение зависимой системы 3 X 3
Напомним, что при решении зависимой системы линейных уравнений с двумя переменными с помощью исключения или замены можно записать решение [латекс](х,у)[/латекс] в терминах x, потому что существует бесконечно много пар (x,y), которые будут удовлетворять зависимой системе уравнений, и все они попадают на прямую [latex](x, mx+b)[/latex]. Теперь, когда вы работаете в трех измерениях, решение будет представлять собой плоскость, поэтому вы должны записать его в общей форме [латекс](x, m_{1}x+b_{1}, m_{2}x+b_{ 2})[/латекс].
Попробуйте
Решите систему методом исключения Гаусса.
[латекс]\begin{array}{c}x+4y-z=4\\ 2x+5y+8z=15\\ x+3y — 3z=1\end{array}[/latex]
Показать Решение
Вопросы и ответы
Можно ли решить любую систему линейных уравнений методом исключения Гаусса?
Да, система линейных уравнений любого размера может быть решена методом исключения Гаусса.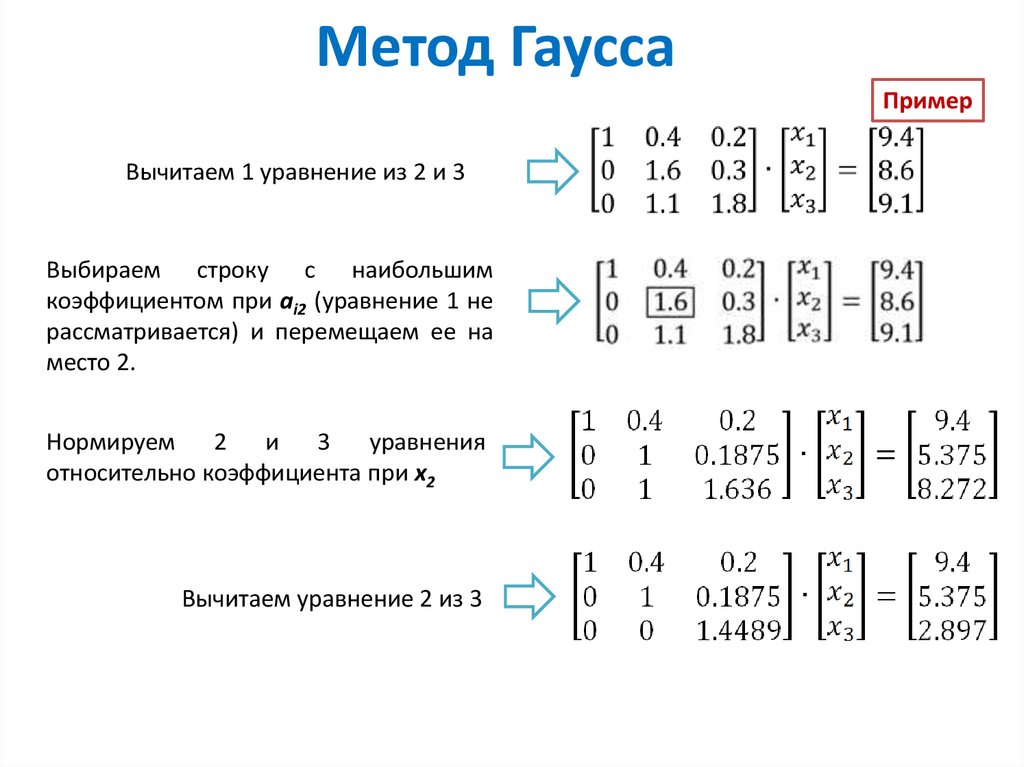
Как: Имея систему уравнений, решить с помощью матриц с помощью калькулятора.
- Сохраните расширенную матрицу как матричную переменную [латекс]\влево[А\вправо],\влево[В\вправо],\влево[С\вправо]\текст{,} \точки [/латекс].
- Используйте функцию ref( в калькуляторе, вызывая каждую матричную переменную по мере необходимости.
Пример: решение системы уравнений с помощью калькулятора
Решите систему уравнений.
[латекс]\begin{array}{r}\hfill 5x+3y+9z=-1\\ \hfill -2x+3y-z=-2\\ \hfill -x — 4y+5z=1\end {массив}[/латекс]
Показать решение
Приложения систем уравнений
Теперь обратимся к приложениям, для которых используются системы уравнений. В следующем примере мы определяем, сколько денег было инвестировано по двум разным ставкам, учитывая сумму процентов, полученных на обоих счетах.
Пример: применение матриц 2 × 2 к финансам
Кэролайн инвестирует в общей сложности 12 000 долларов США в две муниципальные облигации, по одной из которых выплачивается 10,5% годовых, а по другой — 12%.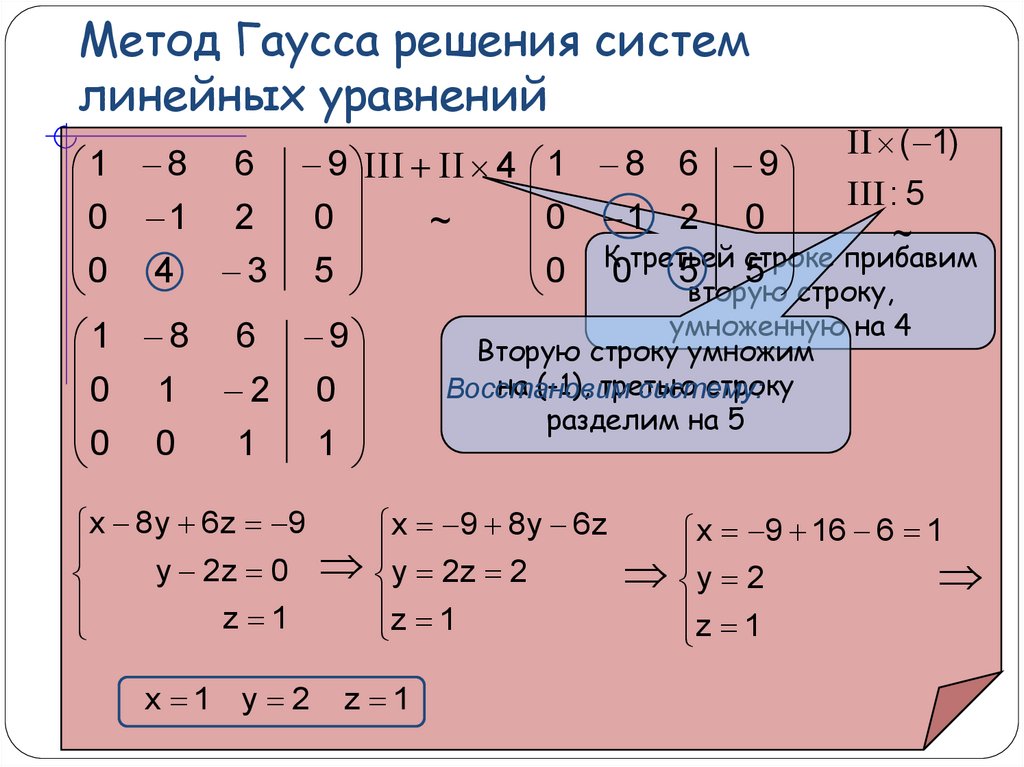 Годовой процент, полученный по двум инвестициям в прошлом году, составил 1335 долларов. Сколько было вложено по каждой ставке?
Годовой процент, полученный по двум инвестициям в прошлом году, составил 1335 долларов. Сколько было вложено по каждой ставке?
Показать раствор
Пример: применение матриц 3 × 3 к финансам
Ava инвестирует в общей сложности 10 000 долларов США в три счета, один из которых приносит 5% годовых, другой — 8% годовых, а третий — 9%. Годовой процент, полученный по трем инвестициям в прошлом году, составил 770 долларов. Сумма, вложенная под 9%, вдвое превышала сумму, вложенную под 5%. Сколько было вложено по каждой ставке?
Показать решение
Попробуй
Небольшая обувная компания взяла кредит в размере 1 500 000 долларов, чтобы расширить свой ассортимент. Часть денег была взята в долг под 7%, часть – под 8%, а часть – под 10%. Сумма займа под 10% в четыре раза превышала сумму займа под 7%, а годовой процент по всем трем кредитам составлял 130 500 долларов. Используйте матрицы, чтобы найти сумму займа по каждой ставке.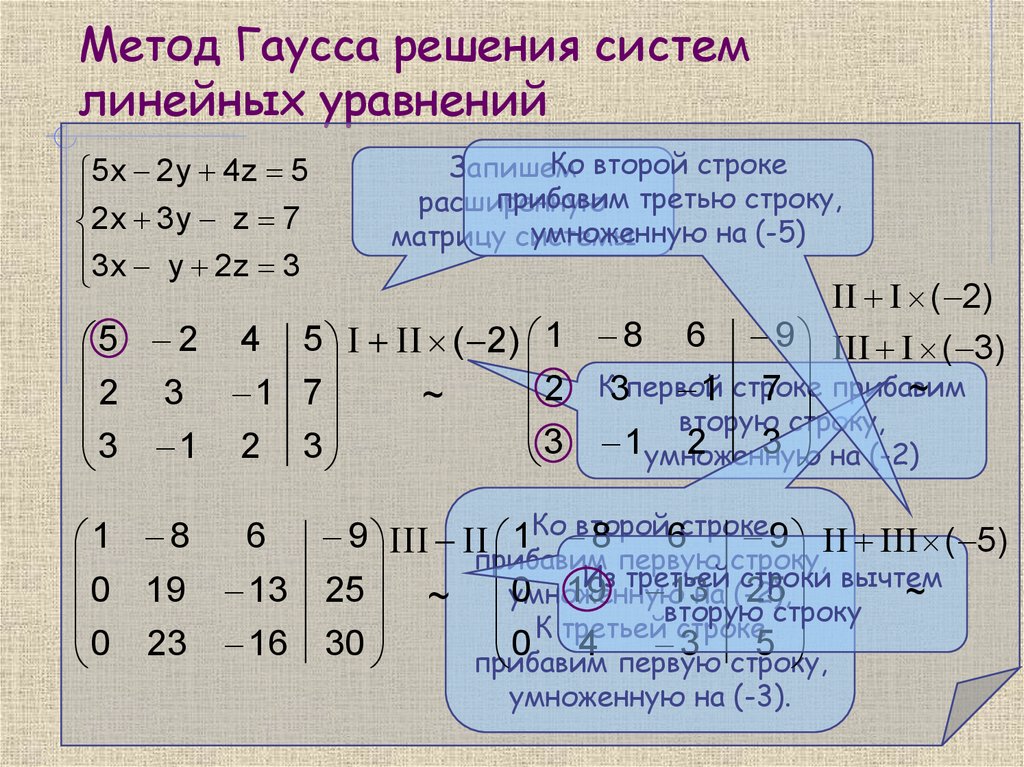

 е. не иметь решений.
е. не иметь решений.
 Поменяйте строки местами или умножьте на константу, если это необходимо.
Поменяйте строки местами или умножьте на константу, если это необходимо.