Метод байеса: просто о сложном / Хабр

alexxlab / / Разное

Содержание

просто о сложном / Хабр

Перевод статьи Bayes’ rule with a simple and practical example под авторством Tirthajyoti Sarkar. Разрешение автора на перевод получено. Мне данная статья понравилась лаконичностью и интересным примером из жизни. Надеюсь, будет полезна и Вам.

В статье продемонстрируем применение Теоремы Байеса на простом практическом примере с использованием языка программирования Python.

Теорема Байеса

Теорема Байеса (или формула Байеса) — один из самых мощных инструментов в теории вероятностей и статистики. Теорема Байеса позволяет описать вероятность события, основываясь на прошлом (априорном) знании условий, которые могут относиться к событиям.

Рис. 1. Связь между апостериорной вероятностью и априорной вероятностью

Например, если заболевание связано с возрастом, то, используя теорему Байеса, возраст человека можно использовать для более точной оценки вероятности заболевания по сравнению с оценкой вероятности заболевания, сделанной без знания возраста человека.

Теорема Байеса позволяет учитывать субъективную оценку или уровень доверия в строгих статистических расчетах. Это один из методов, который позволяет постепенно обновлять вероятность события по мере поступления новых наблюдений или сведений.

Историческая справка

Источник изображения: Википедия

Теорема Байеса названа в честь преподобного Томаса Байеса. Он первым использовал условную вероятность для создания алгоритма (Proposition 9), который использует вероятность для вычисления пределов неизвестного параметра ( опубликовано в «An Essay towards solving a Problem in the Doctrine of Chances»). Байес расширил свой алгоритм на любую неизвестную предшествующую причину.

Независимо от Байеса, Пьер-Симон Лаплас в 1774 году, а затем в своей «Аналитической теории вероятностей» (1812 года) использовал условную вероятность, чтобы сформулировать отношение обновленной апостериорной вероятности к априорной вероятности при наличии данных.

Теорема Байеса позволяет учитывать субъективную оценку или уровень доверия в строгих статистических расчетах.

Логический процесс для анализа данных

Мы начинаем с гипотезы и уровеня доверия к этой гипотезе. Это означает, что на основе знания предметной области или предшествующих других знаний мы приписываем этой гипотезе ненулевую вероятность.

Затем мы собираем данные и обновляем наши первоначальные убеждения. Если новые данные подтверждают гипотезу, то вероятность возрастает, если не подтверждают — вероятность снижается.

Звучит просто и логично, неправда ли?

Исторически в большинстве методов статистического обучения статистических исследований понятие априорного события не используется или недооценивается. Кроме того, вычислительные сложности байесовского обучения не позволяли ему стать мейнстримом более 200 лет.

Но сейчас все меняется с появлением байесовского статистического вывода …

Если новые данные подтверждают гипотезу, то вероятность возрастает, если не подтверждают — вероятность снижается.

Байесовский статистический вывод

Байесовская статистика и моделирование возродились благодаря развитию искуственного интеллекта и систем машинного обучения на основе данных в бизнесе и науке.

Байесовский вывод применяется в генетике, лингвистике, обработке изображений, визуализации мозга, космологии, машинном обучении, эпидемиологии, психологии, криминалистике, распознавании человека, эволюции, визуальном восприятии, экологии и во многих других областях, где большую роль играют извлечение информации из данных и предиктивная (прогнозная) аналитика.

Байесовская статистика и моделирование возродились благодаря развитию искуственного интеллекта и систем машинного обучения на основе данных в бизнесе и науке.

Примеры с кодом на Python

Скрининг-тест на употребление наркотиков

Источник изображения: Pixabay

Мы применим формулу Байеса к скрининг-тесту на употребление наркотиков (который бывает обязательным для допуска к работе на федеральных или других должностях в компаниях, которые обещают рабочую среду, свободную от наркотиков).

Предположим, что тест на применение наркотика имеет 97% чувствительность (комментарий переводчика — по сути это доля истинно положительных результатов) и 95% специфичность (комментарий переводчика — по сути это доля истинно отрицательных результатов).  То есть тест даст 97% истинно положительных результатов для потребителей наркотиков и 95% истинно отрицательных результатов для лиц, не употребляющих наркотики. Эта статистика доступна при тестировании тестов в исследовании до вывода их на рынок. Правило Байеса позволяет нам использовать такого рода знания, основанные на данных, для расчета окончательной вероятности.

Предположим, мы также знаем, что 0,5% населения в целом употребляют наркотики. Какова вероятность того, что случайно выбранный человек с положительным результатом анализа является потребителем наркотиков?

Обратите внимание, что это важнейшая часть «априорной вероятности», которая представляет собой часть обобщенных знаний об общем уровне распространенности. Это наше предварительное суждение о вероятности того, что случайный испытуемый будет употреблять наркотики. Это означает, что если мы выберем случайного человека из общей популяции без какого-либо тестирования, мы можем только сказать, что вероятность того, что этот человек употребляет наркотики, составляет 0,5%.

Как же тогда использовать правило Байеса в этой ситуации? Мы напишем пользовательскую функцию, которая:

  • принимает в качестве входных данных чувствительность и специфичность теста, а также предварительные знания о процентном соотношении потребителей наркотиков

  • и выдает вероятность того, что тестируемый является потребителем наркотиков, на основе положительного результата теста.

Вот формула для вычисления по правилу Байеса:

P(Наркоман) = Уровень распространенности наркомании, P(Не наркоман) = 1 — Уровень распространенности наркомании P(Положительный тест | Наркоман) = Чувствительность теста P(Отрицательный тест | Не наркоман) = Специфичность теста P(Положительный тест | Не наркоман) = 1 — Специфичность теста

Код выложен здесь. Если мы запустим функцию с заданными данными, мы получим следующий результат:

Прошедший тестирование человек может быть не наркоманом. Вероятность, что прошедший тестирование человек является наркоманом: 0,089.

Что здесь интересного?

Даже при использовании теста, который в 97% случаях верно выявляет положительные случаи и который в 95% случаях правильно выявляет отрицательные случаи, истинная вероятность быть наркоманом с положительным результатом этого теста составляет всего 8,9%!

Если вы посмотрите на расчеты, то станет понятным, что это связано с чрезвычайно низким уровнем распространенности. Количество ложных срабатываний превышает количество истинных срабатываний.

Например, если протестировано 1000 человек, ожидается, что будет 995 не наркоманов и 5 наркоманов. Из 995 не наркоманов ожидается 0,05 × 995 ≃ 50 ложных срабатываний. Из 5 наркоманов ожидается 0,95 × 5 ≈ 5 истинно положительных результатов. Из 55 положительных результатов только 5 являются истинно положительными!

Посмотрим, как вероятность меняется с уровнем распространенности (код).

Обратите внимание, что в данном случае наше решение зависит от порога вероятности. В данном примере он установлен на уровне 0,5.  При необходимости его можно понизить. При пороге 0,5 у нас должен быть уровень распространенности почти 4,8%, чтобы поймать наркомана с одним положительным результатом теста.

Какой уровень точности теста необходим для улучшения сценария?

Мы увидели, что чувствительность и специфичность теста сильно влияют на вычисления. В таком случае нам может быть интересно узнать, какая точность теста необходима для повышения вероятности выявления наркоманов (код здесь).

На графиках видно, что даже с чувствительностью, близкой к 100%, мы ничего не выигрываем. Однако имеет место нелинейная зависимость вероятности от специфичности теста, и по мере того, как тест достигает совершенства (с точки зрения специфичности), мы получаем значительное увеличение вероятности. Следовательно, все усилия Отдела разработки (R&D) должны быть направлены на улучшение специфичности теста.

Этот вывод можно интуитивно сделать из того факта, что основной проблемой, связанной с низкой вероятностью, является низкий уровень распространенности.  Следовательно, нам следует сосредоточить внимание на правильном отлове не наркоманов (т.е. улучшении специфичности), потому что их намного больше, чем наркоманов.

Отрицательных примеров в этом примере гораздо больше, чем положительных. Таким образом, специфичность теста должна быть максимальной.

Цепочка расчетов и формула Байеса

Лучшее в байесовском выводе — это возможность использовать предшествующие знания в форме априорного вероятностного члена в числителе теоремы Байеса.

В данной постановке процесса скрининга наркотиков предварительные знания — это не что иное, как вычисленная вероятность теста, которая затем возвращается к следующему тесту .

Это означает, что для этих случаев, когда уровень распространенности среди населения в целом чрезвычайно низок, один из способов повысить уверенность в результате теста — назначить последующий тест, если первый результат теста окажется положительным.

Апостериорная вероятность первого теста становится априорной вероятностью для второго теста, т. е. P (Наркоман) для второго теста уже не общий показатель распространенности, а вероятность из первого теста.

Вот пример кода для демонстрации цепочки.

p1 = drug_user(
  prob_th=0.5,
  sensitivity=0.97,
  specificity=0.95,
  prevelance=0.005)
print("Probability of the test-taker being a drug user, in the first round of test, is:",
      round(p1,3))
print()
p2 = drug_user(
  prob_th=0.5,
  sensitivity=0.97,
  specificity=0.95,
  prevelance=p1)
print("Probability of the test-taker being a drug user, in the second round of test, is:",
      round(p2,3))
print()
p3 = drug_user(
  prob_th=0.5, 
  sensitivity=0.97,
  specificity=0.95,
  prevelance=p2)
print("Probability of the test-taker being a drug user, in the third round of test, is:",
      round(p3,3))

После отработки кода мы получаем следующее:

The test-taker could be an user
Probability of the test-taker being a drug user, in the first round of test, is: 0.089

The test-taker could be an user
Probability of the test-taker being a drug user, in the second round of test, is: 0.

654

The test-taker could be an user
Probability of the test-taker being a drug user, in the third round of test, is: 0.973

Когда мы выполняем тест в первый раз, расчетная (апостериорная) вероятность низка, всего 8,9%, но она значительно возрастает до 65,4% во втором тесте, а третий положительный тест дает апостериорную вероятность 97,3%.

Следовательно, неточный тест можно использовать несколько раз, чтобы обновить наше мнение с помощью последовательного применения правила Байеса.

Лучшее в байесовском выводе — это возможность использовать предшествующие знания в форме априорного вероятностного члена в числителе теоремы Байеса.

Резюме

В этой статье мы рассказываем об основах и применении одного из самых мощных законов статистики — теоремы Байеса. Продвинутое вероятностное моделирование и статистический вывод с применением теоремы Байеса захватили мир науки о данных и аналитики.

Мы продемонстрировали применение правила Байеса на очень простом, но практичном примере тестирования на наркотики и реализовали расчеты на языке програмирования Python.  Мы показали, как ограничения теста влияют на прогнозируемую вероятность и что в тесте необходимо улучшить, чтобы получить результат с высокой степенью достоверности.

Мы также показали истинную силу байесовских рассуждений и как несколько байесовских вычислений можно объединить в цепочку, чтобы вычислить общую апостериорную вероятность.

Для дальнейшего чтения автор рекомендует:

  1. https://www.mathsisfun.com/data/bayes-theorem.html

  2. https://betterexplained.com/articles/an-intuitive-and-short-explanation-of-bayes-theorem/

Скажи Байесу «да!». Забудь про интуицию — просто думай, как Байес завещал

© Олшьга Скворцова, Chrdk.

Моде на так называемое байесовское мышление больше 25 лет, но до сих пор на научных конференциях, в стенах технических факультетов и в курилках ведущих IT-компаний ее часто так горячо обсуждают, как будто она совсем свеженькая. И даже если вы никогда не слышали о том, что такое теорема Байеса, то вы все равно окружены людьми и вещами, использующими байесовский подход постоянно и на каждом шагу. Что делать? Встать на сторону силы.

Встать «на сторону силы», конечно, просто фигура речи. На самом деле наш разговор сейчас лишь о том, как математический инструмент стал широко использоваться на несколько столетий позже момента, когда был сформулирован; как, пользуясь здравым смыслом, не поддаться привычке и дать правильный ответ; о том, как простые и красивые идеи меняют людей и мир вокруг, рождая мечты, прорывы и заблуждения. Но давайте обо всем по порядку. 

А? Байес? Что?

Лондон. 1702 год. В семье одного из первых пресвитерианских священников Англии рождается сын Томас. Он получает домашнее образование, проявляет интерес к математике, но все равно становится священником, как и отец. При своей жизни Томас Байес не опубликовал ни одной научной работы под собственным именем. Однако, даже несмотря на это, в 1742 году он был избран в члены Лондонского Королевского общества, что говорит о том, что в научном сообществе Байес был весьма уважаемым человеком. Ну а знаменитая теорема, о которой пойдет речь, была вообще опубликована после его смерти в «Трудах Лондонского Королевского общества».  

Эта теорема, пожалуй, одна из самых значимых теорем во всей теории вероятностей. Если в общих чертах, она позволяет узнать вероятность определенного события при условии, что произошло какое-то другое, статистически взаимосвязанное с ним. 

И сразу формула: P(A|B) = P(B|A)P(A)P(B) 

P(B|A)P(A)P(B) 

Спокойно, не закрывайте окно браузера, формул в нашем тексте будет не так уж много. 

P(Х) — вероятность того, что произойдет некоторое событие Х. Например, если Х — событие «выпадет решка», то P(X) = ½ или 50%. 

Идем дальше. P(X|Y) называется условной вероятностью. Это вероятность того, что произойдет событие X при условии, что событие Y уже произошло. Такая вероятность вычисляется как P(A|B) = P(A∩B)P(B), где P(A∩B) — вероятность наступления обоих событий сразу. Например, вероятность того, что ваш хомячок (если он у вас есть) проживет два года (событие В) равна 0,6, а вероятность того, что он проживет три года (событие А), равна 0,3. Тогда вероятность того, что хомячок, доживший до двух лет, доживет и до трех, равна P(A|B) = P(A∩B)P(B)= 0,30,6=12=0,5.

P(A∩B)P(B)

P(A∩B)P(B)

0,30,6

Теперь немного математической магии. Заметим, что из формулы условной вероятности следует, что P(A∩B) = P(A|B)P(B)=P(B|A)P(A)=P(A∩B). 

Ну и что? 

А то, что теперь P(A|B) = P(A∪B)P(B)=P(B|A)P(A)P(B), а это и есть наша формула Байеса. 

P(A∪B)P(B)

P(B|A)P(A)P(B)

Здорово, мы вывели формулу. Всё?

Конечно, заслуга Байеса состоит вовсе не в том, что он дважды использовал формулу условной вероятности и получил новую. Его заслуга в том, что именно он объяснил, что это нам дает.

Допустим, у нас есть некоторое убеждение A и мы почему-то знаем вероятность того, что оно истинно (произойдет). Еще у нас есть некое свидетельство B, которое может как-то изменить наше убеждение (А). Так вот. Полученная вероятность P(A|B) — это будет наше новое, измененное свидетельством знание, наше новое убеждение. Дальше существует множество интерпретаций, которые гораздо проще понимать на конкретных примерах, но если говорить об интерпретации самого Байеса, то эта формула показывает, как уровень нашего доверия может кардинально измениться вследствие поступления какой-то новой информации. Совсем просто так: старое знание + новый результат (эксперимент, свидетельство) = новое, более точное знание.

Вероятность события А в данном случае называется априорной вероятностью. То есть это то, что мы знаем к настоящему моменту времени и в чем мы убеждены. Вероятность P(A|B) — апостериорная вероятность. То есть то самое новое, улучшенное знание.

P(B|A) — вероятность наступления события B при истинности гипотезы A, а P(B) — просто вероятность наступления события B.

Но все еще — что с того?

Психологи уже смогли показать, что люди достаточно часто заблуждаются в своих суждениях, основанных на полученном опыте. Поэтому интуитивно ожидаемый результат может очень сильно отличаться от правильного по Байесу. Примером может служить знаменитый парадокс Монти Холла, когда вам нужно выбрать дверь, за которой находится автомобиль, а потом, когда вам откроют одну из дверей, за которой нет автомобиля, поменять свое решение.

Это происходит потому, что мы привыкли рассуждать в парадигме классической, частотной вероятности. Байесовский подход при этом никак ей не противоречит, а скорее наоборот, дополняет.

Ключевое отличие здесь в том, что считать случайной величиной. В частотном или фриквентистском подходе мы под такой величиной подразумеваем значение, которое мы не можем спрогнозировать, не проведя какого-то количества экспериментов. В байесовском же подходе случайная величина — это строго определенный, детерминированный процесс, который можно спрогнозировать целиком, просто мы знаем не все начальные факторы, которые могут влиять на исход.

Самый простой пример — подбрасывание монетки. Если бы мы знали силу, с которой мы ее подбрасываем, ускорение, сопротивление воздуха, скорость ветра и всё-всё-всё, что может как-то повлиять на ее полет, мы бы могли сказать со 100-процентной вероятностью, куда она упадет. Но поскольку мы этого не знаем, мы подбрасываем ее миллион раз и говорим, что примерно половина из этого миллиона раз выпадет орел, а вторую половину раз — решка.

Описание

Разные подходы к одной и той же проблеме «статистика» и «байесовца»

Байесовский подход удобен еще и тем, что мы можем вообще не проводить экспериментов. Но тогда апостериорная вероятность просто-напросто равна априорной. Иначе говоря, такая вероятность будет просто отражением наших представлений об этом процессе. Например, какова вероятность того, что сегодня случится конец света? Если бы мы говорили об этом в терминах частотной вероятности, нам бы нужно было провести ряд экспериментов (то есть несколько раз дождаться конца света), а потом число успехов (концов света) поделить на число всех дней, когда мы наблюдали за этим событием. То есть если вы читаете эту статью, то вероятность того, что конец света наступит сегодня, с точки зрения статистики равна нулю. Но мы же все прекрасно знаем, что вероятности инопланетного вторжения, образования черной дыры внутри БАКа или захвата земли взбунтовавшимися роботами не нулевые. Поэтому, подставив их в качестве априорных в формулу Байеса, мы уже получим ненулевую вероятность.

Таким же достаточно простым способом можно посчитать, например, вероятность того, что вам понравится новый фильм, вышедший в прокат, или что президентом такой-то страны в таком-то году станет такой-то человек.

Кажется, с теорией мы на этом в целом покончили. Но наверняка у вас все еще есть некоторое недопонимание, я уверен. Поэтому вперед — к примерам. Меньше математики, больше веселья!

Зачем мне теорема Байеса, если…

…я случайно переспала с парнем, который не предохранялся, и теперь боюсь за свою загубленную молодость.

Это самый типичный пример, которым очень любят иллюстрировать работу нашей формулы, показывая все ее могущество. 

Допустим, только 1% процент неудачников не успевают избежать беды и становятся молодыми папами. Чтобы узнать это наверняка, вам придется сделать тест, который, вообще говоря, никогда не бывает на 100% надежен. Но мы будем оптимистами и скажем, что наш тест в 99% случаев дает правильный результат. То есть только одна из ста небеременных девушек на несколько дней впадет в отчаяние или только одна из ста беременных опрометчиво успокоится до первых проявлений признаков нечаянного счастья.

Вопрос: какова вероятность того, что, если ваш тест дал положительный результат, вы действительно беременны? Нет, не 99, не 80 и даже не 75 процентов. Вероятность того, что вы на самом деле беременны, всего лишь 50%. Тоже не очень приятно, но сильно лучше, чем 99. 

Почему? А давайте подставим в формулу и проверим.

. A — я беременна,

. В — тест положительный,

. Р(А|В) — я беременна при условии, что результат теста положительный,

. P(A)=0,01 — вероятность забеременеть в принципе,

. P(B|A)=0,99  — вероятность получить положительный результат теста в случае беременности. Она равна 0,99 из точности теста.

А в знаменателе у нас Р(В) — вероятность получить положительный результат теста в принципе. Даже если он и неверный. Для этого умножим вероятность ложного срабатывания на количество небеременных девушек: 0,01 * 0,99, и сложим с вероятностью положительного срабатывания в случае действительной беременности: 0,99 * 0,01. Итого получаем P(A|B)=P(B|A)P(A)P(B)=0,99*0,01(0,01*0,99)+(0,99*0,01)=0,00990,0198=12=50%. Так что не беспокойтесь раньше времени. Возможно, все не так уж и страшно.

P(B|A)P(A)P(B)

0,99*0,01(0,01*0,99)+(0,99*0,01)

0,00990,0198

На самом деле, конечно, это гораздо полезнее знать не девушкам, а врачам, которые, например, занимаются исследованиями рака. Потому что в таких вещах шутить не стоит и каждый лишний процент — это надежда и вера в лучшее. 

…я живу в мире, где все вороны черные, но хочу понять, как это связано с красными яблоками.

Это еще одна хорошая иллюстрация того, как индуктивная логика противоречит интуиции, а байесовское мышление спасает ситуацию. Называется это парадоксом воронов.

Пусть есть некая теория, которая говорит, что все вороны черные. С точки зрения логики утверждение «все вороны черные» эквивалентно выражению «все предметы, не являющиеся черными, не являются воронами». Согласны? Теперь идем дальше. Если я увижу много черных воронов, это должно укрепить мою уверенность в моей теории. А теперь фокус. Если я даже не увижу ни одного черного ворона, но увижу много красных яблок, это, согласно индуктивной логике, должно также увеличить мою уверенность в том, что все вороны черные. Хотя интуитивно так и не кажется. И все же это так и есть. 

В самом деле, чем больше красных яблок я вижу, тем больше убеждаюсь в том, что не черный объект не является вороном, а это, как мы помним,  утверждение, эквивалентное нашей начальной формулировке. Теорема Байеса в этом случае помогает разрешить все математически. Если без формул, то все это будет звучать примерно так: чем больше не черных предметов мы можем наблюдать, тем более мы убеждены в верности нашей теории. То есть тем сильнее меняется наше апостериорное знание. Хотя наблюдение множества красных яблок окажет достаточно слабое воздействие на смещение вероятности того, что утверждение «все вороны черные» верно. Именно поэтому интуитивно нам это и непонятно. Вот если бы мы смогли посмотреть на все не черные предметы Вселенной и убедиться в том, что они не являются воронами, мы бы смогли до конца убедиться в том, что все вороны черные.

…я занимаюсь философией науки и хочу до конца разобраться с критерием фальсифицируемости по Попперу.

Продолжаем погружаться в мышление по Байесу. Для начала несколько слов о самом попперовском критерии.

Описание

Слепые мудрецы выясняют, что такое слон, путем ощупывания

Достаточно долгое время наука была чисто описательной и рецептурной: если долго тереть, можно зажечь огонь, если отрубить голову, остальное тело перестает быть живым, у бабочки есть крылья, голова и туловище, и так далее. Но в какой-то момент все поняли, что описания мало и что хотелось бы знать ответы на вопрос «почему?». Но вот отвечать на вопрос «почему?» оказалось довольно сложно. Точнее, проверять этот ответ.

Тогда пришли ребята, которые сказали: «А давайте просто брать и проверять так это или нет так» — и начали ставить массу экспериментов. Если теория бралась предсказать какой-то результат, а выходило что-то другое, теорию считали плохой. И несмотря на кажущуюся простоту такой схемы, сам принцип был формально сформулирован только в 20-х годах прошлого века и назван «верифицируемостью теории».

Но тут снова началось много неприятного. Оказалось, что сама верифицируемость не верифицируема, а в гуманитарной среде стали рождаться крутые науки, которые многое объясняли, но почти ничего, увы, не могли предсказать. Тут-то и пришел Карл Поппер со своим «научная теория должна быть потенциально фальсифицируемой». То есть, если хотите, чтобы наука могла как-то работать с вашей теорией, предъявите хотя бы мысленный эксперимент, результат которого может ее разрушить.

Например, утверждение о существовании чего-то ненаучно, потому мы не можем это опровергнуть. А вот утверждение о том, что чего-то не существует, научно, так как опровергается непосредственным предъявлением этого чего-то. Еще очень важно не путать научность и истинность. Потому что утверждение о том, что Луна состоит из сыра, тоже научно (можно это опровергнуть), хотя и не истинно. Истинность уже подтверждается доказательствами, экспериментами — вот этим вот всем. Хотя на 100% истинно оно все равно не будет никогда.

Теперь можно вернуться к Байесу. Оказывается, что идея Поппера о том, что научная теория может быть фальсифицирована, но никогда не сможет быть полностью подтверждена, это всего лишь частный случай байесовских правил. Здесь придется немного позанудствовать. Пусть у нас есть некая теория A, предсказывающая Х. Если Р(X|A)≈1 (вероятность того, что если теория А верна, свидетельство Х наступит с вероятностью почти 100%) и теория делает верные предсказания, тогда наблюдение Х~ (не Х) очень сильно фальсифицирует А.

С другой стороны, повторное наблюдение самого Х довольно слабо влияет на истинность теории, так как не несет в себе чего-то нового. Например, увидев черного ворона, мы вновь убедимся в том, что все вороны черные, но укрепит это нашу веру не очень сильно, ведь мы и так знаем, что можем наблюдать черных воронов. А вот чтобы подтвердить наверняка какую-то теорию А, нам нужно было бы найти такое свидетельство Х, чтобы Р(Х|А~) = 0, то есть предоставить такой Х, который при истинности противоположной теории был бы невозможен. Но этого мы сделать не можем, так как не можем рассматривать все возможные альтернативные объяснения. 

То есть мы не сможем предъявить хоть какое-то абсолютно невозможное свидетельство, если будет истинна теория «ни один ворон не является черным». Поэтому ни одна теория не верифицируема на 100%. Формально мы даже можем сказать, что отношение Р(X|A)/Р(Х|А) показывает нам, насколько наше наблюдение Х сильно в качестве свидетельства (насколько сильно оно подтверждает теорию).

Из формулы мы можем увидеть, что фальсификация (сюрприз!) действительно сильнее верификации: сильное свидетельство не является результатом высокой вероятности того, что А ведет к Х, но является результатом очень низкой вероятности того, что не А ведет к Х. Похожим образом мы можем увидеть, что на самом деле фальсифицировать теорию на 100% мы тоже не умеем, так как фальсификация вероятностна по своей природе. Если наблюдение Х является положительным свидетельством для нашей теории, то наблюдение Х опровергает теорию, но лишь в каком-то объеме. 

Получается, что утверждение Поппера о том, что нужна только фальсификация, держится лишь на том, что фальсификация работает гораздо сильнее, хотя по своей сути ничем не отличается от подтверждения. В узких кругах этот вывод стал одной из предпосылок к заявлению о так называемой байесовской революции, хотя по сути это всего лишь некое обобщение и улучшение. 

…я программист, на дворе конец 90-х, и мне нужно придумать, как избавиться от спама в электронной почте.

Теперь поговорим о том, зачем вообще Байес нужен в «народном хозяйстве», о приложениях. 

В данном примере со спамом решение проблемы основывается на принципе так называемого наивного байесовского классификатора, идея которого состоит в том, чтобы, оценив ряд характеристик, отнести объект к тому или иному классу. Модель такого классификатора опирается на использование теоремы Байеса со строгими предположениями о независимости (отсюда и наивность). Такой классификатор, несмотря на достаточно серьезные упрощения, обладает значительным преимуществом. Ему не нужно много начальных данных, чтобы достаточно эффективно справляться со своей задачей. Довольно смутное описание, но сейчас все станет яснее.

Рассмотрим на нашем конкретном примере. Мы получаем какое-то письмо, в котором содержатся какие-то слова в каком-то количестве. Сначала мы просто подсчитываем разные слова, входящие в это письмо, а потом определяем, является письмо спамом или нет. Проделав это некоторое количество раз, мы соберем базу слов вместе с частотой их появления в спаме и в обычных письмах. В итоге получаем табличку, где записаны слово, количество его упоминаний в спаме и общее количество упоминаний. Теперь введем понятие «веса» слова — вероятность того, что сообщение с таким словом является спамом. Например, такой оценкой может быть частота появлений этого слова в спаме, поделенная на частоту появлений этого слова в любом произвольном письме. Теперь скажем, что «вес» всего письма — это усредненный вес всех слов, которые в нем содержатся. Дальше мы просто говорим, что, например, если этот вес больше 80%, то будем считать это сообщение спамом. Мы получили новое письмо, определили спам это или не спам, и к известным нам данным добавилось новое знание про слова, встретившиеся нам в этом письме, поэтому мы запишем в нашу базу новые показатели и пересчитаем «веса». Помните, да? Старое знание + новый опыт = новое, более полное знание. Байес в действии. 

Почему тогда мы все еще иногда получаем спам, раз все так хорошо и просто? Во-первых, алгоритм работает только с текстом. А рекламу можно положить, например, и в картинку. Тогда для борьбы со спамом нужно придумывать что-то еще. Кроме того, данный метод основывается на предположении о том, что какие-то слова чаще встречаются в спаме, а какие-то — в обычных письмах, поэтому если это не так, то система просто не сработает. Некоторые составители рекламы даже специально пользуются так называемым методом байесова отравления — алгоритмом добавления в рекламный текст слов, делающих его менее «спамовым». Тем не менее в основу практически всех современных спам-фильтров входит именно этот алгоритм.

…я суперкомпьютер, и меня попросили придумать новый рецепт печенья.

Это еще один знаменитый кейс про IBM Watson, которого после отличных результатов в медицинской карьере и телевикторинах решили обучить большей креативности и дали ему разбираться в кулинарии. 

Суперкомпьютер изучил миллионы рецептов, превзошел химию и физиологию, почитал про запахи и сочетаемость продуктов и через какое-то время готов был вставать к плите. А точнее — посылать к ней кого-то, у кого есть чем готовить. Придумывал рецепты Watson, опираясь на три основных параметра: новизну, сочетаемость и приятность для человека. Здесь Байес сидит в новизне. Если мы возьмем, например, яблоко с корицей, то мало кому это покажется чем-то новым. А вот каперсы в карамели с креветками уже интереснее. Не факт, что это будет вкусно, но зато уж точно ново. Математическая модель, которая лежала в основе оценивания этой новизны, называется подходом «байесова удивления». Она оценивает разницу между апостериорной вероятностью встретить определенное сочетание продуктов (каперсы+карамель+креветки) в уже существующих рецептах с априорной вероятностью встретить этот же набор продуктов без добавления одного из них (например, креветки в карамели без каперсов наверняка встретить вполне себе можно). После определения новизны компьютер убирал несочетаемые рецепты с точки зрения запахов и вкуса, а потом ранжировал их по степени приятности. Так в недрах компании IBM появились рецепты миндально-шоколадного печенья в испанском стиле, клубничного десерта по-эквадорски и помидоров гриль на гренках с шафраном.  

…я бизнесмен и хочу захватить мир максимизировать прибыль фирмы.

Мы нанимаем новых работников. И конечно же мы хотим, чтобы они были надежные и трудоспособные. 

Сейчас, чтобы определить «качество» работника, HR-менеджеры обычно предлагают соискателю пройти множество психологических тестов, сходить на десяток разных собеседований или просто пытаются дать экспертную оценку самостоятельно. Однако весь этот процесс можно заменить программой, в основе которой лежит теорема Байеса. Например, существует экспертная система получения характеристики личности, где на входе потенциальный сотрудник проходит всего один тест — тест Кеттелла. Сам тест на выходе дает определенное значение шестнадцати факторов, таких как открытость/замкнутость, независимость/податливость и так далее. И, казалось бы, информации не так много, но оказывается, что, имея на руках всего шестнадцать этих значений и использовав теорему Байеса, мы можем достаточно хорошо спрогнозировать результаты и других тестов. Например, авторы этой системы предсказывали результаты теста Лири, который уже рассказывает о представлении субъекта об идеальном «Я» и его моделях поведения в группах. Последовательно получая значения факторов теста Кеттелла, Байес пересчитывал вероятность попадания человека в ту или иную группу «пригодности» для работы, на основе чего эксперты уже могли делать вывод. 

Еще байесовский стиль мышления может пригодиться менеджерам. Например, ваш подчиненный, работающий на макоронопродувательном заводе, пропустил одну макоронинку. Вы смотрите на него и думаете: «Мне срочно нужно наказать этого негодяя, чтобы он больше не допускал такой ужасной ошибки». Я же сижу в головном офисе и просто считаю статистику. И я знаю, что этот рабочий продувает от 10 до 15 тысяч макаронинок в день, а пропускает в среднем 7. И сегодня это была только третья. Обладая априорным знанием, я могу спокойно отнестись к такого рода ошибке. А вы — реагируете на наблюдение (причем с точки зрения математики абсолютно неадекватно). Из этого примера ясно, как важно обладать полнотой знаний и умением принимать решения на основе всех имеющихся данных.

Наконец, известная маркетинговая теория 4P (product, price, promotion, place) становится куда лучше и эффективнее, если добавить туда немного нашей теории. А именно — байесовскую оценку решения. Это такая статистическая оценка, которая может ответить на вопрос «при каких начальных вводных вероятность заработать будет максимальной», ну, или если говорить чуть более правильно, она максимизирует апостериорное математическое ожидание функции полезности. А дальше просто берем и применяем. Например, мы разрабатываем новый продукт. Байес позволяет здесь сравнить дополнительные затраты на проект со стоимостью полученной ценной информации, чтобы снизить затраты на неопределенность. Мы не знаем, будет ли наш новый продукт прибыльным, но, имея вводные данные, можем рассчитать прогнозируемую прибыль (апостериорную). Если эта прибыль приемлема, можно вложить еще денег в это исследование, если нет, проект стоит оставить. Делая такие расчеты с достаточной периодичностью, мы можем значительно уменьшить издержки, особенно в условиях высокого риска. С ценой, рекламой и логистикой схема та же. Есть вводные данные, есть гипотезы насчет каких-то планируемых нововведений. Считаем вероятность прибыли, смотрим, сравниваем. Профит.

…я занимаюсь машинным обучением.

Здесь Байеса стали использовать не так давно, но, судя по результатам, останавливаться не собираются. 

Цель машинного обучения — научить компьютер «думать» не по строго заданному алгоритму, а «по ситуации» (как человек). Тут у нас всегда есть две главные составляющие — множество объектов (ситуаций, вопросов) и набор гипотез (ответов, выходов, реакций). Между объектами и гипотезами существует определенная закономерность, которую обычно называют алгоритмом прогнозирования. В большинстве случаев такую закономерность невозможно задать строгими правилами. Зато у нас есть набор обучающих данных — прецедентов, пар «объект-гипотеза», которые являются некой иллюстрацией этой самой закономерности. Мы подходим к машине, которую хотим обучить, даем ей какую-то программу обучения, показываем обучающую выборку и говорим: «Учись!» Если машина учится, то через некоторое время для любого нового объекта того же класса она сможет выдать нам правильный выход (ответ), хотя никакого формального правила этого определения мы ей не давали. Более того, это правило иногда не знаем даже мы сами. Простейший пример — распознавание образов. Например, вилки. Готов спорить, что вы не сможете придумать однозначного описания вилки, которое не подошло бы чему-то еще. Но вилку-то мы с вами умеем распознавать. 

То есть машина сама ищет модель, которая наиболее точно описывает наши связи «вход-выход» и меньше всего ошибается. Как нетрудно догадаться, вся загвоздка здесь находится в программе обучения. Казалось бы, интуитивно понятно, что мы можем просто перебрать все возможные алгоритмы прогнозирования и посмотреть, какой из них меньше всего ошибается. Однако такой метод, как показывает практика, далеко не всегда работает. Более того, в какой-то момент разработчики в области машинного обучения поняли, что существует определенная зависимость между сложностью алгоритма прогнозирования и величиной ошибки. Так как же найти компромисс? Как найти такой алгоритм, который будет не очень сложным, довольно точным и устойчивым? Байесовский подход может дать нам точный численный критерий для решения такой задачи и обеспечить ряд приятных преимуществ. 

Основная идея такая: мы для каждой гипотезы (алгоритма) будем вычислять апостериорные вероятности получения наших обучающих данных и в итоге выберем ту, для которой такая вероятность окажется максимальной. Такой подход называют maximum a posteriori probability (MAP). Математически доказано, что на выходе такой алгоритм даст нам лучшую гипотезу, лучший алгоритм прогнозирования. Ключевым отличием здесь является то, что на вход мы подаем распределение (зависимость вероятности от параметра, иными словами — функцию), показывающее наше незнание или неопределенность относительно некоторой величины, и на выходе получаем не точечную оценку, а точно такое же распределение. Схема та же. Подаем априорное распределение (незнание) искомой величины, наблюдаем за какими-то косвенными характеристиками (проявлениями) этой величины, изменившимися в результате прохождения цикла обучения, получаем новое, более точное представление о нашей величине в виде апостериорного распределения, которое становится новым априорным. 

Благодаря этому удается получить точное математическое описание процесса обучения и получить не одну гипотезу, которую наша машина посчитала лучшей, а численную оценку достоверности всех возможных гипотез. Например, если это нейросеть, то при обычном подходе она просто находит стабильное состояние при определенном наборе весов (если вы даже примерно не представляете, как работает нейросеть, можно представлять весы как оптические характеристики линз; собрав определенный набор линз с разными диоптриями, вы сможете четко разглядеть любое изображение) на определенной обучающей выборке, и у нас нет никакой уверенности в том, что эта сеть действительно лучшая. В байесовском подходе этого удается избежать. 

Еще одно важное свойство, которое мы приобретаем, — регуляризация, или, другими словами, отсутствие эффекта переобучения. «Переобучение» — это когда мы слишком сильно подгоняем наш алгоритм под имеющиеся обучающие данные. То есть в поисках «правильных» параметров нашего алгоритма мы на самом деле нашли неправильные, но идеально подходящие для нашего конкретного набора. И когда мы подадим на вход какой-то другой объект, не входивший в список обучающих, мы можем получить совсем неправильный выход. В байесовском подходе этого не случится, так как там просто не существует «правильных» параметров. Там сплошные вероятности и распределения. И это очень удобно, потому что чем больше, например, сеть, тем она лучше, а именно на больших моделях чаще всего приходится сталкиваться с эффектом переобучения. К тому же нам будет достаточно не очень большой обучающей выборки, чтобы достаточно хорошо настроить наш алгоритм. Опять же за счет работы именно с распределениями, а не просто численными характеристиками.  

Казалось бы, одни плюсы. Почти не надо учить, получаем спектр правдоподобных гипотез, можем работать с критическими значениями, все математически точно и красиво, и машина сама делает оптимальный выбор. Но тут мы вспоминаем про вычислительную сложность. Байесовский подход основан на том, что мы вычислим вероятности всех возможных алгоритмов для всех обучающих данных. Кроме того, в некоторых моделях приходится не просто просчитывать простые вероятности, а считать, например, для каждой из них интегралы в пространствах с размерностью десятки и сотни тысяч. В общем, очень сложно. Даже компьютеру. С этого момента математики и программисты начинают немного обходить эту сложность стороной, говоря, что полный перебор вовсе не нужен и мы можем посчитать только часть вероятностей, либо используя сведение задачи байесовского вывода к задачам оптимизации, которые мы умеем решать хорошо, либо просто обращаясь к разного рода статистическим и приближенным методам. Но об этом уже лучше почитать отдельно.

…я — Акинатор.

Если вы не знаете, кто такой Акинатор, то это такое приложение, которое довольно быстро определяет загаданного вами персонажа, задавая ряд вопросов.

Байеса, например, Акинатор угадал на 26-м вопросе. Правда, нужно отметить, что над Акинатором успели порядочно поиздеваться, сбив систему введением баллов за правильный ответ, но в лучшие годы он мог отгадать, например, Эйнштейна за шесть вопросов, которые, казалось, никакого прямого отношения к ученому не имеют. Так вот, есть предположение, что Акинатор тоже работает по Байесу. Предположение, потому что точной информации об устройстве интернет-гения мне найти так и не удалось, но зато я нашел несколько статей с рассуждениями и попытками сделать что-то похожее, которые выглядят правдоподобно, поэтому расскажу о них. 

Итак, для начала, чтобы сделать такую игру, нужно решить, что будет происходить внутри. Первое — такая программа должна обучаться. Потому что чем больше персонажей, тем больше уточняющих вопросов необходимо задавать, но когда база героев — несколько сотен тысяч, искать их «в лоб» крайне неудобно. Поэтому программа должна учиться на ходу, используя ответы пользователей. Программа должна уметь прощать ошибки, потому что иногда у человека могут оказаться просто-напросто ложные убеждения насчет какого-нибудь персонажа, но этот «выброс» не должен повлиять на конечный результат. Наконец, программа должна правильно подбирать вопросы, минимизируя их количество. 

Если бы не прощение ошибок, все было бы достаточно просто. Мы могли бы составить древовидную структуру, где в узлах были бы вопросы, а листья были бы персонажами. Тогда задача просто состояла бы в том, чтобы дойти от корня до конкретного персонажа, пройдя по определенным вопросам. Но такое дерево не прощает ошибок. Поэтому, поскольку мы работаем с неопределенностью, но в основе лежит все равно классическая алгебра логики (ответы да/нет), на помощь снова приходит Байес, который в узких кругах считается эталоном рационального мышления, а это как раз то, что нам нужно.

Дальше мы действуем относительно просто. Будем считать Ai событием «загадан персонаж i», который может быть и Нуф-Нуфом, и Эдвардом Сноуденом, и Эллой Фицджеральд. В — множество ответов на вопросы относительно персонажа i. То есть В = {B1,B2,…,Bk} — k разных вопросов в духе «Ваш персонаж мужчина?» или «Есть ли у вашего персонажа рог?» Тогда апостериорная величина P(Ai|B) будет показывать вероятность того, что был загадан именно объект i. С каждым следующим вопросом эта вероятность для каждого i из нашей базы будет меняться, и в какой-то момент, когда она станет достаточно высокой, мы сможем сделать догадку. Кроме того, при k=0, то есть ситуации, когда ни одного вопроса еще не задано, наши вероятности все равно не будут равны для всех i. Ведь, например, Пушкина будут загадывать чаще, чем Дугласа Сполдинга. Поэтому мы должны учесть еще и частоту загадываемых персонажей. Дальше нужно будет сделать еще несколько алгоритмически важных вещей, связанных с избежанием ошибок и проблемой выбора вопросов, но об этом лучше прочитать в оригинале. 

Так или иначе, мы получили достаточно простой алгоритм, который на самом деле очень похож на то, как думаем и мы с вами, но с одним отличием: он не ведется на уловки репрезентативной эвристики. Это когда, например, вам говорят, что есть некая женщина, которая занимается аюрведой, читает гороскопы и носит странную одежду, а потом спрашивают, кто она — учительница или гадалка? Большинство людей скажут, что гадалка, игнорируя тот факт, что вероятность встретить гадалку в жизни существенно меньше, чем встретить учителя. А значит, и вероятность того, что эта женщина — гадалка, вовсе не так велика. Именно поэтому Акинатор зачастую выдает ответ, когда вы этого совсем не ждете. Потому что общая картина складывается изо всей информации, которая у нас есть, но мы почему-то довольно часто не обращаем внимания на, казалось бы, вполне себе очевидные факты.

…я честно прочитал статью до этого момента, но все еще не понимаю, зачем мне Байес.

Для начала я попытаюсь просто перечислить области и сферы деятельности, которые я еще не упомянул, где постоянно используется байесовский подход. Биологи получают наиболее правдоподобные филогенетические деревья, опираясь на байесовские модели. В компьютерной лингвистике проверка гипотез происходит примерно по тем же схемам, что и в филогенетике. Современный эконометрический анализ использует байесовский подход из-за относительно малых выборок, необходимых для построения достаточно точных моделей. Дизайнерские агентства, проводящие A/B-тестирования сайта, используют программы, в основе который лежит Байес. Психологи-когнитивисты предполагают, что на самом деле наш мозг, принимая решения и размышляя, тоже опирается на байесовский алгоритм. Даже в области государственной безопасности не обошлось без него. Сам Гарри Поттер (в книге Юдковского) понял, почему ему никуда не деться от тяги стать Темным Лордом, именно благодаря определению истинности суждения по Байесу. Как вы понимаете, на этом наш список не закончен, длить его можно до бесконечности (ну почти). А теперь еще один небольшой фокус. Если вы ничего до сегодняшнего дня не знали про эту теорему, этого священника и этот подход, но прочитали статью до конца, наверняка ваша уверенность в том, что это что-то стоящее, немного повысилась. Ведь правда? Улавливаете мою мысль? К этому моменту все эти выкладки и размышления кажутся понятными и очевидными, но на самом деле с вами только что все произошло по Байесу.

Эта простая идея на самом деле уже изменила очень многое, и многое обязательно еще изменит. Фанатики поговаривают, что если мы все поголовно погрузимся в эту философию, то сможем познать мир до конца, потому что не останется абсолютно никакой неопределенности и абсолютно все будет просчитано. До мелочей. И мир станет гораздо лучше. 

Но если ты такой умный, то почему же тогда ты такой бедный?

Очень справедливо замечено. Огромная проблема, которая заметна не сразу, это начальная априорная вероятность. Например, в самом первом примере с беременностью мы откуда-то знали, что вероятность стать мамой по неосторожности равна одному проценту. Кто нам это сказал? В жизни — только статистика, являющаяся не самым надежным источником. Более того, в реальной жизни это, скорее всего, будет не конкретное число, а какой-то интервал, что несколько осложняет вычисления. Иногда эта априорная вероятность вообще основывается на чистых догадках, тогда мы даем дорогу субъективизму и серьезной ошибке на самом старте. Из-за этого теорема Байеса не всегда «служит добру», потому что является универсальной для всего на свете. И при качественном подборе априорных данных мы можем получить с помощью нее и значительную вероятность вреда ГМО, и существования рептилоидов, и даже действенности заряженной воды. 

Но на самом деле здесь лежит красивая идея: если вы недостаточно хорошо стараетесь найти альтернативные обоснования уже имеющихся свидетельств, то эти свидетельства лишь сильнее подтвердят то, во что вы верите. Например, увидев странную штуку в небе и рассчитав вероятность ее появления там, можно убедиться в том, что это определенно НЛО. Но если покопаться глубже и подумать о других возможных причинах, то, возможно, все окажется не так интересно и загадочно, как вам, может, и хотелось бы. 

Так все же — что с того?

Попробуем все быстренько обобщить. Теорема Байеса — это не только математический аппарат, который помогает в решении множества прикладных задач. Это в первую очередь стиль мышления, подразумевающий ясность, полноту и непредвзятость. Всегда необходимо помнить, что у любого свидетельства существует множество причин, поэтому никогда не стоит делать поспешных выводов. И даже если вы видите прямо перед собой огромного дракона, дышащего огнем, вспомните, что вы сегодня принимали, как спали, какой сегодня день и где вы находитесь. Возможно, все можно объяснить довольно просто. Наравне с этим нельзя забывать, что любая наша интерпретация такого свидетельства очень сильно зависит от той информации, которая у нас в голове уже есть. Например, я как-то раз в детстве нашел в огороде что-то шарообразное, мягкое, прозрачное и зеленое. Конечно же, я подумал, что это пришелец. А потом оказалось, что это всего-навсего «попрыгунчик». Но мне было лет пять, и о существовании «попрыгунчиков» я тогда еще не знал. Поэтому каждый раз, когда вам встречается что-то новое и вы пытаетесь объяснить это теорией А, которая есть у вас в голове, подумайте о том, что было бы, если бы этой теории не существовало. Могли бы вы тогда все равно увидеть этот инопланетный «попрыгунчик» или нет? Наконец, нужно тщательно подходить к выбору теорий, подтверждающих наши свидетельства. Если теория объясняет явление, которое может объясняться и другой теорией, то такое явление будет плохим доказательством нашей теории и сама теория поэтому будет слабо доказуемой. 

Таким образом, это всего лишь свод простых на первый взгляд правил, который помогает нам ориентироваться в пространстве правдивости, вероятности и неопределенности. Думай обо всем и сразу, учитывай все предпосылки, делай лучшие из возможных выводы. Это идеал, к которому можно стремиться.

И как только мы понимаем, что все, что мы знаем здесь и сейчас, основано на том, что мы знали минуту назад, что было в свою очередь основано на том, что мы знали месяц, год, десятилетие назад, что в свою очередь основано на тех знаниях, которые были у нас при рождении, мы начинаем думать: а все ли наши убеждения о мире вообще верны? А что это вообще за система, в которую мы попали, и откуда взялись все те, начальные предпосылки? А соответствует ли вообще хоть сколько-нибудь то, что я знаю о мире, действительности?

Что ж, think Bayes and go to the truth, ведь, как говорил Джордано Бруно, стремление к истине — единственное занятие, до­стойное героя.

 Егор Антощенко

Теги

МатематикаПопуляризация науки

| алгоритма Байеса (Майкрософт) Документация Майкрософт

  • Статья
  • Чтение занимает 4 мин

Применимо к: SQL Server Analysis Services Azure Analysis Services Power BI Premium

Важно!

Интеллектуальный анализ данных устарел в SQL Server 2017 Analysis Services и теперь прекращен в SQL Server 2022 Analysis Services. Документация не обновляется для устаревших и неподдерживаемых функций. Дополнительные сведения см. в разделе обратной совместимости служб Analysis Services.

Алгоритм Microsoft Naive Bayes — это алгоритм классификации, основанный на теоремах Байеса, который можно использовать как для исследовательского, так и прогнозного моделирования. Слово «упрощенный» в его названии указывает на то, что алгоритм использует методы Байеса, но не учитывает возможные зависимости.

Этот алгоритм является менее вычислительным, чем другие алгоритмы Майкрософт, и, следовательно, полезен для быстрого создания моделей интеллектуального анализа данных для обнаружения связей между входными столбцами и прогнозируемыми столбцами. Этот алгоритм можно использовать для первоначального исследования данных, а затем применить результаты для создания дополнительных моделей интеллектуального анализа с другими алгоритмами, требующими большего количества вычислений и являющимися более точными.

Пример

В рамках постоянной стратегии продвижения отдел маркетинга компании Adventure Works Cycle решил разослать листовки потенциальным клиентам. Чтобы снизить себестоимость, было принято решение рассылать листовки только тем клиентам, которые, вероятно, ответят. Компания хранит в базе данных демографические данные и сведения об ответах на предыдущие рассылки. Необходимо использовать эти данные для определения возможности применения таких демографических показателей, как возраст и место проживания, для прогнозирования ответа на рекламную кампанию путем сравнения потенциальных клиентов с клиентами, которые обладают подобными характеристиками и которые осуществляли покупки в компании в прошлом. Необходимо определить различия между теми клиентами, которые купили велосипед, и теми, которые не купили.

С помощью алгоритма Microsoft Naive Bayes отдел маркетинга может быстро предсказать результат для определенного профиля клиента и, следовательно, определить, какие клиенты, скорее всего, отвечают на листовки. С помощью средства просмотра Microsoft Naive Bayes в SQL Server Data Tools они также могут визуально исследовать, какие входные столбцы влияют на положительные ответы на листовки.

Принцип работы алгоритма

Алгоритм Microsoft Naive Bayes вычисляет вероятность каждого состояния каждого входного столбца, учитывая каждое возможное состояние прогнозируемого столбца.

Чтобы понять, как это работает, используйте средство просмотра Байеса (Майкрософт) в SQL Server Data Tools (как показано на следующем рисунке) для визуального изучения распределения состояний алгоритма.

Здесь средство просмотра Байеса (Майкрософт) перечисляет каждый входной столбец в наборе данных и показывает, как распределяются состояния каждого столбца, учитывая каждое состояние прогнозируемого столбца.

С помощью этого представления модели можно определить входные столбцы, которые важны для разграничения состояний прогнозируемого столбца.

Например, в строке для поля Commute Distance, как показано здесь, распределение входных значений наглядно отличается для покупателей и тех, кто не покупает. Показанные данные указывают на то, что входное значение Commute Distance = 0-1,6 км потенциально имеет влияние на результат прогноза.

Средство просмотра также отображает значения для отдельных классов продуктов таким образом, что можно увидеть, что для клиентов, которые преодолевают расстояние от 1 до 3,3 километра от дома до рабочего места, вероятность приобретения велосипеда составляет 0,387, а вероятность его неприобретения — 0,287. В данном примере для прогнозирования вероятности покупки велосипеда алгоритм использует числовые данные, полученные из характеристик клиентов, например расстояния до работы.

Дополнительные сведения об использовании средства просмотра Байеса (Майкрософт) см. в статье «Обзор модели» с помощью средства просмотра Байеса (Майкрософт).

Данные, необходимые для моделей упрощенного алгоритма Байеса

При подготовке данных, предназначенных для использования в обучении модели упрощенного алгоритма Байеса, следует учитывать требования алгоритма, в том числе необходимый объем данных и способ их использования.

Далее приводятся требования для модели упрощенного алгоритма Байеса.

  • Единичный ключевой столбец Каждая модель должна содержать один числовой или текстовый столбец, который уникальным образом определяет каждую запись. Применение составных ключей не допускается.

  • Входные столбцы . В модели упрощенного алгоритма Байеса все столбцы должны быть дискретными или иметь сегментированные значения. Сведения о том, как дискретизировать (двоичные) столбцы, см. в разделе «Методы дискретизации (интеллектуальный анализ данных)».

  • Переменные должны быть независимыми. Для модели упрощенного алгоритма Байеса также важно обеспечить независимость входных атрибутов друг от друга. Это особенно важно, когда модель используется для прогнозирования. Если использовать два столбца данных, которые тесно связаны между собой, то это приведет к умножению значений этих столбцов, что может затруднить интерпретацию других факторов, влияющих на результат.

    Напротив, возможность алгоритма определять связи между переменными полезна при исследовании модели или набора данных для обнаружения связей между входными данными.

  • По крайней мере один прогнозируемый столбец Прогнозируемый атрибут должен содержать дискретные или дискретизированные значения.

    Значения в прогнозируемом столбце могут рассматриваться как входные. Такая практика может оказаться полезной при исследовании нового набора данных для обнаружения связей между столбцами.

Просмотр модели

Для просмотра модели используется средство просмотра упрощенного алгоритма Байеса (Майкрософт). Средство просмотра показывает, как входные атрибуты связаны с прогнозируемым атрибутом. Также приводится подробный профиль каждого кластера, список атрибутов, отличающих кластер от остальных, и характеристики всего набора данных для обучения. Дополнительные сведения см. в разделе Просмотр модели с помощью средства просмотра упрощенного алгоритма Байеса (Майкрософт).

Если вы хотите узнать больше подробностей, вы можете просмотреть модель в средстве просмотра деревьев содержимого (интеллектуальный анализ данных) Майкрософт. Дополнительные сведения о типе сведений, хранящихся в модели, см. в разделе «Содержимое модели интеллектуального анализа данных» для моделей байеса (службы Analysis Services — интеллектуальный анализ данных).

Составление прогнозов

После обучения модели результаты хранятся в виде набора закономерностей, которые можно исследовать или делать на их основе прогнозы.

Можно создавать запросы, возвращающие прогнозы о связи новых данных с прогнозируемым атрибутом, или получать статистику, описывающую взаимосвязи, обнаруженные моделью.

Дополнительные сведения о создании запросов к модели интеллектуального анализа данных см. в разделе Запросы интеллектуального анализа данных. Примеры использования запросов с моделью упрощенного алгоритма Байеса см. в разделе Примеры запросов к модели упрощенного алгоритма Байеса.

  • Поддерживается использование языка разметки прогнозирующих моделей (PMML) для создания моделей интеллектуального анализа данных.

  • Поддерживается детализация.

  • Не поддерживается создание измерений интеллектуального анализа данных.

  • Поддерживается использование моделей интеллектуального анализа OLAP.

См. также:

Алгоритмы интеллектуального анализа данных (службы Analysis Services — интеллектуальный анализ данных)
Выбор компонентов (интеллектуальный анализ данных)
Примеры запросов к модели упрощенного алгоритма Байеса
Содержимое моделей интеллектуального анализа данных для моделей упрощенного алгоритма Байеса (службы Analysis Services — интеллектуальный анализ данных)
Технический справочник по упрощенному алгоритму Байеса (Майкрософт)

Что такое байесовский анализ? | Международное общество байесовского анализа

Кейт Коулз, Роб Касс и Тони О’Хаган

То, что мы сейчас знаем как байесовскую статистику, не имело четкого применения с 1763 года. Хотя метод Байеса с энтузиазмом подхватили Лаплас и другие ведущие специалисты по вероятностям в то время она приобрела дурную славу в 19 веке, потому что они еще не знали, как правильно обращаться с априорными вероятностями. В первой половине 20-го века была разработана совершенно другая теория, называемая теперь частотной статистикой. Но пламя байесовского мышления поддерживали несколько мыслителей, таких как Бруно де Финетти в Италии и Гарольд Джеффрис в Англии. Современное байесовское движение началось во второй половине 20-го века под руководством Джимми Сэвиджа в США и Денниса Линдли в Великобритании, но байесовский вывод оставался чрезвычайно трудным для реализации до конца 19 века.80-х и начале 1990-х годов, когда мощные компьютеры стали широко доступны и были разработаны новые вычислительные методы. Последующий всплеск интереса к байесовской статистике привел не только к обширным исследованиям байесовской методологии, но и к использованию байесовских методов для решения насущных вопросов в различных прикладных областях, таких как астрофизика, прогнозирование погоды, политика здравоохранения и уголовное правосудие.

Научные гипотезы обычно выражаются через распределения вероятностей наблюдаемых научных данных. Эти распределения вероятностей зависят от неизвестных величин, называемых параметрами. В байесовской парадигме текущие знания о параметрах модели выражаются путем размещения распределения вероятностей по параметрам, называемого «априорным распределением», которое часто записывается как

     

Когда становятся доступными новые данные, содержащаяся в них информация о параметрах модели выражается в «вероятности», которая пропорциональна распределению наблюдаемых данных с заданными параметрами модели, записываемой как

     

Эта информация затем в сочетании с априорным для получения обновленного распределения вероятностей, называемого «апостериорным распределением», на котором основаны все байесовские выводы. Теорема Байеса, элементарное тождество в теории вероятностей, утверждает, как обновление выполняется математически: апостериорное значение пропорционально априорному, умноженному на вероятность, или, точнее,

   

Теоретически апостериорное распределение всегда доступно, но в реально сложных моделях необходимые аналитические вычисления часто трудновыполнимы.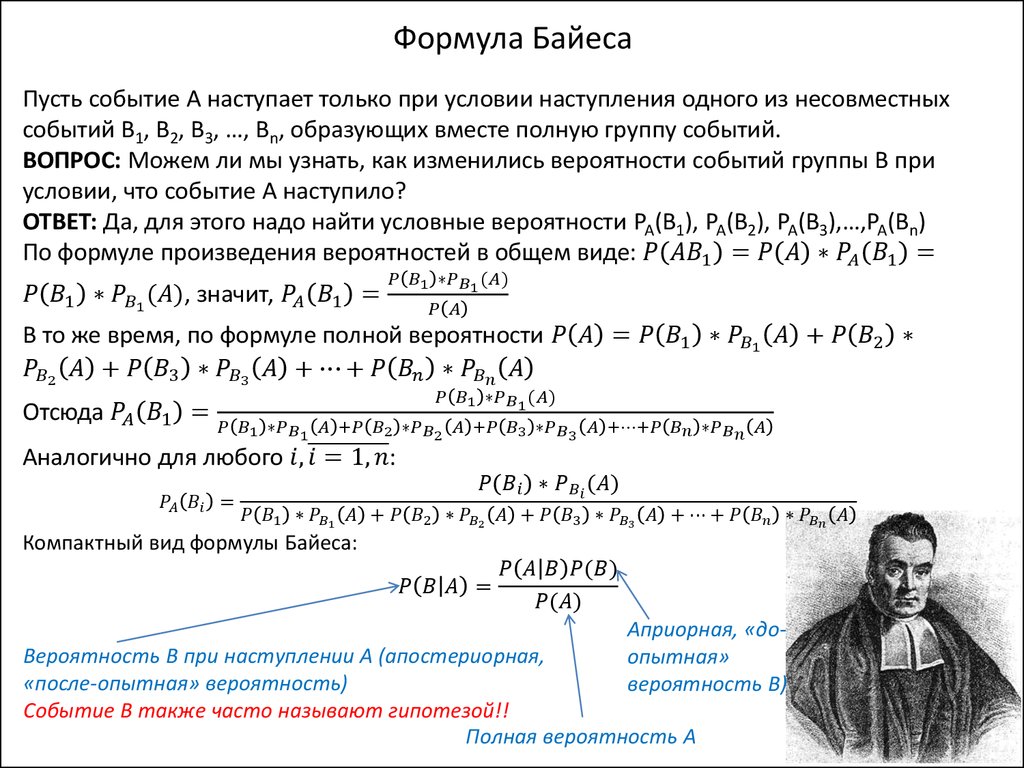 В течение нескольких лет, в конце 1980-х и начале 1990-х годов, стало понятно, что методы получения выборок из апостериорного распределения могут быть очень широко применимы.

Есть много причин для принятия байесовских методов, и их применение появляется в самых разных областях. Многие люди защищают байесовский подход из-за его философской последовательности. Различные фундаментальные теоремы показывают, что если человек хочет принимать последовательные и обоснованные решения в условиях неопределенности, то единственный способ сделать это — использовать байесовские методы. Другие указывают на логические проблемы с частотными методами, которых нет в байесовской модели. С другой стороны, априорные вероятности по своей сути субъективны — ваша априорная информация отличается от моей — и многие статистики считают это фундаментальным недостатком байесовской статистики. Сторонники байесовского подхода утверждают, что это неизбежно и что частотные методы также влекут за собой субъективный выбор, но это было основным источником разногласий между «фундаменталистскими» сторонниками двух статистических парадигм, по крайней мере, в течение последних 50 лет. Напротив, именно прагматические преимущества байесовского подхода способствовали его сильному росту за последние 20 лет и являются причиной его принятия в быстро растущих областях. Мощные вычислительные инструменты позволяют байесовским методам с относительной легкостью решать большие и сложные статистические задачи, в то время как частотные методы могут только приближаться или вообще не срабатывают. Методы байесовского моделирования предоставляют людям во многих дисциплинах естественные способы структурирования своих данных и знаний, а также дают прямые и интуитивно понятные ответы на вопросы практиков.

Существует множество разновидностей байесовского анализа. Самая полная версия байесовской парадигмы отбрасывает статистические проблемы в рамки процесса принятия решений. Это влечет за собой формулирование субъективных априорных вероятностей для выражения ранее существовавшей информации, тщательное моделирование структуры данных, проверку и учет неопределенности в предположениях модели, формулирование набора возможных решений и функции полезности для выражения того, как влияет на ценность каждого альтернативного решения. по неизвестным параметрам модели. Но каждый из этих компонентов может быть опущен. Многие пользователи байесовских методов не используют подлинную априорную информацию либо потому, что она несущественна, либо потому, что им не нравится субъективность. Теоретическая основа принятия решений также широко опускается, и многие считают, что статистический вывод не должен на самом деле формулироваться как решение. Итак, существуют разновидности байесовского анализа и разновидности байесовских аналитиков. Но общая черта, лежащая в основе этого варианта, — это основной принцип использования теоремы Байеса и вероятностного выражения неопределенности относительно неизвестных параметров.

Повышение доступности исследований, данных и фактических данных

Повышение доступности исследований, данных и фактических данных

Байесовские методы исследования позволяют лицам, принимающим решения, обнаруживать, что с наибольшей вероятностью работает, путем сопоставления результатов новых исследований с существующей доказательной базой.

Этот подход также можно использовать для повышения прозрачности, объективности и справедливости.