| ГОСТы, СНиПы Карта сайта TehTab.ru Поиск по сайту TehTab.ru | Навигация по справочнику TehTab.ru: главная страница / / Техническая информация/ / Математический справочник/ / Интегральное и дифференциальное исчисление. Табличные производные и интегралы. Таблица производных. Таблица интегралов. Таблица первообразных. Найти производную. Найти интеграл. Диффуры. / / Таблица первообразных («интегралов»). Табличные неопределенные интегралы. (Простейшие интегралы и интегралы с параметром). Формулы интегрирования по частям. Формула Ньютона-Лейбница.
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Нашли ошибку? Есть дополнения? Напишите нам об этом, указав ссылку на страницу. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
TehTab. Реклама, сотрудничество: [email protected] | Обращаем ваше внимание на то, что данный интернет-сайт носит исключительно информационный характер. Информация, представленная на сайте, не является официальной и предоставлена только в целях ознакомления. Все риски за использование информаци с сайта посетители берут на себя. Проект TehTab.ru является некоммерческим, не поддерживается никакими политическими партиями и иностранными организациями. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Таблица интегралов. Табличные неопределенные интегралы. (Простейшие интегралы и интегралы с параметром). Формулы интегрирования по частям. Формула Ньютона-Лейбница.
Правила интегрирования.
ruПодготовка школьников к ЕГЭ (Справочник по математике — Элементы математического анализа
| Справочник по математике | Элементы математического анализа | Интегралы |
| Определенный интеграл как площадь криволинейной трапеции |
| Производная от определенного интеграла по верхнему пределу |
| Теорема Ньютона — Лейбница |
| Примеры решения задач |
Определенный интеграл как площадь криволинейной трапеции
Рассмотрим на плоскости прямоугольную систему координат Oty , ось абсцисс которой в данном разделе будем обозначать Ot , а не Ox (рис.
1).
Рис.1
Пусть y = f (t) – непрерывная на отрезке [a, b] функция, принимающая только положительные значения.
Определение 1. Фигуру, ограниченную графиком функции y = f (t) сверху, отрезком [a, b] снизу, а справа и слева отрезками прямых t = a и t = b (рис. 2), называют криволинейной трапецией.
Рис.2
Определение 2. Число, равное площади криволинейной трапеции, изображенной на рисунке 2, называют определенным интегралом от функции f (t) в пределах от a до b и обозначают
| (1) |
Формула (1) читается так: «Интеграл от a до b от функции f (t) по dt»
Определение 3. В формуле (1) функцию f (t) называют подынтегральной функцией, переменную t называют переменной интегрирования, отрезок [a, b] называют отрезком интегрирования, число b называют верхним пределом интегрирования, а число a – нижним пределом интегрирования.
Производная от определенного интеграла по верхнему пределу
Если обозначить S (x) площадь криволинейной трапеции, ограниченной с боков отрезками прямых t = a и t = x (рис. 3),
Рис.3
то будет справедлива формула
| (2) |
Теорема 1. Производная от определенного интеграла по верхнему пределу интегрирования равна значению подынтегральной функции в верхнем пределе интегрирования.
Другими словами, справедлива формула
Доказательство. Из формулы (2) следует, что
| (3) |
где через Δx обозначено приращение аргумента x (рис. 4)
Рис.
4
Из формул (3) и (2) получаем, что
| (4) |
где через ΔS обозначено приращение функции S (x), соответствующее приращению аргумента Δx (рис. 5)
Рис.5
Если ввести обозначения
(см. раздел «Наибольшее и наименьшее значение функции на отрезке»), то можно заметить, что выполнено неравенство
| (5) |
смысл которого заключается в том, что площадь криволинейной трапеции, изображенной на рисунке 5, не может быть меньше, чем площадь прямоугольника с основанием Δx и высотой m, и не может быть больше, чем площадь прямоугольника с основанием Δx и высотой M.
Из неравенства (5) следует, что
откуда, переходя к пределу при Δx → 0, получаем
В силу непрерывности функции y = f (t) выполнено равенство
По определению производной функции S (x) имеем
| (6) |
что и завершает доказательство теоремы 1.
Следствие 1. Функция S (x) является первообразной подынтегральной функции f (x) .
Теорема Ньютона — Лейбница
Теорема Ньютона-Лейбница. Если F (x) – любая первообразная функции f (x), то справедливо равенство
| (7) |
Доказательство. Поскольку S (x) и F (x) – две первообразных функции f (x), то существует такое число c, что выполнено равенство
| S (x) = F (x) + c | (8) |
Воспользовавшись равенством (8), из формулы (2) получаем, что
| (9) |
Подставив в формулу (9) значение x = a, получаем равенство
| (10) |
Заметим, что
| (11) |
поскольку площадь криволинейной трапеции, «схлопнувшейся» в отрезок, лежащий на прямой t = a, равна 0 .
Из формул (10) и (11) следует, что
c = – F (a) ,
и формула (9) принимает вид
,
что и завершает доказательство теоремы Ньютона-Лейбница.
Замечание 1. Формулу (7) часто записывают в виде
| (12) |
и называют формулой Ньютона-Лейбница.
Замечание 2. Для правой части формулы Ньютона-Лейбница часто используют обозначение
Замечание 3. Формулу Ньютона-Лейбница (12) можно записывать, как с переменной интегрирования t , так и с любой другой переменной интегрирования, например, x :
Замечание 4.Все определения и теоремы остаются справедливыми не только в случае положительных непрерывных функций f (x), но и для гораздо более широкого класса функций, имеющих произвольные знаки и интегрируемых по Риману, однако этот материал уже выходит за рамки школьного курса математики.
Примеры решения задач
Задача 1. Найти площадь фигуры, ограниченной линиями
y = e – x, y = 0, x = 0, x = ln 3.
Решение. Рассматриваемая фигура является криволинейной трапеции (рис. 6)
Рис.6
Найдем площадь этой криволинейной трапеции:
Ответ.
Задача 2. График функции y = f (x) изображен на рисунке 7.
Рис.7
Вычислить интеграл
| (13) |
Решение. Интеграл (13) равен площади криволинейной трапеции, ограниченной сверху графиком функции y = f (x), ограниченной снизу осью абсцисс Ox и ограниченной с боков отрезками прямых x = 2 и x = 9.
Криволинейная трапеция состоит из квадрата, раскрашенного на рисунке 7 розовым цветом, и трапеции, раскрашенной на рисунке 7 зеленым цветом. Площадь квадрата равна 9, а площадь трапеции равна 20. Таким образом, интеграл (13) равен 29.
Ответ. 29.
Задача 3. Вычислить определенный интеграл
| (14) |
Решение. Поскольку одной из первообразных подынтегральной функции интеграла (14) является функция
то в соответствии с формулой Ньютона-Лейбница получаем
Ответ.
На нашем сайте можно также ознакомиться нашими учебными материалами для подготовки к ЕГЭ по математике.
1.1. Способ непосредственного интегрирования
Предварительно изучите по учебнику Г. М. Фихтенгольца «Основы математического анализа», т. I, главу X, п° 155—159. Обратите особое внимание на примеры, решенные в п° 159.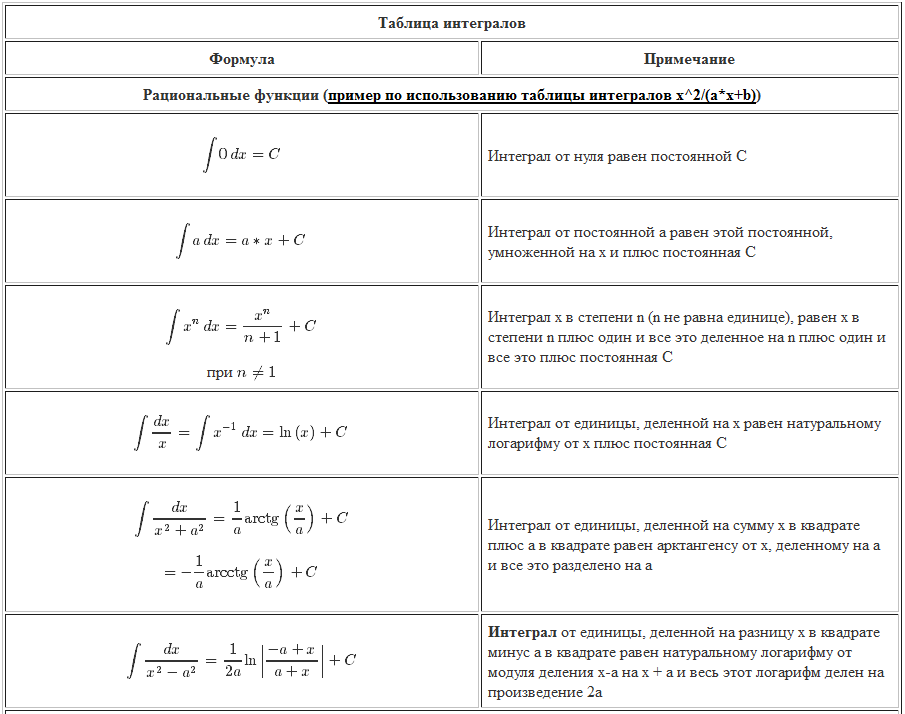
Способ непосредственного интегрирования опирается на таблицу основных интегралов и простейшие правила интегрирования.
Таблица I. Таблица основных интегралов
Все эти формулы справедливы независимо от того, является ли и независимой переменной, либо какой угодно функцией этой независимой переменной. По поводу формул 5), 6), 9), 11) и 12) смотрите учебник п° 159.
Простейшие правила интегрирования (здесь cl?*— постоянная величина,~).
Очень часто встречаются случаи, когда с= I либо 6=0.
При отыскании неопределенных интегралов полезно помнить таблицу дифференциалов, но не в том виде, как она дана в учебнике (см. п° 91), а в немного преобразованном следующем виде (здесь как бы правые и левые части поменялись местами).
Таблица 2. Таблица дифференциалов
Этой таблицей мы в дальнейшем будем широко пользоваться. При этом представление, например, выражения
в видеИли выраженияВ виде Мы будем называть подведением функций соответ ственноИлиПод знак дифференциала.
I. Найти интеграл:
Решение. Записываем подынтегральную функцию в виде степени с отрицательным дробным показателем и применяем формулу I из таблицы I:
2. Найти интеграл:
Решение. Числитель подынтегральной функции делим почленно на знаменатель. Затем применяем правила
II, I и формулу I из таблицы I:
Решение. Возводим числитель в квадрат и делим почленно на знаменатель. Далее поступаем, как в задаче 2:
4. Найти интеграл:
Решение. Сначала исключаем целую часть рациональной дроби, деля числитель на знаменатель. Имеем:
Применяя теперь правило II, получим:
Первые два интеграла правой части (I) вычисляются по формуле I из таблицы I:
К третьему же интегралу правой части применяем правило III интегрирования. В нашем случаеПоэтому на основании формулы 2 из таблицы I имеем:
Итак:
Укажем другой способ рассуждений при вычислении третьего интеграла в правой части равенства (I).
*) Произвольную постоянную мы учтем позднее при написании окончательного ответа. Мы будем поступать так и в дальнейшем.
Легко видеть, что
Интеграл не изменился, так как мы подынтегральное выражение помножили на 2 и одновременно интеграл разделили на 2. Если мы теперь множитель 2 при dx подведем под знак дифференциала (см. формулу I из табл. 2), то получим:
где и = 2х—I. Мы получили табличный интеграл (см. формулу 2 из табл. I).
Итак, окончательно
Замечание. Если подынтегральная функция представляет собой рациональную дробь, у которой степень многочлена числителя больше или равна степени многочлена знаменателя, то прежде всего следует исключить целую часть путем деления числителя рациональной дроби на знаменатель.
5. Найти интеграл:
ся
Решение. Освобождаемся от иррациональности в знаменателе:
Мы воспользовались здесь правилом III и формулой I из таблицы I.
6. Найти интеграл:
Решение.
Имеем:
Мы использовали здесь правило II; подведением соответствующего постоянного множителя под знак дифференциала мы привели интегралы к табличным (см. формулы 6 и 7 из табл. I).
7. Найти интеграл:
Решение. Чтобы свести данный интеграл к табличному (см. формулу 9 из табл. I), достаточно подвести под дифференциал множительИ разделить весь интеграл наТогда, сравнив полученный интеграле формулой 9, увидим, чтоА = 3. Следовательно, получим:
Замечание. Совершенно аналогично следует поступать с интегралами вида
Если в каждом из них мы введем под дифференциал множитель b и разделим интеграл на этот множитель, то приведем данные интегралы к табличным (см. формулы 10, 11, 12 в табл. I), причем и = Ьх.
8. Найти интеграл:
Решение. Вряд ли кому-нибудь придет в голову мысль возвести данный двучлен в 27-ю степень и затем интегрировать сумму из 28-ми слагаемых, хотя такой путь вполне законен. Данный интеграл берется совсем легко с помощью правила III и формулы I из таблицы I.
В самом деле, имеем:
Способ непосредственного интегрирования дает возможность брать интегралы вида
Данный интеграл можно свести к табличному, если ввести множитель 2 под дифференциал и разделить весь интеграл на 2:
где
В самом деле, так как f'(x)dx =Af (х), то
Окончательно имеем:
Итак, если числитель подынтегральной функщш равен производной ее знаменателя (или отличается от нее постоянным множителем), то интеграл равен логарифму модуля знаменателя плюс произвольная постоянная.
Рассмотрим несколько задач.
9. Найти интеграл: так как функция cos л: в числителе есть производная знаменателя sin х.
Решение. Имеем:
Применяя к равенству (2) правило III, мы легко возьмем и более сложный интеграл:
10. Найти интеграл:
Решен ие. Имеем:
Так как производная знаменателя равна 6*, то достаточно в первом интеграле помножить числитель на 6, а весь интеграл разделить на 6:
Второй интеграл равенства (3) берется аналогично интегралу задачи 7:
Окончательно получим:
11.
так как после умножения числителя на 3 он стал равен производной знаменателя.
12.
так как числитель подынтегральной функции равен производной знаменателя.
В задачах 13—26, пользуясь формулами таблицы I и правилами интегрирования I и II, найти заданные интегралы.
Указание. В задаче 25 числитель I подынтегральной функции замените по формуле I = sin2 х 4- cos8 х и разделите почленно на знаменатель. В задаче 26 воспользуйтесь формулой cos 2;r = cos8 х — — Sin2X и разложите на множители.
В задачах 27 — 30 найти интегралы, предварительно исключив целую часть рациональной дроби.
В задачах 29—41, пользуясь правилом интегрирования III или подведением под знак дифференциала, найти заданные интегралы.
При решении задач 42—47 посмотрите решения задач 9—12.
Указание. При решении задачи 43 воспользуйтесь указанием к задаче 25.
В задачах 48, 49 подведите предварительно числитель подынтегральной функции под знак дифференциала.
В задачах 50, 51 подведите предварительно множители х, х% под знак дифференциала.
| Следующая > |
|---|
Формула интегрирования — Примеры | Список формул интегрирования
Формулы интегрирования могут применяться для интегрирования алгебраических выражений, тригонометрических отношений, обратных тригонометрических функций, а также логарифмических и экспоненциальных функций. Интегрирование функций приводит к исходным функциям, для которых были получены производные. Эти формулы интегрирования используются для нахождения первообразной функции. Если мы продифференцируем функцию f на интервале I, то получим семейство функций в I. Если известны значения функций в I, то мы можем определить функцию f. Этот обратный процесс дифференциации называется интеграцией.
Давайте двигаться дальше и узнать о формулах интегрирования, используемых в методах интегрирования.
1. | Что такое формулы интегрирования? |
| 2. | Основные формулы интегрирования |
| 3. | Формулы интегрирования тригонометрических функций |
| 4. | Формулы интегрирования обратных тригонометрических функций |
| 5. | Расширенные формулы интеграции |
| 6. | Различные формулы интегрирования |
| 7. | Применение формул интегрирования |
| 8. | Часто задаваемые вопросы о формулах интеграции |
Что такое формулы интегрирования?
Формулы интегрирования были широко представлены в виде следующих наборов формул. Формулы включают в себя базовые формулы интегрирования, интегрирование тригонометрических отношений, обратные тригонометрические функции, произведение функций и некоторые дополнительные формулы интегрирования. По сути, интеграция — это способ объединения частей для получения целого.
Это обратная операция дифференцирования. Таким образом, основная формула интегрирования такова: ∫ f'(x) dx = f(x) + C. Используя это, получаются следующие формулы интегрирования.
Обсудим эти формулы подробнее.
Основные формулы интегрирования
Используя основные теоремы об интегралах, получены обобщенные результаты, которые запоминаются как формулы интегрирования в неопределенном интегрировании.
- ∫ x n dx = x (n + 1) /(n + 1)+ C
- ∫ 1 дх = х + С
- ∫ е х dx = е х + С
- ∫ 1/x dx = log |x| + С
- ∫ a x dx = a x /log a+ C
- ∫ e x [f(x) + f'(x)] dx = e x f(x) + C
Формулы интегрирования тригонометрических функций
Процесс нахождения интеграла — интегрирование. Вот несколько важных формул интегрирования, которые запомнятся для мгновенных и быстрых вычислений.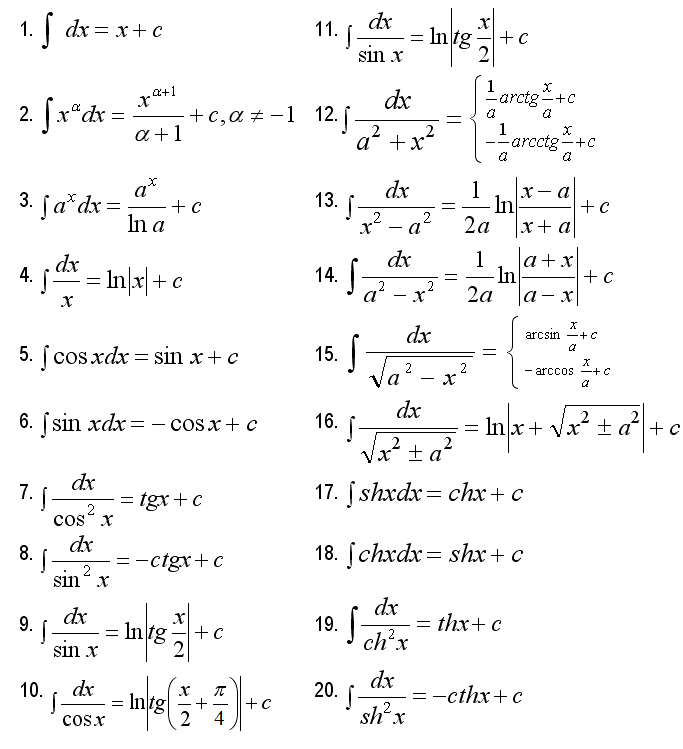
Когда дело доходит до тригонометрических функций, мы упрощаем их и переписываем как интегрируемые функции. Вот список тригонометрических и обратных тригонометрических функций.
- ∫ cos x dx = sin x + C
- ∫ sin x dx = -cos x + C
- ∫ сек 2 х dx = тангенс х + С
- ∫ cosec 2 x dx = -cot x + C
- ∫ сек х тангенс х dx = сек х + C
- ∫ cosec x cot x dx = -cosec x + C
- ∫ тангенс х dx = лог | сек х | + С
- ∫ раскладушка x dx = log |sin x| + С
- ∫ сек х dx = лог | сек х + тангенс х | + С
- ∫ cosec x dx = log |cosec x — cot x| + С
Формулы интегрирования обратных тригонометрических функций
Вот интегральные формулы, которые приводят/дают результат в виде обратных тригонометрических функций.
- ∫1/√(1 — x 2 ) dx = sin -1 x + C
- ∫ 1/√(1 — x 2 ) dx = -cos -1 x + C
- ∫1/(1 + х 2 ) дх = тан -1 х + С
- ∫ 1/(1 + x 2 ) dx = -cot -1 x + C
- ∫ 1/x√(x 2 — 1) dx = сек -1 x + C
- ∫ 1/x√(x 2 — 1) dx = -cosec -1 x + C
Формулы расширенного интегрирования
Вот некоторые продвинутые интегральные формулы, с которыми мы можем столкнуться при решении задач интегрирования.
- ∫1/(x 2 — a 2 ) dx = 1/2a log|(x — a)(x + a| + C
- ∫ 1/(a 2 — x 2 ) dx =1/2a log|(a + x)(a — x)| + С
- ∫1/(x 2 + a 2 ) dx = 1/a tan -1 x/a + C
- ∫1/√(x 2 — a 2 )dx = log |x + √(x 2 — a 2 )| + С
- ∫ √(x 2 — a 2 ) dx = x/2 √(x 2 — a 2 ) -a 2 /2 log |x + √(x 2 — a 2 )| + С
- ∫1/√(a 2 — x 2 ) dx = sin -1 x/a + C
- ∫√(a 2 — x 2 ) dx = x/2 √(a 2 — x 2 ) dx + a 2 /2 sin -1 9007 C
- ∫1/√(x 2 + a 2 ) dx = log |x + √(x 2 + a 2 )| + С
- ∫ √(x 2 + a 2 ) dx = x/2 √(x 2 + a 2 )+ a 2 /2 log |x + √(x 2
2 )| + С
Различные формулы интегрирования
Существует 3 типа методов интегрирования, и каждый метод применяется со своими собственными уникальными методами, связанными с нахождением интегралов.
Это стандартизированные результаты. Их можно запомнить как формулы интегрирования.
Формула интегрирования по частям:
Когда заданная функция является произведением двух функций, мы применяем эту формулу интегрирования по частям или частичное интегрирование и вычисляем интеграл. Формула интегрирования при частичном интегрировании имеет вид:
∫ f(x) g(x) dx = f(x) ∫g(x) dx — ∫ (∫f'(x) g(x) dx) dx + C
Например: ∫ xe x dx имеет вид ∫ f(x) g(x) dx. Таким образом, мы применяем соответствующую формулу интегрирования и вычисляем интеграл.
f(x) = x и g(x) = e x
Отсюда
= xe x — e x + c
Интегрирование по формуле подстановки:
Когда функция является функцией другой функции, тогда мы применяем формулу интегрирования для подстановки. Если I = ∫ f(x) dx, где x = g(t), так что dx/dt = g'(t), то мы пишем dx = g'(t)
. Мы можем написать I = ∫ f(x ) dx = ∫ f(g(t)) g'(t) dt
Например: Рассмотрим ∫ (3x +2) 4 dx
Здесь мы можем использовать формулу интегрирования подстановки.
Пусть u = (3x+2) ⇒ du = 3 dx.
Таким образом, ∫ (3x +2) 4 dx = 1/3 ∫(u) 4 du
= 1/3. u 5 /5 = u 5 /15
= (3x+2) 5 /15
Интегрирование по формуле неполных дробей:
Если нужно найти интеграл от P(x) /Q(x) — неправильная дробь, где степень P(x) < степени Q(x), то используем интегрирование неполными дробями. Мы разделяем дробь, используя разложение частичной дроби, как P(x)/Q(x) = T(x) + P 1 (x)/ Q(x), где T(x) — полином от x, а P 1 (x)/ Q(x) — правильная рациональная функция. Если A, B и C — действительные числа, то у нас есть следующие типы более простых дробей, которые связаны с различными типами рациональных функций.
| Форма рациональных дробей | Форма дробей |
|---|---|
| (px + q)/(x-a)(x — b) | А/(х — а) + В/ (х-б) |
| (px + q)/(x-a) n | A 1 /(x-a) + A 2 /(x-a) 2 + . ……… A n /(x-a) n |
| (px 2 + qx + r)/(ax 2 + bx + c) | (Ax + B)/(ax 2 + bx + c) |
| (px 2 + qx + r)/(ax 2 + bx + c) n | (А 1 х + В 1 )/(ах 2 + бх + в) + (А 2 х + В 2 )/(ах 2 + бх + в) 2 + …(А н x + B n )/(ax 2 + bx + c) n |
| (px 2 + qx + r)/(x-a)(x-b)(x-c) | А/(х-а) + В/ (х-б) + С/ (х-в) |
| (px 2 + qx + r)/ [(x-a) (x 2 +bx +c)] | А/(х-а) + (Вх+С)/(х 2 +бх +в) |
Например: ∫ 3x+7/ x 2 -3x + 2
Разложив на неполные дроби, получим
3x+7/ x 2 -3x + 2 = A/(x- 2) + B/ (x-1)
= A(x-1) + B(x-2)/ (x-2)(x-1)
Приравнивая числители, получаем 3x +7 = A (x-1)+B(x-2)
Найдите B, дав x = 1⇒ 10 = B
Найдите A, дав x = 2⇒ 13 = A
Таким образом, 3x+7/ x 2 — 3x + 2 = 13/(x-2) + 10(x-1)
Применяя формулы интегрирования, получаем
∫ (3x+7/ x 2 -3x + 2) = ∫ 13/(x-2) + ∫ 10(x-1)
∫ (3x+7/ x 2 -3x + 2) ) = 13 log |x-2| — 10 log |x-1| + С
Применение формул интегрирования
Вообще есть два типа интегралов.
Это определенные и неопределенные интегралы.
Определенная формула интегрирования
Это интегрирования, которые имеют ранее существовавшее значение пределов; тем самым окончательное значение интеграла становится определенным.
∫ a b g(x) dx = G(b) — G(a), где g(x) = G'(x).
Неопределенная формула интегрирования
Это интегрирования, которые не имеют ранее существовавшего значения пределов; тем самым делая окончательное значение интеграла неопределенным. Здесь C — постоянная интегрирования. ∫ g'(x) = g(x) + C
Отсюда следует основная теорема исчисления.
Мы применяем формулы интегрирования, обсуждавшиеся до сих пор, для аппроксимации площади, ограниченной кривыми, для оценки среднего расстояния, задач, ориентированных на скорость и ускорение, для нахождения среднего значения функции, для аппроксимации объема и площади поверхности. твердых тел, при нахождении центра масс и работы, при оценке длины дуги, при нахождении кинетической энергии движущегося тела с помощью несобственных интегралов.
Рассчитаем расстояние, пройденное объектом, по формулам интегрирования. Мы знаем, что расстояние есть определенный интеграл скорости.
Дано: скорость объекта = v(t)= -t 2 + 5t. Найдем пройденное перемещение по (1,3).
Начальное и конечное положение объекта 1 и 3 соответственно. Следовательно, применим здесь формулу интегрирования с пределами. ∫ a b g(x) dx = G(b) — G(a)
∫ 1 3 v(t)) dt = v(3) — v(1)
∫ 1 3 v(t)= ∫ 1 3 (-t 2 9 ∫ 1 3 5t
= -t 3 /3 + 5t 2 /2 | 1 3
= [(-27/3 — (-1/3)) + (45/2 — 5/2)]
= 34/3
Водоизмещение = 34/3 ед.
Давайте посмотрим, как использовать формулы неопределенного интегрирования в следующих решенных примерах.
Часто задаваемые вопросы о формулах интеграции
Как вы выполняете интеграцию с помощью формул интеграции?
Мы можем использовать следующие шаги для интеграции:
- Сначала определите небольшую часть объекта в определенных размерах, которые при многократном добавлении составляют весь объект.
- Используйте формулы интегрирования для этой небольшой части по различным измерениям.
Для чего используются формулы интегрирования или интегральные УФ?
Интегральный UV используется для интегрирования произведения двух функций. Формула интегрирования по этому правилу: ∫u v dx = u∫v dx −∫u’ (∫v dx) dx. Здесь u — функция u(x), а v — функция v(x)
Для чего нужны формулы интегрирования?
Интеграция используется для нахождения площади любых объектов. Примеры из реальной жизни — найти центр масс объекта, центр тяжести и момент инерции массы для внедорожника. Он также используется для расчета скорости и траектории объекта, предсказания выравнивания планет и в электромагнетизме. Используйте формулы интегрирования во всех этих случаях.
Какие методы интеграции используются в формулах интеграции?
Замена, интегрирование по частям, правило обратной цепочки и разложение на неполные дроби — вот несколько методов интегрирования.
Что такое формула интегрирования интегрального УФ?
Формула интегрального УФ используется для интегрирования произведения двух функций. Формула интегрирования формы UV задается как ∫ u dv = uv-∫ v du.
Что такое формулы интегрирования тригонометрических функций?
Тригонометрические функции упрощаются до интегрируемых функций, после чего вычисляются их интегралы. Основные формулы интегрирования тригонометрических функций следующие.
- ∫ cos x dx = sin x + C
- ∫ sin x dx = -cos x + C
- ∫ сек 2 х dx = тангенс х + С
- ∫ cosec 2 x dx = -cot x + C
- ∫ сек x.tan x dx = сек x + C
- ∫ cosec x.cot x dx = -cosec x + C
- ∫ тангенс x dx = log|сек x| + С
- ∫ раскладушка x dx = log|sin x| + С
- ∫ сек х dx = log|сек х + тангенс х | + С
- ∫ cosec x dx = log|cosec x — cot x| + С
Как применить формулы интеграции для поиска журнала интеграции x?
∫ log(x) dx имеет UV-форму.
Примените формулу интегрирования по правилу частей.
1) Определить uv: Возьмем u= log(x) и dv = 1 . dx ⇒ du = 1/x и v = x
2) Примените формулу: ∫ uv dx = uv -∫ vdu
= x. журнал(х) — ∫ х. 1/x
= x log(x) — x + C
3) Упростите и оцените интеграл.
Интеграция – свойства, примеры, формулы, методы
Интеграция – это способ объединения частей для получения целого. В интегральном исчислении мы находим функцию, дифференциал которой задан. Таким образом, интегрирование является обратным дифференцированию. Интегрирование используется для определения и вычисления площади области, ограниченной графиком функций. Площадь криволинейной формы аппроксимируется путем отслеживания количества сторон вписанного в нее многоугольника. Этот процесс, известный как метод истощения, позже был принят как интеграция. Мы получаем два вида интегралов, неопределенные и определенные интегралы. Дифференциация и интегрирование являются фундаментальными инструментами исчисления, которые используются для решения задач в математике и физике.
Принципы интеграции были сформулированы Лейбницем. Давайте двинемся дальше и узнаем об интеграции, ее свойствах и некоторых мощных методах.
| 1. | Что такое интеграция? |
| 2. | Интегрирование обратного процесса дифференцирования |
| 3. | Правила интеграции |
| 4. | Методы интеграции |
| 5. | Интеграция рациональных алгебраических функций |
| 6. | Часто задаваемые вопросы по интеграции |
Что такое интеграция?
Интегрирование — это процесс нахождения площади области под кривой. Это делается путем рисования как можно большего количества маленьких прямоугольников, покрывающих площадь, и суммирования их площадей. Сумма приближается к пределу, равному области под кривой функции. Интегрирование — это процесс нахождения первообразной функции.
Если функция интегрируема и ее интеграл по области конечен в указанных пределах, то это определенное интегрирование.
Если d/dx(F(x) = f(x), то ∫ f(x) dx = F(x) +C. Это неопределенные интегралы. Например, пусть f(x) = x Функция F(x) = x 3
| Функция F( х) | Производная F'(x) = f(x) | Первообразная f(x) |
| х 3 + 0 | 3x 2 | x 3 + ? |
| x 3 + 2 | 3x 2 | x 3 + ? |
| x 3 — 4 | 3x 2 | x 3 + ? |
Таким образом, мы находим, что производные F(x) = f(x), однако первообразные f(x) не уникальны. Антипроизводная f(x) — это семейство бесконечно многих функций. На самом деле существуют бесконечные интегралы этой функции, потому что производная любой вещественной константы C равна нулю, и мы можем записать как ∫ cos x.
dx = sin x + C. Правило интегрирования заключается в добавлении произвольной константы C из множества действительных чисел. Таким образом, мы заключаем, что если \(\dfrac{dy}{dx}=f(x)\), то мы пишем \(y=\int f(x) dx\), что читается как «Интеграл от f относительно до х.»
Теорема: Если F(x) — частная первообразная функции f(x) на интервале I, то каждая первообразная функции f(x) на I задается формулой ∫ f(x) dx = F (x) + C.
- Здесь ∫ f(x) dx представляет весь класс интегралов.
- C — произвольная константа, и все первообразные f(x) на I могут быть получены путем присвоения C определенного значения.
- Здесь f(x) — подынтегральная функция,
- Переменная x в dx называется интегратором, а весь процесс нахождения интеграла называется интегрированием. Знак ∫ обозначает сумму.
Интеграция обратного процесса дифференцирования
Нам дают производную функции и просят найти ее первообразную, то есть исходную функцию.
Такой процесс называется антидифференциацией или интеграцией. Если нам дана производная функции, процесс нахождения исходной функции называется интегрированием. Производные и интегралы противоположны друг другу. Рассмотрим функцию f(x)=sinx. Производная от f(x) равна f'(x) = cos x. Мы говорим, что функция cos x является производной функцией sin x. Точно так же мы говорим, что sin x является антипроизводной cos x.
Правила интеграции
Мы уже знаем формулы производных некоторых важных функций. Вот производные и соответствующие им стандартные интегралы нескольких функций, представленных в виде формул интегрирования.
Для нахождения интегралов определены определенные правила. Они включают:
Правила суммирования и разности:
- ∫ [f(x)+g(x)] dx = ∫ f(x) dx + ∫ g(x) dx
- ∫ [f(x)-g(x)] dx =∫ f(x) dx — ∫ g(x) dx
Степенное правило: ∫ x n dx = (x n+1 )/ (n+1)+ C.
(Где n ≠ -1)
Экспоненциальные правила: х дх = е х + С Правило умножения констант: Правило взаимности: Некоторые свойства неопределенных интегралов: Свойства интегрирования
Методы интеграции
Иногда осмотра недостаточно, чтобы найти интеграл некоторых функций.
Существуют дополнительные методы приведения функции к стандартной форме для нахождения ее интеграла. Известные методы обсуждаются ниже.
Методы интегрирования:
- Метод разложения
- Интеграция путем замены
- Интегрирование с использованием частичных дробей
- Интеграция по частям
Метод 1: Интегрирование путем разложения
Функции можно разложить на сумму или разность функций, индивидуальные интегралы которых известны. Заданное подынтегральное выражение будет алгебраическим, тригонометрическим или экспоненциальным, или комбинацией этих функций.
Предположим, нам нужно проинтегрировать (x 2 -x +1)/x 3 dx, мы разложим функцию как: ∫ (х 2 /x 3 — x /x 3 +1/x 3 )
= ∫ (1/x)dx — ∫ (1/x 2 ) dx + x (1/x ∫ 3 )dx
Применяя правило взаимности и правило степени, получаем
∫ (x 2 -x +1)/x 3 dx = log|x| + 1/x — 1/2x 2 + C
Метод 2: Интегрирование подстановкой
Интегрирование методом подстановки позволяет изменить переменную интегрирования так, чтобы подынтегральная функция интегрировалась простым способом.
Допустим, нам нужно найти y =∫ f(x) dx.
Пусть x=g(t). Тогда \(\dfrac{dx}{dt}=g'(t)\).
Итак, y= ∫ f(x) dx можно записать как y= ∫ f(g(t)) g'(t).
Например, найдем интеграл от f(x) = sin(mx) с помощью подстановки.
Пусть mx = t. Тогда \(m\dfrac{dx}{dt}=1\).
\(\begin{align}y&=\int \sin{mx}dx\\&=\dfrac{1}{m}\int \sin{t}dt\\&=-\dfrac{1}{ m} \cos{t}+C\\&=-\dfrac{1}{m} \cos{mx}+C\end{align}\)
y=∫ sin(mx)dx можно записать как ∫ f(g(t)) g'(t)dt
Примечание: Замена переменной интегрирования может также использовать тригнометрические тождества. Вот несколько важных стандартных результатов:
- ∫ tan x dx = log|secx| +С
- ∫ раскладушка x dx = log|sin x| +С
- ∫cosec x dx = log|cosec x -cot x| +С
- ∫ sec x dx = log|secx + tan x| +С
Метод 3: интегрирование с использованием дробей
Предположим, нам нужно найти \(y=\int \dfrac{P(x)}{Q(x)} dx\), где \(\dfrac{P(x)} {Q(x)}\) — несобственная рациональная функция.
Мы уменьшаем его таким образом, что \(\dfrac{P(x)}{Q(x)}=T(x)+\dfrac{P_{1}(x)}{Q(x)}\). Здесь T(x) полиномиальна по x и \(\dfrac{P_{1}(x)}{Q(x)}\) является правильной рациональной функцией. В следующей таблице показаны некоторые рациональные функции и соответствующие им формы частных дробей.
Например, давайте найдем интеграл от \(f(x)=\dfrac{1}{(x+1)(x+2)}\), используя интегрирование по неполным дробям.
Используя неполную дробь, мы имеем \(\dfrac{1}{(x+1)(x+2)}=\dfrac{A}{x+1}+\dfrac{B}{x+2} \ cdots (1)\).
Определим значения A и B.
При сравнении в уравнении (1) получаем 1=A(x+2)+B(x+1).
Отсюда у нас есть набор из двух линейных уравнений.
A+B=0 и 2A+B=1
Решая эти уравнения, получаем A=1 и B=-1.
Итак, уравнение (1) можно записать в виде \(\dfrac{1}{(x+1)(x+2)}=\dfrac{1}{x+1}-\dfrac{1}{x +2}\).
Теперь решим интеграл
\(\begin{align}\int \left(\dfrac{1}{(x+1)(x+2)}\right)dx\\=\int \left( \dfrac{1}{x+1}-\dfrac{1}{x+2}\right)dx\\=\log{|x+1|}-\log{|x+2|}+C\ \=\log{\left|\dfrac{x+1}{x+2}\right|}+C\end{align}\)
Метод 4: Интегрирование по частям
Это правило интегрирования используется для поиска интеграл от двух функций.
По правилу произведения производных имеем \(\dfrac{d}{dx}(uv)=u\dfrac{dv}{dx}+v\dfrac{du}{dx}\;\;\;\ ;\;\;\;\cdots (1)\)
Интегрируя обе части уравнения (1), получаем \(\int u\dfrac{dv}{dx}dx=uv-\int v\dfrac{du}{dx} dx\;\;\ ;\;\;\;\; \cdots (2)\)
Уравнение (2) можно записать в виде \(uv=\int u\dfrac{dv}{dx}dx+\int v\dfrac{du} {dx} dx\)
Пусть u=f(x) и \(\dfrac{dv}{dx}=g(x)\).
Тогда имеем \(\dfrac{du}{dx}=f'(x)\) и v = ∫ g(x)dx.
Итак, уравнение (2) принимает вид
\(\begin{align}\int f(x) g(x)dx\\=f(x) \int g(x)dx-\int [f'( x) \int g(x)dx]dx\end{align}\) 9{x}+C\end{align}\)
Несколько важных стандартных результатов (формула Бернулли):
- ∫ e ax sin bx dx = e ax /(a 2 + b 2 )[a sin bx — b cos bx] + C
- ∫ e ax cos bx dx = e ax /(a 2 + b 2 )[a cos bx + b sin bx] + C
Интеграция рациональных алгебраических функций
Чтобы проинтегрировать рациональные алгебраические функции, числитель и знаменатель которых содержат некоторые положительные целые степени x с постоянными коэффициентами, мы используем интегрирование неполными дробями и получаем несколько стандартных результатов, которые можно непосредственно применять в качестве формул интегрирования.
- ∫1/ (a 2 — x 2 ) dx = (1/2a) log|(a+x)/(a-x)| +С
- ∫1/ (x 2 — a 2 ) dx = (1/2a) log|(x-a)/(x+a)| +С
- ∫1/ √(x 2 — a 2 ) dx = log |x + √(x 2 — a 2 )|+C
- ∫ 1/ √(x 2 + a 2 ) dx = log |x + √(x 2 + a 2 )|+C
- ∫ 1/ √(a 2 — x 2 ) dx = sin -1 (х/д) +C
- ∫1/ (a 2 + x 2 ) dx = (1/a) tan -1 (x/a) + C
Важные примечания
- Интеграция – это процесс, обратный дифференциации.
- Всегда добавляйте постоянную интегрирования после определения интеграла функции.
- Если две функции, например f(x) и g(x), имеют одинаковые производные, то |f(x)-g(x)|= C, где C — некоторая константа.
☛ Также проверьте:
- Интеграция УФ-формулы
- Формула дифференцирования и интегрирования
Часто задаваемые вопросы по интеграции
Что такое интеграция?
Процесс нахождения первообразных функций, также известных как интегралы, называется интегрированием.
Это метод нахождения функции g(x), производная которой d/dx(g(x)), равна функции f(x). Он представляется как ∫ f(x) и называется неопределенным интегралом функции. ∫ f(x)dx представляет собой сумму произведения функции и ее смещения по x.
Какая польза от интеграции?
Определенные интегралы при интегрировании используются для нахождения таких величин, как площадь, объем и т. д., которые можно интерпретировать как площадь под кривой. Установлено, что первообразные помогают при вычислении определенных интегралов.
Что такое интеграция 1?
Интеграция 1 равна (x+C). Интегрирование константы, т. е. ∫ a. dx = ax + C, где a — постоянная. Здесь ∫1. dx = x + C
Каковы методы интегрирования функции?
Существует множество способов интеграции функции. Несколько стандартных интегралов просто находят первообразные, для которых используются основные формулы интегрирования. Есть несколько методов, которым нужно следовать, например, метод замены, интегрирование по частям и интегрирование с использованием неполных дробей.
Они обсуждаются здесь, в этой статье.
Каковы правила интеграции?
Существует множество правил интегрирования, которые помогают нам находить интегралы. правило степени, правила суммы и разности, экспоненциальное правило, правило взаимности, правило констант, правило подстановки и правило интегрирования по частям.
Что такое интегрирование √x?
Согласно степенному правилу интегрирования мы знаем ∫ x n dx = (x n+1 )/ (n+1)+ C.
∴ ∫ x ½ . dx = (x ½+1 )/ (½+1)+ C.
= (x 3/2 )/ (3/2)+ C = (2/3) x 3/2
Как интеграция используется в реальной жизни?
Применение интеграции в реальной жизни упомянуто ниже.
- В электротехнике нам нужен кабель для соединения двух подстанций, которые находятся на расстоянии миль друг от друга. Интеграция помогает нам найти точную длину кабеля.
- В физике интегрирование используется для определения центра масс, центра тяжести, скорости объекта и т. д.
- В эпидемиологии интегральное исчисление используется для изучения распространения инфекционного заболевания.
д.Почему важна интеграция?
Исчисление основано на концепциях производных и интегрирования. В математике мы используем интегрирование для нахождения площадей, объемов, перемещений и т. д. Фактически, концепция интегрирования в исчислении породила интегральное исчисление.
Интегральное исчисление
Интегральное исчислениеДалее: Некоторые полезные формулы Up: тем для изучения Предыдущий: Дифференциальное исчисление
Неопределенные интегралы
Определение : Функция F ( x ) является первообразной функции ( x ), если для всех x в области ,
Основные формулы интегрирования
Общие и логарифмические интегралы
| 1. k ( x ) dx = k ( x ) dx | 2. [( x ) g ( x )] dx = ( x ) dxg ( x ) dx |
| 3. к дх = кх + С | 4. хн дх = + С , н-1 |
| 5. ex dx = ex + С | 6. ах дх = + С , а 0, а1 |
| 7. = пер | х | + С |
Тригонометрические интегралы
| 1. sin x dx = -cos x + C | 2. cos x dx = грех х + С |
3. сек 2 x dx = tan x + C | 4. csc 2 x dx = -кроватка x + C |
| 5. сек x загар x dx = сек x + C | 6. csc x кроватка x dx = -csc x + С |
| 7. tan x dx = -ln |cos x | + С | 8. кроватка x dx = ln |sin x | + С |
| 9. сек x dx = ln |sec x + тангенс x | + С | 10. csc x dx = -ln |csc x + кроватка x | + С |
| 11. | 12. |
| 13. |
Интеграция путем замены
Интеграция по частям
Расстояние, скорость и ускорение ( на Земле )
и ( t ) = с» ( t ) = -32 фут/сек2
v ( t ) = с’ ( t ) = с» ( t ) дт = -32 дт = -32 т + С 1
при t = 0, v 0 = v (0) = (-32)(0) + С 1 = С 1
с ( т ) = v ( т ) дт = (-32 т + v 0) dt = -16 t 2 + v 0 t + С 2
Разделимые дифференциальные уравнения
Иногда можно разделить переменные и записать дифференциал уравнение в виде
( y ) dy + g ( x ) dx = 0 путем интеграции:
| Упражнение : | Найдите |
| 2 x dx + y dy = 0 | |
| х 2 + = С |
приложений к росту и распаду
Часто скорость изменения или переменная y пропорциональна
к самой переменной.
| = тыс. лет назад | разделить переменные | |
| = k dt | интегрировать с обеих сторон | |
| ln | и | = кт + С 1 | ||
| у = Цект | Закон экспоненциального роста и убывания | |
| Экспоненциальный рост при k 0 | ||
| Экспоненциальное затухание при k 0 | ||
Определение определенного интеграла
Определенный интеграл есть предел суммы Римана функции на интервале [ a , b ]
Свойства определенных интегралов
1. [( x ) + г ( x )] дх = ( х ) дх + г ( x ) дх
2.
к ( x ) дх + к(х ) дх
3. ( х ) дх = 0
4. ( х ) дх = -( х ) дх
5. ( x ) dx + ( x ) дх = ( х ) дх
6. Если ( x ) г ( x ) на [ a , b ],
затем ( x ) dx g ( x ) дх
Приближения к определенному интегралу
Суммы Римана
( x ) дх = Sn =
Трапециевидная линейка
( x ) dx [( x 0)
+ ( х 1) + ( х 2)
+ … + ( х -1)
+ ( xn )]
Основная теорема исчисления
Если непрерывно на [ a , b ] и если F’ = , то
Вторая фундаментальная теорема исчисления
Если непрерывна на открытом интервале I , содержащем a , то для каждых x в интервале
Область под кривой
| Если | ( x ) 0 на [ a , b ] | А = ( x ) дх |
| Если | ( x ) 0 на [ a , b ] | А = — ( x ) дх |
| Если | ( x ) 0 на [ a , c ] и | A = ( x ) dx — ( x ) dx |
| ( x ) 0 на [ c , b ] |
| Упражнение | Площадь, ограниченная графиками y = 2 x 2 и y = 4 x + 6, равна: | |
| (A) 76/3 | ||
| (B) 32/3 | ||
| (C) 80/3 | ||
| (D) 64/3 | ||
| ( E) 68/3 | ||
Ответ D. | Пересечение графиков: | 2 х 2 = 4 х + 6 |
| 2 x 2 — 4 x + 6 = 0 | ||
| х = -1, 3 | ||
| А = 4 x + 6 — 2 x 2 | ||
| = (2 х 2 + 6 х — ) | ||
| = 18 + 18 — 18 — (2 — 6 + 2/3) | ||
| = 64/3 | ||
Среднее значение функции на интервале
Объемы твердых тел с известными поперечными сечениями
1. Для поперечных сечений площадью A ( х ), взятых перпендикулярно до оси x :
В = А ( x ) дх
2. Для поперечных сечений площадью A ( y ), взятых перпендикулярно к оси и :
В = А ( y ) dy
Объемы твердых тел вращения: дисковый метод
| В = r 2 dx | |
| Повернута примерно на x -ось: | В = [( x )]2 dx |
| Вращение вокруг оси y : | V = [( y )]2 dy |
Объемы твердых тел вращения: метод промывки
| В = ( прямо 2 дх — ри 2 ) дх | |
| Повернут около x -оси: | V = [(1 ( x )) 2 — (2 ( x )) 2] DX)) 2 — (2 ( x )) 2] DX 91)) 2 — (2 ( x )) 2] DX )) 2 — (2 ( x ). |