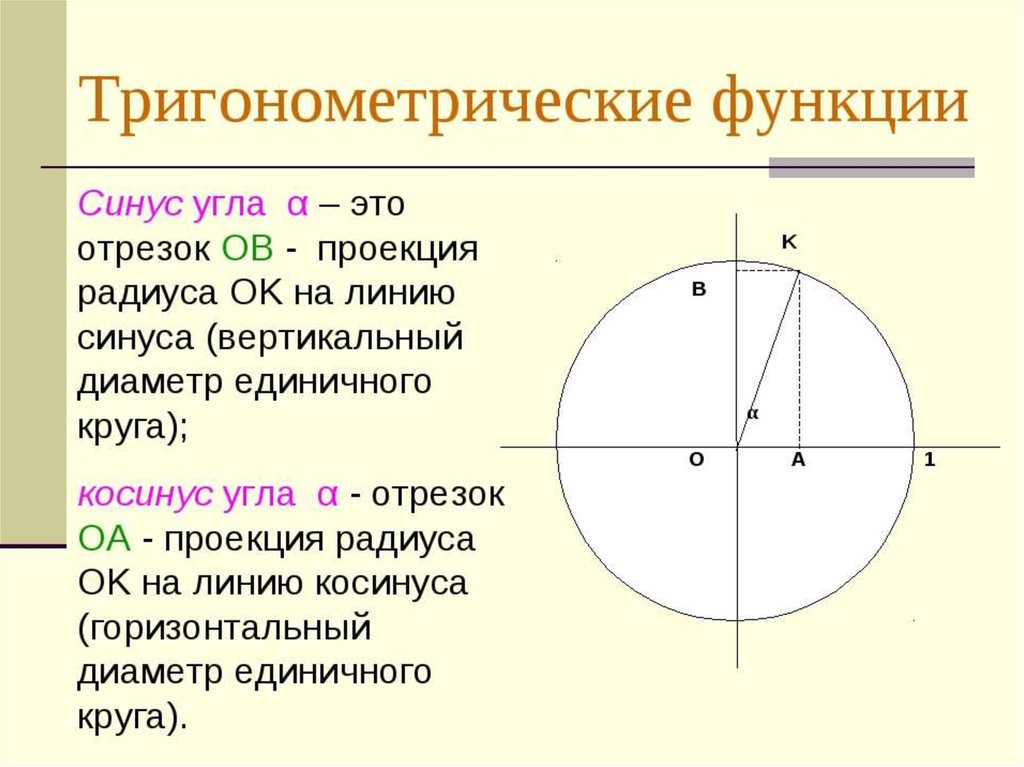
Определение синуса, косинуса и тангенса угла
Вспомним, как в курсе геометрии были введены синус, косинус и тангенс угла из промежутка от до . На координатной плоскости построим полуокружность с центром в начале координат и единичным радиусом, расположенную в первой и второй четвертях. Такую полуокружность называют единичной полуокружностью.
Затем из точки проведём луч , который пересекает нашу полуокружность в точке . Угол между лучом и положительным направлением оси обозначим . При этом, если луч совпадает с положительным направлением оси , то считают, что угол .
Пусть
угол острый.
Опустим из точки перпендикуляр
на
ось и
получим прямоугольный треугольник .
Тогда из этого треугольника имеем: ;
.
– это радиус единичной полуокружности, а значит, равняется . равняется абсциссе точки , то есть . равняется ординате точки , то есть . Подставим эти значения в выражения синуса и косинуса и получим,
что , .
А если угол не является острым, то как определяются синус и косинус этого угла?
Если угол альфа прямой, тупой, развёрнутый или равен нулю, то синус и косинус также определяются по формулам: , .
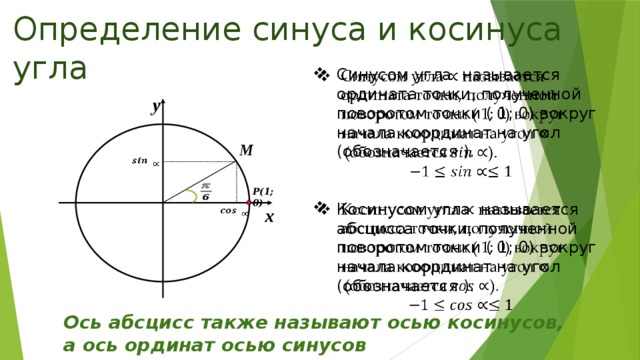
Таким образом, для любого угла альфа из промежутка от до синусом угла называется ордината точки , а косинусом угла – абсцисса точки .
При этом не забудем отметить, что так как координаты и точек единичной полуокружности удовлетворяют неравенствам , а , то для из промежутка от до справедливы неравенства ; .
Тангенсом угла , причём , называется отношение к : . Отметим, что , так как , а в формуле знаменатель не должен обращаться в нуль.
Так как же определяются синус, косинус и тангенс произвольного угла?
Запомните! Синусом угла называется ордината точки , полученной поворотом точки вокруг начала координат на угол . Обозначают: .
Косинусом угла
называется абсцисса точки , полученной поворотом точки вокруг начала координат на угол . Обозначают: .
Обозначают: .Причём угол может выражаться и в градусах, и в радианах.
Давайте найдём значения синуса и косинуса угла , то есть угла . При повороте точки на угол получаем точку . Ордината полученной точки равна , а, следовательно, . Абсцисса полученной точки равна , а, следовательно, .
Отметим, что приведённые выше определения синуса и косинуса произвольного угла в случае, если угол принадлежит промежутку от до , совпадают с определениями синуса и косинуса из курса геометрии, которые мы с вами повторили в начале урока. Так, например, , .
А давайте найдём значения синуса и косинуса угла не из промежутка от до .
Найдём и . Итак, при повороте точки на угол мы осуществим поворот по часовой стрелке и окажемся в точке . Ордината полученной точки равна , следовательно, с. Абсцисса полученной точки равна , следовательно, .
Сейчас давайте решим уравнение . Решить это уравнение означает найти все углы, синус которых
равен .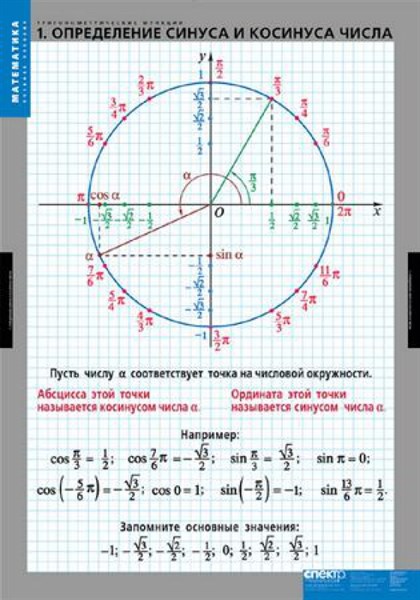 Ординату, равную , имеет точка единичной окружности . Эта точка получается из точки поворотом на угол , на угол , на угол и так далее. А также на угол , на угол и так далее.
Ординату, равную , имеет точка единичной окружности . Эта точка получается из точки поворотом на угол , на угол , на угол и так далее. А также на угол , на угол и так далее.
При этом , , ,
, .
Следовательно, при , где – это любое целое число.
Вы знаете, что множество целых чисел обозначается буквой . Обозначить то, что число принадлежит целым числам можно вот таким образом: . Читают: принадлежит . Тогда ответ к нашей задаче можно записать так: , .
Решим уравнение . Абсциссу, равную , имеет точка . Эта точка получается из точки поворотом на рад, то есть точка остаётся на своём месте; на угол , на угол и так далее. А также на угол , и так далее.
При этом рад мы можем записать как , , , , .
Следовательно, при , .
А что называют тангенсом произвольного угла?
Запомните! Тангенсом угла называется отношение синуса угла к его косинусу. Обозначают: .
Таким образом, можем записать, что .
Иногда используют котангенс угла , который равен отношению косинуса угла к синусу угла : . При этом .
Давайте найдём и .
. Подставим значения синуса и косинуса: . Выполним вычисления и в результате получим .
. Подставим значения косинуса и синуса: . Выполним вычисления и получим .
Также . , а, следовательно, .
Важно помнить, что и определены для любого угла , а их значения заключены в промежутках от до , так как координаты точек единичной окружности заключены в промежутках от до .
А вот определён только для тех углов, для которых , так как делить на нуль нельзя. Найдём углы, косинус которых равен нулю. Итак, абсциссу, равную , имеет точка и . Эти точки получаются поворотом точки на углы , , и так далее. А также на углы , и так далее.
Следовательно, при , .
определён для любых углов, кроме , .
А для каких углов определён ? определён только для тех углов, для
которых . Найдём углы, синус которых равен нулю. Итак, ординату, равную нулю,
имеет точка и точка . Эти точки получаются поворотом точки на углы , , , и так далее. А также на углы , , и так далее.
Итак, ординату, равную нулю,
имеет точка и точка . Эти точки получаются поворотом точки на углы , , , и так далее. А также на углы , , и так далее.
Следовательно, при , .
Тогда определён для любых углов, кроме , .
На следующем слайде приведена таблица значений синуса, косинуса, тангенса и котангенса, с которыми вы будете встречаться чаще всего:
Найдём значение выражения .
Воспользуемся только что приведённой таблицей. Подставим значения в наше выражения: . Теперь выполним вычисления и в результате получим .
Отметим, что значения синуса, косинуса, тангенса и котангенса для углов, которых нет в этой таблице, можно найти с помощью инженерного микрокалькулятора или по четырёхзначным математическим таблицам Брадиса.
что такое? Как найти синус, косинус и тангенс? Формулы двойного угла и сложения аргументов
В этой статье мы покажем, как даются определения синуса, косинуса, тангенса и котангенса угла и числа в тригонометрии . Здесь же мы поговорим об обозначениях, приведем примеры записей, дадим графические иллюстрации. В заключение проведем параллель между определениями синуса, косинуса, тангенса и котангенса в тригонометрии и геометрии.
Здесь же мы поговорим об обозначениях, приведем примеры записей, дадим графические иллюстрации. В заключение проведем параллель между определениями синуса, косинуса, тангенса и котангенса в тригонометрии и геометрии.
Навигация по странице.
Определение синуса, косинуса, тангенса и котангенса
Проследим за тем, как формируются представление о синусе, косинусе, тангенсе и котангенсе в школьном курсе математики. На уроках геометрии дается определение синуса, косинуса, тангенса и котангенса острого угла в прямоугольном треугольнике. А позже изучается тригонометрия, где говорится о синусе, косинусе, тангенсе и котангенсе угла поворота и числа. Приведем все эти определения, приведем примеры и дадим необходимые комментарии.
Острого угла в прямоугольном треугольнике
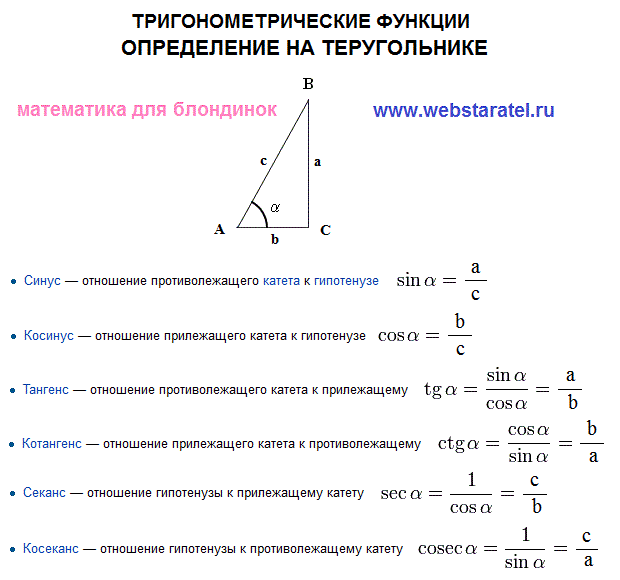
Из курса геометрии известны определения синуса, косинуса, тангенса и котангенса острого угла в прямоугольном треугольнике. Они даются как отношение сторон прямоугольного треугольника. Приведем их формулировки.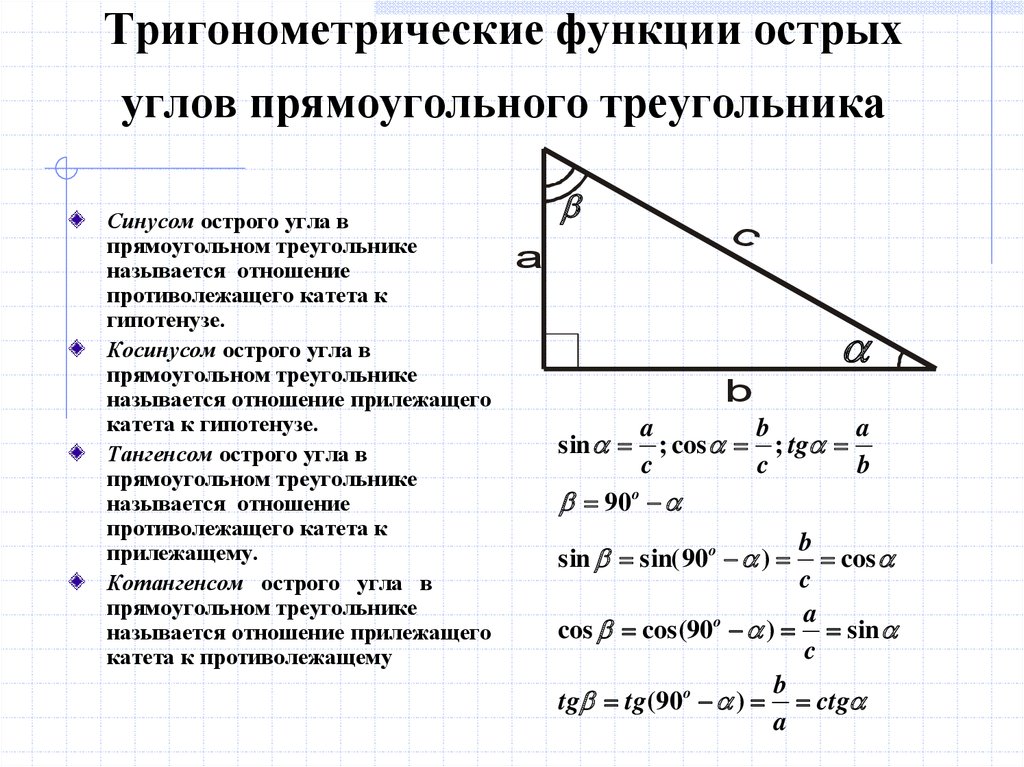
Определение.
Синус острого угла в прямоугольном треугольнике – это отношение противолежащего катета к гипотенузе.
Определение.
Косинус острого угла в прямоугольном треугольнике – это отношение прилежащего катета к гипотенузе.
Определение.
Тангенс острого угла в прямоугольном треугольнике – это отношение противолежащего катета к прилежащему.
Определение.
Котангенс острого угла в прямоугольном треугольнике – это отношение прилежащего катета к противолежащему.
Там же вводятся обозначения синуса, косинуса, тангенса и котангенса – sin , cos , tg и ctg соответственно.
Например, если АВС – прямоугольный треугольник с прямым углом С , то синус острого угла A равен отношению противолежащего катета BC к гипотенузе AB , то есть, sin∠A=BC/AB .
Эти определения позволяют вычислять значения синуса, косинуса, тангенса и котангенса острого угла по известным длинам сторон прямоугольного треугольника, а также по известным значениям синуса, косинуса, тангенса, котангенса и длине одной из сторон находить длины других сторон. Например, если бы мы знали, что в прямоугольном треугольнике катет AC
равен 3
, а гипотенуза AB
равна 7
, то мы могли бы вычислить значение косинуса острого угла A
по определению: cos∠A=AC/AB=3/7
.
Например, если бы мы знали, что в прямоугольном треугольнике катет AC
равен 3
, а гипотенуза AB
равна 7
, то мы могли бы вычислить значение косинуса острого угла A
по определению: cos∠A=AC/AB=3/7
.
Угла поворота
В тригонометрии на угол начинают смотреть более широко — вводят понятие угла поворота . Величина угла поворота, в отличие от острого угла, не ограничена рамками от 0 до 90 градусов, угол поворота в градусах (и в радианах) может выражаться каким угодно действительным числом от −∞ до +∞ .
В этом свете дают определения синуса, косинуса, тангенса и котангенса уже не острого угла, а угла произвольной величины — угла поворота. Они даются через координаты x и y точки A 1 , в которую переходит так называемая начальная точка A(1, 0) после ее поворота на угол α вокруг точки O – начала прямоугольной декартовой системы координат и центра единичной окружности .
Определение.
Синус угла поворота α
— это ордината точки A 1
, то есть, sinα=y
.
Определение.
Косинусом угла поворота α называют абсциссу точки A 1 , то есть, cosα=x .
Определение.
Тангенс угла поворота α — это отношение ординаты точки A 1 к ее абсциссе, то есть, tgα=y/x .
Определение.
Котангенсом угла поворота α называют отношение абсциссы точки A 1 к ее ординате, то есть, ctgα=x/y .
Синус и косинус определены для любого угла α
, так как мы всегда можем определить абсциссу и ординату точки, которая получается в результате поворота начальной точки на угол α
. А тангенс и котангенс определены не для любого угла. Тангенс не определен для таких углов α
, при которых начальная точка переходит в точку с нулевой абсциссой (0, 1)
или (0, −1)
, а это имеет место при углах 90°+180°·k
, k∈Z
(π/2+π·k
рад). Действительно, при таких углах поворота выражение tgα=y/x
не имеет смысла, так как в нем присутствует деление на нуль. Что же касается котангенса, то он не определен для таких углов α
, при которых начальная точка переходит к в точку с нулевой ординатой (1, 0)
или (−1, 0)
, а это имеет место для углов 180°·k
, k∈Z
(π·k
рад).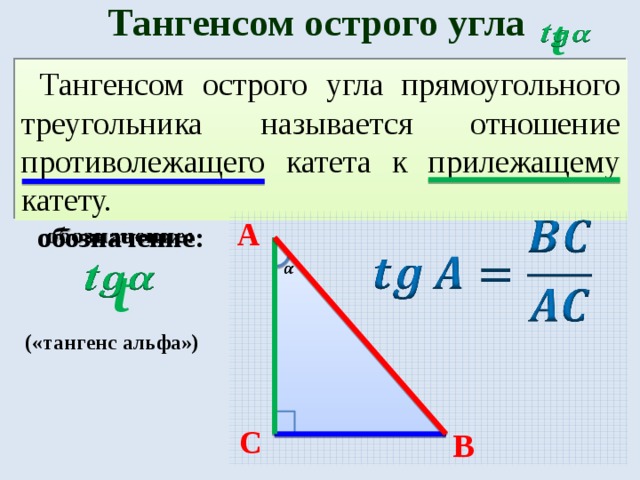
Итак, синус и косинус определены для любых углов поворота, тангенс определен для всех углов, кроме 90°+180°·k , k∈Z (π/2+π·k рад), а котангенс – для всех углов, кроме 180°·k , k∈Z (π·k рад).
В определениях фигурируют уже известные нам обозначения sin , cos , tg и ctg , они используются и для обозначения синуса, косинуса, тангенса и котангенса угла поворота (иногда можно встретить обозначения tan и cot , отвечающие тангенсу и котангенсу). Так синус угла поворота 30 градусов можно записать как sin30° , записям tg(−24°17′) и ctgα отвечают тангенс угла поворота −24 градуса 17 минут и котангенс угла поворота α . Напомним, что при записи радианной меры угла обозначение «рад» часто опускают. Например, косинус угла поворота в три пи рад обычно обозначают cos3·π .
В заключение этого пункта стоит заметить, что в разговоре про синус, косинус, тангенс и котангенс угла поворота часто опускают словосочетание «угол поворота» или слово «поворота». То есть, вместо фразы «синус угла поворота альфа» обычно используют фразу «синус угла альфа» или еще короче – «синус альфа». Это же касается и косинуса, и тангенса, и котангенса.
Это же касается и косинуса, и тангенса, и котангенса.
Также скажем, что определения синуса, косинуса, тангенса и котангенса острого угла в прямоугольном треугольнике согласуются с только что данными определениями синуса, косинуса, тангенса и котангенса угла поворота величиной от 0 до 90 градусов. Это мы обоснуем .
Числа
Определение.
Синусом, косинусом, тангенсом и котангенсом числа t называют число, равное синусу, косинусу, тангенсу и котангенсу угла поворота в t радианов соответственно.
Например, косинус числа 8·π по определению есть число, равное косинусу угла в 8·π рад. А косинус угла в 8·π рад равен единице, поэтому, косинус числа 8·π равен 1 .
Существует и другой подход к определению синуса, косинуса, тангенса и котангенса числа. Он состоит в том, что каждому действительному числу t
ставится в соответствие точка единичной окружности с центром в начале прямоугольной системы координат, и синус, косинус, тангенс и котангенс определяются через координаты этой точки.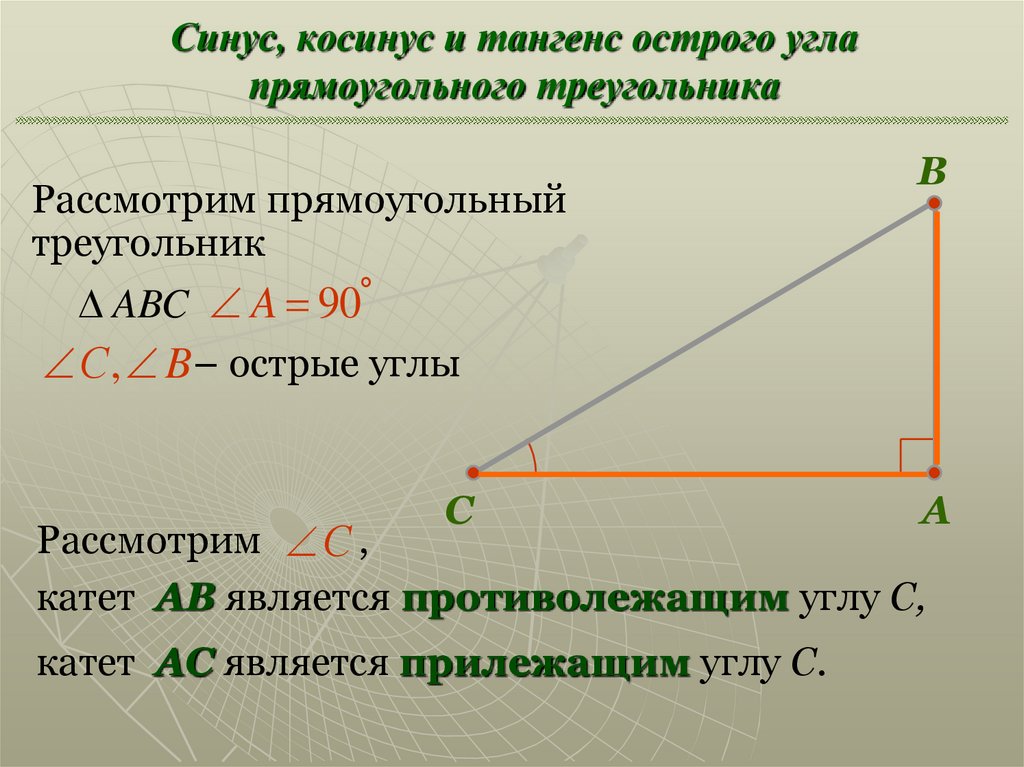 Остановимся на этом подробнее.
Остановимся на этом подробнее.
Покажем, как устанавливается соответствие между действительными числами и точками окружности:
- числу 0 ставится в соответствие начальная точка A(1, 0) ;
- положительному числу t ставится в соответствие точка единичной окружности, в которую мы попадем, если будем двигаться по окружности из начальной точки в направлении против часовой стрелки и пройдем путь длиной t ;
- отрицательному числу t ставится в соответствие точка единичной окружности, в которую мы попадем, если будем двигаться по окружности из начальной точки в направлении по часовой стрелке и пройдем путь длиной |t| .
Теперь переходим к определениями синуса, косинуса, тангенса и котангенса числа t . Допустим, что числу t соответствует точка окружности A 1 (x, y) (например, числу &pi/2; отвечает точка A 1 (0, 1) ).
Определение.
Синусом числа t
называют ординату точки единичной окружности, соответствующей числу t
, то есть, sint=y
.
Определение.
Косинусом числа t называют абсциссу точки единичной окружности, отвечающей числу t , то есть, cost=x .
Определение.
Тангенсом числа t называют отношение ординаты к абсциссе точки единичной окружности, соответствующей числу t , то есть, tgt=y/x . В другой равносильной формулировке тангенс числа t – это отношение синуса этого числа к косинусу, то есть, tgt=sint/cost .
Определение.
Котангенсом числа t называют отношение абсциссы к ординате точки единичной окружности, соответствующей числу t , то есть, ctgt=x/y . Другая формулировка такова: тангенс числа t – это отношение косинуса числа t к синусу числа t : ctgt=cost/sint .
Здесь отметим, что только что данные определения согласуются с определением, данным в начале этого пункта. Действительно, точка единичной окружности, соответствующая числу t , совпадает с точкой, полученной в результате поворота начальной точки на угол в t радианов.
Еще стоит прояснить такой момент. Допустим, перед нами запись sin3
. Как понять, о синусе числа 3
или о синусе угла поворота в 3
радиана идет речь? Обычно это ясно из контекста, в противном случае это скорее всего не имеет принципиального значения.
Допустим, перед нами запись sin3
. Как понять, о синусе числа 3
или о синусе угла поворота в 3
радиана идет речь? Обычно это ясно из контекста, в противном случае это скорее всего не имеет принципиального значения.
Тригонометрические функции углового и числового аргумента
Согласно данным в предыдущем пункте определениям, каждому углу поворота α соответствуют вполне определенное значение sinα , как и значение cosα . Кроме того, всем углам поворота, отличным от 90°+180°·k , k∈Z (π/2+π·k рад) отвечают значения tgα , а отличным от 180°·k , k∈Z (π·k рад) – значения ctgα . Поэтому sinα , cosα , tgα и ctgα — это функции угла α . Другими словами – это функции углового аргумента.
Аналогично можно говорить и про функции синус, косинус, тангенс и котангенс числового аргумента. Действительно, каждому действительному числу t
отвечает вполне определенное значение sint
, как и cost
. Кроме того, всем числам, отличным от π/2+π·k
, k∈Z
соответствуют значения tgt
, а числам π·k
, k∈Z
— значения ctgt
.
Функции синус, косинус, тангенс и котангенс называют основными тригонометрическими функциями .
Из контекста обычно понятно, с тригонометрическими функциями углового аргумента или числового аргумента мы имеем дело. В противном случае мы можем считать независимую переменную как мерой угла (угловым аргументом), так и числовым аргументом.
Однако, в школе в основном изучаются числовые функции, то есть, функции, аргументы которых, как и соответствующие им значения функции, являются числами. Поэтому, если речь идет именно о функциях, то целесообразно считать тригонометрические функции функциями числовых аргументов.
Связь определений из геометрии и тригонометрии
Если рассматривать угол поворота α
величиной от 0
до 90
градусов, то данные в контексте тригонометрии определения синуса, косинуса, тангенса и котангенса угла поворота полностью согласуются с определениями синуса, косинуса, тангенса и котангенса острого угла в прямоугольном треугольнике, которые даются в курсе геометрии. Обоснуем это.
Обоснуем это.
Изобразим в прямоугольной декартовой системе координат Oxy единичную окружность. Отметим начальную точку A(1, 0) . Повернем ее на угол α величиной от 0 до 90 градусов, получим точку A 1 (x, y) . Опустим из точки А 1 на ось Ox перпендикуляр A 1 H .
Легко видеть, что в прямоугольном треугольнике угол A 1 OH
равен углу поворота α
, длина прилежащего к этому углу катета OH
равна абсциссе точки A 1
, то есть, |OH|=x
, длина противолежащего к углу катета A 1 H
равна ординате точки A 1
, то есть, |A 1 H|=y
, а длина гипотенузы OA 1
равна единице, так как она является радиусом единичной окружности. Тогда по определению из геометрии синус острого угла α
в прямоугольном треугольнике A 1 OH
равен отношению противолежащего катета к гипотенузе, то есть, sinα=|A 1 H|/|OA 1 |=y/1=y
. А по определению из тригонометрии синус угла поворота α
равен ординате точки A 1
, то есть, sinα=y
. Отсюда видно, что определение синуса острого угла в прямоугольном треугольнике эквивалентно определению синуса угла поворота α
при α
от 0
до 90
градусов.
Аналогично можно показать, что и определения косинуса, тангенса и котангенса острого угла α согласуются с определениями косинуса, тангенса и котангенса угла поворота α .
Список литературы.
- Геометрия. 7-9 классы : учеб. для общеобразоват. учреждений / [Л. С. Атанасян, В. Ф. Бутузов, С. Б. Кадомцев и др.]. — 20-е изд. М.: Просвещение, 2010. — 384 с.: ил. — ISBN 978-5-09-023915-8.
- Погорелов А. В. Геометрия: Учеб. для 7-9 кл. общеобразоват. учреждений/ А. В. Погорелов. — 2-е изд — М.: Просвещение, 2001. — 224 с.: ил. — ISBN 5-09-010803-X.
- Алгебра и элементарные функции : Учебное пособие для учащихся 9 класса средней школы / Е. С. Кочетков, Е. С. Кочеткова; Под редакцией доктора физико-математических наук О. Н. Головина.- 4-е изд. М.: Просвещение, 1969.
- Алгебра: Учеб. для 9 кл. сред. шк./Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворова; Под ред. С. А. Теляковского.- М.: Просвещение, 1990.- 272 с.
 : ил.- ISBN 5-09-002727-7
: ил.- ISBN 5-09-002727-7 - Алгебра и начала анализа: Учеб. для 10-11 кл. общеобразоват. учреждений / А. Н. Колмогоров, А. М. Абрамов, Ю. П. Дудницын и др.; Под ред. А. Н. Колмогорова.- 14-е изд.- М.: Просвещение, 2004.- 384 с.: ил.- ISBN 5-09-013651-3.
- Мордкович А. Г. Алгебра и начала анализа. 10 класс. В 2 ч. Ч. 1: учебник для общеобразовательных учреждений (профильный уровень)/ А. Г. Мордкович, П. В. Семенов. — 4-е изд., доп. — М.: Мнемозина, 2007. — 424 с.: ил. ISBN 978-5-346-00792-0.
- Алгебра и начала математического анализа. 10 класс: учеб. для общеобразоват. учреждений: базовый и профил. уровни /[Ю. М. Колягин, М. В. Ткачева, Н. Е. Федорова, М. И. Шабунин]; под ред. А. Б. Жижченко. — 3-е изд. — И.: Просвещение, 2010.- 368 с.: ил.- ISBN 978-5-09-022771-1.
- Башмаков М. И. Алгебра и начала анализа: Учеб. для 10-11 кл. сред. шк. — 3-е изд. — М.: Просвещение, 1993. — 351 с.: ил. — ISBN 5-09-004617-4.
- Гусев В.
 А., Мордкович А. Г. Математика (пособие для поступающих в техникумы): Учеб. пособие.- М.; Высш. шк., 1984.-351 с., ил.
А., Мордкович А. Г. Математика (пособие для поступающих в техникумы): Учеб. пособие.- М.; Высш. шк., 1984.-351 с., ил.
Синус острого угла α прямоугольного треугольника – это отношение противолежащего
катета к гипотенузе.
Обозначается так: sin α.
Косинус острого угла α прямоугольного треугольника – это отношение прилежащего
катета к гипотенузе.
Обозначается так: cos α.
Тангенс острого угла α – это отношение противолежащего катета к прилежащему катету.
Обозначается так: tg α.
Котангенс острого угла α – это отношение прилежащего катета к противолежащему.
Обозначается так: ctg α.
Синус, косинус, тангенс и котангенс угла зависят только от величины угла.
Правила:
Основные тригонометрические тождества в прямоугольном треугольнике:
(α – острый угол, противолежащий катету b и прилежащий к катету a . Сторона с – гипотенуза. β – второй острый угол).
β – второй острый угол).
b | sin 2 α + cos 2 α = 1 | |
a | 1 | |
b | 1 | |
a | 1 1 | |
sin α |
При возрастании острого угла sin α и tg α возрастают, а cos α убывает.
Для любого острого угла α:
sin (90° – α) = cos α
cos (90° – α) = sin α
Пример-пояснение :
Пусть в прямоугольном треугольнике АВС
АВ = 6,
ВС = 3,
угол А = 30º.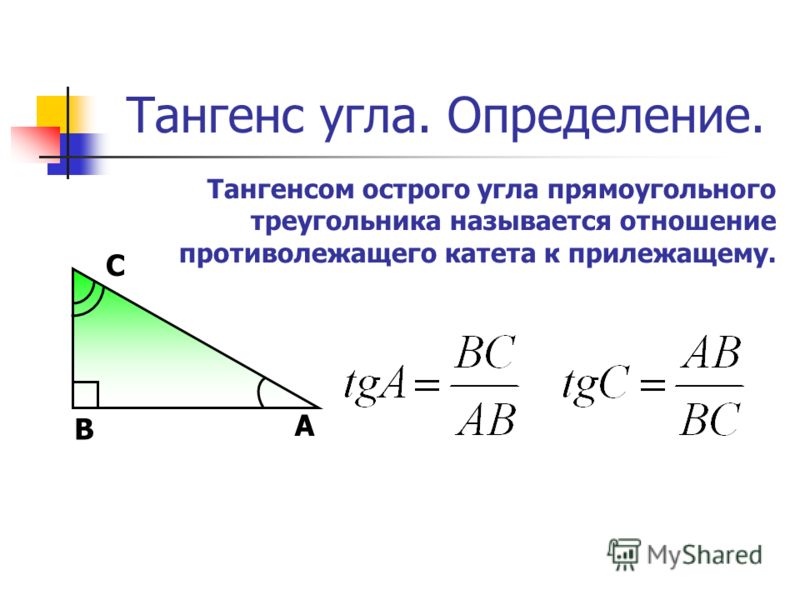
Выясним синус угла А и косинус угла В.
Решение .
1) Сначала находим величину угла В. Тут все просто: так как в прямоугольном треугольнике сумма острых углов равна 90º, то угол В = 60º:
В = 90º – 30º = 60º.
2) Вычислим sin A. Мы знаем, что синус равен отношению противолежащего катета к гипотенузе. Для угла А противолежащим катетом является сторона ВС. Итак:
BC 3 1
sin A = — = — = —
AB 6 2
3) Теперь вычислим cos B. Мы знаем, что косинус равен отношению прилежащего катета к гипотенузе. Для угла В прилежащим катетом является все та же сторона ВС. Это значит, что нам снова надо разделить ВС на АВ – то есть совершить те же действия, что и при вычислении синуса угла А:
BC 3 1
cos B = — = — = —
AB 6 2
В итоге получается:
sin A = cos B = 1/2.
sin 30º = cos 60º = 1/2.
Из этого следует, что в прямоугольном треугольнике синус одного острого угла равен косинусу другого острого угла – и наоборот. Именно это и означают наши две формулы:
sin (90° – α) = cos α
cos (90° – α) = sin α
Убедимся в этом еще раз:
1) Пусть α = 60º. Подставив значение α в формулу синуса, получим:
Подставив значение α в формулу синуса, получим:
sin (90º – 60º) = cos 60º.
sin 30º = cos 60º.
2) Пусть α = 30º. Подставив значение α в формулу косинуса, получим:
cos (90° – 30º) = sin 30º.
cos 60° = sin 30º.
(Подробнее о тригонометрии — см.раздел Алгебра)
Тригонометрические тождества — это равенства, которые устанавливают связь между синусом, косинусом, тангенсом и котангенсом одного угла, которая позволяет находить любую из данных функций при условии, что будет известна какая-либо другая.
tg \alpha = \frac{\sin \alpha}{\cos \alpha}, \enspace ctg \alpha = \frac{\cos \alpha}{\sin \alpha}
tg \alpha \cdot ctg \alpha = 1
Данное тождество говорит о том, что сумма квадрата синуса одного угла и квадрата косинуса одного угла равна единице, что на практике дает возможность вычислить синус одного угла, когда известен его косинус и наоборот.
При преобразовании тригонометрических выражений очень часто используют данное тождество, которое позволяет заменять единицей сумму квадратов косинуса и синуса одного угла и также производить операцию замены в обратном порядке.
Нахождение тангенса и котангенса через синус и косинус
tg \alpha = \frac{\sin \alpha}{\cos \alpha},\enspace
Данные тождества образуются из определений синуса, косинуса, тангенса и котангенса. Ведь если разобраться, то по определению ординатой y является синус, а абсциссой x — косинус. Тогда тангенс будет равен отношению \frac{y}{x}=\frac{\sin \alpha}{\cos \alpha} , а отношение \frac{x}{y}=\frac{\cos \alpha}{\sin \alpha} — будет являться котангенсом.
Добавим, что только для таких углов \alpha , при которых входящие в них тригонометрические функции имеют смысл, будут иметь место тождества , ctg \alpha=\frac{\cos \alpha}{\sin \alpha} .
Например: tg \alpha = \frac{\sin \alpha}{\cos \alpha} является справедливой для углов \alpha , которые отличны от \frac{\pi}{2}+\pi z , а ctg \alpha=\frac{\cos \alpha}{\sin \alpha} — для угла \alpha , отличного от \pi z , z — является целым числом.
Зависимость между тангенсом и котангенсом
tg \alpha \cdot ctg \alpha=1
Данное тождество справедливо только для таких углов \alpha
, которые отличны от \frac{\pi}{2} z
. {2} \alpha = 1
. Это уравнение имеет два решения \cos \alpha = \pm \sqrt{1-\frac34}=\pm\sqrt\frac14
.
{2} \alpha = 1
. Это уравнение имеет два решения \cos \alpha = \pm \sqrt{1-\frac34}=\pm\sqrt\frac14
.
По условию \frac{\pi}{2}
Для того, чтобы найти ctg \alpha , воспользуемся формулой ctg \alpha = \frac{\cos \alpha}{\sin \alpha} . Соответствующие величины нам известны.
ctg \alpha = -\frac12: \frac{\sqrt3}{2} = -\frac{1}{\sqrt 3} .
Понятия синуса, косинуса, тангенса и котангенса являются основными категориями тригонометрии — раздела математики, и неразрывно связаны с определением угла. Владение этой математической наукой требует запоминания и понимания формул и теорем, а также развитого пространственного мышления. Именно поэтому у школьников и студентов тригонометрические вычисления нередко вызывают трудности. Чтобы побороть их, следует подробнее познакомиться с тригонометрическими функциями и формулами.
Понятия в тригонометрии
Чтобы разобраться в базовых понятиях тригонометрии, следует сначала определиться с тем, что такое прямоугольный треугольник и угол в окружности, и почему именно с ними связаны все основные тригонометрические вычисления. Треугольник, в котором один из углов имеет величину 90 градусов, является прямоугольным. Исторически эта фигура часто использовалась людьми в архитектуре, навигации, искусстве, астрономии. Соответственно, изучая и анализируя свойства этой фигуры, люди пришли к вычислению соответствующих соотношений её параметров.
Треугольник, в котором один из углов имеет величину 90 градусов, является прямоугольным. Исторически эта фигура часто использовалась людьми в архитектуре, навигации, искусстве, астрономии. Соответственно, изучая и анализируя свойства этой фигуры, люди пришли к вычислению соответствующих соотношений её параметров.
Основные категории, связанные с прямоугольными треугольниками — гипотенуза и катеты. Гипотенуза — сторона треугольника, лежащая против прямого угла. Катеты, соответственно, это остальные две стороны. Сумма углов любых треугольников всегда равна 180 градусам.
Сферическая тригонометрия — раздел тригонометрии, который не изучается в школе, однако в прикладных науках типа астрономии и геодезии, учёные пользуются именно им. Особенность треугольника в сферической тригонометрии в том, что он всегда имеет сумму углов более 180 градусов.
Углы треугольника
В прямоугольном треугольнике синусом угла является отношение катета, противолежащего искомому углу, к гипотенузе треугольника. Соответственно, косинус — это отношение прилежащего катета и гипотенузы. Оба эти значения всегда имеют величину меньше единицы, так как гипотенуза всегда длиннее катета.
Соответственно, косинус — это отношение прилежащего катета и гипотенузы. Оба эти значения всегда имеют величину меньше единицы, так как гипотенуза всегда длиннее катета.
Тангенс угла — величина, равная отношению противолежащего катета к прилежащему катету искомого угла, или же синуса к косинусу. Котангенс, в свою очередь, это отношение прилежащего катета искомого угла к противолежащему кактету. Котангенс угла можно также получить, разделив единицу на значение тангенса.
Единичная окружность
Единичная окружность в геометрии — окружность, радиус которой равен единице. Такая окружность строится в декартовой системе координат, при этом центр окружности совпадает с точкой начала координат, а начальное положение вектора радиуса определено по положительному направлению оси Х (оси абсцисс). Каждая точка окружности имеет две координаты: ХХ и YY, то есть координаты абсцисс и ординат. Выбрав на окружности любую точку в плоскости ХХ, и опустив с неё перпендикуляр на ось абсцисс, получаем прямоугольный треугольник, образованный радиусом до выбранной точки (обозначим её буквой С), перпендикуляром, проведённым до оси Х (точка пересечения обозначается буквой G), а отрезком оси абсцисс между началом координат (точка обозначена буквой А) и точкой пересечения G. Полученный треугольник АСG — прямоугольный треугольник, вписанный в окружность, где AG — гипотенуза, а АС и GC — катеты. Угол между радиусом окружности АС и отрезком оси абсцисс с обозначением AG, определим как α (альфа). Так, cos α = AG/AC. Учитывая, что АС — это радиус единичной окружности, и он равен единице, получится, что cos α=AG. Аналогично, sin α=CG.
Полученный треугольник АСG — прямоугольный треугольник, вписанный в окружность, где AG — гипотенуза, а АС и GC — катеты. Угол между радиусом окружности АС и отрезком оси абсцисс с обозначением AG, определим как α (альфа). Так, cos α = AG/AC. Учитывая, что АС — это радиус единичной окружности, и он равен единице, получится, что cos α=AG. Аналогично, sin α=CG.
Кроме того, зная эти данные, можно определить координату точки С на окружности, так как cos α=AG, а sin α=CG, значит, точка С имеет заданные координаты (cos α;sin α). Зная, что тангенс равен отношению синуса к косинусу, можно определить, что tg α = y/х, а ctg α = х/y. Рассматривая углы в отрицательной системе координат, можно рассчитать, что значения синуса и косинуса некоторых углов могут быть отрицательными.
Вычисления и основные формулы
Значения тригонометрических функций
Рассмотрев сущность тригонометрических функций через единичную окружность, можно вывести значения этих функций для некоторых углов. k * arcsin α + πk.
k * arcsin α + πk.
Тождества со значением cos х = а, где k — любое целое число:
- cos х = 0, х = π/2 + πk.
- cos х = 1, х = 2πk.
- cos х = -1, х = π + 2πk.
- cos х = а, |a| > 1, нет решений.
- cos х = а, |a| ≦ 1, х = ±arccos α + 2πk.
Тождества со значением tg х = а, где k — любое целое число:
- tg х = 0, х = π/2 + πk.
- tg х = а, х = arctg α + πk.
Тождества со значением ctg х = а, где k — любое целое число:
- ctg х = 0, х = π/2 + πk.
- ctg х = а, х = arcctg α + πk.
Формулы приведения
Эта категория постоянных формул обозначает методы, с помощью которых можно перейти от тригонометрических функций вида к функциям аргумента, то есть привести синус, косинус, тангенс и котангенс угла любого значения к соответствующим показателям угла интервала от 0 до 90 градусов для большего удобства вычислений.
Формулы приведения функций для синуса угла выглядят таким образом:
- sin(900 — α) = α;
- sin(900 + α) = cos α;
- sin(1800 — α) = sin α;
- sin(1800 + α) = -sin α;
- sin(2700 — α) = -cos α;
- sin(2700 + α) = -cos α;
- sin(3600 — α) = -sin α;
- sin(3600 + α) = sin α.

Для косинуса угла:
- cos(900 — α) = sin α;
- cos(900 + α) = -sin α;
- cos(1800 — α) = -cos α;
- cos(1800 + α) = -cos α;
- cos(2700 — α) = -sin α;
- cos(2700 + α) = sin α;
- cos(3600 — α) = cos α;
- cos(3600 + α) = cos α.
Использование вышеуказанных формул возможно при соблюдении двух правил. Во-первых, если угол можно представить как значение (π/2 ± a) или (3π/2 ± a), значение функции меняется:
- с sin на cos;
- с cos на sin;
- с tg на ctg;
- с ctg на tg.
Значение функции остаётся неизменным, если угол может быть представлен как (π ± a) или (2π ± a).
Во-вторых, знак приведенной функции не изменяется: если он изначально был положительным, таким и остаётся. Аналогично с отрицательными функциями.
Формулы сложения
Эти формулы выражают величины синуса, косинуса, тангенса и котангенса суммы и разности двух углов поворота через их тригонометрические функции. 2 x/2) / (2tgx/2), при этом х = π + 2πn.
2 x/2) / (2tgx/2), при этом х = π + 2πn.
Частные случаи
Частные случаи простейших тригонометрических уравнений приведены ниже (k — любое целое число).
Частные для синуса:
| Значение sin x | Значение x |
|---|---|
| 0 | πk |
| 1 | π/2 + 2πk |
| -1 | -π/2 + 2πk |
| 1/2 | π/6 + 2πk или 5π/6 + 2πk |
| -1/2 | -π/6 + 2πk или -5π/6 + 2πk |
| √2/2 | π/4 + 2πk или 3π/4 + 2πk |
| -√2/2 | -π/4 + 2πk или -3π/4 + 2πk |
| √3/2 | π/3 + 2πk или 2π/3 + 2πk |
| -√3/2 | -π/3 + 2πk или -2π/3 + 2πk |
Частные для косинуса:
| Значение cos x | Значение х |
|---|---|
| 0 | π/2 + 2πk |
| 1 | 2πk |
| -1 | 2 + 2πk |
| 1/2 | ±π/3 + 2πk |
| -1/2 | ±2π/3 + 2πk |
| √2/2 | ±π/4 + 2πk |
| -√2/2 | ±3π/4 + 2πk |
| √3/2 | ±π/6 + 2πk |
| -√3/2 | ±5π/6 + 2πk |
Частные для тангенса:
| Значение tg x | Значение х |
|---|---|
| 0 | πk |
| 1 | π/4 + πk |
| -1 | -π/4 + πk |
| √3/3 | π/6 + πk |
| -√3/3 | -π/6 + πk |
| √3 | π/3 + πk |
| -√3 | -π/3 + πk |
Частные для котангенса:
| Значение ctg x | Значение x |
|---|---|
| 0 | π/2 + πk |
| 1 | π/4 + πk |
| -1 | -π/4 + πk |
| √3 | π/6 + πk |
| -√3 | -π/3 + πk |
| √3/3 | π/3 + πk |
| -√3/3 | -π/3 + πk |
Теоремы
Теорема синусов
Существует два варианта теоремы — простой и расширенный.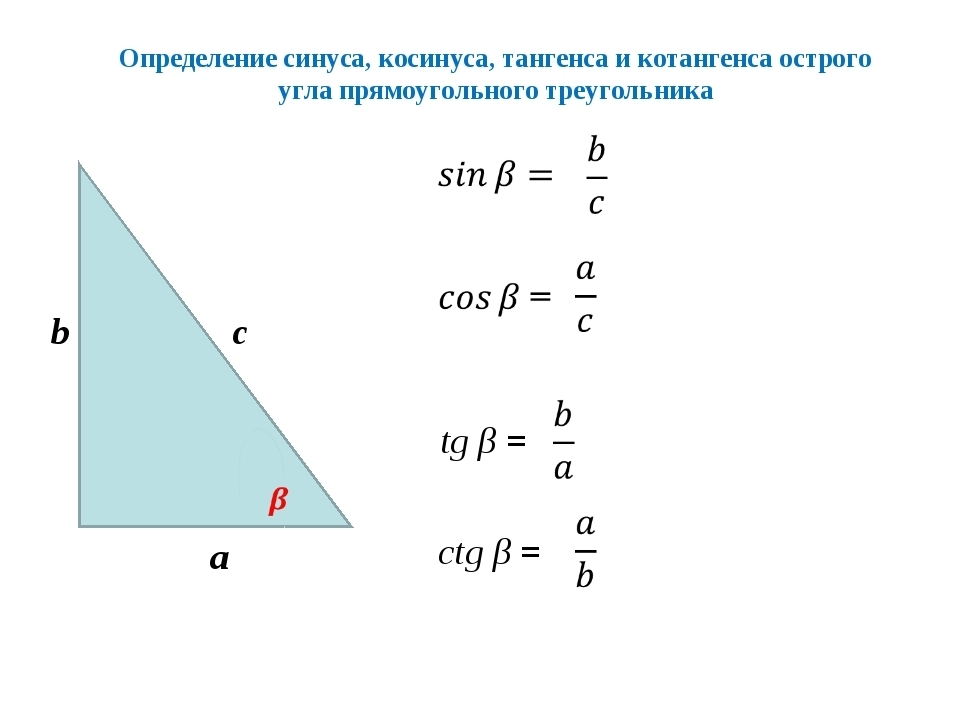 2 — 2*b*c*cos α. В формуле a, b, c — стороны треугольника, и α — угол, противолежащий стороне а.
2 — 2*b*c*cos α. В формуле a, b, c — стороны треугольника, и α — угол, противолежащий стороне а.
Теорема тангенсов
Формула выражает связь между тангенсами двух углов, и длиной сторон, им противолежащих. Стороны обозначены как a, b, c, а соответствующие противолежащие углы — α, β, γ. Формула теоремы тангенсов: (a — b) / (a+b) = tg((α — β)/2) / tg((α + β)/2).
Теорема котангенсов
Связывает радиус вписанной в треугольник окружности с длиной его сторон. Если a, b, c — стороны треугольника, и А, В, С, соответственно, противолежащие им углы, r — радиус вписанной окружности, и p — полупериметр треугольника, справедливы такие тождества:
- ctg A/2 = (p-a)/r;
- ctg B/2 = (p-b)/r;
- ctg C/2 = (p-c)/r.
Прикладное применение
Тригонометрия — не только теоретическая наука, связанная с математическими формулами. Её свойствами, теоремами и правилами пользуются на практике разные отрасли человеческой деятельности — астрономия, воздушная и морская навигация, теория музыки, геодезия, химия, акустика, оптика, электроника, архитектура, экономика, машиностроение, измерительные работы, компьютерная графика, картография, океанография, и многие другие.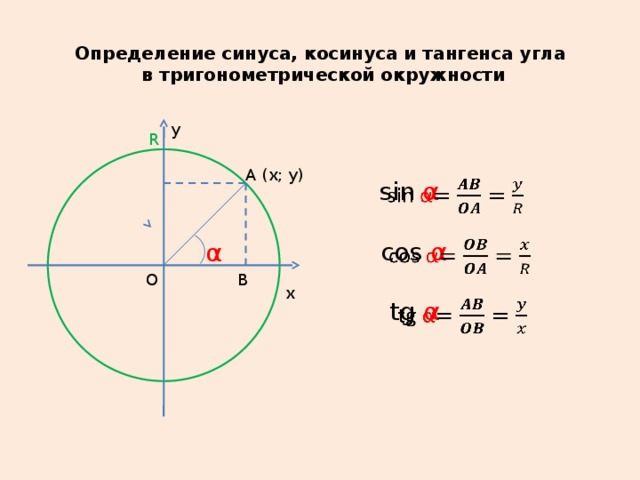
Синус, косинус, тангенс и котангенс — основные понятия тригонометрии, с помощью которых математически можно выразить соотношения между углами и длинами сторон в треугольнике, и найти искомые величины через тождества, теоремы и правила.
Лекция: Синус, косинус, тангенс, котангенс произвольного угла
Синус, косинус произвольного угла
Чтобы понять, что такое тригонометрические функции, обратимся к окружности с единичным радиусом. Данная окружность имеет центр в начале координат на координатной плоскости. Для определения заданных функций будем использовать радиус-вектор ОР , который начинается в центре окружности, а точка Р является точкой окружности. Данный радиус-вектор образует угол альфа с осью ОХ . Так как окружность имеет радиус, равный единице, то ОР = R = 1 .
Если с точки Р опустить перпендикуляр на ось ОХ , то получим прямоугольный треугольник с гипотенузой, равной единице.
Если радиус-вектор двигается по часовой стрелке, то данное направление называется отрицательным , если же он двигается против движения часовой стрелки — положительным .
Синусом угла ОР , является ордината точки Р вектора на окружности.
То есть, для получения значения синуса данного угла альфа необходимо определиться с координатой У на плоскости.
Как данное значение было получено? Так как мы знаем, что синус произвольного угла в прямоугольном треугольнике — это отношение противолежащего катета к гипотенузе, получим, что
А так как R = 1 , то sin(α) = y 0 .
В единичной окружности значение ординаты не может быть меньше -1 и больше 1, значит,
Синус принимает положительное значение в первой и второй четверти единичной окружности, а в третьей и четвертой — отрицательное.
Косинусом угла данной окружности, образованного радиусом-вектором ОР , является абсцисса точки Р вектора на окружности.
То есть, для получения значения косинуса данного угла альфа необходимо определиться с координатой Х на плоскости.
Косинус произвольного угла в прямоугольном треугольнике — это отношение прилежащего катета к гипотенузе, получим, что
А так как R = 1 , то cos(α) = x 0 .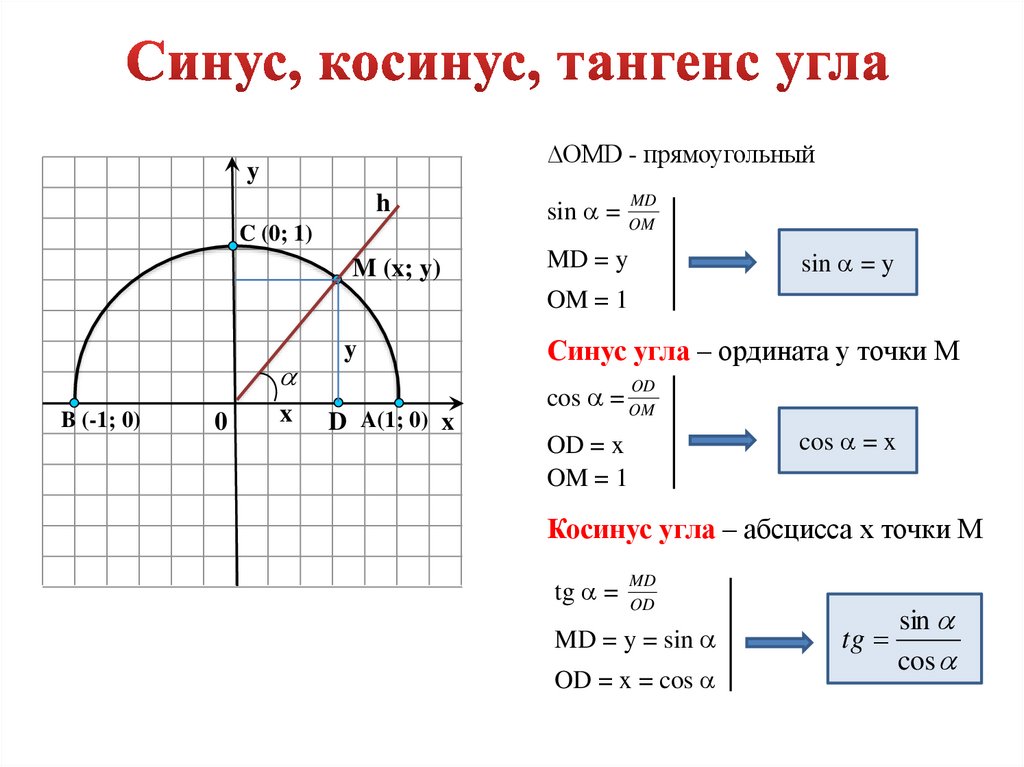
В единичной окружности значение абсциссы не может быть меньше -1 и больше 1, значит,
Косинус принимает положительное значение в первой и четвертой четверти единичной окружности, а во второй и в третьей — отрицательное.
Тангенсом произвольного угла считается отношение синуса к косинусу.
Если рассматривать прямоугольный треугольник, то это отношение противолежащего катета к прилежащему. Если же речь идет о единичной окружности, то это отношение ординаты к абсциссе.
Судя по данным отношениям, можно понять, что тангенс не может существовать, если значение абсциссы равно нулю, то есть при угле в 90 градусов. Все остальные значения тангенс принимать может.
Тангенс имеет положительное значение в первой и третьей четверти единичной окружности, а во второй и четвертой является отрицательным.
1
Первый слайд презентации
Определение синуса, косинуса и тангенса угла
Изображение слайда
2
Слайд 2
Сегодня на уроке
В спомним, что называют синусом, косинусом и тангенсом угла из промежутка от до. 1.
Дадим определение синусу, косинусу и тангенсу произвольного угла.
2.
1.
Дадим определение синусу, косинусу и тангенсу произвольного угла.
2.
Изображение слайда
3
Слайд 3
Чему равны координаты точки, полученной поворотом точки на угол ? А Б В Г
Изображение слайда
4
Слайд 4
А Б В Г Чему равны координаты точки, полученной поворотом точки на угол ?
Изображение слайда
5
Слайд 5
Чему равны координаты точки, полученной поворотом точки на угол ? А Б В Г
Изображение слайда
6
Слайд 6
А Б В Г Чему равны координаты точки, полученной поворотом точки на угол ?
Изображение слайда
7
Слайд 7
Чему равны координаты точки, полученной поворотом точки на угол ? А Б В Г
Изображение слайда
8
Слайд 8
А Б В Г Чему равны координаты точки, полученной поворотом точки на угол ?
Изображение слайда
9
Слайд 9
Вспомним
Синус, косинус и тангенс угла из промежутка от до.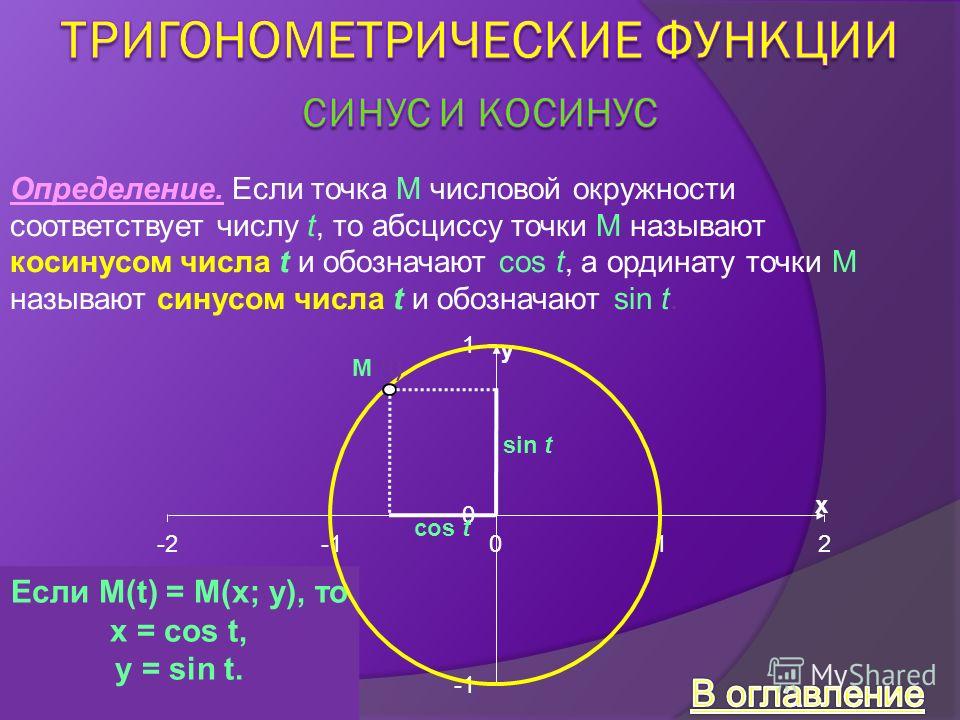 Е сли луч совпадает с положительным направлением оси, то считают, что.
Пусть угол – острый.
– прямоугольный,
т огда,
.
,
,
.
,
.
Единичная полуокружность
Е сли луч совпадает с положительным направлением оси, то считают, что.
Пусть угол – острый.
– прямоугольный,
т огда,
.
,
,
.
,
.
Единичная полуокружность
Изображение слайда
10
Слайд 10
Вспомним Синус, косинус и тангенс угла из промежутка от до. , . А если угол не является острым, то как определяются синус и косинус этого угла? Если угол прямой, тупой, развёрнутый или, то синус и косинус также определяются по формулам Е сли луч совпадает с положительным направлением оси, то считают, что. Единичная полуокружность
Изображение слайда
11
Слайд 11
Вспомним
Синус, косинус и тангенс угла из промежутка от до.
,
Если угол прямой, тупой, развёрнутый или, то синус и косинус также определяются по формулам
Е сли луч совпадает с положительным направлением оси, то считают, что. Единичная полуокружность
Так как координаты точек единичной полуокружности удовлетворяют неравенствам,,
то для из промежутка от до справедливы неравенства,.
,,
так как.
.
Единичная полуокружность
Так как координаты точек единичной полуокружности удовлетворяют неравенствам,,
то для из промежутка от до справедливы неравенства,.
,,
так как.
.
Изображение слайда
12
Слайд 12
Вспомним Синус, косинус и тангенс угла из промежутка от до. Е сли луч совпадает с положительным направлением оси, то считают, что. Единичная полуокружность , Так как же определяются синус, косинус и тангенс произвольного угла?
Изображение слайда
13
Слайд 13
Синусом угла называется ордината точки, полученной поворотом точки вокруг начала координат на угол.
Запомните!
Обозначают:.
Косинусом угла называется абсцисса точки, полученной поворотом точки вокруг начала координат на угол.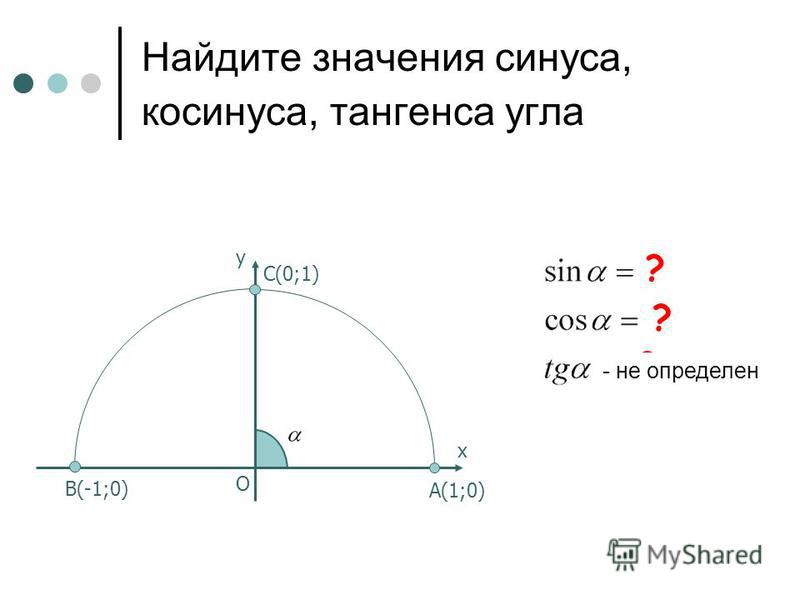 Обозначают:.
Угол может выражаться и в градусах, и в радианах.
Обозначают:.
Угол может выражаться и в градусах, и в радианах.
Изображение слайда
14
Слайд 14
Найдём значения синуса и косинуса угла, то есть угла. Синус и косинус угла , . Определения синуса и косинуса произвольного угла в случае, если угол принадлежит промежутку от до, совпадают с определениями синуса и косинуса из курса геометрии. , . А давайте найдём значения синуса и косинуса угла не из промежутка от до.
Изображение слайда
15
Слайд 15
Найдём и. Синус и косинус угла , .
Изображение слайда
16
Слайд 16
Решим уравнение. Синус и косинус угла
Эта точка получается из точки поворотом на углы,, и т. д.,
а также на углы, и т. д.
,
,
.
,
где – любое целое число.
М ножество целых чисел обозначается буквой.
Обозначить то, что число принадлежит, можно так:
,.
,
,
.
Синус и косинус угла
Эта точка получается из точки поворотом на углы,, и т. д.,
а также на углы, и т. д.
,
,
.
,
где – любое целое число.
М ножество целых чисел обозначается буквой.
Обозначить то, что число принадлежит, можно так:
,.
,
,
.
Изображение слайда
17
Слайд 17
Решим уравнение. Синус и косинус угла Эта точка получается из точки поворотом на углы,, и т. д., а также на углы, и т. д. , , ,. , , . А что называют тангенсом произвольного угла?
Изображение слайда
18
Слайд 18
Тангенсом угла называется отношение синуса угла к его косинусу. Запомните! Обозначают:.
Изображение слайда
19
Слайд 19
М ожем записать, что. Тангенс и котангенс угла
К отангенс угла :
.
,
Тангенс и котангенс угла
К отангенс угла :
.
,
Изображение слайда
20
Слайд 20
Найдём и. Тангенс и котангенс угла , , .
Изображение слайда
21
Слайд 21
и определены для любого угла, Синус, косинус, тангенс и котангенс угла а их значения заключены в промежутках от до, так как координаты точек единичной окружности заключены в промежутках от до.
Изображение слайда
22
Слайд 22
Синус, косинус, тангенс и котангенс угла
определён только для тех углов, для которых,
так как делить на нуль нельзя.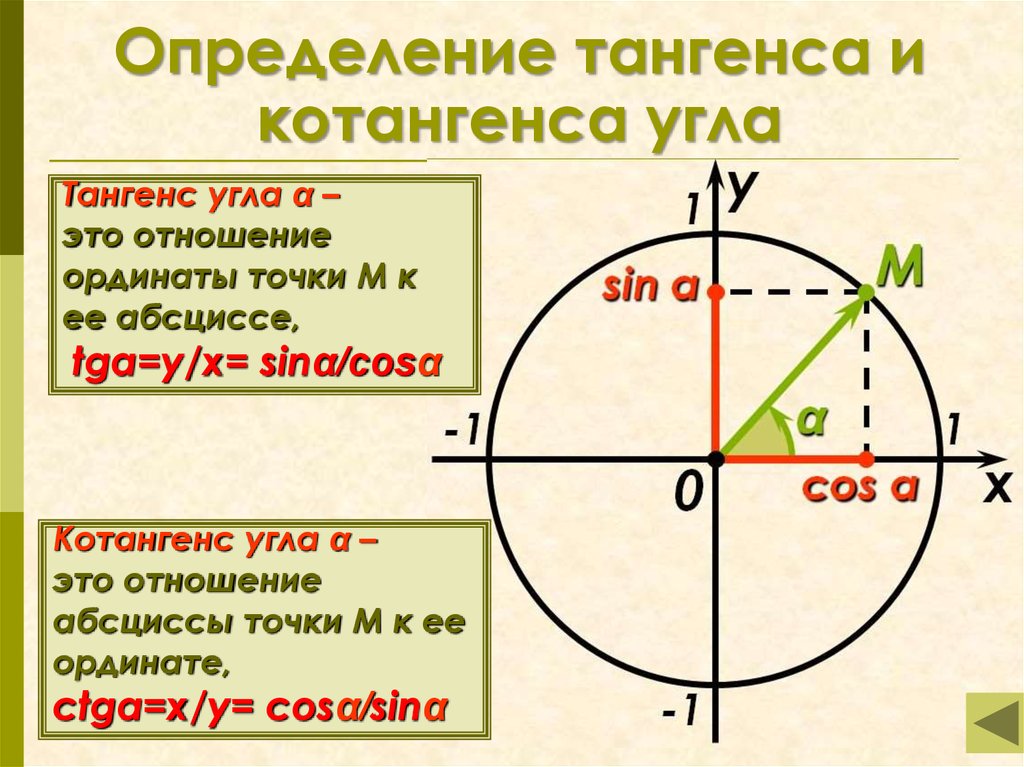 Эти точки получаются поворотом точки на углы,, и т. д.,
а также на углы, и т. д.
при,.
определён для любых углов,
к роме,.
Эти точки получаются поворотом точки на углы,, и т. д.,
а также на углы, и т. д.
при,.
определён для любых углов,
к роме,.
Изображение слайда
23
Слайд 23
Синус, косинус, тангенс и котангенс угла определён только для тех углов, для которых, так как делить на нуль нельзя. Эти точки получаются поворотом точки на углы,,, и т. д., а также на углы,, и т. д. при,. определён для любых углов, к роме,. А для каких углов определён ?
Изображение слайда
24
Слайд 24
Таблица значений синуса, косинуса, тангенса и котангенса Не сущ. Не сущ. Не сущ. Не сущ. Не сущ. Не сущ. Не сущ. Не сущ. Не сущ. Не сущ.
Изображение слайда
25
Слайд 25
Найдём значение выражения.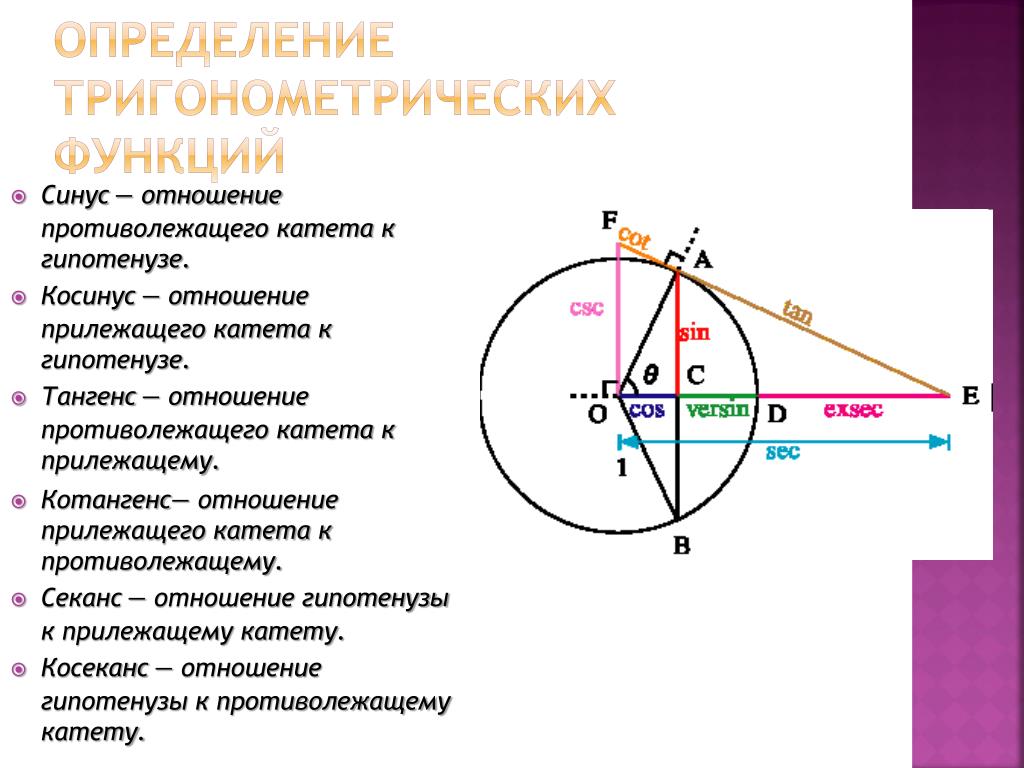 Синус, косинус, тангенс и котангенс угла
.
Синус, косинус, тангенс и котангенс угла
.
Изображение слайда
26
Слайд 26
З начения синуса, косинуса, тангенса и котангенса для углов, которых нет в приведённой выше таблице, можно найти с помощью инженерного микрокалькулятора или по четырёхзначным математическим таблицам Брадиса. Синус, косинус, тангенс и котангенс угла
Изображение слайда
27
Последний слайд презентации: Определение синуса, косинуса и тангенса угла
Итоги урока
Изображение слайда
Исчисление— Какие есть строгие определения для синуса и косинуса?
Задавать вопрос
Спросил
Изменено 11 месяцев назад
Просмотрено 3к раз
$\begingroup$
Вот некоторые из моих идей:
1. \prime(0) = \cos(0) = 1$. 92}}\, дт
\end{align}$$
\prime(0) = \cos(0) = 1$. 92}}\, дт
\end{align}$$
Тогда $\sin x$ является обратным $\arcsin x$, соответствующим образом расширенным до вещественной прямой, и $\cos x$ аналогичен.
Вопрос: Есть ли другие, которые вам нравятся? В частности, есть ли хорошие строгие определения, вытекающие из исходного геометрического определения?
- исчисление
- реальный анализ
- тригонометрия
$\endgroup$
5
$\begingroup$ 9n}{n!}$$
затем определяет функции косинуса и синуса (которые он первоначально называет $C(x)$ и $S(x)$) вещественной переменной посредством
$$C(x)= \frac 12[E(ix)+E(-ix)], \quad S(x)=\frac 1{2i}[E(ix)-E(-ix)]$$
Затем он выводит все обычные свойства (как тригонометрические, так и аналитические) синуса и косинуса всего на двух страницах. Все его доказательства просты и ясны, кроме одного: он показывает, что существуют положительные числа $x$ такие, что $C(x)=0$. Это можно доказать просто другими способами, поэтому аналитическое изложение тригонометрии строго, кратко и ясно. Попутно он также показывает обычную параметризацию единичного круга и показывает обычные школьные определения синуса и косинуса.
Это можно доказать просто другими способами, поэтому аналитическое изложение тригонометрии строго, кратко и ясно. Попутно он также показывает обычную параметризацию единичного круга и показывает обычные школьные определения синуса и косинуса.
Заключение Рудина есть,
Следует подчеркнуть, что мы вывели основные свойства тригонометрические функции из [определений $E(x)$, $C(x)$ и $S(x)$], без обращения к геометрическому понятию угла.
(В этой цитате я заменил ссылки на конкретные уравнения их значением.)
Относительно вашего вопроса «В частности, существуют ли какие-либо хорошие строгие уравнения, вытекающие из исходного геометрического определения?»:
«Исходное геометрическое определение» не является строгим, если у вас нет хорошего определения длины дуги окружности, а также хорошей системы аксиом для действительных чисел или их эквивалента. Евклид не создал такой системы, хотя и пытался. Объяснение, которое я дал от Бэби Рудина, определяет геометрию и тригонометрию на основе анализа. Разработать строгую геометрию, включающую все тригонометрические идеи, не начав с анализа, очень сложно. Даже аксиомы Гильберта для геометрии имели свои проблемы. Я никогда не видел хорошего строгого развития тригонометрии из современной формальной геометрии, хотя где-то оно должно существовать. 9{2k+1}}{(2k+1)!}\end{split}
$$
мы находим обычные определения рядов.
Разработать строгую геометрию, включающую все тригонометрические идеи, не начав с анализа, очень сложно. Даже аксиомы Гильберта для геометрии имели свои проблемы. Я никогда не видел хорошего строгого развития тригонометрии из современной формальной геометрии, хотя где-то оно должно существовать. 9{2k+1}}{(2k+1)!}\end{split}
$$
мы находим обычные определения рядов.
$\endgroup$
2
$\begingroup$
Одно из определений, которое, как мне кажется, имеет очень ясное геометрическое значение, звучит так: на единичной окружности в плоскости $xy$ начертите отрезок прямой от начала координат до точки на окружности. Назовите угол, который отрезок образует с осью $x$ $t$, как показано на рисунке. Определим $x$-компоненту конца отрезка как $\cos(t)$, а $y$-компоненту как $\sin(t)$.
Определение класса триггера «противоположное, смежное, гипотенуза» следует из этого определения.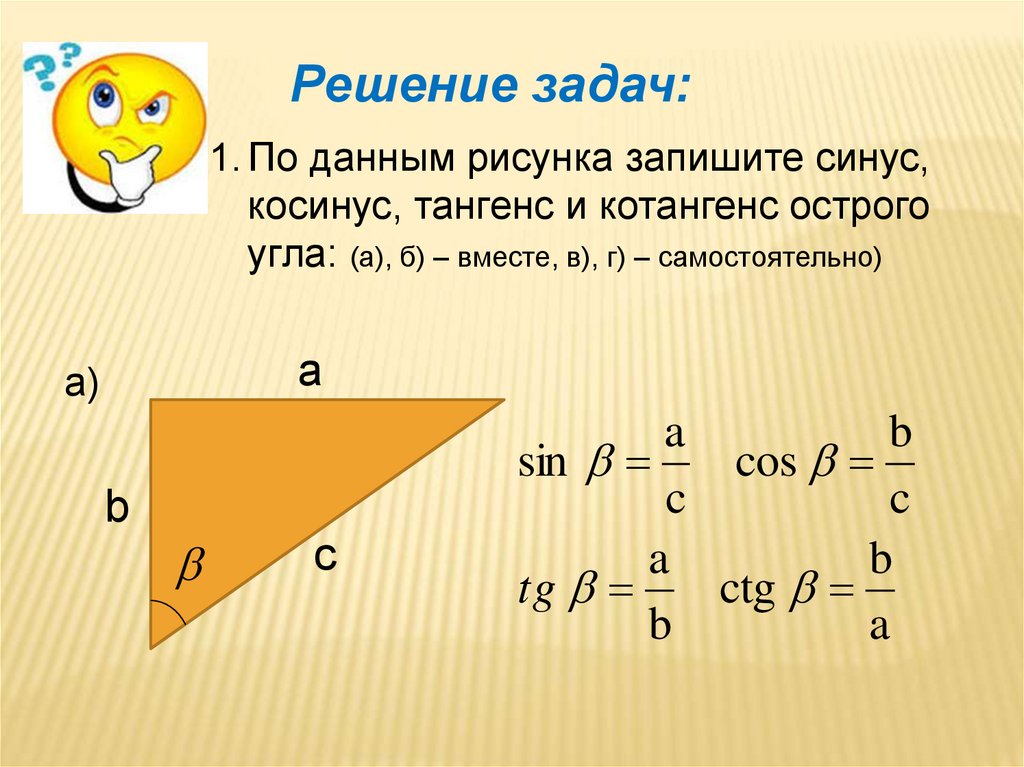 Отсюда также несложно вывести определение интеграла обратной функции. Определение формулы сложения требует немного больше усилий, но существуют геометрические доказательства всех перечисленных фактов.
Отсюда также несложно вывести определение интеграла обратной функции. Определение формулы сложения требует немного больше усилий, но существуют геометрические доказательства всех перечисленных фактов.
$\endgroup$
2
$\begingroup$
Вот один из способов:
- Определите некоторые базовые операции, такие как интегрирование и аналитическое продолжение. 9{-1}$ (обратная функция).
- Расширение $\exp$ с $\mathbb R$ на $\mathbb C$ с помощью аналитического продолжения.
- Окончательно установлен $$ \sin(z)=\frac{\exp(iz)-\exp(-iz)}{2i},\quad \cos(z)=\frac{\exp(iz)+\exp(iz)}{2}. $$
$\endgroup$
$\begingroup$
Вот способ формализовать геометрическую интуицию. Мы можем определить $\sin,\cos$ как проекции спирали $\text{cis}(x)=:(\cos(x),\sin(x))$, где $\text{cis}: \mathbb{R}\to\mathbb{R}^2$ — это единственный выпрямленный путь $C^1$ в единичной окружности, который начинается в точке $(1,0)$ и движется против часовой стрелки.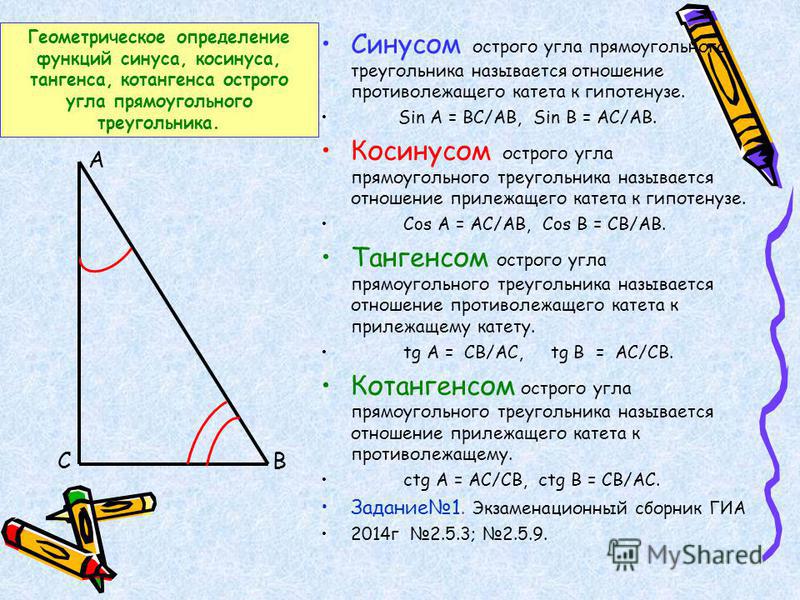 92=1$
92=1$
Первые три условия показывают, что функция $\text{cis}(x):=(\cos(x),\sin(x))$ равна нулю или представляет собой логарифмическую спираль с $\text{cis} (0)=(1,0)$. Четвертое условие сужает его до спирали, а последнее условие определяет ориентацию, а $\pi$ определяет длину волны. Однако вам все равно нужно определить $\pi$, что, к сожалению, требует вычислений. Положительным моментом является то, что $\pi$ отличается только тем, что углы соответствуют длинам дуг.
Например, если вы замените $\pi$ в последнем условии некоторой положительной константой $\lambda$, это задаст триггерные функции в терминах различных единиц измерения углов (например, градусов, если $\lambda=180$ ) и не потребует никаких вычислений, кроме базовой непрерывности. Вы можете опустить условие непрерывности, если вам нужно определить $\sin,\cos$ только для рациональных кратных длин волн $\lambda$.
$\endgroup$
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.
ФУНКЦИИ СИНУСА И КОСИНУСА – ТРИГОНОМЕТРИЯ
функция синусаВ математике синус – это тригонометрическая функция угла. Синус острого угла определяется в контексте прямоугольного треугольника: для указанного угла он равен отношение длины стороны, противоположной этому углу, к длине наибольшей стороны треугольника (гипотенузы) .
В более общем смысле определение синуса (и других тригонометрических функций) может быть расширено до любого действительного значения с точки зрения длины определенного отрезка линии в единичной окружности. Более современные определения выражают синус как бесконечный ряд или как решение определенных дифференциальных уравнений, позволяя их расширение на произвольные положительные и отрицательные значения и даже на комплексные числа.
Функция синуса обычно используется для моделирования периодических явлений, таких как звуковые и световые волны, положение и скорость гармонических осцилляторов, интенсивность солнечного света и продолжительность дня, а также колебания средней температуры в течение года.
Функцию синуса можно проследить до функций jyā и koti-jyā , использовавшихся в индийской астрономии периода Гупта (Арьябхатия, Сурья Сиддханта). Слово «синус» происходит от неправильного латинского перевода арабского jiba 9.0074 , что является транслитерацией санскритского слова, обозначающего половину аккорда, jya-ardha.
Функция синуса обладает следующими свойствами:
- Домен: все действительные числа (R)
- Диапазон: [-1, 1]
- Период: 2π
- x – точки пересечения: x = kπ, где k – целое число.
- г – точки пересечения: г = 0
- Максимальное количество баллов: (π/2 + 2kπ, 1), где k — целое число.
- Минимум баллов: (3π/2 + 2kπ, -1), где k — целое число.
- Симметрия: так как sin(-x) = – sin (x), то sin (x) является нечетной функцией и ее график симметричен относительно начала координат (0 , 0).

- Интервалы: sin x увеличивается на интервалах (0 , π/2) и (3π/2 , 2π) и убывает на интервале (π/2 , 3π/2).
Функция синуса соответствует y-координатам точек на единичной окружности.
Пример: Найдите область определения и диапазон ƒ (x) = 3 sin x + 2.
Решение: Мы знаем, что область определения sin x равна R.
Функция синуса представляет собой непрерывная функция, поэтому мы можем найти диапазон, вычислив максимальное и минимальное значения ƒ (x).
Максимальное значение sin x равно 1, поэтому максимальное значение ƒ (x) равно 3 · 1 + 2 = 5
Минимальное значение sin x равно -1, поэтому минимальное значение ƒ (x) равно 3 · (-1) + 2 = -1
В заключение , диапазон ƒ (x) равен [-1, 5].
В видео ниже объясняется пример графа, домена и диапазона функции синуса:
. Функция
Функция. встречается в тригонометрии. Самый простой способ понять функцию косинуса — использовать единичный круг. Для заданной угловой меры θ нарисуйте единичный круг на координатной плоскости и нарисуйте угол с центром в начале координат, с одной стороной в качестве положительной оси x. Координата x точки, где другая сторона угла пересекает окружность, равна cos(θ), а координата y – sin(θ).
- Домен: все действительные числа (R)
- Диапазон: [-1, 1]
- Период: 2π
- точек пересечения x: x = π/2 + kπ, где k — целое число.

- y-отрезки: y = 1
- Максимальное количество баллов: (2kπ, 1), где k — целое число.
- Минимум баллов: (π + 2kπ, -1), где k — целое число.
- Симметрия: поскольку cos(-x) = cos(x), то cos x является четной функцией и ее график симметричен относительно оси y.
- Интервалы: потому что x убывает на (0, π) и возрастает на (π, 2π).
Функция косинуса соответствует x-координатам точек на единичной окружности.
Пример: Найдите диапазон y = sin 3x · cos 2x + cos 3x · sin 2x + 1.
Решение: Мы знаем (sin 3x · cos 2x) + (cos 3x) 2x) = sin (3x +2x) = sin 5x по формулам суммы и разности. Таким образом, уравнение упрощается до y = sin 5x + 1,9.0307 Кроме того, -1 ≤ sin 5x ≤ 1, поэтому
(-1 + 1) ≤ (sin 5x + 1) ≤ (1 + 1)
В заключение, диапазон y составляет 0 ≤ y ≤ 2.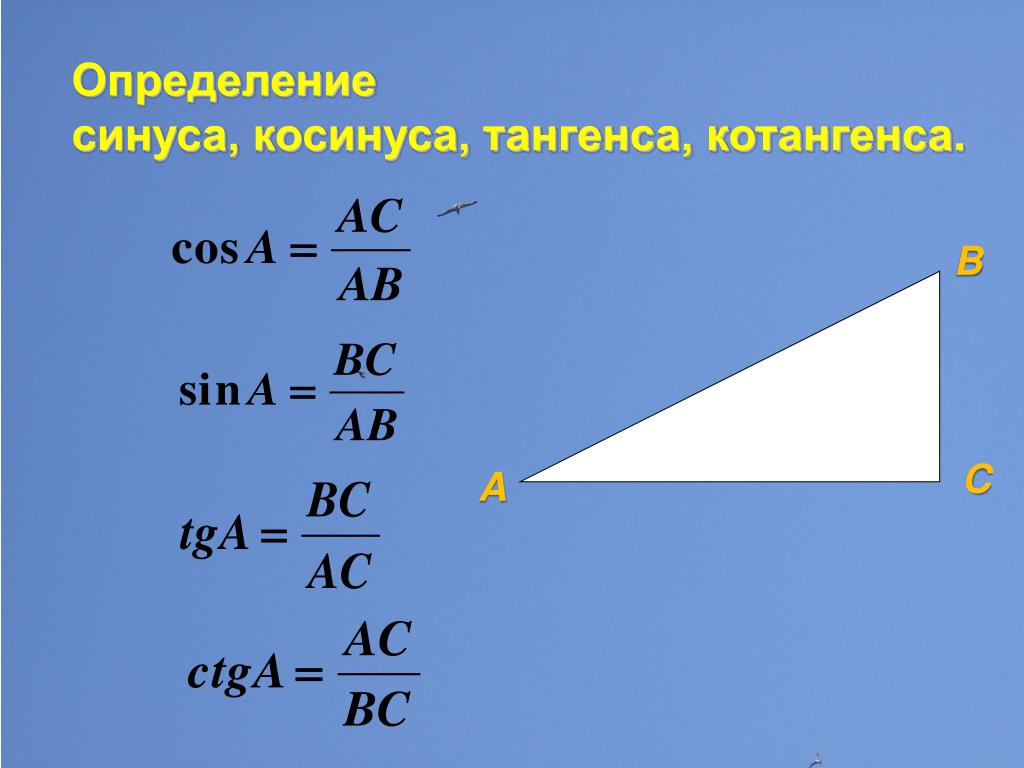
Посмотрите видео ниже, чтобы узнать о происхождении функций косинуса:
Нравится:
Нравится Загрузка…
Определениев кембриджском словаре английского языка
Примеры синуса
синуса
Поступая таким образом, вы можете завоевать доверие — неотъемлемое условие сетевого мира.
От Хаффингтон Пост
Разнообразие во всех его различных аспектах, особенно разнообразие мышления, должно уважаться как sine qua non «ответственности» в коллективе.
От Хаффингтон Пост
Подумайте о трех синусоидальных волнах с разными длинами волн — в определенные моменты времени все три впадины случайно выстроятся в линию.
Из Арс Техника
Свистящий язык и синусоидальная -волновая речь — это не одно и то же: свист сохраняет некоторые свойства, лишенные синусоидальной речи, и теряет другие.
Из Арс Техника
Произношение синусоидальной -волны само по себе трудно, если вообще возможно, понять.
Из Арс Техника
Это могут быть петли чистых тонов, белый шум, синусоиды волновые развертки и даже розовый шум.
Из проводного
Свободный человек выбирает — это sine qua non свободы.
От Хаффингтон Пост
Синеш признал, что в процессе строительства и проектирования возникли проблемы, но сказал, что никогда не считал их достаточно серьезными, чтобы поставить под угрозу весь проект.
Из Балтимора Сан
Динамик приводится в действие усилителем, подключенным к компьютеру, работающему под управлением синусоида программное обеспечение для генерации волн.
От Гизмодо
Строительными блоками формулы являются пи и функции синуса и косинуса из тригонометрии.
Из журнала The New Yorker
На экране компьютера звездное колебание, вызванное одной планетой, выглядит как синусоидальная волна , хотя реальные измерения редко бывают такими четкими.
Из проводного
sine qua non минималистского маркетинга заключается в том, что он опирается на стратегию.
От Хаффингтон Пост
Обсуждение — это не отдельная деятельность, а неотъемлемая часть сайта.
Из Атлантики
Мы можем безвозвратно разорвать узы доверия, являющиеся непременным условием любой демократии.
Из Нью-Йорк Таймс
Эти примеры взяты из корпусов и из источников в Интернете. Любые мнения в примерах не отражают мнение редакторов Кембриджского словаря, издательства Кембриджского университета или его лицензиаров.
Переводы sine
на китайский (традиционный)
正弦…
Подробнее
на китайском (упрощенном)
正弦…
Увидеть больше
на португальском языке
seno…
Увидеть больше
на других языкахна польском
синус…
Подробнее
Нужен переводчик?
Получите быстрый бесплатный перевод!
Как произносится синус ?
Обзор
искренний
С уважением
искренность
синдхи
синус
синусоида
синус умирает
непременное условие
синекура
Проверьте свой словарный запас с помощью наших веселых викторин по картинкам
- {{randomImageQuizHook.


 : ил.- ISBN 5-09-002727-7
: ил.- ISBN 5-09-002727-7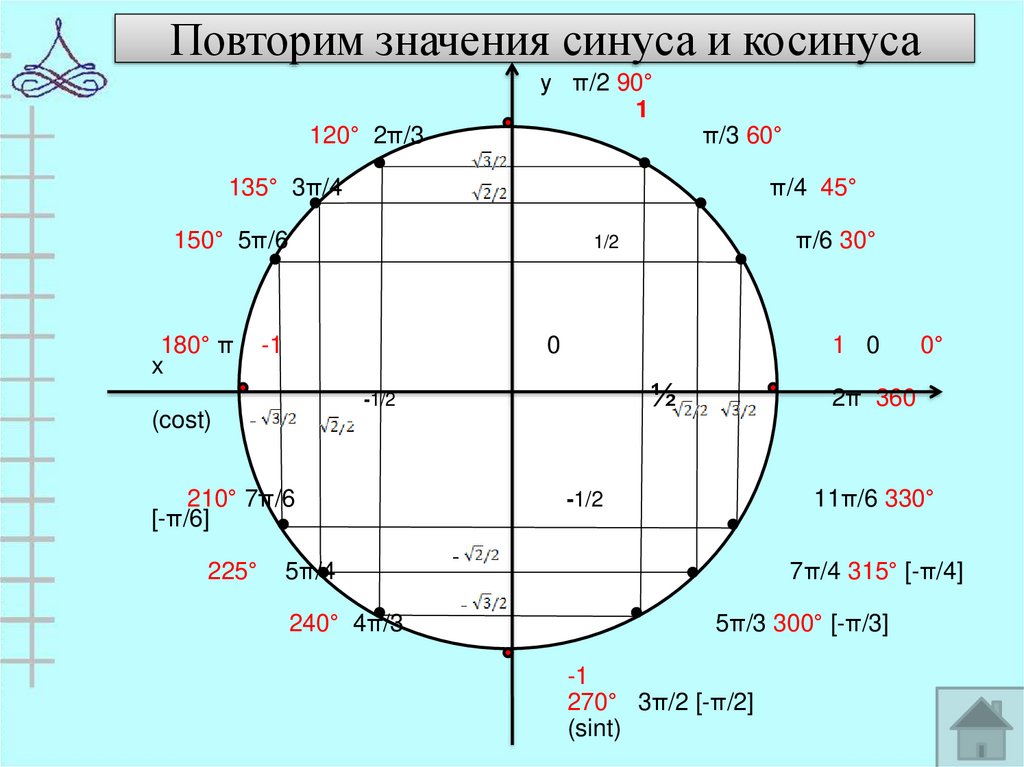 А., Мордкович А. Г. Математика (пособие для поступающих в техникумы): Учеб. пособие.- М.; Высш. шк., 1984.-351 с., ил.
А., Мордкович А. Г. Математика (пособие для поступающих в техникумы): Учеб. пособие.- М.; Высш. шк., 1984.-351 с., ил.