Примеры 5 класс обыкновенные дроби: Понятие обыкновенной дроби — урок. Математика, 5 класс.

Умножение обыкновенных дробей / Обыкновенные дроби / Справочник по математике 5-9 класс

1. Главная
2. Справочники
3. Справочник по математике 5-9 класс
4. Обыкновенные дроби
5. Умножение обыкновенных дробей

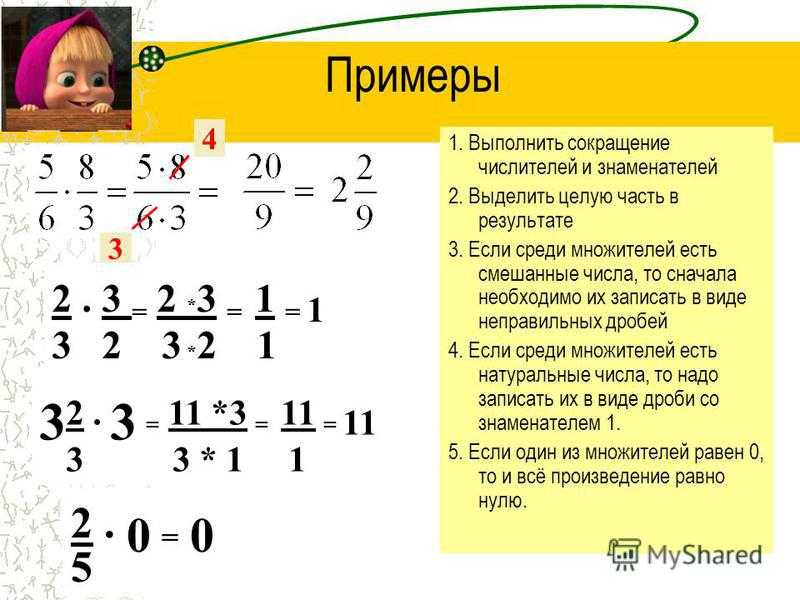
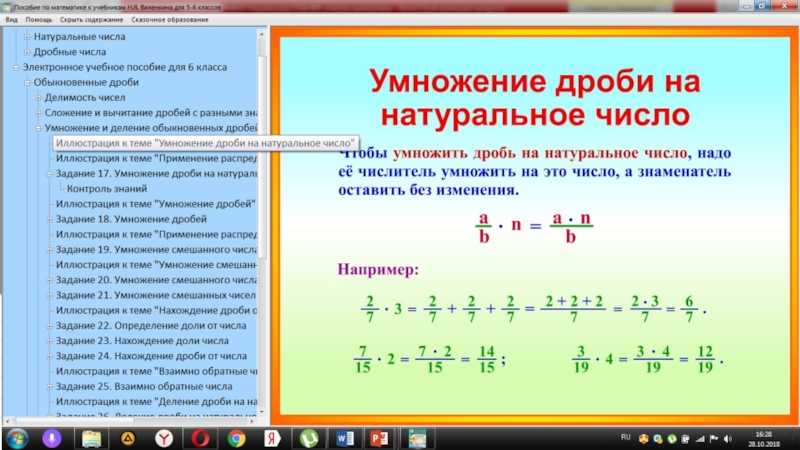
Чтобы умножить обыкновенную дробь на натуральное число, нужно ее числитель умножить на это число, а знаменатель оставить без изменения.

Примеры:

Обратите внимание, если в ответе получается неправильная дробь, то из нее выделяют целую часть.

Если мы умножаем на натуральное число, которое можно сократить с числом, стоящим в знаменателе, то сначала выполняют сокращение, а затем умножение (такой ход действий облегчает вычисления).

Пример:

Произведением двух дробей является дробь, числитель которой равен произведению числителей, а знаменатель — произведению знаменателей.

Пример:

Если мы перемножаем дроби, у которых можно сократить числитель первой и знаменатель второй дроби и (или) знаменатель первой и числитель второй дроби, то сначала выполняют сокращение, а затем умножение (такой ход действий облегчает вычисления).

Примеры:

Умножение смешанных чисел

Чтобы выполнить умножение смешанных чисел, нужно записать эти числа в виде неправильных дробей, а затем воспользоваться правилом умножения дробей.

Примеры:

Для обыкновенных дробей, как и для натуральных чисел, выполняются свойства умножения (переместительное свойство умножения, сочетательное свойство умножения, распределительные свойства умножения относительно сложения и относительно вычитания). Также при умножении дроби на ноль (или нуля на дробь) получаем ноль, и при умножении дроби на единицу (или единицы на дробь) получим равную ей дробь.

Примеры:

Чтобы умножить смешанное число на натуральное число, можно представить смешанное число в виде неправильной дроби, а затем воспользоваться правилом умножения дроби на натуральное число или можно умножить целую часть на натуральное число, далее умножить дробную часть на натуральное число и полученные произведения сложить.

Пример:

Нахождение дроби от числа

Чтобы найти дробь от числа, нужно умножить число на эту дробь.

Примеры:

а) Найти от числа 20.

Решение:

б) Найти 0,6 от числа 9.

Решение:

9·0,6 = 5,4.

в) Найти 30 % от числа 500.

Решение:

1) 30% = 30 : 100 = 0,30 = 0,3

2) 500·0,3 = 150.

Взаимно обратные числа

Два числа, произведение которых равно 1, называют взаимно обратными.

Примеры:

1) , значит, числа — взаимно обратные;

2)

Чтобы определить число обратное смешанному числу, нужно представить это смешанное число в виде неправильной дроби.

Пример:

, значит, числу обратно число .

Запомните:

• Числом, обратным 1, является само число 1.
• Для числа 0 обратного числа не существует.
• Обратным числу является число .
• Если — натуральное число, то обратным ему является число .

Поделись с друзьями в социальных сетях:

Советуем посмотреть:

Доли. Обыкновенные дроби

Сравнение дробей

Делители и кратные

Признаки делимости на 10, на 5 и на 2

Четные и нечетные числа

Признаки делимости на 9 и на 3

Простые и составные числа

Разложение на простые множители

Наибольший общий делитель

Наименьшее общее кратное

Деление и дроби

Сложение и вычитание дробей с одинаковыми знаменателями

Смешанное число

Сложение и вычитание смешанных чисел

Основное свойство дроби

Решето Эратосфена

Приведение дробей к общему знаменателю

Сравнение, сложение и вычитание дробей с разными знаменателями

Деление обыкновенных дробей

Обыкновенные дроби

Правило встречается в следующих упражнениях:

5 класс

Задание 567, Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 1348, Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 1751, Виленкин, Жохов, Чесноков, Шварцбург, Учебник

6 класс

Номер 4, Мерзляк, Полонский, Якир, Учебник

Номер 432, Мерзляк, Полонский, Якир, Учебник

Номер 468, Мерзляк, Полонский, Якир, Учебник

Номер 1036, Мерзляк, Полонский, Якир, Учебник

Задание 445, Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 513, Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 959, Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 1229, Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 1277, Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 1, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 1

7 класс

Номер 48, Мерзляк, Полонский, Якир, Учебник

Номер 70, Мерзляк, Полонский, Якир, Учебник

Номер 115, Мерзляк, Полонский, Якир, Учебник

Номер 2, Мерзляк, Полонский, Якир, Учебник

Номер 7, Мерзляк, Полонский, Якир, Учебник

Номер 503, Мерзляк, Полонский, Якир, Учебник

Номер 578, Мерзляк, Полонский, Якир, Учебник

Номер 646, Мерзляк, Полонский, Якир, Учебник

Номер 650, Мерзляк, Полонский, Якир, Учебник

Номер 1052, Мерзляк, Полонский, Якир, Учебник

---

Обыкновенные дроби 5 класс

УМК: А. Г. Мерзляк и др

Все об обыкновенных дробях

5 класс

Разработано учителем математики МОУ «СОШ» п. Аджером Корткеросского района Республики Коми

Мишариной Альбиной Геннадьевной

Содержание

• Понятие дроби, Правильные и неправильные дроби
• Сравнение дробей
• Сложение и вычитание дробей с одинаковыми знаменателями
• Смешанное число. Преобразование смешанного числа в неправильную дробь. Выделение целого числа из неправильной дроби.
• Сложение и вычитание смешанных чисел

1. Понятие обыкновенной дроби

Дробные числа возникают, когда один предмет

(1 единицу измерения, 1 число) делят на несколько равных частей

Понятие обыкновенной дроби

числитель

— ОБЫКНОВЕННАЯ ДРОБЬ

знаменатель

знаменатель показывает, на сколько долей делят целое,

а

числитель показывает сколько таких долей взято

Назовите получившиеся дроби

Назовите д роби

2. Виды обыкновенных дробей

2. Виды обыкновенных дробей

1).

Если числитель дроби меньше его знаменателя, то такая дробь называется правильной

2. Виды обыкновенных дробей

2).

НЕПРАВИЛЬНАЯ ДРОБЬ – это дробь , в которой ЧИСЛИТЕЛЬ БОЛЬШЕ ЗНАМЕНАТЕЛЯ

или РАВЕН ЕМУ

— НЕПРАВИЛЬНЫЕ ДРОБИ

Можно запомнить

так

Запомним

Определите вид каждой дроби

Решаем из учебника

стр. №

ДРОБНЫЕ ЧИСЛА МОЖНО

СРАВНИВАТЬ,

СКЛАДЫВАТЬ,

ВЫЧИТАТЬ,

УМНОЖАТЬ

и ДЕЛИТЬ

3. Сравнение обыкновенных дробей

Рассмотрим

Значит: из двух дробей с одинаковыми знаменателями та больше, у которой числитель больше

и та меньше, у которой числитель меньше

3. Сравнение обыкновенных дробей

Рассмотрим

Значит: и з двух дробей с одинаковыми числителями та дробь больше, у которой знаменатель меньше

Запомним

• Все правильные дроби меньше единицы, а неправильные – больше или равны единице.

• Каждая неправильная дробь больше любой правильной дроби, а каждая правильная дробь меньше любой неправильной дроби

Например

Сами

Решаем из учебника

стр. №

4). Сложение и вычитание дробей с одинаковыми знаменателями

а). Правило сложения дробей

Например.

4). Сложение и вычитание дробей с одинаковыми знаменателями

б). Правило вычитания дробей

Например.

Запомним

Вычислите

5). Умножение и деление дробей (6 кл)

а). Правило умножения дробей

Например.

5). Умножение и деление дробей (6 кл)

б). Правило деления дробей

Нап р имер.

Решаем из учебника

стр. №

6). Смешанн ое числ о

одна целая две третьих

целая часть

дробная часть

Числа состоящие из целой и дробной частей

называются смешанными числами

Назовите смешанное число, изображённые на рисунках

Рассмотрим где находятся смешанных числа на координатном (числовом) луче?

7).

Например .

Например

Сами

8).

Например

Рассмотрим ещё примеры

Сами

Запомним

Решаем из учебника

стр. №

9). Сложение и вычитание смешанных чисел

Например.

а). ПРИ СЛОЖЕНИИ смешанных чисел

целые части СКЛАДЫВАЮТ отдельно, а дробные — отдельно

9). Сложение и вычитание смешанных чисел

Например .

б). ПРИ ВЫЧИТАНИИ

смешанных чисел

целые части ВЫЧИТАЮТ отдельно, а дробные — отдельно

9). Пр и вычитани и смешанных чисел бывают случаи

а). Как вычесть дробь из единицы

9). Пр и вычитани и смешанных чисел бывают случаи

б). Как вычесть дробь из целого числа?

9). Пр и вычитани и смешанных чисел бывают случаи

в). Как вычесть , если дробная часть уменьшаемого меньше дробной части вычитаемого?

9). Пр и вычитани и смешанных чисел бывают случаи

Проверить решение

Выполните действия самостоятельно

Решаем из учебника

стр. №

Источник и ресурса

Шаблон создан на основе клипарта рамки

• https://img-fotki.yandex.ru/get/6212/39663434.8ee/0_ace11_630a09db_XL.png

И возможностей программы Microsoft PowerPoint 2016

Автор шаблона презентации учитель русского языка и литературы Тихонова Надежда Андреевна , г. Костанай

• А.Г. Мерзляк, В.Б. Полонский, М.С. Якир. Математика: 5 класс: учебник для учащихся общеобразовательных организаций, — 2-е изд., перераб. – М.:Вентана-Граф, 2016

https ://ds03.infourok.ru/ uploads / ex /114d/000604bc-f86d2398/3/hello_html_m73e9c92f.png

https://ds02.infourok.ru/ uploads / ex /0f1f/0002ce3e-2e46c14f/hello_html_m6c4e4d65.jpg

http://900igr.net/ datai / matematika / Doli-obyknovennye-drobi /0006-006-Doli.png

http://900igr. net/ datai / matematika / Doli-obyknovennye-drobi /0006-007-Doli.png

http://fs.nashaucheba.ru/tw_files2/urls_3/1542/d-1541017/img7.jpg

https://fs00.infourok.ru/ images / doc /208/237239/hello_html_55ba06b8.jpg

https://ds02.infourok.ru/ uploads / ex /0d6e/0000e445-8aeb763d/hello_html_m4d8534a6.jpg

http ://fs1.ppt4web.ru/ images /4134/64853/640/img11.jpg

автор и источник заимствования неизвестен

Источник и ресурса

http :// pandia.ru / text /79/418/ images /image002_4.jpg

http://intellect.ml/uploads/news/id1768/6_compare_right_not_right_drob.jpg

https:// allyslide.com / thumbs /134d0c688e4498e549a1bae53efbef31/img7.jpg

http://www.rushkolnik.ru/tw_files2/urls_3/900/d-899561/img3. jpg

http:// bigslide.ru / images /22/21152/831/img8.jpg

https://fs00.infourok.ru/ images / doc /226/36260/3/img13.jpg

https://fs00.infourok.ru/ images / doc /226/36260/3/img12.jpg

https://fs00.infourok.ru/ images / doc /168/192913/640/img5.jpg

https://fs00.infourok.ru/ images / doc /237/136772/2/img19.jpg

http://www.uzluga.ru/potra/ Урок+по+теме.+Дополните+дроби+до+Найди+ошибкуa /img4.jpg

https://ds02.infourok.ru/ uploads / ex /1223/000198c2-57fa5d64/hello_html_3addeb07.png

http://fs1.ppt4web.ru/images/4134/67167/640/img2.jpg

http:// www.matematikus.info / images / arifmetika /smeshan6.png

http:// detskoerazvitie.info / wp-content / uploads / slozhenie-drobej-s-celymi-chislami. jpg

https://fs00.infourok.ru/ images / doc /25/32873/hello_html_6417b52b.jpg

http://poluchisovet.ru/files/00000/02698.jpg

http:// www.mathematics-repetition.com / wp-content / uploads /2012/07/smesh-ch32.jpg

http://fs1.ppt4web.ru/images/5552/84756/640/img1.jpg

https://fs00.infourok.ru/images/doc/243/236091/1/img1.jpg

http://www.for6cl.uznateshe.ru/wp-content/uploads/2013/03/koordinatnijluch3.jpg

http://netnado.ru/tiki-po-teme-sravnenie-drobej-dlya-5-klassa-rabotu/28705_html_7472ab59.jpg

http://school-728.narod.ru/Dorohova/4-.jpg

понятие в математике для 5 класса и основные их свойства

Математика

12.11.21

9 мин.

В средней школе изучается более подробно на уроке математики 5 класса понятие обыкновенной дроби. Это необходимо для перехода к упрощению алгебраических выражений, решению уравнений и другим операциям.

Оглавление:

• Общие сведения
• Определение обыкновенной дроби
• Основные свойства

Здесь важны теоретические знания, поэтому специалисты разработали специальный алгоритм, позволяющий не только рассмотреть эту тему, но и добиться успехов в текущем направлении.

Общие сведения

Любая система обучения строится по определенной методике, состоящей из отдельных пунктов. В некоторых учебных заведениях ученики пишут сочинение об обыкновенных дробях для наилучшего понимания. Такой подход не для всех эффективен, поскольку люди делятся на две категории — гуманитарии и математики. Данное разделение зависит от мышления, а методики обучения не всегда являются универсальными.

В этом случае ученики понимают тему обыкновенных дробных тождеств по-разному. Следовательно, школьная программа не всегда бывает эффективной. Чтобы улучшить понимание, специалисты разработали универсальную методику: они используют последовательное изучение задачи, раскладывая ее на пункты. Последние представляют подзадачи, которые также могут быть разбиты на определенные шаги. Для изучения обыкновенных дробей применяется алгоритм, состоящий из следующих элементов:

1. Определения (формулировки).
2. Свойства.

Первый пункт — определение математического термина с примерами, позволяющими понять математический смысл и как выглядит обыкновенная дробь. Второй компонент включает в свой состав основные свойства дробного тождества определенного типа.

Определение обыкновенной дроби

Наиболее подробно изучаются примеры обыкновенных дробей в 5 классе. Это дает возможность осуществлять более сложные операции, а именно: решать уравнения рационального типа и сокращать или упрощать тождества.

Обыкновенная дробь — это математическое выражение, характеризующее операцию деления без результата операции (незаконченное действие).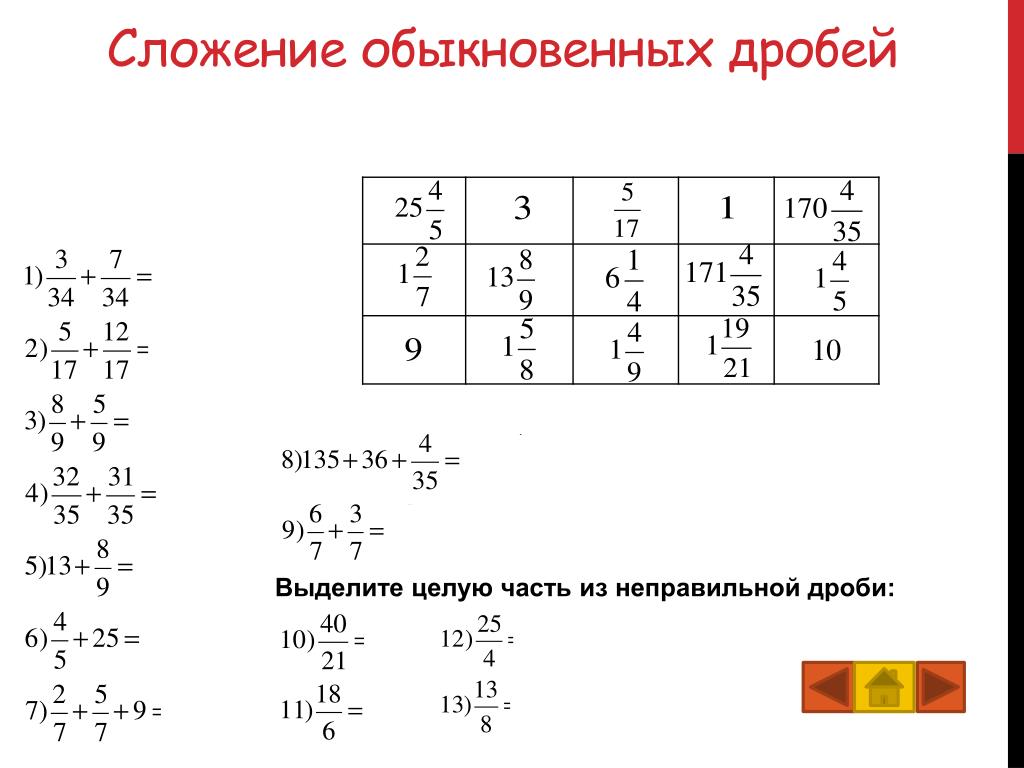 Следует отметить, что она состоит из трех элементов: делимого, делителя и частного. Обыкновенное дробное выражение считается неполной операцией, поскольку состоит только из числителя (делимого) и знаменателя (делителя). Ее результатом является десятичное дробное выражение.

Для примера возьмем дробное выражение обыкновенного вида «½». Оно состоит из числителя «1» и знаменателя «2». В этом случае частное записывается в виде десятичной дроби, т. е. 0,5. Чтение выражение осуществляется таким образом: «одна вторая». Запись выполняется в аналогичном порядке, т. е. «½». Первым указывается числитель, а затем знаменатель.

Чтобы понять саму суть, можно привести такой пример: целый арбуз требуется поровну (куски равны между собой) разделить на 7 человек. Каждому из них достанется только одна часть, т. е. 1/7. Если один человек отдал другому свою долю, то получится 2/7. Следует отметить, что любое единичное значение записывается в общем виде: 7/7, 8/8, 9/9, 11/11 и т. д. Результатом операции является единица, поскольку 7: 7 = 1.

Кроме того, обычные дробные выражения делятся на два вида. К ним относятся следующие:

1. Числитель меньше знаменателя — правильные.
2. Величина знаменателя меньше значения числителя — неправильные.

Следует отметить, что любая неправильная дробь может быть записана в виде смешанного числа, т. е. 7/4=1[¾]. Последнее состоит из целой (1) и дробной (¾) частей. Отделяются они между собой квадратными скобками.

Основные свойства

У обыкновенной дроби есть определенные свойства, позволяющие осуществлять с ней любые арифметические операции преобразования, а также правильно сокращать числитель и знаменатель. К ним относятся следующие:

1. Умножение или деление числителя и знаменателя на одно значение, т. е. (4*2/5*2) или (4:2/5:2).
2. Возможность вынесения общего множителя, чтобы на него сократить числитель и знаменатель, т. е. 4/8=(4*1)/(4*2)=½.
3. Отнимание или прибавление одного и того же значения к числителю или знаменателю, т. е. (7+2−2)/(11−10+10).

Следует отметить, что для понимания каждого свойства, его нужно доказать. Начать следует с первого утверждения. Для этого нужно взять произвольное дробное тождество обыкновенного вида. Например, 8/9. Далее необходимо умножить числитель и знаменатель на 4, т. е. (8*4)/(9*4). После этого требуется представить выражение в виде произведения двух величин: (8/9) * (4/4). Последнее выражение эквивалентно единице. В этом случае утверждение доказано.

Аналогично доказывается и вторая часть утверждения — если разделить числитель и знаменатель на одно число, то величина результирующей дроби не изменится. Для доказательства можно применить следующий алгоритм:

1. Записать выражение: 2/3.
2. Выбрать общий делитель: 7.
3. Записать в математической форме: (2:7)/(3:7).
4. Вынести делитель за скобки: 2/3: 7/7.
5. Последнее выражение в четвертом пункте эквивалентно единице, при делении на которую любое число не меняется.
6. Утверждение доказано.

Второе утверждение доказывать нет необходимости, поскольку в первом случае было вынесение общего множителя за скобку и сокращение на него. Третья формулировка доказывается по следующей методике:

1. Записывается дробь: 6/11.
2. Выбирается один элемент (произвольное число): 5.
3. Коэффициент во втором пункте необходимо прибавить и отнять в числителе, т. е. (6+5−5)/11.
4. Расписывается числитель посредством группировки слагаемых: [6+(5−5)]/11.
5. Осуществляются арифметические операции в числителе: [6+(0)]/11=6/11.
6. Сравниваются конечная и исходная величины: 6/11 = 6/11.
7. Утверждение доказано.

Следует отметить, что аналогично доказывается утверждения и для знаменателя. Так же группируются элементы и складываются. Их результатом является нулевое значение. Кроме того, в школах одним из заданий является создание проекта с примерами свойств обыкновенных дробных тождеств. Для этой цели можно смело применять все алгоритмы, предложенные специалистами в физико-математической сфере.

Таким образом, обыкновенные дробные числа необходимо изучать по определенной методике, предложенной специалистами, для улучшения качества усвоения материала.

Не успеваете написать работу?

Заполните форму и узнайте стоимость

Вид работыПоиск информацииДипломнаяВКРМагистерскаяРефератОтчет по практикеВопросыКурсовая теорияКурсовая практикаДругоеКонтрольная работаРезюмеБизнес-планДиплом MBAЭссеЗащитная речьДиссертацияТестыЗадачиДиплом техническийПлан к дипломуКонцепция к дипломуПакет для защитыСтатьиЧасть дипломаМагистерская диссертацияКандидатская диссертация

Контактные данные — строго конфиденциальны!

Указывайте телефон без ошибок! — потребуется для входа в личный кабинет.

* Нажимая на кнопку, вы даёте согласие на обработку персональных данных и соглашаетесь с политикой конфиденциальности

Подтверждение

Ваша заявка принята.

Ей присвоен номер 0000.
Просьба при ответах не изменять тему письма и присвоенный заявке номер.
В ближайшее время мы свяжемся с Вами.

Ошибка оформления заказа

Кажется вы неправильно указали свой EMAIL, без которого мы не сможем ответить вам.
Пожалуйста проверте заполнение формы и при необходимости скорректируйте данные.

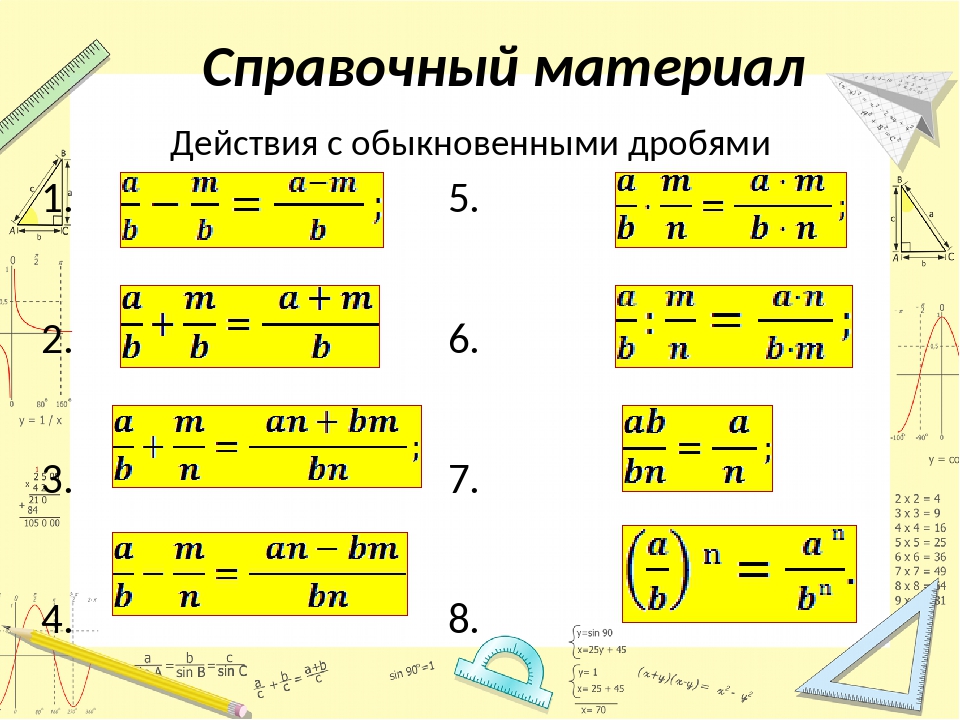
Операции с дробями — Математика 5 класс

Сложение дробей

Дроби являются частями целого. При сложении двух дробей, тем ближе вы к получению целого. Например, если у вас есть половина файла cookie и одна треть файла cookie, вы приближаетесь к тому, чтобы получить целый файл cookie. Чтобы сложить эти дроби вместе, каждую дробь нужно разбить на одинаковое количество частей. Ниже приведены некоторые стратегии, которые помогут вам складывать дроби.

Стратегия: площадная или прямоугольная модель для отображения сложения дробей

Шаг 1: Нарисуйте каждую дробь (одну с горизонтальным разделением, а другое с вертикальным разделением)  6

3 В каждой дроби нарисуйте пунктирные линии так, чтобы они имели общий знаменатель.

Шаг 3: Подсчитайте все заштрихованные части и вычислите сумму дробей

Пример 1:

Пример 2:

Стратегия: Найдите общий знаменатель и добавьте

Шаг 1: Посмотрите на фракции

. : Подумайте, как сделать так, чтобы все дроби имели общий знаменатель (общий множитель)

Шаг 3: Перепишите дроби в эквивалентные дроби с теми же знаменателями

Шаг 4: Найдите сумму фракций

Шаг 5: Напишите сумму фракции в самых низких условиях

. Добавление

9000
. Добавление

. Числа

Стратегия 1: 

Шаг 1. Сначала сложите целые числа

Шаг 2. Затем сложите дробные части (используйте приведенные выше стратегии) 

Шаг 3. Посмотрите на сумму и перепишите дробь в виде необходимо

Мы знаем, что это также эквивалентно 4 и 1/2. дроби

Шаг 2: Найдите общий знаменатель

Шаг 3: Найдите сумму дробей

Шаг 4: Найдите сумму дробей в наименьшем выражении

Затем не забудьте заменить неправильное число смешанным: 

Вычитание дробей

Дроби являются частями целого. Вычитая дроби, вы отнимаете часть дроби. Например, если у вас есть половина файла cookie, и вы дали треть файла cookie, у вас останется меньше половины того, что у вас есть.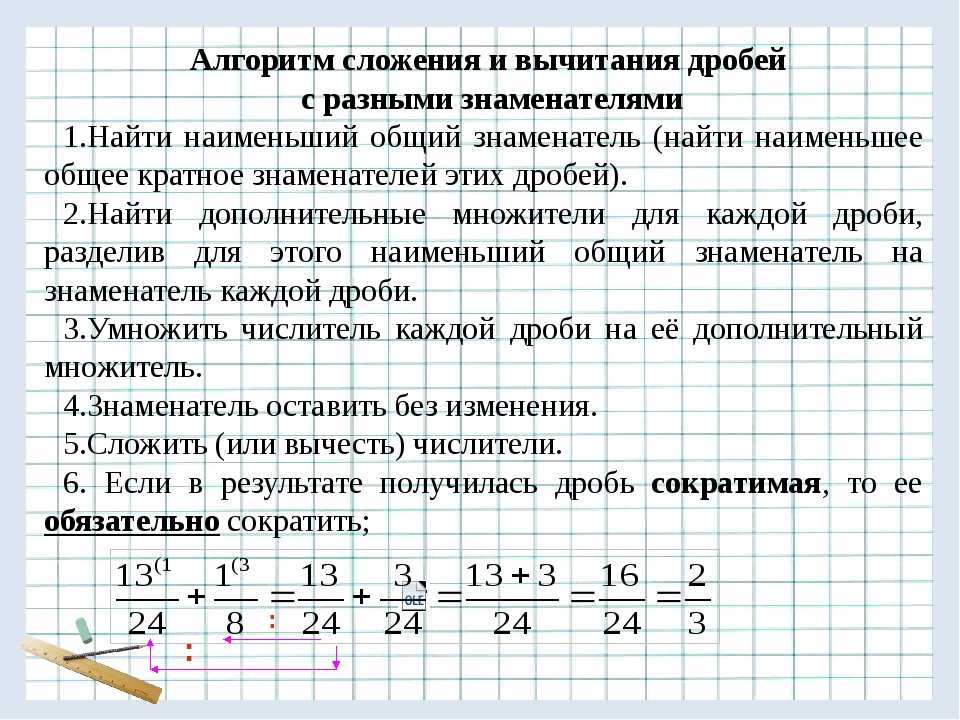 В итоге вы получите одну шестую оставшегося файла cookie.

Вы можете использовать многие из тех же стратегий для решения задач на вычитание, что и в задачах на сложение.

Умножение дробей

Когда мы умножаем дроби, мы думаем о слове «Из». Например:

Что такое 1/2 от 20 или 1/4 от 100. Нам часто кажется, что при умножении дробей мы делим целое число.

Давайте посмотрим на некоторые шаблоны:

Когда оба фактора меньше значения 1, произведение меньше, чем оба фактора.

Примеры:

1/2 x 1/4 —— Подумайте: 1/4 от 1/2               1/2 от 1/4

Таким образом, ответ равен 1/ 8 (произведение меньше, чем 1/2 и 1/4)

Вот еще один:

2/7 x 3/5 —— это как думать, что мне нужно 3/5 2/7 — 6/35 меньше обоих множителей.

Глядя на модели, мы видим, что есть шаги, которые можно сделать, чтобы добраться до продукта.

* Умножить числители

* Умножить знаменатели

* Упростить дробь до наименьшего члена (преобразовать в смешанное число)

Когда один множитель больше единицы, а другой меньше единицы, мы получаем произведение, которое находится между ними из этих факторов.

Примеры:

1 и 2/3 x 1/2 

В этом случае нам нужно подумать. (Точно так же, когда мы думаем, что 23 х 2 = (20 х 2) + (3 х 2)

1 х 1/2 = 1/2

2/3 x 1/2 = (1/2 от 2/3) равно 2/6 или 1/3

1/2 + 1/3 = 3/6 + 2/6 = 5/6 

Мы знаем, что 5/6 больше 1/2, но меньше 1 и 2/3

Когда оба множителя больше единицы, наш продукт будет больше обоих этих множителей.

Пример: 

2 1/2 x 1 2/3 (два смешанных числа)

В этот раз имеет смысл сделать их неправильными дробями.

2 1/2 = 5/2

1 2/3  = 5/3 

5/2 x 5/3 = 25/6 = 4 и 1/6 (произведение больше, чем оба множителя)

Когда один из множителей равен 1, произведение всегда будет другим множителем. (СВОЙСТВО ИДЕНТИЧНОСТИ УМНОЖЕНИЯ)

2/3 x 1 = 2/30010 242/2313 x 1 =  ?????

Когда один из факторов составляет 0, то продукт всегда будет нулевым (нулевое свойство умножения)

2/3 x 0 = 0 110 2/3 x 0 = 0 110 2/3 x 0 = 0 2/3 x 0 = 0

1/5 x 0 = 0

5-й

В пятом классе по математике ваш ребенок будет лучше понимать десятичные числа и дроби, а также изучать числовые выражения, объем и графики. Это много, чтобы покрыть! Помогите своему ребенку добиться успеха в математике в пятом классе, узнав больше о том, что он будет делать.

В течение года ваш ребенок: 

1. Решать числовые выражения

У вашего ребенка большой опыт решения задач с использованием четырех операций. Теперь ваш ребенок разовьет это понимание еще больше, научившись использовать скобки в числовых выражениях и вычислять выражения с их помощью. Ваш ребенок узнает порядок операций и сначала будет решать части выражений в скобках.

Помогите ребенку попрактиковаться в знании порядка операций, дав ему более длинные выражения для оценки как со скобками, так и без них. Дайте ребенку такое же выражение, но с другим расположением скобок. Поговорите с ребенком о том, как скобки повлияли на выражение.

2. Работа с десятичными дробями

В пятом классе учащиеся учатся читать, писать и сравнивать десятичные дроби с тысячными. Они также практикуют сложение, вычитание, умножение и деление десятичных долей до сотых, что может быть непросто!

Поддержите своего ребенка, рассказав о различных стратегиях, которые можно использовать. Пусть ваш ребенок использует рисунки или модели, чтобы попытаться визуализировать десятичные задачи, которые он решает. Например, нарисуйте сетку 10×10 и пусть ваш ребенок увидит каждый квадрат как сотый. Используйте сетку, чтобы визуализировать десятичные дроби при решении задач.

3. Складывать и вычитать дроби с разными знаменателями

В четвертом классе учащиеся научились сравнивать дроби с разными числителями или знаменателями. Теперь они расширят это понимание, научившись складывать и вычитать дроби с разными знаменателями, находя общие знаменатели.

Дайте ребенку возможность выполнять реальные задачи на сложение и вычитание. Например, при приготовлении пищи вы можете попросить ребенка рассчитать ⅓ стакана муки + ½ стакана муки. Помогите ребенку связать общие знаменатели со своими знаниями об умножении, думая об общих кратных. ( Посетите нашу страницу с дробями, чтобы освежить свои знания о дробях!)

4. Умножение и деление дробей

Работа с дробями не заканчивается сложением и вычитанием! Пятиклассники умеют умножать дроби на целые числа или дроби. Они также будут делить единичные дроби (дроби, в которых числитель равен 1) на целые числа и целые числа на единичные дроби.

Эти понятия могут быть сложными, поэтому вместо того, чтобы объяснять их ребенку, пусть он объяснит их вам. Возможность быть учителем может помочь вашему ребенку развить более глубокое понимание и даст вам возможность увидеть, насколько хорошо все усваивается. 

5. Измерьте объем

Четвертоклассники практиковались в измерении длины и веса. Но в этом году они познакомятся с новым типом измерения: объемом. Учащиеся научатся измерять объемы путем подсчета кубических единиц, используя кубические сантиметры, кубические дюймы и кубические футы. Они узнают формулу для вычисления объема кубов и прямоугольных призм (объем = длина x ширина x высота) 

Пусть ваш ребенок заметит количество напитков, которые потребляет ваша семья. Поговорите о том, как контейнеры разного размера, такие как 2-литровые и 1-литровые бутылки, вмещают разное количество жидкости.

6. Нанесение точек на координатную плоскость

В пятом классе учащиеся узнают, как система координат имеет оси x и y, и как точки могут быть представлены их координатами (x,y).

Попросите ребенка нарисовать координатную плоскость на графической бумаге и потренируйтесь, чтобы ребенок находил определенные точки. Такие игры, как Морской бой, также могут быть отличным способом попрактиковаться в использовании координат. Если у вас нет настольной игры, вот как вы можете играть в Морской бой, используя только ручку и бумагу!

На протяжении всего обучения вашего ребенка в пятом классе находите возможности зарегистрироваться и услышать, что он изучает. Математика в пятом классе может быть сложной, так что используйте это как возможность освежить свои навыки!

Нашли это полезным? Ознакомьтесь с нашими руководствами по математике для классов от детского сада до 5-го класса

Написанное Лили Джонс, Лили любит учиться всему. Она работала воспитателем в детском саду и начальных классах, педагогическим тренером, разработчиком учебных программ и тренером для учителей. Она любит смотреть на мир с любопытством и вдохновлять людей всех возрастов любить учиться. Она живет в Калифорнии с мужем, двумя детьми и маленькой собачкой.

О Komodo —  Komodo — это интересный и эффективный способ улучшить математические навыки K-5. Разработанный для детей от 5 до 11 лет для использования дома, Komodo использует небольшой и частый подход к изучению математики (15 минут, три-пять раз в неделю), который вписывается в занятую семейную рутину. Komodo помогает пользователям развить беглость и уверенность в математике — , не заставляя их долго сидеть за экраном .

Узнайте больше о Komodo и о том, как он ежегодно помогает тысячам детей лучше успевать по математике — вы даже можете попробовать Komodo бесплатно.

Снова в школу — 5 советов, которые помогут вам вернуться к рутине

Вот несколько шагов, которые вы можете предпринять, чтобы вывести детей из режима полных каникул, чтобы первая неделя в школе не сбила вас с толку.

Мышление — путь к мастерству

Люди с мышлением роста верят, что у них всегда есть потенциал учиться и совершенствоваться. Они более мотивированы упорно решать сложные задачи, идти на риск и учиться на ошибках.

5 класс | СС | Virtual Nerd

---

Дополнительные темы

в 5 классе

---

Популярные учебные пособия

в 5 классе

• Каковы коммутативные свойства сложения и умножения?

  Свойство коммутативности является фундаментальным строительным блоком математики, но оно работает только для сложения и умножения. В этом руководстве определяется свойство коммутативности и приводятся примеры его использования.

• Каковы ассоциативные свойства сложения и умножения?

  Ассоциативность — это одно из тех фундаментальных свойств математики, благодаря которым математика работает. Вы, вероятно, принимаете это свойство как должное, потому что оно настолько укоренилось, но важно увидеть, как работают нутро математики, поэтому ознакомьтесь с учебным пособием и убедитесь, что вы твердо знаете свои основы!

• Что такое дивиденд и что такое делитель?

  Когда вы решаете задачи на деление, вам нужно знать словарный запас, который люди используют, чтобы описать, какое число делится и какое число выполняет деление. Этот учебник поможет вам сохранить этот словарный запас!

• Как умножать дроби?

  Работа с дробями может быть пугающей, но если вы вооружитесь нужными инструментами, то обнаружите, что работать с дробями не сложнее, чем с простыми числами. В этом уроке вы увидите процесс умножения 3 очень простых дробей. Наслаждаться!

• Как складывать дроби с разными знаменателями?

  Пытаетесь складывать дроби с разными знаменателями? Сначала вам понадобится общий знаменатель! Следуйте этому руководству и посмотрите, что вам нужно сделать, чтобы сложить эти дроби вместе.

• Как умножить целое число на дробь?

  Умножение целого числа на дробь может сбивать с толку, но это руководство поможет разобраться. Проверьте это!

• Каково происхождение?

  Координатная плоскость имеет две оси: горизонтальную и вертикальную. Эти две оси пересекаются друг с другом в точке, называемой началом координат. Узнайте об упорядоченной паре, которая указывает начало координат и ее положение в координатной плоскости, посмотрев этот урок!

• Что такое координатная плоскость?

  Вы не можете изобразить функцию или построить упорядоченные пары без координатной плоскости! Узнайте о координатной плоскости, посмотрев этот урок.

• Что такое координата X?

  Упорядоченные пары являются важной частью построения графика, но вам нужно знать, как определить координаты в упорядоченной паре, если вы собираетесь нанести ее на координатную плоскость. В этом уроке вы увидите, как определить координату x в упорядоченной паре!

• Что такое координата Y?

  Упорядоченные пары являются важной частью построения графика, но вам нужно знать, как определить координаты в упорядоченной паре, если вы собираетесь нанести ее на координатную плоскость. В этом уроке вы увидите, как определить координату Y в упорядоченной паре!

• Что такое ось X?

  Чтобы построить график функции или построить упорядоченную пару, вам нужно использовать координатную плоскость, так что вы должны знать все об этом! В этом уроке вы узнаете об оси x и увидите, где она расположена в координатной плоскости.

• Что такое ось Y?

  Чтобы построить график функции или построить упорядоченную пару, вам нужно использовать координатную плоскость, так что вы должны знать все об этом! В этом уроке вы узнаете об оси Y и увидите, где она расположена в координатной плоскости.

• Что такое оси координат?

  Координатная плоскость имеет две оси: горизонтальную и вертикальную. Узнайте об этих осях и названиях их точек пересечения, посмотрев этот урок!

• Как вы делите целые числа?

  Дивизия — это строительный блок математики. В этом учебном пособии показано, как выполнить деление в длинное число, выполняя процесс по одному шагу за раз.

• Как решить текстовую задачу, разделив целые числа?

  Словесные задачи — отличный способ увидеть математику в реальном мире! Математика может помочь нам ответить на повседневные вопросы. Посмотрите этот урок, чтобы узнать, как деление используется для решения задачи со словами.

• Как найти значение цифры в целом числе?

  Понимание разрядности является строительным блоком понимания чисел. Следуйте этому руководству, чтобы узнать, как найти значение цифры для заданного числа!

• Как упростить выражение, используя порядок операций?

  Вы не можете упростить выражение без полного понимания порядка операций! Следуйте этому руководству, чтобы узнать, как использовать порядок операций для упрощения выражения.

• Как умножить трехзначное число на однозначное?

  Если вы хотите умножить трехзначное число на однозначное, может оказаться полезным выровнять умножение по вертикали. Этот урок проведет вас через процесс умножения!

• Как умножить двузначное число на однозначное?

  Умножение — это строительный блок математики, поэтому важно уметь с ним работать! В этом уроке вы потренируетесь умножать однозначное число на двузначное.

• Как умножить двузначное число на двузначное?

  Когда вы умножаете двузначное число на двузначное число, важно правильно выстроить места. Этот учебник поможет вам попрактиковаться в умножении, сохраняя при этом порядок!

• Как умножить двузначное число на двузначное с помощью частичных произведений?

  Вы можете использовать частичные произведения, чтобы умножить два числа вместе! Следуйте инструкциям в этом руководстве, чтобы увидеть, как частичные произведения могут упростить задачу на умножение!

• Что такое разрядное значение для целых чисел?

  Значение разряда — это строительный блок чисел. Без разрядности мы не смогли бы упорядочить все наши числа! В этом руководстве представлена ​​местная стоимость и показаны части диаграммы разрядной стоимости.

• Какие операции в выражении выполняются в первую очередь?

  Невозможно упростить задачу без порядка действий. В этом уроке вы узнаете об этом специальном порядке и увидите, как использовать его для решения проблемы!

• Как вы конвертируете чашки в пинты?

  Может быть полезно увидеть емкость, указанную в разных единицах измерения. В этом уроке показано, как измерить мерки в чашках и преобразовать их в пинты!

• Как перевести кварты в галлоны?

  Если вы идете в магазин, чтобы купить определенное количество литров молока, а в магазине молоко продается только в галлонах, что вы делаете? Вам нужно преобразовать эти кварты в галлоны! Следуйте этому руководству, чтобы узнать, как это сделать.

• Как перевести миллилитры в литры?

  Миллилитры и литры — это две единицы измерения вместимости. В этом уроке вы увидите, как взять заданное количество миллилитров и преобразовать его в литры!

• Как округлить десятичную дробь с помощью числовой строки?

  Округление — важная часть математики! В этом руководстве вы увидите, как использовать числовую линию, чтобы помочь вам округлить десятичную дробь до выбранного разрядного значения.

• Как использовать предварительную оценку для оценки суммы нескольких десятичных знаков?

  Предварительная оценка может быть отличным способом приблизить сумму. В этом руководстве вы увидите, как использовать предварительную оценку для приблизительной стоимости школьных принадлежностей!

• Как вы оцениваете сумму десятичных знаков с помощью кластеризации?

  Если вы хотите найти приблизительную сумму десятичных знаков, вы можете сначала округлить эти числа! В этом руководстве показано, как округлить десятичные дроби и посмотреть, к каким числам они близки, чтобы упростить сложение.

• Как перегруппировать числа, чтобы мысленно складывать десятичные дроби?

  Складывать числа в уме проще, чем вы думаете! Это может быть быстрый и интересный навык! Этот урок покажет вам, как брать десятичные дроби и складывать их мысленно.

• Как умножить десятичную дробь на целое число?

  Если вы хотите умножить десятичную дробь на целое число, просто игнорируйте десятичную точку и умножайте как обычно! Затем верните десятичную точку для ответа. Этот учебник показывает вам весь процесс шаг за шагом.

• Как умножить десятичную дробь на целое число, используя оценку для размещения десятичной дроби?

  Когда вы умножаете десятичное и целое число, удаление десятичной точки может упростить умножение, но куда девается десятичная точка, когда вы хотите получить ответ? В этом уроке вы увидите, как оценить положение десятичной точки после умножения!

• Как решить задачу со словами, разделив десятичные дроби и округлив ответ в большую сторону?

  Никогда не знаешь, где может появиться дивизия! Эта задача со словами — отличный пример использования деления на длинные числа для решения задачи.

• Как упорядочить дроби и десятичные числа от наибольшего к наименьшему?

  Если вы хотите сравнить различные типы чисел, начните с преобразования их всех в один тип числа! В этом уроке показан пример использования дробей и десятичных знаков!

• Как сложить две дроби с разными знаменателями?

  Если вы складываете дроби с разными знаменателями, вам сначала нужно сделать эти знаменатели одинаковыми! В этом руководстве показано, как записывать дроби, чтобы у них были общие знаменатели, а затем показано, как складывать эти дроби.

• Как вычесть две дроби с разными знаменателями?

  Чтобы вычитать дроби, у них должны быть одинаковые знаменатели. Чтобы получить одинаковые знаменатели, вы можете найти эквивалентные дроби! В этом уроке показано, как вычитать дроби с разными знаменателями.

• Какова формула объема прямоугольной призмы?

  Найдите объем прямоугольной призмы с помощью формулы! Посмотрите этот урок, чтобы узнать больше!

• Как вы делаете длинное умножение?

  Умножение больших чисел? Без проблем! В этом уроке вы увидите, как выполнить длинное умножение, чтобы найти ответ (без использования калькулятора!). Взглянем!

• Как вы переводите фразы в числовые выражения?

  Превратить фразу из слов в математическую задачу может быть сложно, но практика может облегчить этот процесс! В этом уроке вы увидите, как искать ключевые слова, которые могут помочь вам перевести фразу в математику.

• Что такое эквивалентные дроби?

  Нахождение эквивалентных дробей является важной частью таких операций, как сложение, вычитание и сравнение дробей. Но что это такое? В этом уроке вы узнаете, что эквивалентные дроби — это просто дроби, которые имеют одинаковое значение, даже если они могут выглядеть очень по-разному! Взгляните на эквивалентные дроби, посмотрев этот урок!

• Как складывать смешанные дроби с разными знаменателями путем преобразования в неправильные дроби?

  Добавление смешанных фракций? Вы можете сначала преобразовать каждую в неправильную дробь. Если у них нет общих знаменателей, найдите общий знаменатель и используйте его, чтобы переписать каждую дробь. Затем сложите дроби вместе и упростите. В этом уроке вы узнаете, как сложить смешанные дроби с разными знаменателями!

• Как вычитать смешанные дроби с разными знаменателями путем перегруппировки?

  Вычитание смешанных дробей с разными знаменателями? Вы можете сначала найти общий знаменатель и использовать его, чтобы переписать каждую дробь. Затем вычтите целые числа и дроби отдельно. В этом уроке вы познакомитесь с вычитанием смешанных дробей с разными знаменателями!

• Как вычитать смешанные дроби с разными знаменателями путем преобразования в неправильные дроби?

  Вычитание смешанных дробей? Вы можете сначала преобразовать каждую в неправильную дробь. Если у них нет общих знаменателей, найдите общий знаменатель и используйте его, чтобы переписать каждую дробь. Затем вычтите дроби и упростите. В этом уроке вы познакомитесь с вычитанием смешанных дробей с разными знаменателями!

• Как округлить десятичную дробь до заданного разрядного значения?

  Иногда десятичные дроби бывают такими длинными, что вам нужен способ оценить десятичную дробь. В других случаях вам может понадобиться только определенная точность, чтобы получить ответ. Вот где округление десятичных долей до выбранного места может быть очень полезным! Посмотрите этот урок, чтобы узнать, как округлить десятичную дробь до выбранного разряда.

• Что такое разрядное значение?

  Знаете ли вы, что у чисел есть разрядность? В этом учебном пособии вы познакомитесь с термином «место» и покажете некоторые из наиболее часто встречающихся мест. Взглянем!

• Как классифицировать четырехугольники?

  Есть фигура с четырьмя сторонами? Тогда у вас есть четырехугольник! Но есть много специальных типов четырехугольника. Следуйте инструкциям, поскольку этот учебник покажет вам, как определить возможные имена для данного четырехугольника!

• Что такое прямоугольник?

  Прямоугольник — одна из многих основных фигур, встречающихся в математике. Прямоугольники обладают особыми свойствами, которые могут быть очень полезны при решении проблемы. В этом уроке вы познакомитесь с прямоугольниками и объясните их интересные свойства!

• Что такое четырехугольник?

  Термин «четырехугольник» — это действительно причудливо звучащее название для определенного типа многоугольника. Знаете ли вы, что существуют особые типы четырехугольников? Посмотрите этот урок, чтобы узнать о четырехугольниках и их особых типах.

• Что такое квадрат?

  Квадрат — одна из многих основных фигур, встречающихся в математике. Квадраты обладают особыми свойствами, которые могут быть очень полезны при решении проблемы. В этом уроке вы познакомитесь с квадратами и объясните их интересные свойства!

• Что такое ромб?

  Ромб – это особый вид четырехугольника. Знание особых свойств ромба важно для идентификации и использования этих специальных многоугольников.

  No related posts.