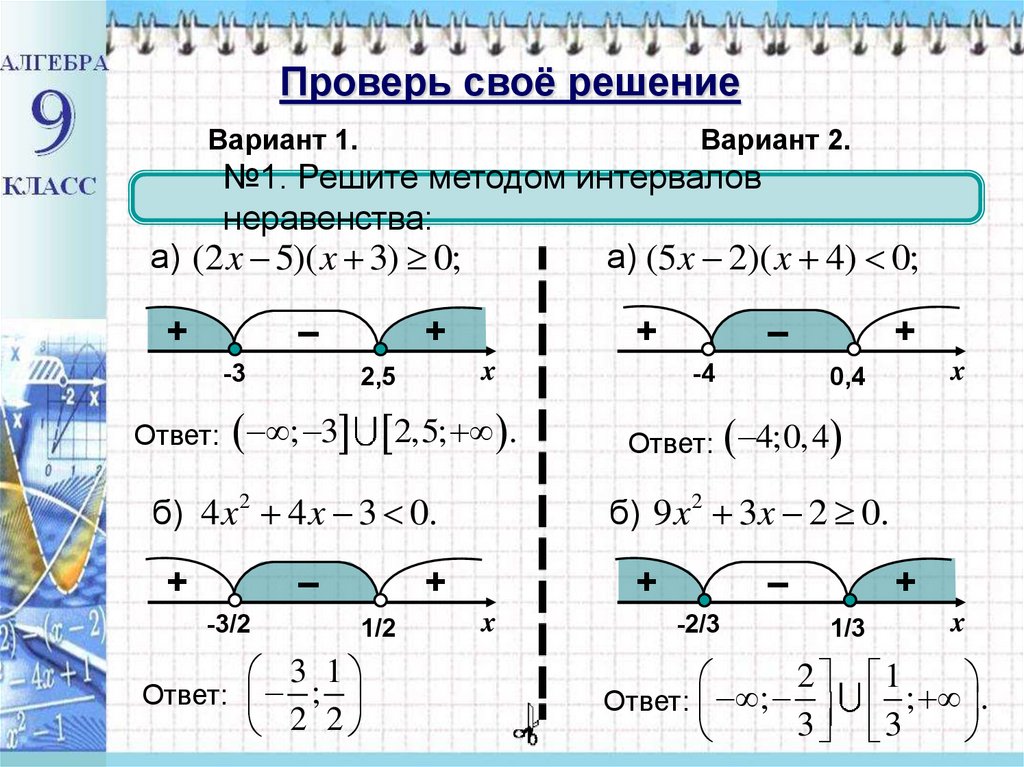
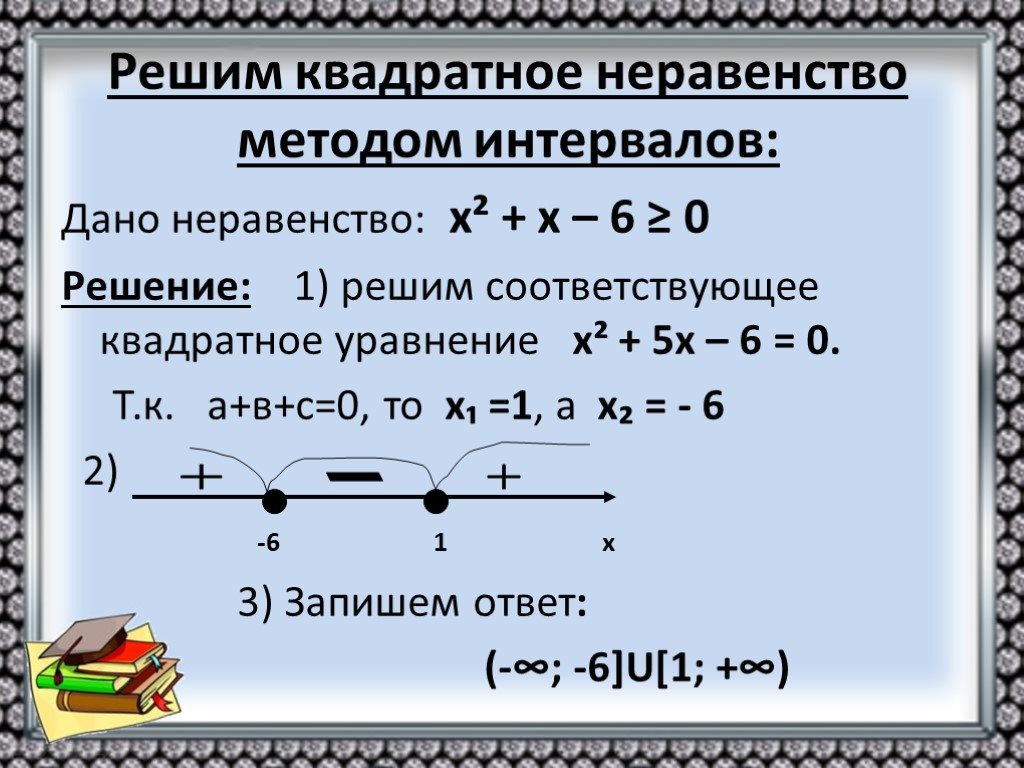
Онлайн калькулятор: Метод бисекции
Калькулятор, который находит приближенное решение уравнения методом бисекции или методом деления отрезка пополам. Небольшая теория под калькулятором.
Метод бисекции
Уравнение
Начальное приближение x0
Начальное приближение x1
Критерий останова (погрешность)
Критерий останова (тип)
Приращение x
Отличие функции от нуля
Точность вычисления
Знаков после запятой: 4
Формула
Файл очень большой, при загрузке и создании может наблюдаться торможение браузера.
Метод бисекции
Существует довольно очевидная теорема: «Если непрерывная функция на концах некоторого интервала имеет значения разных знаков, то внутри этого интервала у нее есть корень (как минимум, один, но может быть и несколько)».
На базе этой теоремы построено несколько методов численного нахождения приближенного значения корня функции. Обобщенно все эти методы называются методами дихотомии, т. е. методами деления отрезка на две части (необязательно равные).
Здесь уже были рассмотрены Метод хорд и Метод секущих, теперь дошла очередь и до самого простого метода дихотомии, называемого методом бисекции, или методом деления отрезка пополам. Как следует из названия, именно в этом методе отрезок делится каждый раз на две равные части. Середина отрезка считается следующим приближением значения корня. Вычисляется значение функции в этой точке, и, если критерий останова не достигнут, выбирается новый интервал. Интервал выбирается таким образом, чтобы на его концах значения функции по прежнему имели разный знак, то есть чтобы он по прежнему содержал корень. Такой подход обеспечивает гарантированную сходимость метода независимо от сложности функции — и это весьма важное свойство. Недостатком метода является то же самое — метод никогда не сойдется быстрее, т.
е. сходимость метода всегда равна сходимости в наихудшем случае.
Итерационная формула проста:
Метод бисекции является двухшаговым, то есть новое приближение определяется двумя предыдущими итерациями. Поэтому необходимо задавать два начальных приближения корня.
Метод требует, чтобы начальные точки были выбраны по разные стороны от корня (то есть корень содержался в выбранном интервале).
В качестве критерия останова берут один из следующих:
— значение функции на данной итерации стало меньше заданого ε.
— изменение хk в результате итерации стало меньше заданого ε. Поскольку интервал на каждом шаге уменьшается в два раза, вместо проверки x можно рассчитать количество требуемых итераций.
Подробнее: Метод бисекции.
Алгебра анализ Математика метод бисекции метод деления отрезка пополам метод дихотомии решение уравнений уравнение уравнения Численные методы
Калькулятор интервальных повторений
| 0 | ||||
| AC | +/- | ÷ | ||
| 7 | 8 | 9 | × | |
| 4 | 5 | 6 | — | |
| 1 | 2 | 3 | + | |
| 0 | 00 | , | = | |
Интервальные повторения — это техника запоминания любой информации, суть которой состоит в повторении материала через определенные интервалы времени, при условии, что каждый последующий интервал возрастает относительно предыдущего.
Интервальные повторения подходят для запоминания любой информации:
заучивания иностранных слов, нот музыкального произведения, математических формул и много другого.
При помощи калькулятора интервальных повторений вы можете составить таблицу дат в которые необходимо будет делать повторенияВыберете дату, когда вы первый раз ознакомились с материалом, который необходимо запомнить
| |||||||||
| Пн | Вт | Ср | Чт | Пт | Сб | Вс | |||
|---|---|---|---|---|---|---|---|---|---|
| 28 | 29 | 30 | 1 | 2 | 3 | 4 | |||
| 5 | 6 | 7 | 8 | 9 | 10 | 11 | |||
| 12 | 13 | 14 | 15 | 16 | 17 | 18 | |||
| 19 | 20 | 21 | 22 | 23 | 24 | 25 | |||
| 26 | 27 | 28 | 29 | 30 | 31 | 1 | |||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 | |||
| Вам могут также быть полезны следующие сервисы |
| Генераторы |
| Генератор примеров по математике |
| Генератор случайных чисел |
| Генератор паролей |
| Калькуляторы линейная алгебра и аналитическая геометрия |
| Калькулятор сложения и вычитания матриц |
| Калькулятор умножения матриц |
| Калькулятор транспонирование матрицы |
| Калькулятор нахождения определителя (детерминанта) матрицы |
| Калькулятор нахождения обратной матрицы |
Длина отрезка. Онлайн калькулятор расстояния между точками |
| Онлайн калькулятор нахождения координат вектора по двум точкам |
| Калькулятор нахождения модуля (длины) вектора |
| Калькулятор сложения и вычитания векторов |
| Калькулятор скалярного произведения векторов через длину и косинус угла между векторами |
| Калькулятор скалярного произведения векторов через координаты |
| Калькулятор векторного произведения векторов через координаты |
| Калькулятор смешанного произведения векторов |
| Калькулятор умножения вектора на число |
| Калькулятор нахождения угла между векторами |
| Калькулятор проверки коллинеарности векторов |
| Калькулятор проверки компланарности векторов |
| Калькуляторы (Комбинаторика) |
| Калькулятор нахождения числа перестановок из n элементов |
| Калькулятор нахождения числа сочетаний из n элементов |
| Калькулятор нахождения числа размещений из n элементов |
| Калькуляторы систем счисления |
| Калькулятор перевода чисел из арабских в римские и из римских в арабские |
| Калькулятор перевода чисел в различные системы счисления |
| Калькулятор сложения, вычитания, умножения и деления двоичных чисел |
| Системы счисления теория |
| N2 | Двоичная система счисления |
| N3 | Троичная система счисления |
| N4 | Четырехичная система счисления |
| N5 | Пятеричная система счисления |
| N6 | Шестеричная система счисления |
| N7 | Семеричная система счисления |
| N8 | Восьмеричная система счисления |
| N9 | Девятеричная система счисления |
| N11 | Одиннадцатиричная система счисления |
| N12 | Двенадцатеричная система счисления |
| N13 | Тринадцатеричная система счисления |
| N14 | Четырнадцатеричная система счисления |
| N15 | Пятнадцатеричная система счисления |
| N16 | Шестнадцатеричная система счисления |
| N17 | Семнадцатеричная система счисления |
| N18 | Восемнадцатеричная система счисления |
| N19 | Девятнадцатеричная система счисления |
| N20 | Двадцатеричная система счисления |
| N21 | Двадцатиодноричная система счисления |
| N22 | Двадцатидвухричная система счисления |
| N23 | Двадцатитрехричная система счисления |
| N24 | Двадцатичетырехричная система счисления |
| N25 | Двадцатипятеричная система счисления |
| N26 | Двадцатишестеричная система счисления |
| N27 | Двадцатисемеричная система счисления |
| N28 | Двадцативосьмеричная система счисления |
| N29 | Двадцатидевятиричная система счисления |
| N30 | Тридцатиричная система счисления |
| N31 | Тридцатиодноричная система счисления |
| N32 | Тридцатидвухричная система счисления |
| N33 | Тридцатитрехричная система счисления |
| N34 | Тридцатичетырехричная система счисления |
| N35 | Тридцатипятиричная система счисления |
| N36 | Тридцатишестиричная система счисления |
| Дроби |
| Калькулятор интервальных повторений |
| Учим дроби наглядно |
| Калькулятор сокращения дробей |
| Калькулятор преобразования неправильной дроби в смешанную |
| Калькулятор преобразования смешанной дроби в неправильную |
| Калькулятор сложения, вычитания, умножения и деления дробей |
| Калькулятор возведения дроби в степень |
| Калькулятор перевода десятичной дроби в обыкновенную |
| Калькулятор перевода обыкновенной дроби в десятичную |
| Калькулятор сравнения дробей |
| Калькулятор приведения дробей к общему знаменателю |
| Калькуляторы (тригонометрия) |
| Калькулятор синуса угла |
| Калькулятор косинуса угла |
| Калькулятор тангенса угла |
| Калькулятор котангенса угла |
| Калькулятор секанса угла |
| Калькулятор косеканса угла |
| Калькулятор арксинуса угла |
| Калькулятор арккосинуса угла |
| Калькулятор арктангенса угла |
| Калькулятор арккотангенса угла |
| Калькулятор арксеканса угла |
| Калькулятор арккосеканса угла |
| Калькулятор нахождения наименьшего угла |
| Калькулятор определения вида угла |
| Калькулятор смежных углов |
| Калькуляторы (Теория чисел) |
| Калькулятор выражений |
| Калькулятор упрощения выражений |
| Калькулятор со скобками |
| Калькулятор уравнений |
| Калькулятор суммы |
| Калькулятор разложения числа на простые множители |
| Калькулятор НОД и НОК |
| Калькулятор НОД и НОК по алгоритму Евклида |
| Калькулятор НОД и НОК для любого количества чисел |
| Калькулятор делителей числа |
| Представление многозначных чисел в виде суммы разрядных слагаемых |
| Калькулятор деления числа в данном отношении |
| Калькулятор процентов |
| Калькулятор перевода числа с Е в десятичное |
| Калькулятор экспоненциальной записи чисел |
| Калькулятор нахождения факториала числа |
| Калькулятор нахождения логарифма числа |
| Калькулятор квадратных уравнений |
| Калькулятор остатка от деления |
| Калькулятор корней с решением |
| Калькулятор нахождения периода десятичной дроби |
| Калькулятор больших чисел |
| Калькулятор округления числа |
| Калькулятор свойств корней и степеней |
| Калькулятор комплексных чисел |
| Калькулятор среднего арифметического |
| Калькулятор арифметической прогрессии |
| Калькулятор геометрической прогрессии |
| Калькулятор модуля числа |
| Калькулятор абсолютной погрешности приближения |
| Калькулятор абсолютной погрешности |
| Калькулятор относительной погрешности |
| Калькуляторы площади геометрических фигур |
| Площадь квадрата |
| Площадь прямоугольника |
| КАЛЬКУЛЯТОРЫ ЗАДАЧ ПО ГЕОМЕТРИИ |
| Генератор Pdf с примерами |
| Тренажёры решения примеров |
| Тренажёр таблицы умножения |
| Тренажер счета для дошкольников |
| Тренажер счета на внимательность для дошкольников |
Тренажер решения примеров на сложение, вычитание, умножение, деление. Найди правильный ответ. |
| Тренажер решения примеров с разными действиями |
| Тренажёры решения столбиком |
| Тренажёр сложения столбиком |
| Тренажёр вычитания столбиком |
| Тренажёр умножения столбиком |
| Тренажёр деления столбиком с остатком |
| Калькуляторы решения столбиком |
| Калькулятор сложения, вычитания, умножения и деления столбиком |
| Калькулятор деления столбиком с остатком |
| Конвертеры величин |
| Конвертер единиц длины |
| Конвертер единиц скорости |
| Конвертер единиц ускорения |
| Цифры в текст |
| Калькуляторы (физика) |
Механика |
| Калькулятор вычисления скорости, времени и расстояния |
| Калькулятор вычисления ускорения, скорости и перемещения |
| Калькулятор вычисления времени движения |
| Калькулятор времени |
Второй закон Ньютона. Калькулятор вычисления силы, массы и ускорения. |
| Закон всемирного тяготения. Калькулятор вычисления силы притяжения, массы и расстояния. |
| Импульс тела. Калькулятор вычисления импульса, массы и скорости |
| Импульс силы. Калькулятор вычисления импульса, силы и времени действия силы. |
| Вес тела. Калькулятор вычисления веса тела, массы и ускорения свободного падения |
Оптика |
| Калькулятор отражения и преломления света |
Электричество и магнетизм |
| Калькулятор Закона Ома |
| Калькулятор Закона Кулона |
| Калькулятор напряженности E электрического поля |
| Калькулятор нахождения точечного электрического заряда Q |
| Калькулятор нахождения силы F действующей на заряд q |
| Калькулятор вычисления расстояния r от заряда q |
| Калькулятор вычисления потенциальной энергии W заряда q |
| Калькулятор вычисления потенциала φ электростатического поля |
| Калькулятор вычисления электроемкости C проводника и сферы |
Конденсаторы |
| Калькулятор вычисления электроемкости C плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления напряженности E электрического поля плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления напряжения U (разности потенциалов) плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления расстояния d между пластинами в плоском конденсаторе |
| Калькулятор вычисления площади пластины (обкладки) S в плоском конденсаторе |
| Калькулятор вычисления энергии W заряженного конденсатора |
Калькулятор вычисления энергии W заряженного конденсатора. Для плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления объемной плотности энергии w электрического поля для плоского, цилиндрического и сферического конденсаторов |
| Калькуляторы по астрономии |
| Вес тела на других планетах |
| Ускорение свободного падения на планетах Солнечной системы и их спутниках |
Бесплатный интервальный калькулятор
Наши пользователи: Не обижайся, но я всегда думал, что математика, особенно алгебра, просто бесполезна всю мою жизнь. Я считаю, что программа очень полезна! Спасибо! Я не могу позволить себе оплачивать отдельные часы занятий с моими близнецами, потому что в алгебре так много различных аспектов, которые они не понимают, но обо всем позаботились; Алгебратор справляется со своей задачей лучше, чем любые репетиторы, которых я нанимал. Теперь я смею надеяться, что мои мальчики поступят в колледж. Я люблю алгебру, но не смог закончить домашнюю работу вовремя. Теперь все изменилось для меня. Сначала я был в замешательстве, покупать это программное обеспечение или нет. Студенты, борющиеся со всевозможными задачами по алгебре, узнают, что наше программное обеспечение спасает им жизнь. Вот поисковые фразы, которые сегодняшние поисковики использовали, чтобы найти наш сайт. Сможете ли вы найти среди них свою?Поисковые фразы, использованные 26 марта 2015 г.:
|
Теперь, когда я это понял, у меня появилось совершенно новое понимание его назначения и необходимости в современном технологическом мире! Кроме того, теперь я могу честно осуществить свою мечту стать создателем видеоигр, и я, вероятно, слишком поздно понял бы, что без продвинутой математики вы просто не сможете этого сделать! 
Но за пять дней я более чем доволен Алгебратором. Я боролся с квадратными уравнениями и неравенствами. Логический и пошаговый подход к решению задач оказался для меня благом, и теперь я люблю решать эти уравнения. 
Как записать уравнение горизонтальной линии?
66 рабочий лист
com
Калькулятор доверительного интервала для коэффициента завершения – измерение U
Джефф Сауро, доктор философии
1 октября 2005 г.
Используйте этот калькулятор для расчета доверительного интервала и наилучшей точечной оценки наблюдаемой скорости завершения. Этот калькулятор предоставляет скорректированные интервалы Вальда, Точного, Счета и Вальда.
Вас также может заинтересовать
Загрузите этот калькулятор в файле Excel
Пояснение
Скорректированный метод Вальда следует использовать практически постоянно. Исключения см. ниже.
Подробное обсуждение биномиальных доверительных интервалов для небольших выборок см. в HFES, а обсуждение наилучшей точечной оценки см. в документе JUS.
Скорректированный метод Вальда
Скорректированный интервал Вальда (также называемый модифицированным интервалом Вальда) обеспечивает наилучшее покрытие для заданного интервала, когда количество выборок меньше примерно 150.
Другими словами, если вам нужен доверительный интервал 95%, используйте этот формула создаст интервал, который будет содержать наблюдаемую пропорцию в СРЕДНЕМ примерно в 95 процентах случаев. Он использует формулу Вальда, но «скорректирован» тем, что добавляет половину квадрата Z-критического значения к числителю и весь квадрат критического значения к знаменателю перед вычислением интервала, т. е. (x + z 2 /2)/(n+z 2 ). Например, при доверительном уровне 95 % используется Z-критическое значение 1,96 или приблизительно 2. Если вы наблюдаете, как 9 из 10 пользователей выполняют задачу, эта формула вычисляет пропорцию как (9 + (1,96 2 /2)) / (10 + (1,96 2 )) = прибл. 11/14 и строит интервал по формуле Вальда. Примечание. До 1 марта 2006 г. этот калькулятор вычислял этот интервал, добавляя одно значение z к числителю и квадрат значения z к знаменателю.
Точный метод
Точный метод был разработан, чтобы гарантировать не менее 95% охвата, в то время как приблизительные методы (с поправкой Вальда и оценки) обеспечивают средний охват 95% только в долгосрочной перспективе.
Используйте точный метод, когда вам нужно быть уверенным, что вы вычисляете интервал 95% или больше, ошибаясь на консервативной стороне. Например, при уровне заполнения 97,8% и метод Score, и скорректированный метод Вальда имели фактическое покрытие, которое упало до 89.%. Когда риск этого уровня фактического охвата не подходит для приложения, метод Exact обеспечивает необходимую точность. ПРИМЕЧАНИЕ. Мы обнаружили проблему с нашим кодом для вычисления этого интервала при больших размерах выборки (n>2000). К счастью, при таком большом размере выборки все методы сходятся на одном и том же интервале, поэтому для больших выборок используйте один из других методов.
Score Method
Score method обеспечивает лучший охват, чем точный метод и метод Wald, но не соответствует скорректированному методу Wald. Кроме того, его недостатком является сложность вычислений и плохое покрытие некоторых значений, когда коэффициент заполнения составляет около 9.
8% или 2%, независимо от размера выборки (Agresti and Coull, 1998). Единственное преимущество использования метода Score заключается в том, что он обеспечивает более точные конечные точки, когда концы интервалов близки к 0 или 1. Для некоторых значений (например, 9/10) скорректированные грубые интервалы Вальда выходят за пределы 0 и 1, и замена >.999 используется. Для метода оценки верхний интервал равен 0,9975.
Метод Вальда
Метода Вальда следует избегать при расчете доверительных интервалов для коэффициентов завершения с размерами выборки менее 100. Его охват слишком далек от номинального уровня, чтобы обеспечить надежную оценку коэффициента завершения генеральной совокупности. Когда размер выборки превышает 100, все четыре метода сходятся к одинаковым интервалам. Используйте Вальда в качестве точки отсчета или для больших размеров выборки.
* Значения «Погрешности» составляют половину ширины доверительных интервалов. Для скорректированных формул Вальда и Вальда можно использовать пропорцию +/- доверительный интервал.
Для точного метода интервалы не симметричны, так как полная пропорция увеличивается от 50% (например, 90% или 15%). Поэтому допустимую погрешность следует использовать только в качестве приближения для точного метода, и следует сообщать фактические значения выше и ниже пропорции.
Когда все пользователи успешно или неудачно
При небольших размерах выборки часто бывает так, что все пользователи в выборке завершат задачу (коэффициент выполнения 100 %) или все пользователи не справятся с задачей (коэффициент выполнения 0 %). Для этих сценариев часто неприятно сообщать о 100% или 0%. В конце концов, насколько вероятно, что истинный параметр популяции достигает 100% или 0%? Поле «Лучшая оценка» обеспечивает наилучшую точечную оценку в этих условиях и использует для расчета метод Лапласа. Хотя это значение может показаться слишком далеким от наблюдаемых 100 %, его привлекательность заключается в том, что оно зависит от размера выборки: чем больше размер выборки, тем ближе это значение будет к 100 %.
Примечание к расчету: Если наблюдаемая степень завершения равна 100 % или 0 %, двусторонний доверительный интервал невозможен (поскольку у вас не может быть больше 100 % или меньше 0 %). В этих случаях необходимо использовать z-критическое значение для одностороннего доверительного интервала. Например, двусторонний доверительный интервал 95% использует z-показатель приблизительно 1,96, односторонний интервал использует z-показатель приблизительно 1,64.
Вероятная степень выполнения задачи
Два варианта в этом раскрывающемся списке:
Между 0,5 и 1
затем выберите «Между 0,5 и 1» в раскрывающемся списке. См. раздел «Наилучшие оценки» ниже, чтобы узнать, как рассчитывается точечная оценка с помощью этой опции. Неизвестно
Если показатели выполнения вашей задачи обычно принимают широкий диапазон значений, равномерно распределенных между 0 и 1, выберите «Неизвестно» в раскрывающемся списке. Если вы не знаете ни того, ни другого, оставьте значение «Неизвестно».
Этот выбор будет использовать метод Лапласа для наилучшей оценки скорости завершения.
Точечные оценки
В то время как доверительный интервал описывает вероятный диапазон или интервал значений, точечная оценка описывает отдельное значение — точка как оценку неизвестного параметра в генеральной совокупности. Вероятность того, что оценка точки выборки совпадает с неизвестной степенью завершения генеральной совокупности, крайне маловероятна. По этой причине вы всегда должны вычислять доверительный интервал, сообщая о степени завершения. Это гораздо более информативно, чем точечная оценка, поскольку она обеспечивает достаточно вероятную границу для степени завершения генеральной совокупности.
Хотя этому методу уделяется мало внимания на вводных занятиях по статистике и он мало повлиял на методы измерения в области инженерии удобства использования, существует богатая история альтернативных методов, разработанных для достижения более точной точечной оценки p, чем простое деление числа успехов.
по количеству попыток (например, см. Chew, 1971; Laplace, 1812; Manning & Schutze, 199).9). Эта потребность наиболее очевидна, когда есть экстремальный результат, в частности, когда x=0 (0%) или x=n (100%) — особенно, но не исключительно, когда размеры выборки малы. Четыре метода оценки, которые относятся к ситуациям, наиболее часто встречающимся в тестировании удобства использования, подробно описаны ниже:
MLE:(Оценка максимального правдоподобия)(x / n)
MLE представляет собой долю выборки или количество успешных пользователей, деленное на общее количество попыток. Это наиболее распространенная точечная оценка.
Лаплас (x+1)/(n+2)
Известная задача большой выборки возникла в основополагающей работе Лапласа начала 1800-х годов. Он поставил вопрос о том, насколько вы можете быть уверены в том, что солнце взойдет завтра, если вы знаете, что оно всходило каждый день в течение последних 5000 лет (1 825 000 дней).
Вы можете быть уверены, что она поднимется, но не можете быть абсолютно уверены. Солнце может взорваться, или большой астероид может разбить Землю на куски. В ответ на этот вопрос он предложил закон наследования Лапласа, который заключается в добавлении единицы к числителю и двух к знаменателю ((x+1)/(n+2)). Применяя эту процедуру, вам будет 99,999945% уверены, что солнце завтра взойдет — близко к 100%, но немного отступили от этой крайности. Величина корректировки больше, когда размеры выборки малы. Например, если вы наблюдаете два успеха из двух и применяете процедуру Лапласа, то ваша оценка p составляет 75% (x+1=3, n+2=4, p=3/4), а не 100%. Если вы наблюдали два отказа, то ваша оценка p составляет 25% (x+1=1, n+2=4, p=1/4), а не 0%. Лаплас, по сути, говорит, что следующий результат — это жеребьевка, поэтому дайте каждой альтернативе равновероятную вероятность появления.
Уилсона (x+z 2 /2)/(n+z 2 )
Точечная оценка Уилсона является средней точкой скорректированного интервала Вальда.
Он получается путем прибавления половины критического значения в квадрате к числителю и квадрата критического значения к знаменателю. Услуги Уилсона более консервативны.
Jeffreys (x+.5)/(n+1)
Jeffreys (1961) предложил компромисс между методами Лапласа и MLE. См. ссылку для технических деталей.
Наилучшая оценка
Наилучшая точечная оценка рассчитывается с использованием следующей логики: Если в раскрывающемся списке Вероятная частота завершения популяции выбрано «Неизвестно», используется метод Лапласа. Чем меньше размер вашей выборки и чем дальше ваша первоначальная оценка p от 0,5, тем больше преимущество над MLE.
Если в раскрывающемся списке «Вероятная частота завершения популяции» выбрано «Между 0,5 и 1», а наблюдаемая скорость завершения составляет:
- Меньше или равно 0,5: используется метод Уилсона.
- Между .5 и .9: используется MLE.
- Более 0,9: используется метод Лапласа (обратите внимание, если 1 > x > 0,9, метод Джеффериса также является приемлемой альтернативой).
Нужна дополнительная информация? Обязательно ознакомьтесь с онлайн-руководством по доверительным интервалам.
Ссылки
- Агрести, А., и Коул, Б. (1998). Приблизительный лучше, чем «точный» для интервальной оценки биномиальных пропорций. Американский статистик, 52, 119-126.
- Чу, В. (1971). Точечная оценка параметра биномиального распределения. Американский статистик, 25, 47-50.
- Джеффрис, Х. (1961) Теория вероятностей (3-е изд.), Clarendon Press, Оксфорд, стр. 179.-192.
- Лаплас, PS (1812). Аналитическая теория вероятностей. Париж, Франция: Курсье.
- Льюис, Дж. Р. и Сауро, Дж. (2006) «Когда 100% на самом деле не 100%: повышение точности оценок показателей завершения для небольшой выборки» в Journal of Usability Studies Issue 3, Vol. 1, май 2006 г., стр. 136-150
- Manning, C.D., & Schutze, H. (1999). Основы статистической обработки естественного языка.
