Четверти координатной плоскости картинки: Метод координат — урок. Информатика, 5 класс.

Рисуем на координатной плоскости

Муниципальное казенное общеобразовательное учреждение

«Песчанская средняя общеобразовательная школа»

Исследовательская работа по математике

«Рисуем на координатной плоскости»

Авторы: ученики 6 класса

Евсиков Александр,

Клюкин Юрий,

Леготин Илья

Руководитель: Е.В. Теплых,

учитель математики

2017-2018 учебный год

Содержание:

№ стр.

1.Введение 3

2.Основная часть

2.1. История возникновения координат. 4-5

2.2. Координатная плоскость. 6-8

3.Заключение 9

4.Список используемой литературы 10

5.Приложение 11

2

1.Введение

При изучении темы «Координатная плоскость» в 6 классе мы познакомились с красивыми заданиями на координатной плоскости. Они вызвали у нас большой интерес. Все учащиеся нашего класса с удовольствием рисовали рисунки.

Мы научились понимать, что из абстрактных точек можно получить знакомый рисунок: изображали не только отдельные точки, но и любые предметы, животных, растения, даже целые сюжеты.

Есть много нетрадиционных задач с новизной заданий, которые можно с успехом использовать при изучении темы «Координатная плоскость», но они не вошли в школьные учебники и методические пособия для учителя.

Мы решили заполнить пробел в учебниках и создать свою работу под названием «Рисуем на координатной плоскости». В приложении работы будут собраны многие интересные задания.

ГИПОТЕЗА: в координатной плоскости можно рисовать

АКТУАЛЬНОСТЬ: данная тема имеет особое место в математике и интересна тем, что в координатной плоскости можно строить не только графики различных функций, но и создавать красивые рисунки.

Цель работы: организовать поиск занимательных задач и создать набор заданий на построение рисунков для работы на уроках математики .

Задачи: Изучение литературы по истории возникновения координат и

системы координат.

Оформить материал в виде рисунков.

Методы: Сбор задач и обработка информации.

Анкетирование учащихся в 7-8 классах по теме

«Координатная плоскость»

Работа с источниками по истории математики.

Работа с компьютером.

3

2. Основная часть.

2.1.История возникновения координат.

За 200 лет до нашей эры греческий ученый Гиппарх ввёл географические координаты. Он предложил нарисовать на географической карте параллели и меридианы и обозначить числами широту и долготу. С помощью этих двух чисел можно точно определить положение острова, поселка, горы или колодца в пустыне и нанести их на карту или глобус, Научившись определять в открытом мире широту и долготу местонахождения корабля, моряки получили возможность выбирать нужное им направление.

Восточную долготу и северную широту обозначают числами со знаком «плюс», а западную долготу и южную широту — со знаком «минус». Таким образом, пара чисел со знаками однозначно определяет точку на земном шаре.

Например, пара +70° , +60° определяет точку в центре острова Вайгач, расположенного в Карском море.

У писателя Жюля Верна, некоторые романы построены на ситуациях, связанных с географическими координатами. Это романы «Удивительные приключения дядюшки Антифера» и «Дети капитана Гранта».

Долгое время лишь география «землеописание»  — пользовалась  этим замечательным изобретением, и только в 14 веке французский математик Никола Орсем (1323-1382) попытался приложить его к «землеизмерению» — геометрии. Он предложил покрыть плоскость прямоугольной сеткой и называть широтой и долготой то, что мы теперь называем абсциссой и ординатой. 

4

На основе этого удачного нововведения возник метод координат, связавший геометрию с алгеброй. Основная заслуга в создании этого метода принадлежит великому французскому математику Рене Декарту (1596 — 1650). В его честь такая система координат называется декартовой, обозначающая место любой точки плоскости расстояниями от этой точки до «нулевой широты» — оси абсцисс » и «нулевого меридиана»  — оси ординат.

По традиции, введенной Декартом, «широта» точки обозначаются буквой x, «долгота» — буквой «y».

На этой системе основаны многие способы указания места.

Например, на билете в кинотеатр стоят два числа: ряд и место — их можно рассматривать как координаты места в зале.

Подобные координаты приняты о шахматах. Вместо одного из чисел берется буква: вертикальные ряды клеток обозначаются буквами латинского алфавита, а горизонтальные — цифрами. Таким образом, каждой клетке шахматной доски ставится в соответствие пэра из буквы и числа, и шахматисты получают возможность записывать свои партии.

Тот же принцип применяется на планах городов. План города разбивают на квадраты занумерованные с помощью букв и цифр, а на оборотной стороне перечисляют все изображенные улицы в алфавитном порядке и указывают, в каком квадрате они находятся.

5

2.2 Координатная плоскость

Координатная плоскость — это плоскость, на которой задана определенная система координат. Такая плоскость задается двумя прямыми, пересекающимися под прямым углом. В точке пересечения этих прямых находится начало координат. Каждая точка на координатной плоскости задается парой чисел, которые называют координатами. В школьном курсе математики школьникам приходится довольно тесно работать с системой координат – строить на ней фигуры и точки, определять, какой плоскости принадлежит та или иная координата, а также определять координаты точки и записывать или называть их.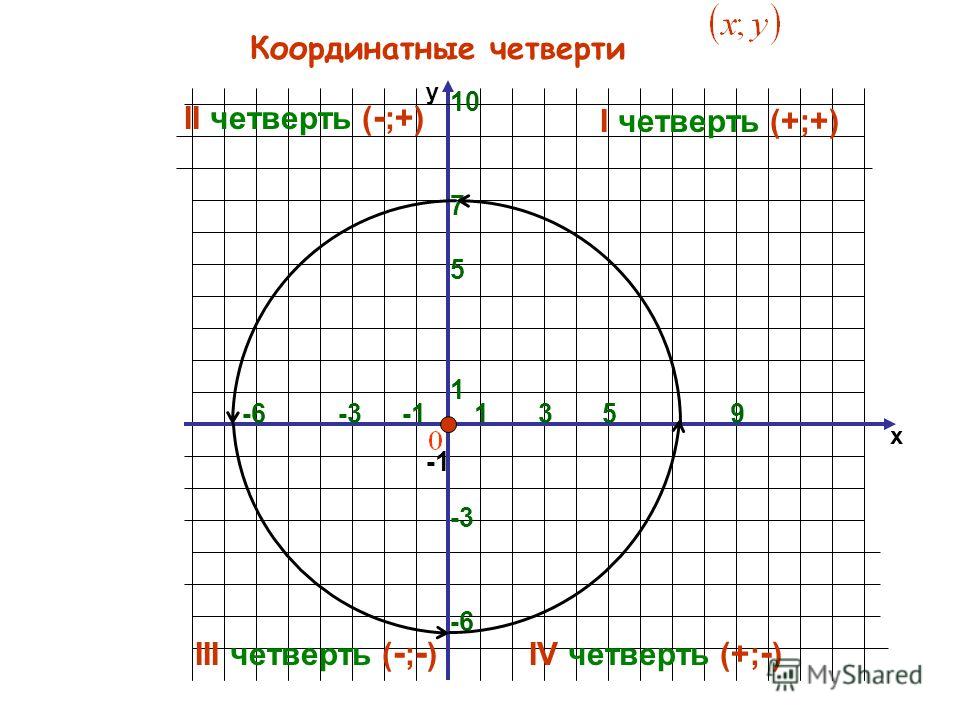

Данная система координат широко применяется не только в математике, логических играх, но и в военном деле, астрономии, физике и многих других науках.

В системе координат выделяют две оси. Первая ось — абсцисс — горизонтальная. Она обозначается как (Оx). Вторая ось — ординат, которая проходит вертикально через точку отсчета и обозначается как (Оy). Именно эти две оси образуют систему координат, разбивая плоскость на четыре четверти. Начало отсчета находится в точке пересечения этих двух осей и принимает значение 0. Только в случае если плоскость образована двумя пересекающимися перпендикулярно осями, имеющими точку отсчета, это координатная плоскость. Также отметим, что каждая из осей имеет свое направление. Обычно при построении системы координат принято указывать направление оси в виде стрелочки. Кроме того, при построении координатной плоскости каждая из осей подписывается.

6

Плоскость разбивается двумя осями на четыре четверти. Каждая из них имеет свой номер, при этом нумерация плоскостей ведется против часовой стрелки. Каждая из четвертей имеет свои особенности. Так, в первой четверти абсцисса и ордината положительная, во второй четверти абсцисса отрицательная, ордината — положительная, в третьей и абсцисса, и ордината отрицательные, в четвертой же положительной является абсцисса, а отрицательной — ордината. Запомнив эти особенности, можно с легкостью определить, к какой четверти относится та или иная точка.

А поговорим о том, как наносить на нее точки, координаты фигур. На координатной плоскости сделать это не так тяжело, как может показаться на первый взгляд. В первую очередь строится сама система, на нее наносятся все важные обозначения. Затем уже идет работа непосредственно с точками или фигурами. При этом даже при построении фигур сначала на плоскость наносятся точки, а затем уже прорисовываются фигуры.

7

Для того чтобы построить координатную плоскость, понадобится только линейка и ручка или карандаш. Сначала рисуется горизонтальная ось абсцисс, затем вертикальная — ординат. При этом важно помнить, что оси пересекаются под прямым углом. Далее на каждой оси указывают направление и подписывают их с помощью общепринятых обозначений x и y. Также отмечается точка пересечения осей и подписывается цифрой 0. Следующим обязательным пунктом является нанесение разметки. На каждой из осей в обоих направлениях отмечаются и подписываются единицы-отрезки. Это делается для того, чтобы затем можно было работать с плоскостью с максимальным удобством.

При построении точек следует помнить, как правильно записываются их координаты. Так, обычно задавая точку, в скобках пишут две цифры. Первая цифра обозначает координату точки по оси абсцисс, вторая — по оси ординат. Строить точку следует таким образом. Сначала отметить на оси Ox заданную точку, затем отметить точку на оси Oy. Далее провести воображаемые линии от данных обозначений и найти место их пересечения — это и будет заданная точка. Нам останется только отметить ее и подписать.

Для того чтобы построить на координатной плоскости любую фигуру, следует знать, как размещать на ней точки.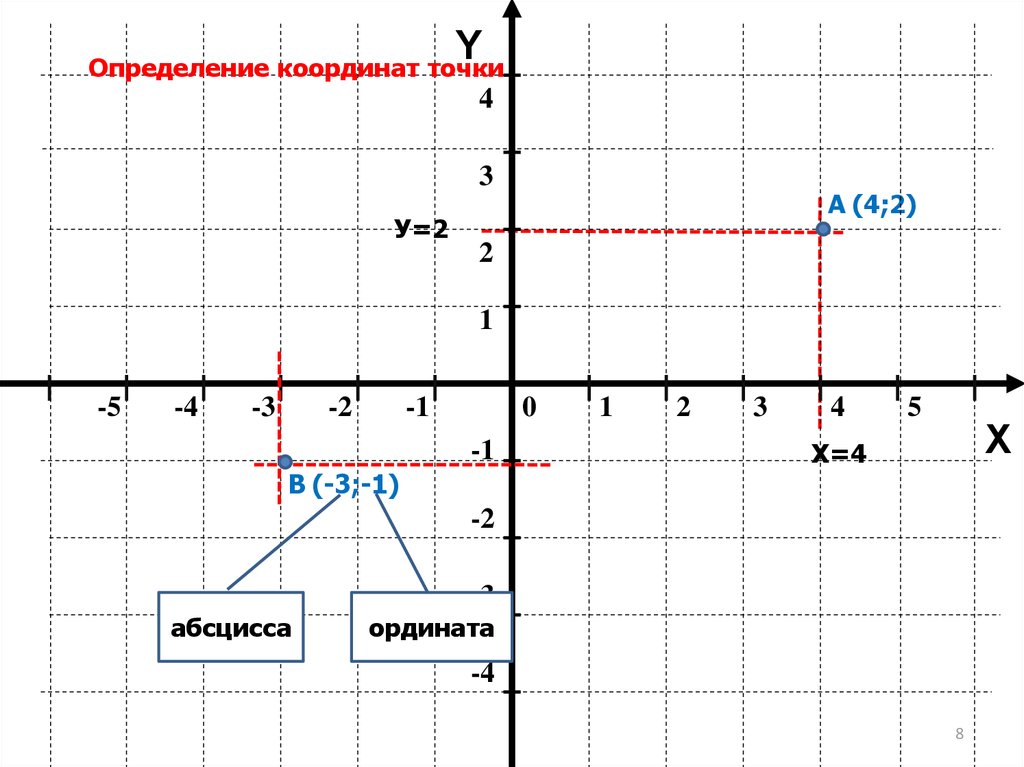 В первую очередь нам понадобятся координаты точек фигуры. Именно по ним мы и будем наносить на нашу систему координат выбранные нами геометрические фигуры или рисунки .

8

3.Заключение

Нам было очень интересно работать над этой темой. Работу мы продолжим и дальше, так как можно самим придумать много разных рисунков по координатам. Главным итогом нашей работы стало создание набора рисунков, которому дали название «Рисунки в координатной плоскости». В нем собраны интересные задания по теме проекта, которые будут полезными при изучении математики.

В свободное время тоже можно порисовать. Красивые рисунки будут получаться даже у тех учеников, которые не умеют хорошо рисовать, потому что эти задания просты по формуле и разнообразны по внешнему выражению.

Выполнение таких заданий заставляют увидеть связь красоты и математики, соприкоснуться с миром прекрасного. Применение такого подхода в процессе обучения позволит сделать уроки математики интересными и красивыми.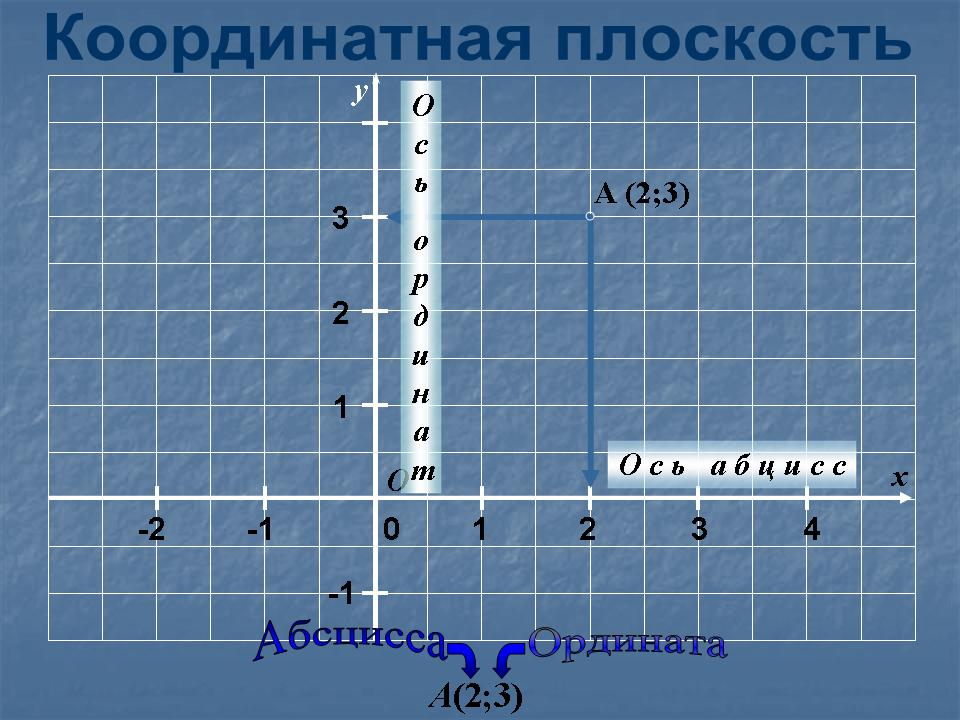

Распределение заданий по уровням сложности и по прикладной тематике позволит выбрать ученику задания в соответствии со своими способностями и познавательными интересами.

Познавательной деятельности ученика можно придать еще большую привлекательность, если при выполнении заданий использовать компьютер.

Мы надеемся, что эти задания будут пользоваться большим спросом у учеников и учителей, потому что их можно применять на уроках математики при изучении темы «Функции и графики», «Координатная плоскость», на занятиях кружка, факультатива.

9

4.Список используемой литературы

Пономарёва Т.Д. «Я познаю мир».

А. Савин. Координаты // Квант. 1977. №9

Журнал Математика в школе №10 от 2001 г.

Ресурсы интернета:

http://www.glena.ru/coordinates;

http://wiki.iteach.ru/images/6/67/Творческое задание.pdf;

http://www.yandex.ru/картинки;

algolist.maru.wikipedia.org/wiki/;

festival.1september.ru/articles/509560/3.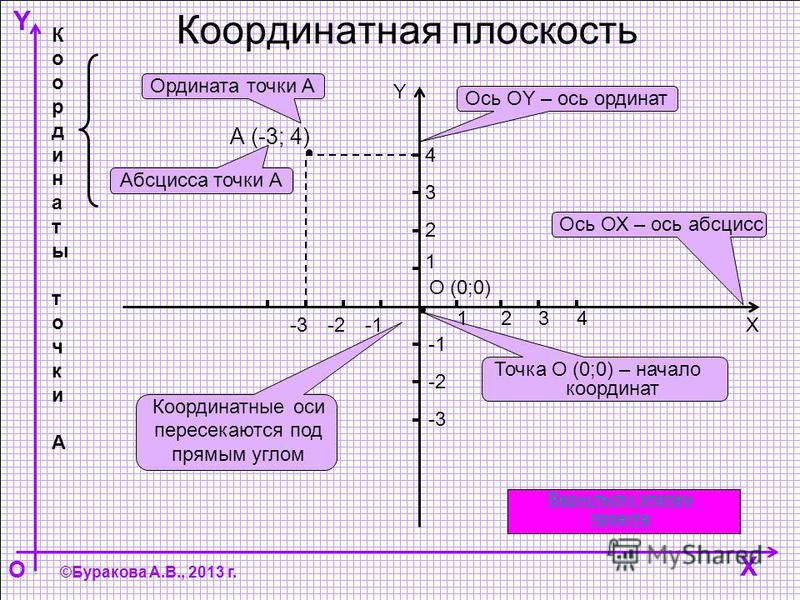

Сайт википедии http://ru.wikipedia.org/wiki

http://kykaraha.beon.ru/29386-228-risunki-na-koordinatnoi-ploskosti-poprobuite-jeto-prikol-no.zhtml

10

5.Приложение

Грибок
1) (6; 0), (6; 2), (5; 1,5), (4; 3), (2; 1), (0; 2,5), (- 1,5; 1,5), (- 2; 5), (- 3; 0,5), (- 4; 2), (- 4; 0).
2) (2; 1), (2,2; 2), (2,3; 4), (2,5; 6), (2,3; 8), (2; 10), (6; 10), (4,8; 12), (3; 13,3), (1; 14),
(0; 14), (- 2; 13,3), (- 3,8; 12), (- 5; 10), (2; 10).
3) (- 1; 10), (- 1,3; 8), (- 1,5; 6), (- 1,2; 4), (- 0,8;2).
Мышонок 1) (3; — 4), (3; — 1), (2; 3), (2; 5), (3; 6), (3; 8), (2; 9), (1; 9), (- 1; 7), (- 1; 6),
(- 4; 4), (- 2; 3), (- 1; 3), (- 1; 1), (- 2; 1), (-2; — 1), (- 1; 0), (- 1; — 4), (- 2; — 4),
(- 2; — 6), (- 3; — 6), (- 3; — 7), (- 1; — 7), (- 1; — 5), (1; — 5), (1; — 6), (3; — 6), (3; — 7),
(4; — 7), (4; — 5), (2; — 5), (3; — 4).
2) Хвост: (3; — 3), (5; — 3), (5; 3).
3) Глаз: (- 1; 5).
Лебедь
1) (2; 7), (0; 5), (- 2; 7), (0; 8), (2; 7), (- 4; — 3), (4; 0), (11; — 2), (9; — 2), (11; — 3),
(9; — 3), (5; — 7), (- 4; — 3).
2) Клюв: (- 4; 8), (- 2; 7), (- 4; 6).
3) Крыло: (1; — 3), (4; — 2), (7; — 3), (4; — 5), (1; — 3).
4) Глаз: (0; 7).
Верблюд
1) (- 9; 6), (- 5; 9), (- 5; 10), (- 4; 10), (- 4; 4), (- 3; 4), (0; 7), (2; 4), (4; 7), (7; 4),
(9; 3), (9; 1), (8; — 1), (8; 1), (7; 1), (7; — 7), (6; — 7), (6; — 2), (4; — 1), (- 5; — 1), (- 5; — 7),
(- 6; — 7), (- 6; 5), (- 7;5), (- 8; 4), (- 9; 4), (- 9; 6).
2) Глаз: (- 6; 7).
Слоник
1) (2; — 3), (2; — 2), (4; — 2), (4; — 1), (3; 1), (2; 1), (1; 2), (0; 0), (- 3; 2), (- 4; 5),
(0; 8), (2; 7), (6; 7), (8; 8), (10; 6), (10; 2), (7; 0), (6; 2), (6; — 2), (5; — 3), (2; — 3).
2) (4; — 3), (4; — 5), (3; — 9), (0; — 8), (1; — 5), (1; — 4), (0; — 4), (0; — 9), (- 3; — 9),
(- 3; — 3), (- 7; — 3), (- 7; — 7), (- 8; — 7), (- 8; — 8), (- 11; — 8), (- 10; — 4), (- 11; — 1),
(- 14; — 3), (- 12; — 1), (- 11;2), (- 8;4), (- 4;5).
3) Глаза: (2; 4), (6; 4).
Конь
1) (14; — 3), (6,5; 0), (4; 7), (2; 9), (3; 11), (3; 13), (0; 10), (- 2; 10), (- 8; 5,5),
(- 8; 3), (- 7; 2), (- 5; 3), (- 5; 4,5), (0; 4), (- 2; 0), (- 2; — 3), (- 5; — 1), (- 7; — 2),

11

(- 5; — 10), (- 2; — 11), (- 2; — 8,5), (- 4; — 8), (- 4; — 4), (0; — 7,5), (3; — 5).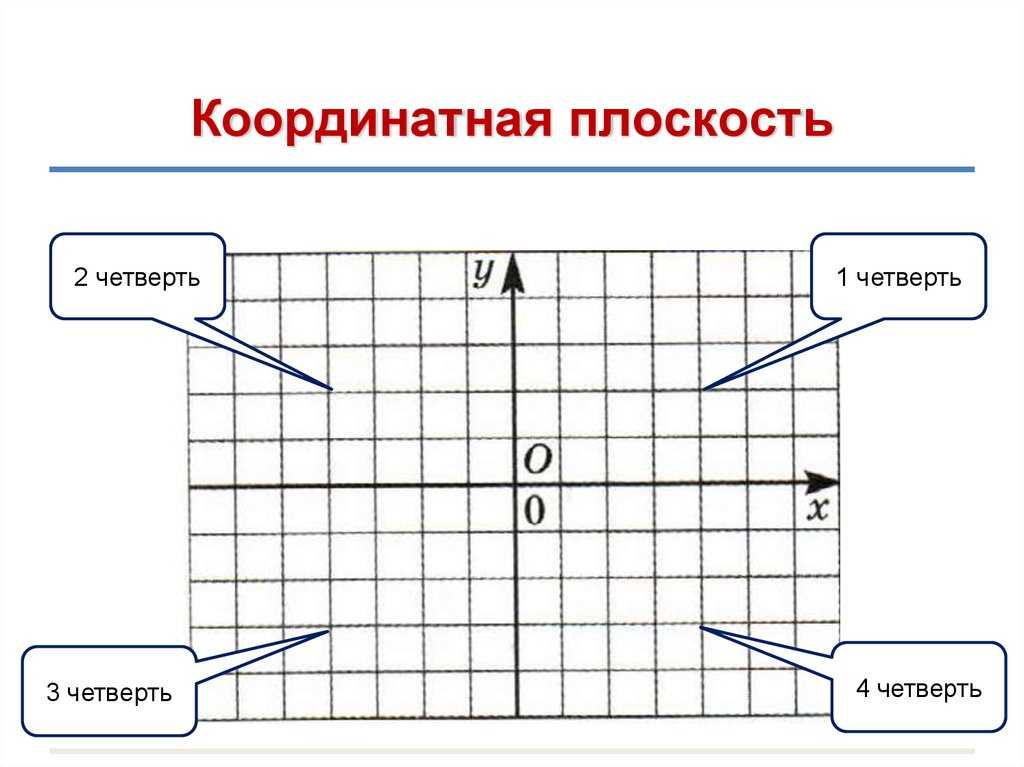
2) Глаз: (- 2; 7).

Звёздочка

(-6;0), (-3;1), (-4;4), (-1;3), (0;6), (1;3), (4;4), (3;1), (6;0), (3;-1), (4;-4),

(1;-3), (0;-6), (-1;-3), (-4;-4), (-3;-1), (-6;0)

Чайник

(2;5), (5;1), (7;1), (10;4), (12;4), (6;-5), (-6;-5), (-6;3), (-3;5), (2;5)

Ручка: (-3;5), (-3;9), (2;9), (2;5)

Бабочка

(-2;-5), (-5;-7), (-8;-7), (-8;-5), (-5;-2), (-9;3), (-8;5), (-6;5), (-2;4), (2;5),

(4;5), (5;3), (1;-2), (4;-5), (4;-7), (1;-7), (-2;-5)

Усики: (-2;4), (-3;6)

(-2;4), (-1;6)

Парусник

(-11;8), (-5;-3), (8;-4), (9;1), (6;1), (7;5), (8;7), (7;8), (7;13), (7;14), (4;15),

(5;14), (4;13), (7;13), (1;4), (-2;4), (-4;6), (-7;7), (-11;8)

Домик

(0;9), (-9;4), (-7;4), (-7;-9), (7;-9), (7;4), (9;4), (0;9)

Окно: (2;2), (-2;2), (-2;-4), (2;-4), (2;2)

Страус

(0;0). (-1;1), (-3;1), (-2;3), (-3;3), (-4;6), (0;8),

(2;5),(2;11), (6;10), (3;9),(4;5), (3;0), (2;0), (1;-7), (3;-8), (0;-8), (0;0)

Глаз: (3;10)

Ёлочка

(0;5), (2;2), (1;2), (3;-1), (2;-1), (4;-4), (1;-4), (1;-5), (-1;-5), (-1;-4),

(-4;-4), (-2;-1), (-3;-1), (-4;2), (-2;2), (0;5)

Утка

(3;0), (1;2), (-1;2), (3;5), (1;8), (-3;7), (-5;8), (-3;4), (-6;3), (-5;2),

(-5;-2), (-2;-3), (-4;-4), (1;-4), (3;-3), (6;1), (3;0) Глаз: (-1;5)

Кит

(4;-0,5), (6,5;-2), (-2;-3), (-10,5;4), (-12,5;7,5), (-9;11), (-13;10),

(- 17;11), (-12,5;7,5), (-10,5;4), (-3;2), (1;4,5), (7,5;3), (6,5;-2)

Глаз: (4;2)

Пёс

(-8;-6), (-9;-4), (-9,5;-2), (-11;0), (-12;-1), (-11;-2), (-11,5;-3), (-11;-4),

(-11;-5), (-10;-6), (-10;-7), (-6;-10), (1;-10), (0,5;-9), (-1;-9), (0;-6),

(-2;- 4), (1;-1), (1;-8), (2;-10), (4;-10), (3,5;-9), (3;-9), (4;-2),

(2;5), (6;4,5), (6;5,5), (4;6), (6;6), (6,5;7,5), (3,5;7,5), (1;12),

(-0,5;10), (-2;9), (-3;7), (-3;5),

(-4;3), (-4,5;1), (-8;-6)

Глаз: (0,5;8), (1;7,5), (2;8) (1;8.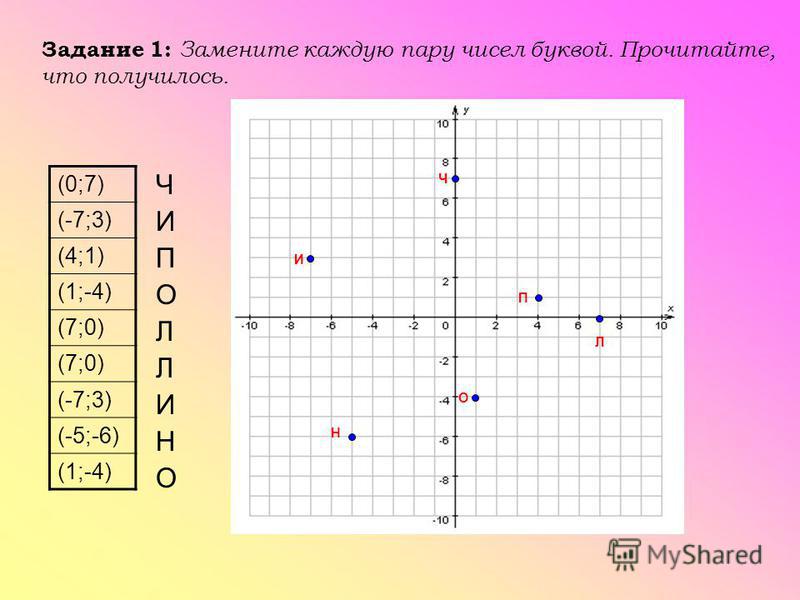 5), (0,5;8)

Рыбка

(3;3), (0;3), (-3;2), (-5;2), (-7;4), (-8;3), (-7;1), (-8;-1), (-7;-2), (-5;0),

(-1;-2), (0;-4), (2;-4), (3;-2), (5;-2), (7;0), (5;2), (3;3), (2;4), (-3;4), (-4;2)

Глаз: (5;0)

Заяц

(1;7), (0;10), (-1;11), (-2;10), (0;7), (-2;5), (-7;3), (-8;0), (-9;1), (-9;0),

(-7;-2), (-2;-2), (-3;-1), (-4;-1), (-1;3), (0;-2), (1;-2), (0;0), (0;3), (1;4),

(2;4), (3;5), (2;6), (1;9), (0;10) Глаз: (1;6)

Сорока

1) (-1;2), (5;6), (7;13), (10;11), (7;5), (1;-4), (-2;-4), (-5;0), (-3;0), (-1;2),

(-2;4), (-5;5), (-7;3), (-11;1), (-6;1), (-7;3),(-5;0), (-6;0), (-10;-1), (-7;1),

(-6;0)

2) Крыло: (0;0), (7;3), (6;1), (1;-3), (0;0)

3) (1;-4), (1;-7), (-1;-4), (-1;-7)

4) Глаз: (-5;3)

Волк

1) (- 9; 5), (- 7; 5), (- 6; 6), (- 5; 6), (- 4; 7), (- 4; 6), (- 1; 3), (8; 3), (10; 1), (10; — 4),

(9; — 5), (9; — 1), (7; — 7), (5; — 7), (6; — 6), (6; — 4), (5; — 2), (5; — 1), (3; — 2), (0; — 1),

(- 3; — 2), (- 3; — 7), (- 5; — 7), (- 4; — 6), (- 4; — 1), (- 6; 3), (- 9; 4), (- 9; 5).

2) Глаз: (- 6; 5)

Бегун

1) (- 8; 1), (- 6; 2), (- 2; 0), (1; 2), (5; 1), (7; — 4), (9; — 3).

2) (- 2; 6), (0; 8), (3; 7), (5; 5), (7; 7).

3) (1; 2), (3; 9), (3; 10), (4; 11), (5; 11), (6; 10), (6; 9), (5; 8), (4; 8), (3; 9).

Ракета

1) (1; 5), (0; 6), (- 1; 5), (0; 4), (0; — 8), (- 1; — 10), (0; 1), (0; — 8).

2) (- 4; — 6), (- 1; 10), (0; 12), (1; 10), (4; — 6), (- 4; — 6).

3) (- 3; — 6), (- 6; — 7), (- 2; 1), (- 3; — 6).

4) (2; 1), (3; — 6), (6; — 7), (2; 1).

Лис

1) (- 8; — 9), (- 6; — 7), (- 3; — 7), (1; 1), (1; 3), (4; 7), (4; 4), (7; 2,5),

(4; 1), (6; — 8), (7; — 8), (7; — 9), (5; — 9), (3; — 3), (1,5; — 6), (3; — 8), (3; — 9), (- 8; — 9).

2) Глаз: (4; 3).

Парусник

1) (0; 0), (- 10; 1), (0; 16), (- 1; 2), (0; 0).

2) (- 9; 0), (- 8; — 1), (- 6; — 2), (- 3; — 3), (5; — 3), (10; — 2), (12; — 1), (13; 0), (- 9; 0).

3) (0; 0), (0; 16), (12; 2), (0; 0).

Лисица

1) (- 3; 0), (- 2; 1), (3; 1), (3; 2), (5; 5), (5; 3), (6; 2), (7; 2), (7; 1,5), (5; 0), (4; 0),

(4; — 1,5), (3; — 1), (3; — 1,5), (4; — 2,5), (4,5; — 2,5), (- 4,5; — 3), (3,5; — 3), (2; — 1,5),

(2; — 1), (- 2; — 2), (- 2; — 2,5), (- 1; — 2,5), (- 1; — 3), (- 3; — 3), (- 3; — 2), (- 2; — 1),

(- 3; — 1), (- 4; — 2), (- 7; — 2), (- 8; — 1), (- 7; 0), (- 3; 0).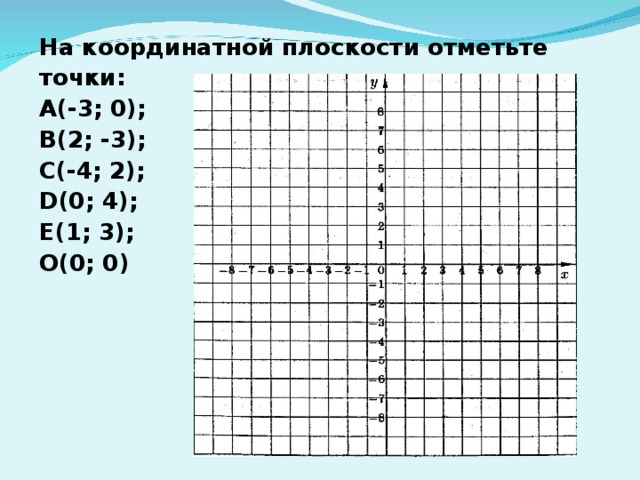

2) Глаз: (5; 2).

Гусь

1) (- 3; 9), (- 1; 10), (- 1; 11), (0; 12), (1,5; 11), (1,5; 7), (- 0,5; 4), (- 0,5; 3), (1; 2),

(8; 2), (10; 5), (9; — 1), (7; — 4), (1; — 4), (- 2; 0), (- 2; 4), (0; 7), (0; 9), (- 3; 9).

2) Крыло: (1; 1), (7; 1), (7; — 1), (2; — 3), (1; 1).

3) Глаз: (0; 10,5).

Кумушка Лиса

1) (- 7; 6), (1; 8), (3; 11), (4; 8), (6; 8), (5; 6), (5; 5), (2; 0), (- 7; 6).

2) (- 4; 0), (8; 0), (5; — 3), (8; — 9), (- 3; — 9), (0; — 3), (- 4; 0).

3) Хвост: (6,5; — 6), (10; — 6), (11; — 8), (11; — 9), (8; — 9).

4) Платок: (- 4; 0), (- 9; — 4), (- 3; — 4), (- 4; 0).

5) Глаз: (1; 6).

Самолёт

1) (- 7; 0), (- 5; 2), (7; 2), (9; 5), (10; 5), (10; 1), (9; 0), (- 7; 0).

2) (0; 2), (5; 6), (7; 6), (4; 2).

3) (0; 1), (6; — 3), (8; — 3), (4; 1), (0; 1).

Вертолёт

1) (- 5; 3), (- 3; 5), (6; 5), (10; 3), (10; 1), (9; 0), (- 2; 0), (- 5; 3).

2) (- 5; 3), (- 10; 7), (- 3; 5).

3) (5; 0), (5; — 1), (6; — 2), (8; — 2), (9; — 2,5), (8; — 3), (- 3; — 3), (- 4; — 2,5), (- 3; — 2),

(- 1; — 2), (- 2; — 1), (- 2; 0).

4) (- 12; 5), (- 8; 9).

5) (- 6; 7), (10; 7).

6) (2; 5), (2; 7).

7) (- 1; 1), (- 1; 4), (2; 4), (2; 1), (- 1; 1).

8) (5; 5), (5; 2), (10; 2).

Настольная лампа

(0; 0), (- 3; 0), (- 3; — 1), (4; — 1), (4; 0), (1; 0), (6; 6), (0; 10), (1; 11), (- 2; 13),

(- 3; 12), (- 7; 12), (0; 5), (0; 9), (5; 6), (0; 0).

Адрес публикации: https://www.prodlenka.org/metodicheskie-razrabotki/323614-risuem-na-koordinatnoj-ploskosti

Подготовка школьников к ЕГЭ и ОГЭ (Справочник по математике — Алгебра

Справочник по математике

Алгебра

Координатная плоскость

Числовая ось

Прямоугольная декартова система координат на плоскости

Формула для расстояния между двумя точками координатной плоскости

Уравнение окружности на координатной плоскости

Числовая ось

      Определение 1. Числовой осью (числовой прямой, координатной прямой)   Ox   называют прямую линию, на которой точка   O   выбрана началом отсчёта (началом координат) (рис.1), направление

O → x

указано в качестве положительного направления и отмечен отрезок, длина которого принята за единицу длины.

Рис.1

      Определение 2. Отрезок, длина которого принята за единицу длины, называют масштабом.

      Каждая точка числовой оси имеет координату, являющуюся вещественным числом. Координата точки   O   равна нулю. Координата произвольной точки   A ,   лежащей на луче   Ox ,   равна длине отрезка   OA .   Координата произвольной точки   A   числовой оси, не лежащей на луче   Ox ,   отрицательна, а по абсолютной величине равна длине отрезка   OA .

Прямоугольная декартова система координат на плоскости

      Определение 3.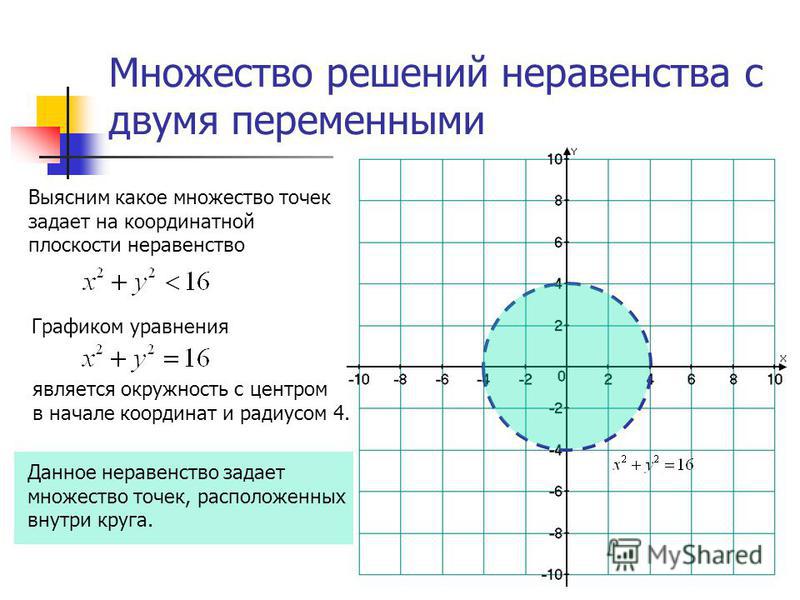 Прямоугольной декартовой системой координат   Oxy   на плоскости называют две взаимно перпендикулярных числовых оси   Ox   и   Oy   с одинаковыми масштабами и общим началом отсчёта в точке   O ,   причём таких, что поворот от луча   Ox   на угол   90°   до луча   Oy   осуществляется в направлении против хода часовой стрелки (рис.2).

Рис.2

      Замечание. Прямоугольную декартову систему координат   Oxy ,   изображённую на рисунке 2, называют правой системой координат, в отличие от левых систем координат, в которых поворот луча   Ox   на угол   90°   до луча   Oy   осуществляется в направлении по ходу часовой стрелки. В данном справочнике мы рассматриваем только правые системы координат, не оговаривая этого особо.

      Если на плоскости ввести какую-нибудь систему прямоугольных декартовых координат   Oxy ,   то каждая точка плоскости приобретёт две координаты – абсциссу и ординату, которые вычисляются следующим образом. Пусть   A   – произвольная точка плоскости. Опустим из точки   A   перпендикуляры   AA₁   и   AA₂   на прямые   Ox   и   Oy   соответственно (рис.3).

Рис.3

      Определение 4. Абсциссой точки   A   называют координату точки   A₁   на числовой оси   Ox ,   ординатой точки   A   называют координату точки   A₂   на числовой оси   Oy .

      Обозначение. Координаты (абсциссу и ординату) точки   A   в прямоугольной декартовой системе координат   Oxy   (рис.4) принято обозначать   A (x ; y)   или   A = (x ; y).

Рис.4

      Замечание. Точка   O ,   называемая началом координат, имеет координаты   O (0 ; 0) .

      Определение 5 . В прямоугольной декартовой системе координат   Oxy   числовую ось   Ox   называют осью абсцисс, а числовую ось   Oy   называют осью ординат (рис. 5).

      Определение 6. Каждая прямоугольная декартова система координат делит плоскость на   4   четверти (квадранта), нумерация которых показана на рисунке 5.

Рис.5

      Определение 7. Плоскость, на которой задана прямоугольная декартова система координат, называют координатной плоскостью.

      Замечание. Ось абсцисс задаётся на координатной плоскости уравнением   y = 0 ,   ось ординат задаётся на координатной плоскости уравнением   x = 0.

Формула для расстояния между двумя точками координатной плоскости

      Утверждение 1. Расстояние между двумя точками координатной плоскости

A₁ (x₁ ; y₁)   и   A₂ (x₂ ; y₂)

вычисляется по формуле

      Доказательство. Рассмотрим рисунок 6.

Рис.6

      Поскольку в прямоугольном треугольнике   A₁A₂B   длина катета   A₁B   равна   | x₂ – x₁|    а длина катета   A₂B   равна   | y₂ – y₁| ,   то по теореме Пифагора

| A1A2|2 = = ( x2 – x1)2 + ( y2 – y1)2 .

(1)

     Следовательно,

что и требовалось доказать.

Уравнение окружности на координатной плоскости

      Рассмотрим на координатной плоскости   Oxy   (рис. 7) окружность радиуса   R   с центром в точке   A₀ (x₀ ; y₀) .

Рис.7

      Поскольку расстояние от любой точки окружности до центра равно радиусу, то, в соответствии с формулой (1), получаем:

( x – x₀)² + ( y – y₀)² = R².

Уравнение (2) и есть искомое уравнение окружности радиуса   R   с центром в точке   A₀ (x₀ ; y₀) .

      Следствие. Уравнение окружности радиуса   R   с центром в начале координат имеет вид

x² + y² = R².

      На сайте можно также ознакомиться с нашими учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.

Координатная плоскость четыре четверти роялти бесплатно векторное изображение

Координатная плоскость четыре четверти роялти бесплатно векторное изображение

org/BreadcrumbList»>
1. лицензионные векторы
2. Векторы координат

ЛицензияПодробнее

Стандарт Вы можете использовать вектор в личных и коммерческих целях. Расширенный Вы можете использовать вектор на предметах для перепродажи и печати по требованию.

Тип лицензии определяет, как вы можете использовать этот образ.

	Станд.	Расшир.
Печатный/редакционный
Графический дизайн
Веб-дизайн
Социальные сети
Редактировать и изменить
Многопользовательский
Предметы перепродажи
Печать по требованию

Право собственности Учить больше

Эксклюзивный Если вы хотите купить исключительно этот вектор, отправьте художнику запрос ниже:

Хотите, чтобы это векторное изображение было только у вас? Эксклюзивный выкуп обеспечивает все права этого вектора.

Мы удалим этот вектор из нашей библиотеки, а художник прекратит продажу работ.

Способы покупкиСравнить

Плата за изображение $ 14,99 Кредиты $ 1,00 Подписка 9 долларов0082 0,69

Оплатить стандартные лицензии можно тремя способами. Цены составляют $ $.

Оплата с помощью	Цена изображения
Плата за изображение $ 14,99 Одноразовый платеж
Предоплаченные кредиты $ 1 Загружайте изображения по запросу (1 кредит = 1 доллар США). Минимальная покупка 30р.
План подписки От 69 центов Выберите месячный план. Неиспользованные загрузки автоматически переносятся на следующий месяц.

Способы покупкиСравнить

Плата за изображение $ 39,99 Кредиты $ 30,00

Существует два способа оплаты расширенных лицензий.

Цены составляют $ $.

Оплата с помощью	Стоимость изображения
Плата за изображение $ 39,99 Оплата разовая, регистрация не требуется.
Предоплаченные кредиты $ 30 Загружайте изображения по запросу (1 кредит = 1 доллар США).

Оплата

Плата за изображение $ 499

Дополнительные услугиПодробнее

Настроить изображение Доступно только с оплатой за изображение 9 долларов0082 85,00

Нравится изображение, но нужно всего лишь несколько модификаций? Пусть наши талантливые художники сделают всю работу за вас!

Мы свяжем вас с дизайнером, который сможет внести изменения и отправить вам изображение в выбранном вами формате.

Примеры

• Изменить текст
• Изменить цвета
• Изменить размер до новых размеров
• Включить логотип или символ
• Добавьте название своей компании или компании

Включенные файлы

Подробности загрузки.

No related posts.