Метод интервалов с дробями: Решение неравенств методом интервалов

Решение неравенств методом интервалов

• Максимова Наталья Александровна

Разделы: Математика, Внеклассная работа

---

Цели:

1. Обобщить использование метода интервалов для решения неравенств,
2. Показать широкие возможности этого метода для решения неравенств, содержащих переменные под знаком log, , и тригонометрические функции.

Мы будем рассматривать неравенства, правая часть которых равна нулю, а левая часть представлена в виде произведения или частного функций.

Идея метода: Знак произведения или частного определяется знаком сомножителей.

Рис.1

Линейная функция с ненулевым угловым коэффициентом меняет знак при переходе через нуль функции, причём справа от нуля знак функции совпадает со знаком углового коэффициента.

Рис.2

Квадратный трёхчлен с D>0 при переходе через каждый нуль функции меняет свой знак, причём правее большего корня знак квадратного трёхчлена совпадает со знаком его старшего коэффициента. [1]

Эти соображения приводят к следующей схеме решения неравенства:

Пример 1:[1]

1. Найдём нули числителя: , , .
2. Найдём нули знаменателя: .
3. Наносим найденные нули на числовую ось. Т.к. неравенство строгое, то все нули изображаем выколотыми точками, которые разбивают числовую ось на интервалы:

Рис. 3

На самом правом из них знак каждого сомножителя совпадает со знаком его старшего коэффициента:

Следовательно, дробь на этом промежутке тоже отрицательна.

1. При переходе через каждый из отмеченных нулей, один и только один из сомножителей меняет знак, и поэтому каждый раз меняется знак дроби. Учитывая это, расставляем в интервалах знаки (как показано на Рис.3).
2. Выбираем интервалы, на которых дробь отрицательна.
3. Записываем ответ: .

В рассмотренном примере 1, знаки в промежутках знакопостоянства функции чередуются. Однако делать обобщение, что так будет происходить всегда, разумеется, не следует.

Пример 2:

1. нули числителя:
   

   -2 – нуль второй кратности

2. нули знаменателя:
   
3. наносим найденные нули на числовую ось, т.к. неравенство не строгое, то нули числителя изображаем заштрихованными точками, а нуль знаменателя мы выкалываем, т.к. это число не входит в область определения неравенства:

Рис.4

Обозначим нуль второй кратности галочкой, чтобы не забыть. Т.к. числитель всегда принимает положительные значения, то на правом крайнем промежутке знак будет зависеть от знака старшего коэффициента знаменателя, т. е. «+». Левее «1» знаменатель будет отрицательным, а числитель положительным, поэтому при переходе через число -2 знак не меняется:

Рис.5

Это поможет понять следующая геометрическая картинка (Рис.6):

Рис.6

4. Для записи ответа выбираем промежуток, где стоит знак «+» и заштрихованную точку , при которой дробь обращается в нуль.
   Ответ:

Вывод: при переходе через нуль чётной кратности, знак не меняется.

Решить по вариантам, с последующим обсуждением у доски.

I вариант

Пример 3:

1. нули числителя:
   
   ;

2. нули знаменателя:
   
   ;
   — нуль второй кратности

Рис.7

Ответ:

II вариант

Пример 4:

1. нули числителя:
   — нуль второй кратности
2. нули знаменателя:
   
   ;
   — нуль третьей кратности

Рис. 8

Ответ:

Применение метода интервалов не ограничивается решением рациональных неравенств.

Универсальность метода основана на достаточно наглядном свойстве непрерывных функций:

«Если на интервале (a;b) функция f(x) непрерывна и не обращается в нуль, то на этом интервале она сохраняет знак».

Пример 5: [1] ,

Будем решать это неравенство по той же схеме, но не на всей оси, а на области определения логарифмической функции, т.е. на промежутке (*):

1. нули числителя:
   
   ; — не входит в (*)
2. нули знаменателя:
   
   ;

Рис. 9

3. на самом правом промежутке
   , ,

Следовательно на этом промежутке левая часть неравенства отрицательна

4. при переходе через каждый корень меняет знак один и только один из сомножителей.
   Учитывая это, расставляем знаки на остальных промежутках.

Ответ: .

Пример 6:

1. нули числителя:
   
   
   корней нет
   
2. нули знаменателя:
   
3. решение изображаем на рис. 10:

Рис.10

Квадратный трёхчлен в числителе не имеет корней и не меняет свой знак. Его знак совпадает со знаком старшего коэффициента, т.е. «+».

Ответ:.

Пример 7: ОДЗ:

Приведём неравенство к такому виду, чтобы в правой части был «0»:

1. нули числителя:
   
   

;;;

2. нули знаменателя:
   
3. решение изображаем на рис. 11:

Рис.11

Ответ:.

Пример 8:

ОДЗ:

Рис.12

1. нули числителя:
   
2. нули знаменателя:
   

, но ОДЗ удовлетворяет только

3. решение изображаем на рис. 13:

Рис.13

Ответ:.

Задание на дом: (Решение предоставлено в Приложении1)

1. Ответ:.
2. Ответ:.
3. Ответ:.
4. Ответ: .
5. Ответ:.

Задания для факультативный занятий предоставлены в Приложении2.

Вывод: Как известно, линейная, квадратичная, степенная, показательная, логарифмическая и тригонометрические функции, а так же их композиции и функции, получаемые из них с помощью арифметических действий, непрерывны в своей области определения. Поэтому метод интервалов можно применять при решении практически всех неравенств школьного курса. Метод интервалов позволяет представить множество решений неравенства в виде объединения промежутков, границы которых либо корни соответствующего уравнения, либо граничные точки области определения.

Список литературы:

[1] «Метод интервалов» //Журнал «Квант» No12, 1985 г.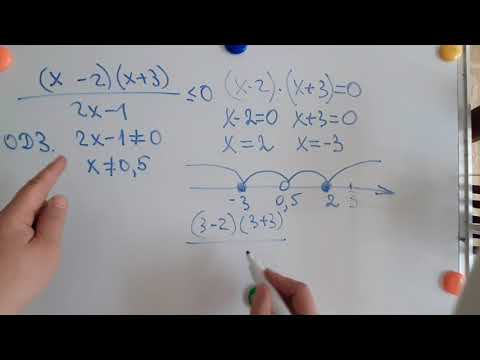

11.08.2009

Метод интервалов

Метод интервалов — универсальный метод решения неравенств. С его помощью можно решить неравенства самого разного вида. Рассмотрим алгоритм метода интервалов, а затем перейдем к примерам решения неравенств этим методом.

Алгоритм решения неравенств методом интервалов.

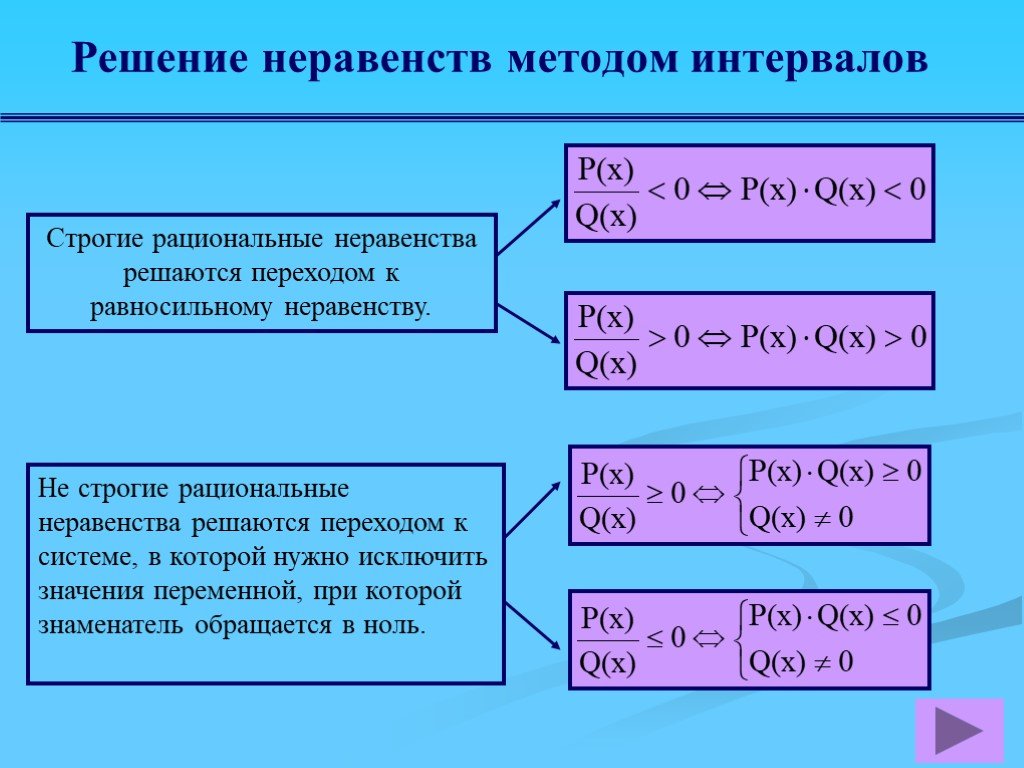
Прежде чем применить метод интервалов для решении неравенства, необходимо все дроби привести к наименьшему общему знаменателю и все слагаемые перенести в левую часть, чтобы справа остался нуль. Для начала рассмотрим алгоритм решения неравенств вида

   

1. Приравниваем к нулю левую часть:

   

(Таким образом мы находим нули функции

   

а также ее область определения).

2.Дробь равна нулю, если числитель равен нулю, а знаменатель отличен от нуля, поэтому это уравнение равносильно системе:

   

   

3. Полученные точки отмечаем на числовой прямой с учетом области определения функции. Точки разбивают числовую прямую на промежутки, в каждом из которых рассматриваемая функция имеет определенный знак. Выбираем любое число из любого промежутка (удобнее всего брать нуль, если он не входит в отмеченные точки), и подставляем это число в последнее неравенство (то есть в упрощенное неравенство, в котором все слагаемые стоят в левой части и дроби приведены к наименьшему общему знаменателю). В результате определяем знак на выбранном промежутке. Остальные знаки расставляем в шахматном порядке.

4. «Петля»

1)Если есть кратный корень четной степени, то в нем — «петля»:

   

2) Если один и тот же корень встречается четное число раз, то в нем — «петля»:

   

так как корень x2 встречается четное количество раз (два раза).

3) Если дискриминант равен нулю, то в соответствующем корне x=-b/2a — «петля».

(В этом случае x₁=x₂, то есть один и тот же корень встретился два раза).

4) Если корень стоит под знаком модуля, а выражение с модулем является множителем (а не слагаемым!), то в таком корне — «петля»:

   

5. Выбираем промежутки с нужным знаком: если в неравенстве знак > или ≥, берем промежутки с «+»; если < или ≤ — с «-«.

Точки, в которых знаменатель обращается в нуль, всегда выколотые!!!

  В остальных случаях запомнить, выколотая точка или закрашенная, можно с помощью ассоциации.

Замечание

Отдельно стоящие закрашенные точки включаем в решение:

   

(Знаки в «петлях» — «виртуальные». В этих точках функция обращается нуль либо не определена. «Петля» служит только для сохранения  порядка чередования знаков).

Кому принадлежит идея «петли», я не знаю. Этот способ очень удобный для расстановки знаков. Почему его нет в литературе? Именно потому, что знак в «петле»- «виртуальный».

Точки, которые мы отмечаем на числовой прямой, являются либо нулями функции, либо не входят в её область определения. Нуль не является ни положительным, ни отрицательным числом (он отделяет положительные числа от отрицательных). Ставя знак в «петлю», мы совершаем грубую ошибку.

Поэтому использовать «петлю» можно, но ставить в неё знак — нельзя. Предлагаю бороться с этим противоречием, либо поставить знак карандашом, а потом его стереть, либо ставить знак в черновик, но не переносить его в чистовик.

Далее рассмотрим различные примеры решения неравенств с помощью этого метода.

Представление дроби на числовой прямой путем определения интервала от 0 до 1: CCSS.Math.Content.3.NF.A.2a

All Common Core: Математические ресурсы для 3-го класса

7 диагностических тестов 226 практических тестов Вопрос дня Карточки Learn by Concept

← Предыдущая 1 2 3 4 Следующая →

Common Core: Справка по математике для 3-го класса » Числа и операции с дробями » Понимание дробей как чисел » Представление дроби на числовой прямой путем определения интервала от 0 до 1: CCSS. Math.Content.3.NF.A.2a

Какая часть числовой строки розовая?

Возможные ответы:

Правильный ответ:

Объяснение:

Числовая строка разбита на равные части. из частей розовый, что означает, что числовая линия розовая.

Сообщить об ошибке

Какая часть числовой строки розовая?

Возможные ответы:

Правильный ответ:

Объяснение:

Числовая строка разбита на равные части. из частей розовый, что означает, что числовая линия розовая.

Сообщить об ошибке

Какая часть числовой строки розовая?

Возможные ответы:

Правильный ответ:

Объяснение:

Числовая строка разбита на равные части.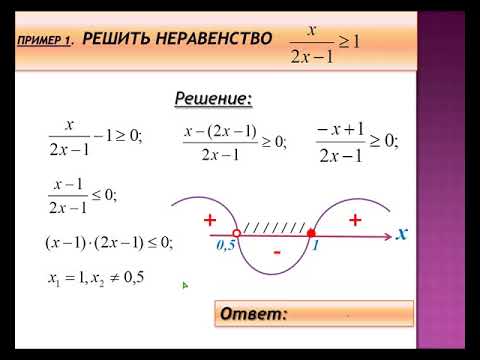 из частей розовый, что означает, что числовая линия розовая.

Сообщить об ошибке

Какая часть числовой строки розовая?

Возможные ответы:

Правильный ответ:

Объяснение:

Числовая строка разбита на равные части. из частей розовый, что означает, что числовая линия розовая.

Сообщить об ошибке

Какая часть числовой строки розовая?

Возможные ответы:

Правильный ответ:

Объяснение:

Числовая строка разбита на равные части. из частей розовый, что означает, что числовая линия розовая.

Сообщить об ошибке

Какая часть числовой строки розовая?

Возможные ответы:

Правильный ответ:

Объяснение:

Числовая строка разбита на равные части. из частей розовый, что означает, что числовая линия розовая.

Сообщить об ошибке

Какая часть числовой строки розовая?

Возможные ответы:

Правильный ответ:

Объяснение:

Числовая строка разбита на равные части. из частей розовый, что означает, что числовая линия розовая.

Сообщить об ошибке

Какая часть числовой строки розовая?

Возможные ответы:

Правильный ответ:

Объяснение:

Числовая строка разбита на равные части. из частей розовый, что означает, что числовая линия розовая.

Сообщить об ошибке

Какая часть числовой строки розовая?

Возможные ответы:

Правильный ответ:

Объяснение:

Числовая строка разбита на равные части. из частей розовый, что означает, что числовая линия розовая.

Сообщить об ошибке

Какая часть числовой строки розовая?

Возможные ответы:

Правильный ответ:

Объяснение:

Числовая строка разбита на равные части. из частей розовый, что означает, что числовая линия розовая.

Сообщить об ошибке

← Предыдущая 1 2 3 4 Следующая →

Уведомление об авторских правах

All Common Core: Математические ресурсы для 3-го класса

7 Диагностические тесты 226 практических тестов Вопрос дня Карточки Learn by Concept

Что такое интервал в математике? Значение, определение, примеры, факты

Интервал в математике

Представьте, что вам нужно постоянно сидеть в классе без перемены или обеденного перерыва.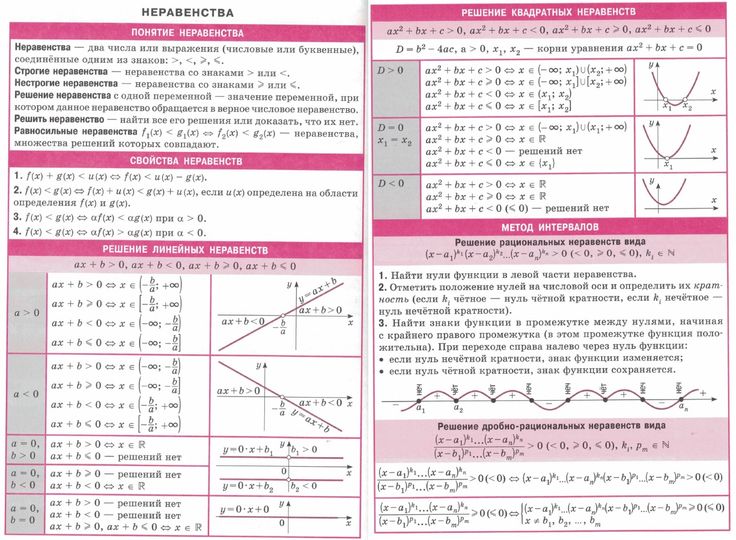 На что это будет похоже?

Большинство вещей не может продолжаться без перерыва. Между ними обычно есть промежуток. Эти промежутки известны как интервалы.

Знаете ли вы, что в математике тоже есть интервалов ? Они помогают нам измерить эти пробелы в цифрах. Давайте разберемся, что такое интервал в математике подробнее.

Родственные игры

Что такое интервал в математике?

Давайте посмотрим на определение интервала в математике.

Интервал — это промежуток между двумя объектами или точками. Давайте лучше разберемся в этом.

Чем отличаются эти две линии?

Первая строка сплошная, а во второй строке есть пробелы.

Чем отличается аварийный мигающий свет машины скорой помощи от ее фары?

Фары постоянно мигают. Однако аварийные проблесковые маячки мигают через определенные промежутки времени. Непрерывный означает без промежутка, тогда как интервал означает с промежутками.

Давайте посмотрим на другой пример, чтобы понять интервалы:

Когда автомобиль движется по дороге, он должен остановиться, когда светофор мигает красным. Однако, если светофор горит зеленым, автомобиль будет продолжать движение, не останавливаясь.

Связанные листы

Интервал в математике

Интервал в математике измеряется числами. Интервал включает в себя все числа, находящиеся между двумя конкретными числами.

Этот диапазон включает все действительные числа между этими двумя числами. Действительные числа — это любые числа, которые вы можете придумать.

Например, интервал между 0 и 10 будет включать не только 1, 2, 3, 4, 5, 6, 7, 8 и 9, но и другие типы чисел между ними. К ним относятся десятичные числа, такие как 1,3, и дроби, такие как 1/10.

Обозначение интервала

Обозначение интервала — это упрощенный способ описания конкретного интервала. Давайте посмотрим, как это делается.

Шаг 1: Пишем первое и последнее число интервала, которые являются конечными точками интервала. Например, если интервал от 6 до 20, мы пишем 6, 20. 

Шаг 2: Мы используем круглую или квадратную скобку с каждой стороны двух чисел. Мы используем:

• Квадратную скобку [ ], если мы хотим включить конечные точки
• Круглая скобка ( ), если мы не хотим включать конечные точки

Итак, в этом примере мы используем: 

• [6, 20], если интервал включает 6 и 20
• (6, 20), если интервал не включает 6 и 20
• (6, 20], если интервал исключает 6, но включает 20
• [6, 20), если интервал включает 6, но исключает 20

Типы интервалов в математике

Итак, мы видим, что некоторые интервалы включают конечные точки, некоторые включают их частично, а некоторые не включают их. Исходя из этого, в математике существует три типа интервалов.

Это:

• Открытый интервал
• Закрытый интервал
• Полуоткрытый и полузакрытый интервал

Открытый интервал

Этот тип интервала не включает конечные точки. Например, (5, 10) не включает конечные точки 5 и 10. 

Закрытый интервал

Этот тип интервала включает конечные точки. Например, [4, 9] включает конечные точки 4 и 9. 

Полуоткрытый и полузакрытый интервал

Этот тип интервала включает только одну из конечных точек.

Например, (6, 16] включает 16, но не включает 6, тогда как [6,16) включает 6, но не включает 16.

Вот как разные типы интервалов выглядят в числовых строках: 

Временной интервал

Давайте узнаем, что такое временной интервал.

Предположим, вы идете из дома в школу. Вы постоянно ходите пешком и добираетесь до школы за 10 минут.

Теперь, возвращаясь домой, вы устаете и решаете посидеть 2 минуты. Вы останавливаетесь на 2 минуты, а затем снова начинаете идти домой. Итак, мы говорим, что вы взяли временной интервал в 2 минуты, возвращаясь домой.

Временной интервал можно определить как время между двумя событиями.

Мы можем показать временные интервалы на временной шкале:

Здесь временная шкала показывает интервалы в 1 час. Мы можем найти время между событиями, используя интервалы.

Например, Сэм начал играть в футбол в 16:30. Он закончил игру в 18:00. Как долго он играл?

Мы можем нарисовать временную шкалу следующим образом:

Интервал с 16:30 до 16:30. до 17:00 составляет полчаса. Затем с 17:00 до 18:00 это час. Итак, получается полтора часа. Сэм играл в футбол полтора часа.

Интересные факты

•  Слово «интервал» происходит от латинского «Inter», что означает «между», и «vallum», что означает «пространство между валами», то есть пространство между защитными стенами замка.

Решенные примеры

Пример 1. Какой интервал между 14:00 и и 18:45?

Решение : Вычтем значения времени:

6:45 – 2:00 = 4:45

Таким образом, между 14:00 и 2:00 4 часа 45 минут. и 18:45

Значит интервал будет 4 часа 45 минут.

Пример 2. Учащиеся в возрасте от 12 до 17 лет могут быть членами школьной футбольной команды. Укажите интервал, который будет представлять эту информацию.

Решение . Допустимый возраст от 12 до 17 лет.

Таким образом, интервал равен [12, 17].

Пример 3: Чтобы сдать экзамен по математике, учащиеся должны набрать более 65 баллов из 100. Как это будет представлено в виде интервала?

Решение . Студенты должны набрать от 65 до 100 баллов.

Интервал для этого будет записан как (65, 100].

(10, 40)

[10, 40]

[10, 40]

(10, 40)

Правильный ответ: [10, 40]
Должно быть не менее 10 учащихся, а максимальное количество учащихся, которое может присутствовать, равно 40. Таким образом, интервал составляет [10, 40].

2

Для проведения спортивных соревнований общее количество участников от школы должно быть менее 30. Однако от школы должно быть не менее 12 участников. Представьте это как интервал.

(12, 30)

[12, 30]

(12, 30)

[12, 30)

Правильный ответ: [12, 30)
Минимальное количество участников — 12, поэтому 12 включены.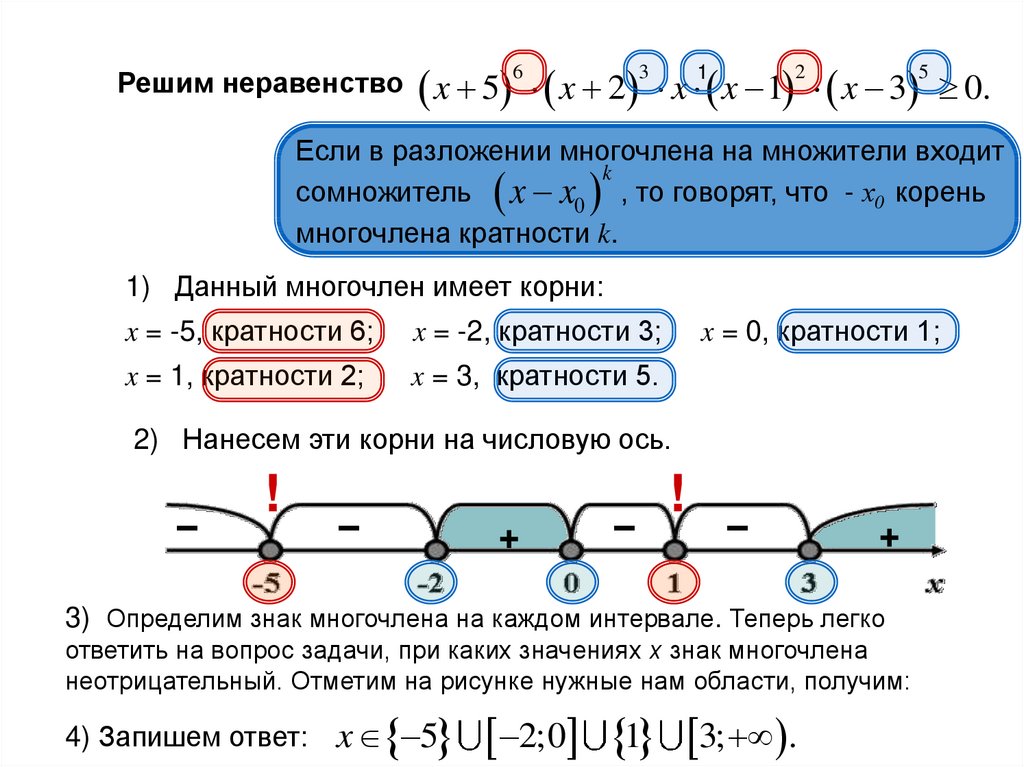 Максимальное количество участников должно быть менее 30, поэтому 30 не учитываются. Следовательно, интервал равен [12, 30).

3

При движении часов от 2 до 3:25 какой интервал проходит минутная стрелка?

125 минут

85 минут

1 час 15 минут

1,5 часа

Правильный ответ: 85 минут
Мы знаем, что интервал между 2 и 3:25 на часах составляет 1 час 25 минут или 85 минут. Таким образом, минутная стрелка покрывает интервал в 85 минут.

4

Ваша мама ведет машину и останавливается на светофоре, который только что загорелся красным светом. Свет остается красным в течение 2 минут. Затем он становится зеленым, и она едет вперед. Каков интервал красного света?

3 минуты

2,5 минуты

200 секунд

2 минуты

Правильный ответ: 2 минуты
Светофор горит красным светом 2 минуты, поэтому он останавливается на 2 минуты. Интервал красного света 2 минуты.