Лекция 06. Метод математической индукции
Лекция 6. Метод математической индукции.
Новые знания в науке и жизни добываются разными способами, но все они (если не углубляться в детали) делятся на два вида – переход от общего к частному и от частного к общему. Первый – это дедукция, второй – индукция. Дедуктивные рассуждения – это то, что в математике обычно называют логическими рассуждениями, и в математической науке дедукция является единственным законным методом исследования. Правила логических рассуждений были сформулированы два с половиной тысячелетия назад древнегреческим учёным Аристотелем. Он создал полный список простейших правильных рассуждений, силлогизмов – «кирпичиков» логики, одновременно указав типичные рассуждения, очень похожие на правильные, однако неправильные (с такими «псевдологическими» рассуждениями мы часто встречаемся в СМИ).
Индукция (induction
– по-латыни наведение)
наглядно иллюстрируется известной
легендой о том, как Исаак Ньютон
сформулировал закон всемирного тяготения
после того, как ему на голову упало
яблоко.
Будем вычислять значение трехчлена при некоторых первых значениях n:
n | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
43 | 47 | 53 | 61 | 71 | 83 | 97 | 113 |
Заметим, что
получаемые в результате вычислений
числа являются простыми.
Лейбниц в 17 веке доказал, что при всяком целом положительном n число делится на 3, число делится на 5 и т.д. На основании этого он предположил, что при всяком нечётном k и любом натуральном n число делится на k, но скоро сам заметил, что не делится на 9.
Рассмотренные
примеры позволяют сделать важный вывод:
утверждение может быть справедливым в
целом ряде частных случаев и в то же
время несправедливым вообще. Вопрос о
справедливости утверждения в общем
случае удается решить посредством
применения особого метода рассуждений,
называемого методом
математической индукции (полной индукции, совершенной индукции).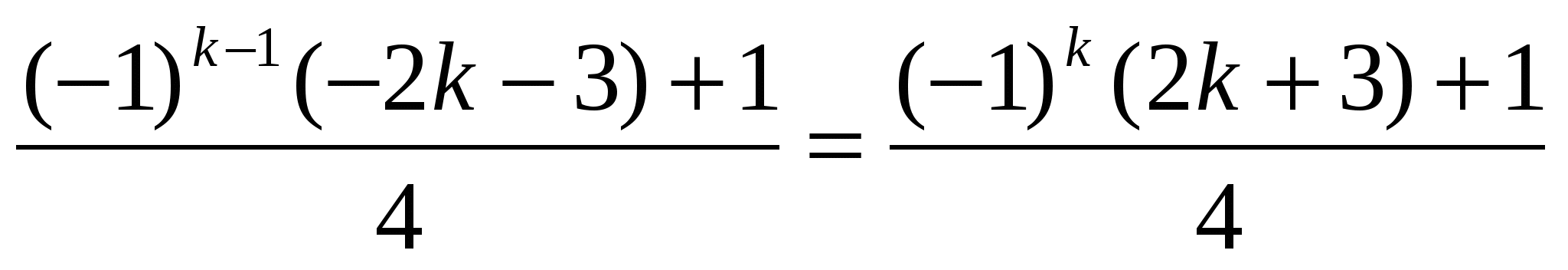
6.1. Принцип математической индукции.
♦ В основе метода математической индукции лежит принцип математической индукции, заключающийся в следующем:
1) проверяется справедливость этого утверждения для n=1 (базис индукции),
2) предполагается справедливость этого утверждения для n=k, где k – произвольное натуральное число 1 (предположение индукции), и с учётом этого предположения устанавливается справедливость его для n=k+1.
Доказательство. Предположим противное, то есть предположим, что утверждение справедливо не для всякого натурального
1) утверждение для n=m несправедливо,
2) для всякого n,
меньшего m,
утверждение справедливо (иными словами, m есть первое натуральное число, для
которого утверждение несправедливо).
Очевидно, что m>1, т.к. для n=1 утверждение справедливо (условие 1). Следовательно, – натуральное число. Выходит, что для натурального числа утверждение справедливо, а для следующего натурального числа m оно несправедливо. Это противоречит условию 2. ■
Заметим, что в доказательстве использовалась аксиома о том, что в любой совокупности натуральных чисел содержится наименьшее число.
Доказательство, основанное на принципе математической индукции, называется методом полной математической индукции.
Пример 6.1. Доказать, что при любом натуральном n число делится на 3.
Решение. Воспользуемся методом полной математической индукции.
1) При n=1 , поэтому a1 делится на 3 и утверждение справедливо при n=1.
2) Предположим, что
утверждение справедливо при n=k,
,
то есть что число делится на 3, и установим, что при n=k+1
число делится на 3.
В самом деле,
.
Т.к. каждое слагаемое делится на 3, то их сумма также делится на 3. ■
Пример 6.2. Доказать, что сумма первых n натуральных нечётных чисел равна квадрату их числа, то есть .
Решение. Воспользуемся методом полной математической индукции.
1) Проверяем справедливость данного утверждения при n=1: 1=12 – это верно.
2) Предположим, что сумма первых k () нечётных чисел равна квадрату числа этих чисел, то есть . Исходя из этого равенства, установим, что сумма первых k+1 нечётных чисел равна , то есть .
Пользуемся нашим предположением и получаем
. ■
Метод полной
математической индукции применяется
для доказательства некоторых неравенств.
Докажем неравенство Бернулли.
Пример 6.3. Доказать, что при и любом натуральном n справедливо неравенство (неравенство Бернулли).
Решение. 1) При n=1 получаем , что верно.
2) Предполагаем, что при n=k имеет место неравенство (*). Используя это предположение, докажем, что . Отметим, что при это неравенство выполняется и поэтому достаточно рассмотреть случай .
Умножим обе части неравенства (*) на число и получим:
, то есть (1+. ■
Доказательство методом неполной математической индукции некоторого утверждения, зависящего от n, где проводится аналогичным образом, но в начале устанавливается справедливость для наименьшего значения n.
В некоторых задачах
явно не сформулировано утверждение,
которое можно доказать методом
математической индукции. В таких случаях
надо самим установить закономерность
и высказать гипотезу о справедливости
этой закономерности, а затем методом
математической индукции проверить
предполагаемую гипотезу.
Пример 6.4. Найти сумму .
Решение. Найдём суммы S1, S2, S3. Имеем , , . Высказываем гипотезу, что при любом натуральном n справедлива формула . Для проверки этой гипотезы воспользуемся методом полной математической индукции.
1) При n=1 гипотеза верна, т.к. .
2) Предположим, что гипотеза верна при n=k, , то есть . Используя эту формулу, установим, что гипотеза верна и при n=k+1, то есть
.
В самом деле,
.
Итак, исходя из предположения, что гипотеза верна при n=k, , доказано, что она верна и при n=k+1, и на основании принципа математической индукции делаем вывод, что формула справедлива при любом натуральном n. ■
Пример 6. 5. В математике доказывается, что сумма
двух равномерно непрерывных функций
является равномерно непрерывной
функцией. Опираясь на это утверждение,
нужно доказать, что сумма любого числа равномерно непрерывных функций является
равномерно непрерывной функцией. Но
поскольку мы ещё не ввели понятие
«равномерно непрерывная функция»,
поставим задачу более абстрактно: пусть
известно, что сумма двух функций,
обладающих некоторым свойством S,
сама обладает свойством S.
Докажем, что сумма любого числа функций
обладает свойством S.
5. В математике доказывается, что сумма
двух равномерно непрерывных функций
является равномерно непрерывной
функцией. Опираясь на это утверждение,
нужно доказать, что сумма любого числа равномерно непрерывных функций является
равномерно непрерывной функцией. Но
поскольку мы ещё не ввели понятие
«равномерно непрерывная функция»,
поставим задачу более абстрактно: пусть
известно, что сумма двух функций,
обладающих некоторым свойством S,
сама обладает свойством S.
Докажем, что сумма любого числа функций
обладает свойством S.
Решение. Базис индукции здесь содержится в самой формулировке задачи. Сделав предположение индукции, рассмотрим функций f1, f2, …, fn, fn+1
 Следовательно, их сумма
обладает свойством S – для двух слагаемых «работает» базис
индукции.
Следовательно, их сумма
обладает свойством S – для двух слагаемых «работает» базис
индукции.Тем самым утверждение доказано и будем использовать его далее. ■
Пример 6.6. Найти все натуральные n, для которых справедливо неравенство
.
Решение. Рассмотрим n=1, 2, 3, 4, 5, 6. Имеем: 21>12, 22=22, 23<32, 24=42, 25>52, 26>62. Таким образом, можно высказать гипотезу: неравенство имеет место для каждого . Для доказательства истинности этой гипотезы воспользуемся принципом неполной математической индукции.
1) Как было установлено выше, данная гипотеза истинна при n=5.
2) Предположим, что
она истинна для n=k,
,
то есть справедливо неравенство
. Используя это предположение, докажем,
что справедливо неравенство
.
Используя это предположение, докажем,
что справедливо неравенство
.
Т. к. и при имеет место неравенство
при ,
то получаем, что . Итак, истинность гипотезы при n=k+1 следует из предположения, что она верна при n=k, .
Из пп. 1 и 2 на основании принципа неполной математической индукции следует, что неравенство верно при каждом натуральном . ■
Пример 6.7. Доказать, что для любого натурального числа n справедлива формула дифференцирования .
Решение. При n=1 данная формула имеет вид , или 1=1, то есть она верна. Сделав предположение индукции, будем иметь:
,
что и требовалось доказать. ■
Пример 6.8. Доказать,
что множество, состоящее из n элементов, имеет
подмножеств.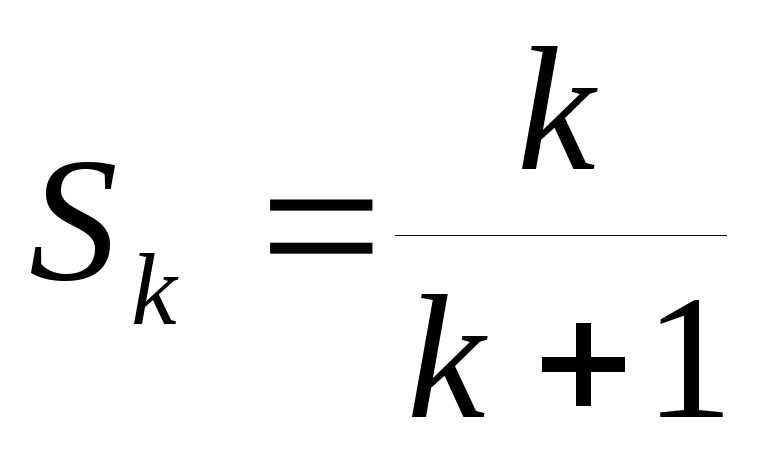
Решение. Множество, состоящее из одного элемента а, имеет два подмножества. Это верно, поскольку все его подмножества – пустое множество и само это множество, и 21=2.
Предположим, что всякое множество из n элементов имеет подмножеств. Если множество А состоит из n+1 элементов, то фиксируем в нём один элемент – обозначим его d, и разобьём все подмножества на два класса – не содержащие d и содержащие d. Все подмножества из первого класса являются подмножествами множества В, получающегося из А выбрасыванием элемента d.
Множество В состоит из n элементов, и поэтому, по предположению индукции, у него подмножеств, так что в первом классе подмножеств.
Но во втором классе
подмножеств столько же: каждое из них
получается ровно из одного подмножества
первого класса добавлением элемента d.
Следовательно, всего у множества А подмножеств.
Тем самым утверждение доказано. Отметим, что оно справедливо и для множества, состоящего из 0 элементов – пустого множества: оно имеет единственное подмножество – самого себя, и 20=1. ■
29
объяснение принципа, примеры решения задач
Основы метода математической индукции
Определение 1Математическая индукция является способом математического доказательства, применимым с целью подтверждения справедливости какого-либо утверждения для любых натуральных чисел.
В процессе реализации метода в первую очередь требуется выполнить проверку того, насколько соответствует истине утверждение под номером 1. Данное утверждение носит название базы, или базиса, индукции.
На следующем этапе нужно представить объяснение справедливости утверждения под номером n+1 в том случае, когда верным является утверждение под номером n. Шагом индукции, или индукционным переходом, называют утверждение под номером n+1.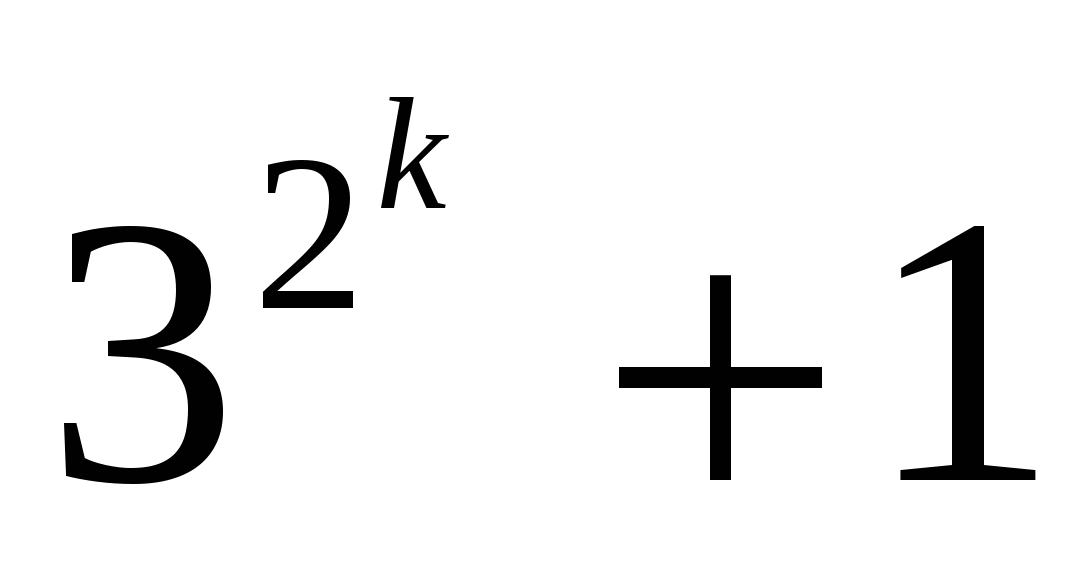
Сформулировать доказательный процесс легко, если вспомнить принцип домино. Предположим, что любое количество фишек домино составлено в ряд так, чтобы каждая из них при падении задевала и опрокидывала фишку, которая за ней следует. В этом состоит смысл индукционного перехода. При опрокидывании первой фишки, которая играет роль базы индукции, все остальные также упадут.
Разберем метод индукции на наглядном примере из данной тематики. Представим, что необходимо доказать то, что верной является неограниченная последовательность утверждений, которые пронумерованы с помощью натуральных чисел:
P1,P2,…,Pn,Pn+1,….
Допустим следующее:
- Фактом является справедливость P1. Данное утверждение примем за базис индукции.
- В случае какого-либо n доказано, что при справедливости Pn, верно Pn+1. Данное утверждение играет роль шага индукции.
При выполнении заданных условий каждое из утверждений рассматриваемой последовательности является верным.
С точки зрения логики, основой для рассматриваемого способа доказательства служит аксиома индукции, пятая из аксиом Пеано, которая определяет натуральные числа. Утверждение того, что этот метод является верным, эквивалентно тому, что в каком-либо непустом подмножестве натуральных чисел имеется минимальный элемент.
Утверждение того, что этот метод является верным, эквивалентно тому, что в каком-либо непустом подмножестве натуральных чисел имеется минимальный элемент.
Принцип полной математической индукции. При наличии ряда утверждений P1,P2,P3, … для какого-либо n из множества натуральных из того, что верны все P1,P2,P3,…,Pn-1, следует также справедливость Pn. Тогда каждое из утверждений в ряду является истинным:
(∀n∈ℕ)((∀i∈{1;…;n-1})Pi⇒Pn\Big)⇒(∀n∈ℕ)Pn.
В рассматриваемом случае база индукции не требуется. Это связано с тем, что данная вариация представляет собой тривиальный частный случай индукционного перехода. В действительности, если n=1, то условие (∀i∈{1;…;n-1})Pi⇒Pn точно является эквивалентным P1 (его истинности не из чего следовать).
С другой стороны, индукционный переход для P1 обычно нуждается в отдельном доказательстве. В связи с этим, целесообразно обособить данную его часть, как базу. Принцип полной математической индукции является эквивалентным аксиоме индукции из аксиом Пеано. Кроме того, данный принцип представляет собой прямое использование более сильной трансфинитной индукции.
Кроме того, данный принцип представляет собой прямое использование более сильной трансфинитной индукции.
Понимание метода математической индукции в роли самостоятельной методики, имеющей большую важность, связано с работами Блеза Паскаля и Герсонида. Стоит отметить, что встречались случаи, когда этот метод применяли в античные времена Прокл и Эвклид. Современный термин сформулировал де Морган в 1838 году.
Применение в разных типах задач
Использование метода математической индукции допустимо при решении следующих видов задач в классе и самостоятельно:
- поиск доказательств делимости и кратности;
- доказательство справедливости равенств и тождеств;
- примеры, содержащие последовательности;
- доказательство того, что верны неравенства;
- вычисление суммы и произведения.
Воспользуемся методом математической индукции, чтобы доказать посредством рассуждений неравенство Бернулли. Согласно этому неравенству, при условии, что x>-1, справедливым для всех натуральных n⩾1является:
(1+x)n⩾1+nx.
Здесь целесообразно воспользоваться индукцией по n. В том случае, когда n = 1 неравенство является верным, что очевидно. Предположим, что данное неравенство справедливо для n, докажем его справедливость для n+1:
(1+x)n+1=(1+x)(1+x)n⩾(1+x)(1+nx)⩾(1+nx)+x=1+(n+1)x, что и требовалось доказать.
В общем виде неравенство Бернулли представляет собой утверждение того, что при условии x>-1 и n∈ℝ:
- когда n∈(-∞;0)∪(1;+∞), имеем, что (1+x)n⩾1+nx;
- когда n∈(0;1) , имеем, что (1+x)n⩽1+nx;
- возможно два случая справедливости данного равенства: ∀x≠-1,n=0,n=1∀n≠0,x=0
В качестве доказательства следует разобрать вариант, когда f(x)=(1+x)n-nx . В данном случае x>-1,n≠0,n≠1 . Если x=x0=0 , то производная равна:
f'(x)=n(1+x)n-1-n=0
Это объясняется тем, что:
n≠0 ˙
Функция f два раза дифференцируется в проколотой окрестности точки x0 . По этой причине:
f»(x)=n(n-1)(1+x)n-2 ˙
В результате:
f»(x)>0 ⇒f(x)⩾f(x0)
Это выполняется, когда:
n∈(-∞;0)∪(1;+∞)
Также получим, что:
f»(x)<0 ⇒f(x)⩽f(x0)
Это выполняется, когда:
n∈(0;1)
Функция обладает следующим значением:
f(x0)=1
Таким образом, данные утверждения верны:
- когда n∈(-∞;0)∪[1;+∞), получим, что (1+x)n⩾1+nx;
- когда n∈(0;1] получим, что (1+x)n⩽1+nx.

Когда имеются соответствующие значения x0=0 или n=0,n=1 , функция равна:
f(x)=f(x0) ˙
В данном случае итоговое неравенство избавляется от ограничений на n , которые записаны в начале доказательства. Это связано с тем, что для них исполняется равенство, что и требовалось доказать.
Заметим, что справедливым рассмотренное неравенство является и для x⩾-2 (при n∈ℕ0). При этом требуется исключение ситуации, при которой получается ноль в степени ноль. При доказательстве рассматриваемого случая x∈-2,-1 допустимо применять метод математической индукции:
(1+x)n+1+(1+x)n=(1+x)n(1+x+1)⩾(1+nx)(1+x+1)=1+(n+1)x+1+nx(1+x)
При условии, что:
(1+x)n⩽1⩽1+nx(1+x)
получим:
(1+x)n+1⩾1+(n+1)x
С помощью метода математической индукции можно рассмотреть сумму геометрической прогрессии. Попробуем найти доказательства того, что при каких-либо натуральных n и вещественных q≠1, справедливо следующее равенство:
∑i=0nqi≡1+q+q2+⋯+qn=1-qn+11-q.
В данном случае рассматривается индукция по n для произвольного q. Представим доказательство базиса для n=1:
1+q= (1-q)(1+q)1-q= 1-q1+11-q.
Докажем, что переход является справедливым. Для этого представим, что в случае n=k выполняется следующее:
1+q+⋯+qk=1-qk+11-q,
В таком случае, для n=k+1, исходя из предположения, имеем:
1+q+⋯+qk+qk+1=1-qk+11-q+qk+1=
=1-qk+1+(1-q)qk+11-q=1-qk+1+qk+1-q(k+1)+11-q=1-q(k+1)+11-q.
Таким образом, руководствуясь принципом математической индукции, заключим, что равенство является справедливым для любого n, что и требовалось доказать.
Стоит отметить, что справедливость утверждения Pn в рассматриваемом доказательстве аналогична тому, что верно следующее равенство:
1+q+⋯+qn= 1-qn+11-q.
Разберем еще один пример применения метода математической индукции под названием «доказательство одноцветности всех лошадей». Эта задача является математическим софизмом, то есть ошибочным подтверждением того факта, что любые из лошадей имеют одинаковый окрас.
Автором этого софизма является венгерский математик Дьердь Пойа. В процессе доказательства выявляют ошибки, причиной возникновения которых является некорректное применение метода математической индукции.
Проиллюстрируем доказательство одноцветности всех лошадей, где шаг индукции не выполняется для K = 1:
Источник: ru.wikipedia.org
Запишем исходные данные.
Утверждение, которое нуждается в доказательстве: все лошади имеют одинаковый окрас.
База индукции: одна лошадь с одним (идентичным) окрасом.
Рассмотрим шаг индукции. Предположим, что имеются доказательства того факта, что какие-либо лошади в любом случае обладают одинаковым окрасом. Разберем K + 1 неких лошадей. Избавимся от одной лошади. (K) лошадей, которые остались, имеют один окрас, исходя из предположения индукции.
Вернем лошадь обратно и исключим любую другую лошадь. (K) лошадей, которые остались в результате, вновь будут иметь один окрас. Таким образом, все K + 1 лошадей обладают одинаковым окрасом. В результате получим, что все лошади не отличаются по цвету, что и требовалось доказать.
В результате получим, что все лошади не отличаются по цвету, что и требовалось доказать.
Ошибка в этом примере формируется уже в базе. Здесь можно наблюдать подмену квантора всеобщности («все») на квантор существования («существует»). Таким образом, противоречие появляется вследствие того, что шаг индукции справедлив только в том случае, когда K⩾2. При K=1 получаемые множества лошадей, которые остались, не обладают пересечениями. В результате доказать равенство окрасов всех лошадей не представляется возможным.
Примеры решения задач
Задача 1Дано равенство, которое требуется доказать:
12+22+32+⋯+n2=n(n+1)(2n+1)6,n∈ℕ.
Решение:
12=1(1+1)(2+1)6=1.
Предположим, что утверждение является справедливым, если n=k:12+⋯+k2=k(k+1)(2k+1)6.
Запишем доказательство того, что утверждение верно для n=k+1:
12+22+⋯+k2⏞k(k+1)(2k+1)6+(k+1)2=
(k+1)(k+2)(2(k+1)+1)6
k(k+1)(2k+1)6+(k+1)2=
(k+1)(k+2)(2k+3)6
k(k+1)(2k+1)+6(k+1)26=
(k+1)(k+2)(2k+3)6
k(2k2+k+2k+1)+6(k2+2k+1)=
(k+1)(2k2+3k+4k+6)
2k3+3k2+k+6k2+12k+6=
2k3+7k2+6k+2k2+7k+6
2k3+9k2+13k+6=
2k3+9k2+13k+6.
Ответ: равенство доказано.
Задача 2Дано следующее неравенство:
n≤2n
Требуется доказать, что данное неравенство верно для любых n из множества натуральных чисел.
Решение
В том случае, когда n=1, неравенство можно записать в таком виде:
1≤2
Заметим, что записанное неравенство является справедливым. Представим, что рассматриваемое неравенство верно, если n=k, а также не обладает противоречиями при n=k+1.
Суммируем предположение индукции k≤2k и неравенство 1≤2≤2k. Выполним вычисления:
k+1≤2k+2k=2k+1, что и требовалось доказать.
Ответ: неравенство доказано.
Задача 3Дана формула, справедливость которой требуется доказать:
1+2+3+…..+n=n(n+1)2.
Решение
Заметим, что в виде формулы записан некий ряд утверждений:
1=1·22
1+2=2·32
1+2+3=3·42
1+2+3+4=4·52и так далее.
Очевидно, что первое утверждение является справедливым. Достаточно просто выполнить проверку того факта, что каждое верное утверждение предшествует верному. Представим, что утверждение k справедливо. Таким образом, является верным следующее равенство:
Представим, что утверждение k справедливо. Таким образом, является верным следующее равенство:
1+2+3+4+….+k=k·(k+1)2
Далее сложим обе части равенства и число (k+1):
1+2+3+4+….+k+(k+1)=k·(k+1)2+k+1=(k+1)·(k+2)2.
Заметим, что записанное утверждение является утверждением k+1, которое следует за утверждением k.
В результате представлено доказательство того, что каждое справедливое утверждение предшествует верному. Исходя из принципа математической индукции, начальная формула является справедливой при каком-либо k.
Ответ: формула доказана.
Рассмотренный пример можно решить альтернативным методом без применения принципа математической индукции. Тогда следует ввести обозначение суммы, которую требуется вычислить, в виде un. Запишем пару равенств:
un=1+2+3+….+(n-2)+(n-1)+n,
un=n+(n-1)+(n-2)+…..+3+2+1
Выполним сложение членов строк:
2un=(n+1)+(n+1)+⋯+(n+1)+(n+1)⏟n=n(n+1)
un=n(n+1)2
В результате равенство доказано.
Требуется доказать, что при каком-либо n (из множества натуральных) число n5-n можно поделить на число 5.
Решение
Воспользуемся методом математической индукции. В том случае, когда n=1, выражение n5-n принимает нулевое значение и может быть поделено на число 5.
Предположим, что k является каким-то числом из множества натуральных. Докажем, что при равенстве n=k число n5-n можно поделить на 5, и выражение (k+1)5-(k+1) аналогично делится на число 5.
Рассмотрим следующее равенство:
(k+1)5=k5+5k4+10k3+10k2+5k+1
Далее запишем число (k+1)5-(k+1) в следующей форме:
(k+1)5-(k+1)=(k5+5k4+10k3+10k2+5k+1)-(k+1)=(k5-k)+5(k4+2k3+2k2+k).
В результате число (k+1)5-(k+1)представляет собой сумму, состоящую из пары слагаемых. Первое слагаемое равно (k5-k) и его можно разделить на число 5, согласно выдвинутому предположению. Второе слагаемое равно 5(k4+2k3+2k2+k) и аналогично может быть поделено на число 5.
В том случае, когда слагаемые можно поделить на число 5, сумма пары этих чисел также делится на 5. В результате:
В результате:
(k+1)5-(k+1) делится на 5.
Оба утверждения являются верными. Исходя из принципа математической индукции, число n5-n можно поделить на число 5 при каких-либо n из множества натуральных.
Ответ: число n5-n можно поделить на число 5 при каких-либо n из множества натуральных.
Полная индукция – Основы математики
Путешествия не всегда приятны. Это не всегда удобно. Иногда это больно, даже сердце разрывается. Но это нормально. Путешествие меняет вас; это должно изменить вас. Оно оставляет следы в вашей памяти, в вашем сознании, в вашем сердце и в вашем теле. Вы берете что-то с собой. Альравель не всегда красивая. Это не всегда удобно. Иногда это больно, даже сердце разрывается. Но это нормально. Путешествие меняет вас; это должно изменить вас. Оно оставляет следы в вашей памяти, в вашем сознании, в вашем сердце и в вашем теле. Вы берете что-то с собой.
Энтони Бурден, Без оговорок: Вокруг света на пустой желудок
Введение — это как восхождение по лестнице. Но есть и другие способы подняться, кроме лестниц. Скалолазы не просто стоят на одной ступеньке. Чтобы подняться на скалу, скалолаз должен использовать все четыре конечности (а не только, как альпинист по лестнице, предыдущий шаг).
Но есть и другие способы подняться, кроме лестниц. Скалолазы не просто стоят на одной ступеньке. Чтобы подняться на скалу, скалолаз должен использовать все четыре конечности (а не только, как альпинист по лестнице, предыдущий шаг).
Подобно скалолазам, нам позволено помнить не только то, что мы находимся всего в одном шаге от того, к чему стремимся, но и то, как мы туда попали. Почему бы не оглянуться назад на столько шагов, сколько нам нужно?
Определение . Мы называем открытое предложение полностью индуктивным , если оно обладает тем свойством, что .
Если индуктивные предложения представляют собой наследственные свойства, то полностью индуктивные предложения представляют свойства, которые переходят к следующему поколению , но, возможно, только в том случае, если этим свойством обладает весь род.
Принцип полной индукции. Предположим, является полностью индуктивным и истинным. Затем .
Как можно использовать такое утверждение, как принцип полной индукции? Давайте посмотрим на пример, а затем вернемся к обоснованию того, что PCI работает.
Основная теорема арифметики. Каждое натуральное число больше 1 имеет простую факторизацию; то есть, учитывая любой с , есть простые числа, так что мы можем написать .
Формулировка этой теоремы содержит два новых термина: простое число и простая факторизация . В самом утверждении мы объяснили, что означает простая факторизация ; но нам все еще нужно знать, что такое простое число .
Определение. Натуральное число простое , если делятся только натуральные числа 1 и .
Приведем пример простого числа.
Лемма. 2 — простое число.
Доказательство. Мы пытаемся размножить 2; то есть написать для некоторых натуральных чисел и ; показать, что 2 является простым, означает, что мы покажем или или . Теперь произведение любых двух натуральных чисел не меньше любого множителя, поэтому имеем и . Так как и натуральные числа, и . Итак, у нас есть и . Но единственными натуральными числами между 1 и 2 (включительно) являются 1 и 2. Итак, либо , либо . .
Теперь произведение любых двух натуральных чисел не меньше любого множителя, поэтому имеем и . Так как и натуральные числа, и . Итак, у нас есть и . Но единственными натуральными числами между 1 и 2 (включительно) являются 1 и 2. Итак, либо , либо . .
Упражнение. Примените это доказательство, чтобы показать, что 3 — простое число.
Упражнение. Докажите, что 5 — простое число.
Теперь мы готовы доказать основную теорему арифметики.
Доказательство основной теоремы арифметики. Докажем утверждение по полной индукции. Мы будем называть .
(базовый случай: .) — условное предложение с ложным антецедентом; так и есть.
(базовый случай: .) означает «Если 2>1, то 2 имеет простую факторизацию». 2 простое, так что есть простая факторизация.
(индуктивный шаг.) Рассмотрим некоторое натуральное число . Предположим, что все верно; то есть предположим, что любое натуральное число с имеет простую факторизацию. Мы будем использовать это предположение, чтобы показать, что имеет простую факторизацию.
Мы будем использовать это предположение, чтобы показать, что имеет простую факторизацию.
Если простое, то это наша простая факторизация.
Если не простое, то имеет множитель, отличный от самого себя и 1. Назовите этот номер . У нас есть некоторое натуральное число . Потому что у нас есть. Более того, произведение любых двух натуральных чисел не меньше любого множителя, поэтому мы знаем и . Потому что , . В общем, у нас
Согласно нашему индуктивному предположению, имеет простую факторизацию, скажем . Индуктивное предположение также применяется, чтобы дать некоторые простые числа с .
Тогда
, так что и в этом случае есть простая факторизация.
В любом случае имеет простую факторизацию; это завершает индуктивный шаг.
По принципу полной индукции мы должны иметь для всех , то есть любое натуральное число больше 1 имеет простую факторизацию.
Несколько замечаний по поводу этого доказательства:
- Такое использование принципа полной индукции делает его более мощным, чем принцип математической индукции.
 Вместо того, чтобы «оглядываться назад» на один шаг, мы должны «оглядываться назад» настолько далеко, насколько нам нужно. Если мы возьмем, например, то мы могли бы использовать и . Вместо того, чтобы полагаться на предыдущий случай (), мы полагаемся на и , которые довольно далеки от .
Вместо того, чтобы «оглядываться назад» на один шаг, мы должны «оглядываться назад» настолько далеко, насколько нам нужно. Если мы возьмем, например, то мы могли бы использовать и . Вместо того, чтобы полагаться на предыдущий случай (), мы полагаемся на и , которые довольно далеки от . - Это доказательство на самом деле представляет собой что-то вроде алгоритма нахождения простых факторизаций, вероятно, того же самого, которому вас учили в начальной школе.
- Как и обычные индуктивные доказательства, полные индукционные доказательства имеют базовый случай и индуктивный шаг.
Один большой класс примеров PCI-доказательств предполагает возврат всего на несколько шагов назад. (Если подумать, вот как работают лестницы, лестницы и ходьба на самом деле .) Вот забавное определение.
Определение. Числа Фибоначчи определяются следующим образом: и . Для любого , .
Такие определения мы называем полностью индуктивные определения , потому что они оглядываются более чем на один шаг назад.
Упражнение. Вычислите первые 10 чисел Фибоначчи.
Как правило, доказательства с использованием чисел Фибоначчи требуют доказательства по полной индукции. Например:
Претензия. Для любого , .
Доказательство. Для индуктивного шага предположим, что для всех , . Покажем, что
Для этого рассмотрим левую часть.
Теперь мы наблюдаем, что и , поэтому мы можем применить индуктивное предположение с и , чтобы продолжить:
по определению чисел Фибоначчи. Это завершает индуктивный шаг.
Теперь о базовом варианте. Заметьте, что, поскольку мы должны были сделать на два шагов назад в нашем индуктивном шаге (чтобы доказать утверждение при , мы должны были посмотреть на и ), наш индуктивный шаг начинает работать только тогда, когда у нас есть два шага, на которые можно положиться. Итак, нам нужно
базовый случай : Утверждение для доказательства .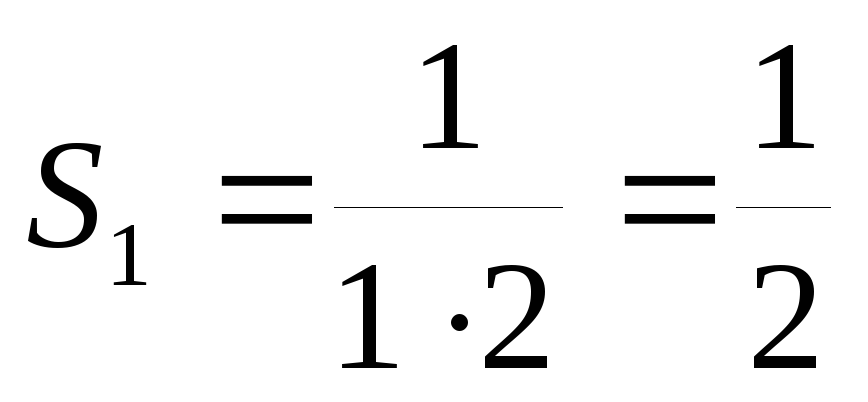 Поскольку , , и , имеем базовый случай.
Поскольку , , и , имеем базовый случай.
базовый случай : Утверждение для доказательства . Поскольку , , и , имеем базовый случай.
По принципу полной индукции мы установили утверждение.
Вот еще пример:
Претензия. Для любого и любого .
Доказательство. Исправить.
Для индуктивного шага предположим, что для всех , . Мы покажем, что
Для этого рассмотрим левую часть.
Теперь мы наблюдаем, что и , поэтому мы можем применить индуктивное предположение с и , чтобы продолжить:
Это завершает индуктивный шаг.
Теперь о базовом варианте. Опять нам нужны два базовых случая, потому что наш индуктивный шаг оглядывался назад на два шага:
базовый случай : Утверждение . Поскольку , это утверждение , что является определением чисел Фибоначчи.
базовый случай : Претензия . Так как и , нам нужно установить, что . Но мы только что доказали это выше.
Но мы только что доказали это выше.
По принципу полной индукции мы установили утверждение.
Теперь, когда мы увидели как работает полная индукция , давайте объясним почему работает полная индукция :
Доказательство принципа полной индукции. Нам дано открытое предложение со свойствами: и является полностью индуктивным.
Рассмотрите предложение . Сначала покажем, что всегда верно.
Сначала обратите внимание на то, что по предположению верно.
Теперь я утверждаю , то есть является индуктивным. Допустим, верно. То есть, . Поскольку полностью индуктивный, мы знаем, что это правда. Тогда верно.
Итак, по (обычной) индукции мы доказали, что .
Почему это установлено? Потому что по определению.
Верно и обратное: мы могли бы принять принцип полной индукции как аксиому и использовать его для доказательства принципа математической индукции . На самом деле вы сделаете это в качестве домашнего задания.
Вот еще один пример доказательства по полной индукции, который показывает, что нам, возможно, придется вернуться на несколько шагов назад (следовательно, у нас будет довольно много базовых случаев для построения):
Утверждение. Если , то существуют неотрицательные натуральные числа и поэтому мы можем написать .
Доказательство.
базовый вариант: . Пусть и .
базовый вариант: . Пусть и .
базовый вариант: . Пусть и .
базовый вариант: . Пусть и .
Теперь предположим, что мы установили, что можем записать любое число до включительно в виде суммы 4 и 5. С тем же успехом мы можем предположить, поскольку с остальными мы уже разобрались. Попробуем записать в виде суммы 4 и 5.
, поэтому мы знаем, что можем написать как сумму 4 и 5, скажем . Но тогда , поэтому мы записали как сумму 4 и 5. Это завершает индуктивный шаг, следовательно, доказательство.
Математическая индукция предоставляет инструмент для доказательства больших задач путем решения меньших приращений
Обзор Развитие математической индукции было одним из величайших шагов вперед в математике. Изящный принцип, сыгравший большую роль в продолжающейся эволюции математической логики и повлиявший на развитие других математических дисциплин, включая алгебру и аналитическую геометрию, математическая индукция, связан с нематематическим процессом, называемым индуктивным рассуждением. В отличие от дедуктивного рассуждения, при котором большая общая истина берется за отправную точку, из которой выводятся более мелкие, более частные истины, индукция давала инструмент для перехода от частного к общему, от малых индивидуальных истин к более крупным общим истинам. В процессе индукции истинность всего математического предложения доказывается шаг за шагом, причем каждый шаг используется в качестве строительного блока для доказательства следующего шага с конечной целью доказательства всего предложения. Природа математической индукции такова, что она предлагает эффективные доказательства определенных предложений, в то же время устраняя необходимость доказывать каждый пример предложения. Хотя многие считают, что индукция воспринималась еще в Древней Греции, этот метод не был четко выражен до 1575 г., когда сицилийский математик Франсиско Мавролико (1494-1575) использовал этот метод для доказательства теоремы. У подхода Мауролико не было названия: его ждал английский математик Джон Уоллис (1616-1703), который описал метод как индукцию в своей книге 1655 года Arithmetica Infinitorum (Бесконечно малая арифметика). Почти десять лет спустя, с посмертной публикацией Блеза Паскаля (1623-1662) Traite du Triangle Arithmetique (Трактат об арифметике треугольников), математическая индукция стала широко известна как эффективный и незаменимый математический инструмент.
Природа математической индукции такова, что она предлагает эффективные доказательства определенных предложений, в то же время устраняя необходимость доказывать каждый пример предложения. Хотя многие считают, что индукция воспринималась еще в Древней Греции, этот метод не был четко выражен до 1575 г., когда сицилийский математик Франсиско Мавролико (1494-1575) использовал этот метод для доказательства теоремы. У подхода Мауролико не было названия: его ждал английский математик Джон Уоллис (1616-1703), который описал метод как индукцию в своей книге 1655 года Arithmetica Infinitorum (Бесконечно малая арифметика). Почти десять лет спустя, с посмертной публикацией Блеза Паскаля (1623-1662) Traite du Triangle Arithmetique (Трактат об арифметике треугольников), математическая индукция стала широко известна как эффективный и незаменимый математический инструмент.
Дедуктивное мышление было одним из величайших достижений человечества. В процессе дедукции большая истина служит отправной точкой, из которой логически выводятся меньшие и более конкретные истины. Но дедуктивное рассуждение было применимо не ко всем областям знания. В математике, в частности, большие истины — или доказательства — часто были неуловимы, к ним можно было приблизиться лишь отрывочно, постепенно.
Но дедуктивное рассуждение было применимо не ко всем областям знания. В математике, в частности, большие истины — или доказательства — часто были неуловимы, к ним можно было приблизиться лишь отрывочно, постепенно.
Но по мере того, как математика становилась все более и более важным и точным инструментом, много размышлений и исследований было посвящено задаче доказательства больших теорем. Эта мысль, исследования и эксперименты привели к развитию математической индукции, также известной как принцип индукции.
Некоторые ученые видят свидетельство математической индукции в работах греческих математиков, в том числе Паппаса (ок. 260–?), в чьих работах собрана большая часть греческих математических работ, сохранившихся до наших дней. Поскольку Паппас был в первую очередь собирателем математических идей, а не их создателем, вполне вероятно, что его работа с индукцией была заимствована у более ранних мыслителей.
Другие свидетельства ранних индуктивных рассуждений можно найти в трудах как исламских, так и талмудических ученых, в частности Леви бен Герсона (1288?-1344?). Говоря о своем подходе к решению сложных проблем, Леви бен Герсон писал, что он следовал математическому процессу «бесконечного подъема шаг за шагом». Этот пошаговый подход является самой сутью индукции, хотя эта сущность не будет формализована еще 250 лет.
Говоря о своем подходе к решению сложных проблем, Леви бен Герсон писал, что он следовал математическому процессу «бесконечного подъема шаг за шагом». Этот пошаговый подход является самой сутью индукции, хотя эта сущность не будет формализована еще 250 лет.
Частично проблема, с которой столкнулся Леви бен Герсон, заключалась в том, что он полагался на слова, а не на символы, когда излагал свои взгляды на алгебру. К 1500-м годам математика находилась в состоянии быстрой эволюции, новые идеи и методологии развивались устойчивыми темпами, а сама наука становилась все более чисто символической деятельностью.
Итальянец (сицилиец) Франсиско Мавролико, монах-бенедиктинец, а также глава сицилийского монетного двора, на протяжении большей части 1500-х годов посвятил себя сбору и переводу мировых математических знаний. Он также написал оригинальные трактаты по математике, в том числе Arithmeticorum Libri Duo (Две книги по математике), в которой он использовал принцип индукции для доказательства теоремы.
Проще говоря, математическая индукция сводит математическое утверждение или теорему к простым утверждениям, которые можно доказать, причем каждое утверждение служит шагом к решению задачи. более крупное предложение. Например, при поиске свойств целых чисел математическая индукция находит простейший пример свойства целого числа, которым, конечно же, является число 1. Следующим шагом является выбор случайного целого числа, представленного как 9.0005 к . Если вы можете доказать, что утверждение, верное для 1, верно и для числа k , вы также доказали, что это верно и для числа k +1.
Доказав эти два утверждения, вы индуцируете , что утверждение верно для всех целых чисел, или n .
Принцип Мауролико привлек некоторое внимание, но оставался безымянным до работы английского математика Джона Уоллиса. Многие считают Уоллиса самым важным английским математиком до Исаака Ньютона (1642–1727), Уоллис внес большой вклад как в математику, так и в науку, в том числе помог основать Английское Королевское общество (наиболее престижное из всех научных обществ) и сформулировал формулировку для первый раз закон сохранения импульса. Он также участвовал во многих ожесточенных научных и математических спорах.
Он также участвовал во многих ожесточенных научных и математических спорах.
Возможно, Уоллис внес наибольший вклад как писатель по математике. Он был одержим историей математики и посвятил себя сохранению этой истории для современного мира. Среди его многочисленных книг была Arithmetica Infinitorum , опубликованная в 1656 году. В этой книге, среди множества примеров математических свойств, включая бесконечные ряды и предсказания интегрального исчисления, Уоллис резюмировал математическую индукцию, назвав ее per modum inductonis 9.0006 (методом индукции) и дал процедуре название, под которым она известна до сих пор.
Однако для того, чтобы математическая индукция стала хорошо известной, потребовалось бы еще почти десятилетие и публикация в 1665 году еще одной книги, которая, по иронии судьбы, была написана до тома Уоллиса.
Это был « Traite du Triangle Arithmetique » Блеза Паскаля («Трактат о треугольнике»), один из ключевых математических трактатов своего времени. Паскаль был сыном математика, хотя его отец изначально был против раннего интереса ребенка к математике. Гений Паскаля быстро стал очевиден, и его отец уступил; мальчик погрузился в математику. Интерес Паскаля вышел за рамки теоретического: к тому времени было 19он изобрел раннюю версию механического калькулятора. Только чрезмерная стоимость производства его калькулятора помешала машинам стать успешными.
Паскаль был сыном математика, хотя его отец изначально был против раннего интереса ребенка к математике. Гений Паскаля быстро стал очевиден, и его отец уступил; мальчик погрузился в математику. Интерес Паскаля вышел за рамки теоретического: к тому времени было 19он изобрел раннюю версию механического калькулятора. Только чрезмерная стоимость производства его калькулятора помешала машинам стать успешными.
Хотя гениальность Паскаля привела его во многие области исследований и размышлений, включая религиозную философию, наибольший вклад он внес в чистую математику, заложив основу (вместе с Пьером де Ферма [1601-1675]) для современной науки вероятности, а также понимания исчисления и геометрии.
Его «Трактат о треугольнике» посвящен свойствам треугольника, состоящего из чисел, а также другим математическим идеям и понятиям. Среди них был его подход к доказательству утверждений, для которых существует бесконечно много случаев. Он сообщил своим читателям, что, столкнувшись с таким предложением, они должны сначала доказать, что предложение верно для первого случая. После этого они должны доказать предложение для данного (или случайного) случая. С этими двумя доказательствами предложение решается для следующего случая и для бесконечного числа других случаев.
После этого они должны доказать предложение для данного (или случайного) случая. С этими двумя доказательствами предложение решается для следующего случая и для бесконечного числа других случаев.
Используя индукцию, Паскаль предложил метод решения биномиальной теоремы, которая была необходима для решения задач, в которых две величины изменяются независимо. Успех книги Паскаля, а также название, которое Уоллис дал этому процессу, обеспечили широкую известность принципа индукции Мауролико и продолжают служить математике по сей день.
Воздействие Математическая индукция, способность доказать для все случаев числового свойства, была важным шагом вперед в переходе математики от чисто практической — счетной — к более теоретической. Вместо того, чтобы ограничиваться конкретными элементами, математика могла иметь дело с переменными, с неизвестными, с отношениями между переменными и неизвестными, с бесконечным набором свойств. Эти способности значительно расширили возможности математики как в отношении вычислений и уравнений, связанных с реальным миром, так и в отношении более чисто теоретических занятий.


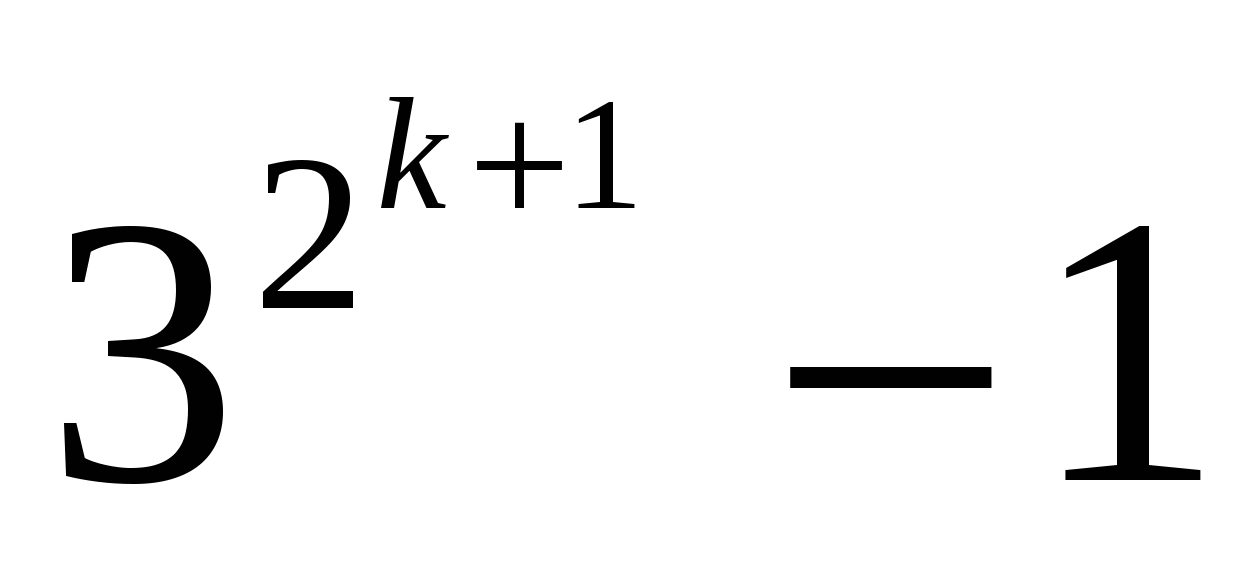 Вместо того, чтобы «оглядываться назад» на один шаг, мы должны «оглядываться назад» настолько далеко, насколько нам нужно. Если мы возьмем, например, то мы могли бы использовать и . Вместо того, чтобы полагаться на предыдущий случай (), мы полагаемся на и , которые довольно далеки от .
Вместо того, чтобы «оглядываться назад» на один шаг, мы должны «оглядываться назад» настолько далеко, насколько нам нужно. Если мы возьмем, например, то мы могли бы использовать и . Вместо того, чтобы полагаться на предыдущий случай (), мы полагаемся на и , которые довольно далеки от .