Формула площади боковой поверхности конуса: Площадь поверхности и объём конуса — урок. Геометрия, 11 класс.

Площадь поверхности конуса

Площадь поверхности конуса (или просто поверхность конуса) равна сумме площадей основания и боковой поверхности.

Площадь боковой поверхности конуса вычисляется по формуле: S = πRl, где R — радиус основания конуса, а l — образующая конуса.

Так как площадь основания конуса равна πR² (как площадь круга), то площадь полной поверхности конуса будет равна: πR² + πRl = πR (R + l ).

Получение формулы площади боковой поверхности конуса можно пояснить такими рассуждениями. Пусть на чертеже изображена развёртка боковой поверхности конуса. Разделим дугу АВ на возможно большее число равных частей и все точки деления соединим с центром дуги, а соседние — друг с другом хордами.

Получим ряд равных треугольников. Площадь каждого треугольника равна ^ah/₂ , где а — длина основания треугольника, a h — его высота.

Сумма площадей всех треугольников составит: ^ah/₂ • n = ^anh/₂ , где n — число треугольников.

При большом числе делений сумма площадей треугольников становится весьма близкой к площади развёртки, т. е. площади боковой поверхности конуса. Сумма оснований треугольников, т. е. an, становится весьма близкой к длине дуги АВ, т. е. к длине окружности основания конуса. Высота каждого треугольника становится весьма близкой к радиусу дуги, т. е. к образующей конуса.

Пренебрегая незначительными различиями в размерах этих величин, получаем формулу площади боковой поверхности конуса (S):

S = ^Cl/₂, где С — длина окружности основания конуса, l — образующая конуса.

Зная, что С = 2πR, где R — радиус окружности основания конуса, получаем: S = πRl.

Примечание. В формуле S = ^Cl/₂ поставлен знак точного, а не приближённого равенства, хотя на основании проведённого рассуждения мы могли бы это равенство считать приближённым. Но в старших классах средней школы доказывается, что равенство

S = ^Cl/₂ точное, а не приближённое.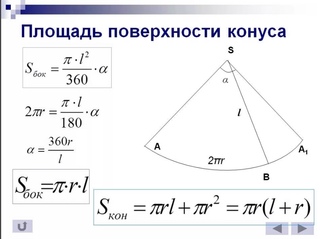

Теорема. Боковая поверхность конуса равна произведению длины окружности основания на половину образующей.

Впишем в конус (рис.) какую-нибудь правильную пирамиду и обозначим буквами р и l числа, выражающие длины периметра основания и апофемы этой пирамиды.

Тогда боковая поверхность её выразится произведением ¹/₂р • l .

Предположим теперь, что число сторон вписанного в основание многоугольника неограниченно возрастает. Тогда периметр р будет стремиться к пределу, принимаемому за длину С окружности основания, а апофема l будет иметь пределом образующую конуса (так как из ΔSAK следует, что SA — SK

¹/₂р• l, будет стремиться к пределу ¹/₂С• L. Этот предел и принимается за величину боковой поверхности конуса. Обозначив боковую поверхность конуса буквой S, можем написать:

S = ¹/₂С • L = С • ¹/₂L

Следствия.
1) Так как С = 2πR, то боковая поверхность конуса выразится формулой:

S = ¹/₂• 2πR • L = πRL

2) Полную поверхность конуса получим, если боковую поверхность сложим с площадью основания; поэтому, обозначая полную поверхность через Т, будем иметь:

T = πRL + πR² = πR(L + R)

Теорема. Боковая поверхность усечённого конуса равна произведению полусуммы длин окружностей оснований на образующую.

Впишем в усечённый конус (рис.) какую-нибудь правильную усечённую пирамиду и обозначим буквами р, р₁ и l числа, выражающие в одинаковых линейных единицах длины периметров нижнего и верхнего оснований и апофемы этой пирамиды.

Тогда боковая поверхность вписанной пирамиды равна ¹/₂ (р + р₁) • l

При неограниченном возрастании числа боковых граней вписанной пирамиды периметры р и р₁ стремятся к пределам, принимаемым за длины С и С₁ окружностей оснований, а апофема l имеет пределом образующую L усечённого конуса. Следовательно, величина боковой поверхности вписанной пирамиды стремится при этом к пределу, равному (С + С₁) L. Этот предел и принимается за величину боковой поверхности усечённого конуса. Обозначив боковую поверхность усечённого конуса буквой S, будем иметь:

S = ¹/₂ (С + С₁) L

Следствия.
1) Если R и R₁ означают радиусы окружностей нижнего и верхнего оснований, то боковая поверхность усечённого конуса будет:

S = ¹/₂ (2πR + 2πR₁) L = π (R + R₁) L.

2) Если в трапеции OO₁А₁А (рис.), от вращения которой получается усечённый конус, проведём среднюю линию ВС, то получим:

ВС = ¹/₂(OA + O₁A₁) = ¹/₂ • (R + R₁),

откуда

R + R₁ = 2ВС.

Следовательно,

S = 2πBC• L,

т.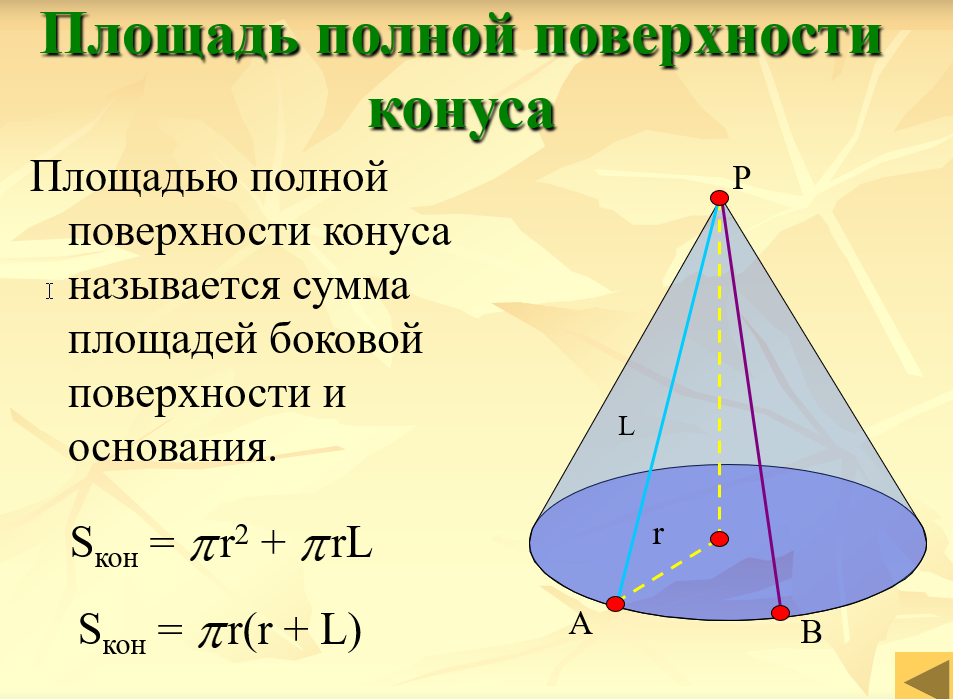 е. боковая поверхность усечённого конуса равна произведению длины окружности среднего сечения на образующую.

3) Полная поверхность Т усечённого конуса выразится так:

T = π( R² + R₁² + RL + R₁L)

Геометрия Площадь поверхности конуса

Материалы к уроку

Конспект урока

 

 Площадь поверхности конуса

Вспомним, что такое конус. Тело, ограниченное конической поверхностью и кругом радиусом R, называется конусом.	Тело, ограниченное конической поверхностью и кругом радиусом R, называется конусом.
Боковую поверхность конуса можно развернуть на плоскость, разрезав ее по одной из образующих. Пусть дан конус с радиусом ОА. Разрежем конус по образующей АВ и развернем его боковую поверхность. В результате получим круговой сектор, радиус которого равен образующей конуса, а длина дуги АА´ сектора равна длине окружности основания конуса.	AA´ = 2πr.
За площадь боковой поверхности конуса принимается площадь его развертки (кругового сектора).   Площадь сектора вычисляется по формуле: пи эль квадрат на угол фи, деленное на 360 градусов, где  φ (фи) — градусная мера дуги АА´. Теперь выразим φ через l и r.   Длина дуги АА´ равна с одной стороны длине окружности, а с другой стороны длине кругового сектора в фи градусов, поэтому получаем формулу:   Выразим из нее φ: 360 умножить на эр и разделить все на эль.
Подставим это выражение в формулу площади боковой поверхности конуса, получим, что площадь боковой поверхности конуса равна произведению половины длины окружности основания на образующую.	Sбок. = πrl
Можно эту формулу выразить через радиус и высоту конуса: Площадь боковой поверхности конуса равна произведению числа π на радиус и  на квадратный корень из суммы квадратов радиуса и высоты.	r–радиус основания h–высота кунуса
Площадью полной поверхности конуса называется сумма площадей боковой поверхности и основания. Основанием конуса является круг.	Sполн. = πr (r + l) где   r — радиус окружности основания,  l- длина образующей конуса.
Можно эту формулу выразить через радиус и высоту конуса:
Задача. Найти высоту конуса, если площадь его осевого сечения равна 6 дм2, а площадь основания равна 8 дм2. Вспомним , что собой представляет осевое сечение конуса: сечение конуса плоскостью, проходящей через его вершину, представляет собой равнобедренный треугольник, у которого боковые стороны являются образующими конуса. Решение   1.Осевое сечение конуса представляет собой треугольник РАВ, который является равнобедренным. Выразим площадь осевого сечения через высоту и радиус основания: площадь треугольника равна половине произведения основания на высоту. АВ равно двум радиусам, подставим в формулу и получим: площадь сечения равна произведению радиуса на высоту конуса. 2. Из этой формулы выразим высоту.   Из формулы площади основания выражаем радиус. Получим, что радиус равен корень квадратный из площади основания деленное на пи. 3. Формулу радиуса подставляем в формулу высоты, после преобразований получаем формулу высоты конуса, и находим её. Высота равна три корня из пи, деленное на корень из двух дм.	Дано конус, РАВ–осевое сечение,                        SΔPAB=6дм2, Sосн=8дм2 Найти h.

 

Остались вопросы по теме? Наши педагоги готовы помочь!

• Подготовим к ЕГЭ, ОГЭ и другим экзаменам

• Найдём слабые места по предмету и разберём ошибки

• Повысим успеваемость по школьным предметам

• Поможем подготовиться к поступлению в любой ВУЗ

Выбрать педагогаОставить заявку на подбор

Площадь поверхности конуса

Горячая математика

общий площадь поверхности из конус есть сумма площадей его основания и боковой (боковой) поверхности.

площадь боковой поверхности

конуса – это площадь только боковой или боковой поверхности.

Поскольку конус тесно связан с пирамида , формулы для их площадей связаны.

Помните, формула площади боковой поверхности пирамиды 1 2 п л а общая площадь поверхности 1 2 п л + Б .

Поскольку основанием конуса является круг, подставляем 2 π р для п и π р 2 для Б где р это радиус основания цилиндра.

Итак, формула для площадь боковой поверхности прямого конуса л . С . А «=» π р л , где л — наклонная высота конуса .

Пример 1:

Найдите площадь боковой поверхности прямого конуса, если радиус 4 см, а наклонная высота 5 см.

л . С . А «=» π ( 4 ) ( 5 ) «=» 20 π ≈ 62,82 см 2

Формула для общая площадь поверхности прямого конуса Т . С . А «=» π р л + π р 2 .

Пример 2:

Найдите площадь полной поверхности прямого конуса, если радиус 6 дюймов, а наклонная высота 10 дюймы.

Т . С . А «=» π ( 6 ) ( 10 ) + π ( 6 ) 2 «=» 60 π + 36 π «=» 96 π дюймы 2 ≈ 301,59 дюймы 2

Боковая часть конуса

Боковая площадь конуса определяется как площадь, покрытая криволинейной поверхностью конуса. Его также называют площадью боковой поверхности (LSA) или площадью криволинейной поверхности (CSA) конуса. Конус — это трехмерный объект, который плавно сужается от плоского круглого основания к точке, называемой вершиной. Другими словами, это форма, образованная набором отрезков, исходящих из основания, которые соединяются с общей точкой (вершиной). Эти отрезки начинаются от точек в основании и заканчиваются в вершине.

1.	Что такое боковая площадь конуса?
2.	Формула площади поперечного сечения конуса
3.	Как найти боковую площадь конуса?
4.	Часто задаваемые вопросы о боковой части конуса

Что такое боковая площадь конуса?

Площадь боковой поверхности конуса представляет собой площадь, занимаемую площадью криволинейной поверхности конуса. Поскольку конус представляет собой трехмерную форму, площадь боковой поверхности конуса также лежит в трехмерной плоскости. Когда много треугольников складываются и вращаются вокруг оси, мы получаем форму, известную как конус. Поскольку он имеет плоское основание, он имеет общую площадь поверхности, а также площадь изогнутой поверхности. Боковая площадь конуса представлена ​​в квадратных единицах, например, см ² , м ² , в ² и др.

Формула боковой площади конуса

Формула поперечной площади конуса: πrL, где r — радиус основания, а L — наклонная высота. Таким образом, если известны наклонная высота и радиус основания конуса, можно найти площадь его боковой поверхности (или площадь криволинейной поверхности). Мы также можем записать площадь кривизны конуса через высоту конуса, поскольку мы знаем соотношение между высотой и наклонной высотой конуса, используя теорему Пифагора. Связь между высотой и наклонной высотой конуса, заданная как L = √(h ² + r ² ), где h — высота конуса. Таким образом, боковая площадь конуса = πrL = πr√(h ² + r ² )

Как найти боковую площадь конуса?

Как мы узнали из предыдущего раздела, боковая площадь конуса равна πrL. Таким образом, мы следуем шагам, показанным ниже, чтобы найти боковую площадь конуса:

• Шаг 1: Определите радиус основания конуса и назовите его r.
• Шаг 2: Определите его высоту и назовите его h.
• Шаг 3: Найдите площадь боковой поверхности конуса по формуле πrL.
• Шаг 4: Представьте окончательный ответ в квадратных единицах.

Пример: Чему равна боковая площадь конуса, имеющего радиус основания = 4 единицы и наклонную высоту = 7 единиц?

Решение: При r = 4 единицах и l = 7 единицах

Как мы знаем, боковая площадь конуса = πrL
⇒ Боковая площадь конуса = (22/7) × 4 × 7 = 88 единиц ²

Ответ: Площадь боковой поверхности конуса 88 единиц ² .

 

Решенные примеры на боковой поверхности конуса

1. Пример 1: Найдите площадь боковой поверхности конуса, имеющего радиус основания 21 единицу и высоту 20 единиц. (Используйте π = 22/7)

   Решение: Учитывая, что r = 21 единица и h = 20 единиц

   Таким образом, наклонная высота конуса, l = √(r ² + h ² ) = √(21 ² + 20 ² ) = √(441 + 400) = √841 = 29 ед.

   Мы знаем, площадь боковой поверхности конуса = πrL
   ⇒ Площадь боковой поверхности конуса = (22/7) × 21 × 29 = 22 × 3 × 29 = 1914 единиц ²

   Ответ:

2. Пример 2: Найдите боковую поверхность конуса высотой 15 единиц и наклонной высотой 17 единиц. (Используйте π = 3,14)

   Решение: Учитывая, что h = 15 единиц и l = 17 единиц

   Радиус конуса (r) = √(L ² — h ² ) = √(17 ² — 15 ² ) = √(289 — 225) = √64 = 8 единиц

   Боковая площадь конуса = πrL
   ⇒ Площадь поперечного сечения конуса = 3,14 × 8 × 17 = 427,04 ед.

перейти к слайдуперейти к слайду

Разбивайте сложные концепции с помощью простых визуальных средств.

Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций.

Записаться на бесплатный пробный урок

Практические вопросы по боковой поверхности конуса

 

перейти к слайдуперейти к слайду

Часто задаваемые вопросы о боковой части конуса

Что такое боковая площадь конуса?

Боковая площадь конуса определяется как площадь, покрываемая криволинейной поверхностью конуса. Его также обычно называют площадью боковой поверхности (LSA) или площадью криволинейной поверхности (CSA) конуса. Единица боковой площади конуса выражается в квадратных единицах, например, см ² , m ² , in ² , и т.д.

Какая формула площади боковой поверхности конуса?

Формула площади поперечного сечения конуса определяется как площадь поперечного сечения конуса = πrL, где «r» и «L» — радиус конуса и наклонная высота конуса. Таким образом, можно определить значение боковой площади конуса, если у нас есть значения обоих размеров конуса.

Какова формула площади поперечного сечения конуса через высоту конуса?

Мы знаем, что формула площади поперечного сечения конуса дается как площадь поперечного сечения конуса = πrL. Мы также знаем, что соотношение между наклонной высотой и высотой конуса равно L = √(h ² + r ² ). Таким образом, боковая площадь конуса по отношению к высоте конуса определяется как πr√(h ² + r ² ).

Как найти боковую площадь конуса?

Боковую площадь конуса можно определить с помощью следующих шагов:

• Шаг 1: Определите радиус основания и высоту конуса.
• Шаг 2: Определите боковую площадь конуса по формуле πrL.
• Шаг 3: После того, как значение боковой площади конуса получено, представьте окончательный ответ в квадратных единицах.

Как найти радиус конуса, если известна боковая площадь конуса?

Мы можем найти радиус конуса, если боковую площадь конуса следующие шаги:

• Шаг 1: Определите заданные размеры конуса и пусть радиус конуса равен «r»
• Шаг 2: Подставьте значения в формулу πrL и получите уравнение.
• Шаг 3: Решите уравнение для «r».
• Шаг 4: После того, как значение радиуса конуса получено, представьте окончательный ответ в единицах.

Что происходит с боковой поверхностью конуса, когда радиус конуса увеличивается вдвое?

Боковая площадь конуса удваивается, когда радиус конуса удваивается, поскольку мы подставляем «2r» вместо «r» в формулу боковой площади конуса. Таким образом, боковая площадь конуса = πrL = π(2r)L = 2(πrL), что в два раза больше первоначального значения боковой площади конуса.

Что происходит с боковой поверхностью конуса, когда наклонная высота конуса уменьшается вдвое?

Боковая площадь конуса уменьшается пополам, когда радиус конуса уменьшается вдвое, поскольку мы подставляем «(L/2)» вместо «L» в формулу боковой площади конуса. Таким образом, боковая площадь конуса = πrL = πr(L/2) = (1/2) × (πrL), что составляет половину первоначального значения боковой площади конуса.