Матрицы методом гаусса онлайн: Онлайн калькулятор. Решение систем линейных уравнений. Метод Гаусса

alexxlab / / Разное

Содержание

Примеры решения системы линейных алгебраических уравнений 4-ого порядка методом Гаусса, пример № 4

СЛАУ 3-его порядка: 1 — 2 — 3 — 4 — 5 — 6 — 7 — 8 — 9 — 10 — 11 — 12
СЛАУ 4-ого порядка: 1 — 2 — 3 — 4 — 5 — 6 — 7 — 8 — 9 — 10 — 11 — 12

Условие

 3x 1 + x 2 — 2x 3 — 2x 4   =   -2
 2x 1 — x 2 + 2x 3 + 2x 4   =   2
 2x 1 + x 2 — x 3 — x 4   =   -1
 x 1 + x 2 — 3x 3 + 2x 4   =   -3

Решение системы линейных алгебраических уравнений методом Гаусс

Для проверки ответов можете воспользоваться нашим онлайн сервисом — Решение системы линейных уравнений методом Гаусса.

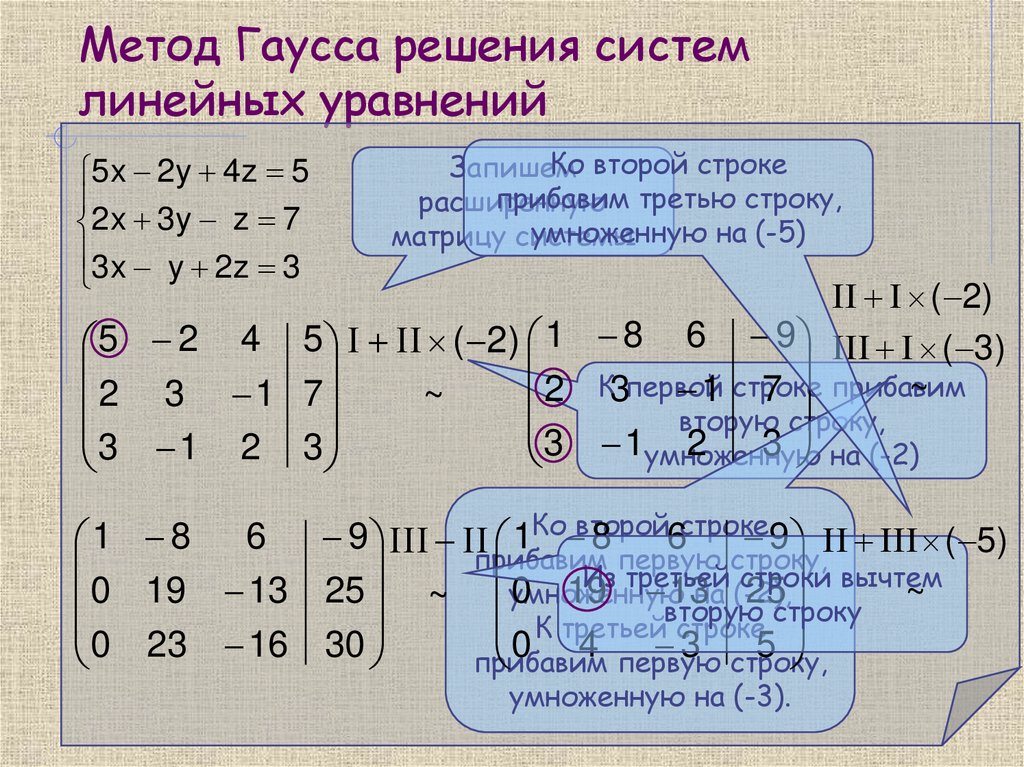
Все действия описанные в данном разделе не противоречат правилам обращения с матрицами и являются элементарными преобразованиями матрицы. Если после изучения примеров решения задач у Вас останутся вопросы, то Вы всегда можете задать их на форуме, и не забывайте про наши онлайн калькуляторы для решения задач по математике и другим предметам!

Перепишем систему линейных алгебраических уравнений в матричную форму. Получится матрица 4 × 5, слева от разделительной линии стоят коэффициенты при переменных, а справа стоят свободные члены.


Проведём следующие действия:

  • Поменяем местами строку № 1 и строку № 4

Получим:

Проведём следующие действия:

  • Из строки № 2 вычтем строку № 1 умноженную на 2 (Строка 2 — 2 × строка 1)
  • Из строки № 3 вычтем строку № 1 умноженную на 2 (Строка 3 — 2 × строка 1)
  • Из строки № 4 вычтем строку № 1 умноженную на 3 (Строка 4 — 3 × строка 1)

Получим:

Проведём следующие действия:

  • Строку № 3 умножим на -1 (Строка 3 = строка 3 * -1)
  • Поменяем местами строку № 2 и строку № 3

Получим:

Проведём следующие действия:

  • К строке № 3 прибавим строку № 2 умноженную на 3 (Строка 3 + 3 × строка 2)
  • К строке № 4 прибавим строку № 2 умноженную на 2 (Строка 4 + 2 × строка 2)

Получим:

Проведём следующие действия:

  • Строку № 4 поделим на -3 (Строка 4 = строка 4 / -3)
  • Поменяем местами строку № 3 и строку № 4

Получим:

Проведём следующие действия:

  • К строке № 4 прибавим строку № 3 умноженную на 7 (Строка 4 + 7 × строка 3)

Получим:

Проведём следующие действия:

  • Строку № 4 поделим на 55 (Строка 4 = строка 4 / 55)
  • Из строки № 3 вычтем строку № 4 умноженную на 6 (Строка 3 — 6 × строка 4)
  • Из строки № 2 вычтем строку № 4 умноженную на 5 (Строка 2 — 5 × строка 4)
  • Из строки № 1 вычтем строку № 4 умноженную на 2 (
    Строка 1 — 2 × строка 4    )

Получим:

Проведём следующие действия:

  • К строке № 2 прибавим строку № 3 умноженную на 5 (Строка 2 + 5 × строка 3)
  • К строке № 1 прибавим строку № 3 умноженную на 3 (Строка 1 + 3 × строка 3)

Получим:

Проведём следующие действия:

  • Из строки № 1 вычтем строку № 2 (Строка 1 — строка 2)

Получим:

В левой части матрицы по главной диагонали остались одни единицы. В правом столбце получаем решение:

х1 = 0
х2 = 0
х3 = 1
х4 = 0


Вы поняли, как решать? Нет?

Другие примеры

Матрицы. Метод Гаусса. Формулы Крамера

Похожие презентации:

Элементы комбинаторики ( 9-11 классы)

Применение производной в науке и в жизни

Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»

Знакомство детей с математическими знаками и монетами

Тренажёр по математике «Собираем урожай». Счет в пределах 10

Методы обработки экспериментальных данных

Лекция 6. Корреляционный и регрессионный анализ

Решение задач обязательной части ОГЭ по геометрии

Дифференциальные уравнения

Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи

1. Матрицы

Метод Гаусса
Формулы Крамера

2. Матрица Определение

Прямоугольная таблица из m, n чисел, содержащая m – строк и n –
столбцов, вида: a a a a
a 11a 12 a 1i a1n
2j
2n
21 22
a a a a
ij
in
i1 i 2
a a a a
mj
mn
m1 m 2
называется
матрицей размера
m n
Числа, из которых составлена матрица, называются элементами матрицы.
Положение элемента аi j в матрице характеризуются двойным индексом:
первый i – номер строки;
второй j – номер столбца, на пересечении которых стоит элемент.
Сокращенно матрицы обозначают заглавными буквами: А, В, С…
Коротко можно записывать так:
A (aij ) ;
i 1, m;
j 1, n

3. Иоганн Карл Фридрих Гаусс (30 апреля 1777, Брауншвейг — 23 февраля 1855, Гёттинген)

4. Метод Гаусса

Метод Гаусса — классический метод решения системы
линейных алгебраических уравнений. Это метод последовательного
исключения переменных, когда с помощью элементарных
преобразований система уравнений приводится к равносильной
системе ступенчатого (или треугольного) вида, из которого
последовательно, начиная с последних (по номеру) переменных,
находятся все остальные переменные.
Система т линейных уравнений с п неизвестными имеет вид:
a11 x1 a12 x2 … a1n xn b1
a 21 x1 a 22 x2 … a 2 n xn b2
………………………………. ……….
a m1 x1 a m 2 x2 … am n xn bn
x1 , x2, …, xn – неизвестные.
ai j — коэффициенты при неизвестных.
bi — свободные члены (или правые части)

5. Типы уравнений

Система линейных уравнений называется совместной, если она
имеет решение, и несовместной, если она не имеет решения.
Совместная система называется определенной, если она имеет
единственное решение и неопределенной, если она имеет
бесчисленное множество решений.
Две совместные системы называются равносильными, если они
имеют одно и то же множество решений.

6. Элементарные преобразования

К элементарным преобразованиям системы отнесем следующее:
1.
2.
3.
перемена местами двух любых уравнений;
умножение обеих частей любого из уравнений на
произвольное число, отличное от нуля;
прибавление к обеим частям одного из уравнений системы
соответствующих частей другого уравнения, умноженных на
любое действительное число.

7. Общий случай

Для простоты рассмотрим метод Гаусса для системы трех линейных уравнений с
тремя неизвестными в случае, когда существует единственное решение:
Дана система:
a11 x1 a12 x2 a13 x3 b1
a21 x1 a22 x2 a23 x3 b2
a x a x a x b
32 2
33 3
3
31 1
(1)
1-ый шаг метода Гаусса
На первом шаге исключим неизвестное х1 из всех уравнений системы (1), кроме
первого. Пусть коэффициент . Назовем его ведущим элементом. Разделим первое
уравнениеa системы (1) на аb11. Получим уравнение:
где
a1 j
(1)
1j
a11
;
j 1,2,3 ;
b1
(1)
1
a11
Исключим х1 из второго и третьего уравнений системы (1). Для этого вычтем из
них уравнение (2), умноженное на коэффициент при х1 (соответственно а21 и а31).
x a x a x b
(2)
Система примет вид:
(1)
1
12
(1)
2
13
(1)
3
1
Верхний индекс (1) указывает, что речь идет о коэффициентах первой
преобразованной системы. x a x a x b
a x a x b
(3)
(1)
1
12
(1)
22
(1)
2
2
13
(1)
23
(1)
3
3
1
(1)
2
a32 x2 a33 x3 b3
(1)
(1)
(1)
2-ой шаг метода Гаусса
На втором шаге исключим неизвестное х2 из третьего уравнения системы (3).
Пусть коэффициент . Выберем его за ведущий элемент и разделим на него второе
уравнение системы (3), получим уравнение: x a x b (4)
( 2)
2
где
a23
( 2)
a23
(1)
a22
(1)
;
b2
( 2)
b2
23
( 2)
3
2
(1)
a22
(1)
Из третьего уравнения системы (3) вычтем уравнение (4), умноженное на
Получим уравнение:
Предполагая, что
a33
( 2)
x3
b3
( 2)
находим
a33
( 2)
0,
x3
b3
( 2)
a33
( 2)
b3
3
(1)
a33 .
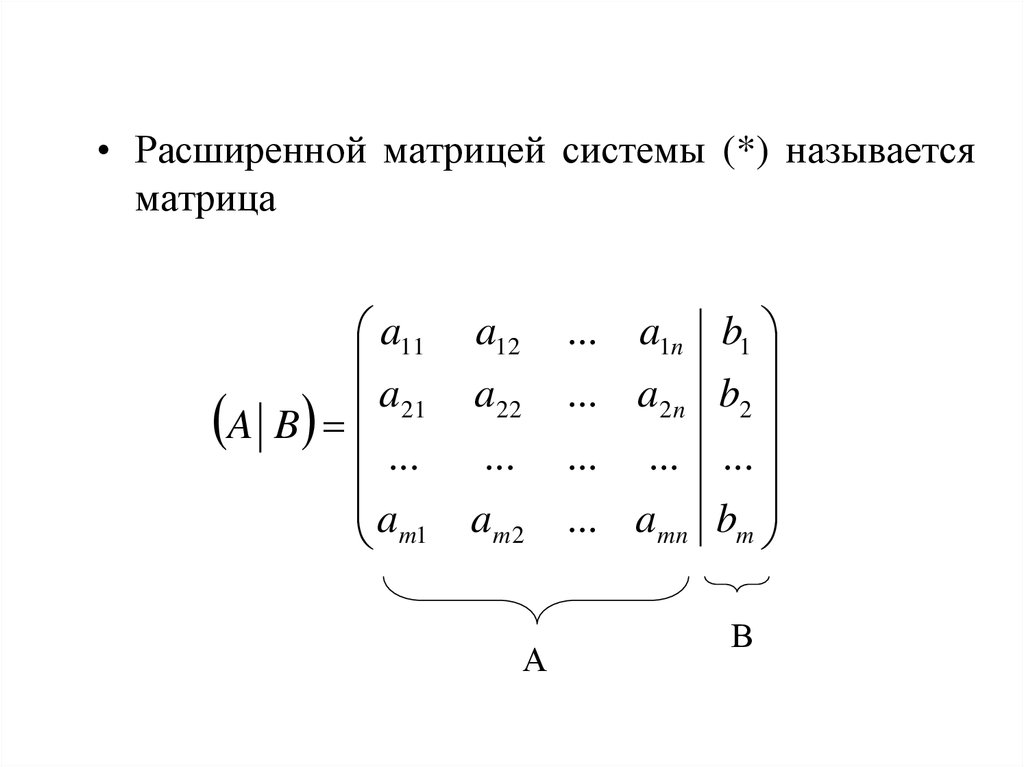
В результате преобразований система приняла вид:
x1 a12 (1) x 2 a13 (1) x3 b1 (1)
( 2)
( 2)
x 2 a 23 x3 b2
( 3)
x3 b3
(5)
Система вида (5) называется треугольной.
Процесс приведения системы (1) к треугольному виду (5)
(шаги 1 и 2) называют прямым ходом метода Гаусса.
Нахождение неизвестных из треугольной системы
называют обратным ходом метода Гаусса.
Для этого найденное значение х3 подставляют во второе
уравнение системы (5) и находят х2. Затем х2 и х3
подставляют в первое уравнение и находят х1.
Если в ходе преобразований системы получается противоречивое
уравнение вида 0 = b, где b 0, то это означает, что система несовместна и
решений не имеет.
В случае совместной системы после преобразований по методу Гаусса,
составляющих прямой ход метода, система т линейных уравнений с п
неизвестными будет приведена или к треугольному или к ступенчатому виду.
Треугольная система имеет вид:
Такая система имеет единственное
решение, которое находится в
x1 c12 x 2 . .. a1n x n d1
x 2 … a 2 n x n d 2
…………….
xn d n
результате проведения обратного хода метода Гаусса.
Ступенчатая система имеет вид:
Такая система имеет бесчисленное
множество решений.
x1 c12 x2 … c1n xn d1
x2 … c2 n xn d 2
…………………
xk … ck n xn d k

11. Рассмотрим на примере

1.
Покажем последовательность решения системы из трех уравнений методом Гаусса
Поделим первое уравнение на 2, затем вычтем его из второго (a21=1, поэтому
домножение не требуется) и из третьего, умножив предварительно на a31=3
2.
Поделим второе уравнение полученной системы на 2, а затем вычтем его из
третьего, умножив предварительно на 4,5 (коэффициент при x2)
3.
x3=-42/(-14)=3;
Тогда
x2=8-2×3=2
x1=8-0,5×2-2×3=1

12. Метод Крамера

Метод Крамера—способ решения квадратных
систем линейных алгебраических уравнений с
ненулевым определителем основной матрицы.
Создан Габриэлем Крамером в 1751 году.

13. Габриэль Крамер (31 июля 1704, Женева, Швейцария—4 января 1752, Баньоль-сюр-Сез, Франция)

14. Рассмотрим систему линейных уравнений с квадратной матрицей A , т.е. такую, у которой число уравнений совпадает с числом неизвестных:

Теорема. Cистема
a11x1+a12x2+…+a1nxn=b1
a21x1+a22x2+…+a2nxn=b2
…
…
an1x1+an2x2+…+annxn=bn

15. Имеет единственное решение тогда и только тогда, когда определитель матрицы этой системы отличен от нуля:

a11 a12 … a1n
a21 a22 … a2n
…
…
an1 an2 … ann
≠0

16. В этом случае решение можно вычислить по формуле Крамера

17. Для получения значения xk в числитель ставится определитель, получающийся из det(A) заменой его k-го столбца на столбец правых частей

Пример. Решить систему уравнений :

18. Решение.

19. Найдите оставшиеся компоненты решения.

Формулы Крамера не представляют практического значения в
случае систем с числовыми коэффициентами: вычислять по
ним решения конкретных систем линейных уравнений
неэффективно, поскольку они требуют вычисления (n+1)-го
определителя порядка n , в то время как метод Гаусса
фактически эквивалентен вычислению одного определителя
порядка n . Тем не менее, теоретическое значение формул
Крамера заключается в том, что они дают явное
представление решения системы через ее коэффициенты.
Например, с их помощью легко может быть доказан результат
Решение системы линейных уравнений с квадратной
матрицей A является непрерывной функцией коэффициентов
этой системы при условии, что det A не равно 0 .

20. Найдите оставшиеся компоненты решения.

Кроме того, формулы Крамера начинают конкурировать по вычислительной
эффективности с методом Гаусса в случае систем, зависящих от параметра.
зависящей от параметра
решения:
, определить предел отношения компонент

21. Решение.

В этом примере определитель матрицы
системы равен
. По теореме Крамера
система совместна при
. Для случая
применением метода Гаусса убеждаемся,
что система несовместна. Тем не менее,
указанный предел существует. Формулы
Крамера дают значения компонент решения
в виде
и, хотя при
каждая из них имеет бесконечный предел, их
отношение стремится к пределу конечному.

22. Ответ.

Приведенный пример поясняет также каким образом система линейных
уравнений, непрерывно зависящая от параметра, становится
несовместной: при стремлении параметра к какому-то критическому
значению (обращающему в нуль определитель матрицы системы) хотя
бы одна из компонент решения «уходит на бесконечность».

23. Использованные источники

1.
В.С. Щипачев, Высшая математика
2.
Ильин В. А., Позняк Э. Г. Линейная
алгебра: Учебник для вузов.
3.
Волков Е.А. Численные методы.
4.
В.Е. Шнейдер и др., Краткий курс
высшей математики,том I.

English     Русский Правила

Калькулятор исключения Гаусса

Выберите порядок матрицы, заполните необходимые поля ввода и нажмите кнопку расчета с помощью калькулятора исключения Гаусса.

Содержание:

  • Калькулятор исключения Гаусса
  • Как выполнить исключение Гаусса?

Дайте нам отзыв

✎

✉

Калькулятор исключения Гаусса 

Калькулятор исключения Гаусса приводит матрицу, образованную системой уравнений, к ее упрощенной форме. Найдите другую информацию и значения, связанные с матрицей, такие как:

  • Матрица, обратная 
  • Определитель
  • Собственные значения
  • Свойства, трассировка и т. д.

    Что такое исключение Гаусса?

    Этот метод назван в честь Карла Фридриха Гаусса. Он использует метод эшелона строк для достижения желаемой формы матрицы. Затем значения переменных математического уравнения легко вычисляются из результирующей матрицы.

    Используется расширенная матрица.

    Как выполнить исключение Гаусса?

    Операции со строками используются в матрице, чтобы сделать диагональные элементы равными 1 с нулями под ними. Далее он используется, чтобы сделать матрицу диагональной матрицей. Таким образом, значения распознаются из самой сокращенной матрицы.

    Прежде всего, вы должны составить уравнение таким образом, чтобы все одинаковые переменные выровнялись по столбцам. Если одно из уравнений не содержит никакой переменной, то вместо нее в матрице ставится 0.

    Давайте посмотрим на пример использования этого метода.

    Пример:

    Найдите значения переменных, используемых в следующих уравнениях, с помощью метода исключения Гаусса-Жордана.

    1x + 1y + 2z = 9

    2x + 4y — 3z = 1

    3x + 6y — 5z = 0

    Решение:

    Шаг 1: .

    3x + 8y — 7 = 0

    6x + 3y — 3 = 0

    9x + 4y — 4 = 0

    Шаг 2: Создайте расширенную матрицу.

    Шаг 3: Выполнить эшелонирование строк.


     
    Вычесть из строки 2 первую строку, умноженную на 2: R 2 = R 2 — 2R 1

     
    Вычесть первую строку, умноженную на 3 из строки 0: R 90 9 0 9 0 8: 3 — 3R 1

    Разделить 1-й ряд на 2: R 2 = R 2 /2

    Из 3-го ряда вычесть 2-й ряд, умноженный на 3: R 3 = R 3 — 3R 2
     
    Умножьте строку 3 на -2: R 3 = -2 R 3
     
    Это конец метода исключения Гаусса. Значения переменных можно легко вычислить по этой матрице. Первый столбец представляет x, второй — y, а третий — переменную z.
     
    В третьей строке только z. Это означает, что z=3. Поместите это во вторую строку, чтобы вычислить y, а затем в первую строку, чтобы найти x.
    Эту матрицу можно еще больше упростить, используя метод Гаусса-Жордана. Для этого:
     
    Добавить строку 3, умноженную на 7/3, к строке 2: 7/3R 3 + R 2

    Вычесть строку 3, умноженную на -2, из строки 1: R 1 = R 1 -2R 3

    Вычесть строку 2 из строки 1: R 1 = R 1 — R2 

    В этой матрице нахождение значений переменных — это вопрос поиска. г=3, у=2 и х=1.

    Исключение Гаусса для плотных матриц: алгебраическая проблема | Прямые методы для разреженных матриц

    Фильтр поиска панели навигации Oxford AcademicDirect Methods for Sparse Matrices (2nd edn)Численный анализOxford Scholarship OnlineBooksJournals Мобильный телефон Введите поисковый запрос

    Закрыть

    Фильтр поиска панели навигации Oxford AcademicDirect Methods for Sparse Matrices (2nd edn)Численный анализOxford Scholarship OnlineBooksJournals Введите поисковый запрос

    Расширенный поиск

    • Иконка Цитировать Цитировать

    • Разрешения

    • Делиться
      • Твиттер
      • Подробнее

    Укажите

    Дафф, И. С., А. М. Эрисман и Дж. К. Рид, «Исключение Гаусса для плотных матриц: алгебраическая проблема», Direct Methods for Sparse Matrices , 2-е изд. (

    Oxford

    , 2017; онлайн-издание, Oxford Academic, 20 апреля 2017 г. ), https://doi.org/10.1093/acprof:oso/9780198508380.003.0003, по состоянию на 22 апреля 2023 г.

    Выберите формат Выберите format.ris (Mendeley, Papers, Zotero).enw (EndNote).bibtex (BibTex).txt (Medlars, RefWorks)

    Закрыть

    Фильтр поиска панели навигации Oxford AcademicDirect Methods for Sparse Matrices (2nd edn)Численный анализOxford Scholarship OnlineBooksJournals Мобильный телефон Введите поисковый запрос

    Закрыть

    Фильтр поиска панели навигации Oxford AcademicDirect Methods for Sparse Matrices (2nd edn)Численный анализOxford Scholarship OnlineBooksJournals Введите поисковый запрос

    Advanced Search

    Abstract

    Мы рассматриваем основные операции прямого решения линейных уравнений, не обращая внимания на ошибку округления, вызванную компьютерной арифметикой.

    Мы рассматриваем связь между исключением Гаусса и LU-факторизацией. Мы сравниваем использование различных вычислительных последовательностей, включая левый и правый взгляды. Мы показываем, что преимуществом симметрии можно воспользоваться, и рассматриваем использование блокировки. Наш выбор материала основан на том, что будет полезно в разреженном случае.

    Ключевые слова: Исключение Гаусса, LU-факторизация, левосторонний, правосторонний, симметричный, блокирующий

    Субъект

    Численный анализ

    Коллекция: Оксфордская стипендия онлайн

    В настоящее время у вас нет доступа к этой главе.

    Войти

    Получить помощь с доступом

    Получить помощь с доступом

    Доступ для учреждений

    Доступ к контенту в Oxford Academic часто предоставляется посредством институциональных подписок и покупок. Если вы являетесь членом учреждения с активной учетной записью, вы можете получить доступ к контенту одним из следующих способов:

    Доступ на основе IP

    Как правило, доступ предоставляется через институциональную сеть к диапазону IP-адресов. Эта аутентификация происходит автоматически, и невозможно выйти из учетной записи с IP-аутентификацией.

    Войдите через свое учреждение

    Выберите этот вариант, чтобы получить удаленный доступ за пределами вашего учреждения. Технология Shibboleth/Open Athens используется для обеспечения единого входа между веб-сайтом вашего учебного заведения и Oxford Academic.

    1. Щелкните Войти через свое учреждение.
    2. Выберите свое учреждение из предоставленного списка, после чего вы перейдете на веб-сайт вашего учреждения для входа.
    3. Находясь на сайте учреждения, используйте учетные данные, предоставленные вашим учреждением. Не используйте личную учетную запись Oxford Academic.
    4. После успешного входа вы вернетесь в Oxford Academic.

    Если вашего учреждения нет в списке или вы не можете войти на веб-сайт своего учреждения, обратитесь к своему библиотекарю или администратору.

    Войти с помощью читательского билета

    Введите номер своего читательского билета, чтобы войти в систему. Если вы не можете войти в систему, обратитесь к своему библиотекарю.

    Члены общества

    Доступ члена общества к журналу достигается одним из следующих способов:

    Войти через сайт сообщества

    Многие общества предлагают единый вход между веб-сайтом общества и Oxford Academic. Если вы видите «Войти через сайт сообщества» на панели входа в журнале:

    1. Щелкните Войти через сайт сообщества.
    2. При посещении сайта общества используйте учетные данные, предоставленные этим обществом. Не используйте личную учетную запись Oxford Academic.
    3. После успешного входа вы вернетесь в Oxford Academic.

    Если у вас нет учетной записи сообщества или вы забыли свое имя пользователя или пароль, обратитесь в свое общество.

    Вход через личный кабинет

    Некоторые общества используют личные аккаунты Oxford Academic для предоставления доступа своим членам. См. ниже.

    Личный кабинет

    Личную учетную запись можно использовать для получения оповещений по электронной почте, сохранения результатов поиска, покупки контента и активации подписок.

    Некоторые общества используют личные аккаунты Oxford Academic для предоставления доступа своим членам.

    Просмотр учетных записей, вошедших в систему

    Щелкните значок учетной записи в правом верхнем углу, чтобы:

    • Просмотр вашей личной учетной записи и доступ к функциям управления учетной записью.

      No related posts.

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *