Методы оптимальных решений задачи с решениями и ответами: Методы оптимальных решений для чайников

Содержание

Решение задач линейного программирования, теории игр и других экономико-математических методов и моделей. Методы оптимальных решений

В этом разделе разобраны типовые задачи методов оптимальных решений. Подробным образом рассматриваются задачи линейного программирования (графический и симплексный методы), транспортная задача. Перед примерами некоторых задач кратко изложены основные теоретические сведения. Данный материал может быть полезен студентам экономических специальностей.

О платной помощи студентам с учебой можно почитать на странице Как заказать решение задач по методам оптимальных решений…

Подробно рассмотрено понятие линейного программирования, даны описания форм записи задач линейного программирования, приведены примеры задач линейного программирования.

Рассмотрен графический метод решения задачи линейного программирования (ЗЛП) с двумя переменными. На примере задачи приведено подробное описание построения чертежа и нахождения решения.

Разобран метод искусственного базиса, применяемый для решения задач линейного программирования. Приведена краткая теория и, в качестве примеров, решены две задачи.

Содержит описание пары взаимно двойственных задач линейного программирования. Приведено правило построения двойственной задачи, сформулированы теоремы двойственности и на конкретных примерах рассмотрено их практическое применение при решении задач линейного программирования.

Подробно рассмотрена транспортная задача, ее математическая модель и методы решения — нахождение опорного плана методом минимального элемента и поиск оптимального решения методом потенциалов.

На конкретных примерах разобраны методы нахождения опорного плана транспортной задачи — северо-западного угла, минимального элемента, Фогеля и двойного предпочтения.

На примере решения задач целочисленного программирования иллюстрируется метод ветвей и границ. Наряду с разобранными задачами, на странице приведены краткие теоретические сведения по данной теме.

На примере решения задачи целочисленного программирования иллюстрируется метод Гомори. Приведены краткие теоретические сведения по данной теме.

На странице даются основные понятия теории игр — платежной матрицы, стратегии игроков, седловой точки, нижней и верхней цены игры. Приведена краткая теория и решены несколько простых задач на тему основных понятий матричных игр.

Содержит изложенные в краткой и доступной форме теоретические сведения о матричной игре без седловой точки и способе сведения такой задачи к задаче линейного программирования, для отыскания ее решения в смешанных стратегиях. Приведен пример решения задачи.

Рассмотрено решение статистической матричной игры в условиях неопределенности с помощью критериев Вальда, Сэвиджа, Гурвица, Лапласа, Байеса. На примере задачи подробно показано построение платежной матрицы и матрицы рисков.

На странице рассмотрено нахождение условного экстремума методом множителей Лагранжа. Показано построение функции Лагранжа на примере решения задачи нелинейного программирования. Решенную задачу предваряет краткая теория.

Приведен образец решения задачи квадратичного выпуклого программирования графическим методом.

Кратко изложены основные принципы динамического программирования (динамического планирования), рассмотрены уравнения Беллмана. Подробно решена задача оптимального распределения ресурсов между предприятиями.

Приведены необходимые теоретические сведения, в частности формулы Эрланга, а также образец решения задачи по теме «Многоканальная система массового обслуживания с отказами». Подробно рассмотрены показатели многоканальной системы массового обслуживания (СМО) с отказами — вероятность отказа и вероятность обслуживания, абсолютная пропускная способность системы и среднее число каналов, занятых обслуживанием заявки.

Приведены необходимые теоретические сведения и образец решения задачи по теме «Многоканальная система массового обслуживания с неограниченной очередью», подробно рассмотрены показатели многоканальной системы массового обслуживания (СМО) с ожиданием обслуживания — среднее число каналов, занятых обслуживанием заявки, длина очереди, вероятность образования очереди, вероятность свободного состояния системы, среднее время ожидания в очереди.

На примере решения задачи рассмотрена основная модель управления запасами (модель Уилсона). Вычислены такие показатели модели как оптимальный размер партии заказа, годовые затраты на хранение, интервал между поставками и точка размещения заказа.

На примере решения задачи рассмотрена межотраслевая модель Леонтьева. Показано вычисление матрицы коэффициентов прямых материальных затрат, матрицы «затраты-выпуск», матрицы коэффициентов косвенных затрат, векторов конечного потребления и валового выпуска.

Методы оптимальных решений Тесты с ответами ИММиФ Тема 4-5

Главная » База вопросов » ИММиФ

Для быстрого поиска по странице нажмите Ctrl+F и в появившемся окошке напечатайте слово запроса (или первые буквы)

Тема 4

Если число ресурсов, которые распределяются по работам равно числу работ и один ресурс назначаются только на одну работу, то задача линейного программирования, к которой сводится задача имеет основные ограничения…

+Все ограничения равенства

Все ограничения неравенства вида ≤

Все ограничения неравенства вида ≥

Ограничения могут быть как равенства, так и неравенства

Матрица эффективности задачи о назначениях при максимизации критерия имеет вид:

Какую матрицу нужно взять за исходную при решении задачи Венгерским методом?

Задача о назначениях с минимизацией критерия имеет матрицу затрат вида:

D E F

А 6 3 4

В 2 8 5

С 1 7 9

Ее решение будет:

+A-E, B-F, C-D

A-D, B-F, C-E

A-F, B-D, C-E

A-F, B-E, C-D

Суммарные затраты для предыдущей задачи равны…

Выберите один ответ.

Какие компьютерные программы предназначены для помощи ЛПР в решении многокритериальных задач о назначении?

Системы управления базами данных

+Интеллектуальные информационные системы

Коммуникационные системы

Системы программирования

Тема 5

В выборах участвуют 3 кандидата: А, В и С. Предпочтения 30 избирателей распределились следующим образом:

или напишите нам прямо сейчас

Написать в WhatsApp

Предпочтения Число голосов Предпочтение Число голосов

А→В→С 6 В→С→А 4

А→С→В 5 С→А→В 4

В→А→С 6 С→В→А 5

Кто победил по методу голосования Кондорсе?

Победил А

Победил В

Победил С

+Однозначно выявить победителя нельзя

Исходные данные о выборах приведены в задании 1.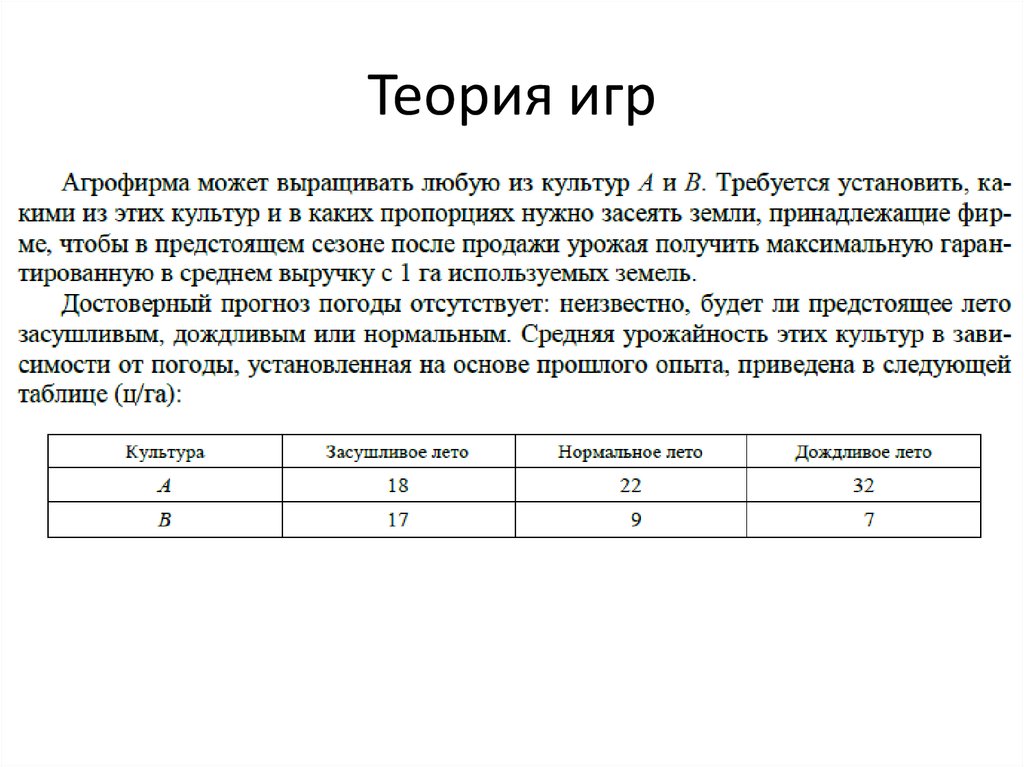 Кто победил по методу голосования Борда?

+Победил А

Победил В

Победил С

Однозначно выявить победителя нельзя

Исходные данные о выборах приведены в задании 1. Кто победил по методу большинства первых мест в одном туре?

+Победил А

Победил В

Победил С

Однозначно выявить победителя нельзя

Как называется принцип голосования «коллективный выбор в системе голосования должен повторять в точности единогласное мнение всех голосующих»?

Аксиома универсальности

+Аксиома единогласия

Аксиома полноты

Аксиома транзитивности

Из двух кандидатов каждый избиратель выбирает лучшего. Побеждает тот, который будет большее число раз выбран лучшим. Какая аксиома Эрроу не может быть проверена в данной системе голосования?

Аксиома универсальности

Аксиома единогласия

Аксиома полноты

Аксиома транзитивности

Несколько конкурентов, выпускающих аналогичный товар, пытаются договориться о объемах выпускаемого товара. Каждый производитель хочет увеличить свой объем выпуска за счет уменьшения выпуска у конкурентов. Какую математическую модель принятия решений целесообразно здесь использовать.

Организацию работы ГПР с помощью посредника

+Теорию игр

Принятие решений в условиях определенности

Метод голосования

Какой этап организации работы ГПР нужно выполнить в первую очередь?

Сбор информации

Разработка шкал оценки по критериям

+Определение списка критериев

Анализ информации

или напишите нам прямо сейчас

Написать в WhatsApp

4.2: Максимизация Симплекс-методом

Последнее обновление
Сохранить как PDF

Идентификатор страницы: 37869

Рупиндер Секон и Роберта Блум
Колледж Де Анза

Цели обучения

В этом разделе вы научитесь решать задачи максимизации линейного программирования с использованием симплекс-метода:

Определить и настроить линейную программу в стандартной форме максимизации
Преобразование ограничений неравенства в уравнения с использованием резервных переменных
Настройте начальную симплексную таблицу, используя целевую функцию и уравнения резерва
Найдите оптимальную симплексную таблицу, выполнив операции поворота.
Определите оптимальное решение по оптимальной симплексной таблице.

В предыдущей главе мы использовали геометрический метод для решения задач линейного программирования, но геометрический подход не работает для задач с более чем двумя переменными. В реальных жизненных ситуациях задачи линейного программирования состоят буквально из тысяч переменных и решаются компьютерами. Мы можем решить эти проблемы алгебраически, но это будет не очень эффективно. Предположим, нам дали задачу, скажем, с 5 переменными и 10 ограничениями. Выбрав все комбинации из пяти уравнений с пятью неизвестными, мы могли бы найти все угловые точки, проверить их на допустимость и найти решение, если оно существует. Но беда в том, что даже для задачи с таким небольшим количеством переменных мы получим более 250 угловых точек, и проверка каждой точки будет очень утомительна. Поэтому нам нужен метод, который имеет систематический алгоритм и может быть запрограммирован для компьютера. Метод должен быть достаточно эффективным, чтобы нам не пришлось оценивать целевую функцию в каждой угловой точке. У нас есть именно такой метод, и он называется симплексный метод .

Симплекс-метод был разработан во время Второй мировой войны доктором Джорджем Данцигом. Его модели линейного программирования помогли союзным войскам решить проблемы с транспортом и планированием. В 1979 году советский ученый Леонид Хачян разработал метод, названный алгоритмом эллипсоида, который должен был стать революционным, но, как оказалось, ничем не лучше симплексного метода. В 1984 году Нарендра Кармаркар, научный сотрудник AT&T Bell Laboratories, разработал алгоритм Кармаркара, который, как было доказано, в четыре раза быстрее, чем симплекс-метод для определенных задач. Но симплекс-метод по-прежнему работает лучше всего для большинства задач.

В симплексном методе используется очень эффективный подход. Он не вычисляет значение целевой функции в каждой точке; вместо этого он начинается с угловой точки области выполнимости, где все основные переменные равны нулю, а затем систематически перемещается от угловой точки к угловой точке, улучшая значение целевой функции на каждом этапе. Процесс продолжается до тех пор, пока не будет найдено оптимальное решение.

Чтобы изучить симплекс-метод, мы попробуем довольно нетрадиционный подход. Сначала мы перечисляем алгоритм, а затем работаем над проблемой. Мы обосновываем обоснование каждого шага в процессе. Тщательное обоснование выходит за рамки данного курса.

Начнем с примера, который мы решили в предыдущей главе графическим методом. Это даст нам некоторое представление о симплекс-методе и в то же время даст нам возможность сравнить несколько допустимых решений, которые мы получили ранее с помощью графического метода. Но сначала приведем алгоритм симплекс-метода.

СИМПЛЕКСНЫЙ МЕТОД

Поставьте задачу. То есть запишите целевую функцию и ограничения неравенства.
Преобразуйте неравенства в уравнения. Это делается путем добавления одной резервной переменной для каждого неравенства.
Построить начальную симплексную таблицу. Запишите целевую функцию в нижней строке.
Самая отрицательная запись в нижней строке идентифицирует сводной столбец.
Вычислите частные. Наименьшее частное определяет строку. Элемент на пересечении столбца, определенного на шаге 4, и строки, определенной на этом шаге, идентифицируется как опорный элемент. Частные вычисляются путем деления крайнего правого столбца на столбец, указанный в шаге 4. Частное, являющееся нулем, отрицательным числом или имеющим ноль в знаменателе, игнорируется.
Выполните поворот, чтобы обнулить все остальные записи в этом столбце. Это делается так же, как и с методом Гаусса-Джордана.
Когда в нижней строке больше нет отрицательных значений, мы закончили; в противном случае начинаем снова с шага 4.
Прочитайте свои ответы. Получить переменные, используя столбцы с 1 и 0. Все остальные переменные равны нулю. Максимальное значение, которое вы ищете, отображается в правом нижнем углу.

Теперь мы используем симплекс-метод для решения примера 3. 1.1, решенного геометрически в разделе 3.1.

Пример $\PageIndex{1}$

Ники работает на двух работах с частичной занятостью: работа I и работа II. Она никогда не хочет работать больше, чем в общей сложности 12 часов в неделю. Она определила, что на каждый час работы на Работе I ей нужно 2 часа времени на подготовку, а на каждый час работы на Работе II ей нужен один час времени на подготовку, и она не может тратить на подготовку более 16 часов. Если она зарабатывает 40 долларов в час на работе I и 30 долларов в час на работе II, сколько часов в неделю она должна работать на каждой работе, чтобы максимизировать свой доход?

Решение

При решении этой задачи будем следовать алгоритму, указанному выше.

ШАГ 1. Поставьте задачу. Запишите целевую функцию и ограничения.

Поскольку симплекс-метод используется для задач, состоящих из многих переменных, нецелесообразно использовать переменные $x$, $y$, $z$ и т. д. Мы используем символы $x_1\ ), \(x_2$, $x_3$ и так далее.

Let

$x_1$ = количество часов в неделю, которое Ники будет работать на работе I и 9.0010
$x_2$ = количество часов в неделю, которое Ники будет работать на задании II.

Принято выбирать переменную, которая должна быть максимизирована как $Z$.

Задача формулируется так же, как и в предыдущей главе.

\[\begin{array}{ll}
\textbf { Развернуть} & \mathrm{Z}=40 \mathrm{x}_{1}+30 \mathrm{x}_{2} \\
\ textbf { При условии: } & \mathrm{x}_{1}+\mathrm{x}_{2} \leq 12 \\
& 2 \mathrm{x}_{1}+\mathrm{x}_ {2} \leq 16 \\
& \mathrm{x}_{1} \geq 0 ; \mathrm{x}_{2} \geq 0
\end{array}\nonumber \]

ШАГ 2. Преобразовать неравенства в уравнения. Это делается путем добавления одной резервной переменной для каждого неравенства.

Например, чтобы преобразовать неравенство $x_1 + x_2 ≤ 12$ в уравнение, мы добавляем неотрицательную переменную $y_1$, и мы получаем

\[x_1 + x_2 + y_1 = 12 \nonumber \]

Здесь переменная $y_1$ восполняет пробел и представляет величину, на которую $x_1 + x_2$ меньше 12. В этой задаче, если Ники работает менее 12 часов, скажем, 10 , тогда $y_1$ равно 2. Позже, когда мы прочитаем окончательное решение из симплексной таблицы, значения резервных переменных будут определять неиспользованные суммы.

Перепишем целевую функцию $Z = 40x_1 + 30x_2$ в виде $- 40x_1 — 30x_2 + Z = 0$.

После добавления резервных переменных наша задача выглядит следующим образом:

\[\begin{array}{ll}
\text { Целевая функция } & — 40x_1 — 30x_2 + Z = 0 \\
\text { С учетом ограничений: } &x_1+x_2+y_1=12\
&2x_1+x_2+y_2=16\
&x1 ≥ 0; x2 ≥ 0
\end{array} \nonumber \]

ШАГ 3. Построить исходную симплексную таблицу . Каждое ограничение неравенства отображается в отдельной строке. (Ограничения неотрицательности заставляют , а не появляться в виде строк в симплексной таблице.) Запишите целевую функцию в нижней строке.

Теперь, когда неравенства преобразованы в уравнения, мы можем представить задачу в виде расширенной матрицы, называемой исходной симплексной таблицей, следующим образом.

Здесь вертикальная линия отделяет левую часть уравнений от правой. Горизонтальная линия отделяет ограничения от целевой функции. Правая часть уравнения представлена столбцом C.

Читатель должен заметить, что последние четыре столбца этой матрицы выглядят как окончательная матрица для решения системы уравнений. Если мы произвольно выберем $x_1 = 0$ и $x_2 = 0$, мы получим

\[\left[\begin{array}{ccccc}
y_{1} & y_{2} & Z & | &С\
1&0&0 & | & 12 \
0 & 1 & 0 & | & 16 \\
0 & 0 & 1 & | & 0
\end{массив}\right]\nonumber \]

, что читается как

\[y_1 = 12 \quad y_2 = 16 \quad Z = 0 \nonumber \]

Решение, полученное путем произвольного присвоения значений некоторым переменным и последующего решения для оставшихся переменных, называется базовым решением , связанным с таблицей . Таким образом, приведенное выше решение является основным решением, связанным с исходной симплексной таблицей. Мы можем пометить базовую переменную решения справа от последнего столбца, как показано в таблице ниже.

ШАГ 4. Самая отрицательная запись в нижней строке идентифицирует сводной столбец.

Самая отрицательная запись в нижней строке -40; поэтому столбец 1 идентифицируется.

Вопрос Почему мы выбираем самую отрицательную запись в нижней строке?

Ответ Самая отрицательная запись в нижней строке представляет наибольший коэффициент в целевой функции — коэффициент, ввод которого увеличит значение целевой функции быстрее всего.

Симплекс-метод начинается с угловой точки, где все основные переменные, переменные с такими символами, как $x_1$, $x_2$, $x_3$ и т. д., равны нулю. Затем он перемещается от угловой точки к соседней угловой точке, всегда увеличивая значение целевой функции. В случае целевой функции $Z = 40x_1+ 30x_2$ имеет смысл увеличить значение $x_1$, а не $x_2$. Переменная $x_1$ представляет количество часов в неделю, которые Ники работает на работе I. Поскольку работа I оплачивается 40 долларов в час, в отличие от работы II, на которой платят всего 30 долларов, переменная $x_1$ увеличит целевую функцию на $40 за единицу увеличения переменной $x_1$.

ШАГ 5. Вычислите частные. Наименьшее частное определяет строку. Элемент на пересечении столбца, определенного на шаге 4, и строки, определенной на этом шаге, идентифицируется как опорный элемент.

Следуя алгоритму, для вычисления частного делим записи в крайнем правом столбце на записи в столбце 1, исключая запись в нижней строке.

Наименьшее из двух частных, 12 и 8, равно 8. Следовательно, идентифицируется строка 2. Пересечение столбца 1 и строки 2 является записью 2, которая выделена. Это наш опорный элемент.

Вопрос Почему мы находим частное и почему наименьшее частное определяет строку?

Ответ Когда мы выбираем самую отрицательную запись в нижней строке, мы пытаемся увеличить значение целевой функции, вводя переменную $x_1$. Но мы не можем выбрать любое значение для $x_1$. Можем ли мы позволить $x_1 = 100$? Точно нет! Это потому, что Ники никогда не хочет работать более 12 часов на обеих работах вместе взятых: $x_1 + x_2 ≤ 12$. Можем ли мы позволить $x_1 = 12$? Опять же, ответ отрицательный, потому что время подготовки к работе I в два раза превышает время, затрачиваемое на работу. Поскольку Ники никогда не хочет тратить на подготовку более 16 часов, максимальное время, которое она может работать, составляет 16 ÷ 2 = 8.9.0034

Теперь вы видите цель вычисления частных; использование частных для определения опорного элемента гарантирует, что мы не нарушаем ограничения.

Вопрос Почему мы идентифицируем поворотный элемент?

Ответ Как мы упоминали ранее, симплекс-метод начинается с угловой точки, а затем переходит к следующей угловой точке, всегда улучшая значение целевой функции. Значение целевой функции улучшается за счет изменения количества единиц переменных. Мы можем добавить количество единиц одной переменной, отбросив единицы другой. Поворот позволяет нам сделать именно это.

Переменная, единицы которой добавляются, называется входной переменной , , а переменная, единицы которой заменяются, называется исходящей переменной . Входной переменной в приведенной выше таблице является $x_1$, и она определяется самой отрицательной записью в нижней строке. Уходящая переменная $y_2$ была идентифицирована наименьшим из всех частных.

ШАГ 6. Выполните поворот, чтобы обнулить все остальные записи в этом столбце.

В главе 2 мы использовали поворот, чтобы получить эшелонированную форму строк расширенной матрицы. Поворот — это процесс получения 1 в местоположении поворотного элемента, а затем обнуления всех остальных записей в этом столбце. Итак, теперь наша задача состоит в том, чтобы сделать наш опорный элемент равным 1, разделив всю вторую строку на 2. Далее следует результат.

Чтобы получить ноль в записи первой над опорным элементом, умножаем вторую строку на -1 и прибавляем к строке 1. Получаем

Чтобы получить ноль в элементе ниже стержня, умножаем вторую строку на 40 и прибавляем к последней строке.

Теперь мы определяем основное решение, связанное с этой таблицей. Произвольно выбирая $x_2 = 0$ и $y_2 = 0$, мы получаем $x_1 = 8$, $y_1 = 4$ и $z = 320$. Если мы напишем расширенную матрицу, левая часть которой представляет собой матрицу со столбцами, в которых одна единица, а все остальные элементы равны нулю, мы получим следующую матрицу, утверждающую то же самое.

\[\left[\begin{array}{ccccc}
\mathrm{x}_{1} & \mathrm{y}_1 & \mathrm{Z} & | & \mathrm{C} \\
0 & 1 & 0 & | & 4 \
1 & 0 & 0 & | & 8 \
0 & 0 & 1 & | & 320
\end{array}\right] \nonumber \]

Мы можем переформулировать решение, связанное с этой матрицей, как $x_1 = 8$, $x_2 = 0$, $y_1 = 4$ , $y_2 = 0$ и $z = 320$. На этом этапе игры написано, что если Ники проработает 8 часов на работе I и ни одного часа на работе II, ее прибыль Z составит 320 долларов. Напомним из примера 3.1.1 в разделе 3.1, что (8, 0) была одной из наших угловых точек. Здесь $y_1 = 4$ и $y_2 = 0$ означают, что у нее останется 4 часа рабочего времени и никакого времени на подготовку.

ШАГ 7. Когда в нижней строке больше нет отрицательных значений, мы закончили; в противном случае мы начинаем снова с шага 4.

Поскольку в нижней строке все еще есть отрицательная запись, -10, нам нужно снова начать с шага 4. На этот раз мы не будем повторять детали каждого шага. , вместо этого мы укажем столбец и строку, которые дают нам опорный элемент, и выделим опорный элемент. Результат следующий.

Делаем опорный элемент 1, умножая строку 1 на 2, и получаем

Теперь, чтобы все остальные записи в этом столбце были равны нулю, мы сначала умножаем строку 1 на -1/2 и прибавляем к строке 2, а затем умножаем строку 1 на 10 и прибавляем к нижней строке.

У нас больше нет отрицательных записей в нижней строке, поэтому мы закончили.

Вопрос Почему мы закончили, если в нижней строке нет отрицательных значений?

Ответ Ответ лежит в нижней строке. Нижняя строка соответствует уравнению:

\[\begin{array}{l}
0 x_{1}+0 x_{2}+20 y_{1}+10 y_{2}+Z=400 \quad \text { or } \\
z=400-20 y 1-10 y 2
\end{array}\nonumber \]

Поскольку все переменные неотрицательны, максимальное значение $Z$ может быть равно 400, и это произойдет только когда $y_1$ и $y_2$ равны нулю.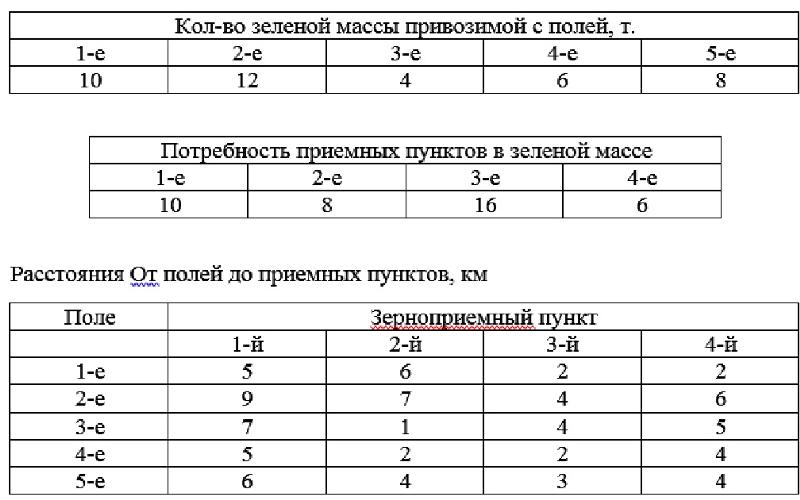

ШАГ 8. Прочитайте ваши ответы.

Теперь мы читаем наши ответы, то есть мы определяем базовое решение, связанное с окончательной симплексной таблицей. Опять же, мы смотрим на столбцы, в которых есть 1, а все остальные записи — нули. Поскольку столбцы с метками $y_1$ и $y_2$ не являются такими столбцами, мы произвольно выбираем $y_1 = 0$ и $y_2 = 0$, и мы получаем

\[\left[\begin{array}{ccccc}
\mathrm{x}_{1} & \mathrm{x}_{2} & \mathrm{Z} & | & \mathrm{C} \\
0 & 1 & 0 & | & 8 \\
1 & 0 & 0 & | & 4 \
0 & 0 & 1 & | & 400
\end{массив}\right] \nonumber \]

Матрица читается как $x_1 = 4$, $x_2= 8$ и $z = 400$.

Окончательное решение гласит, что если Ники будет работать 4 часа на работе I и 8 часов на работе II, она максимизирует свой доход до 400 долларов. Поскольку обе переменные slack равны нулю, значит, она израсходовала бы все рабочее время, а также время на подготовку, и ничего не останется.

Эта страница под названием 4.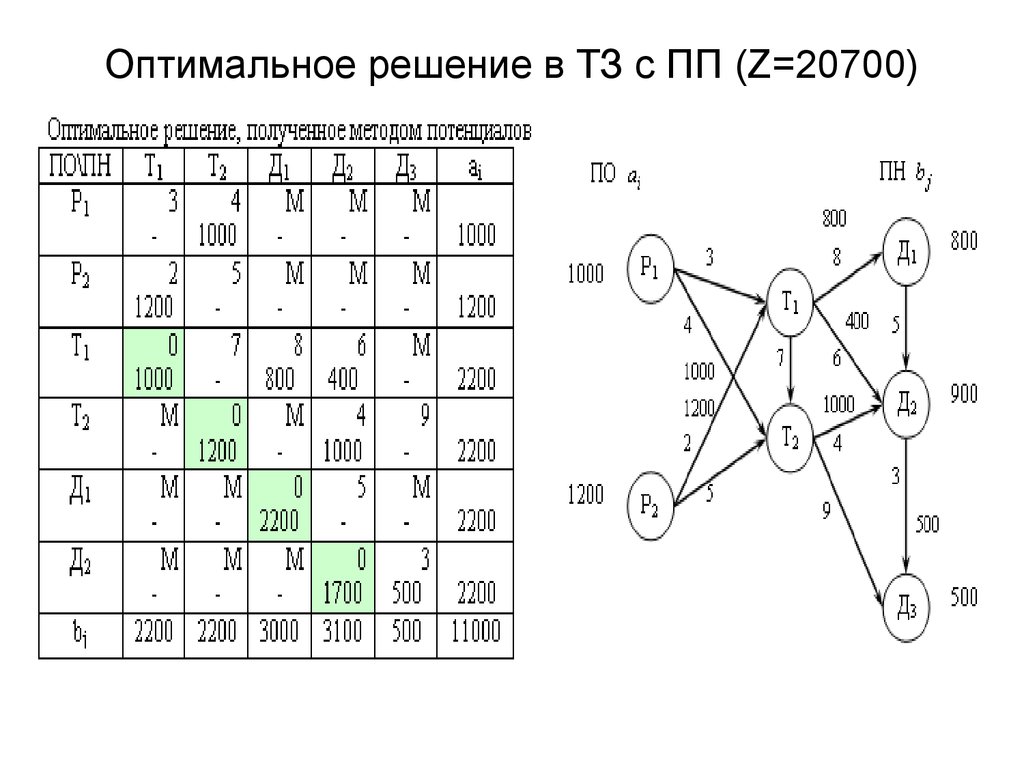 2: Максимизация с помощью симплексного метода распространяется под лицензией CC BY 4.0 и была создана, изменена и/или курирована Рупиндером Секоном и Робертой Блум с использованием исходного контента, который был отредактирован в соответствии со стилем и стандартами LibreTexts. Платформа; подробная история редактирования доступна по запросу.

Наверх

Была ли эта статья полезной?

Тип изделия
Раздел или Страница
Автор
Рупиндер Сехон и Роберта Блум
Лицензия
СС BY
Версия лицензии
4,0
Показать страницу TOC
нет
Теги
1. симплексный алгоритм
2. источник@https://www. deanza.edu/faculty/bloomroberta/math21/afm3files.html.html

Введение в алгоритмы: ГЛАВА 16: ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ

Мы можем использовать динамическое программирование на ориентированном графе G = ( V,E ) для распознавания речи. Каждое ребро ( u,v ) E помечен звуком ( u,v ) из конечного набора звуков. Размеченный граф — это формальная модель человека, говорящего на ограниченном языке. Каждый путь в графе, начинающийся с выделенной вершины v ₀ V , соответствует возможной последовательности звуков, воспроизводимых моделью. Метка направленного пути определяется как объединение меток ребер на этом пути.

а. Опишите эффективный алгоритм, который для графа с помеченными ребрами G с выделенной вершиной v ₀ и последовательности s = ₁ , _{2 9 0 ,…, 9041 0159 символов из , возвращает путь в G , который начинается с v ₀ и имеет метку s , если такой путь существует. В противном случае алгоритм должен вернуть NO-SUCH-PATH. Проанализируйте время работы вашего алгоритма. ( Подсказка: Возможно, вам пригодятся концепции из главы 23.)}

Теперь предположим, что каждому ребру ( u,v ) E также была дана соответствующая неотрицательная вероятность p ( u, v ) пересечения ребра ( u, v ) из вершины u и издавая соответствующий звук. Сумма вероятностей ребер, выходящих из любой вершины, равна 1. Вероятность пути определяется как произведение вероятностей его ребер. Мы можем просмотреть вероятность пути, начинающегося в v ₀ как вероятность того, что «случайное блуждание», начинающееся в v ₀, будет следовать по указанному пути, где выбор того, какое ребро взять в вершине u , производится вероятностно в соответствии с вероятностями доступных ребер, оставляя u .

б. Расширьте свой ответ до части (a) так, чтобы, если возвращается путь, это был наиболее вероятный путь, начинающийся с v ₀ и имеющие маркировку s . Проанализируйте время работы вашего алгоритма.

Р. Беллман начал систематическое изучение динамического программирования в 1955 г. Слово «программирование» и здесь, и в линейном программировании относится к использованию табличного метода решения. Хотя методы оптимизации, включающие элементы динамического программирования, были известны и раньше, Беллман предоставил этой области прочную математическую основу [21].

Ху и Шинг [106] дают O ( n 1 g n )-временной алгоритм для задачи умножения цепочек матриц. Они также демонстрируют соответствие между задачей оптимальной триангуляции полигонов и задачей умножения цепочек матриц.

Алгоритм O ( mn ) времени для задачи о самой длинной общей подпоследовательности кажется народным алгоритмом. Кнут [43] поставил вопрос о существовании субквадратичных алгоритмов для задачи LCS. Масек и Патерсон [143] ответили на этот вопрос утвердительно, предоставив алгоритм, работающий за O ( mn /l g n ) время, где n m и последовательности взяты из набора ограниченного размера.

Методы оптимальных решений задачи с решениями и ответами: Методы оптимальных решений для чайников

Решение задач линейного программирования, теории игр и других экономико-математических методов и моделей. Методы оптимальных решений

Методы оптимальных решений Тесты с ответами ИММиФ Тема 4-5

4.2: Максимизация Симплекс-методом

Цели обучения

СИМПЛЕКСНЫЙ МЕТОД

Пример \(\PageIndex{1}\)

Введение в алгоритмы: ГЛАВА 16: ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ

Добавить комментарий Отменить ответ