9.) Методы решения систем линейных алгебраических уравнений:
Прямые(конечные) методы решения СЛАУ: (позволяют найти решение за определенное число операций.) Метод Крамера Метод обратной матрицы Метод ГауссаИтерационные методы решения линейных алгебраических систем: (основанны на использовании повторяющегося (циклического) процесса и позволяющие получить решение в результате последовательных приближений.)Метод простой итерации или метод Якоби Метод Гаусса – Зейделя
Постановка задачи
Требуется найти решение системы m линейных уравнений, которая записывается в общем виде как
,
Эту систему уравнений можно записать также в матричном виде:
,
где , , .
A – матрица системы, – вектор правых частей, – вектор неизвестных.
При
известных A и требуется
найти такие ,
при подстановке которых в систему
уравнений она превращается в тождество.
Необходимым и достаточным условием существования единственного решения СЛАУ является условие det A≠0, т.е. определитель матрицы A не равен нулю. В случае равенства нулю определителя матрица A называется
Система называется обусловленной (не вырожденной, не особенной), если определитель системы 0, и тогда система имеет единственное решение.
Система называется не обусловленной (вырожденной, особенной), если = 0, и тогда система не имеет решений или имеет бесконечное множество решений.
Система называется плохо обусловленной, если неустранимая погрешность оказывает сильное влияние на решение; у таких систем определитель близок, но не равен 0.
10.) Прямые методы решения слау Метод Крамера:
число
уравнений равно числу неизвестных
переменных и определитель основной
матрицы системы отличен от нуля, то
есть, .
— определитель основной матрицы системы, а — определители матриц, которые получаются из А заменой 1-ого, 2-ого, …, n-ого столбца соответственно на столбец свободных членов:
При таких обозначениях неизвестные переменные вычисляются по формулам метода Крамера как . Так находится решение системы линейных алгебраических уравнений методом Крамера. Основным недостатком метода Крамера является трудоемкость вычисления определителей, когда число уравнений системы больше трех.
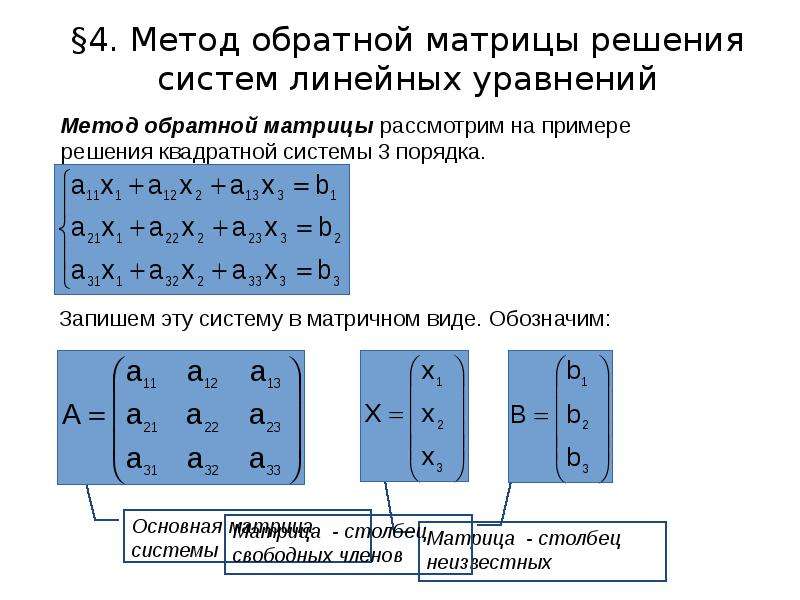
Решение систем линейных алгебраических уравнений матричным методом (с помощью обратной матрицы).
Матричной форма СЛАУ- , где матрица A имеет размерность n на n и ее определитель отличен от нуля.
Так
как ,
то матрица А –
обратима, то есть, существует обратная
матрица .
Если умножить обе части равенства на слева,
то получим формулу для нахождения
матрицы-столбца неизвестных
переменных -решение
системы линейных алгебраических
уравнений матричным методом.
Основная проблема при нахождении решения систем линейных алгебраических уравнений матричным методом заключается в трудоемкости нахождения обратной матрицы, особенно для квадратных матриц порядка выше третьего.
Метод Гаусса- этот метод заключается в последовательном исключении неизвестных. Пусть в системе уравнений
первый элемент . Назовем его ведущим элементом первой строки. Поделим все элементы этой строки на и исключим x1 из всех последующих строк, начиная со второй, путем вычитания первой (преобразованной), умноженной на коэффициент при в соответствующей строке. Получим
.
Если , то, продолжая аналогичное исключение, приходим к системе уравнений с верхней треугольной матрицей
.
Из нее в обратном порядке находим все значения xi:
.
Процесс
приведения к системе с треугольной
матрицей называется прямым
ходом, а нахождения
неизвестных – обратным.
В случае если один из ведущих элементов
равен нулю, изложенный алгоритм метода
Гаусса неприменим.
Кроме того, если
какие–либо ведущие элементы малы, то
это приводит к усилению ошибок округления
и ухудшению точности счета. Поэтому
обычно используется другой вариант
метода Гаусса – схема Гаусса с
выбором главного элемента.
Путем перестановки
строк, а также столбцов
с соответствующей перенумерацией
коэффициентов и неизвестных добиваются
выполнения условия:
, j = i+1,i+ 2, …, m;
т.е. осуществляется выбор первого главного элемента. Переставляя уравнения так, чтобы в первом уравнении коэффициент a11 был максимальным по модулю. Разделив первую строку на главный элемент, как и прежде, исключают x1 из остальных уравнений. Затем для оставшихся столбцов и строк выбирают второй главный элемент и т.д.
Раздел недели: Скоропись физического, математического, химического и, в целом, научного текста, математические обозначения. Математический, Физический алфавит, Научный алфавит. | ||||||||
| Поиск на сайте DPVA Поставщики оборудования Полезные ссылки О проекте Обратная связь Ответы на вопросы. Оглавление Таблицы DPVA.ru — Инженерный Справочник | Адрес этой страницы (вложенность) в справочнике dpva.ru: главная страница / / Техническая информация/ / Математический справочник / / Решение уравнений и неравенств. Системы уравнений. Формулы. Методы. / / Системы уравнений. Понятие системы уравнений. Свойства систем уравнений. Линейные системы уравнений. Основные методы решения систем уравнений / / Методы решения невырожденных систем линейных алгебраических уравнений (СЛАУ) — по формулам Крамера, матричный способ. Метод Гаусса = метод последовательного исключения неизвестных при решения систем линейных алгебраических уравнений. Наличие решений.Поделиться:
| |||||||
Если Вы не обнаружили себя в списке поставщиков, заметили ошибку, или у Вас есть дополнительные численные данные для коллег по теме, сообщите , пожалуйста. | ||||||||
Коды баннеров проекта DPVA.ru Консультации и техническая | Проект является некоммерческим. Информация, представленная на сайте, не является официальной и предоставлена только в целях ознакомления. Владельцы сайта www.dpva.ru не несут никакой ответственности за риски, связанные с использованием информации, полученной с этого интернет-ресурса. Free xml sitemap generator | |||||||
Наличие решений.
Введите свой запрос:Решение систем уравнений матричным методом
Матричный метод решения систем уравнений также известен как метод строк-эшелонов.
Матричный метод аналогичен методу исключения as, но намного чище
, чем метод исключения.
Решение систем уравнений матричным методом включает в себя выражение системы
уравнений в виде матрицы, а затем преобразование этой матрицы в то, что известно как
формы эшелона строк.
Ниже приведены два примера матриц в форме Row Echelon Form
.
Первая представляет собой матрицу 2 x 2 в форме Row Echelon, а вторая представляет собой матрицу 3 x 3
в форме Row Echelon.
Выражение систем уравнений в виде матриц
Учитывая следующую систему уравнений:
Приведенная выше система уравнений с двумя переменными может быть выражена в виде матричной системы как
следует за
Если мы решим приведенное выше, используя правила умножения матриц, мы должны получить
с системой уравнений, с которой мы начали.
Мы можем дополнительно изменить приведенные выше матрицы
и скрыть матрицу, содержащую переменные. Мы не удаляем его, а просто прячем
, чтобы сделать наши вычисления чище.
Вышеупомянутое далее преобразуется в единую матрицу, как показано ниже
Часто вертикальная линия рисуется, чтобы указать, что самый правый столбец представляет
записей справа от знака равенства в системе уравнений.
То же самое можно сделать для системы уравнений с тремя переменными.
Вышеупомянутое может быть выражено как произведение матриц в виде:
Скрывая матрицу, содержащую переменные, мы можем выразить это как:
Затем складываем все это в одну матрицу:
или как
Вышеупомянутая форма называется расширенной матрицей
В расширенной матрице выше мы знаем, что элементы слева представляют коэффициенты к переменным
в системе уравнений.
Метод приведения к форме эшелонирования строк
Прежде чем читать этот раздел, вы должны взглянуть на Сокращение до
Раздел «Форма Эшелона» в разделе «Матрицы».
Теперь, когда вы знаете, как преобразовать матрицу в форму эшелона строк, давайте посмотрим, как применить алгоритм
к расширенным матрицам, сформированным из систем уравнений.
Пример 1:
Найдите решение следующей системы уравнений
Решение:
Первый шаг состоит в том, чтобы выразить приведенную выше систему уравнений в виде расширенной матрицы.
Далее мы маркируем строки:
Теперь мы начнем фактически приводить матрицу к форме эшелона строк.
Сначала мы меняем старший коэффициент
первой строки на 1.
Мы достигаем этого, умножая R 1 на -1 ⁄ 3 :
Далее меняем коэффициент во второй строке, лежащей ниже старшего коэффициента
в первой строке. Это достигается путем умножения R 2 на -1 ⁄ 5
и последующего прибавления результата к R 1 .
Добавление результата к R’ 1 :
Итак, теперь наша новая матрица выглядит так:
На этом этапе мы повторно вводим переменные в строку 2, так как теперь у нас будет единица 9.0003 уравнение переменной:
Мы можем найти y из приведенного выше уравнения:
Теперь, когда у нас есть y , мы можем использовать обратную подстановку для решения x с помощью
, заменив y в уравнении с двумя переменными, составленном из R’ 1 :
Следовательно, решение системы уравнений равно {х, у} = {2,-2}
Пример 2:
Найдите x, y и z в системе уравнений ниже
Решение:
Первый шаг — превратить систему уравнений с тремя переменными в расширенную матрицу 3×4
.
Далее помечаем строки матрицы:
Поскольку в приведенной выше расширенной матрице мы не можем найти ни одной строки с единицей в качестве ведущих
, нам не нужно выполнять операцию переключения строк. Однако нам нужно изменить
строку 1 так, чтобы ее старший коэффициент был равен 1.
Мы можем добиться этого, умножив строку 1 на 1 ⁄ 3 :
Далее нам нужно изменить все записи ниже старшего коэффициента первой строки
на нули.
Для второй строки мы можем добиться этого, сначала умножив на -1 ⁄ 3
, а затем добавить результат в строку 1.
Добавление результата в строку 1:
Затем мы переходим к строке 3; здесь мы умножаем строку на -1 ⁄ 5
, а затем добавляем результат к строке 1, чтобы обнулить первый элемент.
Добавление результата в строку 1:
Нам нужно, чтобы ведущий элемент во второй строке тоже был единицей. Мы получаем этот результат
, умножив вторую строку на -3 ⁄ 2 :
Затем мы обнуляем элемент в третьей строке под старшим коэффициентом во второй строке
. Для этого умножаем третью строку на 5 ⁄ 4
Добавление результата к строке 2:
Наконец, мы умножаем строку 3 на -12, чтобы получить ведущий элемент третьей девятки.0003 ряд как один:
Из приведенной выше матрицы мы находим переменные, начинающиеся с z в последней строке
.
Затем мы находим y, заменяя z в уравнении, образованном второй строкой:
Наконец, мы находим x, подставляя значения y и z в уравнение, сформированное
по первой строке:
Следовательно, решение системы уравнений {x,y,z} = {1,-2,1}
3 метода решения систем уравнений
••• ChristianChan/iStock/GettyImages
Обновлено 14 марта 2018 г.
эс . Подстановка и исключение — это простые методы, с помощью которых можно эффективно решить большинство систем из двух уравнений за несколько простых шагов. Метод дополненных матриц требует больше шагов, но его применение распространяется на большее разнообразие систем.
Подстановка
Подстановка — это метод решения систем уравнений путем удаления всех переменных, кроме одной, в одном из уравнений и последующего решения этого уравнения. Это достигается путем выделения другой переменной в уравнении, а затем подстановки значений этих переменных в другое уравнение. Например, чтобы решить систему уравнений x + y = 4, 2x — 3y = 3, выделите переменную x в первом уравнении, чтобы получить x = 4 — y, затем подставьте это значение y во второе уравнение, чтобы получить 2 (4 — y) — 3y = 3. Это уравнение упрощается до -5y = -5 или y = 1. Подставьте это значение во второе уравнение, чтобы найти значение x: x + 1 = 4 или x = 3,
Исключение
Исключение — это еще один способ решения систем уравнений путем перезаписи одного из уравнений только с одной переменной.
Метод исключения достигает этого путем добавления или вычитания уравнений друг из друга, чтобы отменить одну из переменных. Например, добавление уравнений x + 2y = 3 и 2x — 2y = 3 дает новое уравнение 3x = 6 (обратите внимание, что члены y сокращаются). Затем система решается теми же методами, что и для подстановки. Если невозможно сократить переменные в уравнениях, необходимо будет умножить все уравнение на коэффициент, чтобы коэффициенты совпали.
Расширенная матрица
Расширенные матрицы также могут использоваться для решения систем уравнений. Расширенная матрица состоит из строк для каждого уравнения, столбцов для каждой переменной и расширенного столбца, содержащего постоянный член на другой стороне уравнения. Например, расширенная матрица для системы уравнений 2x + y = 4, 2x — y = 0 равна [[2 1], [2 -1]…[4, 0]].
Определение решения
Следующий шаг включает использование элементарных операций со строками, таких как умножение или деление строки на константу, отличную от нуля, а также сложение или вычитание строк.
Целью этих операций является преобразование матрицы в ступенчато-строковую форму, в которой первый ненулевой элемент в каждой строке равен 1, все элементы выше и ниже этого элемента являются нулями, а первый ненулевой элемент для каждого строка всегда находится справа от всех таких записей в строках над ней. Строково-эшелонная форма для приведенной выше матрицы имеет вид [[1 0], [0 1]…[1, 2]]. Значение первой переменной задается первой строкой (1x + 0y = 1 или x = 1). Значение второй переменной задается второй строкой (0x + 1y = 2 или y = 2).
Приложения
Подстановка и исключение являются более простыми методами решения уравнений и используются гораздо чаще, чем расширенные матрицы в базовой алгебре. Метод подстановки особенно полезен, когда одна из переменных уже изолирована в одном из уравнений. Метод исключения полезен, когда коэффициент одной из переменных одинаков (или его отрицательный эквивалент) во всех уравнениях. Основное преимущество расширенных матриц заключается в том, что их можно использовать для решения систем из трех и более уравнений в ситуациях, когда замена и исключение либо невозможны, либо невозможны.