Методы решения транспортных задач: Ошибка 404. Запрашиваемая страница не найдена

Транспортная задача линейного программирования / Хабр

Прочие статьи цикла

Транспортная задача линейного программирования относится к перечню классических задач, решаемых в практике деятельности людей. Эта задача методами классической математики не решается. В задаче необходимо отыскивать экстремум целевой функции. В задаче целевая функция – линейная. Ограничения на переменные (их может быть очень много) описываются также линейными зависимостями. Казалось бы чего проще. Но как раз ограничения и порождают трудности, связанные не просто с поиском max и min при отсутствии ограничений, а с необходимостью учета таких ограничений. Искать требуется не просто экстремум, а условный экстремум. Методы решения задачи позволяют учитывать особенности структуры задачи и даже отказаться от симплексного метода решения в чистом виде.

I. Основные параметры, термины и обозначения

Для ощущения масштаба задачи приведу парочку изображений того, что рассматривается в транспортной задаче линейного программирования.

Все суда на одной карте в режиме онлайн

Зеленый цвет — пассажирские суда, желтые — грузовые, розовый — частные яхты, оранжевый — танкеры и др. Аналогичная картина наблюдается и для авиационных перевозок, перевозок по железной дороге или автотранспортом. Изображения получены в начальном периоде Пандемии короновируса, что привело к огромным пробкам в узостях мирового Океана (Панамский, Суэцкий и др. каналы). Танкеры отправили отстаиваться на рейде, экипажам судов на берег сойти не разрешалось. Это форс-мажорные обстоятельства, которые в теории должны рассматриваться и учитываться специальным образом, что пока к сожалению перевозчиков не сделано.

Все самолеты мира в режиме онлайн

В теории в тексте задачи Хичкока ничего не говорится о равенстве имеющегося общего запаса судов в портах отправления и общей потребности в судах в портах прибытия (назначения). Если такого равенства нет, то система ограничений несовместна. В случае равенства

транспортная задача называется «сбалансированной». Задачи, в которых условие баланса не задано, должны быть приведены к «сбалансированному» виду. Это можно выполнить использованием «фиктивных» перевозок. Рассматриваем два случая:

Поэтому ранг системы равен не n+m, а n+m – 1, т.е с mn неизвестными. Общее число опорных планов равно числу сочетаний из mn по n+m – 1.. Применение симплекс метода для решения задачи возможно, но требует большого объема вычислений уже при n и m ≈ 10 -15. Заметим также, что каждая неизвестная входит лишь в два уравнения системы (матрица коэффициентов системы ограничений имеет в каждой строке и каждом столбце только два ненулевых элемента). Более того, транспортная задача всегда имеет допустимое решение. Все сказанное вызвало потребность попытаться учесть специфику задачи и создать метод ее решения более простой, чем симплекс метод. Такие методы были найдены и получили названия метода потенциалов и распределительного метода. Это разновидности симплексного метода. Они удобно реализуются, если условие задачи представлено в виде таблиц.

ТАБЛИЦА 1 — Вид данных транспортной задачи линейного программирования

Метод содержит три последовательных этапа:

1. Формирование опорного плана;

2. Проверка опорного плана на оптимальность;

3. Переход к новому опорному плану, если предыдущий не оптимален.

Рисунок 1 — Структурно-логическая схема алгоритма метода потенциалов

II. Формирование опорного плана перевозок

Рассмотрим способ получения начального опорного плана транспортной задачи, названный способом северо-западного (С-З) угла. Способ заключается в заполнении ячеек таблицы m×n значениями переменной x_ij, таким образом, чтобы удовлетворялись условия задачи. При этом план решения Х[m, n] может быть и не оптимальным, но обязательно должен быть допустимым.

В этом способе формируют опорный план, двигаясь по таблице: сверху вниз по строкам и слева направо вдоль строки. Начинают с левого верхнего угла (ячейки), куда вписывают значение x₁₁ =min{a₁, b₁}.Первые строка и столбец из рассмотрения далее исключаются.

Затем, если a₁ > b₁, то определяется остаток (a₁ – b₁) продукта на первом пункте отправления и его запас реализуется на 2-м пункте назначения. Остаток потребностей 2-го пункта назначения удовлетворяется за счет 2-го пункта отправления, остатки которого направляются в 3-й пункт назначения и т. д. Ниже метод будет иллюстрирован числовым примером.

Пример 1. Построение опорного плана методом Северо-Западного угла

Заданы значения: m = 3, n = 4; a₁ = 60, a₂ = 80, a₃ =100, b₁ = 40,b₂ = 60, b₃ = 80, b₄ = 60. Слева в таблице приведены d_ij удельные стоимости перевозок; справа — В_ij стоимости совместно с предложениями a_i и потребностями b_{j .}

Требуется найти план Х [m,n] перевозок, удовлетворяющий условиям на целевую функцию Q и переменные х_ij задачи Q.

РЕШЕНИЕ Построить исходный опорный план способом северо-западного угла. Строим симплексную таблицу:                                        Таблица 3.   Опорный план задачи

В таблице способом северо-западного угла получен опорный план. Базисные переменные (их число = 6): x₁₁ = 40, x₁₂= 20, x₂₂= 40, x₂₃= 40, x₃₃= 40, x₃₄= 60. Свободные переменные: x₁₃= x₁₄= x₂₁= x₂₄= x₃₁= x₃₂= 0 (их число равно 6).

Ячейки таблицы, соответствующие базисным переменным, называют базисными, остальные – свободными. Далее в алгоритме будем следовать идее симплекс метода. Суммарная стоимость перевозок Q, соответствующая плану Х[m,n], получает представление

Q = d₁₁∙x₁₁ + d₁₂∙x₁₂ + d₂₂∙x₂₂ + d₂₃ ∙x₂₃+ d₃₃ ∙x₃₃+ d₃₄ ∙x₃₄ = = 5∙40 + 2∙20 + 10∙40 + 2∙40 + 8∙40 + 5∙60 = 200+40+400 + 80 + 320+ 300 = 1340 ед

Коэффициенты d_ij называются фиктивными или косвенными стоимостями; их выражают через косвенные величины α и β, d’_ij = α_i +β_j . Здесь параметры α_i и ( — β_j ), по аналогии с механикой называют потенциалами i-го пункта отправления и j-го пункта прибытия. Значения потенциалов определяется из системы линейных уравнений: α_i + β_j= d_ij

Каждому из таких уравнений соответствует какая-либо базисная переменная х_ij Система уравнений с потенциалами содержит m+n неизвестных потенциалов, число же уравнений равняется числу базисных ячеек таблицы, т.е. (m + n – 1). Следовательно, один из потенциалов можно задать произвольно, положив его равным, например, нулю.

Решая далее систему уравнений для потенциалов, находим значения потенциалов строк и столбцов, все фиктивные стоимости d_ij и коэффициенты γ_ij. Если для всех свободных клеток γ_rs ≤ 0, то перевод в базис любой свободной переменной не уменьшит значения целевой функции и, следовательно, выбранный опорный план не является оптимальным. Если же некоторые γ_rs >0, то данный план можно улучшить путем перевода в базис свободной переменной, соответствующей max γ_rs, а также путем исключения из базиса, принадлежащей ему переменной, первой обращающейся в нуль. Переход к новому опорному плану и поиск оптимального плана рассмотрим на примере. Другой способ формирования опорного плана предложен Фогелем. Этот способ при первом чтении можно пропустить, так как дальше он в тексте не используется.

Пример 2. Способ аппроксимации Фогеля

В большинстве случаев этот способ дает опорный план наиболее близкий к оптимальному. Удобен для матриц большой размерности. Используется концепция штрафов, взимаемых за выбор не самого оптимального с точки зрения транспортных издержек маршрута. Штраф по каждой строке и каждому столбцу определяется из анализа маршрутов с различными показателями издержек (как разность двух различных уровней транспортных издержек). Первой заполняется клетка матрицы (таблицы), в которой фиксируется самый крупный штраф. После заполнения клетки штрафы пересчитываются и так до тех пор, пока все ресурсы не будут распределены. Исходные данные для этого примера заполняют таблицу слева вверху.

Этапы алгоритма: 1.     Вычисление разностей в каждой строке и в каждом столбце между наименьшей стоимостью и ближайшей к ней по величине. Разности по строкам записываются справа в столбце разностей, разности по столбцам – внизу в строке разностей. Например, для строк А₁ разность равна А₁В₂ – А₁В₃ = 38 – 24 = 14 и т. д.

ТАБЛИЦА 2 — Метод Фогеля для получения опорного плана транспортной задачи

2.     Поиск из всех разностей, как по строкам, так и по столбцам максимальный. В нашем примере максимальная разность равна 38 и находится в строке А₂. Обведем максимальную разность рамкой.

3.     Размещение в клетку, где находится наименьшая стоимость (А₂В₂ = 18) (строка с наибольшей разностью), максимально возможного количества ресурсов. Оно равно 20, т.е. всему ресурсу отправителя А₂. Поскольку все ресурсы отправителя А₂ исчерпаны, строку А₂ исключаем из дальнейших расчетов, для чего отметим все клетки этой строки точками.

4.     Вычисление разностей столбцам и строкам, не принимая во внимание стоимость в клетках, имеющих ресурсы и клетках с точкой (исключенную строку или столбец) и определение максимальной разности в строке или столбце (В₃ = 76).

5.     Поиск минимального элемента в строке или в столбце с максимальной разностью (А₁В₃ = 24) и размещения в данную клетку максимально возможного количества ресурса, возвращение к этапу №4 и т.д. Окончательно

ЦФ Q=23∙19 + 7∙3 + 20∙18 + 2∙10 + 14∙24 + 1∙100 +3∙48 = = 437 + 21 + 360 + 20 +3 36 + 100 + 272 =1546 ед. Это значение соответствует опорному плану Фогеля.

III. Транспортная задача линейного программирования

Как основной метод решения транспортной задачи – используется метод потенциалов. Ни симплексный метод, ни распределительный метод здесь не рассматриваются. У них имеются свои плюсы и минусы, но объем изложения достаточно велик. Возможно этому позднее я уделю внимание и время, но пока отвечаю на пожелание читателя Хабра.

Пример 3 — Транспортная задача. Метод потенциалов

Исходные данные задачи удобно представить двумя матрицами.

ТАБЛИЦА — Исходные данные

Требуется найти план Х [m,n] перевозок, удовлетворяющий условиям на целевую функцию Q и переменные х_ij задачи

Решение задачи:

1.  Формирование начального опорного плана способом Северо-Западного угла.  

Базисные n + m – 1 = 3 + 4 – 1 = 6 переменные:  
x₁₁ =70, x₁₂ = 20, x₂₂ = 10, x₂₃ = 20, x₂₄ = 0, x₃₄ = 40.
Остальные переменные nm – n + m – 1 = 12 – 6 = 6 свободные:
x₁₃ = x₁₄ = x₂₁ = x₂₄ = x₃₁= x₃₂ = 0 .
Суммарная стоимость перевозок для опорного плана получает представление:
Q = d₁₁ ∙x₁₁ + d₁₂∙x₁₂ + d₂₂∙x₂₂ + d₂₃∙x₂₃+ d₂₄∙x₂₄+ d₃₄∙x₃₄ =
=2∙70 + 3∙20 + 3∙10 + 1∙20 + 2∙0 + 2∙40 = 140 + 60 + 30 + 20 + 0 +80  = 330 ед.

2. Проверка опорного плана на оптимальность

Является ли найденный опорный план оптимальным? Ответ может быть получен после составления и решения системы уравнений для потенциалов. Определим систему уравнений для потенциалов и вычислим их значения:

α₁ + β₁ = d₁₁ = 2;
α₁ + β₂ = d₁₂ = 3;
α₂ + β₂ = d₂₂ = 3;
α₂ + β₃ = d₂₃ = 1;
α₂ + β₄ = d₂₄ = 2;
α₃ + β₄ = d₃₄ = 2.

Каждое из этих значений соответствует одной базисной ячейке. Одну из неизвестных в системе можно задавать произвольно. Пусть β₁ = 0. Тогда после решения системы получены значения потенциалов: α₁= 2, α₂= 2, α₃= 2, β₁ =0, β₂=1, β₃ =–1, β₄ =0,

Формируем матрицу фиктивных стоимостей D'[m, n] и матрицу Г [m, n].

Выделяем в Г [m, n] свободные ячейки, содержащие γ_rs. Проверяем наличие положительных переменных γ_i,j > 0. Так как в матрице (в свободных ячейках) имеем γ₃₂ = 2 > 0, то исходный опорный план может быть улучшен, он не является оптимальным.

3. Переход к новому (улучшенному) опорному плану

Переменную x₃₂ =x следует ввести в базис.  Обозначим ее предварительно через x без индексов. С учетом того, что х должна быть положительна х > 0. Найдем значение max x при условии сохранения баланса перевозок. Для этого воспользуемся начальным опорным планом. Будем добавлять переменную х в ячейки таблицы так, чтобы сохранялись условия баланса перевозок

Модификация начального опорного плана

Обозначим ее предварительно через x без индексов. С учетом того, что х должна быть положительна х > 0. Найдем значение max x при условии сохранения баланса перевозок. Для этого воспользуемся начальным опорным планом. Будем добавлять переменную х в ячейки таблицы так, чтобы сохранялись условия баланса перевозок   Очевидно, что наибольшее x определяется теми x_ijв базисных клетках, из которых этот х вычитается. Следовательно, x₁₁ = min{х₂₂, х₃₄} = {10, 40} = 10. При x >10 перевозка х₂₂ становится отрицательной. Переменную х₂₂ исключаем из базиса и переводим ее в разряд свободных переменных. Далее повторяются рекурсивно три пункта алгоритма.

1. Получаем из модифицированного плана новый опорный план

   В нем объемы перевозок распределены иначе чем в начальном опорном плане.

Новый опорный план

Суммарная стоимость перевозок для этого опорного плана получает представление:
Q = d₁₁ ∙x₁₁ + d₁₂∙x₁₂ + d₂₃∙x₂₃ + d₃₂∙x₃₂ + d₂₄∙x₂₄+ d₃₄∙x₃₄ =
=2∙70 + 3∙20 + 2∙10 + 1∙20 + 1∙10 + 2∙30 = 140 + 60 + 20 + 20 + 10 + 60  = 310 ед. Затраты на перевозки при этом плане уменьшились на 330 – 310 = 20 ед.

Является ли найденный опорный план оптимальным? Ответ может быть получен после составления и решения системы уравнений для потенциалов.

2. Проверка опорного плана на оптимальность

Определим систему уравнений для потенциалов и вычислим их значения:
α₁ + β₁ = d₁₁ = 2;
α₁ + β₂ = d₁₂ = 3;
α₂ + β₃ = d₂₃ = 1;
α₂ + β₄ = d₂₄ = 2;
α₃ + β₂ = d₃₂ = 1;
α₃ + β₄ = d₃₄ = 2.

Каждое из этих значений соответствует одной базисной ячейке. Одну из неизвестных в системе можно задавать произвольно. Пустьα₁ = 0. Тогда после решения системы получены значения потенциалов: α₁= 0, α₂= – 2, α₃= –2, β₁ =2, β₂=3, β₃ = 3, β₄ =4.

Формируем матрицу фиктивных стоимостей D'[m, n] и матрицу Г [m, n].

Свободные ячейки матрицы Г [m, n] содержат γ_i,j > 0 (γ₁₄ = 1>0). План не оптимален.

3. Переход к новому (улучшенному) опорному плану

Из свободных переменных с x_ij > 0, выбираем одну x₁₄  для введения ее в базис. Обозначим ее как и ранее через x без индексов. С учетом того, что х должна быть положительна х > 0. Найдем значение max x при условии сохранения баланса перевозок. Для этого воспользуемся очередным опорным планом. Будем добавлять переменную х в ячейки таблицы так, чтобы сохранялись условия баланса перевозок  

модифицированный план

Очевидно, что наибольшее x определяется теми x_ijв базисных клетках, из которых этот х вычитается. Следовательно, x₁₁ = min{х₁₂, х₃₄} = {20, 30} = 20. При х₁₂ >20 перевозка х₁₂ становится отрицательной. Переменную х₁₂ исключаем из базиса и переводим ее в разряд свободных переменных. Переходим к новой итерации

1. Получаем из модифицированного плана новый опорный план.

В нем объемы перевозок распределены иначе чем в предшествующем опорном плане.

Суммарная стоимость перевозок для этого опорного плана получает представление:
Q = d₁₁ ∙x₁₁ + d₁₄∙x₁₄ + d₂₃∙x₂₃ + d₃₂∙x₃₂ + d₂₄∙x₂₄+ d₃₄∙x₃₄ =
=2∙70 + 3∙20 + 1∙20 + 2∙10 + 1∙30 + 2∙10 = 140 + 60 + 20 + 20 + 30 + 20  = 290 ед. Затраты на перевозки при этом плане уменьшились на 310 – 290 = 20 ед. Является ли найденный опорный план оптимальным? Ответ может быть получен после составления и решения системы уравнений для потенциалов.

2. Проверка опорного плана на оптимальность

Определим систему уравнений для потенциалов и вычислим их значения:
α₁ + β₁ = d₁₁ = 2;
α₁ + β₄ = d₁₄ = 3;
α₂ + β₃ = d₂₃ = 1;
α₂ + β₄ = d₂₄ = 2;
α₃ + β₂ = d₃₂ = 1;
α₃ + β₄ = d₃₄ = 2. Каждое из этих значений соответствует одной базисной ячейке. Одну из неизвестных в системе можно задавать произвольно. Пусть β₁ = 0. Тогда после решения системы получены значения потенциалов: α₁= 2, α₂= 2, α₃= 2, β₁ =0, β₂=1, β₃ =–1, β₄ =0.

Формируем матрицу фиктивных стоимостей D'[m, n] и матрицу Г [m, n].

При переходе к новому опорному плану проверяем наличие положительных свободных переменных γ_i,j >0. Но таких переменных не оказалось. Отсюда следует вывод, что полученный последним модифицированный план является оптимальным и ему соответствует значение линейной формы
Q’= 2∙70 + 3∙20 + 1∙20 + 2∙10 + 1∙30 + 2∙10 = 290.

Заключение

Вся теория исследования операций с позиций математики решает неклассические задачи оптимизации целевых функций. Отличие от классики в том, что те ограничения на переменные, которые исследователи вынуждены накладывать в рамках моделей, созданы и вызваны реальностью. Отыскивать требуется экстремумы функций при многих ограничениях, так называемые условные экстремумы. Классика не позволяет этого делать. Взятие производных и приравнивание их нулю «не видит» ограничений. Лучшее, что там имеется это функция Лагранжа, но ее использование также весьма ограничено. Транспортные задачи – частный, но важный случай в исследовании операций. Надеюсь, что читатель разобравшись в приведенных примерах, лучше стал понимать логику задачи и сумеет самостоятельно постигать интересующие его вопросы по другим публикациям в учебниках и журнальных статьях.

Литература

1. Ваулин А. Е. Методы цифровой обработки данных.– СПб.: ВИККИ им. А. Ф. Можайского, 1993.– 106 с.

2. Гэри М., Джонсон Д. Вычислительные машины и трудно решаемые задачи. М.: Мир, 1982.

3. Корбут А.А., Финкельштейн Ю. Ю. Дискретное программирование М. Наука. Гл. ред. физ.-мат. лит. 1969.

4. Макаров И. М. и др. Теория выбора и принятия решений.– М.: Наука, 1982.– 328 с.

5. Пфанцагль  И. Теория измерений. – М.: Наука, 1988.–384 с.

6. Таха Х. А. Введение в исследование операций. 7-е изд. М.: Изд. дом «Вильямс», 2005.

7.  Фишберн П. С. Теория полезности для принятия решений. – М.: Наука,1978. –352 с.

Транспортная задача и методы ее решения

ТРАНСПОРТНАЯ ЗАДАЧА И МЕТОДЫ ЕЕ РЕШЕНИЯ  [c.109]

Мы не будем заниматься интерпретацией или свойствами задачи линейного программирования, не будем говорить и о методах ее решения, отметим лишь тот факт, что, кроме методов решения общей задачи линейного программирования, разработано значительное число методов и стандартных программ, предназначенных для решения ее различных частных случаев. Мы рассмотрим два наиболее распространенных класса задач линейного программирования транспортную задачу и обобщенную транспортную (распределительную) задачу.  [c.151]

Эта задача проще общей задачи линейного программирования, поскольку ее ограничения имеют весьма специальный вид. Интересно, что к транспортной задаче сводятся проблемы планирования экономических объектов разного типа. Поэтому были предприняты значительные усилия по построению эффективных методов решения транспортной задачи, и эти усилия увенчались успехом. В настоящее время умеют решать задачи транспортного типа значительно быстрее и с большим числом неизвестных, чем обычные задачи  [c.151]

Данная задача оптимизации является обобщенной транспортной задачей, так что эффективные методы ее решения существуют и могут быть использованы на практике.  [c.164]

Отметим, что помимо методов решения общей задачи линейного программирования разработано значительное число методов и стандартных программ, предназначенных для решения ее различных частных случаев. Опишем наиболее распространенные специальные задачи линейного программирования транспортную задачу и обобщенную транспортную (распределительную) задачу.  [c.57]

Эта задача проще общей задачи линейного программирования, поскольку ее ограничения имеют весьма специальную форму. Важно отметить, что к транспортной задаче сводятся проблемы планирования экономических объектов разного типа. Поэтому были предприняты значительные усилия по построению эффективных методов решения транспортной задачи и эти усилия увенчались успехом. В настоящее время задачи транспортного типа удается решить значительно быстрее и с большим числом неизвестных, чем обычные задачи линейного программирования. Само название этой задачи связано с ее происхождением она возникла из задачи оптимальной перевозки грузов.  [c.57]

Транспортная задача и задача о назначениях — это частные задачи линейного программирования. Для них в принципе могут быть использованы общие методы решения ЛП-задач (например, симплекс-метод). Однако даже для относительно простых транспортных задач и задач о назначениях характерно большое число переменных решения. Для транспортных задач, имеющих практическое значение, применение таких общих методов может стать неэффективным. Вместе с тем особенности структуры данных и ограничений транспортной задачи обусловливают возможность применения специальных высокоэффективных алгоритмов ее решения.

 [c.118]

Введение в транспортную задачу или в задачу о назначениях не свойственных им дополнительных ограничений приводит к тому, что эффективные «транспортные» методы решения таких задач (метод «северо-западного угла», циклические перестановки и т.п.) перестают быть применимыми. В этом случае задача будет решаться с помощью общих алгоритмов решения ЛП-задач (например, симплекс-методом). Помимо того что эти методы менее эффективны, они не могут гарантировать целочисленного решения, которое обычно предполагается в транспортной задаче и абсолютно необходимо в задаче о назначениях. Прямо е требование  [c.143]

Транспортная задача, в которой имеет место равенство (25.32), называется закрытой и в качестве ЗЛП может быть решена с помощью симплексного метода. Однако благодаря особенностям переменных задачи и системы ограничений разработаны специальные, менее громоздкие методы ее решения.  [c.525]

Оказывается, для того, чтобы решить маршрутную задачу с помощью транспортной модели, нужно принять в качестве однородного груза. .. пустые вагоны, направляемые от пункта выгрузки к пунктам погрузки. Полученное распределение, которое без труда находится на основе транспортной задачи, и дает решение задачи об оптимальной маршрутизации, так как оно определяет пути следования вагонов. Практическое применение транспортной задачи для решения задач оптимальной маршрутизации получило особенное распространение на автотранспорте. В ряде крупных городов производится ежедневный расчет рациональных маршрутов на ЭВМ и на их основе пишутся наряды для значительного процента автомашин. В некоторых небольших автохозяйствах эту методику хорошо освоили и регулярно используют сами диспетчеры. Это позволяет в ряде случаев снижать холостой пробег на 20—40%. Об эффекте ее применения убедительно свидетельствует и такой любопытный факт. В одном автохозяйстве, где проводился эксперимент по введению наилучшей маршрутизации транспорта, шоферы, ездившие по оптимальным маршрутам, найденным с помощью метода. потенциалов, имели на своих машинах отличительные флажки. Через несколько дней после начала эксперимента шоферы наглухо припаяли флажки к машинам, так как они стремились и впредь получать математические наряды. Большая эффективность работы этих машин была выгодна не только для автохозяйства в целом, но и для каждого и,з водителей.  [c.43]

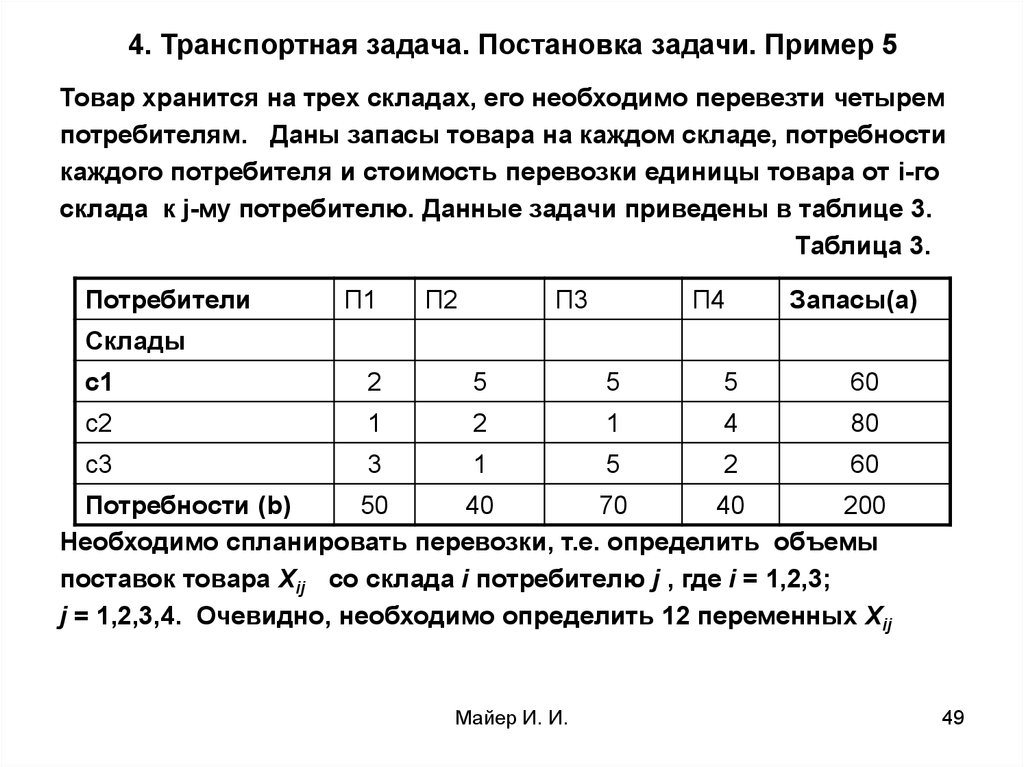
Транспортная задача является представителем класса задач линейного программирования и поэтому обладает всеми качествами линейных оптимизационных задач, но одновременно она имеет и ряд дополнительных полезных свойств, которые позволили разработать специальные методы ее решения.  [c.110]

Для отдельных видов экономических задач созданы специальные методы, значительно сокращающие объем вычислений при их решении. К числу таких задач относится так называемая транспортная задача. Эта задача была поставлена в СССР, и поиски ее решения были связаны с необходимостью получения наиболее рационального плана перевозок.  [c.194]

Наука управления зародилась в Англии во время второй мировой войны, когда группа ученых получила задание на решение сложных военных проблем, таких, как оптимальное размещение сооружений гражданской обороны и огневых позиций, оптимизация глубины подрыва противолодочных бомб и конвоя транспортных караванов.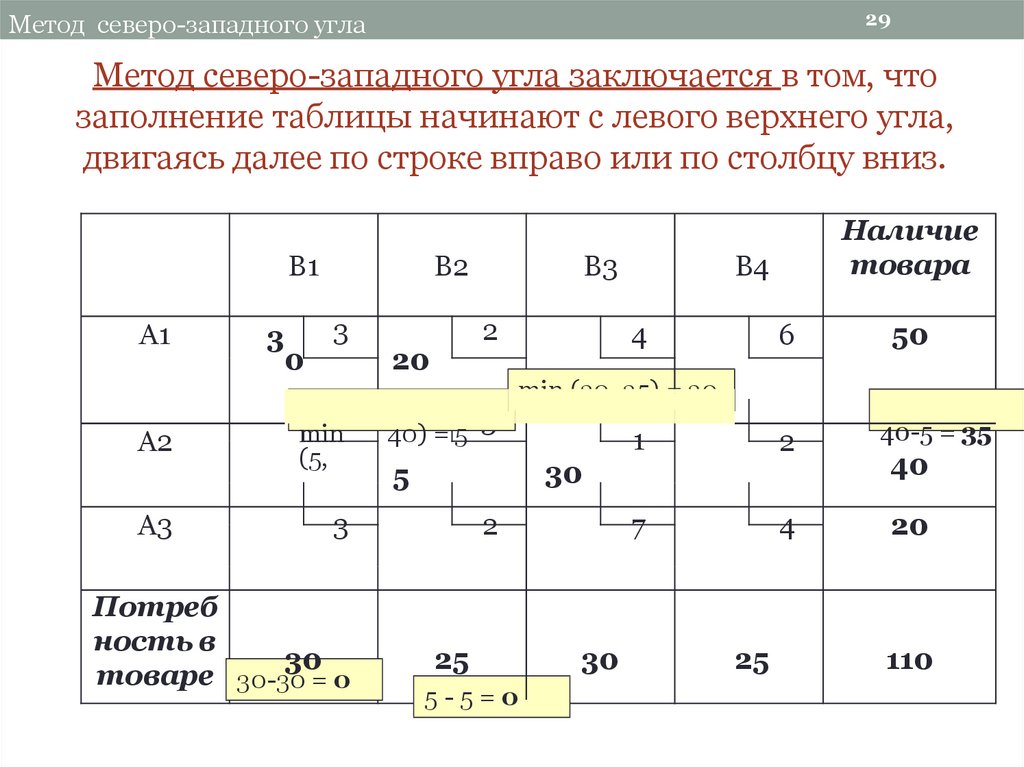 В 50-60-е гг. методология была обновлена, преобразована в целый ряд специфических методов и стала все более широко применяться для решения проблем в промышленности и принятия решений в разных ситуациях. Сегодня модели и методы науки управления используются для решения таких задач, как регулирование транспортных потоков в городах и оптимизация графика движения в аэропортах, составление графиков работы классов и аудиторий в университетах, управление запасами в супермаркетах и универмагах, разработка новых видов продукции, распределение расходов на рекламу различных видов продукции, планирование материального обеспечения, распределение оборудования и трудовых ресурсов для производства разных изделий на заводе, составление графика игр в высшей бейсбольной лиге на сезон.  [c.220]

Зависимость отдельных составляющих целевой функции от числа пунктов разгрузки, включенных в какой-либо вариант внешнего транспортного обеспечения и условно рассматриваемых как непрерывные функции в области целочисленных величин числа пунктов разгрузки пгв, представлена на рис.

27. Как видно из рисунка, с увеличением числа пунктов разгрузки возрастают суммарные затраты на их организацию и уменьшаются транспортные расходы по доставке труб к месту работ. Следовательно, целевая функция как сумма указанных составляющих имеет экстремум при некотором значении числа пунктов разгрузки. Учитывая нелинейную зависимость функционала и его отдельных составляющих от числа вводимых пунктов разгрузки и искомых переменных, для решения поставленной задачи не могут быть применены классические методы математического программирования (например,. линейного). Как известно из курса высшей математики, математическое программирование — область математики, разрабатывающая теорию и методы решения многомерных экстремальных задач с ограничениями, т. е. задач на экстремум функции многих переменных с ограничениями на область изменения этих переменных. Само название программирование взято из линейного программирования, где оно обычно обозначает распределение наилучшим образом ограниченных ресурсов для достижения поставленных целей. Следовательно, термин программирование здесь можно заменить термином планирование .  [c.145]

Фаза регулирования. Здесь решаются функциональные задачи (рис.7.7) календарного планирования и диспетчирования производства, т. е. на основе информации и принятых решений в фазе анализа происходит оперативное воздействие на параметры производственного процесса. Для формального описания задач регулирования привлекаются методы и модели календарного и сетевого планирования, транспортные модели и модели оперативного управления. Результатной информацией этой фазы являются календарные и сетевые графики производства продукции, маршруты, алгоритмы диспетчирования.  [c.273]

Соответствующая задача сводится к сетевой транспортной задаче с дополнительными ограничениями (,СТЗ ДО), где условия СТЗ полностью определяются сетью (графом) задачи, а дополнительные ограничения формируются по информации о связующих дугах. При этом число дополнительных ограничений равно (А —1)7, где / — число цепочек в (7 + 1)-й подсети.

Для решения возникающей задачи могут быть использованы специальные алгоритмы и программы решения СТЗ ДО. Следует подчеркнуть, что в этих алгоритмах существенно используется структура матрицы СТЗ ДО, т. е. на каждой итерации операции преобразования обратной матрицы строятся в соответствии с методом потенциалов решения СТЗ.  [c.70]

СУДЕБНАЯ ЭКСПЕРТИЗА — исследование, проводимое экспертом в порядке, предусмотренном процессуальным законодательством, для установления по материалам уголовного или гражданского дела фактических данных и обстоятельств. Основанием для проведения СУДЕБНОЙ ЭКСПЕРТИЗЫ служит постановление лица, производящего дознание, следователя, прокурора, определение суда о назначении экспертизы. В ходе СУДЕБНОЙ ЭКСПЕРТИЗЫ на основании специальных научных познаний и исследований, необходимых для экспертизы материалов уголовного либо гражданского дела, устанавливаются факты, обстоятельства. Предмет экспертизы предопределяется вопросами, поставленными следователем или судом.

Объектом экспертизы могут быть вещественные доказательства, части трупа, обстановка места происшествия, сравнительные образцы и т.д. Судебные экспертизы проводятся при помощи определенных приемов и с использованием разнообразных технических средств, с учетом предмета экспертизы. Для различных видов СУДЕБНОЙ ЭКСПЕРТИЗЫ разработана специальная методика, т.е. комплекс методов, которые реализуются в определенной последовательности — по этапам исследования, очередности решения частных задач для определения целого и т.п. Проводимые в следственно-судебной практике экспертизы классифицируются по их предмету, объекту, методике исследования и т.д. По степени общности задач, предмета, объектов, методик исследования различают экспертизы криминалистические, инженерно-транспортные, медицинские и психофизиологические, биологические, планово-экономические, в т.ч. бухгалтерские, экологические, инженерно-технические (в их числе можно назвать пожарно-технические, строительно-технические, по технике безопасности и др. ).  [c.215]

Метод коэффициентов интенсивности основан на замене однократного решения нелинейной задачи развития и размещения с дискретными переменными многократным решением серии обычных линейных транспортных задач с непрерывными переменными. Переход от одной транспортной задачи к другой осуществляется взаимосвязанным изменением мощности и соответствующих ей удельных производственных затрат для какого-либо одного пункта производства.  [c.151]

Целью транспортных методов является определение наилучших путей перевозки грузов из нескольких пунктов снабжения в несколько пунктов назначения (потребления), обеспечивающих наименьшие суммарные затраты по производству и транспортировке товаров. Обычно рассматриваются мощности каждого из источников товаров и потребности в этих товарах каждого из пунктов потребления. Каждая фирма, имеющая сеть поставщиков и потребителей, сталкивается с такой задачей. Хотя линейное программирование и может быть использовано для ее решения, более эффективными все-таки являются специальные методы решения транспортной задачи. Как и в линейном программировании, процесс решения транспортной задачи с использованием специальных методов начинается с определения допустимого начального решения, которое затем шаг за шагом улучшается до оптимума. Транспортные методы чрезвычайно просты для решения вручную .  [c.213]

Модель (1) — (4) и ее конкретная реализация (5) — (15) — есть классическая транспортная задача линейного программирования. Найдем численное решение задачи (5) — (15) методом потенциалов.  [c.254]

Большие объемы перевозимых автотранспортом строительных материалов, широкая их номенклатура и значительное количество грузоотправителей и грузополучателей предопределяют мно жество вариантов по их увязке между собой. Выбрать из них наиболее эффективный можно только при помощи современных математических методов и электронно-вычислительных машин (ЭВМ). Задача с большим числом пунктов производства и потребления продукции при сложной системе транспортной сети, называемая транспортной, решается методом линейного программирования с применением ЭВМ. Кроме транспортных затрат, для минимизации задачи могут быть использованы показатели времени перевозки, расстояния транспортировки и др. С помощью линейного программирования решаются также задачи по формированию веерных и кольцевых маршрутов, определению кратчайших расстояний перевозок и др. Решение таких задач позволяет определить объемы поставок, расстояние транспортировки, стоимость производства продукции с учетом мощности предприятий, наличие порожняковых пробегов, состояние дорог и скорость движения на различных ее участках.  [c.337]

ЗАДАЧА О КРАТЧАЙШЕМ ПУТИ (shortest route problem) — задача о нахождении на ориентированном графе пути наименьшей длины между двумя заданными его вершинами Длиной пути такого графа называется сумма длин дуг, составляющих этот путь 3 о к п возникает чаще всего при решении транспортных задач, дискретных задач программирования динамического и др В сетевых методах планирования и управления алгоритмы решения 3 о к п используют для нахождения критического пути Известно несколько эффективных методов ее решения Так, для анализа трансп сетей применяют алгоритм, основанный на методе последовательного анализа вариантов  [c. 69]

Рост масштабов и сложности задач управления, повсеместное внедрение принципа разделения труда и вытекающего из него принципа делегирования части полномочий по принятию решений исполнителям (принцип неокончательности и свободы принятия решений) со временем потребовали решительного снижения ошибок в выборе наилучшего решения. Это, в свою очередь, привело к необходимости обобщить опыт и знания, предложить теорию, которая их превратила бы в стройную систему научных взглядов на управление и разработку решений. Родилась парадигма «рациональных решений». Принципы, заложенные в парадигму рациональных решений, предполагают прежде всего моделирование реальной ситуации, т. е. представление ее в упрощенном для изучения виде с сохранением всех значимых характеристик и связей. После моделирования ситуации моделируют цель, формируя и измеряя требуемые результаты. Это расчленило процесс на более простые фазы, позволило распараллелить работы по разработке решений, на порядок снизить ошибки в принятии решения. Парадигма «рациональных решений» по мере своего развития претерпела ряд изменений. Вначале она делала акцент на использование чисто формальных методов, основанных на «физических измерениях». При этом родились такие классические постановки задач и методы исследования операций, как «транспортная задача», «задача массового обслуживания», «задачи сетевого планирования», «управления запасами», «задача о назначении» и др. Правда, перечисленные формальные задачи и методы не всегда оказывались хорошо приспособлены к практическим делам. Это зачастую приводило к нелепостям и разочарованиям. Самые большие неудачи этой науки связаны с пробле-  [c.65]

При значительных размерах задачи Ю. Ю. Фипксль-штейн предложил специальный метод ее решения, основанный на многократном применении алгоритма транспортной задачи1. Метод этот итеративный и в настоящем пособии не рассматривается.  [c.248]

Предлагаемое пособие написано на основе зарубежных и отечественных журнальных публикаций, а также оригинального материала и легло в основу лекций, прочитанных автором студентам 3-4 курсов математико-механического факультета Уральского госуниверситета, специализирующимся на применении математических методов и информатики в экономике. В пособие включены основные факты из качественной теории конечномерных вариационных неравенств и задач о дополнительности, а также краткий обзор методов их решения, главным образом тех, что используют свойства монотонности входящих в постановки отображений. Отдельно разобран случай линейной задачи о дополнительности и рассмотрены конечные методы ее решения. Приведены разнообразные экономические приложения, в том числе модели равновесия в транспортных сетях и модель общего экономического равновесия Вальраса.  [c.3]

Становление современного математического аппарата оптимальных экономических решений началось в 40-е годы, благодаря первым работам Н. Винера, Р. Беллмана, С. Джонсона, Л. Канторовича. Задача линейного программирования впервые математически сформулирована Л. В. Канторовичем в 1939 г. на примере задачи раскроя материалов для Ленинградского фанерного треста. В 1947 г. Дж. Данциг предложил универсальный алгоритм решения задач линейного программирования, названный им симплекс-методом. В 1941 г. Хичкок и независимо от него в 1947 г. Купсман формулируют транспортную задачу, в 1945 г. Стиглер — задачу о диете. В 1952 г. было проведено первое успешное решение задачи линейного программирования на ЭВМ Sea в Национальном бюро стандартов США.  [c.102]

Составление планов перевозок нефтепродуктов по железным дорогам с помощью экономико-математических методов и ЭВМ — это только первый этап решения транспортной задачи в условиях функционирования АСУнефтеснаб. В данном случае за пункты отгрузки нефтепродуктов принимаются места их производства, т. е. нефтеперерабатывающие заводы, перевалочные нефтебазы, расположенные по берегам морей и рек, железнодорожные пункты налива магистральных нефтепродуктопрово-дов, при этом затраты на доставку нефтепродуктов в указанные пункты водным и трубопроводным транспортом, а также расходы на перевалку не учитываются.  [c.231]

СТОХАСТИЧЕСКОЕ ПРОГРАММИРОВАНИЕ [sto hasti programming] — раздел математического программирования, совокупность методов решения оптимизационных задач вероятностного характера. Это означает, что либо параметры ограничений (условий) задачи, либо параметры целевой функции, либо и те и другие являются случайными величинами (содержат случайные компоненты). В ст. «Транспортная задача «, напр., приведена детерминированная модель. В стохастической постановке та же задача будет более близкой к реальности. Рассмотрим одно условие (заданный объем спроса) и допустим, что спрос Ъ. потребителя j — случайная величина b(w), где w — характеристика распределения этой величины. Тогда в одних случаях (при одних ее реализациях) возникает ущерб от неудовлетворенного спроса — «штраф за дефицит», в других, наоборот, потребитель получает излишний груз и, следовательно, тратит дополнительные средства на хранение и перевозку. Все это усложняет решение задачи, т.е. нахождение оптимального варианта прикрепления поставщиков к потребителям.  [c.348]

ЗАДАЧА О ПЕРЕВОЗКАХ С ПРОМЕЖУТОЧНЫМИ ПУНКТАМИ (transshipment problem) — обобщенная транспортная задача, когда для каждого пункта потребления составляется ур-ние баланса материального 3 о п с п п можно представить в сетевом виде Она является прикладной задачей программирования линейного Для ее решения применяются симплекс-метод, методы графов теории 3 о п с п п применяется при управлении процессами транспортирования грузов через промежуточные базы либо транспортирования сырья с промежуточной переработкой, напр заготовка металлолома у поставщиков, перевозка, переработка его на пунктах промежуточной обработки (прессование и вывоз потребителям — металлургическим заводам) См также Сетевые методы планирования и управления  [c. 69]

Во-вторых, специфика зависимости величины минимума расхода электроэнергии на перекачку от ее объема (в соответствии с принципом 1 это и отображено в критерии оптимальности) такова, что эта зависимость выражается кусочно-линейной выпуклой (вниз) функцией. Это позволило построить точный, быстро сходящийся алгоритм решения задачи, являющейся обобщением метода потенциалов решения сетевой транспортной задачи линейного программирования (СТЗ ЛП) для случая кусочно-линейного выпуклого функционала [41, 47]. Для построения экономико-математической модели задачи введем обозначения г — номер вершины сети 3 (г, s) —дуга сети между вершинами г и s R(E) — множество вершин (дуг) сети Rir(R rвершин сети, из которых выходят дуги, входящие в r-ю вершину (в которые входят дуги, выходящие из г-й вершины) ur(vr) — объем поступления (потребления) нефти в r-й вершине за плановый период . х — объем перекачки нефти по дуге (г, s) за плановый период ars(Prs) — нижний (верхний) предел значений xrs frs(xrs) — функция зависимости расхода электроэнергии от объема перекачки для дуги (г, s).  [c.156]

Формаль ю-математич. особенности модели транспортной задачи, позволяющие применить к ее решению Р. м. л. п. (более простой, чем, напр., симплексный метод), относятся к характеру ограничений, наложенных на значения переменных. Эти особенности заключаются в следующем а) ограничения носят двухсторонний характер, напр., в транспортной задаче — по наличию грузов в пунктах отправления и по потребности в них в пунктах назначения в производственной задаче — по наличной производственной мощности (производительности) оборудования и по потребности в разных видах продукции и т. п. вследствие этого каждая переменная Хц входит в 2 уравнения в сочетании каждый раз с другими переменными б) все переменные. ЗГу входят в уравнения — ограничения с коэффициентом 7, т. е. все эти уравнения представляют простые суммы переменных, взятых в различных сочетаниях.  [c.405]

При огромном количестве различного рода энергетич. потребителей, с одной стороны, при различных условиях н экономич.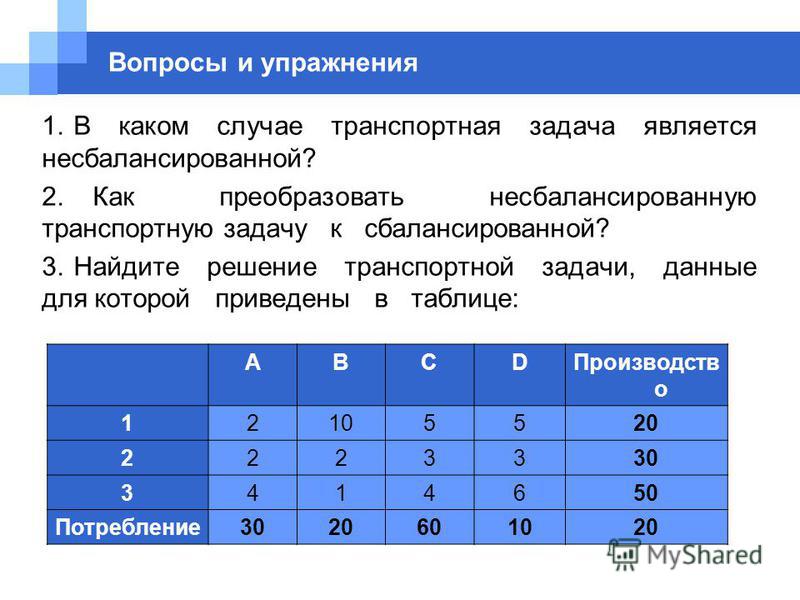 показателях добычи и реализации топливно-энергетич. ресурсов по отдельным районам и месторождениям, с другой стороны, множественности и разнохарактерности транспортных связей между потребителями и источниками энергетич. ресурсов и т. д. решение задачи оптимизации Т.-э. б. требует, как правило, применения методов математич. анализа к эконэмич. расчетам и использования электронно-вычислительной техники. При этом, ввиду нелинейного характера ряда экономич. зависимостей, характеризующих добычу и использование топливно-энергетич. ресурсов и очень сложных зависимостей между экономикой технологич. и энергетич. процессов, обобщающее решение этой задачи пока еще не найдено. Но используемые в СССР частные приближенные решения по оптимизации Т.-э. б. позволили значительно улучшить, теоретически и экономически обосновать перспективные планы развития всех отраслей энергетич. х-ва (см. Топливный баланс оптимальный). А. М. Некрасов, А. Я. Ризник, Е. О. Штейнгауа.  [c.208]

Условие Xtj — 1 или 0, вообще говоря, сильно усложняет задачу и делает невозможным непосредственное применение методов линейного программирования. Далее мы будем специально рассматривать такие задачи в параграфе, посвященном целочисленному программированию. Что же касается задачи о назначениях, то для нее доказано, что можно заменить условие я, 7=1 или 0 на более простое 0 решения транспортной задачи, то в данном случае он автоматически приведет к целым x/j, т. е. к реше нию задачи в ее первоначальной постановке. Таким образом, оказывается, что задача о назначениях также, по существу, описывается моделью транспортной задачи.  [c.47]

Легко заметить, что задача о кратчайшем пути является частным случаем транспортной задачи в сетевой постановке (или, что то же самое, задачи об оптимальном потоке). Для этого достаточно присвоить вершине s единичный запас, вершине t единичную потребность, все остальные вершины положить нейтральными, а дугам присвоить неограниченные пропускные способности. Однако, как правило, более рациональным оказывается использование конкретных свойств данной задачи и решение ее специальными (частными) методами. К их числу относится, например, метод Минти, основные идеи которого мы изложим ниже.  [c.129]

Решение транспортных задач с использованием свойств многомерного пространства



В данной статье рассматриваются понятия четырехмерного пространства и гиперкуба, а также вопросы практического применения тессеракта к решению транспортных задач. Проводится анализ методов решения транспортных задач с помощью гиперкуба, математических формул и САПР MathCAD.

Ключевые слова: гиперкуб, тессеракт, транспортная задача, САПР MathCAD.

Цель работы: изучение методов решения транспортных задач и выбор наиболее рационального.

Задачи работы:

1. Проанализировать специальную литературу по теме исследования.
2. Изучить измерения пространства-времени и обосновать возможно решения транспортной задачи с помощью многомерного пространства.
3. Изучить способы решения транспортных задач.
4. Выявить преимущества и недостатки методов решения транспортных задач.

Введение

Перевозка и доставка грузов, планирование с учётом необходимых товаров в разном регионе, городе является неотъемлемой частью экономики как теоретической, так и практической. Давайте ненадолго представим, что мы предприниматели и открываем новую сеть магазинов. Прибыль у хозяина будет складываться только тогда, когда доходы от продажи будут превышать расходы. Но как минимизировать последние? Как, куда и откуда нужно транспортировать товары с наименьшими затратами на перевозку, когда у тебя десятки вариантов путей? Как наиболее рационально расположить магазины по городу, чтобы они были одновременно близки и к потребителю, и к поставщику?

На эти вопросы отвечает логистика, которая предлагает разные варианты решения задач оптимизации. Есть много способов решения этих задач. В данном исследовании рассмотрена транспортная задача и способы её решения, один из которых предусматривает использование многомерного пространства.

Многомерное пространство.

Пространство — форма существования материальных объектов и процессов. Оно состоит из трёх плюс одного измерения. Первое — это длина. Второе измерение — это ширина. Длинная и ширина вместе образуют двухмерное пространство или плоскость. Третье измерение — это высота. Длинна, ширина и высота образуют объём или пространство. Четвёртое измерение — не является пространственным, как первые три. Оно одно в своём роде. Мы не можем его увидеть или потрогать, однако мы очень хорошо его чувствуем. Четвёртое измерение — это ВРЕМЯ.

На самом деле, количество измерений не ограничено, в математике их может быть сколько угодно, но существуют они для решения разных задач и не имеют общих названий. Для их обозначения в геометрии, существует такое понятие как гиперкуб. Гиперкуб — обобщение куба с произвольным числом измерений

Для решения транспортной задачи рассматривается 4 вида гиперкубов: отрезок, квадрат, куб и тессеракт. Как это может быть видно: все они отлично демонстрируют пространственные и временное измерения, а также их непосредственную взаимосвязь, поскольку существование последующего гиперкуба невозможно без предыдущего.

Рис. 1. Тессеракт

Транспортная задача

Однако, какое это имеет отношение к решению транспортной задачи? Прежде чем ответить на этот вопрос, узнаем, а что такое транспортная задача. Транспортная задача — математическая задача линейного программирования об оптимальном плане перевозок грузов из пунктов отправления в пункты потребления с минимальными затратами.

Условие этой задачи таково. Однородный груз сосредоточен у m поставщиков в объемах a1, a2,… am. Данный груз необходимо доставить n потребителям в объемах b1, b2… bn. Известны C_ij, i=1,2,…m; j=1,2,…n — стоимости перевозки единиц груза от каждого i-го поставщика каждому j-му потребителю. Переменными транспортной задачи являются x_ij — объемы перевозок от i-го поставщика каждому j-му потребителю.

Требуется составить такой план перевозок, при котором запасы всех поставщиков вывозятся полностью, запросы всех потребителей удовлетворяются полностью, и суммарные затраты на перевозку всех грузов являются минимальными.

Таблица 1

Исходные данные транспортной задачи

Математическая формулировка транспортной задачи: найти переменные задачи X=(x_ij), i=1,2,…,m; j=1,2,…,n, удовлетворяющие системе ограничений, при которой запасы всех m поставщиков вывозятся полностью, удовлетворены запросы всех n потребителей, условиям не отрицательности и обеспечивающие минимум целевой функции.

В рассмотренной в рамках данной статьи модели транспортной задачи предполагается, что суммарные запасы поставщиков равны суммарным запросам потребителей. Решаются такие задачи несколькими способами. В статье рассмотрены математический метод, метод с использованием гиперкуба и с помощью системы автоматизированного проектирования (САПР) MathCAD.

Решение транспортной задачи методом потенциалов.

В качестве предмета исследования будет выступать следующая задача. В таблице приведены исходные данные транспортной задачи: расстояние от поставщика к потребителю в километрах, и спрос потребителя в тоннах некоего товара. Сформулируйте экономико-математическую модель транспортной задачи, распределительным методом найдите оптимальный план перевозок.

Таблица 2

Пример транспортной задачи (исходные данные)

Поставщики	Возможности поставщиков	Потребители иих спрос
		I	II	III	IV	V
		150	350	200	100	100
I	500	3	3	5	3	1
II	300	4	3	2	4	5
III	100	3	7	5	4	2

Целевая функция L= в рассматриваемой задаче стремится к минимуму. Проверим условие того, что данная модель задачи закрытая: 150+350+200+100+100=900 и 500+300+100=900. Построим начальный опорный план, методом минимальной стоимости, согласно которому, сперва заполним ячейки с минимальными затратами на перевозку. И когда весь груз распределён, перейдем к оптимизированию полученного плана.

Проверка плана транспортной задачи в описываемом методе на оптимальность осуществляется с помощью потенциалов. Потенциалы — это такие числа, которые по определенным правилам назначаются каждой строке и каждому столбцу. Потенциалы строк обозначим u_i, потенциалы столбцов — v_j. Они могут принимать любые значения. Однако удобнее работать с положительными, целыми и относительно небольшими числами. Такой потенциал первоначально назначается любой строке или столбцу. В нашем случае зададим потенциал второй строке равный нулю (U₂=0). Подсчёт потенциалов осуществим по условию: U_i+V_j=С_ij

Сперва с помощью этой формулы и потенциала 2 строки рассчитаем потенциалы столбцов, а затем потенциалы оставшихся строк. Получим следующую таблицу.

Таблица 3

План перевозок

	150	350	200	100	100	Ui
500	3	3 (+) 100	5(-) 200	3 100	1 100	0
300	4 50	3(-) 250	(+) 2	4	5	0
100	3 100	7	5	4	2	-1
Vj	4	3	5	3	1

Общая стоимость перевозок согласно этому плану равняется 2850 ед. Проверяя условие оптимальности в свободных клетках по условию U_i+V_j≤с_ij, получим что в клетках с координатами (1,1) и (2,3) условие не выполняется, следовательно, требуется улучшение плана. Способ улучшения плана — переброска груза по циклу. Для этого каждой клетке цикла присваивают знаки (+) или (-), чередуя их, начиная с (+) в клетке, в которой не выполняется условие оптимальности. Затем выбирают наименьшую перевозку из базисных клеток со знаком (-) и прибавляют её в клетку со знаком (+) и вычитают в клетках со знаком (-).

В результате получим следующий таблицу стоимости перевозок.

Таблица 4

Оптимизированный план перевозок

	150	350	200	100	100	Ui
500	3 50	3 250	5	3 100	1 100	0
300	4	3 100	2 200	4	5	0
100	3 100	7	5	4	2	0
Vj	3	3	2	3	1

Подсчитаем стоимость — она равно 2300 ед.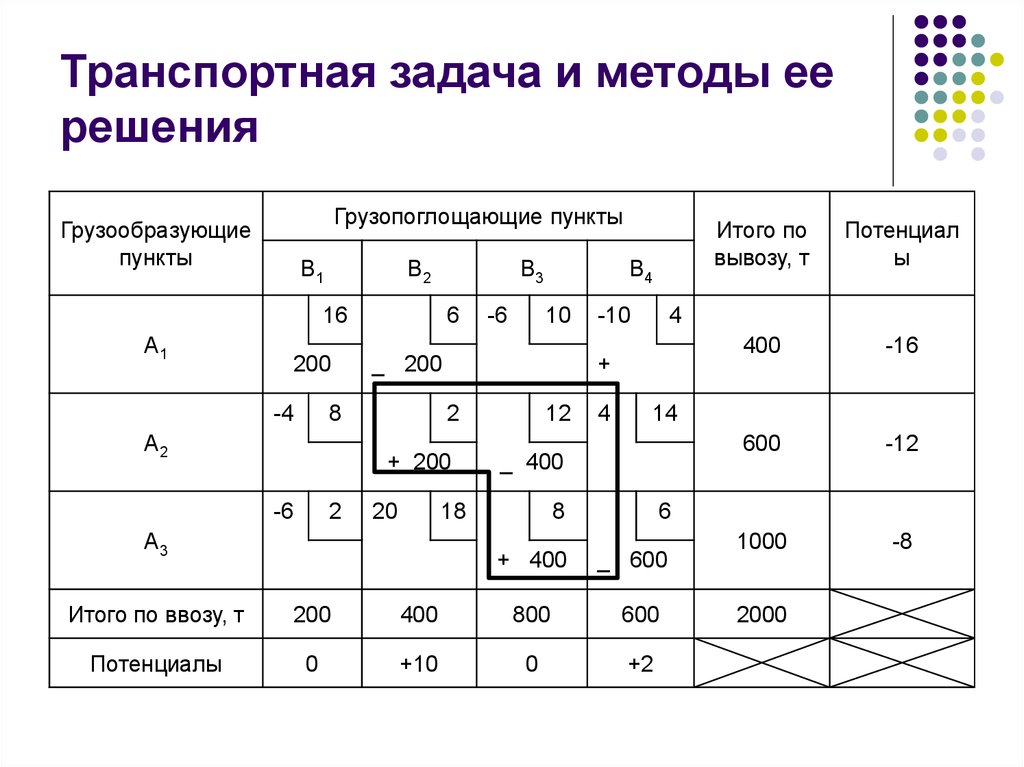 и опять проверим план на оптимальность для базисных и для свободных клеток. Поскольку все условия оптимальности соблюдены, то данный план можно считать оптимальным.

Решение транспортной задачи спомощью гиперкуба.

Теперь рассмотрим решение этой же транспортной задачи методом гиперкуба. Для этого метода начальный опорный план составляется с использованием переменных, значения которых в последствии будут найдены при помощи построения сечения гиперкуба в системе координат.

Таблица 5

Опорный план транспортной задачи («метод гиперкуба»)

Поставщики	Возможности поставщиков	Потребители иих спрос
		I	II	III	IV	V
		150	350	200	100	100
I	500	3x	3 y	5 0	3 z	1 500-x-y-z
II	300	4 0	3 350-y	2 200	4 100-z	5 0
III	100	3 150-x	7 0	5 0	4 0	2 x-50

Как видно из таблицы, некоторые значения были сразу взяты за ноль. Это объясняется невыгодностью перевозок от этого поставщика к этому потребителю.

Учитывая, что все значения, входящие в эту таблицу, должны быть не отрицательны, составим систему неравенств.

Из двух последних уравнений второй строки следует, что xЄ. Эта система определяет некоторый многогранник, а для того, чтобы его построить изобразим сначала многогранник, определяемый первой и второй строкой данной системы. Это параллелепипед ABCDA₁B₁C₁D₁. Уравнение 500-x-y-z определяет плоскость (RGH), пересекающую параллелепипед в точках A1, B, N. На многограннике A₁D₁C₁NADCB выполняются все условия данной системы. Назовём его многогранником ограничений.

Рис. 2. Многогранник ограничений

Теперь найдём общую стоимость перевозок, сложив и перемножив стоимости и объёмы перевозимого товара. Получаем выражение: x-y-2z+2700

Таким образом задача сводится к отысканию наименьшего значения функции F=2700-(y-x+2z) на многограннике ограничений. Для этого достаточно найти наибольшее значение функции f=y-x+2z, тогда F_min=2700-F_max. Вычислив значения F_max в вершинах многогранника, получаем, что равно оно 500 и достигается в точке А1 с координатами (50;350;100). Подставив значения переменных в таблицу получаем план перевозок:

Видно, что полученный ответ не совпадает с ответом, полученным в решении с использованием метода потенциалов. Потребитель II получает свои 350 тонн груза, однако этот груз ему доставляет поставщик I, согласно полученному плану, тем самым полностью исчерпывает свой лимит в 500 тонн груза. Потребитель же V не получает необходимые ему 100 тонн груза, зато у поставщика II остаются лишние 100 тонн груза. Таким образом, полученный план перевозок не был до конца оптимизирован.

В случае, если, оставшиеся 100 тонн груза у второго поставщика, доставить потребителю v, то получиться новый план перевозок, со стоимостью равной 2300 д. е.

Решение транспортной задачи спомощью САПР MathCAD.

Видно, что план перевозок совпадает с планом, полученным при решении методом потенциалов.

Заключение.

Так или иначе, можно сделать вывод о том, какой из этих трёх способов наиболее рационален: метод потенциалов достаточно объёмен, и предусматривает большое обилие вычислений. Плюс ко всему этот метод — есть цикл, во время которого мы проверяем условия для базисных и свободных клеток. Цикл этот может повторяться сколько угодно, и так и не соблюсти все условия, поэтому данный метод решения транспортной задачи рациональным назвать трудно.

Удобство САПР MathCAD проявляется в возможности использовать одну задачу как шаблон для других, просто меняя числа, однако, чтобы сделать этот шаблон, нужно иметь навык работы с программой, ну и разумеется саму программу, которая стоит совсем не дёшево.

Метод гиперкуба не требует обширных знаний в области математики или IT технологий. Он понятен, быстр в использовании, а также не имеет большого объёма вычислений, что делает его практически идеальным способом решения транспортных задач.

Литература:

1. Алексеев Е. Р., Чеснокова О. В. Основы работы в математическом пакете MathCAD. Учебное пособие. — Донецк: ДонНТУ, 2012.
2. Болотов В. П. Начертательная геометрия многомерного пространства. — Владивосток: изд-во Морского государственного университета им. Г. И. Невельского, 2003.
3. Ибаньес Р. Мир математики. Четвёртое измерение: является ли наш мир частью другой вселенной? — М.: DeAgostini, 2014.
4. Рудык Б. М. Ермаков В. И. Общий курс высшей математики для экономистов. — М.: Инфра-М, 2010.
5. Хинтон С. Г. Четвертое измерение.- СПб.: Книгоиздательство «Новый человек», 1915.
6. Черняк А. А., Новиков В. А. Математика для экономистов на базе MathCAD. — СПб.: БХВ-Петербург, 2003.
7. Информационный портал Wikipedia [Электронный ресурс].
8. URL:https://ru.wikipedia.org/wiki/Тессеракт (Дата обращения: 07.11.2015г.)

Основные термины (генерируются автоматически): транспортная задача, III, задача, план перевозок, тонна груза, поставщик, потребитель, многогранник ограничений, многомерное пространство, условие оптимальности.

Транспортная задача. Метод потенциалов и метод минимального элемента. Решение задач и контрольных работ по линейному программированию онлайн

Краткая теория

---

Cимплекс-метод решения задачи линейного программирования является универсальным и применим для решения любых таких задач. Однако существуют некоторые частные типы задач линейного программирования, которые, в силу некоторых особенностей своей структуры, допускают решение более простыми методами. К ним относится, в частности, так называемая транспортная задача.

Классическая транспортная задача линейного программирования формулируется следующим образом:

Имеется  пунктов отправления: , в которых сосредоточены запасы какого-то однородного товара (груза) в количестве соответственно  единиц. Кроме того имеется  пунктов назначения: , подавших заявки соответственно на  единиц товара.

Предполагается, что сумма всех заявок равна сумме всех запасов:

Известная стоимость  перевозки единицы товара от каждого пункта отправления  до каждого пункта назначения . Таблица (матрица) стоимостей перевозки  задана:

Требуется составить такой план перевозок, при котором все заявки были выполнены, и при этом общая стоимость всех перевозок была минимальна.

При такой постановке задачи показателем эффективности плана перевозок является стоимость, поэтому поставленную задачу точнее называют транспортной задачей по критерию стоимости.

Дадим этой задаче математическую формулировку. Обозначим  — количество груза, отправляемого из i-го пункта отправления  и j-й пукнта назначения    Неотрицательные переменные  (число которых, очевидно, равно ) должны удовлетворять следующим условиям:

1. Суммарное количество груза, направляемое из каждого пункта отправления во все пункты назначения, должно быть равно запасу груза в данном пункте. Это даст дам  условий-равенств:

2. Суммарное количество груза, доставляемое в каждый пункт назначения изо всех пунктов отправления, должно быть равно заявке, поданной данным пунктом. Это даст  условий-равенств:

Суммарная стоимость всех перевозок, то есть сумма величин , умноженных на соответствующие стоимости  должна быть минимальной:

Перед нами типичная задача линейного программирования с ограничениями-равенствами.

Как и всякую другую задачу линейного программирования, ее можно было бы решить симплекс-методом, но данная задача имеет некоторые особенности, позволяющие решить ее более просто.

Условимся о терминологии. Значения  количества единиц груза, направляемых из пункта  в пункт  будем называть перевозками.

Любую совокупность значений  будем называть планом перевозок или просто планом.

План  будем называть допустимым, если он удовлетворяет условиям системы равенств (так называемым «балансовым условиям»): все заявки удовлетворены, все запасы исчерпаны.

Допустимый план будем называть опорным, если в нем отличны от нуля не более  базисных перевозок , а остальные перевозки равны нулю.

План  будем называть оптимальным, если он, среди всех допустимых планов, приводит к наименьшей стоимости всех перевозок.

Основные этапы решения транспортной задачи будут такими:

I этап.  Нахождение начального опорного плана .

II этап. Выделение из небазисных переменных вводимой в базис переменной (метод потенциалов). Если все небазисные переменные удовлетворяют условию оптимальности, то следует закончить вычисления; в противном случае — перейти к III этапу.

III этап. Выбор выводимой из базиса переменной (используя условия допустимости) из числа переменных текущего базиса; затем нахождение нового опорного решения и возвращение ко II этапу.

Пример решения задачи

---

В трех пунктах отправления  имеется однородный груз в количестве  соответственно. Этот груз нужно доставить пяти заказчикам . Потребности в грузе в каждом пункте  известны и равны  соответственно. Известны также тарифы перевозки  — стоимость перевозки единицы груза из пункта  в пункт . Нужно найти такой план перевозок, при котором весь груз из пунктов потребления будет вывезен, потребности всех заказчиков будут удовлетворены, и при этом общая стоимость перевозки всего груза будет наименьшей. Данные в таблице,  в клетках которой проставлены элементы матрицы тарифов ; в последнем столбце таблицы указаны значения величин , в последней строке - значения величин .

 

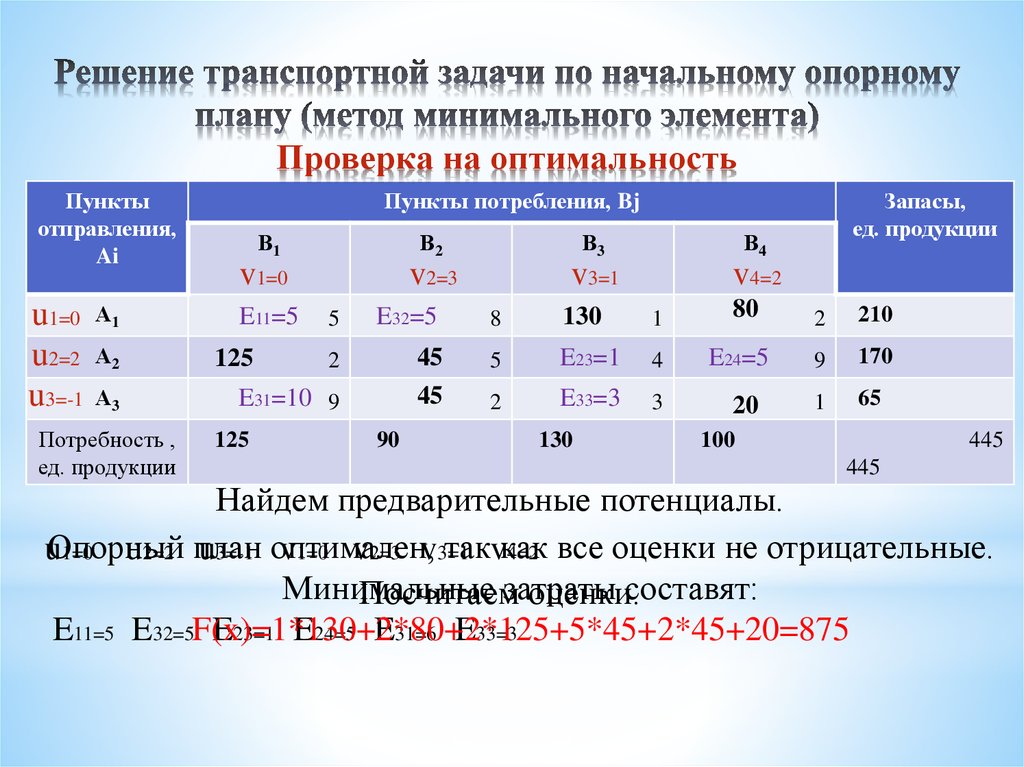
Заказчики Пункты
	4	9	2	5	3	23
	4	6	2	1	8	25
	6	2	3	4	5	17
	14	10	16	10	15

Требуется:

• Составить математическую модель задачи.
• Найти оптимальное решение транспортной задачи методом потенциалов.

Если не находите примера, аналогичного вашему, если сами не успеваете выполнить работу, если впереди экзамен по предмету и нужна помощь — свяжитесь со мной:

ВКонтакте
WhatsApp
Telegram

Я буду работать с вами, над вашей проблемой, пока она не решится.

Решение

Математическая модель задачи

Обозначим через  количество груза, перевозимого от  поставщика  потребителю. Тогда общая стоимость перевозок равна:

Ограничения для поставщиков:

Ограничения для потребителей:

Объем суммарных поставок любого поставщика к потребителю не может быть отрицательным числом, поэтому справедливы ограничения:   

Полученную задачу можно решить симплекс-методом, так как это классическая ЗЛП, однако относительная простота систем уравнений дает возможность использовать метод решения более простой. Особенности систем следующие:

коэффициенты при неизвестных во всех уравнениях равны 1;
1. каждая переменная встречается только в двух уравнениях; система уравнений транспортной задачи симметричная относительно всех переменных ;матрица, составленная из коэффициентов при переменных  состоит из единиц и нулей, причем каждый столбец матрицы содержит два элемента, равных 1, а остальные 0.

Проверка задачи на закрытость модели

Стандартная транспортная задача разрешима только в том случае, когда выполняется условие баланса:

В нашем случае:

Модель транспортной задачи закрытая.

Нахождение начального опорного плана и метод потенциалов

Заполняем таблицу по правилу минимального элемента .

Просматривая таблицу замечаем, что наименьшие затраты соответствуют маршруту , поэтому в клетку помещаем . В этом случае 4-й столбец в расчет не принимается. Просматриваем оставшиеся таблицы клетки. Наименьший тариф имеет клетка

Далее действуя по аналогичной схеме:

 

 Решать задачу будем методом потенциалов. Число занятых клеток должно быть . Потенциал 1-й строки принимаем равным нулю. После этого мы можем вычислить остальные потенциалы (если известны потенциал и тариф занятой клетки, то из соотношения v + u =c легко определить неизвестный потенциал).

Найдем оценки свободных клеток по формуле: 

S ( 1, 1)= 4-( 0-1)=  5	S ( 1, 2)= 9-( 0+ 0)=  9
S ( 1, 4)= 5-( 0-4)=  9	S ( 2, 2)= 6-( 5+ 0)=  1
S ( 2, 3)= 2-( 5+ 2)= -5	S ( 3, 1)= 6-( 2-1)=  5
S ( 3, 3)= 3-( 2+ 2)= -1	S ( 3, 4)= 4-( 2-4)=  6

Для клетки ( 2, 3) с минимальной отрицательной оценкой строим цикл.

Перемещаем груз, равный 1 из вершин, помеченных минусом к вершинам цикла, помеченным плюсом.

Вычисляем потенциалы:

Найдем оценки свободных клеток по формуле

S ( 1, 1)= 4-( 0+ 4)=  0	S ( 1, 2)= 9-( 0+ 0)=  9
S ( 1, 4)= 5-( 0+ 1)=  4	S ( 2, 2)= 6-( 0+ 0)=  6
S ( 2, 5)= 8-( 0+ 3)=  5	S ( 3, 1)= 6-( 2+ 4)=  0
S ( 3, 3)= 3-( 2+ 2)= -1	S ( 3, 4)= 4-( 2+ 1)=  1

 

Для клетки ( 3, 3) с минимальной отрицательной оценкой строим цикл.

Перемещаем груз, равный 7 из вершин, помеченных минусом к вершинам цикла, помеченным плюсом.

Вычисляем потенциалы:

Найдем оценки свободных клеток по формуле

S ( 1, 1)= 4-( 0+ 4)=  0	S ( 1, 2)= 9-( 0+ 1)=  8
S ( 1, 4)= 5-( 0+ 1)=  4	S ( 2, 2)= 6-( 0+ 1)=  5
S ( 2, 5)= 8-( 0+ 3)=  5	S ( 3, 1)= 6-( 1+ 4)=  1
S ( 3, 4)= 4-( 1+ 1)=  2	S ( 3, 5)= 5-( 1+ 3)=  1

Оценки свободных клеток не отрицательны, следовательно, полученный план является оптимальным:

Ответ

Пункт      поставляет 8 единиц груза в пункт   и 15 единиц груза в пункт  

Пункт   поставляет 14 единиц груза в пункт  , 1 единицу груза в пункт  и 10 единиц груза в пункт

Пункт      поставляет 10 единиц груза в пункт   и 7 единиц груза в пункт  

Минимальные транспортные издержки оптимального плана:

Методы нахождения первоначального базисного распределения поставок плана транспортной задачи

Николаева Светлана Ивановнавысшая квалификационная категория, преподаватель математики и информатики, бюджетное образовательное учреждение Чувашской Республики среднего профессионального образования «Алатырский сельскохозяйственный техникум» Минобразования Чувашии, г. Алатырь Чувашская Республика[email protected]

Методы нахожденияпервоначального базисного распределения поставок транспортной задачиАннотацияТранспортная задача относится к классу задач линейного программирования. Транспортная задача решает проблему нахождения оптимального (минимального) по стоимости плана распределения и перемещения ресурсов от производителей к потребителям. Проблема оптимизации стоимости перевозок актуальна и на сегодняшний день, так как позволяет фирмам и предприятиям существенно сократить расходы на транспорт. Правильная организация перевозок позволяет устранить встречные и дублирующие перевозки, сократить количество дальних перевозок. При решении транспортной задачи необходимо:Обеспечить всех потребителей ресурсамиРаспределить все произведенные ресурсыПереместить ресурсы от производителей к потребителям с наименьшими затратамиОт каждого производителя ресурс может перемещаться к любому потребителю и измеряться в одних единицах измерения.Цель:Выявить наиболее оптимальный метод нахождения опорного плана транспортной задачи

Цель определяет задачи:Познакомиться с основными методами нахождения базисного распределения поставок;Рассмотреть алгоритмы методов нахождения опорного плана;Проанализировать преимущества и недостатки каждого метода нахождения опорного плана транспортной задачиИзучив основные методы нахождения базисного плана транспортной задачи, проанализировав их преимущества и недостатки, можно сделать выводы:1)Наиболее простым алгоритмом нахождения базисного плана является метод «северозападного угла», но он является наиболее далеким от оптимального.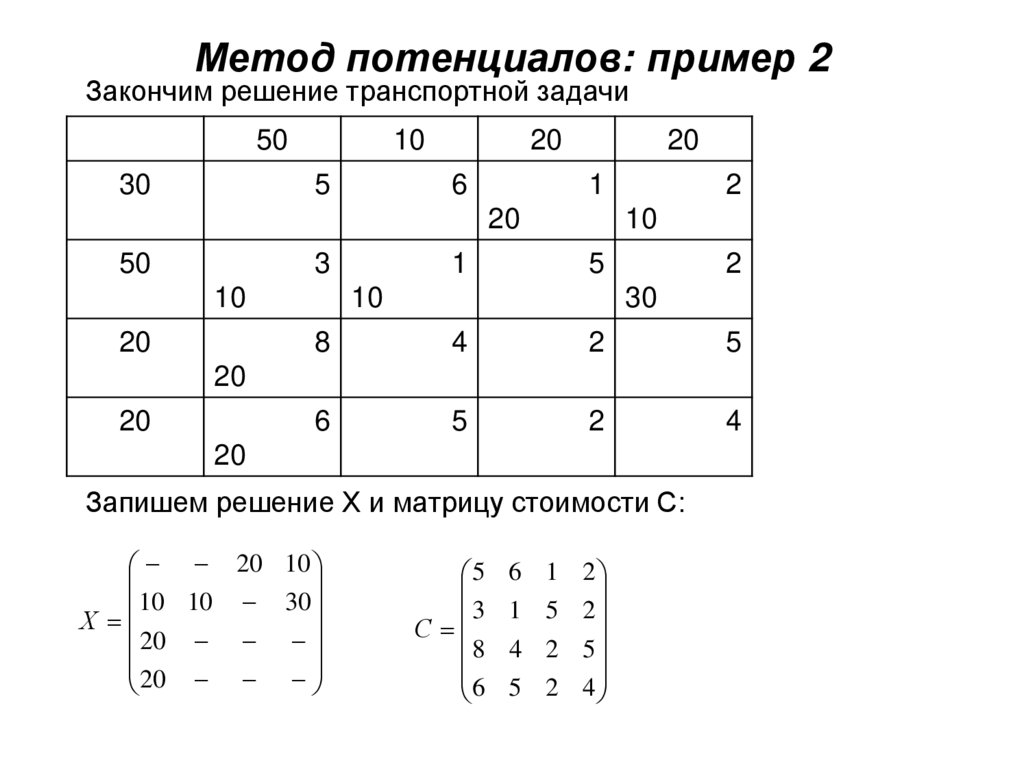 2)Метод Фогеля является достаточно трудоемким, но позволяет получить наименьшие суммарные затраты перевозок3)Для нахождения базисного плана методом Фогеля и симплексным методом можно воспользоваться возможностями программы «Оптимал» и электронной таблицы EXCEL, что ускорит расчеты.

Итак, наиболее близким к оптимальному плану решения транспортной задачи является метод Фогеля. Во многих случаях опорный план транспортной задачи, составленный именно этим методом также является и оптимальным.

Ключевые слова

транспортная задачи, базисный план, программа «Оптимал», симплексный метод, линейное программирование

Список цитируемой литературы:1.Баумоль У. Экономическая теория и исследование операций. –М.; Наука, 2004.2.Павлова Т.Н, Ракова О.А. Линейное программирование. Учебное пособие. Димитровград, 2002.3.Павлова Т.Н, Ракова О.А. Решение задач линейного программирования. Учебноепособие. Димитровград, 20024.Акулич И.Л. Математическое программирование в примерах и задачах: учебное пособие для ВУЗов. М.: Высшая школа, 20045.Исследование операций в экономике; Под ред. проф. Н.Ш. Кремера ЮНИТИ 20036.Красс М. Математика для экономических специальностей. Учебник. 3е изд., перераб и доп. М, Экономист, 2004.

ВведениеВ повседневной жизни мы часто сталкиваемся с необходимостью решать оптимизационные задачи. Например, заходя в магазин, мы стоим перед дилеммой максимального удовлетворения своих потребностей, соизмеряя их с возможностями нашего кошелька. Любой менеджер постоянно решает разнообразные проблемы, начиная с планирования штата сотрудников, фонда зарплаты и заканчивая составлением оптимального плана производства, планированием рекламной кампании по продвижению продукции и оптимизацией капиталовложений.Командиры на военных сборах решают задачи оптимального указания целей и наведения оружия на эти цели в расчете на максимальное поражение противника. Менеджер по транспортным перевозкам решает задачу минимизации транспортных издержек в условиях наиболее полного удовлетворения интересов производителей и потребителей.

Данная статьяпосвящена знакомству с одной из самых популярных и продвинутых экономикоматематических моделей транспортной задаче. Транспортная задача относится к классу задач линейного программирования. Транспортная задача решает проблему нахождения оптимального (минимального) по стоимости плана распределения и перемещения ресурсов от производителей к потребителям. Проблема оптимизации стоимости перевозок актуальна и на сегодняшний день, так как позволяет фирмам и предприятиям существенно сократить расходы на транспорт. Правильная организация перевозок позволяет устранить встречные и дублирующие перевозки, сократить количество дальних перевозок. При решении транспортной задачи необходимо:Обеспечить всех потребителей ресурсамиРаспределить все произведенные ресурсыПереместить ресурсы от производителей к потребителям с наименьшими затратамиОт каждого производителя ресурс может перемещаться к любому потребителю и измеряться в одних единицах измерения.Цель работы:Выявить наиболее оптимальный метод нахождения опорного плана транспортной задачи

Цель работы определяет задачи:Познакомиться с основными методами нахождения базисного распределения поставок;Рассмотреть алгоритмы методов нахождения опорного плана;Проанализировать преимущества и недостатки каждого метода нахождения опорного плана транспортной задачи

1. Общая постановка транспортной задачиОбщая постановка транспортнойзадачисостоит в определении оптимального плана перевозок некоторого однородного груза из тпунктов отправления в ппунктов назначения .При этом в качестве критерия оптимальности обычно берется либо минимальная стоимость перевозок всего груза, либо минимальное время его доставки. Рассмотрим транспортную задачу, в качестве критерия оптимальности которой взята минимальная стоимость перевозок всего груза. Обозначим через тарифы перевозки единицы груза из iго пункта отправления в jйпункт назначения, через –запасы груза в iм пункте отправления, через –потребности в грузе в j–м пункте назначения, а через –количество единиц груза, перевозимого из iго пункта отправления в jйпункт назначения. Тогда математическая постановка задачи состоит в определении минимального значения функции (1) при условиях (2) (3) (4) Поскольку переменные удовлетворяют системам уравнений (2) и (3) и условию неотрицательности(4), обеспечиваются доставка необходимого количества груза в каждый из пунктов назначения, вывоз имеющегося груза из всех пунктов отправления, а также исключаются обратные перевозки.

Определение 1. Всякое неотрицательное решение систем линейных уравнений (2) и (3), определяемое матрицей , называется планомтранспортной задачи. Определение 2. План , при котором функция (1) принимает свое минимальное значение, называется оптимальнымпланомтранспортной задачи. Обычно исходные данные транспортной задачи записывают в виде таблицы 1. Таблица 1. Исходные данные транспортной задачи

Очевидно, общее наличие груза у поставщиков равно , а общая потребность в грузе в пунктах назначения равна единиц. Если общая потребность в грузе в пунктах назначения равна запасу груза в пунктах отправления, т. е. (5) то модель такой транспортной задачи называется закрытой.Если же указанное условие не выполняется, то модель транспортной задачи называется открытой. [1]Теорема 1. Для разрешимости транспортной задачи необходимо и достаточно, чтобы запасы груза в пунктах отправления были равны потребностям в грузе в пунктах назначения, т. е. чтобы выполнялось равенство(5). В случае превышения запаса над потребностью, т. е. вводится фиктивный (n+1)–йпункт назначения с потребностью и соответствующие тарифы считаются равными нулю: Полученная задача является транспортной задачей, для которой выполняется равенство (5). Аналогично, привводится фиктивный (m+1)–йпункт отправления с запасом груза и тарифы полагаются равными нулю: Этим задача сводится к обычной транспортной задаче, из оптимального плана которой получается оптимальный план исходной задачи. В дальнейшем будем рассматривать закрытую модель транспортной задачи. Если же модель конкретной задачи является открытой, то, исходя из сказанного выше, перепишем таблицу условий задачи так, чтобы выполнялось равенство (5). Число переменных в транспортной задаче с тпунктами отправления и ппунктами назначения равно пт, а число уравнений в системах (2) и (3) равно п+т.Так как мы предполагаем, что выполняется условие (5), то число линейно независимых уравнений равно п+т–1. Следовательно, опорный план транспортной задачи может иметь не более п + т–1 отличных от нуля неизвестных. Если в опорном плане число отличных от нуля компонент равно в точности п+т–1, то план является невырожденным, а если меньше –то вырожденным. Как и для всякой задачи линейного программирования, оптимальный план транспортной задачи является и опорным планом. Транспортные задачи бывают:1) открытые m ≠ n (суммарный запас продукции, имеющейся у поставщиков, не совпадает с суммарной потребностью в продукции у потребителей.)2) закрытые m = n (суммарный запас продукции, имеющейся у поставщиков, совпадает с суммарной потребностью в продукции у потребителей.)[1]

2. Методы нахождения опорного плана транспортной задачи

2.1. Симплексный метод

Симплексметодэто итеративный процесс направленного решения системы уравнений по шагам, который начинается с опорного решения и в поисках лучшего варианта движется по угловым точкам области допустимого решения, улучшающих значение целевой функции до тех пор, пока целевая функция не достигнет оптимального значения.Транспортная задача относится к задачам линейного программирования. Одним из методов нахождения опорного плана является симплексный метод.Идея симплексметода относительно проста.[2]

Рассмотрим задачу:Фирма должна отправить некоторое количество кроватей с трёх складов в четыре магазина. На складах имеется соответственно 60, 120и 100кроватей, а для четырехмагазинов требуется соответственно 20, 110, 40и 110кроватей. Стоимости перевозок задаются матрицей:1 2531652

6374

Как следует спланировать перевозку, чтобы её стоимость была минимальной?[3]Решение:Построим экономикоматематическую модель задачи.Данная транспортная задача является закрытой, так как суммарная мощность поставщиков равна суммарной мощности потребителей.Таблица 2. Данные транспортной задачиПоставщикиМощность поставщиковПотребители и их спрос123420110401101601253

21201652

31006374

Пусть Xijпоставка клетки (i,j). Чтобы мощность каждого из поставщиков была реализована, необходимо составить уравнения баланса для каждой строки таблицы поставок:

Х11+Х12+Х13+Х14=60Х21+Х22+Х23+Х24=120Х31+Х32+Х33+Х34=100

Чтобы спрос каждого из потребителей был удовлетворен, подобные уравнения баланса составляются для каждого столбца поставок:

Х11+Х21+Х31=20Х12+Х22+Х32=110Х13+Х23+Х33=40Х14+Х24+Х34=110

Очевидно, что объем перевозимого груза не может быть отрицательным, поэтому Xij≥0, (i=1,2,3,j=1,2,3,4). Суммарные затраты на перевозку выражаются через коэффициенты затрат и поставки следующим образом:F=1Х11+2Х12+5Х13+3Х14+1Х21+6Х22+5Х23+2Х24+6Х31+3Х32+7Х33+4Х34 minДля решения задачи воспользуемся возможностями электронной таблицы EXCELи найдем значения переменных с помощью Поиска решения.

Рисунок 1. Решение транспортной задачи симплексным методом с помощью EXCEL

Рисунок 2. Ответы транспортной задачи симплексным методом с помощью EXCEL

Суммарные затраты равны:1420ден. ед.

2.2. Метод «Северозападного» угла

При использовании «Северозападного» метода опорный план начинают строить с левого верхнего (северозападного угла) матрицы перевозок по следующему алгоритму:1)Первому потребителю назначается ресурс от первого производителя. При этом возможны следующие варианты:Запрос первого потребителя удовлетворен не полностью, тогда недостающий ресурс первому потребителю добавляют от второго производителя и при необходимости от третьего производителя, до тех пор пока потребности первого потребителя не будут полностью удовлетворены. Запрос первого потребителя удовлетворен полностью. Остаток ресурса от первого производителя назначают второму потребителю, а при необходимости и третьему потребителю.Запрос первого потребителя обеспечен полностью ресурсом первого производителя и ресурс первого производителя израсходован полностью. Далее переходим к обеспечению запроса второго потребителя.2)Затем обеспечивают потребности второго потребителя по образцу первого потребителя. И так далее пока не будут обеспечены запросы всех потребителей.[4]

Рассмотрим нахождение базисногоплана транспортной задачи с помощью «северозападного угла»:Дадим переменной Х11максимально возможное значение, или максимально возможную поставку вклетку (1,1) –«северозападный» угол таблицы поставок: Х11=min(60,20)=20.После этого спрос 1 потребителя будет полностью удовлетворен, в результате чего первый столбецвыпадет из рассмотрения. В таблице поставок найдем новый «северозападный» уголклетку (1,2) и дадим в нее максимально возможное значение. Учитывая, что 1 поставщик уже отдал 20 единиц груза и у него осталось только 40=6020 единиц груза, получаем, что Х12=min(40,110)=40. После этого мощность 1 поставщика полностью реализована и из рассмотрения выпадет первая строка таблицы. В оставшейся таблице снова находим «северозападный» угол и т.д. В результате получаем исходное распределение поставок:

Таблица 3. Нахождение базисного плана транспортной задачи методом «северозападного угла»

ПоставщикиМощность поставщиковПотребители и их спрос123420110401101601

202

4053

212016

705

402

1031006374

100

Суммарные затраты: F=1*20+2*40+6*70+5*40+2*10+4*100=1140 Число заполненных клеток в полученном распределении оказалось равным m+n1=3+41=6, то есть числу базисных переменных.Существенный недостаток этого метода состоит в том, что он построен без учета значений коэффициентов затрат задачи.[5]

2.3. Метод наименьших затрат

Суть метода состоит в том, что в матрице стоимостей С = {сij}выбирается стоимость минимальной перевозки сij. Затем назначается максимальный объем ресурса от производителя iк потребителю jдля данной перевозки. При этом возможны три варианта:1) производитель iимеет ресурса больше, чем надо потребителю j.В этом случае удовлетворяется полностью заявка потребителя j’, а остаток произведенного ресурса будет распределен после. Так как потребность потребителя jудовлетворена полностью, то исключается из рассмотрения столбецматрицы стоимости, принадлежащий jму потребителю;2) производитель iимеет ресурса меньше, чем надо потребителю jВ этом случае весь имеющийся ресурс производителя iназначается потребителю jНедостающая часть ресурса потребителю jбудет назначена потом. Так как весь ресурс производителя iисчерпан полностью, то из рассмотрения удаляется строка матрицы стоимости, принадлежащая производителю i3) производитель iимеет ресурса столько, сколько надо потребителю j.В этом случае, аналогично рассмотренным выше случаям, из рассмотрения удаляются и строка, и столбецматрицы стоимости.Затем из матрицы стоимостей выбирается следующая минимальная стоимость перевозки ресурса от производителя к потребителю, удовлетворяются потребности следующего потребителя ресурса (полностью или частично) и удаляется из рассмотрения очередная строка или столбец матрицы стоимостей. Процесс повторяется до тех пор, пока не будет распределен полностью весь произведенный ресурс между всеми потребителями. Так как ресурса произведено ровно столько, сколько нужно потребителям, то задача распределения будет обязательно выполнена.[4]

Рассмотрим нахождение базисного плана транспортной задачи с помощьюметода наименьших затрат:Находим в таблице поставок клетки с наименьшим коэффициентом затрат. Таких клеток две

(1,1) и (2,1), с коэффициентами затрат, равными 1. Сравним максимально возможные поставки для этих клеток: для клетки (1,1) Х11=min(60,20)=20 идля клетки (2,1) Х21=min(120,20)=20. Так как они совпадают, то максимально возможную поставку даем в любую из них. Например, даем поставку, равную 20 единицам в клетку (2,1). В результате спрос первого потребителя удовлетворен и первый столбец таблицы поставок выпадает из последующего рассмотрения.В оставшейся таблицу наименьшим коэффициентом затрат обладают две клетки: С12=С24=2. Сравним максимально возможные поставки этих двух клеток: для клетки (1,2) Х12=min(60,110)=60, для клетки (2,4) Х24=(12020;110)=100. Даем поставку в клетку (2,4), для которой максимально возможная поставка оказалась больше: Х24=100. При этом из рассмотрениявыпадет строка таблицы поставок.

Аналогично заполним все оставшиеся клетки таблицы:

Таблица 4. Нахождение базисного плана транспортной задачи с помощью метода наименьших затрат

ПоставщикиМощность поставщиковПотребители и их спрос123420110401101601 2 6053

21201 206

5

2

100310063 507 404

10

Суммарные затраты: F=1*20+2*60+3*50+2*100+7*40+4*10=810

Как и ожидалось, при использовании метода «северозападного» угла суммарные затраты больше, чем при применении метода наименьших затрат. Таким образом, во втором случае мы находимся ближе к оптимуму, чем в первом.[5]

2.3.Метод Фогеля

При определении опорного плана транспортной задачи методом аппроксимации Фогеля на каждой итерации по всем столбцам и по всем строкам находят разность между двумя записанными в них минимальными тарифами. Эти разности записывают в специально отведенных для этого строке и столбце в таблице условий задачи. Среди указанных разностей выбирают максимальную. В строке (или в столбце), которой данная разность соответствует, определяют минимальный тариф. Клетку, в которой он записан, заполняют на данной итерации. Если минимальный тариф одинаков для нескольких клеток данной строки (столбца), то для заполнения выбирают ту клетку, которая расположена в столбце (строке), соответствующем наибольшей разности между двумя минимальными тарифами, находящимися в данном столбце (строке).[5]Так как метод Фогеля достаточно трудоемкий и требует много времени для решения, воспользуемся специальной программой «Оптимал». Данная программная система предназначена для ускорения процесса обучения студентов решению транспортных задач. Заполним таблицу: Рисунок 3. Заполнение таблицы в программе «Оптимал» для нахождения базисного распределения методом Фогеля

Найдем опорный план методом ФогеляРисунок 4. Нахождение опорного плана транспортной задачи методом Фогеля

Получим: Рисунок 5. Ответы решения транспортной задачи методом Фогеля

Суммарные затраты равны 760 ден. ед.Как правило, применение метода аппроксимации Фогеля позволяет получить либо опорный план, близкий к оптимальному, либо сам оптимальныйплан. Заключение

Транспортная задача линейного программирования получила в настоящее время широкое распространение в теоретических обработках и практическом применении на транспорте и в промышленности. Особенно важное значение она имеет в деле рационализации постановок важнейших видов промышленной и сельскохозяйственной продукции, а также оптимального планирования грузопотоков и работы различных видов транспорта.Кроме того, к задачам транспортного типа сводятся многие другие задачи линейного программирования задачи о назначениях, сетевые, календарного планирования.Изучив основные методы нахождения базисного плана транспортной задачи, проанализировав их преимущества и недостатки, можно сделать выводы:4)Наиболее простым алгоритмом нахождения базисногоплана является метод «северозападного угла», но он является наиболее далеким от оптимального.5)Метод Фогеляявляется достаточно трудоемким, но позволяет получить наименьшие суммарные затраты перевозок6)Для нахождения базисного плана методом Фогеля и симплексным методом можно воспользоваться возможностями программы «Оптимал» и электронной таблицы EXCEL, чтоускорит расчеты.

Итак, наиболее близким к оптимальному плану решения транспортной задачи является метод Фогеля. Во многих случаях опорный план транспортной задачи, составленный именно этим методомтакже является и оптимальным.

Транспортная задача — решение методом потенциалов

Одна из самых распространенных и востребованных оптимизационных задач в логистике — транспортная задача. В классическом виде она предполагает нахождение оптимального (т. е. сопряженного с минимальными затратами) плана грузоперевозок.

Например, у нас есть сеть розничных магазинов, которым требуется определенное количество товаров. Также имеется ряд складов поставщиков, где требуемые товары хранятся. При этом на каждом складе различный объем запасов этих товаров. Кроме этого нам известны тарифы — затраты на перевозку 1 товара от каждого склада к каждому магазину.

Возникает необходимость разработать такой план перевозок, чтобы магазины получили требуемое количество товаров с наименьшими затратами на транспортировку. Вот именно в таких случаях (и во множестве других) приходится решать транспортную задачу.

Содержание:

• теоретический материал по транспортной задаче;
• общий план решения методом потенциалов;
• подробный пример решения транспортной задачи;
• практическое применение транспортной задачи.

Теоретический материал по транспортной задаче

Транспортная задача (задача Монжа — Канторовича) — математическая задача линейного программирования специального вида о поиске оптимального распределения однородных объектов из аккумулятора к приемникам с минимизацией затрат на перемещение.

Для простоты понимания рассматривается как задача об оптимальном плане перевозок грузов из пунктов отправления (например, складов) в пункты потребления (например, магазины), с минимальными общими затратами на перевозки.

Математическая модель транспортной задачи имеет следующий вид:

где: Z — затраты на перевозку грузов;

X — объем груза;

C — стоимость (тариф) перевозки единицы груза;

A — запас поставщика;

B — запрос потребителя;

m — число поставщиков;

n — число потребителей.

Общий план решения транспортной задачи методом потенциалов

Решить транспортную задачу можно различными методами, начиная от симплекс-метода и простого перебора, и заканчивая методом графов. Один из наиболее применяемых и подходящих для большинства случаев методов — итерационное улучшение плана перевозок.

Суть его в следующем: находим некий опорный план и проверяем его на оптимальность (Z → min). Если план оптимален — решение найдено. Если нет — улучшает план столько раз, сколько потребуется, пока не будет найден оптимальный план.

Ниже приведен алгоритм решения транспортной задачи в самом общем виде:

1. Построение транспортной таблицы.
2. Проверка задачи на закрытость.
3. Составление опорного плана.
4. Проверка опорного плана на вырожденность.
5. Вычисление потенциалов для плана перевозки.
6. Проверка опорного плана на оптимальность.
7. Перераспределение поставок.
8. Если оптимальное решение найдено, переходим к п. 9, если нет — к п. 5.
9. Вычисление общих затрат на перевозку груза.
10. Построение графа перевозок.

Подробная инструкция по решению транспортной задачи

1. Построение транспортной таблицы

Заполняем транспортную таблицу с исходными данными, где указываем запасы материалов, имеющиеся на складах поставщиков (A_i), и потребности заводов (B_j) в этих материалах.

В нижний правый угол ячеек таблицы заносим значение тарифов на перевозку груза (C_ij).

2. Проверка задачи на закрытость

Обозначим суммарный запас груза у всех поставщиков символом A, а суммарную потребность в грузе у всех потребителей — символом B.

Тогда:

Транспортная задача называется закрытой, если A = B . Если же A ≠ B , то транспортная задача называется открытой. В случае закрытой задачи от поставщиков будут вывезены все запасы груза, и все заявки потребителей будут удовлетворены. В случае открытой задачи для ее решения придется вводить фиктивных поставщиков или потребителей.

Проверим задачу на закрытость:

A = 10 + 20 + 30 = 60.

B = 15 + 20 + 25 = 60.

A = B, следовательно данная транспортная задача — закрытая.

3. Составление опорного плана

Составляет предварительный (опорный) план перевозок. Он не обязательно должен быть оптимальный. Это просто своеобразный «черновик» или «набросок», итерационно улучшая который мы постепенно придем к оптимальному плану.

Есть разные методы нахождения опорного плана. Наиболее распространены следующие:

а) Метод Северо-Западного угла

Суть метода проста — ячейки транспортной таблицы последовательно заполняются максимально возможными объемами перевозок, в направлении сверху вниз и слева направо. То есть сперва заполняется самая верхняя левая ячейка («северо-западная» ячейка), потом следующая справа и т. д. Затем переходят на новую строку и вновь заполняют ее слева направо. И так пока таблица не будет заполнена полностью.

Подробное описание метода и пример можно посмотреть здесь.

б) Метод минимального элемента

Метод заключается в том, что для заполнения ячеек транспортной таблицы выбирается клетка с минимальным тарифом. Затем выбирается следующая клетка с наименьшим значением тарифа и так продолжается до тех пор, пока таблица не будет заполнена (все запасы и потребности при этом обнулятся).

Подробное описание метода и пример можно посмотреть здесь

в) Аппроксимация Фогеля

Основа метода в нахождении разности (по модулю) между парой минимальных тарифов в каждой строке и столбце. Затем в строке или столбце с наибольшей разностью заполняется клетка с наименьшим тарифом. Затем все эти действия повторяются заново, только при этом уже не учитываются заполненные клетки.

Подробное описание аппроксимации Фогеля и пример можно посмотреть здесь

г) Метод двойного предпочтения

Суть метода в том, что отмечаются клетки с наименьшим тарифом по строкам, а затем по столбцам. Затем ячейки заполняются в следующей очередности: сначала клетки с двумя отметками, потом с одной, наконец без отметок.

Подробное описание метода и пример можно посмотреть здесь

Выберите один из методов и пройдите по ссылке в его описании, чтобы посмотреть как в данном примере был составлен опорный план и заполнена транспортная таблица.

4. Проверка опорного плана на вырожденность

Клетки таблицы, в которые записаны отличные от нуля перевозки, называются базисными, а остальные (пустые) — свободными.

План называется вырожденным, если количество базисных клеток в нем меньше, чем m + n — 1. Если во время решения задачи получился вырожденный план, то его необходимо пополнить, проставив в недостающем числе клеток нулевую перевозку и превратив, тем самым, эти клетки в базисные (общий баланс и суммарная стоимость перевозок плана при этом не изменятся).

Проводить пополнение плана, выбирая клетки произвольно, нельзя. План должен быть ациклическим!

План называется ациклическим, если его базисные клетки не содержат циклов. Циклом в транспортной таблице называется несколько клеток, соединенных замкнутой ломаной линией так, чтобы две соседние вершины ломаной были расположены либо в одной строке, либо в одном столбце. Ниже приведен пример цикла:

Ломаная линия может иметь точки самопересечения, но не в клетках цикла.

В нашем примере количество базисных клеток = 5; m + n — 1 = 3 + 3 — 1 = 5.

Следовательно, первоначальный план перевозок — невырожденный (5 = 5).

5. Вычисление потенциалов для плана перевозки

Для анализа полученных планов и их последующего улучшения удобно ввести дополнительные характеристики пунктов отправления и назначения, называемые потенциалами.

Этот метод улучшения плана перевозок называется методом потенциалов. Есть другие методы итерационного улучшения плана перевозок, но здесь мы их рассматривать не будем.

Итак, сопоставим каждому поставщику A_i и каждому потребителю B_j соответствующие величины U_i и V_j так, чтобы для всех базисных клеток плана было выполнено следующее соотношение: U_i + V_j = C_ij.

Добавим к транспортной таблице дополнительную строку и столбец для U_i и V_j.

Предположим, что U₁ = 0.

Тогда мы сможем найти V₃ = C₁₃ — U₁ = 1 — 0 = 1.

Зная V₃, мы теперь можем найти U₃:

По аналогии вычисляем все оставшиеся потенциалы:

6. Проверка плана на оптимальность методом потенциалов

Для каждой свободной клетки плана вычислим разности ΔC_ij = C_ij — (U_i + V_j ), и запишем полученные значения в левых нижних углах соответствующих ячеек.

План является оптимальным, если все разности ΔC_ij ≥ 0.

В данном случае план — неоптимальный (ΔC₂₂ < 0), и его следует улучшить путем перераспределения поставок.

7. Перераспределение поставок

Найдем ячейку с наибольшей по абсолютной величине (т. е. без учета знака, по модулю) отрицательной разностью ΔC_ij и построим цикл, в котором кроме этой клетки все остальные являются базисными. Такой цикл всегда существует и единственен.

Отметим ячейку с отрицательной разностью ΔC_ij знаком «+», следующую знаком «—», и так далее, поочередно.

Затем находим минимальное значение груза в ячейках цикла имеющих знак «-» (здесь это 5) и вписываем его в свободную ячейку со знаком «+». Затем последовательно обходим все ячейки цикла, поочередно вычитая и прибавляя к ним минимальное значение (в соответствии со знаками, которыми эти ячейки помечены: где минус — вычитаем, где плюс — прибавляем).

Получим новый опорный план перевозок:

Так как базисных клеток стало больше, чем m + n — 1, то базисную клетку с нулевым значением делаем свободной:

Снова вычисляем значения потенциалов и разности ΔC_ij:

На этот раз все разности ΔC_ij ячеек положительные, следовательно, найдено оптимальное решение.

8. Если оптимальное решение найдено, переходим к п. 9, если нет — к п. 5.

В нашем примере оптимальное решение найдено, поэтому переходим к пункту 9.

9. Вычисление общих затрат на перевозку груза

Вычислим общие затраты на перевозку груза (Z), соответствующие найденному нами оптимальному плану, по формуле:

То есть нужно перемножить значения объемов грузоперевозок на соответствующие им тарифы.

Z_min = 10 ⋅ 1 + 15 ⋅ 3 + 5 ⋅ 2 + 15 ⋅ 1 + 15 ⋅ 2 = 110 ден. ед.

В результате общие затраты на доставку всей продукции для оптимального решения составляют 110 ден. ед.

10. Построение графа перевозок

Найдя оптимальный план перевозок, построим граф. Вершинами графа будут «склады» и «магазины». В вершинах укажем соответствующие объемы запасов и потребностей. Дугам, соединяющим вершины графа, будут соответствовать ненулевые перевозки. Каждую такую дугу подпишем, указав объем перевозимого груза.

В результате получится граф, аналогичный изображенному ниже:

Все, транспортная задача решена. Поздравляю!

Практическое применение транспортной задачи

Транспортная задача применяется во многих случаях. В частности:

• оптимизация поставок сырья и материалов на производственные предприятия;
• оптимизация доставок товаров со складов в розничные магазины;
• оптимизация пассажирских перевозок.

Это далеко не полный перечень возможностей прикладного использования транспортной задачи.

Галяутдинов Р.Р.

Источники

1. Галяутдинов Р. Р. Конспект лекций по логистике
2. Решение транспортной задачи в 1С: Предприятие 8. 2 // Волшебный форум (@romix). URL: http://kb.mista.ru/article.php?id=859 (дата обращения: 29.10.2013)
3. Транспортная задача // Википедия. URL: http://ru.wikipedia.org/wiki/Транспортная_задача (дата обращения: 29.10.2013)

© Копирование любых материалов статьи допустимо только при указании прямой индексируемой ссылки на источник: Галяутдинов Р.Р.

Транспортная проблема | Набор 6 (метод MODI — метод UV)

Решение транспортной задачи состоит из двух этапов. На первом этапе необходимо найти начальное базовое допустимое решение, а на втором этапе необходимо оптимизировать начальное базовое допустимое решение, полученное на первом этапе. Существует три метода нахождения начального базового допустимого решения:

1. Метод северо-западного угла
2. Метод ячейки с наименьшими затратами
3. Метод приближения Фогеля

В этой статье мы обсудим, как оптимизировать исходное базовое допустимое решение на объясненном примере. Рассмотрим приведенную ниже транспортную задачу.

Решение:

Шаг 1: Проверьте, сбалансирована ли проблема.
Если общая сумма всех поставок из источников O1 , O2 и O3 равна общей сумме всех потребностей в пунктах назначения D1 , D2 , D3 и D4 , то транспортная задача является сбалансированной транспортной задачей.

Примечание: Если проблема не является несбалансированной, то можно использовать концепцию фиктивной строки или фиктивного столбца для преобразования несбалансированной задачи в сбалансированную, как описано в этой статье.

Шаг 2: Поиск начального базового допустимого решения.
Любой из трех вышеупомянутых методов может быть использован для нахождения начального базисного допустимого решения. Здесь будет использоваться метод северо-западного угла. И в соответствии с методом северо-западного угла это окончательное начальное базовое допустимое решение:

Теперь общая стоимость перевозки составит (200 * 3) + (50 * 1) + (250 * 6) + (100 * 5) + (250 * 3) + (150 * 2) = 3700 .

Этап 3: УФ-метод для оптимизации исходного базового возможного решения.
Ниже приведено начальное базовое допустимое решение:

– Для метода U-V необходимо найти значения u _i и v _j для строк и столбцов соответственно. Как есть три ряда так три u _i значения, т. е. u ₁ для первой строки, u ₂ для второй строки и u ₃ для третьей строки 900.
Аналогично, для четырех столбцов можно найти четыре V _J Посмотрите на изображение ниже:

Для нахождения 9 существует отдельная формула.0023 U _I и V _J ,
U _I + V _J = C _IJ , где C _IJ — это стоимость All All. Об этом подробнее здесь.

Перед применением приведенной выше формулы нам нужно проверить, равно ли m + n — 1 общему количеству выделенных ячеек или нет, где m — это общее количество строк, а n — это общее количество столбцов. .
В этом случае m = 3, n = 4 и общее количество выделенных ячеек равно 6, поэтому m + n – 1 = 6. Случай, когда m + n – 1 не равно общему количеству выделенных ячеек, будет рассмотрен в более поздние посты.

Теперь, чтобы найти значение для u и v, присвоим любому из трех u или любому из четырех v значение 0. Давайте присвоим u ₁ = 0 в этом случае. Тогда, используя приведенную выше формулу, мы получим v ₁ = 3 как u ₁ + v ₁ = 3 (т.е. C ₁₁ ) и v ₂ = 1 как u ₁ + v ₂ = 1 (т. Точно так же мы получили значение для v ₂ = 1 , поэтому мы получаем значение для u ₂ = 5 , что подразумевает v ₃ = 0 . Из значения v ₃ = 0 мы получаем u ₃ = 3 , что означает v ₄ = -1 . Смотрите изображение ниже:

Теперь вычислите штрафы по формуле P _ij = u _i + v _j – C _ij только для незанятых ячеек. У нас есть две нераспределенные ячейки в первой строке, две во второй строке и две в третьей строке. Давайте вычислим это один за другим.

1. для C ₁₃ , P ₁₃ = 0 + 0 -7 = -7 (здесь C ₁₃ = 7 , U ₁ = 0 и , U ₁ = 0 и , U ₁ = 0 и .0023 v ₃ = 0 )
2. для C ₁₄ , P ₁₄ = 0 + (-1) -4 = -5
3. для C ₂₁ ,
9
4. P C ₂₁ ,

   3333 P C ₂₁ ,

9. 21 = 5 + 3 -2 = 6
5. для C ₂₄ , P ₂₄ = 5 + (-1) -9 = -5
6. для C ₃₁ , . P ₃₁ = 3 + 3 – 8 = -2
7. Для C ₃₂ , P ₃₂ = 3 + 1 – 3 = 1

Правило: Если мы получим все значения штрафов как нулевые или отрицательные значения, это означает, что достигнута оптимальность, и этот ответ является окончательным ответом. Но если мы получим какое-либо положительное значение, это означает, что нам нужно перейти к сумме на следующем шаге.

Теперь найдите максимальный положительный штраф. Здесь максимальное значение равно 6, что соответствует ячейке C ₂₁ . Теперь эта ячейка является новой базовой ячейкой. Эта ячейка также будет включена в решение.

Правило рисования замкнутого пути или цикла. Начиная с новой базовой ячейки, начертите замкнутый путь таким образом, чтобы поворот на прямой угол выполнялся только в выделенной ячейке или в новой базовой ячейке. См. изображения ниже:

Назначьте альтернативный знак плюс-минус всем ячейкам с поворотом под прямым углом (или углом) в цикле со знаком плюс, присвоенным новой базовой ячейке.

Рассмотрим ячейки со знаком минус. Сравните выделенное значение (т.е. 200 и 250 в этом случае) и выберите минимум (т.е. выберите 200 в этом случае). Теперь вычтите 200 из ячеек со знаком минус и прибавьте 200 к ячейкам со знаком плюс. И нарисуйте новую итерацию. Работа цикла завершена, и новое решение выглядит так, как показано ниже.

Проверить, что общее количество выделенных ячеек равно (m + n – 1). Снова найдите значения u и значения v, используя формулу u _i + v _j = C _ij , где C _ij — значение стоимости только для выделенной ячейки. Присвоим u ₁ = 0 тогда получим v ₂ = 1 . Точно так же мы получим следующие значения для u _i и v _j .

Найдите штрафы для всех незанятых ячеек по формуле P _ij = u _i + v _j – C _ij .

1. для C ₁₁ , P ₁₁ = 0 + (-3) -3 = -6
2. для C ₁₃ , P ₁₃ = 0 + 0–7 = -7
3. Для C ₁₄ , P ₁₄ = 0 + (-1) – 4 = -5
4. Для C ₂₄ , P ₂₄ = 5 + (-1) – 9 = -5
-11
5. для C ₃₂ , P ₃₂ = 3 + 1 -3 = 1

Существует одно положительное значение, то есть 1 для C ₃₂ . Теперь эта ячейка становится новой базовой ячейкой.

Теперь нарисуйте петлю, начиная с новой базовой ячейки. Назначьте альтернативный знак плюс и минус с новой базовой ячейкой, назначенной в качестве знака плюс.

Выберите минимальное значение из выделенных значений в ячейку со знаком минус. Вычтите это значение из ячейки со знаком минус и прибавьте к ячейке со знаком плюс. Теперь решение выглядит так, как показано на изображении ниже:

Проверьте, равно ли общее количество выделенных ячеек (m + n – 1). Найдите значения u и v, как указано выше.

Теперь снова найдите штрафы за нераспределенные ячейки, как указано выше.

1. Для P ₁₁ = 0 + (-2) – 3 = -5
2. Для P ₁₃ = 0 + 1 – 7 = -6
3. Для P ₁₄ = 0 + 0 – 4 = -4 904
4. Для P ₂₂ = 4 + 1 – 6 = -1
5. Для P ₂₄ = 4 + 0 – 9 = -5 ) – 8 = -8

Все значения штрафа являются отрицательными. Так достигается оптимальность.

Теперь найдите общую стоимость, т.е. (250 * 1) + (200 * 2) + (150 * 5) + (50 * 3) + (200 * 3) + (150 * 2) = 2450

Объяснение транспортной проблемы | Что такое Транспортная проблема?

1. Проблема с транспортом
2. Сбалансированная задача
3. Безбалансированная задача
4. Пример
5. Заключение

. ВОЗДЕЙСТВЕННОСТЬ

.0017

Исследование операций (OR) — это современный подход, используемый для решения проблем и принятия решений. ИЛИ помогает любой организации достичь наилучшей производительности при заданных ограничениях или обстоятельствах. Известные методы ИЛИ:

• Линейное программирование
• Целевое программирование
• Целочисленное программирование
• Динамическое программирование
• Сетевое программирование

Одной из проблем, с которыми сталкиваются организации, является транспортная проблема. Первоначально это означает проблему транспортировки / доставки товаров из отрасли в пункты назначения с наименьшими возможными затратами при удовлетворении ограничений спроса и предложения. Это особый класс методов линейного программирования, разработанный для моделей с линейными целевыми функциями и функциями ограничений. Их применение может быть распространено на другие области деятельности, включая

• Планирование и управление временем
• Сетевая оптимизация
• Управление запасами
• Планирование ресурсов предприятия
• Планирование процессов
• Оптимизация маршрутизации

ЗАМЕТА j) соединение источника (i) и пункта назначения (j)

c _ij 🡪  транспортные расходы на единицу товара

x _ij 🡪 отгруженное количество

a _i   🡪 объем предложения в источнике (i)

b _j   🡪 объем спроса в пункте назначения (j)

Транспортная задача работает таким образом, чтобы минимизировать функцию затрат. Здесь функция затрат представляет собой сумму денег, потраченную поставщиком логистических услуг на транспортировку товаров от места производства или поставщика до места спроса. На стоимость перевозки влияет множество факторов. Он включает в себя расстояние между двумя точками, пройденный путь, вид транспорта, количество перевозимых единиц, скорость транспортировки и т. д. Таким образом, основное внимание здесь уделяется перевозке товаров с минимальными затратами на транспортировку без каких-либо компромиссов в спрос и предложение. Транспортная задача является расширением метода линейного программирования, поскольку транспортные расходы формулируются как линейная функция от объема предложения и спроса. Ознакомьтесь с курсом по транспортной аналитике.

Транспортная проблема существует в двух формах.

1. Сбалансированный 
2. Несбалансированный

Сбалансированный

Это случай, когда общее предложение равно общему спросу.

Несбалансированный

Это случай, когда либо спрос превышает предложение, либо наоборот.

В большинстве случаев задачи принимают сбалансированную форму. Это потому, что обычно производственные подразделения работают, принимая во внимание запасы и спрос. Перепроизводство увеличивает стоимость запасов, в то время как недостаточное производство оспаривается спросом. Следовательно, компромисс должен быть тщательно изучен. Принимая во внимание, что несбалансированная форма существует в ситуации, когда наблюдается беспрецедентный рост или снижение спроса.

Давайте разберемся с этим намного проще на простом примере.

Пример

Предположим, что существует ведущая мировая компания-поставщик автомобилей под названием JIM. JIM имеет свои производственные предприятия во многих странах и поставляет продукцию всем ведущим производителям автомобилей в мире. Например, предположим, что в Индии есть три завода в точках M, N и O. Мощность заводов 700, 300, 550 в сутки. Завод поставляет четырем клиентам A, B, C и D, потребность которых составляет 650, 200, 450, 250 в день. Стоимость перевозки за единицу на километр в индийских рупиях и расстояние между каждым пунктом отправления и пунктом назначения в километрах приведены в таблицах ниже.

Здесь цель состоит в том, чтобы определить неизвестное, удовлетворяя при этом всем ограничениям спроса и предложения. Стоимость доставки от источника до места назначения прямо пропорциональна количеству отправленных единиц.

Решение

Многие сложные языки программирования эволюционировали, чтобы решать задачи OR гораздо проще и легче. Но значение Microsoft Excel не может быть скомпрометировано и обесценено в любое время. Это также дает нам лучшее понимание проблемы, чем другие. Поэтому мы будем использовать Excel для решения проблемы.

Всегда лучше сформулировать рабочую процедуру пошагово, чтобы это помогло лучшему пониманию и предотвратило совершение какой-либо ошибки.

шаги, которые необходимо выполнить, чтобы решить проблему:

1. Создать транспортную матрицу (определить переменные решения)
2. Определите целевую функцию
3. Сформулируйте ограничения
4. Решение с использованием метода LP

. Создание транспортной матрицы:

Транспортная матрица — это способ понять максимальные возможности, которые могут быть осуществлены при отправке. Это также известно как переменные решения, потому что это представляющие интерес переменные, которые мы будем изменять для достижения цели, то есть минимизации функции затрат.

From / To	A	B	C	D	Supply
M	x ma	x mb	x mc	x md	700
N	x na	x nb	x nc	x nd	300
O	x oa	x ob	x oc	x od	550
Demand	650	200	450	250

.

Это функция затрат, то есть общие затраты на транспортировку. Она известна как целевая функция, потому что здесь мы заинтересованы в том, чтобы минимизировать стоимость транспортировки при соблюдении всех ограничений спроса и предложения.

Целевой функцией является общая стоимость. Она получается путем суммирования стоимости за единицу на км и переменных решения (выделено красным), поскольку общая стоимость прямо пропорциональна сумме произведения количества отгруженных единиц и стоимости транспортировки на единицу в расчете на один километр. км.

Столбец «Всего отгружено» представляет собой сумму столбцов A, B, C и D для соответствующих строк, а строка «Общая потребность» представляет собой сумму строк M, N и O для соответствующих столбцов. Эти два столбца вводятся для удовлетворения ограничений количества спроса и предложения при решении функции затрат.

Шаг 3

Сформулируйте ограничения:

Ограничения сформулированы относительно спроса и предложения для соответствующих строк и столбцов. Важность этих ограничений заключается в обеспечении того, чтобы они удовлетворяли всем ограничениям спроса и предложения.

Например, четвертое ограничение, x _ma + x _na + x _oa = 650, используется для обеспечения того, чтобы количество единиц, поступающих с заводов M, N и O потребителю A, не было меньше или выше спроса, который есть у А. Аналогично первое ограничение x _ma + x _mb + x _mc + x _md  = 700 гарантирует, что мощность установки M не будет ниже или выше заданной мощности, следовательно, установка может быть использована в полной мере без компрометация инвентаря.

Шаг 4

Решение с использованием метода LP:

Самый простой и эффективный метод решения — использование решателя. Входные параметры подаются, как указано ниже, и приступают к решению.

Это наилучшая оптимизированная функция стоимости, и нет никакой возможности получить меньшую стоимость, чем эта, при тех же ограничениях.

Из решенного решения видно, что завод M отгружает 100 единиц покупателю A, 350 единиц C и 250 единиц D. Но почему клиенту B ничего не отгружается? Аналогичная тенденция наблюдается и для других растений.

Что может быть причиной этого? Да, вы правильно угадали! Это связано с тем, что некоторые другие заводы отгружают клиенту по более выгодной цене, чем другие, и в результате вы можете найти несколько заводов, поставляющих ноль единиц определенным клиентам.

Итак, когда же эти поставщики нулевой единицы станут прибыльными и смогут поставлять этим клиентам? Ждать! Не паникуйте. Excel тоже сошёл с рук. После перехода к решению появится диалоговое окно, в котором выберите отчет о чувствительности и нажмите ОК. Вы получите замечательный отчет о конфиденциальности, в котором подробно описаны альтернативные издержки или ценность ресурса.

Основное объяснение переменных отчета,

Ячейка: Идентификатор ячейки в Excel

Имя: Соединение поставщика с клиентом

Окончательное значение: Количество отгруженных единиц (после решения)

Сниженная стоимость: Насколько должны быть снижены транспортные расходы на единицу продукции на километр, чтобы сделать завод нулевым поставщиком рентабельно и начать поставки

Объективный коэффициент: Текущая стоимость перевозки на единицу в км для каждой пары клиентов-поставщиков

Допустимое увеличение: Он говорит нам, что максимальная стоимость текущей стоимости перевозки на единицу в км может быть увеличена, что не не вносить никаких изменений в решение

Допустимое снижение: Указывает, насколько может быть снижена текущая стоимость перевозки на единицу на километр, что не вносит никаких изменений в решение

Здесь, посмотрите на первую строку отчета о чувствительности. Завод М поставляет покупателю А. Здесь стоимость транспортировки за единицу на км составляет 14 фунтов стерлингов, и 100 единиц отгружаются покупателю А. В этом случае стоимость транспортировки может увеличиться максимум на 6 фунтов стерлингов и может снизиться максимум до ₹1. Для любого значения в этом диапазоне окончательное решение не изменится.

А теперь кое-что интересное. Посмотрите на второй ряд. Между MB нет ни одной единицы, поставляемой покупателю B с завода M. Текущая стоимость доставки составляет 22 фунта стерлингов, и чтобы сделать эту пару прибыльной и начать бизнес, стоимость должна снизиться на 6 фунтов стерлингов за единицу на км. При этом нет возможности увеличить стоимость даже на рупию. Если стоимость доставки для этой пары снизится до 16 фунтов стерлингов, мы можем ожидать, что между ними начнется бизнес, и окончательное решение изменится соответственно.

Приведенный выше пример представляет собой задачу сбалансированного типа, в которой предложение равно спросу. В случае несбалансированного типа фиктивная переменная добавляется либо к поставщику, либо к покупателю в зависимости от того, как возникает дисбаланс.

Заключение

Таким образом, транспортная задача в Excel не только решает задачу, но и помогает нам понять, как работает модель и что можно изменить, и в какой степени модифицировать решение, что, в свою очередь, помогает определить стоимость и оптимальный поставщик.

Если вы нашли это полезным и хотите узнать больше о таких концепциях, отправляйтесь в Great Learning Academy и запишитесь на бесплатные онлайн-курсы уже сегодня.

Новый метод решения транспортной задачи — метод гармонического среднего — Juniper Publishers | Эллен Стаси

Juniper Publishers — Журнал инженерных технологий с открытым доступом

Транспортная задача — одна из моделей задачи линейного программирования. Целью данной статьи является транспортировка товара из пункта отправления в пункт назначения таким образом, чтобы транспортные расходы были минимизированы, а мы должны минимизировать время транспортировки. Для достижения этого в этой модели предлагается новый подход с использованием среднего гармонического.

Ключевые слова: Транспорт; Гармоническое среднее; Оптимальное решение

Транспортная задача впервые была изучена Ф.Л. Хиткок[1]. В транспортной задаче разные источники обеспечивают спрос в разных пунктах назначения таким образом, что транспортные расходы должны быть минимизированы. Мы можем получить основное допустимое решение тремя способами. Это

1. Метод северо-западного угла
2. Метод наименьших затрат
3. Метод аппроксимации Фогеля (VAM)

Согласно литературным данным, из этих трех методов метод VAM является лучшим. Проверим оптимальность транспортной задачи методом MODI.

Транспортная задача делится на два типа. Это сбалансированная транспортная задача и несбалансированная транспортная задача. Если количество источников равно количеству требований, то это называется сбалансированной транспортной задачей. В противном случае это называется несбалансированной транспортной задачей. Если источник товара больше спроса, то мы должны добавить фиктивный столбец, чтобы сделать проблему сбалансированной. Если спрос больше, чем источник, то мы должны добавить фиктивную строку, чтобы преобразовать данную несбалансированную задачу в сбалансированную транспортную задачу.

В последние годы предложено множество методов для поиска оптимального решения транспортной задачи. Пандиан и Натараджан [2] предложили новый подход к решению транспортной задачи со смешанными ограничениями. Корукоглу и Балли [3] обсудили усовершенствованный метод аппроксимации Фогеля для транспортной задачи. Куддос и др. [4] и Sudhakar et al. [5] разработали новый метод поиска оптимального решения транспортных задач. Рина и др. [6] дал новый глобальный подход к транспортной проблеме. Позже Рина и соавт. [7] расширили свою модель и предложили инновационный подход к оптимальному решению транспортной задачи. Амаравати и др. [8] разработали метод МДМА, чтобы дать оптимальное решение транспортной проблемы. Урашикумари и др. [9] исследовал новую транспортную проблему, используя метод ступенек и его применение. Абдул Калам Азад и др. [10] предложил алгоритмический подход к решению транспортной задачи методом средних полных альтернативных издержек. Джошуа и др. [11] разработал метод северо-восточного угла, чтобы дать начальное базовое возможное решение транспортной задачи.

Трудно дать новую модель, которая соответствовала бы реальным проблемам. В этой статье для нахождения оптимального решения используется новый статистический метод, называемый средним гармоническим. Этот метод дает решение точно так же, как метод MODI, и результаты очень близки к методу VAM. Мы также привели численный пример для нового метода и сравнили наш метод с существующими методами, такими как метод северо-западного угла, метод наименьших затрат, метод аппроксимации Фогеля. Мы проверили оптимальность решения с помощью метода MODI. Здесь мы также рассмотрели сбалансированную транспортную задачу.

Гармоническое среднее = общее количество наблюдений/суммы обратного числа.

1. Шаг 1: Проверить, сбалансирована ли данная транспортная задача. Если нет, сбалансируйте или добавьте фиктивную строку или столбец. Затем перейдите к следующему шагу.
2. Шаг 2: Найдите среднее гармоническое для каждой строки и каждого столбца. Затем найдите среди них максимальное значение.
3. Шаг 3: Разместите минимальный спрос или предложение на месте минимального значения соответствующей строки или столбца.
4. Шаг 4: Повторяйте шаги 2 и 3, пока не будут удовлетворены все потребности и не будут исчерпаны все запасы.
5. Шаг 5: Общая минимальная стоимость = сумма произведения стоимости и соответствующих ей распределенных значений спроса или предложения.

Таблица 1,2

Транспортные расходы:

Таблица 3 и 4

Транспортные расходы:

Сравнение результатов существующего и предлагаемого методов приведено ниже в Таблице 5.

Из сравнительной таблицы видно, что оптимальное решение, полученное предложенным методом, меньше, чем у других методов, и такое же, как у метода MODI. Но предлагаемый метод очень прост, так как у нас меньше вычислительных работ. Таким образом, мы можем заключить, что если мы используем подход гармонического среднего для решения транспортной задачи, мы можем получить глобальное оптимальное решение за меньший шаг.

Для получения дополнительных журналов открытого доступа в Juniper Publishers, пожалуйста, нажмите: https://juniperpublishers.com

Чтобы увидеть больше статей в журнале Open Access Journal of Engineering Technology, нажмите:
https://juniperpublishers.com/etoaj/index.php

Алгоритм решения транспортной задачи

%PDF-1.4 % 60 0 объект > эндообъект 55 0 объект >поток application/pdf

Журнал исследований Национального бюро стандартов является публикацией правительства США. Документы находятся в общественном достоянии и не защищены авторским правом в США. Тем не менее, обратите особое внимание на отдельные работы, чтобы убедиться, что не указаны ограничения авторского права. Для отдельных произведений может потребоваться получение других разрешений от первоначального правообладателя.

Алгоритм решения транспортной задачи

Глейзал, А.

Подключаемый модуль Adobe Acrobat 9.13 Paper Capture2011-01-07T13:47:11-05:00Adobe Acrobat 9.02012-02-27T09:22:04-05:002012-02-27T09:22:04-05:00uuid:0fe8c238-79e9 -4bcb-8eb2-70b3885534ccuuid:4dcd0c7b-90a9-4626-bd98-f4d8f203437euuid:0fe8c238-79e9-4bcb-8eb2-70b3885534ccdefault1

converteduuid:49b7a0ff-a57b-4b9d-b279-af2624148728converted to PDF/A-1bpdfaPilot2012-02-27T09:22 :01-05:00

False1B

http://ns.adobe.com/pdf/1.3/pdfAdobe PDF Schema

internalОбъект имени, указывающий, был ли документ изменен для включения информации треппингаTrappedText

http://ns. adobe.com/xap/1.0/mm/xmpMMXMP Media Management

внутренний идентификатор на основе UUID для конкретного воплощения документаInstanceIDURI

internalОбщий идентификатор для всех версий и представлений документа.OriginalDocumentIDURI

http://www.aiim.org/pdfa/ns/id/pdfaidPDF/A ID Schema

internalPart of PDF/A standardpartInteger

внутреннее изменение стандарта PDF/AamdText

внутренний уровень соответствия стандарту PDF/A, текст

конечный поток эндообъект 42 0 объект > эндообъект 56 0 объект [>] эндообъект 54 0 объект > эндообъект 51 0 объект > эндообъект 52 0 объект > эндообъект 53 0 объект > эндообъект 61 0 объект >/ProcSet[/PDF/Text/ImageB]/XObject>>>/Повернуть 0/Тип/Страница>> эндообъект 1 0 объект >/ProcSet[/PDF/Text/ImageB]/XObject>>>/Повернуть 0/Тип/Страница>> эндообъект 8 0 объект >/ProcSet[/PDF/Text/ImageB]/XObject>>>/Повернуть 0/Тип/Страница>> эндообъект 15 0 объект >/ProcSet[/PDF/Text/ImageB]/XObject>>>/Повернуть 0/Тип/Страница>> эндообъект 16 0 объект [17 0 Р 18 0 Р 190 Р] эндообъект 21 0 объект >поток

Решение транспортной задачи с помощью линейного программирования на Python

10 февраля 2022 г. 30 апреля 2022 г. Авинаш Навлани Линейное программирование, методы оптимизации, PuLP, python, транспортная задача

Узнайте, как использовать Python PuLP для решения транспортных задач с помощью линейного программирования.

В этом уроке мы расширим кругозор задач линейного программирования. Мы обсудим транспортную проблему. Он предлагает различные приложения, связанные с оптимальной транспортировкой товаров. Транспортная модель — это в основном модель минимизации.

Транспортная задача относится к типу задач линейного программирования. В этом типе задач основной целью является транспортировка товаров со складов-источников в различные места назначения с минимальными затратами. Чтобы решить такие проблемы, у нас должны быть объемы спроса, объемы поставок и стоимость доставки из источника и пункта назначения. Имеется m источников или пунктов отправления и n пунктов назначения, каждый из которых представлен узлом. Ребра представляют собой маршруты, соединяющие источники и пункты назначения.

В этом уроке мы рассмотрим следующие темы:

Транспортная проблема

Транспортные модели имеют дело с особым типом задачи линейного программирования, целью которой является минимизация стоимости. Здесь у нас есть однородный товар, который необходимо переместить из разных мест происхождения или фабрик в разные пункты назначения или склады.

Типы транспортных проблем

• Сбалансированный Транспортная задача :  В задаче такого типа общий спрос и предложение равны.
• Несбалансированный Транспортная проблема : В этом типе проблемы общий спрос и предложение не равны.

Методы решения транспортной задачи:

1. Метод северо-западного угла
2. Метод наименьшей стоимости
3. Метод приближения Фогеля (VAM)

Давайте рассмотрим один пример ниже. Компания связалась с тремя складами, чтобы предоставить сырье для своих 3 проектов.

Склад	Снабжение Вместимость
А	300
Б	600
С	600

Стол снабжения

Проект	Спрос Вместимость
1	150
2	450
3	900

Таблица спроса

Из	Проект-1	Проект-2	Проект-3
Склад-А	5	1	9
Склад-Б	4	2	8
Склад- с	8	7	2

Матрица затрат

Это информация, необходимая для решения проблемы. Следующим шагом является организация информации в решаемую транспортную задачу.

Формулировка проблемы

Сначала сформулируем задачу. во-первых, мы определяем склад и его запасы, проект и его потребности, а также матрицу затрат.

 # Создает список всех узлов снабжения
склады = ["А", "Б", "С"]
# Создает словарь для количества единиц снабжения для каждого узла снабжения
поставка = {"A": 300, "B": 600, "C": 600}
# Создает список всех узлов спроса
проекты = ["1", "2", "3"]
# Создает словарь для количества единиц спроса для каждого узла спроса
спрос = {
    «1»: 150,
    «2»: 450,
    «3»: 900,
}
# Создает список затрат каждого пути транспортировки
затраты = [ # проектов
    [5,1,9], # склады А
    [4,2,8], # Б
    [8,7,2]#С
]
# Данные о затратах помещаются в словарь
затраты = makeDict([склады, проекты], затраты, 0) 

Инициализировать модель LP

На этом шаге мы импортируем все классы и функции модуля целлюлозы и создадим задачу минимизации LP, используя класс LpProblem.

 # Импорт функций модуля моделирования PuLP
от импорта целлюлозы *
# Создает переменную 'prob' для хранения данных о проблеме
prob = LpProblem("Проблема поставки материалов", LpMinimize) 

Определить переменную решения

На этом шаге мы определим переменные решения. В нашей задаче у нас есть различные переменные Route. Давайте создадим их с помощью класса LpVariable.dicts() . LpVariable.dicts()  используется с пониманием списков Python. LpVariable.dicts()  будет принимать следующие четыре значения:

• Во-первых, префикс имени того, что представляет эта переменная.
• Во-вторых, это список всех переменных.
• В-третьих, это нижняя граница этой переменной.
• Четвертая переменная — верхняя граница.
• Четвертый по существу тип данных (дискретные или непрерывные). Варианты для четвертого параметра: LpContinuous или LpInteger .

Давайте сначала создадим маршрут списка для маршрута между складом и сайтом проекта и создадим переменные решения, используя метод LpVariable. dicts().

 # Создает список кортежей, содержащих все возможные маршруты транспорта
Маршруты = [(w, b) для w на складах для b в проектах]
# Создается словарь с именем 'Vars', содержащий переменные, на которые ссылаются (маршруты)
vars = LpVariable.dicts("Маршрут", (склады, проекты), 0, Нет, LpInteger) 

Определение целевой функции

На этом шаге мы определим минимальную целевую функцию, добавив ее к объекту LpProblem . lpSum(vector) используется здесь для определения нескольких линейных выражений. Он также использовал понимание списка для добавления нескольких переменных.

 # Минимальная целевая функция сначала добавляется к 'prob'
проблема += (
    lpSum([vars[w][b] * cost[w][b] for (w, b) в Routes]),
    "Сумма_из_транспортных_затрат",
) 

В этом коде мы суммировали значения списка двух переменных (полный рабочий день и неполный рабочий день) аддитивным способом.

Определение ограничений

Здесь мы добавляем два типа ограничений: максимальные ограничения предложения и минимальные ограничения спроса. Мы добавили 4 ограничения, определенные в задаче, добавив их в объект LpProblem .

 # Максимальные ограничения поставок добавляются в prob для каждого узла снабжения (складов)
для ж на складах:
    проблема += (
        lpSum([vars[w][b] для b в проектах]) <= поставка[w],
        "Sum_of_Products_out_of_warehouses_%s" % w,
    )
# Минимальные ограничения спроса добавляются в prob для каждого узла спроса (проекта)
для b в проектах:
    проблема += (
        lpSum([vars[w][b] для w на складах]) >= спрос[b],
        "Sum_of_Products_into_projects%s" % b,
    ) 

Решить модель

На этом шаге мы решим задачу LP, вызвав методsolve(). Мы можем напечатать окончательное значение, используя следующий цикл for.

 # Проблема решена с помощью решения PuLP.
проблема.решить()
# Вывести оптимизированное значение переменных
для v в prob.variables():
    print(v.name, "=", v.varValue)
    
# Значение оптимизированной целевой функции выводится на экран
print("Значение целевой функции = ", value(prob. objective)) 

  Вывод: 
Маршрут_A_1 = 0,0
Маршрут_A_2 = 300,0
Маршрут_A_3 = 0,0
Маршрут_B_1 = 150,0
Маршрут_B_2 = 150,0
Маршрут_B_3 = 300,0
Маршрут_C_1 = 0,0
Маршрут_C_2 = 0,0
Маршрут_C_3 = 600,0
Значение целевой функции = 4800,0 

Из приведенных выше результатов мы можем сделать вывод, что Склад-А поставляет 300 единиц для Проекта -2. Warehouse-B поставляет 150, 150 и 300 на соответствующие проектные площадки. И, наконец, Склад-С поставляет 600 единиц Проекту-3.

Резюме

В этой статье мы узнали о проблемах с транспортировкой, формулировании проблем и реализации с использованием библиотеки Python PuLp. Мы решили транспортную задачу, используя задачу линейного программирования на Python. Конечно, это всего лишь простой пример, мы можем добавить к нему больше ограничений и сделать его более сложным. В следующих статьях мы напишем больше о различных проблемах оптимизации, таких как проблема перегрузки, проблема назначения, проблема сбалансированного питания. Вы можете повторить основы математических понятий в этой статье и узнать о линейном программировании в этой статье.

8 полезных шагов для решения проблем городского транспорта

РЕКЛАМА:

Готового универсально приемлемого решения проблемы городского транспорта не существует. Планировщики, инженеры, экономисты и транспортные технологи имеют свои собственные взгляды, которые при объединении неизменно давали работоспособную стратегию. Любая разработанная политика должна рассматриваться, во-первых, с учетом времени, необходимого для ее реализации, и, во-вторых, все политики должны оцениваться с точки зрения их стоимости.

В решении проблем городского транспорта могут помочь следующие общие шаги:

1. Развитие дополнительной пропускной способности дорог:

Один из наиболее распространенных методов борьбы с заторами на средних и малых дорогах. городов или в районах более крупных центров является строительство объездных путей для отклонения сквозного движения. Этой практике следуют во всем мире, включая Индию. Планировщики середины двадцатого века рассматривали строительство дополнительных дорог в виде новых или улучшенных автомагистралей как приемлемое решение проблемы заторов в крупных городах.

РЕКЛАМА:

Поскольку первые исследования транспорта в 1950-х и 1960-х годах были проведены в городских районах США, где потребности общества, в котором доминируют автомобили, считались первостепенными, обеспечение дополнительной пропускной способности дорог было принято для нескольких десятилетия как наиболее эффективное решение проблемы заторов, а городские автострады были построены в крупных городах, таких как Чикаго, Сан-Франциско и Лос-Анджелес.

Западноевропейские транспортные планировщики включили многие из концепций своих американских коллег в свои собственные программы, а городские автомагистрали фигурировали во многих более крупных проектах (Мюллер, 19 лет).95). Однако вскоре стало очевидно, что создаваемый трафик на этих новых дорогах быстро снижает первоначальные преимущества.

Строительство сети городских автомагистралей с их подъездными путями требует больших площадей земли и неизбежного сноса участков жилой и коммерческой недвижимости. К 1970-м годам планировщики и политики пришли к выводу, что инвестиции в новые автомагистрали, предназначенные для быстрого движения автотранспорта, не обязательно являются наиболее эффективным решением проблем городского транспорта.

2. Мероприятия по управлению дорожным движением:

Временное и частичное облегчение заторов на дорогах может быть достигнуто за счет внедрения схем управления дорожным движением, предусматривающих реорганизацию транспортных потоков и направлений без каких-либо существенных структурных изменений существующей улицы. шаблон. Среди наиболее широко используемых устройств — расширение систем с односторонним движением, поэтапное управление светофорами с учетом изменения интенсивности движения, а также ограничения парковки и загрузки транспортных средств на основных дорогах.

На многополосных автомагистралях с большим объемом пригородного движения определенные полосы могут быть выделены для въезжающих транспортных средств утром и для исходящих транспортных средств во второй половине дня, что создает эффект приливного течения. Недавние эксперименты с использованием информационных технологий были основаны на интеллектуальных системах автомобильных дорог (IVHS) с компьютеризированным управлением светофорами и въездами на автострады, рекомендациями водителям об альтернативных маршрутах во избежание заторов и информацией о погоде и общих дорожных условиях. IVHS может быть подключен к передовым системам управления транспортным средством, используя бортовой компьютер, чтобы исключить ошибки водителя и управлять автоматическим торможением и рулевым управлением, когда авария неизбежна.

РЕКЛАМА:

Управление дорожным движением широко применяется в городских жилых районах, где чрезмерное количество транспортных средств создает шум, вибрацию, загрязнение и, прежде всего, риск несчастных случаев, особенно для молодежи. «Успокоение дорожного движения» было введено во многих европейских городах и направлено на создание среды, в которой автомобили разрешены, но приоритет движения принадлежит пешеходам. Тщательно спланированные изменения ширины улиц, ограничения парковки и устройства контроля скорости, такие как пандусы, объединяются для обеспечения безопасного и приемлемого баланса между автомобилем и пешеходом.

3. Эффективное использование автобусного сообщения :

Многие предложения по планированию транспорта направлены именно на увеличение скорости и надежности расписания автобусного сообщения, и многие европейские города внедрили планы приоритетного автобусного сообщения в попытке повысить привлекательность общественного транспорта. транспорт. Полосы, предназначенные только для автобусов, по направлению движения транспортного потока или против него, выделяются на сильно загруженных дорогах для экономии времени, хотя такая экономия может впоследствии быть растрачена, когда автобусы въезжают в центральные районы города, где приоритетные полосы движения на перекрестках и некоторых улицах могут быть ограничены. только на автобусы, особенно в пешеходных торговых зонах.

Там, где планируются совершенно новые города, есть возможность включить отдельные автобусные сети в систему городских дорог, что позволит автобусам двигаться без заторов. В Соединенном Королевстве Ранкорн-Нью-Таун, построенный как переполненный центр мегаполиса Мерсисайд, был снабжен двухконтурным автобусным маршрутом, соединяющим торговый центр, промышленные зоны и жилые районы.

РЕКЛАМА:

Около 90 % населения города проживало в пяти минутах ходьбы от автобусной дорожки, а эксплуатационные расходы были на 33 % ниже, чем у автобусов на обычных дорогах. Хотя система не используется в той степени, в какой это предполагалось изначально, она успешно иллюстрирует, как общественный транспорт может быть интегрирован в городское развитие. Дороги, предназначенные только для автобусов, также могут быть адаптированы к системам управления транспортными средствами, при этом автобус не управляется, а управляется боковыми колесами с возобновлением обычного управления при повторном въезде в сеть дорог общего пользования.

Такие системы были приняты в Аделаиде, и эксперименты проводились во многих других городах (Управление транзита Аделаиды, 1988). Автобус также может получить дополнительные преимущества в центре города, где реконструируются крупные торговые и транспортные комплексы. Строительство крытых торговых центров и зон может включать в себя автобусные остановки для покупателей, а реконструкция железнодорожных станций также может позволить более тесно интегрировать автобусные перевозки с железнодорожными.

Система «паркуйся и езжай», принятая в настоящее время во многих европейских городах, позволяет сократить количество автомобилей, въезжающих в центры городов, особенно в периоды пиковых покупок в выходные дни. Большие автостоянки, временные или постоянные в зависимости от необходимости, на окраине города связаны автобусом с центром города, при этом стоимость парковки обычно ниже, чем стоимость парковки в центре города.

Преимущества автобуса перед автомобилем как эффективного перевозчика сохраняются, а затраты на обеспечение окраинных парковок значительно меньше, чем в черте города. Железнодорожные пассажиры также могут обслуживаться аналогичным образом с предоставлением вместительных автостоянок, прилегающих к пригородным станциям.

Многие города попытались привлечь пассажиров обратно к автобусному транспорту, повысив его гибкость и уровень реагирования на рыночный спрос. В пригородных районах система дозвона до места назначения имела частичный успех: потенциальные пассажиры бронировали места по телефону в пределах определенной зоны обслуживания.

Такие транспортные средства обычно обслуживают жилые районы вокруг районных торговых центров, и их вместимость ограничена, поэтому они лучше всего подходят для работы в условиях низкого спроса или в непиковые периоды. Стоимость проезда выше, чем на обычных автобусах, поскольку средства контроля и бронирования транспортных средств требуют финансирования.

Были также проведены эксперименты с автобусами малой вместимости, которые можно останавливать и садиться на них так же, как такси, и которые могут легче преодолевать сложные уличные схемы жилых массивов, чем большие автобусы. Однако с широким внедрением рейсовых маршруток проблема перегрузки уменьшилась.

4. Ограничения на парковку :

Как мы видели, невозможно обеспечить достаточно места для всех, кто хотел бы водить машину и парковаться в центральных районах больших городов. Таким образом, парковка должна быть ограничена, и обычно это делается путем запрета парковки в течение всего дня для пассажиров пригородной зоны или ее чрезмерной дороговизны. Ограничения менее строгие — вне пиковой нагрузки, чтобы покупатели и другие краткосрочные посетители, приносящие пользу экономике центра, не сдерживались. Для местных жителей должны быть приняты отдельные меры, возможно, посредством разрешений или зарезервированных мест для парковки.

Таким образом, городские власти могут контролировать общественные места для парковки автомобилей, но многие другие места находятся в частной собственности предприятий и зарезервированы для конкретных сотрудников. Результатом этого является увековечение поездок на работу на машине. Предоставление такого пространства в будущем может быть ограничено разрешением на строительство новых застроек, как это делается в Лондоне, но контроль за использованием существующих частных пространств поднимает проблемные вопросы прав и свобод, с которыми многие страны не хотят сталкиваться.

РЕКЛАМА:

В целом ограничения на парковку имеют то преимущество, что они просты в управлении, гибки в применении и легко понятны общественности. Их ахиллесова пята — правоприменение, поскольку автомобилисты умеют парковаться там и тогда, где и когда не следует, и уклоняться от штрафов, если их поймали.

Штрафы во многих городах настолько низки, что быть пойманным один или два раза в неделю дешевле, чем платить за парковку. Действительно, проведенное в 1982 году в Лондоне исследование показало, что незаконных парковщиков больше, чем законных, и только 60 % штрафов были уплачены. Контроль за парковкой должен быть строгим и обеспечиваться, если он должен внести существенный вклад в уменьшение заторов в городе.

5. Реклама велосипеда :

Преимущества езды на велосипеде давно признаны. Велосипед дешево купить и эксплуатировать, и в городских районах он часто является самым быстрым средством доставки от двери до двери (рис. 5.3). Это безопасный вид транспорта, бесшумный, не загрязняющий окружающую среду, энергоэффективный и компактный, а также не представляющий угрозы для большинства других участников дорожного движения. Город, ориентированный на велосипедистов, будет способствовать фитнесу среди велосипедистов и здоровью среди невелосипедистов. Таким образом, езда на велосипеде является способом обеспечения мобильности, дешевой как для человека, так и для общества.

Сторонники экологического управления дорожным движением (ETM) часто бросают завистливые взгляды на Нидерланды, где планирование циклов осуществляется в контексте национального планирования устойчивого развития. Генеральный план «Велосипед», направленный на увеличение пробега велосипедов не менее чем на 30 процентов в период с 1986 по 2010 год, не только решает традиционные проблемы велосипедной инфраструктуры и безопасности дорожного движения, но также решает вопросы мобильности и выбора вида транспорта; как побудить предприятия повысить роль велосипеда в поездках на работу; сокращение краж велосипедов и увеличение количества и качества парковок; улучшение сочетания велосипедного движения и общественного транспорта; и поощрение рассмотрения велосипеда среди влиятельных лиц, принимающих решения. Эти «притягивающие» меры являются частью национальной транспортной стратегии, направленной на сдерживание использования автомобилей, которая «подталкивает» автомобилистов к использованию велосипедов.

6. Поощрение пеших прогулок :

Ходьба является наиболее важным видом транспорта в городах, однако часто данные о ней не собираются, и многие планировщики не рассматривают ее как вид транспорта. В результате такого пренебрежения приспособления, предназначенные специально для пешеходов, часто либо отсутствуют, либо содержатся в плохом состоянии, а пешеходы составляют самую большую группу смертей участников дорожного движения. Существуют социальные, медицинские, экологические и экономические причины для продвижения ходьбы, поскольку это справедливый, здоровый, экологически чистый и недорогой вид транспорта. Более того, «пешеходные города», как правило, являются приятными местами для жизни, а доступ к удобствам в нескольких минутах ходьбы часто упоминается в качестве ключевого показателя качества жизни в районе.

7. Продвижение общественного транспорта :

Если ETM стремится отказаться от автомобилей, то необходимы привлекательные альтернативы. Езда на велосипеде и ходьба могут быть подходящими для коротких расстояний, но для переноса более длинных поездок требуется наличие качественной системы общественного транспорта, обеспечивающей эффективное функционирование города.

Это означает, что:

1. Плата за проезд должна быть достаточно низкой, чтобы бедные люди могли ее себе позволить;

2. Должно быть достаточно транспортных средств для частого обслуживания в течение дня;

3. Маршруты должны отражать доминирующие линии желаний путешествующего населения, и должен быть обширный пространственный охват города, чтобы никто не находился очень далеко от остановки общественного транспорта;

4. Повысить скорость движения автобусов по сравнению с автомобилями, разгрузив их от заторов;

5. Недостаточно обеспечить общественный транспорт: его еще нужно скоординировать. Мультимодальные билеты могут быть одним из основных компонентов функциональной городской транспортной системы, но ключевым элементом является интеграция услуг путем обеспечения связи между видами транспорта.

8. Другие меры :

Некоторые другие меры, полезные для планирования городского транспорта:

3. Взимание платы за использование дорог на основе соединения или района,

4. Схемы ограничения транспортных средств,

5. Скоростной железнодорожный транспорт,

6. Координация транспорта и

7. Общественный транспорт благоустройство и др.

Планирование городского транспорта представляет собой непрерывный процесс, и оно должно осуществляться в рамках процесса, как показано на рис. 5.4, состоящего из этапов предварительного анализа, технического анализа и последующего анализа.

После определения целей необходимо собрать данные для подготовки инвентаризации землепользования, транспорта и поездок в изучаемой области.

No related posts.