| 1 | Найти точное значение | sin(30) | |
| 2 | Найти точное значение | sin(45) | |
| 3 | Найти точное значение | sin(30 град. ) | |
| 4 | Найти точное значение | sin(60 град. ) | |
| 5 | Найти точное значение | tan(30 град. ) | |
| 6 | Найти точное значение | arcsin(-1) | |
| 7 | Найти точное значение | sin(pi/6) | |
| 8 | cos(pi/4) | ||
| 9 | Найти точное значение | sin(45 град. ) ) | |
| 10 | Найти точное значение | sin(pi/3) | |
| 11 | Найти точное значение | arctan(-1) | |
| 12 | Найти точное значение | cos(45 град. ) | |
| 13 | Найти точное значение | cos(30 град. ) | |
| 14 | Найти точное значение | tan(60) | |
| 15 | Найти точное значение | csc(45 град. ) | |
| 16 | Найти точное значение | tan(60 град. ) | |
| 17 | Найти точное значение | sec(30 град. ) ) | |
| 18 | Найти точное значение | cos(60 град. ) | |
| 19 | Найти точное значение | cos(150) | |
| 20 | Найти точное значение | sin(60) | |
| 21 | Найти точное значение | cos(pi/2) | |
| 22 | Найти точное значение | tan(45 град. ) | |
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | |
| 24 | Найти точное значение | csc(60 град. ) | |
| 25 | Найти точное значение | sec(45 град. ) ) | |
| 26 | Найти точное значение | csc(30 град. ) | |
| 27 | Найти точное значение | sin(0) | |
| 28 | Найти точное значение | sin(120) | |
| 29 | Найти точное значение | cos(90) | |
| 30 | Преобразовать из радианов в градусы | pi/3 | |
| 31 | Найти точное значение | tan(30) | |
| 32 | Преобразовать из градусов в радианы | 45 | |
| 33 | Найти точное значение | cos(45) | |
| 34 | Упростить | sin(theta)^2+cos(theta)^2 | |
| 35 | Преобразовать из радианов в градусы | pi/6 | |
| 36 | Найти точное значение | cot(30 град. ) ) | |
| 37 | Найти точное значение | arccos(-1) | |
| 38 | Найти точное значение | arctan(0) | |
| 39 | Найти точное значение | cot(60 град. ) | |
| 40 | Преобразовать из градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2pi)/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | tan(pi/2) | |
| 45 | Найти точное значение | sin(300) | |
| 46 | Найти точное значение | cos(30) | |
| 47 | Найти точное значение | cos(60) | |
| 48 | Найти точное значение | cos(0) | |
| 49 | Найти точное значение | cos(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | cos(210) | |
| 52 | Найти точное значение | sec(60 град. ) ) | |
| 53 | Найти точное значение | sin(300 град. ) | |
| 54 | Преобразовать из градусов в радианы | 135 | |
| 55 | Преобразовать из градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5pi)/6 | |
| 57 | Преобразовать из радианов в градусы | (5pi)/3 | |
| 58 | Преобразовать из градусов в радианы | 89 град. | |
| 59 | Преобразовать из градусов в радианы | 60 | |
| 60 | Найти точное значение | sin(135 град. ) ) | |
| 61 | Найти точное значение | sin(150) | |
| 62 | Найти точное значение | sin(240 град. ) | |
| 63 | Найти точное значение | cot(45 град. ) | |
| 64 | Преобразовать из радианов в градусы | (5pi)/4 | |
| 65 | Найти точное значение | sin(225) | |
| 66 | Найти точное значение | sin(240) | |
| 67 | Найти точное значение | cos(150 град. ) | |
| 68 | Найти точное значение | tan(45) | |
| 69 | Вычислить | sin(30 град. ) ) | |
| 70 | Найти точное значение | sec(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | csc(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень из 2)/2) | |
| 74 | Найти точное значение | tan((5pi)/3) | |
| 75 | Найти точное значение | tan(0) | |
| 76 | Вычислить | sin(60 град. ) | |
| 77 | Найти точное значение | arctan(-( квадратный корень из 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3pi)/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | Найти точное значение | arcsin(-1/2) | |
| 81 | Найти точное значение | ||
| 82 | Найти точное значение | csc(45) | |
| 83 | Упростить | arctan( квадратный корень из 3) | |
| 84 | Найти точное значение | sin(135) | |
| 85 | Найти точное значение | sin(105) | |
| 86 | Найти точное значение | sin(150 град. ) ) | |
| 87 | Найти точное значение | sin((2pi)/3) | |
| 88 | Найти точное значение | tan((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | pi/4 | |
| 90 | Найти точное значение | sin(pi/2) | |
| 91 | Найти точное значение | sec(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | cos((7pi)/6) | |
| 94 | Найти точное значение | arcsin(0) | |
| 95 | sin(120 град. ) ) | ||
| 96 | Найти точное значение | tan((7pi)/6) | |
| 97 | Найти точное значение | cos(270) | |
| 98 | Найти точное значение | sin((7pi)/6) | |
| 99 | Найти точное значение | arcsin(-( квадратный корень из 2)/2) | |
| 100 | Преобразовать из градусов в радианы | 88 град. |
| 1 | Найти точное значение | sin(30) | |
| 2 | Найти точное значение | sin(45) | |
| 3 | Найти точное значение | sin(30 град. ) ) | |
| 4 | Найти точное значение | sin(60 град. ) | |
| 5 | Найти точное значение | tan(30 град. ) | |
| 6 | Найти точное значение | arcsin(-1) | |
| 7 | Найти точное значение | sin(pi/6) | |
| 8 | Найти точное значение | cos(pi/4) | |
| 9 | Найти точное значение | sin(45 град. ) | |
| 10 | Найти точное значение | sin(pi/3) | |
| 11 | Найти точное значение | arctan(-1) | |
| 12 | Найти точное значение | cos(45 град. ) ) | |
| 13 | Найти точное значение | cos(30 град. ) | |
| 14 | Найти точное значение | tan(60) | |
| 15 | Найти точное значение | csc(45 град. ) | |
| 16 | Найти точное значение | tan(60 град. ) | |
| 17 | Найти точное значение | sec(30 град. ) | |
| 18 | Найти точное значение | cos(60 град. ) | |
| 19 | Найти точное значение | cos(150) | |
| 20 | Найти точное значение | sin(60) | |
| 21 | Найти точное значение | cos(pi/2) | |
| 22 | Найти точное значение | tan(45 град. ) ) | |
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | |
| 24 | Найти точное значение | csc(60 град. ) | |
| 25 | Найти точное значение | sec(45 град. ) | |
| 26 | Найти точное значение | csc(30 град. ) | |
| 27 | Найти точное значение | sin(0) | |
| 28 | Найти точное значение | sin(120) | |
| 29 | Найти точное значение | cos(90) | |
| 30 | Преобразовать из радианов в градусы | pi/3 | |
| 31 | Найти точное значение | tan(30) | |
| 32 | Преобразовать из градусов в радианы | 45 | |
| 33 | Найти точное значение | cos(45) | |
| 34 | Упростить | sin(theta)^2+cos(theta)^2 | |
| 35 | Преобразовать из радианов в градусы | pi/6 | |
| 36 | Найти точное значение | cot(30 град. ) ) | |
| 37 | Найти точное значение | arccos(-1) | |
| 38 | Найти точное значение | arctan(0) | |
| 39 | Найти точное значение | cot(60 град. ) | |
| 40 | Преобразовать из градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2pi)/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | tan(pi/2) | |
| 45 | Найти точное значение | sin(300) | |
| 46 | Найти точное значение | cos(30) | |
| 47 | Найти точное значение | cos(60) | |
| 48 | Найти точное значение | cos(0) | |
| 49 | Найти точное значение | cos(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | cos(210) | |
| 52 | Найти точное значение | sec(60 град. ) ) | |
| 53 | Найти точное значение | sin(300 град. ) | |
| 54 | Преобразовать из градусов в радианы | 135 | |
| 55 | Преобразовать из градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5pi)/6 | |
| 57 | Преобразовать из радианов в градусы | (5pi)/3 | |
| 58 | Преобразовать из градусов в радианы | 89 град. | |
| 59 | Преобразовать из градусов в радианы | 60 | |
| 60 | Найти точное значение | sin(135 град. ) ) | |
| 61 | Найти точное значение | sin(150) | |
| 62 | Найти точное значение | sin(240 град. ) | |
| 63 | Найти точное значение | cot(45 град. ) | |
| 64 | Преобразовать из радианов в градусы | (5pi)/4 | |
| 65 | Найти точное значение | sin(225) | |
| 66 | Найти точное значение | sin(240) | |
| 67 | Найти точное значение | cos(150 град. ) | |
| 68 | Найти точное значение | tan(45) | |
| 69 | Вычислить | sin(30 град. ) ) | |
| 70 | Найти точное значение | sec(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | csc(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень из 2)/2) | |
| 74 | Найти точное значение | tan((5pi)/3) | |
| 75 | Найти точное значение | tan(0) | |
| 76 | Вычислить | sin(60 град. ) | |
| 77 | Найти точное значение | arctan(-( квадратный корень из 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3pi)/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | Найти точное значение | arcsin(-1/2) | |
| 81 | Найти точное значение | sin((4pi)/3) | |
| 82 | Найти точное значение | csc(45) | |
| 83 | Упростить | arctan( квадратный корень из 3) | |
| 84 | Найти точное значение | sin(135) | |
| 85 | Найти точное значение | sin(105) | |
| 86 | Найти точное значение | sin(150 град. ) ) | |
| 87 | Найти точное значение | sin((2pi)/3) | |
| 88 | Найти точное значение | tan((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | pi/4 | |
| 90 | Найти точное значение | sin(pi/2) | |
| 91 | Найти точное значение | sec(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | cos((7pi)/6) | |
| 94 | Найти точное значение | arcsin(0) | |
| 95 | Найти точное значение | sin(120 град. 2+x) $$ 2+x) $$ | |
| log(a,x) | Логарифм x по основанию a | log(3,cos(x)) | $$ log_3(cos(x)) $$ |
| sh(x) | Гиперболический синус | sh(x-1) | $$ sh(x-1) $$ |
| ch(x) | Гиперболический косинус | ch(x) | $$ ch(x) $$ |
| th(x) | Гиперболический тангенс | th(x) | $$ th(x) $$ |
| cth(x) | Гиперболический котангенс | cth(x) | $$ cth(x) $$ |
Почему решение на английском языке?
При решении этой задачи используется большой и дорогой модуль одного «забугорного» сервиса. Решение он выдает в виде изображения и только на английском языке. Изменить это, к сожалению, нельзя. Ничего лучше мы найти не смогли. Зато он выводит подробное и очень качественное решение в том виде в котором оно принято в высших учебных заведениях. Единственное неудобство — на английском языке, но это не большая цена за качество.
Некоторые пояснения по выводу решения.
| Вывод | Перевод, пояснение |
|---|---|
| Solve for x over the real numbers | Решить относительно х в действительных числах (бывают ещё комплексные) |
| Multiply both sides by . | Умножаем обе части на . |
| Simplify and substitute . | Упрощаем и делаем подстановку . |
| Simplify trigonometric functions | Упрощаем тригонометрические функции |
| Bring . together using the commom denominator . | Приводим . к общему знаменателю . |
| The left hand side factors into a product with two terms | Левая часть разбивается на множители как два многочлена |
| Split into two equations | Разделяем на два уравнения |
| Take the square root of both sides | Извлекаем квадратный корень из обоих частей |
| Subtract . from both sides | Вычитаем . из обеих частей уравнения |
Add . (x)\) (x)\) | Арккотангенс. У нас пишут \(arcctg(x)\) |
| \(sec(x)\) | Секанс. У нас пишут также \(sec(x) = \frac\) |
| \(csc(x)\) | Косеканс. У нас пишут \(cosec(x) = \frac\) |
| \(cosh(x)\) | Гиперболический косинус. У нас пишут \(ch(x) = \frac> \) |
| \(sinh(x)\) | Гиперболический синус. У нас пишут \(sh(x) = \frac> \) |
| \(tanh(x)\) | Гиперболический тангенс. У нас пишут \(th(x) = \frac>> \) |
| \(coth(x)\) | Гиперболический котангенс. У нас пишут \(cth(x) = \frac \) |
Если вам что-то осталось не понятно обязательно напишите об этом в Обратной связи и мы дополним эту таблицу.
Данный калькулятор предназначен для решения тригонометрических уравнений.
Тригонометрические уравнения – это уравнения, которые содержат в себе тригонометрические функции неизвестного аргумента. Под тригонометрическими функциями понимают математические функции от величины угла. Как правило, тригонометрические функции определяются как отношения сторон прямоугольного треугольника или длины определенных отрезков в единичной окружности.
Как правило, тригонометрические функции определяются как отношения сторон прямоугольного треугольника или длины определенных отрезков в единичной окружности.
К основным видам тригонометрических уравнений относят простейшие уравнения, содержащие модуль, с параметрами, с целой и дробной частью, со сложными аргументами, с обратными тригонометрическими функциями.
С помощью калькулятора можно вычислить корни тригонометрического уравнения.
Для получения полного хода решения нажимаем в ответе Step-by-step.
Данный калькулятор предназначен для решения тригонометрических неравенств онлайн. Тригонометрические неравенства – это неравенства, в которых переменная стоит под знаком тригонометрической функции.
К простейшим тригонометрическим неравенствам относятся следующие неравенства: sinx ▼a, cosx ▼a, tgx ▼a, ctgx ▼a. Знак ▼ означает любой знак сравнения (≤, ≥, >,
Основным способом решения любых тригонометрических неравенств является сведение их к простейшим тригонометрическим неравенствам, которые указаны выше.
Преимуществом онлайн калькулятора является то, что Вам нет необходимости знать все методы решения тригонометрических неравенств. Чтобы получить ответ, укажите исходное тригонометрическое неравенство. Основные примеры функций для данного калькулятора указаны ниже.
Для получения полного хода решения нажимаем в ответе Step-by-step.
Этот математический калькулятор онлайн поможет вам решить тригонометрическое неравенство. Программа для решения тригонометрического неравенства не просто даёт ответ задачи, она приводит подробное решение с пояснениями, т.е. отображает процесс получения результата.
Данная программа может быть полезна учащимся старших классов общеобразовательных школ при подготовке к контрольным работам и экзаменам, при проверке знаний перед ЕГЭ, родителям для контроля решения многих задач по математике и алгебре. А может быть вам слишком накладно нанимать репетитора или покупать новые учебники? Или вы просто хотите как можно быстрее сделать домашнее задание по математике или алгебре? В этом случае вы также можете воспользоваться нашими программами с подробным решением.
Таким образом вы можете проводить своё собственное обучение и/или обучение своих младших братьев или сестёр, при этом уровень образования в области решаемых задач повышается.
Обязательно ознакомьтесь с правилами ввода функций. Это сэкономит ваше время и нервы.
Правила ввода функций >> Почему решение на английском языке? >> С 9 января 2019 года вводится новый порядок получения подробного решения некоторых задач. Ознакомтесь с новыми правилами >> —> Введите тригонометрическое неравенство
Решить неравенство
Обнаружено что не загрузились некоторые скрипты, необходимые для решения этой задачи, и программа может не работать.
Возможно у вас включен AdBlock.
В этом случае отключите его и обновите страницу.
Т.к. желающих решить задачу очень много, ваш запрос поставлен в очередь.
Через несколько секунд решение появится ниже.
Пожалуйста подождите сек.
Решение тригонометрических неравенств
ПРИМЕР 1. Решим неравенство \( \sin x > \frac \).
Решим неравенство \( \sin x > \frac \).
Так как \( -1 \frac \).
Так как \( -1 1 \).
Очевидно, что решение неравенства будет таким:
$$ x \in \left(\frac + \pi k; \;\; \frac + \pi k\right), \; k \in \mathbb $$
ПРИМЕР 6. Решим неравенство \( tg \;x \frac> \).
Очевидно, что решение неравенства будет таким:
$$ x \in \left( \pi k; \;\; \frac + \pi k \right), \; k \in \mathbb $$
Неравенства вида \( \cos x > a \) и \( \cos x
Пусть дано простейшее неравенство \( \cos x > a \).
1) При \(-1 1\) решением неравенства является любое действительное число: \( x \in \mathbb \)
3) При \(a \leqslant -1\) неравенство не имеет решений.
4) При \(a = 1\) решением неравенства является любое действительное число, отличное от \( 2\pi k, \; k \in \mathbb \)
Неравенства вида \( ctg \;x > a \) и \( ctg \;x
Пусть дано простейшее неравенство \( ctg \;x > a \).
Множество всех решений данного тригонометрического неравенства будем искать с помощью тригонометрического круга.
Из данного рисунка видно, что при любом \(a \in \mathbb \) решение неравенства будет таким:
$$ x \in ( \pi k; \;\; arcctg \;a + \pi k ), \; k \in \mathbb $$
Пусть дано простейшее неравенство \( ctg \;x
Неравенства вида \( tg \;x > a \) и \( tg \;x
Пусть дано простейшее неравенство \( tg \;x > a \).
Множество всех решений данного тригонометрического неравенства будем искать с помощью тригонометрического круга.
Из данного рисунка видно, что при любом \(a \in \mathbb \) решение неравенства будет таким:
$$ x \in \left(arctg \;a + \pi k; \;\; \frac + \pi k \right), \; k \in \mathbb $$
Пусть дано простейшее неравенство \( tg \;x
Тригонометрические неравенства
Неравенства вида \( \sin x > a \) и \( \sin x
Пусть дано простейшее неравенство \( \sin x > a \).
1) При \(-1 1 \) решением неравенства является любое действительное число: \( x \in \mathbb \)
3) При \(а = 1 \) решением неравенства является любое действительное число, отличное от \( \frac + 2\pi k, \; k \in \mathbb \)
4) При \(а \leqslant -1 \) неравенство не имеет решений.
Читайте также:
- Восстановление выносливости ds2
- Spotlight 5 какой уровень
- Выпадение из мира в майнкрафт
- Настольные игры для детей от 4 лет самые
- Hard play герой щита
Решение тригонометрических уравнений
Репетиторы ❯ Математика ❯ Решение тригонометрических уравнений
Автор: Валентин В., онлайн репетитор по математике
●
06.11.2011
●
Раздел: Математика
Мы уже познакомились с формулами корней более простых тригонометрических уравнений
cos x = a, sin x = a, tg x = a. К этим уравнениям сводятся другие тригонометрические уравнения. Для решения большей части таких уравнений необходимо использование формул преобразований тригонометрических выражений. Рассмотрим некоторые способы и примеры решения тригонометрических уравнений.
К этим уравнениям сводятся другие тригонометрические уравнения. Для решения большей части таких уравнений необходимо использование формул преобразований тригонометрических выражений. Рассмотрим некоторые способы и примеры решения тригонометрических уравнений.
1. Уравнения, сводящиеся к квадратам
Задача 1.
Решить уравнение sin2 x + sin x – 2 = 0.
Решение.
Это уравнение является квадратным относительно sin x. Если мы обозначим sin x = у, то наше уравнение примет вид: у2 + у – 2 = 0. Решив это уравнение, мы получаем его корни: у1 = 1, у2 = -2. Таким образом, решение исходного уравнения свелось к решению простейших уравнений sin x = 1 и sin x = -2.
Корнем уравнения sin x = 1 является х = π/2 + 2πn, n € Z; уравнение sin x = -2 не имеет корней.
Ответ. х = π/2 + 2πn, n € Z.
Задача 2.
Решить уравнение 2 cos2x – 5 sin x + 1 = 0.
Решение.
Заменим cos2x на 1 – sin2 x и получим: 2(1 – sin2 x) – 5 sin x + 1 = 0, или 2 sin2 x + 5 sin x – 3 = 0.
Обозначив sin x = у, мы получили: 2у2 + 5у – 3 = 0, откуда у1 = -3, у2 = 1/2.
1) sin x = -3 – уравнение не имеет корней, так как |-3|> 1.
2) sin x = 1/2, х = (-1)n arcsin 1/2 + πn = = (-1)n π/6 + πn, n € Z.
Ответ. х = (-1)n π/6 + πn, n € Z.
2. Уравнения вида а sin x + b cosx = c
Задача 3.
Решить уравнение 2 sin x – 3 cosx = 0.
Решение.
Разделим на cos x обе части уравнения и получим 2 tg x – 3 = 0, tg x = 3/2, х = arctg 3/2 + πn, n € Z.
Ответ. х = arctg 3/2 + πn, n € Z.
При решении этой задачи обе части уравнения 2 sin x – 3 cosx = 0 были разделены на cos x. Мы должны помнить, что в результате деления уравнения на выражение, которое содержит неизвестное, корни могут быть потеряны. Поэтому нужно проверить, не являются ли корни уравнения cos x = 0 корнями данного уравнения. Если cos x = 0, то из уравнения 2sin x – 3 cos x = 0 следует, что sin x = 0. Однако sin x и cos х одновременно не могут быть равными нулю, в силу того что они связаны равенством sin2x + cos2x = 1. Следовательно, при делении уравнения а sin x + b cosx = 0, где а ≠ 0, b ≠ 0, на cos x (или sin x) корни этого уравнения не теряются.
Однако sin x и cos х одновременно не могут быть равными нулю, в силу того что они связаны равенством sin2x + cos2x = 1. Следовательно, при делении уравнения а sin x + b cosx = 0, где а ≠ 0, b ≠ 0, на cos x (или sin x) корни этого уравнения не теряются.
3. Уравнения, решаемые разложением левой части на множители
Многие уравнения, в правой части которых располагается 0, решаются путем разложения на множители их левой части.
Задача 4.
Решить уравнение sin 2x – sinx = 0.
Решение.
Воспользуемся формулой синуса двойного аргумента и запишем уравнение в виде 2 sin x cosx – sin x = 0.
Общий множитель sin x вынесем за скобки и получим sin x(2 cosx – 1) = 0.
1) sin x = 0, х = πn, n € Z.
2) 2 cosx – 1 = 0, cosx = 1/2, х = +/-π/3 + 2πn, n € Z.
Ответ. х = +/-π/3 + 2πn, n € Z.
Задача 5.
Решить уравнение cos 3x + sin 5x = 0.
Решение.
Используя формулу приведения sin α = cos (π/2 – α), запишем уравнение в виде cos 3x + cos (π/2 – 5х)= 0.
Воспользуемся формулой для суммы косинусов и получим:
2 cos(π/4 – х) ∙ cos (4х – π/4)= 0.
1) cos(π/4 – х) = 0, х – π/4 = π/2 + πn, х = 3/4 π + πn, n € Z;
2) cos (4х – π/4)= 0, 4х – π/4 = π/2 + πn, х = 3/16 π + (πn)/4, n € Z.
Ответ. х = 3/4π + πn, х = 3/16π + (πn)/4, n € Z.
Задача 6.
Решить уравнение sin 7x + sin 3x = 3 cos 2х.
Решение.
Применим формулу суммы синусов и запишем уравнение в виде
2 sin 5x ∙ cos 2х = 3 cos 2х, или 2 sin 5x ∙ cos 2х – 3 cos 2х = 0,
откуда cos 2х(sin 5x – 3/2) = 0.
Уравнение cos 2х = 0 имеет корни х = π/4 + (πn)/2, а уравнение sin 5x = 3/2 не имеет корней.
Ответ. х = π/4 + (πn)/2, n € Z.
© blog.tutoronline.ru, при полном или частичном копировании материала ссылка на первоисточник обязательна.
Остались вопросы?
Задайте свой вопрос и получите ответ от профессионального преподавателя.
Задать вопрос
Математика
Курсы по математике 10 класс
Математика
Курсы по математике 9 класс
Математика
Математика 11 класс
Математика
Курсы по геометрии 7 класс
Математика
Курсы по алгебре 7 класс
Математика
Алгебра 8 класс
Математика
Курсы по геометрии 8 класс
Французский язык
Курсы французского языка для начинающих
Тригонометрические уравнения.
 Простейшие тригонометрические уравнения Решить тригонометрическое уравнение sinx 1 2
Простейшие тригонометрические уравнения Решить тригонометрическое уравнение sinx 1 2Основными методами решения тригонометрических уравнений являются: сведение уравнений к простейшим (с использованием тригонометрических формул), введение новых переменных, разложение на множители. Рассмотрим их применение на примерах. Обратите внимание на оформление записи решений тригонометрических уравнений.
Необходимым условием успешного решения тригонометрических уравнений является знание тригонометрических формул (тема 13 работы 6).
Примеры.
1. Уравнения, сводящиеся к простейшим.
1) Решить уравнение
Решение:
Ответ:
2) Найти корни уравнения
(sinx + cosx) 2 = 1 – sinxcosx, принадлежащие отрезку .
Решение:
Ответ:
2. Уравнения, сводящиеся к квадратным.
1) Решить уравнение 2 sin 2 x – cosx –1 = 0.
Решение: Используя формулу sin 2 x = 1 – cos 2 x, получаем
Ответ:
2) Решить уравнение cos 2x = 1 + 4 cosx.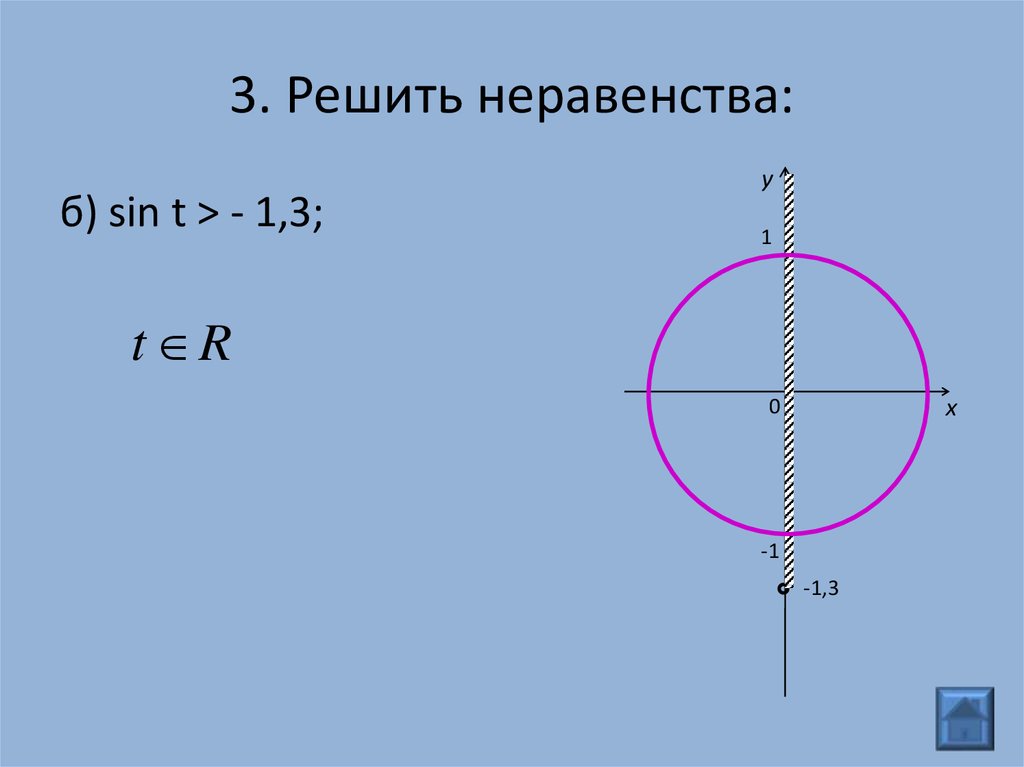
Решение: Используя формулу cos 2x = 2 cos 2 x – 1, получаем
Ответ:
3) Решить уравнение tgx – 2ctgx + 1 = 0
Решение:
Ответ:
3. Однородные уравнения
1) Решить уравнение 2sinx – 3cosx = 0
Решение: Пусть cosx = 0, тогда 2sinx = 0 и sinx = 0 – противоречие с тем, что sin 2 x + cos 2 x = 1. Значит cosx ≠ 0 и можно поделить уравнение на cosx. Получим
Ответ:
2) Решить уравнение 1 + 7 cos 2 x = 3 sin 2x
Решение:
Используем формулы 1 = sin 2 x + cos 2 x и sin 2x = 2 sinxcosx, получим
sin 2 x + cos 2 x + 7cos 2 x = 6sinxcosx
sin 2 x – 6sinxcosx+ 8cos 2 x = 0
Пусть cosx = 0, тогда sin 2 x = 0 и sinx = 0 – противоречие с тем, что sin 2 x + cos 2 x = 1.
Значит cosx ≠ 0 и можно поделить уравнение на cos 2 x. Получим
tg 2 x – 6 tgx + 8 = 0
Обозначим tgx = y
y 2 – 6 y + 8 = 0
y 1 = 4; y 2 = 2
а) tgx = 4, x= arctg4 + 2 k , k
б) tgx = 2, x= arctg2 + 2 k , k .
Ответ: arctg4 + 2 k , arctg2 + 2 k, k
4. Уравнения вида a sinx + b cosx = с, с ≠ 0.
1) Решить уравнение .
Решение:
Ответ:
5. Уравнения, решаемые разложением на множители.
1) Решить уравнение sin2x – sinx = 0.
Корнем уравнения f ( х ) = φ ( х ) может служить только число 0. Проверим это:
cos 0 = 0 + 1 – равенство верно.
Число 0 единственный корень данного уравнения.
Ответ: 0.
Соблюдение Вашей конфиденциальности важно для нас. По этой причине, мы разработали Политику Конфиденциальности, которая описывает, как мы используем и храним Вашу информацию. Пожалуйста, ознакомьтесь с нашими правилами соблюдения конфиденциальности и сообщите нам, если у вас возникнут какие-либо вопросы.
Сбор и использование персональной информации
Под персональной информацией понимаются данные, которые могут быть использованы для идентификации определенного лица либо связи с ним.
От вас может быть запрошено предоставление вашей персональной информации в любой момент, когда вы связываетесь с нами.
Ниже приведены некоторые примеры типов персональной информации, которую мы можем собирать, и как мы можем использовать такую информацию.
Какую персональную информацию мы собираем:
- Когда вы оставляете заявку на сайте, мы можем собирать различную информацию, включая ваши имя, номер телефона, адрес электронной почты и т.д.
Как мы используем вашу персональную информацию:
- Собираемая нами персональная информация позволяет нам связываться с вами и сообщать об уникальных предложениях, акциях и других мероприятиях и ближайших событиях.
- Время от времени, мы можем использовать вашу персональную информацию для отправки важных уведомлений и сообщений.
- Мы также можем использовать персональную информацию для внутренних целей, таких как проведения аудита, анализа данных и различных исследований в целях улучшения услуг предоставляемых нами и предоставления Вам рекомендаций относительно наших услуг.

- Если вы принимаете участие в розыгрыше призов, конкурсе или сходном стимулирующем мероприятии, мы можем использовать предоставляемую вами информацию для управления такими программами.
Раскрытие информации третьим лицам
Мы не раскрываем полученную от Вас информацию третьим лицам.
Исключения:
- В случае если необходимо — в соответствии с законом, судебным порядком, в судебном разбирательстве, и/или на основании публичных запросов или запросов от государственных органов на территории РФ — раскрыть вашу персональную информацию. Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.
- В случае реорганизации, слияния или продажи мы можем передать собираемую нами персональную информацию соответствующему третьему лицу – правопреемнику.
Защита персональной информации
Мы предпринимаем меры предосторожности — включая административные, технические и физические — для защиты вашей персональной информации от утраты, кражи, и недобросовестного использования, а также от несанкционированного доступа, раскрытия, изменения и уничтожения.
Соблюдение вашей конфиденциальности на уровне компании
Для того чтобы убедиться, что ваша персональная информация находится в безопасности, мы доводим нормы соблюдения конфиденциальности и безопасности до наших сотрудников, и строго следим за исполнением мер соблюдения конфиденциальности.
Простейшие тригонометрические уравнения решаются, как правило, по формулам. Напомню, что простейшими называются вот такие тригонометрические уравнения:
sinx = а
cosx = а
tgx = а
ctgx = а
х — угол, который нужно найти,
а — любое число.
А вот и формулы, с помощью которых можно сразу записать решения этих простейших уравнений.
Для синуса:
Для косинуса:
х = ± arccos a + 2π n, n ∈ Z
Для тангенса:
х = arctg a + π n, n ∈ Z
Для котангенса:
х = arcctg a + π n, n ∈ Z
Собственно, это и есть теоретическая часть решения простейших тригонометрических уравнений. Причём, вся!) Совсем ничего. Однако, количество ошибок по этой теме просто зашкаливает. Особенно, при незначительном отклонении примера от шаблона. Почему?
Причём, вся!) Совсем ничего. Однако, количество ошибок по этой теме просто зашкаливает. Особенно, при незначительном отклонении примера от шаблона. Почему?
Да потому, что масса народу записывает эти буковки, не понимая их смысла совершенно! С опаской записывает, как бы чего не вышло…) С этим надо разобраться. Тригонометрия для людей, или люди для тригонометрии, в конце концов!?)
Разберёмся?
Один угол у нас будет равен arccos a, второй: -arccos a.
И так будет получаться всегда. При любом а.
Если не верите, наведите курсор мышки на картинку, или коснитесь рисунка на планшете.) Я изменил число а на какое-то отрицательное. Всё равно, один угол у нас получился arccos a, второй: -arccos a.
Следовательно, ответ можно всегда записать в виде двух серий корней:
х 1 = arccos a + 2π n, n ∈ Z
х 2 = — arccos a + 2π n, n ∈ Z
Объединяем эти две серии в одну:
х= ± arccos а + 2π n, n ∈ Z
И все дела. Получили общую формулу для решения простейшего тригонометрического уравнения с косинусом.
Получили общую формулу для решения простейшего тригонометрического уравнения с косинусом.
Если вы понимаете, что это не какая-то сверхнаучная мудрость, а просто сокращённая запись двух серий ответов, вам и задания «С» будут по плечу. С неравенствами, с отбором корней из заданного интервала… Там ответ с плюсом/минусом не катит. А если отнестись к ответу делово, да разбить его на два отдельных ответа, всё и решается.) Собственно, для этого и разбираемся. Что, как и откуда.
В простейшем тригонометрическом уравнении
sinx = а
тоже получается две серии корней. Всегда. И эти две серии тоже можно записать одной строчкой. Только эта строчка похитрее будет:
х = (-1) n arcsin a + π n, n ∈ Z
Но суть остаётся прежней. Математики просто сконструировали формулу, чтобы вместо двух записей серий корней, сделать одну. И всё!
Проверим математиков? А то мало ли…)
В предыдущем уроке подробно разобрано решение (безо всяких формул) тригонометрического уравнения с синусом:
В ответе получились две серии корней:
х 1 = π /6 + 2π n, n ∈ Z
х 2 = 5π /6 + 2π n, n ∈ Z
Если мы будем решать это же уравнение по формуле, получим ответ:
х = (-1) n arcsin 0,5 + π n, n ∈ Z
Вообще-то, это недоделанный ответ. ) Ученик обязан знать, что arcsin 0,5 = π
/6. Полноценный ответ будет:
) Ученик обязан знать, что arcsin 0,5 = π
/6. Полноценный ответ будет:
х = (-1) n π /6 + π n, n ∈ Z
Тут возникает интересный вопрос. Ответ через х 1 ; х 2 (это правильный ответ!) и через одинокий х (и это правильный ответ!) — одно и то же, или нет? Сейчас узнаем.)
Подставляем в ответ с х 1 значения n =0; 1; 2; и т.д., считаем, получаем серию корней:
х 1 = π/6; 13π/6; 25π/6 и так далее.
При такой же подстановке в ответ с х 2 , получаем:
х 2 = 5π/6; 17π/6; 29π/6 и так далее.
А теперь подставляем значения n (0; 1; 2; 3; 4…) в общую формулу для одинокого х . Т.е возводим минус один в нулевую степень, затем в первую, вторую, и т.д. Ну и, разумеется, во второе слагаемое подставляем 0; 1; 2 3; 4 и т.д. И считаем. Получаем серию:
х = π/6; 5π/6; 13π/6; 17π/6; 25π/6 и так далее.
Вот всё и видно.) Общая формула выдаёт нам точно такие же результаты, что и два ответа по отдельности. Только все сразу, по порядочку. Не обманули математики.)
Формулы для решения тригонометрических уравнений с тангенсом и котангенсом тоже можно проверить. Но не будем.) Они и так простенькие.
Я расписал всю эту подстановку и проверку специально. Здесь важно понять одну простую вещь: формулы для решения элементарных тригонометрических уравнений есть, всего лишь, краткая запись ответов. Для этой краткости пришлось вставить плюс/минус в решение для косинуса и (-1) n в решение для синуса.
Эти вставки никак не мешают в заданиях, где нужно просто записать ответ элементарного уравнения. Но если надо решать неравенство, или далее нужно что-то делать с ответом: отбирать корни на интервале, проверять на ОДЗ и т.п, эти вставочки могут запросто выбить человека из колеи.
И что делать? Да либо расписать ответ через две серии, либо решать уравнение/неравенство по тригонометрическому кругу. Тогда исчезают эти вставочки и жизнь становится легче.)
Тогда исчезают эти вставочки и жизнь становится легче.)
Можно подвести итоги.
Для решения простейших тригонометрических уравнений существуют готовые формулы ответов. Четыре штуки. Они хороши для мгновенной записи решения уравнения. Например, надо решить уравнения:
sinx = 0,3
Легко: х = (-1) n arcsin 0,3 + π n, n ∈ Z
cosx = 0,2
Без проблем: х = ± arccos 0,2 + 2π n, n ∈ Z
tgx = 1,2
Запросто: х = arctg 1,2 + π n, n ∈ Z
ctgx = 3,7
Одной левой: x= arcctg3,7 + π n, n ∈ Z
cos x = 1,8
Если вы, блистая знаниями, мгновенно пишете ответ:
х= ± arccos 1,8 + 2π n, n ∈ Z
то блистаете вы уже, это… того… из лужи.) Правильный ответ: решений нет. Не понимаете, почему? Прочитайте, что такое арккосинус. Кроме того, если в правой части исходного уравнения стоят табличные значения синуса, косинуса, тангенса, котангенса, — 1; 0; √3; 1/2; √3/2 и т. п. — ответ через арки будет недоделанным. Арки нужно обязательно перевести в радианы.
п. — ответ через арки будет недоделанным. Арки нужно обязательно перевести в радианы.
А если уж вам попалось неравенство, типа
то ответ в виде:
х πn, n ∈ Z
есть редкая ахинея, да…) Тут надо по тригонометрическому кругу решать. Чем мы и займёмся в соответствующей теме.
Для тех, кто героически дочитал до этих строк. Я просто не могу не оценить ваши титанические усилия. Вам бонус.)
Бонус:
При записи формул в тревожной боевой обстановке, даже закалённые учёбой ботаны частенько путаются, где πn, а где 2π n. Вот вам простой приёмчик. Во всех формулах стоит πn. Кроме единственной формулы с арккосинусом. Там стоит 2πn. Два пиэн. Ключевое слово — два. В этой же единственной формуле стоят два знака в начале. Плюс и минус. И там, и там — два.
Так что, если вы написали два знака перед арккосинусом, легче вспомнить, что в конце будет два пиэн. А ещё наоборот бывает. Пропустит человек знак ± , доберётся до конца, напишет правильно два пиэн, да и спохватится. Впереди-то два знака! Вернётся человек к началу, да ошибку-то и исправит! Вот так.)
А ещё наоборот бывает. Пропустит человек знак ± , доберётся до конца, напишет правильно два пиэн, да и спохватится. Впереди-то два знака! Вернётся человек к началу, да ошибку-то и исправит! Вот так.)
Кстати, у меня есть ещё парочка интересных сайтов для Вас.)
Можно потренироваться в решении примеров и узнать свой уровень. Тестирование с мгновенной проверкой. Учимся — с интересом!)
можно познакомиться с функциями и производными.
Когда-то я стал свидетелем разговора двух абитуриентов:
– Когда надо прибавить 2πn, а когда – πn? Никак не могу запомнить!
– И у меня такая же проблема.
Так и хотелось им сказать: «Не запоминать надо, а понимать!»
Данная статья адресована прежде всего старшеклассникам и, надеюсь, поможет им с «пониманием» решать простейшие тригонометрические уравнения:
Числовая окружность
Наряду с понятием числовой прямой есть еще и понятие числовой окружности. Как мы знаем, в прямоугольной системе координат окружность,с центром в точке (0;0) и радиусом 1, называется единичной. Вообразим числовую прямую тонкой нитью и намотаем ее на эту окружность: начало отсчета (точку 0), приставим к «правой» точке единичной окружности, положительную полуось обмотаем против движения часовой стрелки, а отрицательную – по направлению (рис. 1). Такую единичную окружность называют числовой.
Вообразим числовую прямую тонкой нитью и намотаем ее на эту окружность: начало отсчета (точку 0), приставим к «правой» точке единичной окружности, положительную полуось обмотаем против движения часовой стрелки, а отрицательную – по направлению (рис. 1). Такую единичную окружность называют числовой.
Свойства числовой окружности
- Каждое действительное число находится на одной точке числовой окружности.
- На каждой точке числовой окружности находятся бесконечно много действительных чисел. Так как длина единичной окружности равна 2π, то разность между любыми двумя числами на одной точке окружности равна одному из чисел ±2π ; ±4π ; ±6π ; …
Сделаем вывод: зная одно из чисел точки A, мы можем найти все числа точки A .
Проведем диаметр АС (рис. 2). Так как x_0 – одно из чисел точки А, то числа x_0±π ; x_0±3π; x_0±5π; … и только они будут числами точки C. Выберем одно из этих чисел, скажем, x_0+π, и запишем с его помощью все числа точки C: x_C=x_0+π+2πk ,k∈Z. Отметим, что числа на точках A и C можно объединить в одну формулу: x_(A ; C)=x_0+πk ,k∈Z (при k = 0; ±2; ±4; … получим числа точки A, а при k = ±1; ±3; ±5; … – числа точки C).
Отметим, что числа на точках A и C можно объединить в одну формулу: x_(A ; C)=x_0+πk ,k∈Z (при k = 0; ±2; ±4; … получим числа точки A, а при k = ±1; ±3; ±5; … – числа точки C).
Сделаем вывод: зная одно из чисел на одной из точек A или C диаметра АС, мы можем найти все числа на этих точках.
- Два противоположных числа находятся на симметричных относительно оси абсцисс точках окружности.
Проведем вертикальную хорду АВ (рис. 2). Так как точки A и B симметричны относительно оси Ox, то число -x_0 находится на точке B и, значит, все числа точки B задаются формулой: x_B=-x_0+2πk ,k∈Z. Числа на точках A и B запишем одной формулой: x_(A ; B)=±x_0+2πk ,k∈Z. Сделаем вывод: зная одно из чисел на одной из точек A или B вертикальной хорды АВ, мы можем найти все числа на этих точках. Рассмотрим горизонтальную хорду AD и найдем числа точки D (рис. 2). Так как BD – диаметр и число -x_0 принадлежит точке В, то -x_0 + π одно из чисел точки D и, значит, все числа этой точки задаются формулой x_D=-x_0+π+2πk ,k∈Z.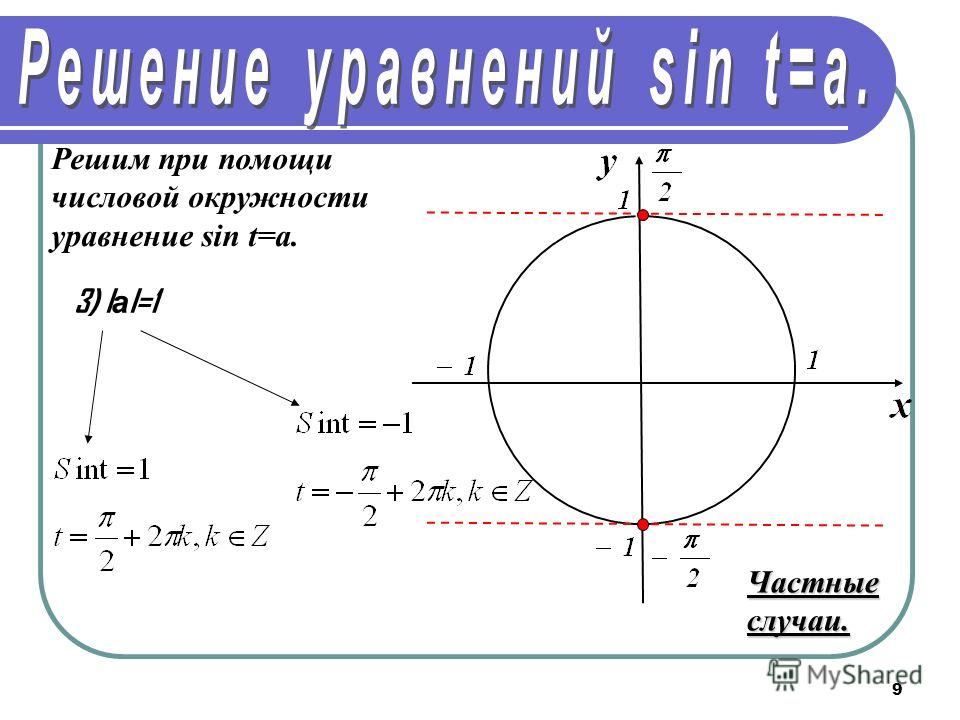 k∙x_0+πk ,k∈Z . (при k= 0; ±2; ±4; … получим числа точки A, а при k = ±1; ±3; ±5; … – числа точки D).
k∙x_0+πk ,k∈Z . (при k= 0; ±2; ±4; … получим числа точки A, а при k = ±1; ±3; ±5; … – числа точки D).
Сделаем вывод: зная одно из чисел на одной из точек A или D горизонтальной хорды AD, мы можем найти все числа на этих точках.
Шестнадцать основных точек числовой окружности
На практике решение большинства простейших тригонометрических уравнений связано с шестнадцатью точками окружности (рис. 3). Что это за точки? Красные, синие и зеленые точки делят окружность на 12 равных частей. Так как длина полуокружности равна π, то длина дуги A1A2 равна π/2, длина дуги A1B1 равна π/6, а длина дуги A1C1 равна π/3.
Теперь можем указать по одному числу на точках:
π/3 на С1 и
Вершины оранжевого квадрата – середины дуг каждой четверти, следовательно, длина дуги A1D1 равна π/4 и, значит, π/4 – одно из чисел точки D1. Воспользовавшись свойствами числовой окружности, мы можем записать с помощью формул все числа на всех отмеченных точках нашей окружности. На рисунке отмечены также и координаты этих точек (опустим описание их получения).
На рисунке отмечены также и координаты этих точек (опустим описание их получения).
Усвоив выше сказанное, мы имеем теперь достаточную подготовку для решения частных случаев (для девяти значений числа a) простейших уравнений.
Решить уравнения
1) sinx=1⁄(2) .
– Что от нас требуется?
– Найти все те числа x, синус которых равен 1/2 .
Вспомним определение синуса: sinx – ордината точки числовой окружности, на которой находится число x . На окружности имеем две точки, ордината которых равна 1/2 . Это концы горизонтальной хорды B1B2 . Значит, требование «решить уравнение sinx=1⁄2 » равнозначно требованию «найти все числа на точке B1 и все числа на точке B2».
2) sinx=-√3⁄2 .
Нам надо найти все числа на точках C4 и C3.
3) sinx=1 . На окружности имеем только одну точку с ординатой 1 – точка A2 и, значит, нам надо найти только все числа этой точки.
Ответ: x=π/2+2πk , k∈Z .
4) sinx=-1 .
Только точка A_4 имеет ординату -1. Все числа этой точки и будут конями уравнения.
Ответ: x=-π/2+2πk , k∈Z .
5) sinx=0 .
На окружности имеем две точки с ординатой 0 – точки A1 и A3 . Можно указать числа на каждой из точек по отдельности, но, учитывая, что эти точки диаметрально противоположные, лучше объединить их в одну формулу: x=πk ,k∈Z .
Ответ: x=πk ,k∈Z .
6) cosx=√2⁄2 .
Вспомним определение косинуса: cosx — абсцисса точки числовой окружности на которой находится число x. На окружности имеем две точки с абсциссой √2⁄2 – концы горизонтальной хорды D1D4 . Нам нужно найти все числа на этих точках. Запишем их, объединив в одну формулу.
Ответ: x=±π/4+2πk , k∈Z .
7) cosx=-1⁄2 .
Надо найти числа на точках C_2 и C_3 .
Ответ: x=±2π/3+2πk , k∈Z .
10) cosx=0 .
Только точки A2 и A4 имеют абсциссу 0, значит, все числа на каждой из этих точках и будут решениями уравнения.
.
Решениями уравнения системы являются числа на точках B_3 и B_4 .Неравенству cosxОтвет: x=-5π/6+2πk , k∈Z .
Заметим,что при любом допустимом значении x второй множитель положителен и, следовательно,уравнение равносильно системе
Решениями уравнения системы являются чила точек D_2 и D_3 . Числа точки D_2 не удовлетворяют неравенству sinx≤0,5 ,а числа точки D_3-удовлетворяют.
blog.сайт, при полном или частичном копировании материала ссылка на первоисточник обязательна.
Пример 2 (4.1)
Решите уравнение
Решение
1 — ,
t2 – 6t +5 = 0;
D = 36 – 20 = 16>0;
+
+
Пример 3 (5.1)
Решите уравнение — = .
Решение
— = ,
+
1 –
.
Обозначим
2t2 –t – 1 = 0; D = 1 + 8 = 9,
t1 =
= — ,
(-1)n+1 + ,
(-1)n+1 + .
,
+
(-1)n+1 + ,
Решение тригонометрических уравнений разложением на множители
Данное выражение представляется в виде произведения нескольких сомножителей. В случае, когда выражение равно нулю, каждый из них приравнивается к нулю и уравнение сводится к более простому.
Пример 1 (4.27)
Решите уравнение
Решение
,
2) +
Ответ: +
Пример 2 (6.23)
Решите уравнение
1 + sin 3x =
Решение
1 + sin 3x =
1 + sin 3x = cos2 sin2
1 + sin3x = 1 – sinx,
sin 3x + sin x = 0,
2sin 2x cos x = 0,
sin2x = 0, 2x
cos x = 0, x = +
Ответ: +
2.
 6 Однородные тригонометрические уравнения
6 Однородные тригонометрические уравненияУравнение, в котором каждое слагаемое имеет одну и ту же степень, называется однородным.
Его можно решать, выполнив деление на старшую степень косинуса (или синуса).
Пример 1( 4.35)
Найдите все решения уравнения принадлежащих отрезку [-2
Решение
делим уравнение почленно на cosx ( заметим: если в данное уравнение подставить cosx =0, то получим sinx = 0, что невозможно, значит, в результате деления на cosx не будет потери корней) и находим:
tg x = 1, x = +
n = 0, x = [-2
n = 1, x = [-2
n = -1, x = [-2
n = -2, x = [-2
Ответ:
Пример
2( 5. 13)
13)
Решите уравнение
6sin2x + sin x cos x – cos2 x = 0.
Решение
6sin2x + sin x cos x – cos2 x = 0, так как cos 2 x 0. То делим почленно на cos2 x
6tg 2 x + tg x – 1 = 0.
Пусть tg x = t, тогда
6t 2 + t – 1 = 0; D = 1 + 24 = 25;
=
tg x =
tg x =
Ответ:
Системы тригонометрических уравнений
Решение
систем тригонометрических уравнений
чаще всего сводится к решению алгебраических
систем относительно sin x, cos x, tg x и т. п.
п.
Необходимо отметить, что при решении простейших уравнений нужно писать различные целочисленные параметры n и k. Если бы мы использовали одну и ту же букву, было бы потеряно бесконечное множество решений.
Есть и иной способ решения систем, в котором может использоваться способ выражения одного переменного через другое и подстановка во второе уравнение.
Решение системы записывается в виде упорядоченных пар (x; y).
Примеры выполнения заданий
Пример 1 (5.15)
Решите систему уравнений
Решение
4y + 10 – 2y = 19,
2y = 9,
y = 4,5;
x = (-1)n + ;
Ответ:
( (-1)n + .
2. Логарифмические выражения, уравнения, неравенства, системы
Справочный материал
Логарифмом числа b по основанию a называется показатель степени, в которую нужно возвести a, чтобы получить b, причем a >0, a ≠ 1, b > 0.
= c , (1)
Основное логарифмическое тождество
(2)
Логарифмическая функция
y=
Свойства
D (y) = R+.
E(y) = R.
При a > 1 функция монотонно возрастает на R+ и при 0 <a <1 функция монотонно убывает на R+.

При x= 1 значение функции y = 0.
| 1 | Найти точное значение | грех(30) | |
| 2 | Найти точное значение | грех(45) | |
| 3 | Найти точное значение | грех(30 градусов) | |
| 4 | Найти точное значение | грех(60 градусов) | |
| 5 | Найти точное значение | загар (30 градусов) | |
| 6 | Найти точное значение | угловой синус(-1) | |
| 7 | Найти точное значение | грех(пи/6) | |
| 8 | Найти точное значение | cos(pi/4) | |
| 9 | Найти точное значение | грех(45 градусов) | |
| 10 | Найти точное значение | грех(пи/3) | |
| 11 | Найти точное значение | арктан(-1) | |
| 12 | Найти точное значение | cos(45 градусов) | |
| 13 | Найти точное значение | cos(30 градусов) | |
| 14 | Найти точное значение | желтовато-коричневый(60) | |
| 15 | Найти точное значение | csc(45 градусов) | |
| 16 | Найти точное значение | загар (60 градусов) | |
| 17 | Найти точное значение | сек(30 градусов) | |
| 18 | Найти точное значение | cos(60 градусов) | |
| 19 | Найти точное значение | cos(150) | |
| 20 | Найти точное значение | грех(60) | |
| 21 | Найти точное значение | cos(pi/2) | |
| 22 | Найти точное значение | загар (45 градусов) | |
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | |
| 24 | Найти точное значение | csc(60 градусов) | |
| 25 | Найти точное значение | сек(45 градусов) | |
| 26 | Найти точное значение | csc(30 градусов) | |
| 27 | Найти точное значение | грех(0) | |
| 28 | Найти точное значение | грех(120) | |
| 29 | Найти точное значение | соз(90) | |
| 30 | Преобразовать из радианов в градусы | пи/3 | |
| 31 | Найти точное значение | желтовато-коричневый(30) | |
| 32 | 92|||
| 35 | Преобразовать из радианов в градусы | пи/6 | |
| 36 | Найти точное значение | детская кроватка(30 градусов) | |
| 37 | Найти точное значение | арккос(-1) | |
| 38 | Найти точное значение | арктан(0) | |
| 39 | Найти точное значение | детская кроватка(60 градусов) | |
| 40 | Преобразование градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2 шт. )/3 )/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | тан(пи/2) | |
| 45 | Найти точное значение | грех(300) | |
| 46 | Найти точное значение | соз(30) | |
| 47 | Найти точное значение | соз(60) | |
| 48 | Найти точное значение | соз(0) | |
| 49 | Найти точное значение | соз(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | cos(210) | |
| 52 | Найти точное значение | сек(60 градусов) | |
| 53 | Найти точное значение | грех(300 градусов) | |
| 54 | Преобразование градусов в радианы | 135 | |
| 55 | Преобразование градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5 дюймов)/6 | |
| 57 | Преобразовать из радианов в градусы | (5 дюймов)/3 | |
| 58 | Преобразование градусов в радианы | 89 градусов | |
| 59 | Преобразование градусов в радианы | 60 | |
| 60 | Найти точное значение | грех(135 градусов) | |
| 61 | Найти точное значение | грех(150) | |
| 62 | Найти точное значение | грех(240 градусов) | |
| 63 | Найти точное значение | детская кроватка(45 градусов) | |
| 64 | Преобразовать из радианов в градусы | (5 дюймов)/4 | |
| 65 | Найти точное значение | грех(225) | |
| 66 | Найти точное значение | грех(240) | |
| 67 | Найти точное значение | cos(150 градусов) | |
| 68 | Найти точное значение | желтовато-коричневый(45) | |
| 69 | Оценить | грех(30 градусов) | |
| 70 | Найти точное значение | сек(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | КСК(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень из 2)/2) | |
| 74 | Найти точное значение | загар((5pi)/3) | |
| 75 | Найти точное значение | желтовато-коричневый(0) | |
| 76 | Оценить | грех(60 градусов) | |
| 77 | Найти точное значение | arctan(-( квадратный корень из 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3 пи)/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | Найти точное значение | угловой синус(-1/2) | |
| 81 | Найти точное значение | sin((4pi)/3) | |
| 82 | Найти точное значение | КСК(45) | |
| 83 | Упростить | арктан(квадратный корень из 3) | |
| 84 | Найти точное значение | грех(135) | |
| 85 | Найти точное значение | грех(105) | |
| 86 | Найти точное значение | грех(150 градусов) | |
| 87 | Найти точное значение | sin((2pi)/3) | |
| 88 | Найти точное значение | загар((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | пи/4 | |
| 90 | Найти точное значение | грех(пи/2) | |
| 91 | Найти точное значение | сек(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | cos((7pi)/6) | |
| 94 | Найти точное значение | угловой синус(0) | |
| 95 | Найти точное значение | грех(120 градусов) | |
| 96 | Найти точное значение | желтовато-коричневый ((7pi)/6) | |
| 97 | Найти точное значение | соз(270) | |
| 98 | Найти точное значение | sin((7pi)/6) | |
| 99 | Найти точное значение | arcsin(-( квадратный корень из 2)/2) | |
| 100 | Преобразование градусов в радианы | 88 градусов |
Предварительное вычисление алгебры — Как бы вы решили уравнение формы $e^{-x} — \sin(x) = 0$?
Спросил
Изменено 2 года, 5 месяцев назад
Просмотрено 913 раз
$\begingroup$
Я пытался сделать это целую вечность. Я беспокоюсь, что это невозможно, но я слышал, что это можно сделать вручную.
Я беспокоюсь, что это невозможно, но я слышал, что это можно сделать вручную.
Пока я могу получить $x$ вручную, я, очевидно, могу рассчитать его стоимость с помощью калькулятора.
Пожалуйста, помогите, я так застрял и отчаянно нуждаюсь в помощи. 9{-x}$ [Синяя линия] и $\sin x$ [Красная линия].
Одним словом решения $x=0.589,3.096,6.285$ и т.д.
Надеюсь, это работает.
$\endgroup$
3
$\begingroup$
Вы не можете найти замкнутую форму для нулей, но можете найти асимптотические приближения.
Пусть $x_n$ — нуль в $(\pi n-\frac \pi 2, \pi n+\frac \pi 2)$. Напишите $x_n=\pi n+\varepsilon_n$ с $|\varepsilon_n|<\frac \pi 2$. 9093}+\cdots$$
$$\слева( \begin{массив}{ccc} n & \text{приближение} & \text{решение} \\ 0 & 0,5625000000000000000 & 0,5885327439818610774 \\ 1 и 3,0963808805403588820 и 3,09636306461156 \\ 2 и 6,28504072431593 и 6,28504
825865338\
3 и 9,4246972547386088459 и 9,4246972547385212191\
4 и 12,5663741016870 и 12,5663741016877 \\
5 и 15,707963117247215942 и 15,707963117247215942 \\
6 и 18. 849555
849555
1171524 и 18.849555
1171524\ 7 и 21,9
574847125823 и 21,9
574847125823 \\
8 и 25.132741228730507464 и 25.132741228730507464\
9 и 28,274333882307613598 и 28,274333882307613598 \\
10 и 31,4155897
6 и 31,4155897
6
\конец{массив}
\справа)$$ $\endgroup$
Твой ответ
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Обязательно, но не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.
7.5 Решение тригонометрических уравнений. Предварительное исчисление 2e
Цели обучения
В этом разделе вы:
- Решение линейных тригонометрических уравнений относительно синуса и косинуса.
- Решите уравнения с одной тригонометрической функцией.
- Решите тригонометрические уравнения с помощью калькулятора.
- Решение тригонометрических уравнений квадратной формы.
- Решите тригонометрические уравнения, используя фундаментальные тождества.
- Решите тригонометрические уравнения с несколькими углами.
- Решение задач на прямоугольный треугольник.
Рисунок
1
Египетские пирамиды стоят рядом с современным городом. (кредит: Oisin Mulvihill)
Фалес Милетский (около 625–547 гг. до н. э.) известен как основатель геометрии. Легенда гласит, что он рассчитал высоту Великой пирамиды в Гизе в Египте, используя теорию подобных треугольника , которые он разработал, измерив тень своего посоха. Основанная на пропорциях, эта теория находит применение в ряде областей, включая фрактальную геометрию, инженерию и архитектуру. Часто угол возвышения и угол наклона находят с помощью подобных треугольников.
Основанная на пропорциях, эта теория находит применение в ряде областей, включая фрактальную геометрию, инженерию и архитектуру. Часто угол возвышения и угол наклона находят с помощью подобных треугольников.
В предыдущих разделах этой главы мы рассмотрели тригонометрические тождества. Тождества верны для всех значений в домене переменной. В этом разделе мы начинаем изучение тригонометрических уравнений для изучения реальных сценариев, таких как определение размеров пирамид.
Решение линейных тригонометрических уравнений с помощью синуса и косинуса
Тригонометрические уравнения, как следует из названия, включают в себя тригонометрические функции. Во многом подобно решению полиномиальных уравнений или рациональных уравнений, только определенные значения переменной будут решениями, если решения вообще есть. Часто мы будем решать тригонометрическое уравнение на заданном интервале. Однако столь же часто нас будут просить найти все возможные решения, а поскольку тригонометрические функции являются периодическими, решения повторяются в каждом периоде. Другими словами, тригонометрические уравнения могут иметь бесконечное число решений. Кроме того, как и в случае с рациональными уравнениями, область определения функции должна быть рассмотрена, прежде чем мы предположим, что какое-либо решение является допустимым. Период как функции синуса, так и функции косинуса равен 2π,2π. Другими словами, через каждые 2π2π единиц y- значения повторяются. Если нам нужно найти все возможные решения, то мы должны добавить 2πk,2πk, где kk — целое число, к исходному решению. Вспомните правило, которое дает формат для формулировки всех возможных решений функции с периодом 2π:2π:
Другими словами, тригонометрические уравнения могут иметь бесконечное число решений. Кроме того, как и в случае с рациональными уравнениями, область определения функции должна быть рассмотрена, прежде чем мы предположим, что какое-либо решение является допустимым. Период как функции синуса, так и функции косинуса равен 2π,2π. Другими словами, через каждые 2π2π единиц y- значения повторяются. Если нам нужно найти все возможные решения, то мы должны добавить 2πk,2πk, где kk — целое число, к исходному решению. Вспомните правило, которое дает формат для формулировки всех возможных решений функции с периодом 2π:2π:
sinθ=sin(θ±2kπ)sinθ=sin(θ±2kπ)
Существуют аналогичные правила для указания всех возможных решений для других тригонометрических функций. Решение тригонометрических уравнений требует тех же методов, что и решение алгебраических уравнений. Читаем уравнение слева направо, по горизонтали, как предложение. Мы ищем известные шаблоны, факторизуем, находим общие знаменатели и заменяем определенные выражения переменной, чтобы упростить процесс решения. Однако с тригонометрическими уравнениями у нас также есть преимущество использования тождеств, которые мы разработали в предыдущих разделах.
Однако с тригонометрическими уравнениями у нас также есть преимущество использования тождеств, которые мы разработали в предыдущих разделах.
Пример
1
Решение линейного тригонометрического уравнения с косинусом
 Основанная на пропорциях, эта теория находит применение в ряде областей, включая фрактальную геометрию, инженерию и архитектуру. Часто угол возвышения и угол наклона находят с помощью подобных треугольников.
Основанная на пропорциях, эта теория находит применение в ряде областей, включая фрактальную геометрию, инженерию и архитектуру. Часто угол возвышения и угол наклона находят с помощью подобных треугольников. Другими словами, тригонометрические уравнения могут иметь бесконечное число решений. Кроме того, как и в случае с рациональными уравнениями, область определения функции должна быть рассмотрена, прежде чем мы предположим, что какое-либо решение является допустимым. Период как функции синуса, так и функции косинуса равен 2π,2π. Другими словами, через каждые 2π2π единиц y- значения повторяются. Если нам нужно найти все возможные решения, то мы должны добавить 2πk,2πk, где kk — целое число, к исходному решению. Вспомните правило, которое дает формат для формулировки всех возможных решений функции с периодом 2π:2π:
Другими словами, тригонометрические уравнения могут иметь бесконечное число решений. Кроме того, как и в случае с рациональными уравнениями, область определения функции должна быть рассмотрена, прежде чем мы предположим, что какое-либо решение является допустимым. Период как функции синуса, так и функции косинуса равен 2π,2π. Другими словами, через каждые 2π2π единиц y- значения повторяются. Если нам нужно найти все возможные решения, то мы должны добавить 2πk,2πk, где kk — целое число, к исходному решению. Вспомните правило, которое дает формат для формулировки всех возможных решений функции с периодом 2π:2π: Однако с тригонометрическими уравнениями у нас также есть преимущество использования тождеств, которые мы разработали в предыдущих разделах.
Однако с тригонометрическими уравнениями у нас также есть преимущество использования тождеств, которые мы разработали в предыдущих разделах.Найдите все возможные точные решения уравнения cosθ=12.cosθ=12.
Решение
Из единичного круга мы знаем, что
cosθ=12 θ=π3,5π3cosθ=12 θ=π3,5π3
Это решения в интервале [0,2π].[0,2π]. Все возможные решения задаются как
π3±2kπ и 5π3±2kππ3±2kπ и 5π3±2kπ
, где kk — целое число.
Пример 2
Решение линейного уравнения с функцией синуса
Найдите все возможные точные решения уравнения sint=12.sint=12.
Решение
Решение для всех возможных значений t означает, что решения включают углы вне периода 2π,2π. Из рисунка 2 видно, что решения равны π6π6 и 5π6,5π6. Но проблема заключается в том, чтобы указать все возможные значения, которые решают уравнение. Поэтому ответ
Из рисунка 2 видно, что решения равны π6π6 и 5π6,5π6. Но проблема заключается в том, чтобы указать все возможные значения, которые решают уравнение. Поэтому ответ
π6±2πk и 5π6±2πkπ6±2πk и 5π6±2πk
, где kk — целое число.
Как
Дано тригонометрическое уравнение, решить с помощью алгебры .
- Ищите шаблон, который предполагает алгебраическое свойство, такое как разность квадратов или факторинговая возможность.
- Замените тригонометрическое выражение одной переменной, например xx или u.u.
- Решите уравнение так же, как решали бы алгебраическое уравнение.
- Замените тригонометрическое выражение на переменную в результирующих выражениях.
- Найдите угол.
Пример 3
Решение тригонометрического уравнения в линейной форме
Точное решение уравнения: 2cosθ−3=−5,0≤θ<2π.2cosθ−3=−5,0≤θ<2π.
Решение
Используйте алгебраические методы для решения уравнения.
2cosθ−3=−5 2cosθ=−2 cosθ=−1 θ=π2cosθ−3=−5 2cosθ=−2 cosθ=−1 0909
Попытайся #1
Решите точно следующее линейное уравнение на отрезке [0,2π):2sinx+1=0.[0,2π):2sinx+1=0.
Решение уравнений с одной тригонометрической функцией
Когда нам даны уравнения, включающие только одну из шести тригонометрических функций, их решения включают использование алгебраических методов и единичной окружности (см. рис. 2). Нам нужно сделать несколько соображений, когда уравнение включает тригонометрические функции, отличные от синуса и косинуса. Проблемы, связанные с обратными величинами основных тригонометрических функций, необходимо рассматривать с алгебраической точки зрения. Другими словами, мы напишем обратную функцию и найдем углы, используя эту функцию. Кроме того, уравнение, включающее функцию тангенса, немного отличается от уравнения, содержащего функцию синуса или косинуса. Во-первых, как мы знаем, период касательной равен π, π, а не 2π,2π. Далее, областью определения тангенса являются все действительные числа, за исключением нечетных целых чисел, кратных π2,π2, если, конечно, проблема не накладывает свои ограничения на область определения.
Кроме того, уравнение, включающее функцию тангенса, немного отличается от уравнения, содержащего функцию синуса или косинуса. Во-первых, как мы знаем, период касательной равен π, π, а не 2π,2π. Далее, областью определения тангенса являются все действительные числа, за исключением нечетных целых чисел, кратных π2,π2, если, конечно, проблема не накладывает свои ограничения на область определения.
Пример 4
Решение задачи с одной тригонометрической функцией
Точно решить задачу: 2sin2θ−1=0,0≤θ<2π.2sin2θ−1=0,0≤θ<2π.
Решение
Так как эту задачу не так просто решить, мы будем решать ее, используя свойство квадратного корня. Во-первых, мы используем алгебру, чтобы изолировать sinθ.sinθ. Потом найдем углы.
2sin2θ — 1 = 0 2sin2θ = 1 sin2θ = 12 sin2 = ± 12 sinθ = ± 12 = ± 22 θ = π4,3π4,5π4,7π42sin2θ — 1 = 0 2sin2 = 1 sin2θ = 12 sin2θ = ± 12 sinθ = ± ± ± ± ± ± ± ± 0 = 0 12=±22 θ=π4,3π4,5π4,7π4
Пример 5
Решение тригонометрического уравнения с косекансом
Точно решить следующее уравнение: cscθ=−2,0≤θ<4π. cscθ=−2,0≤θ<4π.
cscθ=−2,0≤θ<4π.
Решение
Нам нужны все значения θθ, для которых cscθ=−2cscθ=−2 в интервале 0≤θ<4π,0≤θ<4π.
cscθ=-21sinθ=-2sinθ=-12 θ=7π6,11π6,19π6,23π6cscθ=–21sinθ=–2sinθ=–12 θ=7π6,11π6,19π6,23π6
Анализ
Поскольку sinθ=−12,sinθ=−12, обратите внимание, что все четыре решения находятся в третьем и четвертом квадрантах.
Пример 6
Решение уравнения с касательной
Точно решить уравнение: tan(θ−π2)=1,0≤θ<2π.tan(θ−π2)=1,0≤θ<2π.
Решение
Напомним, что тангенс функции имеет период π.π. На интервале [0,π),[0,π) и под углом π4,π4 тангенс имеет значение 1. Однако искомый угол равен (θ−π2).(θ−π2) . Таким образом, если tan(π4)=1,tan(π4)=1, то
θ−π2=π4θ=3π4±kπθ−π2=π4θ=3π4±kπ
На интервале [0,2π),[0 ,2π), имеем два решения:
3π4 и 3π4+π=7π43π4 и 3π4+π=7π4
Попытайся #2
Найдите все решения для tanx=3. tanx=3.
tanx=3.
Пример 7
Найти все решения уравнения с касательной
Найти все точные решения уравнения 2(tanx+3)=5+tanx,0≤x<2π.2(tanx+3)=5+tanx,0≤x <2π.
Решение
Мы можем решить это уравнение, используя только алгебру. Изолируйте выражение tanxtanx слева от знака равенства.
2(tanx)+2(3)=5+tanx2tanx+6=5+tanx2tanx-tanx=5-6tanx=-12(tanx)+2(3)=5+tanx2tanx+6=5+tanx2tanx-tanx =5−6tanx=−1
На единичной окружности есть два угла, тангенс которых равен −1:θ=3π4−1:θ=3π4 и θ=7π4.θ=7π4.
Решение тригонометрических уравнений с помощью калькулятора
Не все функции можно решить точно, используя только единичный круг. Когда мы должны решить уравнение, включающее угол, отличный от одного из специальных углов, нам нужно будет использовать калькулятор. Убедитесь, что он установлен в правильном режиме, либо в градусах, либо в радианах, в зависимости от критериев данной задачи.
Пример 8
Использование калькулятора для решения тригонометрического уравнения с синусом
Использование калькулятора для решения уравнения sinθ=0,8,sinθ=0,8, где θθ выражено в радианах.
Решение
Убедитесь, что для режима установлено значение в радианах. Чтобы найти θ, θ, используйте функцию обратного синуса. На большинстве калькуляторов вам потребуется нажать кнопку 2 ND , а затем кнопку SIN, чтобы вызвать функцию sin-1sin-1. На экране отображается sin-1(.sin-1(. Калькулятор готов к вводу в скобках. Для этой задачи мы вводим sin-1(0.8),sin-1(0.8) и нажимаем ENTER Таким образом, до четырех знаков после запятой,
sin−1(0,8)≈0,9273sin−1(0,8)≈0,9273
Решение
0,9273±2πk0,9273±2πk
Измерение угла в градусах: −53,1∘ ≈126,9∘θ≈53,1∘θ≈180∘−53,1∘ ≈126,9∘
Анализ
Обратите внимание, что калькулятор возвращает только угол в квадрантах I или IV для функции синуса, так как это диапазон обратного синуса. Другой угол получается с помощью π−θ.π−θ.
Другой угол получается с помощью π−θ.π−θ.
Пример 9
Использование калькулятора для решения тригонометрического уравнения с секущей
С помощью калькулятора решите уравнение secθ=−4,secθ=−4, дав ответ в радианах.
Решение
Мы можем начать с алгебры.
secθ=−41cosθ=−4cosθ=−14secθ=−41cosθ=−4cosθ=−14
Убедитесь, что MODE указан в радианах. Теперь используйте функцию арккосинуса.
COS -1 (−14) ≈1,8235 θдоля1,8235+2πkcos — 1 (−14) ≈1,8235 θдоля 1,8235+2πk
с π2,1,57π2 3,57 и πt3,14, π233, 1,57π2,1,57 и πt3,14,14, π233, 1,57 год. эти два числа, таким образом, θ≈1,8235θ≈1,8235 находится в квадранте II. Косинус также отрицателен в квадранте III. Обратите внимание, что калькулятор будет возвращать только угол в квадрантах I или II для функции косинуса, так как это диапазон арккосинуса. См. рис. 2.
Рисунок 2
Итак, нам также нужно найти меру угла в третьем квадранте. В квадранте III опорный угол равен θ’≈π−1,8235≈1,3181,θ’≈π−1,8235≈1,3181. Другое решение в квадранте III равно π+1,3181≈4,4597,π+1,3181≈4,4597.
В квадранте III опорный угол равен θ’≈π−1,8235≈1,3181,θ’≈π−1,8235≈1,3181. Другое решение в квадранте III равно π+1,3181≈4,4597,π+1,3181≈4,4597.
Решения: 1,8235±2πk1,8235±2πk и 4,4597±2πk.4,4597±2πk.
Попытайся #3
Решите cosθ=-0,2.cosθ=-0,2.
Решение тригонометрических уравнений в квадратичной форме
Решение квадратного уравнения может быть более сложным, но опять же, мы можем использовать алгебру, как и для любого квадратного уравнения. Посмотрите на схему уравнения. Есть ли в уравнении более одной тригонометрической функции или только одна? Какая тригонометрическая функция является квадратом? Если представлена только одна функция и один из ее членов возведен в квадрат, подумайте о стандартной форме квадратного числа. Замените тригонометрическую функцию переменной, такой как xx или u.u. Если подстановка делает уравнение похожим на квадратное уравнение, то мы можем использовать те же методы решения квадратного уравнения для решения тригонометрических уравнений.
Пример 10
Решение тригонометрического уравнения в квадратной форме
Точно решить уравнение: cos2θ+3cosθ−1=0,0≤θ<2π.cos2θ+3cosθ−1=0,0≤θ<2π.
Решение
Начнем с подстановки и замены cos θθ на x.x. Нет необходимости использовать подстановку, но это может облегчить визуальное решение проблемы. Пусть cosθ=x.cosθ=x. У нас есть
x2+3x−1=0x2+3x−1=0
Уравнение нельзя разложить на множители, поэтому мы будем использовать квадратичную формулу x=−b±b2−4ac2a.x=−b±b2−4ac2a.
х=-3±(3)2-4(1)(-1)2 =-3±132x=-3±(3)2-4(1)(-1)2 =-3±132
Замените xx на cosθ, cosθ и решите. Таким образом,
cosθ=-3±132 θ=cos-1(-3+132)cosθ=-3±132 θ=cos-1(-3+132)
Обратите внимание, что используется только знак +. Это связано с тем, что мы получаем ошибку, когда решаем θ=cos−1(−3−132)θ=cos−1(−3−132) на калькуляторе, поскольку область определения функции арккосинуса равна [−1,1 ]. [−1,1]. Однако есть и второе решение:
[−1,1]. Однако есть и второе решение:
cos−1(−3+132) ≈1,26cos−1(−3+132) ≈1,26
Эта конечная сторона угла лежит в квадранте I. Поскольку косинус положителен и в квадранте IV, второе решение равно 132) ≈5.02
Пример 11
Решение тригонометрического уравнения в квадратной форме с помощью факторизации
Точно решить уравнение: 2sin2θ−5sinθ+3=0,0≤θ≤2π.2sin2θ−5sinθ+3=0,0≤θ≤2π.
Решение
Используя группировку, этот квадрат можно разложить на множители. Либо сделайте реальную замену, sinθ=u,sinθ=u, либо вообразите ее, поскольку мы факторизуем:
2sin2θ−5sinθ+3=0(2sinθ−3)(sinθ−1)=0 2sin2θ−5sinθ+3=0(2sinθ−3)(sinθ−1)=0
Теперь приравняем каждый фактор к нулю.
2sinθ — 3 = 0 2sinθ = 3 sinθ = 32 sinθ — 1 = 0 sinθ = 12sinθ — 3 = 0 2sinθ = 3 sinθ = 32 sinθ = 0 sinθ = 1
. θ:sinθ≠32, так как диапазон функции синуса равен [−1,1].[−1,1]. Однако sinθ=1,sinθ=1, что дает решение π2. π2.
π2.
Анализ
Обязательно проверьте все решения в данной области, так как некоторые факторы не имеют решения.
Попытайся #4
Решить sin2θ=2cosθ+2,0≤θ≤2π.sin2θ=2cosθ+2,0≤θ≤2π. [Подсказка: сделайте замену, чтобы выразить уравнение только через косинус.]
Пример 12
Решение тригонометрического уравнения с помощью алгебры
Точное решение:
2sin2θ+sinθ=0;0≤θ<2π2sin2θ+sinθ=0;0≤θ<2π
Решение
Эта задача должна показаться знакомой, так как она похожа на квадратичную. Пусть sinθ=x.sinθ=x. Уравнение принимает вид 2×2+x=0,2×2+x=0. Начнем с факторинга:
2×2+x=0x(2x+1)=0 2×2+x=0x(2x+1)=0
Установить каждый коэффициент равным нулю.
x=0 (2x+1)=0 x=−12 x=0 (2x+1)=0 x=−12
Затем подставьте обратно в уравнение исходное выражение sinθsinθ для x. x. Таким образом,
x. Таким образом,
sinθ=0 θ=0,πsinθ=−12 θ=7π6,11π6sinθ=0 θ=0,πsinθ=−12 θ=7π6,11π6
Решения в области 0≤θ<2π0≤θ< 2π равны 0,π,7π6,11π6. 0,π,7π6,11π6.
Если мы предпочитаем не заменять, мы можем решить уравнение, следуя той же схеме разложения на множители и приравняв каждый множитель к нулю.
2sin2θ+sinθ = 0sinθ (2sinθ+1) = 0 sinθ = 0 θ = 0, π 2sinθ+1 = 0 2sinθ = −1 sinθ = −12 θ = 7π6,11π6 2sin2+sinθ = 0sinθ (2sinθ+1) = 0 sinθ = 0 θ = 0, π 2sinθ+1 = 0 2sinθ = −1 sinθ = −12 θ = 7π6,11π6
Анализ
Решения представлены на графике на рис. 3. На интервале 0≤θ<2π,0≤θ<2π график пересекает x- ось четыре раза, при отмеченных решениях. Обратите внимание, что тригонометрические уравнения в квадратной форме могут давать до четырех решений вместо ожидаемых двух, которые можно найти с помощью квадратных уравнений. В этом примере каждое решение (угол), соответствующее положительному значению синуса, даст два угла, которые дадут это значение.
Рисунок 3
Мы также можем проверить решения на единичной окружности на рис. 2.
Пример 13
Решение квадратного тригонометрического уравнения в форме
Точно решить квадратное уравнение в форме: 2sin2θ−3sinθ+1=0,0≤θ<2π.2sin2θ−3sinθ+1=0,0≤θ<2π.
Решение
Мы можем факторизовать, используя группировку. Значения решения θθ можно найти на единичном кругу:
(2sinθ — 1) (sinθ — 1) = 0 2sinθ — 1 = 0 sinθ = 12 θ = π6,5π6 sinθ = 1 θ = π2 (2sinθ — 1) (sinθ — 1) = 0 2sinθ — 1 = 0 sinθ = 12 θ = π6,5π6 sinθ = 1 θ = π2
Попытайся #5
Решите квадратное уравнение 2cos2θ+cosθ=0,2cos2θ+cosθ=0.
Решение тригонометрических уравнений с использованием фундаментальных тождеств
Хотя алгебру можно использовать для решения ряда тригонометрических уравнений, мы также можем использовать фундаментальные тождества, поскольку они упрощают решение уравнений. Помните, что методы, которые мы используем для решения, отличаются от методов проверки личности. Здесь применяются основные правила алгебры, в отличие от переписывания одной стороны тождества, чтобы она соответствовала другой стороне. В следующем примере мы используем два тождества для упрощения уравнения.
Помните, что методы, которые мы используем для решения, отличаются от методов проверки личности. Здесь применяются основные правила алгебры, в отличие от переписывания одной стороны тождества, чтобы она соответствовала другой стороне. В следующем примере мы используем два тождества для упрощения уравнения.
Пример 14
Использование тождеств для решения уравнения
Использование тождеств для точного решения тригонометрического уравнения в интервале 0≤x<2π,0≤x<2π.
cosxcos(2x)+sinxsin(2x)=32cosxcos(2x)+sinxsin(2x)=32
Решение
Обратите внимание, что левая часть уравнения представляет собой формулу разности для косинуса.
cosxcos(2x)+sinxsin(2x)=32 cos(x−2x)=32Формула разности для косинуса cos(−x)=32Используйте отрицательный угол. cosx=32cosxcos(2x)+sinxsin(2x)=32 cos(x−2x)=32Разностная формула для косинуса cos(−x)=32. Используйте тождество отрицательного угла. cosx=32
Используйте тождество отрицательного угла. cosx=32
Из единичного круга на рисунке 2 видно, что cosx=32cosx=32, когда x=π6,11π6.x=π6,11π6.
Пример 15
Решение уравнения с использованием формулы двойного угла
Точное решение уравнения с использованием формулы двойного угла: cos(2θ)=cosθ.cos(2θ)=cosθ.
Решение
У нас есть три варианта выражения для замены двойного угла косинуса. Поскольку проще решать одну тригонометрическую функцию за раз, мы выберем тождество двойного угла, включающее только косинус:
cos (2θ) = cosθ 2cos2θ — 1 = cosθ 2cos2θ -cosθ -1 = 0 (2cosθ+1) (cosθ -1) = 0 2cosθ+1 = 0 cosθ = −12 cosθ -1 = 0 cosθ = 1 cos (2θ) = cosθ 2cos2θ —1 = cosθ 2cos2θ — cosθ — 1 = 0 (2cosθ+1) (cosθ — 1) = 0 2cosθ+1 = 0 cosθ = −12 cosθ — 1 = 0 cosθ = 1
Итак, если cosθ=−12,cosθ=−12, то θ=2π3±2πkθ=2π3±2πk и θ=4π3±2πk;θ=4π3±2πk; если cosθ=1,cosθ=1, то θ=0±2πk.θ=0±2πk.
Пример 16
Решение уравнения с помощью тождества
Решите уравнение точно с помощью тождества: 3cosθ+3=2sin2θ,0≤θ<2π.3cosθ+3=2sin2θ,0≤θ<2π.
Решение
Если мы перепишем правую часть, мы можем записать уравнение через косинус: =0(2 cosθ+1)(cosθ+1)=02 cosθ+1=0cosθ=−12θ=2π3,4π3cosθ+1=0cosθ=−1θ=π3 cosθ+3=2 sin2θ3 cosθ+3=2(1− cos2θ)3 cosθ+3=2−2cos2θ2cos2θ+3 cosθ+1=0(2 cosθ+1)(cosθ+1)=02 cosθ+1=0cosθ=−12θ=2π3,4π3cosθ+1=0cosθ=−1θ= №
Наши решения: 2π3,4π3,π.2π3,4π3,π.
Решение тригонометрических уравнений с несколькими углами
Иногда невозможно решить тригонометрическое уравнение с тождествами, имеющими кратные углы, например sin(2x)sin(2x) или cos(3x).cos(3x). Столкнувшись с этими уравнениями, вспомните, что y=sin(2x)y=sin(2x) — это горизонтальное сжатие в 2 раза функции y=sinx.y=sinx. На интервале 2π,2π мы можем изобразить два периода y=sin(2x),y=sin(2x), а не один цикл y=sinx. y=sinx. Это сжатие графика приводит нас к мысли, что 9 может быть в два раза больше.1043 x — перехваты или решения для sin(2x)=0sin(2x)=0 по сравнению с sinx=0.sinx=0. Эта информация поможет нам решить уравнение.
y=sinx. Это сжатие графика приводит нас к мысли, что 9 может быть в два раза больше.1043 x — перехваты или решения для sin(2x)=0sin(2x)=0 по сравнению с sinx=0.sinx=0. Эта информация поможет нам решить уравнение.
Пример 17
Решение тригонометрического уравнения с несколькими углами
Решите точно: cos(2x)=12cos(2x)=12 на [0,2π).[0,2π).
Решение
Мы видим, что это уравнение является стандартным уравнением с кратным углу. Если cos(α)=12,cos(α)=12, мы знаем, что αα находится в квадрантах I и IV. Хотя θ=cos-112θ=cos-112 даст решения только в квадрантах I и II, мы понимаем, что решения уравнения cosθ=12cosθ=12 будут в квадрантах I и IV.
Следовательно, возможные углы равны θ=π3θ=π3 и θ=5π3.θ=5π3. Итак, 2x=π32x=π3 или 2x=5π3,2x=5π3, значит, x=π6x=π6 или x=5π6.x=5π6. Имеет ли это смысл? Да, потому что cos(2(π6))=cos(π3)=12.cos(2(π6))=cos(π3)=12.
Возможны ли другие ответы? Вернемся к нашему первому шагу.
В квадранте I 2x=π3,2x=π3, так что x=π6x=π6, как уже отмечалось. Давайте снова вернемся по кругу:
2x=π3+2π =π3+6π3 =7π32x=π3+2π =π3+6π3 =7π3
, значит, x=7π6.x=7π6.
Еще одно вращение дает
2x=π3+4π =π3+12π3 =13π32x=π3+4π =π3+12π3 =13π3
x=13π6>2π,x=13π6>2π, поэтому это значение для xx больше чем 2π,2π, так что это не решение на [0,2π).[0,2π).
В квадранте IV 2x=5π3,2x=5π3, поэтому x=5π6x=5π6, как было отмечено. Давайте снова вернемся по кругу:
2x=5π3+2π =5π3+6π3 =11π32x=5π3+2π =5π3+6π3 =11π3
, значит, x=11π6.x=11π6.
Еще одно вращение дает
2x=5π3+4π =5π3+12π3 =17π32x=5π3+4π =5π3+12π3 =17π3
x=17π6>2π,x=17π6>2π, поэтому это значение для xx больше, чем 2π,2π, поэтому это не решение на [0,2π).[0,2π).
Наши решения: π6,5π6,7π6 и 11π6,π6,5π6,7π6 и 11π6. Обратите внимание, что всякий раз, когда мы решаем задачу в виде sin(nx)=c,sin(nx)=c, мы должны пройти единичный круг nn раз.
Решение задач на прямоугольный треугольник
Теперь мы можем использовать все изученные нами методы для решения задач, связанных со свойствами прямоугольных треугольников и теоремой Пифагора. Мы начинаем со знакомой теоремы Пифагора, a2+b2=c2,a2+b2=c2, и моделируем уравнение, соответствующее ситуации.
Пример 18
Использование теоремы Пифагора для моделирования уравнения
Использование теоремы Пифагора и свойств прямоугольных треугольников для моделирования уравнения, соответствующего задаче.
Необходимо заменить один из тросов, которыми колесо обозрения London Eye крепится к земле. Центр колеса обозрения находится на высоте 69,5 метров над землей, а второй якорь на земле — в 23 метрах от основания колеса обозрения. Приблизительно какой длины кабель и каков угол подъема (от земли до центра колеса обозрения)? См. рис. 4.
Рисунок 4
Решение
Используя предоставленную информацию, мы можем нарисовать прямоугольный треугольник. Длину кабеля можно найти по теореме Пифагора.
Длину кабеля можно найти по теореме Пифагора.
A2+B2 = C2 (23) 2+ (69,5) 2≈5359 5359, 73,2 м A2+B2 = C2 (23) 2+ (69,5) 2,5359 5359, 73,2 м
Угол элевации равен θ ,θ, образованный вторым анкером на земле и кабелем, достигающим центра колеса. Мы можем использовать функцию тангенса, чтобы найти его меру. Округлить до двух знаков после запятой.
TANθ = 69,523TAN — 1 (69,523) ≈1,2522 ≈71,69∘ TANθ = 69,523TAN — 1 (69,523) ≈1,2522 ≈71,69∘
Угла поднимая поднимает 71,7∘ 71.7. составляет 73,2 метра.
Пример 19
Использование теоремы Пифагора для моделирования абстрактной задачи
Правила техники безопасности OSHA требуют, чтобы основание лестницы располагалось на расстоянии 1 фута от стены на каждые 4 фута длины лестницы. Найдите угол, под которым лестница любой длины образует землю, и высоту, на которой лестница касается стены.
Решение
Для любой длины лестницы основание должно находиться на расстоянии от стены, равном одной четвертой длины лестницы. Эквивалентно, если основание лестницы находится на расстоянии « а» фута от стены, длина лестницы будет равна 4 а фута. См. рис. 5.
Эквивалентно, если основание лестницы находится на расстоянии « а» фута от стены, длина лестницы будет равна 4 а фута. См. рис. 5.
Рис. 5
Сторона, примыкающая к θθ, равна a , а гипотенуза равна 4a.4a. Таким образом,
cosθ=a4a=14cos−1(14)≈75,5∘ cosθ=a4a=14cos−1(14)≈75,5∘
Высота лестницы образует с землей угол 75,5∘75,5∘. Высоту, на которой лестница касается стены, можно найти с помощью теоремы Пифагора: 4a)2 b2=(4a)2−a2 b2=16a2−a2 b2=15a2 b=15a
Таким образом, лестница касается стены на высоте 15a15a футов от земли.
7.5 Секционные упражнения
Устный
1.
Всегда ли будут решения уравнений тригонометрических функций? Если нет, опишите уравнение, которое не имеет решения. Объясните, почему да или почему нет.
2.
Всегда ли при решении тригонометрического уравнения, включающего более одной тригонометрической функции, мы пытаемся переписать уравнение, чтобы оно выражалось в терминах одной тригонометрической функции? Почему или почему нет?
3.
При решении линейных триггерных уравнений только с помощью синуса или косинуса, как мы узнаем, будут ли решения?
Алгебраический
Для следующих упражнений найдите все решения точно на интервале 0≤θ<2π.0≤θ<2π.
4.
2sinθ=−22sinθ=−2
5.
2sinθ=32sinθ=3
6.
2cosθ=12cosθ=1
7.
2cosθ=−22cosθ=−2
8.
tanθ=-1tanθ=-1
9.
тангенс=1тангенс=1
10.
котх+1=0котх+1=0
11.
4sin2x-2=04sin2x-2=0
12.
csc2x-4=0csc2x-4=0
Для следующих упражнений решите точно на [0,2π).[0,2π).
13.
2cosθ=22cosθ=2
14.
2cosθ=−12cosθ=−1
15.
2sinθ=−12sinθ=−1
16.
2sinθ=−32sinθ=−3
17.
2sin(3θ)=12sin(3θ)=1
18.
2sin(2θ)=32sin(2θ)=3
19.
2cos(3θ)=−22cos(3θ)=−2
20.
потому что (2θ) = −32 cos (2θ) = −32
21.
2sin(πθ)=12sin(πθ)=1
22.
2cos(π5θ)=32cos(π5θ)=3
Для следующих упражнений найдите все точные решения на [0,2π). [0,2π).
[0,2π).
23.
сек(х)sin(x)−2sin(x)=0сек(x)sin(x)−2sin(x)=0
24.
tan(x)−2sin(x)tan(x)=0tan(x)−2sin(x)tan(x)=0
25.
2cos2t+cos(t)=12cos2t+cos(t)=1
26.
2tan2(t)=3сек(t)2tan2(t)=3сек(t)
27.
2sin(x)cos(x)−sin(x)+2cos(x)−1=02sin(x)cos(x)−sin(x)+2cos(x)−1=0
28.
cos2θ=12cos2θ=12
29.
сек2х=1сек2х=1
30.
tan2(x)=-1+2tan(-x)tan2(x)=-1+2tan(-x)
31.
8sin2(x)+6sin(x)+1=08sin2(x)+6sin(x)+1=0
32.
tan5(x)=tan(x)tan5(x)=tan(x)
Для следующих упражнений решите методами, показанными в этом разделе, точно на интервале [0,2π).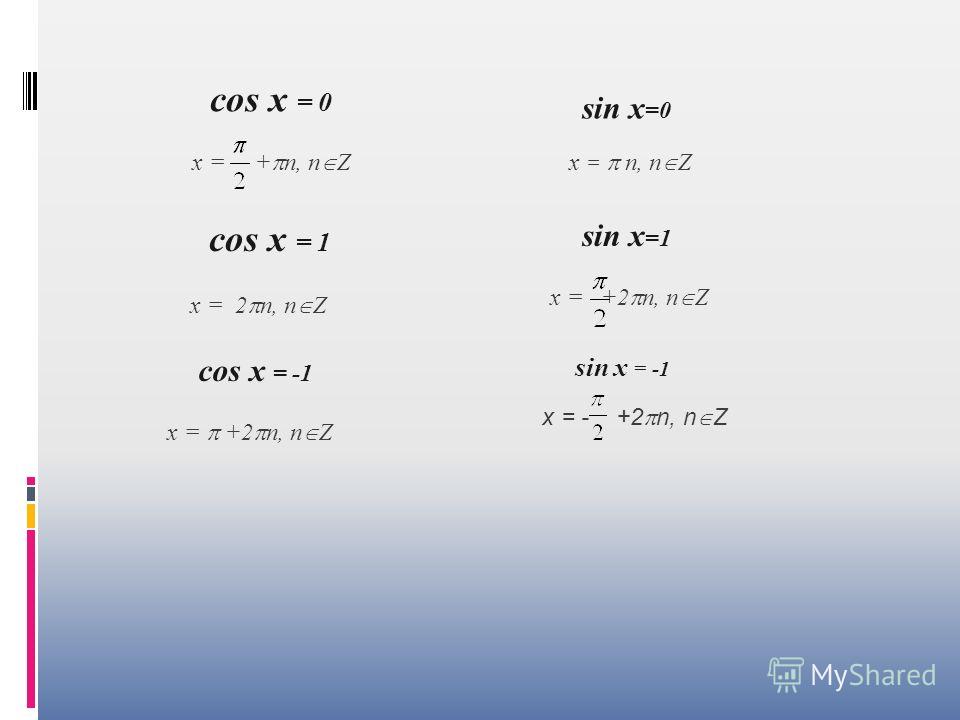 [0,2π).
[0,2π).
33.
sin(3x)cos(6x)−cos(3x)sin(6x)=−0,9sin(3x)cos(6x)−cos(3x)sin(6x)=−0,9
34.
sin(6x)cos(11x)−cos(6x)sin(11x)=−0,1sin(6x)cos(11x)−cos(6x)sin(11x)=−0,1
35.
cos(2x)cosx+sin(2x)sinx=1cos(2x)cosx+sin(2x)sinx=1
36.
6sin(2t)+9sint=06sin(2t)+9sint=0
37.
9cos(2θ)=9cos2θ−49cos(2θ)=9cos2θ−4
38.
sin(2t)=costsin(2t)=стоимость
39.
cos(2t)=sintcos(2t)=sint
40.
потому что (6х) — потому что (3х) = 0 потому что (6х) — потому что (3х) = 0
Для следующих упражнений решите точно на интервале [0,2π).[0,2π). Используйте квадратичную формулу, если уравнения не учитывают.
41.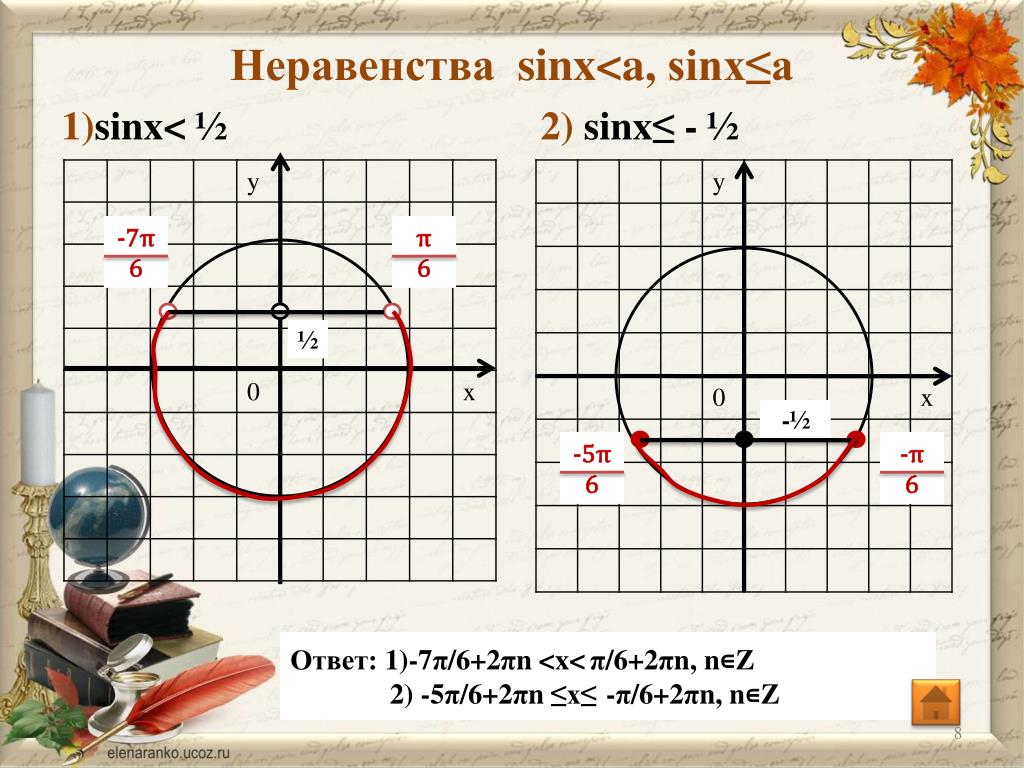
tan2x-3tanx=0tan2x-3tanx=0
42.
sin2x+sinx-2=0sin2x+sinx-2=0
43.
sin2x-2sinx-4=0sin2x-2sinx-4=0
44.
5cos2x+3cosx-1=05cos2x+3cosx-1=0
45.
3cos2x-2cosx-2=03cos2x-2cosx-2=0
46.
5sin2x+2sinx-1=05sin2x+2sinx-1=0
47.
tan2x+5tanx-1=0tan2x+5tanx-1=0
48.
cot2x=-cotxcot2x=-cotx
49.
−tan2x−tanx−2=0−tan2x−tanx−2=0
Для следующих упражнений найдите точные решения на интервале [0,2π).[0,2π). Ищите возможности использовать тригонометрические тождества.
50.
sin2x-cos2x-sinx=0sin2x-cos2x-sinx=0
51.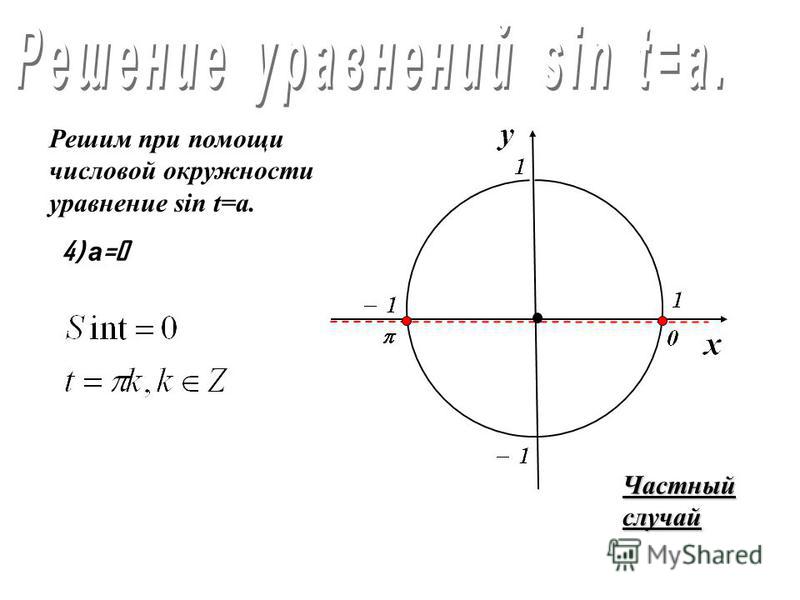
sin2x+cos2x=0sin2x+cos2x=0
52.
sin(2x)−sinx=0sin(2x)−sinx=0
53.
cos(2x)−cosx=0cos(2x)−cosx=0
54.
2tanx2-sec2x-sin2x=cos2x2tanx2-sec2x-sin2x=cos2x
55.
1-cos(2x)=1+cos(2x)1-cos(2x)=1+cos(2x)
56.
сек2х=7сек2х=7
57.
10sinxcosx=6cosx10sinxcosx=6cosx
58.
−3sint=15costsint−3sint=15costsint
59.
4cos2x−4=15cosx4cos2x−4=15cosx
60.
8sin2x+6sinx+1=08sin2x+6sinx+1=0
61.
8cos2θ=3−2cosθ8cos2θ=3−2cosθ
62.
6cos2x+7sinx-8=06cos2x+7sinx-8=0
63.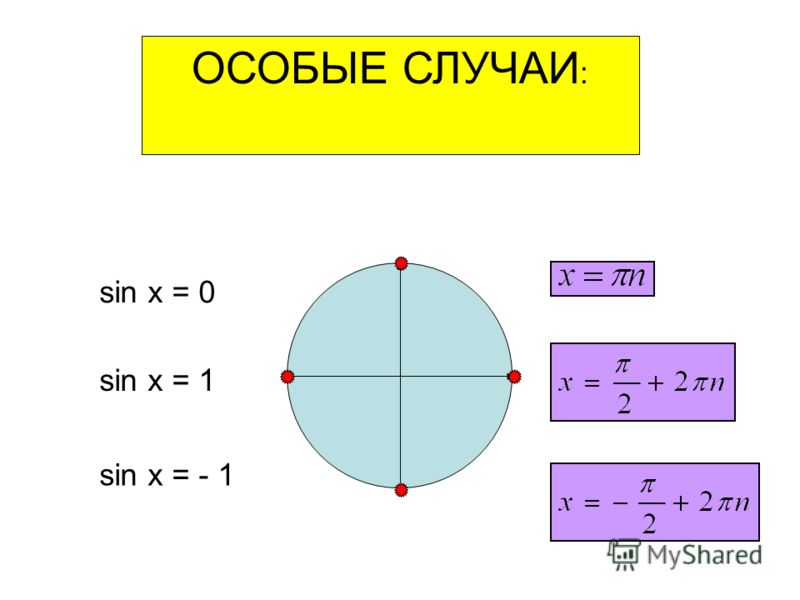
12sin2t+затраты-6=012sin2t+затраты-6=0
64.
tanx=3sinxtanx=3sinx
65.
cos3t=costcos3t=стоимость
Графический
В следующих упражнениях алгебраически точно определите все решения тригонометрического уравнения, затем проверьте результаты, построив уравнение на графике и найдя нули.
66.
6sin2x−5sinx+1=06sin2x−5sinx+1=0
67.
8cos2x-2cosx-1=08cos2x-2cosx-1=0
68.
100tan2x+20tanx-3=0100tan2x+20tanx-3=0
69.
2cos2x-cosx+15=02cos2x-cosx+15=0
70.
20sin2x−27sinx+7=020sin2x−27sinx+7=0
71.
2tan2x+7tanx+6=02tan2x+7tanx+6=0
72.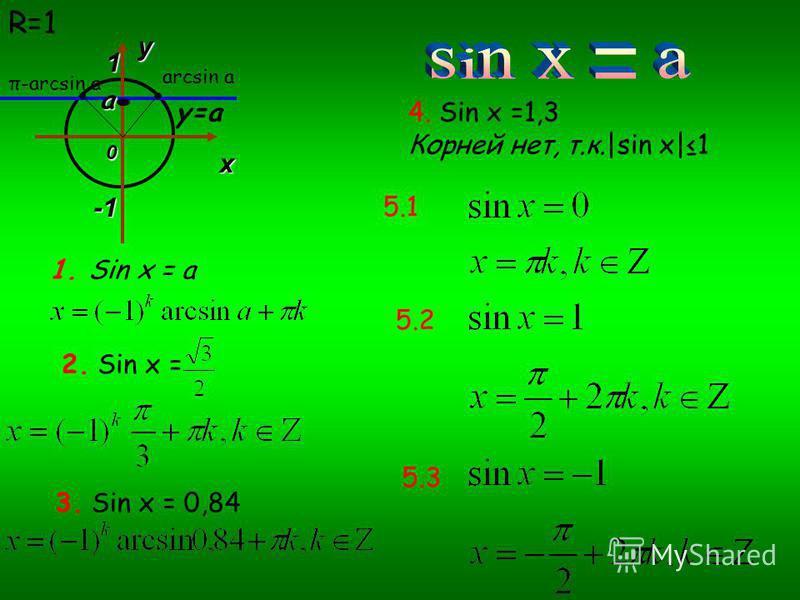
130tan2x+69tanx-130=0130tan2x+69tanx-130=0
Технология
В следующих упражнениях используйте калькулятор, чтобы найти все решения до четырех знаков после запятой.
73.
sinx=0,27sinx=0,27
74.
sinx=-0,55sinx=-0,55
75.
tanx=-0,34tanx=-0,34
76.
cosx=0,71cosx=0,71
В следующих упражнениях решите уравнения алгебраически, а затем с помощью калькулятора найдите значения на интервале [0,2π).[0,2π). Округлите до четырех знаков после запятой.
77.
tan2x+3tanx-3=0tan2x+3tanx-3=0
78.
6tan2x+13tanx=-66tan2x+13tanx=-6
79.
tan2x-secx=1tan2x-secx=1
80.
sin2x-2cos2x=0sin2x-2cos2x=0
81.
2tan2x+9tanx-6=02tan2x+9tanx-6=0
82.
4sin2x+sin(2x)secx−3=04sin2x+sin(2x)secx−3=0
Удлинители
Для следующих упражнений найдите в точности все решения уравнений на отрезке [0,2π).[0,2π).
83.
csc2x-3cscx-4=0csc2x-3cscx-4=0
84.
sin2x-cos2x-1=0sin2x-cos2x-1=0
85.
sin2x(1−sin2x)+cos2x(1−sin2x)=0sin2x(1−sin2x)+cos2x(1−sin2x)=0
86.
3sec2x+2+sin2x-tan2x+cos2x=03sec2x+2+sin2x-tan2x+cos2x=0
87.
sin2x−1+2cos(2x)−cos2x=1sin2x−1+2cos(2x)−cos2x=1
88.
tan2x-1-sec3xcosx=0tan2x-1-sec3xcosx=0
89.
sin(2x)sec2x=0sin(2x)sec2x=0
90.
грех(2x)2csc2x=0sin(2x)2csc2x=0
91.
2cos2x-sin2x-cosx-5=02cos2x-sin2x-cosx-5=0
92.
1sec2x+2+sin2x+4cos2x=41sec2x+2+sin2x+4cos2x=4
Реальные приложения
93.
Бензина у самолета хватит только на то, чтобы долететь до города в 200 милях к северо-востоку от его текущего местоположения. Если пилот знает, что город находится в 25 милях к северу, сколько градусов к северу от востока должен лететь самолет?
94.
Если погрузочная рампа расположена рядом с грузовиком на высоте 4 фута, а длина рампы составляет 15 футов, какой угол образует рампа с землей?
95.
Если погрузочная рампа расположена рядом с грузовиком на высоте 2 фута, а длина рампы составляет 20 футов, какой угол образует рампа с землей?
96.
Женщина наблюдает за запуском ракеты на высоте 11 миль. Если она стоит в 4 милях от стартовой площадки, под каким углом она смотрит вверх от горизонтали?
97.
Космонавт находится в запущенной ракете на высоте 15 миль. Если человек стоит в 2 милях от стартовой площадки, под каким углом она смотрит на него сверху вниз? (Подсказка: это называется углом депрессии.)
98.
Женщина стоит в 8 метрах от 10-метрового здания. Под каким углом она смотрит на крышу здания?
99.
Мужчина стоит в 10 метрах от 6-метрового здания. Кто-то наверху здания смотрит на него сверху вниз. Под каким углом на него смотрит человек?
100.
Здание высотой 20 футов имеет тень длиной 55 футов. Каков угол возвышения солнца?
101.
Здание высотой 90 футов имеет тень длиной 2 фута. Каков угол возвышения солнца?
Каков угол возвышения солнца?
102.
909:06 Прожектор на земле в 3 метрах от человека ростом 2 метра отбрасывает 6-метровую тень на стену в 6 метрах от человека. Под каким углом свет?103.
Прожектор на земле в 3 футах от женщины ростом 5 футов отбрасывает тень высотой 15 футов на стену в 6 футах от женщины. Под каким углом свет?
В следующих упражнениях найдите решение задачи со словами алгебраически. Затем воспользуйтесь калькулятором, чтобы проверить результат. Округлите ответ до десятых долей градуса.
104.
Человек делает стойку на руках, касаясь ногами стены и руками на расстоянии 1,5 фута от стены. Какой угол составляют ноги человека со стеной, если его рост 6 футов?
105.
Человек делает стойку на руках, ноги касаются стены, а руки находятся на расстоянии 3 футов от стены. Если рост человека 5 футов, какой угол составляют его ступни со стеной?
106.
23-футовая лестница расположена рядом с домом. Если лестница соскальзывает на расстоянии 7 футов от дома из-за недостаточного сцепления, какой угол должна составлять лестница с землей, чтобы избежать соскальзывания?
Помогите! Решите 2cosx-sinx=0 для 0
carpe_diem
Участник
- #1
Пожалуйста, покажи свою тренировку!.
Спасибо
* <= в уравнении меньше или равно
БрикХед
Новый член
- #2
перенести sinx на другую сторону, разделить на cos, превратить в tan, tan x = 2, x = 63 и 243
я думаю O_O
2cosx = sinx
2 = tanx
х = 63 градуса и 243 градуса
Найтвивер066
Известный член
- #3
Разделить обе части на cosx
d и m обозначают градусы и минуты.
ролики
Участник
- #4
carpe_diem
Участник
- #5
Большое спасибо! Я понимаю это сейчас
что-то 2ng
На пенсии 14 ноября
Брикхед сказал:
2 = tanx
Нажмите, чтобы развернуть.
..
Я думал, этот метод запрещен?
Не надо приравнивать и решать?
зксрет
Участник
что-то2нг сказал:
Я думал, этот метод был запрещен?
Не надо приравнивать и решать?
Нажмите, чтобы развернуть…
зачем его запрещать? 91/2 = корень 5
a = arctan0.5 = 26 градусов 34 минуты…
отсюда довольно просто. ответ выходит тот же.
Соперник троллей
Сущность, лишенная сна
- #9
2cosx-sinx=0 для 0<=x<=360
2cosx = грех х
2 = sinx/cosx (sinx/cosx = tanx)
тангенс х = 2
Подключитесь к калькулятору для ответа!
что-то 2ng
На пенсии 14 ноября
- 909:25 #10
zxreth сказал:
зачем его запрещать?
Нажмите, чтобы развернуть…
Я не уверен, но это как-то связано с отрицательными значениями A и B.
Лучшее 29 Каково приблизительное значение Sin C
Wiki
14 дней назад Последнее обновление: 23 сентября 2022 г.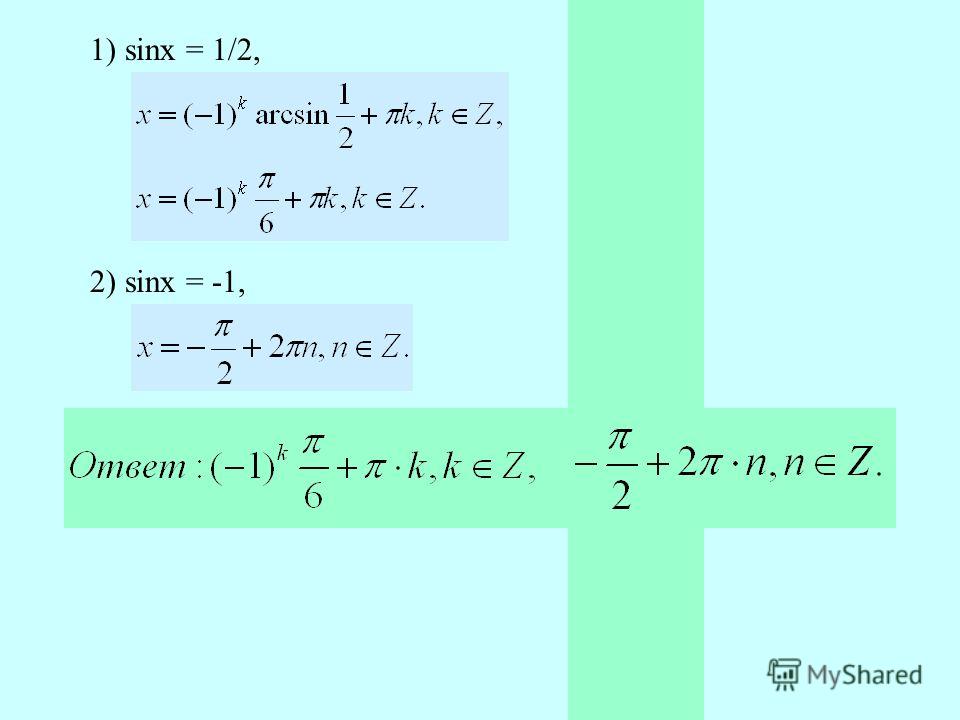
1 11 минут чтения
Ниже приведена лучшая информация и знания о , каково приблизительное значение sin c , собранное и составленное командой hocdientu.net , наряду с другими связанными темами, такими как: каково приблизительное значение tan c, используйте закон косинусов, чтобы найти значение cos округлить ваш ответ до двух знаков после запятой, какую пропорцию можно использовать, чтобы найти длину стороны b, зная, что sin 30 = 1/2 что такое a, какова длина стороны s квадрат, показанный ниже, закон косинусов сводится к теореме Пифагора всякий раз, когда треугольник остроугольный, рассчитайте длину a с точностью до двух знаков после запятой, на диаграмме ниже abc dec каково значение x
Изображение для ключевого слова: каково приблизительное значение sin c
Самые популярные статьи о том, каково приблизительное значение sin c
Содержание
- 1 1. каково приблизительное значение sin c ? а.
 0,92 б. 1,09 в. 2,49 …
0,92 б. 1,09 в. 2,49 … - 2 2. Просмотр вопроса – помогите, пожалуйста,
- 3 3. Каково приблизительное значение sin c? – Soetrust
- 4 4. Приблизительное значение sin по ряду Тейлора – Stack Overflow
- 5 5. Каково приблизительное значение sin C? Пожалуйста помоги! Срочно
- 6 6. Sin 30 Degrees (значение и происхождение) – Byju’s
- 7 7. Каково приблизительное значение sin C?
- 8 8. Каково приблизительное значение sin c? – ForNoob
- 9 9. Приблизительное значение sin 31° равно – Tardigrade App
- 10 10. Найдите приблизительные значения : sin (29° 30′), учитывая, что sin 31 circ is – Collegedunia
- 12 12. Малоугловое приближение – Википедия
- 13 13. Формула синусоидальной аппроксимации Бхаскара I – Википедия
- 14 14. Тригонометрия – используйте тот факт, что sin61=sin(60+1), чтобы получить …
- 15 15. Найдите приблизительное значение синуса 61 градуса
- 16 16. В прямоугольном треугольнике cos A = 0,352 и sin A = 0,936, значение …
- 17 17.
 В прямоугольном треугольнике сторона, противоположная углу – CameraMath
В прямоугольном треугольнике сторона, противоположная углу – CameraMath - 18 18. Решения практических задач (Тригон без слез)
- 19 19. Решено Вычислить приблизительное значение для каждого | Chegg.com
- 20 20. Как решить треугольник с приблизительными значениями, если β = 37,48 …
- 21 21. Приблизительное значение – синус, косинус, тангенс – математические принципы
- 22 22. Выражение функции sin x в виде ряда – Dummies.com
- 23 23. ряд sin(x) Программа на C – Sanfoundry
- 24 24. Найдите приблизительное значение sin 46°, учитывая, что 1° = 0,01745 …
- 25 25. Калькулятор закона синусов
- 26 26. Решение прямоугольных треугольников – тригонометрия | Socratic
- 27 27. Использование дифференциалов для аппроксимации греха 29 – eMathZone
- 28 28. Найдите точное значение sin(60 градусов) – Mathway
- 29 29. Найдите точное значение sin(60 градусов) – Mathway
1. Каково приблизительное значение sin C? а.
 0,92 б. 1,09 в. 2,49 …
0,92 б. 1,09 в. 2,49 …Автор: www.numerade.com
Оценить 3 ⭐ (18653 оценок)
Лучшие по рейтингу: 3 ⭐
Самый низкий рейтинг: 1 ⭐
909:25Совпадение с результатами поиска: В математике абсолютное значение или модуль |x| действительного числа x является его числовым значением независимо от его знака. Абсолютное значение числа можно рассматривать как его расстояние от нуля вдоль числовой прямой; эта интерпретация аналогична функции расстояния, присвоенной действительному числу …
Цитата из источника: …
Резюме: Статьи о том, каково примерное значение sin C? а. 0,92 б. 1,09 в. 2,49 … ·
2. Просмотреть вопрос – помогите пожалуйста
Автор: web2.
 0calc.com
0calc.comОценить 4 ⭐ (29541 оценок)
Лучшие по рейтингу: 4 ⭐
Самый низкий рейтинг: 2 ⭐
Резюме: Статьи о Просмотре вопроса – помогите плиз, какое приблизительное значение sin C? А.0.38. Б.0.93. С.0.36. Д.2.79. XDrakeH 13 января 2017 г. …
Совпадение с результатами поиска: Каково приблизительное значение sin C?
Цитата из источника: …
3. Каково приблизительное значение sin c? – Soetrust
Автор: soetrust.org
Оценить 4 ⭐ (39197 оценок)
Лучшие оценки: 4 ⭐
Самый низкий рейтинг: 2 ⭐
Резюме: Статьи о том Каково приблизительное значение sin c? – Soetrust Найдите приблизительное значение этого C.
 С доказательством. Используя тригнометрическое распознавание … sinC = 0,36 ° (приблизительно). Вариант (Д) правильный. Следовательно, создан … 90 909
С доказательством. Используя тригнометрическое распознавание … sinC = 0,36 ° (приблизительно). Вариант (Д) правильный. Следовательно, создан … 90 909Совпадение с результатами поиска:
Каково приблизительное значение sin c?Цитата из источника: …
4. Приблизительное значение sin по ряду Тейлора
Автор: stackoverflow.com
Оценить 3 ⭐ (3136 оценок)
Лучшие по рейтингу: 3 ⭐
Самый низкий рейтинг: 1 ⭐
Резюме: Статьи о приблизительном значении sin по ряду Тейлора – Stack Overflow Предикат init_sin/4 и mp_sin/4 затем вычисляют синус в обратном направлении от наименьшего слагаемого к наибольшему слагаемому a0 , используя схему Хорнера …
Совпадение с результатами поиска: У меня есть код, который должен найти приблизительное значение sin(15°) по определению ряда Тейлора и сравнить его со встроенной функцией sin.
Цитата из источника: …
5. Каково приблизительное значение sin C? Пожалуйста помоги! Срочно
Автор: Studiesto.com
Оценить 4 ⭐ (28146 оценок)
Лучшие по рейтингу: 4 ⭐
Самый низкий рейтинг: 2 ⭐
Резюме: Статьи о том Каково примерное значение sin C? Пожалуйста помоги! Срочный ответ: 1 📌📌📌 вопрос ➜ Каково приблизительное значение sin C? Пожалуйста помоги! Срочно – ответы на Studiesto.com.
Совпадение с результатами поиска: Значение sin C
Цитата из источника: …
6. Грех 30 градусов (значение и происхождение) – Byju’s
Автор: byjus.com
Оценить 4 ⭐ (29804 оценок)
Лучшие по рейтингу: 4 ⭐
Самый низкий рейтинг: 2 ⭐
Резюме: Статьи о грехе 30 градусов (Значение и вывод) – Byju’s Величина греха 30 градусов равна отношению противолежащего катета и гипотенузы прямоугольного треугольника.
 Научитесь получать значение …
Научитесь получать значение …Совпадение с результатами поиска: Подставьте значение sin 30 и значение AB,
Цитата из источника: …
7. Каково приблизительное значение sin C?
Автор: en-us.januari.live
Оценить 4 ⭐ (32526 оценок)
Лучшие по рейтингу: 4 ⭐
Самый низкий рейтинг: 2 ⭐
Резюме: Статьи о том Каково примерное значение sin C? Найдите приблизительное значение sin C . Чтобы доказать. Используя тригнометрическое тождество. [tex]sin\theta = \frac{Perpendicular}{Гипотенуза}[/tex].
Совпадение с результатами поиска: Подставляя данные значения, мы имеем
Цитата из источника: …
8.
 Каково приблизительное значение sin c? – Для нуба
Каково приблизительное значение sin c? – Для нубаАвтор: fornoob.com
Оценить 4 ⭐ (28318 оценок)
Лучшие по рейтингу: 4 ⭐
Самый низкий рейтинг: 2 ⭐
Резюме: Статьи о том Каково приблизительное значение sin c? – ForNoob Найдите приблизительное значение sin C . Чтобы доказать. Используя тригнометрическое тождество. sintheta = frac {Перпендикуляр {Гипотенуза}. Теперь, как указано в …
Совпадение с результатами поиска: Похоже, в этом месте ничего не найдено. Может попробовать поискать?
Цитата из источника: …
9. Приблизительное значение sin 31° – приложение Tardigrade
Автор: tardigrade.in
Оценить 4 ⭐ (25768 оценок)
Лучшие по рейтингу: 4 ⭐
Самый низкий рейтинг: 2 ⭐
Резюме: статей о Приблизительное значение sin 31° – приложение Тихоходка WBJEE 2018: Приблизительное значение sin 31° составляет (A) > 0,5 (B) > 0,6 (C) < 0,5 (D) < 0,4.
 Проверьте ответ и решение для вышеуказанного вопроса по математике …
Проверьте ответ и решение для вышеуказанного вопроса по математике …Совпадение с результатами поиска: © 2022 Tardigrade®. Все права защищены
Цитата из источника: …
10. Найдите приблизительные значения : sin (29° 30′), учитывая, что 1 …
Автор: www.shaalaa.com
Оценить 4 ⭐ (22919 оценок)
Лучшие по рейтингу: 4 ⭐
Самый низкий рейтинг: 2 ⭐
Сводка: Статьи о Найдите приблизительные значения : sin (29° 30′), учитывая, что 1 … Найдите приблизительные значения : sin (29° 30′), учитывая, что 1°=0,0175°, 3=1,732.
Сопоставьте результаты поиска: Найдите приблизительные значения : sin (29° 30′), учитывая, что 1°= 0,0175°, `sqrt(3) = 1,732`
Цитата из источника: …
11.
 приблизительное значение sin 31 circ is – Collegedunia
приблизительное значение sin 31 circ is – CollegeduniaАвтор: Collegedunia.com
Оценить 3 ⭐ (10842 оценок) 9{\circ}$ есть. … Угол подъема облака C C из точки P, 200 м P , 200 м над неподвижным озером равен 30°.
Совпадение с результатами поиска: Рассмотрим круг радиусом в одну единицу. Кроме того, дуга окружности равна одной единице. Мерой угла является 1 радиан, если дуга стягивается в центре окружности, при условии, что радиус и длина дуги равны. Длина дуги окружности с единичным радиусом эквивалентна углу в радианах.
Цитата из источника: …
12. Малоугловое приближение – Википедия
Автор: en.wikipedia.org
Оценить 4 ⭐ (30148 оценок)
Лучшие по рейтингу: 4 ⭐
Самый низкий рейтинг: 2 ⭐
Резюме: Статьи о малоугловой аппроксимации – Википедия Малоугловые аппроксимации можно использовать для аппроксимации значений основных … \end{align}}} {\displaystyle {\begin{align}\sin\theta & \ ок.

Совпадение с результатами поиска: Число 206265 приблизительно равно количеству угловых секунд в окружности (1296000), деленному на 2π.
Цитата из источника: …
13. Формула приближения синуса Бхаскара I – Википедия
Автор: en.wikipedia.org
Оценить 3 ⭐ (9224 рейтинга)
909:25Самый низкий рейтинг: 1 ⭐
Резюме: Статьи о формуле аппроксимации синусов Бхаскара I – Википедия В математике формула аппроксимации синусов Бхаскара I представляет собой рациональное выражение в одном … приблизительных значениях тригонометрических синусов, открытых Бхаскарой I (c …
Совпадение с результатами поиска:
В математике формула аппроксимации синуса Бхаскары I представляет собой рациональное выражение с одной переменной для вычисления приблизительных значений тригонометрических синусов, открытых Бхаскарой I (ок. 600 – ок. 680), а индийский математик седьмого века.
600 – ок. 680), а индийский математик седьмого века.
Эта формула дана в его трактате…Цитата из источника: …
Лучшие по рейтингу: 3 ⭐
14. тригонометрия – используйте тот факт, что sin61=sin(60+1), чтобы получить …
Автор: math.stackexchange.com
Оценить 3 ⭐ (2039 оценок)
Лучшие по рейтингу: 3 ⭐
Самый низкий рейтинг: 1 ⭐
9{\circ}$, так что выяснить, чему примерно равно $sin(1)$, не составит труда. Следовательно, в этом случае я бы пошел дальше и отослал бы вас к формуле суммы синуса и использовал этот факт для приближения. Вы также знаете, что такое $sin(60)$ из единицы ci…Цитата из источника: …
15. Найдите приблизительное значение синуса 61 градуса
Автор: math.
 stackexchange.com 909:25
stackexchange.com 909:25Лучшие по рейтингу: 3 ⭐
Самый низкий рейтинг: 1 ⭐
Сводка: Статьи о Нахождение приблизительного значения синуса 61 градуса Поскольку вам нужно приблизительное значение, вы можете использовать разложение Тейлора sin(π3+x)=√32+x2−√3×24−x312+O( х4). и сделать x=π180.
Совпадение с результатами поиска: Используйте тот факт, что $\sin 61° = \sin (60°+1°)$, чтобы получить приблизительное значение $\sin 61°$ через $\pi$.
Цитата из источника: …
Оценить 3 ⭐ (13608 оценок)
16. В прямоугольном треугольнике cos A = 0,352 и sin A = 0,936 значение …
Автор: www.cuemath.com
Оценить 3 ⭐ (7908 оценок)
Лучшие по рейтингу: 3 ⭐
Самый низкий рейтинг: 1 ⭐
Резюме: Статьи о В прямоугольном треугольнике cos A = 0,352 и sin A = 0,936, значение … Каково приблизительное значение тангенса A? Тригонометрия — это раздел математики, изучающий прямоугольные треугольники и отношения между их сторонами и …
.
Совпадение с результатами поиска: Тригонометрическое отношение sin A находится по формуле; перпендикуляр/гипотенуза.
Цитата из источника: …
17. В прямоугольном треугольнике сторона противоположна углу – CameraMath
Автор: cameramath.com
Оценить 3 ⭐ (7101 Рейтинг)
Лучшие по рейтингу: 3 ⭐
Самый низкий рейтинг: 1 ⭐
Резюме: Статьи о В прямоугольном треугольнике сторона противоположная углу – CameraMath … сторона противоположная углу β имеет длину 16,4см . Гипотенуза треугольника имеет длину 25,1см. Каково приблизительное значение sin(β) ?
Совпадение с результатами поиска:
Цитата из источника: …
18.
 Решения практических задач (триггер без слез)
Решения практических задач (триггер без слез)Автор: brownmath.com
Оценить 3 ⭐ (5232 оценок)
Лучшие по рейтингу: 3 ⭐
Самый низкий рейтинг: 1 ⭐
Резюме: Статьи о решениях практических задач (Триггер без слез) Зная, что в сумме они составляют 180°, введите значение каждого угла. … Дайте каждый ответ в градусах и радианах. грех А = 0; cos В = √3/2; грех С = 1/2; грех Д …
Совпадение с результатами поиска: Решение:
Arctan x — это угол, тангенс которого равен x, поэтому 9 2015 возможных значений Arctan x — это углы в Q IV и
Q I, касательные которых можно взять. Но тангенс(−π/2)
и тангенс π/2 не существуют,
, поэтому они не являются возможными значениями
Арктан х.Цитата из источника: …
19.
 Решенный Рассчитать приблизительное значение для каждого | Chegg.com
Решенный Рассчитать приблизительное значение для каждого | Chegg.comАвтор: www.chegg.com
Оценить 3 ⭐ (3065 оценок)
Лучшие по рейтингу: 3 ⭐
Самый низкий рейтинг: 1 ⭐
Резюме: Статьи о Решенный Рассчитать примерную стоимость для каждого | Chegg.com 1 cau trả lời
Совпадение с результатами поиска:
Пожалуйста, убедитесь, что в вашем браузере включены Javascript и файлы cookie и что вы не блокируете их загрузку.Цитата из источника: …
20. Как решить треугольник с приблизительными значениями, если β = 37,48 …
Автор: www.quora.com
Оценить 3 ⭐ (6212 оценок)
Лучшие по рейтингу: 3 ⭐
Самый низкий рейтинг: 1 ⭐
Резюме: Статьи о том, как решить треугольник с приближенными значениями, если β = 37,48 … В треугольнике ABC, A=30° b= 8, a= 6, где B= sin⁻¹x тогда каково значение x? 1072 просмотра · Если ab+bc+CA=4 и abc=2, сможете ли вы найти значение 1/a+1/b+1/c?
Совпадение с результатами поиска: Что-то пошло не так.
 Подождите немного и повторите попытку.
Подождите немного и повторите попытку.Цитата из источника: …
21. Приблизительное значение – синус, косинус, тангенс – математические принципы
Автор: www.math-principles.com
Оценить 3 ⭐ (1193 оценок)
Лучшие по рейтингу: 3 ⭐
Самый низкий рейтинг: 1 ⭐
Резюме: Статьи о приближенном значении – синус, косинус, тангенс – математические принципы Нахождение приблизительного значения тригонометрических функций угла без использования калькулятора или тригонометрических таблиц.
Совпадение с результатами поиска: Этот сайт покажет принципы решения математических задач по арифметике, алгебре, плоской геометрии, объемной геометрии, аналитической геометрии, тригонометрии, дифференциальному исчислению, интегральному исчислению, статистике, дифференциальным уравнениям, физике, механике, прочности материалов и химической инженерии Ма…
Цитата из источника: …
22.
 Выражение функции sin x в виде ряда – Dummies.com
Выражение функции sin x в виде ряда – Dummies.comАвтор: www.dummies.com
Оценить 4 ⭐ (29051 оценок)
Лучшие по рейтингу: 4 ⭐
Самый низкий рейтинг: 2 ⭐
Резюме: Статьи о выражении функции sin x в виде ряда – Dummies.com Если вы хотите найти приблизительное значение sin x , вы можете использовать формулу, чтобы выразить его в виде ряда. Эта формула выражает синус … 90 909
Совпадение с результатами поиска: В качестве последнего примера в следующей таблице показано значение sin 10, округленное до восьми членов. Истинное значение sin 10 приблизительно равно –0,54402, так что по любым стандартам это плохая оценка. Тем не менее, если вы продолжаете генерировать термины, эта оценка продолжает становиться все лучше и лучше, к любому…
Цитата из источника: …
23.
 Программа серии sin(x) на C – Sanfoundry
Программа серии sin(x) на C – SanfoundryАвтор: www.sanfoundry.com
Оценить 4 ⭐ (30414 оценок)
Лучшие по рейтингу: 4 ⭐
Самый низкий рейтинг: 2 ⭐
Резюме: статей о sin(x) Программа серии на C – Sanfoundry Эта программа на C вычисляет значение sin(x). Решение проблемы. Это недифференцируемая функция. Начать с нуля, затем подняться до 1, затем вернуться к 0. Но …
Совпадение с результатами поиска: Умножьте значение переменной «x» дважды на значение переменной «term» и произведите отрицание значения, затем разделите значение на переменную «знаменатель». Вычислите сумму значения переменной «sinx» со значением переменной «term».
Цитата из источника: …
24. Найдите приблизительное значение sin 46°, учитывая, что 1° = 0,01745 …
Автор: www.
 sarthaks.com
sarthaks.comОценить 4 ⭐ (35602 оценок)
Лучшие по рейтингу: 4 ⭐
Самый низкий рейтинг: 2 ⭐
Сводка: Статьи о Найдите приблизительное значение sin 46°, если 1° = 0,01745 … ·
Совпадение с результатами поиска: Найдите приблизительное значение sin 46°, учитывая, что 1° = 0,01745 радиуса.
Цитата из источника: …
25. Калькулятор закона синусов
Автор: www.calculatorsoup.com
Оценить 3 ⭐ (3837 оценок)
Лучшие по рейтингу: 3 ⭐
Самый низкий рейтинг: 1 ⭐
Резюме: Статьи о законе синусов Калькулятор Калькулятор показывает уравнения синусов и работу.
 … Схема треугольника с углами A, B и C и сторонами, противоположными этим углам a, A = угол A B = угол B
… Схема треугольника с углами A, B и C и сторонами, противоположными этим углам a, A = угол A B = угол BСовпадение с результатами поиска: Использует закон синусов для вычисления неизвестных углов или сторон треугольника. Для расчета неизвестных значений необходимо ввести 3 известных значения.
Цитата из источника: …
26. Решение прямоугольных треугольников – тригонометрия | Сократ
Автор: socratic.org
Оценить 3 ⭐ (15151 оценок)
Лучшие по рейтингу: 3 ⭐
Самый низкий рейтинг: 1 ⭐
Резюме: Статьи о решении прямоугольных треугольников – тригонометрия | Сократ. Например, допустим, вы знаете длину а и значение угла А в приведенном выше треугольнике. Используя функцию косинуса, вы можете найти с , гипотенузу … 90 909
Совпадение с результатами поиска: Например, предположим, что вы знаете длину #a# и значение угла #A# в приведенном выше треугольнике.
 Используя функцию косинуса, вы можете найти #c#, гипотенузу.
Используя функцию косинуса, вы можете найти #c#, гипотенузу.Цитата из источника: …
27. Использование дифференциалов для аппроксимации Sin 29 – eMathZone
Автор: www.emathzone.com
Оценить 4 ⭐ (24299 оценок)
Лучшие по рейтингу: 4 ⭐
Самый низкий рейтинг: 2 ⭐
Резюме: статей об использовании дифференциалов для аппроксимации греха 29\circ }$$
Цитата из источника: …
28. Найдите точное значение sin(60 градусов) – Mathway
Автор: www.mathway.com
Оценить 4 ⭐ (36973 оценок)
Лучшие по рейтингу: 4 ⭐
Самый низкий рейтинг: 2 ⭐
Резюме: статей о поиске точного значения sin(60 градусов ) — Mathway Бесплатное средство решения математических задач отвечает на ваши домашние вопросы по алгебре, геометрии, тригонометрии, исчислению и статистике с пошаговыми объяснениями, …
Совпадение с результатами поиска: Пожалуйста, убедитесь, что ваш пароль состоит не менее чем из 8 символов и содержит каждый из следующих символов:
Цитата из источника: …
29.
 Найдите точное значение sin(60 градусов) – Mathway
Найдите точное значение sin(60 градусов) – MathwayАвтор: www.mathway.com
Оценить 4 ⭐ (25158 оценок)
Лучшие по рейтингу: 4 ⭐
Самый низкий рейтинг: 2 ⭐
Резюме: Статьи о поиске точного значения sin(60 градусов) – Mathway Бесплатное средство решения математических задач отвечает на ваши домашние вопросы по алгебре, геометрии, тригонометрии, исчислению и статистике с пошаговыми объяснениями, …
Совпадение с результатами поиска: Пожалуйста, убедитесь, что ваш пароль состоит не менее чем из 8 символов и содержит каждый из следующих символов:
Цитата из источника: …
Видеоуроки о том, каково приблизительное значение sin c
com/embed/PDa3B-IL02I» frameborder=»0″ allow=»accelerrometer;autoplay;clipboard-write;encrypted-media;gyroscope;picture-in-picture» allowfullscreen=»»>Связанные статьи
Проверьте также
Закрывать
18 лучших охранников в Afc West
2 дня назад
Решения NCERT для класса 12, математика, глава 7, интегралы, 2019-20, сессия
Темы и подтемы, включенные в главу «Интегралы», следующие:
| Название раздела | Название темы |
| 7 | Интегралы |
| 7.1 | Введение |
| 7.2 | Интеграция как обратный процесс дифференциации |
| 7,3 | Методы интеграции |
| 7,4 | Интегралы некоторых частных функций |
| 7,5 | Интегрирование по дробям |
| 7,6 | Интеграция по частям |
| 7,7 | Определенный интеграл |
| 7,8 | Основная теорема исчисления |
| 7,9 | Вычисление определенных интегралов подстановкой |
7. 10 10 | Некоторые свойства определенных интегралов |
Решения NCERT для математики для 12-го класса, глава 7. Интегралы: Абитуриенты и студенты инженерных специальностей, сдающие экзамены CBSE для 12-го класса, должны серьезно отнестись к учебникам NCERT по математике и закончить их сверху донизу. Они также должны пройти через решения NCERT для математики класса 12 и математики класса 11, чтобы лучше понять различные концепции. В этой статье мы предоставим вам решения NCERT для 12-го класса по математике, глава 7 — интегралы, разработанные лучшими учителями Индии.
Бесплатно скачать Решения NCERT для математики класса 12 Глава 7 Упражнение 7.11, Пример 7.10, Пример 7.9, Пример 7.8, Пример 7.7, Пример 7.6, Пример 7.5, Пример 7.4, Пример 7.3, Пример 7.2, Пример 7.1 Интегралы PDF на хинди Medium as а также на английском языке Medium для студентов CBSE, Uttarakhand, Bihar, MP Board, Gujarat Board, BIE, Intermediate и UP Board, которые используют книги NCERT на основе обновленной программы CBSE для сессии 2019-20.
- Формулы интегрирования
- Интегральные преобразователи класса 12 Ex 7.1
- Интегральный анализ класса 12 Ex 7.1 на языке хинди Medium
- Интегральные преобразователи класса 12 Ex 7.2
- Интегральный анализ класса 12 Ex 7.2 на языке хинди средний
- Интегральные преобразователи класса 12 Ex 7.3
- Интегральный анализ класса 12 Ex 7.3 на языке хинди средний
- Интегральные преобразователи класса 12 Ex 7.4
- Интегральный анализ класса 12 Ex 7.4 на хинди, средний
- Интегральные преобразователи класса 12 Ex 7.5
- Интегральные преобразователи Class 12 Ex 7.5 на языке хинди Medium
- Интегральные преобразователи класса 12 Ex 7.6
- Интегральные преобразователи Class 12 Ex 7.6 на хинди Medium
- Интегральные преобразователи Класс 12 Ex 7.7
- Интегральный анализ класса 12 Ex 7.7 на хинди, средний
- Интегральные преобразователи класса 12 Ex 7.
 8
8 - Интегральные преобразователи Class 12 Ex 7.8 на хинди Medium
- Интегральные преобразователи класса 12 Ex 7.9
- Интегральные преобразователи Class 12 Ex 7.9 на языке хинди Medium
- Интегральные преобразователи класса 12 Ex 7.10
- Интегральный анализ класса 12 Ex 7.10 на языке хинди средний
- Интегральные преобразователи класса 12 Ex 7.11
- Интегральный анализ класса 12 Ex 7.11 на языке хинди средний
- Интегралы Класс 12 Разное Упражнение
- RD Шарма, класс 12, интегральные схемы
- NCERT Пример математических интегралов класса 12
- Интегралы Класс 12 Заметки Математика Глава 7
- Важные вопросы Математические интегралы 12 класса
- JEE Основная математика Определенные и неопределенные интегралы
Математика для класса 12 Глава 7 Решения NCERT Интегралы
Решения NCERT для класса 12 Математика Глава 7 — Интегралы содержит пошаговые и подробные решения для каждого вопроса.
- Введение
- Интеграция как обратный процесс дифференциации
- Геометрическая интерпретация неопределенного интеграла
- Некоторые свойства неопределенного интеграла
- Сравнение дифференциации и интеграции
- Методы интеграции
- Интеграция путем замены
- Интегрирование с использованием тригонометрических тождеств
- Интегралы некоторых частных функций
- Интегрирование неполными дробями
- Интеграция по частям
- Интеграл типа
- Интегралы еще некоторых типов
- Определенный интеграл
- Определенный интеграл как предел суммы
- Основная теорема исчисления
- Функция площади
- Первая фундаментальная теорема интегрального исчисления
- Вторая основная теорема интегрального исчисления
- Вычисление определенных интегралов подстановкой
- Некоторые свойства определенных интегралов 9{ 2 } }{ x } \)
Решение:
Пример 7. 2, математика, класс 12, вопрос 3.
2, математика, класс 12, вопрос 3.
\(\frac { 1 }{ x+xlogx } \)
Решение:
, пример 7.2, математика, класс 12, вопрос 4.
sinx sin(cosx)
Решение:
Пример 7.2 Класс 12 Математика Вопрос 5.
sin(ax+b) cos(ax+b)
Решение:
Пример 7.2 Класс 12 Математика Вопрос 6.
\(\sqrt { ax+b } \)
Решение:
Пример 7.2 Класс 12 Математика Вопрос 7.
\(x\sqrt { x+2 } \)
Решение:
Пример 7.2 Класс 12 Математика Вопрос 8. 9{ 2 } } \)
Решение:
Пример 7.2, класс 12, математика Вопрос 26.
\(\frac { cos\sqrt { x } }{ \sqrt { x } } \)
Решение:
Пример 7.2, класс 12 Математика Вопрос 27.
\(\sqrt { sin2x } cos2x\)
Решение:
Пример 7.2 Класс 12 Математика Вопрос 28.
\(\frac { cosx }{ \sqrt { 1+sinx } } \)
Решение:
Пример 7.2, математика, класс 12, вопрос 29.
cotx log sinx
Решение:
, пример 7.2, математика, класс 12, вопрос 30.
\(\frac { sinx }{ 1+cosx }\) 9{ 2 }x } = } \)
(a) tanx + cotx + c
(b) tanx – cotx + c
(c) tanx cotx + c
(d) tanx – cotx + c
Решение:Перейти к началу → Интегралы класса 12 Глава 7
Интегралы Пример 7.3 Класс 12
Найдите интегралы от функций в упражнениях с 1 по 22.
Пример 7.3 Класс 12 Математика Вопрос 1.
sin²(2x+5)
Решение :
Пример 7.3 Класс 12 Математика Вопрос 2.
sin3x cos4x
Решение:
Пример 7.3 Класс 12 Математика Вопрос 3.
∫COS2X COS4X COS6X DX
Решение:
EX 7,3 Класс 12 Математический Вопрос 4.
∫SIN 3 (2x+1) DX
Решение:
EX 7.3 Математика 12 Класс 12 Вопрос 5.
SIN 3 x COS 3 x
Решение:
EX 7.3 Класс 12 Математический Вопрос 6.
SINX SIN2X SIN3X
Решение:
EX 7,3 Класс 12 Математический Вопрос 7.
SIN 4X SIN 8X
Решение:
EX 7. 3. Вопрос 8.
3. Вопрос 8.
\(\frac { 1-cosx }{ 1+cosx }\) 9{ 2 } } равно } \)
(a) \(\frac { \pi }{ 6 }\)
(b) \(\frac { \pi }{ 12 }\)
(c) \(\frac { \pi }{ 24 }\)
(d) \(\frac { \pi }{ 4 }\)
Решение:Перейти к началу → Интегралы класса 12 Глава 7
Интегрирование класса 12 Пример 7.10
Ex 7.10 класс 12 Математика Вопрос 1:
Решение:
EX 7.10 Класс 12 Математический Вопрос 2:
Решение:
EX 7.10 Класс 12 Математический Вопрос 3:
Решение:
EX 7.10 Класс 12 Математический Вопрос 4:
Решение:
EX 7.10 класс 12 Математика Вопрос 5:
Решение:
EX 7.10 Класс 12 Математический Вопрос 6:
Решение:
EX 7.10 Класс 12 Математический вопрос 7:
Решение:
. Ex 7.10 класс 12 Математика Вопрос 8:
Решение:
EX 7.10 Класс 12 Математический Вопрос 9:
Решение:
EX 7. 10 Класс 12 Математический Вопрос 10:
10 Класс 12 Математический Вопрос 10:
Решение:
EX 7.10 Класс 12 Математический Вопрос 11:
Решение:
EX 7.10 Класс 12 Математический Вопрос 12:
Решение:
EX 7.10 Класс 12 Математический Вопрос 13:
Решение:
EX 7.10. :
EX 7.10 Класс 12 Математический Вопрос 15:
Решение:
EX 7.10 Класс 12 Математический Вопрос 16:
Решение:
EX 7.10.2015 EX 7.10 класс 12 Математика Вопрос 18:
Решение:
EX 7.10 класс 12 Математика Математика 19:
Решение:
EX 7.10 класс 12 Математический Вопрос 20:
Решение:ДОПОЛНЕНИЕ ДЛЯ ТОЧКА. → Class 12 Integrals Chapter 7
NCERT Solutions for Class 2 Maths Integration Class 12 Ex 7.11
.
 0909
0909NCERT Solutions для математики класса 12 Глава 7 Интегралы Разное упражнение
Разное упражнение класс 11 Математика Вопрос 1:
Решение:
. Математика Вопрос 3:
Решение:vРазное Упражнение Класс 11 Математика Вопрос 4:
Решение:
Разное Упражнение Класс 11 Математика Вопрос 5:
Решение:Разное упражнение класс 11 Математика ВОПРОС 6:
Решение:Разное упражнение класс 11 Математический Вопрос 7:
Решение:Miscellese Care Class.
Разное упражнение по математике для 11 класса Вопрос 9:
Решение:Разное упражнение по математике для 11 класса Вопрос 10:
Решение:
Разное упражнение по математике для 11 класса: вопрос 112015
Решение:Разное упражнение класс 11 Математика Вопрос 12:
Решение:Разное упражнение.
Разное упражнение 11 класс математики Вопрос 15:
Решение:Разное упражнение 11 класс математики Вопрос 16:
Решение:Разное упражнение класс 11 Математика Вопрос 17:
Решение:Математика для 11 класса.
 Вопрос 21:
Вопрос 21:
Решение:Разное. Упражнение. Математика для 11 класса. Вопрос 22:
. Решение:.2015
Решение:Разное упражнение класс 11 Математика Вопрос 24:
Решение:
Разное упражнение класс 11 Математический Вопрос 25:
Решение. Мисси.
Разное Упражнение Математика 11 класса Вопрос 27:
Решение:
Разное Упражнение 11 Класс Математика Вопрос 28:
Решение:
Разное упражнение класс 11 Математика Вопрос 29:
Решение:Разное упражнение класс 11 Математический Вопрос 30:
Miscellese Crassed Class 11 Вопрос 31:
.. Математика Вопрос 32:
Решение:
Разное Упражнение Класс 11 Математика Вопрос 33:
Решение:
Разное Упражнение Класс 11 Математика Вопрос 9:2015
Решение:
Вопрос 35:
Решение:Разное упражнение класс 11 Математика Вопрос 36:
Решение:Miscellese Class Class 11:
. Математика для 11 класса Вопрос 38:
Математика для 11 класса Вопрос 38:
Решение:Разное Упражнение Математика для 11 класса Вопрос 39:
Решение:Разное Упражнение для 11 класса Математика Вопрос 40:
Решение:
Разное упражнение класс 11 Математика Вопрос 41:
Решение:
. Решение:
Разное Упражнение Математика 11 класса Вопрос 44:
Решение:
Перейти к началу → Интегралы 12 класса Глава 7
Integration Formulas
Move to Top → Class 12 Integrals Chapter 7
गणित कक्षा 12 समाकलन प्रश्नावली 7.1
निम्नलिखित फलनों के प्रतिअवकलज ( समाकलन) निरीक्षण विधि द्वारा ज्ञात कीजिए ।
EX 7.1 класс 11 Математика Maths प्रश्न 1.
SIN 2X
हल-
∫SIN 2x DX
हम ज हैं कि कि, \ (\ frac {d} {dx} \) cos2x = -2 sin 2x
य in sin 2x = = = -2 sin 2x
य {dx} \). \(-\frac{1}{2} \frac{d}{d x}\)cos2x
\(-\frac{1}{2} \frac{d}{d x}\)cos2x
sin 2x = \(\frac{d}{d x}\)(\(-\frac{1}{2}\)cos2x)
अतः sin 2x का प्रति अवकलज \(-\frac{1}{2} \)cos 2x है।EX 7.1 класс 11 Математика Maths प्रश्न 2.
Cos 3x
हल-
∫cos 3x dx
हम ज ज हैं कि, \ (\ frac {d} {dx} \) sin 3x = 3 cos 3x
अत: cos3x का प्रति अवकलज \(\frac{1}{3}\) sin 3x हैं।EX 7.1 класс 11 Математика प्रश्न 3.
E 2x
हल-
∫e 2x DX
हम ज हैं कि.EX 7.1.2015 (AX + B) ²
हल-
∫ (AX + B) ² DX
हम जानते हैं कि कि,EX 7.1. हैं
Ex 7.1 Class 11 Maths प्रश्न 6.
∫(4e 3x + 1) dx
हल-
∫(4e 3x + 1) dx = 4∫e 3x dx + ∫1 dxПример 7.1 Математика 11 класса प्रश्न 7.
हल-Пример 7.1 Математика 11 класса प्रश्न 8.
∫(ax² + bx + c) dx
हल-
∫(ax² + bx + c) dx = a∫x²dx + b∫xdx + c∫1 dxУпр.
 2x² + E x ) DX
2x² + E x ) DX
हल-
∫ (2x² + E x ) DX = 2∫x² DX + ∫ x DXEX 7.1 Class 11 Maths प्ve 102015
x
x
9015 9015 x 9015 9015.
EX 7.1 класс 11 Математика प्रश्न 11.
हल-EX 7.1 класс 11 Матс प्रश्न 12.
हल-EX 7.1. Матс 112015 हल-
EX 7.1.2015
हल-EX 7.1 класс 11 Математика प्रश्न 14.
0000000000000000000000003
∫ (1-x) √x DX
हल-
∫ (1-x) √x DX
= ∫ (√x-x несоизре внимание) DXEX 7.1 класс 11 Математика प्रश्न 15.
∫√x (3x² + 2x + 3) DX
हल-
∫√x (3x² + 2x + 3) DXEX 7.1 класс 11 Математика प्रश्न 16.
∫ (4.1. 2x- 3Cosx + E x ) DX
हल-
∫ (2x- 3COSX + E x ) DXप्रशFrशvet 17.





 ..
.. 0,92 б. 1,09 в. 2,49 …
0,92 б. 1,09 в. 2,49 …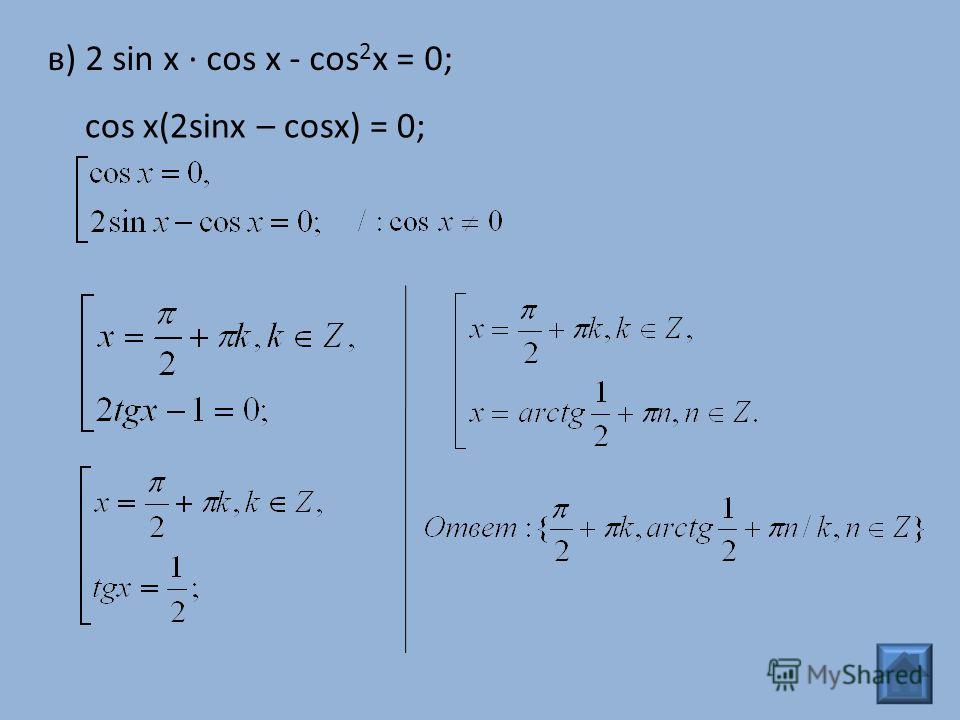 В прямоугольном треугольнике сторона, противоположная углу – CameraMath
В прямоугольном треугольнике сторона, противоположная углу – CameraMath 0calc.com
0calc.com С доказательством. Используя тригнометрическое распознавание … sinC = 0,36 ° (приблизительно). Вариант (Д) правильный. Следовательно, создан … 90 909
С доказательством. Используя тригнометрическое распознавание … sinC = 0,36 ° (приблизительно). Вариант (Д) правильный. Следовательно, создан … 90 909 Научитесь получать значение …
Научитесь получать значение …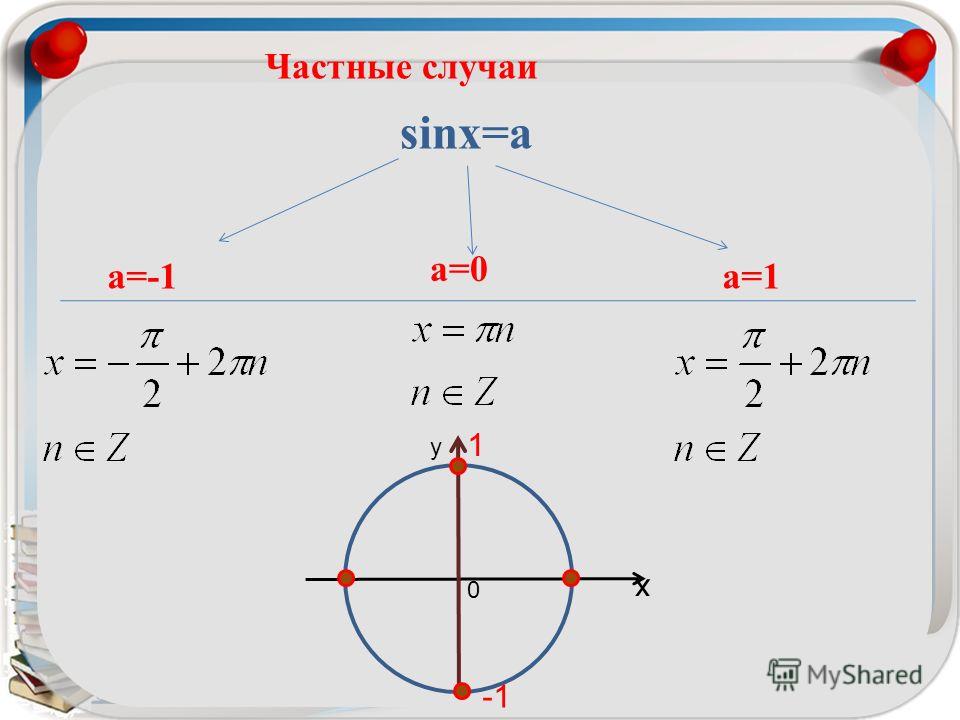 Проверьте ответ и решение для вышеуказанного вопроса по математике …
Проверьте ответ и решение для вышеуказанного вопроса по математике …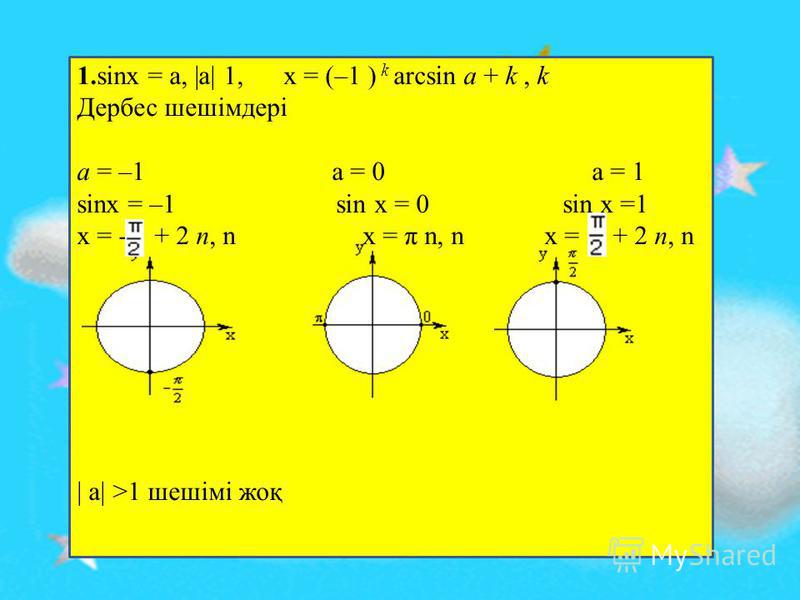
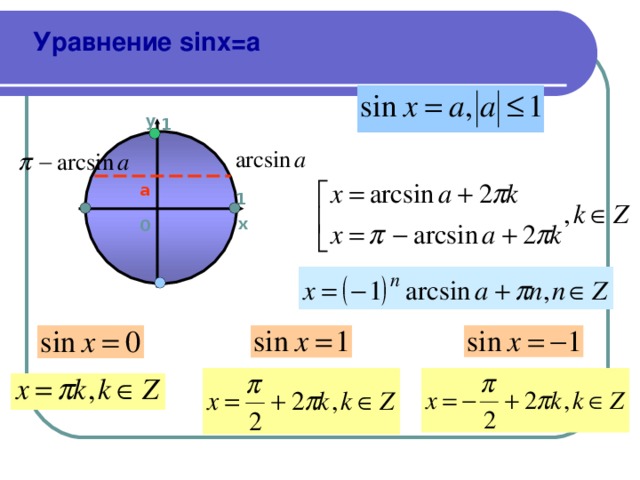 600 – ок. 680), а индийский математик седьмого века.
600 – ок. 680), а индийский математик седьмого века.  stackexchange.com
stackexchange.com
 Подождите немного и повторите попытку.
Подождите немного и повторите попытку. sarthaks.com
sarthaks.com … Схема треугольника с углами A, B и C и сторонами, противоположными этим углам a, A = угол A B = угол B
… Схема треугольника с углами A, B и C и сторонами, противоположными этим углам a, A = угол A B = угол B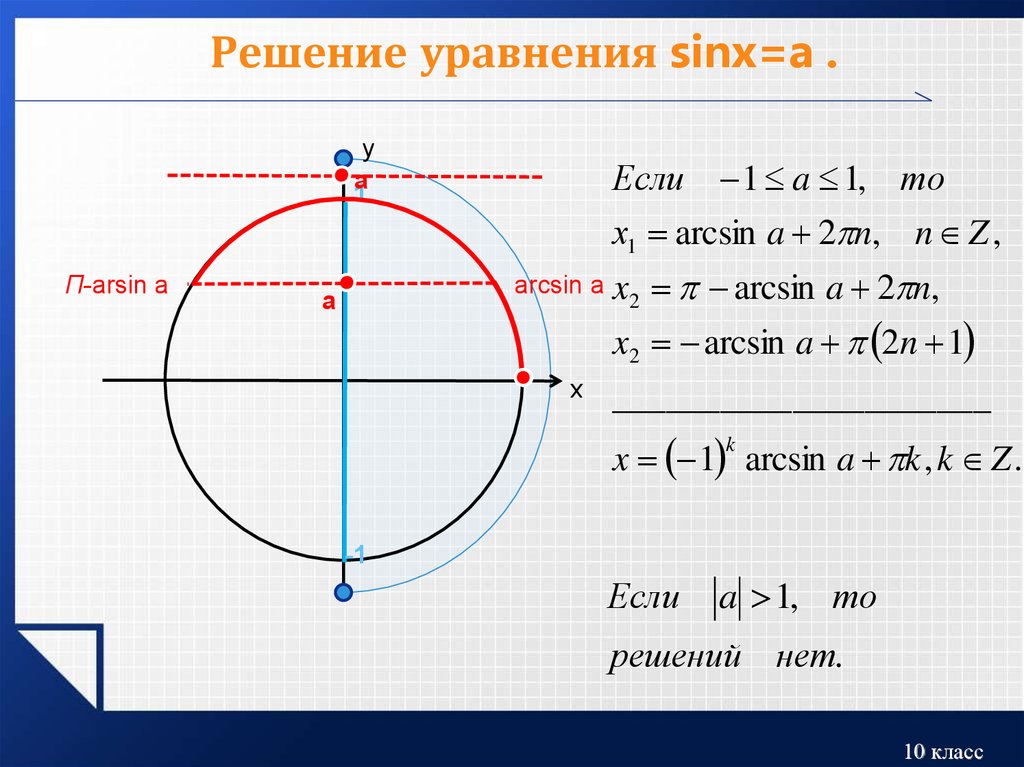 Используя функцию косинуса, вы можете найти #c#, гипотенузу.
Используя функцию косинуса, вы можете найти #c#, гипотенузу. 8
8 2, математика, класс 12, вопрос 3.
2, математика, класс 12, вопрос 3. 
 3. Вопрос 8.
3. Вопрос 8. 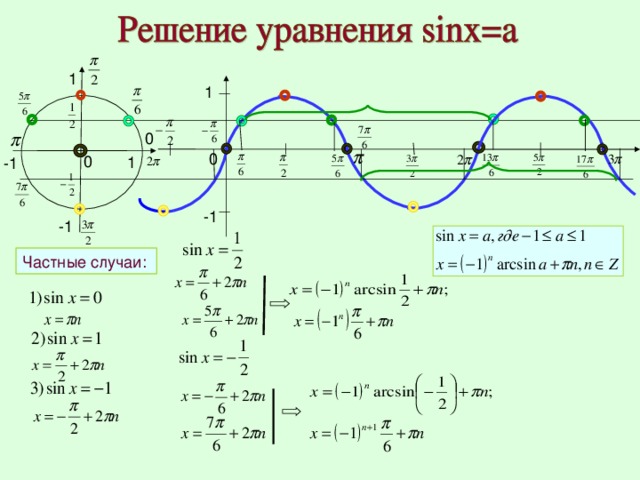 10 Класс 12 Математический Вопрос 10:
10 Класс 12 Математический Вопрос 10:  0909
0909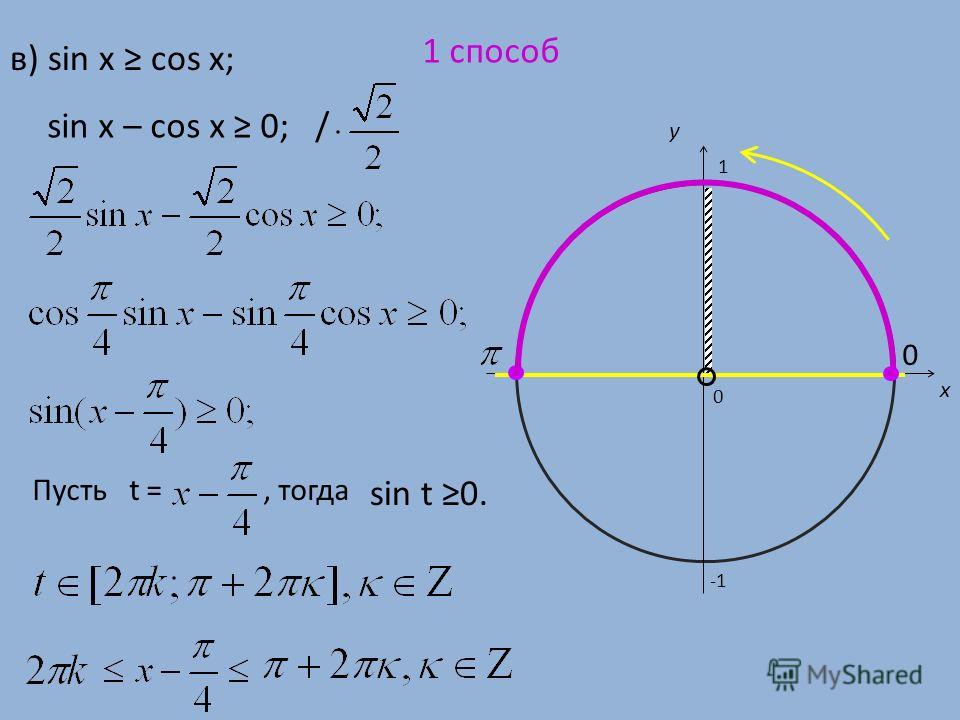 Вопрос 21:
Вопрос 21: 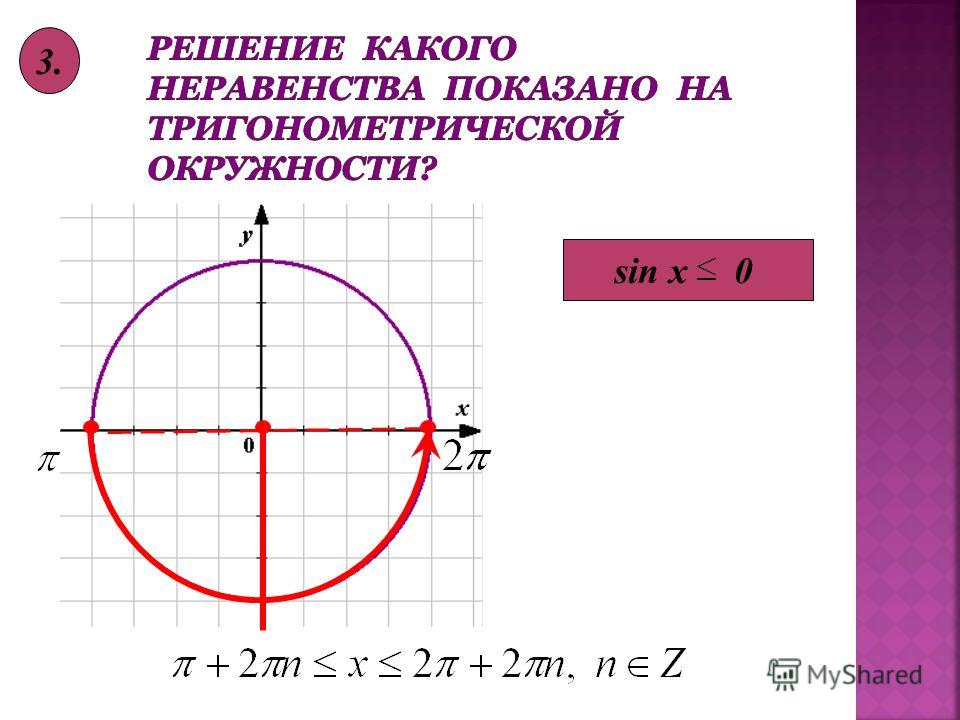 Математика для 11 класса Вопрос 38:
Математика для 11 класса Вопрос 38: 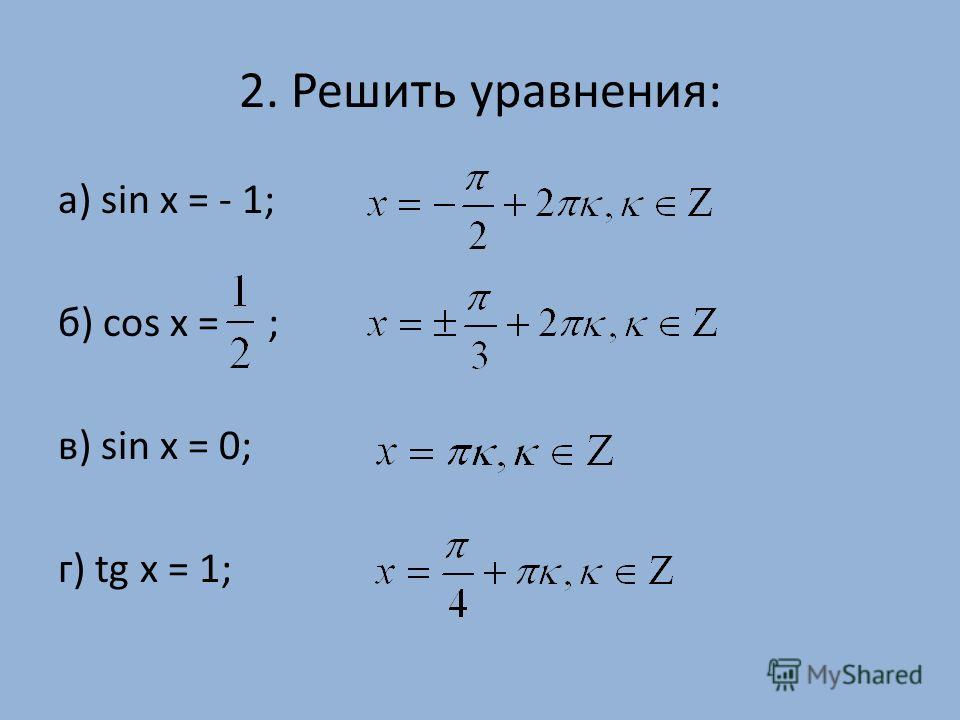 \(-\frac{1}{2} \frac{d}{d x}\)cos2x
\(-\frac{1}{2} \frac{d}{d x}\)cos2x 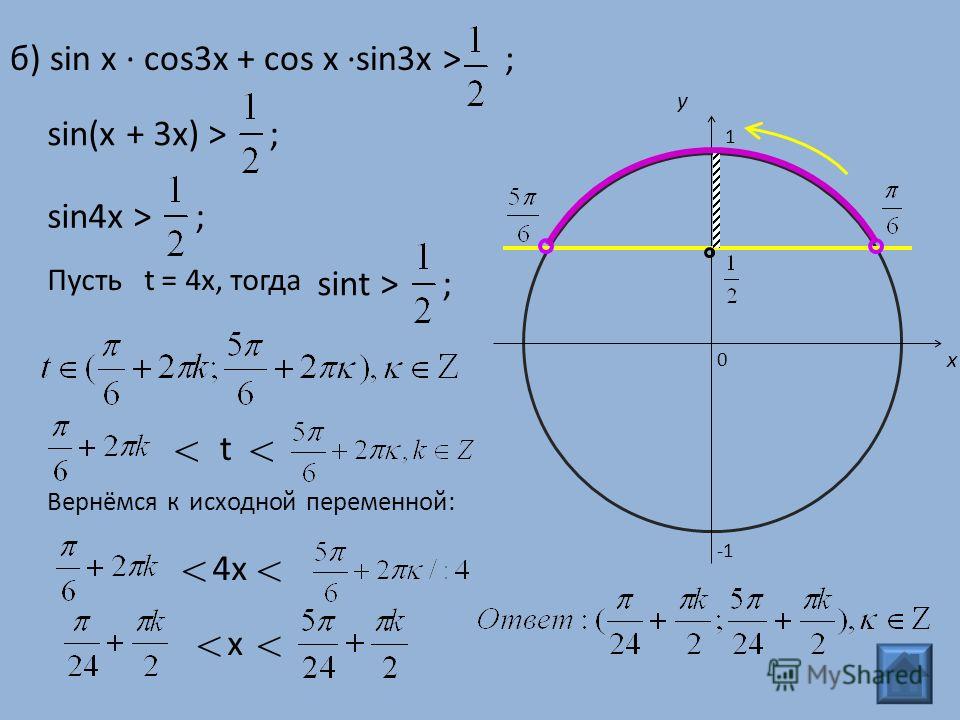 2x² + E x ) DX
2x² + E x ) DX 