§ Вычитание отрицательных чисел. Вычитание рациональных чисел
Координатная прямая Координаты точек на числовой оси Сложение отрицательных чисел Вычитание отрицательных чисел Умножение отрицательных чисел Деление отрицательных чисел
Как известно вычитание — это действие, противоположное сложению.
Если «a» и «b» — положительные числа, то вычесть из числа «a» число «b», значит найти такое число «c», которое при сложении «с» числом «b» даёт число «a».
a − b = с или с + b = a
Определение вычитания сохраняется для всех рациональных чисел. То есть вычитание положительных и отрицательных чисел можно заменить сложением.
Запомните!
Чтобы из одного числа вычесть другое, нужно к уменьшаемому прибавить число противоположное вычитаемому.
Или по другому можно сказать, что вычитание числа «b» — это тоже самое сложение, но с числом
противоположным числу «b».
a − b = a + (−b)
Пример.
6 − 8 = 6 + (− 8) = −2
Пример.
0 − 2 = 0 + (−2) = −2
Запомните!
Стоит запомнить выражения ниже.
0 − a = − a
a − 0 = a
a − a = 0
Как видно из примеров выше вычитание числа «b» — это сложение с числом противоположным числу «b».
Это правило сохраняется не только при вычитании из бóльшего числа меньшего, но и позволяет из меньшего числа вычесть большее число, то есть всегда можно найти разность двух чисел.
Разность может быть положительным числом, отрицательным числом или числом ноль.
Примеры вычитания отрицательных и положительных чисел.
- −3 − (+ 4) = −3 + (−4) = −7
- −6 − (−7) = −6 + (+ 7) = 1
- 5 − (−3) = 5 + (+ 3) = 8
Удобно запомнить правило знаков, которое позволяет уменьшить количество скобок.
Знак «плюс» не изменяет знака числа, поэтому, если перед скобкой стоит плюс, то знак в скобках не меняется.
+ (+ a) = + a
+ (−a) = −a
Знак «минус» перед скобками меняет знак числа в скобках на противоположный.
−(+ a) = − a
−(−a) = + a
Из равенств видно, что если перед и внутри скобок стоят одинаковые знаки, то получаем «+», а если знаки разные, то получаем «−».
(−6) + (+ 2) − (−10) − (− 1) + (− 7) = −6 + 2 + 10 + 1 − 7 = − 13 + 13 = 0
Правило знаков сохраняется и в том случае, если в скобках не одно число, а алгебраическая сумма чисел.
a − (− b + c) + (d − k + n) = a + b − c + d − k + n
Обратите внимание, если в скобках стоит несколько чисел и перед скобками стоит знак «минус», то должны меняться знаки перед всеми числами в этих скобках.
Чтобы запомнить правило знаков можно составить таблицу определения знаков числа.
Правило знаков для чисел
| + (+) = + | + (−) = − |
| − (−) = + | − (+) = − |
Или выучить простое правило.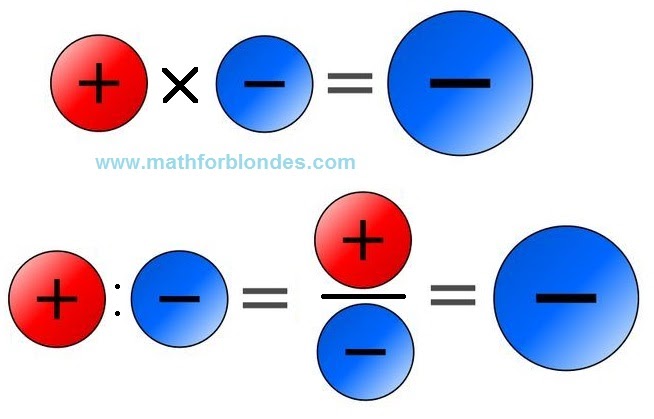
Запомните!
Минус на минус даёт плюс.
Плюс на минус даёт минус.
Координатная прямая Координаты точек на числовой оси Сложение отрицательных чисел Вычитание отрицательных чисел Умножение отрицательных чисел Деление отрицательных чисел
Сложение и вычитание отрицательных чисел – правила (6 класс, математика)
4
Средняя оценка: 4
Всего получено оценок: 308.
Обновлено 11 Января, 2021
4
Средняя оценка: 4
Всего получено оценок: 308.
Обновлено 11 Января, 2021
Отрицательные числа для многих учеников навсегда остаются загадочной частью математики. Всех нас с начальной школы приучают, что отрицательные числа – это не правильно решенный пример, позднее во взрослой жизни отрицательные числа все так же продолжают пугать, что вызывает большое количество ошибок. Чтобы не допускать оплошностей в будущем, рассмотрим во всех подробностях правила сложения и вычитания отрицательных чисел.
Материал подготовлен совместно с учителем высшей категории Харитоненко Натальей Владимировной.
Опыт работы учителем математики — более 33 лет.
Отрицательные числа
Отрицательные числа – это всего лишь числа, которые находятся слева от точки ноль на числовой прямой. Вот и все определение. Его нетрудно запомнить, но трудно понять. Ведь в реальной жизни отрицательных чисел практически нет: нельзя себе представить – 2 яблока или – 3 ручки. Можно понять, что такое реальное число, что такое отсутствие чисел, но что такое отрицательные числа понять куда труднее.
На самом деле можно представить себе любое отрицательное число, как недостаток до нуля. Например, – 3 значит, что при вычитании уменьшаемому не хватило трех единиц, чтобы выйти в ноль. Чаще всего это встречается в бухгалтерских отчетах и финансовых сводках.
Правило знаков
В этой теме часто встречается понятие правила знаков, которое изучается в курсе математики 6 класса. Стоит подробнее остановится на этом вопросе.
На самом деле, правило знаков – это производная от правил умножения отрицательных и положительных чисел. Например:
6-(-6)=6+(-1*-1*6)=6+6 – но расписывать так каждый раз слишком долго, поэтому проще запомнить один раз, что умножение “минуса” на “минус” и “плюса” на “плюс” дает знак “плюс”. А умножение “плюса” на “минус” – “минус”. Эти правила просто запомнить, чтобы не мучиться каждый раз с вынесением множителей.
Сложение и вычитание отрицательных чисел
Рассмотрим в отдельности каждую из операций, чтобы не вызывать лишних вопросов.
Сложение отрицательных чисел
Сложение может происходить между:
Вычитание отрицательных чисел
Вычитание может происходить между:
- Двумя отрицательными числами. В этом случае «”минус” на “минус”» дает “плюс”. После этого, мы увидим выражение из предыдущего пункта, то есть сложение отрицательного числа с положительным. Нужно поменять числа местами и выполнить вычитание.
- Отрицательным и положительным числом.
 В этом случае получается та же ситуация, что при сложении двух отрицательных чисел. Так как, “минус” на “плюс” дает “минус”. Получившиеся числа складываются по модулю, а потом к результату возвращают “минус”.
В этом случае получается та же ситуация, что при сложении двух отрицательных чисел. Так как, “минус” на “плюс” дает “минус”. Получившиеся числа складываются по модулю, а потом к результату возвращают “минус”. - Положительным и отрицательным числом. Этот случай больше прочих любим составителями примеров. В результате преобразования по правилу знаков: «”минус” на “минус”» дает “плюс”. Значит, получится сложение двух положительных чисел.
Стоит добавить, что сложение или вычитание нуля никак не повлияет на отрицательное число. При этом, если из нуля вычесть число, то оно изменит свой знак на противоположный.
Что мы узнали?
Мы поговорили о том, что такое отрицательное число. Выяснили, чем отличается сложение и вычитание отрицательных чисел, и подробно расписали каждый из возможных случаев.
Тест по теме
Доска почёта
Чтобы попасть сюда — пройдите тест.
Джамиля Таджиева
8/10
Мария Воробьева
10/10
Алла Лалаева
7/10
Максим Рачек
10/10
Александра Мальцева
7/10
Оценка статьи
4
Средняя оценка: 4
Всего получено оценок: 308.
А какая ваша оценка?
Почему минус в минус равен плюсу?
Алгебра — одна из старейших областей математики, занимающаяся теорией чисел, геометрией и анализом. Изучение математических символов и правил включает в себя манипулирование этими математическими символами. Алгебра охватывает практически все, от решения простых уравнений до изучения абстракций.
Алгебра также охватывает широкий круг предметов, от решения фундаментальных задач до изучения абстракций. В основном сосредоточены на переменных с неопределенными значениями. Раздел математики имеет дело с переменными и арифметическими операциями, выполняемыми над этими символами. Эти переменные не имеют установленных значений. В повседневной жизни мы сталкиваемся с проблемами. Некоторые значения постоянно меняются.
Эти значения или переменные часто представляются в алгебре такими символами, как a, b, c, d, x, y, z, p или q. Эти переменные обрабатываются с помощью различных математических операций, таких как сложение, вычитание, умножение и деление, для определения их значений.
Выражение представляет собой комбинацию терминов, объединенных вместе с помощью математических операций, таких как вычитание, сложение, умножение и деление.
- Константа — это число или цифра, имеющая фиксированное значение.
- Переменная — это символ с нефиксированным значением.
- Термин определяется как константа, отдельная переменная или комбинация переменной и константы в сочетании с умножением или делением.
Примеры выражений в алгебре: 3x+42, 7y + 12 и т. д.
Теперь
Почему минус в минус равен плюсу?Ответ:
Существуют различные правила отрицательных чисел в различных операциях.
14011119
Тип номеров -3 + (-2) = -5 (-)-(-) 9004 — -OR + -3-(2) = -1
-3-(-4) = 1
(-) × (-) 9004 × + (-3) × (-2) = 6 000447 (-3) (-) ÷ (-) ÷ + (-3) ÷ (-3) = 1 .
даст результат — положительное число, а это означает, что произведение двух отрицательных целых чисел всегда положительно.
То же В правиле деления, когда мы делим отрицательное на отрицательное, результат будет положительным, но эти минус минус плюс невозможны в случае сложения и вычитания.
Решенные примеры
Пример 1: Умножьте -5 и -8.
Решение:
Указанные номера: -5 и -8
Теперь умножьте,
= -5 × -8
= 40 9
После умножения обоих отрицательных чисел получается положительное число.
Пример 2: умножьте -5 и 8.
Решение:
Указанные номера: -5 и 8
Сейчас умножьте,
= -5 × 8
= 40
после умножение одного отрицательного и положительного дает результат отрицательного числа.
Пример 3: Разделить -8 на -4.
Решение:
Указанные цифры: -8 и -4
теперь деление,
= -8 / -4
= 2
после деления оба отрицательных числа, которые он дает в положительное число.
Пример 4. Разделить -8 на 40002 = -8 / 4
= -2
После деления одного отрицательного и положительного числа получается отрицательное число.
Минус, умноженный на минус, будет плюсом
Я видел несколько недавних постов, которые задавались вопросом об интуитивном объяснении того факта, что «минус, умноженный на минус, равен плюсу». Я понимаю, почему люди задаются этим вопросом — как часто учат, это кажется просто произвольным правилом без «почему»! Но на самом деле это вполне логично.
Пол с сайта crossedstreams.com дает объяснение, включающее две величины с реальными интерпретациями, связанными с отрицательными значениями: чистая стоимость (отрицательное значение означает уменьшение чистой стоимости) и время (прошлое отрицательное). Это довольно интуитивно понятно, но в каком-то смысле оно лишь показывает , почему это хорошо, что минус умножить на минус — это плюс, поскольку это позволяет нам смоделировать эту реальную ситуацию; это на самом деле не показывает
Это довольно интуитивно понятно, но в каком-то смысле оно лишь показывает , почему это хорошо, что минус умножить на минус — это плюс, поскольку это позволяет нам смоделировать эту реальную ситуацию; это на самом деле не показывает
Вот как бы я это объяснил. Это совсем не строго, и я даже не полностью удовлетворен этим, но я надеюсь, что это поможет развить некоторую интуицию.
Подумайте о знакомой «числовой прямой»: положительные числа отходят вправо, а отрицательные — влево. Добавление положительного числа соответствует перемещению вправо по числовой прямой. Прибавление отрицательного числа (то есть вычитание положительного) соответствует перемещению влево по числовой прямой. Таким образом, с добавлением мы уже видим эту идею негатива, соответствующую действию «в противоположном направлении».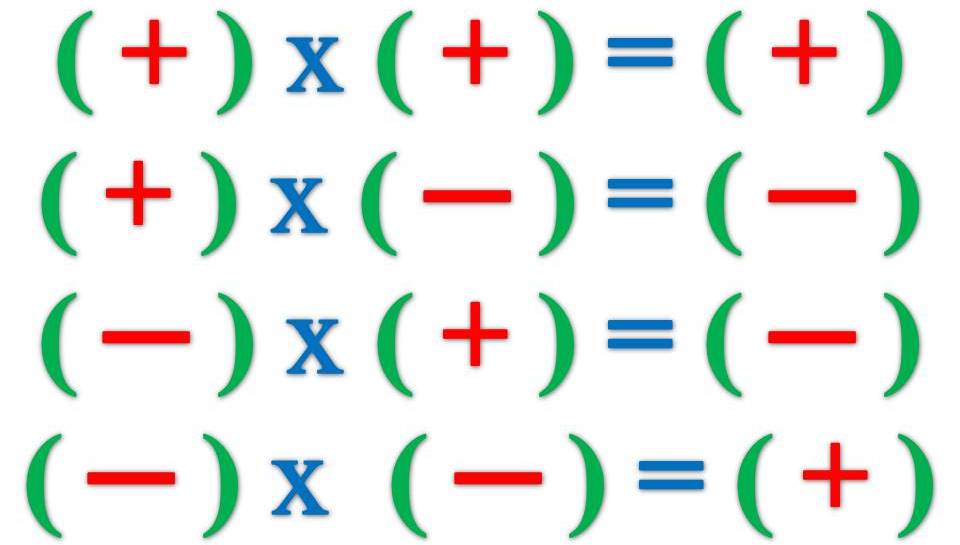
Итак, чему соответствует умножение на числовой прямой? Конечно, умножение соответствует масштабированию или растяжению: например, если мы начнем с точки на числовой прямой и умножим на 3, мы окажемся в точке, в три раза дальше от нуля, чем мы начали. А как насчет умножения на отрицательное число? Это соответствует шкале в другом направлении : например, если мы начнем с точки на числовой прямой и умножим на -3, мы закончим в точке на другая сторона нуля, и в три раза дальше. То есть умножение на отрицательное число означает, что мы переворачиваем с одной стороны нуля на другую. Итак, конечно, если мы начнем с левых нулей (отрицательное число) и умножим на отрицательное, мы закончим правыми нулями (положительное число)!
[Впрочем, я думаю, что попытка объяснить это более глубоко, чем это, действительно требует некоторого введения распределительного свойства — это единственное, что формально связывает сложение (помните, что отрицательные числа определяются как


 В этом случае получается та же ситуация, что при сложении двух отрицательных чисел. Так как, “минус” на “плюс” дает “минус”. Получившиеся числа складываются по модулю, а потом к результату возвращают “минус”.
В этом случае получается та же ситуация, что при сложении двух отрицательных чисел. Так как, “минус” на “плюс” дает “минус”. Получившиеся числа складываются по модулю, а потом к результату возвращают “минус”.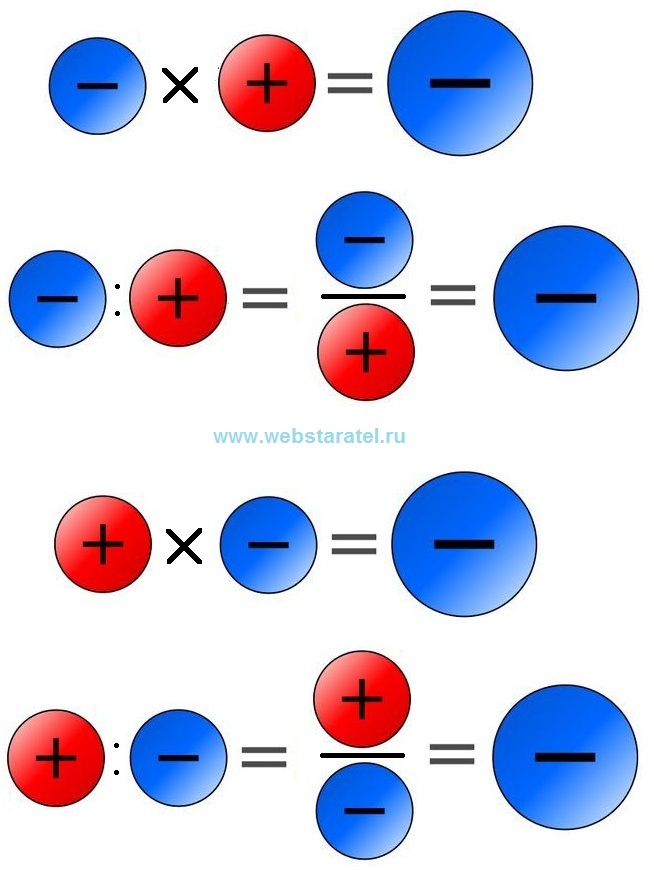 даст результат — положительное число, а это означает, что произведение двух отрицательных целых чисел всегда положительно.
даст результат — положительное число, а это означает, что произведение двух отрицательных целых чисел всегда положительно.