Плюс минус
Плюс минусПлюс и минус — это признаки положительных и отрицательных чисел в математике. Какой результат получается при умножении и делении положительных и отрицательных чисел? Эта простая таблица наглядно показывает результаты умножения и деления двух чисел с разными знаками.
Приведенные в таблице результаты применимы как при умножении и делении целых чисел, так и при умножении и делении дробей. Для определения числовых значений результата умножения или деления воспользуйтесь таблицами умножения и деления, которые можно скачать бесплатно.
При умножении или делении двух положительных чисел в результате получается положительное число. Плюс умноженный на плюс дает плюс, плюс деленный на плюс будет плюс. Это правило математики. Произведение двух положительных чисел — число положительное, частное двух положительных чисел — положительное число.
В математике умножение или деление положительного числа на отрицательное дает в результате отрицательное число.
При делении или умножении отрицательного числа на положительное в результате получается отрицательное число. Минус умноженный на плюс будет минус. Минус деленный на плюс в математике будет минус. Когда числитель дроби отрицательный, а знаменатель положительный — дробь (или целое число) будет отрицательной. Если отрицательную дробь умножить или разделить на положительную дробь получится отрицательное число. Это число может быть целым или дробным, что определяется другими правилами математики. Произведение отрицательного числа на положительное — число отрицательное, частное отрицательного числа на положительное число — отрицательное число.
Когда умножаются или делятся два отрицательных числа, результатом будет положительное число. Минус умноженный на минус дает плюс, минус деленный на минус будет плюс. Произведение двух отрицательного чисел — положительное число, частное двух отрицательного чисел — число положительное. При делении или умножении двух отрицательных чисел получается положительное число. Правила знаков в математике распространяются как на целые, так и на дробные числа. При делении двух отрицательных дробей результат будет положительным. При умножении двух отрицательных дробей результат так же будет положительным, то есть со знаком плюс.
ВОПРОС — ОТВЕТ
Современные знаки плюс «+» и минус «-» появились в Германии в последнее десятилетие пятнадцатого века в книге Видмана, которая была руководством по счету для купцов (“Behende und ubsche Rechenung auf allen Kaufmannschaft”, 1498). Существует предположение, что знаки плюс «+» и минус «-» появились из торговой практики: проданные меры вина отмечались на бочке черточкой «-«, а при восстановлении запаса их перечеркивали, откуда получился знак «+». Здесь я хочу особо подчеркнуть, что знаком «минус» отмечалась не мера (бочка) с «отрицательным» вином, а пустая мера (бочка), что гораздо больше соответствует понятию «ноль». Когда вам математики будут рассказывать об отрицательных числах, всегда помните о пустой бочке, которая по воле математиков превратилась в бочку со знаком «минус». «Минус 6 делить на минус 3 как быть?» — сперва отбрасываем знаки минус и делим просто 6 (шесть) на 3 (три) при помощи таблицы деления и получаем в результате 2 (два). Потом по табличке вверху странички делим минус на минус и получаем плюс.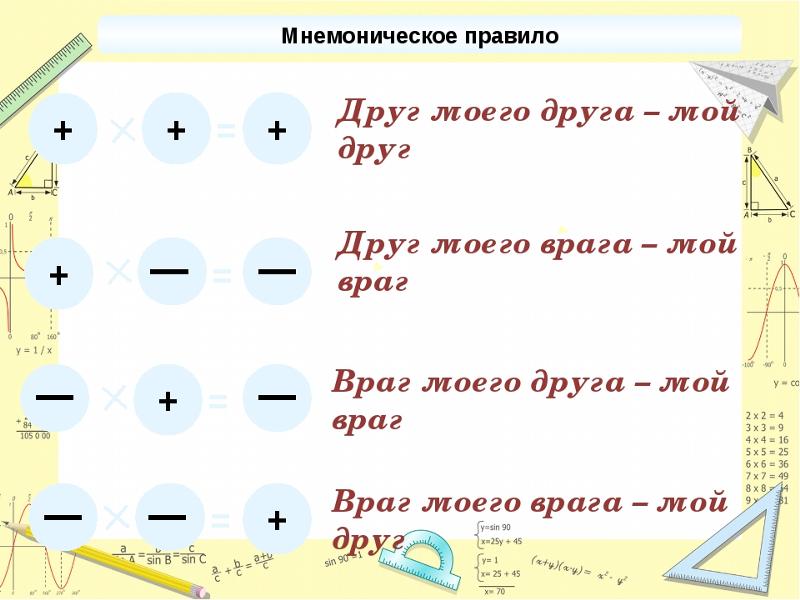
Теперь прилепливаем полученный плюс к ранее полученной двойке
(-6) : (-3) = +2
Впрочем, знак «+» перед числами писать не принято, поэтому красивее и правильнее будет так:
(-6) : (-3) = 2
«Если число со знаком минус спереди умножаем на такое же число?» — решение смотри выше.
13 ноября 2009 года — 22 сентября 2019 года
© 2006 — 2021 Николай Хижняк. Все права защищены.
Почему минус на минус дает плюс?
«Враг моего врага — мой друг».
Проще всего ответить: «Потому что таковы правила действий над отрицательными числами». Правила, которые мы учим в школе и применяем всю жизнь. Однако учебники не объясняют, почему правила именно такие. Мы сначала постараемся понять это, исходя из истории развития арифметики, а потом ответим на этот вопрос с точки зрения современной математики.
Давным-давно людям были известны только натуральные числа: 1, 2, 3, .
.. Их использовали для подсчета утвари, добычи, врагов и т. д. Но числа сами по себе довольно бесполезны — нужно уметь с ними обращаться. Сложение наглядно и понятно, к тому же сумма двух натуральных чисел — тоже натуральное число (математик сказал бы, что множество натуральных чисел замкнуто относительно операции сложения). Умножение — это, по сути, то же сложение, если мы говорим о натуральных числах. В жизни мы часто совершаем действия, связанные с этими двумя операциями (например, делая покупки, мы складываем и умножаем), и странно думать, что наши предки сталкивались с ними реже — сложение и умножение были освоены человечеством очень давно. Часто приходится и делить одни величины на другие, но здесь результат не всегда выражается натуральным числом — так появились дробные числа.
Без вычитания, конечно, тоже не обойтись. Но на практике мы, как правило, вычитаем из большего числа меньшее, и нет нужды использовать отрицательные числа. (Если у меня есть 5 конфет и я отдам сестре 3, то у меня останется 5 – 3 = 2 конфеты, а вот отдать ей 7 конфет я при всем желании не могу.
) Этим можно объяснить, почему люди долго не пользовались отрицательными числами.
В индийских документах отрицательные числа фигурируют с VII века н.э.; китайцы, видимо, начали употреблять их немного раньше. Их применяли для учета долгов или в промежуточных вычислениях для упрощения решения уравнений — это был лишь инструмент для получения положительного ответа. Тот факт, что отрицательные числа, в отличие от положительных, не выражают наличие какой-либо сущности, вызывал сильное недоверие. Люди в прямом смысле слова избегали отрицательных чисел: если у задачи получался отрицательный ответ, считали, что ответа нет вовсе. Это недоверие сохранялось очень долго, и даже Декарт — один из «основателей» современной математики — называл их «ложными» (в XVII веке!).
Рассмотрим для примера уравнение 7x – 17 = 2x – 2. Его можно решать так: перенести члены с неизвестным в левую часть, а остальные — в правую, получится 7x – 2x = 17 – 2, 5x = 15, x = 3. При таком решении нам даже не встретились отрицательные числа.
Но можно было случайно сделать и по-другому: перенести слагаемые с неизвестным в правую часть и получить 2 – 17 = 2x – 7x, (–15) = (–5)x. Чтобы найти неизвестное, нужно разделить одно отрицательное число на другое: x = (–15)/(–5). Но правильный ответ известен, и остается заключить, что (–15)/(–5) = 3.
Что демонстрирует этот нехитрый пример? Во-первых, становится понятна логика, которой определялись правила действий над отрицательными числами: результаты этих действий должны совпадать с ответами, которые получаются другим путем, без отрицательных чисел. Во-вторых, допуская использование отрицательных чисел, мы избавляемся от утомительного (если уравнение окажется посложнее, с большим числом слагаемых) поиска того пути решения, при котором все действия производятся только над натуральными числами. Более того, мы можем больше не думать каждый раз об осмысленности преобразуемых величин — а это уже шаг в направлении превращения математики в абстрактную науку.
Правила действий над отрицательными числами сформировались не сразу, а стали обобщением многочисленных примеров, возникавших при решении прикладных задач. Вообще, развитие математики можно условно разбить на этапы: каждый следующий этап отличается от предыдущего новым уровнем абстракции при изучении объектов. Так, в XIX веке математики поняли, что у целых чисел и многочленов, при всей их внешней непохожести, есть много общего: и те, и другие можно складывать, вычитать и перемножать. Эти операции подчиняются одним и тем же законам — как в случае с числами, так и в случае с многочленами. А вот деление целых чисел друг на друга, чтобы в результате снова получались целые числа, возможно не всегда. То же самое и с многочленами.
Потом обнаружились другие совокупности математических объектов, над которыми можно производить такие операции: формальные степенные ряды, непрерывные функции… Наконец, пришло понимание, что если изучить свойства самих операций, то потом результаты можно будет применять ко всем этим совокупностям объектов (такой подход характерен для всей современной математики).
В итоге появилось новое понятие: кольцо. Это всего-навсего множество элементов плюс действия, которые можно над ними производить. Основополагающими здесь являются как раз правила (их называют аксиомами), которым подчиняются действия, а не природа элементов множества (вот он, новый уровень абстракции!). Желая подчеркнуть, что важна именно структура, которая возникает после введения аксиом, математики говорят: кольцо целых чисел, кольцо многочленов и т. д. Отталкиваясь от аксиом, можно выводить другие свойства колец.
Мы сформулируем аксиомы кольца (которые, естественно, похожи на правила действий с целыми числами), а затем докажем, что в любом кольце при умножении минуса на минус получается плюс.
Кольцом называется множество с двумя бинарными операциями (т. е. в каждой операции задействованы два элемента кольца), которые по традиции называют сложением и умножением, и следующими аксиомами:
- сложение элементов кольца подчиняется переместительному (A + B = B + A для любых элементов A и B) и сочетательному (A + (B + C) = (A + B) + C) законам; в кольце есть специальный элемент 0 (нейтральный элемент по сложению) такой, что A + 0 = A, и для любого элемента A есть противоположный элемент (обозначаемый (–A)), что A + (–A) = 0;
- умножение подчиняется сочетательному закону: A·(B·C) = (A·B)·C;
- сложение и умножение связаны такими правилами раскрытия скобок: (A + B)·C = A·C + B·C и A·(B + C) = A·B + A·C.
Заметим, что кольца, в самой общей конструкции, не требуют ни перестановочности умножения, ни его обратимости (т. е. делить можно не всегда), ни существования единицы — нейтрального элемента по умножению. Если вводить эти аксиомы, то получаются другие алгебраические структуры, но в них будут верны все теоремы, доказанные для колец.
Теперь докажем, что для любых элементов A и B произвольного кольца верно, во-первых, (–A)·B = –(A·B), а во-вторых (–(–A)) = A. Из этого легко следуют утверждения про единицы: (–1)·1 = –(1·1) = –1 и (–1)·(–1) = –((–1)·1) = –(–1) = 1.
Для этого нам потребуется установить некоторые факты. Сперва докажем, что у каждого элемента может быть только один противоположный. В самом деле, пусть у элемента A есть два противоположных: B и С. То есть A + B = 0 = A + C. Рассмотрим сумму A + B + C. Пользуясь сочетательным и переместительным законами и свойством нуля, получим, что, с одной стороны, сумма равна B: B = B + 0 = B + (A + C) = A + B + C, а с другой стороны, она равна C: A + B + C = (A + B) + C = 0 + C = C.
Значит, B = C.
Заметим теперь, что и A, и (–(–A)) являются противоположными к одному и тому же элементу (–A), поэтому они должны быть равны.
Первый факт получается так: 0 = 0·B = (A + (–A))·B = A·B + (–A)·B, то есть (–A)·B противоположно A·B, значит, оно равно –(A·B).
Чтобы быть математически строгими, объясним еще, почему 0·B = 0 для любого элемента B. В самом деле, 0·B = (0 + 0) B = 0·B + 0·B. То есть прибавление 0·B не меняет сумму. Значит, это произведение равно нулю.
А то, что в кольце ровно один ноль (ведь в аксиомах сказано, что такой элемент существует, но ничего не сказано про его единственность!), мы оставим читателю в качестве несложного упражнения.
Ответил: Евгений Епифанов
Знак плюс-минус | Энциклопедия MDPI
Знак плюс-минус (±) — это математический символ с несколькими значениями. Знак обычно произносится как «плюс или минус». В математике это обычно указывает на выбор ровно двух возможных значений, одно из которых является отрицанием другого.
В экспериментальных науках знак обычно указывает на доверительный интервал или ошибку измерения, часто на стандартное отклонение или стандартную ошибку. Знак также может представлять включающий диапазон значений, которые может иметь показание. В технике знак указывает на допуск, который представляет собой диапазон значений, которые считаются приемлемыми, безопасными или соответствующими какому-либо стандарту или контракту. В ботанике используется в морфологических описаниях для обозначения «более или менее». В химии этот знак используется для обозначения рацемической смеси. В шахматах знак указывает на явное преимущество белого игрока; дополнительный знак ∓ указывает на такое же преимущество черного игрока.
1. История
Вариант знака, включающий также французское слово или («или»), был использован в его математическом значении Альбертом Жираром в 1626 г., а знак в его современном виде использовался уже в 9 Уильяма Отреда0008 Clavis Mathematicae (1631).
[1]
2. Применение
2.1. В математике
В математических формулах символ ± может использоваться для обозначения символа, который может быть заменен символами + или -, что позволяет формуле представлять два значения или два уравнения.
Например, для уравнения x 2 = 9 можно дать решение как x = ±3. Это указывает на то, что уравнение имеет два решения, каждое из которых может быть получено заменой этого уравнения одним из двух уравнений 92-4ас}}{2а}. }[/математика]
, описывающее два решения квадратного уравнения x 2 + bx + c = 0. ) = \sin(A) \cos(B) \pm \cos(A) \sin(B). }[/математика]
можно интерпретировать как сокращение двух уравнений: одно с «+» с обеих сторон уравнения, а другое с «-» с обеих сторон. Обе копии знака ± в этом тождестве должны быть заменены одинаковым образом: недопустимо заменять одну из них на «+», а другую на «-».
В отличие от примера с квадратичной формулой, оба уравнения, описываемые этим тождеством, справедливы одновременно. 9{2n+1} + \cdots. }[/математика]
Здесь знак «плюс» или «минус» указывает на то, что знаки терминов чередуются, где (начиная с 0) термины с четным индексом n добавляются, а термины с нечетным индексом вычитаются. Более строгое представление той же формулы умножит каждый член на коэффициент (-1) n , что дает +1, когда n четно, и -1, когда n нечетно.
2.2. В статистике
Использование ⟨±⟩ для приближения чаще всего встречается при представлении числового значения величины вместе с ее допуском или статистической погрешностью. [2] Например, «5,7±0,2» может находиться в диапазоне от 5,5 до 5,9 включительно. В научном использовании это иногда относится к вероятности попадания в указанный интервал, обычно соответствующей 1 или 2 стандартным отклонениям (вероятность 68,3% или 95,4% при нормальном распределении).
Проценты также могут использоваться для указания предела погрешности. Например, 230 ± 10 % В относится к напряжению в пределах 10 % от любой стороны от 230 В (от 207 В до 253 В включительно). Можно также использовать отдельные значения для верхней и нижней границ. Например, чтобы указать, что значение, скорее всего, равно 5,7, но может достигать 5,9.или всего 5,6, можно написать 5,7 + 0,2
-0,1.
2.3. В шахматах
Символы ± и ∓ используются в шахматной системе обозначений для обозначения преимущества белых и черных соответственно. Однако более распространенными шахматными обозначениями будут только + и -. [3] Если есть разница, символы + и — обозначают большее преимущество, чем ± и ∓.
3. Знак минус-плюс
Знак минус-плюс (∓) обычно используется в сочетании со знаком «±» в таких выражениях, как «x ± y ∓ z», что может быть истолковано как означающее x + y — z «и/или» x — y + z «, но не » x + y + z или « x + y + Z 9000″ или « x + + − y − z «.
Верхний «-» в «∓» считается связанным с «+» в «±» (и аналогично для двух нижних символов), даже если нет визуальной индикации зависимости. (Однако знак «±» обычно предпочтительнее знака «∓», поэтому, если они оба появляются в уравнении, можно с уверенностью предположить, что они связаны. С другой стороны, если есть два экземпляра знака «±» в выражении, по одному лишь обозначению невозможно сказать, является ли предполагаемая интерпретация двумя или четырьмя различными выражениями.) Исходное выражение можно переписать как « x ± ( y − z )», чтобы избежать путаницы, но такие случаи, как тригонометрическое тождество
- [math]\displaystyle{ \cos(A \pm B) = \cos(A) \cos (B) \mp \sin(A) \sin(B) }[/math]
лучше всего писать с использованием знака «∓». Приведенное выше тригонометрическое уравнение, таким образом, представляет собой два уравнения:
- [math]\displaystyle{ \begin{align} \cos(A + B) &= \cos(A)\cos(B) — \sin(A) \ sin(B) \\ \cos(A — B) &= \cos(A)\cos(B) + \sin(A) \sin(B) \end{align} }[/math] 92 \mp x + 1\справа) }[/math]
, который представляет собой два уравнения.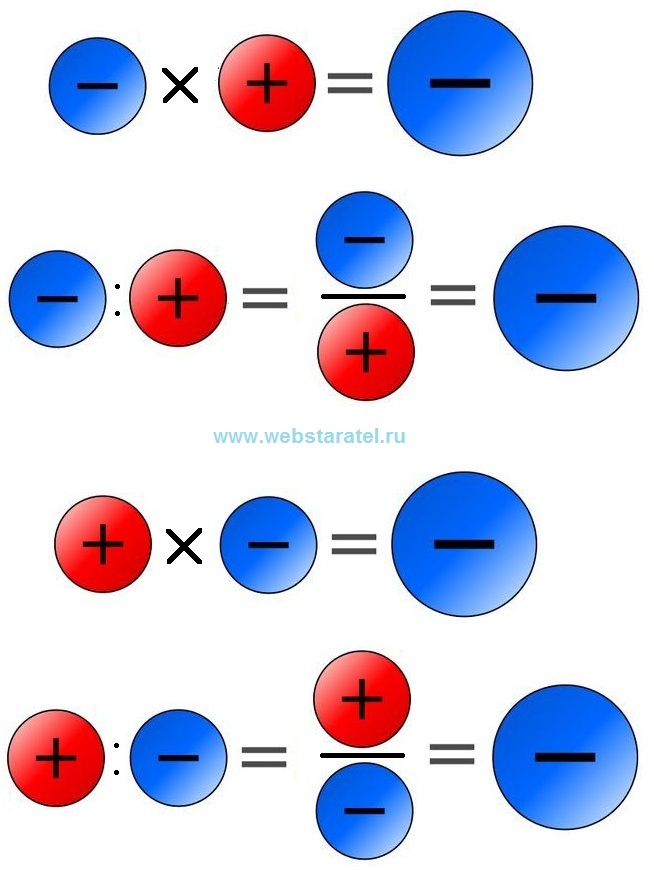
4. Кодировки
- В Unicode: U+00B1 ± ЗНАК ПЛЮС-МИНУС (HTML
±·+) - В ISO 8859-1, -7, -8, -9, -13, -15 и -16 символ плюс-минус задается кодом 0xB1 hex Поскольку первые 256 кодовых точек Unicode идентичны к содержимому ISO-8859-1 этот символ также находится в кодовой точке Unicode U+00B1.
- Символ также имеет HTML-представление сущности
±. - Более редкий знак минус-плюс (∓) обычно не встречается в устаревших кодировках и не имеет именованного объекта HTML, но доступен в Unicode с кодовой точкой U+2213 и поэтому может использоваться в HTML с использованием
∓или∓. - В TeX символы «плюс-или-минус» и «минус-или-плюс» обозначаются
\pmи\mpсоответственно. - Эти символы также могут быть представлены в виде подчеркнутого или надчеркнутого символа + ( + или + ), но будьте осторожны, форматирование может быть удалено позднее, что изменит значение.
Ввод
- В системах Windows его можно ввести с помощью альтернативных кодов, удерживая клавишу ALT при наборе цифр 0177 или 241 на цифровой клавиатуре.
- В Unix-подобных системах его можно ввести, набрав последовательность compose + -.
- В системах Macintosh его можно ввести, нажав опцию shift = (на нецифровой клавиатуре).
- На Chromebook его можно ввести, нажав shift, ctrl и u, а затем написав юникод для плюс-минус (00B1).
5. Подобные символы
Знак плюс-минус напоминает китайские иероглифы 士 и 土, а знак минус-плюс напоминает 干.
Да нет значок галочки плюс минус роялти бесплатно векторное изображение
Да нет значок галочка плюс минус роялти бесплатно векторное изображение- лицензионные векторы
org/ListItem»> Значок векторовЛицензияПодробнее
Стандарт Вы можете использовать вектор в личных и коммерческих целях. Расширенный Вы можете использовать вектор на предметах для перепродажи и печати по требованию.Тип лицензии определяет, как вы можете использовать этот образ.
| Станд. | Экспл. | |
|---|---|---|
| Печатный/Редакционный | ||
| Графический дизайн | ||
| Веб-дизайн | ||
| Социальные сети | ||
| Редактировать и изменять | ||
| Многопользовательский | ||
| Предметы перепродажи | ||
| Печать по требованию |
Владение Узнать больше
Эксклюзивный Если вы хотите купить исключительно этот вектор, отправьте художнику запрос ниже: Хотите, чтобы это векторное изображение было только у вас? Эксклюзивный выкуп обеспечивает все права этого вектора.
Мы удалим этот вектор из нашей библиотеки, а художник прекратит продажу работ.
Способы покупкиСравнить
Плата за изображение $ 14,99 Кредиты $ 1,00 Подписка $ 0,69Оплатить стандартные лицензии можно тремя способами. Цены составляют долларов США долларов США .
| Оплата с | Цена изображения |
|---|---|
| Плата за изображение $ 14,99 Одноразовый платеж | |
| Предоплаченные кредиты $ 1 Загружайте изображения по запросу (1 кредит = 1 доллар США). Минимальная покупка 30р. | |
| План подписки От 69 центов Выберите месячный план. Неиспользованные загрузки автоматически переносятся на следующий месяц. | |
Способы покупкиСравнить
Плата за изображение $ 39,99 Кредиты $ 30,00 Существует два способа оплаты расширенных лицензий.