Аппроксимация функции одной переменной методом наименьших квадратов с дополнительными условиями
Данный калькулятор использует метод наименьших квадратов (МНК) для аппроксимации функции одной переменной, аналогично калькулятору Аппроксимация функции одной переменной. Но, в отличии от указанного калькулятора, данный калькулятор поддерживает аппроксимацию функции с использованием ограничений на ее значения. То есть, можно задать условия равенства аппроксимирующей функции определенным значениям в определенных точках. Формулы аппроксимации будут выведены с учетом этих условий.
Используемый метод (метод множителей Лагранжа) накладывает ограничения на набор аппроксимирующих функций, так что этот калькулятор не поддерживает экспоненциальную аппроксимацию, аппроксимацию степенной функцией и показательную аппроксимацию. Одним словом поддерживается только линейная регрессия. Зато в него были добавлены аппроксимация полиномами 4-ой и 5-ой степени. Формулы и немного теории можно найти под калькулятором.
Если не ввести значения x, калькулятор будет считать, что значение x меняется начиная с 0 с шагом 1.
Аппроксимация функции одной переменной методом наименьших квадратов с дополнительными условиями
83 71 64 69 69 64 68 59 81 91 57 65 58 62Значения x, через пробел
183 168 171 178 176 172 165 158 183 182 163 175 164 175Значения y, через пробел
Ограничения на значения аппроксимирующей функции в точках
| x | y | ||
|---|---|---|---|
Ограничения на значения аппроксимирующей функции в точках
Импортировать данныеОшибка импорта
Данные
Для разделения полей можно использовать один из этих символов: Tab, «;» или «,» Пример: -50.5;-50.5
Загрузить данные из csv файла
Аппроксимирующие функцииЛинейная аппроксимацияКвадратичная аппроксимацияКубическая аппроксимацияАппроксимация полиномом 4-ой степениАппроксимация полиномом 5-ой степениАппроксимация полиномом 6-ой степениАппроксимация полиномом 7-ой степениАппроксимация полиномом 8-ой степениЛогарифмическая аппроксимацияГиперболическая аппроксимацияТочность вычисленияЗнаков после запятой: 4
Квадратичная регрессия
Коэффициент корреляции
Коэффициент детерминации
Средняя ошибка аппроксимации, %
Кубическая регрессия
Коэффициент корреляции
Коэффициент детерминации
Средняя ошибка аппроксимации, %
Полином 4-ой степени
Коэффициент корреляции
Средняя ошибка аппроксимации, %
Полином 5-ой степени
Коэффициент корреляции
Коэффициент детерминации
Средняя ошибка аппроксимации, %
Линейная регрессия
Коэффициент линейной парной корреляции
Коэффициент детерминации
Средняя ошибка аппроксимации, %
Логарифмическая регрессия
Коэффициент корреляции
Коэффициент детерминации
Средняя ошибка аппроксимации, %
Гиперболическая регрессия
Коэффициент корреляции
Коэффициент детерминации
Средняя ошибка аппроксимации, %
Полином 6-ой степени
Коэффициент корреляции
Коэффициент детерминации
Средняя ошибка аппроксимации, %
Полином 7-ой степени
Коэффициент корреляции
Коэффициент детерминации
Средняя ошибка аппроксимации, %
Полином 8-ой степени
Коэффициент корреляции
Коэффициент детерминации
Средняя ошибка аппроксимации, %
Результат
Файл очень большой, при загрузке и создании может наблюдаться торможение браузера.
Метод наименьших квадратов (МНК) — математический метод, применяемый для решения различных задач, основанный на минимизации суммы квадратов отклонений некоторых функций от искомых переменных. Использованием этого метода для вывода формул аппроксимации для различных аппроксимирующих функций можно посмотреть в теоретической части статьи Аппроксимация функции одной переменной.
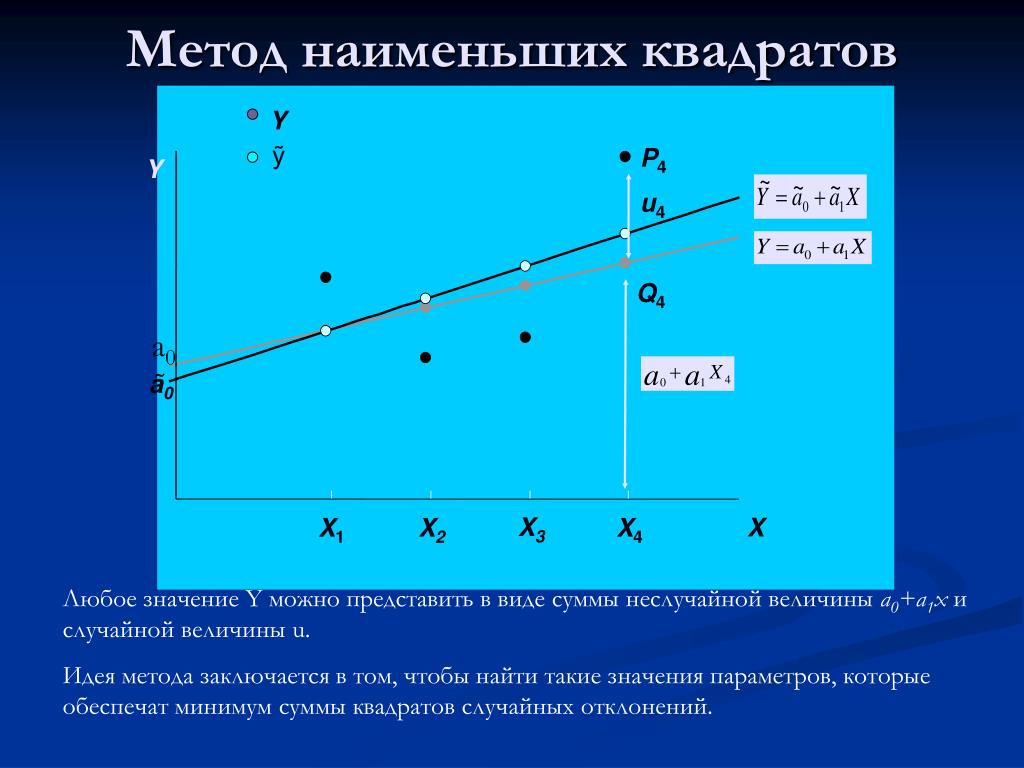
Подход, описанный по ссылке, можно обобщить для случая линейной комбинации параметров (для построения линейной регрессии).
Если аппроксимирующая функция является линейной комбинацией параметров, которые нужно
, то набор значений аппроксимирующей функции в заданных точках можно описать следующим образом
При использовании метода наименьших квадратов нам надо найти набор параметров, минимизирующих функцию
Значение этой функции есть расстояние от вектора y до вектора Xa. Для минимизации этого значения Xa должно быть проекцией на пространство столбцов матрицы X и вектор Xa-y должен быть ортогонален этому пространству (подробнее можно посмотреть здесь).
где v — произвольный вектор в пространстве столбцов. Так как этот вектор может быть любым, очевидно что равенство выполняется только в случае
Последняя формула и используется калькулятором выше для построения линейной регрессии без дополнительных ограничений.
Теперь разберемся с построением линейной регрессии при наличии ограничений. Такими ограничениями могут быть ограничения на значение функции в заданных точках. Например, нам известно, что функция, которую мы аппроксимируем ДОЛЖНА проходить через ноль (точку с координатами 0;0). Также могут существовать ограничения на значения производной функции в некоторых точках (наклона кривой функции). Наличие дополнительных ограничений говорит о том, что нам надо искать условный экстремум, то есть экстремум (в нашем случае минимум) функции, достигнутый при условии что переменные функции удовлетворяют уравнению связи.
Для решения такой задачи используется метод множителей Лагранжа. В методе множителей Лагранжа осуществляют переход от функции к функции Лагранжа через добавление множителей Лагранжа
Далее ищется экстремум данной функции. После всех вычислений, которые я здесь не привожу (их мало где приводят, да и я тоже мог бы написать что-нибудь вроде «очевидно, что» 🙂 ), получается следующая формула для нахождения параметров, при которых функция достигает условного экстремума
После всех вычислений, которые я здесь не привожу (их мало где приводят, да и я тоже мог бы написать что-нибудь вроде «очевидно, что» 🙂 ), получается следующая формула для нахождения параметров, при которых функция достигает условного экстремума
Именно эту формулу использует калькулятор выше для построения линейной регрессии в случае накладывания дополнительных условий на аппроксимирующую функцию.
Калькулятор расчета по методу наименьших квадратов
Метод наименьших квадратов — математический метод, применяемый для решения различных задач, основанный на минимизации суммы квадратов отклонений некоторых функций от искомых переменных.
Калькулятор расчета элементов прямой по методу наименьших квадратов
Онлайн калькулятор нахождения углового коэффициента, точки пересечение и уравнения прямой линии по методу наименьших квадратов
Формула метода наименьших квадратов:
где,
- b = Наклон линии регрессии
- a = Точка пересечения оси Y и линии регрессии.

- X̄ = Среднее значений х
- Ȳ = Среднее значений y
- SDx = Стандартное отклонение x
- SDy = Стандартное отклонение y
- r = (NΣxy — ΣxΣy) / корень ((NΣx2 — (Σx)2) x (NΣy)2 — (Σy)2)
Пример
Найти регрессию методом наименьших квадратов
| Значение X | Значение Y |
| 5 | 6 |
| 2 | 3 |
| 1 | 6 |
| 7 | 9 |
Получаем,
| Значение X | Значение Y |
| 5 | 6 |
| 2 | 3 |
| 1 | 6 |
| 7 | 9 |
Найдем,
Уравнение линии регрессии методом наименьших квадратов
Решение:
Шаг 1 :
Количество значений x.
N = 4
Шаг 2 :
Найдем XY, X2 для полученных значений. Смотрите таблицу ниже
| Значение X | Значение Y | X*Y | X*X |
| 60 | 3.1 | 60 * 3.1 = 186 | 60 * 60 = 3600 |
| 61 | 3.6 | 61 * 3.6 = 219.6 | 61 * 61 = 3721 |
| 62 | 3.8 | 62 * 3.8 = 235.6 | 62 * 62 = 3844 |
| 63 | 4 | 63 * 4 = 252 | 63 * 63 = 3969 |
| 65 | 4.1 | 65 * 4.1 = 266.5 | 65 * 65 = 4225 |
Шаг 3 :
Найдем ΣX, ΣY, ΣXY;, ΣX2 для значений
- ΣX = 311
- ΣY = 18.6
- ΣXY = 1159.7
- ΣX2 = 19359
Шаг 4 :
Подставим значения в приведенную выше формулу.
Наклон(b) = (NΣXY — (ΣX)(ΣY)) / (NΣX2 — (ΣX)2)
- = ((5)*(1159.
 7)-(311)*(18.6))/((5)*(19359)-(311)2)
7)-(311)*(18.6))/((5)*(19359)-(311)2) - = (5798.5 — 5784.6)/(96795 — 96721)
- = 13.9/74
- = 0.19
Шаг 5 :
Подставив значения в формулу
Пересечение (a) = (ΣY — b(ΣX)) / N
- = (18.6 — 0.19(311))/5
- = (18.6 — 59.09)/5
- = -40.49/5
- = -8.098
Шаг 6 :
Подставим значения в уравнение прямой
Уравнение прямой(y) = a + bx
= -8.098 + 0.19x
Предположим, если мы хотим, узнать приблизительное у значение переменной x = 64, необходимо подставить значение в формулу
Уравнение прямой(y) = a + bx
- = -8.098 + 0.19(64)
- = -8.098 + 12.16
- = 4.06
Синонимы: Least-Squares method, МНК
людей нашли эту статью полезной. А Вы?
Monk (сериал, 2002–2009) — IMDb 004
РЕЙТИНГ IMDb
8. 0/10
0/10
79K
ВАШ РЕЙТИНГ
ПОПУЛЯРНОСТЬ
Играть трейлер0 : 9003 2 4450 Видео
99+ Фото
КомедияКриминалДрама
Сериал рассказывает об Адриане Монке, блестящем бывшем детективе из Сан-Франциско, который теперь консультирует полицию в качестве частного консультанта, борющегося с обсессивно-компульсивным расстройством. Сериал рассказывает об Адриане Монке, блестящем бывшем детективе из Сан-Франциско, который теперь консультирует полиции в качестве частного консультанта, который борется с обсессивно-компульсивным расстройством. Сериал рассказывает об Адриане Монке, блестящем бывшем детективе из Сан-Франциско, который теперь консультирует полицию в качестве частного консультанта, который борется с обсессивно-компульсивным расстройством.
- Создатель
- Энди Брекман
- Звезды
- Тони Шалхуб
- Джейсон Грей-Стэнфорд
- Тед Левин 9 0009
 производство, кассовые сборы и информацию о компании
производство, кассовые сборы и информацию о компанииРЕЙТИНГ IMDb
8.0/10
79K
ВАШ РЕЙТИНГ
ПОПУЛЯРНОСТЬ
- Создатель
- Энди Брекман
- Звезды
- Тони Шал hub
- Джейсон Грей-Стэнфорд
- Тед Левин
- 249Отзывы пользователей
- 35Отзывы критиков
- Выигран 8 премий «Эмми» в прайм-тайм
- 22 победы и 47 номинаций всего
Эпизоды125
Просмотреть выпуски
ТопЛучшие рейтинги 8 сезонов 87654321Просмотреть все 8 лет 20092008200720062005200420032002Просмотреть всеВидео 50
Зажим 0:55Смотреть «Дженнифер Лоуренс Дишес» о своем «позорном» первом кредите на IMDb Клип 1:24
Часы Монах : Clip 1
Clip 0:31Watch Monk: Burn Notice Salutes Monk
Clip 0:22Watch Monk: Clip 1
Clip 0:31Watch Monk: Clip 1 9 0011 Клип 0:31
Часы Монах: Монах П. И.
И.
Смотреть Монах: клип 1
Видео 0:32Смотреть Монах: что делал Монах? 1:25 halhoub
- Адриан Монк…
- Рэндалл Дишер
- Капитан Леланд Стоттлмейер…
- Натали Тигер
- Доктор Чарльз Крогер…
- Шарона Флеминг
- Джули Тигер
- Бенджи Флеминг
- Доктор Невен Белл
- Труди Монк…
- Гарольд Крен шоу
- Бенджи Флеминг
- Кевин Дорфман
- Эбигейл Карлайл…
- 2-й патрульный…
- Полицейский в форме…
- Карен Стоттлмейер
- Создатель
- Энди Брекман (главный сценарист)
- Все актеры и съемочная группа
- Производство, кассовые сборы и многое другое на IMDbPro
Больше похоже на это
Психология 9 0032 Последнее дело мистера Монка: фильм о монахе Менталист Замок Числа Кости Белый воротничок Элементарная школа Она написала убийство Обмани меня 9003 2 Уведомление о сожжении CSI: Исследование места преступленияСюжетная линия
Знаете ли вы
- Цитаты
[повторяющаяся строка]
Адриан Монк: Это дар.
 .. и проклятие.
.. и проклятие.
- Connections
Представлены на 60-й церемонии вручения премии «Золотой глобус» (2003)
Обзоры пользователей249
ОбзорПопулярный обзор
Тайна/комедия …кто знал?
Раньше я смотрел «Она написала убийство» вместе с родителями, но никогда особо не увлекался этими историями. Тогда тайны были не для меня. Затем, несколько недель назад, мои родители познакомили меня с сериалом в сети США о детективе-невротике. Так что я посмотрел его, и после одной серии у меня появилось новое любимое шоу.Адриан Монк — детектив с обсессивно-компульсивным расстройством, которое, по-видимому, улучшает его способности восприятия. Большинство его друзей на участке думают, что он просто странный.
Тони Шалхуб играет сумасшедшего сыщика. До этого я не знал, что Тони может играть… ну. Я видел его только в «Людях в черном» в роли Дживса. Но такая роль, как Монк, доказывает мне, что Тони может нести историю.
Но юмор в сериале делает его интересным. Если бы не шутки и шутки, Монах, вероятно, был бы просто еще одним скучным детективом, в котором я тщетно пытаюсь раскрыть дело перед героем. Итак, спасибо вам, Тони Шалхуб, за то, что разгадываете тайны весело.
Если вы поклонник детективов, комедий или того и другого, вам понравится Адриан Монк. 31 марта 2005 г.
ВойтиВ конце открытия первого сезона кредиты Монк видит, что один из его зонтов висит на крючке с ручкой, указывающей не в ту сторону. Поскольку Монк никогда бы не повесил его таким образом, кто это сделал и почему?
О чем Монк?
В какие годы установлен Монах?
Детали
- Дата выпуска
- 12 июля 2002 г.
 (США)
(США)
- 12 июля 2002 г.
- Страна происхождения
- США 9 0009
- Официальные сайты
- dfw.cbsloca
- Телеканал Hallmark Movies & Mysteries
- Язык
- Английский
- Также известен как
- Места съемок
- Торонто, Онтарио, Канада (сезон 1 — эпизоды с 3 по 13)
- Производственные компании
- Mandeville Films
- ABC Signature
- Morat im Produktions
- См.
 больше кредитов компании на IMDbPro
больше кредитов компании на IMDbPro
Технические характеристики
- Время работы
44 минуты
- Цвет
- Звуковой микс
- Стерео
- Соотношение сторон
- 900 03 16 : 9
Связанные новости
Внесите свой вклад в эту страницу
Предложите отредактировать или добавить отсутствующий контент
Еще для изучения
Недавно просмотренные 901 11
У вас нет недавно просмотренных страниц
Ввод MnK перестает работать случайным образом
Июль — последнее редактирование Июль
Перезапуск этой ветки сообщений, так как последняя не обновлялась несколько месяцев.
Июль
Если есть какие-либо USB-устройства, кроме KB и мыши, отключите их. Также, возможно, пришло время обновить драйверы usb.
Все, что я могу придумать.
Июль
Подключены только USB-устройства: беспроводная гарнитура для звука игры, микрофон (проводной) по очевидным причинам, мышь (беспроводная) и клавиатура (проводная). Это странно, потому что это единственный подарок, с которым у меня когда-либо была эта проблема.
Это странно, потому что это единственный подарок, с которым у меня когда-либо была эта проблема.
Июль
Почему мы должны делать, что мой звук USB исправить чертову игру!
Команда EA DICE
Июль
Привет @Schneeeebs, какая у тебя мышь и использует ли она какие-либо драйверы?/Атик
Июль
Я использую Logitech G703 и неоднократно проверял, обновлены ли драйверы через диспетчер устройств. Это клавиатура Corsair RGP3001 (проводная), и я также проверил драйверы для нее.
Июль
@EA_Atic
Я использую Logitech G703 и неоднократно проверял, обновлены ли драйверы с помощью диспетчера устройств. У них клавиатура Corsair RGP3001 (проводная), и я также проверил драйверы для нее.
Август
@EA_Atic
Приветствую, я снова попытался вернуться в игру, но возникла та же проблема.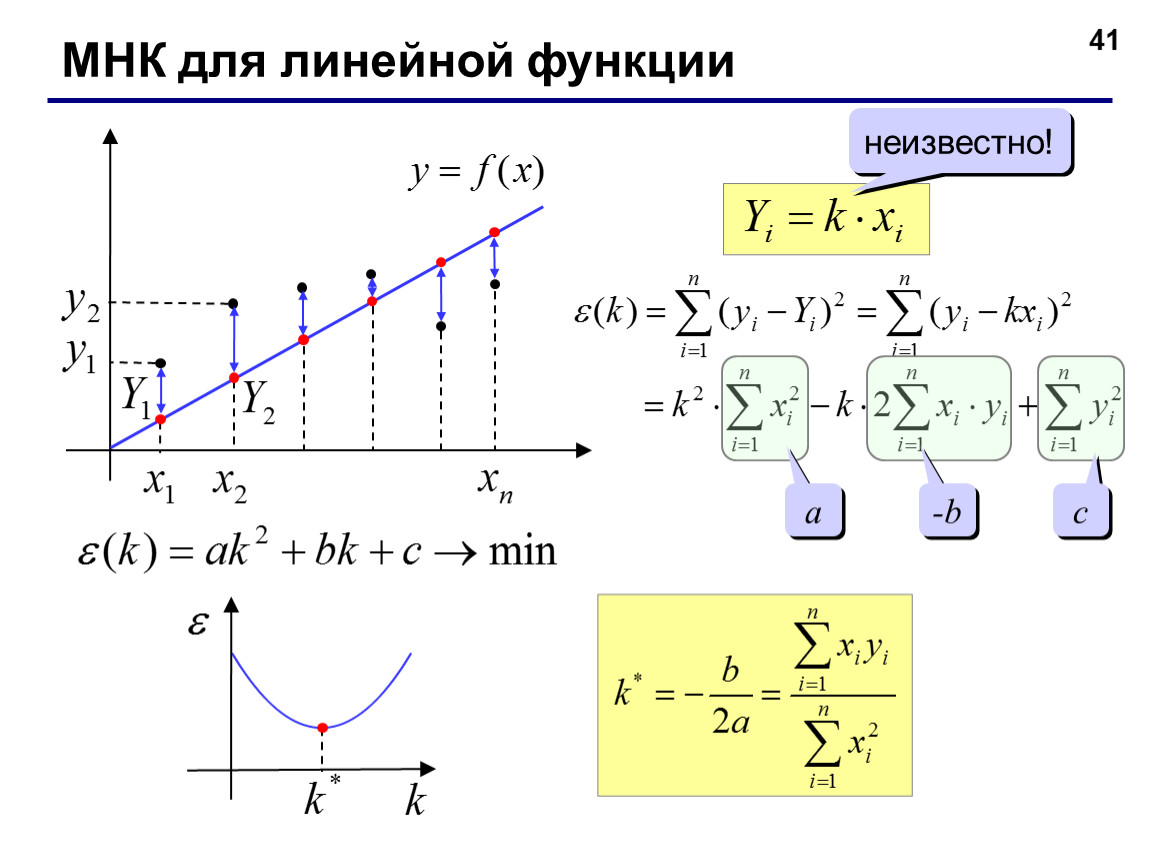

 7)-(311)*(18.6))/((5)*(19359)-(311)2)
7)-(311)*(18.6))/((5)*(19359)-(311)2) .. и проклятие.
.. и проклятие. (США)
(США) больше кредитов компании на IMDbPro
больше кредитов компании на IMDbPro