Правильные и неправильные многогранники презентация. Свойства додекаэдра и интересные факты. Элементы симметрии правильного октаэдра
Одно из древнейших упоминаний о правильных многогранниках находится в трактате Платона (до н. э.) «Тимаус». Поэтому правильные многогранники также называются платоновыми телами (хотя известны они были задолго до Платона). Каждый из правильных многогранников, а всего их пять. Платон ассоциировал с четырьмя «земными» элементами: земля (куб), вода (икосаэдр), огонь (тетраэдр), воздух (октаэдр), а также с «неземным» элементом — небом (додекаэдр).
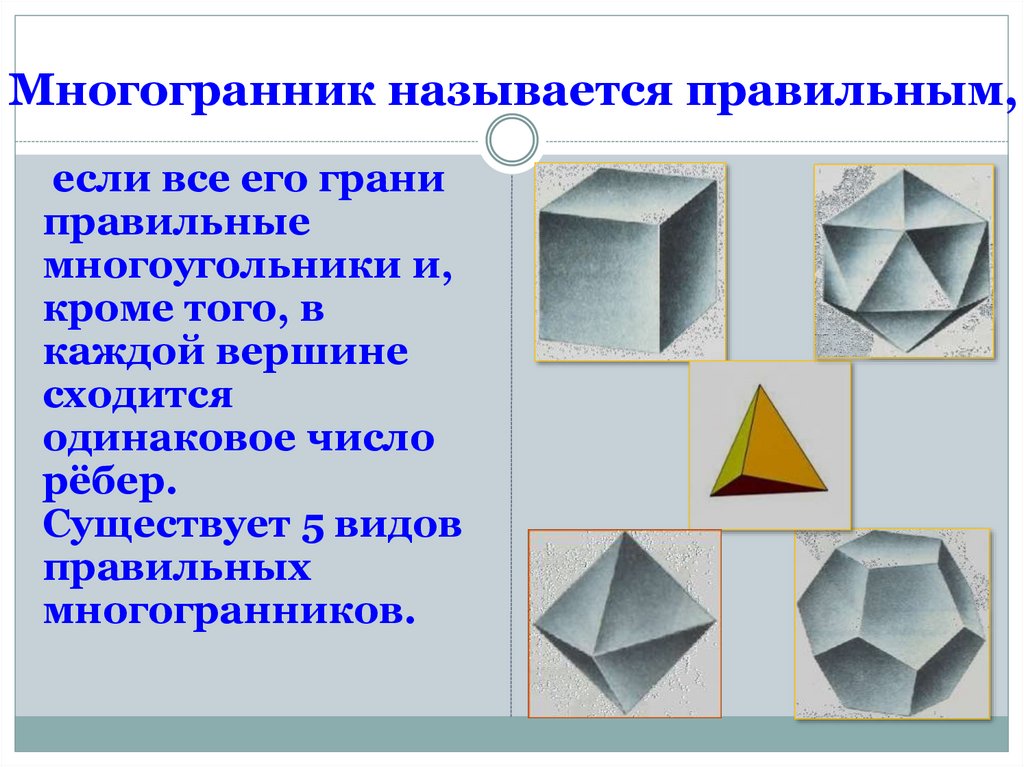
Правильный многогранник, или Платоново тело это выпуклый многогранник с максимально возможной симметрией. Многогранник называется правильным, если: он выпуклый все его грани являются равными правильными многоугольниками в каждой его вершине сходится одинаковое число граней все его двухгранные углы равны
Отметим интересный факт, связанный с гексаэдром (кубом) и октаэдром. Куб имеет 6 граней, 12 ребер и 8 вершин, а октаэдр – 8 граней, 12 ребер и 6 вершин. То есть число граней одного многогранника равно числу вершин другого и наоборот. Как говорят, куб и гексаэдр являются двойственными друг к другу. Это также проявляется в том, что если взять куб и построить многогранник с вершинами в центрах его граней, то, как несложно убедиться, получится октаэдр. Верно и обратное – центры граней октаэдра служат вершинами куба. В этом-то и состоит двойственность октаэдра и куба (рис). Несложно сообразить, что если взять центры граней правильного тетраэдра, то мы вновь получим правильный тетраэдр (рис). Таким образом, тетраэдр двойственен самому себе.
Куб имеет 6 граней, 12 ребер и 8 вершин, а октаэдр – 8 граней, 12 ребер и 6 вершин. То есть число граней одного многогранника равно числу вершин другого и наоборот. Как говорят, куб и гексаэдр являются двойственными друг к другу. Это также проявляется в том, что если взять куб и построить многогранник с вершинами в центрах его граней, то, как несложно убедиться, получится октаэдр. Верно и обратное – центры граней октаэдра служат вершинами куба. В этом-то и состоит двойственность октаэдра и куба (рис). Несложно сообразить, что если взять центры граней правильного тетраэдра, то мы вновь получим правильный тетраэдр (рис). Таким образом, тетраэдр двойственен самому себе.
Знаменитый математик и астроном Кеплер построил модель Солнечной системы как ряд последовательно вписанных и описанных правильных многогранников и сфер. Каков же порядок расположении планет (в соответствии с «требованиями» правильных многогранников) получился у Кеплера? В сферу орбиты Сатурна был вписан куб, в него — сфера орбиты Юпитера; в эту сферу вписался тетраэдр, в него — сфера орбиты Марса; далее: додекаэдр — сфера орбиты Земли — икосаэдр — сфера орбиты Венеры — октаэдр — сфера орбиты Меркурия.
Содержание: Цель пректа Цель пректа Цель пректа Цель пректа Термин Многогранники Термин Многогранники Термин Многогранники Термин Многогранники История История История Платон Платон Платон Платоновы тела Платоновы тела Платоновы тела Платоновы тела Евклид Евклид Евклид Архимед Архимед Архимед Архимедовы тела Архимедовы тела Архимедовы тела Архимедовы тела Иоганн Кеплер Иоганн Кеплер Иоганн Кеплер Иоганн Кеплер Космологическая гипотеза Кеплера Космологическая гипотеза Кеплера Космологическая гипотеза Кеплера Космологическая гипотеза Кеплера Тетраэдр Тетраэдр Тетраэдр Икосаэдр Икосаэдр Икосаэдр Додекаэдр Додекаэдр Додекаэдр Гексаэдр(куб) Гексаэдр(куб) Гексаэдр(куб) Октаэдр Октаэдр Октаэдр Частный случай Частный случай Частный случай Частный случай Развёртки правильных многогранников Развёртки правильных многогранников Развёртки правильных многогранников Развёртки правильных многогранников Теорема Теорема Теорема Таблица хар-к Таблица хар-к Таблица хар-к Таблица хар-к Полуправильные многогранники Полуправильные многогранники Полуправильные многогранники Полуправильные многогранники Нахождение в природе Нахождение в природе Нахождение в природе Нахождение в природе Историческая справка Интересные факты Интересные факты Интересные факты Интересные факты
Многогранник называется правильным, если все его грани – равные между собой правильные многоугольники, из каждой его вершины выходит одинаковое число ребер и все двугранные углы равны.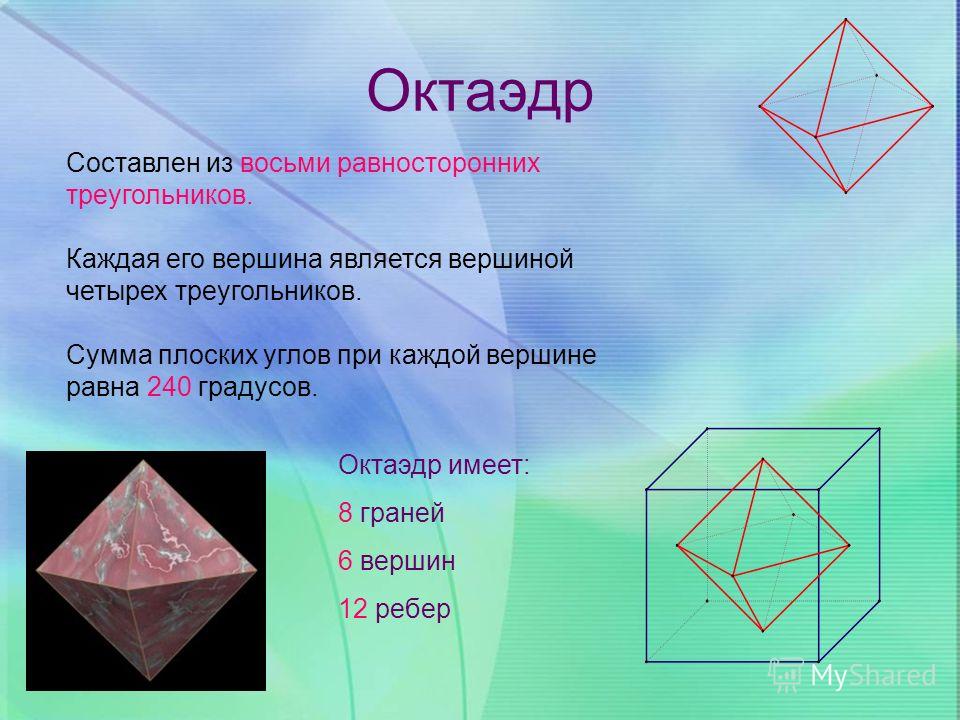 Многогранник называется правильным, если все его грани – равные между собой правильные многоугольники, из каждой его вершины выходит одинаковое число ребер и все двугранные углы равны.
Многогранник называется правильным, если все его грани – равные между собой правильные многоугольники, из каждой его вершины выходит одинаковое число ребер и все двугранные углы равны.
История правильных многогранников Их изучали ученые, ювелиры, священники, архитекторы. Этим многогранникам даже приписывали магические свойства. Древнегреческий ученый и философ Платон (IV–V в до н. э.) считал, что эти тела олицетворяют сущность природы. В своем диалоге «Тимей» Платон говорит, что атом огня имеет вид тетраэдра, земли – гексаэдра (куба), воздуха – октаэдра, воды – икосаэдра. В этом соответствии не нашлось места только додекаэдру и Платон предположил существование еще одной, пятой сущности – эфира, атомы которого как раз и имеют форму додекаэдра. Ученики Платона продолжили его дело в изучении перечисленных тел. Поэтому эти многогранники называют платоновыми телами. Их изучали ученые, ювелиры, священники, архитекторы. Этим многогранникам даже приписывали магические свойства. Древнегреческий ученый и философ Платон (IV–V в до н.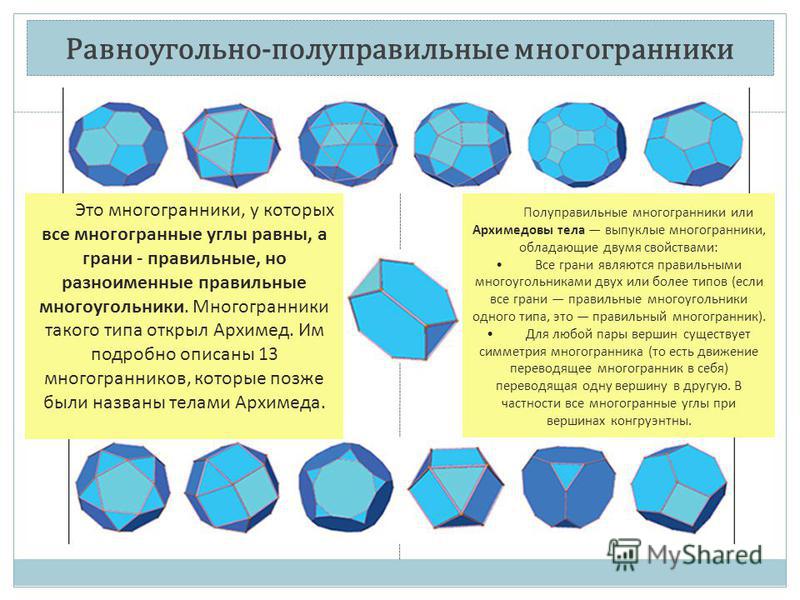
Платон около 429 – 347 гг до н.э. Платоновыми телами называются правильные однородные выпуклые многогранники, то есть выпуклые многогранники, все грани и углы которых равны, причем грани — правильные многоугольники. Платоновы тела — трехмерный аналог плоских правильных многоугольников. Однако между двумерным и трехмерным случаями есть важное отличие: существует бесконечно много различных правильных многоугольников, но лишь пять различных правильных многогранников. Доказательство этого факта известно уже более двух тысяч лет; этим доказательством и изучением пяти правильных тел завершаются «Начала» Евклида.
«Начала Евклида. «…в науке нет царского пути» около 365 – 300 гг. до н.э. Главный труд Евклида – «Начала» (в оригинале «Стохейа». «Начала» состоят из 13 книг, позднее к ним были прибавлены ещё 2. Первые шесть книг посвящены планиметрии. Книги VII – X содержат теорию чисел, XI, XII и XIII книги «Начал» посвящены стереометрии. Из постулатов Евклида видно, что он представлял пространство как пустое, безграничное, изотропное и трёхмерное. Интересно, что «Начала» Евклида открываются описанием построения правильного треугольника и заканчиваются изучением пяти правильных многогранных тел! В наше время они известны как платоновы тела.
Архимед Сиракузский около 287 – 212 гг. до н.э. Математик, физик и инженер Архимед Сиракузский оставил после себя немало изобретений, тринадцать сочинений (таких как «О сфере и цилиндре», «Измерение круга», «Равновесие плоскостей», «Стомахион», «Правильный семиугольник и другие). Архимед, как геометр определил поверхность шара и его объём, исследовал параболоиды и гиперболоиды, изучал «архимедову спираль», определил число «пи», как находящееся между 3,141 и 3,142.
Архимедовы тела Множество архимедовых тел можно разбить на несколько групп. Первую из них составят пять многогранников, которые получаются из платоновых тел в результате их усечения. Так могут быть получены пять архимедовых тел: усечённый тетраэдр, усечённый гексаэдр (куб), усечённый октаэдр, усечённый додекаэдр и усечённый икосаэдр. Другую группу составляют всего два тела, именуемых также квазиправильными многогранниками. Эти два тела носят названия:кубооктаэдр и икосододекаэдр в отличие от большого ромбокубооктаэдра и большого ромбоикосододекаэдра. Два последующих многогранника называются ромбокубооктаэдром и ромбоикосододекаэдром. Иногда их называют также «малым ромбокубооктаэдром» и «малым ромбоикосододекаэдром» в отличие от большого ромбокубооктаэдра и большого ромбоикосододекаэдра. Наконец существуют две так называемые «курносые» модификации одна для куба, другая для додекаэдра.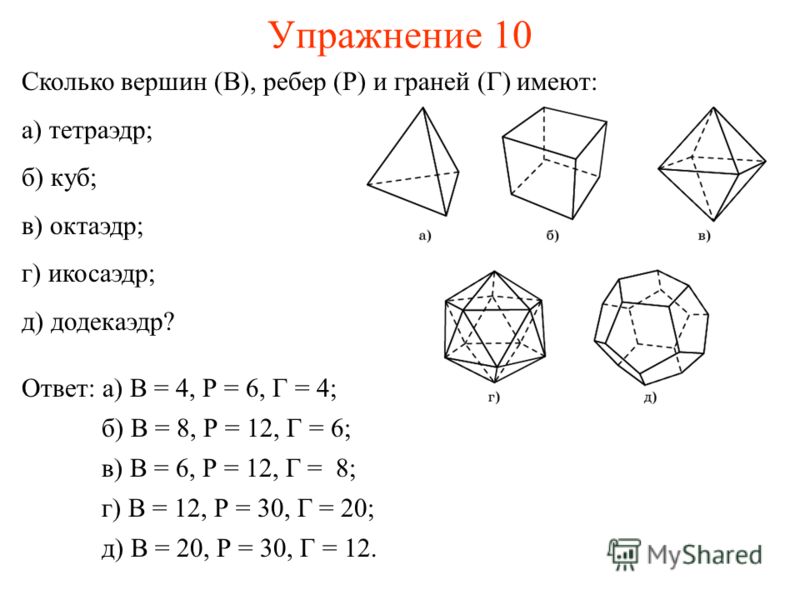
Иоганн Кеплер 1571 – 1630 гг. Немецкий астроном и математик. Один из создателей современной астрономии. Немецкий астроном и математик. Один из создателей современной астрономии. Вклад Кеплера в теорию многогранника — это, во-первых, восстановление математического содержания утерянного трактата Архимеда о полуправильных выпуклых однородных многогранниках. Вклад Кеплера в теорию многогранника — это, во-первых, восстановление математического содержания утерянного трактата Архимеда о полуправильных выпуклых однородных многогранниках. Еще более существенным было предложение Кеплера рассматривать невыпуклые многогранники со звездчатыми гранями, подобными пентаграмме и последовавшее за этим открытие двух правильных невыпуклых однородных многогранников — малого звездчатого додекаэдра и большого звездчатого додекаэдра.
Космологическая гипотеза Кеплера Кеплер попытался связать со свойствами правильных многогранников некоторые свойства Солнечной системы. Он предположил, что расстояния между шестью известными тогда планетами выражаются через размеры пяти правильных выпуклых многогранников (Платоновых тел). Между каждой парой «небесных сфер», по которым, согласно этой гипотезе, вращаются планеты, Кеплер вписал одно из Платоновых тел. Вокруг сферы Меркурия, ближайшей к Солнцу планеты, описан октаэдр. Этот октаэдр вписан в сферу Венеры, вокруг которой описан икосаэдр. Вокруг икосаэдра описана сфера Земли, а вокруг этой сферы — додекаэдр. Додекаэдр вписан в сферу Марса, вокруг которой описан тетраэдр. Вокруг тетраэдра описана сфера Юпитера, вписанная в куб. Наконец, вокруг куба описана сфера Сатурна..
Наконец, вокруг куба описана сфера Сатурна..
Тетраэдр Тетраэдр (tetra – четыре, hedra – грань). Правильный тетраэдр – правильный четырехгранник, то есть тетраэдр с равными ребрами, представляет собой правильный многогранник, все грани которого – правильные треугольники и из каждой вершины которого выходит ровно три ребра Тетраэдр (tetra – четыре, hedra – грань). Правильный тетраэдр – правильный четырехгранник, то есть тетраэдр с равными ребрами, представляет собой правильный многогранник, все грани которого – правильные треугольники и из каждой вершины которого выходит ровно три ребра У него 4 вершины,4 грани,6 ребер У него 4 вершины,4 грани,6 ребер Сумма плоских углов при каждой вершине равна 180 градусов Сумма плоских углов при каждой вершине равна 180 градусов
Икосаэдр (состоит из 20 треугольников) (состоит из 20 треугольников) В каждой вершине икосаэдра В каждой вершине икосаэдра сходятся пять граней. сходятся пять граней. Существует правильный многогранник, у которого все грани – правильные треугольники, и из каждой вершины выходит 5 ребер. Этот многогранник имеет 20 граней, 30 ребер, 12 вершин и называется икосаэдром (icosi – двадцать). Существует правильный многогранник, у которого все грани – правильные треугольники, и из каждой вершины выходит 5 ребер. Этот многогранник имеет 20 граней, 30 ребер, 12 вершин и называется икосаэдром (icosi – двадцать). Сумма плоских углов при каждой вершине равна 300 градусов Сумма плоских углов при каждой вершине равна 300 градусов
Этот многогранник имеет 20 граней, 30 ребер, 12 вершин и называется икосаэдром (icosi – двадцать). Существует правильный многогранник, у которого все грани – правильные треугольники, и из каждой вершины выходит 5 ребер. Этот многогранник имеет 20 граней, 30 ребер, 12 вершин и называется икосаэдром (icosi – двадцать). Сумма плоских углов при каждой вершине равна 300 градусов Сумма плоских углов при каждой вершине равна 300 градусов
Додекаэдр Существует правильный многогранник, у которого все грани правильные пятиугольники и из каждой вершины выходит 3 ребра. Этот многогранник имеет 12 граней, 30 ребер и 20 вершин и называется додекаэдром (dodeka – двенадцать). Существует правильный многогранник, у которого все грани правильные пятиугольники и из каждой вершины выходит 3 ребра. Этот многогранник имеет 12 граней, 30 ребер и 20 вершин и называется додекаэдром (dodeka – двенадцать). Сумма плоских углов при каждой вершине равна 324 градуса Сумма плоских углов при каждой вершине равна 324 градуса
Гексаэдр(куб) Гексаэдр (куб, hexa – шесть).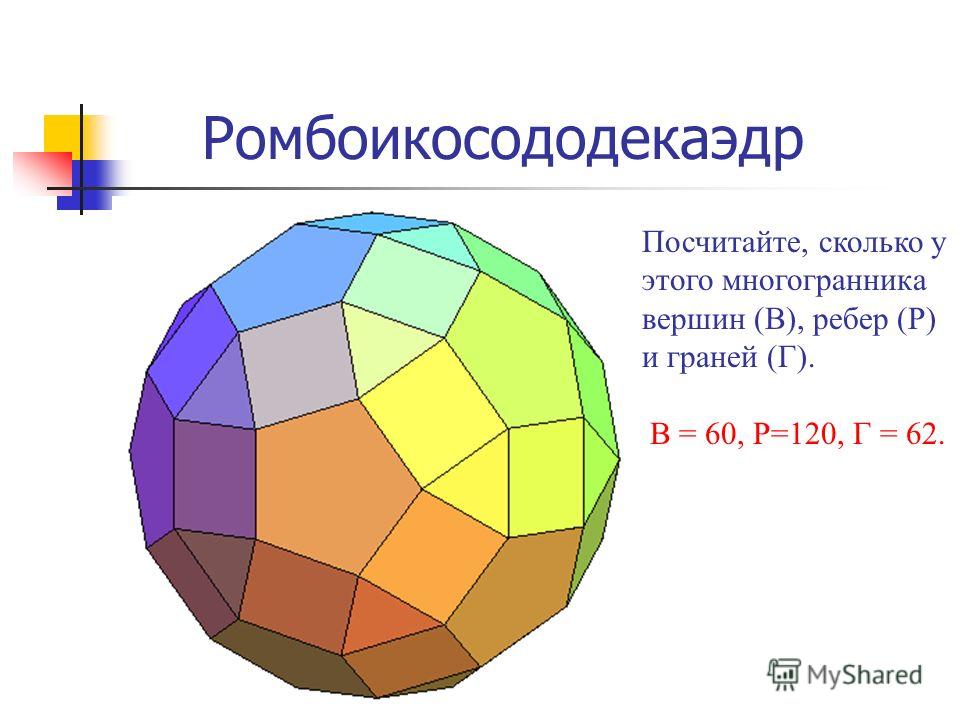 Гексаэдр – правильный многогранник, все грани которого – квадраты, и из каждой вершины выходит три ребра. Гексаэдр (куб, hexa – шесть). Гексаэдр – правильный многогранник, все грани которого – квадраты, и из каждой вершины выходит три ребра. У него 6 граней,8 вершин,12 ребер У него 6 граней,8 вершин,12 ребер Сумма плоских углов при каждой вершине равна 270 градусов Сумма плоских углов при каждой вершине равна 270 градусов
Гексаэдр – правильный многогранник, все грани которого – квадраты, и из каждой вершины выходит три ребра. Гексаэдр (куб, hexa – шесть). Гексаэдр – правильный многогранник, все грани которого – квадраты, и из каждой вершины выходит три ребра. У него 6 граней,8 вершин,12 ребер У него 6 граней,8 вершин,12 ребер Сумма плоских углов при каждой вершине равна 270 градусов Сумма плоских углов при каждой вершине равна 270 градусов
Октаэдр Октаэдр. Это правильный многогранник, все грани которого – правильные треугольники и к каждой вершине прилегают четыре грани Октаэдр. Это правильный многогранник, все грани которого – правильные треугольники и к каждой вершине прилегают четыре грани У него 8 граней,12 ребер,6вершин У него 8 граней,12 ребер,6вершин
Характеристики многогранников. Название:Число ребер при вершине Число сторон грани Число граней Число ребер Число вершин Тетраэдр33464 Куб Октаэдр Додекаэдр Икосаэдр
Полуправильные многогранники Курносый куб. Этот многогранник можно вписать в куб таким образом, что плоскости шести квадратных его граней совпадут с плоскостями граней куба, причем эти квадратные грани курносого куба окажутся как бы слегка повернутыми по отношению к соответственным граням куба. Курносый куб. Этот многогранник можно вписать в куб таким образом, что плоскости шести квадратных его граней совпадут с плоскостями граней куба, причем эти квадратные грани курносого куба окажутся как бы слегка повернутыми по отношению к соответственным граням куба. Ромбоикосододекаэдр. Эта модель принадлежит к числу наиболее привлекательных среди всех других моделей архимедовых тел. Гранями являются треугольники, квадраты и пятиугольники. Ромбоикосододекаэдр. Эта модель принадлежит к числу наиболее привлекательных среди всех других моделей архимедовых тел. Гранями являются треугольники, квадраты и пятиугольники. Ромбоусеченный кубооктаэдр. Этот многогранник, известный также под названием усеченного кубооктаэдра, гранями имеет квадраты, шестиугольники и восьмиугольники.
Этот многогранник можно вписать в куб таким образом, что плоскости шести квадратных его граней совпадут с плоскостями граней куба, причем эти квадратные грани курносого куба окажутся как бы слегка повернутыми по отношению к соответственным граням куба. Курносый куб. Этот многогранник можно вписать в куб таким образом, что плоскости шести квадратных его граней совпадут с плоскостями граней куба, причем эти квадратные грани курносого куба окажутся как бы слегка повернутыми по отношению к соответственным граням куба. Ромбоикосододекаэдр. Эта модель принадлежит к числу наиболее привлекательных среди всех других моделей архимедовых тел. Гранями являются треугольники, квадраты и пятиугольники. Ромбоикосододекаэдр. Эта модель принадлежит к числу наиболее привлекательных среди всех других моделей архимедовых тел. Гранями являются треугольники, квадраты и пятиугольники. Ромбоусеченный кубооктаэдр. Этот многогранник, известный также под названием усеченного кубооктаэдра, гранями имеет квадраты, шестиугольники и восьмиугольники.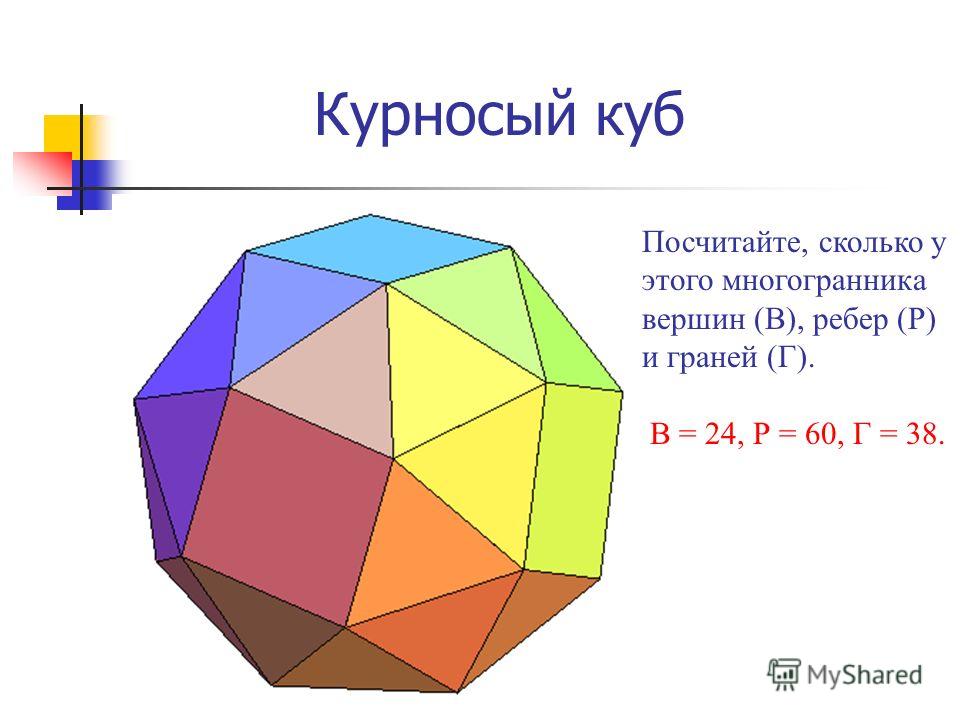 Ромбоусеченный кубооктаэдр. Этот многогранник, известный также под названием усеченного кубооктаэдра, гранями имеет квадраты, шестиугольники и восьмиугольники. Курносый додекаэдр – это последний из семейства выпуклых однородных многогранников. Гранями являются треугольники и пятиугольники. Курносый додекаэдр – это последний из семейства выпуклых однородных многогранников. Гранями являются треугольники и пятиугольники.
Ромбоусеченный кубооктаэдр. Этот многогранник, известный также под названием усеченного кубооктаэдра, гранями имеет квадраты, шестиугольники и восьмиугольники. Курносый додекаэдр – это последний из семейства выпуклых однородных многогранников. Гранями являются треугольники и пятиугольники. Курносый додекаэдр – это последний из семейства выпуклых однородных многогранников. Гранями являются треугольники и пятиугольники.
Ромбододекаэдр. (пролуправильные тела) Он образован помощью семи кубов, образующих пространственный «крест« и додекаэдра.
Нахождение в природе В кристаллических телах частицы располагаются в строгом порядке, образуя пространственные периодически повторяющиеся структуры во всем объеме тела. Для наглядного представления таких структур используются пространственные кристаллические решетки, в узлах которых располагаются центры атомов или молекул данного вещества. Чаще всего кристаллическая решетка строится из ионов (положительно и отрицательно заряженных) атомов, которые входят в состав молекулы данного вещества. Например, решетка поваренной соли содержит ионы Na+ и Cl–, не объединенные попарно в молекулы NaCl. Такие кристаллы называются ионными. В кристаллических телах частицы располагаются в строгом порядке, образуя пространственные периодически повторяющиеся структуры во всем объеме тела. Для наглядного представления таких структур используются пространственные кристаллические решетки, в узлах которых располагаются центры атомов или молекул данного вещества. Чаще всего кристаллическая решетка строится из ионов (положительно и отрицательно заряженных) атомов, которые входят в состав молекулы данного вещества. Например, решетка поваренной соли содержит ионы Na+ и Cl–, не объединенные попарно в молекулы NaCl. Такие кристаллы называются ионными.
Например, решетка поваренной соли содержит ионы Na+ и Cl–, не объединенные попарно в молекулы NaCl. Такие кристаллы называются ионными. В кристаллических телах частицы располагаются в строгом порядке, образуя пространственные периодически повторяющиеся структуры во всем объеме тела. Для наглядного представления таких структур используются пространственные кристаллические решетки, в узлах которых располагаются центры атомов или молекул данного вещества. Чаще всего кристаллическая решетка строится из ионов (положительно и отрицательно заряженных) атомов, которые входят в состав молекулы данного вещества. Например, решетка поваренной соли содержит ионы Na+ и Cl–, не объединенные попарно в молекулы NaCl. Такие кристаллы называются ионными.
Кристаллы Кристаллические решетки металлов часто имеют форму шестигранной призмы (цинк, магний), гранецентрированного куба (медь, золото) или объемно центрированного куба (железо). Кристаллические решетки металлов часто имеют форму шестигранной призмы (цинк, магний), гранецентрированного куба (медь, золото) или объемно центрированного куба (железо). Кристаллические тела могут быть монокристаллами и поликристаллами. Поликристаллические тела состоят из многих сросшихся между собой хаотически ориентированных маленьких кристалликов, которые называются кристаллитами. Большие монокристаллы редко встречаются в природе и технике. Чаще всего кристаллические твердые тела, в том числе и те, которые получаются искусственно, являются поликристаллами. Кристаллические тела могут быть монокристаллами и поликристаллами. Поликристаллические тела состоят из многих сросшихся между собой хаотически ориентированных маленьких кристалликов, которые называются кристаллитами. Большие монокристаллы редко встречаются в природе и технике. Чаще всего кристаллические твердые тела, в том числе и те, которые получаются искусственно, являются поликристаллами.. Простые кристаллические решетки: 1 – простая кубическая решетка; 2 – гранецентрированная кубическая решетка; 3 – объемноцентрированная кубическая решетка; 4 – гексагональная решетка.
Кристаллические тела могут быть монокристаллами и поликристаллами. Поликристаллические тела состоят из многих сросшихся между собой хаотически ориентированных маленьких кристалликов, которые называются кристаллитами. Большие монокристаллы редко встречаются в природе и технике. Чаще всего кристаллические твердые тела, в том числе и те, которые получаются искусственно, являются поликристаллами. Кристаллические тела могут быть монокристаллами и поликристаллами. Поликристаллические тела состоят из многих сросшихся между собой хаотически ориентированных маленьких кристалликов, которые называются кристаллитами. Большие монокристаллы редко встречаются в природе и технике. Чаще всего кристаллические твердые тела, в том числе и те, которые получаются искусственно, являются поликристаллами.. Простые кристаллические решетки: 1 – простая кубическая решетка; 2 – гранецентрированная кубическая решетка; 3 – объемноцентрированная кубическая решетка; 4 – гексагональная решетка.
Кристаллы — многогранники Кальций. При ударах кристаллы кальцита раскалываются правильные фигурки, каждая грань которых имеет форму параллелограмма. Кальций образует разнообразные кристаллы от пластичной до вытянуто- призматичной формы. Кальций. При ударах кристаллы кальцита раскалываются правильные фигурки, каждая грань которых имеет форму параллелограмма. Кальций образует разнообразные кристаллы от пластичной до вытянуто- призматичной формы. Апатит. Они образуют кристаллы в форме прямоугольной призмы. Апатит. Они образуют кристаллы в форме прямоугольной призмы. Бериллий. Обычно встречается в виде столбчатых шестигранных кристаллов. Бериллий. Обычно встречается в виде столбчатых шестигранных кристаллов.
При ударах кристаллы кальцита раскалываются правильные фигурки, каждая грань которых имеет форму параллелограмма. Кальций образует разнообразные кристаллы от пластичной до вытянуто- призматичной формы. Кальций. При ударах кристаллы кальцита раскалываются правильные фигурки, каждая грань которых имеет форму параллелограмма. Кальций образует разнообразные кристаллы от пластичной до вытянуто- призматичной формы. Апатит. Они образуют кристаллы в форме прямоугольной призмы. Апатит. Они образуют кристаллы в форме прямоугольной призмы. Бериллий. Обычно встречается в виде столбчатых шестигранных кристаллов. Бериллий. Обычно встречается в виде столбчатых шестигранных кристаллов.
История правильных многогранников уходит в глубокую древность. Начиная с 7 века до нашей эры в Древней Греции создаются философские школы, в которых происходит постепенный переход от практической к философской геометрии. Большое значение в этих школах приобретают рассуждения, с помощью которых удалось получать новые геометрические свойства. Историческая справка Одной из первых и самых известных школ была Пифагорейская, названная в честь своего основателя Пифагора. Отличительным знаком пифагорейцев была пентаграмма, на языке математики- это правильный невыпуклый или звездчатый пятиугольник. Пентаграмме присваивалось способность защищать человека от злых духов.
Историческая справка Одной из первых и самых известных школ была Пифагорейская, названная в честь своего основателя Пифагора. Отличительным знаком пифагорейцев была пентаграмма, на языке математики- это правильный невыпуклый или звездчатый пятиугольник. Пентаграмме присваивалось способность защищать человека от злых духов.
Земля земля гексаэдр гексаэдр (куб) (куб) вселенная вселеннаяДодекаэдр Пифагорейцы, а затем Платон полагали, что материя состоит из четырех основных элементов: огня, земли, воздуха и воды. Существование пяти правильных многогранников они относили к строению материи и Вселенной. Согласно этому мнению, атомы основных элементов должны иметь форму различных Платоновых тел:
Художники о правильных многогранниках В эпоху Возрождения большой интерес к формам правильных многогранников проявляли скульпторы, архитекторы, ХУДОЖНИКИ. Леонардо да Винчи увлекался теорией многогранников и часто изображал их на своих полотнах. Он проиллюстрировал изображениями правильных и полуправильных многогранников книгу своего друга, монаха Луки Пачоли «О божественной пропорции» В эпоху Возрождения большой интерес к формам правильных многогранников проявляли скульпторы, архитекторы, ХУДОЖНИКИ. Леонардо да Винчи увлекался теорией многогранников и часто изображал их на своих полотнах. Он проиллюстрировал изображениями правильных и полуправильных многогранников книгу своего друга, монаха Луки Пачоли «О божественной пропорции»
Леонардо да Винчи увлекался теорией многогранников и часто изображал их на своих полотнах. Он проиллюстрировал изображениями правильных и полуправильных многогранников книгу своего друга, монаха Луки Пачоли «О божественной пропорции»
На картине художника Сальвадора Дали «Тайная Вечеря» Христос со своими учениками изображён на фоне огромного прозрачного додекаэдра. Форму додекаэдра, по мнению древних, имела ВСЕЛЕННАЯ, т.е. они считали, что мы живём внутри свода, имеющего форму поверхности правильного додекаэдра.
Египетские пирамиды Среди египетских пирамид особое место занимает пирамида фараона Хеопса. Длина стороны её основания L =233,16 м; высота Н =146,6; 148,2 м. Первоначально высота оценивалась не точно. Это связано с осадкой швов, деформацией блоков, предполагаемой частичной разборкой вершины от S 66 до 1010 м. Среди египетских пирамид особое место занимает пирамида фараона Хеопса. Длина стороны её основания L =233,16 м; высота Н =146,6; 148,2 м. Первоначально высота оценивалась не точно. Это связано с осадкой швов, деформацией блоков, предполагаемой частичной разборкой вершины от S 66 до 1010 м.
Первоначально высота оценивалась не точно. Это связано с осадкой швов, деформацией блоков, предполагаемой частичной разборкой вершины от S 66 до 1010 м.
Угол наклона граней =5151. Впервые он был измерен английским полковником Г. Вайзовым в 1837 г tg =1,27306= vd= 1, Угол наклона граней =5151. Впервые он был измерен английским полковником Г. Вайзовым в 1837 г tg =1,27306= vd= 1,27202.
Царская гробница Великая пирамида была построена как гробница Хуфу, известного грекам как Хеопс. Он был одним из фараонов, или царей древнего Египта, а его гробница была завершена в 2580 году до н.э. Позднее в Гизе было построено еще две пирамиды, для сына и внука Хуфу, а также меньшие по размерам пирамиды для их цариц. Пирамида Хуфу, самая дальняя на рисунке, является самой большой. Пирамида его сына находится в середине и смотрится выше, потому что стоит на более высоком месте.
В III веке до н.э. был построен маяк, чтобы корабли могли благополучно миновать рифы на пути в александрийскую бухту.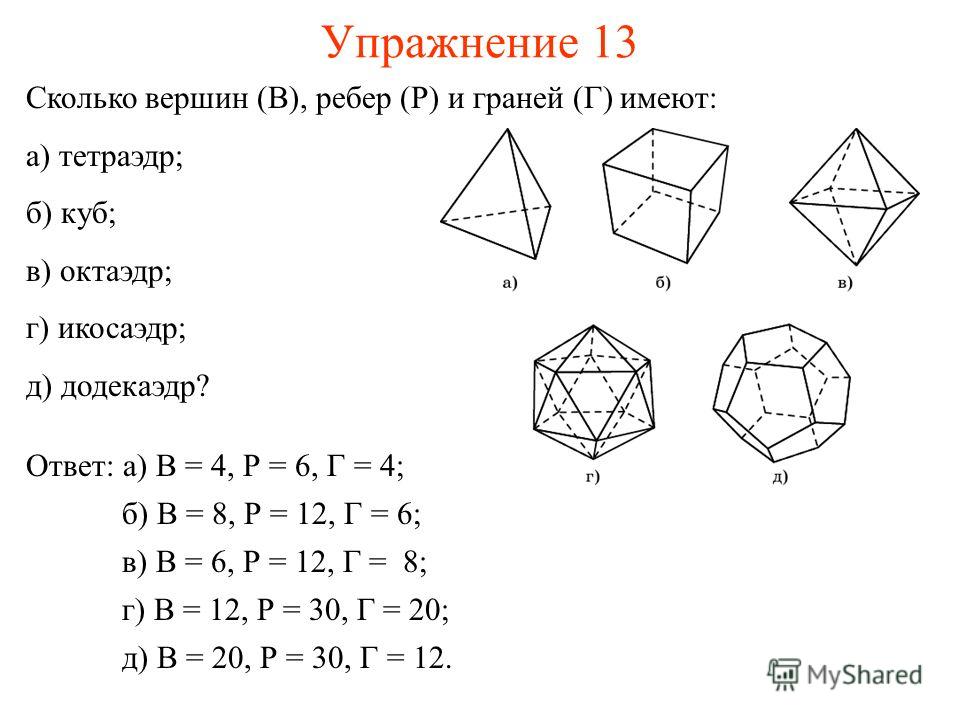 Ночью им помогало в этом отражение языков пламени, а днем — столб дыма. Это был первый в мире маяк, и простоял он 1500 лет Фаросский маяк состоял из трех мраморных башен, стоявших на основании из массивных каменных блоков. Первая башня была прямоугольной, в ней находились комнаты, в которых жили рабочие и солдаты. Над этой башней располагалась меньшая, восьмиугольная башня со спиральным пандусом, ведущим в верхнюю башню. Верхняя башня формой напоминала цилиндр, в котором горел огонь, помогавший кораблям благополучно достигнуть бухты. На вершине башни стояла статуя Зевса Спасителя. Общая высота маяка составляла 117 метров. Александрийский маяк
Ночью им помогало в этом отражение языков пламени, а днем — столб дыма. Это был первый в мире маяк, и простоял он 1500 лет Фаросский маяк состоял из трех мраморных башен, стоявших на основании из массивных каменных блоков. Первая башня была прямоугольной, в ней находились комнаты, в которых жили рабочие и солдаты. Над этой башней располагалась меньшая, восьмиугольная башня со спиральным пандусом, ведущим в верхнюю башню. Верхняя башня формой напоминала цилиндр, в котором горел огонь, помогавший кораблям благополучно достигнуть бухты. На вершине башни стояла статуя Зевса Спасителя. Общая высота маяка составляла 117 метров. Александрийский маяк
Простейшее животное Скелет одноклеточного организма феодарии (Circogonia icosahedra) по форме напоминает икосаэдр. Скелет одноклеточного организма феодарии (Circogonia icosahedra) по форме напоминает икосаэдр. Большинство феодарий живут на морской глубине и служат добычей коралловых рыбок. Но простейшее животное защищает себя двенадцатью иглами, выходящими из 12 вершин скелета. Он больше похоже на звёздчатый многогранник. Большинство феодарий живут на морской глубине и служат добычей коралловых рыбок. Но простейшее животное защищает себя двенадцатью иглами, выходящими из 12 вершин скелета. Он больше похоже на звёздчатый многогранник. Из всех многогранников с тем же числом граней икосаэдр имеет наибольший объём при наименьшей площади поверхности. Это свойство помогает морскому организму преодолевать давление толщи воды.
Он больше похоже на звёздчатый многогранник. Большинство феодарий живут на морской глубине и служат добычей коралловых рыбок. Но простейшее животное защищает себя двенадцатью иглами, выходящими из 12 вершин скелета. Он больше похоже на звёздчатый многогранник. Из всех многогранников с тем же числом граней икосаэдр имеет наибольший объём при наименьшей площади поверхности. Это свойство помогает морскому организму преодолевать давление толщи воды.
Интересно Икосаэдр оказался в центре внимания биологов в их спорах относительно формы вирусов. Икосаэдр оказался в центре внимания биологов в их спорах относительно формы вирусов. Вирус не может быть совершенно круглым, как считалось ранее. Чтобы установить его форму, брали различные многогранники, направляли на них свет под теми же углами, что и поток атомов на вирус. Оказалось, что только один многогранник дает точно такую же тень — икосаэдр.
Выполнила студентка группы Г 2-9 Н.Ю. Коблюк
Руководитель Е.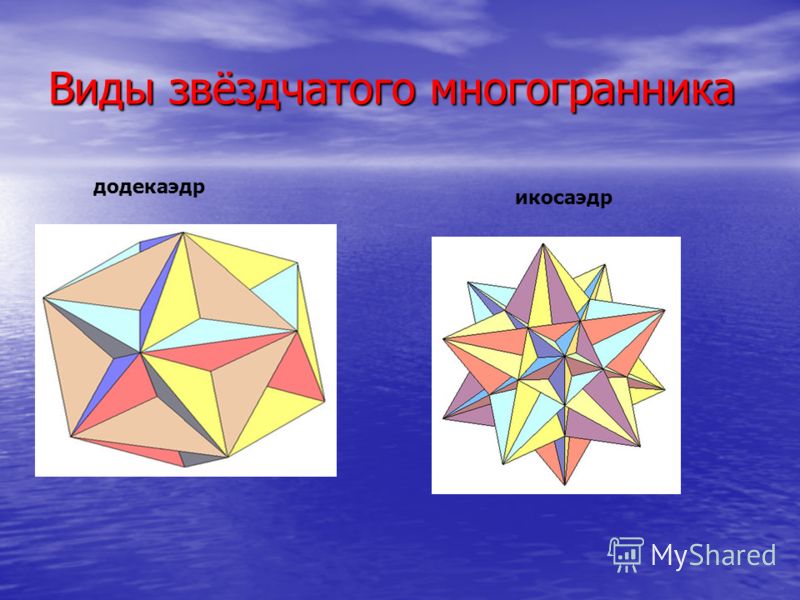 В. Морозова
В. Морозова
Тула 2010
«Математика владеет не только истиной, но и высшей красотой — красотой отточенной и строгой, возвышенно чистой и стремящейся к подлинному совершенству, которое свойственно лишь величайшим образцам искусства»
Бертран Рассел
Многогранник называется правильным , если:
- Он выпуклый.
- Все его грани являются равными правильными многоугольниками.
- В каждой его вершине сходится одинаковое число граней.
- Все его двухгранные углы равны.
Существует всего пять правильных многогранников :
- Тетраэдр (четырёхгранник)
- Куб (шестигранник)
- Октаэдр (восьмигранник)
- Додекаэдр (двенадцатигранник)
- Икосаэдр (двадцатигранник)
Правильный многогранник — это выпуклый многогранник с максимально возможной симметрией.
С древнейших времен наши представления о красоте связаны с симметрией. Наверное, этим объясняется интерес человека к многогранникам — удивительным символам симметрии, привлекавшим внимание выдающихся мыслителей.
История правильных многогранников уходит в глубокую древность. Изучением правильных многогранников занимались Пифагор и его ученики. Их поражала красота, совершенство, гармония этих фигур. Пифагорейцы считали правильные многогранники божественными фигурами и использовали в своих философских сочинениях.
Одно из древнейших упоминаний о правильных многогранниках находится в трактате Платона (427-347 до н. э.) «Тимаус».
Поэтому правильные многогранники также называются платоновыми телами. Каждый из правильных многогранников, а всего их пять, Платон ассоциировал с четырьмя «земными» элементами: земля (куб), вода (икосаэдр), огонь (тетраэдр), воздух (октаэдр), а также с «неземным» элементом — небом (додекаэдр).
Ко времени Платона в античной философии созрела концепция четырех элементов (стихий) – первооснов материального мира: огня , воздуха , воды и земли .
Форма куба – атомы земли, т.к. и земля, и куб отличаются неподвижностью и устойчивостью.
Форма икосаэдра – атомы воды, т.к. вода отличается своей текучестью, а из всех правильных тел икосаэдр – наиболее «катящийся».
Форма октаэдра – атомы воздуха, ибо воздух движется взад и вперед, и октаэдр, как бы направлен одновременно в разные стороны.
Форма тетраэдра – атомы огня, т.к. тетраэдр наиболее остр, кажется, что он мечется в разные стороны.
Платон вводит пятый элемент – «пятую сущность» — мировой эфир, атомам которого придается форма додекаэдра как наиболее близкому к шару.
Платоновыми телами называются правильные однородные выпуклые многогранники, то есть выпуклые многогранники, все грани и углы которых равны, причем грани — правильные многоугольники.
Платоновы тела — трехмерный аналог плоских правильных многоугольников. Однако между двумерным и трехмерным случаями есть важное отличие: существует бесконечно много различных правильных многоугольников, но лишь пять различных правильных многогранников.
около 429 – 347 гг до н.э.
выпуклый многогранник, грани которого являются правильными
многоугольниками с одним и тем же числом сторон и в каждой
вершине которого сходится одно и то же число ребер.
Икосаэдр
Тетраэдр
Октаэдр
Гексаэдр
Додекаэдр
Тело Платона
Геометрия грани
Число
Тетраэдр
Икосаэдр
Гексаэдр
Додекаэдр
Формула Эйлера Г + В – Р = 2
Поверхность тетраэдра состоит из четырех равносторонних треугольников, сходящихся в каждой вершине по три.
У правильного тетраэдра все грани являются равносторонними треугольниками, все двугранные углы при рёбрах и все трёхгранные углы при вершинах равны.
Свойства тетраэдра :
- В тетраэдр можно вписать октаэдр, притом четыре (из восьми) грани октаэдра будут совмещены с четырьмя гранями тетраэдра, все шесть вершин октаэдра будут совмещены с центрами шести рёбер тетраэдра.

- Тетраэдр с ребром х состоит из одного вписанного октаэдра (в центре) с ребром х/2 и четырёх тетраэдров (по вершинам) с ребром х/2.
- Тетраэдр можно вписать в куб двумя способами, притом четыре вершины тетраэдра будут совмещены с четырьмя вершинами куба.
Все шесть рёбер тетраэдра будут лежать на всех шести гранях куба и равны диагонали грани-квадрата.
- Тетраэдр можно вписать в икосаэдр, притом, четыре вершины тетраэдра будут совмещены с четырьмя вершинами икосаэдра.
Правильный многогранник
Правильный треугольник
Граней при вершине
Длина ребра
Площадь поверхности
Элементы симметрии:
Тетраэдр не имеет центра симметрии,
но имеет 3 оси симметрии и 6 плоскостей симметрии
Радиус описанной сферы:
Радиус вписанной сферы:
Площадь поверхности:
Объем тетраэдра:
Куб или гексаэдр — правильный многогранник, каждая грань которого представляет собой квадрат.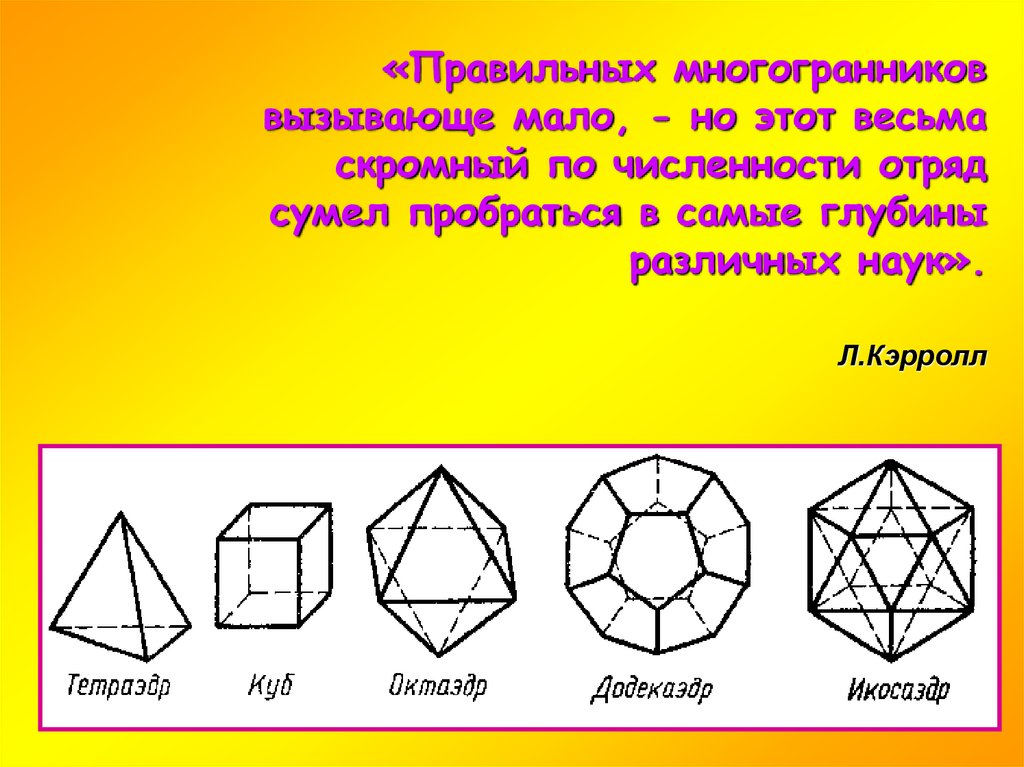 Частный случай параллелепипеда и призмы. Куб имеет шесть квадратных граней, сходящихся в каждой вершине по три.
Частный случай параллелепипеда и призмы. Куб имеет шесть квадратных граней, сходящихся в каждой вершине по три.
Свойства куба :
- В куб можно вписать тетраэдр двумя способами, притом четыре вершины тетраэдра будут совмещены с четырьмя вершинами куба. Все шесть рёбер тетраэдра будут лежать на всех шести гранях куба и равны диагонали грани-квадрата.
- Четыре сечения куба являются правильными шестиугольниками — эти сечения проходят через центр куба перпендикулярно четырём его диагоналям.
- В куб можно вписать октаэдр, притом все шесть вершин октаэдра будут совмещены с центрами шести граней куба.
- Куб можно вписать в октаэдр, притом все восемь вершин куба будут расположены в центрах восьми гранях октаэдра.
- В куб можно вписать икосаэдр, при этом, шесть взаимно параллельных рёбер икосаэдра будут расположены соответственно на шести гранях куба, остальные 24 ребра внутри куба, все двенадцать вершин икосаэдра будут лежать на шести гранях куба.

Правильный многогранник
Граней при вершине
Длина ребра
Площадь поверхности
Элементы симметрии:
Куб имеет центр симметрии — центр куба, 9 осей
симметрии и 9 плоскостей симметрии .
Радиус описанной сферы:
Радиус вписанной сферы:
Площадь поверхности куба:
Объем куба:
S = 6 a 2
V =a 3
Окта́эдр — один из пяти правильных многогранников.
Октаэдр имеет 8 граней (треугольных),
12 рёбер, 6 вершин (в каждой вершине сходятся 4 ребра).
Октаэдр имеет восемь треугольных граней, сходящихся в каждой вершине по четыре .
Свойства октаэдра :
- Октаэдр можно вписать в тетраэдр, притом четыре (из восьми) грани октаэдра будут совмещены с четырьмя гранями тетраэдра, все шесть вершин октаэдра будут совмещены с центрами шести рёбер тетраэдра.
- Октаэдр с ребром у состоит из 6 октаэдров (по вершинам) с ребром у:2 и 8 тетраэдров (по граням) с ребром у:2
- Октаэдр можно вписать в куб, притом все шесть вершин октаэдра будут совмещены с центрами шести граней куба.

- В октаэдр можно вписать куб, притом все восемь вершин куба будут расположены в центрах восьми гранях октаэдра.
Правильный многогранник
треугольник
Граней при вершине
Двойственный многогранник
Элементы симметрии:
Октаэдр имеет центр симметрии — центр октаэдра, 9 осей симметрии и 9 плоскостей симметрии.
Радиус описанной сферы:
Радиус вписанной сферы:
Площадь поверхности:
Объем октаэдра:
Икоса́эдр — правильный выпуклый многогранник, двадцатигранник, одно из Платоновых тел. Каждая из 20 граней представляет собой равносторонний треугольник. Число ребер равно 30, число вершин — 12. Поверхность икосаэдра состоит из двадцати равносторонних треугольников, сходящихся в каждой вершине по пять.
Свойства :
- Икосаэдр можно вписать в куб, при этом, шесть взаимно параллельных рёбер икосаэдра будут расположены соответственно на шести гранях куба, остальные 24 ребра внутри куба, все двенадцать вершин икосаэдра будут лежать на шести гранях куба
- В икосаэдр может быть вписан тетраэдр, притом, четыре вершины тетраэдра будут совмещены с четырьмя вершинами икосаэдра.

- Икосаэдр можно вписать в додекаэдр притом, вершины икосаэдра будут совмещены с центрами граней додекаэдра.
- В икосаэдр можно вписать додекаэдр притом, вершины додекаэдра будут совмещены с центрами граней икосаэдра.
Правильный многогранник
Правильный треугольник
Граней при вершине
Двойственный многогранник
додекаэдр
Элементы симметрии:
Икосаэдр имеет центр симметрии — центр икосаэдра, 15 осей симметрии и 15 плоскостей симметрии.
Радиус описанной сферы:
Радиус вписанной сферы:
Площадь поверхности:
Объем икосаэдра:
Додека́эдр (двенадцатигранник) — правильный многогранник, объёмная геометрическая фигура, составленная из двенадцати правильных пятиугольников. Каждая вершина додекаэдра является вершиной трёх правильных пятиугольников. Имеет двенадцать пятиугольных граней, сходящихся в вершинах по три.
Таким образом, додекаэдр имеет 12 граней (пятиугольных), 30 рёбер и 20 вершин (в каждой сходятся 3 ребра. Сумма плоских углов при каждой из 20 вершин равна 324°.
Сумма плоских углов при каждой из 20 вершин равна 324°.
Додекаэдр применяется как генератор случайных чисел (вместе с другими костями) в настольных ролевых играх.
Правильный многогранник
Правильный пятиугольник
Граней при вершине
Двойственный многогранник
икосаэдр
Элементы симметрии:
Додекаэдр имеет центр симметрии — центр додекаэдра, 15 осей симметрии и 15 плоскостей симметрии.
Радиус описанной сферы:
Радиус вписанной сферы:
Площадь поверхности:
Объем додекаэдра:
Правильные многогранники встречаются в живой природе. Например, скелет одноклеточного организма феодарии ( Circjgjnia icosahtdra ) по форме напоминает икосаэдр.
Чем же вызвана такая природная геометризация феодарий? По-видимому, тем, что из всех многогранников с тем же числом граней именно икосаэдр имеет наибольший объём при наименьшей площади поверхности. Это свойство помогает морскому организму преодолевать давление водной толщи.
Правильные многогранники – самые «выгодные» фигуры. И природа этим широко пользуется. Подтверждением тому служит форма некоторых кристаллов.
Взять хотя бы поваренную соль, без которой мы не можем обойтись. Известно, что она растворима в воде, служит проводником электрического тока. А кристаллы поваренной соли ( NaCl ) имеют форму куба.
При производстве алюминия пользуются алюминиево-калиевыми кварцами ( K [ Al ( SO 4 ) 2 ] 12 H 2 O ), монокристалл которых имеет форму правильного октаэдра.
Получение серной кислоты, железа, особых сортов цемента не обходится без сернистого колчедана ( FeS ). Кристаллы этого химического вещества имеют форму додекаэдра.
В разных химических реакциях применяется сурьменистый сернокислый натрий ( Na 5 ( SbO 4 ( SO 4 )) – вещество, синтезированное учёными. Кристалл сурьменистого сернокислого натрия имеет форму тетраэдра.
Кристалл сурьменистого сернокислого натрия имеет форму тетраэдра.
Последний правильный многогранник – икосаэдр передаёт форму кристаллов бора (В). В своё время бор использовался для создания полупроводников первого поколения.
Феодария
( Circjgjnia icosahtdra )
«Правильных многогранников вызывающе мало, но этот весьма скромный по численности отряд сумел пробраться в самые глубины различных наук»
Л. Кэрролл
Использовались материалы:
http://www.vschool.ru
http://center.fio.ru
http://gemsnet.ru
http://alzl.narod.ru
http://ru.wikipedia.org
Использовались
Многогранник поверхность, составленная из многоугольников и ограничивающих некоторое геометрическое тело. Многогранники бывают выпуклыми и не выпуклыми многоугольников Многогранник называется выпуклым, если он расположен по одну сторону плоскости каждого многоугольника на его поверхности
Октаэдр Окта́эдр (греч. οκτάεδρον, от греч. οκτώ, «восемь» и греч.έδρα «основание») один из пяти выпуклых правильных многогранников, так называемых Платоновых тел.греч. правильных многогранников Платоновых Октаэдр имеет 8 треугольных граней, 12 рёбер, 6 вершин, в каждой его вершине сходятся 4 ребра.
οκτάεδρον, от греч. οκτώ, «восемь» и греч.έδρα «основание») один из пяти выпуклых правильных многогранников, так называемых Платоновых тел.греч. правильных многогранников Платоновых Октаэдр имеет 8 треугольных граней, 12 рёбер, 6 вершин, в каждой его вершине сходятся 4 ребра.
Икосаэдр Икоса́эдр (от греч. εικοσάς двадцать; -εδρον грань, лицо, основание) правильный выпуклый многогранник, двадцатигранник, одно из Платоновых тел. Каждая из 20 граней представляет собой равносторонний треугольник. Число ребер равно 30, число вершин 12. Икосаэдр имеет 59 звёздчатых форм.греч.Платоновых телтреугольникзвёздчатых форм
Додекаэдр Додека́эдр (от греч. δώδεκα двенадцать и εδρον грань),двенадцатигранник правильный многогранник, составленный из двенадцати правильных пятиугольников. Каждая вершина додекаэдра является вершиной трёх правильных пятиугольников.греч.правильный многогранник правильных пятиугольников вершина Таким образом, додекаэдр имеет 12 граней (пятиугольных), 30 рёбер и 20 вершин (в каждой сходятся 3 ребра). Сумма плоских углов при каждой из 20 вершин равна 324°.углов
Сумма плоских углов при каждой из 20 вершин равна 324°.углов
Чтобы пользоваться предварительным просмотром презентаций создайте себе аккаунт (учетную запись) Google и войдите в него: https://accounts.google.com
Многогранник – это такое тело, поверхность которого состоит из конечного числа плоских многоугольников.
Правильные многогранники
Сколько существует правильных многогранников? — Как они определяются, какими свойствами обладают? -Где встречаются, имеют ли практическое применение?
Выпуклый многогранник называется правильным, если все его грани — равные правильные многоугольники и в каждой его вершине сходится одно и то же число ребер.
«эдра» — грань «тетра» — четыре гекса» — шесть «окта» — восемь «додека» — двенадцать «икоса» — двадцать Названия этих многогранников пришли из Древней Греции и в них указано число граней.
Название правильного многогранника Вид грани Число вершин ребер граней граней, сходящихся в одной вершине Тетраэдр Правильный треугольник 4 6 4 3 Октаэдр Правильный треугольник 6 12 8 4 Икосаэдр Правильный треугольник 12 30 20 5 Куб (гексаэдр) Квадрат 8 12 6 3 Додекаэдр Правильный пятиугольник 20 30 12 3 Данные о правильных многогранниках
Вопрос (проблема): Сколько существует правильных многогранников? Как установить их количество?
α n = (180 °(n -2)) : n При каждой вершине многогранника не меньше трех плоских углов, и их сумма должна быть меньше 360 ° . Форма граней Количество граней при одной вершине Сумма плоских углов при вершине многогранника Вывод о существовании многогранника α = 3 α = 4 α = 5 α = 6 α = 3 α = 4 α = 3 α = 4 α = 3
Форма граней Количество граней при одной вершине Сумма плоских углов при вершине многогранника Вывод о существовании многогранника α = 3 α = 4 α = 5 α = 6 α = 3 α = 4 α = 3 α = 4 α = 3
Л. Кэрролл
Великие математики древности Архимед Евклид Пифагор
Подробно описал свойства правильных многогранников древнегреческий ученый Платон. Именно поэтому правильные многогранники называются тела Платона
тетраэдр — огонь куб — земля октаэдр — воздух икосаэдр — вода додекаэдр — вселенная
Многогранники в науках о космосе и земле
Иоганн Кеплер (1571-1630) – немецкий астроном и математик. Один из создателей современной астрономии — открыл законы движения планет (законы Кеплера)
кубок Кеплера Космический
» Экосаэдро — додекаэдровая структура Земли «
Многогранники в искусстве и архитектуре
Альбрехт Дюрер (1471-1528) «Меланхолия»
Сальвадор Дали «Тайная Вечеря»
Современные архитектурные сооружения в виде многогранников
Александрийский маяк
Кирпичный многогранник швейцарского архитектора
Современное здание в Англии
Многогранники в природе ФЕОДАРИЯ
Пирит (сернистый колчедан) Монокристалл алюмокалиевых квасцов Кристаллы красной медной руды ПРИРОДНЫЕ КРИСТАЛЛЫ
Поваренная соль состоит из кристаллов в форме куба Минерал сильвин также имеет кристаллическую решетку в форме куба.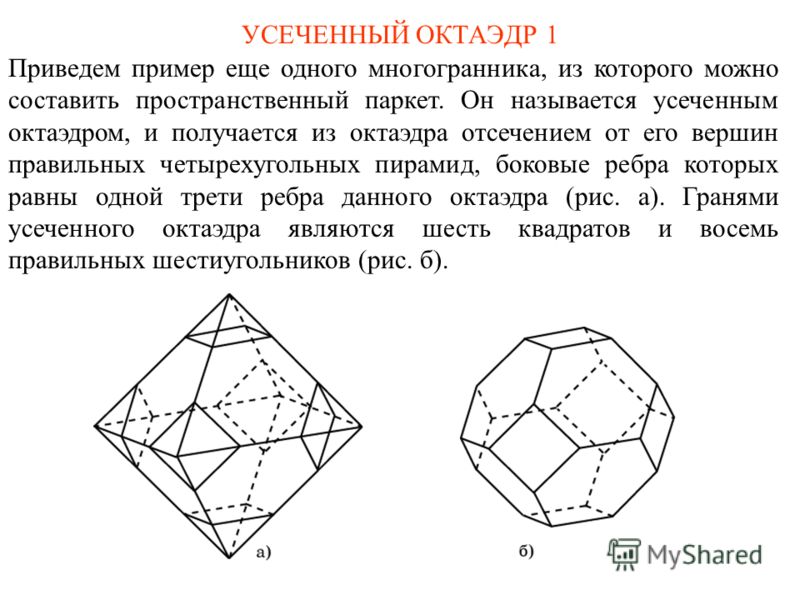 Молекулы воды имеют форму тетраэдра. Минерал куприт образует кристаллы в форме октаэдров. Кристаллы пирита имеют форму додекаэдра
Молекулы воды имеют форму тетраэдра. Минерал куприт образует кристаллы в форме октаэдров. Кристаллы пирита имеют форму додекаэдра
Алмаз В форме октаэдра кристаллизуются алмаз, хлорид натрия, флюорит, оливин и другие вещества.
Исторически первой формой огранки, появившейся в XIV веке стал октаэдр. Алмаз Шах Масса алмаза 88,7 карата
Задача Английская королева дала указание сделать огранку вдоль ребер алмаза золотой нитью. Но огранка не была сделана, так как ювелир не сумел рассчитать максимальную длину золотой нити, а сам алмаз ему не показали. Ювелиру были сообщены следующие данные: число вершин В=54, число граней Г=48, длина наибольшего ребра L= 4мм. Найти максимальную длину золотой нити.
Правильный многогранник Число Граней Вершин Рёбер Тетраэдр 4 4 6 Куб 6 8 12 Октаэдр 8 6 12 Додекаэдр 12 20 30 Икосаэдр 20 12 30 Исследовательская работа «Формула Эйлера»
Теорема Эйлера. Для любого выпуклого многогранника В + Г — 2 = Р где В – число вершин, Г – число граней, Р – число ребер этого многогранника.
ФИЗМИНУТКА!
Задача Найдите угол между двумя ребрами правильного октаэдра, которые имеют общую вершину, но не принадлежат одной грани.
Задача Найти высоту правильного тетраэдра с ребром 12 см.
Кристалл имеет форму октаэдра, состоящего из двух правильных пирамид с общим основанием, ребро основания пирамиды 6 см. высота октаэдра 8 см. Найдите площадь боковой поверхности кристалла
Площадь поверхности Тетраэдр Икосаэдр Додекаэдр Гексаэдр Октаэдр
Задание на дом: mnogogranniki.ru Пользуясь развертками изготовить модели 1-го правильного многогранника со стороной 15 см, 1-го полуправильного многогранника
Спасибо за работу!
Правильные многогранники: элементы, симметрия и площадь
Геометрия прекрасна тем, что, в отличие от алгебры, где не всегда понятно, что и зачем считаешь, дает наглядность объекта. Этот удивительный мир различных тел украшают собой правильные многогранники.
Общие сведения о правильных многогранниках
По мнению многих, правильные многогранники, или как их еще называют Платоновы тела, обладают неповторимыми свойствами.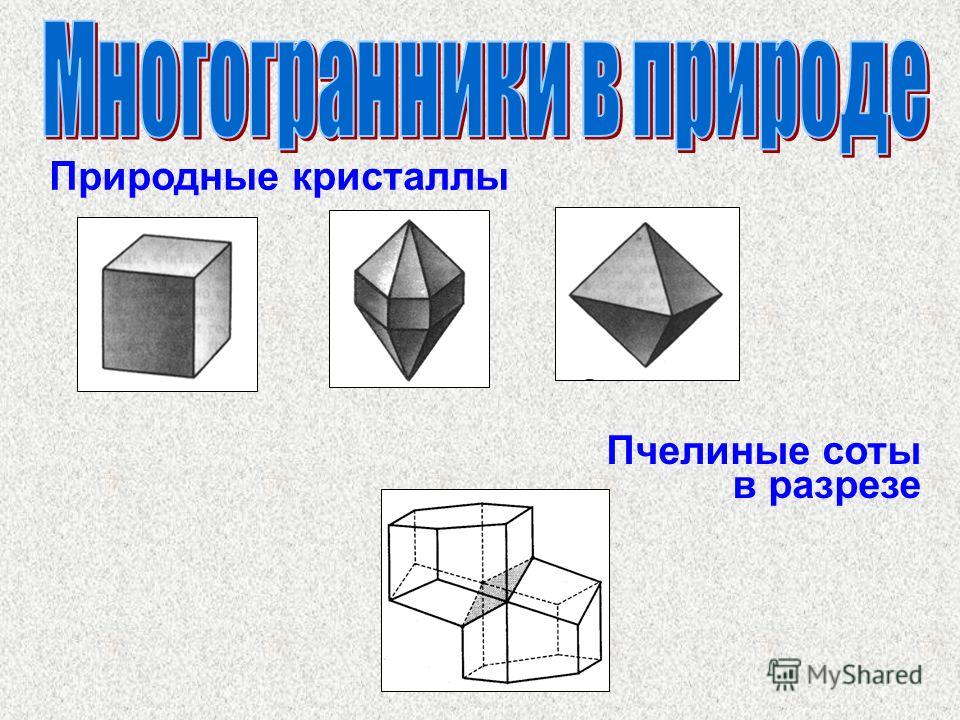 С этими объектами связано несколько научных гипотез. Когда начинаешь изучать данные геометрические тела, понимаешь, что практически ничего не знаешь о таком понятии, как правильные многогранники. Презентация этих объектов в школе не всегда проходит интересно, поэтому многие даже и не помнят, как они называются. В памяти большинства людей остается только куб. Ни одни тела в геометрии не обладают таким совершенством, как правильные многогранники. Все названия этих геометрических тел произошли из Древней Греции. Они означают количество граней: тетраэдр — четырехгранный, гексаэдр — шестигранный, октаэдр — восьмигранный, додекаэдр – двенадцатигранный, икосаэдр — двадцатигранный. Все эти геометрические тела занимали важнейшее место в концепции Платона о мироздании. Четыре из них олицетворяли стихии или сущности: тетраэдр — огонь, икосаэдр — воду, куб — землю, октаэдр — воздух. Додекаэдр воплощал все сущее. Он считался главным, поскольку был символом мироздания.
С этими объектами связано несколько научных гипотез. Когда начинаешь изучать данные геометрические тела, понимаешь, что практически ничего не знаешь о таком понятии, как правильные многогранники. Презентация этих объектов в школе не всегда проходит интересно, поэтому многие даже и не помнят, как они называются. В памяти большинства людей остается только куб. Ни одни тела в геометрии не обладают таким совершенством, как правильные многогранники. Все названия этих геометрических тел произошли из Древней Греции. Они означают количество граней: тетраэдр — четырехгранный, гексаэдр — шестигранный, октаэдр — восьмигранный, додекаэдр – двенадцатигранный, икосаэдр — двадцатигранный. Все эти геометрические тела занимали важнейшее место в концепции Платона о мироздании. Четыре из них олицетворяли стихии или сущности: тетраэдр — огонь, икосаэдр — воду, куб — землю, октаэдр — воздух. Додекаэдр воплощал все сущее. Он считался главным, поскольку был символом мироздания.
Обобщение понятия многогранника
Многогранником является совокупность конечного числа многоугольников такая, что:
- каждая из сторон любого из многоугольников является одновременно и стороной только одного другого многоугольника по той же стороне;
- от каждого из многоугольников можно дойти до других переходя по смежным с ним многоугольникам.

Многоугольники, составляющие многогранник, представляют собой его грани, а их стороны — ребра. Вершинами многогранников являются вершины многоугольников. Если под понятием многоугольник понимают плоские замкнутые ломаные, то приходят к одному определению многогранника. В том случае, когда под этим понятием подразумевают часть плоскости, что ограничена ломаными линиями, то следует понимать поверхность, состоящую из многоугольных кусочков. Выпуклым многогранником называют тело, лежащее по одну сторону плоскости, прилегающей к его грани.
Другое определение многогранника и его элементов
Многогранником называют поверхность, состоящую из многоугольников, которая ограничивает геометрическое тело. Они бывают:
- невыпуклыми;
- выпуклыми (правильные и неправильные).
Правильный многогранник — это выпуклый многогранник с максимальной симметрией. Элементы правильных многогранников:
- тетраэдр: 6 ребер, 4 грани, 5 вершин;
- гексаэдр (куб): 12, 6, 8;
- додекаэдр: 30, 12, 20;
- октаэдр: 12, 8, 6;
- икосаэдр: 30, 20, 12.

Теорема Эйлера
Она устанавливает связь между числом ребер, вершин и граней, топологически эквивалентных сфере. Складывая количество вершин и граней (В + Г) у различных правильных многогранников и сравнивая их с количеством ребер, можно установить одну закономерность: сумма количества граней и вершин равняется числу ребер (Р), увеличенному на 2. Можно вывести простую формулу:
- В + Г = Р + 2.
Эта формула верна для всех выпуклых многогранников.
Основные определения
Понятие правильного многогранника невозможно описать одним предложением. Оно более многозначное и объемное. Чтобы тело было признано таковым, необходимо, чтобы оно отвечало ряду определений. Так, геометрическое тело будет являться правильным многогранником при выполнении таких условий:
- оно выпуклое;
- одинаковое количество ребер сходится в каждой из его вершин;
- все грани его — правильные многоугольники, равные друг другу;
- все двугранные углы его равны.

Свойства правильных многогранников
Существует 5 разных типов правильных многогранников:
- Куб (гексаэдр) — у него плоский угол при вершине составляет 90°. Он имеет 3-гранный угол. Сумма плоских углов у вершины составляет 270°.
- Тетраэдр — плоский угол при вершине — 60°. Он имеет 3-гранный угол. Сумма плоских углов у вершины — 180°.
- Октаэдр — плоский угол при вершине — 60°. Он имеет 4-гранный угол. Сумма плоских углов у вершины — 240°.
- Додекаэдр — плоский угол при вершине 108°. Он имеет 3-гранный угол. Сумма плоских углов у вершины — 324°.
- Икосаэдр — у него плоский угол при вершине — 60°. Он имеет 5-гранный угол. Сумма плоских углов у вершины составляет 300°.
Площадь правильных многогранников
Площадь поверхности этих геометрических тел (S) вычисляется, как площадь правильного многоугольника, умноженная на количество его граней (G):
- S = (a : 2) х 2G ctg π/p.
Объем правильного многогранника
Эта величина вычисляется путем умножения объема правильной пирамиды, в основании которой находится правильный многоугольник, на число граней, а высота ее является радиусом вписанной сферы (r):
- V = 1 : 3rS.

Объемы правильных многогранников
Как и любое другое геометрическое тело, правильные многогранники имеют различные объемы. Ниже представлены формулы, по которым можно их вычислить:
- тетраэдр: α х 3√2 : 12;
- октаэдр: α х 3√2 : 3;
- икосаэдр; α х 3;
- гексаэдр (куб): 5 х α х 3 х (3 + √5) : 12;
- додекаэдр: α х 3 (15 + 7√5) : 4.
Элементы правильных многогранников
Гексаэдр и октаэдр являются дуальными геометрическими телами. Иными словами, они могут получиться друг из друга в том случае, если центр тяжести грани одного принимается за вершину другого, и наоборот. Также дуальными являются икосаэдр и додекаэдр. Сам себе дуален только тетраэдр. По способу Евклида можно получить додекаэдр из гексаэдра с помощью построения «крыш» на гранях куба. Вершинами тетраэдра будут любые 4 вершины куба, не смежные попарно по ребру. Из гексаэдра (куба) можно получить и другие правильные многогранники. Несмотря на то что правильных многоугольников есть бесчисленное множество, правильных многогранников существует всего 5.
Радиусы правильных многоугольников
С каждым из этих геометрических тел связаны 3 концентрические сферы:
- описанная, проходящая через его вершины;
- вписанная, касающаяся каждой его грани в центре ее;
- срединная, касающаяся всех ребер в середине.
Радиус сферы описанной рассчитывается по такой формуле:
- R = a : 2 х tg π/g х tg θ : 2.
Радиус сферы вписанной вычисляется по формуле:
- R = a : 2 х ctg π/p х tg θ : 2,
где θ — двухгранный угол, который находится между смежными гранями.
Радиус сферы срединной можно вычислить по следующей формуле:
- ρ = a cos π/p : 2 sin π/h,
где h величина = 4,6 ,6,10 или 10. Отношение описанных и вписанных радиусов симметрично относительно p и q. Оно рассчитывается по формуле:
- R/r = tg π/p х tg π/q.
Симметрия многогранников
Симметрия правильных многогранников вызывает основной интерес к этим геометрическим телам. Под ней понимают такое движение тела в пространстве, которое оставляет одно и то же количество вершин, граней и ребер. Другими словами, под действием преобразования симметрии ребро, вершина, грань или сохраняет свое первоначальное положение, или перемещается в исходное положение другого ребра, другой вершины или грани.
Под ней понимают такое движение тела в пространстве, которое оставляет одно и то же количество вершин, граней и ребер. Другими словами, под действием преобразования симметрии ребро, вершина, грань или сохраняет свое первоначальное положение, или перемещается в исходное положение другого ребра, другой вершины или грани.
Элементы симметрии правильных многогранников свойственны всем видам таких геометрических тел. Здесь речь ведется о тождественном преобразовании, которое оставляет любую из точек в исходном положении. Так, при повороте многоугольной призмы можно получить несколько симметрий. Любая из них может быть представлена как произведение отражений. Симметрию, которая является произведением четного количества отражений, называют прямой. Если же она является произведением нечетного количества отражений, то ее называют обратной. Таким образом, все повороты вокруг прямой представляют собой прямую симметрию. Любое отражение многогранника — это обратная симметрия.
Чтобы лучше разобраться в элементах симметрии правильных многогранников, можно взять пример тетраэдра. Любая прямая, которая будет проходить через одну из вершин и центр этой геометрической фигуры, будет проходить и через центр грани, противоположной ей. Каждый из поворотов на 120 и 240° вокруг прямой принадлежит к множественному числу симметрий тетраэдра. Поскольку у него по 4 вершины и грани, то получается всего восемь прямых симметрий. Любая из прямых, проходящих через середину ребра и центр этого тела, проходит через середину его противоположного ребра. Любой поворот на 180°, называемый полуоборотом, вокруг прямой является симметрией. Поскольку у тетраэдра есть три пары ребер, то получится еще три прямые симметрии. Исходя из вышеизложенного, можно сделать вывод, что общее число прямых симметрий, и в том числе тождественное преобразование, будет доходить до двенадцати. Других прямых симметрий у тетраэдра не существует, но при этом у него есть 12 обратных симметрий. Следовательно, тетраэдр характеризуется всего 24 симметриями. Для наглядности можно построить модель правильного тетраэдра из картона и убедиться, что это геометрическое тело действительно имеет всего 24 симметрии.
Любая прямая, которая будет проходить через одну из вершин и центр этой геометрической фигуры, будет проходить и через центр грани, противоположной ей. Каждый из поворотов на 120 и 240° вокруг прямой принадлежит к множественному числу симметрий тетраэдра. Поскольку у него по 4 вершины и грани, то получается всего восемь прямых симметрий. Любая из прямых, проходящих через середину ребра и центр этого тела, проходит через середину его противоположного ребра. Любой поворот на 180°, называемый полуоборотом, вокруг прямой является симметрией. Поскольку у тетраэдра есть три пары ребер, то получится еще три прямые симметрии. Исходя из вышеизложенного, можно сделать вывод, что общее число прямых симметрий, и в том числе тождественное преобразование, будет доходить до двенадцати. Других прямых симметрий у тетраэдра не существует, но при этом у него есть 12 обратных симметрий. Следовательно, тетраэдр характеризуется всего 24 симметриями. Для наглядности можно построить модель правильного тетраэдра из картона и убедиться, что это геометрическое тело действительно имеет всего 24 симметрии.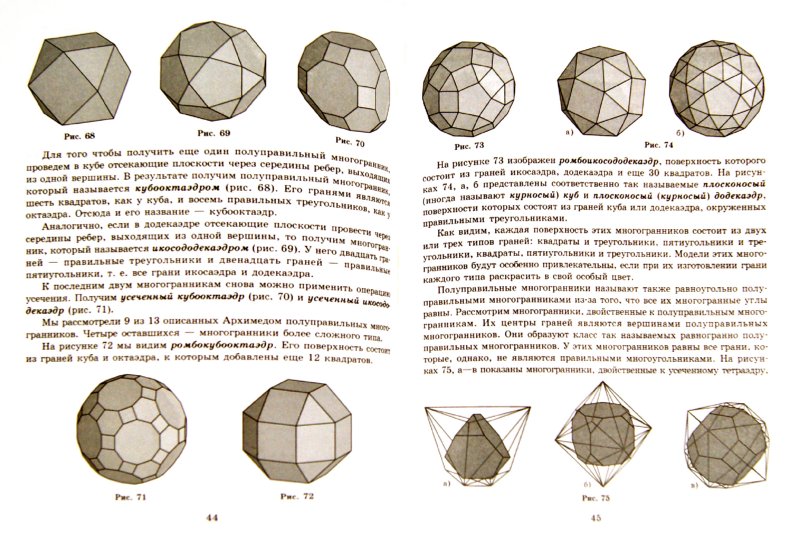
Додекаэдр и икосаэдр — наиболее близкие к сфере тела. Икосаэдр обладает наибольшим числом граней, наибольшим двугранным углом и плотнее всего может прижаться к вписанной сфере. Додекаэдр обладает наименьшим угловым дефектом, наибольшим телесным углом при вершине. Он может максимально заполнить свою описанную сферу.
Развертки многогранников
Правильные многогранники развертки, которых мы все склеивали в детстве, имеют много понятий. Если есть совокупность многоугольников, каждая сторона которых отождествлена с только одной стороной многогранника, то отождествление сторон должно соответствовать двум условиям:
- от каждого многоугольника можно перейти по многоугольникам, имеющим отождествленную сторону;
- отождествляемые стороны должны иметь одинаковую длину.
Именно совокупность многоугольников, которые удовлетворяют эти условия, и называется разверткой многогранника. Каждое из этих тел имеет их несколько. Так, например, у куба их насчитывается 11 штук.
Полуправильные многогранники
Аннотация. Статья посвящена полуправильным многогранникам и их классификации.
Ключевые слова: архимедовы тела, каталановы тела, полуправильные многогранники
Человек проявляет интерес к многогранникам на протяжении всей своей сознательной деятельности — от маленького ребенка, играющего с кубиками, до взрослого человека.
Иоганн Кеплер называл куб «родителем» всех правильных многогранников. На основе куба он смог построить все другие виды правильных многогранников.
Правильные многогранники окружают нас везде, кажется что любая вещь состоит из правильных многогранников. А что же такое полуправильные многогранники и почему они так редко используются в окружающем мире?
Впервые многогранники такое типа открыл Архимед. Им подробно описаны 13 многогранников, которые позже в честь великого ученого были названы телами Архимеда. Архимедовы тела частично получаются из Платоновых тел в результате их усечения. Усеченное тело есть не что иное, как тело с отрезанной верхушкой. Так могут быть получены первые пять архимедовых тел: усеченный тетраэдр (рис.1), усеченный октаэдр (рис.2), усеченный икосаэдр (рис.3), усеченный куб (рис.4), усеченный додекаэдр (рис.5). Вторая группа архимедовых тел представлена двумя многогранниками, являющимися результатом пересечения двух Платоновых тел подходящих размеров и расположенных так, что их центры совпадают. Это кубооктаэдр (рис.6) — результат пересечения куба и октаэдра и икос, икосододекаэдр (рис.7) — результат пересечения икосаэдра и додекаэдра. В результате усечения кубооктаэдра и икосододекаэдра получены следующие два многогранника – ромбокубооктаэдр (рис.8) и ромбоикосододекаэдр (рис.9). Дальнейшее видоизменения могут превратить их в два других многогранника — усеченный кубооктаэдр (рис.10) и усеченный икосододекаэдр (рис.11). Последние два архимедовых тел — «курносый» куб (рис.
Архимедовы тела частично получаются из Платоновых тел в результате их усечения. Усеченное тело есть не что иное, как тело с отрезанной верхушкой. Так могут быть получены первые пять архимедовых тел: усеченный тетраэдр (рис.1), усеченный октаэдр (рис.2), усеченный икосаэдр (рис.3), усеченный куб (рис.4), усеченный додекаэдр (рис.5). Вторая группа архимедовых тел представлена двумя многогранниками, являющимися результатом пересечения двух Платоновых тел подходящих размеров и расположенных так, что их центры совпадают. Это кубооктаэдр (рис.6) — результат пересечения куба и октаэдра и икос, икосододекаэдр (рис.7) — результат пересечения икосаэдра и додекаэдра. В результате усечения кубооктаэдра и икосододекаэдра получены следующие два многогранника – ромбокубооктаэдр (рис.8) и ромбоикосододекаэдр (рис.9). Дальнейшее видоизменения могут превратить их в два других многогранника — усеченный кубооктаэдр (рис.10) и усеченный икосододекаэдр (рис.11). Последние два архимедовых тел — «курносый» куб (рис. 12) и «курносый» додекаэдр (рис.13). Термин курносый означает, что каждую грань многогранника окружили треугольники, что каждое ребро заменили парой треугольников, а в каждой вершине добавили еще один многоугольник.
12) и «курносый» додекаэдр (рис.13). Термин курносый означает, что каждую грань многогранника окружили треугольники, что каждое ребро заменили парой треугольников, а в каждой вершине добавили еще один многоугольник.
Прародителем каждого из 13-ти полуправильных многогранников является один из пяти Платоновых многогранников(рис.14) путем отсечения вершин. При дальнейшем усечении полученных тел мы получаем правильные многогранники, поэтому тел Архимеда только 13.
Каталановы тела
Двойственные архимедовым телам, так называемые каталановы тела, имеют конгруэнтные грани, равные двугранные углы и правильные многогранные углы. Каталановы тела тоже называют полуправильными многогранниками. В этом случае полуправильными многогранниками считается совокупность архимедовых и каталановых тел. Архимедовы тела являются полуправильными многогранниками в том смысле, что их грани — правильные многоугольники, но они не одинаковы, а Каталановы — в том смысле, что их грани одинаковы, но не являются правильными многоугольниками; при этом для тех и других сохраняется условие одного из типов пространственной симметрии: тетраэдрического, октаэдрического или икосаэдрического.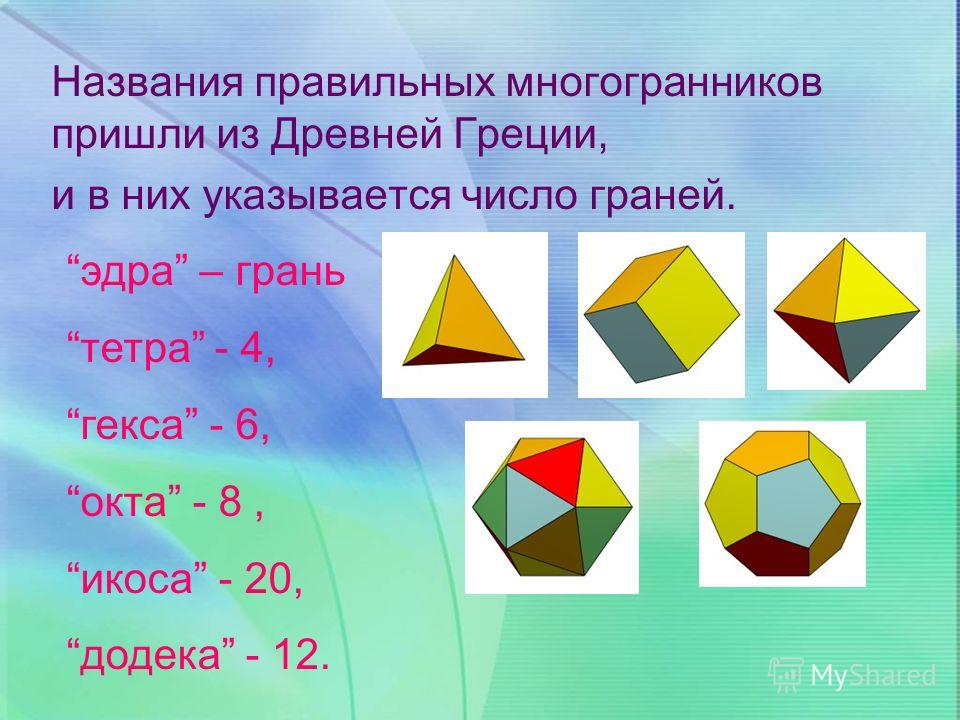
То есть, полуправильными в этом случае называются тела, у которых отсутствует только одно из первых двух из следующих свойств правильных тел:
- Все грани являются правильными многоугольниками;
- Все грани одинаковы;
- Тело относится к одному из трёх существующих типов пространственной симметрии.
Архимедовы — тела, у которых отсутствует второе свойство, у каталановых отсутствует первое, третье свойство сохраняется для обоих видов тел.
Существует 13 архимедовых тел, два из которых (курносый куб и курносый додекаэдр) не являются зеркально-симметричными и имеют левую и правую формы. Соответственно, существует 13 каталановых тел.
Систематизация названий
1. Усеченный октаэдр:
Многие названия созданы на основе греческих приставок, означающих количество граней и корня -едр, означающего грань.
(-hedron- буквально значит место).
Октаэдр (от греч. οκτώ, «восемь»)
2. Усеченный икосододекаэдр:
икосо- (ikosi-) значит 20
додека- значит 2+10
-едр, означает грань
усечение (truncate) отсечение угла многогранника вокруг его вершины
3. Усеченный куб:
Усеченный куб:
усечение (truncate) отсечение угла многогранника вокруг его вершины
4. Усеченный икосаэдр:
усечение (truncate) отсечение угла многогранника вокруг его вершины
икосо- (ikosi-) значит 20
-едр, означает грань
5. Усеченный додекаэдр:
Додека — значит 2+10 и используется для описания двенадцатигранника.
-едр, означает грань
усечение (truncate) отсечение угла многогранника вокруг его вершины
6. Курносый додекаэдр:
Додека — значит 2+10 и используется для описания двенадцатигранника.
7. Усеченный тетраэдр:
тетра- (tetra) – четыре.
8. Икосододекаэдр:
Додека — значит 2+10 и используется для описания двенадцатигранника.
икосо- (ikosi-) значит 20
9. Курносый куб:
10. Кубооктаэдр:
Октаэдр (от греч. οκτώ, «восемь»)
11. Усеченный кубооктаэдр:
усечение (truncate) отсечение угла многогранника вокруг его вершины
Октаэдр (от греч. οκτώ, «восемь»)
12. Ромбокубооктаэдр:
Приставки могут описывать форму граней, чтобы устранять противоречия между двумя многогранниками с одинаковым количеством граней.
13. Ромбоикосододекаэдр:
икосо- (ikosi-) значит 20
Додека — значит 2+10 и используется для описания двенадцатигранника.
Полуправильные многогранники в архитектуре
Национальная библиотека Беларуси(рис.15). Форма книгохранилища — ромбокубооктаэдр.
Библиотека — самый крупный из архитектурных ромбокубооктаэдров, возведенных в мире в настоящее время. Его высота составляет 73,6 м (23 этажа), а вес — 115 000 тонн.
Повторить в архитектуре сложные многогранники (особенно, архимедовы тела — к которым, в том числе, относится и ромбокубооктаэдр) действительно нелегко. И если случается, то в меньшем масштабе, чем Нацбиблиотека, и усеченной форме.
Благодаря оригинальному архитектурному решению в новом здании НББ стало возможным гармонично совмещать искусственные и естественные материалы для отделки интерьеров, создать особый световой колорит во внутреннем пространстве библиотеки за счет сочетания естественного света с искусственным освещением и обеспечить психологический комфорт посетителей и сотрудников
Рис. 16
16
Музей архитектуры Тойо Ито(рис.16) на острове Омишима (Япония) — в основе дизайна музея лежат геометрические фигуры: октаэдр, тетраэдр и кубооктаэдр.
Рис.17
Здание Международного экономического комитета в Киеве(рис.17), купол конференц-зала своими гранями образует икосододекаэдр.
Рис.18
Ботанический сад «Эдем»(рис.18) в Корнуолле (Великобритания) был построен в 2001 году на месте выработанного мелового карьера, а для конструкций сводов использовались формы шестигранных сот. А это еще один вид многогранников — усеченный икосаэдр. Состоит из 12-ти пятиугольников и 20-ти шестиугольников.
Рис.19
Усеченная пирамида пользуется популярностью у современных архитекторов. Например, в Индианополисе (США) в 1972 году закончили строительство офисного комплекса из трех зданий, который так и назвали — The Pyramids(рис.19). Сейчас в нем расположен Институт искусства Индианополиса.
Полуправильные многогранники в привычных вещах
Кресло Hedronics (рис. 20) разработано известным немецким архитектором Даниелем Дендра (Баухаус) специально для недели российского дизайна Sretenka Design Week. В основе форм кресла лежит многогранник производный от плосконосого куба. Подобно оригами, кресло Hedronics выполняется из цельного листа металла и воплощает математическую гармонию строгих геометрических форм. Кресло может быть выполнено из цельного листа металла или из листа с декоративной перфорацией. Перфорированное кресло весит немного и выглядит наполненным воздушными пузырьками.
20) разработано известным немецким архитектором Даниелем Дендра (Баухаус) специально для недели российского дизайна Sretenka Design Week. В основе форм кресла лежит многогранник производный от плосконосого куба. Подобно оригами, кресло Hedronics выполняется из цельного листа металла и воплощает математическую гармонию строгих геометрических форм. Кресло может быть выполнено из цельного листа металла или из листа с декоративной перфорацией. Перфорированное кресло весит немного и выглядит наполненным воздушными пузырьками.
Рис.21
Всемирно известный художник и дизайнер из Дании Олафур Элиассон, выставка которого проходит сейчас в Tate Modern, создал новую световую инсталляцию Your Sound Galaxy (рис.21). Работа состоит из 27 многогранников, свисающих с потолка в виде двух концентрических кругов. Каждая объемная фигура снабжена светодиодом, который освещает пространство сквозь стыки составляющих частей многогранника.
Инсталляцию Your Sound Galaxy нельзя назвать такой прогрессивной и социально важной, однако она, как и многие другие работы Элиассона, выглядит очень загадочно и меняет пространство с помощью света.
Рис.22 Сравнение усечённого икосаэдра(слева) с футбольным мячом
Конструкция из этих 32 многоугольников называется усечённый икосаэдр(рис.22) — достаточно близкая к шару геометрическая фигура, компромисс между несферичностью и количеством швов на покрышке. Сферическая форма придаётся мячу за счёт давления воздуха, закачанного внутрь.
Рис.23
Флористы повинуясь законам математики создают гармоничные букеты на основе полуправильных многогранников(рис.23). На приведенной фотографии букет состоит из элементов двух типов: соприкасающихся крупных роз и заполняющих просветы мелких цветов. В такой форме букета угадывается усеченный додекаэдр, состоящий из 20треугольников и 12десятиугольников.
Ссылки на источники
- Каченовский М.И. Математический практикум по моделированию.-1959.-190с.
- Мотульский Р.С. Национальная библиотека Беларуси: новое здание – новая концепция развития / Национальная библиотека Беларуси.
 – Минск, 2007. – 322 с.
– Минск, 2007. – 322 с. - Смирнов В.А., Смирнова И.М., Ященко И.В. Наглядная геометрия.-М.:МЦНМО, 2013 -272с
- Смирнов В.А., Смирнова И.М., Ященко И.В. Наглядная геометрия. Рабочая тетрадь №4. М.:МЦНМО, 2012 -88с
- Смирнова И., Смирнов В. Что такое «Полуправильный многогранник» Учебно-методическая газета «Математика».- 2007 .-№16-с.23-26
- Тиморин В.А. Комбинаторика выпуклых многогранников.-М.: МЦНМО, 2002.-16с.
- Geometryim.ru
- Arhimedgeom.ru
- Icosogeom.ru
- ru.wikipedia.org/
Симметрия | Бесплатный полнотекстовый | Правильные и неправильные киральные многогранники из диаграмм Кокстера через кватернионы
1. Введение
В фундаментальной физике хиральность играет очень важную роль. Спинор Вейля, описывающий безмассовую частицу Дирака, находится либо в левом, либо в правом состоянии. Такие состояния не могут быть преобразованы друг в друга с помощью собственных преобразований Лоренца.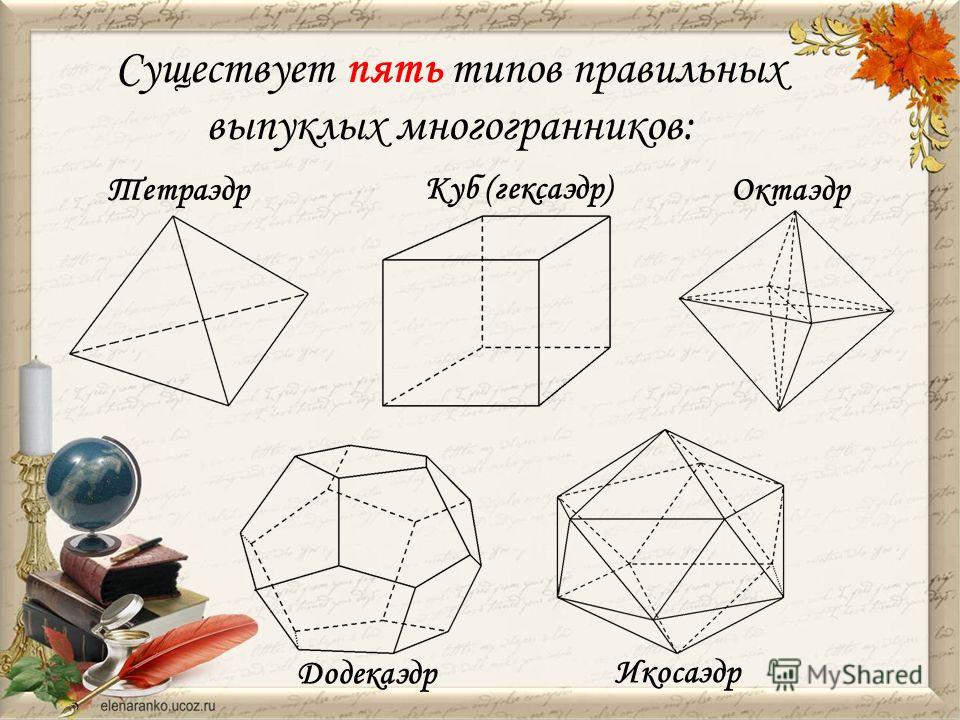 Хиральность — это четко определенное квантовое число для безмассовых частиц. Группы Кокстера и их орбиты [1], полученные из диаграмм Кокстера, описывают молекулярные структуры [2], вирусные симметрии [3,4], кристаллографические и квазикристаллографические материалы [5,6,7]. Хиральность — очень интересная тема в молекулярной химии. Некоторые молекулярные структуры ориентированы либо влево, либо вправо. В трехмерном евклидовом пространстве хиральность можно определить следующим образом: если твердое тело не может быть преобразовано в свое зеркальное отображение с помощью собственных изометрий (собственных вращений, перемещений и их композиций), оно называется хиральным объектом. По этой причине киральные объекты лишены плоскостной и/или центральной инверсионной симметрии. В двух более ранних публикациях [8,9] мы изучили симметрии платоново-архимедовых тел и их двойственных тел — каталонских тел и построили их вершины. Два архимедовых тела, курносый куб и курносый додекаэдр, а также их двойственные формы являются киральными многогранниками, симметрии которых являются собственными вращательными подгруппами группы октаэдра и группы икосаэдра соответственно.
Хиральность — это четко определенное квантовое число для безмассовых частиц. Группы Кокстера и их орбиты [1], полученные из диаграмм Кокстера, описывают молекулярные структуры [2], вирусные симметрии [3,4], кристаллографические и квазикристаллографические материалы [5,6,7]. Хиральность — очень интересная тема в молекулярной химии. Некоторые молекулярные структуры ориентированы либо влево, либо вправо. В трехмерном евклидовом пространстве хиральность можно определить следующим образом: если твердое тело не может быть преобразовано в свое зеркальное отображение с помощью собственных изометрий (собственных вращений, перемещений и их композиций), оно называется хиральным объектом. По этой причине киральные объекты лишены плоскостной и/или центральной инверсионной симметрии. В двух более ранних публикациях [8,9] мы изучили симметрии платоново-архимедовых тел и их двойственных тел — каталонских тел и построили их вершины. Два архимедовых тела, курносый куб и курносый додекаэдр, а также их двойственные формы являются киральными многогранниками, симметрии которых являются собственными вращательными подгруппами группы октаэдра и группы икосаэдра соответственно. Неправильные, нехиральные многогранники обсуждались ранее [10]. Киральные многогранники вообще изучались в контексте абстрактной комбинаторной формы [11,12,13,14]. Киральные архимедовы тела, курносый куб, курносый додекаэдр и их двойники были построены с использованием нескольких других методов [15,16], но кажется, что следующий метод ранее не изучался в этом контексте.
Неправильные, нехиральные многогранники обсуждались ранее [10]. Киральные многогранники вообще изучались в контексте абстрактной комбинаторной формы [11,12,13,14]. Киральные архимедовы тела, курносый куб, курносый додекаэдр и их двойники были построены с использованием нескольких других методов [15,16], но кажется, что следующий метод ранее не изучался в этом контексте.
Мы следуем систематическому методу построения киральных многогранников. Пусть G — граф Кокстера ранга 3, где W(G)+ представляет подгруппу собственных вращений группы Кокстера W(G). Для курносого куба и курносого додекаэдра графы Кокстера — это B3 и h4 соответственно. Чтобы описать общую технику, мы сначала начнем с более простых диаграмм Кокстера A 1 ⊕ A 1 ⊕ A 1 и A3, хотя они описывают ахиральные многогранники, такие как семейства правильных и неправильных тетраэдров и икосаэдров соответственно. Мы явно показываем, что ахиральные многогранники обладают большей собственной вращательной симметрией, превращая их в свои зеркальные отражения. Организуем работу следующим образом. В разделе 2 мы вводим кватернионы и строим группы Кокстера в терминах кватернионов [17]. Расширим группу W (A 1 ⊕ A 1 ⊕ A 1 ) в октаэдрическую группу по группе симметрии Sym(3) диаграммы Кокстера A 1 ⊕ A 1 ⊕ A 1
Организуем работу следующим образом. В разделе 2 мы вводим кватернионы и строим группы Кокстера в терминах кватернионов [17]. Расширим группу W (A 1 ⊕ A 1 ⊕ A 1 ) в октаэдрическую группу по группе симметрии Sym(3) диаграммы Кокстера A 1 ⊕ A 1 ⊕ A 1
7 В разделе 3 мы получаем подгруппу собственных вращений группы Кокстера W (A
1 ⊕ A 1 ⊕ A 1 ) и определяем вершины неправильного тетраэдра. В разделе 4 мы обсуждаем аналогичную проблему для диаграммы Кокстера-Дынкина A3, ведущей к икосаэдру, и снова доказываем, что она может быть преобразована группой W(B 3 ) + к своему зеркальному отображению, из чего следует, что ни тетраэдр, ни икосаэдр не являются киральными телами. Мы сосредоточимся на неправильных икосаэдрах, построенных либо собственной тетраэдрической группой, либо ее расширенной пиритоэдрической группой, и построим связанные с ними двойные твердые тела — тетраид и пиритоэдр.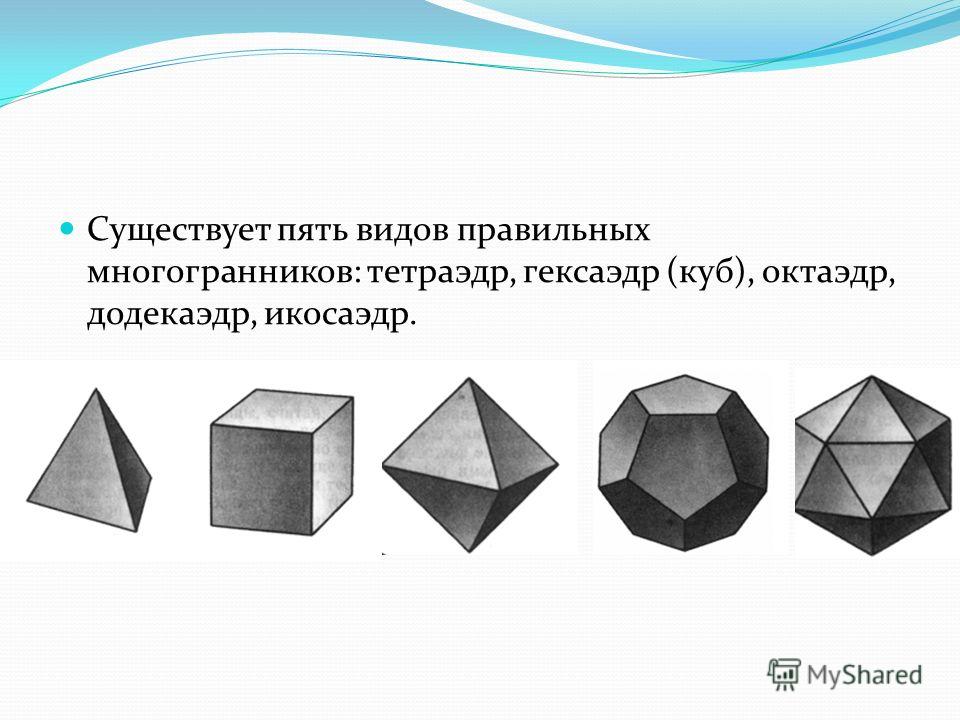 Мы также строим неправильные многогранники, взяв за вершины середины ребер неправильного икосаэдра. Раздел 5 посвящен построению неправильного и правильного курносого куба и их двойственных тел из собственной вращательной октаэдрической симметрии W(B 3 ) + , используя тот же метод, что и в предыдущих разделах. Также обсуждается киральный многогранник, в котором середины являются вершинами неправильного курносого куба. В разделе 6 мы повторяем аналогичную технику для построения неправильных курносых додекаэдров и их двойственных тел, используя собственную группу икосаэдра W(H 3 ) + , которая изоморфна группе четных перестановок пяти букв Alt(5 ). Построены киральные многогранники, вершины которых являются серединами ребер неправильного курносого додекаэдра. Неправильные многогранники переходят в правильные многогранники, когда параметр, описывающий неправильность, оказывается решением некоторых кубических уравнений. В разделе 7 обсуждается техника построения неправильных киральных многогранников.
Мы также строим неправильные многогранники, взяв за вершины середины ребер неправильного икосаэдра. Раздел 5 посвящен построению неправильного и правильного курносого куба и их двойственных тел из собственной вращательной октаэдрической симметрии W(B 3 ) + , используя тот же метод, что и в предыдущих разделах. Также обсуждается киральный многогранник, в котором середины являются вершинами неправильного курносого куба. В разделе 6 мы повторяем аналогичную технику для построения неправильных курносых додекаэдров и их двойственных тел, используя собственную группу икосаэдра W(H 3 ) + , которая изоморфна группе четных перестановок пяти букв Alt(5 ). Построены киральные многогранники, вершины которых являются серединами ребер неправильного курносого додекаэдра. Неправильные многогранники переходят в правильные многогранники, когда параметр, описывающий неправильность, оказывается решением некоторых кубических уравнений. В разделе 7 обсуждается техника построения неправильных киральных многогранников.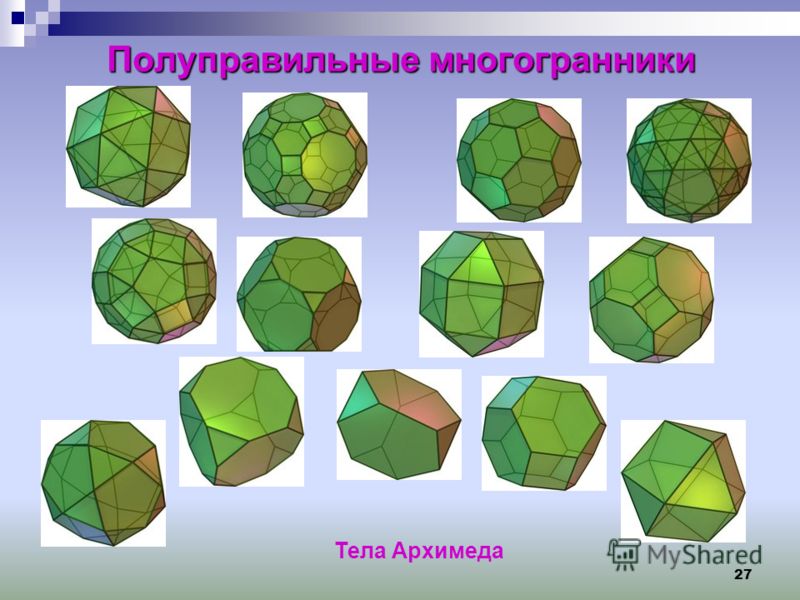
2. Кватернионные конструкции групп Кокстера
Пусть q=q0+qiei, (i=1, 2, 3) — действительный единичный кватернион, сопряженный которому равен q¯=q0−qiei, и норма qq¯ =q¯q=1. Кватернионные мнимые единицы удовлетворяют соотношениям:
где δij и εijk — символы Кронекера и Леви-Чивиты, а суммирование по повторяющимся индексам понятно. Единичные кватернионы образуют группу, изоморфную специальной унитарной группе SU(2). Кватернионы порождают четырехмерное евклидово пространство со скалярным произведением
Диаграмма Кокстера A1⊕A1⊕A1 может быть представлена своими кватернионными корнями, как показано на рисунке 1, где 2 – это просто норма.
Матрица Картана и обратная к ней даются следующим образом:
Простые корни αi и векторы весов ωi для системы корней с простой шнуровкой удовлетворяют скалярному произведению [18,19]
Обратите внимание, что можно выразить корни через веса или наоборот: произвольный кватернион Λ элемент весового пространства ω1, ω2, ω3 может быть представлен в виде [20]:
Тогда нетрудно показать, что riωj=ωj−δijαj. Мы будем использовать обозначения [p,q]*Λ:= pΛ¯q и [p,q]Λ:=pΛq для роторного отражения (объединенного вращения и отражения) и собственного вращения соответственно, где p и q — произвольные единицы кватернионы. Если Λ — чисто мнимый кватернион, то [p,q]*Λ := pΛ¯q= [p,−q]Λ.
Мы будем использовать обозначения [p,q]*Λ:= pΛ¯q и [p,q]Λ:=pΛq для роторного отражения (объединенного вращения и отражения) и собственного вращения соответственно, где p и q — произвольные единицы кватернионы. Если Λ — чисто мнимый кватернион, то [p,q]*Λ := pΛ¯q= [p,−q]Λ.
Группа Кокстера W(A1⊕A1⊕A1)=
Они порождают элементарную абелеву группу W (A 1 ⊕ A 1 ⊕ A 1 ) ≈C2 × C2× C2:= 23 порядка 8. Масштабированная система корней (±e1,±e2,±e3) представляет собой вершины октаэдра и имеет более симметрии, чем группа Кокстера W (A 1 ⊕ A 1 ⊕ A 1 ). Группа автоморфизмов корневой системы может быть получена путем расширения группы Кокстера порядка 8 с помощью симметрии диаграммы Дынкина Sym(3) диаграммы Кокстера на рис. 1. Это очевидно из диаграммы, где образующие группы симметрии Sym( 3) порядка 6 можно выбрать:
Ясно, что генераторы переставляют кватернионные мнимые единицы как:
и удовлетворяют соотношениям sris−1=ri+1, dr1d=r2, dr3d=r3, где индексы рассматриваются по модулю 3.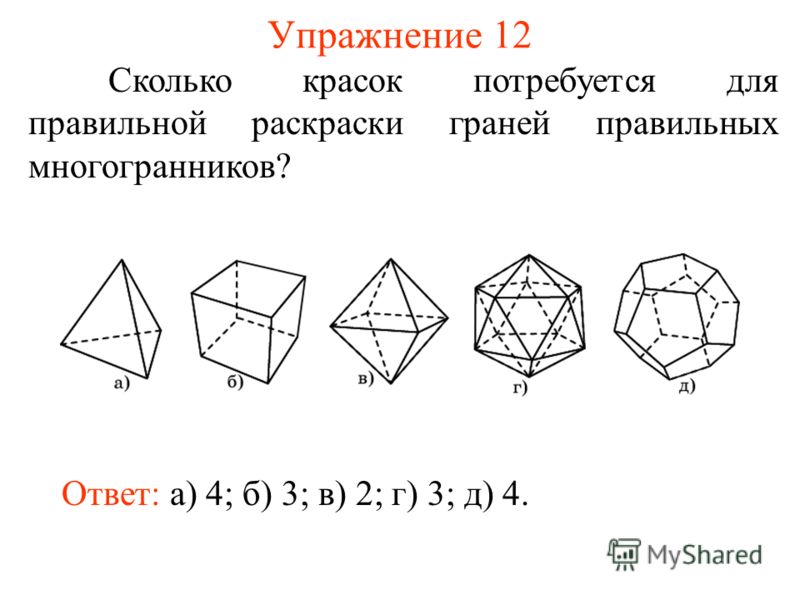
Ясно, что группа Кокстера
где наборы кватернионов T и T’ задаются следующим образом:
Здесь T и T∪T’ представляют бинарную тетраэдрическую группу и бинарную октаэдрическую группу соответственно. Мы использовали сокращенное обозначение групп, например, [T,±T¯] означает множество всех [t,±t¯]∈[T,±T¯] с t∈T. Максимальные подгруппы октаэдрической группы можно записать в виде [21]:
Октаэдрическая группа, как мы увидим далее, также может быть получена как Aut(A3)≈W(B3).
Подгруппа собственных вращений группы Кокстера W(A1⊕A1⊕A1) — это четырехгруппа Клейна C2×C2, представленная элементами:
Заметим также попутно, что четырехгруппа Клейна в (12) инвариантна сопряжением в группе, порожденной s, где s3=1. Четырехгруппа Клейна вместе с групповым элементом s порождают группу тетраэдрических вращений, которая в наших обозначениях представлена как [T, T¯].
Далее мы используем тетраэдрическую группу Td≈W(A3). Диаграмма Коксетера-Дынкина A3 с кватернионными корнями показана на рис. 2.9.0005
Матрица Картана диаграммы Кокстера A3 и ее обратная матрица задаются соответствующими матрицами:
Образующие группы Кокстера W(A3) определяются как:
Образующие в (14) порождают группу Кокстера [ 22,23,24], которая изоморфна тетраэдрической группе Td порядка 24. Группа автоморфизмов Aut(A3)≈W(A3):C2≈Oh, где C2 порождается симметрией диаграммы Дынкина γ=[e1,−e1 ]*, который меняет местами первый и третий простые корни и оставляет второй корень нетронутым на рис. 2.
2.
Диаграмма Кокстера B3, ведущая к октаэдрической группе W(B3)≈Sym(4)×C2≈Oh, показана на рисунке 3. Приведенные ниже образующие порождают октаэдрическую группу, указанную в (9), а весовые векторы имеют вид:
Группа, порожденная вращениями r1r2 и r2r3, изоморфна вращательной октаэдрической группе ]∪[T′,T′¯]}.
Диаграмма Кокстера h4, ведущая к группе икосаэдра, показана на рисунке 4 с кватернионными простыми корнями:
Здесь τ=1+52 — золотое сечение и =1−52. Матрица Картана диаграммы h4, обратная к ней и весовые векторы задаются следующим образом: или, короче, W(h4)=[I,±I¯ ] где I – набор из 120 кватернионных элементов бинарной группы икосаэдра, порожденной кватернионами e1 и 12(τe1+e2+σe3) [20]. Группа икосаэдрического вращения представлена подгруппой собственного вращения W(h4)+=[I,I¯]≈Alt(5). Все конечные подгруппы групп O(3) и O(4) в терминах кватернионов можно найти в ссылках [17,25].
Общий вектор в двойственном пространстве представлен вектором Λ=a1ω1+a2ω2+a3ω3. Мы будем использовать обозначения Λ=a1ω1+a2ω2+a3ω3:(a1a2a3), которые в алгебраической теории представлений Ли [26] называются индексами Дынкина. Мы используем обозначение W(G)Λ:=(a1a2a3)G для орбиты группы Кокстера W(G), порожденной вектором Λ, где буква G обозначает диаграмму Кокстера. Несколько примеров могут быть полезны, чтобы прояснить ситуацию, напомнив отождествления [8]:
Мы будем использовать обозначения Λ=a1ω1+a2ω2+a3ω3:(a1a2a3), которые в алгебраической теории представлений Ли [26] называются индексами Дынкина. Мы используем обозначение W(G)Λ:=(a1a2a3)G для орбиты группы Кокстера W(G), порожденной вектором Λ, где буква G обозначает диаграмму Кокстера. Несколько примеров могут быть полезны, чтобы прояснить ситуацию, напомнив отождествления [8]:
3. Орбита C2×C2(a1a2a3) как неправильный тетраэдр
Подгруппа собственного вращения C2×C2 группы Кокстера W(A1⊕A1⊕A1) преобразует общий вектор Λ следующим образом:
Эти четыре вектора определяют вершины неправильного тетраэдра с четырьмя одинаковыми разносторонними треугольниками с длинами ребер a12 +а22, а22+а32 и а32+а12. Неправильный тетраэдр с a1=1,a2=2,a3=3 изображен на рис. 5.
Середины ребер неправильного тетраэдра заданы векторами ±a1e1,±a2e2,±a3e3, образующими неправильный октаэдр с восемью одинаковыми разносторонними треугольниками со сторонами a12+a22, a22+a32, a32+a12 и соответствующими внутренними углами, скажем, α, β, γ. Вершину a1e1 окружают четыре треугольника с одинаковыми углами между сторонами α. Аналогично остальные 4 треугольника сходятся в противоположной вершине −a1e1. Это верно для каждого угла грани вокруг каждой вершины.
Вершину a1e1 окружают четыре треугольника с одинаковыми углами между сторонами α. Аналогично остальные 4 треугольника сходятся в противоположной вершине −a1e1. Это верно для каждого угла грани вокруг каждой вершины.
Зеркальное отображение неправильного тетраэдра получается применением любого из генераторов отражения к этим векторам, которые приводят к векторам:
Векторы в (20) также могут быть получены из (19) кватернионным сопряжением .
Восемь векторов в (19) и (20) образуют прямоугольную призму с длинами ребер a1,a2 и a3, обладающую симметрией (C2×C2):C2≈D2h порядка 8. Предположим теперь, что мы применяем один из Операторы диаграммной симметрии Дынкина d на векторе Λ и предположим, что:
Если применить образующие вращения, как в (19), мы получим неправильный тетраэдр с одинаковыми четырьмя равнобедренными треугольниками. Зеркальная копия этих векторов может быть получена аналогично процедуре в (20), и когда все они объединены, мы получаем квадратную призму с длинами ребер a и a3.
Более симметричный случай получается, если предположить:
В этом случае симметрия является киральной тетраэдрической группой, а вершины в (19) будут представлять правильный тетраэдр с длиной ребра 2a, который также инвариантен относительно большей тетраэдрической симметрии Td=[T, T¯]⊕[T′, −T′¯], как и ожидалось. Зеркальное отображение правильного тетраэдра получается либо отражениями согласно (20), либо поворотом на 180° вокруг оси e1−e2, что может быть получено групповым элементом:
Тетраэдр не является киральным телом, так как он может быть преобразован в свое зеркальное отображение путем поворота, такого как в (23). Правильный тетраэдр с его зеркальным отображением образует куб, обладающий полной октаэдрической симметрией 48-го порядка. )+ группы Кокстера W(A3) – тетраэдрическая группа 12-го порядка, изоморфная четным перестановкам четырех букв, Alt(4), которая может быть порождена образующими a=r1r2 и b=r2r3, удовлетворяющими соотношениям порождения a3= b3=(ab)2=1. Пусть Λ=(a1a2a3) — общий вектор в весовом пространстве A3. Следующие наборы вершин образуют два равносторонних треугольника.
Пусть Λ=(a1a2a3) — общий вектор в весовом пространстве A3. Следующие наборы вершин образуют два равносторонних треугольника.
с соответствующими длинами ребер 2(a12+a1a2+a22) и 2(a22+a2a3+a32). Еще три треугольника можно получить, соединив вершину r1r3Λ=r3r1Λ с вершинами Λ, r1r2Λ и r3r2Λ и r2r1Λ с r2r3Λ. Новые ребра имеют следующие длины.
Вершины, соединенные с вектором Λ, показаны на рисунке 6.
Факторируя по общему коэффициенту a22≠0 и определяя параметры x=a1a2 и y=a3a2, мы получаем три класса треугольников. Отбрасывая общий множитель a2, получаем
как показано на рисунке 6. Сумма углов между сторонами в вершине Λ (действительно в каждой вершине) равна 2π3+(θ+ ϑ+ φ)=5π3, где θ, ϑ и φ — внутренние углы разносторонних треугольников. Угловой дефицит δ=2π−5π3=π3 такой же, как и в правильном икосаэдре. Используя формулу Декарта, количество вершин также можно получить, как в [27].
Вектор Λ можно записать в терминах кватернионов как Λ=αe1+βe2+γe3, где новые параметры определяются формулой
Орбита киральной тетраэдрической группы W(A3)/C2≈[T, T¯], порожденная вектором Λ, может быть записана как:
Кватернионы в (28) с нечетным числом знаков (−) составляют зеркальное отображение. Элемент вращения, например тот, что в (23), преобразует кватернионы в (28) в их зеркальные отражения. Это доказывает, что множество в (28) не представляет собой киральный многогранник. Прежде чем обсуждать неправильные икосаэдрические структуры, отметим, что для x>0, y=0 или y>0, x=0 набор из 12 векторов описывает усеченный тетраэдр. При x=y=0 он описывает октаэдр. Более интересные случаи возникают, как мы обсудим ниже.
(1) A=B=C, 1+x+x2=1+y+y2=x2+y2
Здесь все ребра равны, что приводит к решению x=y=x2−1⇒x2−x −1=0, ⇒x=τ или x=σ. Подставляя первое решение для =τ, которое дает α=0, β=τ, γ=τ2, набор векторов в (28) можно записать как:
Эти вершины, которые также инвариантны относительно пиритоэдрической симметрии, представляют собой правильный икосаэдр. Обратите внимание, что вектор Λ=τ(e2+τe3) инвариантен относительно 5-кратного поворота на s=[12(σ+e2+τe3),12(σ−e2−τe3)], в то время как другие векторы в (29) переходят друг в друга. Это доказывает, что пиритоэдрическая группа [T,±T¯] может быть расширена до группы икосаэдра [I,±I¯] по образующим так, что множество вершин в (29) инвариантно относительно группы икосаэдра порядка 120. Подчеркнем, что хотя (29) имеет большую симметрию группы икосаэдра, оно получается из ее киральной тетраэдрической подгруппы. Его зеркальное отображение можно получить, повернув его на 180° вокруг вектора e1−e2, что означает, что икосаэдр не является киральным телом.
Обратите внимание, что вектор Λ=τ(e2+τe3) инвариантен относительно 5-кратного поворота на s=[12(σ+e2+τe3),12(σ−e2−τe3)], в то время как другие векторы в (29) переходят друг в друга. Это доказывает, что пиритоэдрическая группа [T,±T¯] может быть расширена до группы икосаэдра [I,±I¯] по образующим так, что множество вершин в (29) инвариантно относительно группы икосаэдра порядка 120. Подчеркнем, что хотя (29) имеет большую симметрию группы икосаэдра, оно получается из ее киральной тетраэдрической подгруппы. Его зеркальное отображение можно получить, повернув его на 180° вокруг вектора e1−e2, что означает, что икосаэдр не является киральным телом.
Существует еще одно тривиальное решение для A=B=C, где x=−1, y=0. Количество вершин в (28) сокращается до 4, что соответствует правильному тетраэдру.
(2) A=B≠C, y=12(−1±1+4(x2+x) )
Для различных значений x и соответствующего y получается неправильный икосаэдр с (4+4) равносторонних треугольников и 12 равнобедренных треугольников. Интересным был бы случай x=y=−τ с 12 вершинами {±τ e1±σe2,±τe2±σe3,±τe3±σe1}, которые представляют собой неправильный икосаэдр с (4+4) равносторонними треугольниками с ребрами длины 2. и 12 равнобедренных треугольников со сторонами 2, 2τ, 2τ (треугольники Робинсона). Любой неправильный икосаэдр с x=y≠0 имеет пиритоэдрическую симметрию порядка 24, как указано в (11). Другое решение квадратного уравнения x=−τ, y=−σ приводит к неправильному икосаэдру из (4+4) равносторонних треугольников с длинами ребер 2 и 12 равнобедренных треугольников с длинами ребер 2, 2,6.
Интересным был бы случай x=y=−τ с 12 вершинами {±τ e1±σe2,±τe2±σe3,±τe3±σe1}, которые представляют собой неправильный икосаэдр с (4+4) равносторонними треугольниками с ребрами длины 2. и 12 равнобедренных треугольников со сторонами 2, 2τ, 2τ (треугольники Робинсона). Любой неправильный икосаэдр с x=y≠0 имеет пиритоэдрическую симметрию порядка 24, как указано в (11). Другое решение квадратного уравнения x=−τ, y=−σ приводит к неправильному икосаэдру из (4+4) равносторонних треугольников с длинами ребер 2 и 12 равнобедренных треугольников с длинами ребер 2, 2,6.
(3) A=C≠B
Это еще один случай с 12 равнобедренными треугольниками, но здесь 4 набора равносторонних треугольников не равны другому набору из 4 равносторонних треугольников. Имеем x=y2−1, x≠τ или σ и x≠0, y≠0. Для значений y=−τ, x=τ неправильный икосаэдр состоит из 4 равносторонних треугольников с длиной ребра 2, 4 равносторонних треугольников с длиной ребра 2τ и 12 треугольников Робинсона с длиной ребра 2,2τ,2τ, как обсуждалось в (2) .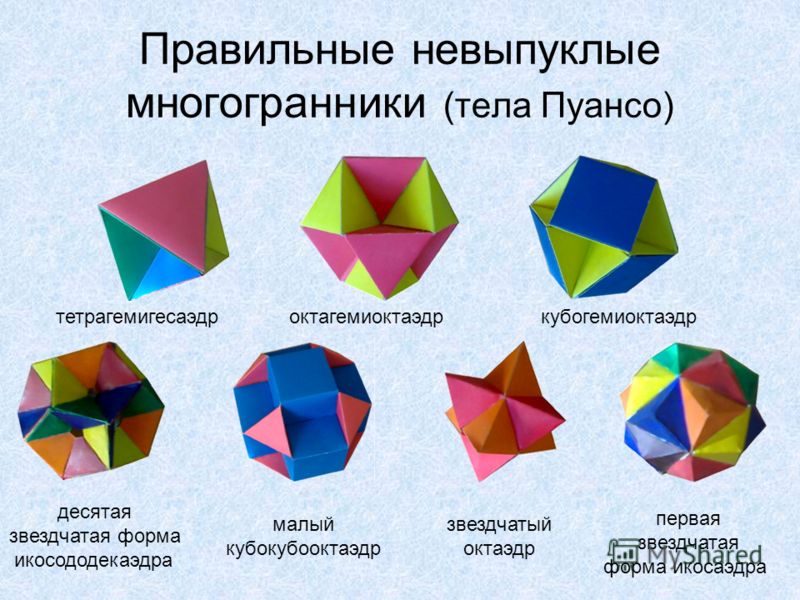
(4) A≠C=B
Здесь y=x2−1, x≠τ или σ. При x=−τ,y=τ грани неправильного икосаэдра такие же, как в случае (3).
(5) A≠C≠B
Теперь у нас есть x≠y2−1 и y≠x2−1. При x=1,y=2 неправильный икосаэдр будет состоять из 4 равносторонних треугольников с длиной ребра 6, 4 равносторонних треугольников с длиной ребра 14 и 12 разносторонних треугольников с ребрами 6, 10 и 14.
4.1. Двойник неправильного икосаэдра
Теперь обсудим построение двойника неправильного икосаэдра. Двойственный неправильному многограннику можно получить, найдя векторы, ортогональные его граням. На рисунке 6 векторы, ортогональные равносторонним граням №1 и №3, можно принять за b1:=ω1 и b3:=ω3, поскольку они инвариантны относительно поворотов r2r3 и r1r2 соответственно. Векторы, ортогональные граням № 2, № 4 и № 5, можно определить как:
где n1=y−x, n2=x+y+2xy, n3=x+y.
Эти векторы должны быть перемасштабированы, чтобы определить плоскость, ортогональную вектору Λ. Переопределим векторы d1:=λω1, d2=b2, d3=ϱb3, d4=b4, d5=b5. Масштабные коэффициенты можно определить как:
Переопределим векторы d1:=λω1, d2=b2, d3=ϱb3, d4=b4, d5=b5. Масштабные коэффициенты можно определить как:
Двойное тело представляет собой неправильный додекаэдр с наборами вершин:
Мы не будем подробно обсуждать, как изменяется неправильный додекаэдр в пяти различных случаях, рассмотренных выше. Достаточно нескольких примеров в порядке возрастания симметрии в сторону регулярности. Случай (5) выше соответствует инвариантности относительно киральной тетраэдрической группы. Подставив x=1, y=2 в (32), получим неправильный додекаэдр, называемый тетратоидом, соответствующий минералу кобальтиту. Вершины d1,d2,d3,d4 и d5 образуют неправильный пятиугольник с тремя разными длинами ребер. Тетартоид с его двойным неправильным икосаэдром изображен на рис. 7.
Так как при пиритоэдрической симметрии x=y вершины в (32) принимают более простой вид где:
Длины ребер неправильного пятиугольника принимают значения:
Неправильный додекаэдр с вершинами (32) с λ а ϱ из (33) называется пиритоэдром.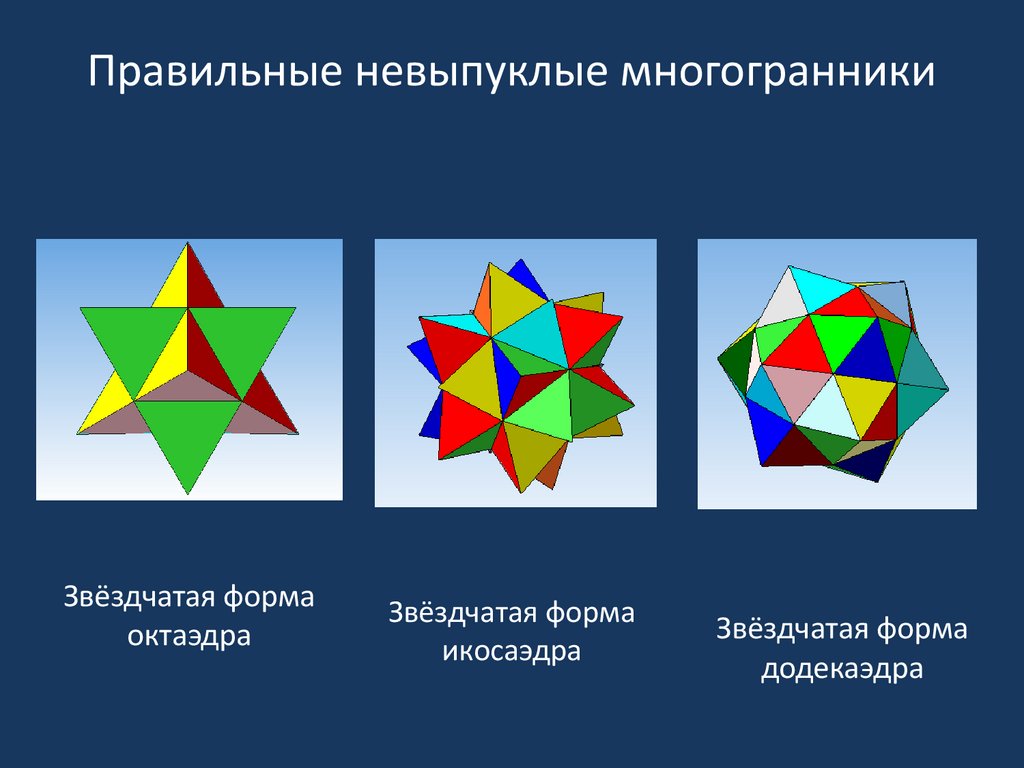 Их также можно переставить и набор можно отдать в стандартном виде:
Их также можно переставить и набор можно отдать в стандартном виде:
где ч=хх+1.
Частный случай x=y=5, обсуждаемый в (2), соответствующий h=56 в (35), показан на рисунке 8.
В пределе либо x=τ, либо x=σ додекаэдр правильный, а пятиугольник оказывается правильным со всеми ребрами, равными либо 4τ, либо −4σ. После масштабирования на 4τ2 набор вершин додекаэдра с x=τ будет следующим:
Каждое указанное выше множество инвариантно относительно пиритоэдрической группы [T,±T¯]. 20 вершин (36) образуют додекаэдр с правильными гранями. Как таковые, они обладают большей икосаэдрической симметрией [I, ±I¯ ].
Первые 8 вершин (36) представляют собой куб, а второй набор из 12 вершин, как мы помним из предыдущих обсуждений, представляет собой неправильный икосаэдр с (4+4) равносторонними треугольниками и 12 треугольниками Робинсона. Двойник неправильного икосаэдра во втором наборе из 12 вершин в (36) является другим неправильным додекаэдром, вершины которого являются объединением куба и правильного икосаэдра, хотя и с разными величинами векторов.
4.2. Правильный и неправильный икосододекаэдр
Хорошо известно, что середины ребер правильного икосаэдра или додекаэдра образуют архимедов телесный икосододекаэдр с 30 вершинами, 32 гранями (12 пятиугольников + 20 треугольников) и 60 ребрами, который можно получить из уравнения Кокстера. граф h4 как орбита (010)h4 [28]. Неправильный икосододекаэдр состоит из неправильных пятиугольных граней и разносторонних треугольников в самом общем случае и будет производным от хиральной тетраэдрической группы и будет расширен пиритоэдрической группой, представляющей большую симметрию. Можно определить пять векторов следующим образом, представляющих вершины неправильного пятиугольника, ортогонального вершине Λ:
С точки зрения x и y вершины читаются:
Здесь c1 с c2, c3 с c4 и c5 определяют три орбиты при киральной тетраэдрической симметрии размеров 12, 12 и 6 соответственно.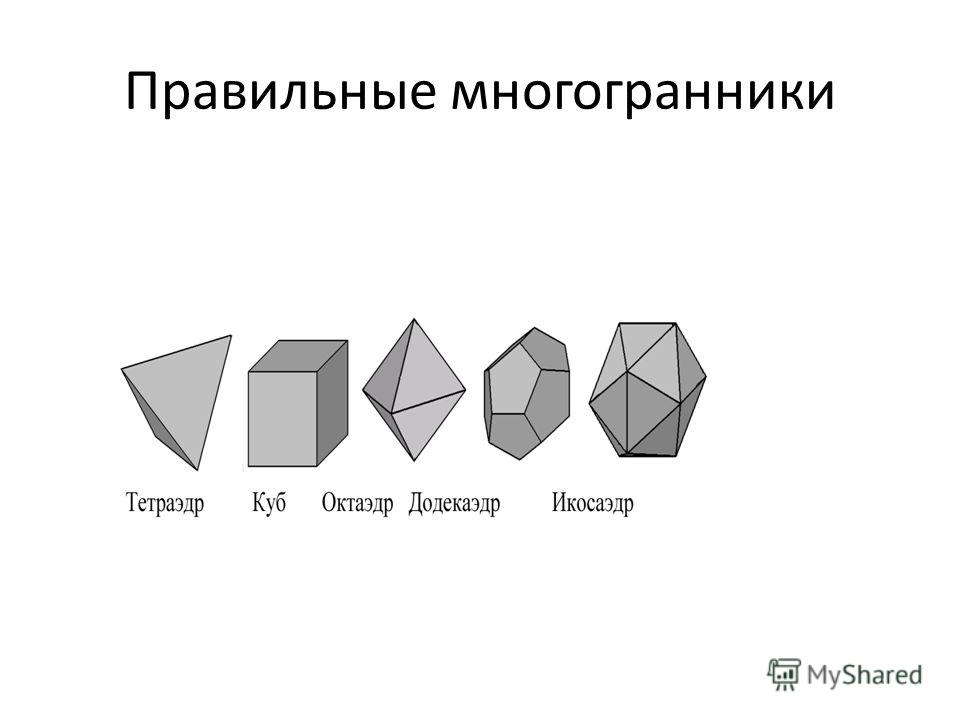 Вводя пиритоэдрическую групповую инвариантность (x=y) и, кроме того, полагая x=τ и деля каждый вектор на масштабный коэффициент 2τ2, получаем обычные кватернионные вершины икосододекаэдра [28]
Вводя пиритоэдрическую групповую инвариантность (x=y) и, кроме того, полагая x=τ и деля каждый вектор на масштабный коэффициент 2τ2, получаем обычные кватернионные вершины икосододекаэдра [28]
Они составляют подмножество кватернионной бинарной группы икосаэдра I. Икосододекаэдр состоит из правильных пятиугольников и равносторонних треугольников, как показано на рисунке 9.а. Общий неправильный икосододекаэдр состоит из 12 пятиугольников с ребрами a, b, c, как показано на рисунке 9b. Кроме того, он имеет 4 равносторонних треугольника с ребрами a, 4 равносторонних треугольника с ребрами b, 12 разносторонних треугольников с ребрами a, b, c, где a, b, c могут быть выражены через x и y.
5. Правильные и неправильные плосковыпуклые кубы, полученные из W(B3)+(a1a2a3)
Плосконосый куб представляет собой киральное архимедово тело с 24 вершинами, 60 ребрами и 38 гранями (8 квадратов, 6+24 равносторонних треугольника). Ее вершины и ее двойник можно определить, используя тот же метод, описанный в разделах 3 и 4. Собственной вращательной подгруппой группы Кокстера W(B3) является вращательная октаэдрическая группа Sym(4)≈{[T, T¯ ] ∪[T′,T′¯]} порядка 24, которая переставляет диагонали куба [21]. Группа порождается двумя образующими вращения a=r3r2 и b=r2r1, удовлетворяющими соотношениям порождения a4=b3=(ab)2=1. Когда Λ берется в качестве общего вектора, следующие наборы вершин образуют равносторонний треугольник и квадрат соответственно:
Собственной вращательной подгруппой группы Кокстера W(B3) является вращательная октаэдрическая группа Sym(4)≈{[T, T¯ ] ∪[T′,T′¯]} порядка 24, которая переставляет диагонали куба [21]. Группа порождается двумя образующими вращения a=r3r2 и b=r2r1, удовлетворяющими соотношениям порождения a4=b3=(ab)2=1. Когда Λ берется в качестве общего вектора, следующие наборы вершин образуют равносторонний треугольник и квадрат соответственно:
с соответствующими длинами ребер 2(a12+a1a2+a22) и 2(a22+a2a3+12a32). С вершиной r1r3Λ=r3r1Λ мы получаем фигуру, состоящую из 7 вершин, как показано на рисунке 10.
Среди 11 ребер есть 3 различных длины ребер, которые задаются как: =a3a2 и α= x+y2+1, β=y2+1, γ= y2 и отбрасывая a2, получают следующие классы граней неправильного курносого куба:
6 равносторонних треугольников с длиной ребра: A= 2(1+х+х2),
8 квадратов с длиной ребра: B=2(1+y+y2),
24 разносторонних треугольника с длиной ребра: A,B, C=2(x2+12y2).

Поскольку угловой дефицит равен δ=π6, количество вершин неправильного курносого куба равно 24.
Вершина Λ=a1ω1+a2ω2+a3ω3 может быть записана в терминах кватернионов как γe3. Орбита, порожденная киральной октаэдрической группой, выглядит следующим образом:
. где Λ′=r1Λ — зеркальное отображение Λ. Вершины (42) представляют собой (1) октаэдр при a1=1,a2=a3=0; (2) усеченный октаэдр для x=1, y=0; (3) куб для a1=a2=0,a3=1 и (4) кубооктаэдр для a1=a3=0,a2=1.
Неправильное киральное выпуклое тело будет иметь 24 вершины, 38 граней (8 квадратных, 6 равносторонних треугольников и 24 разносторонних треугольника) и 60 ребер (24 длины A, 24 длины B, 12 длины C). Далее мы классифицируем их по длинам ребер треугольников и квадратов.
(1) Курносый куб: A=B= C, 1+x+x2=1+y+y2=x2+12y2
Когда все ребра равны, можно исключить переменную, удовлетворяющую y=x2−1, и получить кубическое уравнение x3− x2 − x −1=0, которое также можно записать как x+ x−3=2. Решением является постоянная Трибоначчи x= limn→∞Fn+1Fn ≈1,8393, где Fn — n-й член ряда Трибоначчи 0, 0, 1, 1, 2, 4, 7, 13, 24, 44,….
Решением является постоянная Трибоначчи x= limn→∞Fn+1Fn ≈1,8393, где Fn — n-й член ряда Трибоначчи 0, 0, 1, 1, 2, 4, 7, 13, 24, 44,….
После отбрасывания общего коэффициента 12(x2+1) вершины курносого куба и его зеркального отображения задаются следующим образом:
Для x=1,8393 курносый куб показан на рисунке 11. B≠C, y=−1±(1+2(x2+x)
При x=1, y=−2τ неправильный курносый куб состоит из 6 равносторонних треугольников и 8 квадратов с ребрами 6 соответственно и 24 равнобедренных треугольников ребер 6, 6, 2(2τ+3), как показано на рисунке 12.
(3) A=C≠B, x=12y2 − 1 и x 3 − x 2 − x − 1 ≠ 0
Для y=4 и x=7, соответствующих α=10, β= 3, γ=2, неправильный курносый куб состоит из квадратов с ребрами 13, равносторонних треугольников с ребрами 57 и равнобедренных треугольников с ребрами 57, 57 и 13; все ребра масштабируются в 2 раза. Курносый куб после масштабирования на 2 имеет равносторонние треугольники со сторонами 13, квадраты со сторонами 41 и равнобедренные треугольники со сторонами 41, 41, 13 в качестве граней.
(5) A≠C≠B
Переменные должны удовлетворять неравенствам y≠x2−1 и y2≠2(x+1).
Для x=2 и y=4 неправильный курносый куб состоит из масштабированных равносторонних треугольников со сторонами 7, квадратов со сторонами 13 и разносторонних треугольников со сторонами 7, 13 и 10, как показано на рисунке 13.
5.1. Двойственный нерегулярному курносому кубу
Векторы, ортогональные граням на рисунке 10, могут быть определены как:
Здесь параметры задаются как:
Вершины двойственного неправильного курносого куба могут быть записаны как три набора орбит под киральной октаэдрической группой {[T, T¯ ]⊕[T′,T′¯]},
Зеркальное отображение можно получить из (46) заменой e1↔e2.
Двойник неправильного курносого куба состоит из 24 неправильных пятиугольников с тремя ребрами разной длины. Однако для особого случая y=x2−1 и x3−x2−x−1=0, который соответствует регулярному курносому кубу, параметры задаются как µ=x2, ν=x−32, n1=x(2x+ 1),n2=x, n3=x3.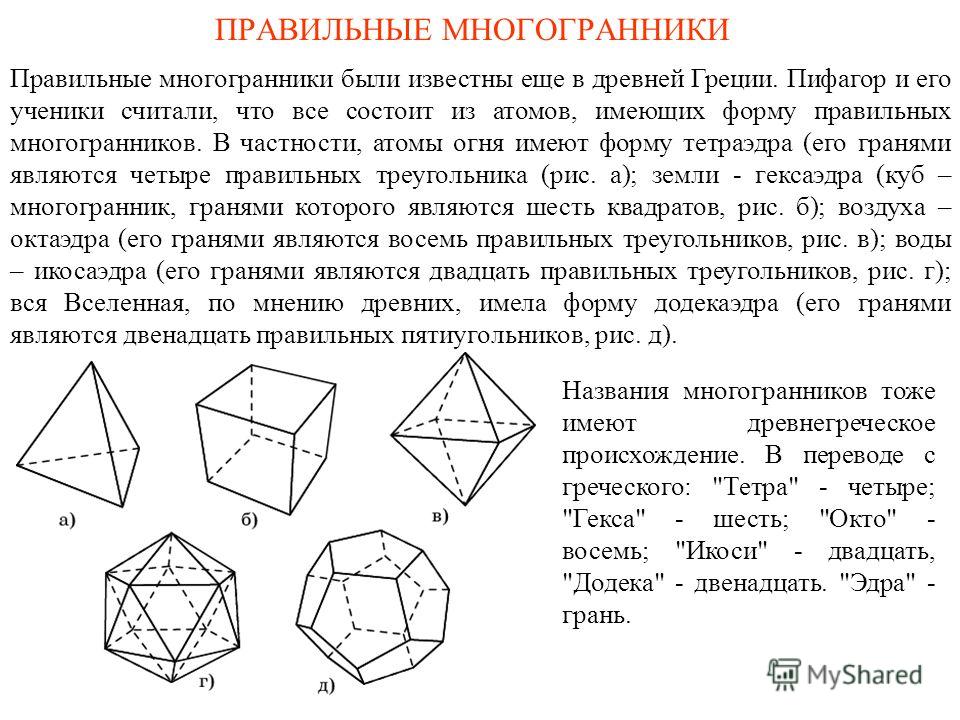 Длины ребер пятиугольника удовлетворяют соотношениям
Длины ребер пятиугольника удовлетворяют соотношениям
где х≈1,8393. Двойник курносого куба показан на рис. 14.
Мы не будем обсуждать все двойники неправильных курносых кубов. Их можно получить, подставив x и y в (45) и (46) в соответствии с каждым случаем выше. Мы проиллюстрируем только случай x=2 и y=4, когда пятиугольник имеет три разные длины ребер. Это двойник неправильного курносого куба, соответствующий случаю (5). Он изображен на рис. 15 с пятиугольными гранями, состоящими из трех ребер разной длины, удовлетворяющих соотношениям |d1−d2|=|d1−d5|, |d2−d3|=|d3−d4|, |d4−d5|.
5.2. Хиральные многогранники с вершинами в серединах ребер неправильного плосковыпуклого куба
Обсуждая аналогично случаю неправильного икосододекаэдра в разделе 4, мы можем построить киральный многогранник, предполагая, что середины ребер неправильного курносого куба равны вершины. Векторы, вершины которых составляют плоскость, ортогональную вектору Λ на рис. 10, построенные аналогично (37) и (38) и равные:
10, построенные аналогично (37) и (38) и равные:
Вершины c1 и c2 находятся на одной орбите размера 24 под киральной октаэдрической группы {[T, T¯ ]∪[T′,T′¯]}, а орбита, включающая c3 и c4, имеет размер 24. Орбита c1 состоит из циклических перестановок коэффициентов единичных кватернионов со всеми возможными изменения знака. Тот же аргумент справедлив и для орбиты c3. Орбита c5 состоит из 12 кватернионов, полученных как циклические перестановки пары кватернионов со всеми изменениями знака. На самом деле орбита c5 сама по себе представляет вершины кубооктаэдра. Для всех допустимых x и y могут отображаться киральные многогранники с 60 вершинами. Однако мы отобразим только многогранник, соответствующий особому случаю, когда 60 вершин, полученных из (48), представляют середины ребер обычного случая, а именно курносого куба. Это получается, как мы обсуждали ранее, заменой y=x2−1 и использованием действительного решения кубического уравнения x3−x2−x−1=0.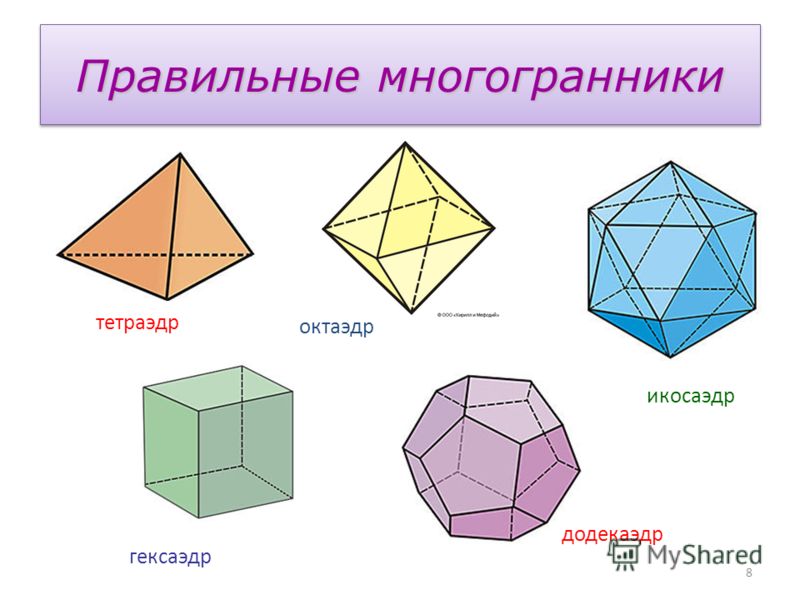 Тогда получается µ′=v′=1, а квадраты длин сторон неправильного пятиугольника, полученные из (48), равны:
Тогда получается µ′=v′=1, а квадраты длин сторон неправильного пятиугольника, полученные из (48), равны:
Вектор, ортогональный этому пятиугольнику, представлен вектором Λ, и вокруг этого пятиугольника есть 4 равносторонних треугольника со сторонами 2×3 и 1 квадрат со сторонами 2×3. С этой пятиугольной гранью хиральный многогранник показан на рисунке 16. Он имеет 60 вершин, 62 грани (6 квадратов, (8+24) равносторонних треугольников и 24 неправильных пятиугольника) и 120 ребер (96 сторон 3,528 и 24 длины 4,989). ).
6. Правильный и неправильный курносый додекаэдр, производный от W(h4)+(a1a2a3)
Курносый додекаэдр представляет собой киральное архимедово тело с 60 вершинами, 92 гранями (20 пятиугольников + 80 треугольников) и 150 ребрами. Мы обсудим, как получить курносый додекаэдр из неправильного курносого додекаэдра. Вершины неправильного курносого додекаэдра, двойственного ему и кирального многогранника, полученного из середин ребер, будут построены с использованием той же техники, которая описана в разделе 5.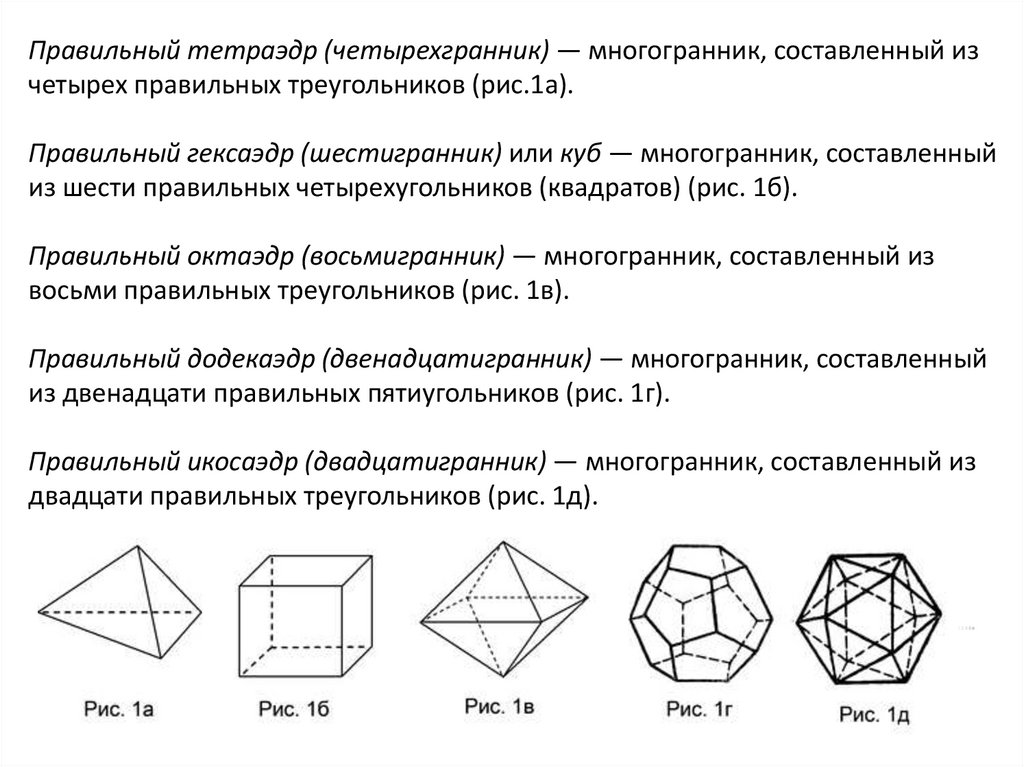 Собственная вращательная подгруппа икосаэдрической группы Кокстера также называется киральной группой икосаэдра. W(h4)+=[I,I¯ ]≈Alt(5), которая является простой группой порядка 60. Они могут быть порождены образующими a=r1r2, b=r2r3, которые удовлетворяют соотношениям порождения a5=b3=( аб)2=1. Пусть Λ=a1ω1+a2ω2+a3ω3 — общий вектор, где ωi, (i=1, 2, 3) может быть получено из (17). Следующие наборы вершин образуют правильный пятиугольник и равносторонний треугольник соответственно:
Собственная вращательная подгруппа икосаэдрической группы Кокстера также называется киральной группой икосаэдра. W(h4)+=[I,I¯ ]≈Alt(5), которая является простой группой порядка 60. Они могут быть порождены образующими a=r1r2, b=r2r3, которые удовлетворяют соотношениям порождения a5=b3=( аб)2=1. Пусть Λ=a1ω1+a2ω2+a3ω3 — общий вектор, где ωi, (i=1, 2, 3) может быть получено из (17). Следующие наборы вершин образуют правильный пятиугольник и равносторонний треугольник соответственно:
с соответствующими длинами ребер 2(a12+τa1a2+a22) и 2(a22+a2a3+a32). С добавлением вершины r1r3Λ=r3r1Λ, как показано на рисунке 17, есть три длины ребра, включая 2(a12+a32). Обсуждение разделов 4 и 5 будет повторено, чтобы получить правильные и неправильные курносые додекаэдры. Двойственный и киральный многогранники, основанные на серединах ребер, следуют той же технике.
Нумерация граней выполнена в соответствии с диаграммой h4 на рис. 4. Разложение на множители a2≠0, переопределение x=a3a2, y=a1a2 и удаление a22 дает неправильный курносый додекаэдр с 12 равносторонними треугольниками с длиной ребра: A =2(1+x+x2), 20 пятиугольников с длиной ребра: B=2(1+τy+y2), 60 разносторонних треугольников с длиной ребра: A,B, C=2(x2+y2).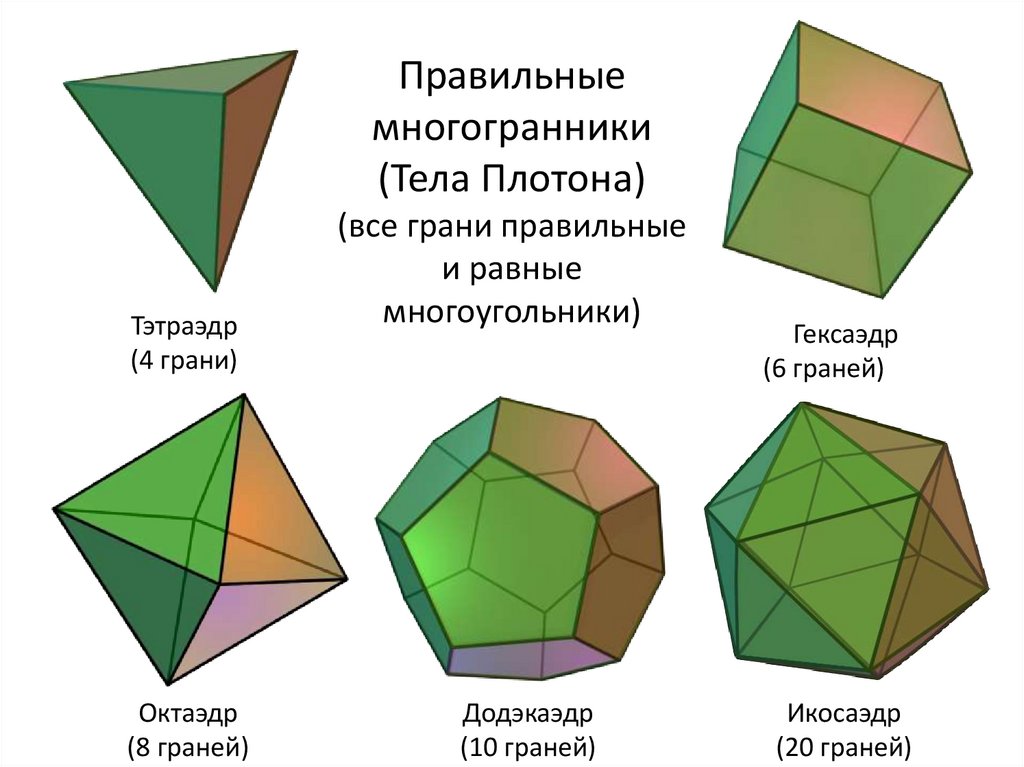 Треугольники с номерами 2, 4 и 5 – это одинаковые разносторонние треугольники, но треугольник 1 – равносторонний. Угловой дефицит равен δ=2π−(π3+3π5+(θ+ ϑ+ φ))=π15, где θ, ϑ и φ — внутренние углы разносторонних треугольников. Формула Декарта проверяет количество вершин N0=60.
Треугольники с номерами 2, 4 и 5 – это одинаковые разносторонние треугольники, но треугольник 1 – равносторонний. Угловой дефицит равен δ=2π−(π3+3π5+(θ+ ϑ+ φ))=π15, где θ, ϑ и φ — внутренние углы разносторонних треугольников. Формула Декарта проверяет количество вершин N0=60.
Орбита [I,I¯ ]Λ, порожденная вектором Λ= − ye1− xe2 − τ(τy+ x+2)e3, включает 60 векторов, представляющих вершины неправильного курносого додекаэдра. Зеркальное отображение [I,I¯ ]Λ′ может быть получено из вектора Λ′= r1Λ= ye1− xe2− τ(τy+x+2)e3. Несколько замечаний, прежде чем мы обсудим обычную классификацию. Для некоторых специальных значений параметров x и y мы получаем некоторые из архимедовых тел. Например,
- (i)
x=1 и y=0: усеченный икосаэдр,
- (ii)
x=0 и y=1: усеченный додекаэдр,
- (iii)
x=y=0: икосододекаэдр.
Давайте, следуя последовательности раздела 5, обсудим правильные и неправильные курносые додекаэдры.
(1) Плосконосый додекаэдр: A=B= C, 1+x+x2=1+τy+y2=x2+y2
Поскольку все ребра равны, это приводит к соотношениям y=σ(1−x2 ) и y2=x+1, что приводит к кубическому уравнению x3−x2−x−τ=0. Реальное решение приблизительно равно x=1,9.43. Курносый додекаэдр показан на рис. 18.
(2) A=B≠ C, y=12(−τ±(τ2+4(x2+x))
Для x=−1, y=− τ, неправильный курносый додекаэдр состоит из 12 равносторонних треугольников и 20 пятиугольников со сторонами 2 и 60 равнобедренных треугольников со сторонами 2,2,2(τ+2)
(3) A=C≠B, y2=x+1 и x3−x2−x−τ≠0
Для y=2 и x=3 соответствующий неправильный курносый додекаэдр состоит из пятиугольников с длиной ребра 2(2τ+5), равносторонних треугольников с длиной ребра 26 и равнобедренных треугольников с длиной ребра 26, 26 и 2(2τ+5)
(4) A≠B=C, x2=τy+1 и x3−x2−x−τ≠0
При y=1, x=τ неправильный курносый додекаэдр имеет пятиугольники со сторонами 2(τ+2 ), равнобедренные треугольники со сторонами 2τ и равнобедренный треугольник со сторонами 2(τ+2), 2(τ+2) и 2τ.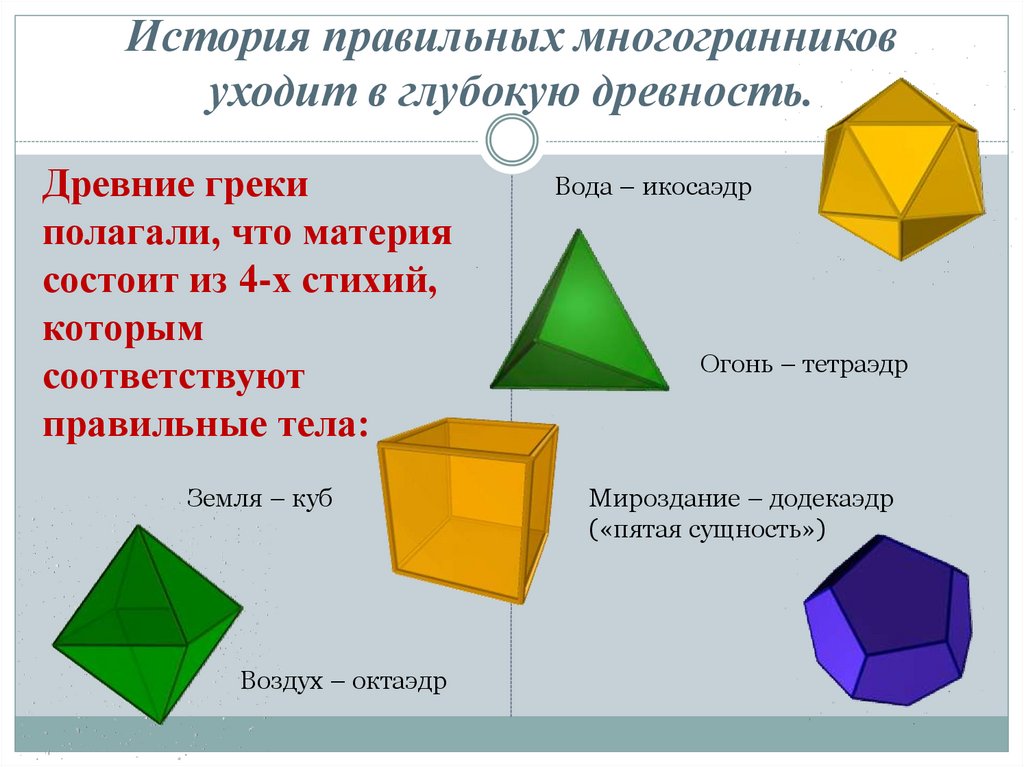
(5) A≠C≠B
При x=2 и y=3 неправильный курносый додекаэдр состоит из равносторонних треугольников со сторонами 14, пятиугольников со сторонами 2(3τ+10) и разносторонних треугольников со сторонами 14, 2(3τ+10) и 26, как показано на рисунке 19.
6.1. Двойник неправильного курносого додекаэдра
Мы получаем 5 векторов следующим образом для определения плоскости, ортогональной вершине Λ:
Орбиты, полученные из этих пяти векторов, представляют собой вершины двойственного тела неправильного курносого додекаэдра. Грани двойственности состоят из неправильных пятиугольников, один из которых представлен вершинами (51). Обратите внимание, что орбиты [I,I¯ ]d1 и [I,I¯ ]d3 представляют собой орбиты размеров 20 и 12 соответственно. Остальные три вершины находятся на той же орбите; поэтому достаточно одного единственного обозначения [I,I¯ ]d2 для этой орбиты размера 60. Следовательно, дуал состоит из 92 вершины, 60 неправильных пятиугольников и 150 ребер. Регулярный случай получается заменой y=σ(1−x2) и x=1,943 в (51). Двойственный курносому додекаэдру, пятиугольный гексаконтаэдр, показан на рисунке 20.
Регулярный случай получается заменой y=σ(1−x2) и x=1,943 в (51). Двойственный курносому додекаэдру, пятиугольный гексаконтаэдр, показан на рисунке 20.
Мы также проиллюстрируем двойственный неправильный курносый додекаэдр, полученный из 5), подставив значения x=2 и y=3 в (51). 92 вершины с этой заменой описывают киральное тело, изображенное на рис. 21.
6.2. Киральные многогранники с вершинами в серединах ребер неправильного курносого додекаэдра
Как и в предыдущем обсуждении, мы можем построить киральный многогранник, имеющий середины ребер неправильного курносого куба в качестве вершин. Векторы, вершины которых составляют плоскость, ортогональную вектору Λ на рисунке 17, определяются как:
В пределе y=σ(1−x2), x3−x2−x−τ=0 и α=β=1 (x =1,943); для курносого додекаэдра вершины в (52) упрощаются, а длины ребер пятиугольника удовлетворяют соотношениям:
Этот киральный многогранник имеет 150 вершин и 152 грани (12 правильных пятиугольников + 60 неправильных пятиугольников и (20+60) равносторонних треугольников, окружающих 60 неправильных пятиугольников), типичный из которых представлен отношениями вершин в (53). Хиральный многогранник с 300 ребрами показан на рис. 22.
Хиральный многогранник с 300 ребрами показан на рис. 22.
7. Заключительные замечания
В этой статье мы представили систематическое построение правильных и неправильных киральных многогранников, курносого куба, курносого додекаэдра и их двойников с использованием собственных вращательных подгрупп группы октаэдра и группы икосаэдра. Также были построены киральные многогранники, вершины которых являются серединами киральных многогранников. Мы использовали диаграммы Кокстера B 3 и H 3 , чтобы получить кватернионное описание соответствующих хиральных групп. Используя ту же технику для диаграмм A 1 ⊕ A 1 ⊕ A 1 и A 3 , неправильные тетраэдры и икосаэдры были включены, хотя они не являются хиральными, поскольку они могут быть преобразованы в свои зеркальные отражения подгруппой правильного вращения октаэдрической группы. .
Двойные тела неправильного икосаэдра, тетартоида и пиритоэдра также построены, представляя хиральные симметрии хиральной тетраэдрической группы и пиритоэдрической группы, соответственно.
Этот метод можно распространить на группы Кокстера более высокой размерности для определения неправильно-правильных киральных многогранников. Например, курносый 24-ячеечный киральный многогранник в 4D евклидовом пространстве можно определить с помощью D 4 Диаграмма Кокстера [29] и ее неправильная форма могут быть получены с использованием той же техники, что и для неправильного икосаэдра.
Четыре правильных невыпуклых многогранника
Четыре правильных невыпуклых многогранникаЧетыре правильных невыпуклых многогранника
| Малый звездчатый додекаэдр | Большой звездчатый додекаэдр | Большой додекаэдр | Большой икосаэдр |
 ..
.. Известно, что пять платоновых многогранников являются единственными правильными выпуклыми многогранниками. Многогранник, рассматриваемый как
тело является выпуклым тогда и только тогда, когда отрезок между любыми двумя точками многогранника полностью принадлежит
твердый. Однако, если мы допустим многогранник невыпуклым, существует четыре больше видов правильных многогранников!
Четыре правильных невыпуклых многогранника известны как многогранников Кеплера-Пуансо . Два из них были описаны Иоганнесом
Кеплером в 1619 г. как регулярные, хотя сами объекты наверняка были известны и раньше. Один из них
появляется на рисунке Ямнитцера 16 века, а другой — на мозаике 15 века на полу собора Сан-Марко.
в Венеции. Два других были описаны Луи Пуансо в 1809 году.но по крайней мере один из них появляется на рисунке того же
Ямницер. В 1810 году французский математик Огюстен-Луи Коши доказал, что пять Платоновских и четыре Кеплера-Пуансо
многогранники — единственно возможные правильные многогранники.
Все четыре многогранника Кеплера-Пуансо можно построить, исходя из правильного додекаэдра или икосаэдра. Это моя цель показать возможную конструкцию для каждого из них.
Два многогранника Кеплера
1. Малый звездчатый додекаэдр
Продлив ребра грани правильного додекаэдра, мы получим пентаграмму. Действуя таким образом для всех двенадцати
граней получаем невыпуклый многогранник. Этот многогранник называется малым звездчатым додекаэдром .
У него 12 граней (пентаграмм),
12 вершин и 30 ребер. В каждой вершине сходятся пять граней. Малый звездчатый додекаэдр можно построить, положив
присвоили пятигранные пирамиды граням данного додекаэдра. Каждая грань этих пирамид представляет собой
«золотой треугольник» (см. напр. Золотое сечение…). Это может быть полезно в
случай материальной конструкции твердого тела. Вершины малого
звездчатый додекаэдр также является вершиной икосаэдра.
2. Большой звездчатый додекаэдр
Начнем с правильного икосаэдра и рассмотрим одну из его вершин. Другие конечные точки пяти ребер, начинающихся из выбранной вершины являются вершинами пятиугольника. Расширяем стороны этого пятиугольника, чтобы получилась пентаграмма. Поскольку у икосаэдра 12 вершин, мы получаем 12 пентаграмм. Это грани невыпуклого многогранника, называемого большой звездчатый додекаэдр . У него 12 граней (пентаграмм), 20 вершин и 30 ребер. В каждой вершине сходятся три грани. Большой звездчатый додекаэдр можно построить, положив присвоили трехгранные пирамиды граням данного икосодра. Каждая грань этих пирамид представляет собой «золотой треугольник» (см. напр. Золотое сечение…). Это может быть полезно в случае материальной конструкции твердого тела. Вершины великого звездчатый додекаэдр также является вершиной додекаэдра.
Два многогранника Пуансо
1. Большой додекаэдр
Большой додекаэдр
Начало очень похоже на большой звездчатый додекаэдр. Начнем с правильного икосаэдра и снова рассмотрим одну из его вершин. Другие конечные точки пяти ребер, начинающихся из выбранной вершины являются вершинами пятиугольника. Поскольку у икосаэдра 12 вершин, мы получаем 12 пятиугольников. Все они расположены внутри икосаэдра. Это грани правильного невыпуклого многогранника, называемого большой додекаэдр . У него 12 граней (пятиугольников), 12 вершин и 30 ребер. В каждой вершине сходятся три грани. Большой додекаэдр имеет те же вершины и ребра, что и икосаэдр, который мы началось с.
2. Большой икосаэдр
Рассмотрим вершины правильного икосаэдра. Если мы соединим каждую вершину с ее пятью «ближайшими соседями», мы получим
грани икосаэдра. Но у каждой вершины также есть пять «ближайших соседей». Пять комбинаций выбранной вершины
и два его «ближайших соседа» образуют равносторонний треугольник. внутри икосаэдра. Поскольку каждая вершина принадлежит пяти треугольникам
равносторонних треугольников 20. Это грани правильного невыпуклого
многогранник, называемый большой икосаэдр . У него 20 лиц
(треугольники), 12 вершин и 30 ребер. В каждой вершине сходятся пять граней.
Большой икосаэдр имеет те же вершины, что и икосаэдр, который мы
началось с.
внутри икосаэдра. Поскольку каждая вершина принадлежит пяти треугольникам
равносторонних треугольников 20. Это грани правильного невыпуклого
многогранник, называемый большой икосаэдр . У него 20 лиц
(треугольники), 12 вершин и 30 ребер. В каждой вершине сходятся пять граней.
Большой икосаэдр имеет те же вершины, что и икосаэдр, который мы
началось с.
вернуться на главную страницу
Последнее обновление: 24 октября 2001 г.
Таблица бесконечных правильных многогранников
Таблица бесконечных правильных многогранников Многогранники — это поверхности, состоящие из многоугольников, каждое ребро которых является смежным.
до двух полигонов (или «граней»). Правильные многогранники – это те, которые составлены
правильного многоугольника только одного типа (у правильных многоугольников все длины ребер
и углы равны). Многогранники, которые замыкаются на себе, имеют конечное число
граней, но можно описать конструкции многогранников, которые
бесконечный. Другими словами, потребовалось бы бесконечное количество полигонов.
завершить такую фигуру, которая затем заполнила бы все пространство решеткой.
Конечно, бесконечная физическая модель не может быть полностью построена.
но можно построить достаточно большие сечения, чтобы показать их геометрию и доказать
их существование. Вот некоторые 2D и 3D
фотографии некоторых физических моделей.
Другими словами, потребовалось бы бесконечное количество полигонов.
завершить такую фигуру, которая затем заполнила бы все пространство решеткой.
Конечно, бесконечная физическая модель не может быть полностью построена.
но можно построить достаточно большие сечения, чтобы показать их геометрию и доказать
их существование. Вот некоторые 2D и 3D
фотографии некоторых физических моделей.
На рисунке выше (любезно предоставлено Стивом Датчом) показано
порции
одной такой фигуры с одинаковыми вершинами, каждая из которых окружена шестью
квадраты.
Щелкните ссылки в таблице ниже, чтобы просмотреть изображения и 3D-модели нескольких
более. Известный математик Х.С.М. Коксетер называет эти цифры «перекосом».
многогранники», в то время как Дж. Ричард Готт, III называет их «псевдополиэдрами».
Я назову их «Бесконечные многогранники», и когда они состоят только из
правильные многоугольники, я буду называть их «бесконечными правильными многогранниками» или просто
«ИРП». Правильные многогранники часто представляются с помощью обозначений, называемых
Символы Шлефли, состоящие из двух чисел в фигурных скобках.
Первое число — это количество сторон каждого многоугольника, а второе
— количество таких многоугольников, окружающих каждую вершину (т.е. угол).
Например, {4,3} — это куб, поскольку каждая вершина окружена тремя
квадраты. Совершенно естественно применять это обозначение к бесконечным многогранникам.
слишком.
Правильные многогранники часто представляются с помощью обозначений, называемых
Символы Шлефли, состоящие из двух чисел в фигурных скобках.
Первое число — это количество сторон каждого многоугольника, а второе
— количество таких многоугольников, окружающих каждую вершину (т.е. угол).
Например, {4,3} — это куб, поскольку каждая вершина окружена тремя
квадраты. Совершенно естественно применять это обозначение к бесконечным многогранникам.
слишком.
На первый взгляд кажется, что конечные и бесконечные многогранники сильно отличаются друг от друга. всякие звери но оказывается что математически их можно посмотреть точно так же через понятие поверхностного «рода». Мощная идея применения концепции рода к IRP, возможно, не нова. но следующее описание и таблица были недавно разработаны Лассе Винквист из Швеции.
Род поверхности является мерой ее сложности. Любая поверхность
который можно плавно деформировать в простую сферу, имеет род 0. Простейшая форма, в которую можно деформировать кофейную чашку, — это тор.
форма пончика), который имеет род 1. Кусок швейцарского сыра с множеством туннелей.
через него имеет род, равный числу тоннелей.
Простейшая форма, в которую можно деформировать кофейную чашку, — это тор.
форма пончика), который имеет род 1. Кусок швейцарского сыра с множеством туннелей.
через него имеет род, равный числу тоннелей.
Эйлер впервые открыл формулу F-E+V = 2-2 г которая связывает количество граней, ребер и вершин
многогранника к его роду. На первый взгляд кажется, что эта формула говорит
что род любого бесконечного многогранника также должен быть бесконечным. Что даже
кажется естественным, поскольку IRP имеют бесконечное количество туннелей. Этот вид
однако вводит в заблуждение. Гораздо более мощное применение формулы Эйлера
к бесконечным многогранникам — это применить его к минимальной повторяющейся единице, которая может
использоваться для создания каждого IRP. Кристаллографам знакомы повторяющиеся единицы.
которые описывают различные кристаллические структуры в терминах небольших кластеров
атомы, которые по-разному расположены в трех измерениях, очень похожие на
способы, которыми кирпичи могут быть выстроены в двух измерениях. Этот метод также полезен
и естественно при описании бесконечных многогранников. Представьте себе минимальное повторение
единица IRP, которая имеет топологию следующего рисунка:
Этот метод также полезен
и естественно при описании бесконечных многогранников. Представьте себе минимальное повторение
единица IRP, которая имеет топологию следующего рисунка:
Любой IRP с топологией, показанной на рисунке выше, будет удовлетворять этим требованиям. уравнения только при g=2. Теперь представьте повторяющийся блок с топологией
рисунок ниже:
уравнения только при g=2. Теперь представьте повторяющийся блок с топологией
рисунок ниже:

Космологи даже спорят, действительно ли сама Вселенная бесконечно, или же пространство повторяет себя именно таким образом. Посмотреть обложку статья в Научном апрельский выпуск журнала American за 1999 г. за прекрасное описание этого проблема. Если это так, то само пространство может иметь точно такую же форму, как требуется для описания некоторых IRP. Другой хорошей ссылкой является веб-страница один из авторов той статьи, которую он посвятил описанию таких мозаичные пространства через фамильяра игры, в которые вы можете играть в таких мозаичных пространствах.
Возможно, упрощенный IRP рода 3 может быть сгенерирован из упаковка кубиков. Щелкните следующую ссылку, чтобы просмотреть модели и описание что {4,6}. Например, бесконечный многогранник очень высокого рода, щелкните следующую ссылку, чтобы просмотреть один с род = 6 ш который может быть получен из упаковки ромбических додекаэдров.
В следующей таблице указано количество граней в повторяющихся единицах
правильные многогранники. Синие клетки представляют конечные регулярные
многогранники, а фиолетовые клетки представляют собой бесконечные правильные многогранники.
Желтые клетки представляют плоские мозаики, которые являются своего рода вырожденным классом
многогранники, которые находятся точно на границе конечных и бесконечных правильных многогранников.
Синие клетки представляют конечные регулярные
многогранники, а фиолетовые клетки представляют собой бесконечные правильные многогранники.
Желтые клетки представляют плоские мозаики, которые являются своего рода вырожденным классом
многогранники, которые находятся точно на границе конечных и бесконечных правильных многогранников.
Подчеркнутые записи таблицы являются ссылками на страницы, содержащие фотографии и описания отдельных IRP, а также ссылки на модели VRML те IRP, которые можно интерактивно вращать, масштабировать и размещать три измерения. Возможность интерактивной мозаики была запрограммирована Владимир Булатов. В настоящее время известно, что он работает со свободным Плагин браузера Cortona VRML от Parallel Graphics.
Владимир Булатов:
изображений и интерактивов
модели некоторых IRP
Стив Датч, «Гиперболические мозаики»
изображения и описания некоторых других
IRP Стива Датча
и еще
больше он взял из Уэллса ниже.


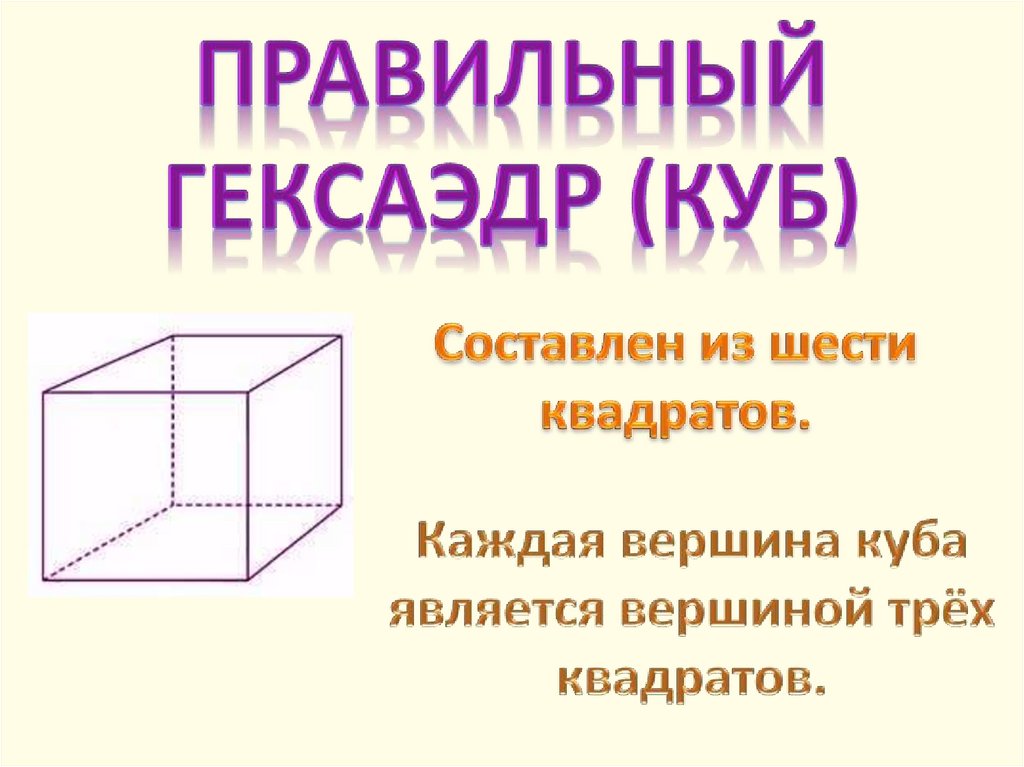

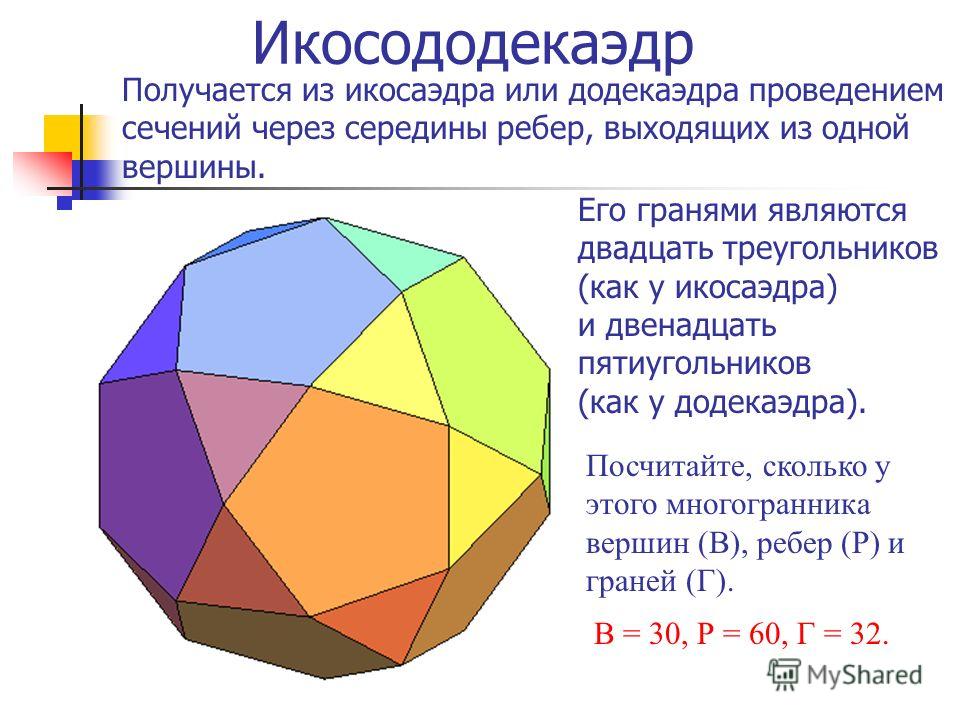


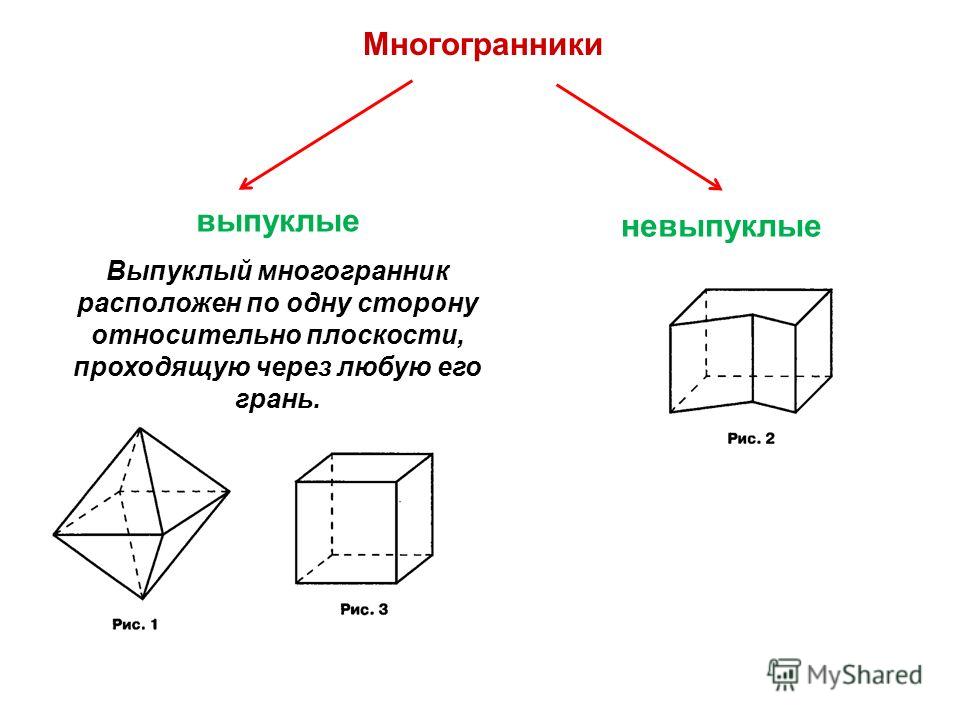
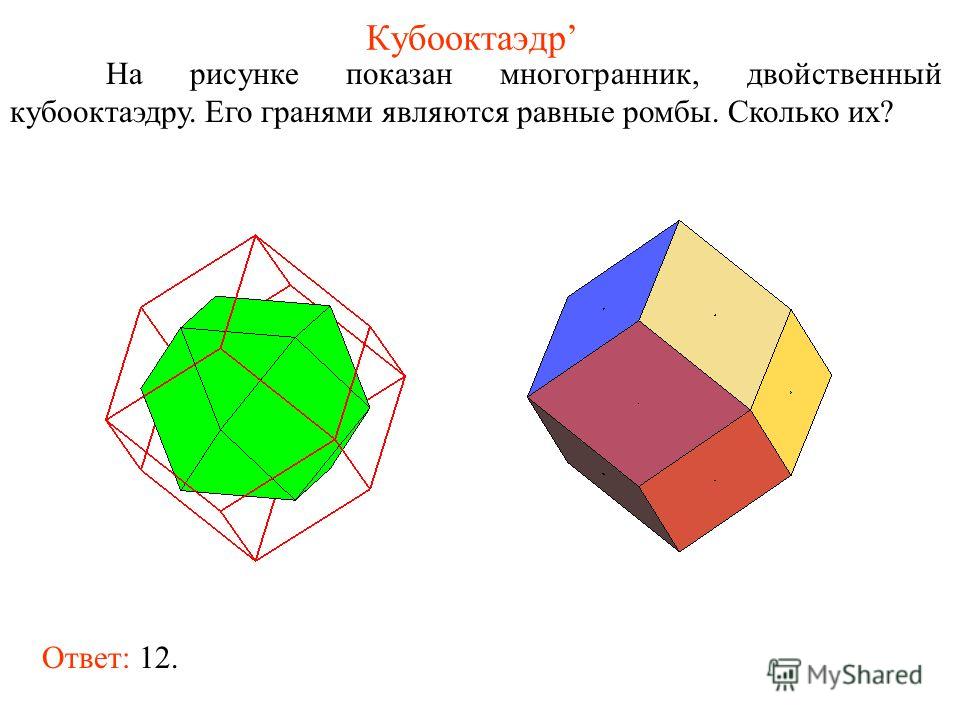
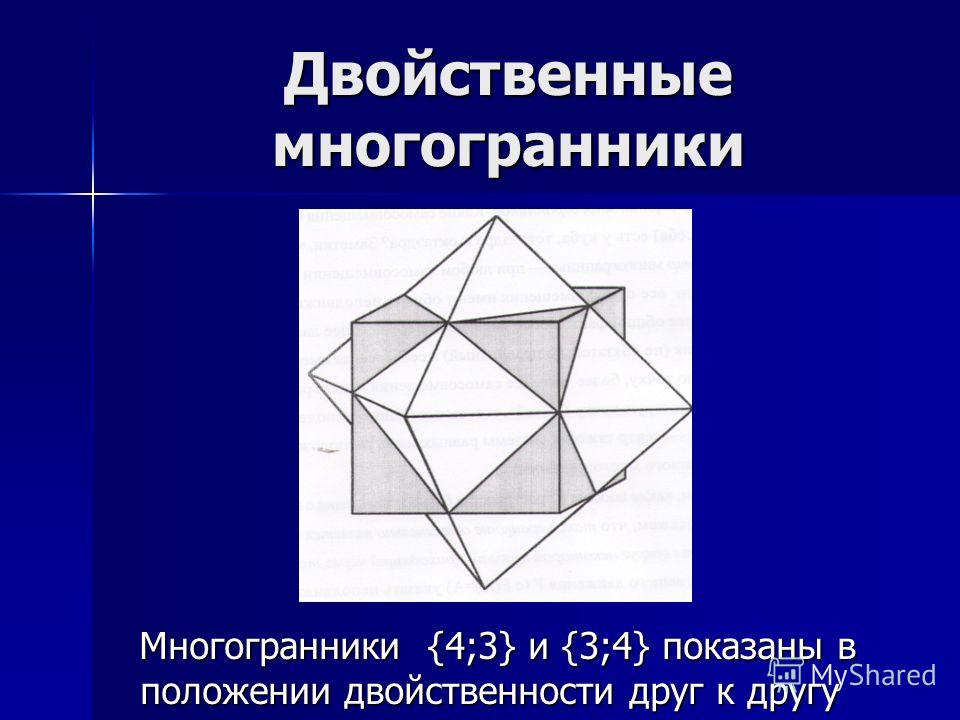 – Минск, 2007. – 322 с.
– Минск, 2007. – 322 с.