Формулы сокращенного умножения определения: Формулы сокращённого умножения — урок. Алгебра, 7 класс.

Фсу формулы сокращенного умножения с названиями. Формулы степеней и корней

Соблюдение Вашей конфиденциальности важно для нас. По этой причине, мы разработали Политику Конфиденциальности, которая описывает, как мы используем и храним Вашу информацию. Пожалуйста, ознакомьтесь с нашими правилами соблюдения конфиденциальности и сообщите нам, если у вас возникнут какие-либо вопросы.

Сбор и использование персональной информации

Под персональной информацией понимаются данные, которые могут быть использованы для идентификации определенного лица либо связи с ним.

От вас может быть запрошено предоставление вашей персональной информации в любой момент, когда вы связываетесь с нами.

Ниже приведены некоторые примеры типов персональной информации, которую мы можем собирать, и как мы можем использовать такую информацию.

Какую персональную информацию мы собираем:

• Когда вы оставляете заявку на сайте, мы можем собирать различную информацию, включая ваши имя, номер телефона, адрес электронной почты и т. д.

Как мы используем вашу персональную информацию:

• Собираемая нами персональная информация позволяет нам связываться с вами и сообщать об уникальных предложениях, акциях и других мероприятиях и ближайших событиях.
• Время от времени, мы можем использовать вашу персональную информацию для отправки важных уведомлений и сообщений.
• Мы также можем использовать персональную информацию для внутренних целей, таких как проведения аудита, анализа данных и различных исследований в целях улучшения услуг предоставляемых нами и предоставления Вам рекомендаций относительно наших услуг.
• Если вы принимаете участие в розыгрыше призов, конкурсе или сходном стимулирующем мероприятии, мы можем использовать предоставляемую вами информацию для управления такими программами.

Раскрытие информации третьим лицам

Мы не раскрываем полученную от Вас информацию третьим лицам.

Исключения:

• В случае если необходимо — в соответствии с законом, судебным порядком, в судебном разбирательстве, и/или на основании публичных запросов или запросов от государственных органов на территории РФ — раскрыть вашу персональную информацию. Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.
• В случае реорганизации, слияния или продажи мы можем передать собираемую нами персональную информацию соответствующему третьему лицу – правопреемнику.

Защита персональной информации

Мы предпринимаем меры предосторожности — включая административные, технические и физические — для защиты вашей персональной информации от утраты, кражи, и недобросовестного использования, а также от несанкционированного доступа, раскрытия, изменения и уничтожения.

Соблюдение вашей конфиденциальности на уровне компании

Для того чтобы убедиться, что ваша персональная информация находится в безопасности, мы доводим нормы соблюдения конфиденциальности и безопасности до наших сотрудников, и строго следим за исполнением мер соблюдения конфиденциальности.

Применяют для упрощения вычислений, а также разложение многочленов на множители, быстрого умножения многочленов. 7.

Решение. Что такое бином Ньютона Вы вероятно уже знаете. Если нет то ниже приведены биномиальные коэффициенты

Они образуются следующим образом: по краю идут единицы, коэффициенты между ними в нижней строке образуют суммированием соседних верхних. Если ищем разницу в каком-то степени, то знаки в расписании чередуются от плюса к минусу. Таким образом для седьмого порядка получим такой расклад

Внимательно также посмотрите как меняются показатели — для первой переменной они уменьшаются на единицу в каждом следующем слагаемом, соответственно для второй — на единицу растут. В сумме показатели всегда должны быть равны степени разложения (=7 ).

Думаю на основе приведенного выше материала Вы сможете решить задачи на бином Ньютона. Изучайте формулы сокращенного умножения и применяйте везде, где это может упростить вычисления и сэкономит время выполнения задания.

Формулы степеней используют в процессе сокращения и упрощения сложных выражений, в решении уравнений и неравенств.

Число c является n -ной степенью числа

a когда:

Операции со степенями.

1. Умножая степени с одинаковым основанием их показатели складываются:

a m ·a n = a m + n .

2. В делении степеней с одинаковым основанием их показатели вычитаются:

3. Степень произведения 2-х либо большего числа множителей равняется произведению степеней этих сомножителей:

(abc…) n = a n · b n · c n …

4. Степень дроби равняется отношению степеней делимого и делителя:

(a/b) n = a n /b n .

5. Возводя степень в степень, показатели степеней перемножают:

(a m) n = a m n .

Каждая вышеприведенная формула верна в направлениях слева направо и наоборот.

Например . (2·3·5/15)² = 2²·3²·5²/15² = 900/225 = 4 .

Операции с корнями.

1. Корень из произведения нескольких сомножителей равняется произведению корней из этих сомножителей:

2. Корень из отношения равен отношению делимого и делителя корней:

3. При возведении корня в степень довольно возвести в эту степень подкоренное число:

4. Если увеличить степень корня в n раз и в тоже время возвести в n -ую степень подкоренное число, то значение корня не поменяется:

5. Если уменьшить степень корня в n раз и в тоже время извлечь корень n -ой степени из подкоренного числа, то значение корня не поменяется:

Степень с отрицательным показателем. Степень некоторого числа с неположительным (целым) показателем определяют как единицу, деленную на степень того же числа с показателем, равным абсолютной величине неположительного показателя:

Формулу a m :a n =a m — n можно использовать не только при m > n , но и при m n .

Например . a 4:a 7 = a 4 — 7 = a -3

.

Чтобы формула a m :a n =a m — n стала справедливой при m=n , нужно присутствие нулевой степени.

Степень с нулевым показателем. Степень всякого числа, не равного нулю, с нулевым показателем равняется единице.

Например . 2 0 = 1,(-5) 0 = 1,(-3/5) 0 = 1.

Степень с дробным показателем. Чтобы возвести действительное число а в степень m/n , необходимо извлечь корень n -ой степени из m -ой степени этого числа а .

Формулы сокращенного умножения (ФСУ) применяются для возведения в степень и умножения чисел и выражений. Часто эти формулы позволяют произвести вычисления более компактно и быстро.

В данной статье мы перечислим основные формулы сокращенного умножения, сгруппируем их в таблицу, рассмотрим примеры использования этих формул, а также остановимся на принципах доказательств формул сокращенного умножения.

Yandex.RTB R-A-339285-1

Впервые тема ФСУ рассматривается в рамках курса «Алгебра» за 7 класс. Приведем ниже 7 основных формул.

Формулы сокращенного умножения

1. формула квадрата суммы: a + b 2 = a 2 + 2 a b + b 2
2. формула квадрата разности: a — b 2 = a 2 — 2 a b + b 2
3. формула куба суммы: a + b 3 = a 3 + 3 a 2 b + 3 a b 2 + b 3
4. формула куба разности: a — b 3 = a 3 — 3 a 2 b + 3 a b 2 — b 3
5. формула разности квадратов: a 2 — b 2 = a — b a + b
6. формула суммы кубов: a 3 + b 3 = a + b a 2 — a b + b 2
7. формула разности кубов: a 3 — b 3 = a — b a 2 + a b + b 2

Буквами a, b, c в данных выражениях могут быть любые числа, переменные или выражения. Для удобства использования лучше выучить семь основных формул наизусть. Сведем их в таблицу и приведем ниже, обведя рамкой.

Первые четыре формулы позволяют вычислять соответственно квадрат или куб суммы или разности двух выражений.

Пятая формула вычисляет разность квадратов выражений путем произведения их суммы и разности.

Шестая и седьмая формулы — соответственно умножение суммы и разности выражений на неполный квадрат разности и неполный квадрат суммы.

Формула сокращенного умножения иногда еще называют тождествами сокращенного умножения. В этом нет ничего удивительного, так как каждое равенство представляет собой тождество.

При решении практических примеров часто используют формулы сокращенного умножения с переставленными местами левыми и правыми частями. Это особенно удобно, когда имеет место разложение многочлена на множители.

Дополнительные формулы сокращенного умножения

Не будем ограничиваться курсом 7 класса по алгебре и добавим в нашу таблицу ФСУ еще несколько формул.

Во-первых, рассмотрим формулу бинома Ньютона.

a + b n = C n 0 · a n + C n 1 · a n — 1 · b + C n 2 · a n — 2 · b 2 + . . + C n n — 1 · a · b n — 1 + C n n · b n

Здесь C n k — биномиальные коэффициенты, которые стоят в строке под номером n в треугольнике паскаля. Биномиальные коэффициенты вычисляются по формуле:

C n k = n ! k ! · (n — k) ! = n (n — 1) (n — 2) . . (n — (k — 1)) k !

Как видим, ФСУ для квадрата и куба разности и суммы — это частный случай формулы бинома Ньютона при n=2 и n=3соответственно.

Но что, если слагаемых в сумме, которую нужно возвести в степень, больше, чем два? Полезной будет формула квадрата суммы трех, четырех и более слагаемых.

a 1 + a 2 + . . + a n 2 = a 1 2 + a 2 2 + . . + a n 2 + 2 a 1 a 2 + 2 a 1 a 3 + . . + 2 a 1 a n + 2 a 2 a 3 + 2 a 2 a 4 + . . + 2 a 2 a n + 2 a n — 1 a n

Еще одна формула, которая может пригодится — формула формула разности n-ых степеней двух слагаемых.

a n — b n = a — b a n — 1 + a n — 2 b + a n — 3 b 2 + . . + a 2 b n — 2 + b n — 1

Эту формулу обычно разделяют на две формулы — соответственно для четных и нечетных степеней.

Для четных показателей 2m:

a 2 m — b 2 m = a 2 — b 2 a 2 m — 2 + a 2 m — 4 b 2 + a 2 m — 6 b 4 + . . + b 2 m — 2

Для нечетных показателей 2m+1:

a 2 m + 1 — b 2 m + 1 = a 2 — b 2 a 2 m + a 2 m — 1 b + a 2 m — 2 b 2 + . . + b 2 m

Формулы разности квадратов и разности кубов, как вы догадались, являются частными случаями этой формулы при n = 2 и n = 3 соответственно. Для разности кубов b также заменяется на — b .

Как читать формулы сокращенного умножения?

Дадим соответствующие формулировки для каждой формулы, но сначала разберемся с принципом чтения формул. Удобнее всего делать это на примере. Возьмем самую первую формулу квадрата суммы двух чисел.

a + b 2 = a 2 + 2 a b + b 2 .

Говорят: квадрат суммы двух выражений a и b равен сумме квадрата первого выражения, удвоенного произведения выражений и квадрата второго выражения.

Все остальные формулы читаются аналогично. Для квадрата разности a — b 2 = a 2 — 2 a b + b 2 запишем:

квадрат разности двух выражений a и b равен сумме квадратов этих выражений минус удвоенное произведение первого и второго выражения.

Прочитаем формулу a + b 3 = a 3 + 3 a 2 b + 3 a b 2 + b 3 . Куб суммы двух выражений a и b равен сумме кубов этих выражений, утроенного произведения квадрата первого выражения на второе и утроенного произведения квадрата второго выражения на первое выражение.

Переходим к чтению формулы для разности кубов a — b 3 = a 3 — 3 a 2 b + 3 a b 2 — b 3 . Куб разности двух выражений a и b равен кубу первого выражения минус утроенное произведение квадрата первого выражения на второе, плюс утроенное произведение квадрата второго выражения на первое выражение, минус куб второго выражения.

Пятая формула a 2 — b 2 = a — b a + b (разность квадратов) читается так: разность квадратов двух выражений равна произведению разности и суммы двух выражений.

Выражения типа a 2 + a b + b 2 и a 2 — a b + b 2 для удобства называют соответственно неполным квадратом суммы и неполным квадратом разности.

С учетом этого, формулы суммы и разности кубов прочитаются так:

Сумма кубов двух выражений равна произведению суммы этих выражений на неполный квадрат их разности.

Разность кубов двух выражений равна произведению разности этих выражений на неполный квадрат их суммы.

Доказательство ФСУ

Доказать ФСУ довольно просто. Основываясь на свойствах умножения, проведем умножение частей формул в скобках.

Для примера рассмотрим формулу квадрата разности.

a — b 2 = a 2 — 2 a b + b 2 .

Чтобы возвести выражение во вторую степень нужно это выражение умножить само на себя.

a — b 2 = a — b a — b .

Раскроем скобки:

a — b a — b = a 2 — a b — b a + b 2 = a 2 — 2 a b + b 2 .

Формула доказана. Остальные ФСУ доказываются аналогично.

Примеры применения ФСУ

Цель использования формул сокращенного умножения — быстрое и краткое умножение и возведение выражений в степень. Однако, это не вся сфера применения ФСУ. Они широко используются при сокращении выражений, сокращении дробей, разложении многочленов на множители. Приведем примеры.

Пример 1. ФСУ

Упростим выражение 9 y — (1 + 3 y) 2 .

Применим формулу суммы квадратов и получим:

9 y — (1 + 3 y) 2 = 9 y — (1 + 6 y + 9 y 2) = 9 y — 1 — 6 y — 9 y 2 = 3 y — 1 — 9 y 2

Пример 2. ФСУ

Сократим дробь 8 x 3 — z 6 4 x 2 — z 4 .

Замечаем, что выражение в числителе — разность кубов, а в знаменателе — разность квадратов.

8 x 3 — z 6 4 x 2 — z 4 = 2 x — z (4 x 2 + 2 x z + z 4) 2 x — z 2 x + z .

Сокращаем и получаем:

8 x 3 — z 6 4 x 2 — z 4 = (4 x 2 + 2 x z + z 4) 2 x + z

Также ФСУ помогают вычислять значения выражений. Главное — уметь заметить, где применить формулу. Покажем это на примере.

Возведем в квадрат число 79 . Вместо громоздких вычислений, запишем:

79 = 80 — 1 ; 79 2 = 80 — 1 2 = 6400 — 160 + 1 = 6241 .

Казалось бы, сложное вычисление проведено быстро всего лишь с использованием формул сокращенного умножения и таблицы умножения.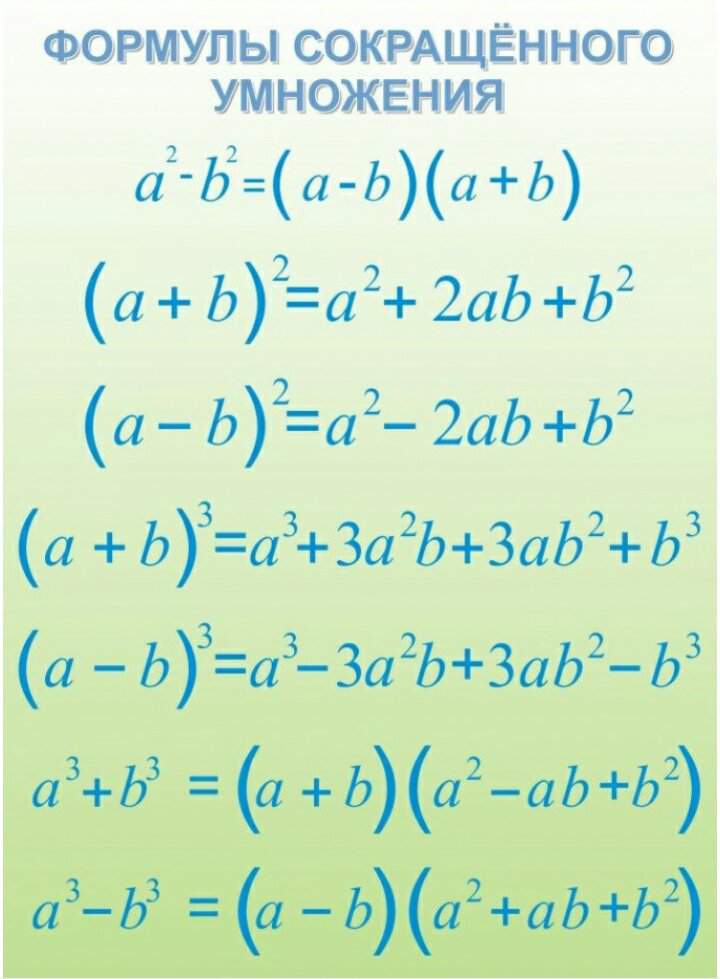

Еще один важный момент — выделение квадрата двучлена. Выражение 4 x 2 + 4 x — 3 можно преобразовать в вид 2 x 2 + 2 · 2 · x · 1 + 1 2 — 4 = 2 x + 1 2 — 4 . Такие преобразования широко используются в интегрировании.

Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter

Соблюдение Вашей конфиденциальности важно для нас. По этой причине, мы разработали Политику Конфиденциальности, которая описывает, как мы используем и храним Вашу информацию. Пожалуйста, ознакомьтесь с нашими правилами соблюдения конфиденциальности и сообщите нам, если у вас возникнут какие-либо вопросы.

Сбор и использование персональной информации

Под персональной информацией понимаются данные, которые могут быть использованы для идентификации определенного лица либо связи с ним.

От вас может быть запрошено предоставление вашей персональной информации в любой момент, когда вы связываетесь с нами.

Ниже приведены некоторые примеры типов персональной информации, которую мы можем собирать, и как мы можем использовать такую информацию.

Какую персональную информацию мы собираем:

• Когда вы оставляете заявку на сайте, мы можем собирать различную информацию, включая ваши имя, номер телефона, адрес электронной почты и т.д.

Как мы используем вашу персональную информацию:

• Собираемая нами персональная информация позволяет нам связываться с вами и сообщать об уникальных предложениях, акциях и других мероприятиях и ближайших событиях.
• Время от времени, мы можем использовать вашу персональную информацию для отправки важных уведомлений и сообщений.
• Мы также можем использовать персональную информацию для внутренних целей, таких как проведения аудита, анализа данных и различных исследований в целях улучшения услуг предоставляемых нами и предоставления Вам рекомендаций относительно наших услуг.
• Если вы принимаете участие в розыгрыше призов, конкурсе или сходном стимулирующем мероприятии, мы можем использовать предоставляемую вами информацию для управления такими программами.

Раскрытие информации третьим лицам

Мы не раскрываем полученную от Вас информацию третьим лицам.

Исключения:

• В случае если необходимо — в соответствии с законом, судебным порядком, в судебном разбирательстве, и/или на основании публичных запросов или запросов от государственных органов на территории РФ — раскрыть вашу персональную информацию. Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.
• В случае реорганизации, слияния или продажи мы можем передать собираемую нами персональную информацию соответствующему третьему лицу – правопреемнику.

Защита персональной информации

Мы предпринимаем меры предосторожности — включая административные, технические и физические — для защиты вашей персональной информации от утраты, кражи, и недобросовестного использования, а также от несанкционированного доступа, раскрытия, изменения и уничтожения.

Соблюдение вашей конфиденциальности на уровне компании

Для того чтобы убедиться, что ваша персональная информация находится в безопасности, мы доводим нормы соблюдения конфиденциальности и безопасности до наших сотрудников, и строго следим за исполнением мер соблюдения конфиденциальности.

Формулы сокращенного умножения:

Квадрат суммы

(a + b)² = a² + 2ab + b²

Квадрат разности

(a — b)² = a² — 2ab + b²

Разность квадратов

a² – b² = (a + b)(a – b)

Куб суммы

(a + b)³ = a³ + 3a²b + 3ab² + b³

Куб разности

(a — b)³ = a³ — 3a²b + 3ab² — b³

Сумма кубов

a³ + b³ = (a + b)( a² — ab + b²)

Разность кубов

a³ – b³ = (a – b)( a² + ab + b²)

Арифметическая прогрессия

Последовательность, у которой задан первый член a₁, а каждый следующий равен предыдущему, сложенному с одним и тем же числом d, называется арифметической прогрессией:

a_n+1 = a_n + d, где d – разность прогрессии.

an = a1 + d(n – 1)	an = ak + d(n – k)
2an = an-1 + an+1	an + am = ak + al, если n + m = k + l

Геометрическая прогрессия

Определение: Последовательность, у которой задан первый член b₁  0, а каждый следующий равен предыдущему, умноженному на одно и то же число q  0, называется геометрической прогрессией:

b_n+1 = b_n q, где q – знаменатель прогрессии.

bn = b1 qn – 1	bn = bk qn – k
bn2 = bn-1 bn+1	bn bm = bk bl, если n + m = k + l
	Бесконечно убывающая геометрическая прогрессия

Степень

Определение

, если n – натуральное число

a – основание степени, n — показатель степени

Формулы

Арифметический квадратный корень

Определение

Арифметическим квадратным корнем из неотрицательного числа a — () — называется неотрицательное число, квадрат которого равен a.

Корнем k–ой степени из a (k — нечетное) называется число, k-ая степень которого равна a.

Квадратное уравнение:

ax² + bx + c = 0

Дискриминант: D = b² – 4ac

Если

D < 0

D = 0

D > 0

то уравнение

не имеет корней

имеет один корень

имеет два корня

x  

x₁

x₁; x₂

Теорема Виета

Приведенное квадратное уравнение: x² + px + q = 0

x₁ + x₂ = — p

x₁  x₂ = q

x₁+x₂ = -b/a

x₁ x₂ = c/a

Логарифм

Определение

Логарифмом числа по b основанию a называется такое число, обозначаемое , что .

a — основание логарифма (a > 0, a  1),

b — логарифмическое число ( b > 0)

Десятичный логарифм:

Натуральный логарифм: где e = 2,71828

Формулы

Дроби

Сложение

Деление с остатком:

	Признак	Пример
На 2	Числа, оканчивающиеся нулём или четной цифрой	……. 6
На 4	Числа, у которых две последние цифры нули или выражают число, делящееся на 4.	……12
На 8	Числа, у которых три последние цифры нули или выражают число, делящееся на 8.	…..104
На 3	Числа, сумма цифр которых делится на 3.	570612
На 9	Числа, сумма цифр которых делится на 9.	359451
На 5	Числа, оканчивающиеся нулём или цифрой 5.	…….5
На 25	Числа, у которых две последние цифры нули или выражают число, делящееся на 25.	……75
На 10	Числа, оканчивающиеся нулём.	……0

Формула деления с остатком: n = mk + r,

где n – делимое, m — делитель, k — частное, r – остаток: 0  r < m

Пример:

Любое число можно представить в виде:

n = 2k + r, где r = {0; 1}

или n = 4k + r, где r = {0; 1; 2; 3}

Вычитание

Умножение

Деление

Составная дробь

Делимость натуральных чисел:

Пусть n : m = k, где n, m, k – натуральные числа.

Тогда m – делитель числа n, а n – кратно числу m.

Число n называется простым, если его делителями являются

только единица и само число n.

Множество простых чисел: {2; 3; 5; 7; 11; 13; . . .; 41; 43; 47 и т.д.}

Числа n и m называются взаимно простыми, если у них нет общихделителей, кроме единицы.

Десятичные числа:

Стандартный вид: 317,3 = 3,173 10² ; 0,00003173 = 3,173 10^-5

Форма записи: 3173 = 3 1000 + 1 100 + 7 10 + 3

Модуль

Формулы Определение

• x  0

• x — y  x — y

• -x=x

• x  y = x  y

• x  x

• x : y =x : y

• x + y  x + y

x² = x²

Неравенства

Определения:

Неравенством называется выражение вида:

a < b (a  b), a > b (a  b)

Основные свойства:

Модуль: уравнения и неравенства

1.

2.

3.

4.

5.

Периодическая дробь

Правило:

Признаки делимости чисел:

Проценты

Определение:

Процентом называется сотая часть от числа. 1%A = 0,01A

Основные типы задач на проценты:

Сколько процентов составляет число A от числа B?

B — 100%

A — x%

Сложные проценты.

Число A увеличилось на 20%, а затем полученное число уменьшили на 25%.

Как, в итоге, изменилось исходное число?

1. A₁ = (100% + 20%)A = 120%A = 1,2A

2. A₂ = (100% — 25%)A₁=75%A₁ = 0,75A₁ = 0,751,2A = 0,9A = 90%A

3. A₁ – A = 90%A – 100%A = -10%A

 Ответ: уменьшилось на 10%. Изменение величины.

Как изменится время, если скорость движения увеличится на 25%?

 Ответ: уменьшится на 20%

 Ответ: уменьшится на 20%

Среднее арифметическое, геометрическое

Среднее арифметическое:

Среднее геометрическое:

Уравнение движения

Пусть — уравнение движения материальной точки, где S – путь, t – время движения.

Тогда: ,

где – скорость, — ускорение.

Определенный интеграл

Первообразная элементарных функций

№	f(x)	F(x)		№	f(x)	F(x)
1				6
2
				7
3
4				8
5				9

Правила вычисления первообразной функции

Определение: Функция F(x) называется первообразной для функции f(x), если .

Функция	Первообразная

Правила вычисления производной функции

	Сложная функция:

7 класс. Алгебра. Формулы сокращенного умножения.

— Формулы сокращенного умножения.

Комментарии преподавателя

На данном уроке мы познакомимся с формулами квадрата суммы и квадрата разности и выведем их. Формулу квадрата суммы докажем геометрически. Кроме того, решим много различных примеров с применением этих формул.

 

Рас­смот­рим фор­му­лу квад­ра­та суммы:

.

Итак, мы вы­ве­ли фор­му­лу квад­ра­та суммы:

.

Сло­вес­но эта фор­му­ла вы­ра­жа­ет­ся так: квад­рат суммы равен квад­ра­ту пер­во­го числа плюс удво­ен­ное про­из­ве­де­ние пер­во­го числа на вто­рое плюс квад­рат вто­ро­го числа.

Дан­ную фор­му­лу легко пред­ста­вить гео­мет­ри­че­ски.

Рас­смот­рим квад­рат со сто­ро­ной :

 – пло­щадь квад­ра­та.

С дру­гой сто­ро­ны, этот же квад­рат можно пред­ста­вить иначе, раз­бив сто­ро­ну на а и b (рис. 1).

Рис. 1. Квад­рат

Тогда пло­щадь квад­ра­та можно пред­ста­вить в виде суммы пло­ща­дей:

.

По­сколь­ку квад­ра­ты были оди­на­ко­вы, то их пло­ща­ди равны, зна­чит:

 .

Итак, мы до­ка­за­ли гео­мет­ри­че­ски фор­му­лу квад­ра­та суммы.

Рас­смот­рим при­ме­ры:

При­мер 1:

.

Ком­мен­та­рий: при­мер решен с при­ме­не­ни­ем фор­му­лы квад­ра­та суммы.

При­мер 2:

.

При­мер 3:

+1.

Вы­ве­дем фор­му­лу квад­ра­та раз­но­сти:

.

Итак, мы вы­ве­ли фор­му­лу квад­ра­та раз­но­сти:

.

Сло­вес­но эта фор­му­ла вы­ра­жа­ет­ся так: квад­рат раз­но­сти равен квад­ра­ту пер­во­го числа минус удво­ен­ное про­из­ве­де­ние пер­во­го числа на вто­рое плюс квад­рат вто­ро­го числа.

Рас­смот­рим при­ме­ры:

При­мер 4:

.

При­мер 5:

.

При­мер 6:

.

Фор­му­лы квад­ра­та суммы и квад­ра­та раз­но­сти могут ра­бо­тать как слева на­пра­во, так и спра­ва на­ле­во. При ис­поль­зо­ва­нии слева на­пра­во это будут фор­му­лы со­кра­щен­но­го умно­же­ния, они при­ме­ня­ют­ся при вы­чис­ле­нии и пре­об­ра­зо­ва­нии при­ме­ров. А при ис­поль­зо­ва­нии спра­ва на­ле­во – фор­му­лы раз­ло­же­ния на мно­жи­те­ли.

Рас­смот­рим при­ме­ры, в ко­то­рых нужно раз­ло­жить за­дан­ный мно­го­член на мно­жи­те­ли, при­ме­няя фор­му­лы квад­ра­та суммы и квад­ра­та раз­но­сти. Для этого нужно очень вни­ма­тель­но по­смот­реть на мно­го­член и опре­де­лить, как имен­но его пра­виль­но раз­ло­жить.

При­мер 7:

.

Ком­мен­та­рий: для того, чтобы раз­ло­жить мно­го­член на мно­жи­те­ли, нужно опре­де­лить, что пред­став­ле­но в дан­ном вы­ра­же­нии. Итак, мы видим квад­рат  и квад­рат еди­ни­цы. Те­перь нужно найти удво­ен­ное про­из­ве­де­ние – это . Итак, все необ­хо­ди­мые эле­мен­ты есть, нужно толь­ко опре­де­лить, это квад­рат суммы или раз­но­сти. Перед удво­ен­ным про­из­ве­де­ни­ем стоит знак плюс, зна­чит, перед нами квад­рат суммы.

При­мер 8:

.

При­мер 9:

.

Ком­мен­та­рий: для ре­ше­ния дан­но­го при­ме­ра нужно вы­не­сти минус за скоб­ки, чтобы можно было уви­деть нуж­ную нам фор­му­лу.

Пе­рей­дем к ре­ше­нию урав­не­ний:

При­мер 10:

;

;

;

;

;

.

Ком­мен­та­рий: для ре­ше­ния дан­но­го урав­не­ния нужно упро­стить левую часть, при­ме­няя фор­му­лу раз­но­сти квад­ра­тов и квад­ра­та раз­но­сти, после этого при­ве­сти по­доб­ные члены. После этого пе­ре­не­сти все неиз­вест­ные в левую часть, а сво­бод­ный член в пра­вую и ре­шить эле­мен­тар­ное ли­ней­ное урав­не­ние.

При­мер 11:

Вы­чис­лить: .

Ком­мен­та­рий: для ре­ше­ния дан­но­го при­ме­ра нужно при­ме­нить фор­му­лы раз­но­сти квад­ра­тов и квад­ра­та суммы, после этого со­кра­тить по­лу­чен­ную дробь.

При­мер 12:

До­ка­зать ра­вен­ство:

.

Раз­ло­жим на мно­жи­те­ли :

.

Из каж­до­го мно­жи­те­ля вы­не­сем минус еди­ни­цу за скоб­ки:

.

Мы до­ка­за­ли ра­вен­ство (a — b)2 = (b — a)2.

Дан­ное ра­вен­ство яв­ля­ет­ся очень по­лез­ным при упро­ще­нии вы­ра­же­ний. Рас­смот­рим при­мер.

При­мер 13:

Раз­ло­жить на мно­жи­те­ли: .

При­мер 14:

До­ка­жи­те, что квад­рат вся­ко­го нечет­но­го числа, умень­шен­ный на еди­ни­цу, де­лит­ся на во­семь.

Пред­ста­вим про­из­воль­ное нечет­ное число как , а его квад­рат, со­от­вет­ствен­но, как . За­пи­шем вы­ра­же­ние со­глас­но усло­вию:

.

Упро­стим по­лу­чен­ное вы­ра­же­ние:

.

Чтобы до­ка­зать, что по­лу­чен­ное вы­ра­же­ние крат­но вось­ми, нам нужно до­ка­зать, что оно де­лит­ся на 2 и на 4. Оче­вид­но, что вы­ра­же­ние крат­но че­ты­рем, так как в нем есть мно­жи­тель 4. По­это­му нам нужно до­ка­зать, что  де­лит­ся на 2.

За­пись  – это про­из­ве­де­ние двух по­сле­до­ва­тель­ных чисел, а оно все­гда крат­но двум, так как из двух по­сле­до­ва­тель­ных чисел одно все­гда будет чет­ным, а вто­рое, со­от­вет­ствен­но, нечет­ным, а про­из­ве­де­ние чет­но­го числа на нечет­ное крат­но двум, зна­чит, вы­ра­же­ние  крат­но вось­ми. Итак, мы до­ка­за­ли, что квад­рат вся­ко­го нечет­но­го числа, умень­шен­ный на еди­ни­цу, де­лит­ся на во­семь.

Вывод: на дан­ном уроке мы вы­ве­ли фор­му­лы квад­ра­та суммы и квад­ра­та раз­но­сти и на­учи­лись ре­шать самые раз­но­об­раз­ные за­да­чи на при­ме­не­ние этих фор­мул.

На данном уроке мы вспомним выученные ранее формулы сокращенного умножения, а именно квадрата суммы и квадрата разности. Выведем формулу разности квадратов и решим много различных типовых задач на применение этой формулы. Кроме того, решим задачи на комплексное применение нескольких формул.

 

На­пом­ним, что на преды­ду­щем уроке мы рас­смот­ре­ли фор­му­лы квад­ра­та суммы и квад­ра­та раз­но­сти. За­пи­шем их:

.

Вы­ве­дем фор­му­лу раз­но­сти квад­ра­тов. Вы­пол­ним умно­же­ние дву­чле­нов по пра­ви­лу:

.

Итак, .

Сло­вес­но дан­ная фор­му­ла вы­гля­дит так: раз­ность квад­ра­тов двух вы­ра­же­ний равна про­из­ве­де­нию суммы этих вы­ра­же­ний на их раз­ность.

 мы на­зы­ва­ем раз­но­стью квад­ра­тов.

 мы на­зы­ва­ем квад­ра­том раз­но­сти, не сле­ду­ет пу­тать два этих вы­ра­же­ния.

Рас­смот­рим при­ме­не­ние фор­мул в ти­по­вых за­да­чах. Нач­нем с задач на пря­мое при­ме­не­ние фор­му­лы.

При­мер 1: .

При­мем  за ,  за , по­лу­чим:

.

Рас­пи­шем со­глас­но фор­му­ле:

.

Пе­рей­дем к ис­ход­ным пе­ре­мен­ным:

.

Стан­дарт­ная ошиб­ка:

по­ме­ня­ем в скоб­ке со зна­ком плюс сла­га­е­мые ме­ста­ми, по­лу­чим:

.

Часто при такой за­пи­си пу­та­ют, какой квад­рат сле­ду­ет вы­честь из ка­ко­го:

.

При­мер 2:

.

Ком­мен­та­рий: если воз­ни­ка­ют за­труд­не­ния, можно, ана­ло­гич­но преды­ду­ще­му при­ме­ру, за­ме­нить одно из вы­ра­же­ний на а, а вто­рое на b, чтобы легче было уви­деть нуж­ную фор­му­лу.

При­мер 3:

.

Ком­мен­та­рий: в дан­ном при­ме­ре сле­ду­ет быть вни­ма­тель­ны­ми и не до­пу­стить ти­по­вую ошиб­ку, опи­сан­ную выше. Для этого удоб­но в пер­вой скоб­ке по­ме­нять сла­га­е­мые ме­ста­ми.

Пе­рей­дем к за­да­чам на об­рат­ное при­ме­не­ние фор­му­лы – раз­ло­же­ние на мно­жи­те­ли.

При­мер 4:

.

Ком­мен­та­рий: при­мер решен из опре­де­ле­ния раз­но­сти квад­ра­тов. Нужно толь­ко опре­де­лить, квад­ра­том ка­ко­го вы­ра­же­ния яв­ля­ет­ся пер­вый од­но­член и вто­рой.

При­мер 5:

.

При­мер 6:

Ком­мен­та­рий: в дан­ном при­ме­ре нужно несколь­ко раз при­ме­нить изу­ча­е­мую фор­му­лу. Может быть за­да­но из по­лу­чен­ной в конце длин­ной фор­му­лы по­лу­чить стан­дарт­ный вид мно­го­чле­на, тогда нужно по­сте­пен­но пе­ре­мно­жать скоб­ки между собой и сво­ра­чи­вать вы­ра­же­ние до про­стей­ше­го.

Сле­ду­ю­щий тип задач – ком­би­ни­ро­ван­ное при­ме­не­ние несколь­ких фор­мул.

При­мер 7 – упро­стить:

.

Ком­мен­та­рий: в дан­ном при­ме­ре нужно при­ме­нить две фор­му­лы: раз­но­сти квад­ра­тов и квад­ра­та раз­но­сти, в по­лу­чен­ном вы­ра­же­нии при­ве­сти по­доб­ные члены.

При­мер 8:

.

Пе­рей­дем к ре­ше­нию урав­не­ний.

При­мер 9:

.

Рас­смот­рим вы­чис­ли­тель­ные за­да­чи.

При­мер 10:

.

При­мер 11:

.

Вывод: на дан­ном уроке мы вы­ве­ли фор­му­лу раз­но­сти квад­ра­тов и ре­ши­ли много раз­лич­ных при­ме­ров, а имен­но урав­не­ния, вы­чис­ли­тель­ные за­да­чи, за­да­ния на пря­мое и об­рат­ное ис­поль­зо­ва­ние вы­ве­ден­ной фор­му­лы и дру­гие. Кроме того, ре­ши­ли несколь­ко задач на ком­плекс­ное при­ме­не­ние несколь­ких фор­мул.

На данном уроке мы продолжим изучать формулы сокращенного умножения, а именно рассмотрим формулы разности и суммы кубов. Кроме того, мы решим различные типовые задачи на применение данных формул.

 

При изу­че­нии фор­мул со­кра­щен­но­го умно­же­ния мы уже изу­чи­ли:

 – квад­рат суммы и раз­но­сти;

 – раз­ность квад­ра­тов.

Вы­ве­дем фор­му­лу раз­но­сти кубов.

.

Наша за­да­ча – до­ка­зать, что при рас­кры­тии ско­бок в пра­вой части и при­ве­де­нии по­доб­ных сла­га­е­мых мы при­дем в ре­зуль­та­те к левой части.

Вы­пол­ня­ем умно­же­ние мно­го­чле­нов:

.

Что и тре­бо­ва­лось до­ка­зать.

Вы­ра­же­ние  на­зы­ва­ет­ся непол­ным квад­ра­том суммы, так как от­сут­ству­ет двой­ка перед про­из­ве­де­ни­ем вы­ра­же­ний.

Опре­де­ле­ние

Раз­ность кубов двух вы­ра­же­ний есть про­из­ве­де­ние раз­но­сти этих вы­ра­же­ний на непол­ный квад­рат их суммы.

Вы­ве­дем фор­му­лу суммы кубов.

.

Вы­пол­ня­ем умно­же­ние мно­го­чле­нов:

.

Что и тре­бо­ва­лось до­ка­зать.

Вы­ра­же­ние  на­зы­ва­ет­ся непол­ным квад­ра­том раз­но­сти, так как от­сут­ству­ет двой­ка перед про­из­ве­де­ни­ем вы­ра­же­ний.

Опре­де­ле­ние

Сумма кубов двух вы­ра­же­ний есть про­из­ве­де­ние суммы этих вы­ра­же­ний на непол­ный квад­рат их раз­но­сти.

При­мер 1 – упро­стить вы­ра­же­ние:

.

Пусть  и , имеем:

.

Это изу­ча­е­мая фор­му­ла – раз­но­сти кубов:

.

При­мер 2 – упро­стить вы­ра­же­ние:

.

Пусть  и , имеем:

.

Это изу­ча­е­мая фор­му­ла – суммы кубов:

.

При­мер 3 – раз­ло­жить на мно­жи­те­ли:

.

Неслож­но за­ме­тить фор­му­лу раз­но­сти кубов:

.

При­ме­ня­ем изу­ча­е­мую фор­му­лу:

.

При­мер 4 – раз­ло­жить на мно­жи­те­ли:

.

Неслож­но за­ме­тить фор­му­лу раз­но­сти кубов:

.

При­ме­ня­ем изу­ча­е­мую фор­му­лу:

.

 

При­мер 5 – ре­шить урав­не­ние:

.

Пусть  и , имеем:

.

Это изу­ча­е­мая фор­му­ла – раз­но­сти кубов:

.

При­мер 6 – ре­шить урав­не­ние:

.

Пусть  и , имеем:

.

Это изу­ча­е­мая фор­му­ла – раз­но­сти кубов:

z3 = -13

z = -1

При­мер 7 – вы­чис­лить при :

.

Пусть  и , имеем:

.

Это изу­ча­е­мая фор­му­ла – раз­но­сти кубов:

.

Под­ста­вим зна­че­ние пе­ре­мен­ной:

.

При­мер 8: до­ка­жи­те, что .

До­ка­за­тель­ство.

При­ме­ним фор­му­лу раз­но­сти кубов и раз­ло­жим за­дан­ное вы­ра­же­ние на мно­жи­те­ли:

.

Вто­рую скоб­ку оста­вим без из­ме­не­ний, вы­пол­ним вы­чис­ле­ния в пер­вой скоб­ке:

.

По­лу­чи­ли про­из­ве­де­ние чисел, со­дер­жа­щее мно­жи­тель 25, оче­вид­но, что дан­ное вы­ра­же­ние крат­но 25.

Вывод: на дан­ном уроке мы рас­смот­ре­ли фор­му­лы раз­но­сти и суммы кубов и их при­ме­не­ние для раз­лич­ных типов задач.

Источник конспекта: http://interneturok.ru/ru/school/algebra/7-klass/mnogochleny-arifmeticheskie-operacii-nad-nimi/formuly-sokraschyonnogo-umnozheniya-kvadrat-summy-i-kvadrat-raznosti?konspekt&chapter_id=7

http://interneturok.ru/ru/school/algebra/7-klass/mnogochleny-arifmeticheskie-operacii-nad-nimi/formuly-sokraschyonnogo-umnozheniya-raznost-kvadratov?konspekt&chapter_id=7

http://interneturok.ru/ru/school/algebra/7-klass/mnogochleny-arifmeticheskie-operacii-nad-nimi/formuly-sokraschyonnogo-umnozheniya-raznost-kubov-i-summa-kubov?konspekt&chapter_id=7

Источник видео: https://www.youtube.com/watch?v=mSYTBWaQIfA

Источник теста: Алгебра. 7-9 классы. Тесты для учащихся общеобразовательных учреждений. А.Г.Мордкович, Е.Е.Тульчинская.

правил применения формул сокращенного умножения. Пример задач с использованием формул на разность квадратов и сумму и разность кубов

В предыдущих уроках мы рассмотрели два способа разложения полинома на множители: круглые скобки и группировка.

В этом уроке мы рассмотрим другой способ разложения многочлена на множители с использованием формул сокращенного умножения .

Мы рекомендуем прописывать каждую формулу не менее 12 раз. Для лучшего запоминания выпишите все формулы сокращенного умножения себе на небольшую шпаргалку.

Вспомним, как выглядит формула разности кубов.

а 3 — б 3 = (а — б) (а 2 + аб + б 2)

Формулу разности кубиков не очень легко запомнить, поэтому мы рекомендуем использовать специальный способ ее запоминания.

Важно понимать, что любая формула сокращенного умножения работает и в обратную сторону.

(а — б) (а 2 + аб + б 2) = а 3 — б 3

Давайте рассмотрим пример. Необходимо учитывать разницу между кубами.

Обратите внимание, что «27a 3» равно «(3a) 3», что означает, что для формулы разности между кубами вместо «a» мы используем «3a».

Используем формулу разности кубов. На месте «а 3» имеем «27а 3», а на месте «б 3», как и в формуле, стоит «б 3».

Применение разности кубов в обратном направлении

Рассмотрим другой пример. Вы хотите преобразовать произведение многочленов в разность кубов, используя формулу сокращенного умножения.

Обратите внимание, что произведение многочленов «(х — 1) (х 2 + х + 1)» напоминает правую часть формулы разности кубов «», только вместо «а» стоит «х», а вместо «b» стоит «1»…

Используем для «(x — 1) (x 2 + x + 1)» формулу разности кубов в обратном направлении.

Рассмотрим более сложный пример. Требуется упростить произведение многочленов.

Если мы сравним «(y 2 — 1) (y 4 + y 2 + 1)» с правой частью формулы разности кубов 92\справа)\]

Формулы сокращенного умножения.

Изучение формул сокращенного умножения: квадрат суммы и квадрат разности двух выражений; разность квадратов двух выражений; куб суммы и куб разности двух выражений; сумма и разность кубов двух выражений.

Применение формул сокращенного умножения при решении примеров.

Для упрощения выражений, факторизации многочленов и приведения многочленов к стандартному виду используются формулы сокращенного умножения. Формулы сокращенного умножения нужно знать наизусть .

Пусть a, b R. Тогда:

1. Квадрат суммы двух выражений равен квадрату первого выражения плюс удвоенное произведение первого выражения на второе плюс квадрат второго выражения .

(a + b) 2 = a 2 + 2ab + b 2

2. Квадрат разности двух выражений равен квадрату первого выражения минус удвоенное произведение первого выражения на второе, плюс квадрат второго выражения.

(a — b) 2 = a 2 — 2ab + b 2

3. Разность квадратов двух выражений равна произведению разности этих выражений на их сумму.

a 2 — b 2 = (a -b) (a + b)

4. Сумма куба двух выражений равна кубу первого выражения плюс утроенный квадрат первого выражения и второе плюс утроенное произведение первого выражения на квадрат второго плюс куб второго выражения.

(a + b) 3 = a 3 + 3a 2 b + 3ab 2 + b 3

5. Куб разности двух выражений равен кубу первого выражения минус утроенный квадрат первого выражения выражение, а второе плюс утроенное произведение первого выражения на квадрат второго минус куб второго выражения.

(a — b) 3 = a 3 — 3a 2 b + 3ab 2 — b 3

6. Сумма кубов двух выражений равна произведению суммы первого и второго выражений на неполный квадрат разности этих выражений.

a 3 + b 3 = (a + b) (a 2 — ab + b 2)

7. Разность кубов двух выражений равна произведению разности первого и второго выражений на неполный квадрат суммы этих выражений.

a 3 — b 3 = (a — b) (a 2 + ab + b 2)

Применение формул сокращенного умножения при решении примеров.

Пример 1.

Вычислить

а) Используя формулу квадрата суммы двух выражений, имеем

(40 + 1) 2 = 40 2 + 2 40 1 + 1 2 = 1600 + 80 + 1 = 1681

б) Используя формулу квадрата разности двух выражений, получаем

98 2 = (100 — 2) 2 = 100 2 — 2 100 2 + 2 2 = 10000 — 400 + 4 = 9604

получаем

Пример 3.

Упростим выражение

(x — y) 2 + (x + y) 2

Используем формулы квадрата суммы и квадрата разности двух выражений

(x — y) 2 + (x + y) 2 = x 2 — 2xy + y 2 + x 2 + 2xy + y 2 = 2x 2 + 2y 2

Формулы сокращенного умножения в одной таблице:

(a + b) 2 = a 2 + 2ab + b 2
(a — b) 2 = a 2 — 2ab + b 2
a 2 — b 2 = (a — b) (a + b)
(a + b) 3 = a 3 + 3a 2 b + 3ab 2 + b 3
(a — b) 3 = a 3 — 3a 2 b + 3ab 2 — b 3
a 3 + b 3 = (a + b) (a 2 — ab + b 2)
a 3 — b 3 = (a — b) (a 2 + ab + b 2)

Правило PEMDAS: порядок действий ПЕМДАС» раньше.

Но что это означает? Здесь мы подробно объясним значение PEMDAS и то, как он используется , прежде чем предоставить вам несколько примеров задач PEMDAS, чтобы вы могли попрактиковаться в том, что вы узнали.

 

PEMDAS Значение: что это значит?

PEMDAS — это аббревиатура, призванная помочь вам запомнить порядок операций, используемых для решения математических задач. Обычно произносится как «пем-дасс», «пем-доз» или «пем-досс».

Вот что означает каждая буква в PEMDAS:

• P арентезы
• E экспоненты
• M умножение и D ivision
• Дополнение и удаление S

Порядок букв показывает порядок решения различных частей математической задачи , где выражения в скобках идут первыми, а сложение и вычитание — последними.

Многие ученики используют этот мнемонический прием, чтобы помочь им запомнить каждую букву: Пожалуйста, извините, моя дорогая тетя Салли .

В Соединенном Королевстве и других странах учащихся обычно изучают PEMDAS как BODMAS . Значение BODMAS такое же, как и значение PEMDAS, просто используется пара разных слов. В этой аббревиатуре буква B означает «скобки» (то, что мы в США называем круглыми скобками), а буква O — «порядки» (или показатели степени).

Теперь, как именно вы используете правило PEMDAS? Давайте взглянем.

 

Как вы используете PEMDAS?

PEMDAS — это аббревиатура, используемая для напоминания людям о порядке операций.

Это означает, что вы не просто решаете математические задачи слева направо; скорее, вы решаете их в заранее определенном порядке, который дается вам через аббревиатуру PEMDAS . Другими словами, вы начнете с упрощения любых выражений в круглых скобках, затем упростите любые показатели степени и перейдете к умножению и т. д.

Но это еще не все. Вот что именно означает PEMDAS для решения математических задач:

• Круглые скобки: Все, что в скобках, должно быть сначала упрощено
• Экспоненты: Все, что имеет экспоненту (или квадратный корень), должно быть упрощено после все в скобках упрощено
• Умножение и деление: После того, как вы разобрались со скобками и показателями степени, решите любое умножение и деление слева направо
• Сложение и вычитание: Разобравшись со скобками, показателями степени, умножением и делением, выполните любое сложение и вычитание слева направо

Если какой-либо из этих элементов отсутствует (например, у вас есть математическая задача без показателей степени), вы можете просто пропустить этот шаг и перейти к следующему.

Теперь давайте рассмотрим пример задачи, чтобы помочь вам лучше понять правило PEMDAS:

4 (5 − 3)² − 10 ÷ 5 + 8

У вас может возникнуть соблазн решить эту математическую задачу слева направо, но это приведет к неправильному ответу! Итак, вместо этого давайте воспользуемся PEMDAS, чтобы помочь нам подойти к этому правильно .

Мы знаем, что скобки должны быть обработаны в первую очередь. В этой задаче один набор скобок: (5 − 3). Упрощение дает нам 2 , так что теперь наше уравнение выглядит так:

4 (2)² − 10 ÷ 5 + 8

Следующая часть PEMDAS — это показатели степени (и квадратные корни). В этой задаче есть один показатель степени, который возводит в квадрат число 2 (то есть то, что мы нашли, упростив выражение в скобках).

Это дает нам 2 × 2 = 4. Теперь наше уравнение выглядит так:

4 (4) − 10 ÷ 5 + 8    ИЛИ    4 × 4 − 10 ÷ 5 + 8 Далее

3 вверх это умножение и деление слева направо . Наша задача содержит и умножение, и деление, которые мы будем решать слева направо (то есть сначала 4 × 4, а затем 10 ÷ 5). Это упрощает наше уравнение следующим образом:

16 − 2 + 8

Наконец, все, что нам нужно сделать сейчас, это решить оставшееся сложение и вычитание слева направо :

16 − 2 + 8
14 + 8
= 22

Окончательный ответ: 22. Не веришь мне? Вставьте все уравнение в свой калькулятор (написанное точно так, как оно указано выше), и вы получите тот же результат!

 

David Goehring/Flickr

 

Примеры математических задач с использованием PEMDAS + ответы

Проверьте, сможете ли вы правильно решить следующие четыре задачи, используя правило PEMDAS. Мы пройдемся по ответам после.

 

Примеры задач PEMDAS

1. 11 − 8 + 5 × 6
2. 8 ÷ 2 (2 + 2)
3. 7 × 4 − 10 (5 − 3) ÷ 2²
4. √25 (4 + 2)² − 18 ÷ 3 (3 − 1) + 2³

 

Ответы

1. 33
2. 16
3. 23
4. 176

 

Объяснение ответов

Здесь мы рассмотрим каждую задачу выше и то, как вы можете использовать PEMDAS, чтобы получить правильный ответ.

 

#1 Ответ Объяснение

11 − 8 + 5 × 6

Эта математическая задача является довольно простым примером PEMDAS, в котором сложение, вычитание и умножение используются только , поэтому здесь не нужно беспокоиться о скобках или показателях степени.

Мы знаем, что умножение предшествует сложению и вычитанию , поэтому вам нужно начать с умножения 5 на 6, чтобы получить 30:

11 − 8 + 30

Теперь мы можем просто работать слева направо на сложение и вычитание:

11 − 8 + 30
3 + 30
= 33

Это приводит нас к правильному ответу , который равен 33 .

 

#2 Ответ Объяснение

8 ÷ 2 (2 + 2)

Если эта математическая задача кажется вам знакомой, это, вероятно, потому, что стала вирусной в августе 2019 года из-за неоднозначной настройки . Многие люди спорили о том, какой правильный ответ: 1 или 16, но, как мы все знаем, в математике (почти всегда!) только один действительно равен 9. 0348 правильный ответ.

Так что это: 1 или 16?

Давайте посмотрим, как PEMDAS может дать нам правильный ответ. В этой задаче есть скобки, деление и умножение. Итак, мы начнем с упрощения выражения в скобках согласно PEMDAS:

8 ÷ 2 (4)

В то время как большинство людей в Интернете соглашались до этого момента, многие не соглашались с тем, что делать дальше: умножить ли 2 на 4 или разделить 8 на 2?

PEMDAS может ответить на этот вопрос: когда дело доходит до умножения и деления, вы всегда работаете слева направо. Это означает, что вы действительно разделите 8 на 2, прежде чем умножать на 4.

Это может помочь взглянуть на проблему таким образом, поскольку люди склонны путаться в скобках (помните, что все, что рядом со скобкой, равно , умноженному на то, что в скобках):

8 ÷ 2 × 4

Теперь решаем уравнение слева направо:

8 ÷ 2 × 4
4 × 4
= 16

Правильный ответ: 16. Любой, кто утверждает, что 1, определенно неправильно — и явно неправильно использует PEMDAS!

 

Если бы эти примеры задач PEMDAS были такими простыми…

 

#3 Ответ Объяснение

7 × 4 − 10 (5 − 3) ÷ 2²

9000 бит хитрее сейчас.

В этой математической задаче есть скобки, показатель степени, умножение, деление, и вычитание. Но не перегружайтесь — давайте работать с уравнением шаг за шагом.

Во-первых, согласно правилу PEMDAS, мы должны упростить то, что в скобках :

7 × 4 − 10 (2) ÷ 2²

Легко, правда? Далее, давайте упростим показатель степени :

7 × 4 − 10 (2) ÷ 4

Теперь осталось только умножение, деление и вычитание. Помните, что с умножением и делением мы просто работаем слева направо:

7 × 4 − 10 (2) ÷ 4
28 − 10 (2) ÷ 4
28 − 20 ÷ 4
28 − 5

умножали и делили, вам просто нужно сделать вычитание , чтобы решить это:

28 − 5
= 23

Это дает нам правильный ответ 23 .

 

#4 Ответ Объяснение

√25 (4 + 2)² − 18 ÷ 3 (3 − 1) + 2³

Эта задача может показаться пугающей, но я обещаю, что это не так! Пока вы будете подходить к ней шаг за шагом, используя правило PEMDAS , вы сможете решить ее в кратчайшие сроки.

Сразу видно, что эта задача содержит все компонентов PEMDAS : круглые скобки (два набора), показатели степени (два и квадратный корень), умножение, деление, сложение и вычитание. Но на самом деле это ничем не отличается от любой другой математической задачи, которую мы решали.

Во-первых, мы должны упростить то, что находится в двух наборах скобок:

√25 (6)² − 18 ÷ 3 (2) + 2³

Затем мы должны упростить все показатели степени — сюда входят и квадратные корни. :

5 (36) − 18 ÷ 3 (2) + 8

Теперь мы должны выполнить умножение и деление слева направо:

5 (36) − 18 ÷ 3 (2) + 8
180 − 18 ÷ 3 (2) + 8
180 − 6 (2) + 8
180 − 12 + 8

Наконец, решаем оставшееся сложение и вычитание слева направо:

180 — 12 + 8
168 + 8
= 176

Это приводит нас к правильному ответу 176 .

 

Что дальше?

Еще одна математическая аббревиатура, которую вы должны знать, это SOHCATOA. В нашем экспертном руководстве вы узнаете, что означает аббревиатура SOHCAHTOAH и как вы можете использовать ее для решения задач, связанных с треугольниками.

Готовитесь к секции SAT или ACT по математике? Тогда вам определенно стоит ознакомиться с нашим полным руководством по SAT Math/ACT Math, в котором вы найдете множество советов и стратегий для этого сложного раздела.

Интересуют действительно большие числа? Узнайте, что такое гугол и гуголплекс, а также почему невозможно записать одно из этих чисел.

 

Нужна дополнительная помощь по этой теме? Проверьте Tutorbase!

Наша проверенная база данных репетиторов включает ряд опытных преподавателей, которые могут помочь вам отшлифовать эссе по английскому языку или объяснить, как производные работают для исчисления. Вы можете использовать десятки фильтров и критериев поиска, чтобы найти идеального человека для ваших нужд.

 

У вас есть друзья, которым тоже нужна помощь в подготовке к экзамену? Поделись этой статьей!

Ханна Муниз

Об авторе

Ханна получила степень магистра японоведения в Мичиганском университете и степень бакалавра в Университете Южной Калифорнии. С 2013 по 2015 год преподавала английский язык в Японии по программе JET. Она увлечена образованием, писательством и путешествиями.

Как умножать в Excel в 2020 (+Примеры и скриншоты)

Microsoft Excel может мгновенно решить практически любую математическую задачу.

Проблема, с которой сталкиваются многие люди, заключается в том, что они не знают, как вводить эти проблемы в Excel.

Вот где я пришел.

Я провел много времени, используя Microsoft Excel. Итак, я могу научить вас, как вычитать в Excel, как складывать в Excel и как делить в Excel. Может быть, немного о том, как объединять ячейки в Excel? Список можно продолжить.

Но в этой конкретной статье я здесь, чтобы научить вас, как умножать в Excel.

• Как умножать в клеточке
• Как умножать клетки
• Как умножить диапазон ячеек

Как умножать в Excel ярлык

Чтобы умножить в Excel, вам нужно написать формулу с арифметическим оператором для умножения, символом звездочки (*). Не забывайте, что все формулы должны начинаться со знака равенства (=)!

Пример. =5*5 дает 25

Теперь приступим.

Если вы хотите умножать в Excel, вам нужно знать, что такое формулы Excel и как их писать.

Формулы Excel — это выражения, используемые в Excel для отображения значений, рассчитанных на основе введенных вами данных, и обычно они используются для выполнения различных математических, статистических и логических операций.

Итак, прежде чем мы перейдем к особенностям умножения в Excel, вот несколько напоминаний, о которых следует помнить при написании формул Excel:

• Все формулы Excel должны начинаться со знака равенства (=). Это , должно быть , чтобы Excel распознал его как формулу.
• В ячейках будет отображаться результат формулы, а не фактическая формула. Таким образом, используя ссылки на ячейки, а не просто ввод данных в ячейку, если вам нужно вернуться позже, значения будут легче понять.
• При использовании арифметических операторов в формуле помните порядок операций (лично я ссылаюсь на аббревиатуру PEMDAS: P арентезис, E возведение в степень, M умножение, D ivision, A дополнение, S вычитание.) Ниже вы найдете пример того, как порядок операций применяется к формулам в Excel.

 

Как умножать в клеточке

Чтобы умножить числа в ячейке, вам нужно будет написать формулу в указанной ячейке. Ваша формула должна начинаться со знака равенства (=) и содержать арифметический оператор (*), необходимый для вычисления. В этом случае вы хотите умножить 10 на 5, поэтому ваша формула =10*5.

 

После того, как вы ввели формулу, нажмите «Ввод», и ваш результат будет заполнен. В этом примере формула умножения =10*5 дает результат 50 (см. ниже).

 

Как умножать клетки

Для этого ваши данные должны быть в отдельных ячейках, чтобы вы могли использовать ссылки на ячейки в формуле.

Ниже видно, что формула умножения была написана в ячейке C1 с использованием ссылок на ячейки, но данные нужно было вводить отдельно в ячейки A1 и B1.

 

После того, как вы ввели формулу, нажмите «Ввод», и ваш результат будет заполнен. В этом примере формула умножения =A1*B1 дает результат 10 (см. ниже).

 

Как умножить диапазон ячеек

Оба приведенных выше значения связаны с умножением двух переменных. Но знаете ли вы, что с помощью Excel вы можете создавать формулы, которые будут умножать за вас целый диапазон чисел? Довольно круто, да?

Для этого вы можете использовать предустановленную формулу, называемую функцией, а именно функцией ПРОИЗВЕД.

No related posts.