Показательные уравнения. Решение показательных уравнений.
Данная статья посвящена теме «Показательные уравнения, решение показательных уравнений». Изучение этой темы стоит начинать со знакомства с показательными уравнениями. Поэтому, в первую очередь будем разбираться с вопросом, что такое показательные уравнения. Следом рассмотрим так называемые простейшие показательные уравнения и на примерах изучим принципы их решения. На основе этой информации мы сможем перейти к основной части материала – к детальному разговору про решение показательных уравнений. В этой части мы запишем алгоритм решения показательных уравнений, изучим все основные методы решения показательных уравнений и рассмотрим примеры решения показательных уравнений разными методами.
Что такое показательные уравнения
Обычно считают, что показательные уравнения – это уравнения, в которых переменная содержится в показателе степени. Например, 5x−3=25, 4x−5·2x+4=0, , — это все показательные уравнения.
Заметим, в вопросе «что такое показательные уравнения» нет строгого единства. Этому свидетельствует тот факт, что определения показательных уравнений, встречающиеся в школьных учебниках и другой математической литературе, отличаются одно от другого. Отличия эти не принципиальные, а касающиеся деталей. При этом взгляд на показательные уравнения как на уравнения с неизвестной величиной в показателе степени является своего рода компромиссным вариантом.
За более детальной информацией обращайтесь к статье «Что такое показательные уравнения». В ней даны определения показательных уравнений из разных учебников, на примерах разобраны различия между ними, приведены примеры показательных уравнений с несколькими переменными и с параметром.
К началу страницы
Простейшие показательные уравнения, их решение
Простейшие показательные уравнения – это уравнения ax=b, где a и b – числа или числовые выражения, причем a>0 и a≠1.
Особую важность с практической точки зрения имеют простейшие показательные уравнения, имеющие вид ax=ac, a>0, a≠1, c – некоторое действительное число (это частный случай уравнений ax=b при b=ac). Вот примеры таких простейших показательных уравнений: 2x=20, (0,3)x=(0,3)−0,1, и др.
Решение простейших показательных уравнений базируется на следующих утверждениях:
- Если b<0 или b=0, то простейшее показательное уравнение ax=b, a>0, a≠1 не имеет решений. Например, простейшие показательные уравнения 4x=−1 и (0,5)x=0 не имеют решений.
-
Если b>0, то уравнение ax=b, a>0, a≠1 имеет единственный корень x=logab, где logab – логарифм числа b по основанию a.
 Приведем пример: простейшее показательное уравнение 2x=7 имеет единственный корень x=log27.
Приведем пример: простейшее показательное уравнение 2x=7 имеет единственный корень x=log27.
В частности, простейшее показательное уравнение ax=ac, a>0, a≠1, c – некоторое действительное число, имеет единственный корень x=c. Например, уравнение 3x=3−4 имеет единственный корень x=−4.
Умение решать простейшие показательные уравнения является одним из самых важных навыков, необходимых для решения более сложных показательных уравнений. Дело в том, что решение показательных уравнений почти всегда сводится к решению одного или нескольких простейших показательных уравнений. Так что с решением простейших показательных уравнений нужно разобраться очень детально. В этом Вам поможет материал «Простейшие показательные уравнения и их решение».
К началу страницы
Алгоритм решения показательных уравнений
Чтобы решить показательное уравнение, надо
- выбрать подходящий метод решения показательного уравнения,
-
провести решение выбранным методом.

К началу страницы
Методы решения показательных уравнений
Для решения показательных уравнений используются практически все методы решения уравнений.
Из списка методов стоит выделить метод уравнивания показателей и метод логарифмирования. Эти методы изучаются именно в рамках разговора про показательные уравнения и преимущественно используются для решения именно показательных уравнений. Остальные методы списка обычно уже хорошо известны к моменту изучения показательных уравнений (кроме метода потенцирования, который больше относится к логарифмическим уравнениям, но, бывает, используется и для решения показательных уравнений, в записи которых присутствуют логарифмы).
Но владение методами решения показательных уравнений должно дополняться умением выбирать подходящий для решения метод. Выработать это умение помогают рекомендации по выбору метода решения показательного уравнения.
К началу страницы
Примеры решения показательных уравнений
Закрепим теорию практикой, то есть, рассмотрим примеры решения показательных уравнений. На них мы разберем все основные нюансы, возникающие при использовании того или иного метода решения показательных уравнений.
Начнем с примеров решения простейших показательных уравнений. В первом примере главный интерес представляют рассуждения, обосновывающие отсутствие корней у простейших показательных уравнений с отрицательными числами в правых частях.
Пример
Решите уравнения:
а) 2x=−7
б)
в)
Смотреть решение
Во втором примере показано, как оформлять решение простейших показательных уравнений с нулями в правых частях.
Пример
Решите уравнения:
а) (0,7)x=0
б)
Смотреть решение
Вот пример решения простейших показательных уравнений, в обеих частях которых находятся степени с одинаковыми основаниями.
Пример
Решите показательные уравнения:
а)
б)
в)
г)
Смотреть решение
Простейшие показательные уравнения в следующем примере требуют изначального приведения уравнения к виду ax=ac.
Пример
Решите уравнения:
а) 7x=1
б)
в)
г)
Смотреть решение
Следующие простейшие показательные уравнения имеют положительное число в правой части и решаются через логарифм.
Пример
Решите уравнения:
а) 5x=7
б)
Смотреть решение
Теперь сосредоточимся на решении показательных уравнений методом уравнивания показателей. В первом примере внимание сосредоточим на самом методе.
В первом примере внимание сосредоточим на самом методе.
Пример
Решите уравнение
Смотреть решение
Для решения следующего показательного уравнения методом уравнивания показателей достаточно вспомнить, что число можно рассматривать как степень этого числа с показателем 1.
Пример
Решите показательное уравнение
Смотреть решение
Для закрепления метода уравнивания показателей предлагаем рассмотреть еще один пример решения показательного уравнения.
Пример
Решите показательное уравнение
Смотреть решение
Дальше на примерах разберем, как проводится решение показательных уравнений методом разложения на множители.
Пример
Решите уравнение
Смотреть решение
Часто перед применением метода разложения на множители требуется провести некоторые преобразования показательного уравнения, чтобы получить произведение в левой части уравнения и нуль в правой части. Решим такой пример.
Решим такой пример.
Пример
Решите показательное уравнение
Смотреть решение
Теперь разберем на примерах, как проводится решение показательных уравнений методом введения новой переменной. Начнем с решения показательного уравнения, в записи которого переменная фигурирует только в составе одинаковых выражений.
Пример
Решите уравнение
Смотреть решение
Метод введения новой переменной используется и для решения показательных уравнений, переменная в которых находится в составе степеней с противоположными показателями. Вот пример решения такого показательного уравнения.
Пример
Решите уравнение
Смотреть решение
Есть и другие типичные показательные уравнения, решающиеся методом введения новой переменной. Вот характерные примеры с решениями.
Вот характерные примеры с решениями.
Пример
Решите показательное уравнение
Смотреть решение
Пример
Решите уравнение
Смотреть решение
Пример
Решите уравнение 25x+9·5x−10=0
Смотреть решение
Пример
Решите уравнение (10x)2+9·10x·2x−10·(2x)2=0
Смотреть решение
Решение многих показательных уравнений упирается в проведение преобразований. Для показательных уравнений наиболее характерны преобразования, базирующиеся на свойствах степеней и на связи корней со степенями. В статье «Решение показательных уравнений через преобразования» Вы найдете массу соответствующих примеров с решениями.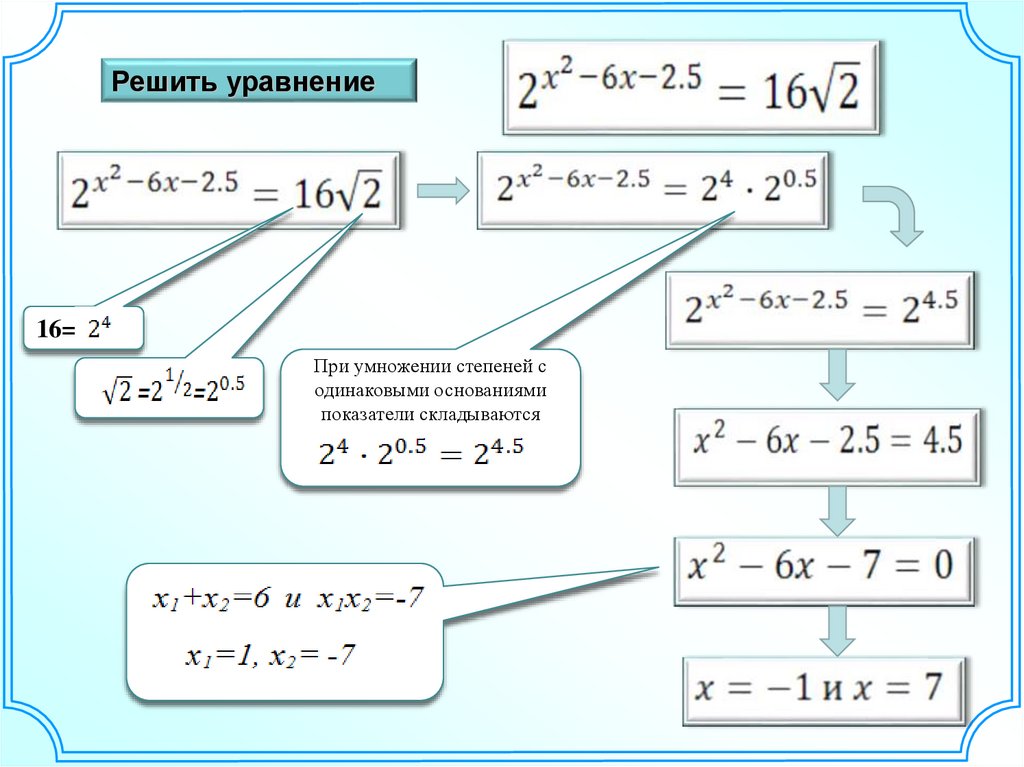
Некоторые показательные уравнения в результате проведения преобразований могут сводиться к числовым равенствам. В статье «Решение показательных уравнений, сводящихся к числовым равенствам» дан принцип их решения. Решение двух показательных уравнений, первое из которых сводится к неверному числовому равенству, а второе – к верному, приведем здесь.
Пример
Решите показательные уравнения:
а)
б)
Смотреть решение
Показательные уравнения, в левой части которых находится некоторая дробь, а в правой – число 0, на области допустимых значений для этих уравнений заменяются уравнениями «числитель равен нулю». Вот примеры решения характерных показательных уравнений из статьи «Решение показательных уравнений дробь равна нулю».
Пример
Решите уравнение
Смотреть решение
Пример
Решите уравнения:
а)
б)
Смотреть решение
Переходим к примерам решения показательных уравнений h(f(x))=h(g(x)) методом освобождения от внешней функции h. Главная сложность при их решении, обычно, заключается в том, чтобы разглядеть соответствующую структуру уравнения и обосновать, что внешняя функция принимает каждое свое значение по одному разу. За более полной информацией обращайтесь к материалу «Решение показательных уравнений методом освобождения от внешней функции», а вот соответствующий пример с решением.
Главная сложность при их решении, обычно, заключается в том, чтобы разглядеть соответствующую структуру уравнения и обосновать, что внешняя функция принимает каждое свое значение по одному разу. За более полной информацией обращайтесь к материалу «Решение показательных уравнений методом освобождения от внешней функции», а вот соответствующий пример с решением.
Пример
Решите уравнение
Смотреть решение
Стоит привести пример решения показательного уравнения методом логарифмирования. Обычно методом логарифмирования решают показательные уравнения, части которого представляют собой степени, произведения или частные степеней, возможно, с числовыми коэффициентами. Дополнительный материал по теме есть в статье «Решение показательных уравнений методом логарифмирования». Сейчас приведем типовое решение показательного уравнения методом логарифмирования.
Пример
Решите уравнение
Смотреть решение
Иногда получить решение показательного уравнения позволяет ОДЗ. Это касается случаев, когда ОДЗ состоит из нескольких чисел или является пустым множеством. Подробнее об этом написано в статье «Решение показательных уравнений через ОДЗ». Здесь же нас интересует пример решения характерного показательного уравнения.
Это касается случаев, когда ОДЗ состоит из нескольких чисел или является пустым множеством. Подробнее об этом написано в статье «Решение показательных уравнений через ОДЗ». Здесь же нас интересует пример решения характерного показательного уравнения.
Пример
Решите показательное уравнение
Смотреть решение
Остается рассмотреть примеры решения показательных уравнений каждым из направлений функционально-графического метода – графическим методом, через возрастание-убывание и методом оценки.
К решению показательных уравнений графическим методом обычно прибегают тогда, когда не видно других более простых методов решения и довольно легко построить графики функций, отвечающих частям уравнения. Этим условиям удовлетворяет показательное уравнение в следующем примере.
Пример
Решите уравнение
Смотреть решение
Решение показательных уравнений через возрастание-убывание обычно проводится тогда, когда очевиден или легко подбирается корень показательного уравнения и при этом очевидно или легко обосновывается, что одна из функций, отвечающих частям уравнения, возрастает, а другая – убывает. Вот соответствующий пример с типовым решением.
Вот соответствующий пример с типовым решением.
Пример
Решите показательное уравнение
Смотреть решение
Наконец, приведем примеры решения показательных уравнений методом оценки. За теорией обращайтесь к статье «Решение показательных уравнений методом оценки».
Пример
Решите уравнение
Смотреть решение
Пример
Решите показательное уравнение
Смотреть решение
Методы решения показательных уравнений
Методы решения показательных уравнений
1. Простейшие показательные уравнения
| Тип уравнения | Вид уравнения | Метод решения | ||
| 1 | (x) | |||
| 2 |
b = a
|
b b>0 |
b b |
|
| = f(x) = 1 |
f(x) = | Решений нет | ||
Примеры.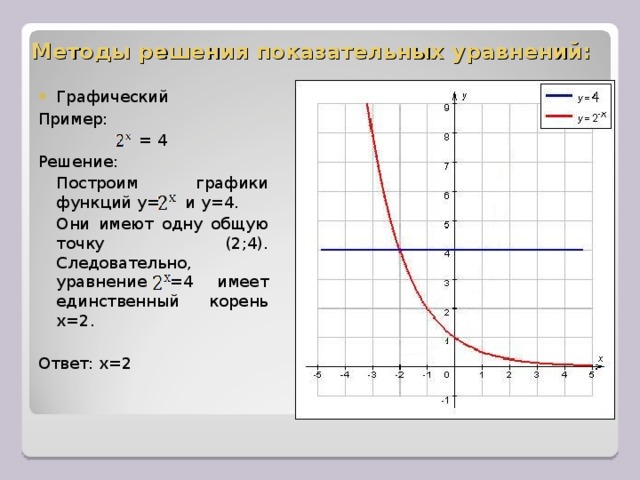
Пример 1. Решите уравнение: 34x-5 = 3x+4 .
Решение.
34x-5 = 3x+4 <=> 4x 5 = x+4 <=> 3x=9<=> x = 3 .
Ответ:3
Пример 2. Решите уравнение: 2x-4 = 3 .
Решение.
2x-4 = 3 <=> x- 4 = x = + 4 <=> x = + <=> x = .
Ответ:.
Пример 3. Решите уравнение:-3x = -7 .
Решение.
-3x = -7 , решений нет, так как -3x > 0 для x R .
Ответ: .
2. Методы преобразования показательных уравнений к простейшим.
A. Метод уравнивания оснований.
Примеры.
Пример 1. Решите уравнение: 27- = 0 .
Решение.
27- = 0 <=> 3334x-9— (32)x+1
= 0 <=> 33+ (4x-9)— 32(x+1) = 0<=> 34x-6-32x+2
= 0 <=> 34x-6 = 32x+2<=> 4x-6=2x+2 <=> 2x =
8 <=> x=4.
Ответ: 4.
Пример 2. Решите уравнение: .
Решение.
0 <=> (22)x3x5x = 604x-15 <=> 4x3x5x = 604x-15 <=> (4x = 604x-15 <=> 60x=604x-15 <=> <=>x=4x-15 <=> 3x=15 <=> x=5.
Ответ: 5.
В. Уравнения, решаемые разложением на множители.
Примеры.
Пример 1. Решите уравнение: x2x = 22x + 8x-16.
Решение.
x2x = 22x + 8x-16 <=> x2x — 22x = 8x-2) <=> 2x(x-2) — 8<=> (x-2) x — 8) = 0 <=> <=> <=> <=> .
Ответ:
Пример 2 . Решите уравнение:
Решите уравнение:
Решение.
52x — 7x — 52x35 +7x = 0 <=> (52x — 7x)((
Ответ: 0.
С. Уравнения, которые с помощью подстановки f(x) = t, t>0 преобразуются к квадратным уравнениям (или к уравнениям более высоких степеней).
Пусть , где А, В, С — некоторые числа. Сделаем замену: >0, тогда A2 + B + C = 0
Решаем полученное уравнение, находим значения t, учитываем условие t >0 , возвращаемся к простейшему показательному уравнению f(x) = t, решаем его и записываем ответ.
Примеры.
Пример 1 . Решите уравнение: 22+x — 22-x = 5.
Решение.
22+x — 22-x = 5 <=> 222x — = 15 <=> 4(2x)2 — 4 = 15x
Делаем замену t = 2x, t > 0. Получаем
уравнение 42 — 4 = 15t <=> 4t2 — 15t — 4=0
Получаем
уравнение 42 — 4 = 15t <=> 4t2 — 15t — 4=0
<=> , t = не удовлетворяет условию t > 0.
Вернемся к переменной х:
2х = 4<=> 2x = 22 <=> x=2.
Ответ: 2
Пример 2. Решите уравнение:
Решение.
5
Делаем замену: , тогда Получаем уравнение:
5 , t = не удовлетворяет условию t
Вернемся к переменной Х:
Ответ: 2.
D. Уравнения, левая часть которых имеет вид A nx + B kx bmx + С bnx, где k, m N, k + m = n
Для решения уравнения такого типа необходимо обе части уравнения разделить либо на nx, либо на nx и получится уравнение типа С).
Примеры.
Пример 1. Решите уравнение: 222x — 5x + 332x = 0.
Решение.
222x — 5x + 332x = 0 <=> 22x — 5x3x + 332x = 0 <=> 2 — + 3 = 0 <=>
<=> 22x — 5x + 3 = 0
Пусть t = x, t>0 , тогда 2t- 5t + 3 = 0 <=> , оба значения t удовлетворяют условию t Вернемся к переменной х:
<=> <=> .
Ответ:
Пример 2. Решите уравнение: 8x + 18x — 227x = 0 .
Решение.
8x + 18x — 227x = 0 <=> + — 2 = 0 <=> 23x + 2x 32x — 233x = 0<=>
<=> + — 2 = 0 <=> + — 2 = 0.
Пусть
= t, t>0 , тогда t3 + t — 2 = 0<=> (t3 — 1) + (t
-1 )= 0 <=> (t-1) (t2 +t +1) + (t — 1) <=> (t — 1) (t2 + t +2) = 0 <=> <=> t -
1= 0 <=> t=1. (t>0)
(t>0)
Вернемся к переменной х: = 1 <=> = x = 0 .
Ответ: 0.
К данному типу уравнений относятся уравнения , левая часть которых имеет вид , где А, В, С -некоторые числа, причем .
Уравнения такого типа решаются с помощью подстановки :
= t , тогда = .
Пример 3. Решите уравнение:
Решение.
Заметим, что произведение оснований степени равно единице:
(. Поэтому можно ввести новую переменную: , причем . Получим уравнение:
t ,оба корня удовлетворяют условию :.
Вернемся к переменной х:
.
Ответ: .
Е. Уравнения, имеющие вид Aam = Bbm.
Для решения необходимо обе части уравнения разделить либо на am, либо на bm. В результате получается простейшее уравнение.
Примеры.
Пример 1. Решите уравнение: 7х = 5х.
Решите уравнение: 7х = 5х.
Решение.
7х = 5х <=> = 1 <=> = <=> x = 0.
Ответ: 0.
Пример 2. Решите уравнение: .
Решение.
.
Ответ: 2.
F. Метод, основанный на использовании свойства монотонности показательной функции .
Примеры.
Пример 1. Решите уравнение: .
Решение.
Заметим, что при х=1 уравнение обращается в тождество. Следовательно, х=1 — корень уравнения. Перепишем уравнение в виде
(*)
Так как при основании, меньшем единицы, показательная функция убывает на R, то при хлевая часть уравнения (*) больше единицы, то есть
Если то левая часть уравнения меньше единицы, то есть
Поэтому, других корней, кроме х=1, уравнение не имеет.
Ответ: 1.
Пример 2. Решите уравнение: .
Решение.
Это уравнение также обращается в тождество при х=1.
Перепишем уравнение в виде:
.
При основании, меньшем единицы, показательная функция убывает на R.
Поэтому при ха при х: . Таким образом, других корней, кроме х=1 , уравнение не имеет.
Ответ: 1.
G. Графический способ решения уравнений вида f(x).
Чтобы графически решить уравнение такого вида, необходимо построить графики функций y=f(x) в одной системе координат и найти (точно или приближенно) абсциссы точек (если они есть) пересечения этих графиков. Абсциссы этих точек — корни данного уравнения (точность результатов определяем только после подстановки в уравнение ).
Примеры.
Пример 1. Решите уравнение: .
Решение.
1.Рассмотрим две функции: f(x) = и g(x) = x+1.
2.Графиком функции f(x) = является кривая, расположенная в верхней полуплоскости, графиком функции g(x) = x+1 является прямая.
3. Зададим таблицы значений этих функций:
х -1 0 1 2 3 f(x) = 1 2 4 х 0 3 g(x)= x+1 1 4
4. Из рисунка видно, что прямая и кривая
пересекаются в двух точках- в точке А и в точке В.
По графику определяем абсциссы этих точек: . Значит,
уравнение имеет два корня: х=3 и х= . Число х=3 — точный
корень заданного уравнения, так как при
подстановке в это уравнение получается верное
числовое равенство:
Из рисунка видно, что прямая и кривая
пересекаются в двух точках- в точке А и в точке В.
По графику определяем абсциссы этих точек: . Значит,
уравнение имеет два корня: х=3 и х= . Число х=3 — точный
корень заданного уравнения, так как при
подстановке в это уравнение получается верное
числовое равенство:
Ответ: 3; .
Пример 2. Решите уравнение: .
Решение.
1. Рассмотрим две функции f(x) = и g(x) = .Используем свойства степени и преобразуем выражение :
= , тогда вторую формулу можно переписать в виде: f(x) = .
2. Функция f(x) = — показательная по основанию и ее графиком является кривая, расположенная в верхней полуплоскости.
Функция g(x) =- прямая пропорциональность и ее график - прямая, проходящая через точку .
3. Зададим таблицы значений этих функций и затем построим их графики в одной системе координат.
х -3 -2 -1 0 1 2 f(x) = 8 4 2 1 х 1 4 g(x) = 2
4. Графики пересекаются в одной точке — в точке
А, ее абсцисса равна единице.Значит, х=1 — корень
заданного уравнения.
Графики пересекаются в одной точке — в точке
А, ее абсцисса равна единице.Значит, х=1 — корень
заданного уравнения.
Примечание:
Если одна часть уравнения содержит убывающую функцию f(x) , а другая часть -возрастающую функцию g(x), и уравнение имеет корень х=, то он -единственный.
В примере 2. : f(x) = убывающая на R функция, а g(x = - возрастающая на R функция, х=1- корень уравнения и он единственный.
Ответ: 1.
Приложение к статье «Методы решения показательных уравнений»
Решение показательных уравнений. Показательные уравнения примеры решения.
- Альфашкола
- Статьи {2x-3}\right)\)
- Свойства корней
- Значение синуса, косинуса и тангенса 30°, 45° и 60°
- МИФИ (Экономическая Безопасность): Проходной балл, учебный план
- Финансовый Университет: факультет Бизнес-Информатики
- Задачи на вклады в банк
- Как решать типовые задачи на кривые второго порядка
- ОГЭ по математике, базовый уровень. Системы уравнений
- Умные по-разному: 8 видов интеллекта, о которых должен знать каждый родитель
- Войти
- Биографии репетитора
- Подготовка к тесту
СРЕДНЯЯ ШКОЛА
- ACT Репетиторство
- SAT Репетиторство
- Репетиторство PSAT
- ASPIRE Репетиторство
- ШСАТ Репетиторство
- Репетиторство STAAR
ВЫСШАЯ ШКОЛА
- Репетиторство MCAT
- Репетиторство GRE
- Репетиторство по LSAT
- Репетиторство по GMAT
К-8
- Репетиторство AIMS
- Репетиторство по HSPT
- Репетиторство ISEE
- Репетиторство ISAT
- Репетиторство по SSAT
- Репетиторство STAAR
Поиск 50+ тестов
- Академическое обучение
репетиторство по математике
- Алгебра
- Исчисление
- Элементарная математика
- Геометрия
- Предварительный расчет
- Статистика
- Тригонометрия
репетиторство по естественным наукам
- Анатомия
- Биология
- Химия
- Физика
- Физиология
иностранные языки
- французский
- немецкий
- Латинский
- Китайский мандарин
- Испанский
начальное обучение
- Чтение
- Акустика
- Элементарная математика
прочие
- Бухгалтерия
- Информатика
- Экономика
- Английский
- Финансы
- История
- Письмо
- Лето
Поиск по 350+ темам
- О
- Обзор видео
- Процесс выбора наставника
- Онлайн-репетиторство
- Мобильное обучение
- Мгновенное обучение
- Как мы работаем
- Наша гарантия
- Влияние репетиторства
- Обзоры и отзывы
- Освещение в СМИ
- О преподавателях университета
- 9
- 9003
- стороны, то можно установить их степени или показатели равными друг другу.
\(3x\ln \left(6\right)=\left(2x-3\right)\ln \left(2\right)\)
\(x=-\frac{3\ln \left(2\right)}{\ln \left(54\right)}\)
Ответ: \(x=-\frac{3\ln \left(2\right)}{\ln \left(54\right)}\).
Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа». Запишитесь на пробное занятие уже сейчас!
Запишитесь на бесплатное тестирование знаний!
Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности
Наши преподаватели
Камо Аркадьевич Филипосян
Репетитор по математике
Стаж (лет)
Образование:
Самаркандский государственный университет
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Репетитор по математике для 8-11 классов и по физике для 7-9 классов. Я твёрдо убежден, что образовательный процесс должен быть пронизан живой, позитивной энергией учителя, находящий ключ к сердцу ученику с помощью индивидуальных подходов к урокам, подаче нового материала. Мое кредо – «Математика – ключ к новым возможностям, добыть его мало, надо найти замок открываемый этим ключом»! Могу помочь с высшей математикой (Арифметика и теория чисел, математическая логика, математический анализ, линейная алгебра, аналитическая геометрия, обыкновенные дифференциальные уравнения.)
Я твёрдо убежден, что образовательный процесс должен быть пронизан живой, позитивной энергией учителя, находящий ключ к сердцу ученику с помощью индивидуальных подходов к урокам, подаче нового материала. Мое кредо – «Математика – ключ к новым возможностям, добыть его мало, надо найти замок открываемый этим ключом»! Могу помочь с высшей математикой (Арифметика и теория чисел, математическая логика, математический анализ, линейная алгебра, аналитическая геометрия, обыкновенные дифференциальные уравнения.)
Алина Владимировна Ваулина
Репетитор по математике
Стаж (лет)
Образование:
Уральский федеральный университет им. Б.Н.Ельцина
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Репетитор по английскому и немецкому языку для 1-9 классов. Я очень люблю английский за звучание и так как без него в современном мире никуда. Знания английского мне помогли в карьере в туризме. Я за индивидуальный подход с интерактивными, игровыми методами. На занятиях со мной ученику будет комфортно и легко. Люблю мотивировать и зажигать любовь к языку!
Я очень люблю английский за звучание и так как без него в современном мире никуда. Знания английского мне помогли в карьере в туризме. Я за индивидуальный подход с интерактивными, игровыми методами. На занятиях со мной ученику будет комфортно и легко. Люблю мотивировать и зажигать любовь к языку!
Елена Сергеевна Соколюк
Репетитор по математике
Стаж (лет)
Образование:
Южный федеральный университет
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Репетитор по математике для 5-9 классов. Подготовка к ОГЭ. Считаю, что математику может знать каждый, ее не нужно «зубрить». Найду подход к каждому ученику, открою пару математических лайфхаков, покажу, как смотреть на задачу под другим углом. Будем учиться мыслить, а не решать шаблонами.
Подготовка к ОГЭ. Считаю, что математику может знать каждый, ее не нужно «зубрить». Найду подход к каждому ученику, открою пару математических лайфхаков, покажу, как смотреть на задачу под другим углом. Будем учиться мыслить, а не решать шаблонами.
Похожие статьи
Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности
Решение экспоненциальных уравнений — Математика средней школы
Звоните прямо сейчас, чтобы записаться на обучение:
(888) 888-0446
Все ресурсы по математике для старших классов
8 Диагностические тесты 613 практических тестов Вопрос дня Карточки Learn by Concept
← Предыдущая 1 2 Следующая →
Справка по математике для средней школы » Алгебра II » Математические отношения и основные графики » Экспоненты » Решение экспоненциальных уравнений и построение графиков » Решение экспоненциальных уравнений
Какое значение удовлетворяет уравнению?
Возможные ответы:
Правильный ответ:
Объяснение:
– единственный выбор из приведенных, который удовлетворяет уравнению. Подстановка вместо дает:
Подстановка вместо дает:
Сообщить об ошибке
Решить для :
Возможные ответы:
Правильный ответ:
Объяснение:
Чтобы найти в уравнении
Вынесите выражение в левой части уравнения на множители:
Используйте метод «разности квадратов», чтобы разложить член в скобках в левой части уравнения на множители.
Любая переменная, которая приводит к тому, что любое из условий в скобках становится , будет допустимым решением уравнения. становится, когда есть, и становится, когда есть, поэтому решения есть и.
Сообщить об ошибке
Найти (ближайшие сотые):
Возможные ответы:
Правильный ответ:
3
3 Explanation:
Take the common logarithm of both sides and solve for :
Report an Error
Solve for (nearest hundredth):
Possible Answers:
Правильный ответ:
Explanation:
, so can be rewritten as
Report an Error
Solve for (nearest hundredth):
Possible Answers:
Correct answer :
Объяснение:
Один из методов: возьмем натуральный логарифм обеих сторон и найдем:
Отчет о ошибке
Решение для:
Возможные ответы:
888888.
Правильный ответ:
Уравнение не имеет решения.
Объяснение:
Так как , мы можем переписать это уравнение, подставив и применив степенное правило:
Это утверждение тождественно ложно, что означает, что исходное уравнение тождественно ложно. Нет решения.
Отчет о ошибке
Решение для:
Возможные ответы:
. Уравнение не имеет решения
9000 28 Правильное ОТВЕТ: 9000 200.0002 Объяснение:
, поэтому мы можем переписать уравнение следующим образом:
. ?
Возможные ответы:
Это уравнение не имеет отрезка у.
Правильный ответ:
Объяснение:
Чтобы найти точки пересечения по оси Y, установите и решите.
Сообщить об ошибке
Что такое Y-отрезки уравнения?
Возможные ответы:
Для этого уравнения нет точек пересечения по оси Y.
Правильный ответ:
Объяснение:
Чтобы найти точки пересечения по оси Y, установите и решите.
Сообщить об ошибке
Каковы абсциссы этого уравнения?
Возможные ответы:
Правильный ответ:
Объяснение:
Чтобы найти точки пересечения, приравняйте числитель к нулю.
Сообщить об ошибке
← Предыдущий 1 2 Далее →
Уведомление об авторских правах
Просмотреть репетиторов
Джоанн
Сертифицированный репетитор
Технологический институт моды, бакалавр искусств, маркетинг.
Посмотреть репетиторов
Келси
Сертифицированный репетитор
Государственный университет Бойсе, бакалавр искусств, писательское мастерство.
Посмотреть репетиторов
Meldorae
Сертифицированный репетитор
Государственный университет Уэйна, бакалавр прикладной психологии. Государственный университет Уэйна, магистр преподавания искусств, история.
Все ресурсы по математике для старших классов
8 диагностических тестов 613 практических тестов Вопрос дня Карточки Learn by Concept
Решение экспоненциальных уравнений без логарифмов
Поиск Показательное уравнение содержит неизвестную переменную в показателе степени. В этом уроке мы сосредоточимся на экспоненциальных уравнениях, которые не требуют использования логарифмов. В алгебре эта тема также известна как решение показательных уравнений с одним и тем же основанием. Почему? Причина в том, что мы можем решить уравнение, заставив обе части экспоненциального уравнения иметь одно и то же основание. 9{\color{red}N}}
В этом уроке мы сосредоточимся на экспоненциальных уравнениях, которые не требуют использования логарифмов. В алгебре эта тема также известна как решение показательных уравнений с одним и тем же основанием. Почему? Причина в том, что мы можем решить уравнение, заставив обе части экспоненциального уравнения иметь одно и то же основание. 9{\color{red}N}}
, тогда {\color{blue}M} = {\color{red}N}
Вам также следует помнить о свойствах показателей, чтобы успешно решать показательные уравнения.
Основные свойства экспоненты
1) Свойство нуля
2) Свойство отрицательной экспоненты
3) Правило произведения
4) Правило частного
5) Правило степени к степени
Давайте рассмотрим несколько примеров!
Примеры решения показательных уравнений без логарифмов
Пример 1: Решите приведенное ниже показательное уравнение, используя основные свойства показателей. 3}.
3}.
Применение свойства отрицательного показателя степени.
- На данный момент основания одинаковы, поэтому установите равные друг другу степени.
- Это просто одношаговое линейное уравнение.
- Чтобы найти x, разделите обе части на 3. Вот и все!
Окончательный ответ: x = — 1.
Пример 2: Решите приведенное ниже показательное уравнение, используя основные свойства экспонент.
98}.
Примените Правило продукта слева, а правило Power to a Power справа.
- Здесь мы готовы установить мощности равными друг другу, так как мы можем создавать единые базы, одинаковые с обеих сторон.
- Решить простое линейное уравнение.
- Вычтите обе стороны на 7x, чтобы выделить x. Сделанный!
Окончательный ответ x=3.
Пример 3: Решите приведенное ниже показательное уравнение, используя основные свойства показателей. 0}, используя нулевое свойство экспоненты.
0}, используя нулевое свойство экспоненты.
- Теперь у нас есть желаемая конфигурация — одинаковые базы с обеих сторон.
- Установите показатель степени левой части уравнения равным показателю степени правой части, затем решите уравнение относительно переменной x.
- Чтобы решить уравнение, начните с добавления обеих сторон по 12, чтобы сдвинуть константу вправо.
- Наконец, разделите обе части на 4, чтобы получить значение x.
Окончательный ответ: х = 3,93}
- Примените свойство отрицательного показателя степени к левой части уравнения.
- Умножьте внутренние показатели на внешние, используя правило степени к степени.
- Поскольку они имеют общую базу, добавьте показатели степени, используя правило произведения.
- Очевидно, что, имея одно и то же основание с обеих сторон, теперь мы можем установить каждую степень равной друг другу.
- Решите линейное уравнение, добавив обе части на 6, чтобы получить x = 93}
- Умножьте внутреннюю и внешнюю экспоненты, применив степень к правилу степени.

- Теперь мы можем сложить показатели степени в левой части уравнения, потому что теперь они имеют общие основания.
- Примените правило произведения, сложив степени, когда основания равны.
- Ясно, что мы можем положить степени обеих частей уравнения равными друг другу.
- Это приводит к простому многоступенчатому уравнению.
- Итак, сначала мы добавляем 6x с обеих сторон. Затем вычтите на 4. И, наконец, разделите на — 1, чтобы полностью изолировать x отдельно!
Ответ: х=7. Легкий!
Пример 6: Решите приведенное ниже показательное уравнение, используя основные свойства показателей.
Решение :
- Дано
- Выразите каждое число по основанию 2.
Затем умножьте внутренние показатели степени на внешние степени, используя правило степени на степень.
- Чтобы сгенерировать одну базу слева, используйте Правило произведения — скопируйте общую базу 2 и добавьте показатели степени.

- Это когда мы применяем правило продукта.
- После сложения показателей у нас есть по одному основанию с каждой стороны.
Пришло время установить силы равными друг другу.
- После приравнивания степеней приходим к этому квадратному уравнению.
Нам нужно переместить все члены на одну сторону, а противоположную сторону сделать равной нулю.
- Решите квадратное уравнение, используя метод факторинга. Вынесите из трехчлена число 5, а затем вынесите простой трехчлен как произведение двух двучленов.
- Используя свойство Zero, мы получаем эти значения для x.
Правильные ответы: x = 2 и x = — 1.
Пример 7: Решите приведенное ниже показательное уравнение, используя основные свойства показателей.
Решение :
- Дано
- Выразите каждое число как экспоненциальное число с основанием 7.

- Примените свойство отрицательного показателя степени с левой стороны.
Кроме того, символ квадратного корня можно переписать как показатель степени \large{1 \over 2}.
- Применение мощности к правилу мощности с левой стороны.
- Выразите левую часть с одним основанием, используя Правило произведения, скопировав общее основание и добавив показатели степени.
- Теперь мы можем установить степени равными друг другу, а затем решить.
- Чтобы найти x, вычтите обе части на 2.
- Упростите
- Чтобы завершить это, разделите обе части на 12.
\более 8}}.
Пример 8: Решите приведенное ниже показательное уравнение, используя основные свойства показателей.
Решение :
- Дано
- Выразите числа по основанию 5.
Затем умножьте внутренний и внешний показатели, используя правило степени на степень.

- Похоже, мы можем использовать правило частного, потому что у нас одинаковые основания для числителя и знаменателя.
- Вычесть показатель степени в числителе на показатель степени в знаменателе.
- Упростить
Теперь можно приравнять «степени» или степени, а затем решить квадратное уравнение.
- Решите квадратное уравнение, разложив трехчлен на два двучлена. Затем установите каждый бином равным 0, чтобы найти x.
- Используя свойство нулевого произведения, мы получаем эти значения x.
Окончательные ответы: x = — 3 и x = 2.
Вам также может понравиться:
Решение экспоненциальных уравнений с помощью логарифмов
Пояснение к уроку: Решение показательных уравнений графическим способом
В этом объяснении мы научимся решать показательные уравнения с помощью графических методов.
Экспоненциальные функции появляются во многих различных областях науки и их приложения включают радиоактивный распад, моделирование населения, сложные проценты и распространение вирусов, и это лишь некоторые из них.

Поскольку экспоненциальные функции используются во многих различных дисциплинах, изучение экспоненциальных функции имеет важное значение. В частности, решение показательных уравнений — это навык, который мы можем применимы ко многим различным проблемам. Например, чтобы определить продолжительность времени, мы бы нужно инвестировать определенную сумму денег в счет сложных процентов, нам нужно было бы решить показательное уравнение.
Прежде чем мы продемонстрируем, как решить показательное уравнение, давайте сначала вспомним определение экспоненциальной функции.
Определение: экспоненциальные функции
Экспоненциальная функция – это функция вида 𝑓(𝑥)=𝑎⋅𝑏, где 𝑎 и 𝑏 действительны константы, 𝑏 положительно, а 𝑏≠1.
Существует множество способов найти решения экспоненциальных уравнений вида 𝑎⋅𝑏=𝑔(𝑥), для некоторой заданной функции 𝑔(𝑥). Например, мы могли бы использовать перестановку. Однако, это не всегда возможно.
 Вместо этого мы найдем решения этих уравнений
графически.
Вместо этого мы найдем решения этих уравнений
графически.Учитывая график экспоненциальной функции 𝑦=𝑎⋅𝑏, любая точка на кривой имеет координаты вида (𝑥,𝑎⋅𝑏). Если начертить 𝑦=𝑔(𝑥) по тем же осям, то любая точка пересечение лежит на обеих кривых. В частности, их 𝑦-координаты будут равны, что дает нам 𝑎⋅𝑏=𝑔(𝑥).
Давайте рассмотрим пример использования этой техники для решения показательного уравнения.
Предположим, нас попросили решить 4=8, учитывая следующий график 𝑦=4.
Мы хотим найти значения 𝑥, которые удовлетворяют этому уравнению. Мы можем сделать это, сделав набросок 𝑦=8 на графике и нахождение координат точек пересечения.
Мы видим, что есть одна точка пересечения, где 𝑥=1,5. Поскольку это лежит на кривая 𝑦=4, мы должны иметь 4=8. Следовательно, 𝑥=1,5 является решением этого уравнения. Фактически, поскольку это единственная точка пересечения, мы можем заключить, что существует только одно решение задачи.
 уравнение. Мы можем записать множество решений уравнения как
{1,5}; это называется
набор решений.
уравнение. Мы можем записать множество решений уравнения как
{1,5}; это называется
набор решений.Стоит отметить, что иногда точки пересечения не будут иметь точного значения для их 𝑥-координата. В этих случаях мы аппроксимируем решения графически и мы можем использовать второстепенные линии сетки, чтобы определить оценку.
Не всегда возможно решить эти уравнения. Например, если бы вместо этого нас попросили решить уравнение 4=−1, тогда мы нарисуем 𝑦=−1 на графике и ищем точки пересечения.
Видим, что точек пересечения нет. На самом деле, мы знаем, что 4 положительно для любого значение 𝑥, поэтому оно никогда не может быть равно −1. Можно сказать, что уравнение не имеет решений или, в качестве альтернативы мы можем сказать, что множество решений уравнения равно ∅.
Также возможно иметь несколько решений. Например, рассмотрим следующую схему 𝑦=4 и 𝑦=73𝑥+53.
Мы видим, что есть две точки пересечения, одна в 𝑥=−0,5, а другой при 𝑥=1.
 Следовательно, это единственные два решения уравнения
4=73𝑥+53.
Следовательно, это единственные два решения уравнения
4=73𝑥+53.Следовательно, мы можем сказать, что множество решений этого уравнения равно {−0,5,1}. Мы можем проверить, что эти являются решениями уравнения путем замены. Например, мы заменяем 𝑥=1 в уравнение, чтобы получить 4=73(1)+534=1234=4.
Поскольку это уравнение истинно, мы подтвердили, что 𝑥=1 является решением уравнения уравнение.
В наших первых нескольких примерах мы будем использовать заданные графики экспоненциальных функций, чтобы найти множество решений показательного уравнения графически.
Пример 1. Определение набора решений экспоненциального уравнения Графически
Использовать заданный график функции 𝑓(𝑥)=2, чтобы найти множество решений уравнения 2=2.
Ответ
Напомним, что множество решений уравнения — это множество всех значений, которые удовлетворяют этому уравнение.
 В этом вопросе мы хотим определить все значения 𝑥, которые делают
уравнение 2=2 верно. Мы можем сделать это, вспомнив, что
любая точка на кривой 𝑦=𝑓(𝑥) будет
имеют координаты (𝑥,𝑓(𝑥)).
В этом вопросе мы хотим определить все значения 𝑥, которые делают
уравнение 2=2 верно. Мы можем сделать это, вспомнив, что
любая точка на кривой 𝑦=𝑓(𝑥) будет
имеют координаты (𝑥,𝑓(𝑥)).Мы можем начать с того, что перепишем данное уравнение в виде 2=2𝑓(𝑥)=2.
Итак, нам нужно найти все значения 𝑥 такие, что 𝑓(𝑥)=2. Мы можем найти их, найдя все точки на кривой с 𝑦-координатой 2; мы рисуем 𝑦=2 на диаграмме и найдите координаты точки пересечения.
Читая 𝑥-координату точки пересечения, мы можем видим, что 𝑓(4)=2, а так как это единственная точка пересечения, это единственное значение 𝑥 такое, что 𝑓(𝑥)=2.
Следовательно, единственным решением уравнения является 𝑥=4. Мы можем убедиться, что это решение, подставляя 𝑥=4 в уравнение: 2=22=22=2.
Поскольку это правда, это подтверждает, что 𝑥=4 является решением уравнения. Следовательно, решение набор уравнения 2=2 равен {4}.

Пример 2. Определение набора решений экспоненциального уравнения Графически
На диаграмме показан график 𝑓(𝑥)=2. Используйте этот график, чтобы найти набор решений уравнение 2=4.
Ответ
Напомним, что множество решений уравнения — это множество всех значений, которые удовлетворяют этому уравнение. Нам дан график 𝑓(𝑥)=2, и поэтому любая точка на этом графике будет иметь координаты вида 𝑥,2. Следовательно, мы можем найдите значения 2, используя 𝑦-координаты кривой. В частности, мы можем переписать данное уравнение как 2=4𝑓(𝑥)=4.
Следовательно, чтобы решить это уравнение, нам нужно найти значения, при которых 𝑓(𝑥) выходов 4. Делаем набросок 𝑦=4 на том же графике и найти координаты точки пересечения.
Координаты точки пересечения (1,4), поэтому мы знаем, что 𝑓(1)=4. С есть только одна точка пересечения, это единственное решение уравнения; следовательно, 𝑥=1 является единственным решением уравнения, а набор решений равен {1}.

Стоит отметить, что мы можем проверить, что 1 является решение путем подстановки 𝑥=1 в уравнение: 2=42=44=4.()
Набор решений уравнения равен {1}.
В наших следующих нескольких примерах мы увидим, как применить этот метод к показательному уравнению что нам нужно переставить в первую очередь.
Пример 3. Поиск набора решений экспоненциального уравнения Графически
На диаграмме показан график 𝑓(𝑥)=2. Используйте этот график, чтобы найти набор решений уравнение 2−12=4.
Ответ
Напомним, что множество решений уравнения — это множество всех значений, которые удовлетворяют этому уравнение. Мы можем переписать и изменить уравнение с точки зрения 𝑓 как 2−12=4𝑓(𝑥)−12=4𝑓(𝑥)=16.
Следовательно, решениями уравнения являются значения 𝑥 такое, что 𝑓(𝑥)=16. Мы можем найдите эти значения, вспомнив, что любая точка на кривой будет иметь вид (𝑥,𝑓(𝑥)), поэтому решениями уравнения являются точки на кривой с 𝑦-координата 16.

На кривой есть только одна точка с 𝑦-координатой 16; Это точка (2,16). Следовательно, 𝑓(2)=16 и единственным решением уравнения является 𝑥=2. Мы можем подтвердить, что это решение в уравнение, подставив 𝑥=2 в исходное уравнение: 2−12=42−12=416−12=44=4.()
Поскольку это уравнение верно, мы подтвердили, что 𝑥=2 является решением уравнения.
Набор решений уравнения 2−12=4 равен {2}.
Пример 4. Поиск набора решений экспоненциального уравнения Графически
На диаграмме показан график 𝑓(𝑥)=2. Используйте этот график, чтобы найти решение система уравнения 2+5=9.
Ответ
Напомним, что множество решений уравнения — это множество всех значений, которые удовлетворяют этому уравнение. Поскольку нам дан график 𝑓(𝑥), мы начнем с переписывания уравнения в термины 𝑓(𝑥) и перестановка: 2+5=9𝑓(𝑥)+5=9𝑓(𝑥)=4.

Следовательно, мы можем решить уравнение, найдя такие значения 𝑥, что 𝑓 выходы 4. Мы можем найдите эти значения, вспомнив, что любая точка на кривой имеет координаты вида (𝑥,𝑓(𝑥)).
Так как мы хотим 𝑓(𝑥)=4, рисуем линию 𝑦=4 и найти координаты любых точек пересечение.
Находим только одну точку пересечения с координатами (4,4). Следовательно, 𝑓(4)=4 и 𝑥=4 — единственное решение уравнения. Мы можем убедиться, что это решение уравнения подставляя 𝑥=4 в данное уравнение: 2+5=92+5=94+5=99=9.
Поскольку это верно, мы проверили, что 𝑥=4 является решение уравнения.
Набор решений данного уравнения равен {4}.
В наших последних двух примерах мы увидим, как применять этот метод, когда экспоненциальная функция равна линейной функции, а не константе.
Пример 5. Решение экспоненциального уравнения по диаграмме
Используйте следующий график, чтобы найти набор решений уравнения 2=𝑥−2.

Ответ
Напомним, что множество решений уравнения — это множество всех значений, которые удовлетворяют этому уравнение. Даны графики 𝑦=2 и 𝑦=𝑥−2, и 𝑦-координата точка на графике говорит нам о выходе функции при этом значении 𝑥. Следовательно, в точках пересечения двух графиков, мы будем иметь 2=𝑥−2. Поэтому мы можем использовать точки пересечения, чтобы найти решения уравнения.
𝑥-координаты точек пересечения равны 3 и 4, поэтому это два решения к уравнению. Мы можем проверить, что это решения, подставив их обратно в исходное уравнение.
Замена 𝑥=3, 2=3−22=11=1.
Замена 𝑥=4, 2=4−22=22=2.
Поскольку оба уравнения верны, мы подтвердили, что оба 𝑥=3 и 𝑥=4 — решения к уравнению.
Набор решений уравнения: {3,4}.
Пример 6: графическое решение экспоненциального уравнения
На следующем графике показана функция 𝑓(𝑥)=2.
 Используйте этот график и постройте
функция
𝑓(𝑥)=𝑥+3 найти решение
система уравнения 2=𝑥+3.
Используйте этот график и постройте
функция
𝑓(𝑥)=𝑥+3 найти решение
система уравнения 2=𝑥+3.Ответ
Напомним, что множество решений уравнения — это множество всех значений, которые удовлетворяют этому уравнение. Любая точка на данной кривой будет иметь координаты вида (𝑥,2). Если мы эскиз 𝑓(𝑥)=𝑥+3, то точки пересечения двух графиков будут равны 𝑥- и 𝑦-координаты. Так как 𝑦-координаты будут равны, мы будем иметь 2=𝑥+3 в эти точки, давая нам решения уравнения.
Есть несколько способов сделать набросок 𝑓(𝑥)=𝑥+3; мы можем заметить, что когда 𝑥=0, 𝑓(0)=0+3=3.
Итак, 𝑦-перехват равен 3. Мы можем решить 𝑓(𝑥)=0, чтобы найти 𝑥-перехват: 0=𝑥+3𝑥=−3.
Итак, 𝑥-перехват равен −3 и прямая проходит через эти две точки.
Затем мы можем считать 𝑥-координату единственного перекрестка точка между линией и кривой как 𝑥=−1, которая является единственным решением данной уравнение.

- Умножьте внутреннюю и внешнюю экспоненты, применив степень к правилу степени.

 Приведем пример: простейшее показательное уравнение 2x=7 имеет единственный корень x=log27.
Приведем пример: простейшее показательное уравнение 2x=7 имеет единственный корень x=log27.






 Вместо этого мы найдем решения этих уравнений
графически.
Вместо этого мы найдем решения этих уравнений
графически. уравнение. Мы можем записать множество решений уравнения как
{1,5}; это называется
набор решений.
уравнение. Мы можем записать множество решений уравнения как
{1,5}; это называется
набор решений. Следовательно, это единственные два решения уравнения
4=73𝑥+53.
Следовательно, это единственные два решения уравнения
4=73𝑥+53. В этом вопросе мы хотим определить все значения 𝑥, которые делают
уравнение 2=2 верно. Мы можем сделать это, вспомнив, что
любая точка на кривой 𝑦=𝑓(𝑥) будет
имеют координаты (𝑥,𝑓(𝑥)).
В этом вопросе мы хотим определить все значения 𝑥, которые делают
уравнение 2=2 верно. Мы можем сделать это, вспомнив, что
любая точка на кривой 𝑦=𝑓(𝑥) будет
имеют координаты (𝑥,𝑓(𝑥)).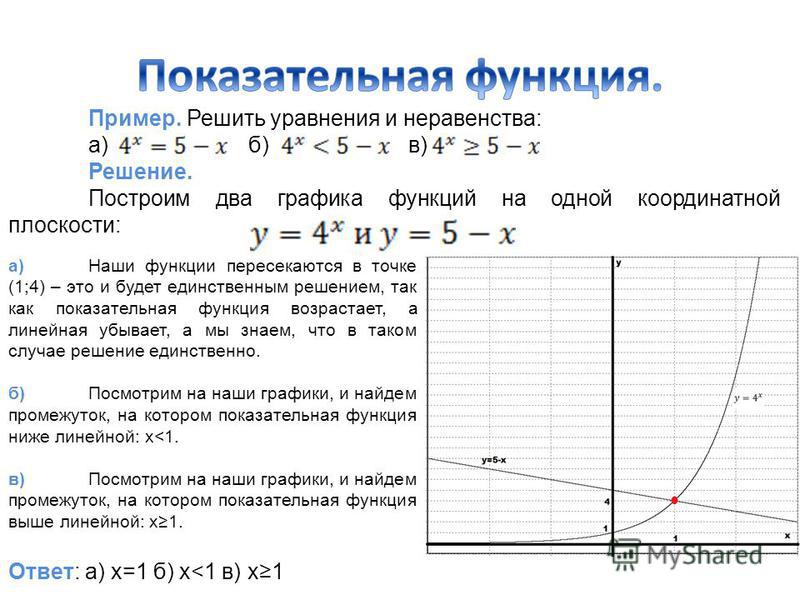




 Используйте этот график и постройте
функция
𝑓(𝑥)=𝑥+3 найти решение
система уравнения 2=𝑥+3.
Используйте этот график и постройте
функция
𝑓(𝑥)=𝑥+3 найти решение
система уравнения 2=𝑥+3.