Множества и операции над ними
1. Множества и операции над ними
МНОЖЕСТВА ИОПЕРАЦИИ НАД НИМИ
2. Понятие множества и операции над ними
ПОНЯТИЕ МНОЖЕСТВА И ОПЕРАЦИИ НАД НИМИПонятие множества является одним из основных понятий
математики и поэтому не определяется через другие.
Множества принято обозначать прописными буквами
латинского алфавита: A, B, C, …, Z.
Множество, не содержащее ни одного объекта,
называется пустым и обозначается так: Ø
Объекты, из которых образованно множество,
называются элементами.
Элементы множества принято обозначать строчными
буквами латинского алфавита: a, b, c, …, z.
Множества бывают конечными (множество дней в
неделе, месяцев в году) и бесконечными (множество
натуральных чисел, точек на прямой)
3. Стандартные обозначения числовых множеств
СТАНДАРТНЫЕ ОБОЗНАЧЕНИЯЧИСЛОВЫХ МНОЖЕСТВ
N – множество всех натуральных чисел
Z – множество всех целых чисел
Q – множество всех рациональных чисел
J – множество всех иррациональных чисел
R – множество всех действительных чисел
4.
 Способы задания множествСПОСОБЫ ЗАДАНИЯ МНОЖЕСТВ
Способы задания множествСПОСОБЫ ЗАДАНИЯ МНОЖЕСТВ1. Способом перечисления всех его
элементов.
Например, если множество А состоит из чисел
1,3,5,7 и 9, то мы зададим это множество, т.к.
все его элементы оказались перечисленными.
При этом используется следующая запись:
{1,3,5,7,9}
Такая форма задания множеств применяется в
том случае, когда оно имеет небольшое
количество элементов.
2. Через характеристическое свойство его
элементов
Характеристическое свойство – это такое
свойство, которым обладает каждый элемент,
принадлежащий множеству, и не обладает ни
один элемент, который ему не принадлежит.
Например, множество А={1,3,5,7,9} можно
задать через характеристическое свойство –
множество однозначных, нечетных
натуральных чисел.
Так множества обычно задают в том случае,
когда множество содержит большое
количество элементов или множество
бесконечно.
6. Символическая форма задания множеств
СИМВОЛИЧЕСКАЯ ФОРМАЗАДАНИЯ МНОЖЕСТВ
А – это множество всех натуральных чисел,
больших 3 и меньших 10 можно записать
таким образом:
А
А = { х|х Є N , 3 < x < 10}
это
всех
множество
больших
натуральных
чисел
меньших
7.
 Отношения между множествамиОТНОШЕНИЯ МЕЖДУ
Отношения между множествамиОТНОШЕНИЯ МЕЖДУМНОЖЕСТВАМИ
I. Рассмотрим 2 множества: А={a, b, c, d,
e}
B={b, d, k, m}
Эти множества имеют общие элементы. В этом случае
говорят, что множества пересекаются.
Множества А и В называются пересекающимися, если они
имеют общие элементы.
Отношения между множествами наглядно представляют
с помощью особых чертежей, называемых кругами
Эллера.
А
a c
e
b d
В
k m
II. Рассмотрим 2 множества: А={a, b, c, d, e}
B={k, m, n, f}
Множества не имеют общих элементов. В этом случае
говорят, что множества не пересекаются.
Множества А и В называются непересекающимися, если они
не имеют общих элементов
А
a
b
c
d
e
k m
n
f
В
III. Рассмотрим 2 множества: А={a, b, c, d, e}
В={b, c, d}
Эти множества называются пересекающимися, и, кроме того,
каждый элемент множества В являются элементом множества А.
В этом случае говорят, что множество В является
подмножеством множества А и пишут: В ⊂ А
Множество В называется подмножеством множества А, если
каждый элемент множества В является также элементом
множества А.

Пустое множество является подмножеством любого
множества. Ø ⊂ А
Любое множество является подмножеством самого себя. А ⊂
А
А
a e
b c
dИ
В
IV. Рассмотрим 2 множества: А={a, b, c, d,
e}
В={c, d, a, b, e}
Эти множества пересекаются, причем каждый элемент
множества А является элементом множества В (А ⊂ В), и
наоборот, каждый элемент множества В является элементом
множества А (В ⊂ А).
В этом случае говорят, что множества равны и пишут: А = В.
Множества А и В называются равными, если А ⊂ В и В ⊂ А
А
a
b
c
d
e
В
11. Операции над множествами
ОПЕРАЦИИ НАД МНОЖЕСТВАМИI. Пересечение множеств
Пересечением множеств А и В называется множество,
содержащее те и только те элементы, которые принадлежат
множеству А и множеству В.
С=А∩В
С={6,8}
А={2,4,6,8}
В={5,6,7,8,9}
А
2
4
8
6
9
7
5
В
II. Объединение множеств
Объединением множеств А и В называется множество,
содержащее те и только те элементы, которые принадлежат
множеству А или множеству В.

А={2,4,6,8}
В={5,6,7,8,9}
А
4
С=А∪В
С={2,4,5,6,7,8,9}
2
6
8
В
7
5
9
III. Вычитание множеств
Разностью множеств А и В называется множество, содержащее
те и только те элементы, которые принадлежат множеству А и
не принадлежат множеству В.
А\В={х|х Є А и х ∉ В}
А
В
b
c
a
d
Дополнением множества В до множества А называется
множество, содержащее те и только те элементы множества А,
которые не принадлежат множеству В.
14. Декартово произведение множеств
ДЕКАРТОВО ПРОИЗВЕДЕНИЕМНОЖЕСТВ
Упорядоченную пару, образованную из элементов множеств А
и В принято записывать, используя круглые скобки (a, b).
Элемент а называют первой координатой (компонентой) пары,
а элемент b – второй координатой (компонентой) пары.
Декартовым произведением множеств А и В называется
множество всех пар, первая компонента которых принадлежит
множеству А, а вторая компонента принадлежит множеству В.

А х В = { (х; у) | х Є А, у Є В }
15. Пример 1
ПРИМЕР 1А={1,3,5}
В={2,4}
А·В={(1;2), (1;4), (3;2), (3;4), (5;2), (5;4)}
16. Пример 2
ПРИМЕР 2А={1,3,5}
В=[2,4] или В={у|у Є R, 2≤у≤4}
17. Пример 3
ПРИМЕР 3А=[1;5]
В={2,4}
18. Пример 4
ПРИМЕР 4А=[1;5]
В=[2,4]
19. Пример 5
ПРИМЕР 5А=[1;5)
В=(2,4]
Конспект. Множества и операции над ними | План-конспект по математике на тему:
Множества и операции над ними
1. Основные понятия о множества.
- Основные определения.
Одним из основных понятий математики является понятие множества, и, как каждое основное понятие, не поддаётся точному определению (например, понятия “точка”, “прямая” являются одними из основных понятий геометрии).
МНОЖЕСТВОМ называется собрание, совокупность объектов, объединенных по какому-нибудь общему признаку, свойству.
Примеры:
- Множество студентов данной учебной группы.

- Множество планет солнечной системы.
- Множество букв русского алфавита.
- Множество натуральных чисел.
Математический смысл слова “множество” отличается от того, как оно используется в обычной речи. Так, в обычной речи понятие “множество” связывают с большим числом предметов, в математике же этого не требуется. Здесь могут рассматриваться множества, содержащие один объект, много объектов, несколько объектов или не содержащие ни одного объекта.
Объекты, из которых состоит множество, называются его ЭЛЕМЕНТАМИ.
Остановимся на символике, обычно использующейся при обращении с множествами.
Множества обозначаются прописными (заглавными) буквами латинского алфавита (без индексов или с индексами). Например: B, C,…,X,Y,…,A1,B1,…
Элементы множества обозначаются строчными (малыми) буквами латинского алфавита. Например: b,c,…,x,y,…,a1,b1,…
В математике особую роль играют множества, элементами которых являются числа.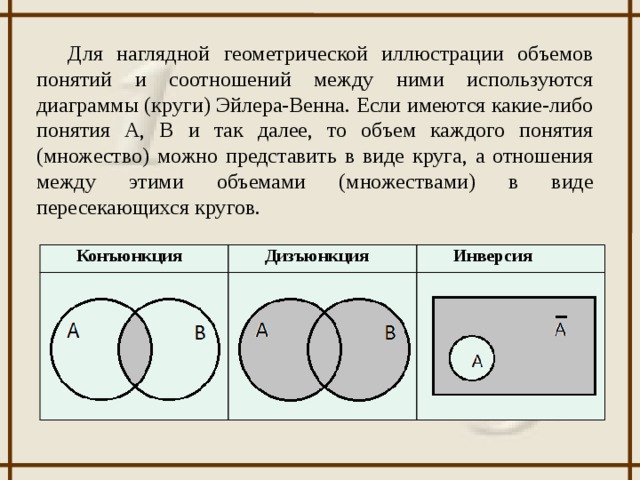 Такие множества называются ЧИСЛОВЫМИ. Некоторые числовые множества имеют специальные обозначения, вводимые для удобства пользования. Один из вариантов этих обозначений, которыми мы будем пользоваться в дальнейшем, выглядит следующим образом:
Такие множества называются ЧИСЛОВЫМИ. Некоторые числовые множества имеют специальные обозначения, вводимые для удобства пользования. Один из вариантов этих обозначений, которыми мы будем пользоваться в дальнейшем, выглядит следующим образом:
N – множество всех натуральных чисел;
Zc (или Z+ или C+) – множество всех целых неотрицательных чисел;
Z (или C) – множество всех целых чисел;
Q – множество всех рациональных чисел;
R – множество всех действительных чисел;
R+ — множество всех действительных положительных чисел.
По числу элементов, входящих в множество, множества делятся на три класса:
1 – конечные, 2 – бесконечные, 3 – пустые.
1. Если элементы множества можно сосчитать, то множество является КОНЕЧНЫМ.
Пример 1.
Множество гласных букв в слове “математика” состоит из трёх элементов – это буквы “а”, “е”, “и”, причем, гласная считается только один раз, т. е. элементы множества при перечислении не повторяются.
е. элементы множества при перечислении не повторяются.
2. Если элементы множества сосчитать невозможно, то множество БЕСКОНЕЧНОЕ.
Пример 2.
Множество натуральных чисел бесконечно.
Пример 3.
Множество точек отрезка [0;1] бесконечно.
3. Множество, не содержащее ни одного элемента, называется ПУСТЫМ. Символически оно обозначается знаком ∅.
Пример 4.
Множество действительных корней уравнения x2 +1=0.
Пример 5.
Множество людей, проживающих на Солнце.
В математике часто приходится определять принадлежность данного элемента конкретному множеству.
Пример 6.
Мы говорим, что число 5 натуральное, т.е. утверждаем, что число 5 принадлежит множеству натуральных чисел. Символически принадлежность множеству записывается с помощью знака ∈. В данном случае символическая запись будет такой: 5 ∈ N. Читается: “5 принадлежит множеству натуральных чисел”.
Число 5,2 не принадлежит множеству натуральных чисел, т.к. не является натуральным числом.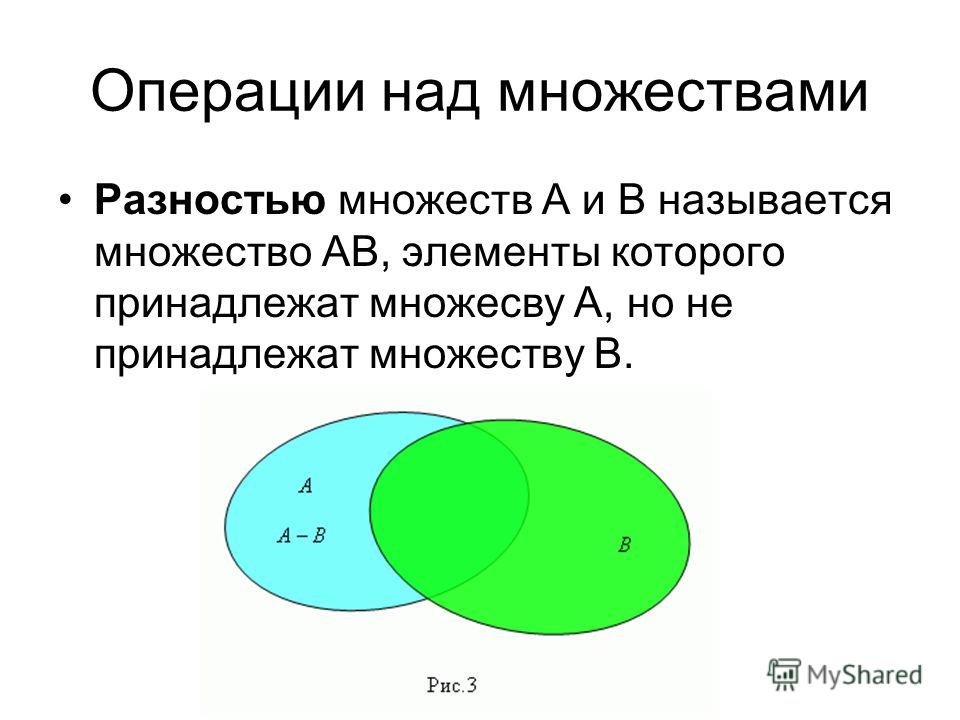 Символически отношение “не принадлежит” записывается с помощью знака (реже ∉). Таким образом, здесь имеем: 5,2 ∉ N
Символически отношение “не принадлежит” записывается с помощью знака (реже ∉). Таким образом, здесь имеем: 5,2 ∉ N
Читается: “5,2 не принадлежит множеству натуральных чисел”.
1.2 Способы задания множеств.
Множество считается заданным, если мы владеем способом, позволяющим для любого данного элемента определить, принадлежит он данному множеству или не принадлежит.
Множество можно задать, непосредственно перечислив все его элементы, причём, порядок следования элементов может быть произвольным. В этом случае названия всех элементов множества записываются в строчку, отделяются точкой с запятой и заключаются в фигурные скобки.
Пример 7.
Множество всех гласных букв русского алфавита:
A={а; я; у; ю; э; е;о; ё; и; ы}.
Пример 8.
Множество цифр десятичной системы счисления:
B={1; 2; 3; 4; 5; 6; 7; 8; 9; 0}.
Очевидно, что такой способ задания множеств удобно применять для конечных множеств с небольшим количеством элементов.
Конечные и бесконечные множества могут быть заданы другим способом: указанием ХАРАКТЕРИСТИЧЕСКОГО СВОЙСТВА, т.е. такого свойства, которым обладает любой элемент данного множества и не обладает ни один элемент, не принадлежащий ему.
Пусть P обозначает некоторое свойство, которым обладают все элементы множества А и не обладают элементы никакого другого множества. Тогда множество всех элементов, обладающих свойством Р, обозначим так:
А={х│х обладает свойством Р}={ х│Р(х)}={х : Р(х)}.
Свойство Р, задающее множество А, есть характеристическое свойство множества А.
Пример 9.
Множество чётных натуральных чисел. Зададим его с помощью характеристического свойства:
В={х │х – чётное натуральное число}={х │ х=2k, k Є N}.
Пример 10.
Множество всех действительных чисел на отрезке от 1 до 3 включительно запишется следующим образом:
R1-3={y│1≤ y≤ 3, y Є R}.
Следует заметить, что в ряде случаев одно и то же множество может быть задано как первым, так и вторым способом.
Пример 11.
Множество натуральных чисел, меньших, чем 10.
Первый способ: N
Второй способ: N
Случается, что одно и то же множество может быть задано с помощью различных характеристических свойств.
Пример 12.
Множество квадратов.
Первый способ: A={x│x – ромб с прямыми углами}.
Второй способ: A={ x│x – прямоугольник с равными сторонами}.
1.3 Отношения между множествами.
Наглядно отношения между множествами изображают при помощи особых чертежей, называемых КРУГАМИ ЭЙЛЕРА (или диаграммами Эйлера – Венна).
Для этого множества, сколько бы они ни содержали элементов, представляют в виде кругов или любых других замкнутых кривых (фигур) – рис.1.
рис. 1.
1. Пусть даны два множества: X={a; b; c; d} и Y={l; k; m; b; c}. Множества Х и Y содержат некоторые одинаковые элементы, а именно “b” и “c” . В данном случае говорят, что множества X иY находятся в отношении ПЕРЕСЕЧЕНИЯ. С помощью кругов Эйлера данное отношение можно представить в виде рис.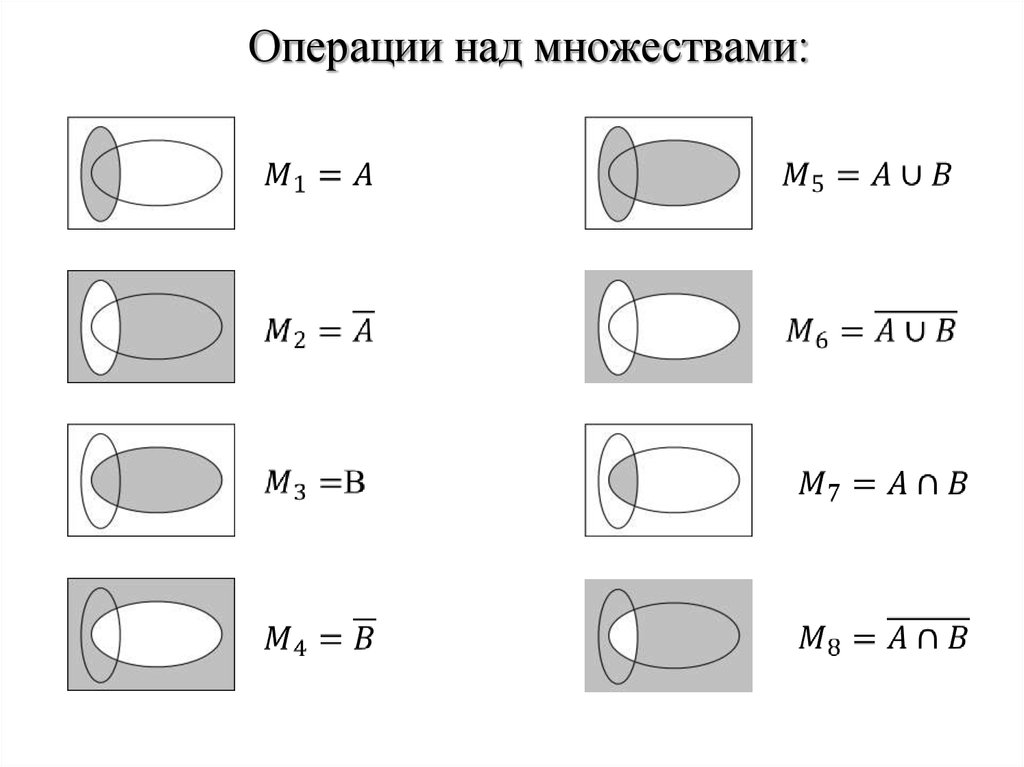 2.
2.
X Y B1 B2
рис. 2. рис. 3.
- Пусть даны множества B1={1; 2; 3} и B2={4; 5; 6}.
Данные множества различны, у них нет одинаковых элементов. В таком случае говорят, что множества B1 и B2 находятся в отношении НЕПЕРЕСЕЧЕНИЯ.
С помощью кругов Эйлера данное отношение показано на рис. 3.
- Пусть даны множества A={a; b; c; d; e} и B={a; b; c}.
Очевидно, что эти множества пересекаются; кроме того, каждый элемент
множества В является в то же время (одновременно) и элементом множества А. Тогда говорят, что множество В ВКЛЮЧЕНО в множество А, или что В есть ПОДМНОЖЕСТВО множества А.
Определение 1.1
Множество В является подмножеством множества А тогда и только тогда, когда каждый элемент множества В является элементом множества А.
Отношение “включено” обозначается знаком ⊂.
Соответственно отношение “включает” – знаком ⊃.
Определение 1.1 символически записывается так: В⊂А или А⊃В. С помощью кругов Эйлера данное отношение между множествами показано на рис.4.
Из определения подмножества следует, что всякое непустое множество А содержит по крайней мере два
множества: Ø и А, которые называются НЕСОБСТВЕННЫМИ
ПОДМНОЖЕСТВАМИ МНОЖЕСТВА. Все остальные подмножества (если они существуют) называются СОБСТВЕННЫМИ ПОДМНОЖЕСТВАМИ МНОЖЕСТВА. То есть, если В – собственное подмножество множества А, то имеем: Ø⊂ В⊂А, или иначе: А⊃В⊃ Ø.
4. Пусть даны множества C={x; y; z}, D={x; y; z}, которые состоят из одних и тех же элементов. В таком случае говорят, что множества С и D равны и пишут C=D.
Определение 1.2
Множества С и D называются равными, если они состоят из одних и тех же элементов.
Используя понятие “включено”, можно дать другое определение равенства множеств.
Определение 1.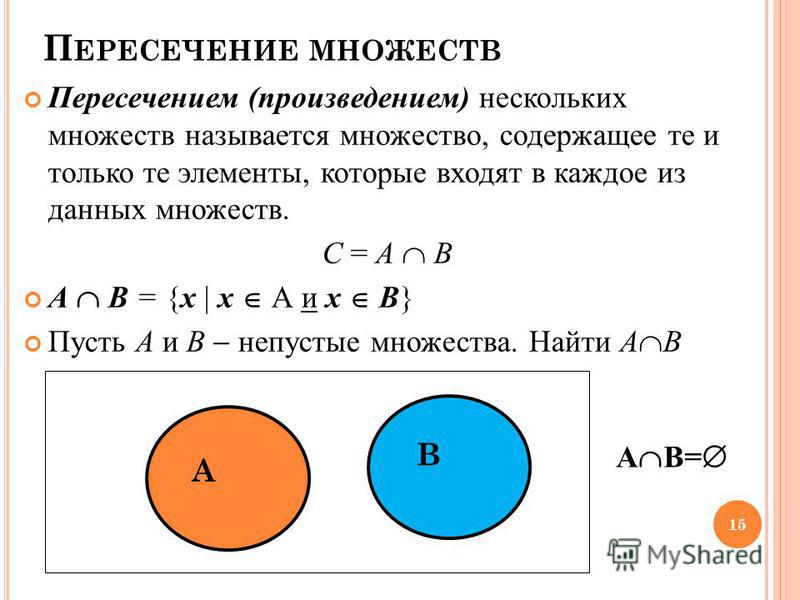 3
3
Множества C и D называются равными тогда и только тогда, когда множество С является подмножеством множества D, и наоборот.
Символически данное определение можно записать так:
С = D ⇔ С ⊂ D и D ⊂ С, или С = D ⇔ С ⊂ D ∧ D ⊂ С,
где знак ⇔ означает “эквивалентность” (равнозначность), а знак ∧ (конъюнкция) означает одновременность (совместность) осуществления тех операций (или событий), которые он соединяет.
С помощью кругов Эйлера отношение “равенство” показано на рис.5.
рис.5. рис.6.
УНИВЕРСАЛЬНОЕ МНОЖЕСТВО
Пусть U (или T – total) – некоторое фиксированное множество. Рассмотрим только такие множества А, В, С,…, которые являются подмножествами множества U. В этом случае множество U называется универсальным множеством всех множеств А, В, С,…
Примером универсального множества может служить множество действительных чисел, множество людей на планете Земля…
Мы его будем изображать прямоугольником с буквой U в правом верхнем углу (рис. 6), внутри которого будут размещаться те или иные множества.
6), внутри которого будут размещаться те или иные множества.
2. Операции над множествами
Рассмотрим некоторые операции над множествами.
2.1 Пересечение множеств
Пусть даны два множества: А={a; b; c; d} иB={c; d; e}.образуем новое множество Р, состоящее из всех элементов, принадлежащих одновременно и множеству А, и множеству В, т.е. Р={c;d}. Тогда говорят, что множество Р является пересечением множеств А и В.
Определение 1.4
Пересечением множеств А и В называется множество, состоящее их всех тех и только тех элементов, которые принадлежат множествам А и В одновременно.
Символически пересечение множеств А и В обозначается так: А∩В, где символ ∩ — знак пересечения множеств. Используя характеристическое свойство, определение 1.4 можно записать следующим образом:
Р=А∩В= {x ⎪x∈A и x∈B}={x ⎪ x∈A ∧ x∈B}. (1)
Таким образом, (1) есть характеристическое свойство пересечения двух множеств.
Союз “и” иногда заменяют фигурной скобкой, и тогда (1) будет иметь вид:
(2)
Для обозначения одновременной принадлежности множеству А и множеству В используется также знак ∧ (конъюнкция, или логическое “и”):
x∈A∩B ⇒ x∈A ∧ x∈B (2а)
Читаются выражения (2) и (2а) одинаково: если х принадлежит пересечению множеств А и В, то х принадлежит как множеству А, так и множеству В.
Если мы имеем ситуацию, когда х не принадлежит пересечению множеств А и В, то это означает, что х не принадлежит или множеству А, или множеству В.
Символически это может быть записано так:
(3)
где квадратная скобка заменяет союз “или”.
В символической записи союз “или” может быть заменен также знаком ∨ (дизъюнкция, логическое “или”):
х∉А∩В ⇒ х∉А ∨ х∉В. (3а)
Читаются выражения (3) и (3а) одинаково: если х не принадлежит пересечению множеств А и В, то х не принадлежит или множеству А, или множеству В.
Графическая иллюстрация вариантов пересечения двух множеств приведена на рис. 7÷10 (пересечение заштриховано).
рис. 7 рис. 8 рис. 9 рис. 10
2.2 Объединение множеств
Множества А и В входят в их объединение только один раз. Это вполне соответствует толкованию множества, принятому в математике: ни один элемент не может содержаться в множестве несколько раз.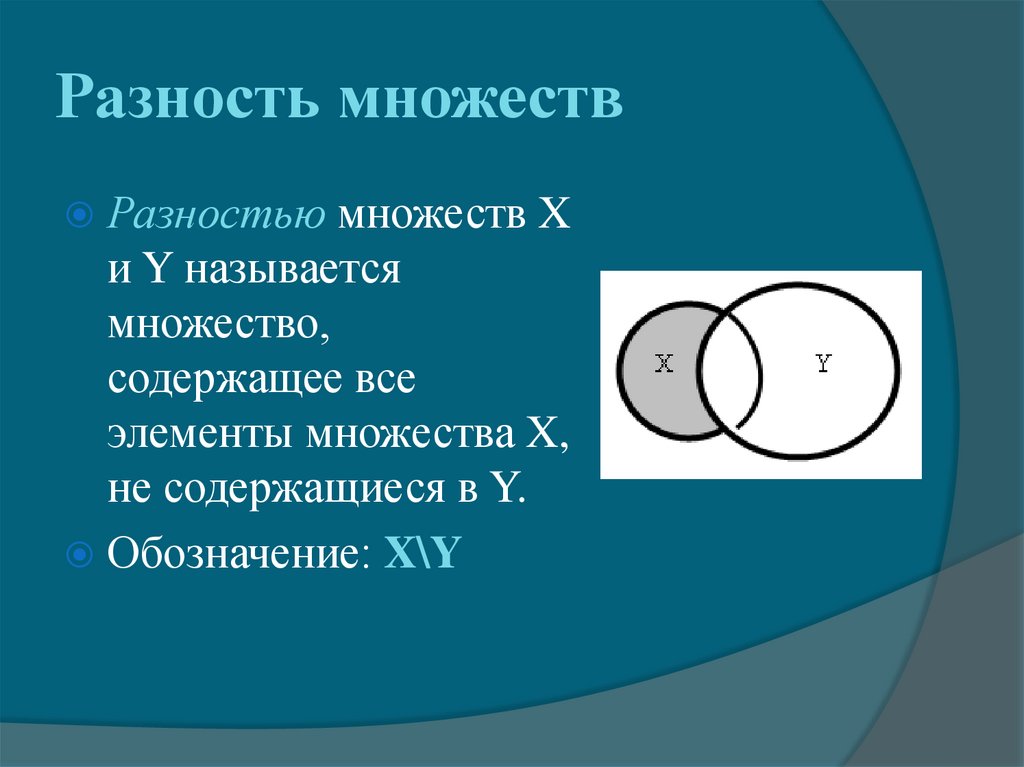
Определение 1.5
Объединением двух множеств А и В называется такое множество С, которое состоит из всех тех элементов, которые принадлежат хотя бы одному из множеств А или В.
Символически объединение двух множеств А и В обозначается так:
А ∪ В, где ∪ — символ объединения множеств. Определение 1.5 можно записать с помощью характеристического свойства:
С= А ∪ В={x⎪ x∈A или x∈B}. (4)
Союз “или” иногда заменяют квадратной скобкой
(5)
а также знаком дизъюнкции
х ∈А ∪ В ⇒ х∈А ∨ х∈В. (5а)
Читаются эти знаки одинаково: если элемент х принадлежит объединению двух множеств А и В, то он принадлежит множеству А или множеству В.
Если же элемент х не принадлежит объединению множеств А и В, то он не принадлежит ни множеству А, ни множеству В.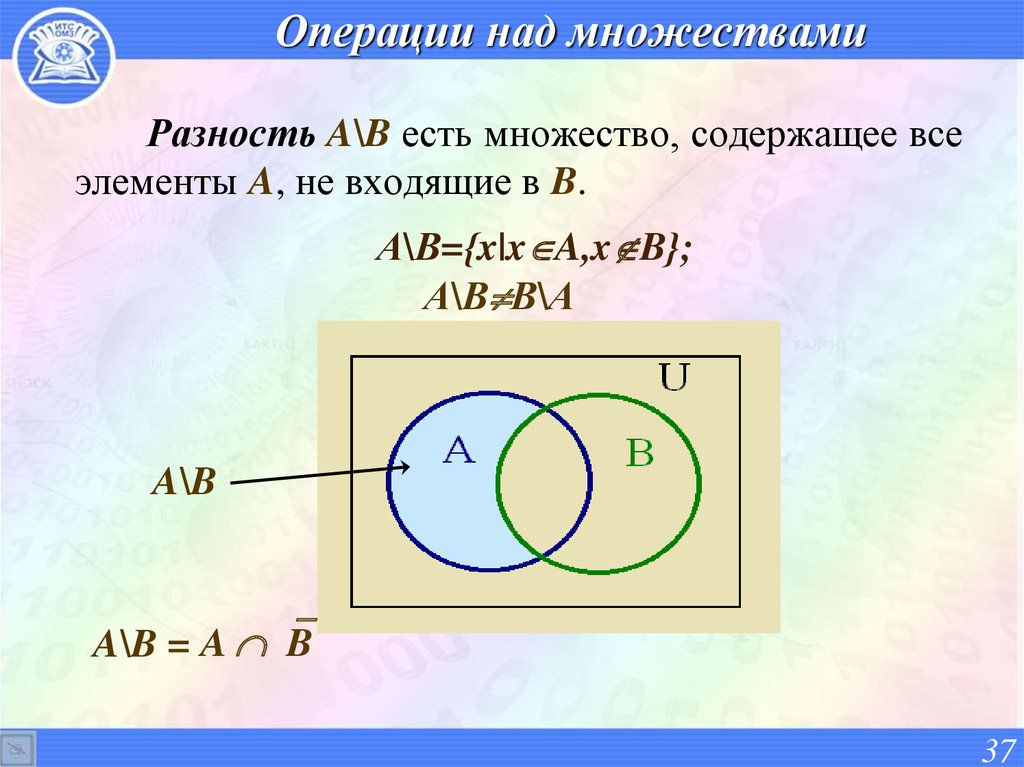 Символически это может быть записано так:
Символически это может быть записано так:
(6)
или
x ∉A∪B ⇒ x∉A ∧ x∉B. (6а)
Графически варианты объединения двух множеств показаны на рис. 11÷14 (объединение заштриховано).
рис. 11 рис. 12 рис. 13 рис. 14
Отметим некоторые очевидные свойства операции объединения двух множеств:
А∪А=А, А∪∅=А, А∪U=U. (7)
Замечание1.
Если А1, А2,…, Аn – несколько множеств, то аналогично тому, как это делалось для двух множеств, определяется их пересечение, т.е. составляется множество, представляющее их общую часть:
Р= А1∩ А2∩…∩ Аn={x ⎪ x∈∀ Ai, i=},
Где символ ∀ (квантор всеобщности) заменяет слово “все”, и, таким образом, мы символически обозначили ту часть множеств Ai, которая принадлежит каждому множеству одновременно.
Замечание 2.
Если А1, А2,…, Аn – несколько множеств, то аналогично тому, как это делалось для двух множеств, определяется их объединение – составляется множество, состоящее из элементов, которые принадлежат хотя бы одному их них:
C= A1∪A2∪…∪An={x ⎪ x∈A1 или x∈A2 или …или x∈An}.
Замечание 3.
Если в выражении есть знаки ∪ и ∩ и нет скобок, то сначала выполняется операция пересечения, а потом – операция объединения (аналог сложению и умножению в арифметике).
2.3 Разность множеств
Определение 1.6
Разностью двух множеств А и В называется множество, состоящее из всех тех и только тех элементов, которые принадлежат множеству А и не принадлежат множеству В.
Символически разность двух множеств обозначается так:
А В, где символ является знаком разности для множеств. С помощью характеристического свойства запишем определение 1.6 следующим образом:
C=A B={x ⎪ x∈A и x∉B} (8)
Или
(9)
а также x∈AB ⇒ x∈A ∧ x∉B. (9а)
(9а)
Пример 1.
Если E1={2; 4; 6} и E2={6; 8; 10}, то E3=E1E2={2; 4}, E4=E2E1={8;10}.
Пример 2.
Если M1={x1; x2; x3}, M2={y1; y2}, то M3=M1M2={ x1; x2; x3},
M4=M2M1={y1; y2}.
Пример 3.
Если K1={1; 3; 5; 7; 9}, K2={5; 7; 1}, то K3=K1K2={3; 9}, K4=K2K1=∅.
Графическое представление вариантов разности двух множеств А и В показано на рис. 15÷18, где множество А В заштриховано.
рис. 15 рис. 16 рис. 17 рис. 18
2.4 Дополнение к множеству
Определение 1.7
Пусть В ⊂ А. Множество всех элементов множества А, не принадлежащих множеству В, называют дополнением к множеству В и обозначают или .
Если ясно, о каком множестве идёт речь, то индекс А опускается и пишут или .
Определение 1.8
Пусть А – некоторое множество, являющееся частью универсального (основного) множества U. Дополнением множества А называется множество, состоящее из всех тех и только тех элементов их множества U, которые не принадлежат А. Его обозначают или .
Дополнением множества А называется множество, состоящее из всех тех и только тех элементов их множества U, которые не принадлежат А. Его обозначают или .
Это определение может быть записано в виде:
= {x ⎪ x∉A}. (10)
Графически дополнения (соответственно определениям 1.7 и 1.8) изображены на рис. 19 и 20 соответственно, на которых дополнения заштрихованы.
рис. 19 рис. 20
Множества и операции над ними, их геометрическое истолкование
Понятие множества относится к числу первичных в математике: его нельзя определить через другие понятия. Для наших целей оказывается достаточным интуитивного представления о множестве, и поэтому можно ограничиться его описанием и примерами.
Множество состоит из элементов и полностью определяется ими. Принадлежность элемента a множеству A обозначают ; запись означает, что a – не элемент A.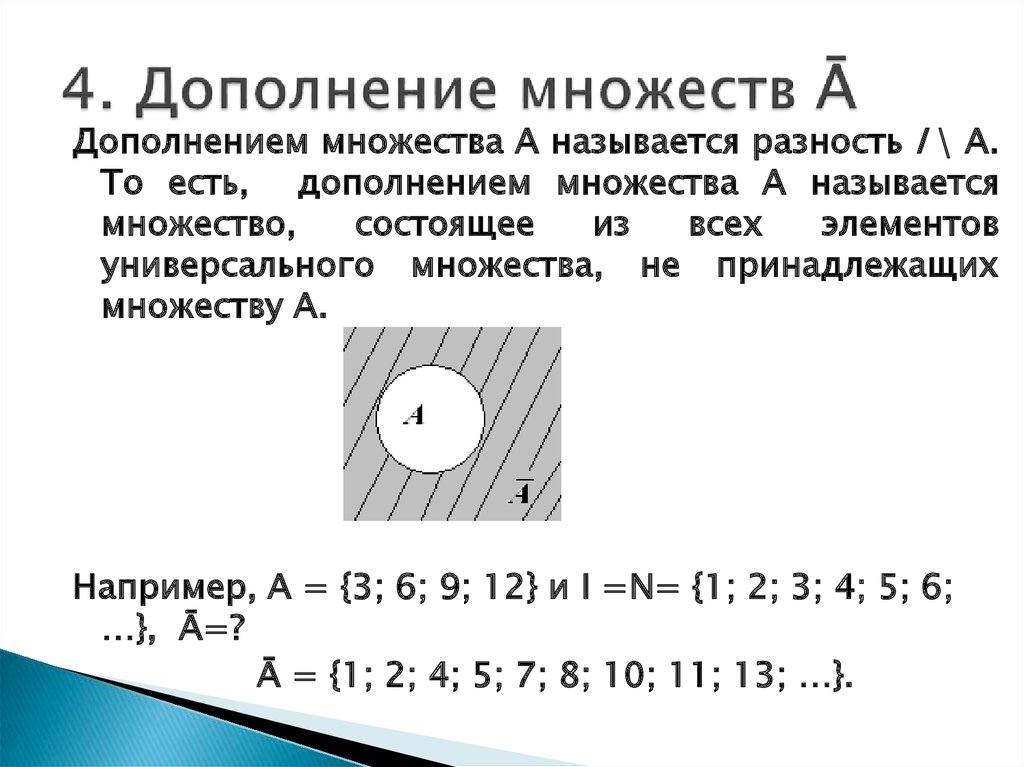
Множество можно задать либо непосредственным перечислением его элементов, либо указанием некоторого свойства, которым обладают элементы этого множества, и только они. В первом случае используют запись вида ( в фигурных скобках через запятую перечисляются элементы множества). Во втором случае записывают , что означает, что множество A состоит из тех и только тех элементов, для которых выполняется свойство .
Примеры 1.1
1) Запись вида означает, что множество A состоит из трех элементов a, b и c.
2) {человек│человек является студентом СПбГЭУ}. Множество A – множество студентов СПбГЭУ.
Множество, не содержащее ни одного элемента, называется пустым и обозначается знаком .
Два множества называются равными, если они состоят из одних и тех же элементов. Равенство множеств A и B обозначают: .
Множество A называется подмножеством множества B если каждый элемент множества A является элементом множества B. В этом случае также говорят, что имеет место включение множества A в множество B и обозначают (или ).
В этом случае также говорят, что имеет место включение множества A в множество B и обозначают (или ).
.
Для любого множества A верно, что и .
Очевидно, что тогда и только тогда, когда и .
При доказательстве равенства двух множеств можно пользоваться формулой:
Операции над множествами
Объединением множеств A и B называется множество, обозначаемое , состоящее из элементов, каждый из которых принадлежит хотя бы одному из множеств A или B:
.
Пересечением множеств A и B называется множество, обозначаемое , состоящее из элементов, каждый из которых принадлежит как множеству A, так и множеству B:
.
Пример 1.2. Пусть и . Тогда , .
Следующие свойства операций объединения и пересечения множеств следуют непосредственно из определений:
1) Коммутативность объединения и пересечения множеств
(переместительный закон):
; .
2) Ассоциативность объединения и пересечения множеств
(сочетательный закон):
; .
3) ; .
4) ; .
Следующие два свойства называются дистрибутивностью объединения и пересечения множеств (распределительным законом):
5) .
6) .
Замечание. Для обозначения объединения множеств
используют обозначение . Аналогичное обозначение используют для пересечения множеств: .
Разностью множеств A и B (или дополнением множества B в
множестве A) называется множество, обозначаемое A\B, состоящее из элементов множества A, не входящих в множество B:
A\B
Пример1. 3. Пусть и . Тогда A\B , B\A .
3. Пусть и . Тогда A\B , B\A .
Операции с множествами – объединение, пересечение и разность (дополнение) – связаны между собой так называемыми соотношениями двойственности: дополнение к объединению множеств равно пересечению их дополнений, а дополнение к пересечению – объединению дополнений. Действительно, пусть A, B и C – три множества. Докажем, что:
\ \A) \B).
Пусть . Это означает, что
Второе соотношение двойственности: доказывается аналогично.
Будем считать, что все множества в рассматриваемой задаче содержатся в одном и том же множестве U (универсальном множестве). Тогда дополнение множества
В этих обозначениях соотношения двойственности принимают вид:
и ,
и известны как формулы де Моргана.
Прямым (декартовым) произведением двух множеств A и B называется множество, обозначаемое , элементами которого являются упорядоченные пары , где :
.
Пример 1.4. , . Тогда и .
Пример 1.5. , . На рисунке изображены множества , . Двойной штриховкой обозначено множество .
Числовые множества
Перечислим общепринятые обозначения числовых множеств.
– множество натуральных чисел.
– множество целых чисел.
Q – множество рациональных чисел. Рациональным числом называется число, которое может быть представлено в виде отношения , где , .
R – множество действительных чисел.
Дата добавления: 2021-02-19; просмотров: 200; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
МНОЖЕСТВА И ОПЕРАЦИИ НАД НИМИ презентация, доклад, проект
МНОЖЕСТВА
И ОПЕРАЦИИ НАД НИМИ
«Множество есть многое, мыслимое нами как единое»
(Георг Кантор)
КАНТОР (Cantor) Георг (1845—1918) —
немецкий математик, логик, теолог, создатель теории трансфинитных (бесконечных) множеств, оказавшей определяющее влияние на развитие математических наук на рубеже 19— 20 вв.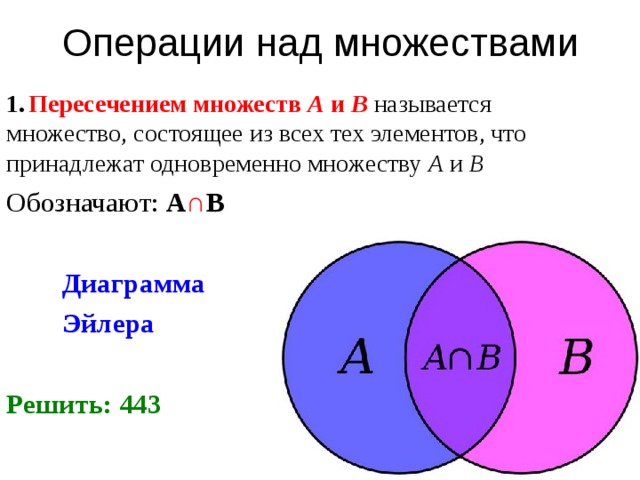
Теория множеств появилась на свет 7 декабря 1873 года.
Кантора заинтересовал вопрос, каких чисел больше – натуральных или действительных?
В одном из писем адресованных к своему приятелю Рихарду Дедекинду, Кантор писал, что ему удалось доказать посредством множеств, что действительных чисел больше, чем натуральных. День, которым было датировано это письмо, математики считают днем рождения теории множеств.
МНОЖЕСТВО
Множество — одно из основных понятий современной математики, используемое почти во всех её разделах.
К сожалению, основному понятию теории – понятию множества – нельзя дать строгого определения.
Можно сказать, что множество – это «совокупность», «собрание», «ансамбль», «коллекция», «семейство», «система», «класс» и т. д.
Понятие множества поясняется при помощи примеров: множество книг на полке, множество точек на прямой (точечное множество) и т.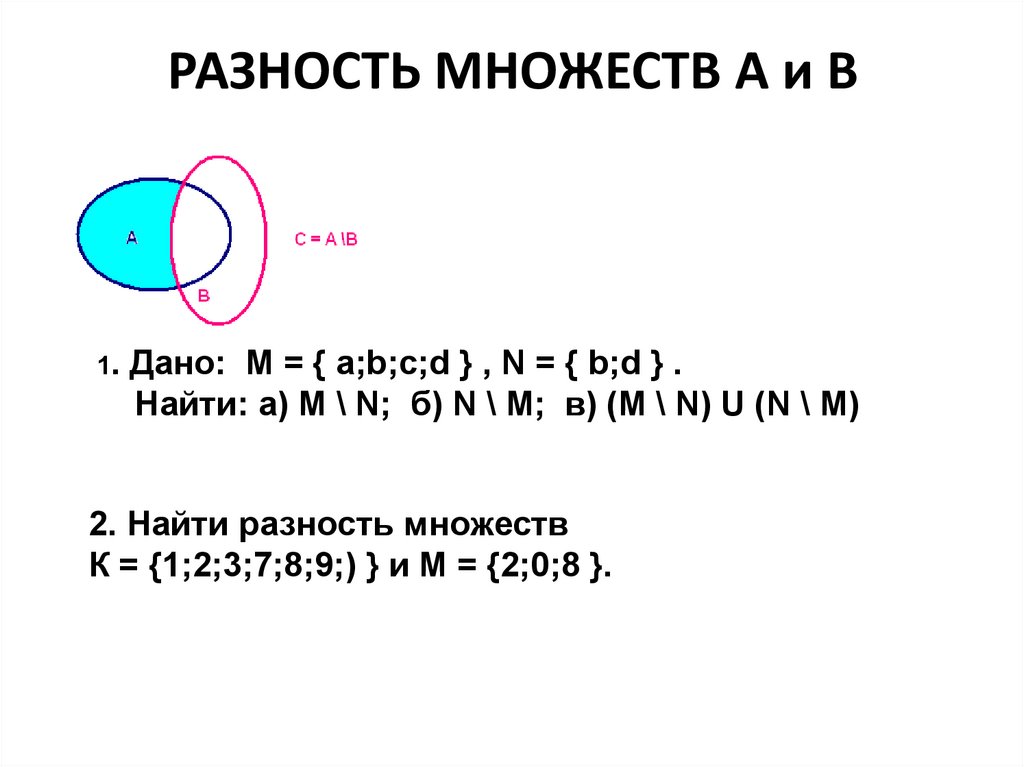
Множества принято обозначать прописными буквами латинского алфавита: A, B, C… Z.
Объекты, составляющие данное множество, называют его элементами.
Множество обычно обозначают большими латинскими буквами, а элементы множества − малыми латинскими буквам.
Если элемент, а принадлежит множеству А, то пишут:
а А
Если а не принадлежит А, то пишут:
а А.
А = {1, 2, 3, 4, 5, 6, 7, 8, 9}
B = {Маша, Даша, Саша}
Множество ЧЁТНЫХ чисел: свойство, которым обладает каждый элемент данного множества, — «ДЕЛИТСЯ НА 2».
СПОСОБЫ ЗАДАНИЯ МНОЖЕСТВ
МНОЖЕСТВО ПЛАНЕТ СОЛНЕЧНОЙ СИСТЕМЫ
МНОЖЕСТВО ЗНАКОВ ЗОДИАКА
ЧИСЛОВЫЕ МНОЖЕСТВА
Для самых основных числовых множеств утвердились следующие обозначения:
N — множество всех натуральных чисел;
Z — множество всех целых чисел;
Q — множество всех рациональных чисел;
R — множество всех действительных чисел. Приняты также обозначения Z+ , Q+, R+ соответственно для множеств всех неотрицательных целых, рациональных и действительных чисел, и Z¯, Q¯, R¯ -для множеств всех отрицательных целых, рациональных и действительных чисел.
Приняты также обозначения Z+ , Q+, R+ соответственно для множеств всех неотрицательных целых, рациональных и действительных чисел, и Z¯, Q¯, R¯ -для множеств всех отрицательных целых, рациональных и действительных чисел.
Два множества А и В называются равными
( А = В ), если они состоят из одних и тех же элементов, то есть каждый элемент множества А является элементом множества В и наоборот, каждый элемент множества В является элементом множества А.
Если каждый элемент множества А является
элементом множества В, то множество А называется подмножеством В.
Обозначение: А В.
Знак « » — знак включения.
ОПЕРАЦИИ НАД МНОЖЕСТВАМИ
Пересечением
двух множеств А и В, называется множество, которое состоит из всех элементов, лежащих одновременно в множестве А и в множестве В.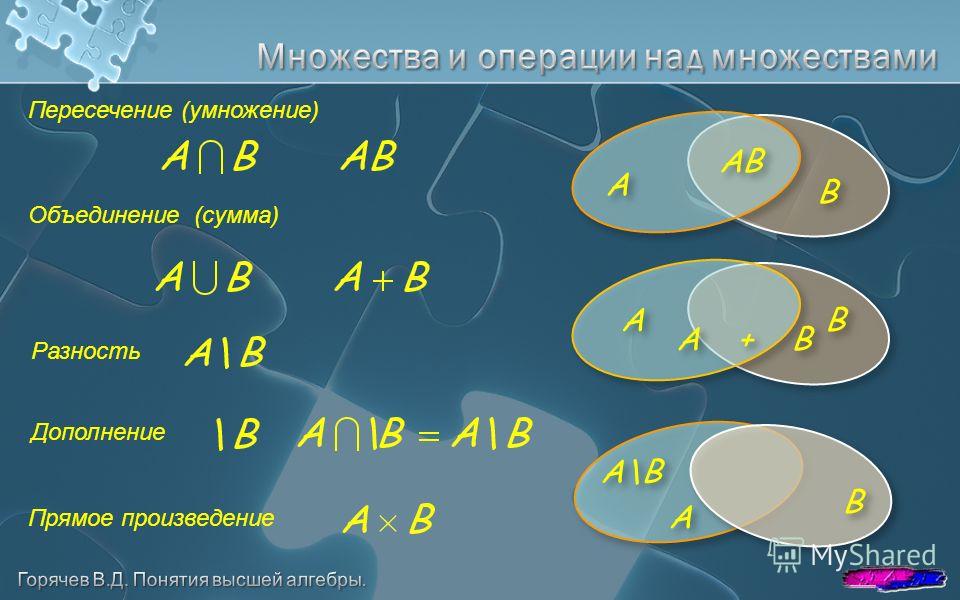
Объединением
двух множеств А и В называется множество, которое состоит из всех элементов, принадлежащих хотя бы одному из множеств — или А или В.
АВ= {x xA и xB}
А В={x xA или xB}
Разность множеств
Разностью А\В множеств А и В называется множество, состоящее из всех элементов множества А, которые не принадлежат множеству В
ЗАКРЕПЛЕНИЕ ИЗУЧЕННОГО
Приведите примеры множества, элементами которого являются:
а) животные;
б) составные числа;
в) простые числа;
г) треугольники.
Перечислите элементы множеств:
а) частей света;
б) деревьев;
в) материков;
г) цветов радуги.
Среди перечисленных ниже множеств укажите конечные и бесконечные множества:
а) множество чисел, кратных 11;
б) множество делителей числа 5;
в) множество океанов;
г) множество натуральных чисел;
д) множество рек Ростовской области;
е) множество корней уравнения х — 3 = 10;
Даны множества:
А – множество фруктов в корзине;
В – множество яблок в этой корзине;
С – множество груш в этой корзине;
Д – множество слив в этой корзине.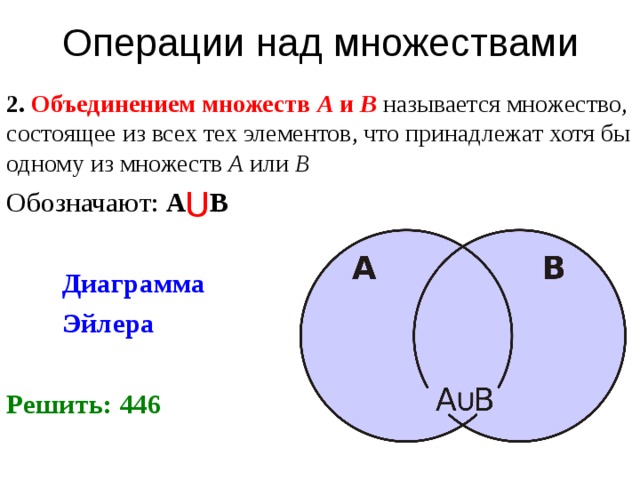
Чем являются множества В, С и Д для множества А?
БЛИЦ-ОПРОС
БЛИЦ-ОПРОС
земноводные, млекопитающие, хладнокровные и т.п.
Какие названия применяются для обозначения множеств животных?
БЛИЦ-ОПРОС
рота, взвод, полк, дивизия и т.п.
Какие названия применяются для обозначения множеств военно-служащих?
БЛИЦ-ОПРОС
букет
Как называется множество цветов, стоящих в вазе?
БЛИЦ-ОПРОС
флотилия, эскадра
Какие названия применяют для обозначения множеств кораблей?
БЛИЦ-ОПРОС
династия
Как называется множество царей (фараонов, императоров и т.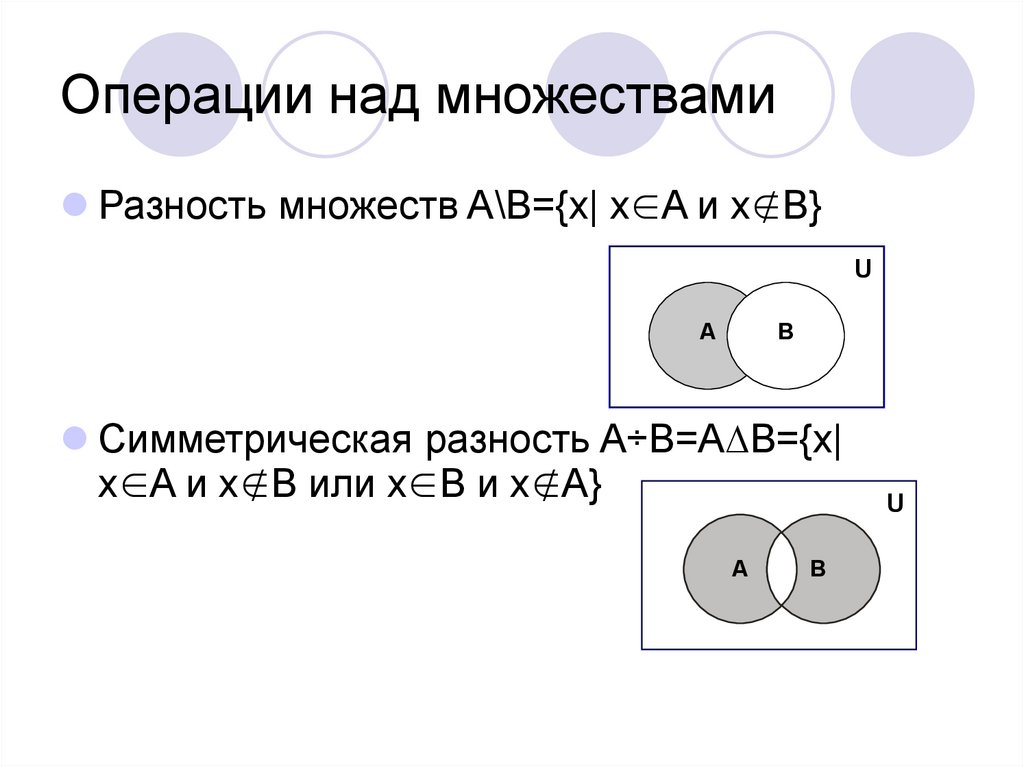 д.) данной страны, принадлежащих одному семейству?
д.) данной страны, принадлежащих одному семейству?
БЛИЦ-ОПРОС
экватор
Как называется множество точек земной поверхности, равноудаленных от обоих полюсов?
БЛИЦ-ОПРОС
деревня, село, город, посёлок
Как называется множество населённых людьми мест?
БЛИЦ-ОПРОС
выставка, галерея
Как называется множество картин?
БЛИЦ-ОПРОС
архив
Как называется множество документов?
Множества и операции над ними. Решение задач с помощью кругов Эйлера
Современный математический язык более краток и
заменяет разговорный язык специальными
буквенными и символьными выражениями. Понятия и
обозначения языка теории множеств
составляет фундамент современного
математического языка. Всякий объект, входящий
во множество, называют его элементом.
Например, если множество – дни недели, то
понедельник элемент этого множества.
Всякий объект, входящий
во множество, называют его элементом.
Например, если множество – дни недели, то
понедельник элемент этого множества.
Блок 1. Множества и операции над ними.
Презентация. (Слайд 2) Вопросы к слайду 2:
- Перечислите элементы множеств:
а) арабских цифр; (0; 1; 2; 3; 4; 5; 6; 7; 8; 9)
б) натуральных чисел; (1; 2; 3; 4;…)
в) целых чисел (…-2; -1; 0; 1; 2;…). - Как называется множество цветов, стоящих в вазе? (букет).
- Перечислите элементы множества планет солнечной системы. (Меркурий, Венера, Земля, Марс, Юпитер, Сатурн, Уран, Нептун).
- Как называется множество фруктовых деревьев и кустарников растущих у дома? (сад).
- Приведите примеры множеств, элементами которого являются геометрические фигуры.
- Какие названия применяют для обозначения
множеств животных? (млекопитающие, земноводные,
хладнокровные и т.
 п.).
п.). - Перечислите элементы множества видов спорта (футбол, теннис, волейбол и т. п.).
- Какие названия применяют для обозначения множеств кораблей? (флотилия, эскадра).
Задайте сами множество описанием.
(Слайд 3) Множества обычно обозначают большими буквами латинского алфавита: А, В, С, Д, и т. д. Некоторые числовые множества столь часто встречающиеся в различных разделах математики, что для них ввели специальные обозначения:
N – множество натуральных чисел;
Z – множество целых чисел;
Q – множество рациональных чисел;
I – множество иррациональных чисел;
R – множество действительных чисел.
(Слайд 4) Чтобы не забыть, что перечисляемые
элементы объединены вместе в некоторое
множество, такое перечисление производят внутри
фигурных скобок {,}.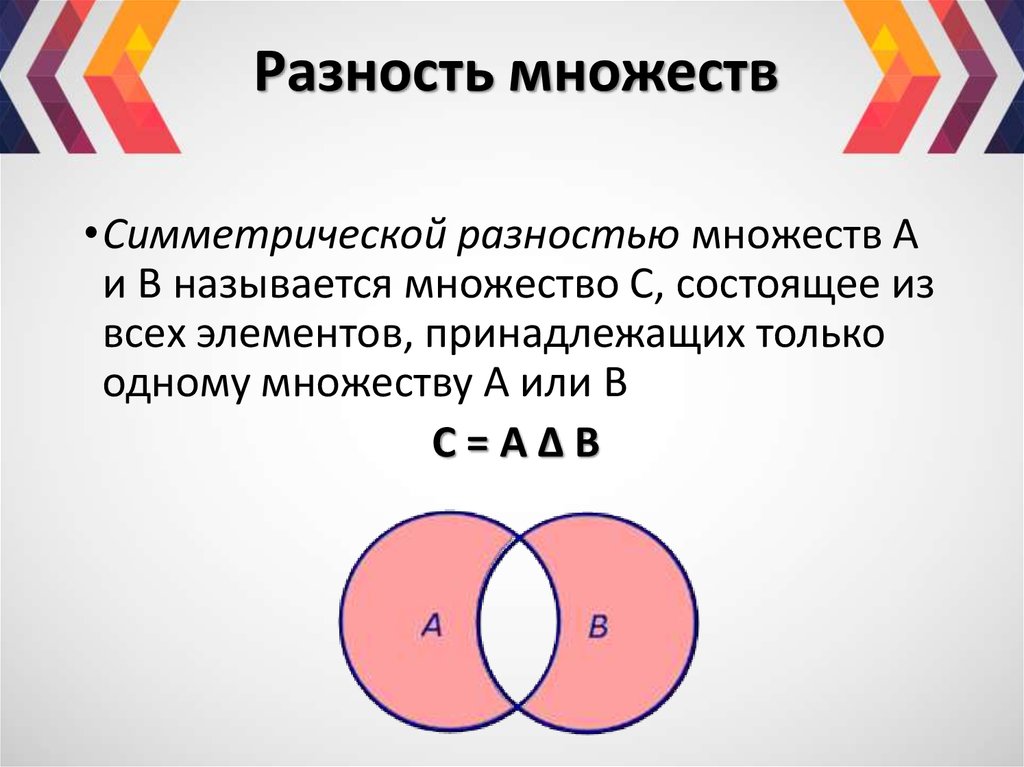
Например, цифры десятичной системы счисления задаются множеством
{0, 1, 2, 3, 4, 5, 6, 7, 8, 9}.
Если множество состоит из чисел, то при их перечислении иногда удобнее использовать не запятую, а знак препинания “ ; ” – точку с запятой. Так как “перечислительную” запятую можно спутать с “десятичной” запятой.
Элементы множества можно перечислять в произвольном порядке. От изменения порядка перечисления элементов само множество не меняется. Например, множество гласных букв русского алфавита задается {А, Е, Ё, И, О, У, Ы, Э, Ю, Я} или {Э, Е, А, Ё, Я, О, Ы, И, У, Ю}.
Эти множества состоят из одних и тех же элементов, их называют равными, а для записи равенства двух множеств употребляют знак “ = ”.
{А, Е, Ё, И, О, У, Ы, Э, Ю, Я} = {Э, Е, А, Ё, Я, О, Ы, И, У, Ю}.
Чтобы задать конечное множество, можно просто перечислить все его элементы.
Например, запись А = {2; 3; 5; 7; 11; 13} означает, что
множество А состоит из первых шести простых
чисел.
Однако задавать множество путем перечисления его элементов удобно только в том случае, когда их число невелико. Если число элементов множества достаточно велико или множество бесконечно, то явное перечисление элементов такого множества невозможно.
Способы задания, описания множеств весьма разнообразны. Например, множество всех квадратов натуральных чисел можно записать {1; 4; 9; 16; 25; …}, а множество всех чисел, которые больше 5 и меньше 12 записать {х | 5< х <12} или (5; 12). В примерах использован оборот “ … и так далее” и символ “ | ” внутри фигурных скобок заменяющий комбинацию слов “ … таких, что …”. (Множество всех х таких, что 5< х <12).
Описав словами некоторое множество, нельзя
гарантировать, что найдется хотя бы один объект,
отвечающий этому описанию. Предположим, о
множестве С сказано, что оно состоит из чисел,
делящихся на 6, но не делящихся на 3. Таких чисел
просто нет. В подобных случаях множество
называют пустым и обозначают символом O, в
фигурные скобки его не ставят, так как никакого
перечисления элементов пустого множества не
происходит.
В подобных случаях множество
называют пустым и обозначают символом O, в
фигурные скобки его не ставят, так как никакого
перечисления элементов пустого множества не
происходит.
(Слайд 5) Задание 1. [3]
1) Задайте множество цифр, с помощью которых записывается число:
а) 3254; б) 8797; в) 11000; г) 555555.
2) Задайте множество А описанием:
а) А = {1, 3, 5, 7, 9}; б) А = {– 2, – 1, 0, 1, 2}; в) А = {11, 22, 33, 44, 55, 66, 77, 88, 99}; г) А = {0,1; 0,01; 0,001; 0,0001; …}; д) А = {1/2, 2/3, 3/4, 4/5, … }.
3) Задание с выбором ответа. Даны множества: М = {5,4,6}, Р = {4,5,6}, Т = {5,6,7},
S = {4, 6}. Какое из утверждений неверно?
а) М = Р. б) Р S. в) М Т. г) Р = Т.
(Слайд 6) Словесные обороты, как “элемент х принадлежит множеству А” или “х – элемент множества А”, достаточно длинны и не всегда удобны в записи решений конкретных задач.
В математике эти выражения кратко записывают
так: х А, где – знак принадлежности.
Например, 5N, лучше читать не буквально, а в “литературном переводе”, “5 – число натуральное”. Наряду со знаком принадлежит используют и его “отрицание” – знак (знак не принадлежит). Запись 0 N означает, что нуль не натуральное число.
(Слайд 7) Задание 2. [3; 1]
1. Запишите на символическом языке следующее утверждение:
а) число 10 – натуральное; б) число – 7 не является натуральным; в) число – 100 является целым; г) число 2,5 – не целое.
2. Верно ли, что:
а) – 5 N; б) -5 Z; в) 2,(45) Q?
3. Верно ли, что:
а) 0,7 {х | х2 – 1 < 0}; б) – 7 {х | х2 + 16х ? – 64}?
(Слайд 8) Возьмем множество А = {2; 4; 6} и В = {1; 2; 3; 4; 5; 6; 7}. Каждый элемент множества А принадлежит также и множеству В. В таких случаях говорят, что множество А является подмножеством множества В, и пишут: А В.
Знак “” называют
знаком включения.
Соотношения между множествами А и В можно проиллюстрировать на рисунке с помощью так называемых кругов Эйлера (Леонард Эйлер российский ученый — математик, механик, физик и астроном.). Множество изображается в виде некоторого круга, а его элементы изображаются точками этого круга (рис 1).
Рис. 1
Пустое множество считают подмножеством любого множества. А В. Будем считать, что все элементы рассматриваемых множеств взяты из некоторого одного и того же “универсального” множества К. Это множество будем изображать квадратом, а рассматриваемые множества А, В, С, … – подмножества множества К – кругами (или другими полученными из них фигурами, которые выделим штриховкой).
(Слайд 9) Задание 3. [3; 1]
1. Даны множества: А = {10}, В = {10, 15}, С = {5, 10, 15}, D = {5, 10, 15, 20}.
Поставьте вместо … знак включения ( или ) так, чтобы получилось верное утверждение:
а) А… D; б) А…В; в) С…А; г) С…В.
2. Даны три множества А = {1, 2, 3,…, 37}, В = {2, 4, 6, 8, …}, С = {4, 8, 12, 16,…,36}.
Верно ли, что: а) А В; б) В С; в) С А; г) С В?
(Слайд 10) Из данных множеств с помощью специальных операций можно образовывать новые множества:
1) Пересечением множества А и В
называют множество, состоящие из всех общих
11элементов множеств А и В, т. е. из всех элементов,
которые принадлежат и множеству А, и множеству В
(рис. 2). Пересечение множеств А и В обозначают так:
АВ. Это определение
можно записать и так: АВ
= {х | х А и х В}. Иными словами,
пересечение двух множеств – это их общая часть.
Например, если А = {3; 9; 12} и В = {1; 3; 5; 7; 9; 11}, то АВ = {3; 9}. Если А = {10; 20; …90; 100}
и В = {6; 12; 18;…}, то АВ = {30;
60; 90}. Можно рассматривать пересечение не только
двух, но трех, четырех и т. д. множеств.
Пересечение множеств В, С и D обозначают так: ВСD.
д. множеств.
Пересечение множеств В, С и D обозначают так: ВСD.
Рис. 2
(Слайд 11) Задание 4. [3; 1]
1. Даны множества: А = {2; 3; 8}, В = {2; 3; 8; 11}, С = {5; 11}.
Найдите: а) АВ; б) АС; в) СВ.
2. Даны множества: А – множества всех натуральных чисел, кратных 10, В = {1; 2; 3;…, 41}.
Найдите АВ.
3. Даны множества: А = {a, b, c, d}, B = {c, d, e, f}, C = {c, e, g, k}.
Найдите (АВ) С.
(Слайд 12)
2) Объединением множеств А и В называют множество, состоящее из всех элементов, которые принадлежат хотя бы одному из этих множеств – или множеству А, или множеству В (рис. 3). Объединение множеств А и В обозначают так: АUВ.
Рис. 3
Это определение можно записать и так:
АUВ = {х | х А или х В}. Например, если А = {3; 9;
12} и В = {1; 3; 5; 7; 9; 11}, то АUВ = {1; 3; 5; 7; 9; 11; 12}. Можно
рассматривать объединение не только двух, но
трех, четырех и т.д. множеств. Объединение
множеств В, С и D обозначают так: ВUСUD.
Можно
рассматривать объединение не только двух, но
трех, четырех и т.д. множеств. Объединение
множеств В, С и D обозначают так: ВUСUD.
(Слайд 13) Задание 5. [3; 1]
1. Даны множества: А = {2; 3; 8}, В = {2; 3; 8; 11}, С = {5; 11}.
Найдите: а) АUВ; б) АUС; в) СUВ.
2. Даны множества: А = {a, b, c, d}, B = {c, d, e, f}, C = {c, e, g, k}.
Найдите (АUВ)UС.
3. Даны три числовых промежутка: А = (7,7; 11), В = [; ], С = (; 13].
Найдите (АUВ)UС.
Продолжение статьи
Приложение
Презентация
9 класс. Алгебра. Множества и операции над ними. — Множества
Комментарии преподавателяМножества в реальной жизни
Математика отражает реальную жизнь, а в реальной жизни мы наблюдаем выделение отдельных объектов, людей в единую совокупность. Например, родственников мы выделяем в единую совокупность и называем семьей, группу книг называем библиотекой и т. д. В математике соответствующим понятием является понятие множества.
д. В математике соответствующим понятием является понятие множества.
Множества обозначаются большими буквами латинского алфавита (). Множества в математике состоят из элементов, которые обозначаются малыми латинскими буквами ().
Тот факт, что элемент принадлежит множеству , записывается как . Тот факт, что элемент не принадлежит множеству , записывается как .
Два множества называются равными, если они содержат одни и те же элементы. Например: множество содержит цифры 1, 2, 3 и множество содержит эти цифры (), значит, множества равны друг другу (.
Способы задания множества:
1) Перечисление всех элементов множества. Например: .
2) С помощью характеристического свойства – свойства, которым обладают элементы множества (рис. 1).
Множество простых чисел – все натуральные числа, которые имеют ровно два обычных делителя.
Расположенные на оси x числа, между числами 1 и 2: .
Рис. 1. Задание множества с помощью характеристического свойства
Множество всех москвичей, которых зовут Дмитрий.
Пример
Рассмотрим множество корней уравнения. Зададим его характеристическим свойством: . Допустим, теперь следует задать то же множество, но с помощью перечисления его элементов. Для этого решим уравнение:
Тогда и т.д., порядок элементов здесь не важен.
Мы видим, что переход к новому виду множества может быть содержательной математической задачей. Здесь – это решение уравнения.
Аналогичный пример: описать множество корней уравнения: .
Мы знаем, что для любого , , тогда , значит, уравнение не имеет смысла, то есть у него нет корней. В этом случае записывается так называемое пустое множество .
По аналогии с нулем пустое множество – это множество в котором нет ни одного элемента.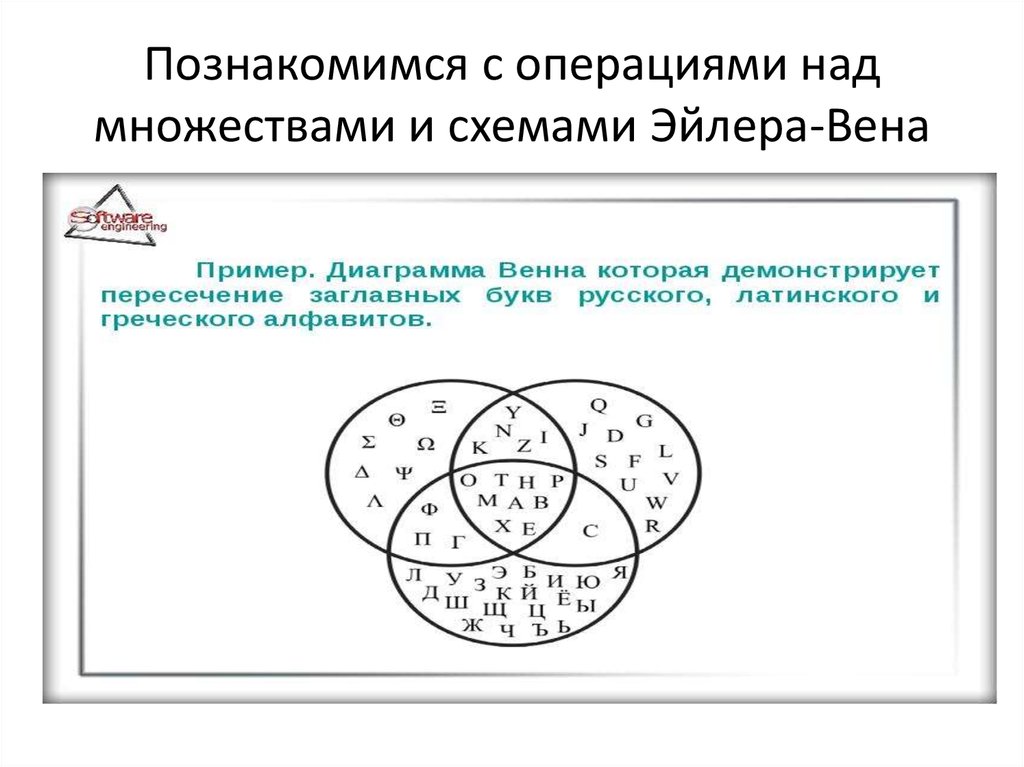
Характеристическое множество всегда должно быть сформулировано четко. Вот пример не очень удачной характеристики множества: окружностью называется множество точек плоскости, равноудаленных от одной точки. Если представить квадрат, то можно увидеть, что все его вершины равноудалены от одной точки – точки пересечения диагоналей (рис. 2).
Рис. 2. Иллюстрация примера не очень удачной характеристики множества
Но множество вершин квадрата не является окружностью, пропущено ключевое слово «…всех точек плоскости…».
Еще один пример о способах задания бесконечных множеств. Теорема: серединный перпендикуляр к отрезку есть геометрическое место точек, равноудаленных от его концов.
Возьмем отрезок , его центр – точка . Перпендикуляр, проведенный через точку к отрезку () – это серединный перпендикуляр, любая его точка равноудалена от концов отрезка (рис.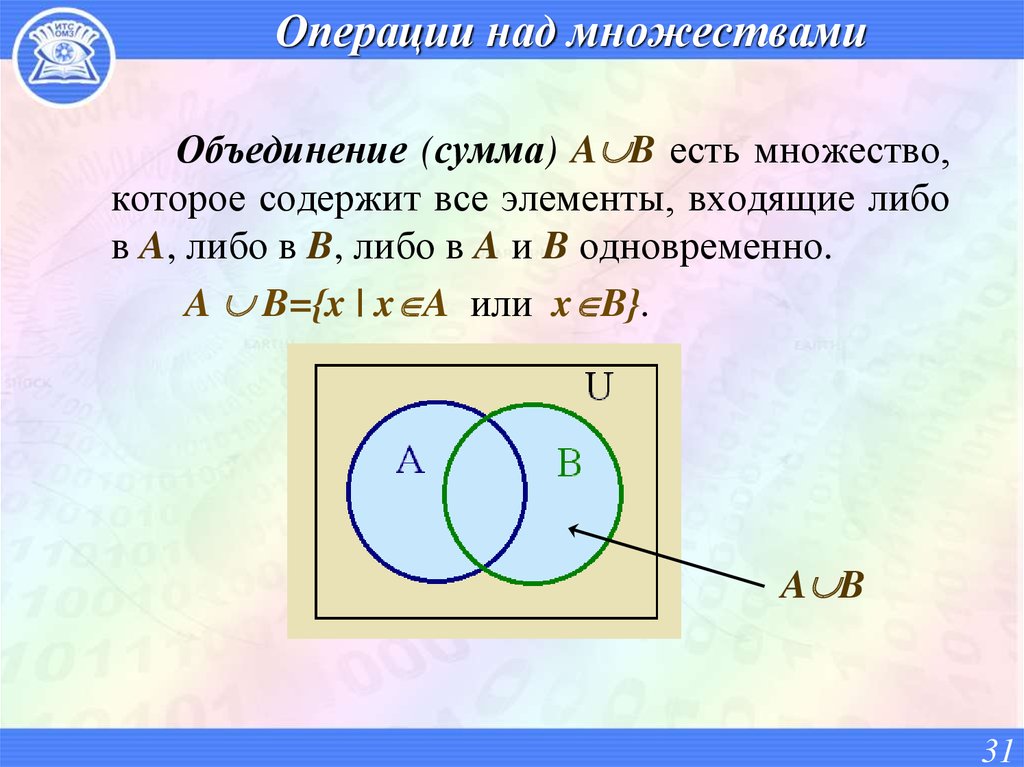 3). Точка принадлежит перпендикуляру () тогда и только тогда, когда . Смысл этой теоремы в том, что есть множество, которое задано характеристическим свойством, то есть равноудаленностью от концов отрезка, то есть множество задано неявно. Теорема утверждает, что это множество совпадает с серединным перпендикуляром к отрезку, то есть может быть задано явно – в том смысле, что может быть указан способ его построения, в данном случае построение циркулем и линейкой.
3). Точка принадлежит перпендикуляру () тогда и только тогда, когда . Смысл этой теоремы в том, что есть множество, которое задано характеристическим свойством, то есть равноудаленностью от концов отрезка, то есть множество задано неявно. Теорема утверждает, что это множество совпадает с серединным перпендикуляром к отрезку, то есть может быть задано явно – в том смысле, что может быть указан способ его построения, в данном случае построение циркулем и линейкой.
Рис. 3. Пример к теореме о серединном перпендикуляре к отрезку
Еще один пример: при изучении вписанных окружностей доказывают такую теорему – биссектриса есть геометрическое место точек, равноудаленных от сторон угла.
Имеем угол с вершиной , биссектриса , точка на биссектрисе. Опускаем перпендикуляры на стороны угла, к точкам и (рис. 4). Эти перпендикуляры, а значит, и расстояние от точки до лучей угла равны между собой. Точка принадлежит биссектрисе () тогда и только тогда, когда .
Точка принадлежит биссектрисе () тогда и только тогда, когда .
Рис. 4. Пример для теоремы о биссектрисе угла
Смысл этой теоремы в том, что есть множество с заданным характеристическим свойством: геометрическое место точек, равноудаленных от сторон угла, то есть множество задано неявно. Теорема утверждает, что это множество может быть задано явно, то есть может быть указан способ его построения, в данном случае построение циркулем и линейкой. Оно совпадает с биссектрисой. В данном случае мы опять сталкиваемся с тем, что задача перехода от одного описания множества к другому, может быть содержательной математически. Обратим внимание на то, что для бесконечных множеств, задание множества перечислением невозможно, а явное построение служит заменой этого способа.
Подмножество.С понятием «множество» вы уже знакомы.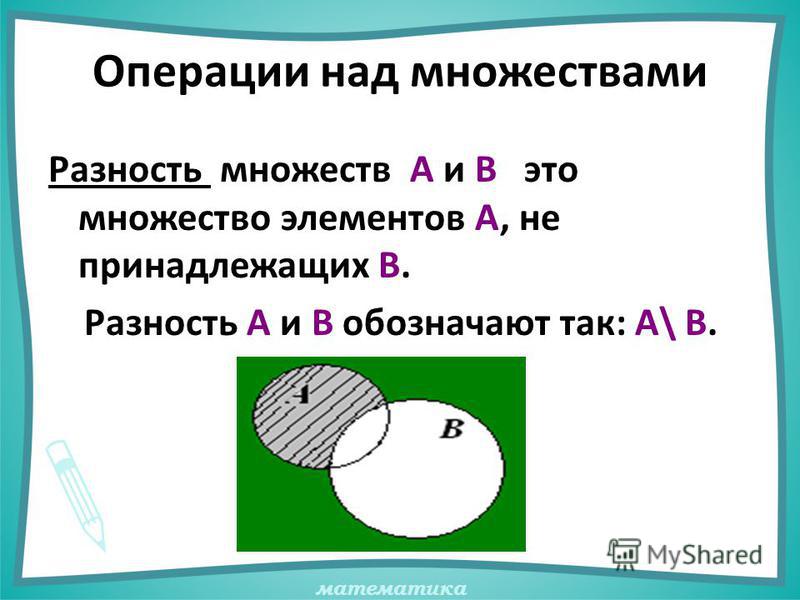 Подмножество, как можно догадаться из названия, – это определенная часть множества. Например:
Подмножество, как можно догадаться из названия, – это определенная часть множества. Например:
А – это множество всех учеников в классе.
В – это множество девочек указанного выше класса.
С – множество всех мальчиков класса.
D – множество всех отличников данного класса.
Е – множество всех мальчиков-отличников этого класса.
Таким образом, были перечислены множество (А) и его подмножества (В, С, D, Е). Теперь мы можем дать определение, что такое «подмножество».
Если каждый элемент множества В является элементом множества А, то множество В называют подмножеством множества А.
В ⊂ А
Как пример, девочки класса из примера выше (множество В) являются ученицами класса (множество А). Значит, В входит в А.
Мальчики тоже являются частью класса, значит, С ⊂ А.
Все отличники являются частью класса, D ⊂ A.
Как и мальчики, отличники – это ученики класса, то есть Е ⊂ А.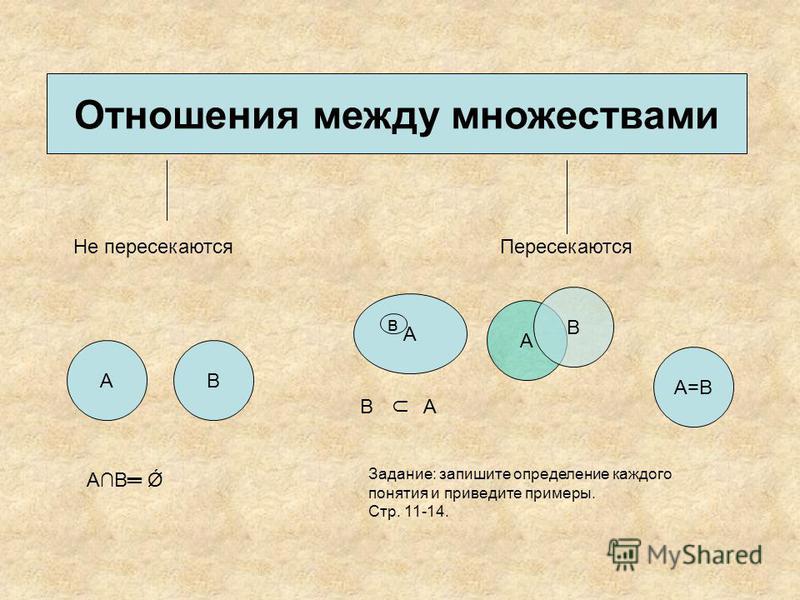
Если у нас а ∈ А, то это значит, что а принадлежит А.То есть, это один элемент a принадлежит множеству А.
Если же подмножество В входит в А, то мы пишем В ⊂ А.
То есть между значками есть разница.
N – множество натуральных чисел (с их помощью мы считаем предметы, природу и так далее.)
N =
Z – множество целых чисел.
Z =
Ясно, что натуральные числа – это подмножество целых чисел, то есть N ⊂ Z.
Q – множество рациональных чисел.
Q =
Если к множеству рациональных чисел добавить множество иррациональных чисел, то мы получим множество всех действительных чисел.
R – множество действительных чисел.
R =
Запишем правильные включения:
N ⊂ Z ⊂ Q ⊂ R
Пусть множество А – это множество всех четырехугольников: A, B, C, D (рис. 1).
Рис. 1. Множество А
Пусть множество В – это множество четырехугольников с парой равных параллельных сторон: A, B, C, D (рис. 2).
2).
BC = AD BC || AD
Рис. 2. Множество В
Множество С – это множество таких четырехугольников, у которых диагонали, пересекаясь, делятся пополам: AB, CD – диагонали, т. О – точка пересечения диагоналей, АО = ОС, BO = OD (рис. 3).
Рис. 3. Множество С
Итак, было рассмотрено 3 множества четырехугольников: множество произвольных четырехугольников; множество четырехугольников, у которых парные стороны равны и параллельны; множество четырехугольников, у которых диагонали, пересекаясь, точкой пересечения делятся пополам.
Рассмотрим еще 2 множества.
Множество D – это множество всех параллелограммов, и множество Е – множество параллелограммов с прямым углом (рис. 4).
Рис. 4. Множества D и Е
Таким образом, мы имеем 5 множеств четырехугольников.
Написать верное включение (то есть, какое множество является подмножеством другого множества) (рис. 5).
5).
Рис. 5. Иллюстрация к задаче
Наиболее богатое – это множество всех четырехугольников. Значит:
B ⊂ A; C ⊂ A; D ⊂ A; E ⊂ A
Множества В, С, D и Е являются подмножествами множества А.
Далее вспомним определение параллелограмма:
Параллелограммом называется такой четырехугольник, у которого противоположные стороны попарно параллельны.
Для того чтобы убедиться, что фигура является параллелограммом, необходимо вспомнить его признаки:
1. Если 2 стороны параллельны и равны, то такой четырехугольник является параллелограммом.
Значит, В – это множество всех параллелограммов.
2. Если в четырехугольнике диагонали пересекаются и точкой пересечения делятся пополам, то эта фигура – параллелограмм.
Значит, С – это множество всех параллелограммов.
Про множество D напрямую было сказано, что это множество всех параллелограммов.
Если будет стоять вопрос, какие множества равны между собой, то можно ответить, что:
В = С = D – это множества всех параллелограммов.
3. Если в параллелограмме хотя бы один угол равен 900, то такой параллелограмм является прямоугольником.
Значит, Е – это множество всех прямоугольников. Множество всех прямоугольников является подмножеством (частным случаем) произвольного четырехугольника и подмножеством параллелограмма. Отсюда имеем:
Е ⊂ А; E ⊂ B; E ⊂ C; E ⊂ D
Мы рассмотрели множества четырехугольников, из которых самое богатое множество – это множество всех четырехугольников, далее по-разному заданы множества параллелограммов и, наконец, Е – это множество всех прямоугольников. Были даны ответы на вопросы, где верные включения, какие множества равны между собой.
Мы уже знакомы с понятием множеств. Знаем, что каждое множество состоит из элементов.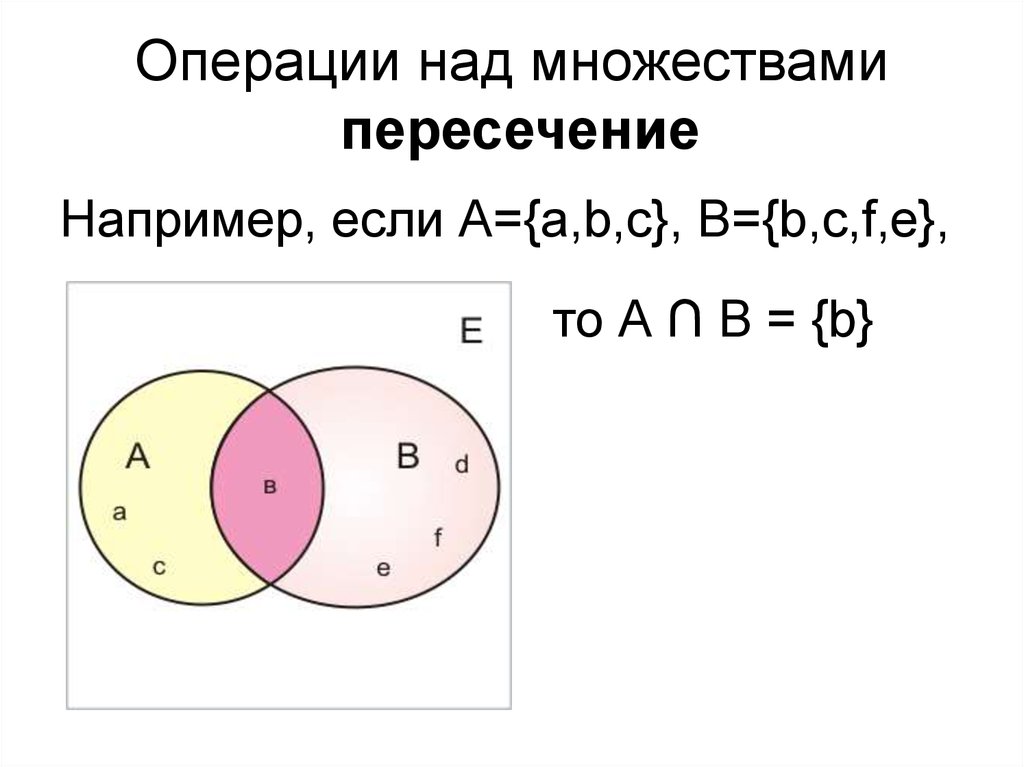 Сегодня мы рассмотрим примеры пересечения и объединения множеств.Обозначение:
Сегодня мы рассмотрим примеры пересечения и объединения множеств.Обозначение: a∈Ab∉A∈ – принадлежит, ∉ – не принадлежит.Число элементов в множестве может быть конечным, бесконечным и пустым.A={a;b;c} – конечное множествоB={x| 2≤x≤3} – бесконечное множество∅ – пустое множество
Пересечение и объединение множеств – операции над множествами.
Пример: В классе 19 учеников: 10 девочек, 9 мальчиков.
10 девочек – это множество .
9 мальчиков – это множество .
Класс из 19 учеников – это множество С, которое объединяет два множества.
Пусть в классе 5 отличников – это множество D.
Из них 2 мальчика – это множество E.
Из какие элементов состоит множество Е?
Мальчики входят в множества В, так как 2 мальчика – отличники, они входят в множество D.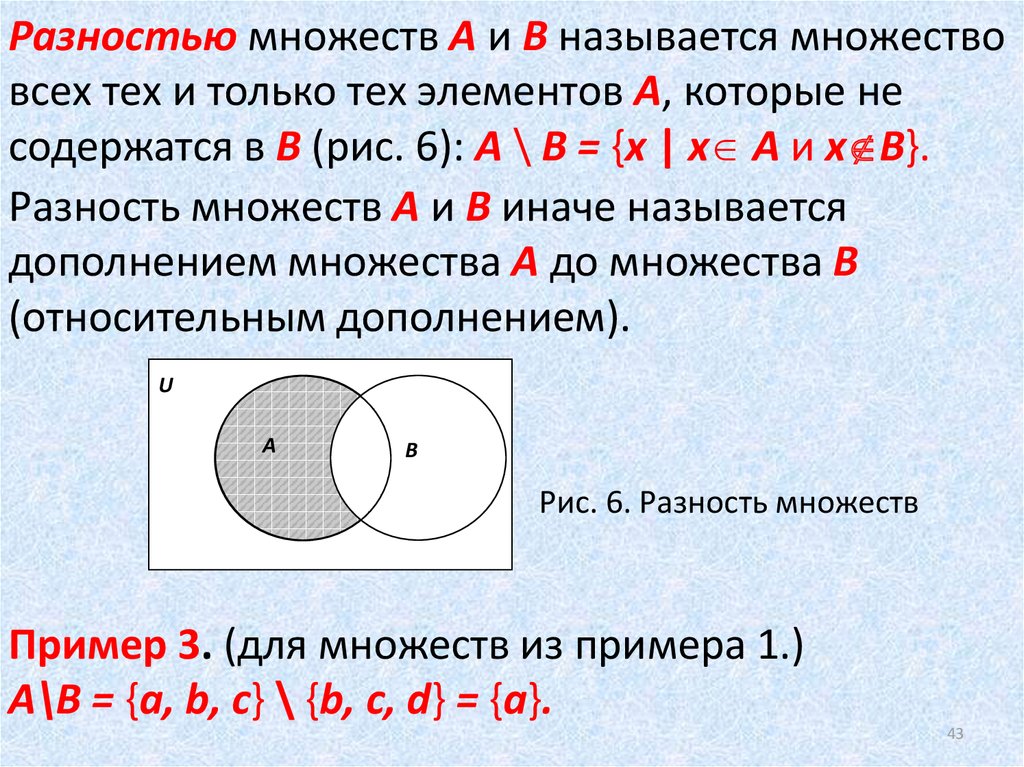
Рис. 1. Пересечение двух множеств
Множество Е есть пересечение двух множеств В и D(рис. 1).
Определение: объединением множеств А и В называется новое множество, состоящее из тех и только тех элементов, которые входят хотя бы в одно из множеств А или В (рис. 3).
Рис. 2. Множества
Рис. 3. Объединение множеств
– знак объединения.
Множество состоит из всех элементов , которые входят или в множество , или в множество . Это можно записать следующим образом:
Дано множество = и .
Найти объединение множеств .
Решение:
Дано множество и .
Найти объединение множеств .
Решение:
Имеем совокупность неравенств:
Решить квадратное неравенство .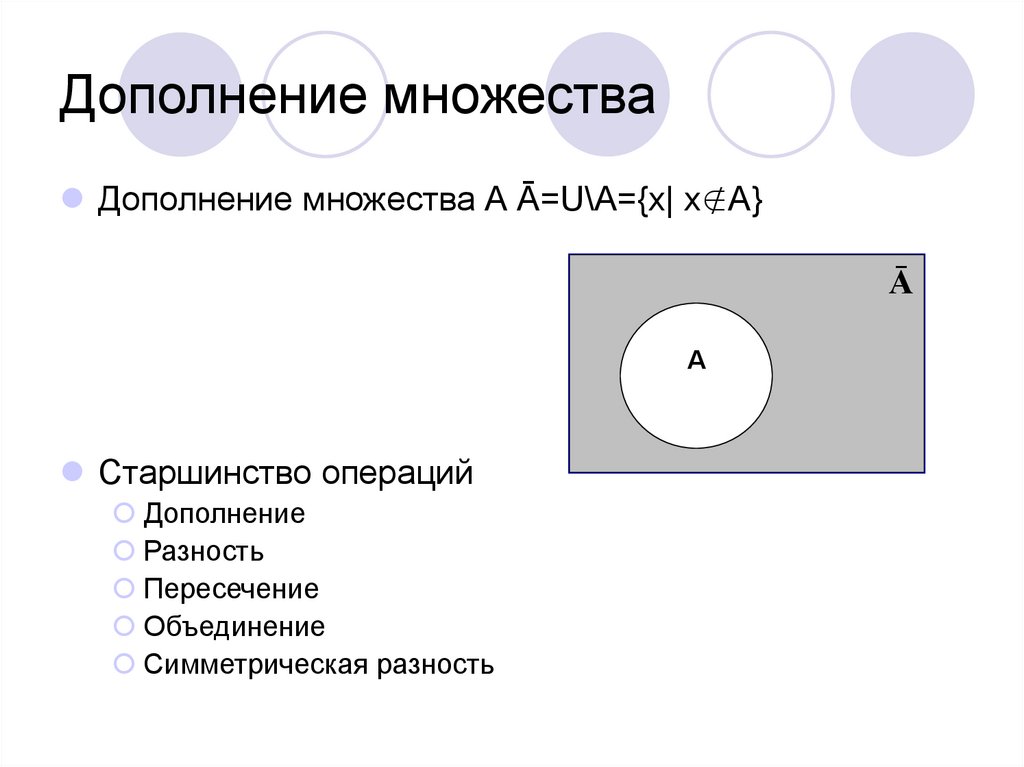
Решение:
Рассмотрим функцию .
Найдём корни функции .
По теореме Виета: .
Имеем объединение двух множеств .
Схематически изобразим график функции:
при или .
Ответ:.
Пересечение множеств
Пересечением множеств Aи B называется новое множество, содержащее те и только те элементы, которые входят одновременно и в множество А, и в множество В.
– знак пересечения
Рис. 4а. Пересечение множеств
– пересечение множеств на рис. 4а
Рис. 4б. Пересечения множеств нет
На рис. 4б множества не пересекаются, их пересечение – пустое множество
Даны множества и . Найти пересечение множеств .
Решение
По определению пересечения, решением будут те элементы, которые одновременно входят в оба множества:
– пересечение множеств.
Сравним с объединением:
C= – объединение множеств.
Найти пересечение бесконечных множеств
Решение
Нужно найти такие х, которые принадлежат пересечению :
Нужно решить систему неравенств. На оси изображаем множества и находим их пересечение
Ответ:
.
Сравним с объединением множеств:
Решить систему неравенств
Решение:
Рассмотрим ось х:
Ответ:
Пересечением множеств будет:
Источник конспекта: http://interneturok.ru/ru/school/algebra/9-klass/sistemy-racionalnyh-neravenstv/ponyatie-mnozhestva?konspekt&chapter_id=22
http://interneturok.ru/ru/school/algebra/9-klass/sistemy-racionalnyh-neravenstv/peresechenie-i-ob-edinenie-mnozhestv?konspekt&chapter_id=22
Источник видео: http://www.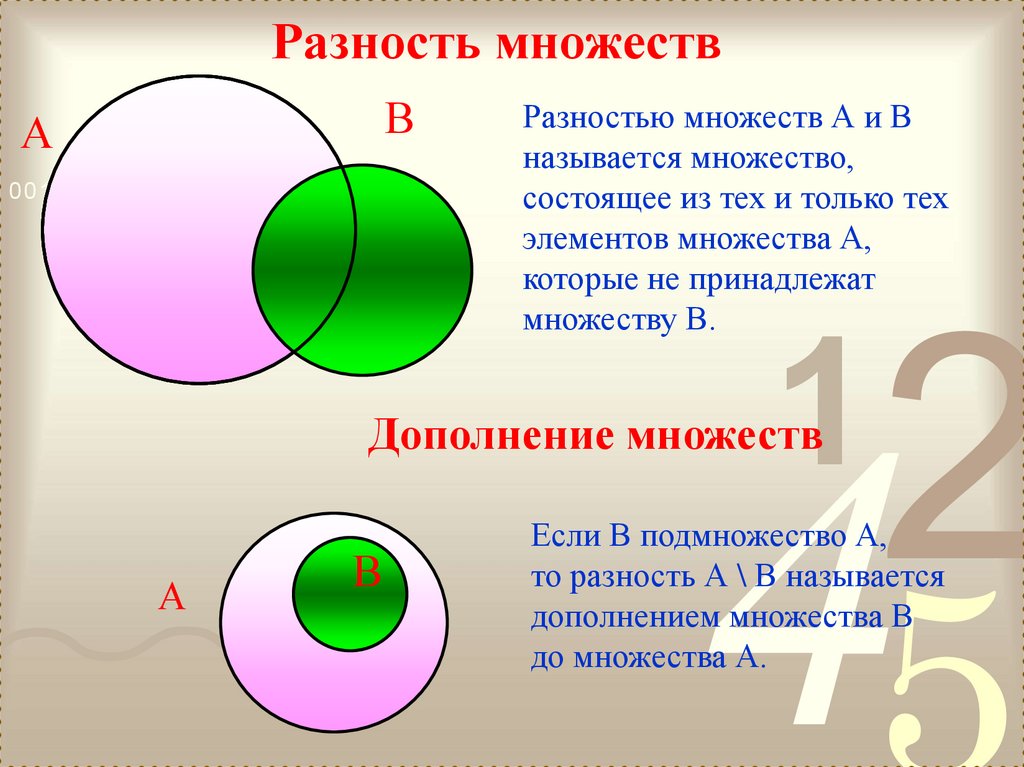 youtube.com/watch?v=s0As4waawqA
youtube.com/watch?v=s0As4waawqA
Набор операций
- Объединение двух множеств — это множество, содержащее все элементы из обоих этих множеств.
- Написано \(A\чашка B\) и определено \[A\cup B = \{x \mid x\in A\vee x\in B\}\,.\]
- Например, \[\{1,2,3,4\}\чашка\{3,4,5,6\} = \{1,2,3,4,5,6\}\,\\ \mathbf{R} = \mathbf{Q} \cup \overline{\mathbf{Q}}\,.\]
- Пересечение двух множеств — это множество, содержащее элементы, которые входят в оба этих множества.
- Написано \(A\cap B\) и определено \[A\cap B = \{x \mid x\in A\клин x\in B\}\,\\ \mathbf{Q} \cap \overline{\mathbf{Q}}=\emptyset\,.\]
- Например, \[\{1,2,3,4\}\cap\{3,4,5,6\} = \{3,4\}\,.\]
- Разница между двумя наборами — это набор значений в одном, но не в другом:
\[A-B = \{x \mid x\in A\text{ и } x\notin B\}\,.\]
- Например,
\[\{1,2,3,4\}-\{3,4,5,6\} = \{1,2\}\,\\
\overline{\mathbf{Q}} = \mathbf{R}-\mathbf{Q} \,.
 \]
\] - Также иногда пишут \(A\setminus B\).
- Например,
\[\{1,2,3,4\}-\{3,4,5,6\} = \{1,2\}\,\\
\overline{\mathbf{Q}} = \mathbf{R}-\mathbf{Q} \,.
- Теорема: Для любых множеств \(|AB|\le|A|\).
Доказательство: Предположим, что \(|A-B|>|A|\). Тогда должен быть элемент \(x\) с \(x\in(AB)\), но \(x\не в A\). Таким образом, \(AB\not\subseteq A\).
Но из определения разности множества мы видим, что \[ A-B = \{x \mid x\in A\text{ и } x\notin B\} \subseteq \{x \mid x\in A\} =A\,. \] Это противоречие, поэтому \(|AB|\le|A|\).∎
- С подобными доказательствами мы могли бы доказать следующее:
Теорема: Для любых множеств \(|A\cap B|\le|A|\) и \(|A\cap B|\le|B|\).
Теорема: Для любых множеств \(|A\cup B|\ge|A|\) и \(|A\cup B|\ge|B|\).
- При выполнении операций над множествами нам часто нужно определить универсальный набор , \(U\).
- Как и домен для квантификаторов, это набор всех возможных значений, с которыми мы работаем.
- Часто не определяется явно, а подразумевается в зависимости от проблемы, которую мы рассматриваем.

- напр. когда мы работаем с действительными числами, вероятно, \(U=\mathbf{R}\).
- дополнение набора \(S\) записывается как \(\overline{S}\) и представляет собой набор всех значений , а не в \(S\):
\[\overline{S} = \{x\mid x\notin S\} = U-S \,.\]
- Стандартная запись иррациональных чисел теперь должна иметь большой смысл: с универсальным набором \(\mathbf{R}\) иррациональные числа (\(\overline{\mathbf{Q}}\)) являются дополнением рациональные числа (\(\mathbf{Q}\)).
- Теорема: Для любого множества \(S\cap\overline{S}=\emptyset\).
Доказательство: Предположим противное, что существует элемент \(x\in S\cap\overline{S}\). Тогда по определению операторов \[ х\in S\cap\overline{S}\\ х\in S \клин х\in\overline{S} \\ х\in S \клин х\notin{S}\,. \] Это противоречие, поэтому мы должны иметь \(S\cap\overline{S}=\emptyset\).∎
- Обратите внимание на сходство между соответствующим набором и логическими операторами: \(\vee,\cup\) и \(\wedge,\cap\) и \(\overline{\mbox{S}},\neg\).

- Это больше, чем похожие символы.
- Вот несколько важных наборов идентификаторов:
Имя Идентификатор Идентификатор \(A\cap{U}= A\\A\cup\emptyset= A\) Доминирование 9000\cup = {U}\\A\cap\emptyset= \emptyset\) Идемпотент \(A\cap A= A\\A\cup A= A\) Двойное отрицание \ (\overline{(\overline{A})}= А\) Коммутативный \(A\чашка B = B\чашка A\\A\крышка B = B\крышка A\) Ассоциативный \((A\чашка B)\чашка C = A\cup(B\cup C)\\(A\cap B)\cap C = A\cap(B\cap C)\) Распределительный \(A\cup(B\cap C) =(A\чашка B)\крышка(A\чашка C)\\A\крышка(B\чашка C) = (A\крышка B)\чашка(A\крышка B)\) Закон де Моргана \(\overline{A\cap B}=\overline{A} \cup \overline{B}\\\overline{A\cup B}= \overline{A} \cap \overline{B}\) Поглощение \(A\чашка(A\крышка B) = A \\ A\крышка(A\чашка B) = A\) Отрицание \(A\cup\overline{ A} = {U}\\A\cap\overline{A} = \emptyset\) - Выглядит знакомо? Это таблица логических эквивалентов с некоторым поиском и заменой.

- В качестве примера мы можем доказать один из законов Де Моргана (книга доказывает другой).
- Мы будем осторожны с этим и будем манипулировать нотацией построителя наборов.
Теорема: Для любых множеств \(\overline{A\cup B}= \overline{A} \cap \overline{B}\).
Доказательство: По определению операций множества, \[\начать{выравнивать*} \overline{A\чашка B} &= \{x\mid x\notin (A\cup B)\} \\ &= \{x\mid \neg(x \in (A\cup B))\} \\ &= \{x\mid \neg(x \in A\vee x\in B)\} \\ &= \{x\mid\neg(x\in A)\клин \neg(x\in B)\} \\ &= \{x\mid x \in \overline{A}\wedge x \in \overline{B} )\} \\ &= \{x\mid x \in (\overline{A}\cap\overline{B}))\} \\ &= \overline{A}\cap\overline{B}\,.\quad{}∎ \конец{выравнивание*}\]
- Можно было бы привести и менее формальное доказательство. (Для этого см. раздел 2.2, пример 10.)
- Это тот случай, когда, вероятно, проще быть более формальным: писать все детали в предложениях настолько мучительно, что семь шагов в этом доказательстве приятнее читать.
 (См. также пример 10.)
(См. также пример 10.)
- Это доказательство может подсказать, почему таблицы эквивалентностей и множественных тождеств так похожи.
- Для любой из операций над множествами мы можем использовать нотацию построителя множеств, а затем использовать логические эквивалентности для управления условиями.
- Так как мы проделываем те же манипуляции, то и таблицы у нас получились одинаковые.
- Будьте осторожны с другими операциями. То, что это сработало для них, не означает, что вы можете считать, что все одинаково. Не существует логической версии установленного различия или установленной версии исключающего или (по крайней мере, насколько мы определили).
Теорема: Для любых множеств \(AB = A\cap\overline{B}\).
Менее формальное доказательство: Набор \(A-B\) представляет собой значения из \(A\) с удаленными значениями из \(B\).
Набор \(\overline{B}\) — это набор всех значений, не входящих в \(B\).
 Таким образом, пересечение с \(\overline{B}\) приводит к тому, что остаются только значения, не входящие в \(B\). То есть \(A\cap\overline{B}\) — это \(A\) со всеми удаленными значениями из \(B\). Таким образом, мы видим, что эти множества содержат одни и те же элементы. ∎
Таким образом, пересечение с \(\overline{B}\) приводит к тому, что остаются только значения, не входящие в \(B\). То есть \(A\cap\overline{B}\) — это \(A\) со всеми удаленными значениями из \(B\). Таким образом, мы видим, что эти множества содержат одни и те же элементы. ∎Более формальное доказательство: По определению операций над множествами \[\начать{выравнивать*} А-Б &= \{х\середина х\в А \клин х\не в В\} \\ &= \{x\mid x\in A \wedge x\in \overline{B}\} \\ &= \{x\mid x\in (A \cap \overline{B})\} \\ &= A\cap\overline{B}\,.\quad{}∎ \конец{выравнивание*}\]
- Я думаю, что любое из этих доказательств является действительным.
- «Менее формальная» версия должна быть написана достаточно тщательно, чтобы убедить читателя (или ТА в вашем случае).
- В «более формальной» версии больше шагов и отсутствует интуитивная причина (она может помочь вам вспомнить почему).
- Мы можем использовать тождества множеств для доказательства других фактов о множествах.
 Например:
Например:Теорема: \(A-(B\чашка C)= (A-B)\cap(A-C)\).
Доказательство: Для множеств \(A,B,C\) из приведенной выше теоремы имеем \[\начать{выравнивать*} А-(В\чашка С) &= A\cap \overline{B\cup C} \\ &= A\cap \overline{B}\cap \overline{C} \\ &= A\cap \overline{B}\cap A\cap \overline{C} \\ &= (A-B)\cap (A-C)\,.\quad{}∎ \конец{выравнивание*}\]
- Эти тождества должны убедить вас в том, что порядок объединения и пересечения не имеет значения (точно так же, как сложение, умножение, конъюнкция и дизъюнкция: все они являются коммутативными операциями).
- Таким образом, мы можем написать их кучу без скобок, как сложение/умножение/соединение/дизъюнкция: \[A\чашка B\чашка C \чашка D\,\\A\крышка B\крышка C \крышка D\,.\]
- Если нам нужно выполнить объединение/пересечение множества вещей, иногда используется такое обозначение, как суммирование.
- Например, предположим, что в этом семестре ZJU предлагает \(n\) курсов.
 {n} S_i\,.\]
Студенты берут 92\,.\]
{n} S_i\,.\]
Студенты берут 92\,.\]
- Например, предположим, что в этом семестре ZJU предлагает \(n\) курсов.
Наборы: основное определение и операции
Мы затронем темы:
Определение наборов
Операции: Объединение, пересечения, дополнение, множество разностей.
Диаграммы Венна
Кардинальность: принцип включения-исключения
Определяющие наборы
Пока удобно предположить, что существует вселенная из элементов .
Понятие множества является настолько базовым в математике, что не поддается простому определение. Большинство определений просто переходят к , набор — это набор :-).
Существует два способа определить набор:
Явно : Просто перечислите его элементы. напр., .
Неявно : Напишите описание того, что входит в набор, на английском языке или еще лучше на логике. напр., .
На данный момент, всякий раз, когда мы обсуждаем наборы, необходимо прояснить вселенную.
Наивная теория множеств
Понятие теории множеств, которое мы изучаем в этой лекции, называется наивной теорией множеств .
Причина, которую мы называем наивной, заключается в допущении универсального множества . До 20 века математики и философы представляли набор всех возможных сущностей и назвал его универсальный набор. В этом наборе есть буквально все, что можно представить: козы , муравьи , Бозоны Хиггса , столы , стулья , номера , группы и все такое. Подумайте об этом, и престо !, в универсальном наборе есть. Но работы математиков таких как Кантор и Бертран Рассел в начале 20 века доказали, что универсальное множество не может существовать, так как его существование ведет к парадоксам или противоречиям.
Поэтому в этих заметках мы продолжим описывать версию, которая
мы будем называть неофициально «полу-наивным» (обратите внимание, что это наш собственный
изобретение, а не стандартный термин в математике).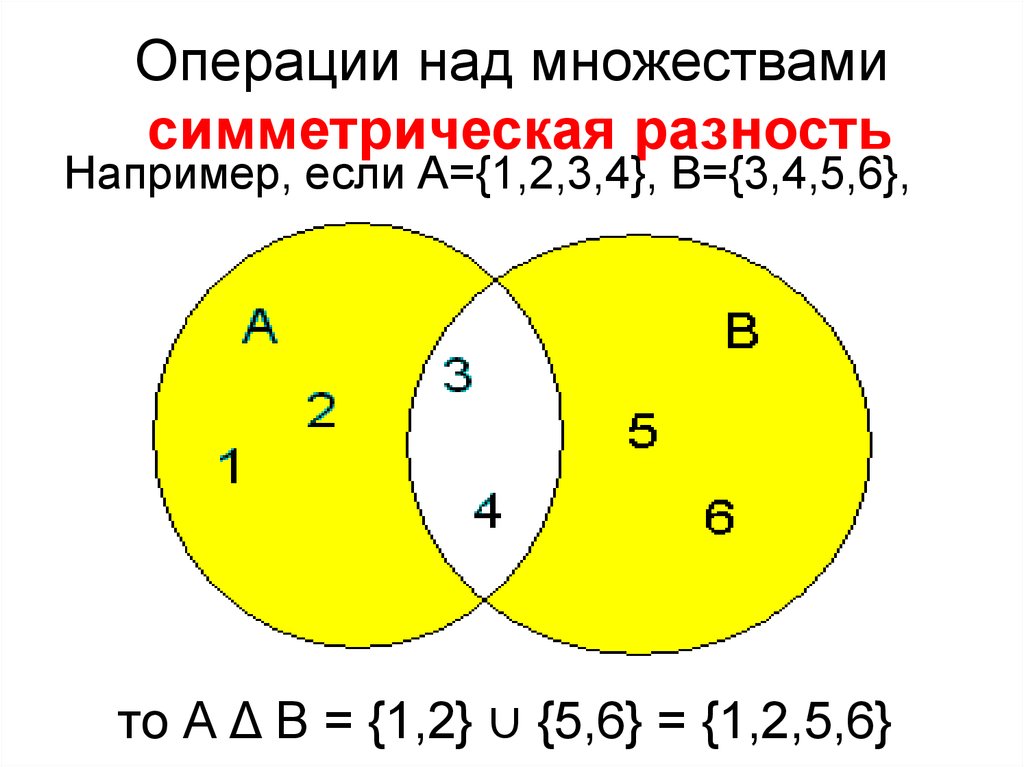 Где это возможно,
мы отметим изменения, необходимые из-за отсутствия
универсальный набор.
Где это возможно,
мы отметим изменения, необходимые из-за отсутствия
универсальный набор.
Пример 1: Целые числа
Мы предполагаем, что вселенная ограничена множеством всех целых чисел.
Что определяют следующие наборы:
Обратите внимание, что ограничение нашей вселенной набором целых чисел не создает противоречия или парадокса в приведенных выше определениях.
Пример 2: Животные
Пусть вселенная будет всеми видами животных на планете Земля.
Обратите внимание, что ограничение вселенной только всеми видами животных на планете Земля делает наборы выше четко определенными и свободными. противоречий.
Пустые/универсальные наборы
Наивная теория множеств часто добавляет специальное универсальное множество. В качестве отмечалось ранее, универсального набора не существует, и его нужно будет необученный.
Однако во многих контекстах мы будем специально называть набор, например
(множество всех действительных чисел), чтобы быть ограниченным
вселенная . Так как это четко определенное множество, можно
принять такое множество как ограниченную вселенную.
Так как это четко определенное множество, можно
принять такое множество как ограниченную вселенную.
Союз, Пересечение, Разность и Дополнение.
Позвольте обозначить наборы, взятые из ограниченной вселенной .
Операция дополнения определяется в наивной теории множеств.
.
Если мы действуем в ограниченной вселенной, то .
Иначе не существует, строго говоря, потому что универсального набора, содержащего все, не существует.
Пример 1
Позвольте быть ограниченной вселенной, заданной набором всех целых чисел.
Позвольте быть набором всех нечетных целых чисел, быть набором всех четных целых чисел, быть набором всех простых целых чисел и быть набором всех составных чисел (не являются ни простыми, ни составными).
Что такое наборы?
Пример-2
То же, что и ? Как насчет ?
То же, что и ? Приведите простой пример.
Конечный Против. Бесконечные наборы
Конечные множества — это те, которые имеют конечное число элементов.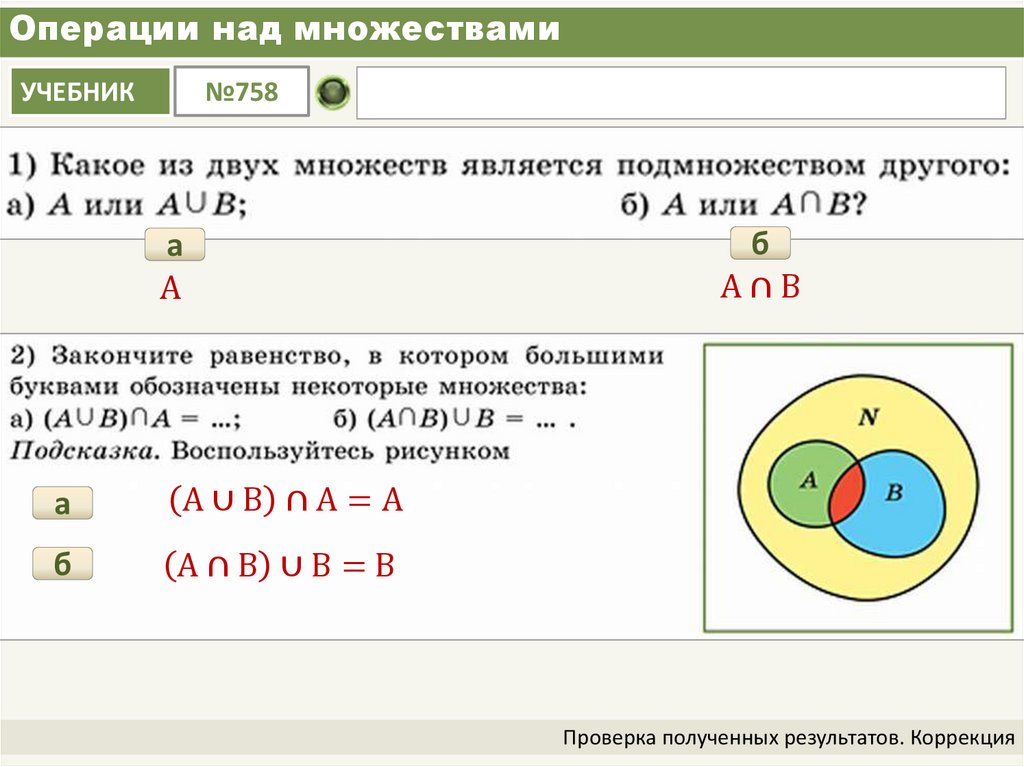 Бесконечные наборы,
с другой стороны, имеют бесконечно много элементов. Мы определим
бесконечные множества, и в ближайшее время подробно рассмотрим бесконечные множества.
Бесконечные наборы,
с другой стороны, имеют бесконечно много элементов. Мы определим
бесконечные множества, и в ближайшее время подробно рассмотрим бесконечные множества.
Диаграммы Венна
Диаграммы Венна — это простые графические способы визуализации множеств и операций между ними. Мы предполагаем, что вы уже много знаете о это (на самом деле это школьный материал). Мы сделаем несколько быстрых подведение итогов в классе.
С другой стороны, диаграммы Венна — это не так уж и чихать. статья в Википедии о Венне диаграммы или на этом сайте есть много интересной информации.
Диаграммы Венна можно использовать для доказательства некоторых свойств множеств.
Мощность
Мощность множества — это количество элементов в нем. На данный момент это
имеет смысл говорить о мощности только для конечных множеств. Мы будем
обсудим вопрос о бесконечных множествах и мощности после того, как мы
охватывающие отношения и функции. Мощность пустого множества равна
конечно ноль. Мощность множества никогда не может быть отрицательной.
Мощность множества никогда не может быть отрицательной.
Какова мощность следующих множеств:
(Ответ: 21).
(Ответ 15).
(Ответ: 26)
? (Ответ: 10)
?
?
Мощность множества обозначается или иногда . Мы будем использовать .
Обратите внимание на следующий интересный факт: . Почему это правда?
Используя диаграмму Венна, мы можем вывести, что
Приведенное выше отношение называется принципом исключения включения .
Мы можем расширить его до трех наборов:
Обратите внимание на любопытное изменение знака!!
Пример-1
Пусть и .
Проверить принцип включения-исключения для ?
Мы это видим.
Мы также можем увидеть это, используя принцип исключения включения:
Пример-2
Если мы посмотрим на все числа от до .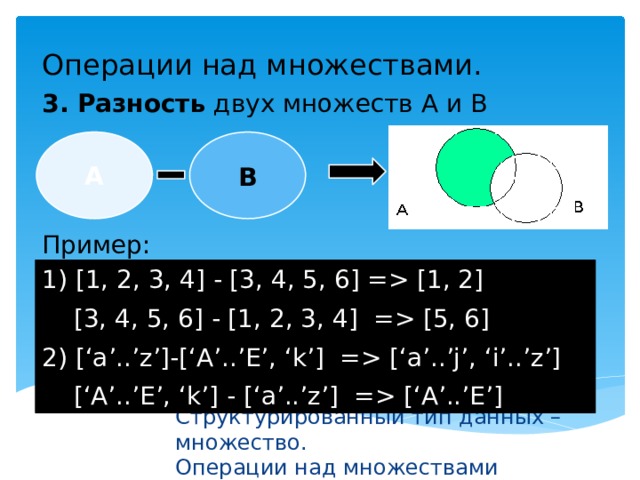 Сколько чисел содержит ?
Сколько чисел содержит ?
На первый взгляд, такие расчеты сложны. У нас есть цифры с во второй цифре () и числа с a в первой цифре . Следовательно, существует общее количество чисел, в которых есть a. Однако примечание это было учтено дважды. Так что ответ должен быть.
Используя включение-исключение: пусть будет множество всех чисел с во второй цифре и быть всеми числами с первой (старшей) цифрой. Наш аргумент выше использует принцип включения-исключения:
Пример -3
Сколько чисел между и делится на или на или на ?
Давайте исправим вселенную, чтобы она была .
Пусть . Аналогично, пусть — числа, которые делятся на и быть числа делятся на .
Мы ищем .
У нас есть
.
.
.
.
.
Всего = = .
(могу ошибиться в расчетах, проверьте).
Общий принцип исключения включения
Мы видели исключение включения для кардинальности . Предположим, у нас есть наборы, мы можем обобщить это до
.Головоломка (Подсчет простых чисел)
Имея список простых чисел от до , покажите, как этот список можно использовать для подсчета количества простых чисел от до с помощью включение исключение.
Давайте рассмотрим более простой случай подсчета простых чисел из . Вместо простых чисел будем считать составные. Как только мы посчитаем композиты, мы можем сразу же сделать вывод, сколько существует простых чисел.
Универсальный набор. Определим множество. Мы опускаем, поскольку оно не является ни простым, ни составным.
Мы принимаем исходный набор простых чисел равным .
Теорема Каждое составное число из делится на или . Другими словами, каждое составное число имеет или в качестве одного из своих простых делителей.
Другими словами, сначала будем считать по принципу включения-исключения. Это даст нам количество композитов с оговоркой . включает ,
а также . Итак, какова бы ни была мощность их объединения, нам нужно вычесть из них, чтобы получить действительно составные числа.
Это даст нам количество композитов с оговоркой . включает ,
а также . Итак, какова бы ни была мощность их объединения, нам нужно вычесть из них, чтобы получить действительно составные числа.
Пишем
Заметим, что это просто . Мы знаем, потому что есть числа, которые делятся на .
Следовательно,
Таким образом, количество составных частей равно (почему мы вычли ?) Количество простых чисел будет (почему из? почему не здесь?). Убедитесь, что действительно есть простые числа от до : .
Тот же расчет может быть выполнен для всех простых чисел. За это получаем:
Используя это, число композитов равно . Отсюда делаем вывод, что простые числа существуют. Дополнительные четыре простых числа за .
Существует очень тесная связь между этим способом подсчета и ситом Эратостена для перечисления все простые числа. Следовательно, принцип включения-эксклюзия часто называют принципом сита .
как забавное упражнение: реализуйте счетчик для решения головоломки.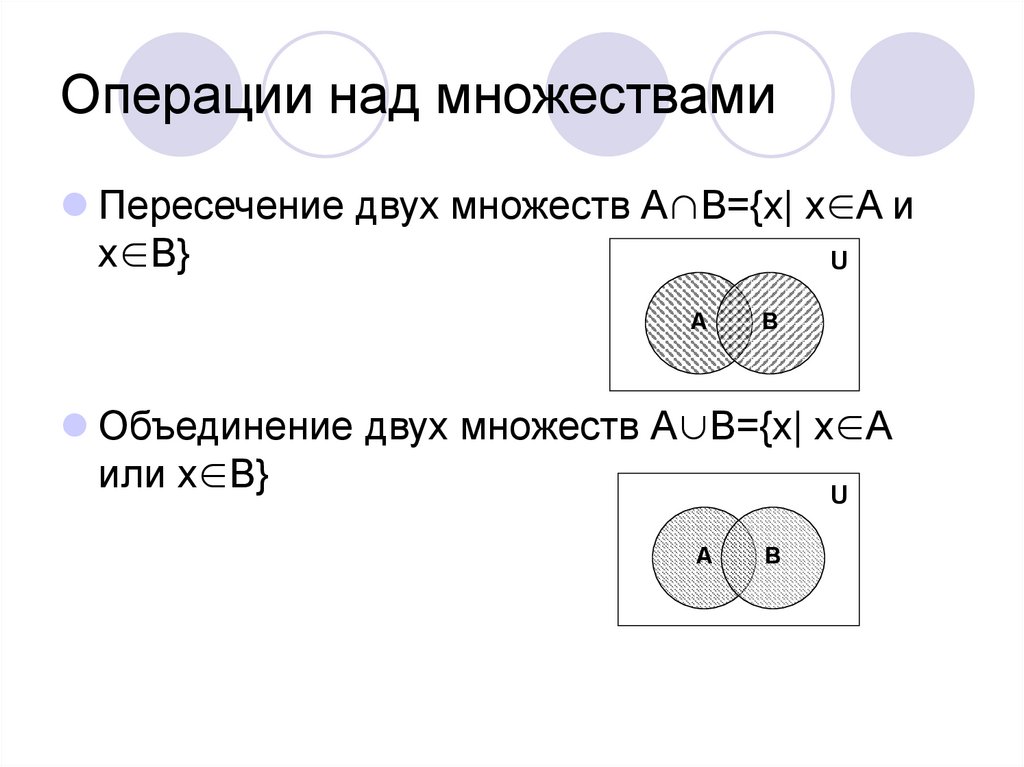 Вам обязательно нужно будет написать программу скорее
чем пытаться сделать это вручную.
Вам обязательно нужно будет написать программу скорее
чем пытаться сделать это вручную.
Декартовы произведения и мощности
Теперь рассмотрим две другие операции над множествами:
Декартовы произведения
Силовые наборы
Декартово произведение
Возьми наборы и над какой-нибудь вселенной. Декартово произведение определяется как
Другими словами, мы строим набор из всех 2-кортежей , где первый компонент из набора и второй компонент из набора.
Мы можем распространить декартово произведение не только на множества:
Здесь мы берем декартово произведение множеств, и в результате получается множество 3-кортежей .
Пример-1
Если множество всех действительных чисел представлено вещественной линией, то что это за множество?
Ответ: состоит из всех наборов вещественных чисел вида где и — вещественные числа.
Другими словами, мы перешли от однозначных чисел к -мерным координатам.
Для простоты произведение множества на себя записывается .
Что такое ?
Пример 2: пустой набор
Чему равно декартово произведение пустого множества на множество?
Ответ: Пустое множество.
Мощность декартовых произведений
Правило декартова произведения состоит в том, что
Мы можем убедиться сами, нарисовав таблицу всех записей. Допустим и .
| а | б | в | |
| 1 | (1,а) | (1,б) | (1,в) |
| 2 | (2,а) | (2,б) | (2,в) |
Порядок декартова произведения имеет значение
Если для множеств, то заметим, что не будет равно. Другими словами, имеет значение в кортеже, который идет первым и идет вторым. Например, если я попрошу вас нарисовать пиксель в точке , это не то же самое, что нарисовать пиксель в , верно?
Если , однако, это тривиально, что все одно и то же.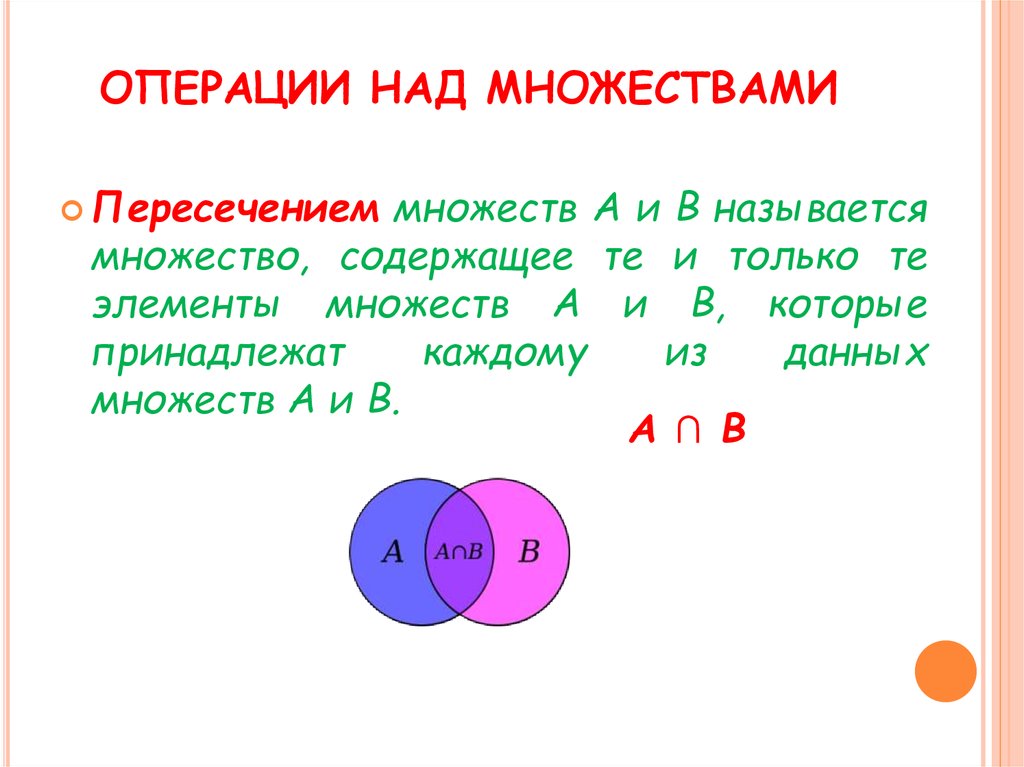
Пример
Какова величина декартова произведения, если ?
Подмножество
Set является подмножеством написанного тогда и только тогда, когда каждый элемент также является элементом .
Примеры
?
?
Верно ли, что для любого набора ?
Верно ли, что для всех наборов?
Верно ли, что для всех наборов?
Ответы: да, нет, да, нет, да!
Набор Python (с примерами)
В этом руководстве вы узнаете все о наборах Python; как они создаются, добавляются или удаляются из них элементы, и все операции, выполняемые над множествами в Python.
Набор — это неупорядоченный набор элементов. Каждый элемент набора уникален (без дубликатов) и должен быть неизменным (не может быть изменен).
Однако сам набор может изменяться. Мы можем добавлять или удалять элементы из него.
Множества также можно использовать для выполнения математических операций над множествами, таких как объединение, пересечение, симметричная разность и т. д.
д.
Создание наборов Python
Набор создается путем помещения всех элементов (элементов) в фигурные скобки {} , разделенных запятой, или с помощью встроенной функции set() .
Может иметь любое количество элементов, и они могут быть разных типов (целые числа, числа с плавающей запятой, кортежи, строки и т. д.). Но множество не может иметь в качестве своих элементов изменяемые элементы, такие как списки, наборы или словари.
# Различные типы наборов в Python
# набор целых чисел
мой_набор = {1, 2, 3}
печать (мой_набор)
# набор смешанных типов данных
my_set = {1.0, "Привет", (1, 2, 3)}
печать (мой_набор) Выход
{1, 2, 3}
{1.0, (1, 2, 3), "Привет"} Попробуйте также следующие примеры.
# набор не может иметь дубликатов
# Вывод: {1, 2, 3, 4}
my_set = {1, 2, 3, 4, 3, 2}
печать (мой_набор)
# мы можем сделать множество из списка
# Вывод: {1, 2, 3}
my_set = установить ([1, 2, 3, 2])
печать (мой_набор)
# в наборе не может быть изменяемых элементов
# здесь [3, 4] — изменяемый список
# это вызовет ошибку. my_set = {1, 2, [3, 4]}
my_set = {1, 2, [3, 4]} Вывод
{1, 2, 3, 4}
{1, 2, 3}
Traceback (последний последний вызов):
Файл "", строка 15, в
my_set = {1, 2, [3, 4]}
TypeError: unhashable type: 'list' Создать пустой набор немного сложно.
Пустые фигурные скобки {} создаст пустой словарь в Python. Чтобы создать набор без каких-либо элементов, мы используем функцию set() без каких-либо аргументов.
# Различать набор и словарь при создании пустого набора
# инициализируем {}
а = {}
# проверить тип данных a
печать (тип (а))
# инициализируем с помощью set()
а = установить ()
# проверить тип данных a
печать (тип (а)) Выход
<класс 'словарь'>
Изменение набора в Python
Наборы изменяемы. Однако, поскольку они неупорядочены, индексация не имеет смысла.
Мы не можем получить доступ к элементу набора или изменить его с помощью индексации или нарезки. Установить тип данных не поддерживает его.
Установить тип данных не поддерживает его.
Мы можем добавить один элемент, используя метод add() , и несколько элементов, используя метод update() . 9Метод 0701 update() может принимать в качестве аргумента кортежи, списки, строки или другие множества. Во всех случаях дубликаты избегаются.
# инициализировать my_set
мой_набор = {1, 3}
печать (мой_набор)
# мой_набор[0]
# если вы раскомментируете строку выше
# вы получите сообщение об ошибке
# TypeError: объект 'set' не поддерживает индексацию
# добавить элемент
# Вывод: {1, 2, 3}
my_set.add(2)
печать (мой_набор)
# добавить несколько элементов
# Вывод: {1, 2, 3, 4}
my_set.update([2, 3, 4])
печать (мой_набор)
# добавить список и установить
# Вывод: {1, 2, 3, 4, 5, 6, 8}
my_set.update([4, 5], {1, 6, 8})
печать (мой_набор) Выход
{1, 3}
{1, 2, 3}
{1, 2, 3, 4}
{1, 2, 3, 4, 5, 6, 8} Удаление элементов из набора
Конкретный элемент можно удалить из набора с помощью методов discard() и remove() .
Единственная разница между ними состоит в том, что функция discard() оставляет набор без изменений, если элемент отсутствует в наборе. С другой стороны, функция remove() вызовет ошибку в таком состоянии (если элемент отсутствует в наборе).
Следующий пример иллюстрирует это.
# Разница между discard() и remove()
# инициализировать my_set
my_set = {1, 3, 4, 5, 6}
печать (мой_набор)
# отбросить элемент
# Вывод: {1, 3, 5, 6}
my_set.discard(4)
печать (мой_набор)
# удалить элемент
# Вывод: {1, 3, 5}
my_set.remove(6)
печать (мой_набор)
# отбросить элемент
# отсутствует в my_set
# Вывод: {1, 3, 5}
my_set.discard(2)
печать (мой_набор)
# удалить элемент
# отсутствует в my_set
# вы получите сообщение об ошибке.
# Вывод: KeyError
my_set.remove(2) Выход
{1, 3, 4, 5, 6}
{1, 3, 5, 6}
{1, 3, 5}
{1, 3, 5}
Traceback (последний последний вызов):
Файл "", строка 28, в
KeyError: 2 Точно так же мы можем удалить и вернуть элемент, используя метод pop() .
Поскольку набор является неупорядоченным типом данных, невозможно определить, какой элемент будет извлечен. Это совершенно произвольно.
Мы также можем удалить все предметы из набора, используя метод очистки() .
# инициализировать my_set
# Вывод: набор уникальных элементов
my_set = установить ("HelloWorld")
печать (мой_набор)
# извлекаем элемент
# Вывод: случайный элемент
печать (my_set.pop())
# извлечь другой элемент
my_set.pop()
печать (мой_набор)
# очистить my_set
# Вывод: установить()
my_set.clear()
print(my_set) Вывод
{'H', 'l', 'r', 'W', 'o', 'd', 'e'}
ЧАС
{'г', 'В', 'о', 'д', 'е'}
set() Python Операции над множествами
Наборы можно использовать для выполнения математических операций над множествами, таких как объединение, пересечение, разность и симметричная разность. Мы можем сделать это с помощью операторов или методов.
Рассмотрим следующие два набора для следующих операций.
>>> А = {1, 2, 3, 4, 5}
>>> B = {4, 5, 6, 7, 8} Set Union
Set Union в PythonUnion of A и B представляет собой набор всех элементов из обоих наборов.
Объединение выполняется с помощью | оператор. То же самое можно сделать с помощью метода union() .
# Установить метод объединения
# инициализируем А и Б
А = {1, 2, 3, 4, 5}
В = {4, 5, 6, 7, 8}
# использовать | оператор
# Вывод: {1, 2, 3, 4, 5, 6, 7, 8}
напечатать (А | В) Выход
{1, 2, 3, 4, 5, 6, 7, 8} Попробуйте выполнить следующие примеры в оболочке Python.
# использовать функцию объединения
>>> А.союз(Б)
{1, 2, 3, 4, 5, 6, 7, 8}
# используем функцию объединения на B
>>> Б.союз(А)
{1, 2, 3, 4, 5, 6, 7, 8} Пересечение множества
Пересечение множества в Python Пересечение A и B — это набор элементов, общих для обоих наборов.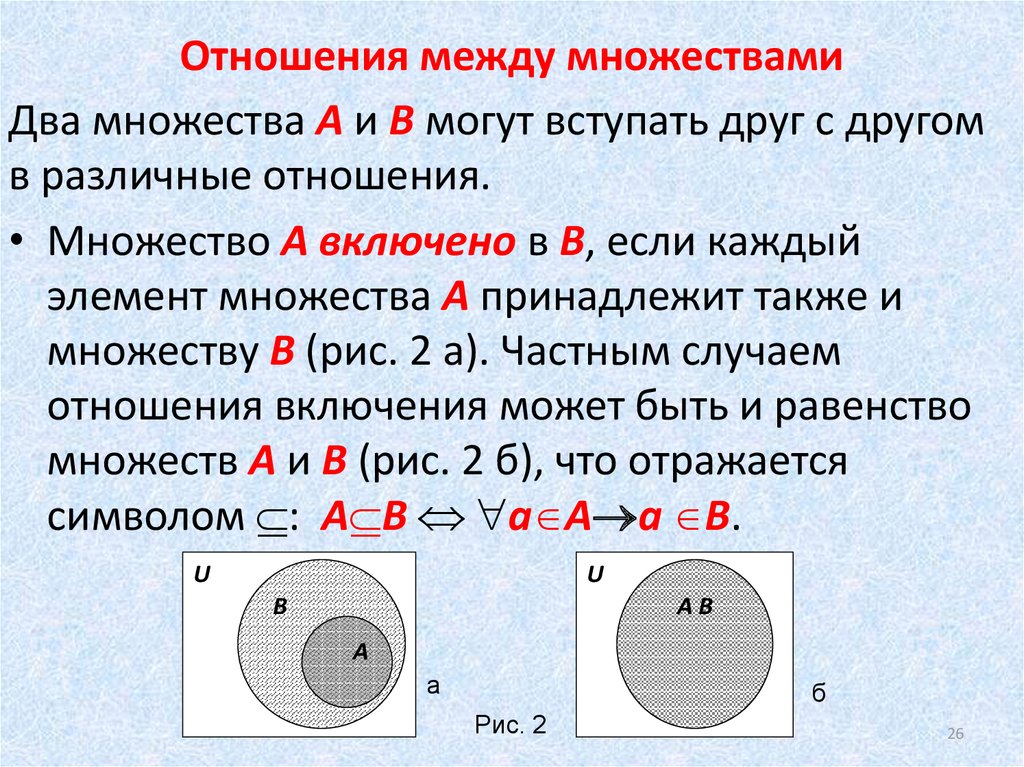
Пересечение выполняется с помощью 9Оператор 0701 и . То же самое можно сделать, используя метод пересечения() .
# Пересечение множеств
# инициализируем А и Б
А = {1, 2, 3, 4, 5}
В = {4, 5, 6, 7, 8}
# использование и оператор
# Вывод: {4, 5}
печать(A и B) Вывод
{4, 5} Попробуйте выполнить следующие примеры в оболочке Python.
# использовать функцию пересечения на A
>>> А.пересечение(Б)
{4, 5}
# используем функцию пересечения на B
>>> Б.пересечение(А)
{4, 5} Set Difference
Set Difference в PythonОтличие набора B от набора A ( A — B ) это набор элементов, которые есть только в 3 B 83 B но не . Точно так же B — A является набором элементов в B , но не в A .
Различие выполняется с помощью оператора - . То же самое можно сделать с помощью метода разницы().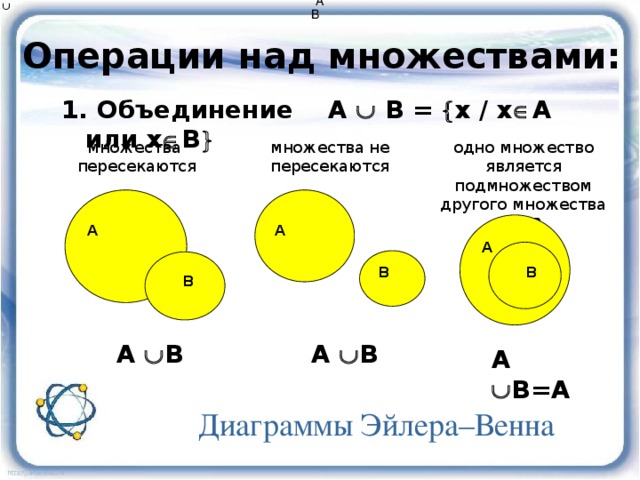
# Разница двух наборов
# инициализируем А и Б
А = {1, 2, 3, 4, 5}
В = {4, 5, 6, 7, 8}
# use - оператор на A
# Вывод: {1, 2, 3}
печать(A - B) Вывод
{1, 2, 3} Попробуйте выполнить следующие примеры в оболочке Python.
# использовать функцию разницы на A
>>> А.разница(Б)
{1, 2, 3}
# use - оператор на B
>>> Б - А
{8, 6, 7}
# используем функцию разности на B
>>> Б.разница(А)
{8, 6, 7} 9Б)
Выход
{1, 2, 3, 6, 7, 8} Попробуйте выполнить следующие примеры в оболочке Python.
# использовать функцию symmetric_difference на A
>>> А.симметричная_разница(Б)
{1, 2, 3, 6, 7, 8}
# использовать функцию symmetric_difference на B
>>> Б. симметричная_разница (А)
{1, 2, 3, 6, 7, 8} Другие методы установки Python
Существует множество методов установки, некоторые из которых мы уже использовали выше. Вот список всех методов, которые доступны с установленными объектами:
| Метод | Описание |
|---|---|
| добавить() | Добавляет элемент в набор |
| очистить() | Удаляет все элементы из набора |
| копировать() | Возвращает копию набора |
| разница() | Возвращает разницу двух или более наборов в виде нового набора |
| разность_обновление() | Удаляет все элементы другого набора из этого набора |
| отбросить() | Удаляет элемент из набора, если он является членом.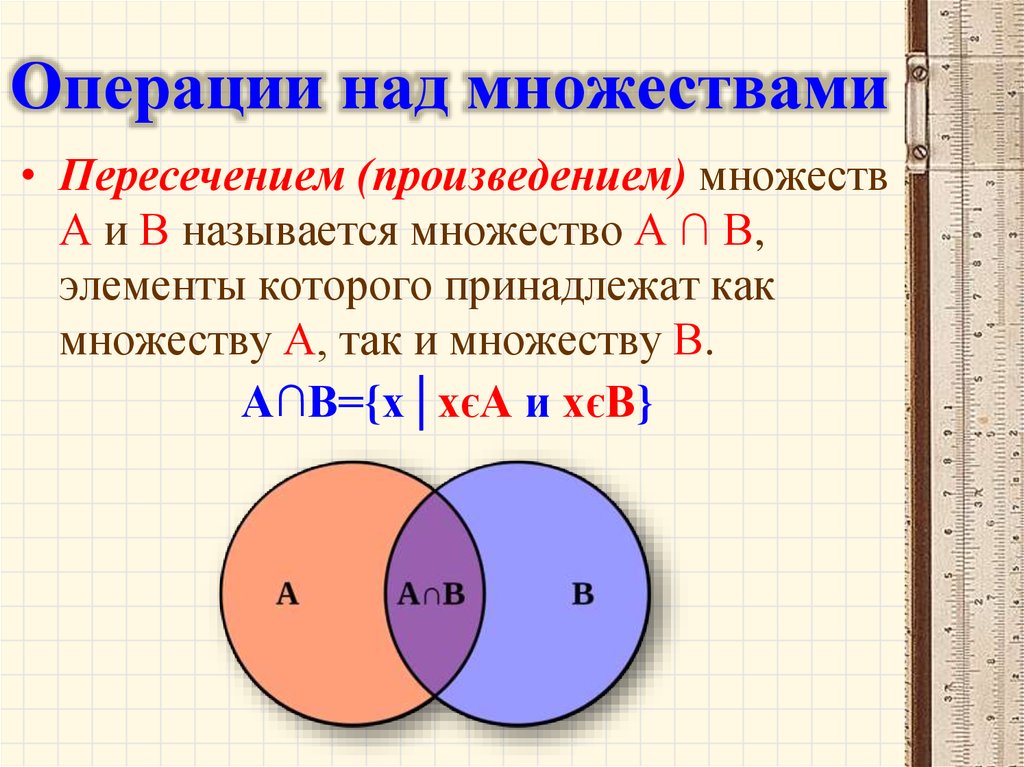 (Ничего не делать, если элемента нет в наборе) (Ничего не делать, если элемента нет в наборе) |
| пересечение() | Возвращает пересечение двух наборов как новый набор |
| cross_update() | Обновляет набор пересечением себя и другого |
| непересекающийся() | Возвращает Истинно , если два набора имеют нулевое пересечение |
| issubset() | Возвращает True , если другой набор содержит этот набор |
| issuperset () | Возвращает True , если этот набор содержит другой набор |
| поп() | Удаляет и возвращает произвольный элемент множества. Вызывает KeyError , если набор пуст |
| удалить() | Удаляет элемент из набора. Если элемент не является членом, вызывает ошибку KeyError | .
| симметричная_разность() | Возвращает симметричную разность двух наборов в виде нового набора |
| симметричная_разница_обновление() | Обновляет набор с симметричной разностью себя и другого |
| объединение() | Возвращает объединение наборов в новый набор |
| обновление() | Обновляет набор объединением себя и других |
Другие операции над множествами
Проверка принадлежности множества
Мы можем проверить, существует ли элемент в множестве, используя ключевое слово в .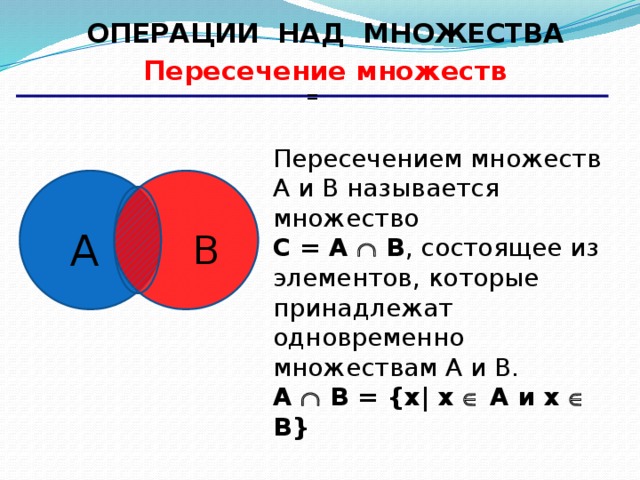
# в ключевом слове в наборе
# инициализировать my_set
my_set = установить ("яблоко")
# проверяем, присутствует ли 'a'
# Вывод: Истина
print('a' в my_set)
# проверить, присутствует ли 'p'
# Вывод: Ложь
print('p' нет в my_set) Выход
Верно False
Перебор набора
Мы можем перебирать каждый элемент набора с помощью цикла for .
>>> для письма в наборе ("яблоко"):
... печать (письмо)
...
а
п
е
l Встроенные функции с набором
Встроенные функции, такие как all() , any() , enumerate() , len() , max()
отсортировано() , sum() и т. д. обычно используются с наборами для выполнения различных задач.| Функция | Описание |
|---|---|
| все() | Возвращает True , если все элементы набора истинны (или если набор пуст). |
| любой() | Возвращает True , если любой элемент набора истинен. Если набор пуст, возвращает False . |
| перечислить() | Возвращает перечисляемый объект. Он содержит индекс и значение для всех элементов набора в виде пары. |
| лен() | Возвращает длину (количество элементов) в наборе. |
| макс() | Возвращает самый большой элемент в наборе. |
| мин() | Возвращает наименьший элемент в наборе. |
| отсортировано() | Возвращает новый отсортированный список из элементов набора (сам набор не сортируется). |
| сумма() | Возвращает сумму всех элементов набора. |
Python Frozenset
Frozenset — это новый класс, обладающий характеристиками набора, но его элементы нельзя изменить после назначения. В то время как кортежи — это неизменяемые списки, замороженные наборы — неизменные наборы.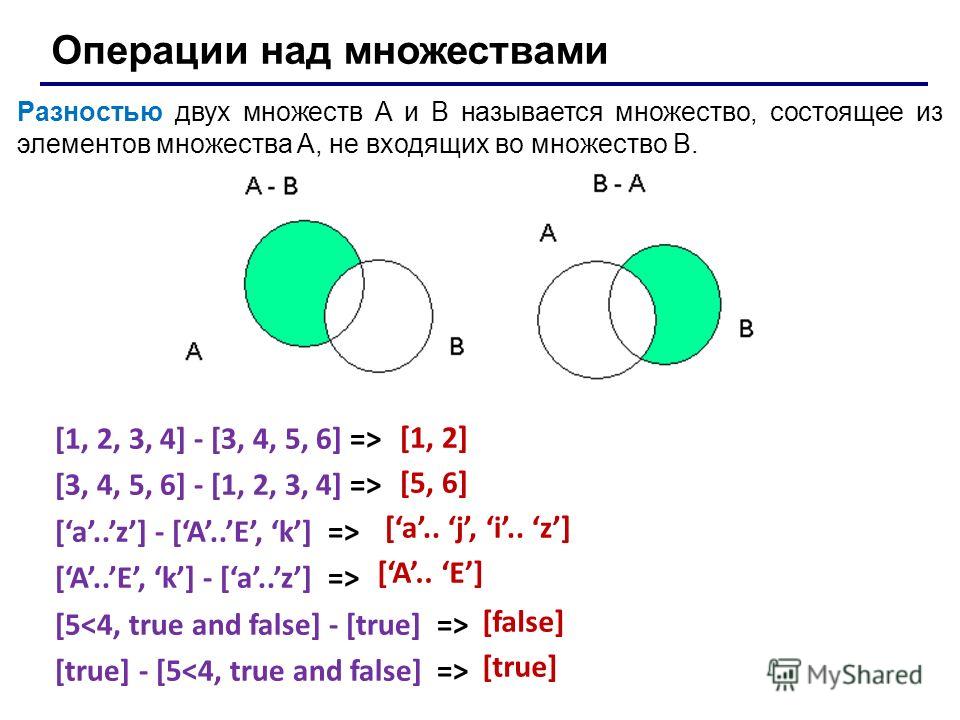
Изменяемые наборы нельзя хешировать, поэтому их нельзя использовать в качестве ключей словаря. С другой стороны, наборы заморозки можно хешировать и использовать в качестве ключей к словарю.
Frozensets можно создавать с помощью функции Frozenset().
Этот тип данных поддерживает следующие методы: союз() . Будучи неизменным, он не имеет методов, которые добавляют или удаляют элементы.
# Фрозенсеты # инициализируем А и Б A = замороженный набор ([1, 2, 3, 4]) B = замороженный набор ([3, 4, 5, 6])
Попробуйте эти примеры в оболочке Python.
>>> A.isdisjoint(B)
ЛОЖЬ
>>> А.разница(Б)
замороженный набор ({1, 2})
>>> А | Б
замороженный набор ({1, 2, 3, 4, 5, 6})
>>> А.добавить(3)
...
AttributeError: объект 'frozenset' не имеет атрибута 'add' Логические и математические рассуждения, введение в корректуру
\(\require{mathrsfs}\newcommand{\abs}[1]{\left| #1 \right|} \renewcommand{\emptyset}{\varnothing} \DeclareMathOperator{\dom}{dom} \DeclareMathOperator{\range}{rng} \DeclareMathOperator{\пермь}{пермь} \новая команда{\lt}{<} \новая команда{\gt}{>} \newcommand{\amp}{&} \)
¶ Теперь, когда мы определили множества, давайте напомним себе, что мы уже знаем о некоторых: \(\mathbb{N} \subseteq \mathbb{Z} \subseteq \mathbb{Q} \subseteq \mathbb{R} \subseteq \mathbb{C}\text{,}\) натуральные числа, целые числа, рациональные числа, действительные числа и комплексные числа. Определив наборы, мы также хотим знать, как их можно комбинировать для формирования новых наборов, что и является целью этого раздела.
Определив наборы, мы также хотим знать, как их можно комбинировать для формирования новых наборов, что и является целью этого раздела.
Определение 2.2.1 Объединение, пересечение, различие
Имея два множества \(A,B\), мы можем выполнить три основные бинарные операции.
- штуцер
- \(A \cup B = \{ x \mid x \in A \vee x \in B \}\)
- перекресток
- \(A \cap B = \{ x \mid x \in A \wedge x \in B \}\)
- разница
- \(A \setminus B = \{ x \mid x \in A \wedge x \notin B \}\)
Легко видеть, что объединение и пересечение коммутативны и ассоциативны, поскольку дизъюнкция (\(\vee\)) и конъюнкция (\(\клин\)) таковы. Более того, они распределяются друг над другом по той же причине. Кроме того, вы можете думать о разнице множеств как об аналоге отрицания (\(\neg\)), момент, который будет прояснен позже. Эти факты заключены в следующей теореме, которую я предлагаю вам доказать для себя, используя доказательства равенства множеств по принципу «тогда и только тогда».
Теорема 2.2.2
Бинарные операции объединение и пересечение коммутативны, ассоциативны и распределяются друг над другом. То есть
\начать{выравнивать*} A \cup B = B \cup A \quad&\text{and}\quad A \cap B = B \cap A,\\ (A \чашка B) \чашка C = A \чашка (B \чашка C) \quad&\text{and}\quad (A \cap B) \cap C = A \cap (B \cap C),\\ (A \чашка B) \cap C = (A \cap C) \cup (B \cap C) \quad&\text{and}\quad (A \cap B) \cup C = (A \cup C) \ крышка (В\чашка С). \конец{выравнивание*}Более того, с той разницей, что они удовлетворяют своего рода законам Де Моргана:
\начать{выравнивать*} A \setminus (B \cup C) &= (A \setminus B) \cap (A \setminus C),\\ A \setminus (B \cap C) &= (A \setminus B) \cup (A \setminus C). \конец{выравнивание*}Кроме того, разность множеств удовлетворяет своего рода исключению двойного отрицания, а именно,
\begin{уравнение*} A \setminus \big( A \setminus ( A \setminus B) \big) = A \setminus B. \end{уравнение*}Определение 2.2.3 Непересекающиеся
Множества \(A,B\) называются непересекающимися , если их пересечение пусто, т. е. \(A \cap B = \emptyset\text{.}\) 9с = U\)
е. \(A \cap B = \emptyset\text{.}\) 9с = U\)
Еще один способ создания новых наборов — создание упорядоченных кортежей . Помните, множества неупорядочены, но очень полезно иметь объекты с упорядоченным расположением. Например, когда мы рассматривали точки на плоскости в алгебре и исчислении, мы обычно представляли их парами действительных чисел, например \((a,b)\), где \(a\) — горизонтальное смещение от начало координат, а \(b\) — вертикальное смещение. Ясно, что \((0,1) \not= (1,0)\text{,}\) поэтому порядка имеют значение .
Определение 2.2.6 Декартово произведение
Для множеств \(A,B\) мы можем составить их декартово произведение (или просто произведение ), которое состоит из всех упорядоченных пар, где первая компонента является элементом \(A\), а вторая компонента является элемент \(B\text{.}\) Символически,
\begin{уравнение*} A \times B := \{ (a,b) \mid a \in A, b \in B \}. \end{уравнение*} Обратите внимание, что в вашей книге декартово произведение называется «перекрестным произведением».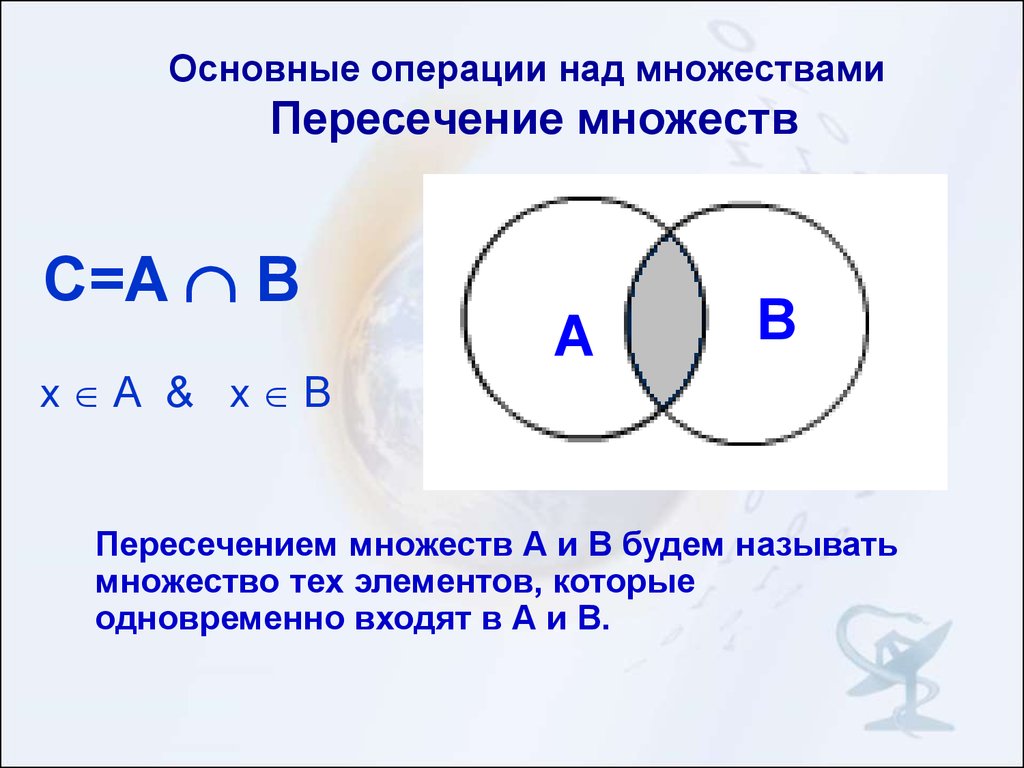 Это просто неверно; никто не относится к этому так. Взаимные произведения — это либо операции с трехмерными (или семи) мерными векторами, которые вы изучили в исчислении, либо гораздо более сложные объекты, включающие групповые действия (вы не должны знать, что такое групповое действие). Только никогда не используйте термин перекрестное произведение вместо декартова произведения. 92\text{,}\), то есть он лежит в плоскости, поэтому мы можем его визуализировать! В частности, \(A \times B\) — это (открытый) прямоугольник на плоскости, \(x\)-значения которого находятся между \(2\) и \(3\), а \(y\)-значения находятся между \(6\) и \(7\text{.}\). Итак, когда у вас есть какое-то свойство о декартовых произведениях и вы хотите узнать, верно ли оно и/или почему оно верно, сначала представьте, что ваши декартовы произведения являются прямоугольниками в плоскости. Надеюсь, это поможет вашей интуиции для следующей теоремы.
Это просто неверно; никто не относится к этому так. Взаимные произведения — это либо операции с трехмерными (или семи) мерными векторами, которые вы изучили в исчислении, либо гораздо более сложные объекты, включающие групповые действия (вы не должны знать, что такое групповое действие). Только никогда не используйте термин перекрестное произведение вместо декартова произведения. 92\text{,}\), то есть он лежит в плоскости, поэтому мы можем его визуализировать! В частности, \(A \times B\) — это (открытый) прямоугольник на плоскости, \(x\)-значения которого находятся между \(2\) и \(3\), а \(y\)-значения находятся между \(6\) и \(7\text{.}\). Итак, когда у вас есть какое-то свойство о декартовых произведениях и вы хотите узнать, верно ли оно и/или почему оно верно, сначала представьте, что ваши декартовы произведения являются прямоугольниками в плоскости. Надеюсь, это поможет вашей интуиции для следующей теоремы.
Теорема 2.2.7
Предположим, что \(A,B,C,D\) — множества. Затем
Затем
- \(A \times (B \times C) = (A \times B) \cup (A \times C)\)
- \(A \times (B \cap C) = (A \times B) \cap (A \times C)\)
- \(A \times\emptyset = \emptyset\)
- \((A \times B) \cap (C \times D) = (A \cap C) \times (B \cap D)\)
- \((A \times B) \cup (C \times D) \subseteq (A \cup C) \times (B \cup D)\)
Набор операций и диаграмм Венна
Набор операций и диаграмм ВеннаНаборы рассматриваются как математические объекты. Подобно числам, мы можем выполнять определенные математические операции над множествами. Ниже мы рассмотрим основные операции, связанные с пересечением, объединением, разностью, симметрической разностью и дополнением множеств.
Для визуализации операций над множествами мы будем использовать диаграммы Венна. На диаграмме Венна прямоугольник показывает универсальное множество, а все остальные множества обычно представляются кружками внутри прямоугольника. Заштрихованная область представляет собой результат операции.
Пересечение наборов
Пересечение двух множеств \(A\) и \(B\) — это множество элементов, которые входят в оба множества \(A\) и \(B.\). Пересечение двух множеств записывается как \( А \крышка Б.\)
Рис. 1.Два множества называются непересекающимися, если они не имеют общих элементов.
Примеры:
- \(A = \left\{ {a,b,c} \right\},\) \(B = \left\{ {k,\ell,m} \right\}.\) Эти два множества не пересекаются, так как не имеют общих элементов. Их пересечение — пустое множество.
\[A \cap B = \left\{ {a,b,c} \right\} \cap \left\{ {k,l,m} \right\} = \varnothing.\]
- \(C = \left\{ {1,2,3,4} \right\},\) \(D = \left\{ {2,4,6,7} \right\}.\) пересечение этих множеств есть
\[C \cap D = \left\{ {1,2,3,4} \right\} \cap \left\{ {2,4,6,7} \right\} = \left\{ { 2,4} \право\}.\]
Союз наборов
Объединение двух множеств \(A\) и \(B\) определяется как множество элементов, которые находятся либо в множестве \(A\), либо в множестве \(B\), либо в обоих \(A\) и \(B.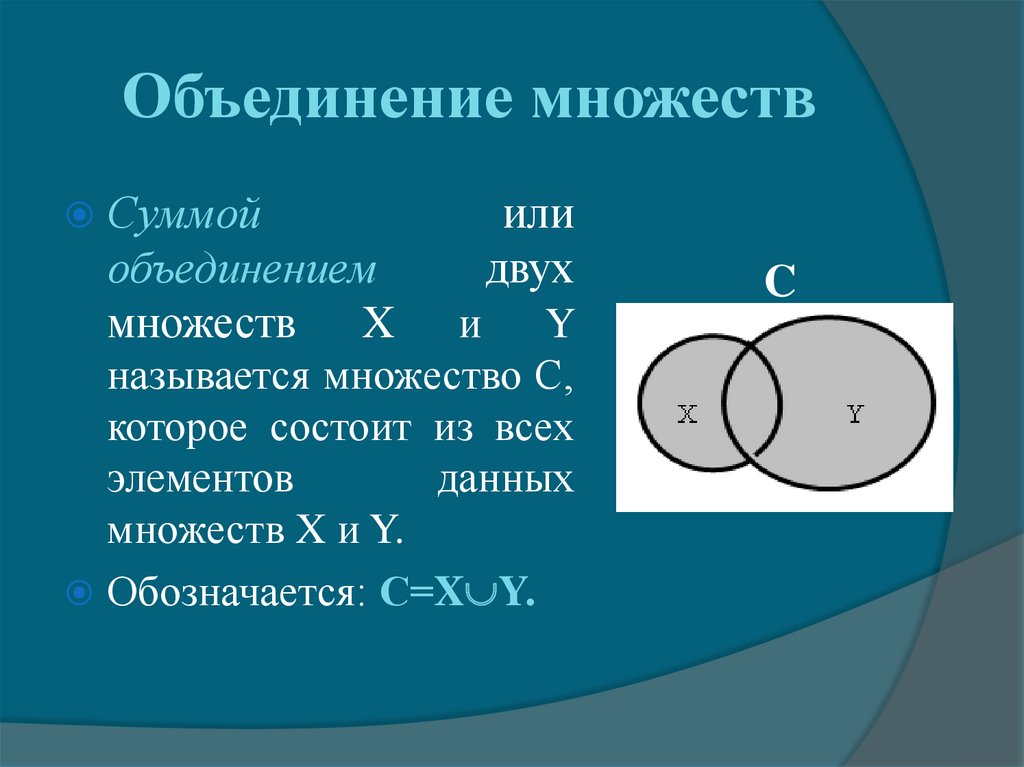 \) Эта операция обозначается символом \(\cup\).
\) Эта операция обозначается символом \(\cup\).
Примеры:
- \(A = \left\{ {a,b,c} \right\},\) \(B = \left\{ {k,\ell,m} \right\}.\) Объединение два набора задаются
\[A \cup B = \left\{ {a,b,c} \right\} \cup \left\{ {k,l,m} \right\} = \left\{ {a,b, в,к,л,м} \право\}.\]
- \(C = \left\{ {1,2,3,4} \right\},\) \(D = \left\{ {2,4,6,7} \right\}.\) объединение множеств задается выражением
\[C \cup D = \left\{ {1,2,3,4} \right\} \cup \left\{ {2,4,6,7} \right\} = \left\{ { 1,2,3,4,6,7} \право\}.\]
Принцип включения-исключения
Мощность конечного множества \(A,\), обозначаемого через \(\left| A \right|,\), равна количеству элементов в нем. Мощность объединения двух конечных множеств \(A\) и \(B\) определяется следующим соотношением:
\[\слева| {А \чашка Б} \право| = \ влево | А \право| + \влево| Б \ справа | — \влево| {A \cap B} \right|,\]
где \(\left| {A \cap B} \right|\) — мощность пересечения \(A\) и \(B.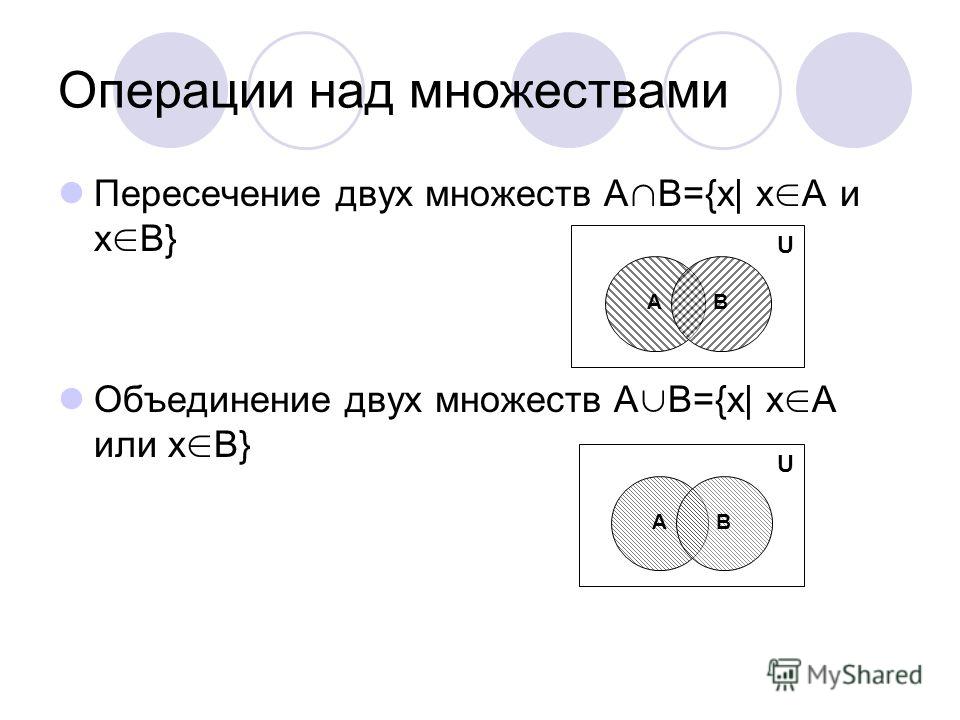 \)
\)
Аналогичная формула существует для объединения \(3\) конечных множеств:
\[\слева| {A \чашка B \чашка C} \right| = \ влево | А \право| + \влево| Б \ справа | + \влево| С \ справа | — \влево| {А \заглавная Б} \право| — \влево| {A \cap C} \right| — \влево| {B \cap C} \право| + \влево| {A \cap B \cap C} \right|.\]
Разница двух наборов
Разность двух множеств \(A\) и \(B\) — это множество, которое содержит ровно все элементы из \(A\), но не из \(B.\) Разность двух множеств \(A\) а \(B\) обозначается \(A \обратная косая черта B\) или \(A — B.\)
Рисунок 3.Примеры:
- \(A = \left\{ {a,b,c} \right\},\) \(B = \left\{ {k,\ell,m} \right\}.\) Разница между два непересекающихся множества равно исходному множеству. Итак, у нас есть
\[A \backslash B = A \backslash \left( {A \cap B} \right) = A \backslash \varnothing = A = \left\{ {a,b,c} \right\}.\]
- \(C = \left\{ {1,2,3,4} \right\},\) \(D = \left\{ {2,4,6,7} \right\}.
 \) разность двух множеств \(C\) и \(D\) определяется выражением
\) разность двух множеств \(C\) и \(D\) определяется выражением\[C \обратная косая черта D = \left\{ {1,2,3,4} \right\} — \left\{ {2,4,6,7} \right\} = \left\{ {1 ,3} \право\}.\]
Симметричная разность
Симметричная разность двух множеств \(A\) и \(B\) — это множество всех элементов, принадлежащих ровно одному из двух исходных множеств. Эта операция записывается как \(A \,\triangle\, B\) или \(A \oplus B.\)
Рис. 4.В терминах объединений и пересечений симметричная разность двух множеств \(A\) и \(B\) может быть выражена как
\[A \,\треугольник\, B = \left( {A \cup B} \right) \backslash \left( {A \cap B} \right).\]
Примеры:
- \(A = \left\{ {a,b,c} \right\},\) \(B = \left\{ {k,\ell,m} \right\}.\) Симметричная разность двух непересекающихся множеств равно их объединению:
\[A \,\треугольник\, B = \left( {A \cup B} \right) \backslash \left( {A \cap B} \right) = \left( {A \cup B} \right ) \обратная косая черта \varnothing = A \cup B = \left\{ {a,b,c,k,\ell,m} \right\}.
 \]
\] - \(C = \left\{ {1,2,3,4} \right\},\) \(D = \left\{ {2,4,6,7} \right\}.\) симметричная разность множеств \(C\) и \(D\) определяется выражением 9с} = \{- 4,3,4\} .\]
См. решенные проблемы на стр. 2.
Страница 1 Страница 2
Теория множеств > Базовая теория множеств (Стэнфордская энциклопедия философии)
Множества — это хорошо определенные наборы, полностью
характеризуется своими элементами. Таким образом, два множества равны тогда и только тогда, когда
если они имеют точно такие же элементы. Основное отношение в множестве
Теория есть теория элементальности или членства. Мы пишем \(a\in A\) в
указать, что объект \(a\) является элемент или
элемент множества \(A\). Мы также говорим, что \(a\) принадлежит
до \(А\). Таким образом, множество \(А\) равно множеству \(В\) тогда и только тогда, когда для
каждое \(а\), \(а\в А\) тогда и только тогда, когда \(а\в В\). В частности, есть
только один набор без каких-либо элементов.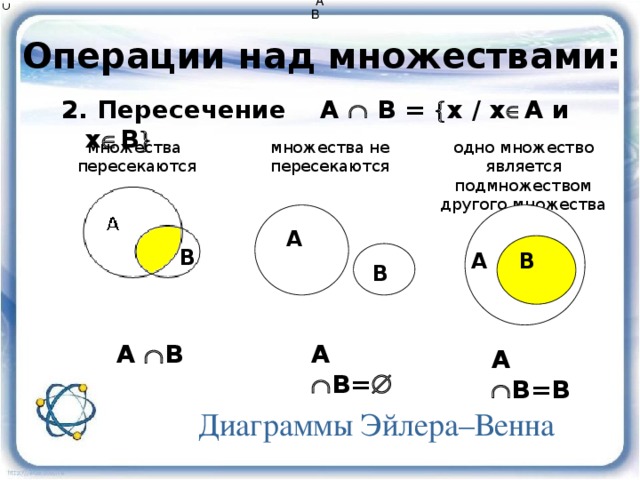 Это множество называется, естественно,
пустой набор и представлен символом
\({\varничего}\).
Это множество называется, естественно,
пустой набор и представлен символом
\({\varничего}\).
Мы говорим, что \(A\) есть подмножество множества \(B\), записанное как \(A\subseteq B\), если каждый элемент \(A\) является элементом \(B\). Таким образом, \(A=B\), если и только если \(A\subseteq B\) и \(B\subseteq A\). Заметь \({\varnothing}\subseteq A\), для каждого набора \(A\).
Имея наборы \(A\) и \(B\), можно выполнить некоторые основные операции с из них получаются следующие множества:
Множество \(A\cup B\), называемое объединением \(A\) и \(B\), чьи элементами являются элементы \(A\) и элементы \(B\).
Множество \(A\cap B\), называемое пересечением точек \(A\) и \(B\), элементами которого являются элементы, общие для \(A\) и \(B\).
Множество \(A-B\), называемое разность \(A\) и \(B\), чьи элементами являются те элементы \(A\), которые не являются членами \(В\).

Проверка того, что эти операции удовлетворяют следующим свойства:
Ассоциативность:
Коммутативность:
Распределение:
Идемпотентность:
\(А \чашка А=А\)
\(А \крышка А=А\)
\(A \cup {\varnothing}=A\)
\(A\cap {\varnothing}={\varnothing}\)
\(A — A={\varnothing}\)
Если \(A\subseteq B\), то
Имея объект \(a\), мы можем сформировать множество, в котором \(a\) является единственным
элемент. Это множество обозначается через \(\{ a \}\). В более общем плане, учитывая
\(a,b,c,\ldots\), мы можем сформировать множество, имеющее \(a,b,c,\ldots\) в качестве
элементы, которые мы обозначаем через \(\{ a,b,c, \ldots\}\). Конечно можем
на самом деле запишите все элементы множества, когда их не слишком много.
многие из них.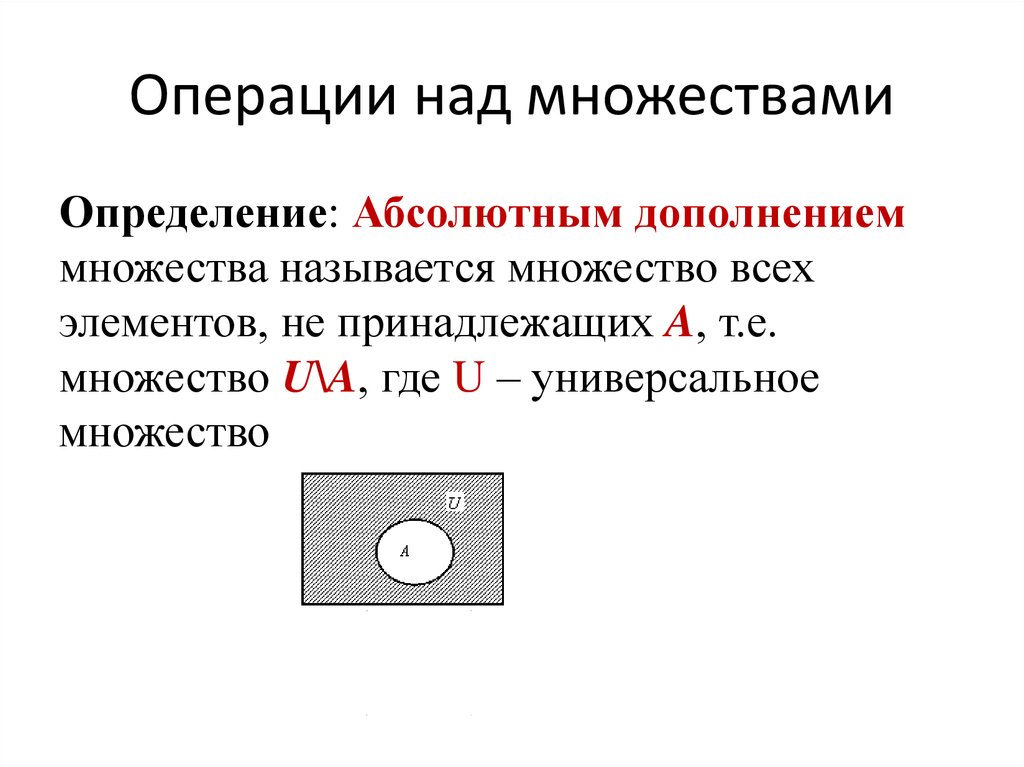 В случае бесконечных множеств это явно не так.
возможный.
В случае бесконечных множеств это явно не так.
возможный.
Если \(a=b\), то \(\{ a,b\}=\{ a\}\). Кроме того, для любых \(a\) и \(b\) пара \(\{ a,b\}\) совпадает с парой \(\{ b,a\}\). Итак, если мы хотим принять во внимание порядок, в котором два элемента пары Учитывая, нам нужно найти другой способ представления пары. Таким образом, мы определить упорядоченную пару \((a,b)\) как набор \(\{ \{ a\},\{ а, б\}\}\). Легко проверить, что две упорядоченные пары \((a,b)\) и \((c,d)\) равны тогда и только тогда, когда \(a=c\) и \(b=d\). Заказ сейчас важно, ибо если \(a\ne b\), то \((a,b)\ne (b,a)\).
Декартово произведение \(A\times B\) двух множеств, \(A\) и \(B\), определяется как множество всех упорядоченных пар \((a,b)\) таких, что \(а\в А\) и \(б\в В\).
Определив упорядоченные пары, теперь можно определить упорядоченных
тройки \((a,b,c)\) как \((a,(b,c))\), или вообще заказано
\(n\)-кортежи \((a_1,\ldots ,a_n)\) как \((a_1, (a_2,\ldots ,a_n))\).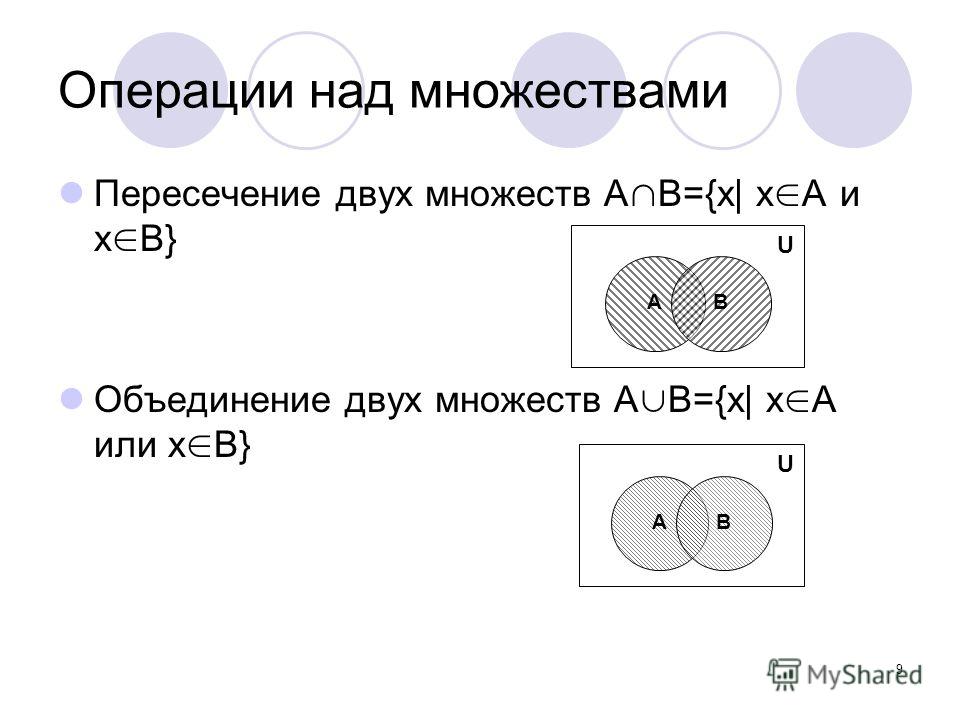 n\).
n\).
Бинарное отношение \(R\) на множестве \(A\) называется рефлексивным , если \((a,a)\in R\) для каждого \(a\in A\). Он называется симметричным , если \((b,a)\in R\) всякий раз, когда \((a,b)\in R\). И это называется транзитивным , если \((a,c)\in R\) всякий раз, когда \((a,b)\in R\) и \((b,c)\в R\). Отношение, которое является рефлексивным, симметричным и транзитивным называется отношением эквивалентности . Отношение тождества на любое множество \(A\) является парадигматическим примером эквивалентности связь. Другим примером является отношение на множестве всех конечных множества натуральных чисел, состоящие из всех пар \((a,b)\) таких, что \(a\) и \(b\) имеют одинаковое количество элементов.
Если \(R\) является отношением эквивалентности на множестве \(A\) и \((a,b)\в R\),
тогда мы говорим, что \(a\) и \(b\) \(R\)-эквивалентны . За
каждый \(a\in A\), класса эквивалентности \(a\), обычно обозначаемый
через \([a]_R\), это множество всех элементов \(A\), которые являются \(R\)-эквивалентными
к \(а\). Множество всех классов \(R\)-эквивалентности называется
фактор-множество и обозначается \(A/R\). Можно легко
проверьте, что \(A/R\) является разделом \(A\), то есть ни один элемент
из \(A/R\) пусто, любые два элемента из \(A/R\) не пересекаются, и каждый
\(a\in A\) принадлежит (ровно) одному элементу \(A/R\), а именно классу
\([а]_Р\).
Множество всех классов \(R\)-эквивалентности называется
фактор-множество и обозначается \(A/R\). Можно легко
проверьте, что \(A/R\) является разделом \(A\), то есть ни один элемент
из \(A/R\) пусто, любые два элемента из \(A/R\) не пересекаются, и каждый
\(a\in A\) принадлежит (ровно) одному элементу \(A/R\), а именно классу
\([а]_Р\).
Если \(R\) является бинарным отношением, то вместо него обычно пишут \(aRb\) из \((a,b)\in R\).
Бинарное отношение \(R\) на множестве \(A\) называется антисимметричным если \(a=b\), когда \(aRb\) и \(bRa\). Отношение \(R\) на множестве \(A\), т.е.
рефлексивной, антисимметричной и транзитивной, называется
(возвратный) частичный заказ . Если удалить из \(R\) все пары
\((a,a)\), для каждого \(a\in A\), мы получаем строгих частичных
заказ. Отношение \(\subseteq\) на любом множестве множеств является примером
частичный заказ. Частичный порядок на заданном множестве \(A\) обычно
представленный символом \(\leq\), и соответствующий строгий частичный
упорядочение по \(<\). Частичный порядок \(\leq\) на множестве \(A\) с
дополнительное свойство, состоящее в том, что либо \(a\leq b\), либо \(b\leq a\) для всех
элементы \(a\) и \(b\) из \(A\), называется 92\) также является линейным порядком на
\(В\). Если \(\leq\) — линейный порядок на множестве \(A\), то говорят, что \(a\in
A\) является \(\leq\)-наименьшим элементом \(A\), если нет \(b\in A\) различных
из \(a\) такое, что \(b\leq a\). Число \(0\) является наименьшим элементом
\(\mathbb{N}\), но \(\mathbb{Z}\) не имеет наименьшего элемента.
Частичный порядок \(\leq\) на множестве \(A\) с
дополнительное свойство, состоящее в том, что либо \(a\leq b\), либо \(b\leq a\) для всех
элементы \(a\) и \(b\) из \(A\), называется 92\) также является линейным порядком на
\(В\). Если \(\leq\) — линейный порядок на множестве \(A\), то говорят, что \(a\in
A\) является \(\leq\)-наименьшим элементом \(A\), если нет \(b\in A\) различных
из \(a\) такое, что \(b\leq a\). Число \(0\) является наименьшим элементом
\(\mathbb{N}\), но \(\mathbb{Z}\) не имеет наименьшего элемента.
Линейный порядок \(\leq\) на множестве \(A\) является хорошим порядком, если каждое непустое подмножество \(A\) имеет \(\leq\)-наименьший элемент. Эквивалентно, если нет бесконечного строго убывающего последовательность \[\ldots < a_2< a_1< a_0\] элементов \(A\). Таким образом, обычный порядок \(\mathbb{N}\) является правильным порядком. Но обычное порядок на \(\mathbb{Z}\) не такой, потому что в нем нет наименьшего элемента.
2. Функции
A (\(1\)-арные) функция на множестве \(A\) является бинарным отношением \(F\)
на \(A\) такие, что для каждого \(a\in A\) существует ровно одна пара
\((а,б)\в F\).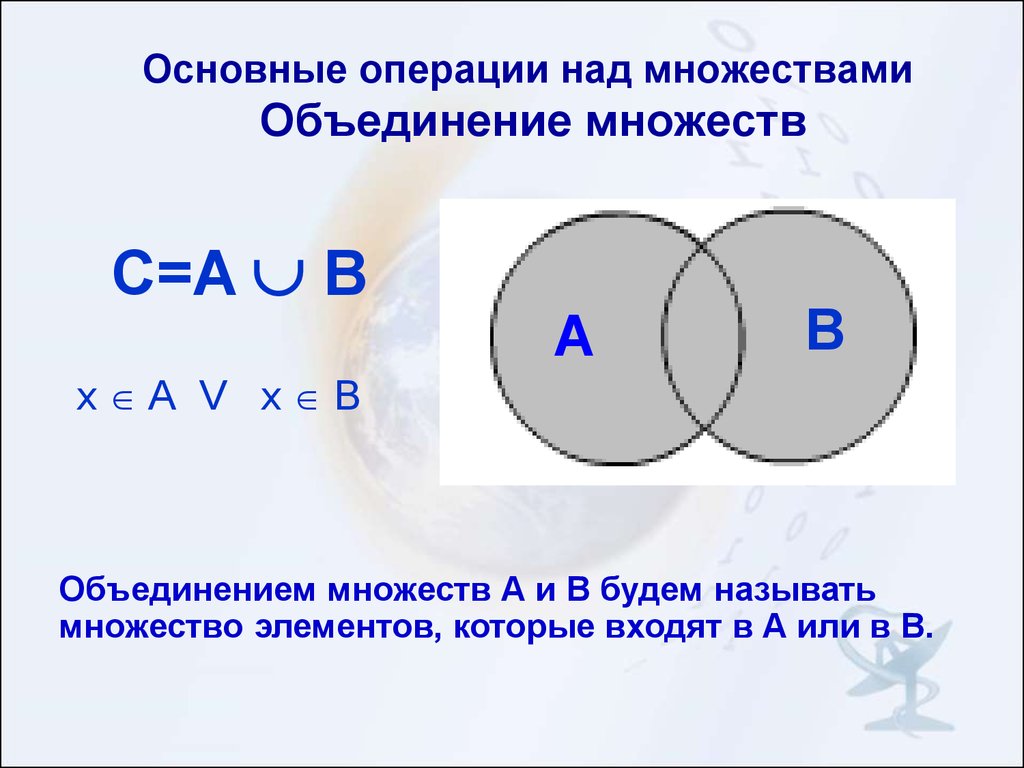 Элемент \(b\) называется значением элемента \(F\) на
\(a\) и обозначается через \(F(a)\). А множество \(A\) называется
домен из \(F\). Обозначение \(F:A\to B\) указывает, что \(F\)
есть функция с областью определения \(A\) и значениями в множестве \(B\). Для \(n\geq
2\), \(n\)-арная функция 9п\к Б\),
для некоторого \(B\).
Элемент \(b\) называется значением элемента \(F\) на
\(a\) и обозначается через \(F(a)\). А множество \(A\) называется
домен из \(F\). Обозначение \(F:A\to B\) указывает, что \(F\)
есть функция с областью определения \(A\) и значениями в множестве \(B\). Для \(n\geq
2\), \(n\)-арная функция 9п\к Б\),
для некоторого \(B\).
Функция \(F:A\to B\) является однозначной , если для всех элементов
\(a\) и \(b\) из \(A\), если \(a\ne b\), то \(F(a)\ne F(b)\). А также
есть на , если для каждого \(b\in B\) существует некоторое \(a\in A\) такое
что \(F(a)=b\). Наконец, \(F\) является биективным , если оно является взаимно однозначным.
и на. Таким образом, биекция \(F:A\to B\) устанавливает взаимно-однозначное
соответствие между элементами \(A\) и элементами \(B\), а \(A\)
является биективным с \(B\), если существует такой
биекция. тождественная функция на множестве \(A\), обозначаемая
\(Id:A\to A\) и состоит из всех пар \((a,a)\), где \(a\in
A\) тривиально является биекцией.
Даны функции \(F:A\to B\) и \(G:B\to C\), композиция \(F\) и \(G\) , записанные \(G\circ F\), есть функция \(G\circ F:A\to C\), элементами которого являются все пары \((a,G(F(a)))\), где \(a\in A\). Если \(F\) и \(G\) биекции, то и \(G\circ F\).
3. Наборы и формулы
Формальные язык теории множеств является языком первого порядка язык, единственным нелогическим символом которого является символ бинарного отношения \(\в\).
Дана любая формула \(\varphi(x,y_1,\ldots ,y_n)\) языка теории множеств и множеств \(A,B_1,\ldots ,B_n\), можно сформировать множество всех те элементы \(A\), которые удовлетворяют формуле \(\varphi(x,B_1,\ldots ,В_п)\). Это множество обозначается \(\{ a\in A: \varphi(a,B_1,\ldots ,В_п)\}\). Ниже приведены некоторые примеры
\({\varnothing}=\{ a\in A: a\ne a\}\)
\(А=\{а\в А: а=а\}\)
\(A-B=\{ a\in A: a\not \in B\}\).
\(A\cap B=\{ a\in A: a\in B\}\).

И если \(B\) и \(C\) являются подмножествами \(A\), то
Учитывая подмножество \(C\subseteq A\times B\), проекция \(C\) (по первой координате) есть множество
\(\{ a\in A: \существует b\in B ((a,b)\in C)\}\).
Однако это не тот случай, когда при любой формуле \(\varphi(x,y_1,\ldots,y_n)\) и множеств \(B_1,\ldots,B_n\), можно сформировать множество всех тех множеств, которые удовлетворяют формуле \(\varphi(x,B_1,\ldots,B_n)\). Пусть \(\varphi(x)\) будет формулой \(х\не \в х\). Если бы \(A\) было множеством всех множеств, удовлетворяющих формулы, то \(А\в А\) тогда и только тогда, когда \(А\не \в А\). Противоречие! Это противоречие известно как Парадокс Рассела , после Бертран Рассел, открывший его в 1901 г. (см. парадокс Рассела).
4. Порядковые номера
Первый порядковый номер — \({\varnothing}\). Учитывая порядковый номер
\(\alpha\), следующий больший порядковый номер, называемый
(немедленно) преемник \(\alpha\), это набор \(\alpha \cup \{
\альфа\}\). Таким образом, преемником \(\alpha\) является просто набор \(\alpha\)
вместе с еще одним элементом, а именно \(\alpha\)
сам. конечных порядковых числа получены
начиная с \({\varnothing}\) и многократно беря преемника.
Таким образом, преемником \(\alpha\) является просто набор \(\alpha\)
вместе с еще одним элементом, а именно \(\alpha\)
сам. конечных порядковых числа получены
начиная с \({\varnothing}\) и многократно беря преемника.
В теории множеств натуральных числа определяются как конечные ординалы. Таким образом,
\(0= {\varnothing}\)
\(1= {\varnothing}\cup \{ {\varnothing}\}=\{ {\varnothing}\}\)
\(2= \{ {\varnothing}\} \cup \{\{{\varnothing}\}\}=\{ {\varnothing}, \{ {\varnothing}\}\}\)
\(3= \{ {\varnothing}, \{ {\varnothing}\}\}\cup \{ \{ {\varnothing}, \{ {\varnothing}\}\}\} =\{ {\varnothing}, \{ {\varnothing}\}, \{ {\varnothing}, \{ {\varnothing}\}\}\}\)
\(\вдоц\)
Обратите внимание, что \(1=\{ 0\}\), \(2=\{ 0,1\}\), \(3=\{ 0,1,2\}\) и в
вообще имеем \(n=\{ 0,1,2,\ldots ,n-1\}\). Итак, каждое натуральное число
\(n\) — это просто набор своих предшественников.
Множество \(A\) является конечным , если существует однозначное соответствие между некоторым натуральным числом \(n\) и элементами \(A\), т. е. биекция \(F:n\to A\), и в этом случае мы говорим, что \(A\) имеет \(n\) элементов. Набор бесконечен , если он не конечен.
Множество всех конечных ординалов обозначается греческой буквой омега
(\(\омега\)). Таким образом, \(\omega\) — это просто набор \(\mathbb{N}\) натуральных
числа. \(\omega\) также является порядковым номером, первым бесконечным
порядковый. Обратите внимание, что \(\omega\) не является преемником какого-либо порядкового номера, и
поэтому он называется предельным порядковым номером . Когда у нас есть \(\omega\), мы можем
продолжайте генерировать больше порядковых номеров, взяв его преемника \(\omega \cup
\{ \omega \}\), затем его преемник \((\omega \cup \{\omega\}) \cup
\{\omega \cup \{\omega \}\}\) и так далее. Все порядковые числительные больше
чем \(0\) производятся таким образом, а именно, либо путем взятия
преемник последнего произведенного порядкового номера, или, если такого последнего нет
порядковый номер, взяв набор всех произведенных до сих пор ординалов, как в
случай \(\omega\), который дает новый предельный порядковый номер. Обратите внимание, однако,
что нельзя взять набор из все порядковые номера, для этого
множество было бы новым предельным ординалом, что невозможно, так как мы
уже все были.
Обратите внимание, однако,
что нельзя взять набор из все порядковые номера, для этого
множество было бы новым предельным ординалом, что невозможно, так как мы
уже все были.
Как и в случае с конечными ординалами, каждый бесконечный ординал — это просто набор его предшественники. Одним из следствий этого является то, что отношение \(\in\) является строгим порядком на любом множестве ординалов. Таким образом, для любых ординалов \(\alpha\) и \(\beta\) мы определяем \(\alpha <\beta\) тогда и только тогда, когда \(\альфа\в\бета\). Тогда соответствующий рефлексивный порядок равен определяется как \(\alpha \leq \beta\) тогда и только тогда, когда \(\alpha <\beta\) или \(\альфа=\бета\). Заметим теперь, что \(\alpha \subseteq \beta\), если и только если \(\alpha \leq \beta\).
5. Счетные и несчетные множества
Если \(A\) конечное множество, то существует биекция \(F:n\to A\) между
натуральные числа \(n\) и \(A\). Любая такая биекция дает
a , считая элементов \(A\), а именно \(F(0)\) есть
первый элемент \(A\), \(F(1)\) — второй и так далее. Каждое бесконечное подмножество счетного множества также счетно: для
предположим, что \(F:\omega \to A\) является биекцией, а \(B\subseteq A\) является
бесконечный. Тогда множество \(\{ n\in \omega: F(n)\in B\}\) является бесконечным
подмножество \(\omega\), следовательно, счетно, и поэтому существует биекция
\(G:\omega \to \{n\in \omega : F(n)\in B\}\). Тогда состав
функция \(F\circ G:\omega \to B\) является биекцией. Объединение счетного множества и конечного множества также
исчисляемый. Более того, объединение двух счетных множеств тоже счетно: поскольку
мы уже показали, что объединение счетного множества и конечного
множество также счетно, достаточно убедиться, что объединение двух
непересекающиеся счетные множества также счетны. Итак, предположим, что \(A\) и \(B\) равны
счетные множества и \(F:\omega \to A\) и \(G:\omega \to B\)
биекций, то функция \(H:\omega \to A\cup B\), состоящая из всех
пар \((2n,F(n))\), плюс все пары \((2n+1, G(n))\) — биекция. Так как любое рациональное число задается парой целых чисел, т.е.
частное \(\frac{m}{n}\), где \(m,n\in \mathbb{Z}\) и \(n\ne 0\),
множество \(\mathbb{Q}\) рациональных чисел также счетно. Однако Георг Кантор обнаружил, что множество \(\mathbb{R}\) вещественных
числа не исчисляются. Предположим, что, стремясь к противоречию,
что \(F:\omega \to \mathbb{R}\) является биекцией. Пусть \(a_0=F(0)\). Выбирать
наименьшее \(k\) такое, что \(a_0 Существование несчетных множеств следует из гораздо более общего
факт, также обнаруженный Кантором. А именно, для любого множества \(A\) множество
все его подмножества, называемые степенным набором множества \(A\), и обозначаемые
\(\mathcal{P}(A)\), не является биективным с \(A\): предположим, что \(F:A\to
\mathcal{P}(A)\) является биекцией. Существуют также неисчисляемые порядковые номера. множество всех конечных и
исчисляемые ординалы также являются порядковыми номерами, называемыми \(\omega_1\), и
первый неисчисляемый порядковый номер. Точно так же множество всех ординалов, которые
биективный с некоторым порядковым номером, меньшим или равным \(\omega_1\), также
порядковое число, называемое \(\omega_2\), и не биецируется с \(\omega_1\),
и так далее. Мощность или размер конечного множества \(A\) есть
единственное натуральное число \(n\), такое что существует биекция \(F:n\to
А\). В случае бесконечных множеств их мощность определяется не
натуральным числом, а бесконечным порядковым номером. Однако, в отличие от
конечные множества, бесконечное множество \(A\) биективно со многими различными
порядковые номера. В частности, мощность порядкового числительного \(\alpha\) равна
наименьший порядковый номер \(\каппа\), который биецируется с ним. Заметь
\(\kappa\) не биективен ни с каким меньшим порядковым номером, иначе
будет \(\альфа\). Порядковые числа, которые не биективны с
любые меньшие порядковые числа называются количественными числами . Таким образом, все
натуральные числа являются количественными, как и \(\omega\), \(\omega_1\),
\(\omega_2\) и так далее. В общем, для любого кардинала \(\каппа\)
множество всех ординалов, которые биективны с некоторым ординалом \(\leq
\каппа\) тоже кардинал; это наименьший кардинал больше, чем
\(\каппа\). Бесконечные кардиналы представлены буквой алеф
(\(\алеф\)) еврейского алфавита. Таким образом, наименьший бесконечный
кардинал — \(\omega =\aleph_0\), следующий — \(\omega_1=\aleph_1\),
который является первым несчетным кардиналом, затем следует
\(\omega_2=\aleph_2\) и т. д. Мощность любого множества \(A\), обозначаемого \(|A|\), является единственным
кардинальное число, биективное с \(A\). Мы уже видели, что
\(|\mathbb{R}|\) несчетно, следовательно, больше, чем \(\aleph_0\), но
неизвестно, какое это кардинальное число. Гипотеза о том, что
\(|\mathbb{R}|=\aleph_1\), сформулированная Кантором в 1878 г., является
знаменитый Гипотеза континуума . Таким образом, все
конечные множества счетны. Бесконечное множество \(A\) есть
называется счетным , если существует биекция \(F:\omega \to A\)
между множеством натуральных чисел и \(A\). Набор \(\mathbb{N}\) из
натуральные числа (тривиально) счетны. Если \(A\) бесконечное подмножество
\(\omega\), то \(A\) также счетно: ибо пусть \(F:\omega \to A\) будет
такой, что \(F(n)\) является наименьшим элементом \(A\), не входящим в множество
\(\{ F(m)\in A: m
Таким образом, все
конечные множества счетны. Бесконечное множество \(A\) есть
называется счетным , если существует биекция \(F:\omega \to A\)
между множеством натуральных чисел и \(A\). Набор \(\mathbb{N}\) из
натуральные числа (тривиально) счетны. Если \(A\) бесконечное подмножество
\(\omega\), то \(A\) также счетно: ибо пусть \(F:\omega \to A\) будет
такой, что \(F(n)\) является наименьшим элементом \(A\), не входящим в множество
\(\{ F(m)\in A: m Для заданных множеств \(A\) и \(B\), которые без потери
общности, мы можем предположить, что они не пересекаются, и при заданных биекциях
\(F:\omega \to A\) и \(G:n\to B\), для некоторого \(n<\omega\) пусть \(H:\omega
\to A\cup B\) — биекция, заданная формулой: \(H(m)=G(m)\), для каждого
\(m
Для заданных множеств \(A\) и \(B\), которые без потери
общности, мы можем предположить, что они не пересекаются, и при заданных биекциях
\(F:\omega \to A\) и \(G:n\to B\), для некоторого \(n<\omega\) пусть \(H:\omega
\to A\cup B\) — биекция, заданная формулой: \(H(m)=G(m)\), для каждого
\(m
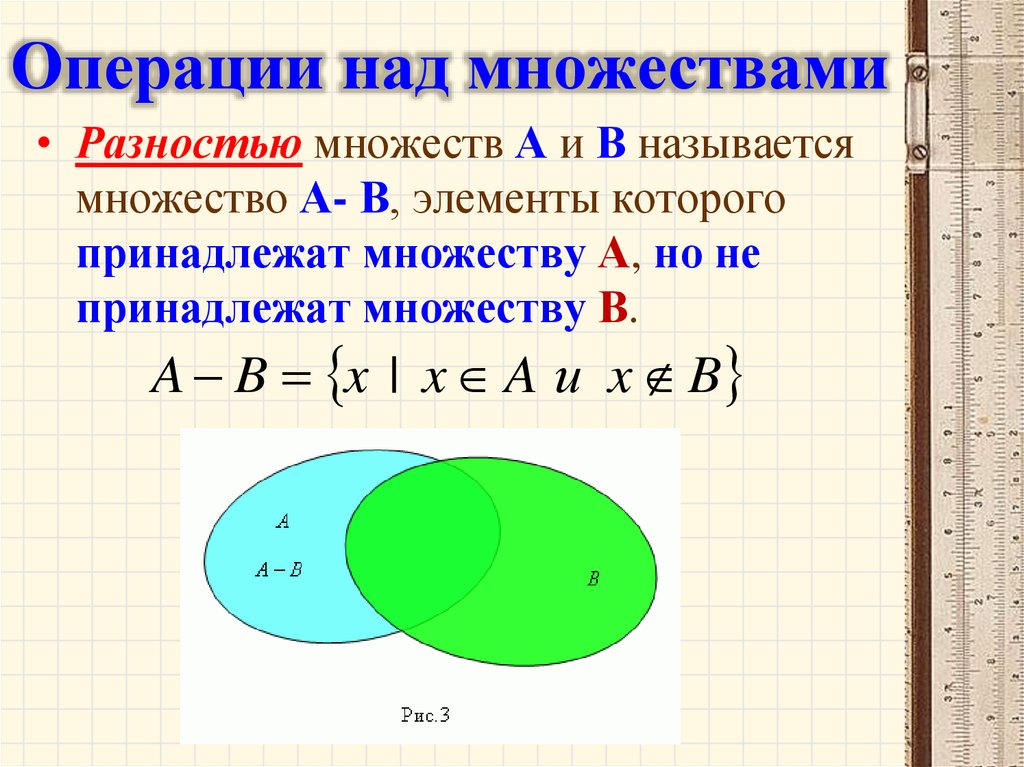 Тогда подмножество \(\{ a\in A: a\not \in
F(a)\}\) множества \(A\) есть значение \(F(a)\) некоторого \(a\in A\). Но тогда \(a\in
F(a)\) тогда и только тогда, когда \(a\not \in F(a)\). Следовательно, если \(А\) — любое бесконечное
множество, то \(\mathcal{P}(A)\) несчетно.
Тогда подмножество \(\{ a\in A: a\not \in
F(a)\}\) множества \(A\) есть значение \(F(a)\) некоторого \(a\in A\). Но тогда \(a\in
F(a)\) тогда и только тогда, когда \(a\not \in F(a)\). Следовательно, если \(А\) — любое бесконечное
множество, то \(\mathcal{P}(A)\) несчетно. 5.1 Кардиналы
 Например, множество \(\mathbb{N}\) биективно с
\(\omega\), но и с его преемником \(\omega \cup \{\omega\}\): by
присваивая \(0\) \(\omega\) и \(n+1\) \(n\), для всех \(n\in \omega\), мы
получить биекцию между \(\omega \cup \{\omega \}\) и \(\omega\). Но
поскольку ординалы хорошо упорядочены, мы можем определить мощность
бесконечное множество как наименьший ординал, биективный с ним.
Например, множество \(\mathbb{N}\) биективно с
\(\omega\), но и с его преемником \(\omega \cup \{\omega\}\): by
присваивая \(0\) \(\omega\) и \(n+1\) \(n\), для всех \(n\in \omega\), мы
получить биекцию между \(\omega \cup \{\omega \}\) и \(\omega\). Но
поскольку ординалы хорошо упорядочены, мы можем определить мощность
бесконечное множество как наименьший ординал, биективный с ним.
Дополнительная литература



 п.).
п.). \]
\]
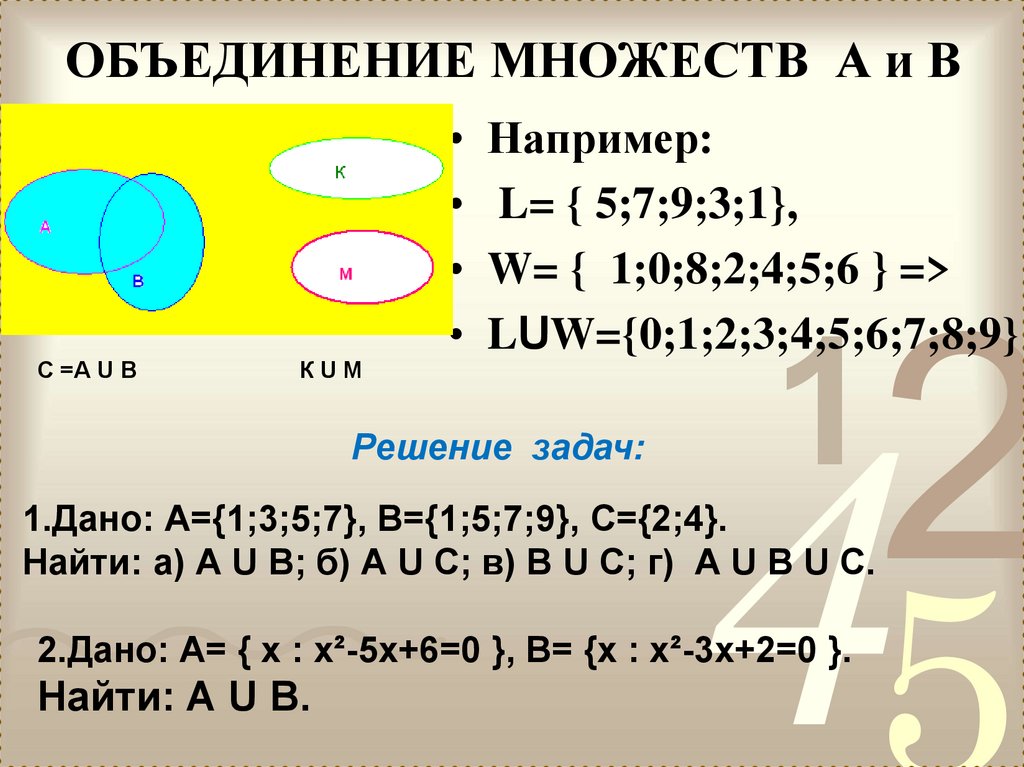
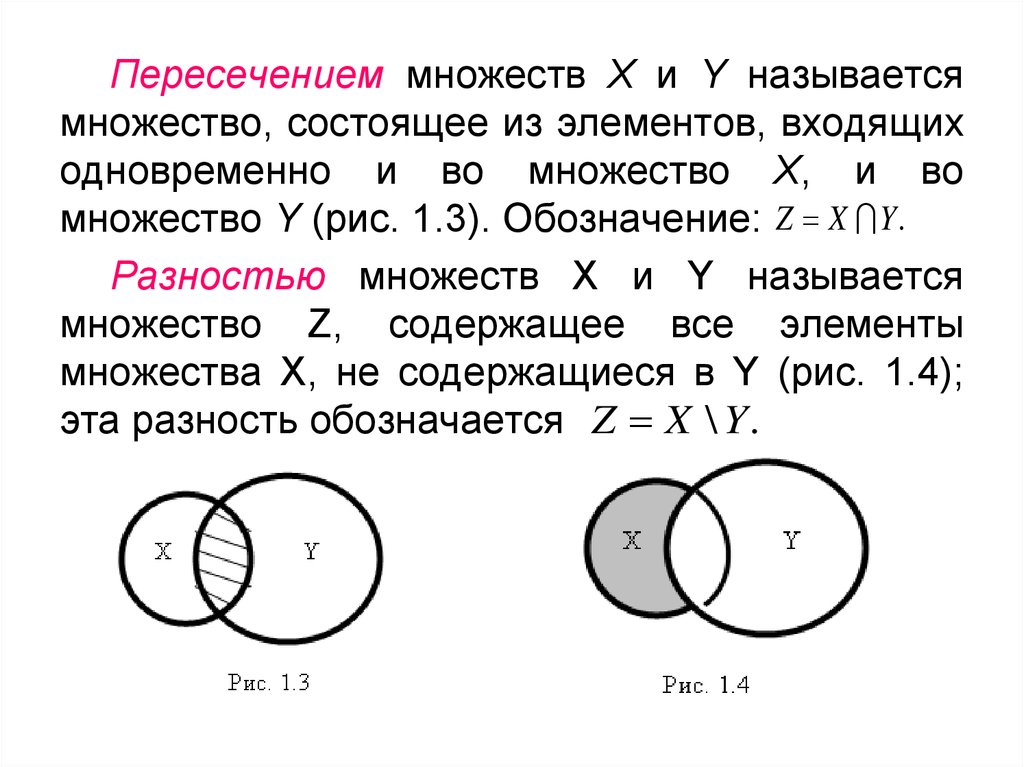
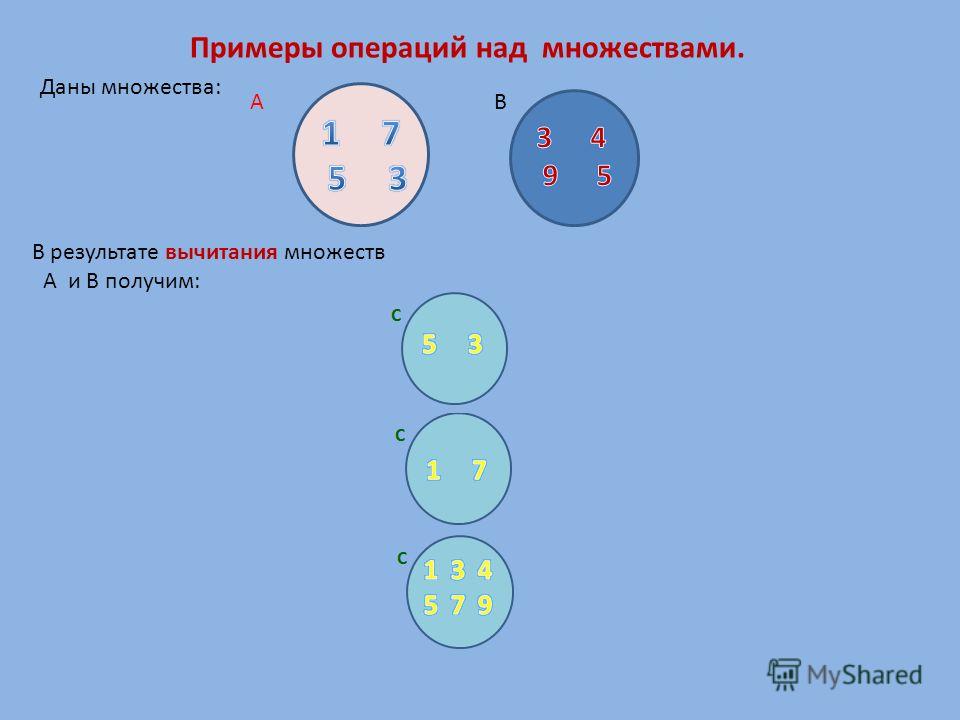 (См. также пример 10.)
(См. также пример 10.) Таким образом, пересечение с \(\overline{B}\) приводит к тому, что остаются только значения, не входящие в \(B\). То есть \(A\cap\overline{B}\) — это \(A\) со всеми удаленными значениями из \(B\). Таким образом, мы видим, что эти множества содержат одни и те же элементы. ∎
Таким образом, пересечение с \(\overline{B}\) приводит к тому, что остаются только значения, не входящие в \(B\). То есть \(A\cap\overline{B}\) — это \(A\) со всеми удаленными значениями из \(B\). Таким образом, мы видим, что эти множества содержат одни и те же элементы. ∎ Например:
Например: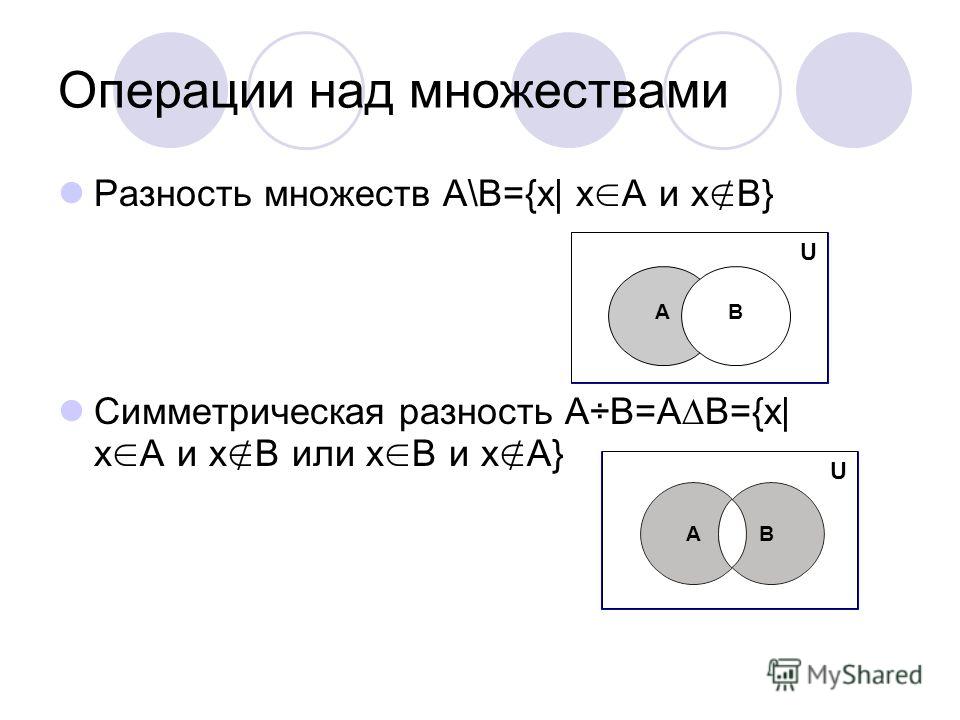 {n} S_i\,.\]
Студенты берут 92\,.\]
{n} S_i\,.\]
Студенты берут 92\,.\] my_set = {1, 2, [3, 4]}
my_set = {1, 2, [3, 4]} 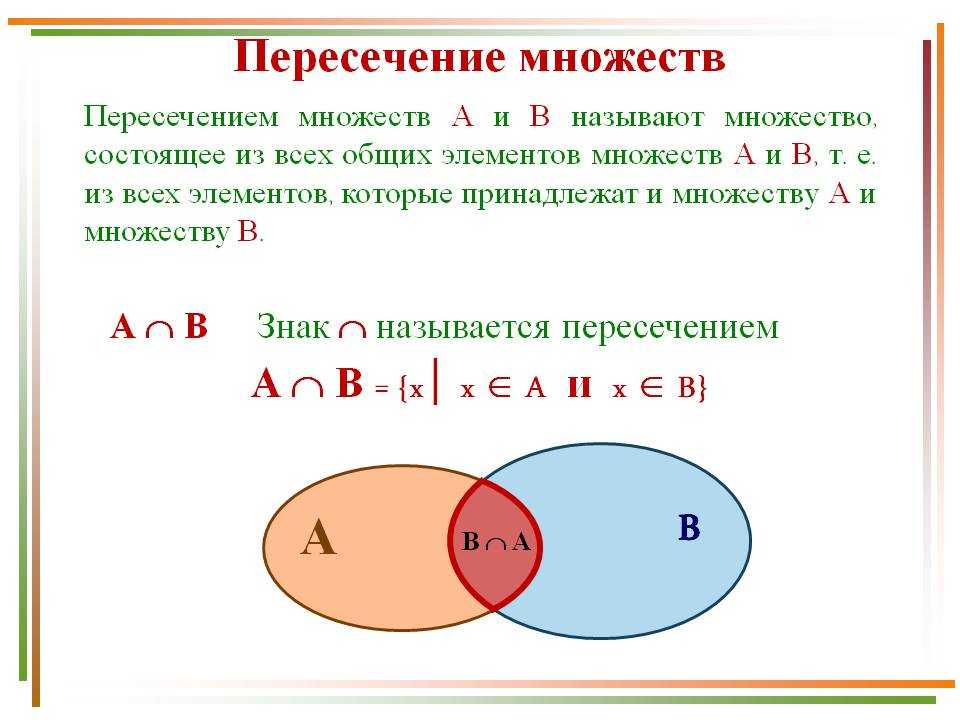 \) разность двух множеств \(C\) и \(D\) определяется выражением
\) разность двух множеств \(C\) и \(D\) определяется выражением \]
\]
