2+n-72)=1/(n+9)Умножение многочлена на многочлен — как правильно?
Определение многочлена
Прежде чем мы расскажем, как умножить один многочлен на другой многочлен, разберемся в основных понятиях.
Одночлен — это произведение чисел, переменных и степеней.
Многочлен— алгебраическое выражение, которое представляет из себя сумму или разность нескольких одночленов.
Стандартный вид многочлена — представление многочлена в виде суммы одночленов стандартного вида, среди которых нет подобных одночленов.
Как привести многочлен к стандартному виду:
- Привести к стандартному виду все одночлены, которые входят в многочлен.
- Привести подобные члены.
Вспомним, как умножать многочлен на одночлен, двучлен на двучлен, трехчлен на трехчлен:
- Правило умножения двучленов:
(a + b) * (c + d) = ac + ad + bc + bd.
- Правило умножения двучлена на трехчлен:
(a + b + c) * (x + y) = ax + bx + cx + ay + by + cy.
- Правило перемножения трехчленов:
(a + b + c)2 = a2 + b2 + c2 + 2ab + 2ac + 2bc.
Эти правила можно описать так: чтобы умножить один многочлен на другой, нужно каждый член первого умножить на каждый член второго многочлена. Затем полученные произведения сложить и привести результат к многочлену стандартного вида, если это возможно.
Практикующий детский психолог Екатерина Мурашова
Бесплатный курс для современных мам и пап от Екатерины Мурашовой. Запишитесь и участвуйте в розыгрыше 8 уроков
Правило умножения многочлена на многочлен
Рассмотрим пример, а после решения сформулируем правило умножения многочлена на многочлен:
- Возьмем два многочлена (a + b) и (c + d) и выполним их умножение.
- Сначала составим их произведение: (a + b)(c + d).
- Теперь обозначим (c + d) как x. После этой замены произведение примет вид: (a + b)x.
- Выполним умножение многочлена на одночлен: (a + b)x = ax + bx.
- Проведем обратную замену x на (c + d):
a(c + d) + b(c + d). Преобразуем: ac + ad + bc + bd. - Как изменилось произведение исходных многочленов:
(a + b)(c + d) = ac + ad + bc + bd.
Как раз так и выглядит формула умножения многочлена на многочлен.
Запоминаем!
Результат умножения многочлена на многочлен — всегда многочлен.
Правило умножения многочлена на многочлен Чтобы умножить многочлен на многочлен, надо каждый член первого многочлена умножить на каждый член второго многочлена и все полученные произведения сложить. |
Алгоритм умножения многочлена на многочлен:
- Первый член первого многочлена умножить на каждый член второго многочлена. Второй член первого многочлена умножить на каждый член второго многочлена.
И так далее.
- Сложить полученные произведения.
- Преобразовать полученную сумму в многочлен стандартного вида.
Второй член первого многочлена умножить на каждый член второго многочлена.
И так далее.Запоминаем!
Умножение трех, четырех и большего количества многочленов нужно свести к последовательному умножению двух многочленов. То есть, сначала умножаем первые два многочлена, затем результат умножаем на третий многочлен, и этот результат умножаем на четвертый многочлен и так далее.
Рассмотрим пример умножения многочлена на многочлен:
(6x – 2a) * (4 – 3x).
Как решаем:
- Умножим последовательно первый одночлен 6x из первой скобки на оба одночлена второй скобки.
- Уумножим второй одночлен −2a первой скобки на оба одночлена второй скобки.
Ответ: (6x – 2a) * (4 – 3x) = 24x – 18x2 – 8a + 6ax.
Рассмотрим пример умножения трех многочленов:
(x – 2) * (3x + 1) * (4x – 3).
Как решаем:
- Умножим первый многочлен на второй. Результат запишем в скобках.
- Перемножим получившийся многочлен и третий многочлен. Приведем подобные одночлены.
Ответ: (x – 2) * (3x + 1) * (4x – 3) = 12x3 – 29x2 + 7x + 6.
Теперь мы знаем все из темы умножения многочлена на многочлен. Осталось отточить на практике новый навык и ловить хорошие и отличные отметки на контрольных.
Курсы ОГЭ по математике от Skysmart придадут уверенности в себе и помогут освежить знания перед экзаменом.
Примеры умножения многочлена на многочлен
Рассмотрим еще несколько примеров, чтобы закрепить пройденный материал.
Пример 1. Выполнить умножение многочленов:
2 − 3x и x2 − 7x + 1.
Как решаем:
Запишем произведение: (2 − 3x)(x2 − 7x + 1).
Составим сумму произведений каждого члена многочлена (2 − 3x) на каждый член многочлена (x2 − 7x + 1). Для этого первый член первого многочлена «2» умножим на каждый член второго многочлена: 2x2
, 2(−7x) и 2*1.Теперь второй член первого многочлена «−3x» умножим на каждый член второго многочлена: −3xx2, −3x(−7x) и −3x*1.
Из полученных выражений составим сумму: 2x2 + 2(−7x) + 2*1 − 3xx2 − 3x(−7x) − 3x*1.
Чтобы убедиться, что мы все сделали правильно, посчитаем количество членов в полученной сумме. Их шесть. Так и должно быть, так как исходные многочлены состоят из 2 и 3 членов: 2 * 3 = 6.
Осталось полученную сумму преобразовать в многочлен стандартного вида:
2x2 + 2(−7x) + 2*1 − 3xx2 − 3x(−7x) − 3x*1 = 2x2 − 14 x + 2 − 3x3 + 21x2 − 3x = (2x2 + 21x2) + (−14x − 3x) + 2 − 3x3 = 23x2 − 17x + 2 − 3x3.
Получается, что (2 − 3x)(x2 − 7x + 1) = 23x2 − 17x + 2 − 3x3.
Ответ: (2 − 3x)(x2
Пример 2. Найти произведение трех многочленов:
x2 + xy − 1, x + y и 2y − 3.
Как решаем:
Запишем их произведение: (x2 + xy − 1)(x + y)(2y − 3).
Умножим первые два многочлена:
(x2 + xy − 1)(x + y) = x2x + x2y + xyx + xyy − 1x − 1y = x3 + 2x2y + xy2 − x − y.
Таким образом: (x2+ xy − 1)(x + y)(2y − 3) = (x3 + 2x2y + xy2 − x − y)(2y − 3).
Снова выполним умножение двух многочленов:
(x3 + 2x2y + xy2 − x − y)(2y − 3) = x32y + x3(−3) + 2x2y2y + 2x2y(−3) + xy22y + xy2(−3) − x2y − x(−3) − y2y − y(−3) = 2x3y − 3x3 + 4x2y2 − 6x2y + 2xy3 − 3xy 2 − 2xy + 3x − 2y2 + 3y.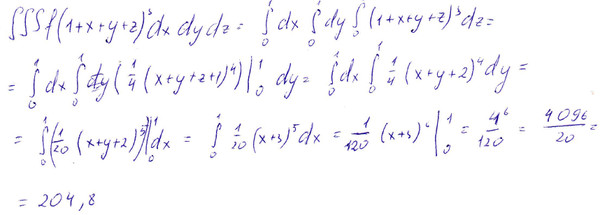
Ответ: (x2 + xy − 1)(x + y)(2y − 3) = 2x3y − 3x3 + 4x2y2 − 6x2y + 2xy3 − 3xy2 − 2xy + 3x − 2y2 + 3y.
Многочлен Стандартного Вида. Примеры.
Определение многочлена
Многочлен — это сумма одночленов. Получается, что многочлен — не что иное, как несколько одночленов, собранных «под одной крышей».
Одночлен — это произведение, состоящее из числового множителя и одной или нескольких переменных, каждая из которых взята в неотрицательной степени.
Рассмотрим примеры многочленов:
- 15x + 7x
- 4ab − b + 3
Если многочлен состоит из двух одночленов, его называют двучленом:
- 10x − 3x2
- 10x — одночлен
- −3x2 — одночлен
Многочлен — это сумма одночленов, поэтому знак «минус» относится к числовому коэффициенту одночлена. Именно поэтому мы записываем −3x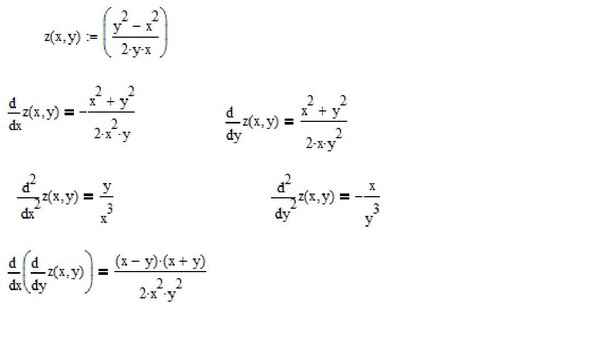
Этот же многочлен можно записать вот так:
- 10x – 3x2 = 10x − 3x2 = 10x + (−3x2).
Это значит, что каждый одночлен важно рассматривать вместе со знаком, который перед ним стоит.
Многочлен вида 10x − 3x2 + 7 называется трехчленом.
Линейный двучлен — это многочлен первой степени: ax + b. a и b здесь — некоторые числа, x — переменная.
Если разделить многочлен с переменной x на линейный двучлен x − b (где b — некоторое положительное или отрицательное число) — остаток будет только многочленом нулевой степени. То есть некоторым числом N, которое можно определить без поиска частного.
Если многочлен содержит обычное число — это число является свободным членом многочлена.
- Например, в многочлене 6a + 2b − x + 2 число 2 — свободный член.
Свободный член многочлена не имеет буквенной части. Кроме того, любое числовое выражение — это многочлен. Например, вот такие числовые выражения — тоже многочлены:
- 16 + 13
- (7 − 2) ∙ 9
- (25 + 25) : 5
Такие выражения состоят из свободных членов.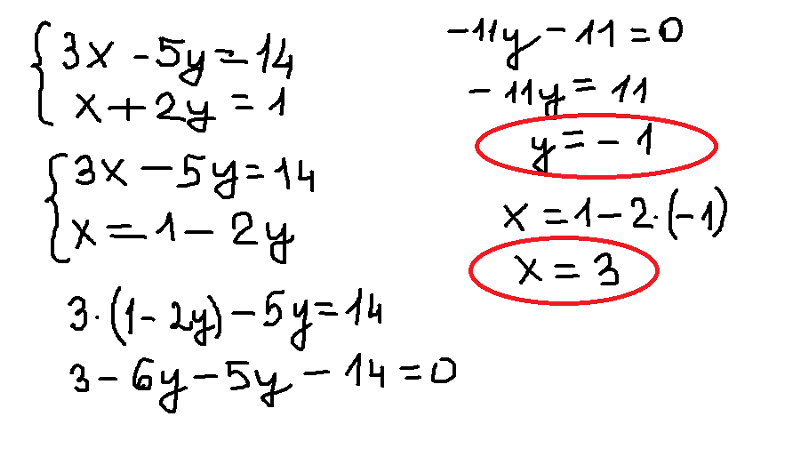
Практикующий детский психолог Екатерина Мурашова
Бесплатный курс для современных мам и пап от Екатерины Мурашовой. Запишитесь и участвуйте в розыгрыше 8 уроков
Коэффициенты многочлена
Коэффициенты членов многочлена — это числа, которые указаны перед переменными множителями. Если перед переменной нет числа, то коэффициент этого члена = 1.
Иными словами — коэффициенты членов многочлена — это члены многочлена, представленные в виде стандартных одночленов.
Например:
Дан многочлен 2x + 5x − 18y
Все одночлены имеют стандартный вид. 2, 5 и 18 — коэффициенты членов данного многочлена.
Многочлен стандартного вида
Недостаточно просто знать, что такое многочлен и что такое одночлен. Это целая алгебраическая экосистема, где у всего есть названия, определения и особенности.
Давайте разберемся, что такое многочлен стандартного вида. Многочленом стандартного вида называют многочлен, каждый член которого имеет одночлен стандартного вида и не содержит подобных членов.
Получается, что всякий многочлен можно привести к стандартному виду. Таким образом можно получить многочлен, работать с которым гораздо проще и приятнее.
К стандартному виду многочлен приводится очень просто. Нужно лишь привести в нем подобные слагаемые.
Подобные слагаемые — это подобные члены многочлена. Приведение подобных слагаемых в многочлене — приведение его подобных членов. Тут же возникает резонный вопрос: Что такое подобные члены многочлена? Это члены с одинаковой буквенной частью.
Давайте разберем на примере, как «нестандартный» многочлен приводится к стандартному виду.
Дан красавец многочлен: 3x + 5xy2 + x − xy2
Приведем подобные слагаемые. Для этого найдем все члены с одинаковыми буквенными составляющими:
- 3x и x — подобные слагаемые.
- 5xy2 и −xy2 — подобные слагаемые.
Получаем многочлен вот такого вида: 3x + 5xy2 + x − xy2 = 4x + 4xy2.
Как видите, в получившемся многочлене нет подобных членов. Такой многочлен — это многочлен стандартного вида.
Онлайн-подготовка к ОГЭ по математике — отличный способ снять стресс и закрепить знания перед экзаменом.
Учёба без слёз (бесплатный гайд для родителей)
Пошаговый гайд от Екатерины Мурашовой о том, как перестать делать уроки за ребёнка и выстроить здоровые отношения с учёбой.
Степень многочлена
Многочлен может иметь степень — имеет на это полное право.
Степень многочлена стандартного вида — это наибольшая из степеней, входящих в него одночленов.
Из определения можно сделать вывод, что степень многочлена возможно определить только после приведения его к стандартному виду.
- Приводим многочлен к стандартному виду.
- Выбираем одночлен с наибольшей степенью.
Рассмотрим на примере:
Дан многочлен 6x + 4xy2 + x + xy2
Сначала приводим многочлен к стандартному виду — для этого приводим подобные слагаемые:
- 6x и x — подобные слагаемые
- 4xy2 и xy2 — подобные слагаемые
Получаем многочлен стандартного вида 6x + 4xy2 + x + xy2 = 7x + 5xy2.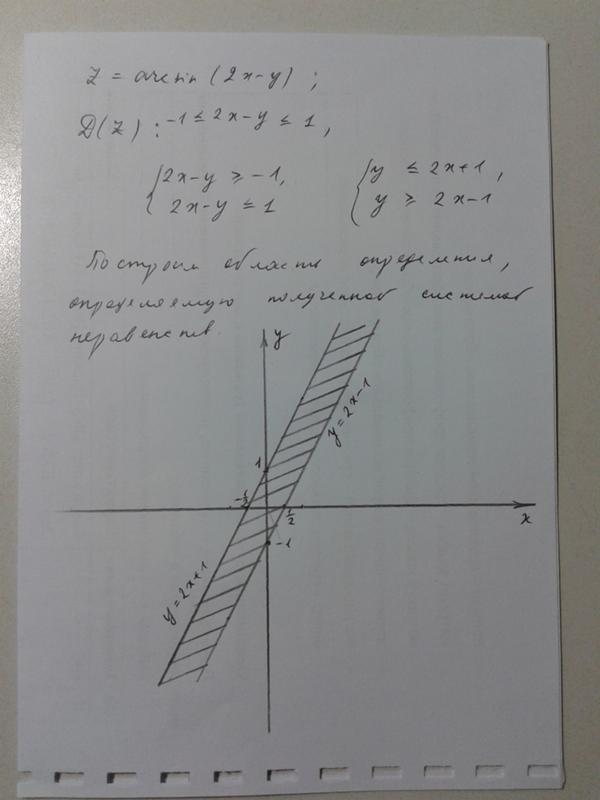
- Степень первого одночлена (7x) — 1.
- Степень второго одночлена (5xy2) — 3.
- Наибольшая из двух степеней — 3.
Отсюда делаем вывод, что многочлен 7x + 5xy2 — многочлен третьей степени.
Кроме того, можно сделать вывод, что и исходный многочлен 6x + 4xy2 + x + xy2 — многочлен третьей степени, поскольку оба многочлена равны друг другу.
В некоторых случаях необходимо сначала привести к стандартному виду одночлены многочлена, а затем уже и сам многочлен.
Пример:
Дан многочлен 6xx2 + 5xx2 − 3xx3 − 3x2x
Приведем его к стандартному виду: 6xx3 + 5xx2 − 3xx3 − 3x2x = 6x4 + 5x3 − 3x4 − 3x3
Получившийся многочлен без труда приводим к стандартному виду. Приводим подобные слагаемые:
- 5x3 и −3x3 — подобные слагаемые.
- 6x4 и −3x4 — подобные слагаемые.
- 6x4 + 3x3 − 3x4 − 3x3 = 3x4 − 2x3
- 6xx3 + 5xx2 − 3xx3 − 3x2x — многочлен четвертой степени.
Практика
Кажется, со стандартным видом многочлена все понятно. Чтобы без труда приводить любой многочлен к стандартному виду, нужно потренироваться, ведь в 7 классе только и разговоров, что о многочленах. Давайте разберем несколько примеров. Попробуйте решить их самостоятельно, сверяясь с ответами.
Задание раз. Приведите многочлен к стандартному виду и определите его степень: 4x + 6xy2 + x − xy2.
Как решаем: приведем подобные слагаемые. Для этого найдем все члены с одинаковыми буквенными составляющими:
- 4x и x — подобные слагаемые.
- 6xy2 и −xy2 — подобные слагаемые.
Получаем многочлен стандартного вида: 4x + 6xy2 + x − xy2 = 5x + 5xy2.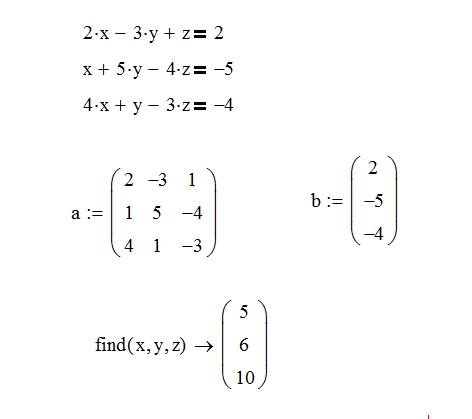
Ответ: стандартный вид многочлена 5x + 5xy2. Данный многочлен — многочлен второй степени.
Задание два. Приведите многочлен к стандартному виду: 2x2y3 − xy3 − x4 − x2y3 + xy3 + 2x4.
Как решаем: сначала необходимо привести все одночлены к стандартному виду: 2x2y3 − xy3 − x4 − x2y3 + xy3 + 2x4 = (−x4 + 2x4) + (2x2y3 − x2y3) + (− xy3 + xy3) = x4 + x2y3 + 0 = x4 + x2y3.
Многочлен приведен к стандартному виду.
Ответ: x4 + x2y3
Задание три. Приведите многочлен к стандартному виду и определите его степень: 8x + 8xy2 − x + xy2.
Как решаем: приведем подобные слагаемые.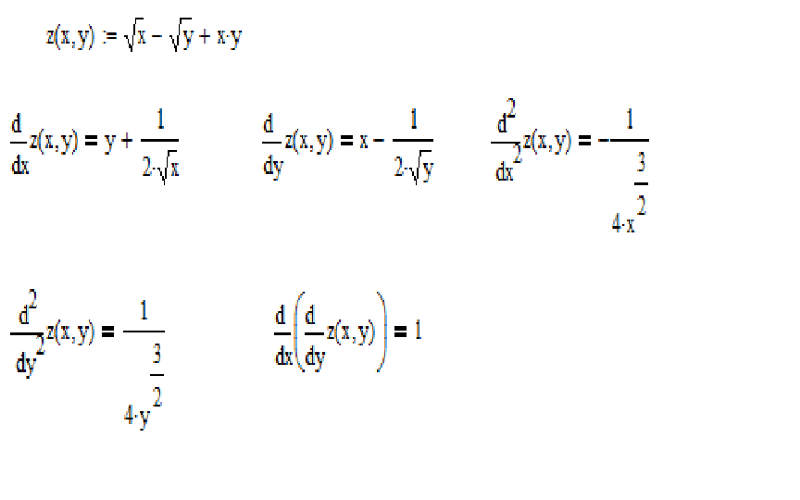
Для этого найдем все члены с одинаковыми буквенными составляющими:
- 8x и −x — подобные слагаемые.
- 8xy2 и xy2 — подобные слагаемые.
Получаем многочлен стандартного вида: 8x + 8xy2 − x + xy2 = 7x + 9xy2.
Ответ: стандартный вид многочлена 7x + 9xy2, данный многочлен — многочлен третьей степени.
Разобраться в многочленах не так-то просто. В этой теме немало нюансов и подводных камней. Чтобы не запутаться в множестве похожих одно на другое определений, побольше практикуйтесь. Чтобы перейти на следующую ступень и начать выполнение арифметических действий с многочленами, важно научиться приводить многочлен к стандартному виду.
| 1 | Найдите количество возможностей | 7 выбрать 3 | |
| 2 | Найдите количество возможностей | 8 выбрать 3 | |
| 3 | Найдите количество возможностей | 5 выбрать 2 | |
| 4 | Найдите количество возможностей | 4 выбрать 2 | |
| 5 | Найдите количество возможностей | 8 выбрать 4 | |
| 6 | Найдите количество возможностей | 10 выбрать 3 | |
| 7 | Найдите количество возможностей | 7 выбрать 4 | |
| 8 | Найдите количество возможностей | 6 выбрать 3 | |
| 9 | Найдите количество возможностей | 9 выбрать 3 | |
| 10 | Найдите количество возможностей | 3 выбрать 2 | |
| 11 | Найдите количество возможностей | 6 выбрать 4 | |
| 12 | Найдите количество возможностей | 5 выбрать 4 | |
| 13 | Найдите количество возможностей | 7 переставить 3 | |
| 14 | Найдите количество возможностей | 7 выбрать 2 | |
| 15 | Найдите количество возможностей | 10 выбрать 5 | |
| 16 | Найдите количество возможностей | 10 выбрать 6 | |
| 17 | Найдите количество возможностей | 13 выбрать 5 | |
| 18 | Найдите количество возможностей | 3 выбрать 3 | |
| 19 | Найдите количество возможностей | 4 выбрать 1 | |
| 20 | Найдите количество возможностей | 4 выбрать 4 | |
| 21 | Найдите количество возможностей | 5 выбрать 1 | |
| 22 | Найдите количество возможностей | 6 переставить 3 | |
| 23 | Найдите количество возможностей | 8 выбрать 5 | |
| 24 | Найдите количество возможностей | 9переставить 4 | |
| 25 | Найдите количество возможностей | 13 выбрать 3 | |
| 26 | Найдите количество возможностей | 12 выбрать 2 | |
| 27 | Найдите количество возможностей | 12 выбрать 4 | |
| 28 | Найдите количество возможностей | 12 выбрать 3 | |
| 29 | Найдите количество возможностей | 9 выбрать 5 | |
| 30 | Найдите количество возможностей | 9 выбрать 2 | |
| 31 | Найдите количество возможностей | 7 выбрать 5 | |
| 32 | Найдите количество возможностей | 6 переставить 6 | |
| 33 | Найдите количество возможностей | 8 переставить 5 | |
| 34 | Найдите количество возможностей | 8 переставить 3 | |
| 35 | Найдите количество возможностей | 7 переставить 5 | |
| 36 | Найдите количество возможностей | 52 выбрать 5 | |
| 37 | Найдите количество возможностей | 5 переставить 3 | |
| 38 | Найдите количество возможностей | 12 выбрать 5 | |
| 39 | Найдите количество возможностей | 3 выбрать 1 | |
| 40 | Найдите количество возможностей | 11 выбрать 5 | |
| 41 | Найдите количество возможностей | 10 выбрать 2 | |
| 42 | Найдите количество возможностей | 15 выбрать 3 | |
| 43 | Найдите количество возможностей | 52 выбрать 4 | |
| 44 | Найдите количество возможностей | 9 выбрать 4 | |
| 45 | Найдите количество возможностей | 9 переставить 3 | |
| 46 | Найдите количество возможностей | 7 переставить 4 | |
| 47 | Найдите количество возможностей | 7 переставить 2 | |
| 48 | Найдите количество возможностей | 11 выбрать 4 | |
| 49 | Найдите количество возможностей | 11 выбрать 2 | |
| 50 | Найдите количество возможностей | 11 выбрать 3 | |
| 51 | Найдите количество возможностей | 10 переставить 5 | |
| 52 | Найдите количество возможностей | 5 выбрать 5 | |
| 53 | Найдите количество возможностей | 6 выбрать 1 | |
| 54 | Найдите количество возможностей | 8 переставить 4 | |
| 55 | Найдите количество возможностей | 8 выбрать 6 | |
| 56 | Найдите количество возможностей | 13 выбрать 4 | |
| 57 | Оценить | и | |
| 58 | Найти любое уравнение, перпендикулярное прямой | -7x-5y=7 | |
| 59 | Найдите количество возможностей | 13 выбрать 2 | |
| 60 | Найдите количество возможностей | 10 переставить 2 | |
| 61 | Найдите количество возможностей | 10 переставить 3 | |
| 62 | Найдите количество возможностей | 10 выбрать 7 | |
| 63 | Найдите количество возможностей | 20 выбрать 4 | |
| 64 | Найдите количество возможностей | 6 переставить 4 | |
| 65 | Найдите количество возможностей | 5 переставить 4 | |
| 66 | Найдите количество возможностей | 6 выбрать 5 | |
| 67 | Найдите количество возможностей | 52 выбрать 3 | |
| 68 | Найдите количество возможностей | 4 выбрать 0 | |
| 69 | Найдите количество возможностей | 9переставить 7 | |
| 70 | Найдите количество возможностей | 6 выбрать 2 | |
| 71 | Найдите количество возможностей | 5 переставить 5 | |
| 72 | Найдите количество возможностей | 5 переставить 2 | |
| 73 | Найдите количество возможностей | 6 выбрать 6 | |
| 74 | Найдите количество возможностей | 7 выбрать 6 | |
| 75 | Найдите количество возможностей | 8 переставить 6 | |
| 76 | Найдите количество возможностей | 7 переставить 7 | |
| 77 | Найдите количество возможностей | 9 переставить 5 | |
| 78 | Найдите количество возможностей | 2 переставить 2 | |
| 79 | Найдите количество возможностей | 10 выбрать 8 | |
| 80 | Найдите количество возможностей | 12 выбрать 7 | |
| 81 | Найдите количество возможностей | 15 выбрать 5 | |
| 82 | Найдите обратное | [[1,0,1],[2,-2,-1],[3,0,0]] | |
| 83 | Найти диапазон | 1/4x-7 | |
| 84 | Найдите количество возможностей | 10 переставить 7 | |
| 85 | Найдите количество возможностей | 12 выбрать 6 | |
| 86 | Найдите количество возможностей | 2 выбрать 1 | |
| 87 | Найдите количество возможностей | 30 выбрать 3 | |
| 88 | Найдите количество возможностей | 9 выбрать 6 | |
| 89 | Найдите количество возможностей | 8 переставить 2 | |
| 90 | Найдите количество возможностей | 7 выбрать 1 | |
| 91 | Найдите количество возможностей | 6 перестановка 2 | |
| 92 | Найдите количество возможностей | 4 переставить 2 | |
| 93 | Найдите количество возможностей | 4 переставить 3 | |
| 94 | Найдите количество возможностей | 3 переставить 3 | |
| 95 | Найдите количество возможностей | 46 выбрать 6 | |
| 96 | Найдите количество возможностей | 5 переставить 1 | |
| 97 | Найдите количество возможностей | 52 выбрать 7 | |
| 98 | Найдите количество возможностей | 52 переставить 5 | |
| 99 | Найдите количество возможностей | 9выбрать 1 | |
| 100 | Найдите количество возможностей | 9 переставить 6 |
Q8 Вычесть x 2y z из суммы 3x y z и x y 3z.
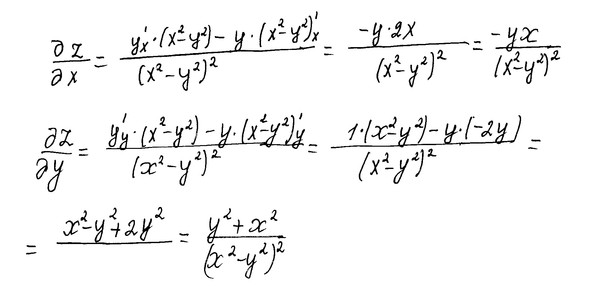..Перейти к
- Упражнение 19 (А)
- Упражнение 19(Б)
- Упражнение 19(С)
- Упражнение 19(Г)
- Система счисления (закрепление чувства числа)
- Предварительный расчет
- Числа в Индии и международной системе (со сравнением)
- Место Значение
- Натуральные числа и целые числа (включая шаблоны)
- Отрицательные числа и целые числа
- Номер строки
- HCF и LCM
- Игра с числами
- Наборы
- Соотношение
- Доля (включая словесные задачи)
- Унитарный метод
- Фракции
- Десятичные дроби
- Процент (Процент)
- Представление о скорости, расстоянии и времени
- Основные понятия (алгебра)
- Основные операции (связанные с алгебраическими выражениями)
- Замена (включая использование скобок в качестве группирующих символов)
- Обрамление алгебраических выражений (включая вычисление)
- Простые (линейные) уравнения (включая текстовые задачи)
- Основные понятия (геометрия)
- Углы (с их типами)
- Свойства углов и линий (включая параллельные линии)
- Треугольники (включая типы, свойства и конструкцию)
- четырехугольник
- Полигоны
- Круг
- Повторное упражнение по симметрии (включая построения по симметрии)
- Распознавание твердых тел
- Периметр и площадь плоских фигур
- Обработка данных (включая пиктограмму и гистограмму)
- Среднее и медиана
Главная >
Селина Солюшнс
Класс 6
Математика
>
Глава 19.
Основные операции (связанные с алгебраическими выражениями)
>
Упражнение 19(Б)
>
Вопрос 16
Вопрос 16 Упражнение 19(B)
В8) Вычтите x – 2y – z из суммы 3x – y + z и x + y – 3z.
Ответ:
Алгебраическое выражение, состоящее из трех членов и арифметических знаков (+ или -), называется трехчленом. Сложите два выражения вместе, затем вычтите последнее, поставив знак минус перед скобкой. Снимите скобки, изменив знаки каждого вычитаемого члена, хотя знаки добавляемых выражений останутся прежними. Теперь сложите все подобные члены вместе и выполните расчет.
Решение 8:
(3x — y + z) + (x + y — 3z) — (x — 2y — z)
= 3x — y + z + x + y — 3z — x + 2y + z
= 3x + x — x — y + y + 2y + z + z — 3z
= 3x + 2y — z
Поэтому , когда x – 2y – z вычитается из суммы 3x – y + z и x + y – 3z, мы получаем 3x + 2y – z.
Похожие вопросы
Q1) Найдите сумму: (i) 3a+4b+7c, -5a+3b-6c и 4a-2b-4c(ii) (iii) (iv) (v) (vi)
Q1) Найдите сумму: (i) 3a+4b+7c, -5a+3b-6c и 4a-2b-4c(ii) (iii) (iv) (v) (vi)
Q2) Добавьте следующие выражения: (i) (ii) (iii)
Q2) Добавьте следующие выражения: (i) (ii) (iii)
Q3) Оценить: (i) 3a-(a+2b)(ii) (5x-3y) — (x+y)(iii) (8a+15b) — (3b-7a)(iv) (8x+7y) — (4у-3х)(т) 7-.
..
Q3) Оценить: (i) 3a-(a+2b)(ii) (5x-3y) — (x+y)(iii) (8a+15b) — (3b-7a)(iv) (8x+7y) — (4у-3х)(т) 7-…
Фейсбук WhatsApp
Копировать ссылку
Было ли это полезно?
Упражнения
Упражнение 19(A)
Упражнение 19(B)
Упражнение 19(C)
Упражнение 19(D)
Главы
Система счисления (Закрепление чувства числа)
Оценка
Числа в Индии и международной системе (с сравнением)
Значение места
Натуральные числа и целые числа (включая паттерны)
Отрицательные числа и целые числа
НОМЕР ЛИНИЯ
HCF
НОМЕР ЛИНИЯ
HCF
.
Множества
Соотношение
Доля (включая текстовые задачи)
Унитарный метод
Дроби
Десятичные дроби
Проценты (проценты)
Представление о скорости, расстоянии и времени
Основные понятия (алгебра)
Основные операции (относящиеся к алгебраическим выражениям)
Подстановка (включая использование скобок в качестве группирующих символов)
Обрамление алгебраических выражений (включая простые 909 вычисления) 7 (Линейные) уравнения (включая текстовые задачи)
Основные понятия (геометрия)
Углы (с их типами)
Свойства углов и прямых (включая параллельные прямые)
Triangles (Including Types, Properties and Construction)
Quadrilateral
Polygons
The Circle
Revision Exercise on Symmetry (Including Constructions on Symmetry)
Recognition of Solids
Perimeter and Area of Plane Figures
Data Handling (включая пиктограмму и гистограмму)
Среднее и медиана
Курсы
Быстрые ссылки
Условия и политика
Условия и политика
2022 © Quality Tutorials Pvt Ltd.
Все права защищены.
К сожалению, в прошлом году рекламный блок начал отключать загрузку почти всех изображений на нашем сайте, что привело к тому, что mathwarehouse стало непригодным для использования пользователями adlbock.
Все вместе на 1 странице!
Чтобы узнать больше о любом из перечисленных ниже свойств, посетите отдельную страницу этого свойства.
Распределительное свойство
Ассоциативное свойство
Коммутативное свойство
Свойства и Операции Давайте посмотрим, как (и если) эти свойства работают со сложением, умножением, вычитанием и делением.
Дополнение
| Имущество | Пример с дополнением | |
|---|---|---|
| Распределительное свойство | ||
| Ассоциативный | ||
| Коммутативный | ||
Сводка: Все 3 из этих свойств применимы к сложению. | ||
Умножение
| Имущество | Пример с умножением | |
|---|---|---|
| Распределительное свойство | Распределительное свойство — это применение умножения (поэтому здесь нечего показывать). | |
| Ассоциативный | ||
| Коммутативный | ||
Сводка: Все 3 из этих свойств применимы к умножению. | ||
Вычитание
| Имущество | Пример с вычитанием | |
|---|---|---|
| Распределительное свойство | ||
| Ассоциативный | ||
| Коммутативный | ||
Summary: Распределительное свойство — единственное, которое применимо к вычитанию. | ||
Подразделение
| Имущество | Пример с вычитанием | |
|---|---|---|
| Распределительное свойство | ||
| Ассоциативный | ||
| Коммутативный | ||
Резюме: Ни одно из этих свойств не относится к делению. | ||
Какие из следующих утверждений иллюстрируют распределительное, ассоциированное и коммутативное свойство?
Направления: Нажмите на каждую кнопку ответа, чтобы увидеть, какое свойство соответствует утверждению слева .
| Заявление | Собственность |
|---|---|
| 7 + 2 = 2 + 7 | Коммутативное свойство |
| 6 + (2 + 11) = (6 + 2) + 11 | Ассоциативное свойство |
| 5 (2 + 4) = 5 • 2 + 5 • 4 | Распределительное свойство |
| (12 • 44) • 13 • 5 = 12 • 44 • (13 • 5) | Ассоциативное свойство |
| 5 • 3 • 11 = 11 • 5 • 3 | Коммутативное свойство |
| 6 (3 + 11 + 4) = 6 • 3 + 6 • 11 + 6 • 4 | Распределительное свойство |
Все три из этих свойств также могут быть применены к алгебраическим выражениям.
Какие из следующих утверждений иллюстрируют распределительное, ассоциированное и коммутативное свойство?
Направления: Нажмите на каждую кнопку ответа, чтобы увидеть, какое свойство соответствует утверждению слева .
| Заявление | Собственность |
|---|---|
| а + с = с + а | Коммутативное свойство |
| а (х + у + г) = а • х + а • у + а • г | Распределительное свойство |
| (а • у) • х • г = а • у • (х • г) | Ассоциативное свойство |
Распределительное свойство
Ассоциативное свойство
Коммутативное свойство
Решения NCERT для математики класса 7 Глава 7
NCERT Solutions for Class 7 Math Chapter 7 Algebraic Expressions представлены здесь с простыми пошаговыми объяснениями.
Эти решения для алгебраических выражений чрезвычайно популярны среди учащихся 7 класса по математике. Решения для алгебраических выражений пригодятся для быстрого выполнения домашних заданий и подготовки к экзаменам. Все вопросы и ответы из Книги NCERT по математике для 7-го класса, глава 7, предоставляются здесь для вас бесплатно. Вам также понравится возможность без рекламы в решениях NCERT от Meritnation. Все решения NCERT для математики класса 7 подготовлены экспертами и на 100% точны.
Страница № 7.13:
Вопрос 1:
Добавить следующее:
(I) 3 x и 7 x
(II) −5 xy и 16 1771771771771771771771771771771771771717717717177171771717717171717177171717177171771717171717109R7. У нас есть
(i) 3x + 7x = (3 + 7)x = 10x
(ii) -5xy + 9xy = (-5 + 9)xy = 4xy
Страница № 7.13:
Вопрос 2:
Упрощение каждый из следующих:
(i) 7 x 3 y + 9 yx 3
(ii) 12 A 2 B + 3 BA 2
Ответ:
Упрощение данных выражений, мы имеем
(I) 7x 3 666.
x 3 Y = 16x 3 Y
(II) 12A 2 B + 3BA 2 = (12 + 3) A 2 B = 15A 2 B 9107 44444444444444444444444444 4.114444444444444444444444444 4. Вопрос 3:
Добавьте следующее:
(i) 7 abc , −5 abc , 9 abc , −8 abc
(ii) 2 x 2 y , − 4 x 2 y , 6 x 2 y , −5 x 2 y
Ответ:
Складывая данные члены, мы имеем
(i) 7abc + (- 5abc) + (9 abc) + (- 8abc)
= 7abc — 5abc + 9abc 9abc — 4 80 (7 — 5 + 9 — 8)abc
= (16 — 13)abc
= 3abc
(ii) 2x 2 y + (- 4x 2 y) + 6x 2 Y + ( — 5x 2 Y)
= 2x 2 Y — 4x 2 Y + 6x 2 Y — 5x 2 6660 = 2-1 Y — 5x 2 6666 = .
4 + 6 — 5) x 2 Y
= (8 — 9) x 2 Y
= -x 2 Y
Страница № 7.14:
Вопрос 4:
Добавить следующие выражения: 9145
. (i) x3-2x2y+3xy2-y3, 2×3-5xy2+3x2y-4y3
(ii) a4-2a3b+3ab3+4a2b2+3b4,-2a4-5ab3+7a3b-6a2b2+b4
Ответ:
Сложение заданные выражения, мы имеем
(i) x 3 — 2x 2 Y + 3XY 2 — Y 3 + 2x 3 — 5xy 2 + 3x 2 Y — 3x . like terms together, we get
x 3 + 2x 3 — 2x 2 y + 3x 2 y + 3xy 2 — 5xy 2 — y 3 — 4y 3
= 3x 3 + x 2 y — 2xy 2 — 5y 3
(II) (A 4 — 2A 3 B + 3AB 3 + 4A 2 B 2 + 3B 4 ) + (-2A 4 4 4 ) + (-2A 4 4 4 ) + (-2A 4 4 4 ).
3 b — 6a 2 b 2 + b 4 )
a 4 — 2a 3 b + 3ab 3 + 4a 2 b 2 + 3b 4 — 2a 4 — 5ab 3 + 7a 3 b — 6a 2 b 2 + b 4
Собирая положительные и отрицательные 9 подобных членов вместе, мы получаем1440 a 4 — 2a 4 — 2a 3 b + 7a 3 b + 3ab 3 — 5ab 3 + 4a 2 b 2 — 6a 2 b 2 + 3b 4 + b 4
= — a 4 + 5a 3 b — 2ab 3 — 2a 2 b 2 + 4b 4
Page No 7.14:
Вопрос 5:
Добавьте следующие выражения:
(i) 8a-6ab+5b, -6a-ab-8b и -4a+2ab+3b
(ii) 5×3+7+6x-5×2, 2×2-8-9x, 4x-2×2+3×3, 3×3-9x-x2 и x-x2-x3-4
Ответ:
(i) Требуемое выражение = ( 8a — 6ab + 5b) + (- 6a — ab — 8b) + ( — 4a + 2ab + 3b)
Собирая положительные и отрицательные подобные члены вместе, мы получаем
8a — 6a — 4a — 6ab — ab + 2ab + 5b — 8b + 3b
= 8a — 10a — 7ab + 2ab + 8b — 8b
= — 2a — 5ab
(ii) Требуемое выражение = (5x 3 + 7 + 6x — 5x 2 2) — 8 — 9х) + (4х — 2х 2 + 3х 3 ) + (3х 3 — 9х — х 2 ) + ( х — х 2 — х 3 — 4 0 4) 91 4 negative like terms together, we get
5x 3 + 3x 3 + 3x 3 — x 3 — 5x 2 + 2x 2 — 2x 2 — x 2 — x 2 + 6x — 9x + 4x — 9x + x + 7 — 8 — 4
= 11x 3 — x 3 — 7x 2 + 11x — 18x + 7 — 12
= 10x 3 — 7x 2 — 7x — 5
Страница № 7.
14:Вопрос 6:
Добавьте следующее:
(i) x-3y+94z-08x3x37y (ii) 4ab-5bc+7ca-3ab+2bc-3ca5ab-3bc+4ca
Ответ:
(i) Требуемое выражение = (x — 3y — 2z) + (5x +7y — 8z) +(3x — 2y + 5z)
Собирая положительные и отрицательные подобные члены вместе, мы получаем
x + 5x + 3x — 3y + 7y — 2y — 2z — 8z + 5z
= 9x — 5y + 7y — 10z + 5z
= 9x + 2y — 5z
(ii) Требуемое выражение = (4ab — 5bc + 7ca) + (- 3ab + 2bc — 3ca ) + (5ab — 3bc + 4ca)
Собирая положительные и отрицательные подобные члены вместе, мы получаем
4ab — 3ab + 5ab — 5BC + 2BC — 3BC + 7CA — 3CA + 4CA
= 9AB — 3AB — 8BC + 2BC + 11 CA — 3CA
= 6AB — 6BC + 8CA
Страница № 7.14:
Вопрос 7:
Добавить 2
6 x 7777777:. Добавить 2
6 x 77777777:. 2 − 3 x + 1 в сумме 3 x 2 − 2 x и 3 x + 7.
Ответ:
Сумма 3x 2 — 2x и 3x + 7
= (3x 2 — 2x) + (3x +7) 6 x 5 + 3 — 2926 x 5 2946 + 7
= (3x 2 + x + 7)
Теперь требуется выражение = (2x 2 — 3x + 1) + (3x 2 + x + 7)
= 2x 2 + 3X 5555555 2 — 3x + x + 1 + 7
= 5x 2 — 2x + 8
Страница № 7.
14:Вопрос 8:
Добавить x 2 + 2 xy + y 2 к сумме x 2 к сумме x 2 . 2 x 2 − y 2 + 9.
Answer:
Sum of x 2 — 3y 2 and 2x 2 — y 2 + 9
= (x 2 — 3 года 2 ) + (2x 2 — год 2 + 9)
= x 2 + 2x 2 — 3y 2 — y 2 + 9
= 3x 2 — 4y 2 + 9
Now, required expression = (x 2 + 2xy + y 2 ) + (3x 2 — 4y 2 + Добавить A 3 + B 3 — 3 к сумме 2 A Сначала нужно найти сумму 2a 3 — 3b 3 — 3ab + 7 и — a 3 + b 3 + 3ab — 9. — 2 . искомое выражение = (a 3 + b 3 — 3) + (a 3 — 2b 3 — 2). (II) Требуемое выражение = — 3 XY — 4xy Вычесть: (i) Требуемое выражение = (3y) -(-4x) (ii) Требуемое выражение = (-5y) -(-2x) Вычесть: (i) Требуемое выражение = (4 — 5x + 6x 2 — 8x 3 ) — (6x 3 — 7x 2 + 5x — 3) (III) Требуемое выражение = (Y 3 — 3xy 2 — 4x 2 Y) — (x 3 +666 +666 +666 + 2 Y) — (x 3 +666 + 2 Y) — (x 3 + 2 Y) — (x 3 + 2 Y) — (x 3 — 4x 2 Y) — (x 3 — 4x 2 Y) — (x 3 2x 2 у + 6xy 2 — у 3 ) From (I) Требуется выражение = (P 3 — 4 + 3P 2 ) -(5P — 4 + 3P 2 ) -(5P — 4 + 3P 2 ) -(5P — 4 + 3P 2 ) -(5P — 4 + 3P 2 ) -(5P 5 — 4 + 3P 2 5 3 — 4 + 3P 2 — 41465. (ii) Требуемое выражение = (7 + x — x 2 ) — (9 + x + 3x 2 + 7x 3 ) 6 (III) (III). 2 ) — (Y 3 + 7y 2 + Y + 1) (iv) Требуется экспрессия = (X 3 — 5x 6666 6 (iv). Required выражение = {(3x 2 — 5x + 2) + (- 5x 2 — 8x + 9)} — (4x 2 — 7x + 9) Вычтите сумму 13 x — 4 Y + 7 Z и -6 Z + 6 x + 3 Y от суммы 6 x – 41316 y от суммы 6 x – 41316 y от суммы 6 x – 41316 y от суммы 6 x — 41316 y . z и 2 x + 4 y − 7. Сумма (13x — 4y + 7z) и ( — 6z + 6x + 3y) Сумма (6x — 4y — 4z) и (2x + 4y − 7) Теперь требуемое выражение = {(8x — 4z — 7) — (19x — y + z)} С суммы x 2 . (x 2 9146 4146. 2x 2 — y 2 + 8xy), (y 2 + 8) и (x 2 — 3xy) Теперь требуемое выражение = (4x 1 — 6 х 9 4 + + 8) — (- 3x 2 + 4y 2 — xy + x — y + 3) Что следует добавить в xy — 3 16 yz 13131316 16 16 16. zx , чтобы получить 4 xy − 3 zx + 4 yz + 7? Искомое выражение можно получить, вычитая xy — 3yz + 4zx из 4xy — 3zx + 4yz + 7. Что нужно вычесть из x 2 − xy + y 2 − x + y + 3 to obtain − x 2 + 3 y 2 − 4 xy + 1? Пусть ‘M’ будет искомым выражением. Тогда имеем Сколько будет x − 2 y + 3 z больше 3 x + 5 y − 7? Требуемое выражение = (x — 2y + 3z) — (3x + 5y — 7) Требуемое выражение = (2x 2 — 3Y 2 + xy) — (x 2 — 2xy + 3y 2 ) Требуемое выражение = (a 2 — 3ab + 2b 2 ) — (2a 2 — 7ab + 9B 2 ) Что должно быть добавлено к 12 x 3 — 4 x 2 + 3 x — 7, чтобы сделать сумму x 3 + 2 x 3 + 2 x 3 + 2 x 3 + 2 x 3 + 2 . х + 2? Пусть ‘M’ будет искомым выражением. Если P = 7 x 2 + 5 xy − 9 y 2 , Q = 4 y 2 − 3 x 2 − 6 xy and R = −4 x 2 + XY + 5 Y 2 , показать, что P + Q + R = 0, Мы имеем 07. If P = a 2 − b 2 + 2 ab , Q = a 2 + 4 b 2 − 6 ab , R = b 2 + b , S = a 2 − 4 ab a nd T = −2 a 2 + б 2 − аб + а . Имеем Напишите каждое из следующих утверждений, используя соответствующие группирующие символы: (i) Сумма a − b и 3a − 2b + 5 = {(a − b) + (3a − 2b + 5)}. (ii) Умноженная на три суммы 2x + y − {5 − (x − 3y)} и 7x − 4y + 3 = 3[(2x + y) − {5 − (x − 3y)} + (7x − 4у + 3)]. (iii) Произведение вычитания x 2 − y 2 + 4xy из 2x 2 + y 2 − 3xy равно — (x 2 — y 2 + 4xy)}. Имеем Упростите каждое из следующих алгебраических выражений, удалив символы группировки. У нас есть Упростите каждое из следующих алгебраических выражений, удалив символы группировки. Имеем Упростите каждое из следующих алгебраических выражений, удалив символы группировки. We имеем Упростите каждое выражение из следующих алгебраических символов, сгруппировав их. У нас есть следующие алгебраические выражения, удалив символы группировки. У нас есть Упростите каждое из следующих алгебраических выражений, удалив символы группировки. Сначала мы должны удалить круглые скобки ( ), затем фигурные скобки, { }, а затем квадратные скобки [ ]. Упростите каждое из следующих алгебраических выражений, удалив символы группировки. Сначала мы должны удалить маленькие скобки ( ) или скобки , затем фигурные скобки { }, а затем квадратные скобки [ ]. Упростите каждое из следующих алгебраических выражений, удалив группировку символы. Сначала мы должны удалить скобки, ( или ), затем фигурные скобки { }, а затем квадратные скобки [ ]. следующие алгебраические выражения, удаляя символы группировки. Сначала мы должны убрать скобки, ( или ), затем фигурные скобки { }, а затем квадратные скобки [ ]. Упростите каждое из следующих алгебраические выражения путем удаления символов группировки. Сначала мы должны удалить маленькие скобки или круглые скобки ( ), затем фигурные скобки { }, а затем квадратные скобки [ ]. Упростите каждое из следующих алгебраических выражений, удалив символы группировки. First мы должны удалить маленькие скобки или круглые скобки ( ), затем фигурные скобки { }, а затем квадратные скобки [ ]. Упростите каждое из следующих алгебраические выражения путем удаления символов группировки. Сначала мы должны удалить маленькие скобки или круглые скобки ( ), затем фигурные скобки { }, а затем квадратные скобки [ ]. Упростите каждое из следующих алгебраических выражений, удалив символы группировки. Сначала мы должны удалить маленькие скобки или круглые скобки ( ), затем фигурные скобки { }, а затем квадратные скобки [ ] . Упростите каждое из следующих алгебраических выражений, удалив символы группировки. Упростите каждое из следующих алгебраических выражений, удалив символы группировки. скобки или круглые скобки ( ), затем фигурные скобки { }, а затем квадратные скобки [ ]. Упростите каждое из следующих алгебраических выражений, удалив символы группировки. Определите одночлены, двучлены, трехчлены и четырехчлены из следующих выражений: Напишите все члены каждого из следующих алгебраических выражений: Укажите подобные члены, а также укажите числовые коэффициенты этих членов: Like terms Численные коэффициенты Определите одинаковые члены в следующих алгебраических выражениях: Подобные члены в данных алгебраических выражениях таковы. (ii) В данном алгебраическом выражении одинаковыми членами являются -2yz и 52zy. Запишите коэффициент x следующим образом: Коэффициенты при x следующие. Write the coefficient of x 2 in the following: Коэффициенты x 2 следующие. (iii) Численный коэффициент x 2 равен 57z. Напишите коэффициент: Коэффициенты следующие. (i) Коэффициент y равен -3. Числовой коэффициент каждого из приведенных слагаемых выглядит следующим образом. Запишите числовой коэффициент каждого члена в следующих алгебраических выражениях: Числовой коэффициент каждого члена в данных алгебраических выражениях выглядит следующим образом. (I) 4x 2 Y 4 (II) -53x2y -53 (II) -53x2y -53 (II) -53X2Y -53 .1440 3 3 Write the constant term of each of the following algebraic expressions: Оцените каждое из следующих выражений для x = − 2, y = −1, z = 3: Имеем x = −2, y = −1 и z = 3 . (ii) x 2 + y 2 + z 2 — xy — yz — zx Оцените каждое из следующих алгебраических выражений для x = 1, y = 7 , Имеем x = 1, y = −1, z = 2, a = −2, b = 1 и c = −2. (ii) ax 2 + by 2 — cz 2 Касательные плоскости Пусть z = f(x,y) — функция двух переменных. F(x,y,z) = 0 х = х(т),
y = y(t) z = z(t) F(x(t), y(t), z(t)) =
0 F x (x, y, z) x’ + F y (x,
у, з) у’
+ F z (x, y, z) z’ = 0 ГрадФ . Град F(x 0 ,y 0 ,z 0 ) Пример z = 3x 2 — xy Решение Допустим F(x,y,z) = 3 x 2 — ху — я Град F = <6x - y,
-х, -1> Град F(1,2,1) = <4, -1, -1> . <4, -1, -1> . 4(х — 1) — (у — 2) — (г — 1) =
0 4x – y – z = 1 Нормальные линии Даны вектор и точка, существует единственная линия, параллельная этой
вектор, проходящий через точку. Определение GradF(x 0 , y 0 , z 0 ) х(т)
= x 0 + F x (x 0 , y 0 , z 0 )
t y(t) = y 0 + F y (x 0 , г 0 , г 0 )
t z(t) = z 0 + F z (x 0 ,y 0 ,z 0 )
т Найдите параметрические уравнения для нормальной прямой к х 2 уз — у
+ г — 7 = 0 Раствор Вычисляем градиент Град F = <2xyz, x 2 z —
1, x 2 y + 1> = <12, 2, 3> х(т) = 1 + 12т
y(t) = 2 + 2t z(t) = 3 + 3t Диаграмма
ниже отображается поверхность и нормальная линия. Угол наклона Дана плоскость с вектором нормали n угол наклона , q определяется F(x,y,z)
= 0 — это поверхность, чем угол
наклон в точке (x 0 , y 0 ,
я 0 )
определяется углом наклона касательной плоскости в точке. Найдите угол наклона x 2 у 2 я 2 в точке (1,1,2). Решение Первое вычисление Град F = Град F(1,1,2) = <1/2,
1/2, 1/2> |<1/2, 1/2, 1/2> . к | = 1/2 ||<1/2, 1/2, 1/2>|| знак равно
/ 2 cosq =
(1/2)/[()/2] =
1/ д =
arccos(1/) @
0,955 радиан Касательная линия к кривой х 2 + у 2 +
я 2 = 30 г = х 2 + у 2 Находим Grad двух поверхностей в точке Град (х 2 + у 2 + z 2 ) = <2x, 2y, 2z> = <2, 4,10> Град (х 2 + у 2 — z) = <2x, 2y, -1> = <2, 4, -1> Отсюда уравнение касательной х(т) = 1 —
44т
y(t) = 2 + 22t z(t) = 5 Назад к функциям нескольких
Страница переменных Назад
на домашнюю страницу Math 107 Назад на домашнюю страницу математического факультета электронная почта
Вопросы и предложения Базовые векторы в двумерных декартовых координатах — это единичный вектор i в положительном направлении. Вектор положения точки P ( x , y ) в двух измерениях равен x i + y j.
Мы будем часто обозначать этот важный вектор через r (см. рисунок внизу справа). В трех измерениях вектор положения равен r = x i + y j + z k. Векторный дифференциальный оператор ∇, называемый «дель» или «набла», определяется в трех измерениях как: — обратите внимание, что это частных производных ! Этот векторный оператор может быть применен к (дифференцируемым) скалярным функциям (скалярным полям), и результат является частным случаем векторного поля,
называется градиентным векторным полем. Вот два разминочных упражнения на частичное дифференцирование: Тест 1: Выберите следующую частную производную: ∂ / ∂z ( xyz x ): (a) x 2 yz x −1 Правильно — молодец! (b) 0 Неверно — попробуйте еще раз! (c) xy log x ( z ) Неверно – попробуйте еще раз! (d) yz x −1 Неверно — попробуйте еще раз! Решение: Частная производная от xyz x по переменной z равна: ∂ / ∂z ( xyz x )
= xy × ∂ / ∂z ( z x )
= xy × x × z x −1 = x 2 YZ 9475 2 YZ 9475 2 YZ 9475 2 . (a)cos ( y ) Правильно — молодец! (b)cos ( y ) − x sin ( y ) + 1 Неверно – попробуйте еще раз! (c) cos ( y ) + x sin ( y ) + 1 Неверно – попробуйте еще раз! (d)−sin ( y ) Решение: Рассмотрим функцию ƒ ( x , y ) = x cos ( y ) + y . Его производная по переменной x равна: Градиент функции ƒ ( x , y ) в двух измерениях определяется как: Градиент функции представляет собой поле вектора . Пример 1: Градиент функции ƒ ( x , y ) = x + y 2 определяется как: Викторина 3: Выберите градиент ƒ ( x , y ) = x 2 y 3 : (a) 2 x i + 3 y 2 j Неверно — попробуйте еще раз! (b) x 2 i + y 3 j Неверно — попробуйте еще раз! (в) 2 xy 3 i + 3 x 2 y 2 j Правильно — молодец! (г) у 3 я + х 2 у Решение: Градиент функции ƒ ( x , y ) = x 2 y 3 определяется выражением Определение градиента может быть расширено до функций, определенных в трех измерениях ƒ ( x , y , z ): Упражнение 1: Вычислите градиент следующих функций: (a) ƒ ( x , y ) = x + 3 y 2 Решение: Функция ƒ ( x , y ) = x + 3 y 2 имеет градиент: (б) ƒ ( х , у )
= √ x 2 + у 2 Решение: Градиент функции ƒ ( x , y )
= √ х 2 + y 2 = ( x 2 + y 2 ) ½ определяется как: (в) ƒ ( х , у , г )
= 3 x 2 √ y + cos (3 z ) Решение: Градиент функции ƒ ( x , y , z )
= 3 x 2 √ y + cos (3 z )
= 3 x 2 y ½ + cos (3 z ) определяется по формуле: (d) ƒ ( x , y , z )
=1/ √ x 2 + у 2 + у 2 Решение: Частная производная функции ƒ ( x , y , z )
= 1/ √ x 2 + y 2 + z 2 = ( x 2 + y 2 + z 2 ) ½ относительно переменной x: ∂ƒ / ∂x =
− ( x 2 + y 2 + z 2 ) ½−1 × ∂ ( x 2 )/ ∂x = − x / ( x 2 + y 2 + z 2 ) 3 ⁄ 2 7 6
Точно так же производные ∂ƒ / ∂y и ∂ƒ / ∂z это: ∂ƒ / ∂y = y / ( x 2 + y 2 + z 2 ) 3 ⁄ 2 and z соответственно Следовательно, градиент равен: ∇ ƒ ( x , y , z ) = − x i + y j + z k / ( x 2 + y 2 + z 2 ) 3 ⁄ 2 (E) ƒ ( x , Y ) 4 Y / ( x 2 9466 + 1) 1) ( x 2 + 1) 1). (F) ƒ ( x , Y , Z ) = SIN ( x ) E Y LN () () () (). Следовательно, градиент равен: ∇ ƒ ( x , y , z )
= cos ( x ) E Y LN ( Z ) I + SIN ( x ) E Y LN ( Z ) J + SIN J +) J + SIN J +) J +) J +) J +) J +) J +) J +) J +) J +) J +) J +) J +) J +) J +). Чтобы интерпретировать градиент скалярного поля ∇ ƒ ( x , y , z )
= ∂ƒ / ∂x i + ∂ƒ / ∂y j + ∂ƒ / ∂z k заметим, что его составляющая в направлении i является частной производной от ƒ по x. Это скорость изменения ƒ в направлении x, поскольку y и z остаются постоянными. В общем случае составляющая ∇ƒ в любом направлении представляет собой скорость изменения ƒ в этом направлении. Пример 2: Рассмотрим скалярное поле ƒ ( x , y ) = 3 x + 3 в двух измерениях.
Он не зависит от y и линейен по x. Его градиент определяется выражением: Как и следовало ожидать, градиент имеет нулевую составляющую в направлении y, а его составляющая в направлении x постоянна (3). Quiz 4: Select a point from the answers below at which the scalar field ƒ( x , y , z ) = x 2 yz − xy 2 z убывает в направлении y. (a)(1, −1, 2) Неверно — попробуйте еще раз! (б)(1, 1, 1) Правильно — молодец! (c)(−1, 1, 2) Неверно — попробуйте еще раз! (d)(1, 0, 1) Неверно — попробуйте еще раз! Решение: частная производная скалярной функции1466 z по отношению к y: ∂ƒ / ∂y ( x , y , z ) = x 2 Z x 2 Z x 2 Z x 2 Z x 2 Z x 2 Z x )
Оценка его в точке (1, 1, 1) дает: ∂ƒ / ∂y (1, 1, 1)
= 1 2 × 1 − 2 × 1 × 1 × 1 = 1 − 2 = −1 Это отрицательно, и поэтому функция ƒ убывает в направлении y в этой точке. Можно проверить, что функция не убывает по оси y ни при каких других
три точки. Пример 3: Найдите производную по направлению от ƒ ( x , y , z )
= x 2 yz в направлении 4i − 3k в
точка (1, −1, 1). Решение: Вектор 4i − 3k имеет величину √4 2 + (−3) 2 = √25 = 5.
Единичный вектор в направлении
Таким образом, 4i− 3k равно 1/5(4i−3k). Градиент ƒ: поэтому искомая производная по направлению равна: 0 k) Таким образом, в точке (1, −1, 1) искомая производная по направлению равна: ⋅ ∇ ƒ = 1/5 [8 × (−1) − 3 × (−1)] = −1 Упражнение 2: Вычислите производную по направлению следующих функций в заданных направлениях и в указанных точках: (а) ƒ = 3 x 2 − 3 y 2 в направлении j в (1, 2, 3). Решение: Производная по направлению функции ƒ = 3 x 2 − 3 y 2 в направлении единичного вектора j определяется скалярным произведением j ⋅ ∇. Градиент функции ƒ равен ∇ ƒ = 6 x i − 6 y й Следовательно, производная по направлению в направлении единичного вектора j равна: j ⋅ ∇ ƒ = j ⋅ (6 x i − 6 y j)
= −6 г а в точке (1, 2, 3) имеет значение −6 × 2 = −12. (б) ƒ = √ x 2 + y 2 в направлении 2i + 2j + k в точке (0, −2, 1). Решение: Производная функции по направлению
определяется вектором 2i + 2j + k, задается скалярным произведением ⋅ ∇ ƒ , где единичный вектор равен: = 2i + 2j + k / √2 2 + 2 2 + 1 2 = 2i + 2j + k / √9 = 2/3i + 2/3j + 1/3k Градиент функции ƒ равен: ∇ ƒ = x / √ x 2 + y 2 i + y / √ x 2 + y 2 j + 0k = x i + y i/ √ x 2 + y 2 Следовательно, требуемая производная по направлению равна: ⋅ ∇ ƒ = ( 2/3i + 2/3j + 1/3k ) ⋅ ( x i + y i/ √ x 2 + y 2 ) = 2/3 x + y / √ x 2 + y 2 В точке (0, −2, 1) он равен: 2/3 0 − 2/ √0 2 + (−2) 2 = 2/3 × −2/2 = − 2/3 (c) ƒ = sin ( x ) + cos ( y ) + sin ( z ) в направлении π i + π j в точке (π, 0, π). Решение: Производная по направлению функции ƒ = sin ( x ) + cos ( y ) + sin ( z ) в направлении, определяемом вектором π 1 π 1 9470 i + 9 задается скалярным произведением ⋅ ∇ ƒ , где единичный вектор равен: = π i + π j / √ π 2 + π 2 = i + j / √2 ∇ ƒ =
cos ( x )i − sin ( y )j + cos ( z )k Следовательно, производная по направлению равна: ⋅ ∇ ƒ = (i + j / √2 ) ⋅ [cos ( x ) I — sin ( y ) J + cos ( z ) K] = cos ( x . ) − sin ( y ) / √2 а в точке (π, 0, π) становится cos ( π ) − sin (0) / √2 =
− 1 / √2 Теперь сформулируем без доказательства два полезных свойства производной по направлению и градиента: Пример 4: Рассмотрим поверхность xy 3 = z + 2.
Чтобы найти его единичную нормаль в точке (1, 1, −1), нам нужно записать ее как: ƒ = xy 3 − z = 2 и вычислить градиент ƒ: ∇ƒ = г 3 i + 3 xy 2 j − k В точке (1, 1, −1) это ∇ƒ = i + 3j − k. величина эта максимальная скорость изменения равна √1 2 + 3 3 + (−1) 2 = √11 Таким образом, единичные нормали к поверхности равны: 1/√11 (i + 3j − k). Тест 5: Какой из следующих векторов является нормальным к поверхности x 2 yz = 1 в (1, 1, 1)? (a) 4i + j + 17k Неверно — попробуйте еще раз! (b) 2i + j + 2k Неверно. (c) i + j + k Неверно — попробуйте еще раз! (d) −2i − j − k Правильно – молодец! Объяснение: Поверхность определяется уравнением: х 2 yz = 1 Чтобы найти его единичную нормаль в (1, 1, 1), нам нужно оценить градиент функции ƒ ( x , y , z ) = x 2 yz : ∇ ƒ = 2 xyz i + x 2 z j + x 2 4 ∇ ƒ = i + j + k Таким образом, требуемые нормали к поверхности равны ±(i + j + k).
Следовательно, (d) — вектор нормали к поверхности. Тест 6: Какой из следующих векторов является единичной нормалью к поверхности cos ( x ) yz = −1 в точке (π, 1, 1)? (a) − 1 / √2 j + 1 / √2 k Неверно — попробуйте еще раз! (b) π i + j + 2 / √ π k Неверно – попробуйте еще раз! (c) i Неверно — попробуйте еще раз! (г) − 1 / √2 j − 1 / √2 k Правильно — молодец! Объяснение: Поверхность определяется уравнением: cos ( x ) yz = −1 Чтобы найти его единичную нормаль в точке (π, 1, 1), нам нужно оценить градиент ƒ = cos ( x ) yz : ∇ ƒ = −sin ( x ) yz i + cos ( x ) z j + cos ( x ) y k В точке (π, 1, 1) это: ∇ ƒ = 0i + (−1)j + (−1)k = −j −k Величина этого вектора: √(−1) 2 + (−1) 2 = √2 Следовательно, нормальная единица равна: = — 1 / √2 j — 1 / √2 k Тест 7: Выберите единицу нормали к (сферически-симметричной) поверхности x 2 + y 2 + z 2 = 109, 169 at (2, 1): (a) i + 1 /6 j − 1 /6 k Неверно — попробуйте еще раз! (b) 1 /3 i + 1 /3 j + 1 /3 k Неверно — попробуйте еще раз! (в) 5 /13 i + 12 /13 k Правильно — молодец! (d) − 5 /13 i + 12 /13 k Неверно — попробуйте еще раз! Объяснение: Поверхность определяется уравнением: x 2 + y 2 + z 2 = 169 Чтобы найти его единичную нормаль в точке (5, 0, 12), нам нужно оценить градиент ƒ = x 2 + y 2 + г 2 : ∇ ƒ = 2 x i + 2 y j + 2 z k В точке (5, 0, 12) это: ∇ ƒ = 2 × 5i + 0 × j + 2 × 12k = 10i + 24k Величина этого вектора: √(2 × 5) 2 + (2 × 12) 2 = √4 × (25 + 144) = 2 √169 = 2 × 13 Следовательно, нормальная единица равна: = 5 / 13 к + 12 91 465 91 466 / 13 к Выберите решения из предложенных вариантов 1. (A) I + J + Z −2 K (B) Y / Z I + x / Z J + x / Z 14 J + x / Z J + x / Z J + x / Z J + x / Z J + x / Z I + x / к (в) YZ −1 I + XZ -1 J + XYZ -2 K (D) — 1/ Z .9179.9797979797979797979797979797979797797779779797979797979797967 9. . (а)0 (б)− n /2 i + j + k / r n +1 (c) − n r / r n +2 (d) − n /2 r / r n +2 3.
= x 2 + 3x 2 + 2xy + y 2 9146 — 41465 26 2 2 2 2 2 2 2 2 . = 4x 2 + 2xy — 3y 2 +
Стр. № 7.14:
Вопрос 9:
Ответ:
= (2a 3 — 3b 3 — 3ab + 7) + (- a 3 + b 3 + 3ab — 9)
Собирая положительные и отрицательные подобные члены вместе, Получим
= 2A 3 — A 3 — 3B 3 + B 3 — 3AB + 3AB + 7 —
= A 3 — 2B 3 — 2
= a 3 + A 3 + B 3 — 2B 3 — 3 — 2
= 2A 3 — B 3 — 5
(I) 7 A 2 B из 3 A 2 B
(II) 4 XY B
(II) 4 xy от −3 (II) 4 XY от −3
(II) 4 XY от −3
(II) 4 XY от −3
(II) 4 xy от
(II) 4 xy от
(II) 4 xy .
Требуемое выражение = 3a 2 b — 7a 2 B
= (3 — 7) A 2 B
= — 4A 2 B
= — 7xy Стр. № 7.1440 41444444444444444444444444444444444444444444444444444444444444444444440
. :
(i) −4 x из 3 y
(ii) −2 x из −5 y Ответ:
= 3y + 4x
= -5y + 2x Страница № 7.14:
Вопрос 12:
(i) 6×3-7×2+5x-3 из 4-5x+6×2-8×3
(ii) -x2-3z из 5×2-y+z+7
(iii) x3+ 2x2y+6xy2-y3 из y3-3xy2-4x2y Ответ:
= 4 — 5x + 6x 2 — 8x 3 — 6x 3 + 7x 2 — 5x + 3
= — 8x 3 — 6x 3 + 7x 2 + 6x 2 — 5x — 5x + 3 + 4
= — 14x 3 + 13x 2 -10x +7 + 13x 2 -10x +7.
Требуемое выражение = (5x 2 — y + z + 7) — ( — x 2 — 3Z)
= 5x 2 — Y + z + 7 + x 2 + 3Z
= 5x 2 + x 2 — Y + z + 3Z + 7
= 6x 2 — Y + 4Z + 7
= Y 3 — 3xy 2 — 4x 2 Y — x 3 — 2x 2 Y — 6xy 2 + Y 3 Y — 6xy 2 + y 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 .
— 3xy 2 — 6xy 2 — 4x 2 y — 2x 2 y — x 3
= 2y 3 — 9xy 2 — 6x 2 y — x 3 Page No 7.14:
Question 13:
(i) p 3 − 4 + 3 p 2 , take away 5 p 2 − 3 p 3 + p − 6
(ii) 7 + x − x 2 , take away 9 + x + 3 x 2 + 7 x 3
(iii) 1 − 5 д 2 , забрать д 3 + 7 y 2 + y + 1
(iv) x 3 − 5 x 2 + 3 x + 1, take away 6 x 2 — 4 x 3 + 5 + 3 x Ответ:
3 + p — 6)
= p 3 — 4 + 3p 2 — 5p 2 + 3p 3 — p + 6
= p 3 + 3p 3 + 3p 2 — 5p 2 — p — 4+ 6
= 4p 3 — 2p 2 — P + 2
= 7 + x — x 2 — 9 — х — 3х 2 — 7х 3
= — 7x 3 — x 2 — 3x 2 + 7 —
= — 7x 3 — 4x 2 — 2
= 1 — 5y 2 — Y 3 — 7y 2 — Y -1
= -Y 2 — Y -1
= -Y 2 — Y 3 1465 3 — 5y 2 — 7y 2 — Y
= — Y 3 — 12y 2 — Y
1) — (6x 2 — 4x 3 + 5 + 3x)
= x 3 — 5x 2 + 3x + 1 — 6x 2 + 4x 3 — 5 — 3x + 4x 3 9146 — 5 — 5 — 3x + 4x 3 9146 — 5 — 5 — 3x . 3 + 4x 3 — 5x 2 — 6x 2 + 1 — 5
= 5x 3 — 11x 2 — 4 Страница № 7.14:
Вопрос 14:
6666666666666666666666666666. Сим. 2 − 5 x + 2 and −5 x 2 − 8 x + 9 subtract 4 x 2 − 7 x + 9. Answer:
= {3x 2 — 5x + 2 — 5x 2 — 8x + 9} — (4x 2 — 7x + 9)
= {3x 2 — 5x 2 — 5x — 8x + 2 + 9} — (4x 2 — 7x + 9)
= { — 2x 2 — 13x +11}} — (4x 2 — 13x +11}} 2 — 7x + 9)
= — 2x 2 — 13x + 11 — 4x 2 + 7x — 0 = — 2x 2 — 4x 2 — 13x + 7x + 11 —
= — 6x 2 — 6x + 2 Страница № 7.
14:44444444444.
.
Ответ:
= {(13x — 4y + 7z) + (- 6z + 6x + 3y)
={ 13x — 4y + 7z — 6z + 6x + 3y}
= {13x + 6x — 4y + 3y + 7z — 6z}
= 19x — y + z
= (6x − 4y − 4z) + (2x + 4y − 7)
= 6x − 4y − 4z + 2x + 4y − 7
= 8x − 4z − 7
= 8x — 4z — 7 — 19x + y — z
= 8x — 19x + y — 4z — z — 7
= — 11x + y — 5z — 7 Стр. № 7,14:
Вопрос 16:
Ответ:
= {(x 2 + 3y 2 — 6 2 — у 2 + 8xy) + ( y 2 + 8) + (x 2 — 3xy)}
= {x 2 + 3y 2 — 6x9y + 21465 2 — Y 2 + 8xy + y 2 + 8 + x 2 — 3xy}
= {x 2 + 2x 2 + x 2 + 2x 2 + x 2 + 3Y 2 + x 2 + 2 2 + x 2 + 2 2 + x + 2 + 2 2 + 2 + 2 2 + 2 .
2 + y 2 — 6xy + 8xy — 3xy + 8}
= 4x 2 + 3y 2 — xy + 8
= 4x 2 + 3y 2 — xy + 8 + 3x 2 — 4y 2 + xy — x + y — 3
= 4x 2 + 3x 2 + 3y 2 — 4y 2 — 3y 2 — 4y 2 + 3Y 2 — 4y 2 + 3y 2 — 4y 2 + 3y 2 — 41465 2 + 3y 2 — 41465 2 + 3y 2 — 41465 2 + 3y 2 — 41465 — 3 + 8
= 7x 2 — Y 2 — x + y + 5 Страница № 7,14:
Вопрос 17:
Ответ:
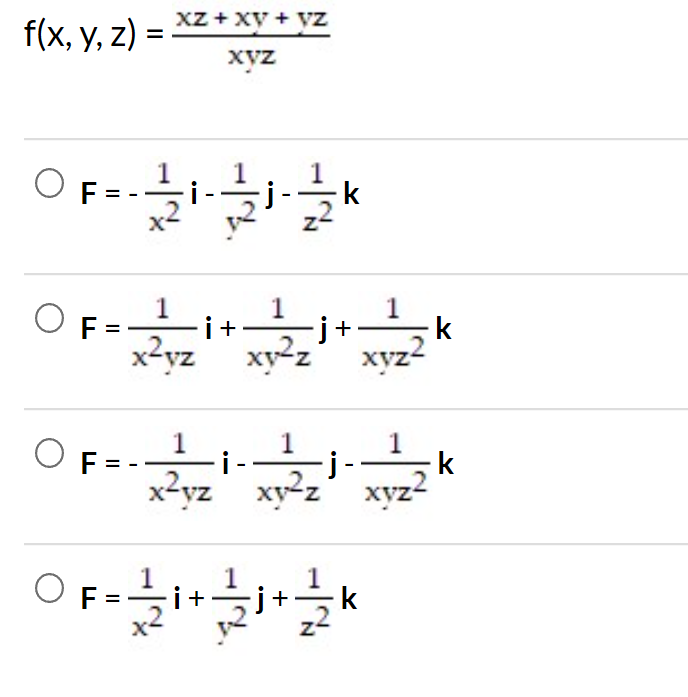
Следовательно, искомое выражение = (4xy — 3zx + 4yz + 7) — (xy — 3yz + 4zx )
= 4xy — 3zx + 4yz + 7 — xy + 3yz — 4zx
= 4xy — xy — 3zx — 4zx + 4yz + 3yz + 7
= 3xy — 7zx + 7yz + 7 no 7.14:
4444444. 18
. :
Ответ:
х 2 — ху + у 2 — х + у + 3 — М = — х 2 + 3у 2 — 4ху + 1
Следовательно,
М = (5 х 29146 — ху + у 2 — х + у + 3) — (- х 2 + 3Y 2 — 4xy + 1)
= x 2 — xy + y 2 — x + y + 3 + x 2 — 3Y 2 + 4xy — 1 — 3Y 2 + 4xy — 1 — 3Y 2 + 4xy — 1 — 3Y 2 + 4xy — 1 — 3Y 2 + 4xy — 1 — 3Y 2 + 4xy 41465 — и отрицательные члены вместе, мы получаем
x 2 + x 2 — xy + 4xy + y 2 — 3y 2 — x + y + 3 — 1
= 2x 2 + 91×466--y 2 года 2 — x + y + 2 Номер страницы 7.
14: Вопрос 19:
Ответ:
— 3x — 2y — 5y + 3z + 7
= — 2x — 7y + 3z + 7 № страницы 7.14:
Вопрос 20:
9016 г 2 меньше 2 x 2 − 3 г 2 + xy ? Ответ:
= 2x 2 — 3y )
= 2x 2 — 3y )
= 2x 2 — 3 )
= 2x 2 — 3 ) x 2 + 2xy — 3y 2
Собирая вместе положительные и отрицательные подобные члены, мы получаем
2x 2 — x 2 — 3y 2 — 3y 2 + xy + 2xy
= x 2 — 6y 2 + 3xy.
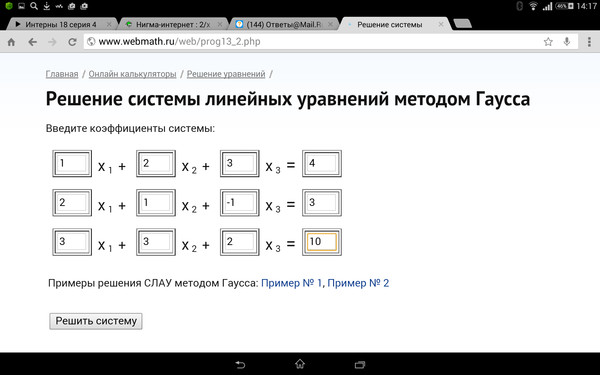2 − 3 ab + 2 b 2 больше 2 a 2 − 7 ab + 9 b 2 ? Ответ:
= A 2 — 3AB + 2B 2 — 2A 2 + 7AB — 2
Сбор положительных и отрицательных условий, как термины, мы получим
=
. 2 — 3AB + 7AB + 2B 2 — 9B 2
= — A 2 + 4AB — 7B 2 Страница № 7.14:
444466 22:
444.1145
2 Ответ:
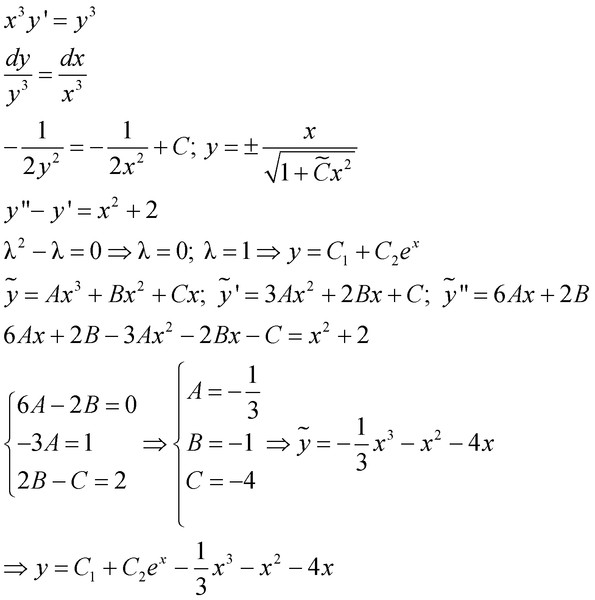Таким образом, имеем
12x 3 — 4x 2 + 3x — 7 + M = x 3 + 2x 2 — 3x + 2
Следовательно,
M = (x 1 + 29146 — 3х + 2) — (12х 3 — 4x 2 + 3x — 7)
= x 3 + 2x 2 — 3x + 2 — 12x 3 + 4x 2 — 3x + 7
. , мы получаем
x 3 — 12x 3 + 2x 2 + 4x 2 — 3x — 3x + 2 + 7
= — 11x 3 + 6x 2
— 11x 3 + 6x 2 9144 2
2
2
. Страница № 7.14: Вопрос 23:
Ответ:
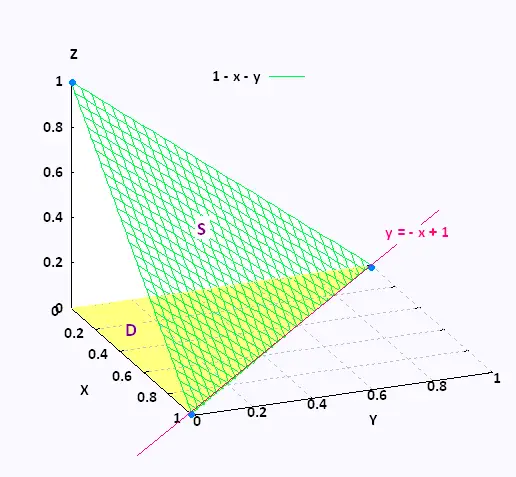— 9 лет 2 ) + (4 года 2 — 3x 2 — 6xy) + (- 4x 2 + xy + 5y 2 )
= 7x 2 + 5xy — 9y 2 + 4y 2 — 3x 2 — 6xy — 4x 2 9146 + xy + 5y 914. negative like terms together, we get
7x 2 — 3x 2 — 4x 2 + 5xy — 6xy + xy — 9y 2 + 4y 2 + 5y 2
= 7x 2 — 7x 2 + 6xy — 6xy — 9y 2 + 9y 2
= 0 Page No 7.14:
Question 24:
Найдите P + Q + R + S − T. Ответ:
P + Q + R + S — T = {(a 2 — b 2 92ab)66 + (a 2 + 4b 2 — 6ab) + (b 2 + b) + (a 2 — 4ab)} — (-2a 2 + b 2 — ab + a)
= {a 2 — b 2 + 2ab + a 2 + 4b 2 — 6AB + B 2 + B + A 2 — 4AB} — ( — 2A 2 + B 2 — AB + A)
= {3A 2 + 4B 2 9146 2 9146 2 9146 2 9146 2 9146 2 9146 2 9146 2 9146 2
= {3A 2 + 4B 2 2 2 = {3A 2 . 8AB + B} — (-2A 2 + B 2 — AB + A)
= 3A 2 + 4B 2 — 8AB + B + 2A 2 — B 2 + AB — A -A 2 — B 2 + AB -AB -AB -AB -AB -AB 2 — B 2 + 2A 2 — B
Собирая вместе положительные и отрицательные подобные члены, мы получаем
3a 2 + 2a 2 + 4B 2 — B 2 — 8AB + AB — A + B
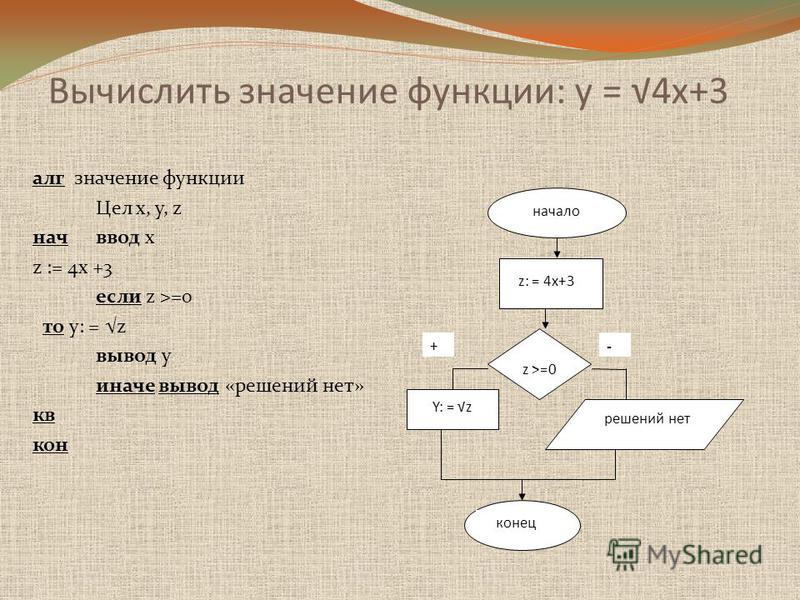
= 5A 2 + 3B 2 — 7AB — A + B Page NO 7.
16:. два последних члена следующих выражений в скобках со знаком минус:
(i) x + y − 3 z + y
(ii) 3 x − 2 7 y − 5 z − 4
(iii) 3 a − 2 b + 4 c − 5
(IV) 7 A + 3 B + 2 C + 4
(V) 2 A 2 — B 2 — 3 B 2 — 3 B 2 — 3 . A 2 + B 2 — C 2 + AB — 3 AC AB — 3 AC
(ii) 3x — 2y — 5z — 4 = 3x — 2y — (5z + 4)
(iii) 3a — 2b + 4c — 5 = 3a — 2b — (- 4c + 5)
(iv) 7a + 3b + 2c + 4 = 7a + 3b — (- 2c — 4)
(v) 2a 2 — b 2 — 3ab + 6 = 2a 2 — b 2 — (3ab — 6)
(vi) a 2 + b 2 − c 2 + ab − 3ac = a 2 + b 2 − c + 2 91 ) Страница № 7.
16: Вопрос 2:
(i) Сумма a − b и 3 a − 2 b + 5 вычитается из 4 a + 2 b − 7.
(ii) Тройная сумма 2 x + 7 y 5 { — ( x — 3 y )} и 7 x — 4 y + 3 вычитается из 3 x — 4 y + 7. x 91 (iii) Вычитание числа 91 2 − y 2 + 4 xy из 2 x 2 + y 2 − 3 xy добавляется к 9 x 2 − 3 y 2 − xy . Ответ:
Это вычитается из 4a + 2b — 7.
Таким образом, искомое выражение равно {4a + 2b — 7) — {(a — b) + (3a — 2b + 5)}.
Это вычитается из 3x — 4y +7.
Таким образом, искомое выражение равно (3x — 4y +7) — 3[(2x + y) — {5 — (x — 3y)} + (7x — 4y + 3)].
Когда приведенное выше уравнение добавляется к 9x 2 − 3y 2 − xy, мы получаем
{(2x 2 + y 2 − 3xy) — (x 2 − y 2 + 4xy)} + (9x 2 − 3y 2 − xy) Стр. № 7.20:
Вопрос 1:
.
2 x + (5 x − 3 y ) Ответ:
2x + (5x − 3y)
Поскольку знак «+» стоит перед скобками, каждого члена в скобках, когда мы их удаляем.
= 2х + 5х — 3у
= 7x — 3y Страница № 7.20:
Вопрос 2:
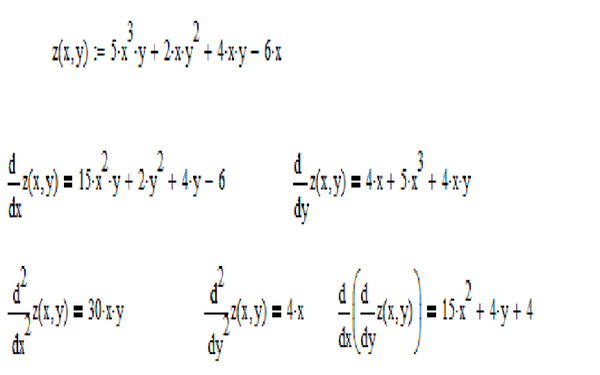
3 x — ( y — 2 x ) Ответ:
3x — (y — 2x)
Поскольку знак «-» стоит перед скобками, мы должны изменить знак каждый термин в круглых скобках, когда мы их удаляем. Таким образом, мы имеем
3x − y + 2x
= 5x − y Страница № 7.20:
Вопрос 3:
5 a − (3 b − 2 a + 4 c ) Ответ:
5a − (3b − 2a + 4c) перед скобками
‘ , мы должны изменить знак каждого члена в скобках, когда мы их удаляем.
= 5a — 3b + 2a — 4c
= 7a — 3b — 4c Страница № 7.20:
Вопрос 4:
−2 ( x 2 − y 2 + xy ) − 3( x 2 + y 2 − xy ) Answer:
— 2(x 2 — y 2 + xy) — 3(x 2 + y 2 — xy)
Поскольку знак «-» стоит перед скобками, мы должны изменить знак каждый термин в круглых скобках, когда мы их удаляем.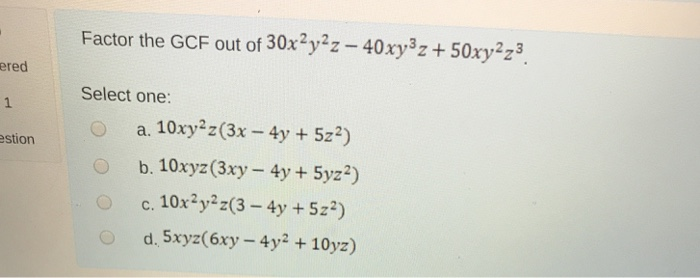
= — 2x 2 + 2y 2 — 2xy — 3x 2 — 3y 2 + 3xy
= — 2x 2 + 3xy
= — 2x 2 + 3xy
= — 2x 2
— 3xy
= — 2x 2 + 3xy
= — 2x 2 + 3xy
= — 2x 2 . 2 — 2xy + 3xy
= — 5x 2 — y 2 + xy Страница № 7.20:
Вопрос 5:
3 х + 2 у — { х — (2 у − 3)} Ответ:
3x + 2y − {x − (2y − 3)}
. Во-первых, мы должны удалить маленькие квадратные скобки (или скобки): ( ). Затем мы должны удалить фигурные скобки (или фигурные скобки): { }.
Следовательно,
= 3x + 2y — {x — 2y + 3}
= 3x + 2y — x + 2y — 3
= 2x + 4y — 3 Страница № 7.
20: Вопрос 6:
5 а — {3 а − (2 − a ) + 4} Ответ:
5a − {3a − (2 − a) + 4}
. Во-первых, мы должны удалить маленькие квадратные скобки (или скобки): ( ). Затем мы должны удалить фигурные скобки (или фигурные скобки): { }.
Следовательно,
= 5а — {3а — 2 + а + 4}
= 5а — 3а + 2 — а — 4
= 5а — 4а — 2
= а — 2 Страница № 7.20:
Вопрос 7:
a − [ b − { a − ( b − 1) + 3 a }] Ответ:
Следовательно, имеем
а — [b — {а — (b — 1) + 3а}]
= а — [b — {а — b + 1 + 3а}]
= а — [b — {4а — b + 1}]
= a — [b — 4a + b — 1]
= a — [2b — 4a — 1]
= a — 2b + 4a + 1
= 5a — 2b + 1 Страница № 7.
20 : Вопрос 8:
a — [2 b — {3 a — (2 b — 3 c )}] Ответ:
Следовательно, имеем
а — [2b — {3a — (2b — 3c)}]
= a — [2b — {3a — 2b + 3c}]
= a — [2b — 3a + 2b — 3c]
= a — [4b — 3a — 3c]
= a — 4b + 3a + 3c
= 4a — 4b + 3c Страница № 7.20:
Вопрос 9:
— x + [5 y — {2 x — (3 y — 5 x )}] Ответ:
Следовательно, имеем
— х + [5у — {2х — (3у — 5х)}]
= — х + [5у — {2х — 3у + 5х}]
= — х + [5у — {7х — 3у}]
= — x + [5y — 7x + 3y]
= — x + [8y — 7x]
= — x + 8y — 7x
= — 8x + 8y Страница № 7.
20: Вопрос 10:
2 a − [4 b − {4 a − 3(2 a − b )}] Ответ:
Следовательно, имеем
2а — [4b — {4а — 3(2а — b)}]
= 2а — [4b — {4а — 6а + 3b}]
= 2а — [4b — {- 2а + 3b} ]
= 2a — [4b + 2a — 3b]
= 2a — [b + 2a]
= 2a — b — 2a
= — b Страница № 7.20:
Вопрос 11:
− a − [ a + { a + b − 2 a − ( a − 2 b )} − b ] Ответ:
Следовательно, имеем
— а — [а + {а + b — 2а — (а — 2b)} — b]
= — а — [а + {а + b — 2а — а + 2b} — b]
= — а — [а + {- 2а + 3b} — b]
= — а — [а — 2а + 3b — b]
= — а — [- а + 2b]
= — а + а — 2b
= — 2b Страница № 7.
20: Вопрос 12:
2 x − 3 y − [3 x − 2 y − { x − z − ( x − 2 y )}] Answer:
Следовательно, имеем
2x — 3y — [3x — 2y — {x — z — (x — 2y)}]
= 2x — 3y — [3x — 2y — {x — z — x + 2y}]
= 2x — 3y — [3x — 2y — {- z + 2y}]
= 2x — 3y — [3x — 2y + z — 2y]
= 2x — 3y — [3x — 4y + z]
= 2x — 3y — 3x + 4y — z
= — x + y — z Страница № 7.20:
Вопрос 13:
5 + [ x — {2 y — (6 x + y — 4) + 2 x } — { x — ( y ) 70 9 19 4 ] :
Следовательно, имеем
5 + [х — {2у — (6х + у — 4) + 2х} — {х — (у — 2)}]
= 5 + [х — {2у — 6х — у + 4 + 2x} — {x — y + 2}]
= 5 + [x — {y — 4x + 4} — {x — y + 2}]
= 5 + [x — y + 4x — 4 — x + y — 2]
= 5 + [4x — 6]
= 5 + 4x — 6
= 4x — 1 Страница № 7.20:
Вопрос 14:
x 2 — [3 x + {2 x — ( x 2 − 1) + 2}] Ответ:
Следовательно, имеем
х 2 — [3х + {2х — (х 2 — 1)} + 2]
= х 2 — [3х + {2х — х 2 + 1} + 2]
= x 2 — [3x + 2x — x 2 + 1+ 2]
= x 2 — [5x — x 2 + 3]
= x + 2 — 5x 2 — 3
= 2x 2 — 5x — 3 Страница № 7.
20: Вопрос 15:
20 — [5 xy + 3 { x 2 — ( xy — y ) — ( x — y ) — ( x — y ) — ( x — y )}
707070707070707. маленькие скобки или круглые скобки ( ), затем фигурные скобки { }, а затем квадратные скобки [ ].
Следовательно, имеем
20 — [5xy + 3{x 2 — (xy — y) — (x — y)}]
= 20 — [5xy + 3{x 2 — xy + y — x + у}]
= 20 — [5ху + 3{х 2 — ху + 2у — х}]
= 20 — [5ху + 3х 2 — 3ху + 6у — 3х]
= 20 — [2ху + 3x 2 + 6y — 3x]
= 20 — 2xy — 3x 2 — 6y + 3x
= — 3x 2 — 2xy — 6y + 3x + 20 Страница № 7.20:
44445:
.
85 — [12 x — 7(8 x — 3) — 2 {10 x — 5(2 — 4 x )}] Ответ:
Следовательно, имеем
85 — [12x — 7(8x — 3) — 2{10x — 5(2 — 4x)}]
= 85 — [12x — 56x + 21 — 2{10x — 10 + 20x}]
= 85 — [12x — 56x + 21 — 2{30x — 10}]
= 85 — [12x — 56x + 21 — 60x + 20]
= 85 — [12x — 116x + 41]
= 85 — [- 104x + 41]
= 85 + 104x — 41
= 44 + 104x Страница № 7.20:
Вопрос 17:
XY [ YZ — ZX — { YX — (3 Y — XZ ) — ( XY – ) — ( XY – ) — ( XY – ) удалите маленькие скобки или круглые скобки ( ), затем фигурные скобки { }, а затем квадратные скобки [ ].
Следовательно, имеем
xy — [yz — zx — {yx — (3y — xz) — (xy — zy)}]
= xy — [yz — zx — {yx — 3y + xz — xy + zy}]
= xy — [yz — zx — {- 3y + xz + zy}]
= xy — [yz — zx + 3y — xz — zy]
= xy — [- zx + 3y — xz]
= xy — [ — 2zx + 3y]
= xy + 2xz — 3y Страница № 7.
7: Вопрос 1:
(i) a7
7 (ii) а 2 − b 2
(iii) x 3 + y 3 + z 3
(iv) x 3 + y 3 + Z 3 + 3 XYZ
(V) 7 + 5
(VI) ABC + 1
(VII) 3 x + 1
(vii) 3 x + 1
(VII) 3 x + 1
(VII) 3 x + 1
(VII) 3 . х — 3 х + 4
(ix) ху + yz + zx
(x) AX 3 + до н.э. 2 + CX + D .
(i) a 2 является мономом, так как содержит только один член.
(ii) a 2 — b 2 является биномиальным выражением, поскольку оно содержит два термина.
(iii) x 3 + y 3 + z 3 является трехчленным выражением, поскольку оно содержит три члена.
(iv) x 3 + y 3 + z 3 + xyz представляет собой четырехчленное выражение, поскольку оно содержит четыре члена.
(v) 7 + 5 = 12 является мономом, так как содержит только один член.
(vi) abc +1 является биномиальным выражением, поскольку оно содержит два термина.
(vii) 3x — 2 + 5 = 3x + 3 является биномиальным выражением, поскольку оно содержит два члена.
(viii) 2x — 3y + 4 является трехчленным выражением, поскольку оно содержит три члена.
(ix) xy + yz + zx — это трехчленное выражение, поскольку оно содержит три члена.
(x) ax 3 +bx 2 +cx + d является четырехчленным выражением, поскольку оно содержит четыре члена. Страница № 7.8:
Вопрос 2:
(i) 3 x
(ii) 2 x − 3
(iii) 6 x 91 2 — 7
(IV) 2 x 2 + y 2 — 3 xy + 4.
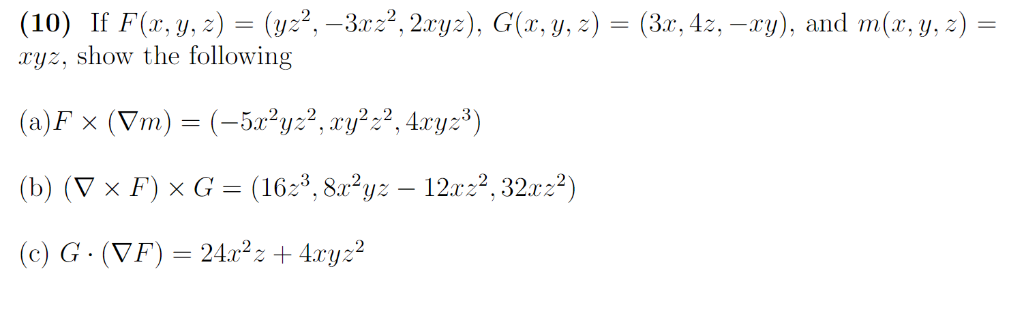
(i) 3x — единственный член данного алгебраического выражения.
(ii) 2x и -3 являются членами данного алгебраического выражения.
(iii) 2x 2 и -7 являются членами данного алгебраического выражения.
(iv) 2x 2 , y 2 , -3xy и 4 являются членами данного алгебраического выражения. Страница № 7.8:
Вопрос 3:
(i) 4 xy , −5 x 2 y , −3 yx , 2 xy 2
(ii) 7a2bc, -3ca2b, -52abc2, 32abc2, -43cba2 Answer:
(i) 4xy, -3yx 4, -3
(II) {7a 2 BC, -3CA 2 B, -43CBA2} {7, -3, -43}
{-52AB 32abc2 } {-52,32} Страница № 7.8:
Вопрос 4:
(i) a2+b2-2a2+c2+4a
(ii) 3x+4xy-2yz+52zy
(iii ) abc+ab2c+2acb2+3c2ab+b2ac-2a2bc+3cab2 Ответ:
(i) В данном алгебраическом выражении одинаковыми членами являются a 2 и -2a 2 .
(iii) В данном алгебраическом выражении одинаковыми членами являются ab 2 c, 2acb 2 , b 2 ac и 3cab 2 . Страница № 7.8:
Вопрос 5:
(i) −12 x
(ii) −7 xy 1 13 x (6 iii) (iv) −7 ax
Ответ:
(i) Числовой коэффициент x равен -12.
(ii) Числовой коэффициент x равен -7y.
(iii) Числовой коэффициент x равен yz.
(iv) Числовой коэффициент x равен -7a. Page No 7.8:
Question 6:
(i) −3 x 2
(ii) 5 x 2 yx
(iii) 57x2z
(iv) -32ax2+yx Ответ:
(i) Числовой коэффициент x 2 равен -3.
(ii) Числовой коэффициент x 2 равен 5yz.
(iv) Численный коэффициент x 2 равен -32a. Страница № 7,8:
Вопрос 7:
(I) Y в -3 Y
(II) A в 2 AB
(II) A в 2 AB
(II) A в 2 AB
(II) A . в −7 xyz
(IV) P в -3 PQR
(V) Y 2 в 9 XY 2 Z
(vI) Z
(ri) Z
(vii) x 2 дюймов − x 2 Ответ:
(ii) Коэффициент а равен 2b.
(iii) Коэффициент z равен -7xy.
(iv) Коэффициент при p равен -3qr.
(v) Коэффициент y 2 равен 9xz.
(vi) Коэффициент x 3 равен 1.
(vii) Коэффициент x 2 равен — 1. Стр. the following:
(i) xy
(ii) −6 yz
(iii) 7 abc
(iv) −2 x 3 y 2 z Ответ:
(i) Числовой коэффициент в члене xy равен 1.
(ii) Числовой коэффициент в члене -6yz равен — 6.
(iii) Числовой коэффициент в члене 7abc равен 7.
(iv) Числовой коэффициент коэффициент в члене -2x 3 y 2 z is — 2. Страница № 7.8:
Вопрос 9:
(i) 4x2y- 32xy+52xy2
(ii) -53x2y+74xyz+3 Ответ:
Термин Коэффициент
-32xy -32
52xy2 52
74XYZ 74
74XYZ 74
7407
Page No 7.8:
Question 10:
(i) x 2 y − xy 2 + 7 xy − 3
(ii) a 3 − 3 a 2 + 7 a + 5 Ответ:
90 .
(i) Постоянный член в данном алгебраическом выражении равен -3.
(ii) Постоянный член в данном алгебраическом выражении равен 5. Страница № 7.8:
Вопрос 11:
(i) xy+yz+zx
(ii) x2+y2+z2-xy-yz-zx Ответ:
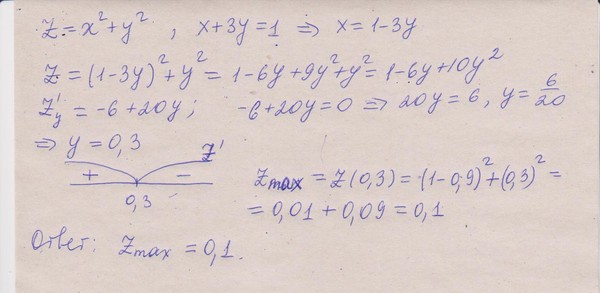
Таким образом,
(i)
xy+yz+zx=-2-1+-13+3-2=2-13-32=12-2-96=12-116=16
= (-2) 2 + (-1) 2 6 9 — 5 1 + (3) (-2)(-1) — (-1)(3) — (3)(-2)
= 4 + 1 + 9 — 2 + 3 + 6
= (4 + 1 + 9 + 3 + 6) — 2
= 23 — 2 = 21 Страница № 7.8:
Вопрос 12:
6 = −1, 19316 а = -2, б = 1, c = −2: 6 В точке (1, 1, 1) это:
(i) ax + by + cz
(ii) ax 2 + by 2 − cz 2
(iii) axy + byz + cxy Ответ:
Таким образом,
(i) ax + by + cz
= (-2)(1) + (1)(-1) + (-2)(2)
= — 2 + (- 1) + (- 4 )
= — 2 -1 — 4 = -7
= (-2)(1) 2 + (1)(-1) 2 — (-2)(2) 2
= -2 x 1 + 1 — (-2 x 4)
= -2 + 1 — (-8)
= -2 + 1 + 8 ) axy + byz + cxy
= (-2)(1)(-1) + (1)(-1)(2) + (-2)(1)(-1)
= 2 + (-2) + 2
= 2 — 2 + 2
= 4 — 2
= 2 Касательные плоскости и нормальные линии
Касательные плоскости и нормальные линии
Мы можем определить новый
функция F(x,y,z) трех переменных путем вычитания
я. Это имеет
состояние
Теперь рассмотрим любую кривую, заданную параметрически с помощью
Мы можем написать,
Дифференцирование обеих сторон по t и использование цепного правила дает
Обратите внимание, что это скалярное произведение функции градиента и вектора <х', у', z'>,
В частности, вектор градиента ортогонален касательной любой
кривая на поверхности. Это приводит к Определение
Пусть F(x,y,z)
определить поверхность, которая
дифференцируемый в точке (x 0 , y 0 , z 0 ),
затем касательная плоскость к
F(x, y, z) в
( х 0 , у 0 , я 0 ) это плоскость с вектором нормали
который проходит через точку (x 0 , y 0 , z 0 ).
В частности, уравнение касательной плоскости имеет вид
Найдите уравнение касательной плоскости к
в точке (1,2,1)
затем
В точке (1,2,1) вектор нормали равен
Теперь используйте формулу точечной нормали для плана
или
В итоге получаем
В контексте поверхностей мы
имеют вектор градиента поверхности в данной точке. Это приводит
к следующему определению.
Пусть F(x,y,z)
определить поверхность, дифференцируемую в
точка (x 0 , y 0 , z 0 ), затем нормальная линия к
F(x,y,z) в
( х 0 , у 0 , я 0 ) это линия с вектором нормали
который проходит через точку (x 0 , y 0 , z 0 ).
В частности уравнение нормальной линии
Пример
в точке (1,2,3).
Теперь используйте формулу, чтобы найти
| н . к |
cosq =
|| н ||
В более общем случае, если
|град F(x 0 , y 0 , z 0 ) . к |
cosq =
||Град F(x 0 , y 0 , z 0 )||
Пример
+
+
= 1
4
4 8
Теперь подключитесь, чтобы получить
У нас есть
Также
Отсюда
Значит угол наклона равен
Пример
Найдите касательную к кривой пересечения сферы
и параболоид
в точке (1,2,5).
Решение
и
Оба эти вектора будут перпендикулярны касательной к
кривая в точке, следовательно, их векторное произведение будет параллельно этому
касательная линия. Вычисляем PPLATO | Базовая математика | Градиенты и производные по направлениям
оси x и единичного вектора j в направлении y (см. рисунок внизу слева).
В трех измерениях нам также требуется k, единичный вектор в направлении z. ∇ = ∂ / ∂x i + ∂ / ∂y j + ∂ 5 к 
0906 Тест 2: Выберите следующую частную производную ∂ / ∂x ( x cos ( y ) + y ): ∂ / ∂x ƒ ( x , y ) = ∂ / ∂x cos ( y ) + y = ∂ / ∂x ( x ) × cos ( y )
+ ∂ / ∂x у = 1 × cos ( y ) + 0 = cos ( y ) град ƒ ( x , y )
= ∇ ƒ ( x , y )
= ∂ƒ / ∂x i + ∂ƒ / ∂y j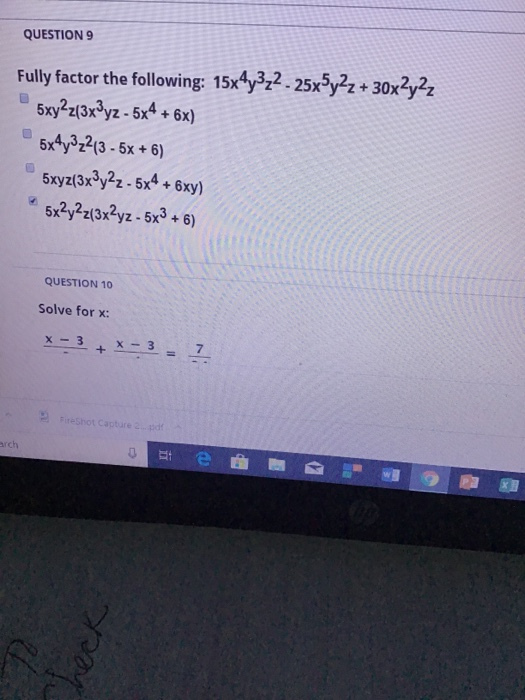 
Он получается применением векторного оператора ∇ к
скалярная функция ƒ ( x , y ). Такое векторное поле называется градиент
(или консервативное) векторное поле . ∇ ƒ ( x , y ) = ∂ƒ / ∂x i + ∂ƒ / ∂y j = ∂ / ∂x ( x + y 2 )i + ∂ / ∂y ( x + y 2 )j = (1 + 0)i + (0 + 2y)j = я + 2yj ∇ ƒ ( x , y ) = ∂ƒ / ∂x i + ∂ƒ / ∂y j = ∂ / ∂x ( x 2 y 3 )i + ∂ / ∂y ( x 2 y 3 )j = ∂ / ∂x ( x 2 ) × y 3 i + x 2 × ∂ / ∂y ( y 3 )j = 2 x 2−1 × y 3 i + 3 x 2 × y 3−5 j 6 = 2 x у 3 i + 3 x 2 г 2 г ∇ ƒ ( x , y , z )
= ∂ƒ / ∂x i + ∂ƒ / ∂y j + ∂ƒ / ∂z k ∇ ƒ ( x , y ) = ∂ƒ / ∂x i + ∂ƒ / ∂y j = ∂ / ∂x ( x + 3 y 2 ) I + ∂ / ∂y ( x / ∂y ( x / ∂ ( x / ∂ ( x / ∂ ( / ∂ / ∂ /.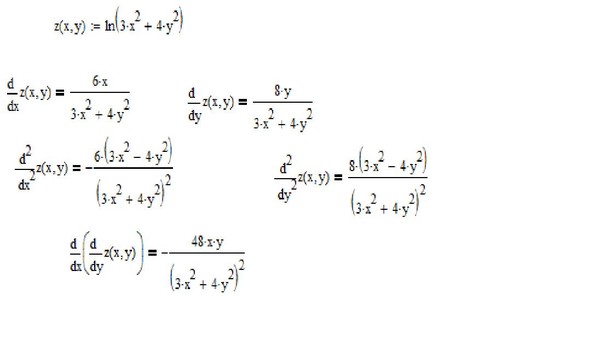 
= (1 + 0)i + (0 + 3 × 2 г 2−1 )j = я + 6 у у ∇ ƒ ( x , y ) = ∂ƒ / ∂x i + ∂ƒ / ∂y j = ∂ / ∂x ( x 2 + y 2 ) ½ i + ∂ / ∂y ( x 2 + у 2 ) ½ у = 1/2 ( x 2 + y 2 ) ½−1 × ∂ / ∂x ( x 2 )i + 1/2 ( x 2 + y 2 ) ½−1 × ∂ / ∂y ( y 2 0) = 1/2 ( x 2 + y 2 ) −½ × 2 x 2–1 I + 1/2 ( x 2–1 I + 1/2 ( x
5 2–1 I + 1/2 ( x
5 2-1 I + 1/2 ( x
5 2 I + 1/2 ( x 9465 2 I + 1/2 ( x 2 I + 1/2.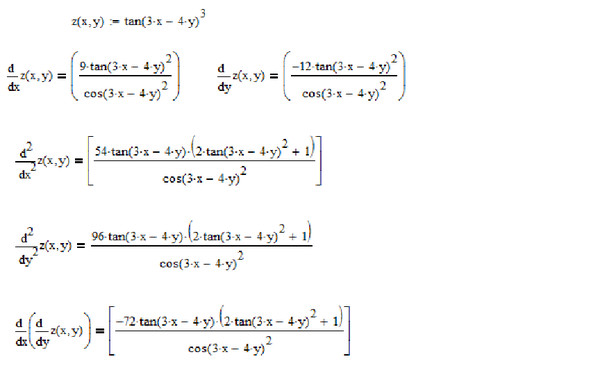
2 ) −½ × 2 у 2−1 у = ( x 2 + у 2 ) −½ x я +
( x 2 + у 2 ) −½ у у = x / √ x 2 + Y 2 I + Y / √ x 2 + Y 7141479147 ∇ ƒ ( x , y , z ) = ∂ƒ / ∂x i + ∂ƒ / ∂y j + ∂ƒ / ∂z k = 3 y ½ ∂ / ∂x ( x 2 )i +
3 x 2 ∂ / ∂y ( y ½ )j + ∂ / ∂y (cos (3 z ))k = 3 y ½ × 2 x 2−1 i +
3 x 2 × 1/2 y ½−1 j − 3 sin (3 z )k = 6 г ½ x i + 3/2 x 2 y −½ j − 3 sin (3 z )k = 6 x √ y i + 3/2 x 2 / √ y j − 3 sin 90k(3 z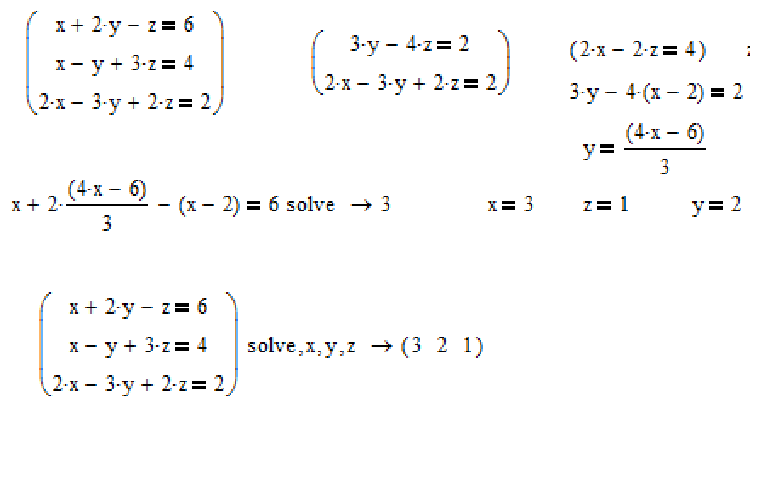 
Решение: Градиент функции ƒ ( x , y ) 4 y / ( x 2 + 1) = 4 y ( x 2 + 1) −1 равно: ∇ ƒ ( x , y ) = 4 y × ∂ / ∂x ( x 2 + 1) −1 i +
( x 2 + 1) −1 × ∂ / ∂y 4 y j = 4 y × (−1)( x 2 + 1) −1−1 ∂ / ∂x ( x 2 + 1) 2 i + 4 ( x 2 + 1) −1 j = −4 y ( x 2 + 1) −2 × 2 x i + 4( x 2 + 1) −1 j = − 8 xy / ( x 2 + 1) 2 i + 4/ ( x 2 + 1)j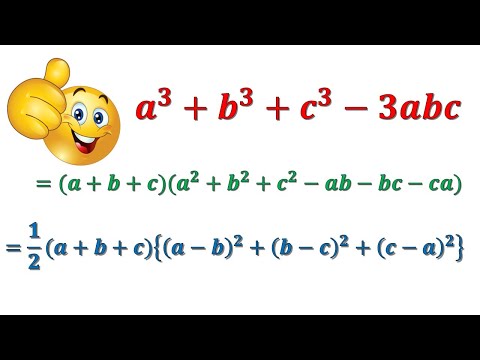 
Решение: Частные производные функции ƒ ( x , y , z ) = sin ( x ) e y ln( 9:7 z 94 ln ∂ƒ / ∂x = ∂ / ∂x (sin ( x )) e y ln( z )
= cos ( x ) e y ln( z ) ∂ƒ / ∂y = sin ( x ) ∂ / ∂y (e y ) ln( z )
= sin ( x ) e y ln( z ) ∂ƒ / ∂z = sin ( x ) e y ∂ / ∂z (ln( z )) = sin ( x ) e y 1/ z 
у ∇ ƒ = ∂ / ∂x (3 x + 3)i + ∂ / ∂y (3 x + 3)j = 3i + 0j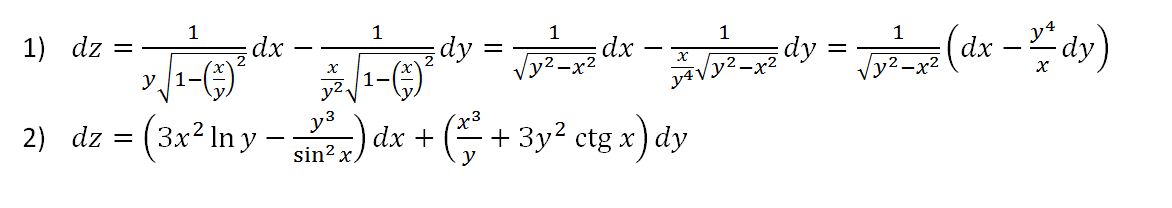 
Определение: если единичный вектор, то ⋅ ∇ƒ называется производной от ƒ по направлению в направлении .
Производная по направлению — это скорость изменения ƒ в направлении . ∇ ƒ = ∂ / ∂x ( x 2 yz )i + ∂ / ∂y ( x 2 yz )j + ∂ / ∂z ( х 2 yz )k = 2 xyz i + x 2 z j + x 2 у к ⋅ ∇ ƒ = 1/5 (4i − 3k) ⋅ (2 xyz i + x 2 z j + x 2 y = 1/5 [4 × 2 xyz + 0 − 3 × x 2 y ] 
Повторите попытку!
Каков градиент ƒ ( x , y , z ) = xyz −1 ?