Решите неравенство методом интервалов » задачи
неравенства »
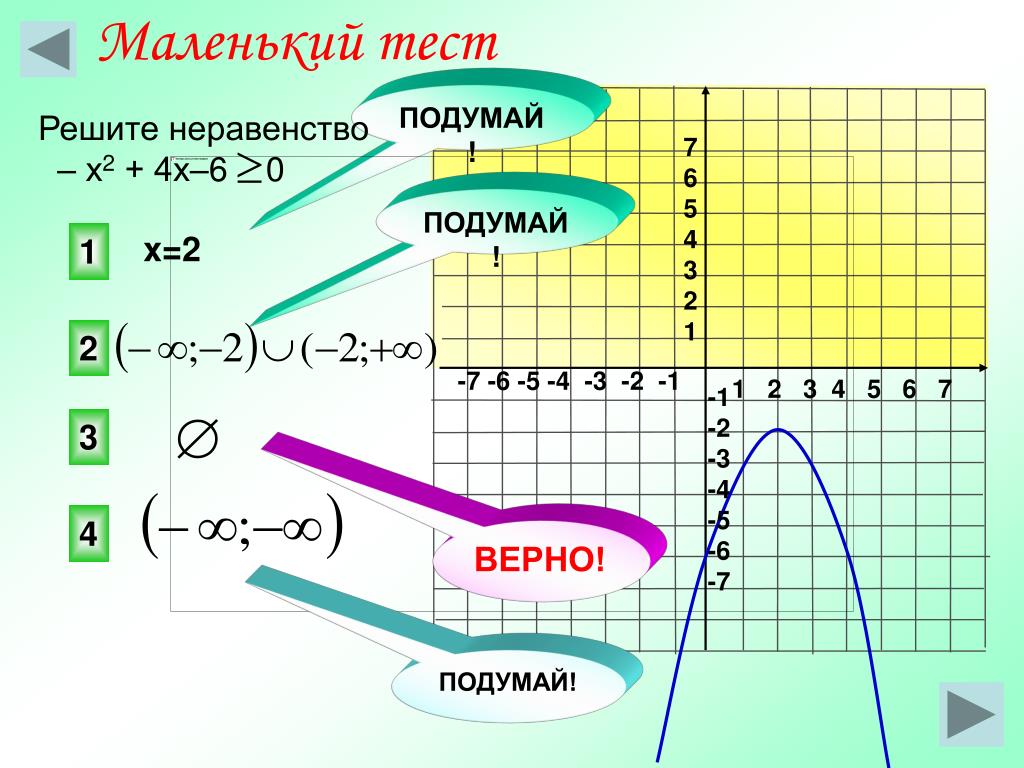
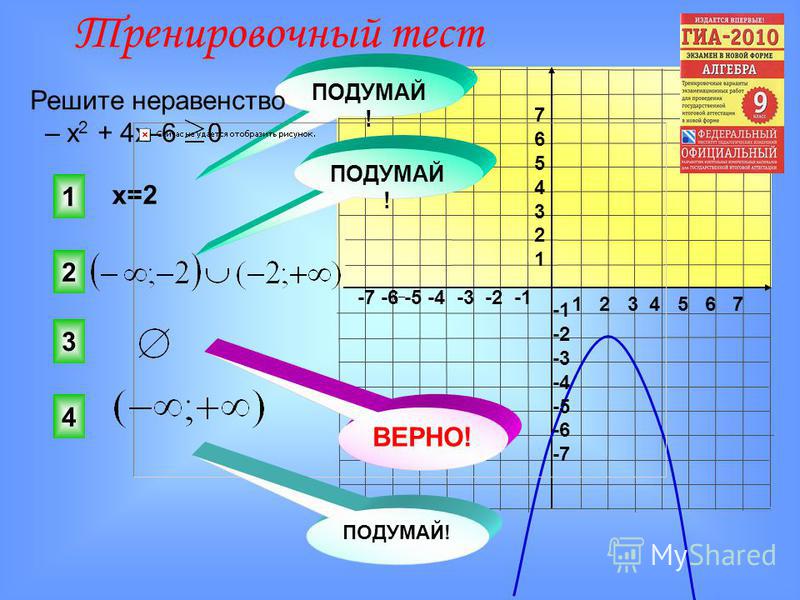
Решите неравенство методом ИНТЕРВАЛОВ
1)(5-х)(х+6)2)(х-10)(15-х)> ЛИБО РАВНО 0
3)(7-х)(11+х)>0
4)х-2.7/х-3 ( и все это
5)Х-7/х-1 (и все это > ЛИБО РАВНО НУЛЮ)
6)х(х-18)(х+1.7)
Решение: 1)(5-х)(х+6) 5-х=0 х+6=0 х-10=0 15-х=0
х=5 х=-6 х=10 х=15
— + — — + —
—— -6———— 5————— ———- 10 ————— 15———
х∈(-∞; -6) и (5; +∞) х∈[10;15] или 10≤х≤153) (7-х)(11+х)>0 4) [(х-2,7)/(х-3)]≤0
7-х=0 11+х=0 х-2,7=0 х-3=0
х=7 х=-11 х=2,7 х=3— + — + — +
——- -11 ———— 7 ———— ——— 2,7———— 3 ————-
х∈(-11; 7) или -115) (х-7)/(х-1) ≥0 6) х(х-18)(х+1,7) х-7=0 х-1=0 х=0 х-18=0 х+1,7=0
х=7 х=1 х=18 х=-1,7+ — + — + — +
——— 1 ———— 7———— ——— -1,7 ——- 0 ————- 18 ———
х∈(-∞; 1) и [7; +∞) х∈(-∞; -1,7) и (0; 18)Решите неравенство методом интервалов (x(2x-x^2)(2-x^2)(x^2-5x+6))/((4+x^2)(x^3-8)(x^2+x+200))
Решение: X(2x-x²)(2-x²)(x²-5x+6)/(4+x²)(x³-8)(x²+x+200)≤0
x²(2-x)(√2-x)(√2+x)((x-2)(x-3)/(4+x²)(x-2)(x²+2x+4)(x²+x+200)≤0
x≠2
x²(x-2)(x-√2)(x+√2)(x-3)/(4+x²)(x²+2x+4)(x²+x+200)≤0
4+x²>0 при любом х,x²+2x+4>0 при любом х,x²+x+200>0 при любом х т. к.Dx²(x-2)(x-√2)(x+√2)(x-3)≤0
к.Dx²(x-2)(x-√2)(x+√2)(x-3)≤0
x=0 x=2 x=√2 x=-√2 x=3
+ — — + _ +
——————————————————
-√2 0 √2 2 3
x∈[-√2;√2] U (2;3]Решите неравенство методом интервалов (2-3x) (3-2x) (2x-1)≤
0
Решение: Находим нули функции
у=(2-3x) (3-2x) (2x-1)
Решаем уравнение:
(2-3x) (3-2x) (2x-1)= O
2-3х = 0 или 3-2х = 0 или 2х-1 = 0
-3х = -2 -2х = -3 2х = 1
х= 2/3 х=3/2 х=1/2Отмечаем эти точки на числовой прямой и расставляем знаки функции. Знаки чередуются:
— + — +
—————-[1/2]——[2/3]————————[3/2]—————
Ответ. [1/2; 2/3] U [3/2;+∞)решить неравенство методом интервалов x ²(х-3) (х+6)
Решение: находим нули функции и изображаем на числовой прямойx ²(х-3) (х+6)
x² = 0, x — 3 = 0, x + 6 = 0
x = 0 x = 3 x = -6
x ∈ (-∞; -6) — положительный знак;
х ∈ (-6; 0) — отрицательной
х ∈ (0; 3) — отрицательной
х ∈ (3; +∞) — положительной.
 4-15x²-16≤0
4-15x²-16≤0
Решение: X⁴ — 15x² — 16 ≤ 0,
Решаем биквадратное уравнение
x⁴ — 15x² — 16 = 0
Замена переменной
х²=t
x⁴=t²
t² — 15t — 16 = 0
D=225+4·16=289=17²
t=(15-17)/2=-1 или t=(15+17)/2=16
обратная замена
х²=-1 — уравнение не имеет решений
х²=16 ⇒ х=-4 или х=4
Отмечаем корни на числовой прямой сплошным кружком или квадратными скобками [ ]
—————————[-4]—————-[4]——————-
Находим знак на [4;+∞) например при х=10
10⁴-15·10²-16=10000-1500-16>0
Ставим знак «+» и знаки чередуем
+ — +
—————————[-4]—————-[4]——————-Решение неравенства -4 ≤ х ≤ 4
Ответ. [-4;4]Решить неравенство методом интервалов:(2х+7)*(3х-4)*(х+5)≥0
Решение: (2х+7)*(3х-4)*(х+5)≥0
находим нули функции
2х+7 = 0
2х = -7
х = -3.5
3х-4 = 0
3х = 4
х = 1 1/3
х+5 = 0
х = -5
_-_-5__+__-3. 2-16)>0
2-16)>0
x(x+4)(x-4)>0,
В знаменателе всегда выкалываем точки,т.к. на 0 нельзя делить.
12 3 > >>
(х − 1) ∙ (х − 2) 0
Ответ:
asel07071
14.09.2020 12:27
Х Є [1; 2]
0,0(0 оценок)
Ответ:
alonsoqureaz
08.11.2020 18:02
0,0(0 оценок)
Ответ:
Maksimka087
08.11.2020 18:02
Решение во вложении…….
0,0(0 оценок)
Ответ:
dhhfdghgxdyhfdfcc
08.11.2020 18:02
х+4≥0х-1≥0х-2≥0
х≥0-4х≥0+1х≥0+2
х≥-4х≥1х≥2
ответ: х1≥-4, х2≥1, х3≥2
Проверка:
(-4+4)(1-1)(2-2)≥0
0≥0
0,0(0 оценок)
Ответ:
JaikHit533
08. 11.2020 18:02
11.2020 18:02
Только первое
Объяснение:
Всё на фото
0,0(0 оценок)
Ответ:
00002017
08.11.2020 18:02
решим интервалов:
где «-» там принимает отрицательные значения..
значит (-9;11) ⇒ (11;12) «(» и «)» означает что граничные корни не входят
-8,-7,-6,-5,-4,-3,-2,-1,0,1,2,3,4,5,6,7,8,9,10
0,0(0 оценок)
Ответ:
planeta88
08.11.2020 18:02
а = -6, в=7
Объяснение:
0,0(0 оценок)
Ответ:
Никитар456
08.11.2020 18:02
a=7 b=-6
Объяснение:
0,0(0 оценок)
Ответ:
dania45451
08.11.2020 18:02
3x²+6x+x+2-3x²+3≥19
7x≥14
x≥2
0,0(0 оценок)
Ответ:
zora3
08. 2 + 3 = 7x + 5
2 + 3 = 7x + 5
11 x < 1 —> x < 1\11 (ПРИМЕРНО 0.09)
0.3 — 0.3x < 0.1x + 0.7
0.4x > — 0.4
x > — 0.1
оТВЕТ: ОТ — 0.1 ДО 0.09
мОДА
0,0(0 оценок)
Ответ:
sasd3
08.11.2020 18:02
3-x+1>6-2x-2
-x+2x>6-2-3
x>1
Целое наименьшее число 2
0,0(0 оценок)
Ответ:
romanilblockp08hg1
08.11.2020 18:02
-3(х+2)+2(х-1)>3(х-3)+2,- 3х — 6 + 2х — 2 > 3x — 9 + 2,
-3x + 2x — 3x > — 9 + 2 + 2 + 6,
— 4x > 1
x < — 1/4
(-1/4)
ответ. (-∞; — 1/4)
0,0(0 оценок)
Ответ:
Gjjsg
08. 2-3х-10
2-3х-10
-4>-10
2)
а)ас <вс
б)а+с > в+с
в)а/с <в/с
3)
4)
а) -5х < -5у
б) 8+х > 8+у
г) х-1,1 > у-1,1
0,0(0 оценок)
Ответ:
султа65
08.11.2020 18:02
-3х-6+2х-3>3х-9+2
-3х+2х-3х>-9+2+6+3
2х>2
х>1
0,0(0 оценок)
Ответ:
Кисаааа123
08.11.2020 18:02
-3(х+2)+2(х-1)>3(х-3)+2
-3х-6+2х-2>3х-9+2
-3х+2х-3х>-9+2+6+2
-4х>1|: (-4)
х>0,25
ответ: ( от 0,25, до +бесконечности)
0,0(0 оценок)
Ответ:
sabinabaigali
08.11.2020 18:02
-3(х+2)+2(х-1)>3(х-3)+2
-3х-6+2х-2>3х-9+2
-3х+2х-3х>-9+2+2+6
-4х>1
х<-0,25
х€(-оо;-0,25)
0,0(0 оценок)
Ответ:
Masha07041
08.
-3(х+2)+2(х-1)>3(х-3)+2
-3х(х+2)+2(х-1)-3(х-3)+2=-3х-6+2х-2-3х+9+2=-4х+3<0,значит неравенство верно не при всех значениях х.
0,0(0 оценок)
Ответ:
lychik1111
08.11.2020 18:02
-3(х+2)+2(х-1)>3(х-3)+2,
-3x-6+2x-2>3x-9+2,
-4x>1,
x<-1/4.
ответ: x<1/4.
0,0(0 оценок)
Ответ:
Ksyusha891
08.11.2020 18:02
ツответ……………………….
0,0(0 оценок)
77-я Генассамблея ООН открылась в Нью-Йорке. Что сказал ее председатель
Материалы ИноСМИ содержат оценки исключительно зарубежных СМИ и не отражают позицию редакции ИноСМИ
Читать inosmi.ru в
В Нью-Йорке стартовала 77-я сессия Генассамблеи ООН. Ее председатель, венгерский дипломат Чаба Кереши, посвятил свое выступление целям устойчивого развития и призвал Совбез организации относиться к населению мира более «равномерно». Кроме того, Череши сделал несколько заявлений на иностранных языках, в том числе на русском.
Кроме того, Череши сделал несколько заявлений на иностранных языках, в том числе на русском.
Г-н Генеральный секретарь,
уважаемые главы государств и правительств,
Ваши превосходительства,
друзья,
миру нужны решения, основанные на солидарности, устойчивом развитии и науке.
Решения — потому что мы разработали множество соглашений, поставили прекрасные цели, но сделали слишком мало.
Нам нужна солидарность, потому что неравенство достигло рекордных высот.
Нам нужна устойчивость, потому что мы обязаны оставить после себя нашим детям пригодный для жизни мир.
Нам нужна наука, потому что она даёт нам нейтральные доказательства для того, чтобы действовать.
Искренне благодарю всех стран-членов, особенно Венгрию и группу восточноевропейских государств за то, что дали мне мандат воплотить этот девиз в жизнь.
Ваши превосходительства,
мы собрались здесь сегодня в самый важный момент за последние четыре десятилетия.
Des chaleurs extrêmes aux inondations dévastatrices — le changement climatique est ébranlent
nos communautés.
Notre consommation et nos méthodes de production lacèrent notre planète — de ses sols à ces
cieux. Nous vivons dans un état de crise humanitaire permanent.
(Перевод с французского: из-за изменения климата мы страдаем от аномальной жары, наводнений и засухи. Неустойчивое потребление и производство оставляют шрамы на всей нашей окружающей среде — от неба до морей. Мы как будто живём в состоянии постоянной гуманитарной чрезвычайной ситуации).
.أكثر من ثلاثمائة ملیون شخص في حاجة ماسة للمساعدات الإنسانیة والحمایة ـوذلك بزیادة قدرھا عشرة فيالمائة منذ ینایر
كما وصلت أزمة الجوع العالمیة إلىمستویات تنذر بالخطر بسبب تغیر المناخ والنزاعات وجائحة كوفید تسعة عشر
.وفي الأشھر الستة الماضیة، دفعتضخم أسعار الغذاء والطاقة بسبعین ملیون شخص على الأقل إلى الفقر
(Перевод с арабского: Более 300 миллионов людей остро нуждаются в гуманитарной помощи и защите. С января их стало больше на 10%. Из-за изменения климата, COVID-19 и конфликтов голод во всём мире достиг тревожного уровня. За последние полгода продовольственная и энергетическая инфляция поверг в нищету не менее 70 миллионов человек).
За последние полгода продовольственная и энергетическая инфляция поверг в нищету не менее 70 миллионов человек).
Инфляция, тем временем, находится на самом высоком за сорок лет уровне.
Четверть всего населения Земли проживает в районах, охваченных конфликтами, боевыми действиями и политической нестабильностью.
Редко когда насилие по всему миру бывало столь жестоким.*
Кто бы мог подумать, что война вернется в Европу? Что ядерная угроза вернется в политический дискурс, как способ урегулирования спора с соседом?
Прошло 203 дня с тех пор, как Генеральная Ассамблея приняла резолюцию, осуждающую военную кампанию против Украины. К сожалению, кровопролитие и страдания еще не прекратились.
Херсон и «народные республики» в Донбассе хотят инсценировать референдумы о вступлении в состав РоссииУкраинские регионы, освобожденные из-под контроля Киева, запросили референдумы о присоединении к России, сообщает Spiegel. Некоторые читатели издания опасаются ядерной войны. Другие указывают, что в Донбассе живут русские люди, а Москва их защищает.
Некоторые читатели издания опасаются ядерной войны. Другие указывают, что в Донбассе живут русские люди, а Москва их защищает.
20.09.2022
За это время ООН и ее партнеры предоставили еду и кров миллионам беженцев из этой страны.
Знаковое соглашение о коммерческом экспорте зерна из мировой житницы вселяет надежду.
Дипломатия работает над тем, чтобы начались поставки удобрений, чтобы дефицит, который мы наблюдаем сегодня, не привёл к голоду в следующем году.
Инспекторы ООН по атомной энергии находятся на одном из ключевых ядерных объектов Европы, чтобы предотвратить возможную катастрофу.
Ваши превосходительства,
тема наших 77-х общих прений: «Переломный момент: преобразующие решения взаимосвязанных проблем».
Я выражаю солидарность народу Пакистана, где разрушительные наводнения смыли сотни деревень.
Вы видели душераздирающие сцены разрушений: возможно, таким будет наше будущее.
Но в борьбе с изменением климата у нас есть решения.
Они основаны на достижениях в области научного сотрудничества и климатической дипломатии.
Но мы должны захотеть применить их на практике.
Международная группа экспертов по изменению климата зарекомендовала себя как бесценный инструмент поддержки политических решений по борьбе с изменением климата и адаптации к его последствиям.
Нам следует подумать о том, чтобы повторить её успех в области водных ресурсов, энергетики, продовольствия и биоразнообразия.
Это позволило бы нам обрести общепризнанную научную основу для действий.
По окончании этой недели высокого уровня я планирую начать серию консультаций с научными сообществами и попросить их о помощи.
Необходимо доносить знания от микроскопов к микрофонам.
77-я сессия Генеральной Ассамблеи станет ключевой в подготовке Саммита по целям в области устойчивого развития (ЦУР) в 2023 году и Саммита будущего в 2024 году.
В следующем году мы будем оценивать ЦУР-6 на Конференции ООН по водным ресурсам — первой с 1977 года.
Это очень срочный призыв. Вода станет следующей главной движущей силой конфликтов по всему миру.
У проблемы воды три грани. Слишком много воды. Недостаточно воды. Небезопасная вода.
У нас есть шанс изменить жизнь 2,1 миллиарда человек, не имеющих доступа к чистой воде.
Давайте сотрудничать, чтобы сделать Программу действий по водным ресурсам настолько трансформационной, практичной и осуществимой, насколько это возможно.
В ходе сессии мы также оценим Сендайскую рамочную программу и подумаем над тем, как повысить устойчивость к стихийным бедствиям.
Крайне важно, чтобы эти возможности приводили к значительным результатам.
Элементы для преобразования и достижения трансформации находятся в нашем распоряжении. Повестка дня до 2030 года, Сендайская рамочная программа, Парижское соглашение, Аддис-Абебская программа действий и наша общая повестка — все они направлены на одни цели.
Они описывают мир, к которому мы стремимся, и предлагают пути для достижения цели.
Меня обнадеживает тот факт, что предложения генерального секретаря и важные инициативы стран-членов дополняют друг друга.
Вызовы большие, и они взаимосвязаны, но их можно преодолеть.
Дамы и господа,
без всеобщего уважения к верховенству права, очень легко угодить в зыбкую почву.
Как нам всем известно, во времена кризиса в первую очередь оказываются под угрозой права человека.
Когда права человека оказываются под угрозой, это сигнал тревоги, призыв к действию.
И, говоря о правах человека, было бы упущением не отметить фундаментальную вещь, которая, как выяснилось, актуален в большинстве обществ мира. Это права женщин.
Просто недопустимо, чтобы каждая третья женщина в своей жизни подвергалась насилию.
В данный момент половину человечества слишком часто исключают из процесса принятия решений и руководства.
Но нам нужно, чтобы каждый мужчина и каждая женщина смогли в полной мере реализовать свой потенциал.
Мы сможем найти решения стоящим перед нами вызовам, только если вовлечём в процесс всех и будем ценить знания всех.
Платформа женщин-лидеров ГА ООН, организованная в сотрудничестве со структурой ООН-женщины, сегодня может стать ответом на этот призыв.
Женщины-лидеры стран и правительств предложат свои решения сложных проблем общества.
«Все легкие процессы заняты поляками». Почему украинцы начали устраивать забастовки на заводах в ПольшеВ Польше украинские рабочие все чаще идут на конфликт с местными работодателями, пишет «Страна». Мигранты жалуются на нарушения прав и низкую зарплату. На заводах начали устраивать забастовки.
20.09.2022
Данные говорят о том, что решение кризиса более эффективно, когда женщины берут на себя ведущую роль.
Я призываю вас предметно заняться этим вопросом: он касается справедливости и равенства, но, в первую очередь, человеческого достоинства.
Ваши превосходительства,
Во всех наших начинаниях я рассчитываю на тесное сотрудничество с Генеральным секретарем, Советом Безопасности, ЭКОСОС (Экономический и Социальный Совет ООН) и другими важными органами ООН.
Я готов поддержать государства-члены, чтобы определить преобразующие, продуктивные, системные и устойчивые решения.
Я обещаю сотрудничать со всеми заинтересованными сторонами, в том числе с гражданским обществом, молодежью, женщинами, научным сообществом.
Агентства, фонды и программы ООН очень важны для того, чтобы наши усилия вышли из стен этого зала и реализовались в обществе.
Чтобы реализовать сформулированную государствами-членами повестку, я рассчитываю на ваше конструктивное участие, сотрудничество и взаимное уважение друг к другу.
Подчеркиваю, что активизация деятельности ООН и Генеральной Ассамблеи должна продолжаться.
От того, насколько компетентно мы сможем улучшить нашу организацию, будет зависеть её значимость в глазах людей по всему миру.
Я хотел бы продвинуть переговоры о реформе Совета Безопасности: Совету пора представлять население мира более равномерно и следовать за реалиями XXI века.
Это вопрос доверия ко всей нашей организации и многостороннему порядку.
Дамы и господа,
Кризисное управление и трансформация потребуют от нас последовательных усилий, которые выходят далеко за рамки одной лишь сессии Генеральной Ассамблеи.
И на этой ноте позвольте мне закончить парой вечных мудрых слов о шансах и риске их упустить:
«Улучшения происходят тогда, когда мы над ними работаем. Ухудшения происходят тогда, когда мы упускаем стоящие перед нами возможности».
Наши возможности в наших руках. Давайте действовать.
Благодарю вас.
*эту часть выступления Кереши произнес на русском языке — прим. ИноСМИ
Журнал Театр. • Активизм и травма: есть ли связь?
Журнал ТЕАТР. предложил выпускнице МиГИП (Московского института гештальта и психодрамы), окончившей театроведческую магистратуру РГИСИ и сейчас совмещающей практику психолога с работой над диссертацией о театре Дмитрия Волкострелова, поразмышлять о природе активизма и реакций на него в обществе.
Активизм в России — явление разнородное и разноприродное, оно складывается из нескольких напластований.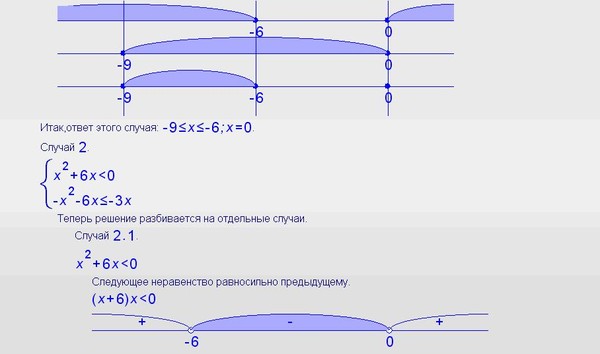 С одной стороны, мы все видим, как гражданский активизм последнего десятилетия объединяет людей, позволяет надеяться на формирование гражданского самосознания и, как следствие, гражданского общества. Волонтером быть теперь не просто модно, им просто неприлично не быть (финансовая поддержка тоже считается). С другой — государство как открыло со времен процесса против Pussy Riot новый сезон охоты, так до сих пор не может закрыть и преследует ЛГБТК+, полит-, фем- и, наконец, арт-активистов. Действия властей плюс пропаганда приводят к поляризации общества, в которой все делится на крайности, а люди маркируются как «свои» и «чужие». Представители современного искусства, говорящие порой на малодоступном среднестатистическому россиянину языке, да к тому же эпатирующие публику то наготой, то изображениями табуированных частей человеческого тела, да и просто нарушающие «правила общественного общежития», гораздо чаще попадают в категорию «чужие». Но если внимательно и уважительно расспросить людей, которых оскорбляет активизм, может оказаться, что их резкое неприятие в большой степени зиждется не на «патриотизме» или отвращении к конкретной идее, но на способе репрезентации, попросту говоря — на форме.
С одной стороны, мы все видим, как гражданский активизм последнего десятилетия объединяет людей, позволяет надеяться на формирование гражданского самосознания и, как следствие, гражданского общества. Волонтером быть теперь не просто модно, им просто неприлично не быть (финансовая поддержка тоже считается). С другой — государство как открыло со времен процесса против Pussy Riot новый сезон охоты, так до сих пор не может закрыть и преследует ЛГБТК+, полит-, фем- и, наконец, арт-активистов. Действия властей плюс пропаганда приводят к поляризации общества, в которой все делится на крайности, а люди маркируются как «свои» и «чужие». Представители современного искусства, говорящие порой на малодоступном среднестатистическому россиянину языке, да к тому же эпатирующие публику то наготой, то изображениями табуированных частей человеческого тела, да и просто нарушающие «правила общественного общежития», гораздо чаще попадают в категорию «чужие». Но если внимательно и уважительно расспросить людей, которых оскорбляет активизм, может оказаться, что их резкое неприятие в большой степени зиждется не на «патриотизме» или отвращении к конкретной идее, но на способе репрезентации, попросту говоря — на форме.
В 2013 году в журнале European Journal of Social Psychology было опубликовано исследование «Парадоксальное воздействие активистов: как негативные стереотипы уменьшают возможности социальных изменений», посвященное экспериментальному изучению восприятия активистов. В первой части эксперимента референтная группа выбрала характеристики трех условных типажей: «типичные активисты», «нетипичные» и «люди с неопределенными целями», затем смотрела, как влияет агент на восприятие его послания (спойлер: влияет, и сильно). Америка, имеющая репутацию самой политкорректной страны мира, удивила всех. В качестве примера рассматривались образы типичных феминисток и тех, кого мы обычно называем «зелеными».
 Защитников окружающей среды назвали «хиппи», tree-hugger, «наркоман». Из любопытного: в обеих категориях более 70 респондентов выбрали слово «либерал». Из важного: более 40 раз было выбрано слово «нетолерантный»[1].
Защитников окружающей среды назвали «хиппи», tree-hugger, «наркоман». Из любопытного: в обеих категориях более 70 респондентов выбрали слово «либерал». Из важного: более 40 раз было выбрано слово «нетолерантный»[1].Помимо удивительной, противоречащей устоявшемуся образу страны выборки (сделанной, кстати, случайными американцами — их наняли специально для этого опроса на одной из крупнейших платформ для фрилансеров), в этом исследовании действительно значимым представляется то, что, соглашаясь в целом с самими идеями, во второй части эксперимента респонденты, тем не менее, не хотели присоединяться и даже идентифицировать свои убеждения с убеждениями тех, кто попадает в их представление о «типичном активисте». Но так ли это удивительно, если вспомнить, какой образ ассоциируется с таким человеком?
В нашей стране институт гражданского активизма во многом пока еще формируется, хотя очевидно, что очень многие активисты также становятся заложниками негативных стереотипов. Откуда они берутся?
Откуда они берутся?
Преодолевая общественную стигму, активисты ищут способ быть услышанными. Многие из них находятся в постоянном поиске такой формы, которая не позволит оставаться равнодушным к их высказыванию. После левого (по своей природе) поворота в искусстве перформанса в конце 1960‑х, когда «в рамках новой эстетики производство предметов искусства начали считать совершенно лишним»
[2], художники стали рассматривать в качестве материала свое тело. Этот ставший привычным сегодня подход с точки зрения науки о психике может объясняться таким понятием, как диссоциация. Согласно психологическому словарю, это «такое состояние, при котором два или более психических процесса сосуществуют, не будучи связанными или интегрированными», а как иначе можно описать состояние человека в тот момент, когда он является и творцом, и тем, из чего он творит? Диссоциативные состояния и расстройства опознаются психикой здорового человека как необъяснимые и пугающие (если у них нет приемлемого объяснения) состояния другого, при котором он перестает присутствовать в реальности.
Примерно тогда же, в конце 1960‑х, логичным шагом после объективации собственного тела становится распространение такого направления перформанса, которое определяется саморазрушительным поведением автора. Роузли Голдберг относит большую часть этих перформансов к разделу «ритуал»[3], отмечая при этом, что «характерной чертой венских акционистов был их интерес к психологии: труды Зигмунда Фрейда и Вильгельма Райха породили перформансы, где искусство рассматривалось как своего рода психотерапия»[4]. Идея психотерапевтического воздействия такого перформанса на зрителей во многом опирается на понятие катарсиса, согласно которому, переживая благодаря театру (то есть безопасно) ужас и сострадание, мы сами очищаемся, но в такой концепции незаметно теряется разница между театром и перформансом: в театре у зрителей есть точное знание о том, что перед ними представление, иллюзия. Аутоагрессивный же перформанс — насилие, пусть и совершенное над собой, происходящее на глазах у публики или даже творимое ею, что переживается присутствующими совершенно иначе. Знаменитая формула Уолтера Кэннона «замри — беги — дерись — сдавайся» основана на исследовании инстинктивных реакций организма на опасность. Ситуация перформанса для зрителей — рамка с двойным, противоречивым посланием. С одной стороны, если кто‑то на наших глазах подвергается опасности, значит, она в принципе присутствует. С другой — зрители понимают, что они находятся в ситуации искусства, то есть в безопасности. При таком конфликте контекстов организм предпочтет выбрать реакцию замирания, то есть невмешательства в происходящее, и зритель чаще всего останется безучастным наблюдателем. Но это безучастие скорее сопоставимо с бессилием в связи с невозможностью интерпретировать обстоятельства. Если же в результате акции перформер получает повреждения, высока вероятность того, что многими зрителями впоследствии эта ситуация будет восприниматься как травматическая — поскольку они никак не помогли человеку спастись.
Аутоагрессивный же перформанс — насилие, пусть и совершенное над собой, происходящее на глазах у публики или даже творимое ею, что переживается присутствующими совершенно иначе. Знаменитая формула Уолтера Кэннона «замри — беги — дерись — сдавайся» основана на исследовании инстинктивных реакций организма на опасность. Ситуация перформанса для зрителей — рамка с двойным, противоречивым посланием. С одной стороны, если кто‑то на наших глазах подвергается опасности, значит, она в принципе присутствует. С другой — зрители понимают, что они находятся в ситуации искусства, то есть в безопасности. При таком конфликте контекстов организм предпочтет выбрать реакцию замирания, то есть невмешательства в происходящее, и зритель чаще всего останется безучастным наблюдателем. Но это безучастие скорее сопоставимо с бессилием в связи с невозможностью интерпретировать обстоятельства. Если же в результате акции перформер получает повреждения, высока вероятность того, что многими зрителями впоследствии эта ситуация будет восприниматься как травматическая — поскольку они никак не помогли человеку спастись.
2.
Перформеры, ориентированные на левую повестку, часто рассматривают свои аутоагрессивные работы как исследование социума, его реакций и состояния. По реакциям случайной и часто нерелевантной выборки они могут делать выводы о готовности или неготовности общества быть активным и свободным, но при этом не учитываются чисто психологические факторы, влияющие в этих обстоятельствах на людей. И самое главное — не учитываются невидимые еще последствия. Как отреагирует тот или иной зритель на то, что стал свидетелем насилия? Скорее всего, ему не придет в голову, что сам политический перформанс, работающий с травмой, может тоже стать травмой. То есть то, что является терапевтическим актом для исполнителя, для наблюдателя может оказаться травмирующим событием.
3.
Меняется искусство, меняется и его публика — в последнее время появляются работы, вызывающие резонанс именно с точки зрения этичности или неэтичности по отношению к зрителям. В 2018 году был показан неудачный эскиз Олега Христолюбского по пьесе «Человек из Подольска»: стремясь заострить тему насилия со стороны тех, кто обладает властью, над теми, у кого власти нет, режиссер перенес эту ситуацию на зрителей. Описанный в fb личный зрительский опыт (человеку, приглашенному из зала на сцену, сковывали руки пусть пластиковыми, но все же наручниками, пригибали лицом к столу и грубо требовали подчинения) породил мощную дискуссию о допустимом в театре; тему взаимодействия со зрителем и возможных непрогнозируемых воздействий на него подняли на своих страницах несколько профильных изданий. Сложные этические вопросы были подняты не впервые, но, видимо, к 2018‑му театральное сообщество накопило ресурсы и доросло до того, что авторы стали учитывать возможные психологические последствия тех или иных художественных решений для зрителей.
Описанный в fb личный зрительский опыт (человеку, приглашенному из зала на сцену, сковывали руки пусть пластиковыми, но все же наручниками, пригибали лицом к столу и грубо требовали подчинения) породил мощную дискуссию о допустимом в театре; тему взаимодействия со зрителем и возможных непрогнозируемых воздействий на него подняли на своих страницах несколько профильных изданий. Сложные этические вопросы были подняты не впервые, но, видимо, к 2018‑му театральное сообщество накопило ресурсы и доросло до того, что авторы стали учитывать возможные психологические последствия тех или иных художественных решений для зрителей.
Создатели спектакля Locker Room Talk, работающие с темой сексизма, специально проводили несколько показов «на своих», чтобы сформулировать достаточный и все учитывающий trigger warning. «Груз 300» Катрин Ненашевой, созданный как реакция на преодоление собственного ПТСР после примененных к авторке пыток[5], с его игрой в Шавку и Командира, открыто моделирующей ситуацию насилия, вызвал шквал разнообразных реакций. Несмотря на существующие предупреждения и возможность после показа пообщаться с психологом, часть зрителей все же говорила о том, что это не была просто смоделированная ситуация, что к ним — зрителям — было применено насилие со стороны авторов проекта. Справедливости ради стоит отметить, что немало голосов прозвучало и в защиту спектакля: другая часть зрителей считала, что насилия не было, была свобода выбора, как актерского, так и зрительского.
Несмотря на существующие предупреждения и возможность после показа пообщаться с психологом, часть зрителей все же говорила о том, что это не была просто смоделированная ситуация, что к ним — зрителям — было применено насилие со стороны авторов проекта. Справедливости ради стоит отметить, что немало голосов прозвучало и в защиту спектакля: другая часть зрителей считала, что насилия не было, была свобода выбора, как актерского, так и зрительского.
Похожая дискуссия разгорелась в конце 2019 года после показа в Петербурге спектакля «Игрушки» датской компании SIGNA. В этой работе звучало много актуальных левых тем: восприятие женщины как объекта, социальное неравенство и его последствия, модель капиталистических отношений как нездоровье, иерархическая структура как пространство насилия и многое другое. Зрители попадали в болезненную атмосферу с порога и на протяжении четырех часов находились в ней, имея приблизительно такой же выбор, как и персонажи: уйти, конечно, было можно, но при этом ты все терял (это было прописано достаточно жестко: покинувшим спектакль людям право на возвращение не давалось). В том числе и возможность что‑то изменить в самом перформансе.
В том числе и возможность что‑то изменить в самом перформансе.
Но сейчас, в контексте нашего разговора, самой интересной частью спектакля кажется его исходная точка: по легенде Леди (Хозяйка дома) рано лишилась матери и, похоже, неоднократно терпела насилие со стороны отца. Теперь, собрав вокруг себя таких же девчонок-сирот, Леди при помощи своей челяди устраивает «челленджи»: воссоздает ситуации из прошлого, вынуждая свои «игрушки» переживать такое же насилие каждый день. Если смотреть на происходящее по внутренним законам спектакля, то Леди срежиссировала для себя этот бесконечный перформанс, чтобы преодолеть собственную травму. Все перформерки совершеннолетние люди, точно знающие, зачем и для чего они сюда пришли, у них есть свободный выбор. Но разве это отменяет травмы, которые они получают в процессе? Если даже мы, зрители, окунувшись в это на четыре часа, чувствовали себя физически плохо и от двойных посланий (когда нам транслируется идея заботы и добровольности, а в реальности мы наблюдаем насилие и психологическую незрелость), и от общей нездоровой атмосферы, и от бессилия и невозможности объяснить девочкам, что им нужно вырваться отсюда, уйти куда угодно, лишь бы не оставаться здесь и не подвергаться насилию и дальше.
Можно предположить, что Леди — не просто садистка, что она таким образом дает своим «воспитанницам» возможность отрастить собственные клыки: научиться сопротивляться, выбирать приоритеты, ценить жизнь и здоровье, не поддаваться насилию. В общем, совершить тот выбор, который пришлось совершать нам, гостям. Ужас и гениальность этого решения в том, что именно так очень часто ведут себя люди с травмой и ПТСР. Они снова и снова, осознанно или бессознательно, воссоздают свой кошмар. Чтобы справиться с ним, чтобы найти решение, которое не приходило в голову в момент травматического события, с целью преодолеть собственное бессилие. К сожалению, еще Фрейд заметил, что «психическая травма или воспоминание о ней воздействует по типу инородного тела, которое еще долгое время после проникновения должно выступать воздействующим в настоящее время фактором»[6].
4.
Одним из последствий такого попадания инородного тела в нашу психику становится пограничное состояние, в которое может проваливаться человек при встрече с триггером. И тогда прерывается контакт с реальностью, носитель оказывается в своем внутреннем мире, где он все еще находится в небезопасной ситуации. Часто встречающийся элемент такого состояния — перенос — широко известное явление, описанное Фрейдом и его последователями как механизм для психоаналитической работы. От внимания широкой публики обычно ускользает тот факт, что перенос возникает не только в кабинете психотерапевта, но и в жизни. Это феномен бессознательного проецирования чувств, ожиданий и реакций с одного человека на другого (переживания из прошлого проецируются на любой объект, находящийся рядом). Интересно, что под влиянием переноса люди, не обученные распознавать его (как психологи и психотерапевты), так же бессознательно попадают под его конструкцию и начинают вести себя именно так, как ожидает этого носитель переноса. Например, человек, у которого сработал триггер на травмирующее событие, где к нему, беззащитному, проявляли агрессию, проваливается в это переживание. И начинает видеть вокруг не реальных людей, а агрессоров из прошлого — и взаимодействовать с ними из своей субъективной картины мира.
И тогда прерывается контакт с реальностью, носитель оказывается в своем внутреннем мире, где он все еще находится в небезопасной ситуации. Часто встречающийся элемент такого состояния — перенос — широко известное явление, описанное Фрейдом и его последователями как механизм для психоаналитической работы. От внимания широкой публики обычно ускользает тот факт, что перенос возникает не только в кабинете психотерапевта, но и в жизни. Это феномен бессознательного проецирования чувств, ожиданий и реакций с одного человека на другого (переживания из прошлого проецируются на любой объект, находящийся рядом). Интересно, что под влиянием переноса люди, не обученные распознавать его (как психологи и психотерапевты), так же бессознательно попадают под его конструкцию и начинают вести себя именно так, как ожидает этого носитель переноса. Например, человек, у которого сработал триггер на травмирующее событие, где к нему, беззащитному, проявляли агрессию, проваливается в это переживание. И начинает видеть вокруг не реальных людей, а агрессоров из прошлого — и взаимодействовать с ними из своей субъективной картины мира. Редко какой человек устоит перед таким мощным бессознательным ожиданием, его реакцией действительно становится
Редко какой человек устоит перед таким мощным бессознательным ожиданием, его реакцией действительно становится
агрессивность.
К сожалению, в арт-среде не принято исследовать художественные акции и реакцию зрителей через изучение переноса. Принимая во внимание воспоминания Марины Абрамович о травматичном детстве и постоянном домашнем насилии, можно прийти к выводу, что предлагая (в знаменитом «Ритме 0») публике делать с ее телом что угодно с использованием разложенных перед ней предметов, да еще и усугубив это самообязательством никак не вмешиваться в происходящее, она наверняка внесла в перформанс свою проекцию детской беззащитности и таким образом повлияла на его ход. Или Петр Павленский, зашивший себе рот в поддержку известной акции Pussy Riot, произвел, с одной стороны, мощный художественный жест, а с другой — отсутствие реакции было им почти запрограммировано: бездействие, молчание как метафора. Он пришел к Казанскому собору, представляя общество 2013 года именно таким образом. И общество его не подвело: даже полиция не вступила с ним во взаимодействие, вместо этого молча вызвав ему «скорую».
И общество его не подвело: даже полиция не вступила с ним во взаимодействие, вместо этого молча вызвав ему «скорую».
Есть и другой вариант объяснения подобных реакций: объективация свидетелей (или вовлеченных пространством пассивных участников). Создатель «Театра. На вынос» Алексей Ершов и художница Дарья Каминская (оба в разное время были студентами РГИСИ) устроили перформанс «Идиот» со сжиганием денег в декоративном пластиковом камине в здании института. Камин по‑настоящему загорелся и испускал токсичный дым. Находиться в здании института, продолжать лекции и показ курсовых спектаклей было невозможно: всех, кто находился внутри, эвакуировали. Очевидно, что авторы концепта не задавались вопросом, как повлияет перформанс на тех, кто находился рядом. Вынесем за скобки вариант настоящего пожара, но после ужасающей трагедии в «Зимней вишне» теми, кто находился внутри, подобные обстоятельства могли переживаться как катастрофические. Но если авторы все же задумывались об этом, то получается, что случайные участники изначально воспринимались ими как объекты — как безымянная часть институции, не обладающая правом на личностные реакции.
Справедливости ради вспомним, что годом ранее Ершов провел перформанс «31‑е» — вышел в одиночный пикет на Красную площадь с плакатом «Против системы Станиславского». Его и оператора, снимающего процесс в режиме прямой трансляции (для зрителей, собравшихся в зале Театра на Таганке), задержали, но, думается, это было вшито в идею акции: задержание было ее частью. Дополнительной ценностью этой работы можно считать то, что автор вступил в конфронтацию с властью в одиночестве, не включая в живой процесс ни зрителей, ни свидетелей. Не подвергая их никакому риску — и это в контексте нашего разговора важнее, чем далеко не оригинальная идея выступления против Станиславского.
Новые левые сегодня — сила, обретшая голос, их много, они громко и бесстрашно заявляют о себе, но делают это такими неоднозначными способами, которые сами становятся предметом бесконечных дискуссий. Феминистская оптика, деколониальный дискурс, #metoo, трансгендерный дискурс, BLM — новая этика стала тем, что в очередной раз раскололо мировое сообщество на враждующие лагеря. Кто‑то поддерживает ее безоглядно, кто‑то называет новой цензурой и насилием. Российское театральное сообщество двигается сразу в нескольких направлениях. С одной стороны, существуют и множатся проекты, работающие с темой через собственную травму: в них велик риск ретравматизации участников и зрителей. Самые уязвимые места таких практик — неучтенные при создании произведения искусства психологические факторы, влияющие на результат и способ восприятия. Но это лишь вопрос психологического просвещения и доброй воли создателей, а также их способность прочитать и воспринять мой текст не как нападение на их опыт и точку зрения.
Кто‑то поддерживает ее безоглядно, кто‑то называет новой цензурой и насилием. Российское театральное сообщество двигается сразу в нескольких направлениях. С одной стороны, существуют и множатся проекты, работающие с темой через собственную травму: в них велик риск ретравматизации участников и зрителей. Самые уязвимые места таких практик — неучтенные при создании произведения искусства психологические факторы, влияющие на результат и способ восприятия. Но это лишь вопрос психологического просвещения и доброй воли создателей, а также их способность прочитать и воспринять мой текст не как нападение на их опыт и точку зрения.
С другой стороны, всегда существуют гораздо менее громкие проекты, зачастую работающие на тот же результат, но созданные без такой личной вовлеченности, благодаря чему их создателям легче учитывать риски и контекст. Это спектакли, тем или иным способом рассказывающие об экологических проблемах (например, «Лицо Земли» Евгении Сафоновой в ТЮЗе имени Брянцева, «Что ответили птицы Франциску Ассизскому» Всеволода Лисовского в ЦТИ «Трансформатор» совместно с орнитарием парка «Сокольники» и др. ). Тему гендера и телесности уже несколько лет исследует тихий петербургский театр Maailmanloppu, появляются спектакли, рассматривающие квирность не только и не столько в ракурсе социальной трагедии (пример — «Зарница» Юрия Квятковского в ЦИМе). Спектакль «Кариес капитализма» (авторки Ада Мухина, Алена Папина, Ольга Тараканова и Дарья Юрийчук), критикующий капитализм, создан хоть и с учетом личного опыта, но сохраняет для зрителей возможность подключиться с безопасного расстояния. Список далеко не исчерпывающий, однако явственно говорящий о том, что опыт ненасильственного, осмелюсь даже сказать — «нетипичного» театрального активизма — возможен и вполне расцветает на ниве отечественного искусства.
). Тему гендера и телесности уже несколько лет исследует тихий петербургский театр Maailmanloppu, появляются спектакли, рассматривающие квирность не только и не столько в ракурсе социальной трагедии (пример — «Зарница» Юрия Квятковского в ЦИМе). Спектакль «Кариес капитализма» (авторки Ада Мухина, Алена Папина, Ольга Тараканова и Дарья Юрийчук), критикующий капитализм, создан хоть и с учетом личного опыта, но сохраняет для зрителей возможность подключиться с безопасного расстояния. Список далеко не исчерпывающий, однако явственно говорящий о том, что опыт ненасильственного, осмелюсь даже сказать — «нетипичного» театрального активизма — возможен и вполне расцветает на ниве отечественного искусства.
Наконец, невозможно не упомянуть, что, кроме практиков, свой активистский путь ищут и теоретики — критики, телеграм-блогеры, создатели подкастов. Правда, сегодня становится все труднее отделить теоретика от практика: многие, начинавшие как авторы каналов о театре, при первой возможности отправились исследовать интересующий их предмет практически. Это породило еще одно направление российского театрального активизма, странным образом микширующее его типичную и нетипичную инкарнации. Новые левые безапелляционны и нападают буквально на каждую попытку любого из коллег остаться в пределах предшествующих представлений и об искусстве, и об этике. Они не приемлют авторитетов и если чувствуют возможность их появления, сразу вносят underprivileged-дискурс. Они участвуют в лабораториях ЦИМа, но не забывают критиковать позицию его арт-директора. Они говорят о феминистских спектаклях, сбрасывая остальные с парохода современности; среди пьес, присланных на «Любимовку», они цепким взором выбирают только те, что попадают в деколониальную (в случае с Россией — анти-имперскую) оптику; они не забывают поставить на вид даже друг другу несоответствие между поступками в частной жизни и декларируемой позицией. Они бесконечно критикуют институции, забывая, что за ними тоже стоят люди, и если, выходя за пределы привычной модели разговоров в поле практики, сталкиваются с агрессивной же реакцией, оказываются не готовы брать за нее ответственность.
Это породило еще одно направление российского театрального активизма, странным образом микширующее его типичную и нетипичную инкарнации. Новые левые безапелляционны и нападают буквально на каждую попытку любого из коллег остаться в пределах предшествующих представлений и об искусстве, и об этике. Они не приемлют авторитетов и если чувствуют возможность их появления, сразу вносят underprivileged-дискурс. Они участвуют в лабораториях ЦИМа, но не забывают критиковать позицию его арт-директора. Они говорят о феминистских спектаклях, сбрасывая остальные с парохода современности; среди пьес, присланных на «Любимовку», они цепким взором выбирают только те, что попадают в деколониальную (в случае с Россией — анти-имперскую) оптику; они не забывают поставить на вид даже друг другу несоответствие между поступками в частной жизни и декларируемой позицией. Они бесконечно критикуют институции, забывая, что за ними тоже стоят люди, и если, выходя за пределы привычной модели разговоров в поле практики, сталкиваются с агрессивной же реакцией, оказываются не готовы брать за нее ответственность.
Одним из любимых тезисов новых левых «от театра» является идея (разумеется, сама по себе далеко не новая) о том, что профессионализм в этой сфере невозможен, не нужен и даже вреден (они критикуют государственное образование, говоря о его абьюзивной и архаичной природе, и призывают бойкотировать его). В последнем тезисе есть своя логика: отсутствие диплома не гарантирует умение мыслить по‑новому, но, возможно, позволяет сохранить дистанцию между автором и его работой — какой бы важной для него темы она ни касалась. Что же касается перформативного и/или партисипативного театра, выходящего на прямую коммуникацию со зрителем, то тут у меня своя боль — очень хочется, чтобы у тех, кто берется за него, было в анамнезе если не психологическое образование, то хотя бы пройденные курсы (или личная терапия), которые дадут возможность оценить собственную степень вовлеченности и умение сканировать реальность. В таком случае эти работы станут более безопасными для зрителей. Впрочем, допускаю, что немалое количество арт-проектов при таких условиях просто не появится.
[1] Bashir N., Lockwood P., Chasteen A., Nadolny D., Noyes I. The ironic impact of activists: Negative stereotypes reduce social change influence // European Journal of Social Psychology, Eur. J. Soc. Psychol. 43, 614—626 (2013). Published online in Wiley Online Library (wileyonlinelibrary.com) DOI: 10.1002/ejsp. 1983.
[2] Голдберг Р. Искусство перформанса. От футуризма до наших дней. Пер. с англ. Асланян А. М.: Ад Маргинем пресс, 2017. С. 189.
[3] Голдберг Р. Искусство перформанса. От футуризма до наших дней. Пер. с англ. Асланян А. М.: Ад Маргинем пресс, 2017. С. 206—2011.
[4] Там же. С. 207.
[5] Пытки — это “немодная” тема»: Как устроен проект «Груз 300». Саша Старость, Катрин Ненашева, Полина Андреевна и Олеся Гудкова о совместной работе. www.wonderzine.com/wonderzine/opportunities/partners/242259‑gruz-300 (дата обращения 14.08.2020).
[6] Фрейд З., Брейер Й. О психическом механизме истерических феноменов. Критически-историческое исследовательское издание под ред. С. Ф. Сироткина. Пер. с нем. М. М. Бочкаревой. — Ижевск:
Критически-историческое исследовательское издание под ред. С. Ф. Сироткина. Пер. с нем. М. М. Бочкаревой. — Ижевск:
ERGO, 2018. — VII, с. 6.
Неравенство Пошаговая математическая решатель
Неравенство
9. 1 Основные свойства
1 Основные свойства
Из главы 1, мы вспоминаем, что реальные цифры рассматриваются по реальным номерам. Множество действительных чисел представляет собой объединение трех непересекающихся множеств:
P : положительные действительные числа
N: отрицательные действительные числа
{0}: множество с единственным нулевым элементом
Кроме того, каждое действительное число a либо положительно, либо равно 0, либо -a положительно, а умножение и сложение подчиняются следующим правилам вычисления:
(положительно) ⋅ (положительно) = (положительно)
(отрицательно) ⋅ (отрицательно) = (положительно)
(положительно) ⋅ (отрицательно) = (отрицательно)
(отрицательно) ⋅ (положительно) = (отрицательно)
) + (положительно) = (положительно)
(отрицательно) + (отрицательно) = (отрицательно)
Отношение упорядочения меньше, чем в действительной системе счисления, определяется с помощью множества положительных действительных чисел. Пусть a и b — любые действительные числа.
Пусть a и b — любые действительные числа.
a меньше b, обозначается (a)<(b), тогда и только тогда, когда b-a положительное
Три других отношения порядка:
a меньше или равно b, обозначается a<=b, тогда и только тогда, когда (a)<(b) или a=b
a больше, чем b, обозначаемое a>b, тогда и только тогда, когда (b)<(a)
a больше или равно b , обозначаемый как a>=b, если (b)<(a) или b=a
Иногда мы хотим подчеркнуть, что отношение порядка a к b равно <, а не ≤ , и в этом случае мы говорим, что a строго меньше, чем b.
Любое утверждение, использующее одно из четырех отношений порядка, называется неравенством. В вычислениях с неравенствами используются пять основных правил.
I.1 Если a и b — любые действительные числа, то верно ровно одно из следующих
:
(a)<(b), a=b, (b)<(a) Если (a)<(b) и (b)<(c), то (a)<(c).
I.3 Если (a)<(b) и c — любое действительное число, то a+c=b+c.
I.4 Если (a)<(b) и c>0, тогда (ac)<(bc).
I.5 Если (a)<(b) и (c)<0, то ac>bc.
В наших вычислениях наиболее полезными являются правила I.3, I.4 и I.5.
В более продвинутых курсах доказывается, что правила с I.1 по I.5 верны для действительных чисел, используя определение < и свойства P, N. и {0}, перечисленные выше. Для интересующихся мы приводим в качестве образца доказательство 1.2.
Если (a) < (b) и (b) < (c), то по определению b-a положительно, а c-b положительно. Из того свойства P, что (положительное) + (положительное) = (положительное), следует, что (c — b) + (b — a) положительно. Но
(c-b)+(b-a)=c-b+b-a=c-a
Таким образом, c — a положительно, поэтому по определению (a) < (c).
Используя прямую с действительными числами, мы видим, что (a) < (b) тогда и только тогда, когда a находится левее b. Другие отношения порядка имеют аналогичную интерпретацию. Используя геометрическую интерпретацию <, мы можем интерпретировать пять основных правил.
I. 1 Если a и b точки на прямой с действительными числами, то ровно одна из
1 Если a и b точки на прямой с действительными числами, то ровно одна из
верно следующее:
a находится слева от b, a = b, b находится слева от a
I.2 Если a находится слева от b и b слева от c, то a находится слева от c
I.3 Если a находится слева от b и c — любое действительное число, +c находится слева от b+c.
I.4 Если a находится слева от b и c больше 0, то ac находится слева от bc.
I.5 Если a находится слева от b, а c меньше 0, то be находится слева от ac.
В главах 6 и 7 мы рассмотрели методы решения уравнений с одной или несколькими переменными. В этой главе мы рассмотрим методы решения неравенств с одной или двумя переменными. Под множеством решений неравенства с одной переменной мы понимаем все те действительные числа, которые удовлетворяют неравенству. Часто такие наборы решений представляют собой объединение отрезков и полустрок на прямой с действительными числами. Некоторые условные обозначения показаны ниже:
Первые три подмножества линии являются интервалами, а четвертое — полупрямой или лучом.
Множество решений неравенства с двумя переменными — это множество всех пар чисел, удовлетворяющих неравенству. Его график представляет собой область координатной плоскости.
Два неравенства, имеющие одно и то же множество решений, эквивалентны. Как и в случае с уравнениями, решение данного неравенства получается путем поиска эквивалентного неравенства, набор решений которого известен.
Мы завершим этот раздел несколькими примерами, связанными с отношениями неравенства.
Пример 1. Что из следующего верно? (а) -1/2<-3/7, (б) 3,2>=17/5.
(a) Компьютер -3/7-(-1/2).
-3/7-(-1/2)
=-3/7+1/2
=-6/14+7/14
=1/14
/33-1/2)=1/14 положительно, неравенство верно.
(b) Вычислить 3.2-17/5.
3.2-17/5
= 32/10-17/5
= 16/5-17/5
= -1/5
, так как 3,2-17/5 = -1/5-отрицательный, отрицательный, отрицательный неравенство неверно.
Пример 2. Нарисуйте графически каждое из следующих чисел и запишите в виде интервалов,1813
(a)
(b)
(c)
(a)
= (-3+∞) {Intersect} (-ЩЕСТ 1)
= (-3+∞) {Intersect} (-эйт. , 1)
, 1)
(b)
= (1,4) {Union} [2,5
= (1,5)
Lets’s Посмотрите на то, как наша математическая соль соль соль. Нажмите кнопку «Решить подобное», чтобы увидеть больше примеров.
Решить похожую задачуВведите свою проблему
(c)
= (1,+∞) {Union} (-3,0)
Из графа мы видим, что дальнейшая упрощение не возможно
9.2 Lineare Inqualitiation in in in in in neabitities in in neabitities in in neabitities in in neabitities in in in neabilities
9.2.
Мы можем использовать свойства неравенств, которые мы перечислили в предыдущем разделе, для решения линейных неравенств с одной переменной, то есть любого неравенства, которое элементарными операциями может быть преобразовано к одному из следующих видов.
ax+b<0
AX+B <= 0
AX+B> 0
AX+B> = 0
Пример 1. Решение неравенства
4x-3> = 2x+5
Добавить -2x к оба к обоим к обоим 4x-3> = 2x+5
. Стороны (I.3)
Стороны (I.3)
2x-3> = 5
Добавить 3 к обеим сторонам (I.3)
2x> = 8
Умножение обеих сторон на 1/2 (I.4)
x> =4
Таким образом, набор решений равен
= (4,+∞)
Геометрически это представлено числом
Пример 2. Решение неравенства
(2x+1)/(-3) <= 2
Умножение на -3
2x+1> =-6
. число обращает неравенство.
Добавьте -1 к обеим сторонам, затем умножьте на 1/2. (I.3, i.4)
x> =-7/2
Набор решений, следовательно,
= (-7/2,+∞)
Это иллюстрируется геометрически
.1813
Пример 3. Решите неравенство
-3 <3x-2 <= 7
Это неравенство означает, что x должен удовлетворить систему неравенств
-2 <3x-2
3x-2 <= 7
Однако мы можем решить оба неравенства одновременно.
-2<3x-2<=7
Прибавьте 2 ко всем трем выражениям
0<3x<=9
Умножьте все три выражения на 1/3.
0<(x)<=3
Таким образом, набор решений равен
= (0,3)
Это представлено геометрически
Пример 4. Решить неравенство
-8 <= 2-3x <6
-2.
-10<=-3x<4
Умножить на -1/3, изменив направление обоих неравенств.
10/3>=x>-4/3
Следовательно, набор решений равен1813
Давайте посмотрим, как наш решатель неравенств решает эту и подобные задачи. Нажмите кнопку «Решить подобное», чтобы увидеть больше примеров.
Решите похожую задачуВведите свою задачу
9.3 Неравенства, включающие абсолютные значения
Вспомните из главы 1, что расстояние между x и a на прямой с действительными числами равно |x-a|. Если x, a и b — действительные числа и |x-a| < (b), то x должен находиться на расстоянии меньшем, чем b, от a. Геометрически это представлено на рис. 1.
Рисунок 1
Мы видим, что неравенство
|x- a| < (b)
имеет своим решением множество
=(a-b,a+b)
Аналогично, если x удовлетворяет неравенству
|-a| < (b)
тогда x должен находиться на расстоянии, большем чем b, от a. Это представлено на рис. 2.
Это представлено на рис. 2.
Рис. 2.
Мы видим, что неравенство |x- a| < (b) имеет в качестве решения множество
= (-∞, A-B) {Union} (A+B,+∞)
Пример 1. Решение неравенства
| x-1/2 | <5
Граф.
Набор решений составляет
= (-9/2,11/2)
Пример 2. Решите неравенство
| X-2 |> 3
GRAPTIALE
| X-2 |> 3
GRAPTIALE
| X-2 |> 3
1818131310
| X-2 |> 3
GRAPTINGTION
| X-2 |> 3
GRAPTINGTION.
Набор решений равен
=(-∞,-1) {union} (5,+∞)
Пример 3. Решите неравенство
|x+1|<=3
Сначала заметим, что
|x+1|=|x-(-1)|
, так что |x+1| Расстояние от x до -1
График. Решите неравенство
|4-x|>5
Заметим, что |4-x| есть расстояние между 4 и x, такое же, как расстояние между x и 4, а именно |x-4|. Таким образом, приведенное выше неравенство эквивалентно неравенству
Таким образом, приведенное выше неравенство эквивалентно неравенству
| X-4 |> 5
чей график составляет
Набор решения
= (-∞, -1) {Союз} (9,+∞)
с тех пор | U | = |u-0|, которое является расстоянием от u до 0, неравенство
|u|<(a)
эквивалентно
|u-0|<(a)
что эквивалентно
(-a)<(u)<(a)
Если u=ax+b, мы видим, что
|ax+b|<(c)
эквивалентно
(-c)<(ax+b)<(c)
, которое можно решить, как в предыдущем разделе. Аналогично
| AX+B |> (C)
эквивалентен
Пример 5. Решение неравенства
| 2x-3 | <4
Это неравенство является эквивалентом к
-3. 2x-3<4
Прибавляем 3 и умножаем на 1/2.
-1<(2x)<7
-1/2<(x)<7/2
Набор решений равен
=(-1/2,7/2)
Давайте посмотрим, как наш решатель неравенств решает эту и подобные задачи. Нажмите кнопку «Решить подобное», чтобы увидеть больше примеров.
Нажмите кнопку «Решить подобное», чтобы увидеть больше примеров.
Решить похожую задачуВведите свою задачу
Пример 6. Выразите -1<(x)<5 в виде |x-a|<(b).
График -1<(x)<5 равен
Середина этого интервала равна
(5+(-1))/(2)=2
3, которая находится на расстоянии a 3 конечные точки -1 и 5. Таким образом, x должно быть a. расстояние менее 3 от середины 2, что дает нам 92+2x+c>=0
где a!=0. Любое неравенство, которое с помощью наших элементарных операций может быть преобразовано в неравенство указанного выше типа, конечно, может быть обработано теми же методами.
Мы будем использовать следующие свойства действительных чисел.
R.1 Если AB<0, то возможны два случая:
(a) A<0 и B>0
(b) A>0 и B<0
тогда возможны два случая:
(a) А>0 и В>0
92+5x-3> 0 Мы первым фактором для получения
(2x-1) (x+3)> 0
Из R. 2 Существует два случая:
2 Существует два случая:
(a) 2x- 1>0 и x+3>0
(b) 2x-1<0 и x+3<0
Поскольку число x является решением исходного неравенства тогда и только тогда, когда оно удовлетворяет либо (a), либо ( б) полный набор решений исходного неравенства представляет собой объединение набора решений (а) с набором решений (б).
(a) 2x-1>0 и x+3>0
Следовательно,
2x-1>0 и x+3>0
2x>1 и x>-3
x>1/2 и x>-3
for (a) is
=
= (1/2,+∞)
Geometrically,
(b) 2x-1<0 and x+3<0
Следовательно,
2x-1<0 и x+3<0
2x<1 и x<-3
x<1/2 and x<-3
The solution set for (b) is
=
=(-∞,-3)
Geometrically,
Recall that the множество решений исходного уравнения является объединением множеств, полученных в пунктах (б) и (а), а именно,
S=S_b {объединение} S_a
=(-∞,-3) {объединение} (12, +∞)
Геометрически,
Еще один метод решения квадратного неравенства заключается в указании на числовой прямой, где каждый множитель положительный, отрицательный или нулевой. Применяя этот метод к примеру 1, мы имеем
Применяя этот метод к примеру 1, мы имеем
Поскольку произведение (x+3)(2x-1) должно быть положительным, набор решений задается областями, в которых оба множителя имеют одинаковый знак. Из диаграммы видно, что это S = (-∞, -3) {union} (1/2,+∞)
Этот метод проще в использовании, чем первый, особенно если линейных множителей больше двух.
Пример 2. Решите неравенство
(x-2)(x+1)(x-1)<=0
— те числа, у которых хотя бы один из сомножителей равен нулю или нечетное число сомножителей отрицательно.
Таким образом, набор решений равен
S=(-∞,-1) {union} [1,2
Этот метод также применим к рациональному выражению, числитель и знаменатель которого можно разложить на линейные множители.
Пример 3. Решите неравенство
(x-1)/(x+2)<=2
Сначала преобразуем это неравенство в эквивалентное неравенство с нулем в правой части.
(x-1)/(x+2)-2<=2
(x-1-2(x+2))/(x+2)<=0
(-x-5)/(x+2)<=0
Как и прежде,
Обратите внимание, что -2 исключается, поскольку знаменатель здесь равен нулю. Набор решений:
Набор решений:
S=(-∞,-5) {union} (-2,+∞)
Давайте посмотрим, как наш решатель неравенств решает эту и подобные задачи. Нажмите кнопку «Решить подобное», чтобы увидеть больше примеров.
Решить похожую задачуВведите свою задачу
9.5 Линейные неравенства с двумя переменными
Неравенство любого из видов и b не равно нулю, называется линейным неравенством с двумя переменными.
Множеством решений такого неравенства является одна из двух полуплоскостей, определяемых линией ax+ по формуле + c = 0.
Чтобы убедиться, что множество решений на самом деле является одной из полуплоскостей прямой, решим неравенство для y, получив
y>2x+2
Точки (x,y), удовлетворяющие y>2x+2, это те, которые находятся выше точек на прямой y = 2x +2, а именно точки в полуплоскости над прямой . Поскольку неравенство строгое, точки на прямой не входят в множество решений. Обозначим это пунктирной линией.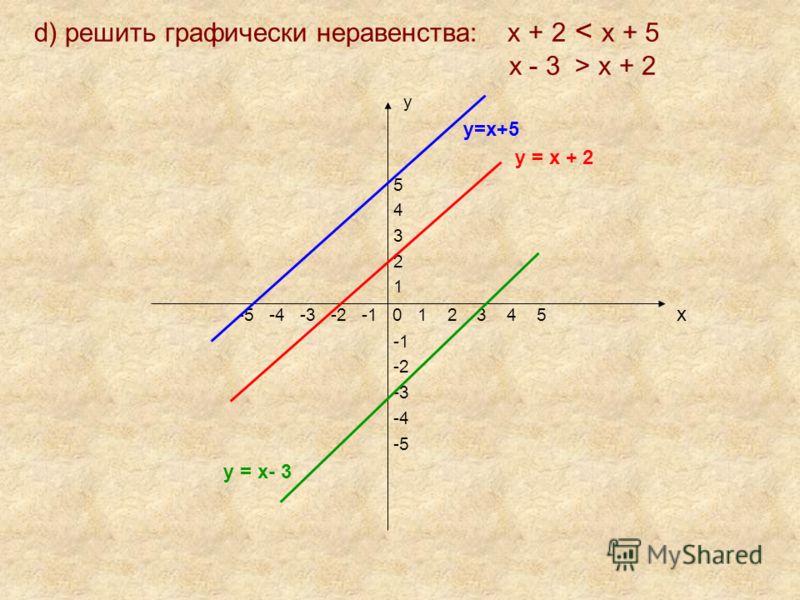
Алгебраически, набор решений-
Пример 2. Решить неравенство
X-3Y+2> = 0
Соли.1813
x>=3y-2
Поскольку x больше справа, множество решений представляет собой полуплоскость справа от прямой x-3y+2=0. Поскольку неравенство не является строгим, точки прямой включаются в множество решений. Сначала мы рисуем линию, а затем заштриховываем полуплоскость.
Альтернативный метод обнаружения полуплоскости решения состоит в том, чтобы подставить в неравенство координаты точки, не лежащей на прямой. Если неравенство выполнено, множество решений представляет собой полуплоскость, включающую эту точку, и другую полуплоскость в противном случае. Точку (0,0) легко использовать, если она не находится на прямой. В примере 2 подставляя (0,0) получаем
x-3y+2>0
(0)-3(0)+2>0
2>0
Поскольку (0,0) удовлетворяет неравенству, множество решений представляет собой полуплоскость, содержащую (0 ,0).
С системами неравенств можно работать аналогичным образом. Мы получаем набор решений графически, находя пересечение полуплоскостей решений отдельных неравенств в системе.
Пример 3. Решить неравенство1813
График Соответствующие строки L_1L_2:
L_1 Y-2x+3 = 0
L_2 2y+x-1 = 0
одним или другим методам выше. (1) представляет собой полуплоскость над l_1, тогда как набор решений S_2 из (2) представляет собой полуплоскость ниже l_2. Набор решений S_1 показан вертикальными линиями, а S_2 показан горизонтальными линиями. Следовательно, множество решений S системы равно
S=S_1 {пересечение} S_2
=
, то есть область, в которой пересекаются горизонтальные и вертикальные линии.
Пример 4. Решение системы
(1) x-y+1> = 0
(2) x <1
(3) y> =-3
Рассмотрим следующие уравнения. Находим, что решение набор S_2 из (2) — это полуплоскость слева от l_2, а набор решений S_3 из (3) — это полуплоскость над la. Набор решений равен 9.2
Набор решений равен 9.2
Множество решений S_p — это множество всех точек над параболой и на ней, а множество решений S_l — это множество всех точек внутри и на окружности. Таким образом, набор решений исходной системы равен
S=S_p {intersect} S_l
Решение неравенств: обзор
Решение Неравенства: обзор (стр. 3 из 3) Секции: линейные неравенства, квадратные неравенства, Другие неравенства Общие полиномиальные неравенства
Во-первых, я фактор, чтобы найти нули: x 5 + 3 x 4 23 x 3 51 x 2 + 94 х + 120 …так х = 5, 3, 1, 2, и 4 нули этого многочлена. (Посмотрите, как решить многочлены, если вы не знаете, как получить это решение.) Решить с помощью Test-Point Метод, я бы выбрал точку выборки в каждом интервале, интервалы быть (отрицательный бесконечность, 5), (5, 3), (3, 1), (1, 2), (2, 4) и (4, положительная бесконечность). Как видите, если ваша полиномиальная или рациональная функция имеет много факторов, Метод контрольных точек может занять довольно много времени. г. Решить с помощью коэффициента
Метод, я бы решил каждый фактор для его положительности: x + 5 > 0 для x > 5; х + 3 > 0 для x > 3; х + 1 > 0 для x > 1; х 2 > 0 для x > 2; и х 4 > 0 для x > 4. …и введите: …и решить: Тогда решение (вспоминая включить конечные точки, потому что это «или равно» неравенство) представляет собой набор x -значений в промежутках [5, 3], [1, 2], и [4, положительная бесконечность] . Как видите, если ваш полиномиальная или рациональная функция имеет много факторов, факторный метод может быть намного быстрее. Рациональные неравенства
Прежде всего, я должен
помните, что я не могу начать решать, пока не получу неравенство в «=
формат 0». Теперь мне нужно преобразовать к общему знаменателю: …и тогда я могу упростить:
Авторские права
Элизабет Стапель 1999-2011 Все права защищены Два фактора x + 6 и х 3. Обратите внимание, что x не может равняться 3,
иначе я бы делил на ноль, что недопустимо. Первый
фактор, x + 6, равно нулю
когда х = 6. Другой множитель, х 3, равно нулю
когда х = 3. Теперь х на самом деле не может равняться 3,
поэтому эта конечная точка не будет включена ни в один интервал решения (даже
хотя это неравенство «или равно»), но мне нужно
значение, чтобы выяснить, каковы мои интервалы. В этом случае мой
интервалы (отрицательная бесконечность, 3),
(3, 6],
и [6,
положительная бесконечность). Использование контрольной точки Метод, я бы выбрал точку в каждом интервале и проверил знак на результат. Я мог бы использовать, скажем, x = 0, х = 4 и х = 7, Используя факторный метод, Я решаю каждый фактор: x + 6 > 0 для x > 6 или x < 6; х 3 > 0 для x > 3. Потом делаю сетку: …заполните знаки по факторам: …и решить для знак рациональной функции: Так что решение все х в промежутках (отрицательный
бесконечность, 3 )
и [6 ,
положительная бесконечность). Есть еще один способ решить неравенства. Вам все еще нужно найти нули ( x -перехваты) сначала, а потом строишь график функции, и просто смотришь: где график выше оси x , функция положительная; где бы она ни находилась ниже оси, функция отрицательно. Например, для первого квадратное упражнение, г = х 2 3 х + 2 > 0, мы нашли нули на x = 1 и х = 2. Теперь посмотрим на график: На графике решение очевидно: вы бы взяли два интервала (но не конечные точки интервала) где линия выше оси x . Или тот огромный многочлен
мы сделали в верхней части этой страницы: x 5 + 3 x 4 23 x 3 51 x 2 + 94 х + 120 > 0. На фото раствор очевидно: возьмите три интервала (вместе с конечными точками интервала) где линия выше оси x . Как вы, наверное, догадались, графический калькулятор может сэкономить вам много времени на этих неравенствах если ты понимаешь, что делаешь. Вы все равно должны показать свою работу и рассуждения, но не стесняйтесь использовать картинки для подтверждения алгебры. г.<< Предыдущий Топ | 1 | 2 | 3 | Возвращаться к индексу
|
|
|
Решение квадратных неравенств — промежуточная алгебра, но на этот раз клонировано, не импортировано
Цели обучения
К концу этого раздела вы сможете:
- Решать квадратные неравенства графически
- Алгебраическое решение квадратных неравенств
Прежде чем приступить к работе, пройдите этот тест на готовность.
- Решить:
Если вы пропустили эту проблему, просмотрите (рисунок).
- Решить: .
Если вы пропустили эту проблему, просмотрите (рисунок).
- Решить
Если вы пропустили эту проблему, просмотрите (рисунок).
Ранее мы научились решать линейные неравенства и рациональные неравенства. Некоторые из методов, которые мы использовали для их решения, были одинаковыми, а некоторые отличались.
Сейчас мы научимся решать неравенства, имеющие квадратное выражение. Мы будем использовать некоторые приемы решения линейных и рациональных неравенств, а также квадратных уравнений.
г.Квадратные неравенства будем решать двумя способами — и графически, и алгебраически.
Решить квадратное неравенство графически
Квадратное уравнение имеет стандартный вид, если его записать в виде x 2 + bx + c = 0.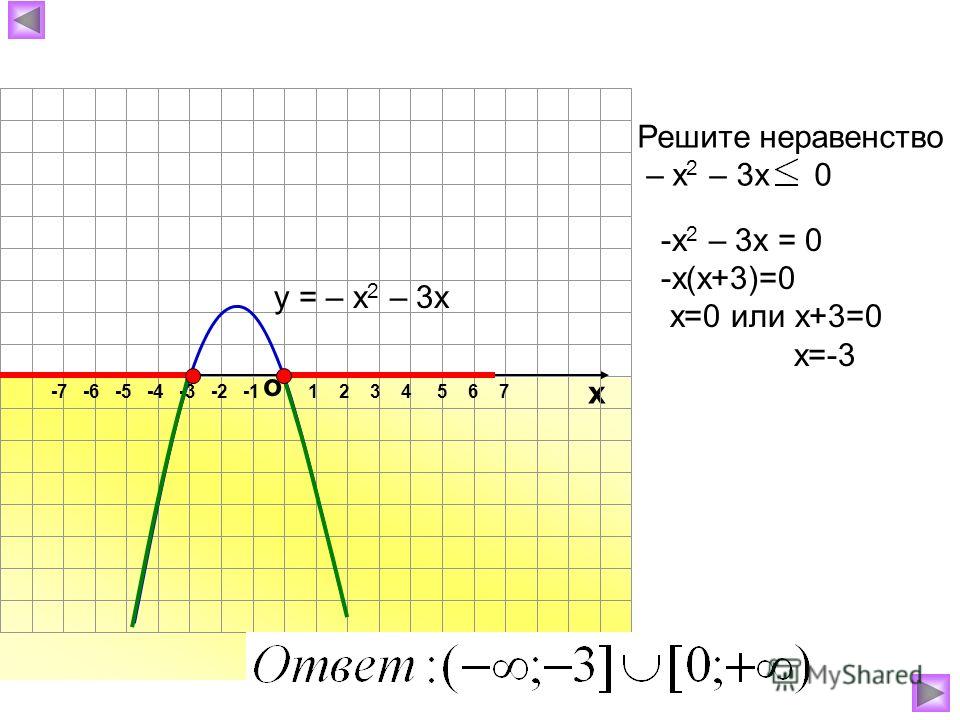 Если мы заменим знак равенства знаком неравенства, мы получим квадратное неравенство в стандартной форме.
Если мы заменим знак равенства знаком неравенства, мы получим квадратное неравенство в стандартной форме.
Квадратное неравенство
Квадратное неравенство — это неравенство, содержащее квадратное выражение.
Стандартная форма квадратного неравенства записывается:
График квадратичной функции Когда мы спрашиваем, когда ax 2 + bx + c < 0, мы спрашиваем, когда f( x ) < 0. Мы хотим знать, когда парабола находится ниже x — ось.
Когда мы спрашиваем, когда топор 2 + bx + c > 0, мы спрашиваем, когда f ( x ) > 0. Мы хотим знать, когда парабола выше оси y .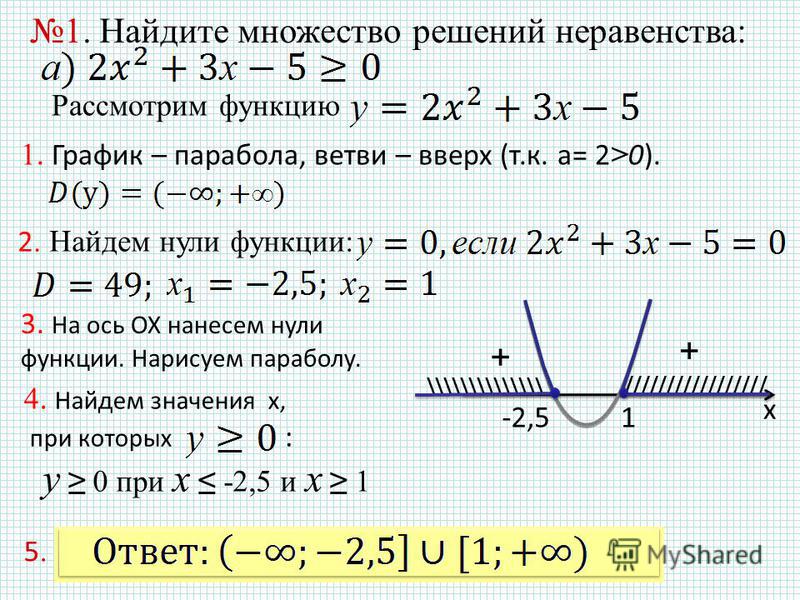
Как решить квадратное неравенство графически
Решить графически. Запишите решение в интервальной записи.
ⓐ Решите графически и ⓑ запишите решение в интервальной записи.
ⓐ
ⓑ
ⓐ Решите графически и ⓑ запишите решение в интервальной записи.
ⓐ
ⓑ
Перечислим шаги, необходимые для графического решения квадратного неравенства.
Решите квадратное неравенство графически.
- Запишите квадратное неравенство в стандартной форме.
- График функции
- Определите решение по графику.
В последнем примере парабола открылась вверх, а в следующем — вниз. В обоих случаях мы ищем ту часть параболы, которая ниже 9.3113 x , но обратите внимание, как положение параболы влияет на решение.
Решить графически. Запишите решение в интервальной записи.
The quadratic inequality in standard form is negative x squared minus 8 times x minus 12 less than or equal to 0. Graph the function f of x equals negative x squared minus 8 times x minus 12 to find that the parabola opens upward. Find the line of symmetry by using the equation x equals negative b divided by 2 times a. Substitute in to get x equals negative negative 8 divided by 2 times negative 1 to find x equals negative 4. Find the vertex of f of x equals negative x squared minus 8 times x minus 12 by finding that f of negative 4 equals negative negative 4 squared minus 8 times negative 4 minus 12. That gives you f of negative 4 equals negative 16 minus 32 minus 12, which then reduces to f of negative 4 equals 4. The vertex is (negative 4, 4). Find the x-intercepts. Let f of x equal 0. Take the original function, f of x equals negative x squared minus 8 times x minus 12, then make it 0 equals negative x squared minus 8 times x minus 12. Factor to get 0 equals negative 1 times the quantity x plus 6 times the quantity x plus 2.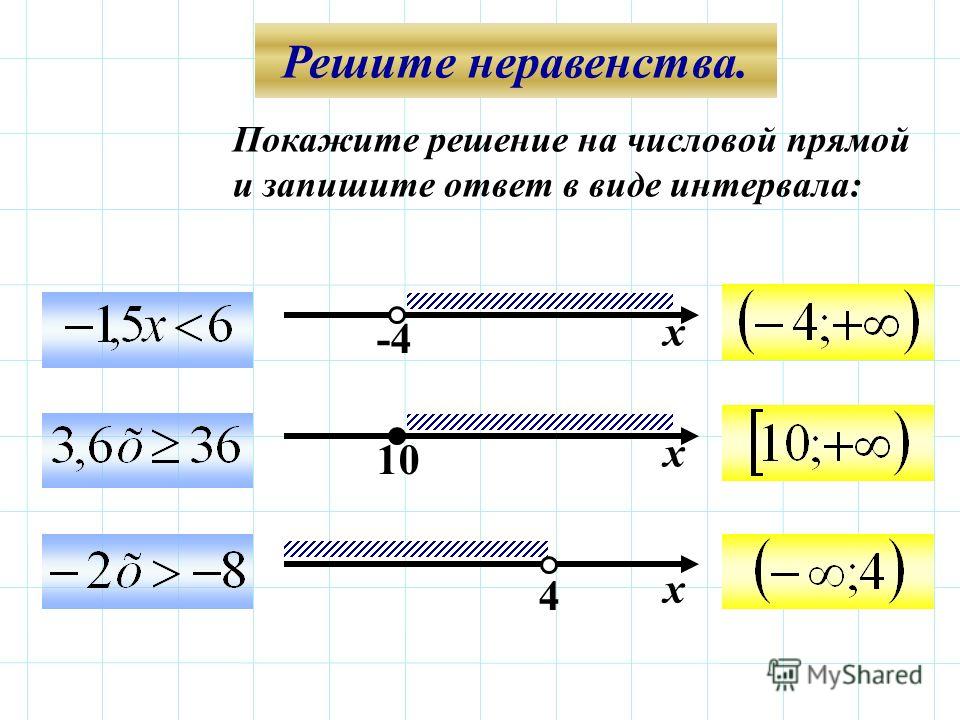 Use the Zero Product Property to get x equals negative 6 and x equals negative 2. The x-intercepts are (negative 6, 0) and (negative 2, 0). The graph shown is the curve formed when plotting all the points just found. Then, determine the solution from the graph, (negative infinity, negative 6] in union with [negative 2, infinity). We include the x-intercepts as the inequality is “less than or equal to.”» data-label=»»>
Use the Zero Product Property to get x equals negative 6 and x equals negative 2. The x-intercepts are (negative 6, 0) and (negative 2, 0). The graph shown is the curve formed when plotting all the points just found. Then, determine the solution from the graph, (negative infinity, negative 6] in union with [negative 2, infinity). We include the x-intercepts as the inequality is “less than or equal to.”» data-label=»»>| Квадратное неравенство в стандартной форме. | ||
| График функции . | Парабола открывается вниз. | |
| Найдите линию симметрии. | ||
| : Найдите вершину. | вершина | |
Найдите пересечения x . Позволять . Позволять . | ||
| Фактор. Использовать свойство нулевого продукта. | ||
| Постройте параболу. | x -перехваты | |
| Определите решение по графику. Мы включаем x -отрезков как неравенство — «меньше или равно». |
ⓐ Решите графически и ⓑ запишите решение в интервальной записи.
ⓐ
ⓑ
ⓐ Решите графически и ⓑ запишите решение в интервальной записи.
ⓐ
ⓑ
Алгебраическое решение квадратных неравенств
Алгебраический метод, который мы будем использовать, очень похож на метод, который мы использовали для решения рациональных неравенств. Найдем критические точки неравенства, которые будут решениями соответствующего квадратного уравнения. Помните, что полиномиальное выражение может менять знак только тогда, когда оно равно нулю.
Найдем критические точки неравенства, которые будут решениями соответствующего квадратного уравнения. Помните, что полиномиальное выражение может менять знак только тогда, когда оно равно нулю.
Мы будем использовать критические точки, чтобы разделить числовую прямую на интервалы, а затем определить, будет ли квадратное выражение положительным или отрицательным в интервале. Затем находим решение неравенства.
Алгебраическое решение квадратных неравенств
Алгебраическое решение. Запишите решение в интервальной записи.
Решить алгебраически. Запишите решение в интервальной записи.
Решить алгебраически. Запишите решение в интервальной записи.
В этом примере, поскольку выражение хорошо учитывается, мы также можем найти знак в каждом интервале так же, как мы делали это при решении рациональных неравенств. Находим знак каждого из сомножителей, а затем знак произведения. Наша числовая строка будет выглядеть так:
Результат будет таким же, как и при использовании другого метода.
Здесь мы суммируем шаги.
Алгебраически решить квадратное неравенство.
- Запишите квадратное неравенство в стандартной форме.
- Определите критические точки — решения соответствующего квадратного уравнения.
- Используйте критические точки, чтобы разделить числовую прямую на интервалы.
- Над числовой прямой покажите знак каждого квадратного выражения, используя контрольные точки из каждого интервала, подставленного в исходное неравенство.
- Определите интервалы, на которых неравенство верно. Запишите решение в интервальной записи.
Решить алгебраически. Запишите решение в интервальной записи.
Determine the critical points by solving the related quadratic equation, x squared minus 6 times x plus 7 equals 0. Write the quadratic formula, x equals negative b plus or minus the square root of b squared minus 4 times a times c all divided by 2 times a. Then substitute in the values of a, b, c, to get x equals negative negative 6 plus or minus the square root of negative 6 squared minus 4 times 1 times 7 all divided by 2 times 1. Simplify to get x equals 6 plus or minus the square root of 8 divided by 2. Remove the common factor of 2, x equals 2 times the quantity 3 plus or minus square root of 2 divided by 2 which gives x equals 3 plus or minus square root of 2. If x equals 3 plus square root of 2, x is approximately 1 and 6 tenths. If x equals 3 minus square root of 2, x is approximately 4 and 4 tenths. Use the critical points to divide the number line into intervals. A number line is shown with 1 and 6 tenths and 4 and 4 tenths. Test the numbers from each interval in the original inequality. On the number line, negative x squared plus 6 times x minus 7 is shown with the signs negative, positive, and negative. Determine the intervals where the inequality is correct. Write the solution in interval notation. negative x squared plus 6 times x minus 7 is greater than or equals to 0 in the middle interval, so the final answer is [3 minus square root of 2, 3 plus square root of 2″ data-label=»»>
On the number line, negative x squared plus 6 times x minus 7 is shown with the signs negative, positive, and negative. Determine the intervals where the inequality is correct. Write the solution in interval notation. negative x squared plus 6 times x minus 7 is greater than or equals to 0 in the middle interval, so the final answer is [3 minus square root of 2, 3 plus square root of 2″ data-label=»»>| Запишите квадратное неравенство в стандартной форме. | |
| Умножьте обе части неравенства на . Не забудьте поменять знак неравенства. | |
| Определите критические точки, решив соответствующее квадратное уравнение. | |
Напишите квадратную формулу. | |
| Затем подставьте значения . | |
| Упрощение. | |
| Упростите радикальное. | |
| Удалить общий делитель, 2. | |
| Используйте критические точки для разделения номер строки на интервалы. Тестовые номера из каждого интервала в исходном неравенстве. | |
| Определите интервалы, в которых
9Неравенство 1810 верно. Напишите решение в интервальной записи. | в среднем интервале |
Решить алгебраически. Запишите решение в интервальной записи.
Решить алгебраически. Запишите решение в интервальной записи.
Решениями квадратных неравенств в каждом из предыдущих примеров были либо интервал, либо объединение двух интервалов. Это произошло из-за того, что в каждом случае было найдено два решения соответствующего квадратного уравнения x 2 + bx + c = 0. Затем эти два решения дали нам либо две точки пересечения x- для графика, либо две критические точки для деления числовой прямой на интервалы.
Это коррелирует с нашим предыдущим обсуждением количества и типа решений квадратного уравнения с использованием дискриминанта.
Для квадратного уравнения вида ах 2 + bx + с = 0,
Последняя строка таблицы показывает нам, когда параболы никогда не пересекают ось x . Используя квадратную формулу для решения квадратного уравнения, подкоренное число является отрицательным. Получаем два комплексных решения.
Используя квадратную формулу для решения квадратного уравнения, подкоренное число является отрицательным. Получаем два комплексных решения.
В следующем примере решения квадратного неравенства будут результатом комплексного решения квадратного уравнения.
Решите, записав любое решение в интервальной записи:
ⓐⓑ
ⓐ
Simplify to get x equals 3 plus or minus the square root of negative 7 divided by 2. Simplify the radicand to get x equals 3 plus or minus the square root of 7 times i divided by 2. The complex solutions tell us that parabola does not intercept the x-axis. Also, the parabola opens upward. This tells us that the paprabola is completely above the x-axis, as the image of an upward-facing parabola that does not cross the x-axis shows.» data-label=»»>| Запишите квадратное неравенство в стандартной форме. | |
| Определите критические точки, решив соответствующее квадратное уравнение. | |
| Напишите квадратную формулу. | |
Затем подставьте значения .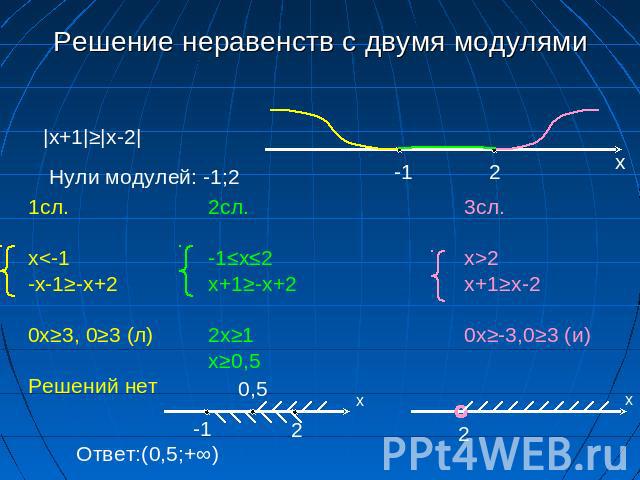 | |
| Упрощение. | |
| Упростите подкоренное число. | |
| Комплексные решения говорят нам о
Парабола не пересекает x оси. Также парабола открывается вверх. это говорит нам, что парабола находится полностью над осью x . | Комплексные решения |
Требуется найти решение задачи Поскольку для всех значений графика выше оси x , все значения x делают неравенство верным. В интервальной записи запишем
ⓑ
Поскольку соответствующее квадратное уравнение такое же, как в части (а), парабола будет такой же. Парабола открывается вверх и находится полностью над 9Ось 3113 x — ни одна из ее частей не находится ниже оси x .
Парабола открывается вверх и находится полностью над 9Ось 3113 x — ни одна из ее частей не находится ниже оси x .
Нам нужно найти решение задачи Поскольку для всех значений x график никогда не находится ниже оси x , никакие значения x не делают неравенство верным. Неравенство не имеет решения.
Решите и запишите любое решение в интервальной записи:
ⓐ ⓑ
ⓐ
ⓑ нет решения
Решите и запишите любое решение в интервальной записи:
ⓐ ⓑ
ⓐ нет решения
ⓑ
Ключевые понятия
- Графическое решение квадратного неравенства
- Запишите квадратное неравенство в стандартной форме.
- Постройте график функции, используя свойства или преобразования.
- Определите решение по графику.
- Как решить квадратное неравенство алгебраически
- Запишите квадратное неравенство в стандартной форме.

- Определите критические точки — решения соответствующего квадратного уравнения.
- Используйте критические точки, чтобы разделить числовую прямую на интервалы.
- Над числовой прямой покажите знак каждого квадратного выражения, используя контрольные точки из каждого интервала, подставленного в исходное неравенство.
- Определите интервалы, на которых неравенство верно. Запишите решение в интервальной записи.
- Запишите квадратное неравенство в стандартной форме.
Раздельные упражнения
Практика делает совершенным
Решайте квадратные неравенства графически
В следующих упражнениях ⓐ решите графически и ⓑ запишите решение в интервальной записи.
В следующих упражнениях решите каждое неравенство алгебраически и запишите любое решение в интервальной записи.
no solution
Writing Exercises
Explain critical points and how they are used to solve quadratic inequalities алгебраически.
Ответы будут разными.
Решите как графически, так и алгебраически. Какой метод вы предпочитаете и почему?
Опишите шаги, необходимые для графического решения квадратного неравенства.
Ответы будут разными.
Опишите шаги, необходимые для алгебраического решения квадратного неравенства.
Самопроверка
ⓐ После выполнения упражнений используйте этот контрольный список, чтобы оценить свое мастерство в выполнении целей этого раздела.
ⓑ По шкале от 1 до 10, как бы вы оценили свое знание этого раздела в свете ваших ответов на контрольный список? Как вы можете улучшить это?
Упражнения по обзору глав
Решение квадратных уравнений с использованием свойства квадратного корня
Решение квадратных уравнений вида x 2 = k Использование свойства квадратного корня
В следующих упражнениях решите, используя свойство квадратного корня.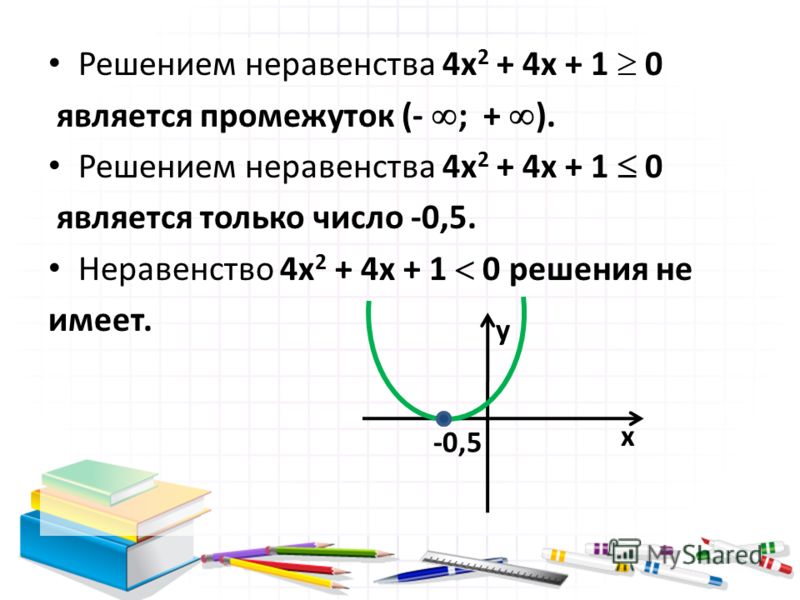
11.
Solve Quadratic Equations of the Form Using the Square Root Property
: В следующих упражнениях решите, используя свойство квадратного корня.
Solve Quadratic Equations by Completing the Square
Solve Quadratic Equations Using Completing the Square
In the following exercises , завершите квадрат так, чтобы получился идеальный квадратный трехчлен. Затем запишите результат в виде бинома в квадрате.
В следующих упражнениях решите, заполнив квадрат.
Solve Quadratic Equations of the form ax 2 + bx + c = 0, заполнив квадрат
В следующих упражнениях решите, заполнив квадрат.
Solve Quadratic Equations Using the Quadratic Formula
In the following exercises, solve by using the Quadratic Formula.
Use the Discriminant to Predict the Количество решений квадратного уравнения
В следующих упражнениях определите количество решений для каждого квадратного уравнения.
ⓐ 1 ⓑ 2 ⓒ 2 ⓓ 2
Определите наиболее подходящий метод для решения квадратного уравнения
решить каждое квадратное уравнение. Не решить.
ⓐ множитель ⓑ Квадратная формула ⓒ квадратный корень
Решение уравнений в квадратной форме
Решение уравнений в квадратной форме
В следующих упражнениях решите.
Solve Applications of Quadratic Equations
Solve Applications Modeled by Quadratic Equations
In the following упражнения, решите, используя метод факторинга, принцип квадратного корня или квадратную формулу. Округлите свои ответы до десятых, если необходимо.
Найдите два последовательных нечетных числа, произведение которых равно 323.
Найдите два последовательных четных числа, произведение которых равно 624.
Два последовательных четных числа, произведение которых равно 624, это 24 и 26, а также -24 и -26.
Треугольный баннер имеет площадь 351 квадратный сантиметр. Длина основания на два сантиметра больше, чем в четыре раза больше высоты. Найдите высоту и длину основания.
Юлий построил треугольную витрину для своей коллекции монет. Высота витрины на шесть дюймов меньше, чем удвоенная ширина основания. Площадь задней части корпуса составляет 70 квадратных дюймов. Найдите высоту и ширину корпуса.
Высота витрины на шесть дюймов меньше, чем удвоенная ширина основания. Площадь задней части корпуса составляет 70 квадратных дюймов. Найдите высоту и ширину корпуса.
Высота 14 дюймов, ширина 10 дюймов.
Плитка-мозаика в форме прямоугольного треугольника используется в качестве угла прямоугольной дорожки. Гипотенуза мозаики равна 5 футам. Одна сторона мозаики в два раза длиннее другой. Каковы длины сторон? Округлите до десятых.
Прямоугольный кусок фанеры имеет диагональ на два фута больше ширины. Длина фанеры в два раза больше ширины. Какова длина диагонали фанеры? Округлите до десятых.
Длина диагонали 3,6 фута.
Проход от улицы к дому Пэм имеет площадь 250 квадратных футов. Его длина в два раза меньше ширины в четыре раза. Найдите длину и ширину тротуара. Округлите до десятых.
Для выпускного вечера Софии несколько столов одинаковой ширины будут расставлены встык, чтобы получился сервировочный стол общей площадью 75 квадратных футов. Общая длина столов будет в два раза больше ширины. Найдите длину и ширину сервировочного стола, чтобы София могла купить скатерть нужного размера. Ответ округлить до десятых.
Общая длина столов будет в два раза больше ширины. Найдите длину и ширину сервировочного стола, чтобы София могла купить скатерть нужного размера. Ответ округлить до десятых.
Ширина сервировочного стола 4,7 фута, а длина 16,1 фута.
Мяч брошен вертикально в воздух со скоростью 160 футов/сек. Используйте формулу ч = -16 t 2 + v 0 t , чтобы определить, когда мяч будет на высоте 384 фута от земли. Округлите до десятых.
Пара на маленьком самолете совершила быстрый перелет в винную страну для романтического ужина, а затем вернулась домой. Самолет летел в общей сложности 5 часов и в одну сторону расстояние составило 360 миль. Если самолет летел со скоростью 150 миль в час, какова была скорость ветра, действовавшего на самолет?
Скорость ветра была 30 миль в час.
Эзра плыл вверх по реке и обратно в общей сложности за 6 часов.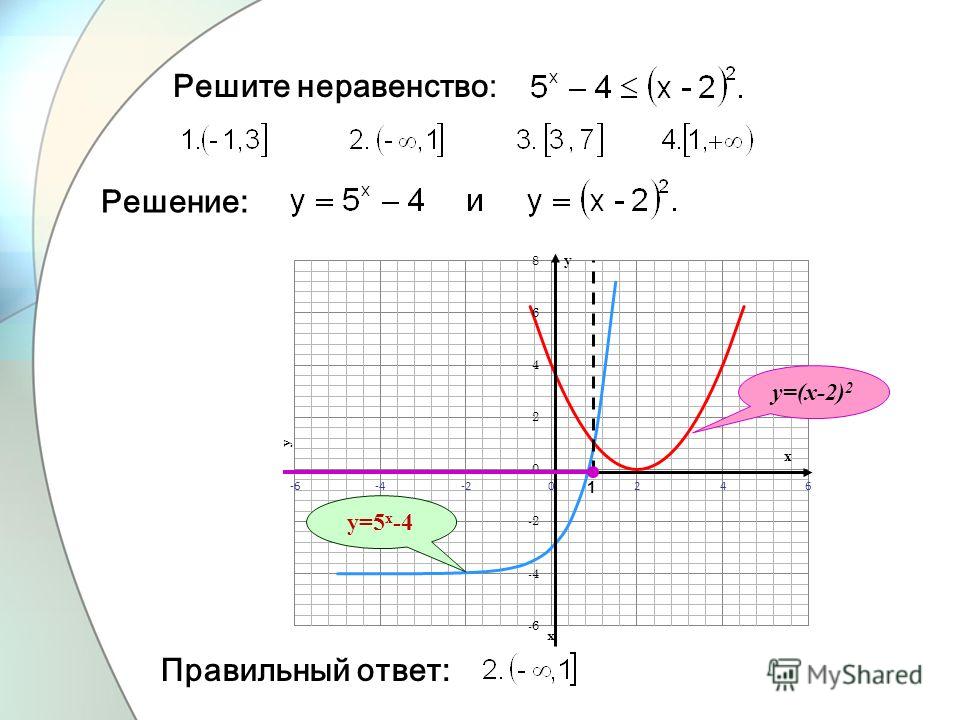 Путь был 4 мили в одну сторону, и течение было трудным. Если Рой плыл на байдарке со скоростью 5 миль в час, какова была скорость течения?
Путь был 4 мили в одну сторону, и течение было трудным. Если Рой плыл на байдарке со скоростью 5 миль в час, какова была скорость течения?
Два мастера могут сделать ремонт дома за 2 часа, если они будут работать вместе. Одному из мужчин требуется на 3 часа больше, чем другому, чтобы закончить работу самостоятельно. Сколько времени требуется каждому мастеру на ремонт дома индивидуально?
Один человек тратит 3 часа, а другой 6 часов, чтобы закончить ремонт в одиночку.
График квадратичных функций с использованием свойств
Распознавание графика квадратичной функции
В следующих упражнениях постройте график по точкам.
График
График
В следующих упражнениях определите, раскрываются ли следующие параболы вверх или вниз.
ⓐ
ⓑ
ⓐ
ⓑ
ⓐ вверх ⓑ вниз
Найдите ось симметрии и вершину параболы
В следующих упражнениях найдите ⓐ уравнение оси симметрии и ⓑ вершину.
Найдите точки пересечения параболы
В следующих упражнениях найдите точки пересечения x и y .
Постройте график квадратичных функций с использованием свойств
В следующих упражнениях постройте график, используя его свойства.
Solpe Maximum и минимальные применения
Solpe Maximum и минимальные применения
.
Максимальное значение равно 2, когда x = 2,
В следующих упражнениях решите. Округление ответов до десятых.
Мяч брошен вверх с земли с начальной скоростью 112 футов/сек.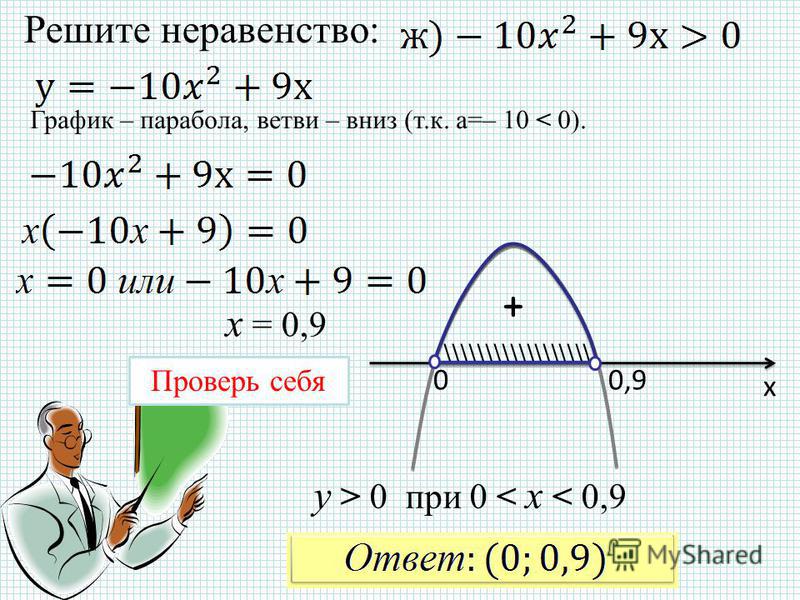 Используйте квадратное уравнение ч = -16 t 2 + 112 t , чтобы найти, сколько времени потребуется мячу, чтобы достичь максимальной высоты, а затем найдите максимальную высоту.
Используйте квадратное уравнение ч = -16 t 2 + 112 t , чтобы найти, сколько времени потребуется мячу, чтобы достичь максимальной высоты, а затем найдите максимальную высоту.
Детский сад огораживает прямоугольную площадку вдоль стены своего здания, чтобы дети могли играть на открытом воздухе. Им нужно максимально увеличить площадь, используя 180-футовое ограждение с трех сторон двора. Квадратное уравнение A = −2 x 2 + 180 x дает площадь A двора для длины x здания, которое будет граничить со двором. Найдите длину здания, которое должно граничить с двором, чтобы площадь была максимальной, а затем найдите максимальную площадь.
Примыкающая к зданию длина составляет 90 футов, что дает максимальную площадь 4050 квадратных футов.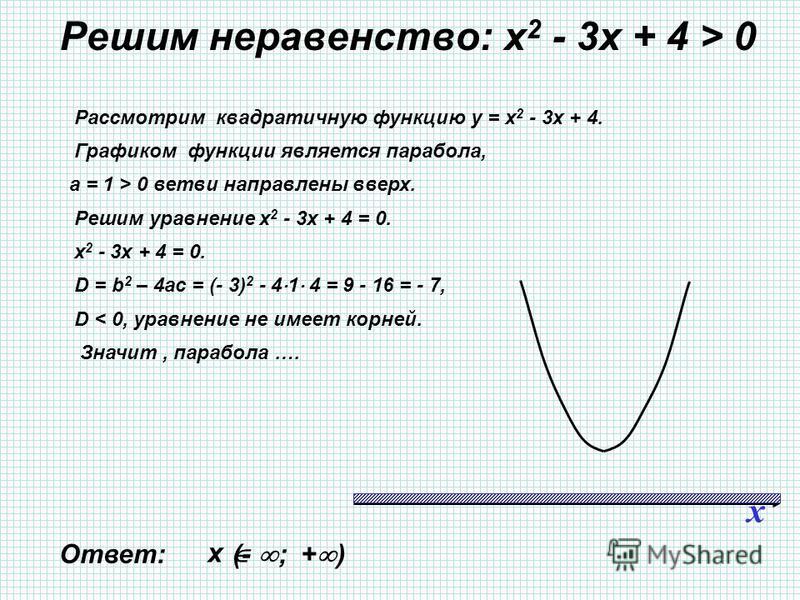
График квадратичных функций с использованием преобразований
График квадратичных функций вида
В следующих упражнениях постройте график каждой функции, используя сдвиг по вертикали.
В следующих упражнениях постройте график каждой функции, используя сдвиг по горизонтали.
В следующих упражнениях постройте график каждой функции, используя преобразования.
График квадратичных функций вида
В следующих упражнениях постройте график каждой функции.
График квадратичных функций с использованием преобразований
В следующих упражнениях перепишите каждую функцию в форме, заполнив квадрат.
В следующих упражнениях ⓐ перепишите каждую функцию в форме и ⓑ нарисуйте ее, используя преобразования.
В следующих упражнениях ⓐ перепишите каждую функцию в форме и ⓑ нарисуйте ее, используя свойства.
Найдите квадратичную функцию по ее графику
В следующих упражнениях запишите квадратичную функцию в форме.
Решение квадратных неравенств
Решение квадратных неравенств графически
В следующих упражнениях решите графически и запишите решение в интервальной записи.
В следующих упражнениях решите каждое неравенство алгебраически и запишите любое решение в интервальной записи.
нет решения
Практический тест
Использование свойства «Квадратный корень» для решения квадратного уравнения
Использование «Заполнение квадрата» для решения квадратного уравнения
Использование формулы квадратного уравнения для решения квадратного уравнения
Решите следующие квадратные уравнения. Используйте любой метод.
Используйте любой метод.
Используйте дискриминант для определения количества и типа решений каждого квадратного уравнения.
2 комплекса
Решите каждое уравнение.
Для каждой параболы найти ⓐ направление, в котором она раскрывается, ⓑ уравнение оси симметрии, ⓒ вершину, ⓓ x- и y -максимальные точки пересечения, и e) или минимальное значение.
ⓐ вниз ⓑ
ⓒ ⓓ
ⓔ минимальное значение, когда
Постройте график каждой квадратичной функции, используя точку пересечения, вершину и уравнение оси симметрии.
В следующих упражнениях постройте график каждой функции, используя преобразования.
В следующих упражнениях решите каждое неравенство алгебраически и запишите любое решение в интервальной записи.
Смоделируйте ситуацию квадратным уравнением и решите любым методом.
Найдите два последовательных четных числа, произведение которых равно 360.
Длина диагонали прямоугольника в три раза больше ширины. Длина прямоугольника в три раза больше ширины. Найдите длину диагонали. (Округлите до десятых.)
Длина диагонали составляет 3,8 единицы.
Воздушный шар с водой запускается вверх со скоростью 86 футов/сек. Используя формулу ч = −16 t 2 + 86 t , найдите, сколько времени потребуется воздушному шару, чтобы достичь максимальной высоты, а затем найдите максимальную высоту. Округлите до десятых.
г.Глоссарий
- квадратное неравенство
- Квадратное неравенство — это неравенство, содержащее квадратное выражение.
19.5: Решение квадратных неравенств — Mathematics LibreTexts
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 46460
Цели обучения
К концу этого раздела вы сможете:
- Решать квадратные неравенства графически
- Алгебраическое решение квадратных неравенств
Прежде чем приступить к работе, пройдите этот тест на готовность. {2}+y=15\). 9{2}+2 x-8}>0\)
{2}+y=15\). 9{2}+2 x-8}>0\)
Если вы пропустили эту проблему, просмотрите пример 7.56.
Ранее мы научились решать линейные неравенства и рациональные неравенства. Некоторые из методов, которые мы использовали для их решения, были одинаковыми, а некоторые отличались. Теперь мы научимся решать неравенства, имеющие квадратное выражение. Мы будем использовать некоторые приемы решения линейных и рациональных неравенств, а также квадратных уравнений. Мы будем решать квадратные неравенства двумя способами — графически и алгебраически. 9{2}-6(\color{red}{0}\color{black}{)}+8} \\ {f(0)=8}\end{массив}\)
\(y\ )-перехват равен \((0.8)\).
Мы используем ось симметрии, чтобы найти точку, симметричную \(y\)-перехвату. \(y\)-отрезок находится в \(3\) единицах слева от оси симметрии, \(x=3\). Точка \(3\) единиц справа от оси симметрии имеет \(x=6\).
Точка, симметричная \(y\)-перехвату
Точка \((6,8)\).
Решаем \(f(x)=0\).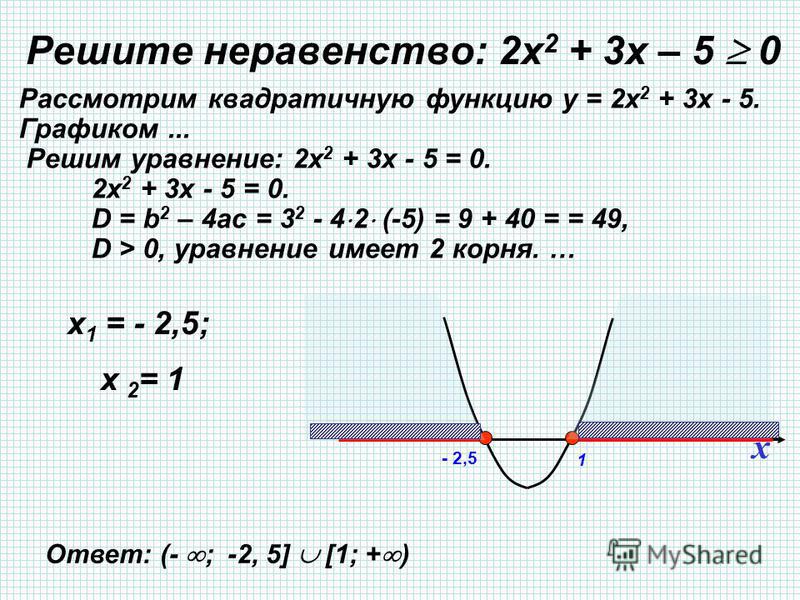
- Ответить
-
Рисунок 9.8.5 - \((-\infty, 2] \cup[6, \infty)\)
-
Перечислим шаги, необходимые для графического решения квадратного неравенства.
Графическое решение квадратного неравенства
- Запишите квадратное неравенство в стандартной форме. 9{2}-8 x-12 \end{выровнено}\) Фактор: использование свойства нулевого продукта. \(\begin{массив}{l}{0=-1(x+6)(x+2)} \\ {x=-6 \quad x=-2}\end{массив}\) Постройте параболу.
\(x\)-отрезки \((-6,0), (-2.0)\)
Рисунок 9.8.7 Определите решение по графику. Мы включаем \(x\)-перехваты, поскольку неравенство «меньше или равно». 9{2}+10x−16≤0\) графически
9{2}+10x−16≤0\) графически - Запишите решение в интервальной записи
- Ответить
-
Рисунок 9.8.9 - \((-\infty, 2] \cup[8, \infty)\)
-
Алгебраическое решение квадратных неравенств
Алгебраический метод, который мы будем использовать, очень похож на метод, который мы использовали для решения рациональных неравенств. Найдем критические точки неравенства, которые будут решениями соответствующего квадратного уравнения. Помните, что полиномиальное выражение может менять знак только тогда, когда оно равно нулю. 9{2}-x-12=0} \\ {(x+3)(x-4)=0} \\ {x+3=0 \quad x-4=0} \\ {x=-3 \ четверка х=4}\конец{массив}\) Шаг 3 : Используйте критические точки, чтобы разделить числовую прямую на интервалы. Используйте \(-3\) и \(4\), чтобы разделить числовую прямую на интервалы. Шаг 4 : Над числовой линией покажите знак каждого квадратного выражения, используя контрольные точки из каждого интервала, подставленного из исходного неравенства. 9{2}−x−12\) хорошо размножаются, мы также можем найти знак в каждом интервале так же, как мы это делали, когда решали рациональные неравенства. Находим знак каждого из сомножителей, а затем знак произведения. Наша числовая линия будет выглядеть так:
Шаг 4 : Над числовой линией покажите знак каждого квадратного выражения, используя контрольные точки из каждого интервала, подставленного из исходного неравенства. 9{2}−x−12\) хорошо размножаются, мы также можем найти знак в каждом интервале так же, как мы это делали, когда решали рациональные неравенства. Находим знак каждого из сомножителей, а затем знак произведения. Наша числовая линия будет выглядеть так:
Результат будет таким же, как и при использовании другого метода.
Здесь мы суммируем шаги.
Алгебраическое решение квадратного неравенства
- Запишите квадратное неравенство в стандартной форме.
- Определите критические точки — решения соответствующего квадратного уравнения. 9{2}-4 \cdot 1 \cdot(7)}}{2 \cdot 1}\) Упрощение. \(x=\frac{6 \pm \sqrt{8}}{2}\) Упростите радикальное.
 \(x=\frac{6 \pm 2 \sqrt{2}}{2}\) Удалить общий множитель \(2\). \(\begin{array}{l}{x=\frac{2(3 \pm \sqrt{2})}{2}} \\ {x=3 \pm \sqrt{2}} \\ { x=3+\sqrt{2}} \quad x=3-\sqrt{2} \\ {x \приблизительно 1,6}\quad\quad\:\:\: x\приблизительно 4,4\end{массив}\) 9{2}+bc+c=0, a≠0\). Рисунок 9.8.14
\(x=\frac{6 \pm 2 \sqrt{2}}{2}\) Удалить общий множитель \(2\). \(\begin{array}{l}{x=\frac{2(3 \pm \sqrt{2})}{2}} \\ {x=3 \pm \sqrt{2}} \\ { x=3+\sqrt{2}} \quad x=3-\sqrt{2} \\ {x \приблизительно 1,6}\quad\quad\:\:\: x\приблизительно 4,4\end{массив}\) 9{2}+bc+c=0, a≠0\). Рисунок 9.8.14Последняя строка таблицы показывает нам, когда параболы никогда не пересекают ось \(x\). Используя квадратную формулу для решения квадратного уравнения, подкоренное число является отрицательным. Получаем два комплексных решения.
В следующем примере решения квадратного неравенства будут результатом комплексного решения квадратного уравнения.
Пример \(\PageIndex{5}\)
Решить, записав любое решение в интервальной записи:
- 9{2}-4 \cdot 1 \cdot(4)}}{2 \cdot 1}\) Упрощение. \(x=\frac{3 \pm \sqrt{-7}}{2}\) Упростите подкоренное число.
- Определите решение по графику.
 \(x=\frac{3 \pm \sqrt{7 i}}{2}\) Комплексные решения говорят нам, что парабола
\(x=\frac{3 \pm \sqrt{7 i}}{2}\) Комплексные решения говорят нам, что парабола
не пересекает ось \(x\).
Также парабола открывается вверх. Это число
говорит нам, что парабола находится полностью над осью \(х\). 9{2}+bx+c\) с использованием свойств или преобразований. - Как решить квадратное неравенство алгебраически
- Запишите квадратное неравенство в стандартной форме.
- Определите критические точки — решения соответствующего квадратного уравнения.
- Используйте критические точки, чтобы разделить числовую прямую на интервалы.
- Над числовой прямой покажите знак каждого квадратного выражения, используя контрольные точки из каждого интервала, подставленного в исходное неравенство.
- Определите интервалы, на которых неравенство верно.


 к.Dx²(x-2)(x-√2)(x+√2)(x-3)≤0
к.Dx²(x-2)(x-√2)(x+√2)(x-3)≤0 4-15x²-16≤0
4-15x²-16≤0 2-16)>0
2-16)>0
 Потом рисую
сетка:
Потом рисую
сетка:
 Обратите внимание на использование квадратных скобок, чтобы указать, что 6
можно включить в решение, но это 3
не может.
Обратите внимание на использование квадратных скобок, чтобы указать, что 6
можно включить в решение, но это 3
не может.
 Мы нашли нули
многочлена, равного x = 5, х = 3, х = 1, х = 2, и х = 4. Теперь посмотрим
на графике:
Мы нашли нули
многочлена, равного x = 5, х = 3, х = 1, х = 2, и х = 4. Теперь посмотрим
на графике: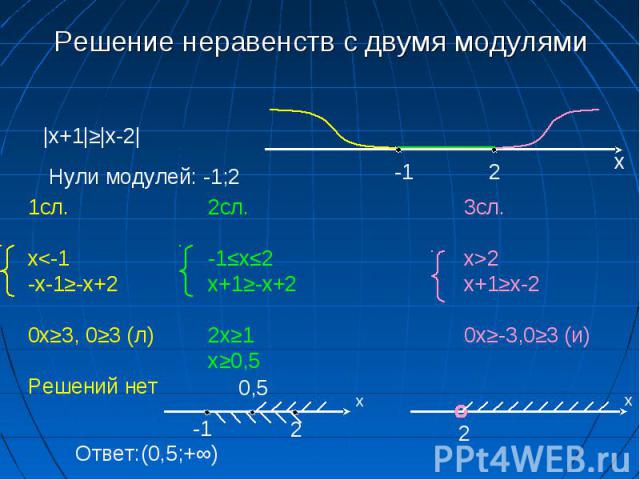 «Решение неравенства: обзор». Пурпурная математика .
Доступно по номеру
«Решение неравенства: обзор». Пурпурная математика .
Доступно по номеру 

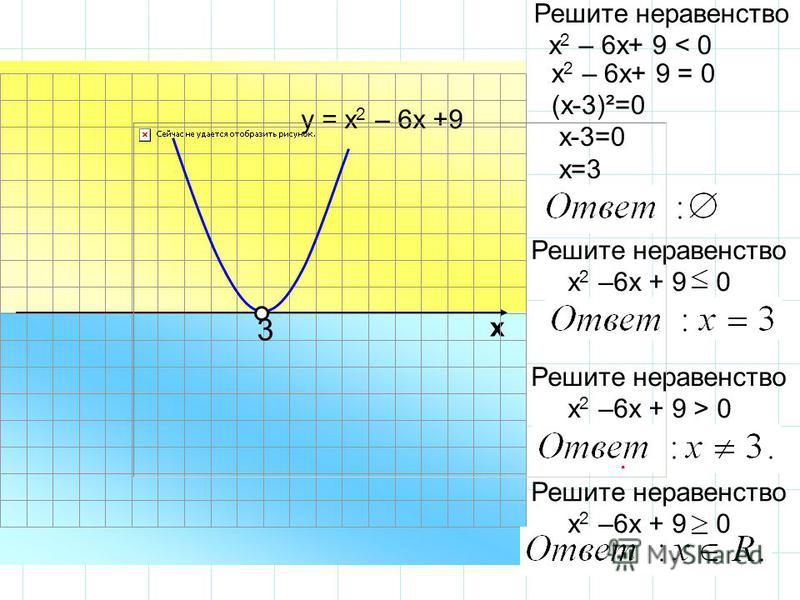 9{2}+10x−16≤0\) графически
9{2}+10x−16≤0\) графически \(x=\frac{6 \pm 2 \sqrt{2}}{2}\) Удалить общий множитель \(2\). \(\begin{array}{l}{x=\frac{2(3 \pm \sqrt{2})}{2}} \\ {x=3 \pm \sqrt{2}} \\ { x=3+\sqrt{2}} \quad x=3-\sqrt{2} \\ {x \приблизительно 1,6}\quad\quad\:\:\: x\приблизительно 4,4\end{массив}\) 9{2}+bc+c=0, a≠0\). Рисунок 9.8.14
\(x=\frac{6 \pm 2 \sqrt{2}}{2}\) Удалить общий множитель \(2\). \(\begin{array}{l}{x=\frac{2(3 \pm \sqrt{2})}{2}} \\ {x=3 \pm \sqrt{2}} \\ { x=3+\sqrt{2}} \quad x=3-\sqrt{2} \\ {x \приблизительно 1,6}\quad\quad\:\:\: x\приблизительно 4,4\end{массив}\) 9{2}+bc+c=0, a≠0\). Рисунок 9.8.14 \(x=\frac{3 \pm \sqrt{7 i}}{2}\) Комплексные решения говорят нам, что парабола
\(x=\frac{3 \pm \sqrt{7 i}}{2}\) Комплексные решения говорят нам, что парабола 