Как найти напряжение через ЭДС и сопротивление?
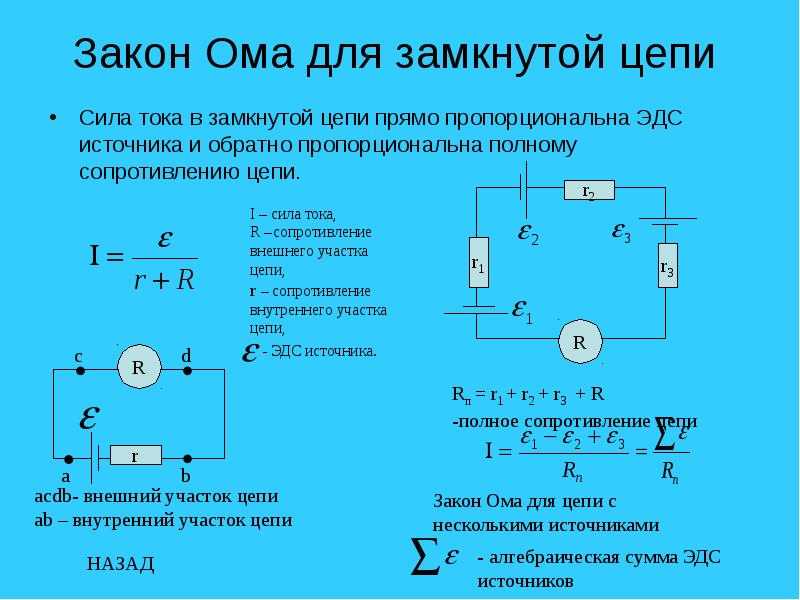
Закон Ома для замкнутой цепи
Если к источнику питания подключить внешнюю цепь сопротивлением R, в цепи пойдёт ток с учётом внутреннего сопротивления источника:
I – Сила тока в цепи.
– Электродвижущая сила (ЭДС) – величина напряжения источника питания не зависящая от внешней цепи (без нагрузки). Характеризуется потенциальной энергией источника. r – Внутреннее сопротивление источника питания.
Для электродвижущей силы внешнеее сопротивление R и внутреннее r соединены последовательно, значит величина тока в цепи определится значением ЭДС и суммой сопротивлений: I = /(R+r) .
Напряжение на выводах внешней цепи определится исходя из силы тока и сопротивления R соотношением, которое уже рассматривалось выше: U = IR. Напряжение U, при подключении нагрузки R, всегда будет меньше чем ЭДС на величину произведения I*r, которую называют падением напряжения на внутреннем сопротивлении источника питания. С этим явлением мы сталкиваемся достаточно часто, когда видим в работе частично разряженные батарейки или аккумуляторы. По мере разряда, увеличивается их внутреннее сопротивление, следовательно, увеличивается падение напряжение внутри источника, значит уменьшается внешнее напряжение U = – I*r. Чем меньше ток и внутреннее сопротивление источника, тем ближе по значению его ЭДС и напряжение на его выводах U. Если ток в цепи равен нулю, следовательно, = U. Цепь разомкнута, ЭДС источника равна напряжению на его выводах.
По мере разряда, увеличивается их внутреннее сопротивление, следовательно, увеличивается падение напряжение внутри источника, значит уменьшается внешнее напряжение U = – I*r. Чем меньше ток и внутреннее сопротивление источника, тем ближе по значению его ЭДС и напряжение на его выводах U. Если ток в цепи равен нулю, следовательно, = U. Цепь разомкнута, ЭДС источника равна напряжению на его выводах.
В случаях, когда внутренним сопротивлением источника можно пренебречь (r ≈ 0), напряжение на выводах источника будет равно ЭДС ( ≈ U ) независимо от сопротивления внешней цепи R. Такой источник питания называют источником напряжения.
Разомкнутая электрическая цепь
При отсутствии потока электронов необходимое напряжение источника цепи проявляется на концах точек. В этом случае происходит процесс ожидания момента соединения концов точек, чтобы возобновился поток электронов. Подобную цепь принято называть разомкнутой.
Замечание 1При связывании концов проводов, где существует разрыв, непрерывность всей цепи восстановится. Это основная разница между замкнутой и разомкнутой цепью.
Это основная разница между замкнутой и разомкнутой цепью.
При включении и выключении электрического освещения (лампы) требуется постоянно осуществлять похожие процессы. Для удобства были созданы специальные устройства. Их называют выключателями или рубильниками. Они в автоматическом режиме по сигналу управляют потоками электронов в цепи, контролируя начало и завершение работы электрооборудования.
Рубильники практически идеально подходят для демонстрации принципов работы выключателей и переключателей. Однако при использовании их в больших электрических цепях существует немало проблем, связанных с безопасной эксплуатацией. Так как некоторые части рубильников открыты, то существует вероятность воспламенения горючих материалов. В современных выключателях применяются подвижные и неподвижные контакты, которые защищены изоляционным корпусом.
Простейшая электрическая цепь представляет собой нагрузку, подключенную к источнику питания. Для управления цепью в нее последовательно включают замыкающее устройство (ключ).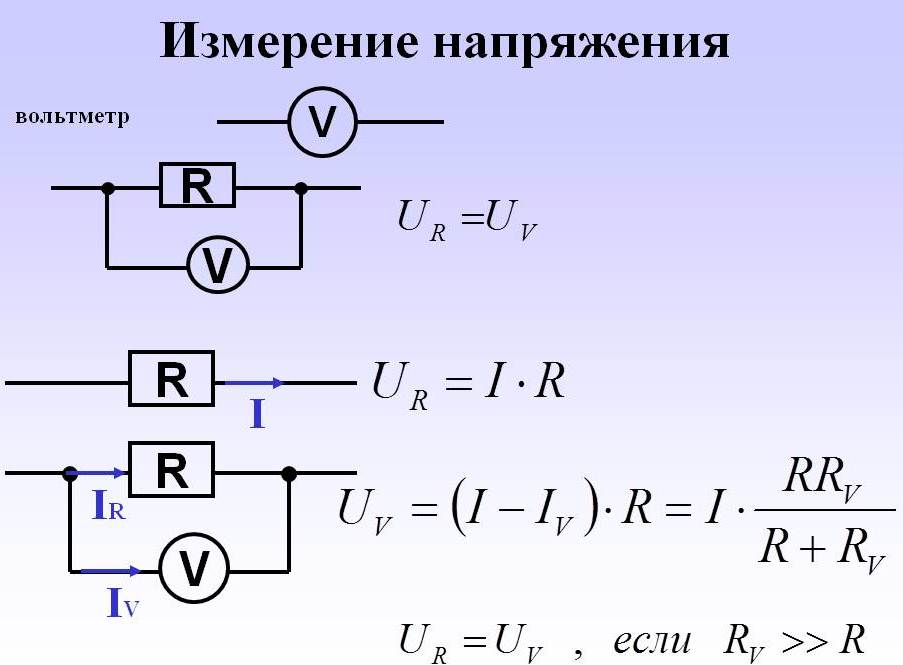 При замкнутом ключе в цепи возникает электрический ток, а при разомкнутом – ток отсутствует. Именно от положения ключа (замкнутый/разомкнутый) напрямую зависит – какую электрическую цепь называют замкнутой и разомкнутой.
При замкнутом ключе в цепи возникает электрический ток, а при разомкнутом – ток отсутствует. Именно от положения ключа (замкнутый/разомкнутый) напрямую зависит – какую электрическую цепь называют замкнутой и разомкнутой.
[custom_ads_shortcode1]
Закон Ома для переменного тока
При наличии индуктивности или ёмкости в цепи переменного тока необходимо учитывать их реактивное сопротивление. В таком случае запись Закона Ома будет иметь вид:
I = U/Z
Здесь Z – полное (комплексное) сопротивление цепи – импеданс. В него входит активная R и реактивная X составляющие. Реактивное сопротивление зависит от номиналов реактивных элементов, от частоты и формы тока в цепи. Более подробно ознакомится с комплексным сопротивлением можно на страничке импеданс.
С учётом сдвига фаз φ, созданного реактивными элементами, для синусоидального переменного тока обычно записывают Закон Ома в комплексной форме:
Элементы электрической цепи
Электрическую цепь разделяют на 2 участка – внутренний и внешний. Внутренним участком считается источник питания постоянного или переменного напряжения, а внешним – система, состоящая из нагрузки, приборов и соединительных элементов (проводов). Кроме обязательных элементов – источника и нагрузки, электрическая цепь может включать выключатели, реостаты, предохранительные плавкие или автоматические устройства, приборы контроля и индикации. Нагрузка также может состоять из различных потребителей, подключенных в цепь параллельно или последовательно.
Внутренним участком считается источник питания постоянного или переменного напряжения, а внешним – система, состоящая из нагрузки, приборов и соединительных элементов (проводов). Кроме обязательных элементов – источника и нагрузки, электрическая цепь может включать выключатели, реостаты, предохранительные плавкие или автоматические устройства, приборы контроля и индикации. Нагрузка также может состоять из различных потребителей, подключенных в цепь параллельно или последовательно.
[custom_ads_shortcode2]
Нелинейные элементы и цепи
Закон Ома не является фундаментальным законом природы и может быть применим в ограниченных случаях, например, для большинства проводников. Его невозможно использовать для расчёта напряжения и тока в полупроводниковых или электровакуумных приборах, где эта зависимость не является пропорциональной и её можно определять только с помощью вольтамперной характеристики (ВАХ). К данной категории элементов относятся все полупроводниковые приборы (диоды, транзисторы, стабилитроны, тиристоры, варикапы и т. д.) и электронные лампы. Такие элементы и цепи, в которых они используются, называют нелинейными.
д.) и электронные лампы. Такие элементы и цепи, в которых они используются, называют нелинейными.
Напряжение, ток и сопротивление
Электрическая цепь образуется, когда создается проводящий путь, позволяющий электрическому заряду непрерывно перемещаться. Это непрерывное движение электрического заряда по проводникам цепи называется током, и о нем часто говорят как о «потоке», как о потоке жидкости через полую трубу.
Сила, побуждающая носители заряда «течь» по цепи, называется напряжением. Напряжение – это особая мера потенциальной энергии, которая всегда относительна между двумя точками. Когда мы говорим об определенной величине напряжения, присутствующего в цепи, мы имеем в виду измерение потенциальной энергии для перемещения носителей заряда из одной конкретной точки этой цепи в другую конкретную точку. Без упоминания двух конкретных точек термин «напряжение» не имеет значения.
Ток, как правило, проходит через проводники с некоторой степенью трения или противодействия движению.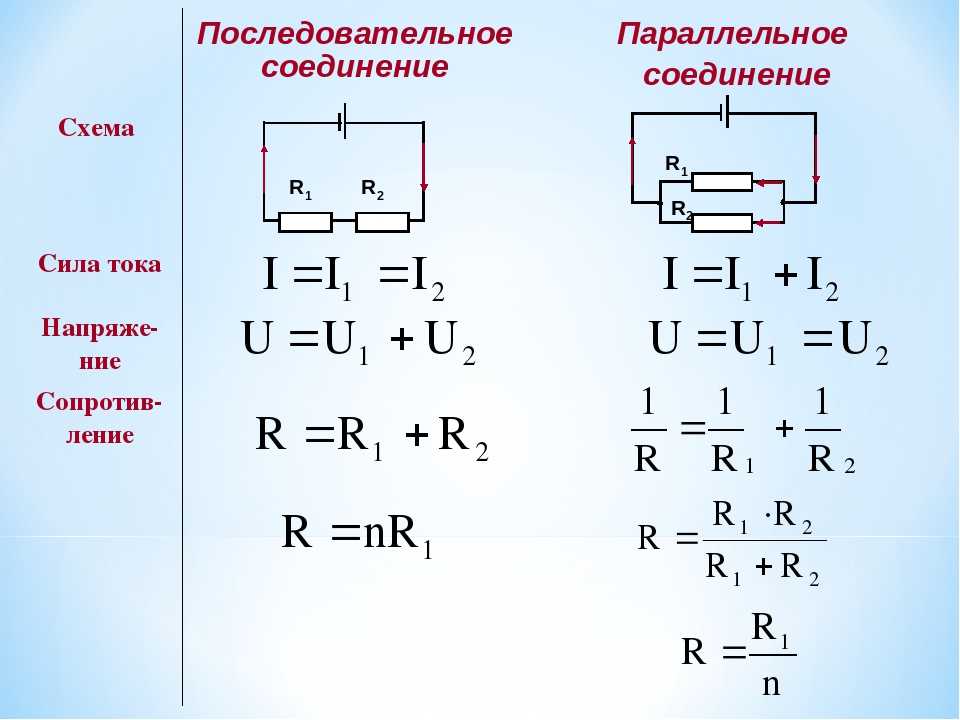 Это противодействие движению правильнее называть сопротивлением. Величина тока в цепи зависит от величины напряжения и величины сопротивления в цепи, препятствующего прохождению тока. Как и напряжение, сопротивление – это величина, измеряемая между двумя точками. По этой причине величины напряжения и сопротивления часто указываются как «между» двумя точками в цепи.
Это противодействие движению правильнее называть сопротивлением. Величина тока в цепи зависит от величины напряжения и величины сопротивления в цепи, препятствующего прохождению тока. Как и напряжение, сопротивление – это величина, измеряемая между двумя точками. По этой причине величины напряжения и сопротивления часто указываются как «между» двумя точками в цепи.
Идеальный источник ЭДС
Электродвижущая сила (E) – физическая величина, определяющая степень воздействия внешних сил на перемещение в замкнутой цепи носителей заряда. Иными словами, от ЭДС будет зависеть то, как сильно ток стремится течь по проводнику.
При объяснении подобных непонятных явлений отечественные школьные учителя любят обращаться к методу гидравлических аналогий. Если проводник – это труба, а электрический ток – это количество протекающей по ней воды, то ЭДС – это давление, которое развивает насос, чтобы качать жидкость.
Термин электродвижущая сила родственен такому понятию, как напряжение. Она, ЭДС, так же измеряется в вольтах (ед. изм. – «В»). Каждый источник питания, будь то батарейка, генератор или солнечная панель, обладает своей собственной электродвижущей силой. Зачастую эта ЭДС близка к выходному напряжению (U), но всегда немного меньше его. Вызвано это внутренним сопротивлением источника, на котором неизбежно падает часть вольтажа.
Она, ЭДС, так же измеряется в вольтах (ед. изм. – «В»). Каждый источник питания, будь то батарейка, генератор или солнечная панель, обладает своей собственной электродвижущей силой. Зачастую эта ЭДС близка к выходному напряжению (U), но всегда немного меньше его. Вызвано это внутренним сопротивлением источника, на котором неизбежно падает часть вольтажа.
Советуем изучить — Закалка стали
По этой причине идеальный источник ЭДС – это скорее абстрактное понятие или физическая модель, не имеющая места в реальном мире, ведь внутреннее сопротивление элемента питания Rвн хоть и весьма низкое, но всё же отлично от абсолютного нуля.
Идеальный и реальный источник ЭДС
Кулон и электрический заряд
Одна из основных единиц электрических измерений, которую часто преподают в начале курсов электроники, но нечасто используют впоследствии, – это кулон – единица измерения электрического заряда, пропорциональная количеству электронов в несбалансированном состоянии. Один кулон заряда соответствует 6 250 000 000 000 000 000 электронов.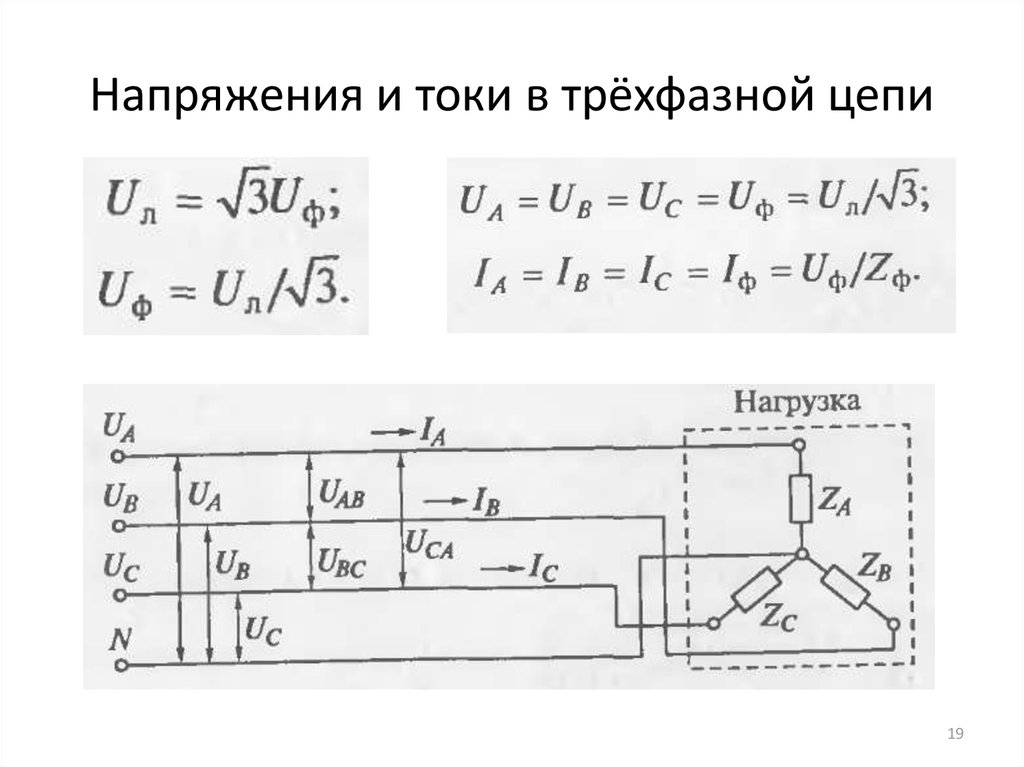 Символом количества электрического заряда является заглавная буква «Q», а единица измерения кулонов обозначается «Кл». Единица измерения тока, ампер, равна 1 кулону заряда, проходящему через заданную точку в цепи за 1 секунду. В этом смысле, ток – это скорость движения электрического заряда через проводник.
Символом количества электрического заряда является заглавная буква «Q», а единица измерения кулонов обозначается «Кл». Единица измерения тока, ампер, равна 1 кулону заряда, проходящему через заданную точку в цепи за 1 секунду. В этом смысле, ток – это скорость движения электрического заряда через проводник.
Как указывалось ранее, напряжение – это мера потенциальной энергии на единицу заряда, доступная для стимулирования протекания тока из одной точки в другую. Прежде чем мы сможем точно определить, что такое «вольт», мы должны понять, как измерить эту величину, которую мы называем «потенциальной энергией». Общей метрической единицей измерения энергии любого вида является джоуль, равный количеству работы, совершаемой силой в 1 ньютон при движении на 1 метр (в том же направлении). В этих научных терминах 1 вольт равен 1 джоулю электрической потенциальной энергии на (деленному на) 1 кулон заряда. Таким образом, 9-вольтовая батарея выделяет 9 джоулей энергии на каждый кулон заряда, проходящего через цепь.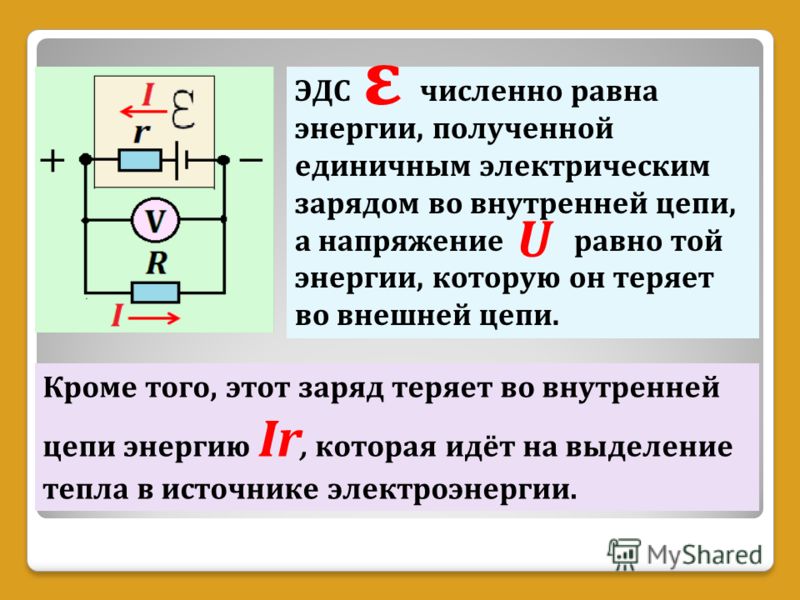
Эти единицы и символы электрических величин станут очень важны, когда мы начнем исследовать отношения между ними в цепях.
Формула закона Ома
Основное открытие Ома заключалось в том, что величина электрического тока, протекающего через металлический проводник в цепи, при любой заданной температуре прямо пропорциональна напряжению, приложенному к нему. Ом выразил свое открытие в виде простого уравнения, описывающего взаимосвязь напряжения, тока и сопротивления:
[E=IR]
В этом алгебраическом выражении напряжение (E) равно току (I), умноженному на сопротивление (R). Используя алгебру, мы можем преобразовать это уравнение в других два варианта, решая его для I и R соответственно:
Метода треугольника закона Ома
Закон Ома – очень простой и полезный инструмент для анализа электрических цепей. Он так часто используется при изучении электричества и электроники, что студент должен запомнить его. Если вы не очень хорошо умеете работать с формулами, то для его запоминания существует простой прием, помогающий использовать его для любой величины, зная две других.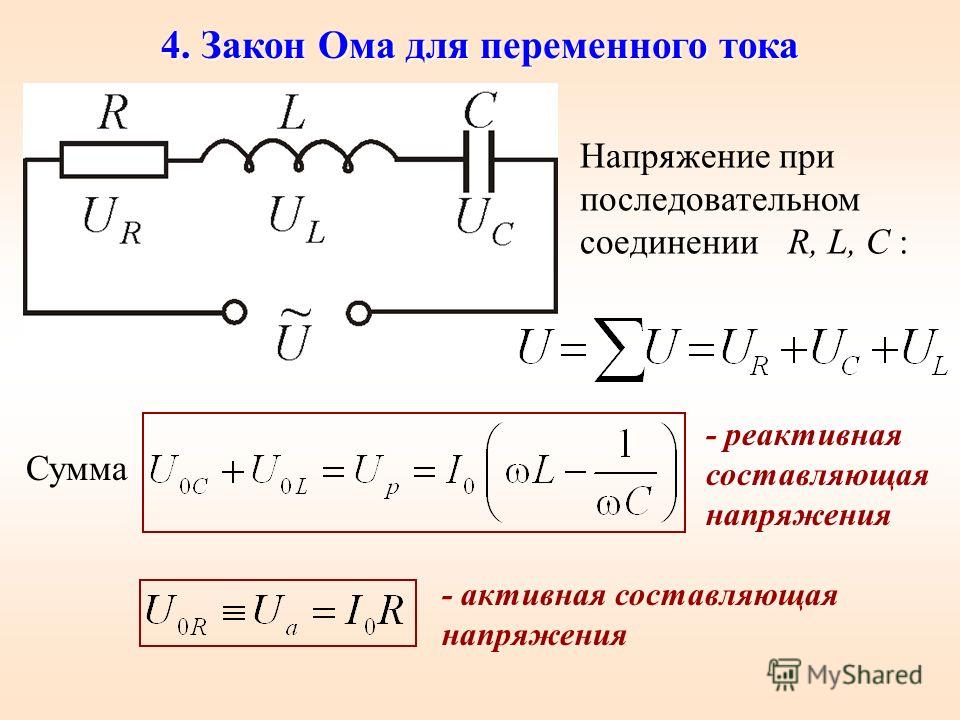 Сначала расположите буквы E, I и R в виде треугольника следующим образом:
Сначала расположите буквы E, I и R в виде треугольника следующим образом:
Рисунок 5 – Треугольник закона Ома
Если вы знаете E и I и хотите определить R, просто удалите R с картинки и посмотрите, что осталось:
Рисунок 6 – Закон Ома для определения R
Если вы знаете E и R и хотите определить I, удалите I и посмотрите, что осталось:
Рисунок 7 – Закон Ома для определения I
Наконец, если вы знаете I и R и хотите определить E, удалите E и посмотрите, что осталось:
Рисунок 8 – Закон Ома для определения E
В конце концов, вам придется научиться работать с формулами, чтобы серьезно изучать электричество и электронику, но этот совет может облегчить запоминание ваших первых вычислений. Если вам удобно работать с формулами, всё, что вам нужно сделать, это зафиксировать в памяти E = IR и вывести из нее две другие формулы, когда они вам понадобятся!
Что нам дает параллельное и последовательное соединение?
Теоретические знания — это хорошо, но как их применить на практике? Параллельно и последовательно могут соединяться элементы любого типа.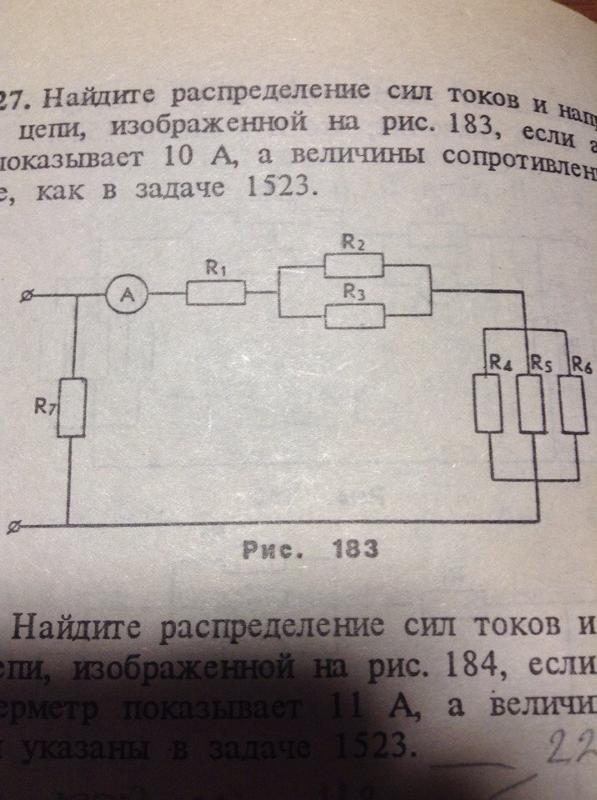 Но мы рассматривали только простейшие формулы, описывающие линейные элементы. Линейные элементы — это сопротивления, которые еще называют «резисторы». Итак, вот как можно использовать полученные знания:
Но мы рассматривали только простейшие формулы, описывающие линейные элементы. Линейные элементы — это сопротивления, которые еще называют «резисторы». Итак, вот как можно использовать полученные знания:
В общем, это наиболее распространенные варианты использования этих соединений.
Работа и мощность электрического тока
Электрическое поле, создавая упорядоченное движение заряженных частиц в проводнике, выполняет работу, которую принято называть работой тока.
Работа электрического тока А — физическая величина, характеризующая: изменение электрической энергии тока — превращение ее в другие виды. Единица работы электрического тока — джоуль, 1 Дж. В быту и технике используют также внесистемная единица — киловатт-час (кВт • ч), 1 кВт • ч = 3,6 • 106 Дж.
Советуем изучить — Статическое и астатическое регулирование
Если рассматривать внешний участок электрической цепи, то работа тока определяется как А = qU = UIt, где q — заряд, прошедший через поперечное сечение проводника за время t, U — электрическое напряжение на участке цепи, I — сила тока.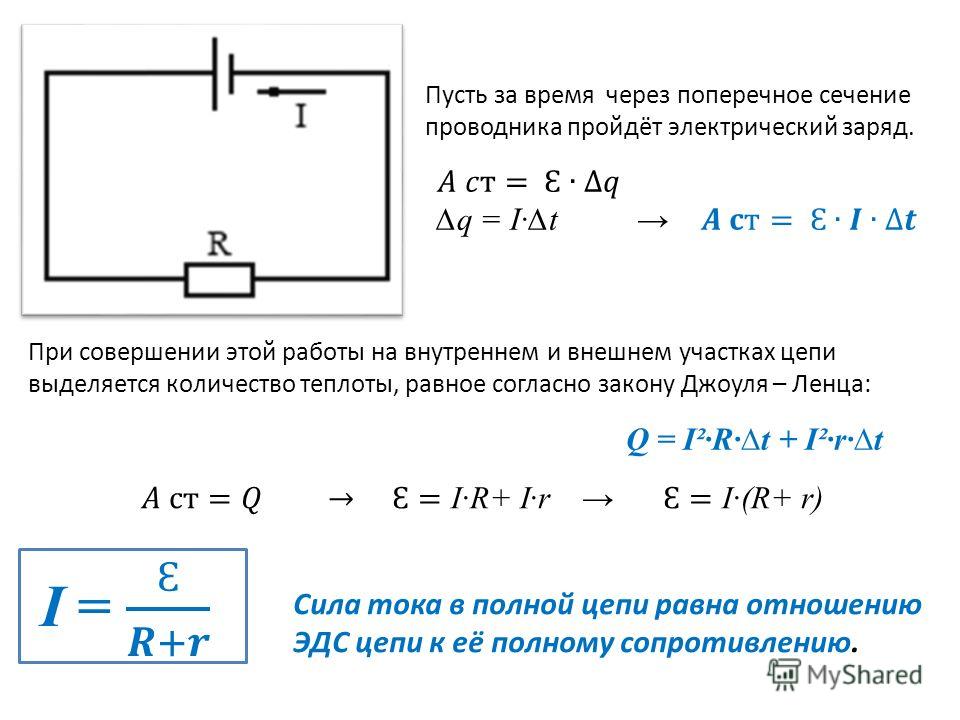
Если на участке цепи, по которой проходит ток, не выполняется механическая работа и не происходят химические реакции, то результатом работы электрического тока будет только нагрев проводников. Нагретый проводник вследствие теплообмена отдает полученную энергию в окружающую среду. Согласно закону сохранения энергии, количество выделенной теплоты равна работе тока: Q = А и вычисляется по закону Джоуля — Ленца: количество теплоты Q, выделяемой за время t в проводнике с сопротивлением R во время прохождения по нему тока силой I, равна Q = I2Rt.
Воспользовавшись законом Ома I = U/R, математически можно получить и такие формулы закона Джоуля — Ленца: Q =U2t/R и Q = UIt. Однако, если в цепи выполняется механическая работа или происходят химические реакции, эти формулы использовать нельзя.
Мощность электрического тока Р — физическая величина, характеризующая способность электрического тока выполнять определенную работу и измеряется работой, выполненной в единицу времени, Р = A/t, здесь А — работа электрического тока, t — время, за которое эта работа выполнена.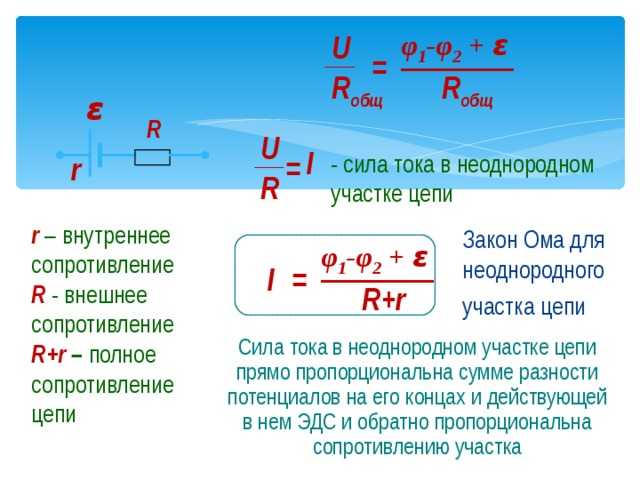 Мощность во внешнем участке электрической цепи можно определить по формулам Р = UI, Р = I2R, Р = U2/R, где U — электрическое напряжение, I — сила тока, R — электрическое сопротивление участка цепи. Единица мощности — ватт, 1 Вт = 1.
Мощность во внешнем участке электрической цепи можно определить по формулам Р = UI, Р = I2R, Р = U2/R, где U — электрическое напряжение, I — сила тока, R — электрическое сопротивление участка цепи. Единица мощности — ватт, 1 Вт = 1.
Если цепь состоит из нескольких потребителей, то при параллельном их соединения общая мощность тока во всей цепи равна сумме мощностей отдельных потребителей
Это стоит принять во внимание. В быту мы пользуемся мощными электрическими приборами
Если одновременно их включить, то общая мощность может превышать ту, на которую рассчитана электрическая сеть в помещении.
Выясним, в каком случае в электрической цепи выделяется максимальная мощность. Для этого запишем закон Ома для полной цепи в таком виде: ε = IR + Ir. Умножив обе части уравнения на I, получим: εI = I 2 R + I 2 r, где εI — полная мощность, которую развивает источник тока, I2R — мощность потребителей внешней участка цепи, I2г — мощность, которую потребляет внутренняя часть круга.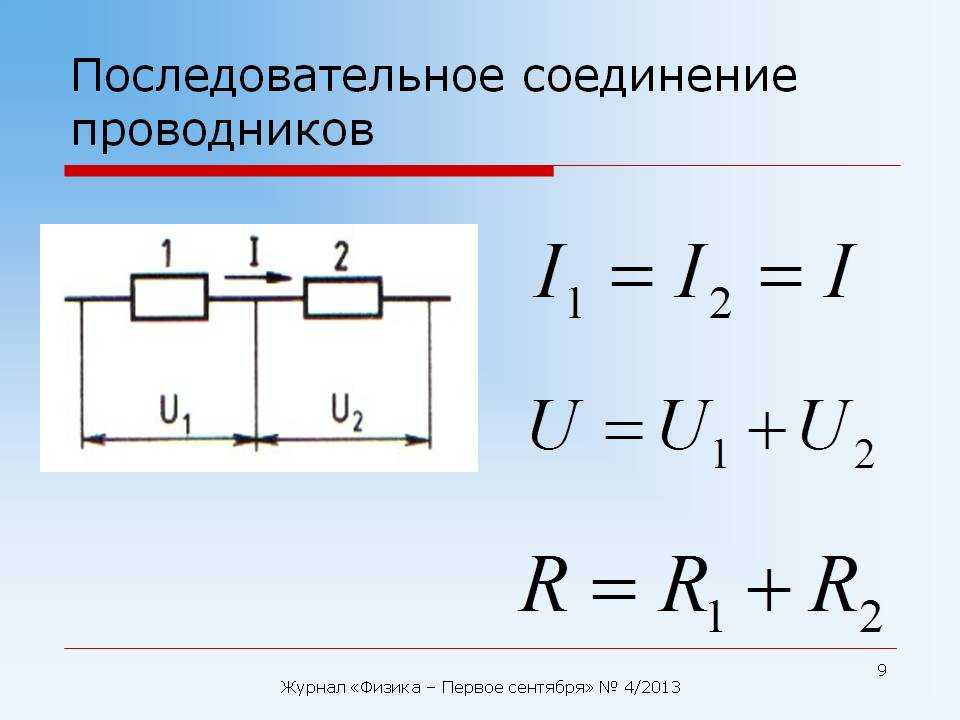 Итак, потребляемая мощность внешней частью цепи, составляет: P = εI – I 2 r.
Итак, потребляемая мощность внешней частью цепи, составляет: P = εI – I 2 r.
График зависимости потребляемой мощности во внешней части цепи от силы тока
Графиком зависимости Р (I) является парабола, вершина которой имеет координаты {ε/2r;ε2/4r}. Из графика видно, что максимальная мощность потребляется во внешнем цепи при силе тока I = ε/2r.
Параллельное и последовательное соединение
В электрике элементы соединяются либо последовательно — один за другим, либо параллельно — это когда к одной точке подключены несколько входов, к другой — выходы от тех же элементов.
Закон Ома для параллельного и последовательного соединения
Параллельное соединение
Параллельное соединение — это когда начала проводников/элементов сходятся в одной точке, а в другой — соединены их концы. Постараемся объяснить законы, которые справедливы для соединений этого типа. Начнем с тока. Ток какой-то величины подается в точку соединения элементов. Он разделяется, протекая по всем проводникам. Отсюда делаем вывод, что общий ток на участке равен сумме тока на каждом из элементов: I = I1 + I2 + I3.
Отсюда делаем вывод, что общий ток на участке равен сумме тока на каждом из элементов: I = I1 + I2 + I3.
Теперь относительно напряжения. Если напряжение — это работа по перемещению заряда, тоо работа, которая необходима на перемещение одного заряда будет одинакова на любом элементе. То есть, напряжение на каждом параллельно подключенном элементе будет одинаковым. U = U1=U2=U3. Не так весело и наглядно, как в случае с объяснением закона Ома для участка цепи, но понять можно.
Законы для параллельного соединения
Для сопротивления все несколько сложнее. Давайте введем понятие проводимости. Это характеристика, которая показывает насколько легко или сложно заряду проходить по этому проводнику. Понятно, что чем меньше сопротивление, тем проще току будет проходить. Поэтому проводимость — G — вычисляется как величина обратная сопротивлению. В формуле это выглядит так: G = 1/R.
Закон Ома — формулировка простыми словами, определение
Сопротивление
Представьте, что есть труба, в которую затолкали камни.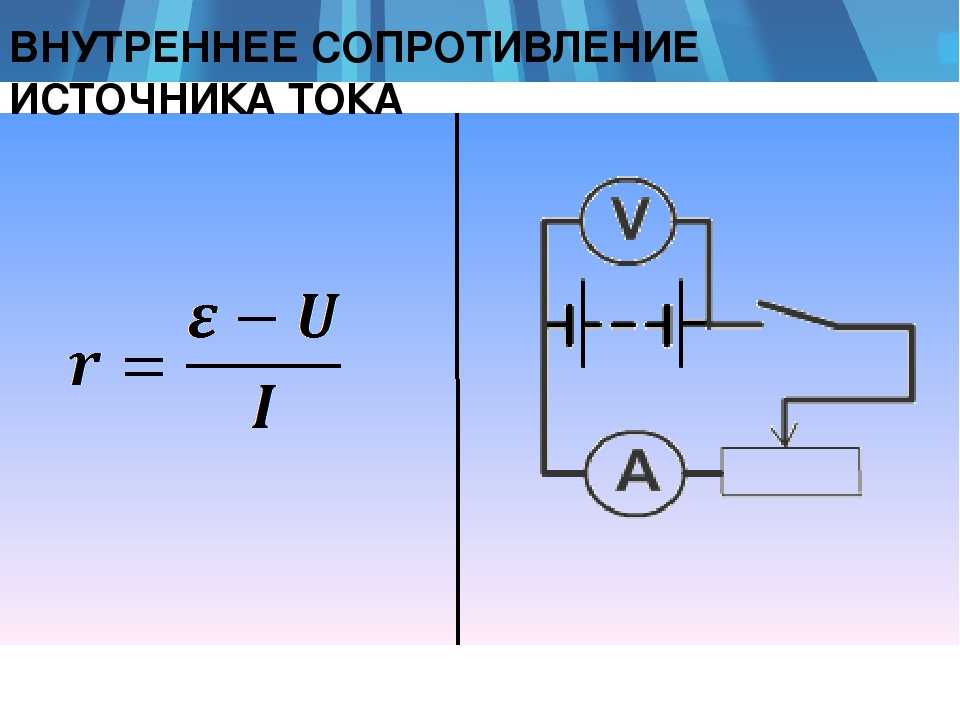 Вода, которая протекает по этой трубе, станет течь медленнее, потому что у нее появилось сопротивление. Точно также будет происходить с электрическим током.
Вода, которая протекает по этой трубе, станет течь медленнее, потому что у нее появилось сопротивление. Точно также будет происходить с электрическим током.
Сопротивление — физическая величина, которая показывает способность проводника пропускать электрический ток. Чем выше сопротивление, тем ниже эта способность.
Теперь сделаем «каменный участок» длиннее, то есть добавим еще камней. Воде будет еще сложнее течь.
Сделаем трубу шире, оставив количество камней тем же — воде полегчает, поток увеличится.
Теперь заменим шероховатые камни, которые мы набрали на стройке, на гладкие камушки из моря. Через них проходить тоже легче, а значит сопротивление уменьшается.
Электрический ток реагирует на эти параметры аналогичным образом: при удлинении проводника сопротивление увеличивается, при увеличении поперечного сечения (ширины) проводника сопротивление уменьшается, а если заменить материал — изменится в зависимости от материала.
Эту закономерность можно описать следующей формулой:
Сопротивление R = ρ · l/S R — сопротивление [Ом] l — длина проводника [м] S — площадь поперечного сечения [мм2] ρ — удельное сопротивление [Ом · мм2/м] |
Единица измерения сопротивления — ом. Названа в честь физика Георга Ома.
Будьте внимательны!
Площадь поперечного сечения проводника и удельное сопротивление содержат в своих единицах измерения мм2. В таблице удельное сопротивление всегда дается в такой размерности, да и тонкий проводник проще измерять в мм2. При умножении мм2 сокращаются и мы получаем величину в СИ.
Но это не отменяет того, что каждую задачу нужно проверять на то, что там мм2 в обеих величинах! Если это не так, то нужно свести не соответствующую величину к мм2.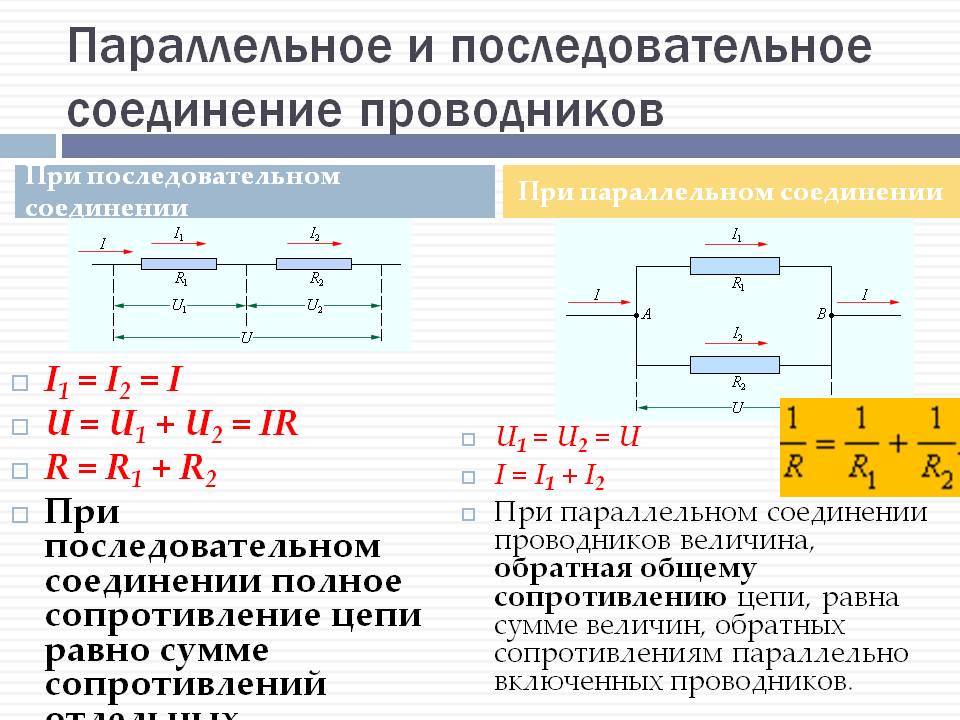
Знайте!
СИ — международная система единиц. «Перевести в СИ» означает перевод всех величин в метры, килограммы, секунды и другие единицы измерения без приставок. Исключение составляет килограмм с приставкой «кило».
Удельное сопротивление проводника — это физическая величина, которая показывает способность материала пропускать электрический ток. Это табличная величина, она зависит только от материала.
Практикующий детский психолог Екатерина Мурашова
Бесплатный курс для современных мам и пап от Екатерины Мурашовой. Запишитесь и участвуйте в розыгрыше 8 уроков
Таблица удельных сопротивлений различных материалов
Материал | Удельное сопротивление ρ, Ом · мм2/м |
Алюминий | 0,028 |
Бронза | 0,095–0,1 |
Висмут | 1,2 |
Вольфрам | 0,05 |
Железо | 0,1 |
Золото | 0,023 |
Иридий | 0,0474 |
Константан (сплав NiCu + Mn) | 0,5 |
Латунь | 0,025–0,108 |
Магний | 0,045 |
Манганин (сплав меди марганца и никеля — приборный) | 0,43–0,51 |
Медь | 0,0175 |
Молибден | 0,059 |
Нейзильбер (сплав меди, цинка и никеля) | 0,2 |
Натрий | 0,047 |
Никелин (сплав меди и никеля) | 0,42 |
Никель | 0,087 |
Нихром (сплав никеля, хрома, железа и марганца) | 1,05–1,4 |
Олово | 0,12 |
Платина | 0,107 |
Ртуть | 0,94 |
Свинец | 0,22 |
Серебро | 0,015 |
Сталь | 0,103–0,137 |
Титан | 0,6 |
Хромаль | 1,3–1,5 |
Цинк | 0,054 |
Чугун | 0,5–1,0 |
Резистор
Все реальные проводники имеют сопротивление, но его стараются сделать незначительным. В задачах вообще используют словосочетание «идеальный проводник», а значит лишают его сопротивления.
В задачах вообще используют словосочетание «идеальный проводник», а значит лишают его сопротивления.
Из-за того, что проводник у нас «кругом-бегом-такой-идеальный», чаще всего за сопротивление в цепи отвечает резистор. Это устройство, которое нагружает цепь сопротивлением.
Вот так резистор изображается на схемах:
В школьном курсе физики используют европейское обозначение, поэтому запоминаем только его. Американское обозначение можно встретить, например, в программе Micro-Cap, в которой инженеры моделируют схемы.
Вот так резистор выглядит в естественной среде обитания:
Полосочки на нем показывают его сопротивление.
На сайте компании Ekits, которая занимается продажей электронных модулей, можно выбрать цвет резистора и узнать значение его сопротивления:
Источник: сайт компании Ekits
О том, зачем дополнительно нагружать сопротивлением цепь, мы поговорим в этой же статье чуть позже.
Учёба без слёз (бесплатный гайд для родителей)
Пошаговый гайд от Екатерины Мурашовой о том, как перестать делать уроки за ребёнка и выстроить здоровые отношения с учёбой.
Реостат
Есть такие выключатели, которые крутишь, а они делают свет ярче-тусклее. В такой выключатель спрятан резистор с переменным сопротивлением — реостат.
Стрелка сверху — это ползунок. По сути, он отсекает ту часть резистора, которая находится от него справа. То есть, если мы двигаем ползунок вправо — мы увеличиваем длину резистора, а значит и сопротивление. И наоборот — двигаем влево и уменьшаем.
По формуле сопротивления это очень хорошо видно, так как длина проводника находится в числителе:
Сопротивление R = ρ · l/S R — сопротивление [Ом] l — длина проводника [м] S — площадь поперечного сечения [мм2] ρ — удельное сопротивление [Ом · мм2/м] |
Закон Ома для участка цепи
С камушками в трубе все понятно, но не только же от них зависит сила, с которой поток воды идет по трубе — от насоса, которым мы эту воду качаем, тоже зависит. Чем сильнее качаем, тем больше течение. В электрической цепи функцию насоса выполняет источник тока.
Чем сильнее качаем, тем больше течение. В электрической цепи функцию насоса выполняет источник тока.
Например, источником может быть гальванический элемент (привычная батарейка). Батарейка работает на основе химических реакций внутри нее. В результате этих реакций выделяется энергия, которая потом передается электрической цепи.
У любого источника обязательно есть полюса — «плюс» и «минус». Полюса — это его крайние положения, по сути клеммы, к которым присоединяется электрическая цепь. Собственно, ток как раз течет от «+» к «−».
У нас уже есть две величины, от которых зависит электрический ток в цепи — напряжение и сопротивление. Кажется, пора объединять их в закон.
Сила тока в участке цепи прямо пропорциональна напряжению на его концах и обратно пропорциональна его сопротивлению.
Математически его можно описать вот так:
Закон Ома для участка цепи I = U/R I — сила тока [A] U — напряжение [В] |
Напряжение измеряется в Вольтах и показывает разницу между двумя точками цепи: от этой разницы зависит, насколько сильно будет течь ток — чем больше разница, тем выше напряжение и ток будет течь сильнее.
Сила тока измеряется в амперах, а подробнее о ней вы можете прочитать в нашей статье. 😇
Давайте решим несколько задач на закон Ома для участка цепи.
Задача раз
Найти силу тока в лампочке накаливания торшера, если его включили в сеть напряжением 220 В, а сопротивление нити накаливания равно 880 Ом.
Решение:
Возьмем закон Ома для участка цепи:
I = U/R
Подставим значения:
I = 220/880 = 0,25 А
Ответ: сила тока, проходящего через лампочку, равна 0,25 А
Давайте усложним задачу. И найдем силу тока, зная все параметры для вычисления сопротивления и напряжение.
Задача два
Найти силу тока в лампочке накаливания, если торшер включили в сеть напряжением 220 В, а длина нити накаливания равна 0,5 м, площадь поперечного сечения 0,01 мм2, а удельное сопротивление нити равно 1,05 Ом · мм2/м.
Решение:
Сначала найдем сопротивление проводника.
R = ρ · l/S
Площадь дана в мм2, а удельное сопротивления тоже содержит мм2 в размерности.
Это значит, что все величины уже даны в СИ и перевод не требуется:
R = 1,05 · 0,5/0,01 = 52,5 Ом
Теперь возьмем закон Ома для участка цепи:
I = U/R
Подставим значения:
I = 220/52,5 ≃ 4,2 А
Ответ: сила тока, проходящего через лампочку, приблизительно равна 4,2 А
А теперь совсем усложним! Определим материал, из которого изготовлена нить накаливания.
Задача три
Из какого материала изготовлена нить накаливания лампочки, если настольная лампа включена в сеть напряжением 220 В, длина нити равна 0,5 м, площадь ее поперечного сечения равна 0,01 мм2, а сила тока в цепи — 8,8 А
Решение:
Возьмем закон Ома для участка цепи и выразим из него сопротивление:
I = U/R
R = U/I
Подставим значения и найдем сопротивление нити:
R = 220/8,8 = 25 Ом
Теперь возьмем формулу сопротивления и выразим из нее удельное сопротивление материала:
R = ρ · l/S
ρ = RS/l
Подставим значения и получим:
ρ = 25 · 0,01/0,5 = 0,5 Ом · мм2/м
Обратимся к таблице удельных сопротивлений материалов, чтобы выяснить, из какого материала сделана эта нить накаливания.
Ответ: нить накаливания сделана из константана.
Закон Ома для полной цепи
Мы разобрались с законом Ома для участка цепи. А теперь давайте узнаем, что происходит, если цепь полная: у нее есть источник, проводники, резисторы и другие элементы.
В таком случае вводится закон Ома для полной цепи: сила тока в полной цепи равна отношению ЭДС цепи к ее полному сопротивлению.
Так, стоп. Слишком много незнакомых слов — разбираемся по порядку.
Что такое ЭДС и откуда она берется
ЭДС расшифровывается, как электродвижущая сила. Обозначается греческой буквой ε и измеряется, как и напряжение, в Вольтах.
ЭДС — это сила, которая движет заряженные частицы в цепи. Она берется из источника тока. Например, из батарейки.
Химическая реакция внутри гальванического элемента (это синоним батарейки) происходит с выделением энергии в электрическую цепь. Именно эта энергия заставляет частицы двигаться по проводнику.
Зачастую напряжение и ЭДС приравнивают и говорят, что это одно и то же. Формально, это не так, но при решении задач чаще всего и правда нет разницы, так как эти величины обе измеряются в Вольтах и определяют очень похожие по сути своей процессы.
В виде формулы Закон Ома для полной цепи будет выглядеть следующим образом:
Закон Ома для полной цепи I — сила тока [A] ε — ЭДС [В] R — сопротивление нагрузки [Ом] r — внутреннее сопротивление источника [Ом] |
Любой источник не идеален. В задачах это возможно («источник считать идеальным», вот эти вот фразочки), но в реальной жизни — точно нет. В связи с этим у источника есть внутреннее сопротивление, которое мешает протеканию тока.
Решим задачу на полную цепь.
Задачка
Найти силу тока в полной цепи, состоящей из одного резистора сопротивлением 3 Ом и источником с ЭДС равной 4 В и внутренним сопротивлением 1 Ом
Решение:
Возьмем закон Ома для полной цепи:
Подставим значения:
A
Ответ: сила тока в цепи равна 1 А.
Когда «сопротивление бесполезно»
Электрический ток — умный и хитрый парень. Если у него есть возможность обойти резистор и пойти по идеальному проводнику без сопротивления, он это сделает. При этом с резисторами просто разных номиналов это не сработает: он не пойдет просто через меньшее сопротивление, а распределится согласно закону Ома — больше тока пойдет туда, где сопротивление меньше, и наоборот.
А вот на рисунке ниже сопротивление цепи равно нулю, потому что ток через резистор не пойдет.
Ток идет по пути наименьшего сопротивления.
Теперь давайте посмотрим на закон Ома для участка цепи еще раз.
Закон Ома для участка цепи I = U/R I — сила тока [A] U — напряжение [В] R — сопротивление [Ом] |
Подставим сопротивление, равное 0. Получается, что знаменатель равен нулю, а на математике говорят, что на ноль делить нельзя. Но мы вам раскроем страшную тайну, только не говорите математикам: на ноль делить можно. Если совсем упрощать такое сложное вычисление (а именно потому что оно сложное, мы всегда говорим, что его нельзя производить), то получится бесконечность.
То есть:
I = U/0 = ∞
Такой случай называют коротким замыканием — когда величина силы тока настолько велика, что можно устремить ее к бесконечности. В таких ситуациях мы видим искру, бурю, безумие — и все ломается.
Это происходит, потому что две точки цепи имеют между собой напряжение (то есть между ними есть разница). Это как если вдоль реки неожиданно появляется водопад. Из-за этой разницы возникает искра, которую можно избежать, поставив в цепь резистор.
Именно во избежание коротких замыканий нужно дополнительное сопротивление в цепи.
Параллельное и последовательное соединение
Все это время речь шла о цепях с одним резистором. Рассмотрим, что происходит, если их больше.
ЭДС. Закон Ома для полной цепи
Автор статьи — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев
Темы кодификатора ЕГЭ: электродвижущая сила, внутреннее сопротивление источника тока, закон Ома для полной электрической цепи.До сих пор при изучении электрического тока мы рассматривали направленное движение свободных зарядов во внешней цепи, то есть в проводниках, подсоединённых к клеммам источника тока.
Как мы знаем, положительный заряд :
• уходит во внешнюю цепь с положительной клеммы источника;
• перемещается во внешней цепи под действием стационарного электрического поля, создаваемого другими движущимися зарядами;
• приходит на отрицательную клемму источника, завершая свой путь во внешней цепи.
Теперь нашему положительному заряду нужно замкнуть свою траекторию и вернуться на положительную клемму. Для этого ему требуется преодолеть заключительный отрезок пути — внутри источника тока от отрицательной клеммы к положительной. Но вдумайтесь: идти туда ему совсем не хочется! Отрицательная клемма притягивает его к себе, положительная клемма его от себя отталкивает, и в результате на наш заряд внутри источника действует электрическая сила , направленная против движения заряда (т.е. против направления тока).
Сторонняя сила
Тем не менее, ток по цепи идёт; стало быть, имеется сила, «протаскивающая» заряд сквозь источник вопреки противодействию электрического поля клемм (рис. 1).
Рис. 1. Сторонняя сила
Эта сила называется сторонней силой; именно благодаря ей и функционирует источник тока. Сторонняя сила не имеет отношения к стационарному электрическому полю — у неё, как говорят, неэлектрическое происхождение; в батарейках, например, она возникает благодаря протеканию соответствующих химических реакций.
Обозначим через работу сторонней силы по перемещению положительного заряда q внутри источника тока от отрицательной клеммы к положительной. Эта работа положительна, так как направление сторонней силы совпадает с направлением перемещения заряда. Работа сторонней силы называется также работой источника тока.
Во внешней цепи сторонняя сила отсутствует, так что работа сторонней силы по перемещению заряда во внешней цепи равна нулю. Поэтому работа сторонней силы по перемещению заряда вокруг всей цепи сводится к работе по перемещению этого заряда только лишь внутри источника тока. Таким образом, — это также работа сторонней силы по перемещению заряда по всей цепи.
Мы видим, что сторонняя сила является непотенциальной — её работа при перемещении заряда по замкнутому пути не равна нулю. Именно эта непотенциальность и обеспечивает циркулирование электрического тока; потенциальное электрическое поле, как мы уже говорили ранее, не может поддерживать постоянный ток.
Опыт показывает, что работа прямо пропорциональна перемещаемому заряду . Поэтому отношение уже не зависит от заряда и является количественной характеристикой источника тока. Это отношение обозначается :
(1)
Данная величина называется электродвижущей силой (ЭДС) источника тока. Как видим, ЭДС измеряется в вольтах (В), поэтому название «электродвижущая сила» является крайне неудачным. Но оно давно укоренилось, так что приходится смириться.
Когда вы видите надпись на батарейке: «1,5 В», то знайте, что это именно ЭДС. Равна ли эта величина напряжению, которое создаёт батарейка во внешней цепи? Оказывается, нет! Сейчас мы поймём, почему.
Закон Ома для полной цепи
Любой источник тока обладает своим сопротивлением , которое называется внутренним сопротивлением этого источника. Таким образом, источник тока имеет две важных характеристики: ЭДС и внутреннее сопротивление.
Пусть источник тока с ЭДС, равной , и внутренним сопротивлением подключён к резистору (который в данном случае называется внешним резистором, или внешней нагрузкой, или полезной нагрузкой).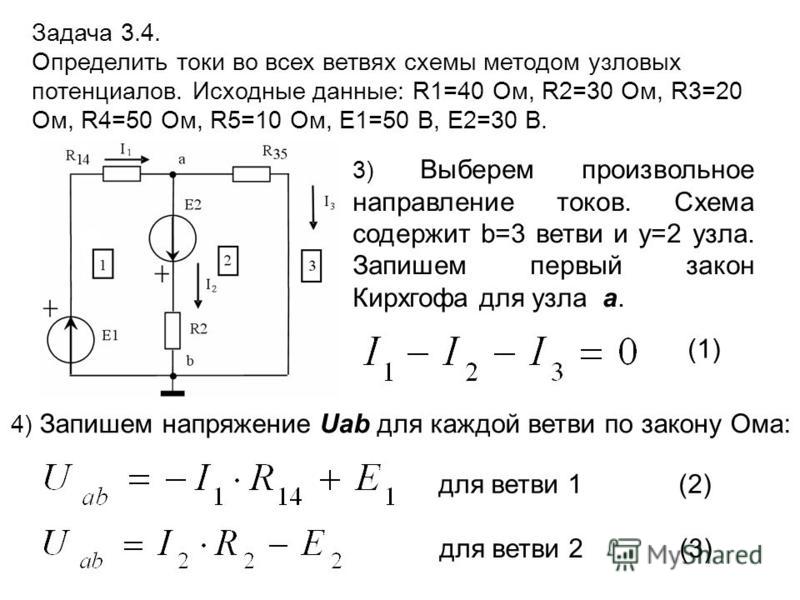 Всё это вместе называется полной цепью (рис. 2).
Всё это вместе называется полной цепью (рис. 2).
Рис. 2. Полная цепь
Наша задача — найти силу тока в цепи и напряжение на резисторе .
За время по цепи проходит заряд . Согласно формуле (1) источник тока совершает при этом работу:
(2)
Так как сила тока постоянна, работа источника целиком превращается в теплоту, которая выделяется на сопротивлениях и . Данное количество теплоты определяется законом Джоуля–Ленца:
(3)
Итак, , и мы приравниваем правые части формул (2) и (3):
После сокращения на получаем:
Вот мы и нашли ток в цепи:
(4)
Формула (4) называется законом Ома для полной цепи.
Если соединить клеммы источника проводом пренебрежимо малого сопротивления , то получится короткое замыкание. Через источник при этом потечёт максимальный ток — ток короткого замыкания:
Из-за малости внутреннего сопротивления ток короткого замыкания может быть весьма большим. Например, пальчиковая батарейка разогревается при этом так, что обжигает руки.
Например, пальчиковая батарейка разогревается при этом так, что обжигает руки.
Зная силу тока (формула (4)), мы можем найти напряжение на резисторе с помощью закона Ома для участка цепи:
(5)
Это напряжение является разностью потенциалов между точками и (рис. 2). Потенциал точки равен потенциалу положительной клеммы источника; потенциал точки равен потенциалу отрицательной клеммы. Поэтому напряжение (5) называется также напряжением на клеммах источника.
Мы видим из формулы (5), что в реальной цепи будет — ведь умножается на дробь, меньшую единицы. Но есть два случая, когда .
1. Идеальный источник тока. Так называется источник с нулевым внутренним сопротивлением. При формула (5) даёт .
2. Разомкнутая цепь. Рассмотрим источник тока сам по себе, вне электрической цепи. В этом случае можно считать, что внешнее сопротивление бесконечно велико: . Тогда величина неотличима от , и формула (5) снова даёт нам .
Смысл этого результата прост: если источник не подключён к цепи, то вольтметр, подсоединённый к полюсам источника, покажет его ЭДС.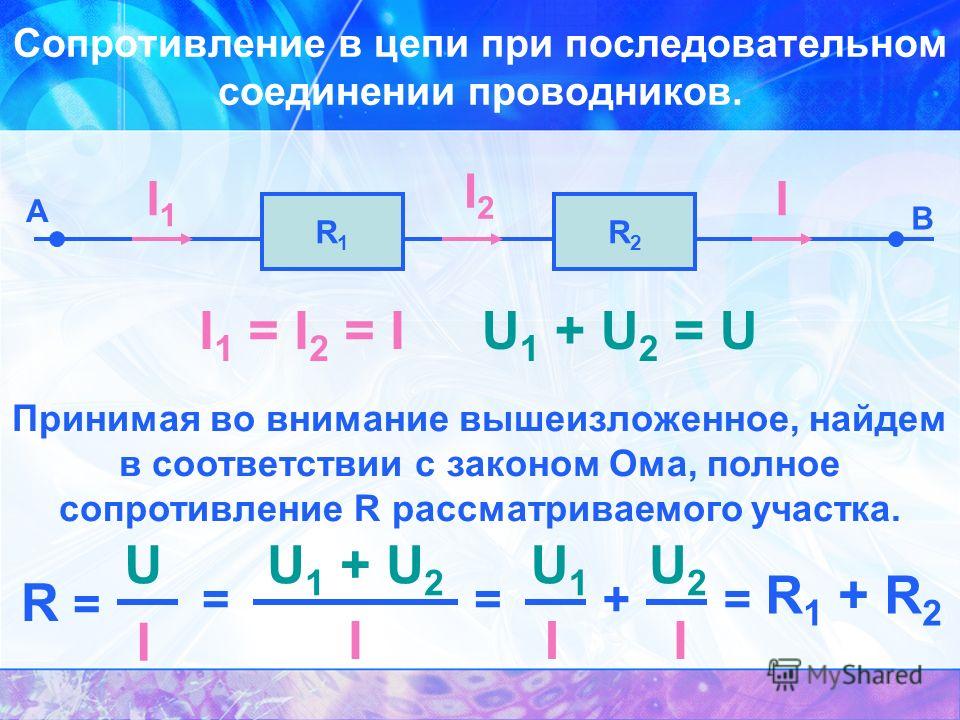
КПД электрической цепи
Нетрудно понять, почему резистор называется полезной нагрузкой. Представьте себе, что это лампочка. Теплота, выделяющаяся на лампочке, является полезной, так как благодаря этой теплоте лампочка выполняет своё предназначение — даёт свет.
Количество теплоты, выделяющееся на полезной нагрузке за время , обозначим .
Если сила тока в цепи равна , то
Некоторое количество теплоты выделяется также на источнике тока:
Полное количество теплоты, которое выделяется в цепи, равно:
КПД электрической цепи — это отношение полезного тепла к полному:
КПД цепи равен единице лишь в том случае, если источник тока идеальный .
Закон Ома для неоднородного участка
Простой закон Ома справедлив для так называемого однородного участка цепи — то есть участка, на котором нет источников тока. Сейчас мы получим более общие соотношения, из которых следует как закон Ома для однородного участка, так и полученный выше закон Ома для полной цепи.
Сейчас мы получим более общие соотношения, из которых следует как закон Ома для однородного участка, так и полученный выше закон Ома для полной цепи.
Участок цепи называется неоднородным, если на нём имеется источник тока. Иными словами, неоднородный участок — это участок с ЭДС.
На рис. 3 и источник тока. ЭДС источника равна , его внутреннее сопротивление считаем равным нулю (усли внутреннее сопротивление источника равно , можно просто заменить резистор на резистор ).
Рис. 3. ЭДС «помогает» току:
Сила тока на участке равна , ток течёт от точки к точке . Этот ток не обязательно вызван одним лишь источником . Рассматриваемый участок, как правило, входит в состав некоторой цепи (не изображённой на рисунке), а в этой цепи могут присутствовать и другие источники тока. Поэтому ток является результатом совокупного действия всех источников, имеющихся в цепи.
Пусть потенциалы точек и равны соответственно и . Подчеркнём ещё раз, что речь идёт о потенциале стационарного электрического поля, порождённого действием всех источников цепи — не только источника, принадлежащего данному участку, но и, возможно, имеющихся вне этого участка.
Подчеркнём ещё раз, что речь идёт о потенциале стационарного электрического поля, порождённого действием всех источников цепи — не только источника, принадлежащего данному участку, но и, возможно, имеющихся вне этого участка.
Напряжение на нашем участке равно: . За время через участок проходит заряд , при этом стационарное электрическое поле совершает работу:
Кроме того, положительную работу совершает источник тока (ведь заряд прошёл сквозь него!):
Сила тока постоянна, поэтому суммарная работа по продвижению заряда , совершаемая на участке стационарным элетрическим полем и сторонними силами источника, целиком превращается в тепло: .
Подставляем сюда выражения для , и закон Джоуля–Ленца:
Сокращая на , получаем закон Ома для неоднородного участка цепи:
(6)
или, что то же самое:
(7)
Обратите внимание: перед стоит знак «плюс». Причину этого мы уже указывали — источник тока в данном случае совершает положительную работу, «протаскивая» внутри себя заряд от отрицательной клеммы к положительной. Попросту говоря, источник «помогает» току протекать от точки к точке .
Причину этого мы уже указывали — источник тока в данном случае совершает положительную работу, «протаскивая» внутри себя заряд от отрицательной клеммы к положительной. Попросту говоря, источник «помогает» току протекать от точки к точке .
Отметим два следствия выведенных формул (6) и (7).
1. Если участок однородный, то . Тогда из формулы (6) получаем — закон Ома для однородного участка цепи.
2. Предположим, что источник тока обладает внутренним сопротивлением . Это, как мы уже упоминали, равносильно замене на :
Теперь замкнём наш участок, соединив точки и . Получим рассмотренную выше полную цепь. При этом окажется, что и предыдущая формула превратится в закон Ома для полной цепи:
Таким образом, закон Ома для однородного участка и закон Ома для полной цепи оба вытекают из закона Ома для неоднородного участка.
Может быть и другой случай подключения, когда источник «мешает» току идти по участку. Такая ситуация изображена на рис. 4. Здесь ток, идущий от к , направлен против действия сторонних сил источника.
Такая ситуация изображена на рис. 4. Здесь ток, идущий от к , направлен против действия сторонних сил источника.
Рис. 4. ЭДС «мешает» току:
Как такое возможно? Очень просто: другие источники, имеющиеся в цепи вне рассматриваемого участка, «пересиливают» источник на участке и вынуждают ток течь против . Именно так происходит, когда вы ставите телефон на зарядку: подключённый к розетке адаптер вызывает движение зарядов против действия сторонних сил аккумулятора телефона, и аккумулятор тем самым заряжается!
Что изменится теперь в выводе наших формул? Только одно — работа сторонних сил станет отрицательной:
Тогда закон Ома для неоднородного участка примет вид:
(8)
или:
где по-прежнему — напряжение на участке.
Давайте соберём вместе формулы (7) и (8) и запишем закон Ома для участка с ЭДС следующим образом:
Ток при этом течёт от точки к точке . Если направление тока совпадает с направлением сторонних сил, то перед ставится «плюс»; если же эти направления противоположны, то ставится «минус».
Если направление тока совпадает с направлением сторонних сил, то перед ставится «плюс»; если же эти направления противоположны, то ставится «минус».
основные понятия, нахождение через силу тока и сопротивление
При проектировании схем различных устройств радиолюбителю необходимо производить точные расчеты c помощью измерительных приборов и формул. В электротехнике используются формулы для вычислений величин электричества (формулы напряжения, сопротивления, силы тока и так далее).
- Общие сведения об электрическом токе
- Физический смысл
- Пагубное влияние на человека
- Единицы измерения
- Цепи переменного и постоянного тока
- Переменное однофазное напряжение
- Рекомендации по выбору прибора
Общие сведения об электрическом токе
Электрическим током является процесс движения заряженных частиц (свободных электронов), имеющий вектор направленности. Частицы перемещаются под действием напряженности электрического поля, имеющей векторное направление.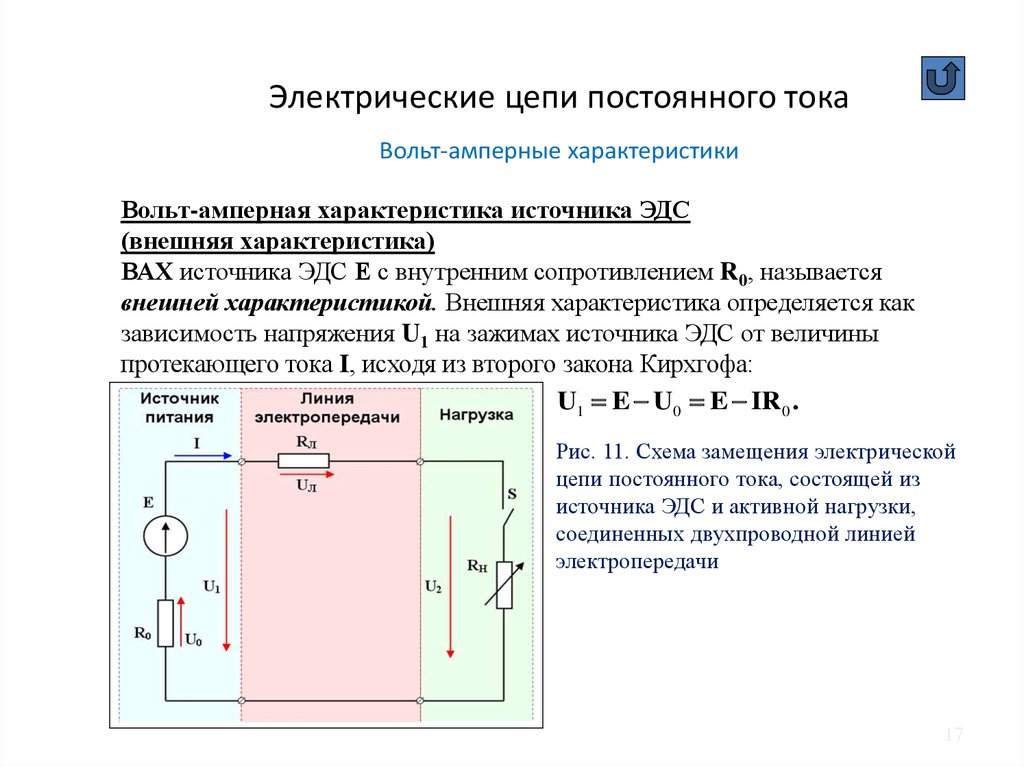 Это поле совершает работу по перемещению этих частиц. Влияют на работу электрического поля сила тока, напряжение и сопротивление.
Это поле совершает работу по перемещению этих частиц. Влияют на работу электрического поля сила тока, напряжение и сопротивление.
Физический смысл
Под физическим смыслом понимается работа тока на участке, соотносящаяся с величиной заряда. Положительный заряд перемещается из одной точки, обладающей одним потенциалом, в другую, причем потенциал в этой точке отличается от предыдущего. В результате этого и возникает разность потенциалов, именуемая напряжением или ЭДС (электродвижущей силой).
Для полного понимания этого физического процесса и выяснения физического смысла напряжения необходимо провести аналогию с трубой. Допустим, труба наполнена водой и к ней прикручен кран для слива воды. Эта труба также оборудована краном для заливания воды с помощью мощного насоса.
Для демонстрации аналогии нужно открыть кран полностью, вода начнет выливаться и можно сделать вывод о незначительном давлении.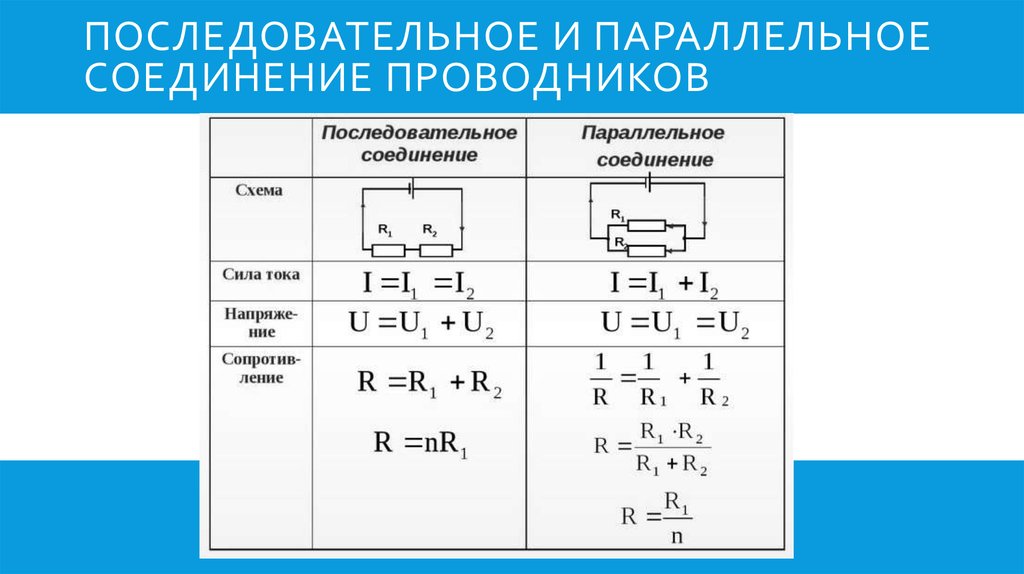 Во втором случае спускной кран открыт не полностью и происходит набор воды при помощи насоса. В трубе создается давление и напор усиливается. Насос, создающий давление, и является в этом примере напряженностью электрического поля.
Во втором случае спускной кран открыт не полностью и происходит набор воды при помощи насоса. В трубе создается давление и напор усиливается. Насос, создающий давление, и является в этом примере напряженностью электрического поля.
Электричество, если его не контролировать и не знать о пагубном влиянии на организм человека, способно создать множество проблем начиная от сгорания приборов и пожаров, и заканчивая угрозой жизни и здоровью человека. Техника безопасности очень важна в любой сфере.
Пагубное влияние на человека
Электричество очень опасно и является причиной несчастных случаев. Радиолюбители подвержены риску поражения электрическим током довольно часто. Некоторые радиолюбители пробуют наличие напряжения пальцами и пренебрегают техникой безопасности. Большинство из них считает опасным для жизни напряжение от 500 В, а 110 и 220 — не наносящими вреда здоровью. Удары от маломощных источников тока (маломощный силовой трансформатор, конденсатор), по их мнению, являются неопасными.
Согласно технике безопасности при работах с электричеством, они ошибаются, но есть и другая сторона этого вопроса: организм каждого человека индивидуален, обладает разными параметрами. Из этого утверждения следует, что смертельные характеристики электричества (напряжение и ток) индивидуальны для каждого человека. Одних может ударить 36 В, а других не пробивает и 220 В.
Действие электричества на организм человека зависит от нескольких факторов: силы и частоты, времени и пути прохождения через организм, сопротивления организма или участка тела, по которому протекает ток.
Исследованиями ученых установлено, что величина смертельного тока, поражающего сердце, составляет более 100 мА. Токи от 50 мА до 100 мА вызывают потерю сознания при кратковременном касании к поверхности, которая проводит ток. Токи до 50 мА могут стать причиной травм, например, падения с лестницы, выпускания из рук токоведущего проводника и т. д.
д.
Влияние на фактор поражения еще оказывает и сопротивление тела человека. Сопротивление для каждого индивида определить сложно и диапазон его составляет от 30 кОм до 200 кОм. Эта величина зависит от множества факторов: толщины кожи, влажности тела и окружающей среды, усталости, нервно-эмоционального состояния, болезни и других факторов. Сопротивление резко уменьшается при повышенной влажности воздуха и работе на влажных участках.
Формула расчета напряжения, опасного для жизни, предполагая, что Rч = 2кОм и I = 60 мА, выглядит так: U = I * R = 0,06 * 2000 = 120 В. В этой ситуации опасным напряжением можно считать 120 В и выше.
Частота тока является еще одной опасной характеристикой, обладающей поражающим действием. При увеличении частоты опасность уменьшается прямо пропорционально. Ток оказывает и тепловое действие, поэтому считать высокочастотные токи безопасными нельзя.
Травмы, происходящие из-за электричества, называются электротравмами.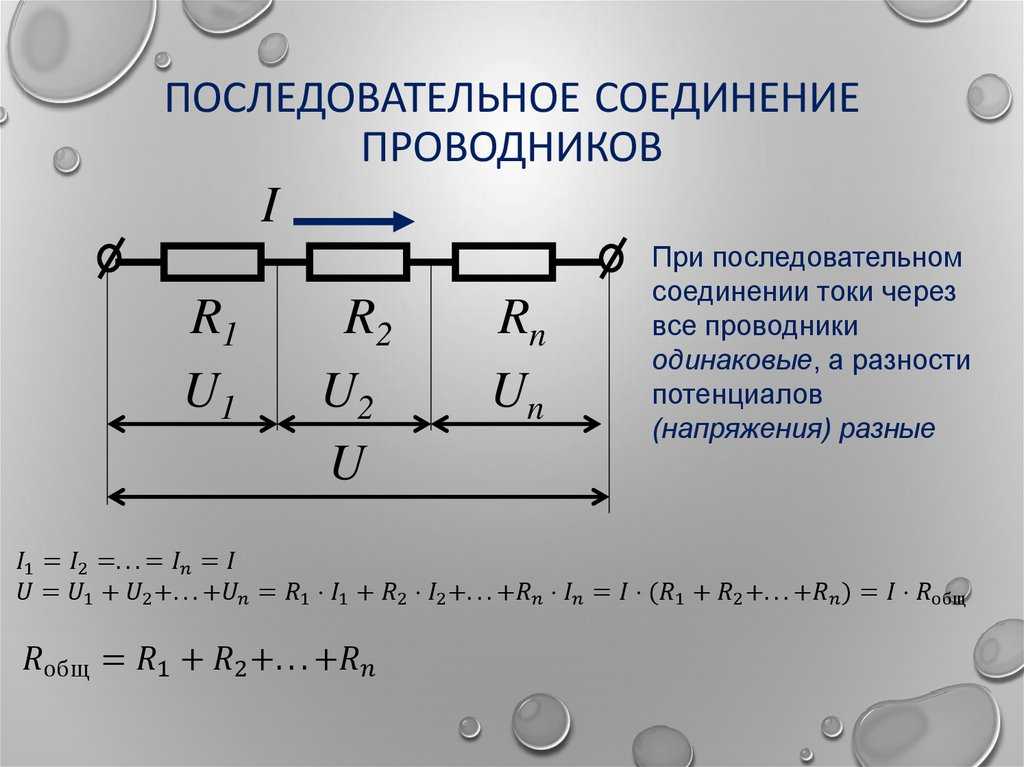 Каждая из них несет в себе меньшую или большую опасность. Наиболее опасными являются травмы, полученные от электрической дуги, которая обладает высокой температурой от 5 тыс. до 12 тыс. градусов по Цельсию. Виды электрических травм:
Каждая из них несет в себе меньшую или большую опасность. Наиболее опасными являются травмы, полученные от электрической дуги, которая обладает высокой температурой от 5 тыс. до 12 тыс. градусов по Цельсию. Виды электрических травм:
- Электрические ожоги происходят при тепловом воздействии на ткани организма человека, по которым течет ток.
- Обожженные участки на коже возникают при прямом контакте ее с токоведущей частью проводника. Пораженный участок приобретает серый или бледно-серый цвет.
- Металлизация кожи — пропитывание кожи частицами металла при коротком замыкании или сварке.
- Механические повреждения — самопроизвольная судорога мышц, приводящая к падению. При падении происходят переломы, ушибы вывихи суставов и т. д.
- Электроофтальмия — воспаление слизистой оболочки глаз при воздействии излучения электрической дуги.
Существует еще один вид поражения — электрический удар. Этот вид поражения можно условно разделить на 5 групп: без потери сознания; с потерей сознания, связанной с нарушением сердечной деятельности или без нее; клиническая смерть и электрический шок.
Единицы измерения
Работа электрического поля по перемещению заряда измеряется в Дж (Джоуль), заряд в Кл (кулон). Вот, как обозначается напряжение или его единица измерения: отношение этих величин (работа по перемещению в Дж к электрическому заряду в Кл) и является разностью потенциалов, измеряется в вольтах (В) и обозначается U. Разность потенциалов бывает:
- Переменной (амплитуда и полярность изменяются с течением времени, в зависимости от характерной частоты).
- Постоянной (имеет постоянное значение амплитуды и полярность есть величина постоянная).
А также у единиц измерения есть приставки, например, кВ (Киловольт = 1000В) и МВ (мегавольт = 1000000В). Существуют о совсем низкие значения, например, мВ (милливольт = 0,001В).
Цепи переменного и постоянного тока
В цепях постоянного и переменного тока U обладает различными свойствами и производит иные влияния на проводники.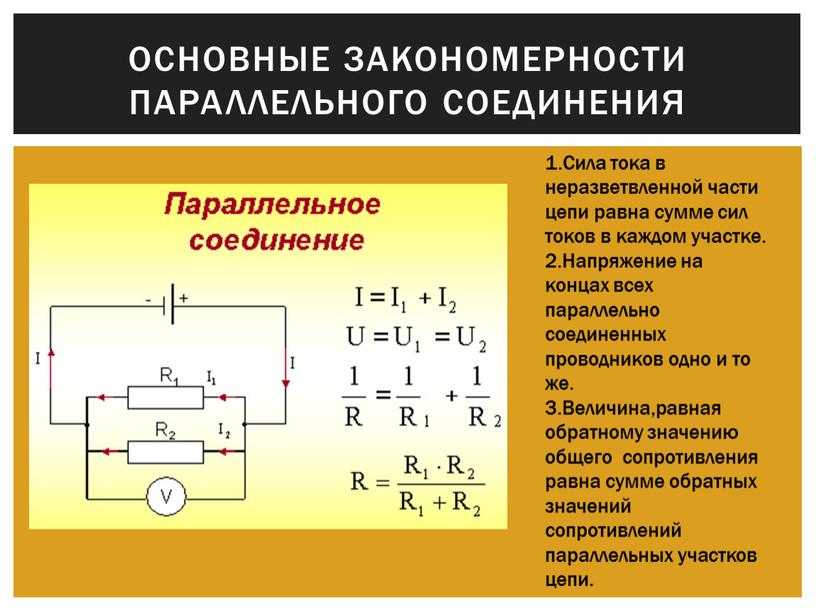 Для постоянного напряжения существуют законы по вычислению его характеристик, но для переменного способы вычисления показателей заметно отличаются. Разберем более подробно все различия и сходства.
Для постоянного напряжения существуют законы по вычислению его характеристик, но для переменного способы вычисления показателей заметно отличаются. Разберем более подробно все различия и сходства.
Расчет и анализ цепей выполняется при помощи закона Ома: сила тока полной цепи прямо пропорциональна напряжению и обратно пропорциональна сумме сопротивлений цепи и источника питания.
Следствие из закона при условии пренебрежения внутренним сопротивлением источника электричества: сила тока участка цепи прямо пропорциональна ЭДС и обратно пропорциональна сопротивлению этого участка.
Запись закона Ома, из которого следует формула напряжения, тока и сопротивления: I = U / (Rц + Rвн), где I — сила тока, U — ЭДС, Rц — сопротивление цепи, Rвн — внутреннее сопротивление источника питания.
Формула силы тока через сопротивление и напряжение: I = U / Rц.
Формула напряжения электрического тока: U = I * Rц.
Для расчета мощности необходимо U умножить на I: P = U * I = U * U / R, где P — мощность.
Переменное однофазное напряжение
В цепях для переменного тока происходят совершенно другие явления и процессы, для них справедливы другие законы. Различают такие основные виды:
- Мгновенное (разность потенциалов в конкретный промежуток времени: u = u (t)).
- Амплитудное значение (максимальное значение мгновенного U в момент времени: u (t) = Uм * sin (wt + f), где w — угловая частота, t — конкретный момент времени и f — угол начальной фазы напряжения).
- Среднее значение (для синусоиды равно нулю).
- Среднеквадратичное — Uq (U за весь период колебаний и для синусоиды имеет вид: Uq = 0,707 * Uм).
- Средневыпрямленное — Uv (среднее значение модуля U: Um примерно равно 0,9 * Uq).
В цепях 3-фазного тока различают 2 вида напряжений: линейное (фаза-фаза) и фазное (фаза-ноль). При соединении в цепь «треугольником» фазное и линейное U равны. В случае соединения «звездой» — фазное в 1,732050808 раз меньше линейного.
Рекомендации по выбору прибора
Для расчетов необходимо измерять значения величин электричества. Существуют специальные приборы, которые помогают произвести точные расчеты. Для измерения разности потенциалов применяют вольтметр.
Вольтметр (вольт — единица измерения ЭДС, метр — измеряю) — прибор для измерения ЭДС в цепи, подключаемый параллельно участку, на котором необходимо провести замер.
Для конкретного случая необходимо применять тот или иной прибор. Для более точных расчетов приобретаются приборы с высоким классом точности. Классификация вольтметров:
- Принцип действия: электромеханические (стрелочные) и электронные.
- Назначение: постоянного и переменного тока, импульсные, селективные и универсальные.
- Конструктивное исполнение: щитовые, переносные и стационарные.
Аналоговый электромеханический вольтметр имеет большие погрешности измерений в высокоомных цепях, но отлично зарекомендовал себя в низкоомных цепях и возможностью модернизации (увеличение значений измерения U за счет добавочного резистора).
Выпрямительный вольтметр обладает более высоким классом точности. Состоит из самого измерительного прибора (обладает чувствительностью к постоянному току) и выпрямительного устройства. Они получили не очень широкое распространение из-за высоких погрешностей, и применяются в качестве сигнальных приборов (примерное значение U).
Цифровые вольтметры применяются в комбинированных приборах-мультиметрах. Поступающее напряжение на клеммы (измерительные щупы) прибора преобразовывается в сигнал при помощи аналого-цифрового преобразователя (АЦП). Происходит отображение на цифровом табло. Этот вид приборов получил широкое применение благодаря высокой точности и универсальности.
Импульсный вольтметр необходимо применять при измерении амплитуд импульсных сигналов и одиночных импульсов.
Основным применением фазочувствительных вольтметров является измерение квадратурных составляющих комплексного напряжения (наличие мнимой и действительной частей) первичной гармоники. Они, как правило, снабжены 2-мя индикаторами для выявления мнимой и действительной частей. Они получили широкое применение в измерении АФХ (амплитудно-фазовая характеристика) для подбора деталей и настройки усилителей.
Они, как правило, снабжены 2-мя индикаторами для выявления мнимой и действительной частей. Они получили широкое применение в измерении АФХ (амплитудно-фазовая характеристика) для подбора деталей и настройки усилителей.
Для измерения номинала постоянного напряжения используются вольтметры подгруппы В2 (вольтметры для постоянного напряжения), а также В7 (универсальные).
Для определения переменного напряжения необходимо использовать устройства из подгруппы В3 или универсального типа (В7). Однако часто в этих вольтметрах применяются специальные преобразователи из переменного напряжения в постоянное.
В3 и В7 рассчитаны только для определения среднеквадратического гармонического напряжения. В этих электроизмерительных приборах возможно применение детекторов (преобразователей): пикового, выпрямительного и квадратичного. Оптимальным вариантом является вольтметр на квадратичном детекторе, при этом измеряемое значение выдается напрямую без всяких преобразований. Измерительные приборы на пиковых и выпрямительных детекторах пересчитывают значения, тем самым уменьшая точность измерений. Для измерения периодического негармонического напряжения выбирают вольтметр на квадратичном детекторе.
Для измерения периодического негармонического напряжения выбирают вольтметр на квадратичном детекторе.
Таким образом, расчет напряжения играет важную роль в электротехнике. Расчеты для переменных и постоянных цепей электрического тока существенно отличаются, в результате чего необходимо определить сначала тип тока, а затем производить расчеты. Но также необходимо соблюдать технику безопасности при работах с электричеством. Ведь ее основные положения основаны на горьком опыте человечества.
Глава 21. Электрический ток. Законы Ома и Джоуля-Ленца
Для решения задач ЕГЭ на постоянный ток надо знать определения тока, напряжения, сопротивления, закон Ома для участка цепи и замкнутой цепи, закон Джоуля-Ленца, а также уметь находить эквивалентные сопротивления простейших электрически цепей. Рассмотрим эти вопросы.
Электрическим током называют упорядоченное движение заряженных частиц. Силой тока в некотором сечении проводника называется отношение заряда , протекшего через это сечение за интервал времени , к этому интервалу времени
(21. |
Чтобы в проводнике тек электрический ток, в проводнике должно быть электрическое поле, или, другими словами, потенциалы различных точек проводника должны быть разными. Но при движении электрических зарядов по проводнику потенциалы различных точек проводника будут выравниваться (см. гл. 19). Поэтому для протекания тока в течение длительного времени на каких-то участках цепи необходимо обеспечить движение зарядов в направлении противоположном полю. Такое движение может быть обеспечено только силами неэлектрической природы, которые в этом контексте принято называть сторонними. В гальванических элементах («батарейках») сторонние силы возникают в результате электрохимических превращений на границах электродов и электролита. Эти превращения обеспечивают перемещение заряда противоположно направлению поля, поддерживая движение зарядов по замкнутому пути.
Сила тока в однородном участке проводника пропорциональна напряженности электрического поля внутри проводника. А поскольку напряженность поля внутри проводника связана с разностью потенциалов его концов (или электрическим напряжением на проводнике ), то
А поскольку напряженность поля внутри проводника связана с разностью потенциалов его концов (или электрическим напряжением на проводнике ), то
(21.2) |
Коэффициент пропорциональности , который принято записывать в знаменатель формулы (21.2), является характеристикой проводника и называется его сопротивлением. В результате формула (21.2) принимает вид
(21.3) |
Формула (21.3) называется законом Ома для однородного участка цепи, а сам участок цепи часто называют резистором (от английского слова resistance — сопротивление).
Если проводник является однородным и имеет цилиндрическую форму (провод), то его сопротивление пропорционально длине и обратно пропорционально площади сечения
(21.4) |
где коэффициент пропорциональности зависит только от материала проводника и называется его удельным сопротивлением.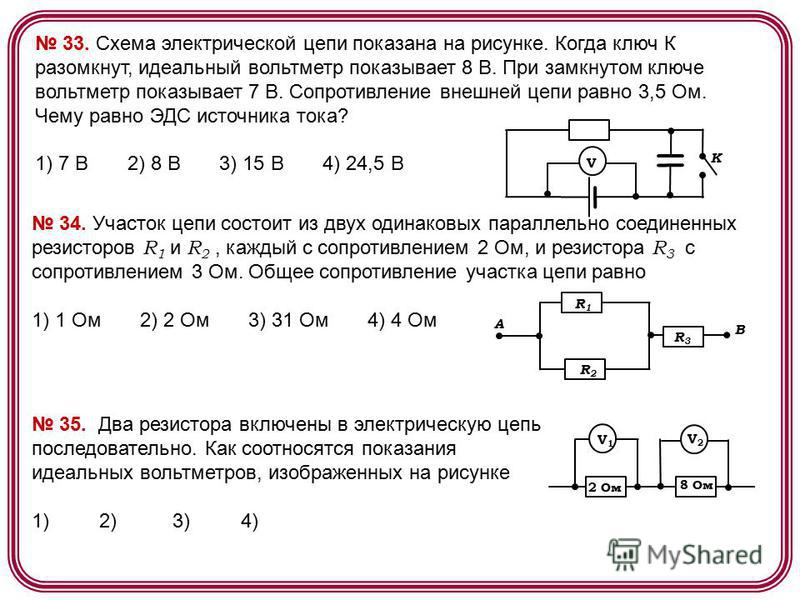
Если участок цепи представляет собой несколько последовательно соединенных однородных проводников с сопротивлениями (см. рисунок), то сила тока через каждый проводник будет одинаковой , электрическое напряжение на всем участке цепи равно сумме напряжений на каждом проводнике , а эквивалентное сопротивление всего участка равно сумме сопротивлений отдельных проводников
(21.4) |
Если участок цепи представляет собой несколько однородных проводников с сопротивлениями , соединенных параллельно (см. рисунок), то электрическое напряжение на каждом проводнике будет одинаковым , ток через участок будет равен сумме токов, текущих через каждый проводник , а величина, обратная эквивалентному сопротивлению всего участка, равно сумме обратных сопротивлений отдельных проводников
(21. |
Рассмотрим теперь закон Ома для замкнутой электрической цепи. Пусть имеется замкнутая электрическая цепь, состоящая из источника сторонних сил с внутренним сопротивлением и внешнего сопротивления . Пусть при прохождении заряда через источник сторонние силы совершают работу . Электродвижущей силой источника (часто используется аббревиатура ЭДС) называется отношение работы сторонних сил к заряду
(21.6) |
В этом случае сила тока в цепи равна
(21.7) |
Формула (21.7) называется законом Ома для замкнутой электрической цепи.
При прохождении электрического тока через участок цепи электрическое поле совершает работу (часто эту работу называют работой тока, хотя термин этот не очень точный). Очевидно, вся эта работа превращается в тепло. Поэтому если через участок цепи прошел заряд , где — сила тока в цепи, — время, то количество выделившейся теплоты равно
(21. |
(для получения последнего и предпоследнего равенств использован закон Ома для участка цепи). Формулы (21.8) называются законом Джоуля-Ленца. Из формулы (21.8) следует, что количество выделившейся при протекании электрического тока теплоты линейно зависит от времени наблюдения. Поэтому отношение
(21.9) |
которое называется мощностью тока, не зависит от времени наблюдения. Формулу (21.9) также называют законом Джоуля-Ленца.
Рассмотрим теперь задачи.
Структура металла кратко обсуждалась в гл. 16: положительно заряженные ионы расположены в узлах кристаллической решетки, образовавшиеся в результате диссоциации валентные электроны могут свободно перемещаться по проводнику (свободные электроны). Они и осуществляют проводимость металла (задача 21.1.1 — ответ 2).
Согласно определению (21.1) находим среднюю силу тока в канале молнии (задача 21.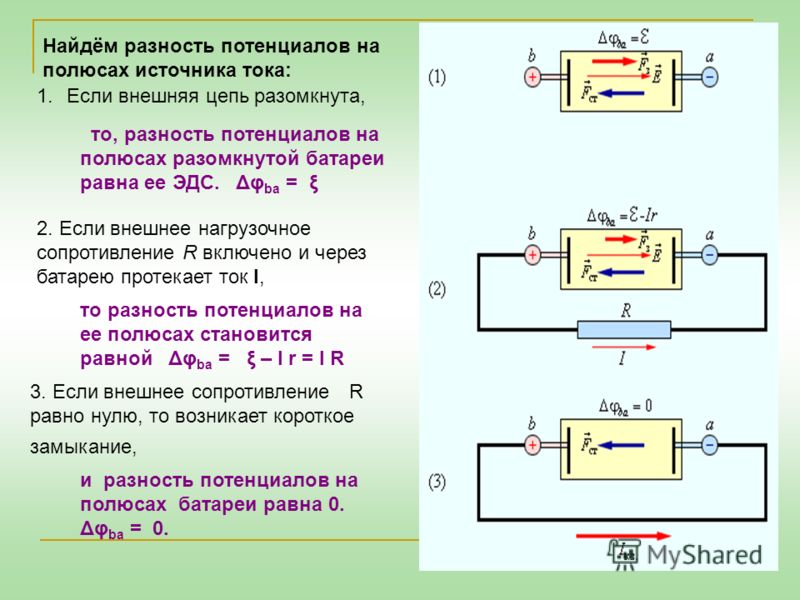 1.2)
1.2)
(ответ 2).
Если за 1 мин через сечение проводника протекает заряд 60 Кл (задача 21.1.3), то сила тока в этом проводнике равна А. Применяя далее к этому проводнику закон Ома для участка цепи, получаем В (ответ 2).
По закону Ома для участка цепи имеем для силы тока через участок цепи после изменения его сопротивления и электрического напряжения на нем (задача 21.1.4)
Таким образом, сила тока уменьшилась в 4 раза (ответ 3).
Согласно закону Ома для участка цепи сопротивление — это коэффициент пропорциональности между напряжением на этом участке и силой тока в нем. Поэтому в задаче 21.1.5 имеем, например, используя крайнюю точку графика
(ответ 2). Из-за линейной зависимости тока от напряжения вычисления можно было выполнить и по другим точкам графика, ответ был бы таким же.
Согласно формуле (21.4) имеем для первой проволоки в задаче 21.1.6
где — удельное сопротивление меди, — длина проводника, — его радиус. Для медной проволоки с вдвое большей длиной и втрое бóльшим радиусом сечения имеем
(ответ 3).
Как следует из формулы (21.4) при двукратном уменьшении длины проводника вдвое уменьшается его сопротивление. Поэтому из закона Ома для участка цепи (21.3) заключаем, что при двукратном уменьшении напряжения на проводнике и двукратном уменьшении его длины (задача 21.1.7) сила тока в проводнике не изменится (ответ 4).
В задаче 21.1.8 следует использовать закон Ома для замкнутой электрической цепи (21.7). Имеем
где — ЭДС источника, — сопротивлении е внешней цепи, — сопротивление источника (ответ 1).
В задаче 21.1.9 следует применить закон Ома для замкнутой электрической цепи (21.7) к какому-нибудь значению внешнего сопротивления, по графику найти силу тока в цепи, а затем и ЭДС источника. Проще всего применить закон Ома к случаю . Из графика находим силу тока . Поэтому
где — внутреннее сопротивление источника (ответ 3).
Из формулы (21.9) следует, что при фиксированном сопротивлении участка цепи увеличение электрического напряжения в 2 раза (задача 21.1.10) приведет к увеличению мощности тока в 4 раза (ответ 2).
В задаче 21.2.1 удобно использовать вторую из формул (21.9) . Имеем Вт (ответ 3).
Часто школьники не могут ответить на такой вопрос: из формулы для мощности тока следует, что мощность линейно растет с ростом сопротивления, а из формулы — убывает с ростом сопротивления. А как же в действительности мощность зависит от сопротивления? Давайте разберемся в этом вопросе на примере задачи 21. 2.2. Конечно, оба предложенных «решения» неправильны: в них молчаливо предполагалось, что сила тока, текущего через это сопротивление, или напряжение на этом сопротивлении не зависят от его величины. А на самом деле эти величины от сопротивления зависят, причем эти зависимости могут быть разными для разных источников тока. Внутреннее сопротивление бытовых электрических сетей очень мало. В этом случае из законов Ома для замкнутой цепи и участка цепи (21.7), (21.3) следует, что напряжение на любом элементе, включенном в такую сеть, не зависит от сопротивления этого элемента и равно номинальному напряжению сети . Поэтому из формулы заключаем, что мощность, которая выделяется на таком элементе обратно пропорциональна его сопротивлению (ответ 3). Отметим, что из проведенного рассуждения следует, что выделяемая мощность будет очень большой (опасная в быту ситуация!) для малого сопротивления внешнего участка цепи, т.е. в случае короткого замыкания, которого, таким образом, необходимо избегать.
2.2. Конечно, оба предложенных «решения» неправильны: в них молчаливо предполагалось, что сила тока, текущего через это сопротивление, или напряжение на этом сопротивлении не зависят от его величины. А на самом деле эти величины от сопротивления зависят, причем эти зависимости могут быть разными для разных источников тока. Внутреннее сопротивление бытовых электрических сетей очень мало. В этом случае из законов Ома для замкнутой цепи и участка цепи (21.7), (21.3) следует, что напряжение на любом элементе, включенном в такую сеть, не зависит от сопротивления этого элемента и равно номинальному напряжению сети . Поэтому из формулы заключаем, что мощность, которая выделяется на таком элементе обратно пропорциональна его сопротивлению (ответ 3). Отметим, что из проведенного рассуждения следует, что выделяемая мощность будет очень большой (опасная в быту ситуация!) для малого сопротивления внешнего участка цепи, т.е. в случае короткого замыкания, которого, таким образом, необходимо избегать.
Если бы внутреннее сопротивление источника было бы много больше внешнего сопротивления, ток в цепи определялся бы, главным образом, внутренним сопротивлением источника, а от внешнего сопротивления зависел бы слабо. В этом случае мощность тока была бы прямо пропорциональна сопротивлению участка цепи.
Как обсуждалось в решении предыдущей задачи, сопротивление элемента, работающего в бытовой электросети равно , где — номинальная мощность данного элемента, — напряжение в сети. Поэтому отношение сопротивлений ламп мощностью Вт и Вт, рассчитанных на работу в одной и той же бытовой электрической сети (задача 21.2.3) равно
(ответ 2).
Поскольку резисторы в задаче 21.2.4 соединены последовательно, то сила тока в них одинакова. Поэтому из закона Ома для участка цепи заключаем, что
(ответ 2).
При параллельном соединении ламп (задача 21.2.5) напряжение на них одинаково (см. введение к настоящей главе). Поэтому из закона Ома для участка цепи следует, что
(ответ 1).
Рассматриваемый в задаче 21.2.6 участок представляет собой два последовательных соединенных элемента, один из которых есть резистор 6 Ом, второй — два таких же резистора, соединенных параллельно. По правилам сложения сопротивлений находим эквивалентное сопротивление второго участка
а затем и эквивалентное сопротивление всей цепи
(ответ 3).
При разомкнутом ключе сопротивление участка цепи, данного в задаче 21.2.7, можно найти как в предыдущей задаче , где — сопротивление каждого резистора. Если ключ замкнут, то цепь сводится к одному резистору (т. к. параллельно двум резисторам включается проводник с пренебрежимо малым сопротивлением). Поэтому в этом случае сопротивление цепи равно . Таким образом, сопротивление второй цепи составляет две трети от сопротивления первой (ответ 1).
к. параллельно двум резисторам включается проводник с пренебрежимо малым сопротивлением). Поэтому в этом случае сопротивление цепи равно . Таким образом, сопротивление второй цепи составляет две трети от сопротивления первой (ответ 1).
Как обсуждалось в решении задачи 21.2.2, сопротивление элемента номинальной мощности , работающего в бытовой электросети равна
где В — напряжение сети. Из этой формулы следует, что чем больше номинальная мощность элемента, тем меньше должно быть его сопротивление. Если две лампы накаливания включены последовательно (задача 21.2.8), то сила тока в них одинакова и отношение мощностей тока в этих лампах равно отношению их сопротивлений. Отсюда следует, что отношение реально выделяемых в лампах мощностей и обратно отношению номинальных мощностей этих ламп:
(ответ 2).
Работа, совершаемая электрическим полем в проводнике при протекании по нему электрического тока, превращается в энергию тока, которая затем превращается в тепловую энергию. Поэтому работу поля можно найти из закона Джоуля-Ленца. Для работы поля за время получаем . Из этой формулы находим сопротивление проводника в задаче 21.2.9 —
(ответ 1).
Поскольку при последовательном соединении резисторов ток через каждый из них одинаков, из закона Джоуля-Ленца (22.8) заключаем, что из двух сопротивлений и (задача 21.2.10; см. рисунок) наибольшей будет мощность тока на сопротивлении , из двух сопротивлений и — на сопротивлении . Сравним мощности тока на этих сопротивлениях. Учитывая, что при параллельном соединении элементов электрическое напряжение на каждом элементе одинаковое, а при последовательном — складываются значения сопротивлений, получим из законов Ома для верхнего и нижнего участков цепи и закона Джоуля-Ленца
где — электрическое напряжение, приложенное ко всей цепи. Поскольку то в представленной схеме наибольшая мощность будет выделяться на сопротивлении (ответ 2).
Поскольку то в представленной схеме наибольшая мощность будет выделяться на сопротивлении (ответ 2).
Закон Ома для участка цепи. Закон Джоуля — Ленца. Работа и мощность электрического тока. Виды соединения проводников.
Основные ссылки
CSS adjustments for Marinelli theme
Объединение учителей Санкт-Петербурга
Форма поиска
Поиск
Вы здесь
Главная » Закон Ома для участка цепи. Закон Джоуля -…
| Закон Ома для участка цепи. | ||||
Сила тока в участке цепи прямо пропорциональна напряжению на концах этого участка и обратно пропорциональна сопротивлению этого участка.
Выполняется для металлов и электролитов. | ||||
Закон Джоуля — Ленца. Дж. Джоуль (1841—1843) Э. X. Ленц (1842—1843) независимо друг от друга экспериментально установили | ||||
В электрической цепи происходит преобразование энергии упорядоченного движения заряженных частиц в тепловую. Согласно з-ну сохранения энергии работа тока равна количеству выделившегося тепла. | ||||
Количество теплоты, выделившееся при прохождении электрического тока по проводнику, прямо пропорционально квадрату силы тока, сопротивлению проводника и времени, в течение которого шел ток: | ||||
Работа и мощность электрического тока. | ||||
Работа электрического тока: | ||||
Мощность электрического тока (работа в единицу времени): | ||||
В электричестве иногда применяется внесистемная единица работы — кВт. | 1 кВт.ч = 3,6.106 Дж. | |||
Виды соединения проводников. | ||||
Последовательное соединение. 1. Сила тока во всех последовательно соединенных участках цепи одинакова: I1=I2=I3=…=In=… 2. Напряжение в цепи, состоящей из нескольких последовательно соединенных участков, равно сумме напряжений на каждом участке: U=U1+U2+…+Un+… 3. Сопротивление цепи, состоящей из нескольких последовательно соединенных участков, равно сумме сопротивлений каждого участка: R=R1+R2+. Если все сопротивления в цепи одинаковы, то: R=R1. N При последовательном соединении общее сопротивление увеличивается (больше большего). | Параллельное соединение. 1. Сила тока в неразветвленном участке цепи равна сумме сил токов во всех параллельно соединенных участках. I=I1+I2+…+In+… | |||
2. Напряжение на всех параллельно соединенных участках цепи одинаково: U1=U2=U3=…=Un=… 3. При параллельном соединении проводников проводимости складываются (складываются величины, обратные сопротивлению): Если все сопротивления в цепи одинаковы, то: При параллельном соединении общее сопротивление уменьшается (меньше меньшего). | ||||
4. Работа электрического тока в цепи, состоящей из последовательно соединенных участков, равна сумме работ на отдельных участках: A=A1+A2+…+An+… т.к. A=I2Rt=I2(R1+R2+…+Rn+…)t. 5. Мощность электрического тока в цепи, состоящей из последовательно соединенных участков, равна сумме мощностей на отдельных участках: P=P1+P2+…+Pn+… 6. Т.к. силы тока во всех участках одинаковы, то: U1:U2:…:Un:… = R1:R2:…:Rn:… Для двух резисторов: — чем больше сопротивление, тем больше напряжение. | 4. Работа электрического тока в цепи, состоящей из параллельно соединенных участков, равна сумме работ на отдельных участках: A=A1+A2+. т.к. .
5. Мощность электрического тока в цепи, состоящей из параллельно соединенных участков, равна сумме мощностей на отдельных участках: P=P1+P2+…+Pn+… 6. Т.к. напряжения на всех участках одинаковы, то: I1R1= I2R2=…= I3R3=… Для двух резисторов: — чем больше сопротивление, тем меньше сила тока. | |||
Теги:
конспект
цепей простой серии | Последовательные и параллельные цепи
На этой странице мы изложим три принципа, которые вы должны понимать в отношении последовательных цепей:
- Ток : Величина тока одинакова через любой компонент в последовательной цепи.
- Сопротивление : Общее сопротивление любой последовательной цепи равно сумме отдельных сопротивлений.

- Напряжение : Напряжение питания в последовательной цепи равно сумме отдельных падений напряжения.
Давайте рассмотрим несколько примеров последовательных схем, демонстрирующих эти принципы.
Начнем с последовательной цепи, состоящей из трех резисторов и одной батареи:
Первый принцип, который нужно понять о последовательных цепях, заключается в следующем:
Величина тока в последовательной цепи одинакова для любого компонента в цепи.
Это связано с тем, что в последовательной цепи имеется только один путь для протекания тока. Поскольку электрический заряд течет по проводникам подобно шарикам в трубке, скорость потока (скорость шариков) в любой точке цепи (трубки) в любой конкретный момент времени должна быть одинаковой.
Использование закона Ома в последовательных цепях
По тому, как устроена 9-вольтовая батарея, мы можем сказать, что ток в этой цепи будет течь по часовой стрелке, от точки 1 к точке 2, к точке 3, к точке 4 и обратно к 1. Однако у нас есть один источник напряжения и три сопротивления. Как здесь использовать закон Ома?
Однако у нас есть один источник напряжения и три сопротивления. Как здесь использовать закон Ома?
Важная оговорка к Закону Ома заключается в том, что все величины (напряжение, ток, сопротивление и мощность) должны соотноситься друг с другом с точки зрения одних и тех же двух точек в цепи. Мы можем увидеть эту концепцию в действии в приведенном ниже примере схемы с одним резистором.
Использование закона Ома в простой цепи с одним резистором
С помощью схемы с одной батареей и одним резистором мы можем легко рассчитать любую величину, поскольку все они относятся к одним и тем же двум точкам в цепи:
Поскольку точки 1 и 2 соединены вместе проводом с пренебрежимо малым сопротивлением, как и точки 3 и 4, можно сказать, что точка 1 электрически общая с точкой 2, а точка 3 электрически общая с точкой 4. Поскольку мы знаем, что у нас 9вольт ЭДС между точками 1 и 4 (непосредственно на аккумуляторе), а так как точка 2 общая с точкой 1 и точка 3 общая с точкой 4, то и между точками 2 и 3 (непосредственно на резисторе) должно быть 9 вольт .
Следовательно, мы можем применить закон Ома (I = E/R) к току через резистор, потому что мы знаем напряжение (E) на резисторе и сопротивление (R) этого резистора. Все термины (E, I, R) относятся к одним и тем же двум точкам цепи, к одному и тому же резистору, поэтому мы можем безоговорочно использовать формулу закона Ома.
Использование закона Ома в цепях с несколькими резисторами
В цепях, содержащих более одного резистора, мы должны быть осторожны в применении закона Ома. В примере схемы с тремя резисторами ниже мы знаем, что у нас есть 9 вольт между точками 1 и 4, что является величиной электродвижущей силы, управляющей током через последовательную комбинацию R 1 , R 2 и R 3 . Однако мы не можем взять значение 9 вольт и разделить его на 3 кОм, 10 кОм или 5 кОм, чтобы попытаться найти значение тока, потому что мы не знаем, какое напряжение находится на каждом из этих резисторов в отдельности.
Цифра 9 вольт – это суммарных величин для всей цепи, тогда как цифры 3k, 10k и 5k Ω – это индивидуальных величин для отдельных резисторов. Если бы мы подставили цифру полного напряжения в уравнение закона Ома вместе с цифрой индивидуального сопротивления, результат не был бы точно связан с какой-либо величиной в реальной цепи.
Если бы мы подставили цифру полного напряжения в уравнение закона Ома вместе с цифрой индивидуального сопротивления, результат не был бы точно связан с какой-либо величиной в реальной цепи.
Для R 1 закон Ома будет соотносить величину напряжения на R 1 с током через R 1 , при заданном сопротивлении R 1 , 3кОм:
напряжение, подаваемое батареей через комбинацию из трех резисторов), и мы не знаем ток через R 1 , мы не можем выполнять какие-либо вычисления ни по одной из формул. То же самое касается R 2 и R 3 : мы можем применить уравнения закона Ома тогда и только тогда, когда все члены представляют их соответствующие величины между одними и теми же двумя точками в цепи.
Так что мы можем сделать? Нам известно напряжение источника (9 вольт), приложенное к последовательной комбинации R 1 , R 2 и R 3 , и мы знаем сопротивление каждого резистора, но, поскольку эти величины не входят в В том же контексте мы не можем использовать закон Ома для определения тока в цепи. Если бы мы только знали, каково общее сопротивление для цепи: тогда мы могли бы рассчитать общий ток с нашим значением для общего напряжения (I = E/R).
Если бы мы только знали, каково общее сопротивление для цепи: тогда мы могли бы рассчитать общий ток с нашим значением для общего напряжения (I = E/R).
Объединение нескольких резисторов в эквивалентный общий резистор
Это подводит нас ко второму принципу последовательных цепей:
Общее сопротивление любой последовательной цепи равно сумме отдельных сопротивлений.
Это должно быть интуитивно понятно: чем больше последовательно соединенных резисторов, через которые должен протекать ток, тем сложнее будет протекать току.
В примере задачи у нас были последовательные резисторы 3 кОм, 10 кОм и 5 кОм, что дало нам общее сопротивление 18 кОм:
По сути, мы рассчитали эквивалентное сопротивление R 1 , R 2 и R 3 вместе взятых. Зная это, мы могли бы перерисовать схему с одним эквивалентным резистором, представляющим последовательную комбинацию R 1 , R 2 и R 3 :
Теперь у нас есть вся необходимая информация для расчета тока цепи, потому что у нас есть напряжение между точками 1 и 4 (9вольт) и сопротивление между точками 1 и 4 (18 кОм):
Расчет напряжений компонентов по закону Ома
Зная, что ток одинаков во всех компонентах последовательной цепи (и мы только что определили ток
Теперь, когда мы знаем величину тока через каждый резистор, мы можем использовать закон Ома для определения падение напряжения на каждом из них (применяя закон Ома в правильном контексте):
Обратите внимание на падение напряжения на каждом резисторе и на то, как сумма падений напряжения (1,5 + 5 + 2,5) равна напряжению батареи (питания): 9 вольт.
Это третий принцип последовательного соединения:
Напряжение питания в последовательном соединении равно сумме отдельных падений напряжения.
Анализ простых последовательных цепей с помощью «табличного метода» и закона Ома
Однако метод, который мы только что использовали для анализа этой простой последовательной цепи, можно упростить для лучшего понимания. Используя таблицу для перечисления всех напряжений, токов и сопротивлений в цепи, становится очень легко увидеть, какие из этих величин могут быть правильно связаны в любом уравнении закона Ома:
Правило для такой таблицы заключается в применении закона Ома только к значениям в каждом вертикальном столбце. Например, E R1 только с I R1 и R 1 ; E R2 только с I R2 и R 2 ; и т. д. Вы начинаете свой анализ с заполнения тех элементов таблицы, которые даны вам с самого начала:
Как видно из расположения данных, мы не можем применить 9вольт ET (общее напряжение) к любому из сопротивлений (R 1 , R 2 или R 3 ) в любой формуле закона Ома, потому что они находятся в разных столбцах. Напряжение батареи 9 вольт равно , а не , приложенных непосредственно к контактам R 1 , R 2 или R 3 . Однако мы можем использовать наши «правила» последовательных цепей, чтобы заполнить пустые места в горизонтальном ряду. В этом случае мы можем использовать правило последовательностей сопротивлений, чтобы определить общее сопротивление из сумма отдельных сопротивлений:
Напряжение батареи 9 вольт равно , а не , приложенных непосредственно к контактам R 1 , R 2 или R 3 . Однако мы можем использовать наши «правила» последовательных цепей, чтобы заполнить пустые места в горизонтальном ряду. В этом случае мы можем использовать правило последовательностей сопротивлений, чтобы определить общее сопротивление из сумма отдельных сопротивлений:
Теперь, со значением полного сопротивления, вставленным в крайний правый столбец («Общее»), мы можем применить закон Ома I=E/R к общему напряжению и общему сопротивление для получения полного тока 500 мкА:
Затем, зная, что ток распределяется поровну между всеми компонентами последовательной цепи (еще одно «правило» последовательных цепей), мы можем заполнить токи для каждого резистора из только что рассчитанного значения тока:
Наконец, мы можем использовать закон OHM для определения падения напряжения на каждом резисторе, по одному столбцу за время:
Проверка расчетов с помощью компьютерного анализа (Spice)
для забавно, мы можем использовать компьютер для автоматического анализа этой же самой схемы. Это будет хороший способ проверить наши расчеты, а также ближе познакомиться с компьютерным анализом. Во-первых, мы должны описать схему компьютеру в формате, распознаваемом программным обеспечением.
Это будет хороший способ проверить наши расчеты, а также ближе познакомиться с компьютерным анализом. Во-первых, мы должны описать схему компьютеру в формате, распознаваемом программным обеспечением.
Программа SPICE, которую мы будем использовать, требует, чтобы все электрически уникальные точки в цепи были пронумерованы, а размещение компонентов понимается по тому, какие из этих пронумерованных точек или «узлов» они разделяют. Для ясности я пронумеровал четыре угла схемы нашего примера от 1 до 4. Однако SPICE требует, чтобы где-то в схеме был нулевой узел, поэтому я перерисую схему, немного изменив схему нумерации:
Все, что я здесь сделал, это перенумеровал левый нижний угол схемы на 0 вместо 4. Теперь я могу ввести несколько строк текста в компьютерный файл, описывающий схему в терминах, которые SPICE поймет, завершить с парой дополнительных строк кода, предписывающих программе отображать данные о напряжении и токе для нашего удовольствия. Этот компьютерный файл известен как список соединений в терминологии SPICE:
Этот компьютерный файл известен как список соединений в терминологии SPICE:
последовательная цепь v1 1 0 р1 1 2 3к р2 2 3 10к р3 3 0 5к .dc v1 9 9 1 .print DC v (1,2) v (2,3) v (3,0) .конец
Теперь все, что мне нужно сделать, это запустить программу SPICE для обработки списка соединений и вывода результатов:
| v1 | v(1,2) | в(2,3) | v(3) | я (v1) |
|---|---|---|---|---|
| 9.000E+00 | 1.500E+00 | 5.000E+00 | 2.500E+00 | -5.000Е-04 |
Эта распечатка говорит нам, что напряжение батареи составляет 9 вольт, а падение напряжения на резисторах R 1 , R 2 и R 3 составляет 1,5 вольт, 5 вольт и 2 соответственно. . Падения напряжения на любом компоненте в SPICE обозначаются номерами узлов, между которыми находится компонент, поэтому v(1,2) ссылается на напряжение между узлами 1 и 2 в цепи, которые являются точками, между которыми R 1 находится.
Порядок номеров узлов важен: когда SPICE выводит число для v(1,2), он учитывает полярность так же, как если бы мы держали вольтметр с красным щупом в узле 1 и черным щупом на узле 2. У нас также есть дисплей, показывающий ток (хотя и с отрицательным значением) на уровне 0,5 миллиампер или 500 микроампер. Итак, наш математический анализ был подтвержден компьютером. Эта цифра отображается как отрицательное число в анализе SPICE из-за особенностей того, как SPICE обрабатывает текущие вычисления.
Таким образом, последовательная цепь определяется как имеющая только один путь, по которому может течь ток. Из этого определения следуют три правила последовательных цепей: все компоненты имеют одинаковый ток; сопротивления добавляются к большему общему сопротивлению; и падения напряжения складываются, чтобы равняться большему общему напряжению. Все эти правила уходят корнями в определение последовательной цепи. Если вы полностью понимаете это определение, то правила — не что иное, как сноски к определению.
ОБЗОР:
- Компоненты в последовательной цепи имеют одинаковый ток: I Итого = I 1 = I 2 = . . . я п
- Общее сопротивление в последовательной цепи равно сумме отдельных сопротивлений: RTotal = R 1 + R 2 + . . . Р п
- Общее напряжение в последовательной цепи равно сумме отдельных падений напряжения E Total = E 1 + Е 2 + . . . EN
Попробуйте наш Калькулятор закона Ома в нашем разделе Инструменты .
СВЯЗАННЫЕ РАБОЧИЕ ТАБЛИЦЫ:
- Серия
- Практическое задание по цепям постоянного тока с ответами Рабочий лист
- Работа с алгебраическими уравнениями для электрических цепей. Лист .
– Основное электричество
Электрические цепи
Три закона для последовательных цепей
Существуют три основных соотношения, касающихся сопротивления, тока и напряжения для всех последовательных цепей. Важно, чтобы вы усвоили три основных закона для последовательных цепей.
Важно, чтобы вы усвоили три основных закона для последовательных цепей.
Сопротивление
Всякий раз, когда отдельные сопротивления соединены последовательно, они имеют тот же эффект, что и одно большое комбинированное сопротивление. Поскольку в последовательной цепи есть только один путь для протекания тока, и поскольку каждый из резисторов находится на линии, чтобы действовать как противодействие этому протеканию тока, общее сопротивление представляет собой комбинированное сопротивление всех встроенных резисторов.
Общее сопротивление последовательной цепи равно сумме всех отдельных сопротивлений в цепи .
Rt = R1 + R2 + R3…
Используя эту формулу, вы находите, что общее сопротивление цепи составляет:
RT = 15 Ом + 5 Ом + 20 Ом = 40 Ом
Рисунок 16. Последовательная схема
Текущий
Поскольку в последовательной цепи существует только один путь для потока электронов, ток в любой точке цепи имеет одинаковую величину.
Полный ток в последовательной цепи равен току через любое сопротивление цепи.
ИТ = И1 = И2 = И3…
Учитывая 120 В в качестве общего напряжения и определяя общее сопротивление цепи как 40 Ом, теперь вы можете применить закон Ома для определения полного тока в этой цепи:
IT = 120 В/ 40 Ом = 3 А
Этот общий ток цепи будет оставаться одинаковым для всех отдельных резисторов цепи.
Напряжение
Прежде чем какой-либо ток будет протекать через сопротивление, должна быть доступна разность потенциалов или напряжение. При последовательном соединении резисторов они должны «делить» общее напряжение источника.
Общее напряжение в последовательной цепи равно сумме всех отдельных падений напряжения в цепи.
Когда ток проходит через каждый резистор в последовательной цепи, он создает разность потенциалов на каждом отдельном сопротивлении. Это обычно называют падением напряжения, и его величина прямо пропорциональна значению сопротивления. Чем больше значение сопротивления, тем выше падение напряжения на этом резисторе.
Чем больше значение сопротивления, тем выше падение напряжения на этом резисторе.
ЭТ = Е1 + Е2 + Е3…
Используя закон Ома, вы можете определить напряжение на каждом резисторе.
3 А × 15 Ом = 45 В
3 А × 5 Ом = 15 В
3 А × 20 Ом = 60 В
Общее напряжение источника равно сумме отдельных падений напряжения:
45 В + 15 В + 60 В = 120 В
Обрыв в последовательной цепи
Если вводится обрыв, ток в цепи прерывается. Если ток отсутствует, падение напряжения на каждом из резистивных элементов равно нулю. Однако разность потенциалов источника появляется поперек обрыва. Если вольтметр подключен через разомкнутую цепь, показания будут такими же, как если бы он был подключен непосредственно к клеммам источника питания.
Рис. 17. Разомкнутая цепьПоследствия падения и потери линии
Медь и алюминий используются в качестве проводников, потому что они мало противодействуют току. Хотя при простом анализе цепей сопротивлением часто пренебрегают, в практических приложениях может возникнуть необходимость учитывать сопротивление линий.
Хотя при простом анализе цепей сопротивлением часто пренебрегают, в практических приложениях может возникнуть необходимость учитывать сопротивление линий.
Отвод линии
Рисунок 18. Падение напряжения
Поскольку через каждую линию с сопротивлением 0,15 Ом протекает ток 10 А, на каждой линии возникает небольшое падение напряжения. Это падение напряжения на линейных проводах обычно называют отбрасывание строки .
Поскольку имеется две линии, общее падение составляет 2 × 1,5 В = 3 В. Чистое напряжение на нагрузке (117 В) меньше напряжения источника.
В некоторых ситуациях может быть необходимо использовать более крупные проводники с меньшим сопротивлением, чтобы падение напряжения в линии не слишком сильно снижало напряжение нагрузки.
Потеря линии
Другим термином, связанным с проводниками, являются потери в линии. Это потери мощности, выраженные в ваттах и связанные с рассеиванием тепловой энергии при протекании тока через сопротивление линейных проводников. Потери в линии рассчитываются с помощью одного из уравнений мощности.
Потери в линии рассчитываются с помощью одного из уравнений мощности.
Используя предыдущий пример:
P = I 2 × R
P = (10 А) 2 × 0,3 Ом
P = 30 Вт
*Помните:
- Падение напряжения в линии выражается в вольтах.
- Потери в линии выражены в ваттах.
Напряжение холостого хода: что это такое? (И как его найти и протестировать)
Содержание
Что такое напряжение холостого хода?
Когда в каком-либо устройстве или цепи возникает состояние разомкнутой цепи, разность электрических потенциалов между двумя клеммами называется напряжением разомкнутой цепи. В сетевом анализе напряжение холостого хода также известно как напряжение Тевенина. Напряжение холостого хода часто сокращается до OCV или V OC в математических уравнениях.
В условиях разомкнутой цепи внешняя нагрузка отключена от источника.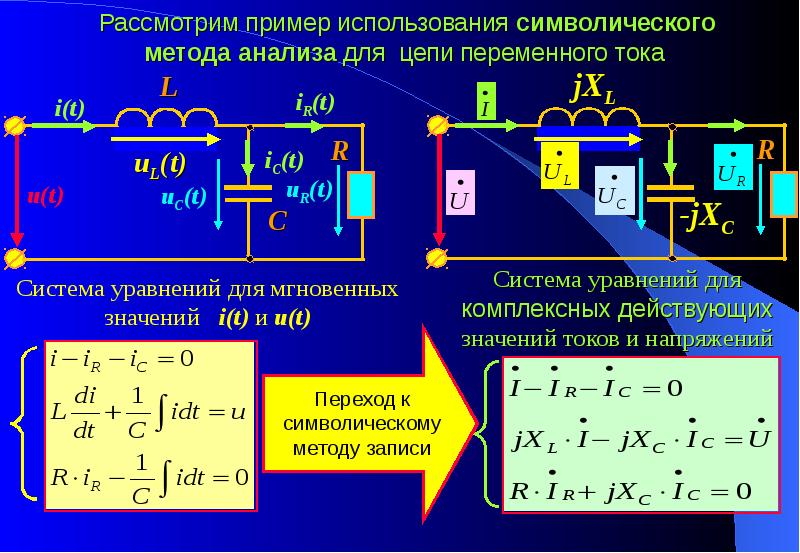 Электрический ток не будет течь по цепи.
Электрический ток не будет течь по цепи.
Когда нагрузка подключена и цепь замкнута, напряжение источника делится на нагрузку. Но когда полная нагрузка устройства или цепи отключена и цепь разомкнута, напряжение холостого хода равно напряжению источника (предположим, что источник идеальный).
Напряжение холостого хода используется для обозначения разности потенциалов в солнечных элементах и батареях. Однако оно будет зависеть от определенных условий, таких как температура, уровень заряда, освещение и т. д.
Как определить напряжение разомкнутой цепи?
Чтобы найти напряжение холостого хода, нам нужно рассчитать напряжение между двумя клеммами, от которых цепь разомкнута.
Если вся нагрузка отключена, напряжение источника равно напряжению холостого хода. Падение напряжения происходит только на аккумуляторе. И это будет очень мало.
Состояние разомкнутой цепи с одиночной нагрузкой Если частичная нагрузка отключена, напряжение источника распределяется между другой нагрузкой. И если вы хотите найти напряжение холостого хода, его можно получить так же, как напряжение Тевенина. Давайте разберемся на примере.
И если вы хотите найти напряжение холостого хода, его можно получить так же, как напряжение Тевенина. Давайте разберемся на примере.
На приведенном выше рисунке резисторы A, B, C и нагрузка подключены к источнику постоянного тока (V). Предположим, что нагрузка отключена от источника и размыкает цепь между клеммами P и Q.
Теперь найдем напряжение на клеммах P и Q. Следовательно, мы должны найти ток, проходящий через контур-1, используя Закон Ома.
Это ток, проходящий через контур-1. И такой же ток будет протекать через резисторы А и В.
Второй контур — разомкнутая цепь. Итак, ток, проходящий через резистор С, равен нулю. А падение напряжения на резисторе С равно нулю. Таким образом, резистором C можно пренебречь.
Падение напряжения на резисторе B равно напряжению, имеющемуся между контактами P и Q разомкнутой цепи. напряжение цепи или напряжение Thevenin.
Проверка напряжения разомкнутой цепи
Напряжение холостого хода — это разность потенциалов между положительной и отрицательной клеммами.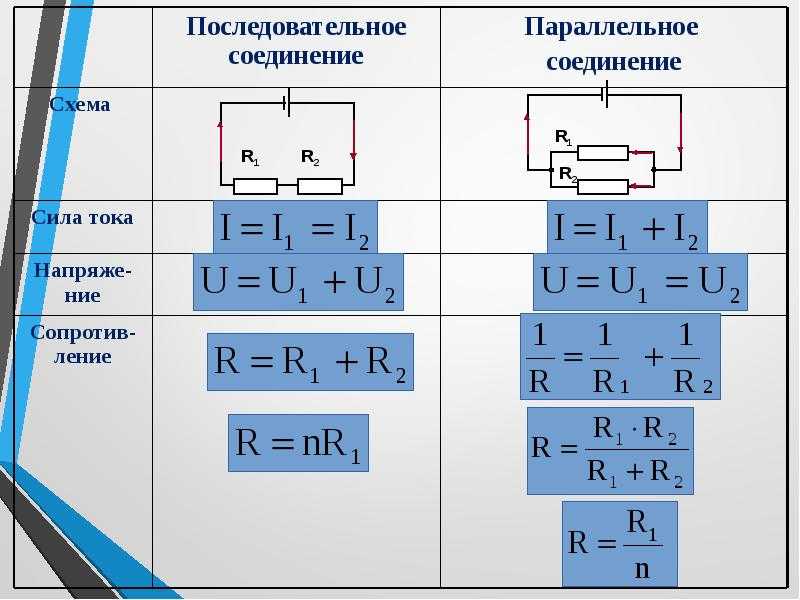 Испытание напряжения холостого хода выполняется на батареях и солнечных элементах для определения потенциала электрического потенциала.
Испытание напряжения холостого хода выполняется на батареях и солнечных элементах для определения потенциала электрического потенциала.
Батарея используется для преобразования химической энергии в электрическую. И есть два типа батарей; аккумуляторная батарея и основная батарея.
Проверка напряжения холостого хода применяется к обоим типам батарей. И данные этого теста используются для расчета состояния заряда (SOC) аккумуляторных батарей.
Стандартное напряжение холостого хода взято из спецификации производителя батареи. Напряжение, указанное на аккумуляторе, является напряжением холостого хода.
Проверка напряжения холостого хода измеряет напряжение батареи, когда нагрузка не подключена. Таким образом, чтобы выполнить проверку напряжения холостого хода, снимите аккумулятор, если это возможно, или возьмите клеммы для проверки.
Теперь установите цифровой мультиметр на постоянное напряжение. И измерьте показания на клеммах аккумулятора. Это напряжение близко к стандартному напряжению. Если измеренное напряжение низкое, батарея повреждена.
Если измеренное напряжение низкое, батарея повреждена.
Для перезаряжаемых батарей этот тест выполняется для проверки того, заряжена или разряжена батарея. В этом случае для проверки состояния выполняется тест емкости.
Почему напряжение не равно нулю при разомкнутой цепи?
Напряжение определяется как разность потенциалов между двумя клеммами. Итак, две точки не соединены друг с другом и обе точки соединены с разными уровнями напряжения. В этом состоянии из-за разности потенциалов напряжение присутствует между двумя точками.
Аналогично, при разомкнутой цепи обе клеммы разомкнуты, но она подключена к аккумулятору или другому источнику напряжения. И обе клеммы батареи находятся на разных уровнях напряжения.
Следовательно, создается разность потенциалов и присутствует напряжение между двумя клеммами в условиях разомкнутой цепи.
Напряжение холостого хода солнечной батареи
В солнечной батарее максимальное напряжение доступно при нулевом токе. И это напряжение известно как напряжение холостого хода.
И это напряжение известно как напряжение холостого хода.
Когда фотоны попадают на солнечные элементы, ток генерируется из-за смещения контактов солнечных элементов. Напряжение холостого хода представляет собой прямое напряжение смещения на солнечном элементе.
В характеристиках ВАХ солнечного элемента напряжение холостого хода показано на рисунке ниже.
IV Характеристики солнечной батареиУравнение напряжения холостого хода:
Где,
I 0 = темновой ток насыщения
I L = световой ток
N = Коэффициент идеальности
T = Температура
k = Постоянная Больцмана
q = Электронный заряд
Из приведенного выше уравнения V oc и температура прямо пропорциональны. Следовательно, V oc линейно возрастают в зависимости от температуры. Но на самом деле этого не происходит. Потому что ток насыщения также быстро увеличивается с ростом температуры. Поэтому влияние температуры на напряжение холостого хода представляет собой сложную задачу. Если ток насыщения изменяется с изменением температуры, напряжение холостого хода уменьшается с температурой.
Если ток насыщения изменяется с изменением температуры, напряжение холостого хода уменьшается с температурой.
Напряжение холостого хода Примеры вопросов
Метод определения напряжения холостого хода такой же, как и для определения напряжения Тевенина. Давайте разберемся, как найти напряжение холостого хода на примере.
Пример-1
На приведенном выше рисунке нагрузка R L подключена к источнику постоянного тока. Теперь мы отключаем нагрузку от источника, и оставшаяся схема выглядит так, как показано на рисунке ниже.
Из-за разомкнутой цепи ток, проходящий через нагрузку и резистор 10 Ом, равен нулю. А напряжение холостого хода такое же, как напряжение на резисторе 3 Ом.
Применить КВЛ в шлейфе-1;
Напряжение на резисторе 3 Ом равно; Пример 2 Следовательно, оставшаяся цепь после разомкнутой цепи выглядит так, как показано ниже.
Напряжение холостого хода равно напряжению на резисторе 6 Ом. Итак, нам нужно найти ток, проходящий через резистор сопротивлением 6 Ом.
Итак, нам нужно найти ток, проходящий через резистор сопротивлением 6 Ом.
Теперь примените KVL во внешнем цикле;
(1)
Мы можем выразить источник тока 3 А в терминах контурных токов.
(2)
Теперь, решая уравнения-1 и уравнения-2, мы можем найти ток I 1 и I 2 . Но нам нужен только ток, проходящий через резистор 6 Ом. И этот ток равен I 2 .
Что такое закон Ома? | Fluke
Закон Ома — это формула, используемая для расчета соотношения между напряжением, током и сопротивлением в электрической цепи.
Для студентов, изучающих электронику, закон Ома (E = IR) так же важен, как уравнение относительности Эйнштейна (E = mc²) для физиков.
E = I x R
При расшифровке это означает напряжение = ток x сопротивление , или вольт = ампер x ом , или В = A x Ω .
Назван в честь немецкого физика Георга Ома (1789 г.).-1854), Закон Ома обращается к ключевым величинам, действующим в цепях:
| Количество | Закон Ома символ | Единица измерения (аббревиатура) | Роль в цепях 6 | Давление, запускающее поток электронов0318 | I | Ampere, amp (A) | Rate of electron flow | I = intensity |
|---|---|---|---|---|---|---|---|---|
| Resistance | R | Ohm (Ω) | Flow inhibitor | Ω = Greek letter omega |
Если два из этих значений известны, технические специалисты могут переконфигурировать закон Ома для расчета третьего. Просто измените пирамиду следующим образом:
Если вы знаете напряжение (E) и силу тока (I) и хотите знать сопротивление (R), уменьшите X R в пирамиде и рассчитайте оставшееся уравнение (см. первое или последнее уравнение). слева, пирамида вверху).
Примечание: Сопротивление нельзя измерить в работающей цепи, поэтому закон Ома особенно полезен, когда его необходимо рассчитать.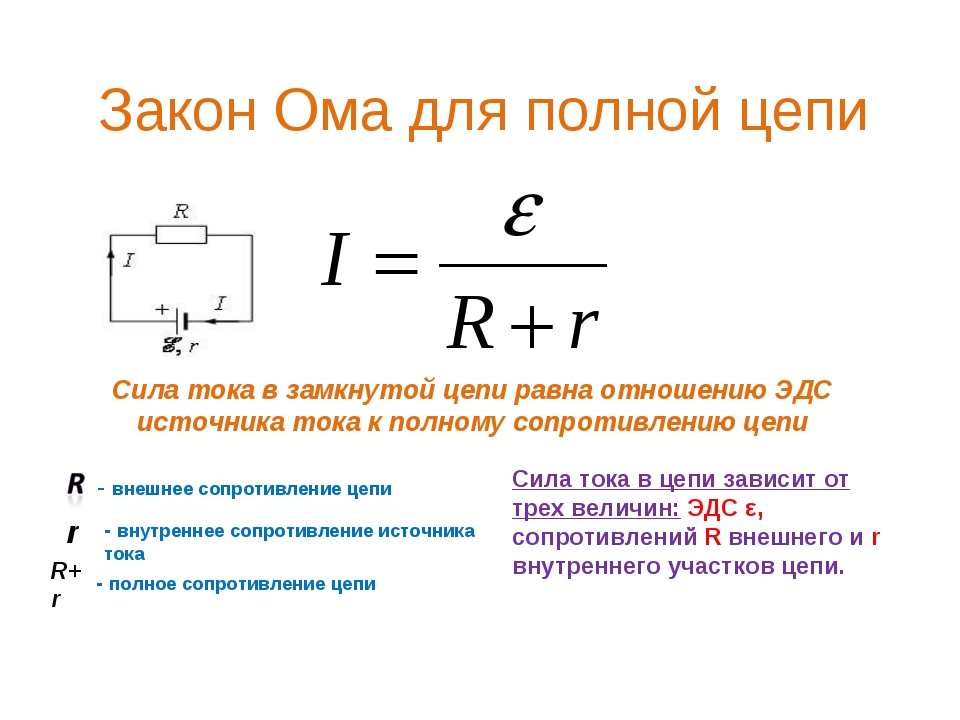 Вместо того, чтобы отключать цепь для измерения сопротивления, технический специалист может определить R, используя приведенный выше вариант закона Ома.
Вместо того, чтобы отключать цепь для измерения сопротивления, технический специалист может определить R, используя приведенный выше вариант закона Ома.
Теперь, если вы знаете напряжение (E) и сопротивление (R) и хотите узнать ток (I), вычеркните X из I и вычислите оставшиеся два символа (см. среднюю пирамиду выше).
А если вы знаете ток (I) и сопротивление (R) и хотите знать напряжение (E), умножьте нижние половины пирамиды (см. третью, или крайнюю правую, пирамиду вверху).
Попробуйте выполнить несколько расчетов на основе простой последовательной цепи, включающей только один источник напряжения (батарея) и сопротивление (свет). В каждом примере известны два значения. Используйте закон Ома, чтобы вычислить третий.
Пример 1: Напряжение (E) и сопротивление (R) известны.
Какой ток в цепи?
I = E/R = 12 В/6 Ом = 2 А
Пример 2: Напряжение (E) и ток (I) известны.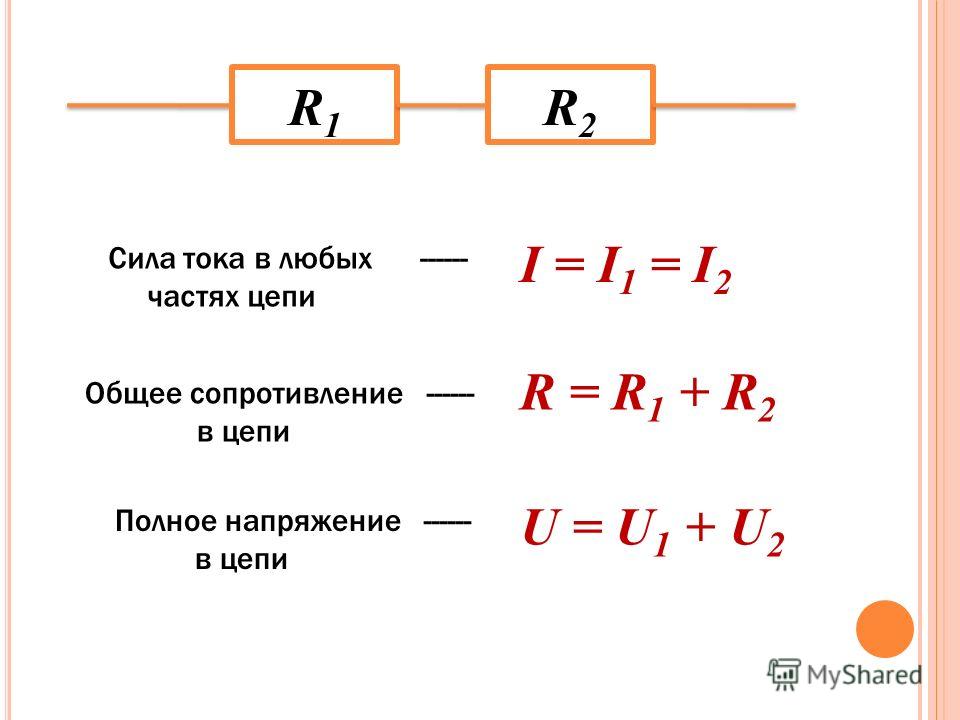
Какое сопротивление создает лампа?
R = E/I = 24 В/6 А = 4 Ом
Пример 3: Ток (I) и сопротивление (R) известны. Какое напряжение?
Какое напряжение в цепи?
E = I x R = (5A)(8Ω) = 40 В
Когда Ом опубликовал свою формулу в 1827 году, его ключевой вывод заключался в том, что количество электрического тока, протекающего через проводник, равно прямо пропорционально приложенному к нему напряжению. Другими словами, требуется один вольт давления, чтобы протолкнуть один ампер тока через сопротивление в один ом.
Что проверять с помощью закона Ома
Закон Ома можно использовать для проверки статических значений компонентов схемы, уровней тока, источников напряжения и падения напряжения. Если, например, контрольно-измерительный прибор обнаруживает измеренный ток выше нормального, это может означать, что сопротивление уменьшилось или напряжение увеличилось, что привело к возникновению ситуации с высоким напряжением. Это может указывать на проблему с питанием или цепью.
Это может указывать на проблему с питанием или цепью.
В цепях постоянного тока (постоянного тока) измерение тока ниже нормального может означать, что напряжение уменьшилось или сопротивление цепи увеличилось. Возможными причинами повышенного сопротивления являются плохие или ослабленные соединения, коррозия и/или поврежденные компоненты.
Нагрузки в цепи потребляют электрический ток. Нагрузками могут быть любые компоненты: небольшие электрические устройства, компьютеры, бытовая техника или большой двигатель. К большинству этих компонентов (нагрузок) прикреплена заводская табличка или информационная наклейка. Эти паспортные таблички содержат сертификаты безопасности и несколько идентификационных номеров.
Технические специалисты обращаются к шильдикам компонентов, чтобы узнать стандартные значения напряжения и силы тока. Если во время тестирования техники обнаруживают, что обычные значения не регистрируются на их цифровых мультиметрах или токоизмерительных клещах, они могут использовать закон Ома, чтобы определить, какая часть цепи дает сбой, и исходя из этого определить, в чем может заключаться проблема.
Основы науки о цепях
Цепи, как и вся материя, состоят из атомов. Атомы состоят из субатомных частиц:
- Протонов (с положительным электрическим зарядом)
- Нейтроны (бесзарядные)
- Электроны (отрицательно заряженные)
Атомы остаются связанными силами притяжения между ядром атома и электронами в его внешней оболочке. Под влиянием напряжения атомы в цепи начинают реформироваться, и их компоненты проявляют потенциал притяжения, известный как разность потенциалов. Взаимно притягивающиеся свободные электроны движутся навстречу протонам, создавая поток электронов (ток). Любой материал в цепи, который ограничивает этот поток, считается сопротивлением.
Ссылка: Принципы цифрового мультиметра Глена А. Мазура, American Technical Publishers.
Связанные статьи
- Устранение неполадок неисправных двигателей с помощью проверки сопротивления изоляции
- Безопасность электрических испытаний – Подготовка к тестированию без напряжения
Как рассчитать падение напряжения на резисторе, подробное объяснение чтобы рассчитать падение напряжения на резисторе, то вот полная теория и практические примеры падения напряжения на резисторе.
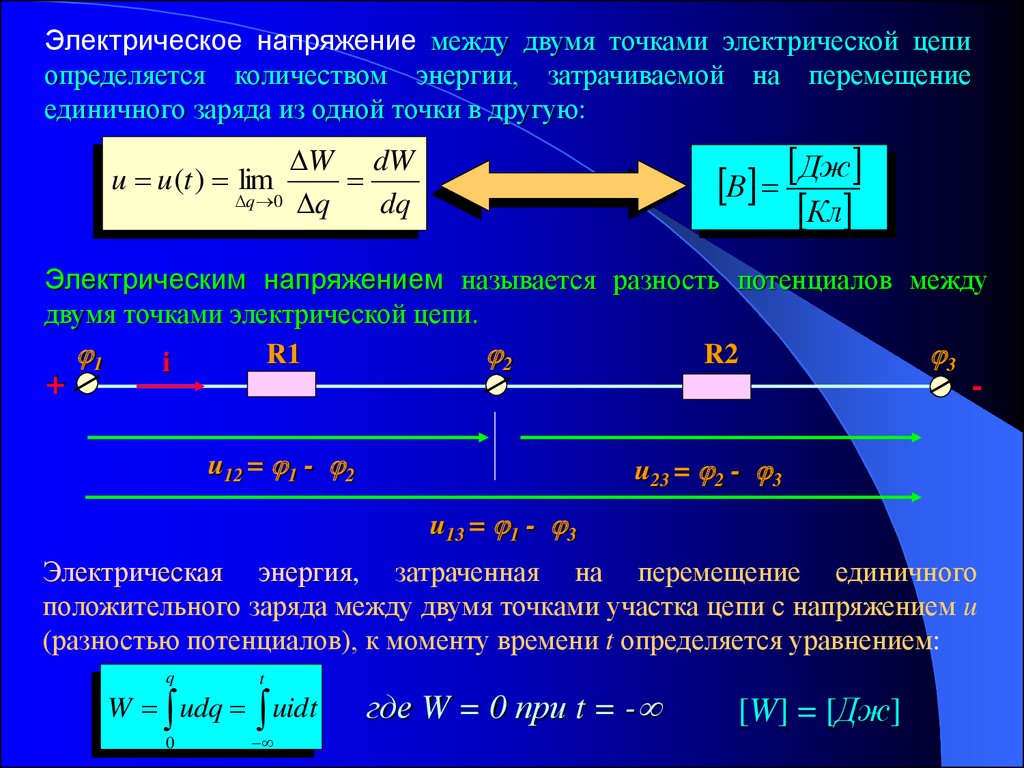
Перед этим давайте освежим представление о законе Ома: (прокрутите вниз, если у вас все хорошо)
- Обычный способ показать поведение схемного устройства — это его характеристика.
-
Это график зависимости тока I, проходящего через устройство, от приложенного к нему напряжения V. Это устройство, резистор, имеет простую линейную характеристику В – I , показанную на рис. выше. - Эта линейная зависимость устройства выражается Закон Ома :
V = IR - Здесь константа пропорциональности R называется сопротивлением устройства и равна наклону ВАХ. Единицей сопротивления является ом, условное обозначение Ом . Любое устройство с линейной характеристикой VI можно рассматривать как резистивное по своей природе.
Каково падение напряжения на резисторе?
- Падение напряжения на резисторе — это не что иное, как значение напряжения на резисторе.
 Иногда его также называют «напряжение на резисторе» или просто «падение напряжения».
Иногда его также называют «напряжение на резисторе» или просто «падение напряжения». - Обычно обозначается как:
‘V(drop ) ’ или ‘Vr’ или ‘Vd’
Для нескольких резисторов это записывается как Vr1, Vr2, Vr3 и т. д.
Как мы все знаем, резистор — это устройство, оказывающее сопротивление протекающему через него току. Тогда, применяя закон Ома, резистор будет создавать падение напряжения на резистивном устройстве, и оно определяется как:
В ( падение ) = I × R
где, I = ток через резистор в (А) амперах
R = сопротивление в (Ом) омах
В( падение ) = падение напряжения в (В) вольтах
Как рассчитать напряжение Пошаговое падение сопротивления:
Шаг 1: Упростите данную схему. Если, скажем, цепь полна резисторов, соединенных последовательно и параллельно, то переподключите ее, чтобы упростить.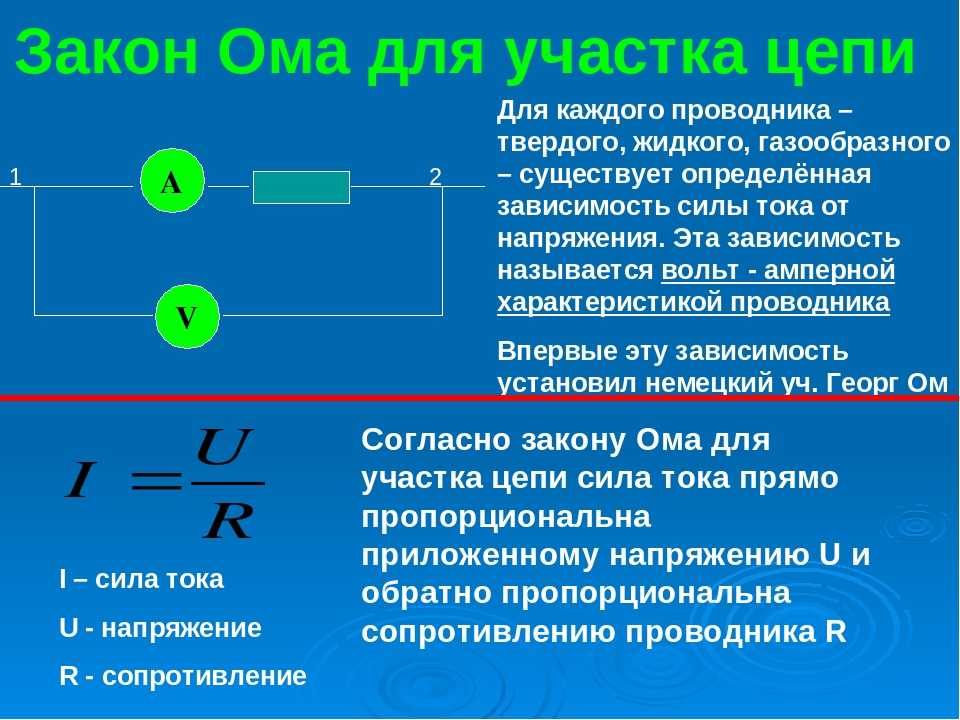 (проверьте практический пример ниже)
(проверьте практический пример ниже)
Шаг 2: Затем найдите эквивалентный резистор.
Для параллельного подключения: 1 / Треб. = 1 / R1 + 1 / R2 …
Для серии: Необх. = R1 + R2 + . . .
Шаг 3: Найдите ток через каждый резистор. (Ток через последовательный резистор одинаков, а ток через параллельные резисторы отличается и зависит от его значения)
Шаг 4 : Примените формулу из закона Ома для расчета падения напряжения.
V=IR
Напряжение последовательной цепи. Практические примеры:
Случай I:
Если последовательно с батареей или источником питания подключен только один резистор, как показано на этой схеме.
В этой схеме падение напряжения на резисторе такое же, как и у источника питания. Это связано с тем, что оба компонента имеют общие потенциальные точки, общие между ними (точка A и точка B)
∴ Vs = Vdrop = 5 вольт (скажем)
Случай II:
два или более резистора последовательно с батареей, как показано на этой схеме.
В этой цепи мы должны рассчитать общий ток «I» через цепь.
I (общий) = V(питание) / R(эквивалент)
∴ I(общий) = 5 / 30 = 0,166 A
Тогда падение напряжения на R1 будет: Vr1 = I × R1
Падение напряжения на R2 будет: Vr2 = I × R2
Падение напряжения на Rn будет: Vrn = I × Rn
- Vr1 =I × R1 = 0,166 × 10 = 1,66 9 вольт0078 и VR2 = I × R2 = 0,166 × 20 = 3,33 вольт
Напряжение на параллельных резисторах:
Случай I:
как показано на этой схеме.
В этой схеме падение напряжения на этих параллельных резисторах такое же, как и у источника питания.
Это связано с тем, что оба резистора имеют общие потенциальные точки, общие для них (точка A и точка B), поэтому напряжение будет одинаковым, а ток будет разным.
∴Vs = Vdrop = Vr1 = Vr2 = 5 вольт (скажем)
Случай II:
В этой схеме имеется один резистор и два резистора, соединенных последовательно, и два резистора с источником питания, как показано на рисунке.
В этой схеме нам нужно рассчитать ток «I» через каждый компонент.
- i1 = I (общий) = Is = V (предложение) / R (эквивалент), где R (эквивалент) = R1 + Rp
, где 1 / Rp = 1 / R2 + 1 / R3 ∴ Rp = 12 Ом и R ( эквивалент ) = 22 Ом - I2 = I1 * (R3/(R2+R3))
I3 = I1 * (R2/(R2+R3))
- 910000000000.
- Падение напряжения на R1 будет Vr1 = R1 * i1
Падение напряжения на R2 будет Vr2 = R2 * i2
Падение напряжения на R3 будет Vr3 = R2 * i3 Теперь i1 = V (питание) / R (эквивалент) = 5/22 = 0,227 А
∴ i1 = 0,227 АПадение напряжения на сопротивлении 10 Ом -> Vr1 = 10 * i1 = 10 × 0,227 вольт
∴ Vr1 = 2,27 вольтТеперь (R06+92 i4 *, i2) ∴ I2 = 0,1362 A
Падение напряжения на 20 Ом -> VR2 = 20 * I2 = 20 × 0,1362 вольт
∴ VR2 = 2,724 ВольтаТеперь, I1 * I1 * I1 * I1 * I1 * I1 * I1 * I1 /(R1+R2))
∴ i3 =0,09 AПадение напряжения на сопротивлении 30 Ом -> Vr2 = 30 * i2 = 30 × 0,09 Вольт
∴ VR3 = 2,7 вольтМетод 2:
- Найти I1 = V (Supply) / R (эквивалент) = 77777777777777777777777777777 гг.

Тогда падение напряжения на R1 будет Vr1 = R1 * i1 = 10 × 0,227 = 2,27 вольт∴ Эквивалентное напряжение в точке «А» будет равно
Veq = Va = Vs – Vr1 ∴ 06 Va=
5 – 2,27 = 2,73 вольта
Следовательно, мы получаем одинаковое потенциальное значение для R2 и R3. - Таким образом, Va = Vr2 = Vr3 = 2,73 вольта
Метод 3:
В этом методе мы можем использовать цифровой мультиметр или вольтметр. Все, что вам нужно, это установить мультиметр в режим измерения напряжения.
Теперь двумя его щупами проверьте напряжение на требуемом резисторе, подключив к нему щупы. (на рис. показания вольтметра только для индикации)Вуаля !! Ты понял.
Это самый простой способ найти падение напряжения на резисторе в любой цепи.
Преобразователь 12 В в 6 В — коллекция лучших 5 цепей 18650 Технические характеристики батареи: технические данные и свойства при последовательном соединении или при параллельном соединении.
 Когда все устройства подключены с помощью параллельных соединений, цепь называется 9.0006 параллельная цепь . В параллельной схеме каждое устройство размещается в своей отдельной ветке . Наличие ответвлений означает, что существует несколько путей, по которым заряд может проходить по внешней цепи. Каждый заряд, проходящий через петлю внешней цепи, пройдет через один резистор, присутствующий в одной ветви. По прибытии в место разветвления или узел плата делает выбор в отношении того, через какую ветвь пройти на обратном пути к терминалу с низким потенциалом.
Когда все устройства подключены с помощью параллельных соединений, цепь называется 9.0006 параллельная цепь . В параллельной схеме каждое устройство размещается в своей отдельной ветке . Наличие ответвлений означает, что существует несколько путей, по которым заряд может проходить по внешней цепи. Каждый заряд, проходящий через петлю внешней цепи, пройдет через один резистор, присутствующий в одной ветви. По прибытии в место разветвления или узел плата делает выбор в отношении того, через какую ветвь пройти на обратном пути к терминалу с низким потенциалом.Короткое сравнение и противопоставление последовательной и параллельной цепей было сделано в предыдущем разделе Урока 4. В этом разделе подчеркивалось, что добавление большего количества резисторов в параллельную цепь приводит к довольно неожиданному результату в виде меньшего общего сопротивление. Поскольку существует несколько путей, по которым может течь заряд, добавление еще одного резистора в отдельную ветвь обеспечивает еще один путь, по которому можно направить заряд через основную область сопротивления в цепи.
 Это уменьшенное сопротивление в результате увеличения количества ответвлений приведет к увеличению скорости протекания заряда (также известной как ток). Чтобы сделать этот довольно неожиданный результат более разумным, была введена аналогия с платной дорогой. Пункт взимания платы является основным местом сопротивления автомобильному потоку на платной дороге. Добавление дополнительных пунктов взимания платы в пределах их собственной ветки на платной дороге обеспечит больше путей для движения автомобилей через пункт взимания платы. Эти дополнительные пункты взимания платы снизят общее сопротивление потоку автомобилей и увеличат скорость их движения.
Это уменьшенное сопротивление в результате увеличения количества ответвлений приведет к увеличению скорости протекания заряда (также известной как ток). Чтобы сделать этот довольно неожиданный результат более разумным, была введена аналогия с платной дорогой. Пункт взимания платы является основным местом сопротивления автомобильному потоку на платной дороге. Добавление дополнительных пунктов взимания платы в пределах их собственной ветки на платной дороге обеспечит больше путей для движения автомобилей через пункт взимания платы. Эти дополнительные пункты взимания платы снизят общее сопротивление потоку автомобилей и увеличат скорость их движения.
ТокСкорость, с которой заряд течет по цепи, называется током. Заряд НЕ накапливается и не начинает накапливаться в любом заданном месте, так что ток в одном месте больше, чем в других местах. Заряд НЕ расходуется резисторами таким образом, чтобы ток в одном месте был меньше, чем в другом. В параллельной цепи заряд делит на отдельные ветви, так что в одной ветви может быть больше тока, чем в другой.
 Тем не менее, если взять в целом, общая сумма тока во всех ветвях при суммировании равна сумме тока в точках за пределами ветвей. правило, что тока везде тот же до сих пор работает, только с изюминкой. Ток вне ветвей равен сумме токов в отдельных ветвях. Это все тот же ток, только разделенный на более чем один путь.
Тем не менее, если взять в целом, общая сумма тока во всех ветвях при суммировании равна сумме тока в точках за пределами ветвей. правило, что тока везде тот же до сих пор работает, только с изюминкой. Ток вне ветвей равен сумме токов в отдельных ветвях. Это все тот же ток, только разделенный на более чем один путь.В форме уравнения, этот принцип можно записать как
I Всего = I 1 + I 2 + I 3 + … , где I . общая сумма тока вне ветвей (и в аккумуляторе) и I 1 , I 2 и I 3 представляют ток в отдельных ветвях цепи.
На протяжении всего этого модуля широко использовалась аналогия между потоком заряда и потоком воды. Еще раз вернемся к аналогии, чтобы проиллюстрировать, как сумма текущих значений в ветвях равна сумме вне ветвей. Течение заряда в проводах аналогично течению воды в трубах. Рассмотрим приведенные ниже схемы, на которых поток воды в трубах разделяется на отдельные ветви.
 В каждой , узел (место разветвления), вода идет двумя или более отдельными путями. Скорость, с которой вода поступает в узел (измеряется в галлонах в минуту), будет равна сумме расходов в отдельных ответвлениях за пределами узла. Точно так же, когда две или более ветвей впадают в узел, скорость, с которой вода вытекает из узла, будет равна сумме скоростей потока в отдельных ветвях, впадающих в узел.
В каждой , узел (место разветвления), вода идет двумя или более отдельными путями. Скорость, с которой вода поступает в узел (измеряется в галлонах в минуту), будет равна сумме расходов в отдельных ответвлениях за пределами узла. Точно так же, когда две или более ветвей впадают в узел, скорость, с которой вода вытекает из узла, будет равна сумме скоростей потока в отдельных ветвях, впадающих в узел.Тот же принцип разделения потока применяется к электрическим цепям. Скорость, с которой заряд течет в узел, равна сумме скоростей потока в отдельных ветвях за пределами узла. Это показано в примерах, показанных ниже. В примерах вводится новое обозначение схемы — буква А, заключенная в круг. Это символ амперметра — устройства, используемого для измерения силы тока в определенной точке. Амперметр способен измерять ток, оказывая незначительное сопротивление потоку заряда.
На диаграмме A показаны два резистора, соединенных параллельно с узлами в точке A и точке B.
 Заряд поступает в точку A со скоростью 6 ампер и делится на два пути — один через резистор 1, а другой — через резистор 2. Ток в ответвлении с резистором 1 равен 2 ампера, а ток в ответвлении с резистором 2 равен 4 ампера. После того, как эти две ветви снова встречаются в точке B и образуют единую линию, сила тока снова становится равной 6 ампер. Таким образом, мы видим, что справедлив принцип, согласно которому ток вне ветвей равен сумме токов в отдельных ветвях.
Заряд поступает в точку A со скоростью 6 ампер и делится на два пути — один через резистор 1, а другой — через резистор 2. Ток в ответвлении с резистором 1 равен 2 ампера, а ток в ответвлении с резистором 2 равен 4 ампера. После того, как эти две ветви снова встречаются в точке B и образуют единую линию, сила тока снова становится равной 6 ампер. Таким образом, мы видим, что справедлив принцип, согласно которому ток вне ветвей равен сумме токов в отдельных ветвях.I всего = I 1 + I 2 6 ампер = 2 ампера + 4 ампера
Схема B, приведенная выше, может быть немного сложнее, если на ней три резистора расположены параллельно. На диаграмме идентифицированы четыре узла, обозначенные A, B, C и D. Заряд течет в точку A со скоростью 12 ампер и делится на два пути: один проходит через резистор 1, а другой направляется к точке B (и резисторы 2). и 3). Ток 12 ампер делится на путь 2 ампера (через резистор 1) и путь 10 ампер (направленный к точке B).
 В точке В происходит дальнейшее разделение потока на два пути — один через резистор 2, а другой через резистор 3. Подходящий к точке В ток силой 10 ампер разделяется на 6-амперный путь (через резистор 2) и 4-амперный путь. -амперный тракт (через резистор 3). Таким образом, видно, что значения тока в трех ветвях составляют 2 ампера, 6 ампер и 4 ампера и что сумма значений тока в отдельных ветвях равна току вне ветвей.
В точке В происходит дальнейшее разделение потока на два пути — один через резистор 2, а другой через резистор 3. Подходящий к точке В ток силой 10 ампер разделяется на 6-амперный путь (через резистор 2) и 4-амперный путь. -амперный тракт (через резистор 3). Таким образом, видно, что значения тока в трех ветвях составляют 2 ампера, 6 ампер и 4 ампера и что сумма значений тока в отдельных ветвях равна току вне ветвей.I всего = I 1 + I 2 + I 3 12 ампер = 2 ампера + 6 ампер + 4 ампера
Можно также провести анализ потока в точках C и D, и видно, что сумма расходов потока, направляющихся в эти точки, равна расходу, который находится непосредственно за этими точками.
Эквивалентное сопротивлениеФактическая величина тока всегда обратно пропорциональна величине общего сопротивления. Существует четкая зависимость между сопротивлением отдельных резисторов и общим сопротивлением набора резисторов.
 Чтобы исследовать эту взаимосвязь, давайте начнем с простейшего случая двух резисторов, размещенных на параллельных ветвях, каждый из которых имеет одинаковое значение сопротивления 4 Ом. Поскольку схема предлагает два равно путям для потока заряда, только половина заряда выберет для прохождения через данную ветвь. В то время как каждая отдельная ветвь оказывает сопротивление 4 Ом любому заряду, проходящему через нее, только половина всего заряда, протекающего через цепь, встретит сопротивление 4 Ом этой отдельной ветви. Таким образом, что касается батареи, которая качает заряд, наличие двух 4-омных резисторов, включенных параллельно, было бы эквивалентно наличию в цепи одного 2-омного резистора. Точно так же наличие двух резисторов 6 Ом параллельно будет эквивалентно наличию в цепи одного резистора 3 Ом. А наличие двух 12-омных резисторов параллельно было бы эквивалентно наличию в цепи одного 6-омного резистора.
Чтобы исследовать эту взаимосвязь, давайте начнем с простейшего случая двух резисторов, размещенных на параллельных ветвях, каждый из которых имеет одинаковое значение сопротивления 4 Ом. Поскольку схема предлагает два равно путям для потока заряда, только половина заряда выберет для прохождения через данную ветвь. В то время как каждая отдельная ветвь оказывает сопротивление 4 Ом любому заряду, проходящему через нее, только половина всего заряда, протекающего через цепь, встретит сопротивление 4 Ом этой отдельной ветви. Таким образом, что касается батареи, которая качает заряд, наличие двух 4-омных резисторов, включенных параллельно, было бы эквивалентно наличию в цепи одного 2-омного резистора. Точно так же наличие двух резисторов 6 Ом параллельно будет эквивалентно наличию в цепи одного резистора 3 Ом. А наличие двух 12-омных резисторов параллельно было бы эквивалентно наличию в цепи одного 6-омного резистора.Теперь давайте рассмотрим еще один простой случай с тремя параллельными резисторами, каждый из которых имеет одинаковое сопротивление 6 Ом.
 С тремя равными путями для прохождения заряда через внешнюю цепь, только одна треть заряда выберет прохождение через данную ветвь. Каждая отдельная ветвь оказывает сопротивление 6 Ом проходящему через нее заряду. Однако тот факт, что только одна треть заряда проходит через конкретную ветвь, означает, что общее сопротивление цепи равно 2 Ом. Что касается батареи, которая качает заряд, наличие трех резисторов 6 Ом параллельно будет эквивалентно наличию в цепи одного резистора 2 Ом. Таким же образом присутствие трех 9Параллельное подключение резисторов сопротивлением Ω эквивалентно наличию в цепи одного резистора сопротивлением 3 Ω. А наличие трех 12-омных резисторов параллельно будет эквивалентно наличию в цепи одного 4-омного резистора.
С тремя равными путями для прохождения заряда через внешнюю цепь, только одна треть заряда выберет прохождение через данную ветвь. Каждая отдельная ветвь оказывает сопротивление 6 Ом проходящему через нее заряду. Однако тот факт, что только одна треть заряда проходит через конкретную ветвь, означает, что общее сопротивление цепи равно 2 Ом. Что касается батареи, которая качает заряд, наличие трех резисторов 6 Ом параллельно будет эквивалентно наличию в цепи одного резистора 2 Ом. Таким же образом присутствие трех 9Параллельное подключение резисторов сопротивлением Ω эквивалентно наличию в цепи одного резистора сопротивлением 3 Ω. А наличие трех 12-омных резисторов параллельно будет эквивалентно наличию в цепи одного 4-омного резистора.Это концепция эквивалентного сопротивления. Эквивалентное сопротивление цепи представляет собой величину сопротивления, которая потребуется одному резистору, чтобы уравнять общий эффект набора резисторов, присутствующих в цепи.
 Для параллельных цепей математическая формула расчета эквивалентного сопротивления (R Уравнение ) IS
Для параллельных цепей математическая формула расчета эквивалентного сопротивления (R Уравнение ) IS1 / R EQ = 1 / R 1 + 1 / R 2 + 1 / R 3 + … , где R 1 , R 2 и R 3 — значения сопротивления отдельных резисторов, соединенных параллельно. Приведенные выше примеры можно рассматривать как простые случаи, когда все пути оказывают одинаковое сопротивление отдельному заряду, проходящему через них. Простые случаи выше были выполнены без использования уравнения. Тем не менее, уравнение подходит как для простых случаев, когда резисторы ответвления имеют одинаковые значения сопротивления, так и для более сложных случаев, когда резисторы ответвления имеют разные значения сопротивления. Например, рассмотрим применение уравнения к одному простому и одному сложному случаю ниже.
Вариант 1 : Три резистора 12 Ом подключены параллельно 1/R экв.  = 1/R 1 + 1/R 2 + 1/R 3
= 1/R 1 + 1/R 2 + 1/R 3 1/R экв. = 1/(12 Ом) + 1/(12 Ом) + 1/(12 Ом)
Использование калькулятора…
1/R экв. = 0,25 Ом -1
Ч экв. = 1 / (0,25 Ом -1 )
R экв. = 4,0 Ом
Вариант 2 : Резистор 5,0 Ом, 7,0 Ом и 12 Ом подключен параллельно 1/R экв. = 1/R 1 + 1/R 2 + 1/R 3 1/R экв. = 1/(5,0 Ом) + 1/(7,0 Ом) + 1/(12 Ом)
Использование калькулятора…
1/R экв. = 0,42619 Ом-1
R экв. = 1 / (0,42619 Ом -1 )
R экв. = 2,3 Ом
Ваша очередь попробоватьНужно больше практики? Используйте Два резистора параллельно виджет ниже, чтобы попробовать некоторые дополнительные проблемы.
 Введите любые два значения сопротивления, которые вы хотите. Используйте свой калькулятор, чтобы определить значения R eq . Затем нажмите кнопку Отправить , чтобы проверить свои ответы. Попробуйте сколько угодно раз с разными значениями сопротивления.
Введите любые два значения сопротивления, которые вы хотите. Используйте свой калькулятор, чтобы определить значения R eq . Затем нажмите кнопку Отправить , чтобы проверить свои ответы. Попробуйте сколько угодно раз с разными значениями сопротивления.Падение напряжения для параллельных ветвей внешний контур. Общее падение напряжения во внешней цепи равно приросту напряжения при прохождении заряда по внутренней цепи. В параллельной цепи заряд не проходит через каждый резистор; скорее, он проходит через один резистор. Таким образом, полное падение напряжения на этом резисторе должно соответствовать напряжению батареи. Не имеет значения, проходит ли заряд через резистор 1, резистор 2 или резистор 3, падение напряжения на резисторе, которое оно выбирает для прохождения должно быть равно напряжению батареи. В виде уравнения этот принцип можно выразить следующим образом:
В батарея = В 1 = В 2 = В 3 = .  ..
.. от 12-вольтовой батареи, то падение напряжения на каждом из трех резисторов составляет 12 вольт. Заряд, протекающий по цепи, столкнется только с одним из этих трех резисторов и, таким образом, столкнется с одним падением напряжения в 12 вольт.
Диаграммы электрических потенциалов были представлены в Уроке 1 этого модуля и впоследствии использовались для иллюстрации последовательных падений напряжения, возникающих в последовательных цепях. Диаграмма электрических потенциалов — это концептуальный инструмент для представления разности электрических потенциалов между несколькими точками электрической цепи. Рассмотрим принципиальную схему ниже и соответствующую ей диаграмму электрических потенциалов.
Как показано на диаграмме электрических потенциалов, позиции A, B, C, E и G имеют высокий электрический потенциал. Один заряд выбирает только один из трех возможных путей; таким образом, в положении B один заряд будет двигаться к точке C, E или G, а затем пройдет через резистор, который находится в этой ветви.
 Заряд не теряет своего высокого потенциала до тех пор, пока он не пройдет через резистор, либо от C к D, от E к F, либо от G к H. Как только он проходит через резистор, заряд возвращается почти к 0 вольт и возвращается к отрицательному клемму аккумулятора для повышения напряжения. В отличие от последовательных цепей, заряд в параллельной цепи сталкивается с единичным падением напряжения на своем пути через внешнюю цепь.
Заряд не теряет своего высокого потенциала до тех пор, пока он не пройдет через резистор, либо от C к D, от E к F, либо от G к H. Как только он проходит через резистор, заряд возвращается почти к 0 вольт и возвращается к отрицательному клемму аккумулятора для повышения напряжения. В отличие от последовательных цепей, заряд в параллельной цепи сталкивается с единичным падением напряжения на своем пути через внешнюю цепь.Ток через данную ветвь можно предсказать, используя уравнение закона Ома и падение напряжения на резисторе и сопротивление резистора. Поскольку падение напряжения одинаково на каждом резисторе, фактором, определяющим, что резистор имеет наибольший ток, является сопротивление. Резистор с наибольшим сопротивлением испытывает наименьший ток, а резистор с наименьшим сопротивлением испытывает наибольший ток. В этом смысле можно сказать, что заряд (как у людей) выбирает путь наименьшего сопротивления. В форме уравнения это можно записать как
. 
I 1 = Δ В 1 / R 1 I 2 = Δ В 2 / R 2 I 3 = Δ В 3 / Р 3 Этот принцип иллюстрируется схемой, показанной ниже. Произведение I•R одинаково для каждого резистора (и равно напряжению батареи). Но ток в каждом резисторе разный. Ток больше там, где сопротивление наименьшее, а ток меньше там, где сопротивление больше.
Математический анализ параллельных цепейПриведенные выше принципы и формулы можно использовать для анализа параллельной цепи и определения значений тока при и разности электрических потенциалов на каждом из резисторов в параллельной цепи.
 Их использование будет продемонстрировано математическим анализом схемы, показанной ниже. Цель состоит в том, чтобы использовать формулы для определения эквивалентного сопротивления цепи (R eq ), тока через батарею (I tot ), а также падения напряжения и тока для каждого из трех резисторов.
Их использование будет продемонстрировано математическим анализом схемы, показанной ниже. Цель состоит в том, чтобы использовать формулы для определения эквивалентного сопротивления цепи (R eq ), тока через батарею (I tot ), а также падения напряжения и тока для каждого из трех резисторов.Анализ начинается с использования значений сопротивления отдельных резисторов для определения эквивалентного сопротивления цепи.
1 / R eq = 1 / R 1 + 1 / R 2 + 1 / R 3 = (1/17 Ом) + (1/12 Ом) + (1/11 Ом) 1 / R экв. = 0,23306 Ом -1
R экв. = 1 / (0,23306 Ом -1 )
R экв. = 4,29Ом
(округлено от 4,29063 Ом)
Теперь, когда известно эквивалентное сопротивление, ток в батарее можно определить с помощью уравнения закона Ома. При использовании уравнения закона Ома (ΔV = I • R) для определения тока в батарее важно использовать напряжение батареи для ΔV и эквивалентное сопротивление для R.
 Расчет показан здесь:
Расчет показан здесь:I tot = ΔV батареи / R eq = (60 В) / (4,29063 Ом) I to = 14,0 ампер
(округлено от 13,98396 ампер)
Напряжение батареи 60 В представляет собой прирост электрического потенциала за счет заряда, проходящего через батарею. Заряд теряет такое же количество электрического потенциала при любом данном проходе через внешнюю цепь. То есть падение напряжения на каждом из трех резисторов такое же, как напряжение, полученное в батарее:
ΔV батареи = ΔV 1 = ΔV 2 = ΔV 3 = 60 В Осталось определить три значения — ток в каждом из отдельных резисторов. Закон Ома используется еще раз для определения значений тока для каждого резистора — это просто падение напряжения на каждом резисторе (60 вольт), деленное на сопротивление каждого резистора (данное в условии задачи).
 Расчеты показаны ниже.
Расчеты показаны ниже.я 1 = ΔV 1 / R 1 I 1 = (60 В) / (17 Ом)
I 1 = 3,53 А
I 2 = ΔV 2 / R 2 I 2 = (60 В) / (12 Ом)
I 2 = 5,00 ампер
I 3 = ΔV 3 / R 3 I 3 = (60 В) / (11 Ом)
I 3 = 5,45 А
В качестве проверки точности выполненных математических расчетов имеет смысл проверить, удовлетворяют ли рассчитанные значения принципу, согласно которому сумма значений тока для каждого отдельного резистора равна общему току в цепи (или в батарее). Другими словами, я tot = I 1 + I 2 + I 3 ?
I to = I 1 + I 2 + I 3 ? Является ли 14,0 ампер = 3,53 ампер + 5,00 ампер + 5,45 ампер?
Является ли 14,0 ампер = 13,98 ампер?
Да!!
(Разница в 0,02 ампера является просто результатом предварительного округления значения I до от 13,98.
 )
)Математический анализ этой параллельной цепи включал смесь концепций и уравнений. Как это часто бывает в физике, отрыв понятий от уравнений при решении физической задачи — опасный поступок. Здесь необходимо учитывать концепцию, что падение напряжения на каждом из трех резисторов равно напряжению батареи и что сумма тока в каждом резисторе равна общему току. Это понимание необходимо для завершения математического анализа. В следующей части урока 4 будут исследованы комбинированные или составные схемы, в которых одни устройства включены параллельно, а другие последовательно.
Больше практикиСоздавайте, решайте и проверяйте свои собственные проблемы с помощью виджета Equivalent Resistance ниже. Составьте себе задачу с любым количеством резисторов и любых номиналов. Решать проблему; затем нажмите кнопку «Отправить», чтобы проверить свой ответ.

Мы хотели бы предложить …Зачем просто читать об этом и когда вы могли бы взаимодействовать с ним? Взаимодействие — это именно то, что вы делаете, когда используете один из интерактивов The Physics Classroom. Мы хотели бы предложить вам совместить чтение этой страницы с использованием нашего интерактивного конструктора цепей постоянного тока. Вы можете найти его в разделе Physics Interactives на нашем сайте. Конструктор цепей постоянного тока предоставляет учащимся набор для создания виртуальных схем. Вы можете легко перетаскивать источники напряжения, резисторы и провода на рабочее место, располагать и соединять их так, как пожелаете. Вольтметры и амперметры позволяют измерять падение тока и напряжения. Прикосновение к резистору или источнику напряжения позволяет изменить сопротивление или входное напряжение. Это просто. Это весело. И это безопасно (если только вы не используете его в ванной).

Посетите: DC Circuit BuilderПроверьте свое понимание 1. По мере того, как в цепь параллельно добавляются все новые и новые резисторы, эквивалентное сопротивление цепи ____________ (увеличивается, уменьшается) и общий ток цепи ____________ (увеличивается, уменьшается).
2. Три одинаковые лампочки подключены к D-элементу, как показано ниже. P, Q, X, Y и Z представляют местоположения вдоль цепи. Какое из следующих утверждений верно?
а. Ток Y больше тока Q.
б. Ток на Y больше, чем ток на P.
в. Ток в Y больше, чем ток в Z.
д. Ток на P больше, чем ток на Q.
е. Ток на Q больше, чем ток на P.
ф. Ток одинаков во всех местах.
3.
 Три одинаковые лампочки подключены к D-элементу, как показано ниже. P, Q, X, Y и Z представляют местоположения вдоль цепи. В каком месте(ах), если таковые имеются, ток будет …
Три одинаковые лампочки подключены к D-элементу, как показано ниже. P, Q, X, Y и Z представляют местоположения вдоль цепи. В каком месте(ах), если таковые имеются, ток будет …a. … такой же, как у X?
б. … так же, как в Q?
в. … такой же, как у Y?
д. … меньше, чем на Q?
эл. … меньше, чем у P?
ф. … вдвое больше, чем у Z?
г. … в три раза больше, чем у Y?
4. Какие корректировки можно внести в схему ниже, чтобы уменьшить ток в ячейке? Перечислите все, что применимо.
а. Увеличьте сопротивление лампы X.
б. Уменьшите сопротивление лампы X.
в. Увеличьте сопротивление лампы Z.
д. Уменьшить сопротивление лампы Z.
эл. Увеличьте напряжение ячейки (как-то).
ф. Уменьшить напряжение ячейки (каким-то образом).
г. Снимите лампу Y.
.
5. Аккумулятор 12 В, резистор 12 Ом и резистор 4 Ом подключены, как показано на рисунке. Ток в резисторе сопротивлением 12 Ом в _____ раз больше, чем у резистора сопротивлением 4 Ом.
а. 1/3
б. 1/2
в. 2/3
д. то же, что
эл. 1,5 раза
ф. дважды
г. три раза
ч. четыре раза
6. Аккумулятор 12 В, резистор 12 Ом и резистор 4 Ом подключены, как показано на рисунке. Падение напряжения на резисторе 12 Ом в ____ раз меньше, чем на резисторе 4 Ом.

а. 1/3
б. 1/2
в. 2/3
д. то же, что
эл. 1,5 раза
ф. дважды
г. трижды
ч. четыре раза
7. Аккумулятор 12 В и резистор 12 Ом подключены, как показано на схеме. Резистор на 6 Ом добавляется к резистору на 12 Ом, чтобы создать схему Y, как показано на рисунке. Падение напряжения на резисторе 6 Ом в цепи Y в _____ раз меньше, чем на резисторе в X.
a. больше, чем
б. меньше
в. то же, что
8. Используйте свое понимание эквивалентного сопротивления, чтобы завершить следующие утверждения:
a.
 Два резистора 6 Ом, включенные параллельно, обеспечат сопротивление, эквивалентное одному резистору _____ Ом.
Два резистора 6 Ом, включенные параллельно, обеспечат сопротивление, эквивалентное одному резистору _____ Ом.б. Три резистора 6 Ом, включенные параллельно, обеспечат сопротивление, эквивалентное одному резистору _____ Ом.
с. Три резистора 8 Ом, включенные параллельно, обеспечат сопротивление, эквивалентное одному резистору _____ Ом.
д. Три резистора с сопротивлением 2 Ом, 4 Ом и 6 Ом соединены параллельно. Они обеспечат сопротивление, эквивалентное одному резистору _____-Ом.
эл. Три резистора с сопротивлением 5 Ом, 6 Ом и 7 Ом соединены параллельно. Они обеспечат сопротивление, эквивалентное одному резистору _____-Ом.
ф. Три резистора с сопротивлением 12 Ом, 6 Ом и 21 Ом включены параллельно. Они обеспечат сопротивление, эквивалентное одному резистору _____-Ом.
9. На основании ваших ответов на приведенный выше вопрос дополните следующее утверждение:
Общее или эквивалентное сопротивление трех параллельно соединенных резисторов будет _____.

- Найти I1 = V (Supply) / R (эквивалент) = 77777777777777777777777777777 гг.

 1)
1) 5)
5) 8)
8)
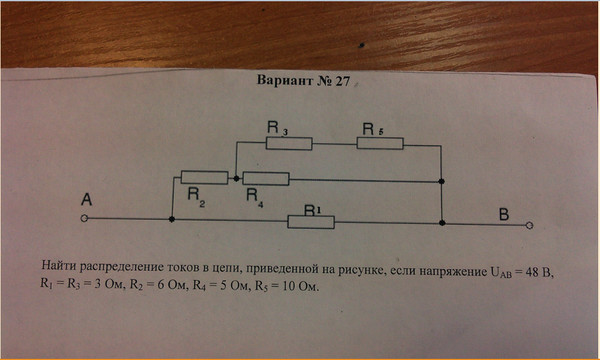 ч (киловатт-час).
ч (киловатт-час). ..+Rn+…
..+Rn+…
 ..+An+…
..+An+… 
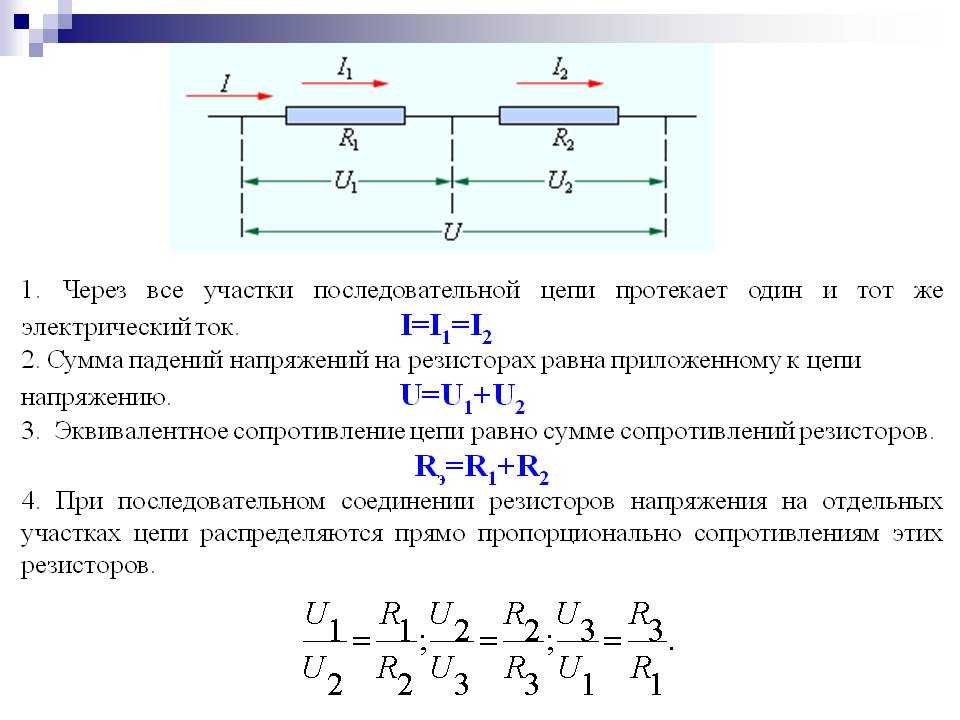 Иногда его также называют «напряжение на резисторе» или просто «падение напряжения».
Иногда его также называют «напряжение на резисторе» или просто «падение напряжения».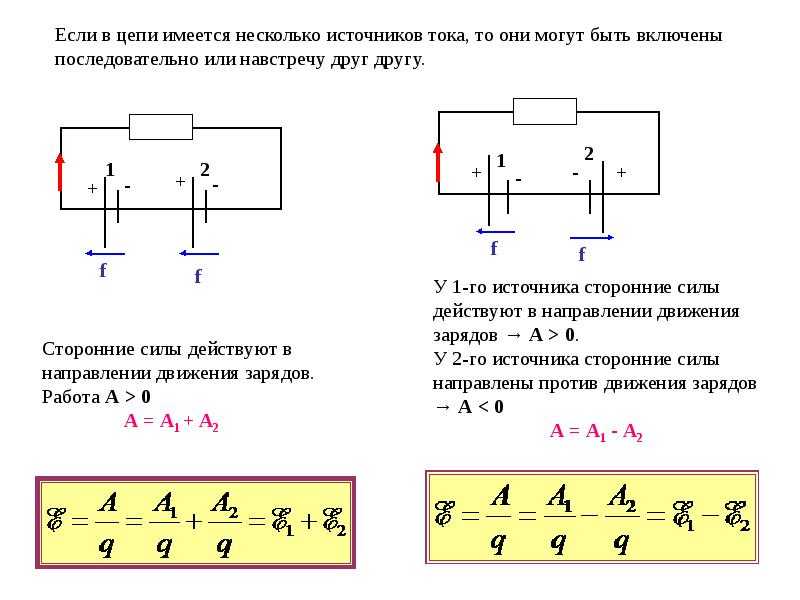
 Когда все устройства подключены с помощью параллельных соединений, цепь называется 9.0006 параллельная цепь . В параллельной схеме каждое устройство размещается в своей отдельной ветке . Наличие ответвлений означает, что существует несколько путей, по которым заряд может проходить по внешней цепи. Каждый заряд, проходящий через петлю внешней цепи, пройдет через один резистор, присутствующий в одной ветви. По прибытии в место разветвления или узел плата делает выбор в отношении того, через какую ветвь пройти на обратном пути к терминалу с низким потенциалом.
Когда все устройства подключены с помощью параллельных соединений, цепь называется 9.0006 параллельная цепь . В параллельной схеме каждое устройство размещается в своей отдельной ветке . Наличие ответвлений означает, что существует несколько путей, по которым заряд может проходить по внешней цепи. Каждый заряд, проходящий через петлю внешней цепи, пройдет через один резистор, присутствующий в одной ветви. По прибытии в место разветвления или узел плата делает выбор в отношении того, через какую ветвь пройти на обратном пути к терминалу с низким потенциалом. Это уменьшенное сопротивление в результате увеличения количества ответвлений приведет к увеличению скорости протекания заряда (также известной как ток). Чтобы сделать этот довольно неожиданный результат более разумным, была введена аналогия с платной дорогой. Пункт взимания платы является основным местом сопротивления автомобильному потоку на платной дороге. Добавление дополнительных пунктов взимания платы в пределах их собственной ветки на платной дороге обеспечит больше путей для движения автомобилей через пункт взимания платы. Эти дополнительные пункты взимания платы снизят общее сопротивление потоку автомобилей и увеличат скорость их движения.
Это уменьшенное сопротивление в результате увеличения количества ответвлений приведет к увеличению скорости протекания заряда (также известной как ток). Чтобы сделать этот довольно неожиданный результат более разумным, была введена аналогия с платной дорогой. Пункт взимания платы является основным местом сопротивления автомобильному потоку на платной дороге. Добавление дополнительных пунктов взимания платы в пределах их собственной ветки на платной дороге обеспечит больше путей для движения автомобилей через пункт взимания платы. Эти дополнительные пункты взимания платы снизят общее сопротивление потоку автомобилей и увеличат скорость их движения. Тем не менее, если взять в целом, общая сумма тока во всех ветвях при суммировании равна сумме тока в точках за пределами ветвей. правило, что тока везде тот же до сих пор работает, только с изюминкой. Ток вне ветвей равен сумме токов в отдельных ветвях. Это все тот же ток, только разделенный на более чем один путь.
Тем не менее, если взять в целом, общая сумма тока во всех ветвях при суммировании равна сумме тока в точках за пределами ветвей. правило, что тока везде тот же до сих пор работает, только с изюминкой. Ток вне ветвей равен сумме токов в отдельных ветвях. Это все тот же ток, только разделенный на более чем один путь. В каждой , узел (место разветвления), вода идет двумя или более отдельными путями. Скорость, с которой вода поступает в узел (измеряется в галлонах в минуту), будет равна сумме расходов в отдельных ответвлениях за пределами узла. Точно так же, когда две или более ветвей впадают в узел, скорость, с которой вода вытекает из узла, будет равна сумме скоростей потока в отдельных ветвях, впадающих в узел.
В каждой , узел (место разветвления), вода идет двумя или более отдельными путями. Скорость, с которой вода поступает в узел (измеряется в галлонах в минуту), будет равна сумме расходов в отдельных ответвлениях за пределами узла. Точно так же, когда две или более ветвей впадают в узел, скорость, с которой вода вытекает из узла, будет равна сумме скоростей потока в отдельных ветвях, впадающих в узел. Заряд поступает в точку A со скоростью 6 ампер и делится на два пути — один через резистор 1, а другой — через резистор 2. Ток в ответвлении с резистором 1 равен 2 ампера, а ток в ответвлении с резистором 2 равен 4 ампера. После того, как эти две ветви снова встречаются в точке B и образуют единую линию, сила тока снова становится равной 6 ампер. Таким образом, мы видим, что справедлив принцип, согласно которому ток вне ветвей равен сумме токов в отдельных ветвях.
Заряд поступает в точку A со скоростью 6 ампер и делится на два пути — один через резистор 1, а другой — через резистор 2. Ток в ответвлении с резистором 1 равен 2 ампера, а ток в ответвлении с резистором 2 равен 4 ампера. После того, как эти две ветви снова встречаются в точке B и образуют единую линию, сила тока снова становится равной 6 ампер. Таким образом, мы видим, что справедлив принцип, согласно которому ток вне ветвей равен сумме токов в отдельных ветвях. В точке В происходит дальнейшее разделение потока на два пути — один через резистор 2, а другой через резистор 3. Подходящий к точке В ток силой 10 ампер разделяется на 6-амперный путь (через резистор 2) и 4-амперный путь. -амперный тракт (через резистор 3). Таким образом, видно, что значения тока в трех ветвях составляют 2 ампера, 6 ампер и 4 ампера и что сумма значений тока в отдельных ветвях равна току вне ветвей.
В точке В происходит дальнейшее разделение потока на два пути — один через резистор 2, а другой через резистор 3. Подходящий к точке В ток силой 10 ампер разделяется на 6-амперный путь (через резистор 2) и 4-амперный путь. -амперный тракт (через резистор 3). Таким образом, видно, что значения тока в трех ветвях составляют 2 ампера, 6 ампер и 4 ампера и что сумма значений тока в отдельных ветвях равна току вне ветвей. Чтобы исследовать эту взаимосвязь, давайте начнем с простейшего случая двух резисторов, размещенных на параллельных ветвях, каждый из которых имеет одинаковое значение сопротивления 4 Ом. Поскольку схема предлагает два равно путям для потока заряда, только половина заряда выберет для прохождения через данную ветвь. В то время как каждая отдельная ветвь оказывает сопротивление 4 Ом любому заряду, проходящему через нее, только половина всего заряда, протекающего через цепь, встретит сопротивление 4 Ом этой отдельной ветви. Таким образом, что касается батареи, которая качает заряд, наличие двух 4-омных резисторов, включенных параллельно, было бы эквивалентно наличию в цепи одного 2-омного резистора. Точно так же наличие двух резисторов 6 Ом параллельно будет эквивалентно наличию в цепи одного резистора 3 Ом. А наличие двух 12-омных резисторов параллельно было бы эквивалентно наличию в цепи одного 6-омного резистора.
Чтобы исследовать эту взаимосвязь, давайте начнем с простейшего случая двух резисторов, размещенных на параллельных ветвях, каждый из которых имеет одинаковое значение сопротивления 4 Ом. Поскольку схема предлагает два равно путям для потока заряда, только половина заряда выберет для прохождения через данную ветвь. В то время как каждая отдельная ветвь оказывает сопротивление 4 Ом любому заряду, проходящему через нее, только половина всего заряда, протекающего через цепь, встретит сопротивление 4 Ом этой отдельной ветви. Таким образом, что касается батареи, которая качает заряд, наличие двух 4-омных резисторов, включенных параллельно, было бы эквивалентно наличию в цепи одного 2-омного резистора. Точно так же наличие двух резисторов 6 Ом параллельно будет эквивалентно наличию в цепи одного резистора 3 Ом. А наличие двух 12-омных резисторов параллельно было бы эквивалентно наличию в цепи одного 6-омного резистора. С тремя равными путями для прохождения заряда через внешнюю цепь, только одна треть заряда выберет прохождение через данную ветвь. Каждая отдельная ветвь оказывает сопротивление 6 Ом проходящему через нее заряду. Однако тот факт, что только одна треть заряда проходит через конкретную ветвь, означает, что общее сопротивление цепи равно 2 Ом. Что касается батареи, которая качает заряд, наличие трех резисторов 6 Ом параллельно будет эквивалентно наличию в цепи одного резистора 2 Ом. Таким же образом присутствие трех 9Параллельное подключение резисторов сопротивлением Ω эквивалентно наличию в цепи одного резистора сопротивлением 3 Ω. А наличие трех 12-омных резисторов параллельно будет эквивалентно наличию в цепи одного 4-омного резистора.
С тремя равными путями для прохождения заряда через внешнюю цепь, только одна треть заряда выберет прохождение через данную ветвь. Каждая отдельная ветвь оказывает сопротивление 6 Ом проходящему через нее заряду. Однако тот факт, что только одна треть заряда проходит через конкретную ветвь, означает, что общее сопротивление цепи равно 2 Ом. Что касается батареи, которая качает заряд, наличие трех резисторов 6 Ом параллельно будет эквивалентно наличию в цепи одного резистора 2 Ом. Таким же образом присутствие трех 9Параллельное подключение резисторов сопротивлением Ω эквивалентно наличию в цепи одного резистора сопротивлением 3 Ω. А наличие трех 12-омных резисторов параллельно будет эквивалентно наличию в цепи одного 4-омного резистора. Для параллельных цепей математическая формула расчета эквивалентного сопротивления (R Уравнение ) IS
Для параллельных цепей математическая формула расчета эквивалентного сопротивления (R Уравнение ) IS = 1/R 1 + 1/R 2 + 1/R 3
= 1/R 1 + 1/R 2 + 1/R 3  Введите любые два значения сопротивления, которые вы хотите. Используйте свой калькулятор, чтобы определить значения R eq . Затем нажмите кнопку Отправить , чтобы проверить свои ответы. Попробуйте сколько угодно раз с разными значениями сопротивления.
Введите любые два значения сопротивления, которые вы хотите. Используйте свой калькулятор, чтобы определить значения R eq . Затем нажмите кнопку Отправить , чтобы проверить свои ответы. Попробуйте сколько угодно раз с разными значениями сопротивления. ..
..  Заряд не теряет своего высокого потенциала до тех пор, пока он не пройдет через резистор, либо от C к D, от E к F, либо от G к H. Как только он проходит через резистор, заряд возвращается почти к 0 вольт и возвращается к отрицательному клемму аккумулятора для повышения напряжения. В отличие от последовательных цепей, заряд в параллельной цепи сталкивается с единичным падением напряжения на своем пути через внешнюю цепь.
Заряд не теряет своего высокого потенциала до тех пор, пока он не пройдет через резистор, либо от C к D, от E к F, либо от G к H. Как только он проходит через резистор, заряд возвращается почти к 0 вольт и возвращается к отрицательному клемму аккумулятора для повышения напряжения. В отличие от последовательных цепей, заряд в параллельной цепи сталкивается с единичным падением напряжения на своем пути через внешнюю цепь.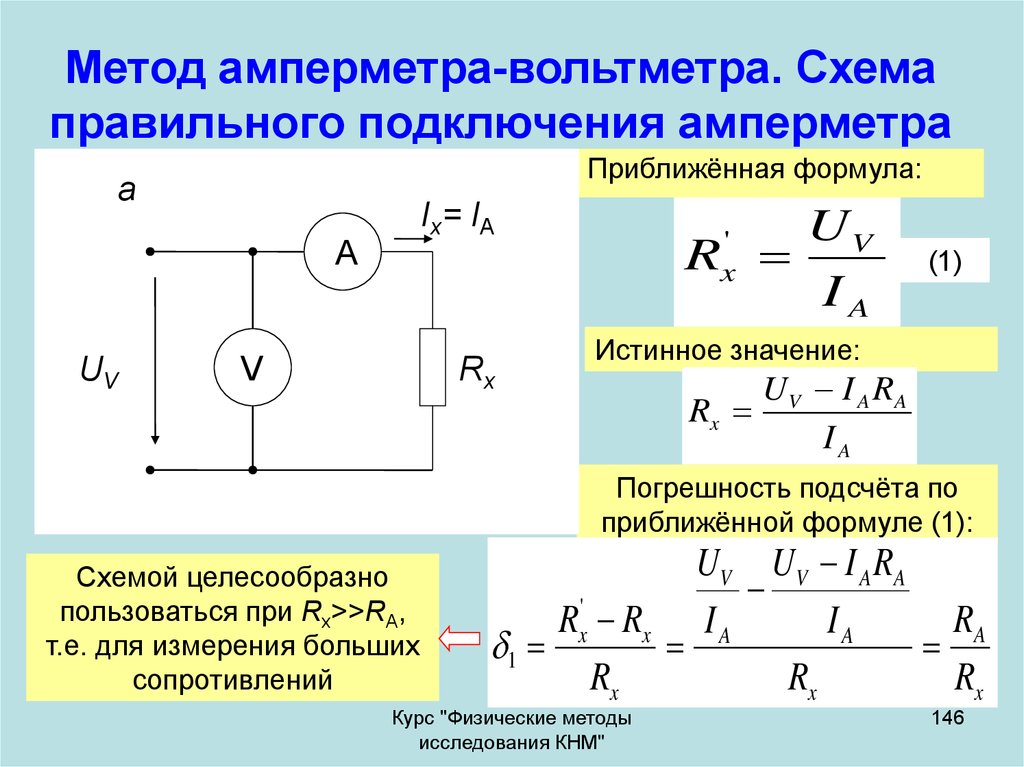
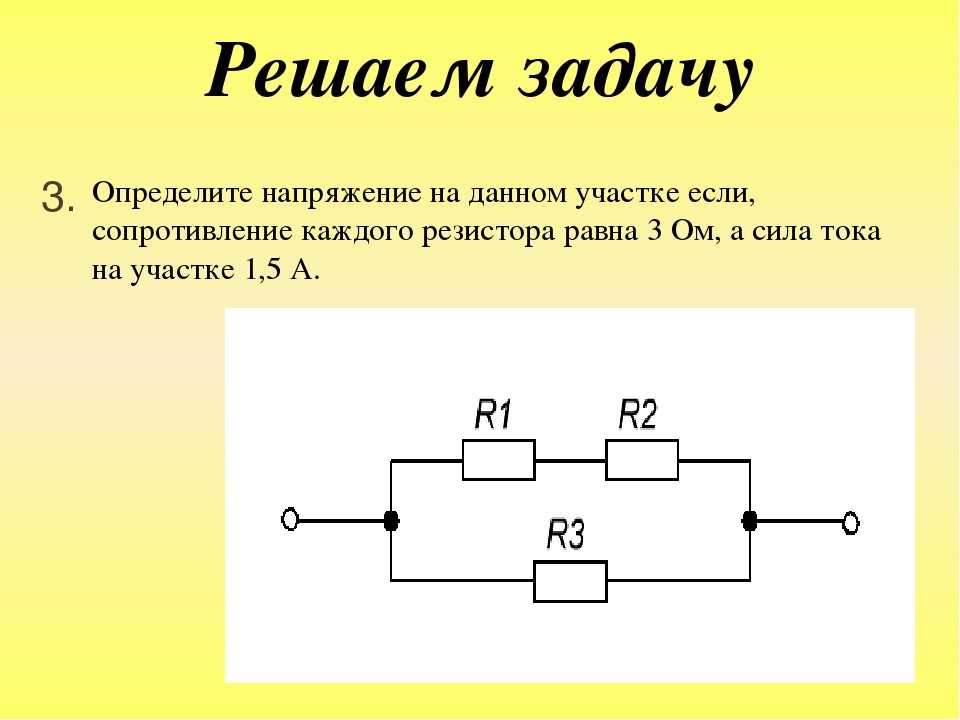 Их использование будет продемонстрировано математическим анализом схемы, показанной ниже. Цель состоит в том, чтобы использовать формулы для определения эквивалентного сопротивления цепи (R eq ), тока через батарею (I tot ), а также падения напряжения и тока для каждого из трех резисторов.
Их использование будет продемонстрировано математическим анализом схемы, показанной ниже. Цель состоит в том, чтобы использовать формулы для определения эквивалентного сопротивления цепи (R eq ), тока через батарею (I tot ), а также падения напряжения и тока для каждого из трех резисторов. Расчет показан здесь:
Расчет показан здесь: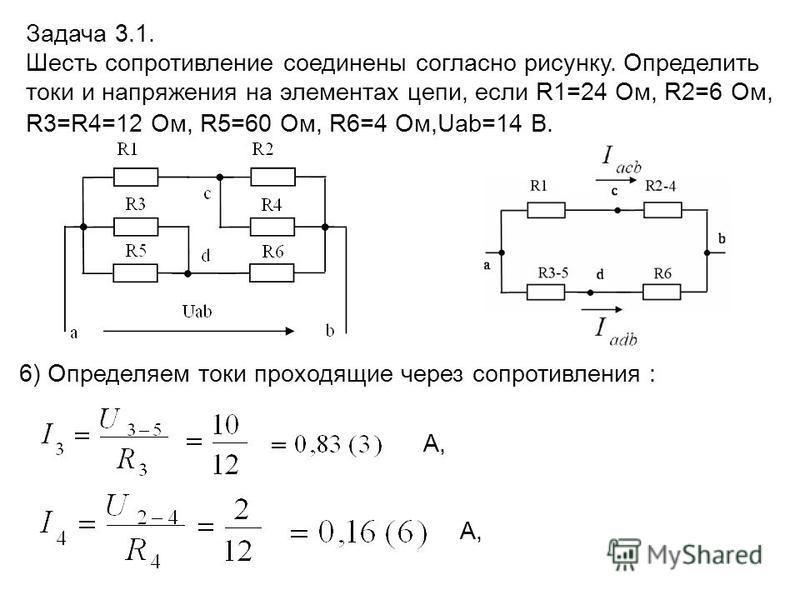 Расчеты показаны ниже.
Расчеты показаны ниже.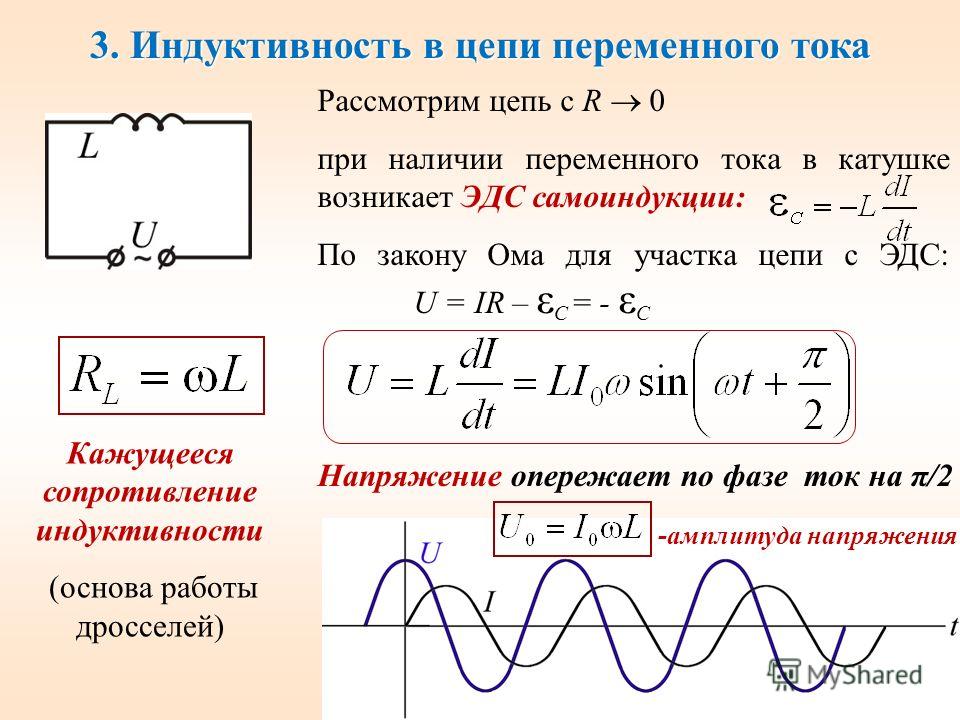 )
)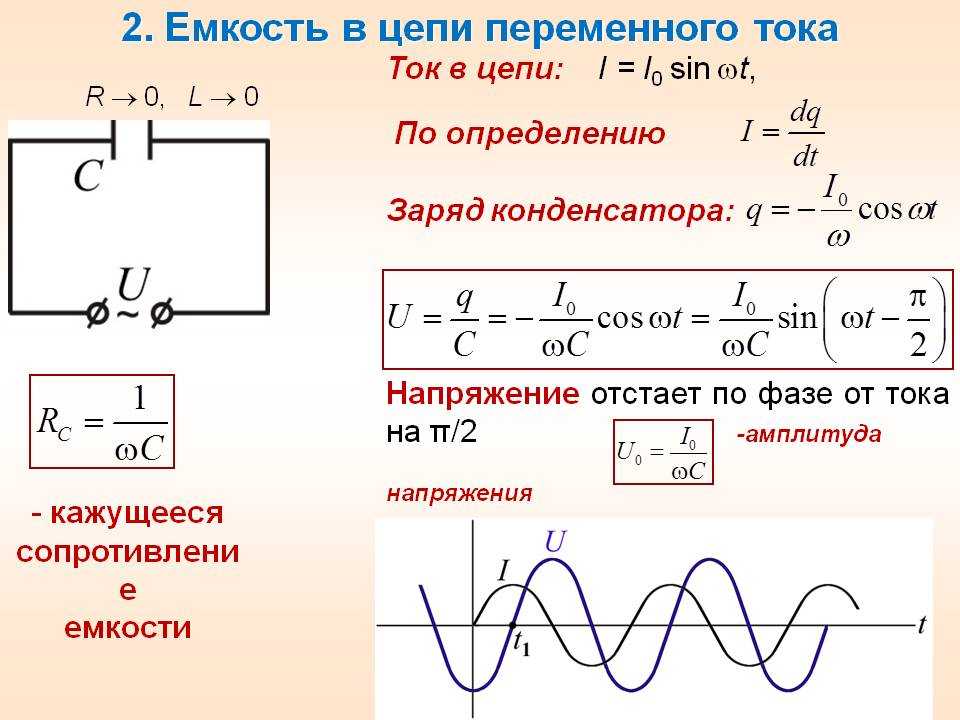
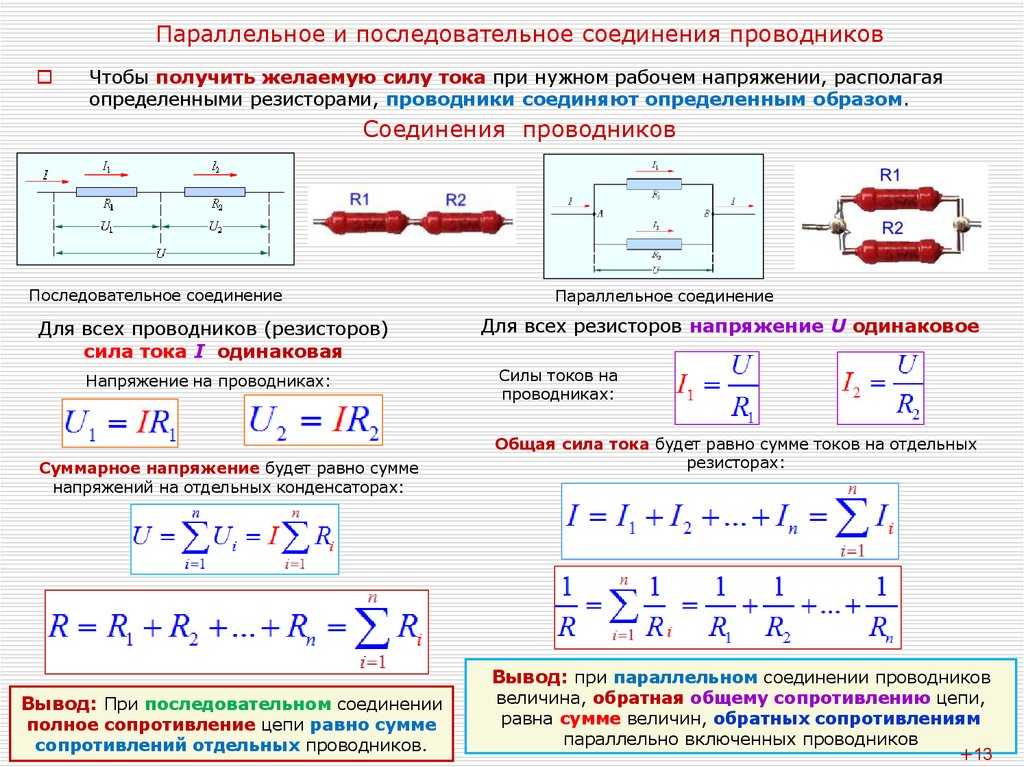 Три одинаковые лампочки подключены к D-элементу, как показано ниже. P, Q, X, Y и Z представляют местоположения вдоль цепи. В каком месте(ах), если таковые имеются, ток будет …
Три одинаковые лампочки подключены к D-элементу, как показано ниже. P, Q, X, Y и Z представляют местоположения вдоль цепи. В каком месте(ах), если таковые имеются, ток будет …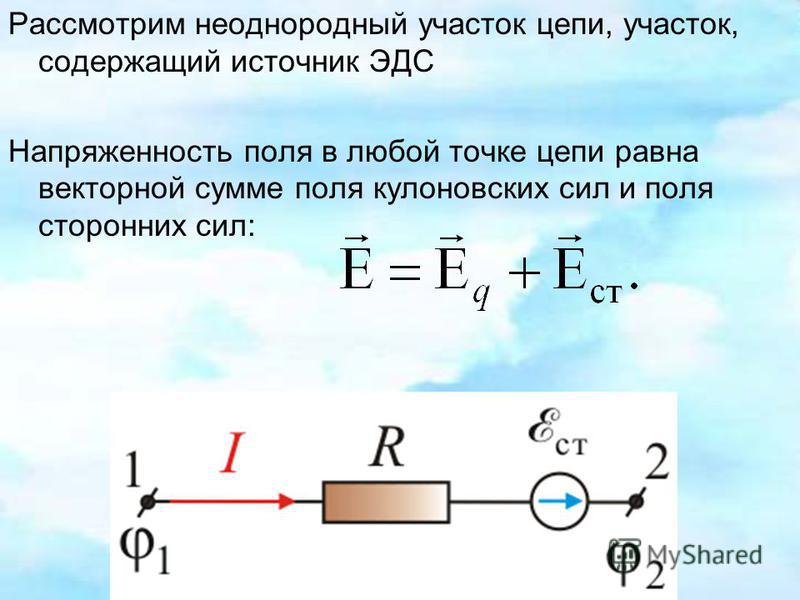

 Два резистора 6 Ом, включенные параллельно, обеспечат сопротивление, эквивалентное одному резистору _____ Ом.
Два резистора 6 Ом, включенные параллельно, обеспечат сопротивление, эквивалентное одному резистору _____ Ом.