Модуль функции график: Графики функций с модулем

Модуль. Графики функций, содержащих переменную под знаком модуля

Похожие презентации:

Элементы комбинаторики ( 9-11 классы)

Применение производной в науке и в жизни

Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»

Знакомство детей с математическими знаками и монетами

Тренажёр по математике «Собираем урожай». Счет в пределах 10

Методы обработки экспериментальных данных

Лекция 6. Корреляционный и регрессионный анализ

Решение задач обязательной части ОГЭ по геометрии

Дифференциальные уравнения

Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи

1. Урок-презентация на тему: «Модуль»

Учитель: Матюшева В.И.

2. Графики функций, содержащих переменную под знаком модуля

1. Преобразование графиков
2. Построение графиков
3. Решение уравнений
4. Дидактический материал

3. 1.Преобразование графиков функций, содержащих переменную под знаком модуля

4.

Функция у =|х|График функции у =|х| получается из графика у=х
следующим образом:
— часть графика у=х, лежащая над осью Ох, сохраняется ;
— часть его, лежащая под осью Ох , отображается
симметрично относительно оси Ох.
у
у=|x|
0
у=х
х

5. Функция у=|х|+а

График функции
у=|х|+а
получается
параллельным переносом графика у=|х| в
— положительном направлении оси Оу(вверх) на а ед.отрезков
при а>0 или
— в отрицательном направлении оси Оу(вниз) на |а| при а<0.
y
у=IxI+a
у=I x I
у=IxI-a
a
0
-a
x
Функция у=а|х|
График функции у=а|х| получается:
— сжатием графика у=|х| к оси Оу в а раз при а>1;
— растяжением от этой оси в а раз при 0 < a < 1.
y
у=a|x|, а>1
у=| x|
у =а|x|, 0 <a< 1
0
x

7. Функция у=|x+a|

График функции у=|x+a| получается
параллельным
переносом графика y=|x|:
-в положительном направлении оси Ох (вправо) на |a| при a<0
— в отрицательном направлении оси Ох (влево) на |а| при а>0
y
у=|x+ a|
у = |x|
у=|x-a|
о
-a
a
х

8.

Функция y= — |x|График функции y = — |x| получается симметричным
отображением графика y = |x| относительно оси Ох.
у
у = |x|
о
х
у = — IxI

9. Функция y = f(|x|)

График функции y = f(|x|) получается из графика y = f(x)
следующим образом:
1)строится график f(x) при х>0
2) полученная часть графика f(x) отображается симметрично относительно оси Оу.
у
у= 1
IxI
у= 1
x
х
о

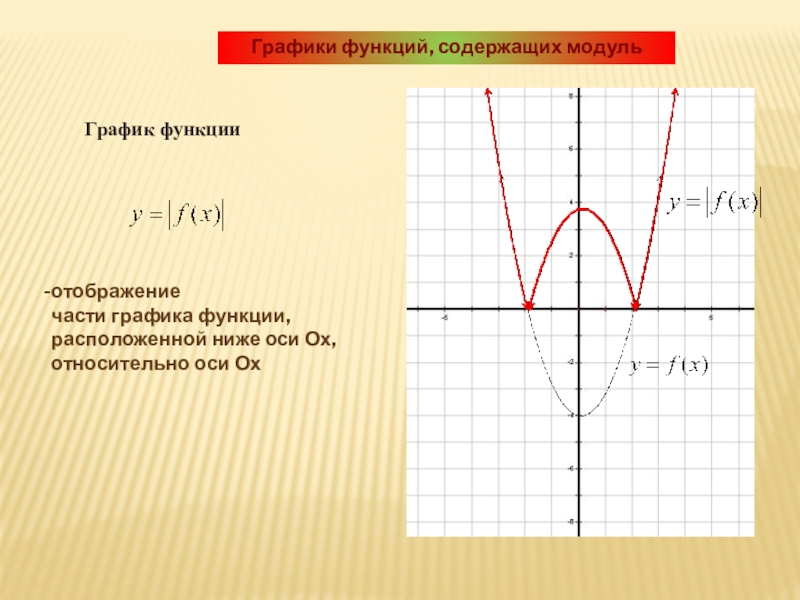
10. Функция y=|f(x)|

График функции y=|f(x)| получается из графика y=f(x)
следующим образом :
1) часть графика f(x), лежащая над осью Ох, сохраняется ;
2) часть графика f(x), лежащая под осью Ох, отображается
симметрично относительно оси Ох.
у
y=f(x)
y=|f(x)|
х
о

11. 2.Построение графиков функций, содержащих переменную под знаком модуля

12. Задание №1.

Построить график функции у=||x|-2|.
План построения:
1) Строим график y=|x|
2) Смещаем его по оси Оу вниз на 2 ед. отрезка.
3) Отображаем часть графика, расположенного под осью Ох,
в верхнюю полуплоскость
у
у=||x|-2|
у = |x|
2
о
у=|x|- 2
-2
х

13. Задание №2.

Построить график функции у=||x-2|-2|.
План построения:
1) Строим график y=|x|
2) смещаем его по оси Ох вправо на 2 ед.отрезка;
3) смещаем его по оси Оу вниз на 2 ед.отрезка;
4) отображаем часть графика, расположенного под осью Ох,
у
в верхнюю полуплоскость
у = |x|
2
о
у=||x-2|-2|
х
2
у=|x- 2|
-2

14. 3.а)Решение уравнений, содержащих переменную под знаком модуля; б)решение уравнений с параметром.

15. Задание №1.

Решить уравнение ||x-2|-2|=2.
Решение.
1) Строим график y=I|x-2|-2I
2) строим прямую у=2;
3) абсциссы точек пересечения графиков являются решениями данного уравнения;
у
у=||x-2|-2|
у=2
2
о
-2
2
6
Ответ: -2; 2; 6.
х

16. Задание №2.

В зависимости от параметра а определить количество
корней уравнения
||x|-2|=а.
Решение.
1) Строим график y= ||x|-2|;
2) Строим прямые:
у = а, при а > 2 ;
у = а, при а = 2 ;
у = а, при 0 < a < 2 ;
y = a, при а = 0 ;
у = а, при а < 0 .
3) Определяем число корней по количеству точек
пересечения прямой у=а и графика функции y= ||x|-2|.
Решение.
у
у=||x|-2|
у=а,при а>2
1
2
2
У= а, при 0<a<2
y=a, при а=0
3
5
о
4
у=а, при а=2
х
у=а, при а<0

18. 4. Дидактический материал

A. Построить график функции:
а) у=IxI+2; б) y=Ix+2I; в) y=-Ix+2I-1.
Б. a) y= 1/ Ix-2I+3;
б) y=- IIIxI-2I-3I;
в) у=IIII2xI-1I-1I-2I.
В. Решить уравнение: IIх+4I-3I = 2
Г. В зависимости от параметра а определить количество
корней уравнения
а)
IIIxI-2I-3I=a;
б) III2xI-1I-1I=a;
в) при каких k уравнение IIII4xI-2I-1I-1I=k имеет
наибольшее количество корней?

English     Русский Правила

Обработка графиков

Многие из модулей обработки данных создают графики в результате своей работы. Графики можно экспортировать в текстовый файл или продолжать анализировать их в Gwyddion с помощью нескольких модулей обработки графиков. Эти модули доступны в меню График основного окна Gwyddion. Следует заметить, что число модулей обработки графиков на данный момент невелико, и они состоят в основном из простейших модулей для операций, которые часто встречаются при анализе данных СЗМ. Для более сложных аналитических операций лучше использовать вашу любимую программу для обработки графиков.

В этой секции кратко описываются имеющиеся в Gwyddion модули обработки графиков.

Базовые операции

Прежде всего, функции масштабирования и чтения данных доступны непосредственно в окне графика:

• Логарифмический масштаб осей – горизонтальные и вертикальные оси могут переключаться между линейным и логарифмическим режимом с использованием кнопок логарифмического масштаба. Переключение на логарифмический масштаб доступно только для положительных значений (либо по абсциссе, либо по ординате).
• Увеличение и уменьшение масштаба – после выбора режима приближения можно нарисовать мышью область, которую нужно увеличить. Уменьшение восстанавливает тот масштаб, при котором видны все данные.
• Измерение расстояний – позволяет выбрать несколько точек на графике и показать расстояния и углы между ними.

Перевернуть график

Перевернуть график переворачивает график вертикально. Другими словами, ордината инвертируется, при этом абсцисса остаётся нетронутой. Функция непосредственно меняет данные кривой, она не затрагивает только презентацию данных.

Инвертировать график

Инвертировать график переворачивает график горизонтально. Другими словами, абсцисса инвертируется, при этом ордината остаётся нетронутой. Функция непосредственно меняет данные кривой, она не затрагивает только презентацию данных.

Обрезать график

Обрезать график – очень простой модуль, который обрезает кривые графиков до выбранного диапазона (либо заданного численно, либо выбранного на графике с помощью мыши) и создаёт новый график. Если выбрано Обрезать все кривые, все кривые обрезаются и переносятся на новый график, в противном случае операция применяется только к выбранной кривой.

Выравнивание графиков

Выравнивание графика – очень простой модуль, который на данный момент производит линейную аппроксимацию каждой из кривых графика и вычитает аппроксимирующую линейную функцию из них.

Подровнять

Функция подровнять сдвигает кривые графиков горизонтально таким образом, чтобы максимизировать их взаимные корреляции, т.е. чтобы общие особенности кривых соответствовали друг другу. Это может быть полезным, например, для сравнения профилей, снятых в разных местах образца.

Логарифмический масштаб

Элементы управления окном графика позволяют переключаться между линейным и логарифмическим масштабом осей. Однако, для аппроксимации зависимостей наподобие степенных может оказаться полезно физически преобразовать данные взятием логарифма от значений. Функция преобразования графика в логарифмический масштаб осуществляет такое преобразование.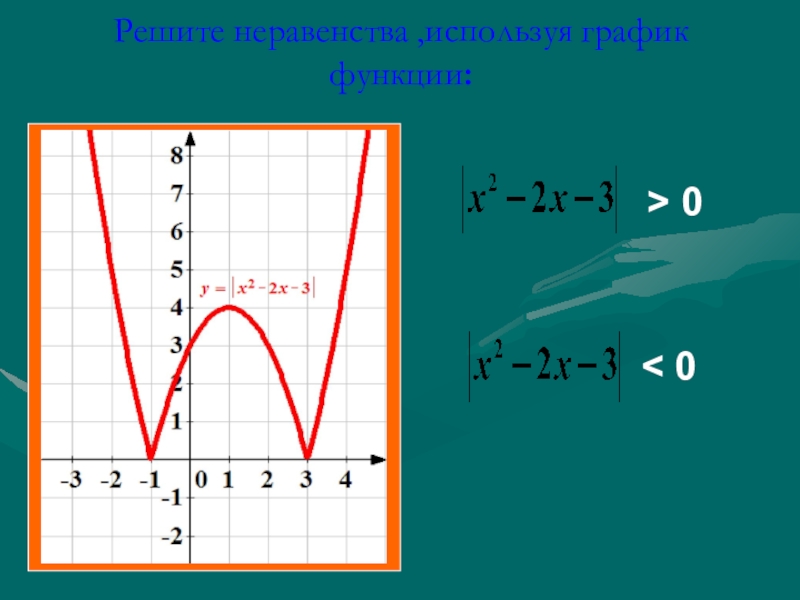 Можно выбрать, какую из осей нужно преобразовать (x, y или обе), что делать с неположительными значениями, если они появляются, и выбрать основание логарифма. После этого создаётся новый график и все кривые преобразуются заданным образом.

Экспорт графиков кривых

Данные графиков кривых могут быть экспортированы в текстовые файлы с использованием меню Экспортировать текст. Диалоговое окно экспорта позволяет выбрать между несколькими вариантами стилей, которые потом проще импортировать в другие пакеты программного обеспечения. Опции Экспорт меток, Экспорт единиц измерения и Экспорт метаданных позволяют добавить строки с дополнительной информацией перед блоком числовых данных. Это может оказаться полезным как напоминание, какие данные содержал исходный файл, но может вызывать проблемы при чтении файла другим программным обеспечением.

Опция Формат чисел POSIX принудительно заставляет использовать стандартное машиночитаемое научное представление чисел с десятичной точкой. В противном случае значения записываются в соответствии с настройками текущей локали (офисное программное обеспечение может более охотно читать такой формат, научное программное обеспечение обычно поддерживает его хуже).

Другой важной опцией, которая влияет на структуру всего файла является Общая объединённая абсцисса. По умолчанию отдельные кривые записываются в файл последовательно, разделённые пустыми строками. Если эта опция включена, экспорт кривых записывает единую таблицу с несколькими столбцами, представляющими данные всех кривых, и общую абсциссу первым столбцом. Если кривые не были дискретизированы одинаково, некоторые строки будут естественно содержать значения только для части кривых, где они определены. Экспортируемый файл с двумя отдельными кривыми может выглядеть следующим образом:

в то время, как с общей объединённой осью абсцисс те же данные будут сохранены как:

Также можно экспортировать векторное (EPS) или растровое (PNG) графическое представление графика используя пункты меню Экспортировать PostScript или Экспортировать растр. Однако, эти опции предоставляют достаточно ограниченные возможности. Gwyddion не является специальным программным обеспечением для построения графиков, и если вам нужны красивые графики, лучше использовать то, которое является – например, gnuplot или matplotlib.

Статистика

Модуль статистики графика показывает сводную информацию о полной кривой графика или о выбранных диапазонах. Диалоговое окно показывает две основные группы величин, которые вычисляются различным способом.

Простые параметры рассчитываются из набора значений ординат, никак не учитывая абсциссы. Это важно иметь в виду в том случае, когда кривая дискретизирована неравномерно, т.е. расстояние между значениями по оси абсцисс меняется, возможно сильно. Часть кривой, в которой точки дискретизации идут более плотно, будет оказывать более сильное влияние на результат. Доступные параметры включают в себя базовые характеристики с тем же значением, что и для двумерных данных. Некоторые из них также совпадают с основными параметрами шероховатости, которые рассчитываются инструментом Шероховатость.

С другой стороны Интегралы получаются интеграцией по правилу трапеций (или с помощью похожей аппроксимации). Следовательно, более длинные интервалы вносят больший вклад в результат. Доступные величины включают в себя:

Длина проекции

Длина выбранного диапазона (или полный диапазон значений по оси абсцисс, если диапазон не выбран).

Длина полного профиля

Сумма длин линейных сегментов, соединяющих точки кривой.

Вариация

Интеграл модуля производной — рассчитывается как сумма модулей попарных разностей значений ординаты.

Среднее значение

Площадь под кривой делённая на длину проекции.

Площадь под кривой

Полный интеграл (сумма положительной и отрицательной площади).

Положительная площадь

Интеграл под отрезками кривой, где она положительна.

Отрицательная площадь

Интеграл под отрезками кривой, где она отрицательна.

Среднеквадратичное

Интеграл возведённых в квадрат значений делённый на длину проекции кривой.

Статистические функции

Одномерные статистические функции рассчитываются для графиков используя те же самые определения, что и для изображений. Они подробно описаны в разделе Инструмент статистические функции. Доступные функции включают в себя распределения высот и углов, функцию автокорреляции, функцию корреляции высота-высота и функцию спектральной плотности мощности. Они могут быть расчитаны для выбранной кривой или для всех кривых сразу если включена опция Все кривые.

Главное различие между изображениями и графиками состоит в том, что кривые графика не обязательно должны иметь равномерные интервалы между значениями абсцисс (равномерную дискретизацию). В этом случае кривая будет заново дискретизирована при расчёте статистических функций на равномерно распределенные интервалы. Шаг между отсчётами по умолчанию берётся таким, чтобы сохранить количество точек. Однако, это можно изменить используя опцию Избыточная дискретизация, которая задаёт насколько больше точек новая кривая должна иметь по сравнению с оригинальной.

Иногда может быть полезно использовать избыточную дискретизацию больше 1 даже для кривых графиков с правильными интервалами между точками.

Аппроксимировать функцией

Аппроксимация функцией разрабатывалась для аппроксимации данных статистическими функциями, используемыми при оценке параметров шероховатости. Следовательно, большая часть доступных здесь функций является статистическими функциями поверхностей с гауссовой или экспоненциальной функцией автокорреляции. Тем не менее, здесь доступно несколько распространённых функций общего назначения. Подробнее они описаны в списке аппроксимирующих функций.

В модуле аппроксимации можно задать область, на которой будет производиться аппроксимация (с помощью мыши или численно), сначала надо задать начальные параметры или дать модулю самому угадать их, и, затем, можно аппроксимировать данные используя алгоритм Левенберга – Маркардта.

В результате получается аппроксимированная кривая и набор её параметров. Отчёт об аппроксимации можно сохранить в файл используя кнопку Сохранить. Нажатие кнопки OK добавляет аппроксимирующую кривую к графику, если это нежелательно, закройте диалоговое окно с помощью кнопки Отмена.

Аппроксимировать кривую сила-расстояние

Модуль аппроксимации кривых сила-расстояния весьма похож на модуль аппроксимации любых кривых, он просто специально сделан для данного типа кривых. На настоящий момент модуль может использоваться для аппроксимации части со скачком на кривой сила-расстояния (которая показывает силы притяжения) используя различные модели:

• силу Ван-дер-Ваальса между полусферой и полупространством
• силу Ван-дер-Ваальса между пирамидой и полупространством
• силу Ван-дер-Ваальса между усечённой пирамидой и полупространством
• силу Ван-дер-Ваальса между сферой и полупространством
• силу Ван-дер-Ваальса между двумя сферами
• силу Ван-дер-Ваальса между конусом и полупространством
• силу Ван-дер-Ваальса между цилиндром и полупространством
• силу Ван-дер-Ваальса между параболоидом и полупространством

Следует отметить, что аппроксимируемая кривая должна быть именно кривой сила-расстояние, а не смещение-расстояние или сигнал датчика-расстояние. Пересчёт отклонения кантелевера в силу должен быть сделан до вызова этого модуля.

Также следует отметить, что для кантелеверов с малой постоянной упругости количество полезных данных в области притяжения ограничено эффектом перескока в состояние контакта.

Габаритный размер

Модуль определения габаритных размеров можно использовать для аппроксимации некоторых «типичных» объектов, которые можно встретить на профилях полученных с микросхем и похожих на них объектов. Эти объекты обнаруживаются на графике, после чего рассчитываются их свойства.

Интерфейс модуля практически ничем не отличается от модуля аппроксимации функциями.

Спектр плотности состояний

Модуль расчёта спектра плотности состояний предназначен для расчёта этих спектров из ВАХ туннельного контакта между СТМ-зондом и локальной точкой поверхности. Он рассчитывает

и строит полученную функцию в виде графика.

Найти пики

Наиболее выделяющиеся пики на кривых графиков можно автоматически выделять с точностью, превышающей точность дискретизации. Можно задать число наиболее выделяющихся пиков как Количество пиков и функция выделит их на графике. Выделение пиков зависит от их высоты, площади и расстояний до других пиков. Обычно представление данной функции о наиболее выделяющихся пиках неплохо совпадает с ручным выбором. Если вам не нравится текущий выбор, можно увеличить количество пиков и игнорировать ненужные. Также возможно искать отрицательные пики, т.е. впадины, включив опцию Инвертировать (найти впадины).

Таблица всех пиков показывается в левой части отсортированной в соответствии с выбором опции Упорядочить пики по…. Сортировка по положению означает что пики будут перечислены в том же порядке, как они показаны на графике слева направо. Сортировка по выдающести означает, что наиболее выделяющиеся пики будут показаны первыми.

Для каждого пика показывается несколько его основных характеристик: положение (абсцисса) x, высота h, площадь A и ширина (или отклонение) w. Положение определяется по квадратичному субпиксельному уточнению максимума пика. Остальные значения зависят от того, как определён фон у пика. Возможные варианты включают в себя Нуль, означающий что за основание пика всегда будет браться уровень нуля, и Двусторонний минимум, что означает что фоном пика будет функция гладкой ступени проходящая через ближайшие минимумы кривой слева и справа от пика.

Период/шаг

Существует много методов измерения периода/шага периодических профилей, таких как решетки. Модуль измерения периода на графиках реализует несколько из них (см. ссылку [1] для их описания). Лоя достаточно хорошо измеренной решетки все хорошие методы

• Уточненное преобразование Фурье
• Многопиковая АКФ
• Пересечение нуля
• Центры притяжения

должны давать сравнимые результаты, но при этом они отличаются чувствительностью к различным артефактам в данных. Уточненное преобразование Фурье это наиболее устойчивый метод для нечетных форм повторяющихся элементов. Однако, он не предоставляет никакой оценки ошибок.

Два базовых метода также включены, простое преобразование Фурье и простая АКФ, которые просто находят положение основного пика на спектре мощности или АКФ.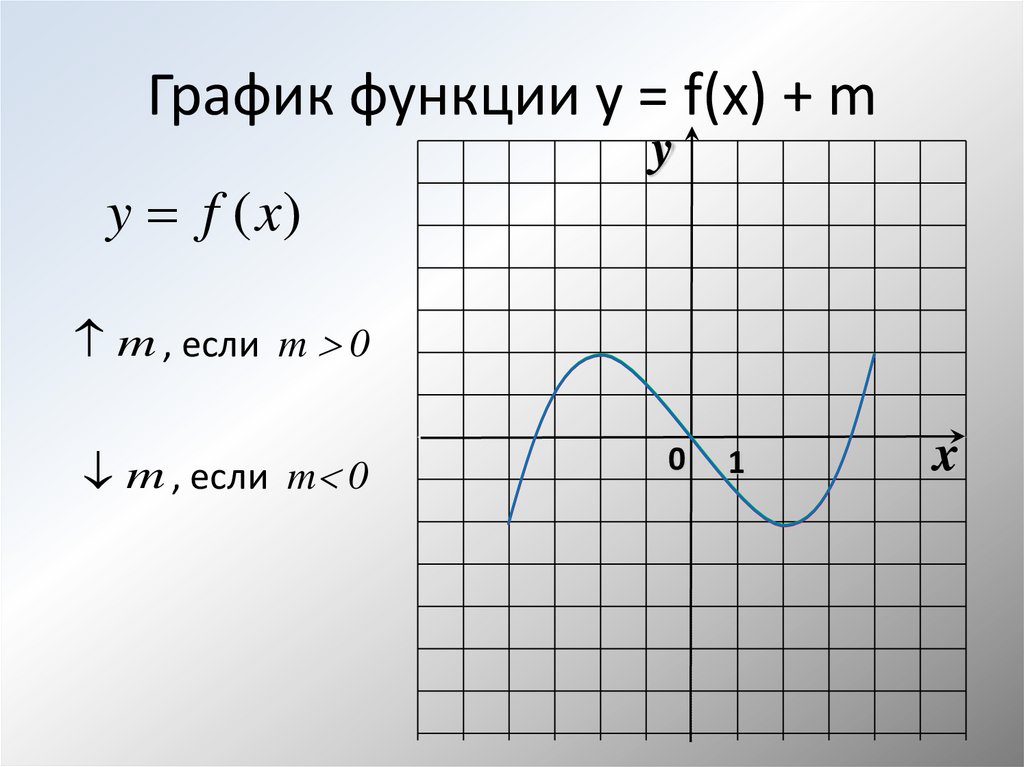 Они не должны использоваться для оценки и представлены в основном для полноты.

Если профиль был уже правильно выровнен и выбрана нулевая линия, функция может рассчитать данные для профиля без всякой предобработки. В противном случае, нужно включить опцию Вычесть фон чтобы убрать фон на основе хорошо определенной процедуры (см. снова [1]). В этом случае опция Показать выровненную кривую может использоваться чтобы показать обработанный профиль наряду с не модифицированными данными.

Террасы

Террасы или структуры по типу амфитеатров могут быть измерены используя одномерные профили так же, как они измеряются по данным изображения в модуле Террасы. Модули для графиков и для изображений почти идентичны. Следовательно, дальнейшее описывает только основные различия:

• Ядро поиска ступени и уширение будут одномерными. Они по прежнему измеряются в пикселях, что соответствует среднему расстоянию между точками кривой. Минимальная площадь террасы заменяется минимальной длиной, измеренной как доля всего диапазона абсцисс.

• Отсутствует опция использования маски. Вместо этого, террасы могут быть выделены вручную на графике с помощью мыши если опция Выбрать области вручную включена.

• Присутствует дополнительный выбор в меню Показать, Детекция ступеней. Он показывает результат работы фильтра поиска краёв и показывает выбранный порог используя красную пунктирную линию. Это один из наиболее полезных графиков при настройке параметров.

• Площадь в пикселях A_px заменяется на N_px, количество точек кривой, из которых состоит терраса.

Источники

[1] D. Nečas, A. Yacoot, M. Valtr, P. Klapetek: Demystifying data evaluation in the measurement of periodic structures. Measurement Science and Technology 34 (2023) 055015, 10.1088/1361-6501/acbab3

Модуль Microsoft.Graph.Users.Functions | Microsoft Узнайте

Твиттер LinkedIn Фейсбук Электронная почта

• Артикул

Командлеты Microsoft Graph PowerShell

Export-MgUserDeviceAndAppManagementData	Вызов функции exportDeviceAndAppManagementData
Get — Мгаллусерчатмессаже	Вызвать функцию getAllMessages
Get-MgUserCalendarEventDelta	Вызов функции дельта
Get-MgUserChatMessageDelta	Вызов функции дельта
Get-MgUserChatMessageReplyDelta	Вызов функции дельта
Get-MgUserContactDelta	Вызов функции дельта
Get-MgUserContactFolderChildFolderContactDelta	Вызов функции дельта
Get-MgUserContactFolderChildFolderDelta	Вызов функции дельта
Get-MgUserContactFolderContactDelta	Вызов функции дельта
Get-MgUserContactFolderDelta	Вызов функции дельта
Get-MgUserDelta	Вызов функции дельта
Get-MgUserDriveItemActivityByInterval	Вызов функции getActivitiesByInterval
Get-MgUserDriveItemDelta	Вызов функции дельта
Get-MgUserDriveItemListItemActivityByInterval	Вызов функции getActivitiesByInterval
Get-MgUserDriveListContentTypeCompatibleHubContentType	Вызов функции getCompatibleHubContentTypes
Get-MgUserDriveListItemActivityByInterval	Вызов функции getActivitiesByInterval
Get-MgUserDriveRootActivityByInterval	Вызов функции getActivitiesByInterval
Get-MgUserDriveRootDelta	Вызов функции дельта
Get-MgUserDriveRootListItemActivityByInterval	Вызов функции getActivitiesByInterval
Get-MgUserEventDelta	Вызов функции дельта
Get-MgUserEventInstanceDelta	Вызов функции дельта
Get-MgUserMailFolderChildFolderDelta	Вызов функции дельта
Get-MgUserMailFolderChildFolderMessageDelta	Вызов функции дельта
Get-MgUserMailFolderDelta	Вызов функции дельта
Get-MgUserMailFolderMessageDelta	Вызов функции дельта
Get-MgUserManagedAppDiagnosticStatuses	Получает статус проверки диагностики для данного пользователя.
Get-MgUserManagedAppPolicy	Получает ограничения приложения для данного пользователя.
Get-MgUserManagedDeviceWithAppFailure	Получает список устройств со сбойными приложениями
Get-MgUserMessageDelta	Вызов функции дельта
Get-MgUserOnenoteRecentNotebook	Вызвать функцию getRecentNotebooks
Get-MgUserTodoListDelta	Вызов функции дельта
Get-MgUserTodoListTaskDelta	Вызов функции дельта
Invoke-MgCalendarUserCalendarAllowedCalendarSharingRoles	Функция вызова разрешенаCalendarSharingRoles
Invoke-MgGraphUserDrive	Вызов функции sharedWithMe
Invoke-MgPreviewUserOnenotePage	Вызов функции предварительного просмотра
Invoke-MgRecentUserActivity	Недавняя функция вызова
Invoke-MgRecentUserDrive	Недавняя функция вызова
Invoke-MgSupportedUserOutlookLanguage	Поддерживаемые языки вызова функции
Invoke-MgTimeUserOutlook	Функция вызова поддерживается TimeZones
Invoke-MgViewUserReminder	Вызов функции напоминания View
Поиск-MgUserDrive	Вызов функции поиска
Search-MgUserDriveItem	Вызов функции поиска
Поиск-MgUserDriveRoot	Вызов функции поиска
Test-MgUserDriveListContentTypePublished	Вызов функции isPublished

Прочитано: Графические линейные функции | Средний уровень алгебры |

Модуль 4: Функции и обозначения функций

Цели обучения

• График линейных функций с использованием таблицы значений

Полезным первым шагом при построении графика функции является создание таблицы значений. Это особенно полезно, когда вы не знаете общую форму функции. Вы, наверное, уже знаете, что линейная функция — это прямая линия, но давайте сначала составим таблицу, чтобы посмотреть, чем она может быть полезна.

При создании таблицы рекомендуется включать отрицательные значения, положительные значения и ноль, чтобы обеспечить линейную функцию.

Составьте таблицу значений для

f(x)=3x+2f(x)=3x+2f(x)=3x+2

.

Сделать таблицу из двух столбцов. Пометьте столбцы x и f ( x ).

х	ф ( x )

Выберите несколько значений для x и поместите их в отдельные строки в столбце x . Это ВАШ ВЫБОР — нет «правильных» или «неправильных» значений, просто действуйте.

Совет: Всегда полезно включать 0, положительные и отрицательные значения, если это возможно.

х	ф ( x )
−2-2−2
−1-1−1
000
111
333

Оцените функцию для каждого значения x и запишите результат в столбец f ( x ) рядом с использованным значением x .

Когда

x=0x=0x=0

,

f(0)=3(0)+2=2f(0)=3(0)+2=2f(0)=3(0) +2=2

,

f(1)=3(1)+2=5f(1)=3(1)+2=5f(1)=3(1)+2=5

,

f(-1)=3(-1)+2=-3+2=-1f(-1)=3(-1)+2=-3+2=-1f(-1)=3(- 1)+2=-3+2=-1

и т. д.

х	ф ( x )
−2-2−2	−4-4−4
−1-1−1	−1-1−1
000	222
111	555
333	111111

(Обратите внимание, что ваша таблица значений может отличаться от чьей-либо. Каждый из вас может выбрать разные числа для x .)

Теперь, когда у вас есть таблица значений, вы можете использовать ее, чтобы помочь вам нарисовать как форму, так и местоположение функции. Важно: График функции покажет все возможные значения x и соответствующие значения y . Вот почему график представляет собой линию, а не просто точки, составляющие точки в нашей таблице.

График

f(x)=3x+2f(x)=3x+2f(x)=3x+2

.

Используя таблицу значений, которую мы создали выше, вы можете представить f ( x ) как y, каждая строка образует упорядоченную пару, которую вы можете нанести на координатную сетку.

х	ф ( x )
−2-2−2	−4-4−4
−1-1−1	−1-1−1
000	222
111	555
333	111111

Постройте точки.

Поскольку точки лежат на линии, используйте линейку, чтобы провести линию. Попробуйте пройти через каждую точку, не двигая линейку.

Попробуем еще. Прежде чем смотреть ответ, попробуйте сами составить таблицу и нарисовать график на листе бумаги.

В следующем видео мы покажем еще один пример того, как построить график линейной функции на наборе координатных осей.

Эти графики представляют линейную функцию. Помните, что функция — это соответствие между двумя переменными, такими как x и y .

A Общее примечание: линейная функция

Линейная функция — это функция, график которой представляет собой линию. Линейные функции могут быть записаны в виде линии с пересечением наклона

f(x)=mx+bf\left(x\right)=mx+bf(x)=mx+b

где

bbb

 – начальное или начальное значение функции (при вводе

x=0x=0x=0

), а

mmm

 является постоянной скоростью изменения или наклоном функции.