Модуль числа
— Образовательные: Повторить основные понятие по теме «Противоположные числа». Закрепить новое понятие в ходе решения упражнений.
— Развивающие: Совершенствование устной речи учащихся по отработке понятийного аппарата
— Воспитательные: формирование у учащихся внимания и навыков контроля и самоконтроля
Оборудование: интерактивная доска, проектор, ноутбук, индивидуальные карточки, таблица «Модуль числа», электронное приложение к УМК, электронное приложение «Наглядная математика» 6 класс.
• регулятивными УУД: — формулировать вопросы по теме на основе опорных (ключевых и вопросительных) слов,
• познавательными УУД: -выделять и структурировать информацию, существенную для решения проблемы под руководством учителя,
• личностные УУД: -осуществлять рефлексию своего отношения к содержанию темы по заданному алгоритму.
У учащихся недостаточно сформированы: • коммуникативные УУД: — эффективно сотрудничать, осуществляя взаимопомощь и взаимоконтроль.
Цели урока как планируемые результаты обучения, планируемый уровень достижения целей:
Вид планируемых учебных действий | Учебные действия | Планируемый уровень достижения результатов обучения |
Предметные | вводят и определяют понятия «модуль», | 1-2 уровень — понимание, адекватное употребление в речи, выборочно — воспроизведение |
знакомятся со свойствами модуля; отрабатывают умение находить модуль и применять свойства модуля. | 1-2 уровень — понимание, адекватное употребление в речи, выборочно — воспроизведение | |
Регулятивные | • самостоятельно ставят новые учебные задачи путем задавания вопросов о неизвестном | 2 уровень — самостоятельное действие учащихся по заданному алгоритму |
• планируют собственную деятельность, определяют средства для ее осуществления | 2 уровень— совместное с учителем действие учащихся на основе знания видов источников информации и способов работы с ними | |
Познавательные | •извлекают необходимую информацию из прослушанного и прочитанного материала | 2 уровень — самостоятельное выполнение действий в условиях взаимопомощи и взаимоконтроля |
•структурируют информации в виде записи выводов и определений | 2 уровень — совместные действия учащихся в условиях взаимопомощи и взаимоконтроля | |
Коммуникативные | • эффективно сотрудничать и способствовать продуктивной кооперации | 1 уровень — выполнение действий по алгоритму под управлением учителя |
Личностные | умение правильно излагать свои мысли, понимать смысл поставленной задачи, личностная саморегуляция в процессе взаимоконтроля | 2 уровень — самостоятельное выполнение действий с опорой на известный алгоритм |
Этапы урока | Деятельность | |||||||||||||||||||||||||
учителя | учащихся | |||||||||||||||||||||||||
Организационный этап | Учитель приветствует учащихся, проверяет их готовность к уроку. «Я сегодня быстро встал, В школу рано прибежал. Очень я хочу учиться, Не лениться, а трудиться» | 1.Учащиеся готовы к началу работы. Настраиваются на успех. | ||||||||||||||||||||||||
Этап актуализация знаний. | Учитель: Новые знания нам будет очень трудно осваивать без умения быстро и верно считать, поэтому, как всегда, начнем урок с устных заданий: 1. Дан ряд чисел: — 256; 3000; 4 ; -7 ; 0 ; — 19; -1000. — Дать определение положительного числа и выбрать их. — Дать определение отрицательного числа и выбрать их. — Есть ли среда этих чисел противоположные? Дать определение. — К каким числам относится число 0? — Что такое координатная прямая? — Где на координатной прямой расположены положительные числа? Отрицательные? 2. 3. Между какими целыми числами лежит число На каждом уроке вы, ребята, приобретаете новые знания, которые когда-то открыли великие математики. Знания, полученные сегодня, помогут вам в дальнейшем при изучении многих тем не только в курсе математики, но и при изучении нового курса, который называется алгебра. Чтобы узнать тему урока, решите ребус. — Исходя из названия темы, давайте сформулируем цель нашего урока. Модуль числа — Для того чтобы достичь цели урока, какие задачи нам надо поставить? — Где можно узнать информацию по данной теме? | 1. Учащиеся внимательно слушают учителя и отвечают на вопросы: 2. Называют все целые числа, удовлетворяющие условию задания. 3. Называют числа, между которыми лежит число -6целых одна третья. 4. Учащиеся решают ребус и называют тему урока. 5. Учащиеся формулируют цели урока: узнать, что такое модуль; изучить свойства модуля; изучить материал учебника по этой теме; внимательно слушать учителя; делать необходимые записи в тетрадях. 7. Называют источники информации: учебник, учитель. | ||||||||||||||||||||||||
Этап изучение нового материала | Построим координатную прямую; что нужно, чтобы такая прямая существовала? (начало отсчета, положительное направление, единичный отрезок). Задание 1. Отметим на координатной прямой точки А(5), В(2), С(-6), К(-5). Найдем расстояние от начала отсчета до каждой из точки. 9. Модуль числа 1 На электронной доске проектируется таблица с интерактивной моделью Или учитель показывает на таблице, или на доске Для такого расстояния придумано специальное название — модуль. Модулем числа a называют расстояние (в единичных отрезках) от начала координат до точки А(a), изображающей число a. Пишут: |-5|=5; |3|=3, |-7|=7, |-5|=5. Читают: «Модуль числа 3 равен 3. Задание 2. Найдите модули чисел 3; ; 8. , Числа 3; ; 8 — какие? А их модули? Сделайте вывод. (Модуль положительного числа равен самому этому числу, т.е. если a — положительное, то |a|=а). Задание 3. Найдите модули чисел -2; -3; -4 Числа -2; -3; — какие? А их модули? Сделайте вывод. (Модуль отрицательного числа равен числу ему противоположному, т.е. если a — отрицательное, то |a|= — а). А чему равен модуль нуля? |0|=0. (Модуль нуля равен нулю.) Числа 4 и -4; 3 и -3; 2 и -2; 1 и -1 — какие? (противоположные) А модули каждой пары чисел? (равные) Сделайте вывод. (Модули противоположных чисел равны. Модуль любого числа есть число неотрицательное). | 1. Отвечают на вопрос — что нужно, чтобы такая прямая существовала 2. Строят координатную прямую и отмечают на ней точки. 3. Находят расстояние от начала отсчета до каждой точки. Запись учащихся: А(5), ОА=5 В(3), ОВ=3 С(-3), ОС=3 К(-5), ОК=5 Проговариваем: -Точка А с координатой 5, отрезок ОА равен 5 единичным отрезкам 4. 5. Выполняют задание. Делают вывод. Записывают вывод в тетрадь. 6. Выполняют задание. Делают вывод. Записывают вывод в тетрадь. 7. Выполняют задание. Делают вывод. Записывают вывод в тетрадь. | ||||||||||||||||||||||||
Этап первичное осмысление и закрепление знаний | Выполните задание и сделайте взаимопроверку.
| — Учащиеся выполняют работу на индивидуальных карточках, после выполнения проводят взаимопроверку с соседом по столу На доске слайд с ответами | ||||||||||||||||||||||||
Физпауза | Ветер дует нам в лицо, Закачалось деревцо, Ветерок все тише-тише, Деревцо все выше-выше. | Выполняют упражнение стоя, изображая ветер, дерево, становятся на носочки и приседают. | ||||||||||||||||||||||||
Этап закрепление изученного материала | Стр. 48 учебника, найдите и прочитайте правило Читайте внимательно, что нового еще вы узнали? (модуль – это абсолютная величина) Устно № 217 Стр 49 посередине Электронное приложение к учебнику УМК Никольского Вычисли модуль и расшифруй число КОТС | Анализируют текст учебника, выделяют неизвестное. 1. Осмысливают и приступают применять новый способ решения на практике. 2. Делают записи в тетрадь. После выполнения задания сверяют с доской. Один из учеников решает у доски с комментарием. 3.Решают самостоятельно, сверяют с доской. | ||||||||||||||||||||||||
Этап подведение итогов. Домашнее задание. | -Наш урок подходит к концу, сначала запишем домашнее задание, затем подведем итоги. — На доске: Домашнее задание: п. 2.2, выучить правила. № 218, №222, № 223. — А теперь подведем итоги: Что мы хотели узнать? Что мы узнали? На все ли вопросы мы получили ответы? — Давайте еще раз вспомним определение модуля, свойства модуля Слайд рефлексия «Сегодня на уроке я узнал…» — Итог урока каждый из вас подведет с помощью телеграммы; то есть в виде одного краткого предложения, которое выразит ваше отношение к уроку. Если останется время закончить одно из предложений письменно. Всем спасибо! | 1. Ребята записывают домашнее задание в дневниках. 2. Просматривают домашнее задание, задают вопросы 3. Проводят самоанализ, отвечают на вопросы; вспоминают правила; определение модуля, свойства модуля. 4. В конце своей работы каждый ученик пишет телеграмму. По желанию зачитывают на весь класс | ||||||||||||||||||||||||
Модуль числа. Исследовательская работа по математике
Похожие презентации:
Элементы комбинаторики ( 9-11 классы)
Применение производной в науке и в жизни
Проект по математике «Математика вокруг нас.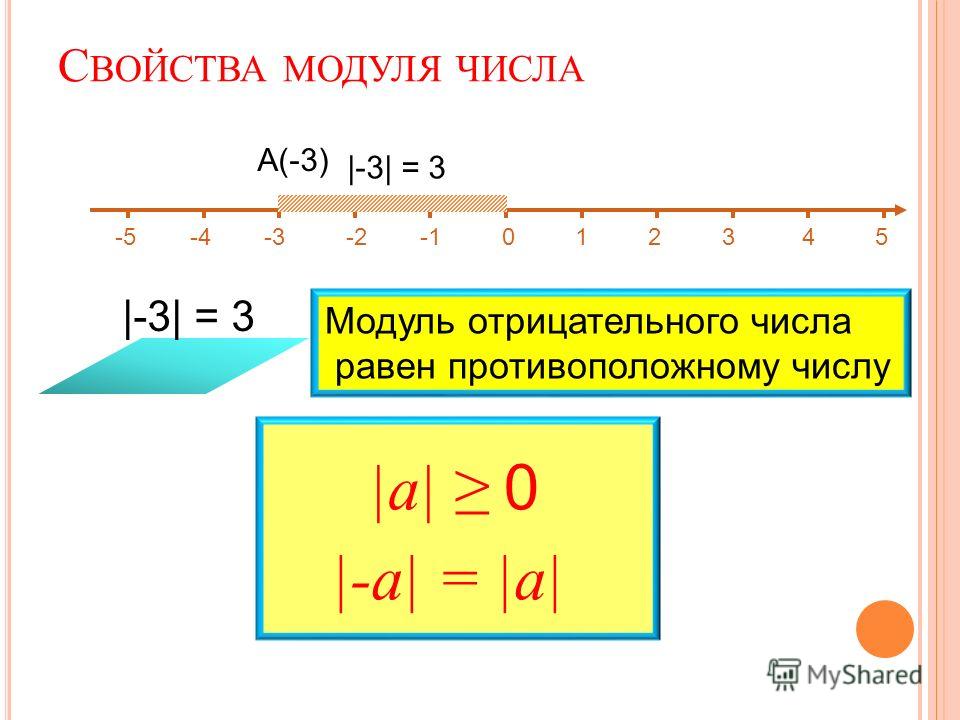 Узоры и орнаменты на посуде»
Узоры и орнаменты на посуде»
Знакомство детей с математическими знаками и монетами
Тренажёр по математике «Собираем урожай». Счет в пределах 10
Методы обработки экспериментальных данных
Лекция 6. Корреляционный и регрессионный анализ
Решение задач обязательной части ОГЭ по геометрии
Дифференциальные уравнения
Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи
МКОУ «Осыпнобугорская СОШ»
Ученица
7 а класса
Лукманова
Регина
2. Исследовательская работа по математике
3. Ц Е Л Ь:
изучение понятия модуля,применение определения модуля
при выполнении задач
4. З А Д А Ч И
ЗАДАЧИразвивать умение применять теоретический
материал при решении практических задач;
развивать интерес к предмету через поиск задач по
данной теме;
расширить математический кругозор ;
приобрести навыки исследовательской работы.
5. Значимость и актуальность работы:
Задачи, связанные сабсолютной
величиной, часто
встречаются на
математических
олимпиадах и
вступительных
экзаменах.

Понятие модуля
широко
применяется в
различных
разделах
школьного курса
математики.
6. Методы исследования:
• Исследованиелитературы по теме.
• Проведение поиска
задач по теме.
7. ПОНЯТИЕ МОДУЛЯ
Понятие абсолютнойвеличины (модуля) –
существенная характеристика
числа .
Модулем числа называют расстояние от
точки, изображающей число на
координатной прямой до начала отсчета.
8. МОДУЛЬ ЧИСЛА
Модуль (modulus) впереводе с латинского
языка означает “мера,
размер”.
Термин “модуль” ввёл в
1806 г. французский
математик Жорж
Аргон.
9. Геометрический смысл модуля
Модулем числа а называют расстояние (в единичныхотрезках) от начала координат до точки А(а).
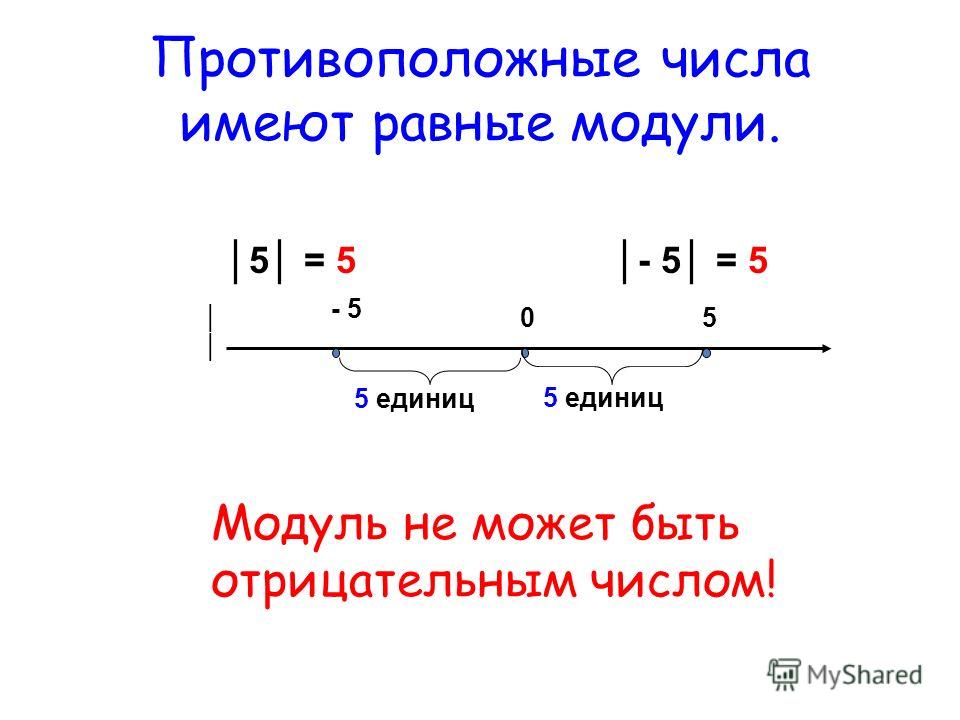
|5| = 5
|-6| = 6
10. Доказательство теоремы
ТеоремаАбсолютная величина действительного числа a ≠ 0
равна большему из двух чисел a или -a.
Доказательство:
1. Если число a положительно, то -a отрицательно, т.
 е.
е.-a < 0 < a. Отсюда следует, что -a < a.
Например, число 5 положительно, тогда
-5 – отрицательно и -5 < 0 < 5, отсюда -5 < 5.
В этом случае |a| = a, т.е. |a| совпадает с большим из
двух чисел a и — a.
2. Если a отрицательно, тогда -a положительно и a < — a,
т. е. большим числом является -a. По определению, в
этом случае, |a| = -a — равно большему из двух чисел -a и
a.
11. Алгоритм нахождения модуля числа БЛОК-СХЕМА
12. Отработка алгоритма
13. РАЗМИНКА
• Запишите число,противоположное данному:
-4
+3
6,3
4
-3
-6,3
Найдите модуль каждого
из чисел:
|- 6 |
| 9 |
| — 5 |
| 0 |
|0,8 |
Найти расстояние от М
(-7) и N(6) до начала
отчета на
координатной прямой
15. Решение задач, содержащих модуль числа
Основной прием –В некоторых случаях
раскрытие знака модуля
модуль раскрывается
в соответствии с его
однозначно:
свойствами.

|x2 + y2| = x2 + y2
так как x2 + y2 ≥ 0 при
любых х и у.
|–z2 – 1| = z2 + 1
–z2 – 1 < 0 при любых z.
16. Способы решения задач, содержащих модуль
алгебраический,графический,
последовательное
раскрытие модулей,
метод интервалов.
17. РЕШЕНИЕ УРАВНЕНИЙ
Решить уравнение |x| = 3. Решить уравнение.|x — 3| = 4.Мы видим, что на
Это уравнение можно
числовой прямой есть две прочитать так: расстояние от
точки, расстояние от
точки до точки равно 4. С
которых до нуля равно
помощью графического
трём. Это точки 3 и -3.
метода можно определить, что
Значит, уравнение |x| = 3
уравнение имеет два решения:
имеет два решения:
— 1 и 7.
x = 3 и x = -3.
18. РЕШЕНИЕ НЕРАВЕНСТВ
Решить неравенство:|x + 7| < 4.
Можно прочитать как:
расстояние от точки до
точки меньше четырёх.
Ответ: (-11; -3).
Решить неравенство:
|10 — x| ≥ 7.
Расстояние от точки 10
до точки х больше или
равно семи.

Ответ: (-∞; 3] U [17, +∞)
19. График функции y = |x|
Для x ≥ 0 имеем y = x.Для x < 0 имеем y =
-x.
20. ЗАКЛЮЧЕНИЕ
В результате работы я:повторила школьный материал по данной теме,
изучила решение уравнений и неравенств,
содержащих знак модуля.,
научилась строить график функции вида y = |x|,
различного уровня сложности, а также
олимпиадные и экзаменационные задачи.
English Русский Правила
Ошибка
From Academic Kids
Запрошенный заголовок страницы недействителен, пуст или неправильно связанный межъязыковой или межвики-заголовок.
Вернуться на главную страницу.
Навигация
Академическое детское меню
- Искусство и культура
- Искусство ( http://www.academickids.com/encyclopedia/index.php/Art )
- Архитектура ( http://www.academickids.com/encyclopedia/index.php/Architecture )
- Культуры ( http://www.
 academickids.com/encyclopedia/index.php/Cultures )
academickids.com/encyclopedia/index.php/Cultures ) - Музыка ( http://www.academickids.com/encyclopedia/index.php/Music )
- Музыкальные инструменты ( http://academickids.com/encyclopedia/index.php/List_of_musical_instruments )
- Биографии ( http://www.academickids.com/encyclopedia/index.php/Biographies )
- Клипарт ( http://www.academickids.com/encyclopedia/index.php/Clipart )
- География ( http://www.academickids.com/encyclopedia/index.php/Geography )
- Страны мира ( http://www.academickids.com/encyclopedia/index.php/Countries )
- Карты ( http://www.academickids.com/encyclopedia/index.php/Maps )
- Флаги ( http://www.academickids.com/encyclopedia/index.php/Flags )
- Континенты ( http://www.academickids.com/encyclopedia/index.php/Continents )
- История ( http://www.
 academickids.com/encyclopedia/index.php/History )
academickids.com/encyclopedia/index.php/History )- Древние цивилизации ( http://www.academickids.com/encyclopedia/index.php/Ancient_Civilizations
- Промышленная революция ( http://www.academickids.com/encyclopedia/index.php/Industrial_Revolution )
- Средневековье ( http://www.academickids.com/encyclopedia/index.php/Middle_Ages )
- Предыстория ( http://www.academickids.com/encyclopedia/index.php/Prehistory )
- Ренессанс ( http://www.academickids.com/encyclopedia/index.php/Renaissance )
- Хронология ( http://www.academickids.com/encyclopedia/index.php/Timelines )
- США ( http://www.academickids.com/encyclopedia/index.php/United_States )
- Войны ( http://www.academickids.com/encyclopedia/index.php/Wars )
- Всемирная история ( http://www.academickids.com/encyclopedia/index.php/History_of_the_world )
- Древние цивилизации ( http://www.academickids.com/encyclopedia/index.php/Ancient_Civilizations
- Тело человека ( http://www.
 academickids.com/encyclopedia/index.php/Human_Body )
academickids.com/encyclopedia/index.php/Human_Body ) - Математика ( http://www.academickids.com/encyclopedia/index.php/Mathematics )
- Ссылка ( http://www.academickids.com/encyclopedia/index.php/Reference )
- Наука ( http://www.academickids.com/encyclopedia/index.php/Science )
- Животные ( http://www.academickids.com/encyclopedia/index.php/Animals )
- Авиация ( http://www.academickids.com/encyclopedia/index.php/Aviation )
- Динозавры ( http://www.academickids.com/encyclopedia/index.php/Dinosaurs )
- Земля ( http://www.academickids.com/encyclopedia/index.php/Earth )
- Изобретения ( http://www.academickids.com/encyclopedia/index.php/Inventions )
- Физические науки ( http://www.academickids.com/encyclopedia/index.php/Physical_Science )
- Растения (
- Ученые ( http://www.
 academickids.com/encyclopedia/index.php/Scientists )
academickids.com/encyclopedia/index.php/Scientists )
- Социальные науки ( http://www.academickids.com/encyclopedia/index.php/Social_Studies )
- Антропология ( http://www.academickids.com/encyclopedia/index.php/Anthropology )
- Экономика ( http://www.academickids.com/encyclopedia/index.php/Economics )
- Правительство ( http://www.academickids.com/encyclopedia/index.php/Government )
- Религия ( http://www.academickids.com/encyclopedia/index.php/Religion )
- Праздники ( http://www.academickids.com/encyclopedia/index.php/Holidays )
- Космос и астрономия
- Солнечная система ( http://www.academickids.com/encyclopedia/index.php/Solar_System )
- Планет ( http://www.academickids.com/encyclopedia/index.php/Planets )
- Спорт ( http://www.academickids.com/encyclopedia/index.php/Sports )
- Хронология ( http://www.
 academickids.com/encyclopedia/index.php/Timelines )
academickids.com/encyclopedia/index.php/Timelines ) - Погода ( http://www.academickids.com/encyclopedia/index.php/Weather )
- Штаты США ( http://www.academickids.com/encyclopedia/index.php/US_States )
Информация
- Домашняя страница ( http://academickids.com/encyclopedia/index.php )
- Свяжитесь с нами ( http://www.academickids.com/encyclopedia/index.php/Contactus )
- Картинки ( http://classroomclipart.com )
Search
Набор инструментов
- Специальные страницы
Персональные инструменты
Математический модуль Python
Некоторые из самых популярных математических функций определены в математическом модуле. К ним относятся тригонометрические функции, функции представления, логарифмические функции, функции преобразования углов и т. д. Кроме того, в этом модуле также определены две математические константы.
Пи — известная математическая константа, которая определяется как отношение длины окружности к диаметру круга и имеет значение 3,141592653589793.
>>> импортировать математику >>>math.pi 3.141592653589793
Другая известная математическая константа, определенная в математическом модуле, — e . Оно называется числом Эйлера и является основанием натурального логарифма. Его значение равно 2,718281828459.045.
>>> импортировать математику >>> math.e 2,718281828459045
Математический модуль содержит функции для вычисления различных тригонометрических соотношений для заданного угла. Функциям (sin, cos, tan и т. д.) в качестве аргумента требуется угол в радианах.
Мы, с другой стороны, привыкли выражать угол в градусах. В математическом модуле представлены две функции преобразования углов: градусов() и радиан() , чтобы преобразовать угол из градусов в радианы и наоборот. Например, следующие операторы преобразуют угол 30 градусов в радианы и обратно (Примечание: π радиан эквивалентно 180 градусам).
Например, следующие операторы преобразуют угол 30 градусов в радианы и обратно (Примечание: π радиан эквивалентно 180 градусам).
>>> импортировать математику >>> мат.радианы(30) 0,5235987755982988 >>> math.степени(math.pi/6) 29,999999999999996
Следующие утверждения показывают 9Соотношения 0269 sin, cos и tan
>>> импортировать математику >>> math.sin(0.5235987755982988) 0,49999999999999994 >>> math.cos(0.5235987755982988) 0,8660254037844387 >>> math.tan(0.5235987755982988) 0,5773502691896257
Вы можете вспомнить, что sin(30)=0,5 , cos(30)=32 (что равно 0,8660254037844387 ) и tan(30)= 13 (что равно 0, 5773502691896257 ).
мат.лог()
Метод math. возвращает натуральный логарифм заданного числа. Натуральный логарифм рассчитывается по основанию  log()
log() e .
>>> импортировать математику >>>math.log(10) 2.302585092994046
мат.log10()
Метод math.log10() возвращает логарифм заданного числа по основанию 10. Он называется стандартным логарифмом.>>> импортировать математику >>>math.log10(10) 1,0
мат.выражение()
math.exp() 9Метод 0270 возвращает число с плавающей запятой после возведения e в степень заданного числа.
Другими словами, exp(x) дает e**x .
>>> импортировать математику >>>math.exp(10) 22026.465794806718
Это можно проверить с помощью оператора экспоненты.
>>> импортировать математику >>>math.

 И обращает внимание учащихся на доску, на которой написаны следующие слова:
И обращает внимание учащихся на доску, на которой написаны следующие слова: Назовите все целые числа, которые лежат между числами -2 и 3.
Назовите все целые числа, которые лежат между числами -2 и 3.
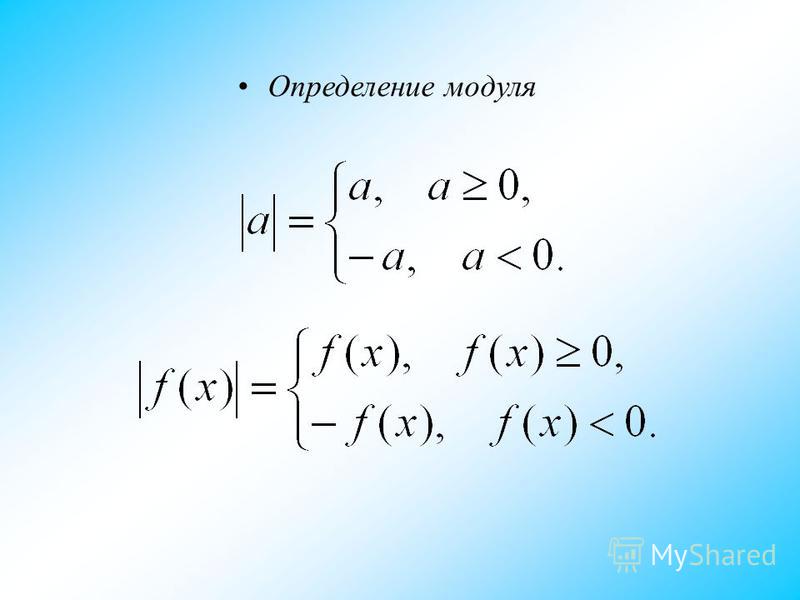 Модуль числа -7 равен 7 и т.д. «.
Модуль числа -7 равен 7 и т.д. «.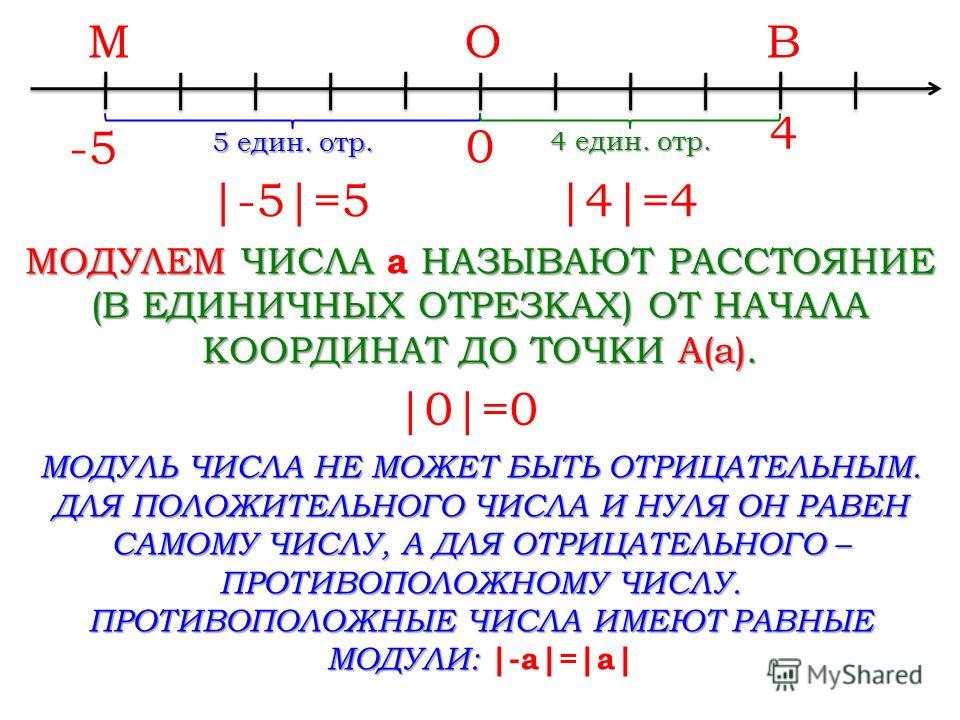 Записывают в тетрадь определение модуля.
Записывают в тетрадь определение модуля.

 academickids.com/encyclopedia/index.php/Cultures )
academickids.com/encyclopedia/index.php/Cultures ) academickids.com/encyclopedia/index.php/History )
academickids.com/encyclopedia/index.php/History ) academickids.com/encyclopedia/index.php/Human_Body )
academickids.com/encyclopedia/index.php/Human_Body ) academickids.com/encyclopedia/index.php/Scientists )
academickids.com/encyclopedia/index.php/Scientists ) academickids.com/encyclopedia/index.php/Timelines )
academickids.com/encyclopedia/index.php/Timelines )