Модуль суммы меньше суммы модулей: Лекции по алгебре

Содержание

Лекции по алгебре

ПРЕДИСЛОВИЕ
ГЛАВА I. ЦЕЛЫЕ ЧИСЛА
§ 1. Теория делимости целых чисел
2. Деление с остатком.
3. Наибольший общий делитель.
4. Алгоритм Евклида.
5. Взаимно простые числа.
6. Простые числа.
§ 2. Теория сравнений
2. Действия над классами.
3. Приведенная система вычетов и примитивные классы.
§ 3. Некоторые общие понятия алгебры
2. Кольца и поля.
3. Изоморфизм.
ГЛАВА II. КОМПЛЕКСНЫЕ ЧИСЛА
§ 1. Обоснование комплексных чисел
3. Свойства действий.
4. Возвращение к обычной форме записи.
5. Вычитание и деление комплексных чисел.
§ 2. Тригонометрическая форма комплексного числа
2. Модуль и аргумент комплексного числа.
3. Тригонометрическая запись комплексного числа.
4. Неравенства для модуля суммы и модуля разности двух комплексных чисел.

5. Умножение комплексных чисел в тригонометрической записи.
6. Возведение комплексного числа в степень с целым показателем и формула Муавра.
7. Применения формулы Муавра к преобразованиям тригонометрических выражений.
§ 3. Извлечение корня из комплексного числа
2. Исследование формулы извлечения корня.
3. Извлечение квадратного корня.
§ 4. Корни из единицы
§ 5. Показательная и логарифмическая функции комплексной переменной
ГЛАВА III. ПРОСТЕЙШИЕ СВЕДЕНИЯ ОБ АЛГЕБРЕ ПОЛИНОМОВ
§ 1. Полиномы от одной буквы
2. Высший член и степень полинома.
3. Степени элемента в ассоциативном кольце.
4. Значение полинома.
5. Схема Хорнера и теорема Безу.
6. Число корней полинома в коммутативной области целостности.
7. Теорема о тождестве.
§ 2. Алгебраическое решение уравнений третьей и четвертой степени
2. Исследование формулы Кардано.
3. Решение уравнений четвертой степени.
§ 3. Полиномы от нескольких букв

3. Теорема о тождестве.

4. Теорема о несущественности алгебраических неравенств.
ГЛАВА IV. МАТРИЦЫ И ОПРЕДЕЛИТЕЛИ
§ 1. Матрицы и действия над ними
2. Сложение матриц и умножение матрицы на число.
3. Умножение матриц.
4. Транспонирование матриц.
5. Обзор действий над матрицами.
§ 2. Теория определителей
2. Элементарные сведения теории перестановок.
3. Определитель порядка n. Определение.
4. Свойства определителя.
5. Алгебраические дополнения и миноры.
6. Вычисление определителей.
7. Определитель Вандермонда.
9. Некоторые следствия из теоремы Крамера.
§ 3. Линейная зависимость и линейная независимость строк (столбцов)
2. Линейные зависимости столбцов матрицы с линейно зависимыми строками.
3. Теорема о линейной зависимости линейных комбинаций.
4. Базис и ранг совокупности строк.
5. Линейно эквивалентные совокупности строк.
6. Ранг матрицы.
7. Условие линейной зависимости множества строк квадратной матрицы.
8. Ранг матрицы в терминах определителей.

9. Определение ранга матрицы при помощи элементарных преобразований.
§ 4. Системы линейных уравнений общего вида
§ 5. Дальнейшие свойства определителей
2. Умножение матриц, разбитых на клетки.
3. Умножение матрицы на вспомогательную матрицу как линейное преобразование строк (столбцов).
4. Определитель произведения двух квадратных матриц.
5. Примеры применения теоремы об определителе произведения квадратных матриц к вычислению определителей.
6. Теорема Бине — Коши.
§ 6. Обращение квадратных матриц
§ 7. Характеристический полином матрицы
2. Теорема Кэли—Гамильтона.
ГЛАВА V. КВАДРАТИЧНЫЕ ФОРМЫ
§ 1. Преобразование квадратичной формы к каноническому виду линейной подстановкой букв

§ 2. Закон инерции квадратичных форм
2. Критерий Сильвестра положительности квадратичной формы.
3. Закон инерции квадратичных форм.
§ 3. Ортогональное преобразование квадратичной формы к каноническому виду
2. Собственные значения вещественной симметричной матрицы.

3. Построение ортогональных матриц.
4. Ортогональное преобразование квадратичной формы к каноническому виду.
5. Коэффициенты канонического вида квадратичной формы и столбцы преобразующей ортогональной матрицы.
6. Одновременные преобразования двух квадратичных форм к каноническому виду.
§ 4. Эрмитовы формы
2. Свойства эрмитовых форм.
ГЛАВА VI. ПОЛИНОМЫ И ДРОБИ
§ 1. Теория делимости для полиномов от Одной буквы
§ 2. Производная
2. Разложение полинома по степеням линейного двучлена.
3. Разделение множителей различной кратности.
§ 3. Рациональные дроби
2. Поле частных.
3. Правильные рациональные дроби.
4. Разложение рациональной дроби на простейшие.
5. Разложение рациональной дроби на простейшие над полем С комплексных чисел.
6. Разложение рациональной дроби на простейшие над полем R вещественных чисел.
7. Разложение на простейшие правильной рациональной дроби, знаменатель которой разложен на попарно простые линейные множители.

§ 4. Интерполяция
2. Интерполяционная формула Лагранжа.
3. Способ интерполяции Ньютона.
4. Приближенная интерполяция.
ГЛАВА VII. СРАВНЕНИЯ В КОЛЬЦЕ ПОЛИНОМОВ И РАСШИРЕНИЯ ПОЛЕЙ
§ 1. Сравнения в кольце полиномов над полем
§ 2. Расширение полей
2. Конструирование простых расширений.
ГЛАВА VIII. ПОЛИНОМЫ С ЦЕЛЫМИ КОЭФФИЦИЕНТАМИ. ПОЛИНОМЫ НАД ФАКТОРИАЛЬНЫМИ КОЛЬЦАМИ
§ 1. Полиномы с целыми коэффициентами

§ 2. Полиномы от одной буквы над факториальным кольцом
ГЛАВА IX. РАСПРЕДЕЛЕНИЕ КОРНЕЙ ПОЛИНОМА
§ 1. Существование корней в С
§ 2. Распределение корней на плоскости комплексной переменной
2. Принцип аргумента.
3. Теорема Руше.
4. Непрерывность корней полинома.
§ 3. Распределение вещественных корней полинома с вещественными коэффициентами
2. Теорема Штурма.
3. Построение ряда Штурма.
§ 4. Обобщенная теорема Штурма
§ 5. Приближенное вычисление корней полинома
2. Метод непрерывных дробей.
ГЛАВА X. ЭЛЕМЕНТЫ ТЕОРИИ ГРУПП
§ 2.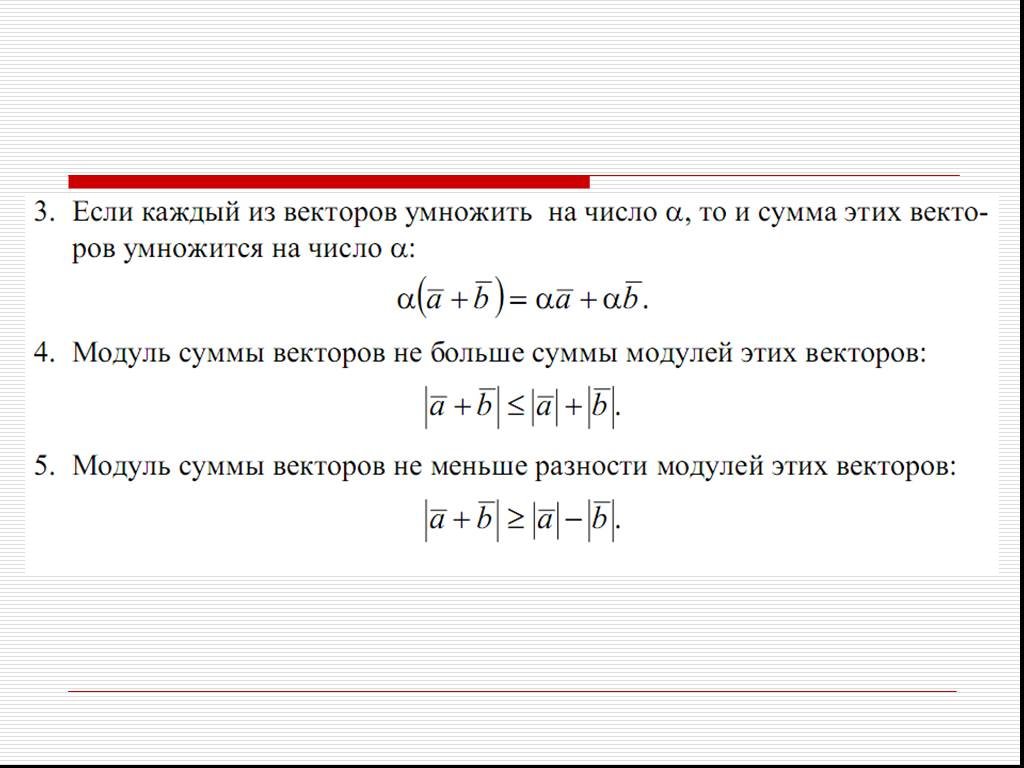

Нормальные подгруппы и факторгруппы
§ 3. Гомоморфизм
§ 4. Прямое произведение групп
§ 5. Группы преобразований
2. Классы сопряженных элементов.
3. Строение однородных пространств.
4. К теории подстановок.
5. Примеры из геометрии.
6. Централизатор элемента и нормализатор подгруппы.

7. Центр p-группы.
8. Преобразования.
9. Автоморфизмы группы.
§ 6. Свободная группа
§ 7. Свободные произведения групп
§ 8. Конечные абелевы группы
§ 9. Конечно порожденные абелевы группы
ГЛАВА XI. СИММЕТРИЧЕСКИЕ ПОЛИНОМЫ
§ 1. Выражение симметрических пэлииов через основные
§ 2. Значения симметрических полиномов от корней полинома
2. Степенные суммы.
3. Дискриминант полинома.
4. Алгебраическое решение уравнений третьей и четвертой степени в свете теории симметрических полиномов.
§ 3. Результант
2. Другой способ построения результанта.
3. Линейное представление результанта.
4. Применение результанта к исключению неизвестного из системы двух алгебраических уравнений с двумя неизвестными.

5. Связь дискриминанта полинома с результантом полинома и его производной.
ГЛАВА XII. ВЕКТОРНЫЕ ПРОСТРАНСТВА

2. Линейные комбинации, линейная зависимость и линейная независимость.
3. Координаты вектора.
4. Замена базиса и преобразование координат.
§ 2. Подпространства
3. Прямая сумма подпространств.
4. Относительная линейная независимость и относительный базис.
5. Факторпространство.
§ 3. Линейные функции
§ 4. Линейные отображения векторных пространств
§ 5. Линейные операторы в векторном пространстве
2. Действия над операторами.
3. Инвариантные подпространства.
4. Циклическое подпространство и минимальный аннулятор вектора.
5. Матрица оператора на циклическом подпространстве и ее характеристический полином.
6. Минимальный полином оператора.
7. Разложение пространства с оператором в прямую сумму примарных подпространств.
8. Разложение примарного пространства в прямую сумму циклических примарных подпространств.
9.

Модули над кольцом главных идеалов.
10. Некоторые следствия.
11. Каноническая форма матрицы оператора.
12. Оператор проектирования.
13. Полуобратные линейные отображения.
§ 6. Операторы в векторных пространствах над полем С комплексных чисел
2. Корневые векторы.
3. Нильпотентный оператор.
4. Каноническая форма Жордана матрицы оператора.
5. Пример.
§ 7. Операторы в векторных пространствах над полем R вещественных чисел
ГЛАВА XIII. ЕВКЛИДОВО И УНИТАРНОЕ ПРОСТРАНСТВА
1. Скалярное произведение.
§ 2. Подпространства унитарного (или евклидова) пространства
§ 3. Пространства, сопряженные с евклидовым и унитарным пространствами
§ 4. Операторы в унитарном пространстве
§ 5. Операторы в евклидовом пространстве
§ 6. Преобразование уравнения гиперповерхности второго порядка к каноническому виду
§ 7. Линейные отображения унитарного пространства в унитарное
§ 8. Объем параллелепипеда в евклидовом пространстве

ГЛАВА XIV. ЭЛЕМЕНТЫ АЛГЕБРЫ ТЕНЗОРОВ
§ 2.

Действия над тензорами
§ 3. Симметричные и антисимметричные тензоры
§ 4. Тензорные произведения векторных пространств
ГЛАВА XV. АЛГЕБРЫ
1. Определение и простейшие свойства алгебр.
2. Структурные константы алгебры.
3. Некоторые классы алгебр.
4. Идеалы алгебры.
5. Присоединение единицы.
6. Вложение ассоциативной алгебры в алгебру матриц.
§ 2. Алгебра кватернионов
§ 3. Внешняя алгебра
СПИСОК ЛИТЕРАТУРЫ

Основные свойства модуля действительного числа

Password recovery

Восстановите свой пароль

Ваш адрес электронной почты

MicroExcel.ru Математика Алгебра Основные свойства модуля действительного числа

Ниже представлены основные свойства модуля действительного числа (т.е. положительного, отрицательного и нуля).

Свойство 1
Свойство 2
Свойство 3
Свойство 4
Свойство 5
Свойство 6
Свойство 7
Свойство 8

Свойство 1

Модуль числа представляет собой расстояние, которое не может быть отрицательным. Следовательно, и модуль не может быть меньше нуля.

|a| ≥ 0

Свойство 2

Модуль положительного числа равняется этому же числу.

|a| = a, при a > 0

Свойство 3

Модуль отрицательного числа равняется этому же числу, но с противоположным знаком.

|-a| = a, при a < 0

Свойство 4

Модуль числа ноль равняется нулю.

|a| = 0, при a = 0

Свойство 5

Модули противоположных чисел равны между собой.

|-a| = |a| = a

Свойство 6

Модуль числа a – это квадратный корень из a².

Свойство 7

Модуль произведения равняется произведению модулей чисел.

|ab| = |a| ⋅ |b|

Свойство 8

Модуль частного равняется делению одного модуля на другой.

|a : b| = |a| : |b|

ЧАЩЕ ВСЕГО ЗАПРАШИВАЮТ

Таблица знаков зодиака

Нахождение площади трапеции: формула и примеры

Нахождение длины окружности: формула и задачи

Римские цифры: таблицы

Таблица синусов

Тригонометрическая функция: Тангенс угла (tg)

Нахождение площади ромба: формула и примеры

Нахождение объема цилиндра: формула и задачи

Тригонометрическая функция: Синус угла (sin)

Геометрическая фигура: треугольник

Нахождение объема шара: формула и задачи

Тригонометрическая функция: Косинус угла (cos)

Нахождение объема конуса: формула и задачи

Таблица сложения чисел

Нахождение площади квадрата: формула и примеры

Что такое тетраэдр: определение, виды, формулы площади и объема

Нахождение объема пирамиды: формула и задачи

Признаки подобия треугольников

Нахождение периметра прямоугольника: формула и задачи

Формула Герона для треугольника

Что такое средняя линия треугольника

Нахождение площади треугольника: формула и примеры

Нахождение площади поверхности конуса: формула и задачи

Что такое прямоугольник: определение, свойства, признаки, формулы

Разность кубов: формула и примеры

Степени натуральных чисел

Нахождение площади правильного шестиугольника: формула и примеры

Тригонометрические значения углов: sin, cos, tg, ctg

Нахождение периметра квадрата: формула и задачи

Теорема Фалеса: формулировка и пример решения задачи

Сумма кубов: формула и примеры

Нахождение объема куба: формула и задачи

Куб разности: формула и примеры

Нахождение площади шарового сегмента

Что такое окружность: определение, свойства, формулы

Любое комплексное число можно записать в виде суммы комплексных чисел по модулю 1?

Задавать вопрос

спросил 9 лет, 6 месяцев назад

Изменено 9 лет, 6 месяцев назад

Просмотрено 334 раза

$\begingroup$

Я нашел эту задачу в учебнике, решения не предложил. Мне любопытно, потому что это кажется очень интересным результатом. Полное утверждение:

Пусть $M \subseteq \mathbb{C}$, набор со следующими свойствами:
1. если $x\in{\mathbb{C}}$ с $|x|=1$, тогда $x \in{M}$
2. если $x=a_1+a_2$ и $a_1,a_2 \in{M}$, то $x \in{M}$

Покажите, что $M=\mathbb {С} $.

Приветствуются любые предложения, заранее спасибо 🙂

комплексные числа

9{я(\фи-\тета)}. $$

$\endgroup$

$\begingroup$

Думай геометрически. Начните с любой точки комплексной плоскости и нарисуйте окружность единичного радиуса с центром в вашей точке. Выберите точку на окружности ближе к началу координат и используйте ее в качестве центра другой единичной окружности. Повторяйте этот процесс, пока не получите цепочку единичных окружностей, последняя из которых пересекает единичную окружность с центром в начале координат.

Теперь соедините центры этих окружностей от начала координат до вашей точки. Вуаля. Ваше комплексное число выставляется как сумма комплексных чисел по модулю единицы.

$\endgroup$

$\begingroup$

Геометрически равно тому, что между любыми двумя точками на плоскости можно провести цепочку из окружностей единичного радиуса, центр каждой из которых находится на окружности предыдущей. В конце концов они должны пересечься. Плоскость становится диаграммой Аргана.

Предположим, вы начинаете с точки $a+bi$. Можно нарисовать окружность, чтобы найти новую точку $a-1 + bi$, и постоянно уменьшать действительную и мнимую составляющие до значения, меньшего единицы. Тогда имеется точка $A+Bi$, лежащая в единичной окружности. Окружность, проведенная вокруг этой точки, пересечет единичную окружность в точке $c+di$. Окружность, проведенная в точке $c+di$, пройдет через точку $A+Bi$, и по цепочке можно будет вернуться к точке $a+bi$.

$\endgroup$

Как найти модуль комплексного числа

Как найти модуль комплексного числа

Как найти модуль комплексного числа?

Пусть z = a + ib — комплексное число.

Модуль или абсолютное значение z, обозначаемое | г | определяется как

Модуль свойств комплексных чисел

Свойство 1 :

Модули суммы двух комплексных чисел всегда меньше или равны сумме их модулей.

Приведенное выше неравенство может быть немедленно распространено по индукции на любое конечное число комплексных чисел, т. е. для любых n комплексных чисел z ₁ , z ₂ , z ₃ , …, z _n

90 002 |г ₁ + z ₂ + z ₃ + … + zn | ≤ | я ₁ | + | я ₂ | + … + | я _н |

Свойство 2 :

Модуль разности двух комплексных чисел всегда больше или равен разности их модулей.

Свойство 3 :

Модуль произведения двух комплексных чисел равен произведению их модулей.

Свойство 4 :

Модуль отношения двух комплексных чисел равен отношению их модулей.

Давайте рассмотрим несколько примеров, основанных на приведенной выше концепции.

Пример 1:

Найдите модуль следующего комплексного числа

− 2 + 4i

Решение:

Пусть z = -2 + 4i

|z| = √(-2 + 4i)

|z| = √(-2) ² + 4 ²

= √4 + 16

= √20

Разложив число внутри корня, получим

90 002 = √(2 ⋅ 2 ⋅ 5)

= 2√5

Пример 2:

Найдите модуль следующего комплексного числа

2 − 3i

Решение: 900 03

Пусть z = 2 − 3i

|з| = √(2 — 3i)

|z| = √2 ² + (-3) ²

= √4 + 9

= √13

Пример 3 : 900 03

Найдите модуль следующего комплексного числа

− 3 − 2i

Решение:

Пусть z = − 3 − 2i

|z| = √(− 3 − 2i)

|z| = √(-3) ² + (-2) ²

= √9 + 4

= √13

Пример 4 :

Найдите модуль следующего комплексного числа

4 + 3i

Решение:

Пусть z = 4 + 3i

|z| = √(4 + 3i)

|z| = √4 ² + 3 ²

= √16 + 9

= √25

Разложив число внутри корня, получим

900 02 = √(5 ⋅ 5)

= √5

Давайте рассмотрим следующий пример «Как найти модуль комплексного числа».

Пример 5:

Найдите модуль или абсолютное значение

[(1 + 3i) (1 — 2i)] / (3 + 4i)

Решение:

900 02 |[(1 + 3i ) (1 — 2i)] / (3 + 4i) | = |(1 + 3i) (1 — 2i)| / |3 + 4i|

= |(1 + 3i)| |(1 — 2i)| / |3 + 4i|

= √(1 ² + 3 ² ) √(1 ² + (-2) ² ) / √3 ² + 4 ²

= ( √(1 + 9 ) √(1 + 4)) / √(9+ 16)

= ( √10 √5) / √25

= √50 / √25 = 5√2/5 = √2 90 003

Модуль суммы меньше суммы модулей: Лекции по алгебре

Лекции по алгебре

Оглавление

Основные свойства модуля действительного числа

Свойство 1

Свойство 2

Свойство 3

Свойство 4

Свойство 5

Свойство 6

Свойство 7

Свойство 8

ЧАЩЕ ВСЕГО ЗАПРАШИВАЮТ

Любое комплексное число можно записать в виде суммы комплексных чисел по модулю 1?

Как найти модуль комплексного числа

Модуль свойств комплексных чисел

Похожие темы

Добавить комментарий Отменить ответ