Определитель матрицы второго и третьего порядков и правила вычисления
Матрица содержит в себе векторы-столбцы. Они по-разному ориентированы в пространстве. Характеристикой этого расположения и того матричного преобразования, которое может дать матрица, выступает определитель матрицы.
Содержание
Определитель матрицы 2×2
Пусть дана квадратная матрица второго порядка:
A=\begin{pmatrix} a_{11}& a_{12}\\ a_{21}& a_{22} \end{pmatrix}
Определителем (или детерминантом) второго порядка, соответствующим данной матрице, называется число a_{11}a_{22}-a_{12}a_{21}.
Определитель второго порядка записывается так:
detA=\begin{vmatrix} a_{11}& a_{12}\\ a_{21}& a_{22} \end{vmatrix}=a_{11}a_{22}-a_{12}a_{21}
Геометрический смысл определителя
Если нам дана квадратная матрица
A=\begin{pmatrix} a_{11}& a_{12}\\ a_{21}& a_{22} \end{pmatrix}
То первый столбец дает нам координаты одного вектора, а второй столбец чисел — координаты второго вектора.
Начало данных векторов — в точке начала координат.
Тогда определитель матрица дает нам площадь параллелограмма, построенного на данных векторах.
Рассмотрим на примере
Пусть нам дана матрица с координатами:
A=\begin{pmatrix} 3& 1\\ 1& 2 \end{pmatrix}
Нарисуем координатную плоскость и отметим на ней данные векторы.
Векторы и
Где у вектора \overline{a} координаты (3; 1), а у вектора \overline{b} координаты (2; 1).
Теперь построим на этих векторах параллелограмм, считая, что векторы a и b его стороны. Получим:
Параллелограмм на векторах и
Площадь данного параллелограмма и будет являться определителем матрицы. Площадь данного параллелограмма S_{ABCD}=5. И определитель матрицы:
detA=\begin{vmatrix} 3& 1\\ 1& 2 \end{vmatrix}=3 \cdot 2-1 \cdot 1=6-1=5
Однако, обычно в линейной алгебре говорят не о площади параллелограмма, а о матричном преобразовании. То есть о том, в какую фигуру матрица преобразует единичный квадрат, построенный на единичных векторах.
Насколько она ее масштабирует в пространстве. То есть вот из такого квадрата (синий цвет) матричное преобразование делает параллелограмм с определенной площадью (отмечено красным цветом), равной по модулю определителю матрицы.
Матричное преобразование площади определитель матрицы
Однако иногда определитель матрицы может быть отрицательным числом. В этом случае площадь фигуры, построенной на векторах матрицы, будет равна модулю данного числа, а знак минус означает, что ориентация данной фигуры отрицательна.
Геометрический смысл определителя матрицы
Определитель показывает какой будет площадь единичного квадрата при матричном преобразовании. Она будет равна площади параллелограмма, который будет построен на векторах-столбцах матрицы. Первый столбец матрицы дает нам координаты первого вектора, а второй столбец — координаты второго вектора.
Можно расширить геометрический смысл матрицы и на матрицы другого размера.
Таким образом, определитель матрицы 1×1 дает длину вектора, 2×2 — площадь параллелограмма, 3×3 — объем параллелепипеда, а nxn — объем n-мерного параллелепипеда.
2=0
Ответ: 0
Определитель третьего порядка
Пусть дана квадратная матрица третьего порядка:
A=\begin{pmatrix} a_{11}& a_{12} & a_{13}\\ a_{21}& a_{22} & a_{23} \\ a_{31}& a_{32} & a_{33} \end{pmatrix}
Определителем (или детерминантом) третьего порядка, соответствующим данной матрице, называется число:
a_{11}a_{22}a_{33}+a_{21}a_{32}a_{13}+a_{12}a_{23}a_{31}-a_{13}a_{22}a_{31}-a_{12}a_{33}a_{21}-a_{11}a_{23}a_{32}
Определитель третьего порядка будет:
detA=\begin{vmatrix} a_{11}& a_{12} & a_{13}\\ a_{21}& a_{22} & a_{23} \\ a_{31}& a_{32} & a_{33}\end{vmatrix}= \\ =a_{11}a_{22}a_{33}+a_{21}a_{32}a_{13}+a_{12}a_{23}a_{31}-a_{13}a_{22}a_{31}-a_{12}a_{33}a_{21}-a_{11}a_{23}a_{32}
Правило треугольников
При вычислении определителей третьего порядка удобно пользоваться правилом треугольников (правилом Саррюса). Это правило проиллюстрируем на схеме:
Правило треугольников или правило Саррюса
Как пользоваться правилом треугольника:
На схеме есть две картинки — красная и синяя, красная картинка дает нам три положительных слагаемых в формуле определителя третьего порядка, а синяя — три отрицательных.
Умножаем так — сначала умножаем элементы матрицы по главной диагонали потом в вершинах одного треугольника и в вершинах другого треугольника: . Все полученные множители складываем.
Теперь обратимся к синей картинке. Тут мы начинаем сначала перемножать элементы по побочной диагонали: , а потом элементы в вершинах двух треугольников: и . Полученные множители записываем в формулу со знаком минус.
Примеры на вычисление определителя третьего порядка
a) Вычислить определитель матрицы:
A=\begin{pmatrix} 2& 3 & 4\\ 6& 5 & 7 \\ 9& 0& 8 \end{pmatrix}
Решение:
det A=\begin{vmatrix} 2& 3 & 4\\ 6& 5 & 7 \\ 9& 0 & 8 \end{vmatrix}=2 \cdot 5 \cdot 8+ 3 \cdot 7 \cdot 9+6\cdot 0 \cdot 4 — 4 \cdot 5 \cdot 9 — 3 \cdot 6 \cdot 8 — 7 \cdot 0 \cdot 2=80+189+0-180-144-0=-55
Ответ: det A=-55
б) Вычислить определитель матрицы 3×3:
A=\begin{pmatrix} 2& 3 & 1\\ 1& -5 & 6\\ 2& -3& 4 \end{pmatrix}
Решение:
Используем формулу определителя третьего порядка
det B=\begin{vmatrix} 2& 3 & 1\\ 1& -5 & 6\\ 2& -3& 4 \end{vmatrix}=2 \cdot (-5) \cdot 4+ 3 \cdot 6 \cdot 2+1\cdot 1 \cdot (-3) — 1 \cdot (-5) \cdot 2 — 2 \cdot 6 \cdot (-3) — 3 \cdot 1 \cdot 4=-40+36-3+10+36-12=27
Ответ: det B=27
в) Вычислите определитель единичной матрицы 3×3.
Решение:
Единичная матрица 3×3 имеет вид:
A=\begin{pmatrix} 1& 1 & 1\\ 1& 1 & 1\\ 1& 1& 1 \end{pmatrix}
Используем формулу определителя третьего порядка
det A=\begin{vmatrix} 1& 1 & 1\\ 1& 1 & 1\\ 1& 1& 1 \end{vmatrix}=1 \cdot 1 \cdot 1+ 1 \cdot 1 \cdot 1+1\cdot 1 \cdot 1 — 1 \cdot 1 \cdot 1 — 1 \cdot 1 \cdot 1 — 1 \cdot 1 \cdot 1=1+1+1-1-1-1=0
Действительно, в столбцах единичной матрицы три совпадающих вектора, на которых невозможно построить объемную фигуру, объем которой и определяет определитель матрицы третьего порядка. Поэтому мы и получили число 0.
Вообще говоря, любая матрица с одинаковыми строками и столбцами дает определитель, равный нулю. Можете проверить самостоятельно.
Ответ: 0
Разложение определителя по строке или столбцу, а также его свойства, миноры и дополнения элементов определителя рассмотрим далее.
Определитель матрицы второго и третьего порядков и правила вычисления
Матрица содержит в себе векторы-столбцы.
Они по-разному ориентированы в пространстве. Характеристикой этого расположения и того матричного преобразования, которое может дать матрица, выступает определитель матрицы.
Содержание
Определитель матрицы 2×2
Пусть дана квадратная матрица второго порядка:
A=\begin{pmatrix} a_{11}& a_{12}\\ a_{21}& a_{22} \end{pmatrix}
Определителем (или детерминантом) второго порядка, соответствующим данной матрице, называется число a_{11}a_{22}-a_{12}a_{21}.
Определитель второго порядка записывается так:
detA=\begin{vmatrix} a_{11}& a_{12}\\ a_{21}& a_{22} \end{vmatrix}=a_{11}a_{22}-a_{12}a_{21}
Геометрический смысл определителя
Если нам дана квадратная матрица
A=\begin{pmatrix} a_{11}& a_{12}\\ a_{21}& a_{22} \end{pmatrix}
То первый столбец дает нам координаты одного вектора, а второй столбец чисел — координаты второго вектора. Начало данных векторов — в точке начала координат.
Тогда определитель матрица дает нам площадь параллелограмма, построенного на данных векторах.
Рассмотрим на примере
Пусть нам дана матрица с координатами:
A=\begin{pmatrix} 3& 1\\ 1& 2 \end{pmatrix}
Нарисуем координатную плоскость и отметим на ней данные векторы.
Векторы и
Где у вектора \overline{a} координаты (3; 1), а у вектора \overline{b} координаты (2; 1).
Теперь построим на этих векторах параллелограмм, считая, что векторы a и b его стороны. Получим:
Параллелограмм на векторах и
Площадь данного параллелограмма и будет являться определителем матрицы. Площадь данного параллелограмма S_{ABCD}=5. И определитель матрицы:
detA=\begin{vmatrix} 3& 1\\ 1& 2 \end{vmatrix}=3 \cdot 2-1 \cdot 1=6-1=5
Однако, обычно в линейной алгебре говорят не о площади параллелограмма, а о матричном преобразовании. То есть о том, в какую фигуру матрица преобразует единичный квадрат, построенный на единичных векторах.
Насколько она ее масштабирует в пространстве. То есть вот из такого квадрата (синий цвет) матричное преобразование делает параллелограмм с определенной площадью (отмечено красным цветом), равной по модулю определителю матрицы.
Матричное преобразование площади определитель матрицы
Однако иногда определитель матрицы может быть отрицательным числом. В этом случае площадь фигуры, построенной на векторах матрицы, будет равна модулю данного числа, а знак минус означает, что ориентация данной фигуры отрицательна.
Геометрический смысл определителя матрицы
Определитель показывает какой будет площадь единичного квадрата при матричном преобразовании. Она будет равна площади параллелограмма, который будет построен на векторах-столбцах матрицы. Первый столбец матрицы дает нам координаты первого вектора, а второй столбец — координаты второго вектора.
Можно расширить геометрический смысл матрицы и на матрицы другого размера.
Таким образом, определитель матрицы 1×1 дает длину вектора, 2×2 — площадь параллелограмма, 3×3 — объем параллелепипеда, а nxn — объем n-мерного параллелепипеда.
2=0
Ответ: 0
Определитель третьего порядка
Пусть дана квадратная матрица третьего порядка:
A=\begin{pmatrix} a_{11}& a_{12} & a_{13}\\ a_{21}& a_{22} & a_{23} \\ a_{31}& a_{32} & a_{33} \end{pmatrix}
Определителем (или детерминантом) третьего порядка, соответствующим данной матрице, называется число:
a_{11}a_{22}a_{33}+a_{21}a_{32}a_{13}+a_{12}a_{23}a_{31}-a_{13}a_{22}a_{31}-a_{12}a_{33}a_{21}-a_{11}a_{23}a_{32}
Определитель третьего порядка будет:
detA=\begin{vmatrix} a_{11}& a_{12} & a_{13}\\ a_{21}& a_{22} & a_{23} \\ a_{31}& a_{32} & a_{33}\end{vmatrix}= \\ =a_{11}a_{22}a_{33}+a_{21}a_{32}a_{13}+a_{12}a_{23}a_{31}-a_{13}a_{22}a_{31}-a_{12}a_{33}a_{21}-a_{11}a_{23}a_{32}
Правило треугольников
При вычислении определителей третьего порядка удобно пользоваться правилом треугольников (правилом Саррюса). Это правило проиллюстрируем на схеме:
Правило треугольников или правило Саррюса
Как пользоваться правилом треугольника:
На схеме есть две картинки — красная и синяя, красная картинка дает нам три положительных слагаемых в формуле определителя третьего порядка, а синяя — три отрицательных.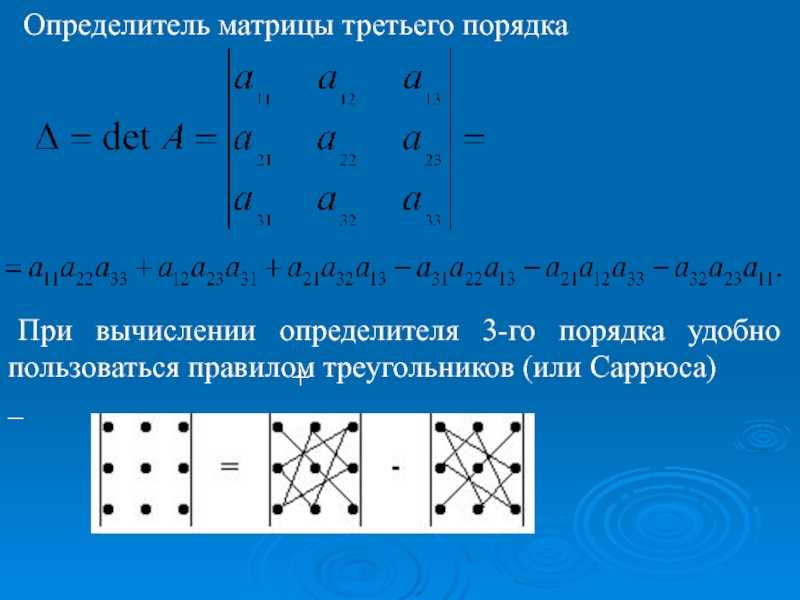
Умножаем так — сначала умножаем элементы матрицы по главной диагонали потом в вершинах одного треугольника и в вершинах другого треугольника: . Все полученные множители складываем.
Теперь обратимся к синей картинке. Тут мы начинаем сначала перемножать элементы по побочной диагонали: , а потом элементы в вершинах двух треугольников: и . Полученные множители записываем в формулу со знаком минус.
Примеры на вычисление определителя третьего порядка
a) Вычислить определитель матрицы:
A=\begin{pmatrix} 2& 3 & 4\\ 6& 5 & 7 \\ 9& 0& 8 \end{pmatrix}
Решение:
det A=\begin{vmatrix} 2& 3 & 4\\ 6& 5 & 7 \\ 9& 0 & 8 \end{vmatrix}=2 \cdot 5 \cdot 8+ 3 \cdot 7 \cdot 9+6\cdot 0 \cdot 4 — 4 \cdot 5 \cdot 9 — 3 \cdot 6 \cdot 8 — 7 \cdot 0 \cdot 2=80+189+0-180-144-0=-55
Ответ: det A=-55
б) Вычислить определитель матрицы 3×3:
A=\begin{pmatrix} 2& 3 & 1\\ 1& -5 & 6\\ 2& -3& 4 \end{pmatrix}
Решение:
Используем формулу определителя третьего порядка
det B=\begin{vmatrix} 2& 3 & 1\\ 1& -5 & 6\\ 2& -3& 4 \end{vmatrix}=2 \cdot (-5) \cdot 4+ 3 \cdot 6 \cdot 2+1\cdot 1 \cdot (-3) — 1 \cdot (-5) \cdot 2 — 2 \cdot 6 \cdot (-3) — 3 \cdot 1 \cdot 4=-40+36-3+10+36-12=27
Ответ: det B=27
в) Вычислите определитель единичной матрицы 3×3.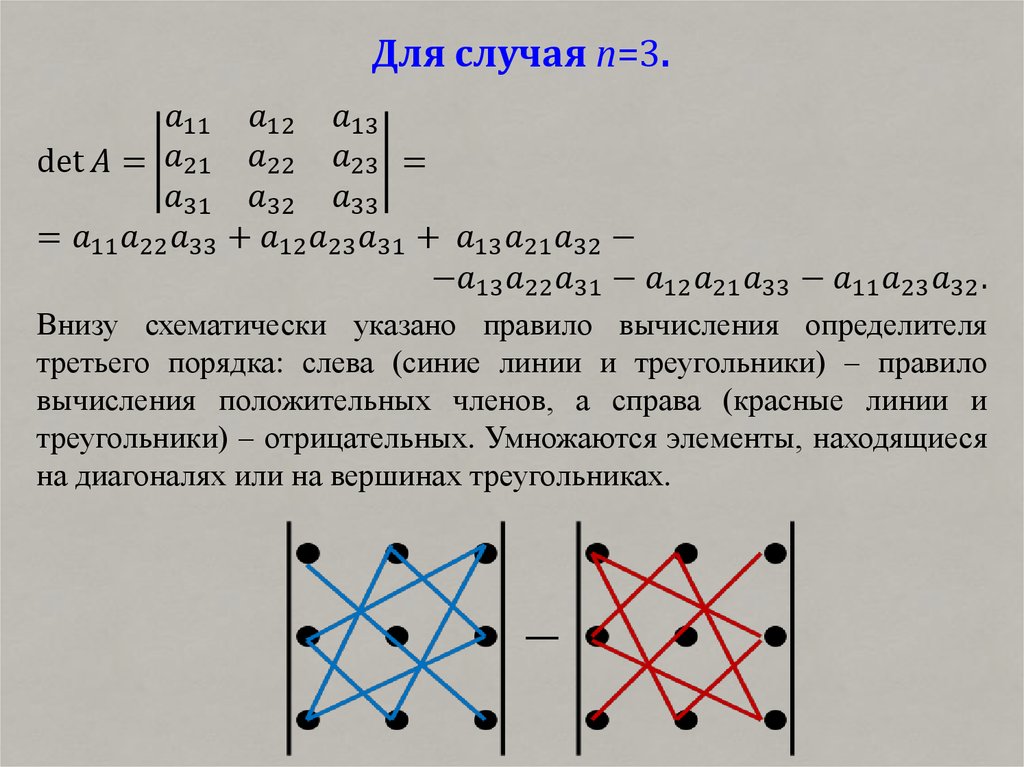
Решение:
Единичная матрица 3×3 имеет вид:
A=\begin{pmatrix} 1& 1 & 1\\ 1& 1 & 1\\ 1& 1& 1 \end{pmatrix}
Используем формулу определителя третьего порядка
det A=\begin{vmatrix} 1& 1 & 1\\ 1& 1 & 1\\ 1& 1& 1 \end{vmatrix}=1 \cdot 1 \cdot 1+ 1 \cdot 1 \cdot 1+1\cdot 1 \cdot 1 — 1 \cdot 1 \cdot 1 — 1 \cdot 1 \cdot 1 — 1 \cdot 1 \cdot 1=1+1+1-1-1-1=0
Действительно, в столбцах единичной матрицы три совпадающих вектора, на которых невозможно построить объемную фигуру, объем которой и определяет определитель матрицы третьего порядка. Поэтому мы и получили число 0.
Вообще говоря, любая матрица с одинаковыми строками и столбцами дает определитель, равный нулю. Можете проверить самостоятельно.
Ответ: 0
Разложение определителя по строке или столбцу, а также его свойства, миноры и дополнения элементов определителя рассмотрим далее.
линейная алгебра — Является ли определитель этой матрицы положительным или отрицательным?
спросил
Изменено 8 лет, 3 месяца назад
Просмотрено 10 тысяч раз
$\begingroup$
$\left( \begin{массив}{ccc} 1 и 1000 и 2 и 3 и 4\\ 5 и 6 &7&1000 &8\\ 1000&9&8&7&6\\ 5 и 4&3&2&1000\\ 1&2&1000&3&4\\ \end{array} \right)$
Когда я вычисляю определитель онлайн, я обнаруживаю, что он положительный, но я должен «видеть» что-то в матрице, что позволяет мне знать, что определитель положительный .
Какие свойства этой конкретной матрицы позволяют сделать вывод, что определитель будет положительным?
- линейная алгебра
- определитель
$\endgroup$
$\begingroup$
Используя позицию, занимаемую членами $1000$, мы можем записать определитель более красивым образом
$$\left| \begin{массив}{ccc}
1 и 1000 и 2 и 3 и 4\\
5 и 6 &7&1000 &8\\
1000&9&8&7&6\\
5 и 4&3&2&1000\\
1&2&1000&3&4\\ \end{массив} \right|=-\left| \begin{массив}{ccc}
1000 и 1 и 2 и 3 и 4\\
6 и 5 &7&1000 &8\\
9& 1000&8&7&6\\
4 и 5&3&2&1000\\
2&1&1000&3&4\\ \end{массив} \right|\\=\left| \begin{массив}{ccc}
1000 и 3 и 2 и 3 и 4\\
6 и 1000 &7&5 &8\\
9& 7 &8&1000&6\\
4 и 2&3&5&1000\\
2&3&1000&1&4\\ \end{массив} \right|=-\left| \begin{массив}{ccc}
1000 и 3 и 3 и 2 и 4\\
6 и 1000 &5&7 &8\\
9&7 &1000&8&6\\
4 и 2&5&3&1000\\
2&3&1&1000&4\\ \end{массив} \right|\\=\left| \begin{массив}{ccc}
1000 и 3 и 3 и 4 &2\\
6 и 1000 &5&8 &7\\
94$, что положительно.
$\endgroup$
$\begingroup$
При четном количестве перестановок соседних строк вы можете положить $1000$ по диагонали. Этот определитель должен быть положительным. Используя алгоритм, который рассматривает второстепенные члены, наибольший член всегда положителен.
$\endgroup$
2
$\begingroup$
Вы можете использовать 1000 в каждой строке, чтобы исключить другой элемент, чтобы получить верхнюю треугольную матрицу, и в процессе для 1000 достаточно большой, вы можете считать, что элемент в другом столбце не изменится. Тогда вы можете получить все элементы по диагонали равные 1000, что показывает, что определитель положителен.`
$\endgroup$
Геометрические свойства определителя
Определитель квадратной матрицы — это одно число, которое, среди прочего,
могут быть связаны с площадью или объемом региона.
В частности, определитель матрицы отражает то, как линейное преобразование, связанное с матрицей, может масштабировать или отражать объекты.
Здесь мы обрисовываем три свойства определителей, которые можно понять в этом геометрическом контексте.
Эффект масштабирования матрицы
Поскольку линейное преобразование всегда можно записать в виде $\vc{T}(\vc{x}) = A\vc{x}$ для некоторой матрицы $A$, применение линейного преобразования к вектору $\vc{ x}$ — это то же самое, что умножение на матрицу. Для квадратных матриц $A$ абсолютное значение определителя показывает, как применение $\vc{T}$ расширяет или сжимает объекты. Характер расширения или сжатия зависит от основного измерения. Одномерные линейные преобразования увеличивают длину в $| \det(A)|$, двумерные линейные преобразования расширяют площадь в $| \det(A)|$, а трехмерные линейные преобразования увеличивают объем в $| \дет(А)|$.
Как повлияет расширение линейного преобразования, если мы масштабируем $A$? Например, если мы удвоим каждый элемент $A$, сформировав матрицу $B=2A$, то как разложение линейного преобразования $\vc{\tilde{T}}=B\vc{x}$ будет сравниваться с что исходного $\vc{T} = A\vc{x}$?
В одном измерении эффект удвоения каждого вектора просто удвоит увеличение длины на $\vc{\tilde{T}}$.
3=8$ больше, чем исходный $\vc{T}$. Удвоение каждого измерения трехмерного объекта должно привести к восьмикратному увеличению объема. 9n |\det(A)|.$$
А как насчет отрицательных чисел и знака определителя? Знак определителя определяет, сохраняет или меняет ориентацию линейное преобразование. В одном измерении умножение одного компонента матрицы на отрицательное число будет соответствовать отражению в этом одном измерении. Следовательно, умножение на отрицательное число изменит размер определителя. Мы можем заключить, что для одного измерения $\det(cA)=c\det(A)$ для любого числа $c$. (Этот результат до боли очевиден, поскольку определитель как раз равен единице числа $A$, но мы обсуждаем одномерный случай только для того, чтобы дать представление о более высоких измерениях.)
В двух измерениях ситуация иная. Если мы умножим каждый компонент $A$ на отрицательное число, изменение будет соответствовать переворачиванию объекта один раз по оси $x$, а затем один раз по оси $y$.
2\det(A)$ в двух измерениях. Это уравнение резюмирует, как умножение на число не может изменить знак определителя в двух измерениях. 9n \det(A).\end{gather}
Эффект перемножения матриц
Геометрическая интерпретация позволяет быстро вывести определитель произведения $AB$ для $n\times n$ матриц $A$ и $ Б$. Если мы применим линейное преобразование $\vc{S}(\vc{x}) = AB\vc{x}$ к объекту, это то же самое, что сначала применить линейное преобразование $\vc{\tilde{T} }(\vc{x}) = B\vc{x}$, а затем применив линейное преобразование $\vc{T}(\vc{x}) = A \vc{x}$. (Это следует из того факта, что умножение матриц ассоциативно.)
Так как $\vc{T}$ расширяется в $|\det(A)|$ раз, а $\vc{\tilde{T}}$ расширяется в $|\det(B)|$ раз, применение обоих преобразований последовательно должно увеличиваться в множителе $|\det(A)||\det(B)|$. Более того, комбинация двух преобразований может изменить ориентацию только в том случае, если есть только одно из направлений $\vc{T}$ или $\vc{\tilde{T}}$.