Серия N 1/2/3 кВА (старые модели)
ИБП
- Семейство Amplon (>1 кВА)
- Семейство Ultron (>10 кВА)
- Семейство Modulon (модульные ИБП)
- Семейство Agilon (≤1,5 кВА)
- Аксессуары
- ПО Управление ИБП
- Серии сняты с производства
- Серия DPS 60/80/100/120 kBA
- Серия GAIA 1/2/3 кВА
- Серия H 15/20/30 кВА
- Серия N 1/2/3 кВА (старые модели)
- Серия NH Plus 20-120 кВА
- Серия R 1/2/3 кВА (старые модели)
- Серия RT 1/2/3 кВА (старые модели)
- Серия RT 5/6/10 кВА (старые модели)
- Серия VX 600 ВА
Выбор Продукта
Выберите направлениеИБПЦОДРешения для Телекома
Выберите семействоСемейство Agilon ( Семейство Amplon (>1 кВА)Семейство Ultron (>10 кВА)Семейство Modulon (модульные ИБП)Выберите продуктСистема ПитанияСтойки и АксессуарыСистема Мониторинга и УправленияВыберите продуктInD — Системы питания DC & ACOutD — Внешние системы питанияГибридная возобновляемая энергияВыпрямителиКонвертерыЗарядные устройстваsИнверторы и бесконтактные коммутаторыКонтроллеры
ИБП » Серии сняты с производства » Серия N 1/2/3 кВА (старые модели)
- Введение
- Технические характеристики
- Скачать
Введение
Сняты с производства :
рекомендуемая замена N 1/2/3 кВА. |
Amplon N-Series — источники бесперебойного питания с двойным преобразованием, компактных габаритов (для вертикальной установки). Эта серия разработана для обеспечения бесперебойного электропитания рабочих станций, торговых терминалов, банкоматов, бытовых приборов и пр.
В случае внутренней неисправности ИБП происходит автоматическое переключение на байпас для бесперебойного питания нагрузки. Также UPS 1000 va, 2000 и 3000 va серии Amplon N имеют встроенные батареи, обеспечивающие постоянное и устойчивое электропитание критической нагрузки при перебоях в электроснабжении. Для увеличения времени резервного электропитания есть возможность подключения дополнительных батарейных модулей. UPS 1000 va, 2000 и 3000 может быть запущен от аккумулятора, без питающей электросети.
Широкий диапазон входного напряжения и регулируемый ток заряда увеличивают срок службы батарей, а интеллектуальное управление предотвращает глубокий разряд аккумулятора ИБП.
Применения:
Cерверы Cети Безопасность Медицина Торговые терминалы Банкоматы
вверх
Доказательство того, что T(n)=n(n+1)/2
Доказательство того, что T(n)=n(n+1)/2 Здесь мы приводим три доказательства того, что n-е треугольное число 1+2+3+…+n равно n(n+1)/2. Первый — визуальный, включающий только формулу площади прямоугольник. Затем следуют два доказательства с использованием алгебры. В первом используется обозначение «…», а во втором вы знакомитесь с Сигма-обозначение, которое делает доказательство более точным.Наглядное доказательство того, что 1+2+3+…+n = n(n+1)/2
Мы можем визуализировать сумму 1+2+3+…+n как треугольник из точек . Числа, имеющие такое расположение точек, называются Треугольные (или треугольные) числа , записанные T(n), сумма целых чисел от 1 до n :| n | 1 | 2 | 3 | 4 | 5 | 6 | T(n) as a sum | 1 | 1+2 | 1+2+3 | 1 +2+3+4 | 1. | 1..6 |
|---|---|---|---|---|---|---|---|
| T(n) в виде треугольника | … | ||||||
| T(n)= | 1 | 3 | 6 | 10 | 15 | 21 |
Для этого мы совместим две копии треугольника из точек вместе , одну красную и перевернутую копию зеленого цвета.
Например. Т(4)=1+2+3+4
- Обратите внимание, что
- мы получаем прямоугольник , который имеет такое же количество строк (4), но имеет один дополнительный столбец (5)
- , поэтому прямоугольник 4 на 5
- поэтому содержит 4×5=20 шаров
- , но мы взяли две копии T(4), чтобы получить этот
- , поэтому у нас должно быть 20/2 = 10 шаров в T(4), что мы легко можем проверить.
Это визуальное доказательство применимо к любому размеру треугольного числа.
Вот это снова на T (5):
Итак, T(5) — это половина прямоугольника из точек 5 в высоту и 6 в ширину, то есть половина из 30 точек, поэтому T(5)=15.
Попробуйте формулу для себя с этой викториной (нажмите на кнопку), которая откроется в новом окне. После викторины закройте ее окно и снова нажмите эту кнопку для другого вопроса викторины.
Для T(n)=1+2+3+…+n мы берем две копии и получаем прямоугольник, который равен n на (n+1).
T(n) = 1 + 2 + 3 + … + n = n(n + 1)/2
То же доказательство с использованием алгебры!
Вот как математик мог бы написать приведенное выше доказательство, используя алгебру:| Т(н)+Т(н) | = | 1 + | 2 + | 3 + | … + | (N-1) + | N | |
| + | N + | (N-1) + | (N-2) (N-2) (N-2) (N-2) (N-2) (N-2) (N-2) (N-2) (N-2). + | … + | 2 + | 1 | Две копии, одна красная, а другая перевернутая, зеленого цвета | |
| = | (1 + n) + | (2 + n-1) + | (3 + n-2) + | … + | (н-1 + 2) + | (n + 1) | парные термины, красный с зеленым | |
| = | (n+1) + | (n+1) + | (n+1) + | … + | ( n+1) + | (n+1) | Все суммы n пар равны (n+1) | |
| 2 T(n) | = | n (n+1) | ||||||
| T(n) | = | n (n+1) / 2 | ||||||
Использование сигма-обозначения
Некоторые люди считают «…» слишком расплывчатым и хотят более точной альтернативы. По этой причине при суммировании ряда используется обозначение сигма . Сигма — это название греческой буквы английского «s», написанной как (как буква М на боку) как с большой буквы и (как маленькая b, которая упала) в нижнем регистре.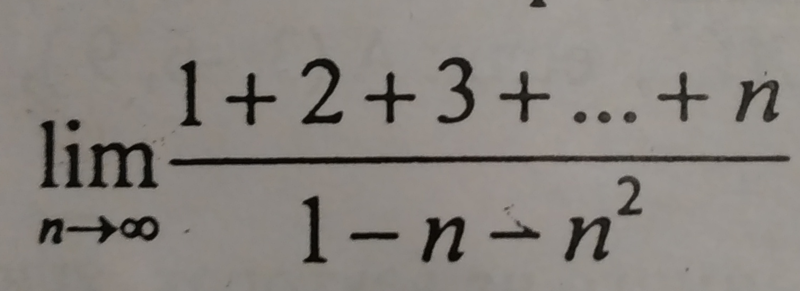
В этом случае «s» означает «сумма». (Высокая фигурная форма S дает
математический символ для интегрирования
|
На самом деле формулу после сигмы можно записать через любую переменную, а не только i , например k, но тогда надо указать, какая
это буква, которая варьируется в сумме под сигмой.
Часто переменная опускается выше сигмы, но никогда не пропускал ниже сигмы.
Вот некоторые примеры:
| Сумма 10 2 +11 2 +12 2 , где добавленные числа представляют собой квадратных числа i 2 : |
| |||||||
| 0087 например, как сумма квадратных чисел (i+9) 2 где на этот раз я иду от 1 до 3 |
| |||||||
где на этот раз i изменяется от -1 до 1 (т.е. i = -1, 0 и 1) |
| |||||||
Сумма 1+2+3 равна T+9 или 0,1+2+9. |
| |||||||
| Вот T(n), которое равно 1+2+3+…+n, на этот раз опуская второе использование i над сигмой: |
| 2 | 2
и на этот раз у нас есть T(n), но записанное наоборот: n+ (n-1) + … 3 + 2 + 1 где i -й -й член теперь равен n+1i для i от 1 до n: |
|
количество терминов будет
задается начальным и конечным значениями. Здесь все члены фиксированы (постоянны) на уровне 3:| i=7 | 3 = 3+3+3+3 = 12 |
| i=4 |
Вот приведенное выше алгебраическое доказательство, но теперь записанное с использованием сигма-обозначения:
| Т(н)+Т(н) | = |
| + |
| Две копии, одна красная, а другая перевернутая, зеленого цвета | ||||||||
| 2 T(n) | = |
4 | пара с терминами, красный с зеленым | ||||||||||
| 2 T(n) | = |
| n копий (n+1): i не фигурирует в формуле, поэтому все термины одинаковы | ||||||||||
| T(n) | = | n (n+1) / 2 | |||||||||||
Назад на страницу результатов Runsums
| © 2003 Доктор Рон Нотт |
| 12 февраля 2003 г. |
comБесконечность или -1/12? | plus.maths.org
В последнее время очень странный результат ходит по кругу. Это говорит что если сложить все натуральные числа
1+2+3+4+…
, то ответом на эту сумму будет -1/12. Идея, представленная в Numberphile видео (см. ниже), которое претендует на доказательство результата, а также говорит, что оно использовалось повсюду в физике. Люди сочли эту идею настолько поразительной, что она даже попала в Новый Йорк Таймс . Так что все это значит?
Математика
Прежде всего, бесконечная сумма всех естественных число не равно -1/12. Вы можете легко убедиться в этом, набрав в калькуляторе частичных сумм
и так далее. Чем больше и больше становится, тем больше становится, то есть тем больше натуральных чисел вы включаете. На самом деле, вы можете сделать столько, сколько хотите, выбрав достаточно большой.
Например, для вас получить
и для вас получить
Вот почему математики говорят, что сумма
расходится в бесконечность. Или, выражаясь более свободно, что сумма равна бесконечности.
Шриниваса Рамануджан
Так откуда взялось -1/12? Неправильный результат на самом деле появился в работе известного индийского математика Шринивасы Рамануджана в 1913 г. (дополнительную информацию см. в этой статье). Но Рамануджан знал, что делал, и имел на то причины. записать это. Он работал над тем, что называется Дзета-функция Эйлера . Чтобы понять, что это такое, сначала рассмотрим бесконечная сумма
Вы можете узнать это как сумму, которую вы получите, если возьмете каждое натуральное число, возведете его в квадрат, а затем возьмете обратное:
Теперь эта сумма не расходится.
Если вы возьмете последовательность частичных сумм, как мы сделали выше,
, то результаты, которые вы получите, будут сколь угодно близки, но никогда не превысят число, которое, по словам математиков, сходится к или . более грубо, что оно равно
Теперь, что произойдет, если вместо того, чтобы возводить эти натуральные числа в знаменателе в степень 2, вы возведете его в другую степень? Оказывается, соответствующая сумма
сходится к конечному значению, если мощность является числом больше . Для каждого выражение имеет четко определенное конечное значение. это то, что называется функцией , и она называется дзета-функцией Эйлера в честь плодовитого математика 18-го века Леонарда Эйлера.
Пока все хорошо. Но что произойдет, если вы подставите значение меньше 1? Например, что, если вы подключите ? Посмотрим.
Итак, вы восстанавливаете нашу первоначальную сумму, которая, как мы знаем, расходится. То же верно и для любых других значений, меньших или равных 1: сумма расходится.
Расширение дзета-функции Эйлера
В существующем виде дзета-функция Эйлера S(x) определена для действительных чисел x , которые больше 1. Действительные числа являются частью более крупного семейства чисел, называемых комплексными числами . И в то время как действительные числа соответствуют всем точкам на бесконечно длинной прямой, комплексные числа соответствуют всем точкам на плоскости, содержащей прямую с действительными числами. Эта плоскость называется сложной плоскостью. Точно так же, как вы можете определять функции, принимающие на вход вещественные числа, вы можете определять функции, принимающие на вход комплексные числа.
Одна удивительная особенность функций комплексных чисел заключается в том, что если вы знаете функцию достаточно хорошо для некоторый набор входных данных, то (вплоть до некоторых технических подробностей) вы можете знать значение функции везде на комплексной плоскости. Этот метод расширения определения функции известен как аналитическое продолжение . Дзета-функция Эйлера определена для действительных чисел больше 1. Поскольку действительные числа также являются комплексными числами, мы можем рассматривать ее как комплексную функцию, а затем применить аналитическое продолжение, чтобы получить новую функцию, определенную на всей плоскости, но согласующуюся с эйлеровой дзета-функция для действительных чисел больше 1. Это дзета-функция Римана.
Но есть еще одна вещь, которую вы можете сделать. Используя некоторую мощную математику (известную как комплексный анализ , см. рамку) существует способ распространить определение дзета-функции Эйлера на числа, меньшие или равные 1, таким образом, чтобы получить конечные значения.
Другими словами, есть способ определить новую функцию, назвать ее так, чтобы для
и для функции были четко определенные конечные значения. Этот метод расширения называется аналитическим продолжением , а новая функция, которую вы получаете, называется дзета-функцией Римана в честь математика 19-го века Бернхарда Римана. (Для того, чтобы эта новая функция давала вам конечные значения для, нужно ловко вычесть другую расходящуюся сумму, так что бесконечность из первой расходящейся суммы минус бесконечность из второй расходящейся суммы дает вам что-то конечное.)
ОК. Итак, теперь у нас есть функция, которая согласуется с дзета-функцией Эйлера, когда вы подставляете значения. Когда вы подставляете значения, дзета-функция дает конечный результат. Какое значение вы получаете, когда подключаетесь к дзета-функции? Вы уже догадались:
Если вы сейчас ошибетесь, полагая, что для , то вы получите (неправильное) выражение
Это один из способов понять загадочное выражение лица Рамануджана.
Уловка
Так как же люди в видео Numberphile «доказали», что все натуральные числа дают в сумме -1/12? Настоящий ответ заключается в том, что они этого не сделали. Смотреть это видео — все равно, что смотреть на фокусника и пытаться увидеть, как он сует кролика в шляпу. Первый шаг «доказательства» пытается убедить вас в кое-чем довольно глупом, а именно в том, что бесконечная сумма
равно
Видео не останавливается на этом долго и, кажется, подразумевает, что это очевидно. Но давайте посмотрим на это немного ближе, чтобы увидеть, имеет ли это вообще смысл. Предположим, что сумма имеет конечное значение и назовем ее . Прибавляя к себе, вы получаете бесконечную сумму
Но это всего лишь исходная сумма, из которой следует
Так как следует то, что является ерундой.
Поэтому утверждение, что бесконечную сумму можно принять равной 1/2, неверно.
На самом деле, вы можете получить любые результаты, возясь с бесконечные суммы, которые расходятся (см. здесь). Это трюк!
Физика
Но как этот любопытный, неверный результат попал в учебник физики, как показано в видео? Вот где все действительно стать интересным. Предположим, вы берете две проводящие металлические пластины и размещаете их в вакууме так, чтобы они были параллельны друг другу. Согласно классической физике, между ними не должно быть никакой чистой силы. тарелки.
Иллюстрация эффекта Казимира. Изображение: Эмок.
Но классическая физика не считается со странными эффектами
вы видите, когда смотрите на мир в очень малых масштабах. Чтобы сделать это,
вам нужна квантовая физика, которая говорит нам много очень странных вещей. Один
из них то, что вакуум не пуст, а кипит
Мероприятия. Так называемые виртуальных частицы появляются и исчезают все время.
время. Это действие дает так называемую энергию нулевой точки : самая низкая энергия, которую что-либо может иметь, никогда не равна нулю (см. здесь для более подробной информации).
Когда вы пытаетесь рассчитать общую плотность энергии между двумя пластинами, используя математика квантовой физики, вы получаете бесконечную сумму
Эта бесконечная сумма также является результатом подстановки значения в дзета-функцию Эйлера:
Это прискорбно, потому что сумма расходится (она расходится даже быстрее, чем ), что подразумевало бы бесконечную плотность энергии . Это явно ерунда. Но что, если вы дерзко предположите, что бесконечная сумма равна дзета-функции Римана, а не дзета-функции Эйлера, оцениваемой при ? Ну, тогда вы получаете конечную плотность энергии. Это означает, что между металлическими пластинами должна существовать сила притяжения, что также кажется нелепым, поскольку классическая физика предполагает, что силы быть не должно.
А вот и сюрприз. Когда физики провели эксперимент, они обнаружили, что сила действительно существует — и она соответствует плотности энергии, точно равной !
Этот удивительный физический результат известен как эффект Казимира. в честь голландского физика Хендрика Казимира.
Найдите минутку, чтобы понять это. Квантовая физика говорит, что плотность энергии должна быть
Это вздор, но эксперименты показывают, что если вы (ошибочно) считаете эту сумму дзета-функцией, оцененной в , вы получите правильный ответ. Таким образом, кажется, что природа последовала идеям, которые мы изложили выше. Он расширил дзета-функцию Эйлера, включив в нее значения, меньшие 1, ловко вычитая бесконечность, и, таким образом, получил конечное значение. Это замечательно!
Причина, по которой мы видим и в видео Numberphile, и в учебнике физики, а не в том, что когда вы представляете эффект Казимира происходящим в одном измерении (вдоль линии, а не в 3D), плотность энергии, которую вы вычисляете, скорее чем .