На какие числа делятся: Признаки делимости | Онлайн калькуляторы, расчеты и формулы на GELEOT.RU

Признаки делимости ➗ свойства кратности, правила делимости натуральных чисел

Дроби с кратными от 1 до 5

На единицу делится любое целое число.

Самым простым правилом является делимость на число два: если натуральное число оканчивается на четную цифру, то оно кратно двум. Если в конце стоит нечетная цифра, какими являются 1, 3, 5, 7, 9, то число на два не делится. То есть чтобы поделить многозначное число на два, в конце числа должна стоять одна из таких цифр: 2, 4, 6, 8, 0.

Пример: 6942 является четным, поскольку в конце четная цифра, поэтому оно кратно двум; число 19678456 также кратно двум, так как в конце стоит четная цифра 6. А вот число 6796345 не делится на 2, поскольку оно нечетное. Также нельзя получить ответ без остатка с такой суммы, как 398573 по этой же причине.

Деление на три имеет свое правило: нужно сложить все цифры, а затем проверить, делится ли сумма на три. Если да, то и данность разделится на три. Если нет, значит, не делится.

Например, возьмем 3576. Складываем 3+5+7+6=21. Полученную сумму 21 делим на три, получается семь. Значит, оно кратно трем без остатка. Проведем разложение шестизначного номера 353388. Оно раскладывается на три, поскольку сумма равна тридцати (3+5+3+3+8+8=30). Еще возьмем, например, 5819. Складываем: 5+8+1+9=23, полученная сумма не делится на три без остатка. Также и 2947 невозможно разделить, поскольку остаются тройки.

Правило делимости на четыре звучит так: если две последние цифры номера кратны четырем либо оно в конце имеет два нуля, то отношение получится без остатка.

Например, 1000 делится на четыре, поскольку в конце 00. Делится также и 3824, так как в конце 24, которое кратно этому делителю. А вот 2986 не делится на четыре, так как 86 не кратно четырем, и 29087 тоже не может остаться целым, поскольку с 87 нельзя произвести расчета.

Еще пример: четырехзначный номер 2648 можно разделить на этот делитель, так как 48:4=12.

Довольно простым правилом является делимость на пять. Частное получается без остатка, если в конце заданного числа стоит 5 или 0. Если оно не заканчивается одной из этих цифр, то при делении возникнет остаток.

Проверим правило, взяв пятизначное число 45765. Оно кратно пяти без остатка, так как заканчивается на пять. Также 45030 можно разделить, поскольку в конце ноль. А вот четырехзначное число 4321 без остатка не делится.

Свойства делителей от 6 до 10

Составное шесть состоит из произведения двух последовательных чисел — 2 и 3. Теория кратности такова: число 6 составное, поэтому необходимо, чтобы одновременно действовали два правила признака делимости. Нужно, чтобы число было кратно и двум, и трем сразу.

Например, проверке подвергаются трехзначные числа 756 и 168. Они четные, поэтому делятся на два. Теперь нужно сложить 7+5+6=18, становится ясно, что сумма 18 делится на 3. Число 165 при разложении на однозначные цифры с последующим сложением превращается в 12, которое может разделиться на три. Оба числа кратны одновременно 2 и 3, значит, кратны шести.

Определение отношения с делимостью на семь довольно сложное: число делится, если при удвоении последней цифры и полученной разности результат кратен семи или равен нулю.

Пример, трехзначное число 679 кратно 7. (Калькулятор выдал 97). Узнать можно так:

• 2*9=18.
• 67−18=49.
• 49:7=7.

Из примера видно, что удвоилось последнее число, затем получена разность, после чего — отношение-доказательство.

В классе было дано задание доказать, что число 497 делится на семь. Порядок решения:

• 2*7=14.
• 49−14=35.
• 35:7=5.

Найти признак делимости на 8 очень легко. Формулировка закона такова: последние три цифры должны быть 000 или 888. Легко можно произвести вычисления с 789000: оно делится на 8, так как оканчивается на 000. Множество 289673888 тоже кратно 8, поскольку заканчивается на 888.

Свойство при делителе 9 похоже на правило с 3. Формула делимости на 9 довольно простая: сумма цифр должна быть кратна девяти. Маленький пример: из 46980 возможно получить целое, 4+6+9+8+0= 27. Получившаяся сумма кратна 9. Еще одно задание: найти отношение с использованием признака кратности 9 при делимом 29565. Рассуждение: 2+9+5+6+5=27. Полученная сумма может разделиться на девять.

Разрядные единицы

Любое число можно разделить на разрядную единицу, если у него одинаковое или большее количество нулей в конце. Например, 5790 можно поделить на 10, так как в конце один ноль. Еще примеры:

• 4958700:100=49587.
• 374000:1000=374.
• 5781000:100=5781.
• 97430:10=9743.

Невозможно разделить 128700 на 1000, так как у разрядной единицы нулей больше, а также 237480 на 100 и другие подобные.

Делители от 11 и выше

Чтобы получилось деление на 11, необходимо сложить четные по счету номера, а затем нечетные, затем произвести вычитание. Если в процессе вычислений получился ноль или одиннадцать, то остатка не будет.

Онлайн-задание с ответом: 7535, 74019 и 50486.

Нечетные в первом случае 7 и 3, четные 5 и 5. Считаем:

• 7+3=10,
• 5+5=10,
• 10−10=0.

Четные во втором примере 4 и 1, нечетные — 7, 0, 9. Вычисление:

• 7+0+9=16.
• 4+1=5.
• 16−5=11.

В третьем примере нечетные 5, 4, 6, четные 0 и 8. Решаем:

• 5+4+6=15.
• 0+8=8.
• 15−8=7.

Ответ: в первом и втором примере десятых, сотых, тысячных и так далее не останется, а в третьем — останется.

Чтобы разделить на двузначный делитель 12, нужно произвести общие вычисления, характерные для делителей 3 и 4 одновременно. К примеру, 900 и 3432. Сначала следует разложить на слагаемые 9+0+0=9, значит, можно поделить на 3. В конце стоит два нуля — можно делить на 4. Проверка: 900:12=75. Первая часть задания решена, теперь делаем вторую: 3+4+3+2=12, 12:3=4. Таким образом проверяется кратность трем. Теперь четырем: в конце стоит 32, что указывает на кратность 4, значит, остатка не будет. Таким образом, оба примера кратны 12.

Дробь, кратная 13, разрешится без остатка, если последнюю цифру умножить на 4, после чего сложить число и последнюю цифру. Если полученная сумма кратна 13 или равно 0, то деление получится.

Например, 6942:

• 2*4=8.
• 694+8=702.
• 702:13=54.

Еще пример — 754:

• 4*4=16.
• 75+16=91.
• 91:13=7.

Признак делимости на составное число

Если делитель составной, необходимо его разложить на простые множители, которые не имеют общих кратных, кроме единицы. Пример: 15 раскладывается на 3 и 5. Любое неизвестное кратно 15, если одновременно кратно трем и пяти.

Также и с другим составным: 18 раскладывается на 2 и 9. Нельзя брать множители 3 и 6, так как они не простые, у них общее кратное 3. Например, 456 кратно трем, проверка: 4+5+6=15, также кратно 6 (при разложении на 2 и 3). Однако калькулятор выводит запятую. Если взять множители 2 и 9, будет видно, что двум — кратно, а девяти — нет, ведь сумма равна 15, которая не кратна 9.

Таблица кратных от 2 до 10

Для удобства школьникам и их родителям предлагается таблица признаков делимости чисел от 2 до 10. Она наглядно и кратко демонстрирует всю вышеизложенную теоретическую часть:

Делимость на:	Признак числа:
2	Оканчивается четной цифрой: 0, 2, 4,6, 8
3	Сумма цифр, их которой оно состоит, делится на 3
4	Две последние цифры делятся на 4
5	Окончание на 5 или 0
6	Одновременная кратность 2 и 3
8	Три последние цифры кратны 8
9	Сумма цифр кратна 3
10	Окончание равно нулю

Вышеизложенное доказывает, что к любому натуральному числу можно подобрать простой или составной признак кратности. На практике выходит, что чем больше число, тем сложнее его признак. Часто не хочется тратить время на проверку делимости, ведь за этот промежуток уже можно выполнить само деление. Поэтому любой школьник может воспользоваться простейшими признаками делимости.

Страница 17 — ГДЗ Математика 3 класс. Моро, Бантова. Учебник часть 2

1. Главная
2. ГДЗ
3. 3 класс
4. Математика
5. org/ListItem»> Моро, Бантова. Учебник
6. Деление суммы на число
7. Страница 17. Часть 2

Вернуться к содержанию учебника

Деление суммы на число

Вопрос

1. Вычисли и проверь решение умножением.

81:3    96:6     51:3     58:2

Ответ

Вопрос

2. Объясни решение уравнения и его проверку.

х : 2 = 14 х = 14 • 2 х = 28

Проверка: 28 : 2 = 14 14 = 14

Ответ

Вопрос

3. В деревне 19 домов, а в посёлке в 4 раза больше. Объясни, что обозначают выражения:

19 • 4, 19 • 4 — 19.

Ответ

Вопрос

4. Один рабочий изготавливал за день 23 детали, а другой — 21 деталь. Сколько деталей изго­товят оба рабочих за 2 дня?

Ответ

Вопрос

5. 1) Запиши числа от 19 до 30 и подчеркни те из них, которые делятся на 4 без остатка.

2) Запиши числа от 20 до 30 и подчеркни те из них, которые делятся на 3 без остатка.

Ответ

Вопрос

6. 

31 • 3 — 56	90 — 65 : 5	78 — 36 — 42 : 6
4 • 17 + 32	84 : 7 + 27	21 + 49 : 7 — 6

Ответ

Вопрос

Вычисли и выполни проверку.

76:4      69:3

Ответ

Вопрос

Лабиринт:

Ответ

Вернуться к содержанию учебника

---

Делимость

— Как узнать, делится ли число на $60$?

спросил 3 года, 1 месяц назад

Изменено 5 месяцев назад

Просмотрено 2к раз

$\begingroup$

Я изучал Вавилонскую цивилизацию (Вавилон), я вижу, что насчет числа $60$, теперь я собираюсь найти хитрость или быстрый способ узнать остаток делимости на число $60$, например: 9{2}+51,60+29$

$2567=42,60+47$

Я знаю, что число $60$ делится на $1,2,3,4,5,6$

Так что мне нужно быстро узнать метод Я имею в виду как остальные ? Я не могу ли мы обобщить или нет? Пожалуйста, мне нужен быстрый метод без использования калькулятора!

Например, $17894=?$

См. это: $2177,12=2177+0,12$

$2177=36,60+17$ $0,12=\frac{3}{25}=\frac{60,3}{25,60}=?$ Мне нужно написать в базе $60$?

• теория чисел
• делимость

$\endgroup$

2

$\begingroup$

Делимость на 60$ эквивалентна кратности одновременно на 3,20$. Таким образом, мы можем использовать для них проверку на делимость, которая проста в базе $ 10 $. Делимость на $20$ означает, что последние $2$ цифры должны быть четными, за которыми следует $0$. Признак делимости на $3$ означает, что сумма цифр делится на $3$.

$\endgroup$ 9n=Mx+t\space \text{для }n\ge3 $$ Это следует методу, который мы применяем здесь, в частности, к числу $17894$, предложенному О.П. $$17894=Nx+(1+7+8)t+94=Nx+16\cdot40+94=Nx+734$$ теперь легко проверить, что $17894=Nx+734\equiv734\equiv14\pmod{60}$

Метод . -Если $N=a_na_{n-1}\cdots a_2a_1a_0\equiv x\pmod{60}$, то $x\equiv 40(a_n+\cdots a_2)+a_1a_0$, поэтому, если $a_n+\cdots +a_2\equiv h\pmod3$, затем $$\boxed{x\equiv 40h+a_1a_0\pmod{60}}$$, где $h$ равно $0,1$ или $2$.

$\endgroup$

$\begingroup$

Если я правильно понимаю, вам нужен быстрый способ конвертировать число в основание $60$ без использования калькулятора.

Стандартный способ преобразования числа в двоичное с помощью компьютера состоит в том, чтобы вычесть $1$, если оно нечетное, затем несколько раз разделить на $2$, пока не получите $0$. Мы можем обобщить этот метод на базу $60$.

С вашим примером, $6689$, вы можете следовать этому методу. Вам нужно найти наибольшее число, меньшее этого, которое делится на $60$. В данном случае это $6660$. Итак, 6689 долларов.=6660+29$. Затем вы можете разделить число на 60 долларов, 6689 долларов = 60 (111) + 29 долларов. Теперь мы можем сделать то же самое за $111$. Нам нужно наибольшее число меньше $111$, которое делится на $60$. В этом случае 111$=1(60)+51$. Таким образом, мы можем написать: 6689 долларов = 60 (60 (1) + 51) + 29 долларов. Теперь мы опустились до $ 1 $ в средних скобках, так что мы можем остановиться. Таким образом, 6689 долларов США из базовых 60 долларов будут составлять 1,51,29 долларов США.

Вопрос теперь только в том, как найти наибольшее число, меньшее вашего числа, которое делится на $60$. Вы можете сделать это либо путем догадок и интуиции, либо использовать модульную арифметику (если вы знаете о модульной арифметике, то прочитайте следующий абзац).

Например, мы снова можем использовать $6689$. Нам нужно число по модулю $2,3,10$ (остаток при делении на эти числа). $6689$ нечетно, поэтому оно сравнимо с $1$ по модулю $2$. В $6689$ сумма цифр равна $29$, что на $2$ больше, чем кратное $3$, поэтому $6689$ сравнимо с $2$ по модулю $3$. Последняя цифра $6689$ равна $9$, поэтому $6689$ соответствует модулю $9$ на $10$.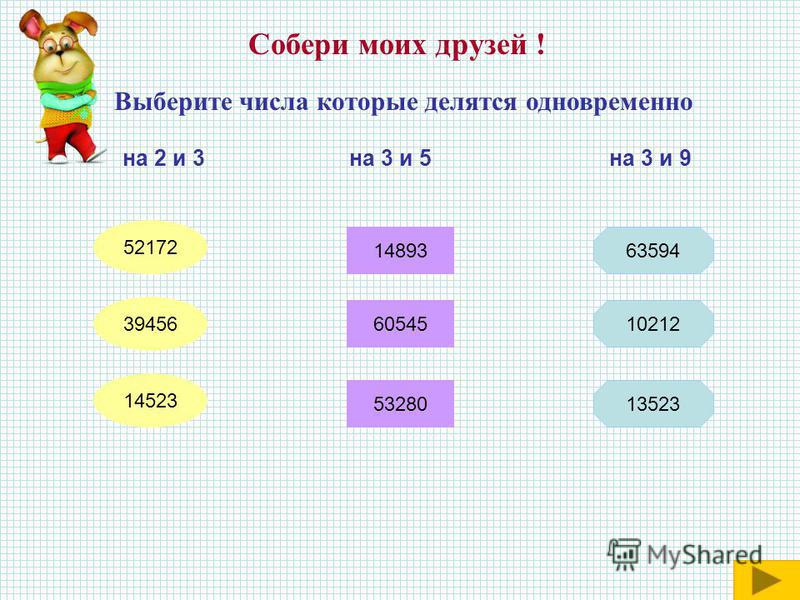 Мы можем использовать эту информацию, чтобы найти $6689$ mod $60$. Вы можете использовать китайскую теорему об остатках или просто использовать логику. Сначала находим мод $6$. Нам нужно число от $0$ до $6$, что является нечетным, и на $2$ больше, чем кратное $3$, что составляет $5$. Таким образом, $6687$ соответствует модулю $5$ по модулю $6$. Теперь нам нужно число от $0$ до $60$, которое на $5$ больше, чем кратное $6$, и оканчивается на $9.2)*3*5 = 4*3*5 .

Теперь мы должны убедиться, что число делится на $3, 4, 5$. Чтобы число делилось на $5$, последняя цифра должна быть либо $0$, либо $5$. Чтобы число делилось на $4$, последние две цифры должны делиться на $4$. Следовательно, здесь, чтобы число делилось на $4$ и $5$, последние цифры должны быть $0$, и предпоследние цифры должны быть четными.

Далее, чтобы число делилось на $3$, сумма цифр должна делиться на $3$.

$\endgroup$

Изучите определение, правила и примеры

Вы, должно быть, слышали слово «делимость» в математике. Смысл делимости в способности быть полностью разделенным без остатка. Чтобы проверить эту делимость, необходимо соблюдать некоторые правила делимости. Без фактического деления, как мы можем угадать числа, делящиеся на 4 или нет? В этой статье вы изучите делящиеся на 4 или правила делимости на 4. В этой статье будет рассмотрено правило делимости на 4 с примерами и то, как его можно использовать для проверки, делится ли число на 4.

Делимость Правило 4

Что вы подразумеваете под делимостью?

Делимость определяется как правило или способ определения, делится ли данное большое или малое число на данное фиксированное число (делитель).

Число делится на другое число, если оно делится на это число поровну или если при этом получается целое число. Например, поскольку 6, деленное на 3, дает 2, а 2 — целое число, то 6 делится на 3 (мы говорим: «3 делит 6»).

Набор общих рекомендаций, известных как «правила делимости», часто используется для определения того, делится ли одно число на другое число без остатка.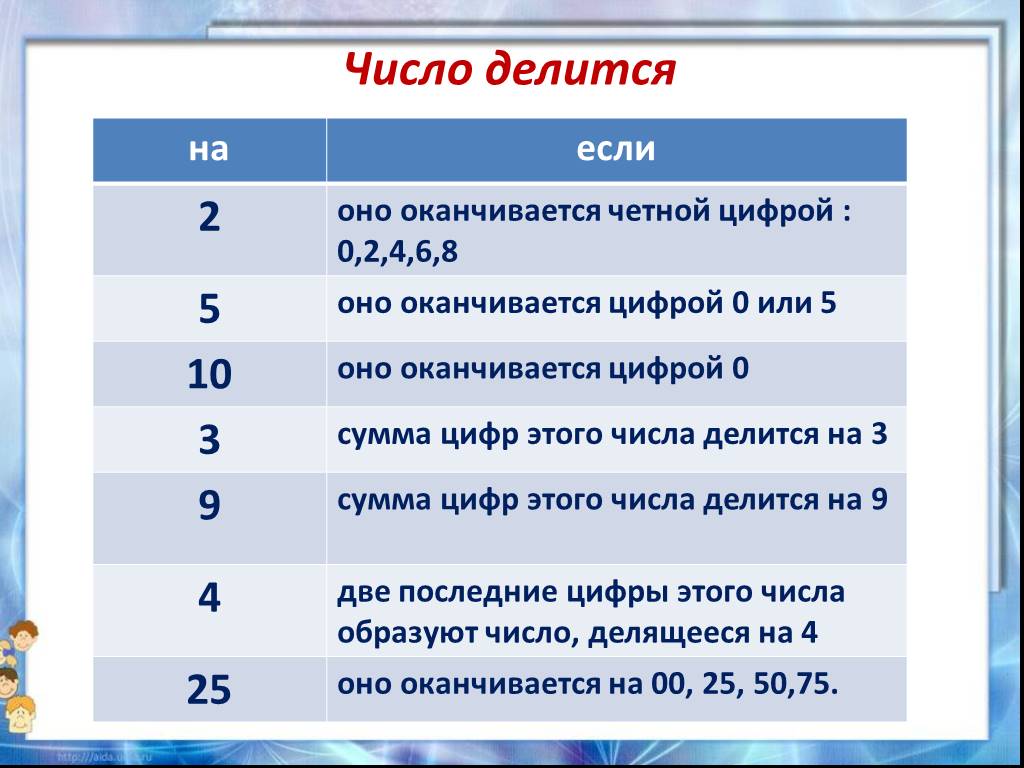 Например, если нам нужно проверить, делится ли число 432 на 4 или нет.

Заданное число = 432

Фиксированное число или делитель = 4

Подробно мы узнаем в следующем разделе о числах, делящихся на 4.

Итак, для некоторых чисел у нас есть некоторое правило делимости, чтобы выяснить, число делится на делитель или нет.

Деление на 4 части

Правило делимости на 4

Правило делимости на 4 определяется как данное число делится на 4, если последние две цифры данного числа являются нулями или кратны 4 (4 , 8,12,16,20,24,…..).

Это правило помогает учащимся узнать, делится ли заданное число на 4 или нет.

Некоторые из целых чисел, которые полностью делятся на 4, равны 0,4,8,12,16. Мы все знаем таблицу 4. Следовательно, эти числа, кратные 4, полностью делятся на 4.

Как проверить делимость на 4?

В этом трюке мы должны выполнить два условия, чтобы проверить признак делимости на 4, заданный следующим образом:

1. Проверить, являются ли последние две цифры заданного числа нулями. Если да, то данное число будет делиться на 4. Если нет, то проверьте второе условие, приведенное ниже. Нули должны стоять в разряде единиц и десятков.

Например, 700 — это число, в котором нули стоят на единицах и десятках. Следовательно, мы можем сказать, что 700 делится на 4 без каких-либо вычислений.

2. Проверить, являются ли последние две цифры данного числа точно кратными 4 или входят в таблицу 4, тогда мы можем сказать, что данное число делится на 4.

Например, 736 чеков двузначные числа выделены жирным шрифтом и подчеркнуты.

36 входит в таблицу 4 или кратно 4. Следовательно, мы можем сказать, что 736 полностью делится на 4.

Правило делимости на 4 с примером

Некоторые примеры числа делящиеся на 4

1. Проверить, делятся ли заданные числа на 4 или нет.

1. 1700

2. 6500

ANS:

1. 1700

. Дайский номер — 1700

. 1700 делится на 4.

1700 ÷ 4 = 425

2. 6500

.6 Последние две цифры числа -00

Следовательно, правило делимости 1 выполняется, и 6500 делится на 4.

6500 ÷ 4 = 1625

Практические вопросы

4? Отметьте правильный вариант.

1. 766

2. 222

3. 336

4. 811

ANS: 36

96969

Div: 36

969696. Отметьте правильный вариант.

1. 555

2. 840

3. 114

4. 106

ANS: 840

САМЕЧА делится на заданное фиксированное число (делитель).