Комплексные числа — Математика — Уроки
Комплексные числа и квадратные уравнения.
10 класс ( профильный уровень).
«Мысль выражать все числа знаками
настолько проста, что именно из-за
этой простоты сложно осознать,
сколь она удивительна»
Пьер Симон Лаплас
Цели урока:
1.Обучающая:
формирование у школьников различных приёмов мыслительной деятельности;
включение новой информации в структуру прежних знаний;
расширить сведения учащихся о числах;
2. Воспитательная:
привитие интереса к предмету;
формирование уверенности в своих знаниях.
воспитание чувства ответственности.
3. Развивающая:
Развивающая:
Задачи урока:
Обобщить и систематизировать знания, умения и навыки учащихся по теме урока.
Развивать умения применять теоретические знания при решении заданий; умение анализировать, сравнивать, обобщать, устанавливать причинно-следственные связи; классифицировать.
Формировать навыки самостоятельной деятельности
Учебно-методическая карта фрагмента урока
№ | Этап урока | Содержание этапа | Методы и методические приемы | Формируемые компетенции |
1 | Организационный момент | Приветствие | ||
2 | Мотивация и целеполагание. | Мотивация Определение целей урока (слайды 2-4) |
| |
3 | Актуализация | Историческая справка Решение кроссворда (для сильных) Тест (для слабых) (слайд 5-6) Индивидуальная работа (на карточках) | ( проверка через документ камеру) |
|
4 | Сообщение новых знаний | Решение квадратных уравнений на множестве комплексных чисел. (слайд 7-8) | ||
5 | Этап обобщения и систематизации | Индивидуальная работа. (слайд 9-10) Индивидуальная работа (на карточках) |
| |
6 | Домашнее задание | Задания различного уровня сложности | ||
7 | Рефлексия | Ответы на вопросы (слайд 11-12) |
| |
8 | Итог урока | Качественная характеристика работы учащихся |
| |
На прошлых уроках мы познакомились с понятием комплексного числа, алгебраической формой записи комплексного числа, научились выполнять различные действиями над комплексными числами, научились находить модуль и аргумент комплексного числа.
Актуализация
Работа в парах — решение кроссворда (историческая справка), для слабых тестирование. (проверка)
Индивидуальная работа. Заполняют лист само оценивания.
Вариант 1
1. Даны два комплексных числа Z1= (10 + 2i ) и Z2=(1 – 6i ). Найдите их сумму, разность, произведение и частное.
Вариант 2.
Даны два комплексных числа z1= (12 + 2i ) и z2=(3 – 4i ). Найдите их сумму, разность, произведение и частное.
Ответы:
Вариант 1
1. Z1+ Z2=11 – 4i
2. Z1— Z2=9 +8i
3. Z1 Z2=22 -58i
4.
Вариант 2
1. Z1+ Z2=15 – 2i
2. Z1— Z2=9 +6i
3. Z1 Z2=44 -42i
4. (Проверка по тетрадям учащихся через документ камеру)
Решите квадратные уравнения:
х2 – 5х + 6=0 х2 +6х+9=0 9х2-12х + 5 = 0
Решение квадратных уравнений в поле комплексных чисел
ax2 + bx + c = 0
1 cлучай: D0, 2 корня, х1,2 =
2 случай D=0, 1 коре нь, х1,2 =
3 cлучай: D1,2 =
Сколько корней может иметь записанное на доске квадратное уравнение?
9х2-12х + 5 = 0
У доски решает ученик:
9х2-12х+5=0
D= 144-180= -36, считаем, что
-Теперь вы можете блеснуть эрудицией, услышав, что при D
— Вот и сделали мы шаг в глубину математического айсберга. Комплексные числа широко применяются в электротехнике, в аэродинамике. Отец русской авиации, Н.Г. Жуковский использовал их при разработке теории крыла самолета. Возможно, они пригодились для получения промежуточного результата.
Комплексные числа широко применяются в электротехнике, в аэродинамике. Отец русской авиации, Н.Г. Жуковский использовал их при разработке теории крыла самолета. Возможно, они пригодились для получения промежуточного результата.
x 2– 4x + 13 = 0.
9 x 2+ 12x + 29 = 0.
Взаимопроверка
Ответы:
1) 𝑥=(4+6𝑖)/2=2+3i 𝑥=(4−6𝑖)/2=2-3i
2) 𝑥=(−12−30𝑖)/18=(−2)/3 − 5/3 𝑖 , 𝑥=(−12+30𝑖)/18=(−2)/3+ 5/3 𝑖
Самопроверка.
1. Решите уравнение x2 – 4x + 5 = 0.
Решение. D = – 4 уравнение имеет мнимые корни: 2+i, 2-i
2. Решите уравнение x2 – x + 10 = 0.
Решение. D = – 39 , уравнение имеет мнимые корни:
3. Решите уравнение x2 – 4x + 13 = 0.
Решение. D = – 36 уравнение имеет мнимые корни: 2+3i, 2-3i
4. Решите уравнение x2 – 2x + 15 = 0.
Решение. D = – 56 , уравнение имеет мнимые корни:
А как бы вы решили следующее квадратное уравнение?
х2 + (5 – 2i) x + 5(1– i) = 0;???????
Вот над этой проблемой будем работать на следующем уроке, а желающие могут попробовать самостоятельно попробовать свои силы.
Домашнее задание п.35 №7-8(а, б),10.
Спасибо за урок!
Вариант 1
1. Даны два комплексных числа Z1= (10 + 2i ) и Z2=(1 – 6i ). Найдите их сумму, разность, произведение и частное.
2. Проверьте правильность следующих утверждений:
а) Сумма и разность чисто мнимых чисел есть чисто мнимое число.
Для проверки возьмите числа: Z1=2i, Z2=-3i
б) Произведение двух чисто мнимых чисел равно действительному числу.
Для проверки возьмите числа: Z1=-5i, Z2=3i
в) Квадрат чисто мнимого числа равен действительному отрицательному числу.
Для проверки возьмите числа: Z1=10i
г) Произведение чисто мнимого числа на действительное равно чисто мнимому числу.
Для проверки возьмите числа: Z1=7i, Z2=3
которых равны 2.
Вариант 2.
Даны два комплексных числа z1= (12 + 2i ) и z2=(3 – 4i ). Найдите их сумму, разность, произведение и частное.
Найдите их сумму, разность, произведение и частное.
2. Проверьте правильность следующих утверждений:
а) Сумма и разность чисто мнимых чисел есть чисто мнимое число.
Для проверки возьмите числа: Z1=2i, Z2=-3i
б) Произведение двух чисто мнимых чисел равно действительному числу.
Для проверки возьмите числа: Z1=-5i, Z2=3i
в) Квадрат чисто мнимого числа равен действительному отрицательному числу.
Для проверки возьмите числа: Z1=10i
г) Произведение чисто мнимого числа на действительное равно чисто мнимому числу.
Для проверки возьмите числа: Z1=7i, Z2=3
1. Решите уравнение x2 – 4x + 5 = 0. 2+i, 2-i
2. Решите уравнение x2 – x + 10 = 0.
3. Решите уравнение x2 – 4x + 13 = 0. 2+3i, 2-3i
4. Решите уравнение x2 – 2x + 15 = 0.
1. Решите уравнение x2 – 4x + 5 = 0. 2+i, 2-i
Решите уравнение x2 – 4x + 5 = 0. 2+i, 2-i
2. Решите уравнение x2 – x + 10 = 0.
3. Решите уравнение x2 – 4x + 13 = 0. 2+3i, 2-3i
4. Решите уравнение x2 – 2x + 15 = 0.
1 | |||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||
| 2 | 3 | |||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
| |||||||||||||||||||||||||||||||||||||||
|
|
| 5 | ||||||||||||||||||||||||||||||||||||||||||||
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |||||||||||||||||||||||||||||
|
|
|
| ||||||||||||||||||||||||||||||||||||||||||||
| 6 |
|
|
|
|
|
| 8 | |||||||||||||||||||||||||||||||||||||||
| 7 |
|
|
|
|
|
|
|
| ||||||||||||||||||||||||||||||||||||||
|
|
| |||||||||||||||||||||||||||||||||||||||||||||
|
|
| |||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||
9 |
|
|
|
|
|
|
| ||||||||||||||||||||||||||||||||||||||||
| 10 |
|
|
|
|
|
| ||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||
11 |
|
|
|
|
|
| |||||||||||||||||||||||||||||||||||||||||
ВОПРОСЫ: | |||||||||||||||||||||||||||||||||||||||||||||||
По горизонтали: | |||||||||||||||||||||||||||||||||||||||||||||||
3. | Кто впервые упомянул о мнимых числах, назвав их «софически отрицательными»? | ||||||||||||||||||||||||||||||||||||||||||||||
4. |
| ||||||||||||||||||||||||||||||||||||||||||||||
6. | Чье имя носит формула = ? | ||||||||||||||||||||||||||||||||||||||||||||||
7. | arg z. | ||||||||||||||||||||||||||||||||||||||||||||||
9. | Длина вектора соответствующего комплексного числа. | ||||||||||||||||||||||||||||||||||||||||||||||
10. | bi — …… часть числа. | ||||||||||||||||||||||||||||||||||||||||||||||
11. | Геометрическая интерпретация комплексного числа. | ||||||||||||||||||||||||||||||||||||||||||||||
По вертикали: | |||||||||||||||||||||||||||||||||||||||||||||||
1. | Кто ввел название «мнимые числа»? | ||||||||||||||||||||||||||||||||||||||||||||||
2. | Французский математик, предложивший изображать комплексные числа на координатной плоскости. | ||||||||||||||||||||||||||||||||||||||||||||||
3. |
| ||||||||||||||||||||||||||||||||||||||||||||||
5. | Числа | ||||||||||||||||||||||||||||||||||||||||||||||
8. | Сколько форм записи комплексных чисел Вы знаете? | ||||||||||||||||||||||||||||||||||||||||||||||
Карточка само оценивания.
Ф. И. _______________________________________________
Система оценивания:
«+» — справился с заданием без затруднений,
«±» — справился с заданием, но возникали сложности,
«-» — не справился с заданием.
№ задания | Задание | Оценка | Оценка учителя |
1 | Работа в парах | ||
2 | Работа по карточкам | ||
3 | Решение квадратных уравнений (взаимопроверка) | ||
4 | Решение квадратных уравнений (самопроверка) | ||
5 | Итого: ваша оценка за урок |
Если у вас: 5- 4,5 «+» — ставим оценку «5»;
4- 3,5 «+» — «4»;
3- 2,5 «+» — «3».
Рождение комплексных чисел — Ugukalka — LiveJournal
Рождение комплексных чисел
6th-Apr-2013 01:57 am
| |||||
This page was loaded Oct 3rd 2022, 8:19 am GMT.
Обратная связь ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса — ваш вокал Как цель узнает о ваших желаниях прежде, чем вы начнете действовать. Целительная привычка Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Тренинг уверенности в себе Вкуснейший «Салат из свеклы с чесноком» Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Как слышать голос Бога Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека — Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т. Отёска стен и прирубка косяков — Когда на доме не достаёт окон и дверей, красивое высокое крыльцо ещё только в воображении, приходится подниматься с улицы в дом по трапу. Дифференциальные уравнения второго порядка (модель рынка с прогнозируемыми ценами) — В простых моделях рынка спрос и предложение обычно полагают зависящими только от текущей цены на товар. |
ПОНЯТИЕ О КОМПЛЕКСНЫХ ЧИСЛАХ Для решения алгебраических уравнений недостаточно действительных чисел.
ДЕЙСТВИЯ С КОМПЛЕКСНЫМИ ЧИСЛАМИ Решение многих задач математики, физики сводится к решению алгебраических уравнений, т.е. уравнений вида , где a0 , a1 , …, an действительные числа. Поэтому исследование алгебраических уравнений является одним из важнейших вопросов в математике. Например, действительных корней не имеет квадратное уравнение с отрицательным дискриминантом. Простейшим таким уравнением является уравнение х2 +1 = 0. Отсюда х2 = -1. Число х, квадрат которого равен –1, называется мнимой единицей и обозначается i. Таким образом , i2 = -1, откуда i = . Числа вида 4+3i и 4-3i называют комплексными числами. Символ называется мнимой единицей. С его помощью и с помощью пары действительных чисел и составляется выражение вида: Число а называется действительной частью комплексного числа, bi-мнимой частью этого числа, b— коэффициентом мнимой части комплексного числа. Для их обозначения используются символы , . Комплексные числа вида являются действительными числами и, следовательно, множество комплексных чисел содержит в себе множество действительных чисел. Комплексные числа вида называются чисто мнимыми. Два комплексных числа вида и называются равными, если равны их действительные и мнимые части, т. , . Алгебраическая запись комплексных чисел позволяет производить операции над ними по обычным правилам алгебры. Сложение комплексных чисел.Суммой двух комплексных чисел z1 = a + bi и z2 = c + di называется комплексное число z = (a+c) + (b+d)i. Числа a + bi и a-bi называются сопряженными. Их сумма равна действительному числу 2а, (а+bi) + (а-bi) = 2а. Числа а+bi и -a-bi называются противоположными. Их сумма равна нулю. Комлексные числа равны, если равны их действительные части и коэффициенты мнимых частей: а+bi = c+di, если a = c, b = d. Комплексное число равно нулю тогда, когда его действительная часть и коэффициент мнимой части равны нулю, т.е. z = a + bi = 0, если a = 0,b = 0. Действительные числа являются частным случаем комплексных чисел. Если b = 0, то a + bi = a — действительное число. Если а = 0, b 0, то a + bi = bi – чисто мнимое число. Для комплексных чисел справедливы переместительный и сочетательный законы сложения. Вычитание комплексных чисел определяется как действие, обратное сложению: разностью двух комплексных чисел a + bi и с + di называется комплексное число х + уi, которое в сумме с вычитаемым дает уменьшаемое. Отсюда, исходя из определения сложения и равенства комплексных чисел получим два уравнения, из которых найдем, что х = а-с, у = b-d. Значит, (а+bi) — (c+di) = (a-c) + (b-d)i. Произведение комплексных чисел z 1= a + bi и z2 = c + di называется комплексное число z = (ac-bd) + (ad + bc)i, z1z2 = (a + bi)(c + di) = (ac — bd) + (ad + bc)i. Легко проверить, что умножение комплексных чиcел можно выполнять как умножение многочленов с заменой i2 на –1. Из определения умножения получим, что произведение сопряженных комплексных чисел равно действительному числу: (a + bi)(a — bi) = a2 + b2 Деление комплексных чисел,кроме деления на нуль, определяется как действие, обратное умножению. Конкретное правило деления получим, записав частное в виде дроби и умножив числитель и знаменатель этой дроби на число, сопряженное со знаменателем: (a + bi):(c + di) = = = +
1. Коммутативный (переместительный) закон сложения: . 2. Ассоциативный (сочетательный) закон сложения: . 3. Коммутативный закон умножения: . 4. Ассоциативный закон умножения: . 5. Дистрибутивный (распределительный) закон умножения относительно сложения: . 6. . 7. . 8. . 9. Любому комплексному числу соответствует противоположное комплексное число такое, что . 10. Всякому комплексному числу отличному от нуля, соответствует обратное комплексное число такое, что .
Доверь свою работу ✍️ кандидату наук! Имя Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно — исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое Нажимая кнопку «Продолжить», я принимаю политику конфиденциальности |
Уравнения с комплексными числами — Алгебра II
Все ресурсы по Алгебре II
10 Диагностических тестов 630 практических тестов Вопрос дня Карточки Learn by Concept
Алгебра II Помощь » Математические отношения и основные графики » Воображаемые числа » Уравнения с комплексными числами
– это действительные числа.
Оценить.
Возможные ответы:
Правильный ответ:
Пояснение:
Чтобы два мнимых числа были равны друг другу, их мнимые части должны быть равны. Поэтому мы устанавливаем и решаем для in:
Сообщить об ошибке
Если и действительные числа, и , что если ?
Возможные ответы:
Правильный ответ:
Объяснение:
Чтобы решить для , мы должны сначала решить уравнение с комплексным числом для и . Поэтому нам необходимо сопоставить действительную часть комплексного числа с действительной частью выражения, а мнимую часть комплексного числа с мнимой частью выражения. Таким образом, мы получаем:
Поэтому нам необходимо сопоставить действительную часть комплексного числа с действительной частью выражения, а мнимую часть комплексного числа с мнимой частью выражения. Таким образом, мы получаем:
и
. Мы можем использовать подстановку, заметив, что первое уравнение можно переписать как и подставив его во второе уравнение. Таким образом, мы можем решить для :
С этим значением мы можем решить для:
, так как теперь мы имеем, и мы можем решить:
Наш окончательный ответ.
Сообщить об ошибке
Решить если .
Возможные ответы:
Правильный ответ:
Объяснение:
Решите эту задачу так же, как и любую другую задачу по алгебре, следуя своему порядку действий. Сначала мы оценим, что находится внутри скобок: . На этом этапе нам нужно знать следующие свойства :
На этом этапе нам нужно знать следующие свойства :
Следовательно, и исходное выражение становится
Сообщить об ошибке
.
Возможные ответы:
Ни один из других ответов.
Правильный ответ:
Объяснение:
Первым шагом является вычисление выражения. Преобразовав выражение в FOIL, мы получим:
Теперь нам необходимо упростить любые условия, которые мы можем, используя свойства
Поэтому выражение становится
. С. Ошибка
Решите для:
Возможные ответы:
Правильный ответ:
Объяснение:
Чтобы решить эту задачу, нам нужно сначала упростить наше уравнение. Первое, что мы должны сделать, это распределить квадрат, что дает нам
Первое, что мы должны сделать, это распределить квадрат, что дает нам
Теперь на самом деле это просто . Таким образом, это становится
Теперь все, что нам нужно сделать, это решить в уравнении:
, что дает нам
Наконец, мы получаем
, и, следовательно, наше решение —
4
, и, следовательно, наше решение —
4
, и, следовательно, наше решение —
4
, и поэтому наше решение —
Сообщить об ошибке
Решите для и :
Возможные ответы:
Правильный ответ:
Объяснение:
Помните, что
Итак, степени цикличны. Это означает, что когда мы пытаемся вычислить значение показателя степени , мы можем игнорировать все степени, кратные , потому что они заканчиваются умножением конечного результата на , и, следовательно, ничего не делают.
Это означает, что
Теперь, помня отношения показателей степени , мы можем упростить это до:
Поскольку элементы слева и справа должны соответствовать (без смешивания и сопоставления!), мы получаем отношения:
Независимо от того, как вы ее решаете, вы получаете значения , .
Сообщить об ошибке
Решить
Возможные ответы:
Все действительные числа
Нет решения
Правильный ответ:
Нет решения
Объяснение:
Чтобы решить
Вычтите из обеих сторон:
Что никогда не верно, поэтому решения нет.
Сообщить об ошибке
Уведомление об авторских правах
Все ресурсы по алгебре II
10 Диагностические тесты 630 практических тестов Вопрос дня Карточки Учитесь по концепции
Алгебра — комплексные числа
Показать мобильное уведомление Показать все примечания Скрыть все примечания
Мобильное уведомление
Похоже, вы находитесь на устройстве с «узкой» шириной экрана ( т. е. вы, вероятно, на мобильном телефоне). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.
е. вы, вероятно, на мобильном телефоне). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.
Раздел 1-7: Комплексные числа
Последняя тема в этом разделе на самом деле не связана с большей частью того, что мы сделали в этой главе, хотя, как мы увидим, она в некоторой степени связана с разделом радикалов. Нам также не понадобится этот материал так часто в оставшейся части этого курса, но есть пара разделов, в которых он нам понадобится, поэтому лучше убрать его с дороги на этом этапе.
В разделе радикалов мы отметили, что из квадратного корня из отрицательного числа нельзя получить действительное число. Например, \(\sqrt { — 9} \) не является действительным числом, так как нет никакого реального числа, которое мы могли бы возвести в квадрат и получить ОТРИЦАТЕЛЬНУЮ 9.
Теперь мы также видели, что если \(a\) и \ (b\) оба были положительными, тогда \(\sqrt {ab} = \sqrt a \,\sqrt b \). На секунду забудем об этом ограничении и сделаем следующее.
\[\ sqrt { — 9} = \ sqrt {\ влево ( 9 \ вправо) \ влево ( { — 1} \ вправо)} = \ sqrt 9\sqrt {- 1} = 3\sqrt {- 1} \]
Итак, \(\sqrt { — 1} \) не является действительным числом, но если подумать, мы можем сделать это для любого квадратного корня из отрицательного числа. Например,
\[\begin{align*}\sqrt { — 100} & = \sqrt {100} \sqrt { — 1} = 10\sqrt { — 1} \\ \sqrt { — 5} & = \sqrt 5 \, \,\sqrt { — 1} \\ \sqrt { — 290} & = \sqrt {290} \,\,\sqrt { — 1} \hspace{0.25in}и т. д.\end{align*}\]
Таким образом, даже если число не является полным квадратом, мы всегда можем уменьшить квадратный корень из отрицательного числа до квадратного корня из положительного числа (с которым мы или калькулятор можем справиться), умноженное на \(\sqrt {- 1} \).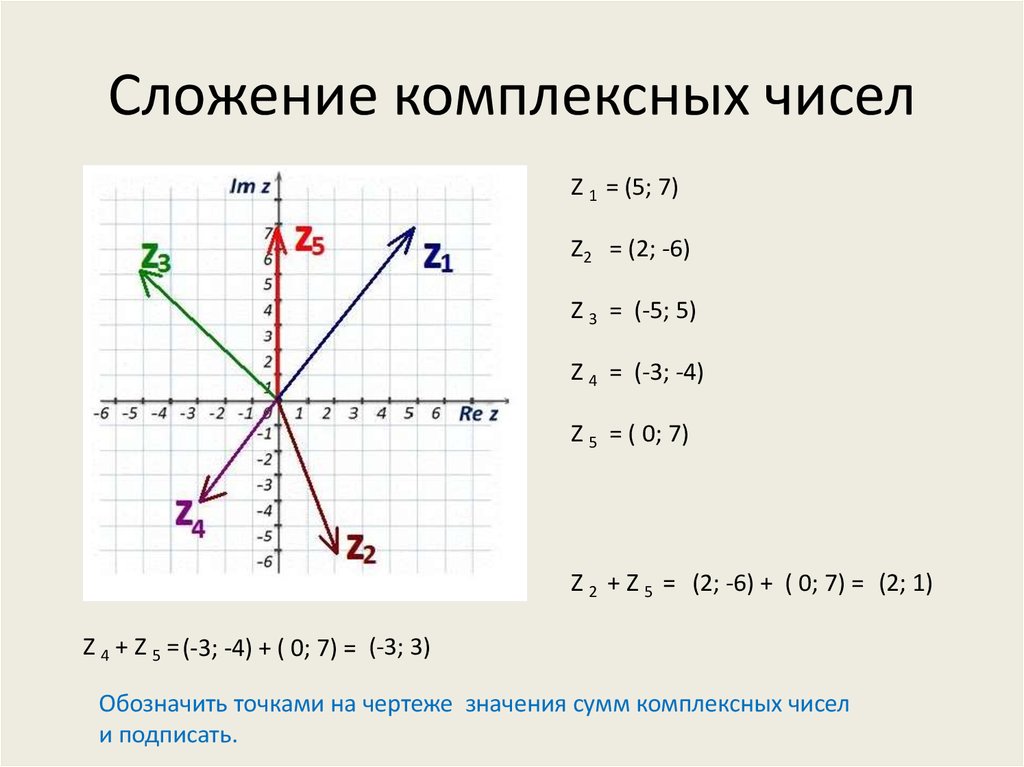
Итак, если бы у нас был способ работать с \(\sqrt { — 1} \), мы могли бы работать с квадратными корнями из отрицательных чисел. Что ж, реальность такова, что на этом уровне просто нет способа справиться с \(\sqrt { — 1} \), поэтому вместо того, чтобы иметь дело с ним, мы, так сказать, «заставим его уйти», используя следующее определение.
\[\require{bbox} \bbox[2pt,border:1px сплошной черный]{{i = \sqrt { — 1} }}\]
Обратите внимание, что если возвести в квадрат обе стороны, мы получим 92} = — 1}}\]
Это важно запомнить позже. Это показывает, что в некотором роде \(i\) — единственное «число», которое мы можем возвести в квадрат и получить отрицательное значение.
Используя это определение, все приведенные выше квадратные корни становятся
\[\begin{align*}\sqrt { — 9} & = 3\,i & \hspace{0.5in}\sqrt {- 100} & = 10\,i\\ \sqrt {- 5} & = \ sqrt 5 \,i & \hspace{0. 5in} \sqrt {- 290} & = \sqrt {290} \,i\end{align*}\]
5in} \sqrt {- 290} & = \sqrt {290} \,i\end{align*}\]
Это все примеры комплексных чисел .
В этот момент возникает естественный вопрос: зачем нам это? Ответ заключается в том, что, как мы увидим в следующей главе, иногда мы будем сталкиваться с квадратными корнями из отрицательных чисел, и нам понадобится способ с ними справиться. Итак, чтобы разобраться с ними, нам нужно будет обсудить комплексные числа.
Итак, давайте начнем с некоторых основных определений и терминологии комплексных чисел. стандартная форма комплексного номера
\[а + би\]
где \(a\) и \(b\) — действительные числа, и они могут быть любыми, положительными, отрицательными, нулями, целыми, дробными, десятичными, это не имеет значения. Когда в стандартной форме \(a\) называется действительной частью комплексного числа, а \(b\) называется мнимой частью комплексного числа.
Вот несколько примеров комплексных чисел.
\[3 + 5i\hspace{0.25in}\,\,\,\,\sqrt 6 — 10i\,\,\,\,\,\,\,\frac{4}{5} + i\, \,\,\,\,\,\,16i\,\,\,\,\,\,\,\,\,113\]
Последние два, вероятно, нуждаются в небольшом пояснении. Вполне возможно, что \(а\) или \(b\) могут быть равны нулю, и поэтому в 16\(i\) действительная часть равна нулю. Когда действительная часть равна нулю, мы часто будем называть комплексное число чисто мнимым числом . В последнем примере (113) мнимая часть равна нулю, а на самом деле мы имеем действительное число. Итак, думая о числах в этом свете, мы можем видеть, что действительные числа — это просто подмножество комплексных чисел.
Конъюгат комплексного числа \(a + bi\) является комплексным числом \(a — bi\). Другими словами, это исходное комплексное число с измененным знаком мнимой части. Вот несколько примеров комплексных чисел и их сопряженных.
\[\begin{array}{*{20}{c}}{{\mbox{комплексное число}}}&{\hspace{0,25 дюйма}{\mbox{сопряженное}}}\\{3 + \frac{ 1}{2}i}&{\hspace{0. 25in}3 — \frac{1}{2}i}\\{12 — 5i}&{\hspace{0.25in}12 + 5i}\\{1 — i}&{\hspace{0.25in}1 + i}\\{45i}&{\hspace{0.25in} — 45i}\\{101}&{\hspace{0.25in}101}\end{массив }\hspace{0,25 дюйма}\]
25in}3 — \frac{1}{2}i}\\{12 — 5i}&{\hspace{0.25in}12 + 5i}\\{1 — i}&{\hspace{0.25in}1 + i}\\{45i}&{\hspace{0.25in} — 45i}\\{101}&{\hspace{0.25in}101}\end{массив }\hspace{0,25 дюйма}\]
Обратите внимание, что сопряженное вещественное число представляет собой само себя без изменений.
Теперь нам нужно обсудить основные операции над комплексными числами. Начнем со сложения и вычитания. Самый простой способ думать о сложении и/или вычитании комплексных чисел — думать о каждом комплексном числе как о многочлене и выполнять сложение и вычитание так же, как мы складываем или вычитаем многочлены.
Пример 1 Выполните указанную операцию и запишите ответы в стандартной форме.
- \(\влево( { — 4 + 7i} \вправо) + \влево( {5 — 10i} \вправо)\)
- \(\влево( {4 + 12i} \вправо) — \влево( {3 — 15i} \вправо)\)
- \(5i — \влево({- 9 + i} \вправо)\)
Показать решение
Здесь действительно нечего делать, кроме добавления или вычитания.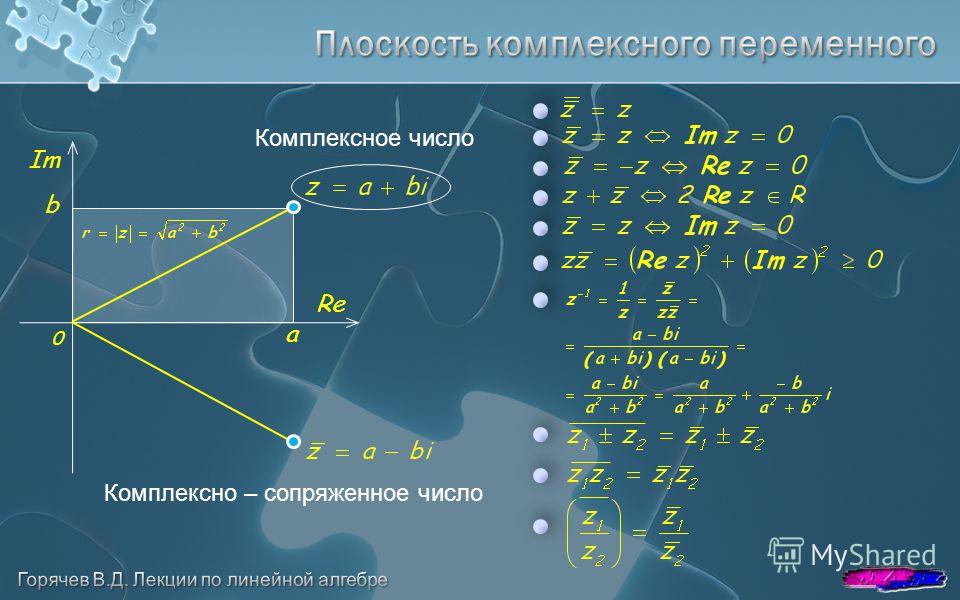 Обратите внимание, что круглые скобки в первых терминах нужны только для того, чтобы указать, что мы думаем об этом термине как о комплексном числе, и в общем случае не используются.
Обратите внимание, что круглые скобки в первых терминах нужны только для того, чтобы указать, что мы думаем об этом термине как о комплексном числе, и в общем случае не используются.
a \(\left( { — 4 + 7i} \right) + \left( {5 — 10i} \right) = 1 — 3i\)
b \(\left( {4 + 12i} \right ) — \left( {3 — 15i} \right) = 4 + 12i — 3 + 15i = 1 + 27i\)
c \(5i — \left( { — 9 + i} \right) = 5i + 9 — i = 9 + 4i\)
Далее рассмотрим умножение. Опять же, с одним небольшим отличием, вероятно, проще всего думать о комплексных числах как о многочленах, поэтому умножайте их, как многочлены. Единственное отличие появится на последнем шаге, как мы увидим.
Пример 2 Умножьте каждое из следующих чисел и запишите ответы в стандартной форме.
- \(7i\влево( { — 5 + 2i} \вправо)\)
- \(\влево( {1 — 5i} \вправо)\влево( { — 9 + 2i} \вправо)\)
- \(\влево({4+i}\вправо)\влево({2+3i}\вправо)\)
- \(\влево( {1 — 8i} \вправо)\влево( {1 + 8i} \вправо)\)
Показать все решения Скрыть все решения
a \(7i\left( { — 5 + 2i} \right)\) Показать решение 92} = — 1\]
Используя это, мы получаем,
\[7i\влево( { — 5 + 2i} \вправо) = — 35i + 14\влево( { — 1} \вправо) = — 14 — 35i\]
Мы также изменили порядок, чтобы реальная часть шла первой. 2}\). 92}}}\]
2}\). 92}}}\]
Теперь мы привели эту формулу с комментарием, что она будет удобна при делении комплексных чисел, так что давайте рассмотрим пару примеров.
Пример 3 Запишите каждое из следующих утверждений в стандартной форме.
- \(\displaystyle \frac{{3 — i}}{{2 + 7i}}\)
- \(\displaystyle \frac{3}{{9 — i}}\)
- \(\displaystyle \frac{{8i}}{{1 + 2i}}\)
- \(\displaystyle \frac{{6 — 9я}}{{2i}}\)
Показать все решения Скрыть все решения
Показать обсуждение
Итак, в каждом случае мы действительно рассматриваем деление двух комплексных чисел. Однако основная идея здесь заключается в том, что мы хотим записать их в стандартной форме. Стандартная форма не позволяет никаким \(i\) стоять в знаменателе. Итак, нам нужно получить \(i\) из знаменателя.
На самом деле это довольно просто, если вспомнить, что комплексное число, умноженное на его сопряженное, является действительным числом. Итак, если мы умножим числитель и знаменатель на сопряженное знаменателю, мы сможем исключить \(i\) из знаменателя. 92}}} = \frac{{16 + 8i}}{5} = \frac{{16}}{5} + \frac{8}{5}i\]
d \(\displaystyle \frac{{6 — 9i}}{{2i}}\) Показать решение
Этот немного отличается от предыдущих, так как знаменатель является чисто мнимым числом. Это можно сделать так же, как и предыдущие, но есть немного более простой способ решить задачу.
Сначала разбейте дробь следующим образом.
\[\фракция{{6 — 98} & = 1\конец{выравнивание*}\]
Вы видите узор? Все степени if \(i\) можно свести к одному из четырех возможных ответов, и они повторяются через каждые четыре степени. Это может быть удобным фактом для запоминания.
Теперь нам нужно решить проблему с квадратными корнями из отрицательных чисел. Из раздела о радикалах мы знаем, что можем сделать следующее.
\[6 = \sqrt {36} = \sqrt {\left( 4 \right)\left( 9 \right)} = \sqrt 4 \,\sqrt 9= \влево( 2 \вправо)\влево( 3 \вправо) = 6\]
Другими словами, мы можем разложить произведение квадратного корня на произведение квадратных корней, если оба числа положительны.
Оказывается, мы можем сделать то же самое, если одно из чисел отрицательное. Например,
\[6i = \sqrt { — 36} = \sqrt {\left( { — 4} \right)\left( 9 \right)} = \sqrt { — 4} \,\sqrt 9 = \left( {2i } \вправо)\влево( 3 \вправо) = 6i\] 92} = — 6\]
Мы можем обобщить это как набор правил. Если \(a\) и \(b\) оба положительные числа, то
\[\begin{align*}\sqrt a \,\sqrt b & = \sqrt {ab} \\ \sqrt { — a} \,\sqrt b & = \sqrt { — ab} \\ \sqrt a \ , \ sqrt { — b} & = \ sqrt { — ab} \\ & \\ \ sqrt { — a} \, \ sqrt { — b} & \ ne \ sqrt {\ left ( { — a} \ right) \left( { — b} \right)} \end{align*}\]
Почему это так важно, чтобы об этом беспокоиться? Рассмотрим следующий пример.
Пример 4 Умножьте следующие числа и запишите ответ в стандартной форме. \[\left( {2 — \sqrt { — 100} } \right)\left( {1 + \sqrt { — 36} } \right)\]
Показать решение
Если бы мы умножили это в его нынешнем виде, мы бы получили
\[\left( {2 — \sqrt { — 100} } \right)\left( {1 + \sqrt { — 36} } \right) = 2 + 2\sqrt { — 36} — \sqrt { — 100 } — \sqrt { — 36} \, \sqrt { — 100} \]
Теперь, если бы мы не были осторожны, мы, вероятно, объединили бы два корня в последнем члене в один, что невозможно!
Итак, есть общее практическое правило при работе с квадратными корнями из отрицательных чисел. Столкнувшись с ними, первое, что вы всегда должны делать, это преобразовать их в комплексные числа. Если мы будем следовать этому правилу, мы всегда получим правильный ответ.
Итак, давайте решим эту задачу так, как надо. 2} = 62 + 2i\]
2} = 62 + 2i\]
Эмпирическое правило, приведенное в предыдущем примере, достаточно важно, чтобы повторить его. Столкнувшись с квадратными корнями из отрицательных чисел, первое, что вы должны сделать, это преобразовать их в комплексные числа.
Есть еще одна тема, которую нам нужно затронуть, прежде чем покинуть этот раздел. Как мы уже отмечали в разделе о радикалах, хотя \(\sqrt 9 = 3\) на самом деле есть два числа, которые мы можем возвести в квадрат, чтобы получить 9. Мы можем возвести в квадрат и 3, и -3.
То же верно и для квадратных корней из отрицательных чисел. Как мы видели ранее \(\sqrt { — 92} = — 9\]
и поэтому, если возвести в квадрат -3\(i\), мы также получим -9. Итак, при извлечении квадратного корня из отрицательного числа на самом деле есть два числа, которые мы можем возвести в квадрат, чтобы получить число под радикалом. Однако мы ВСЕГДА будем брать положительное число в качестве значения квадратного корня точно так же, как мы делаем это с квадратным корнем из положительных чисел.
Что такое комплексные числа?
Диаграмма Аргана
Вводя комплексные числа и обозначения для них, эта статья объединяет в одну большую «картину» некоторые тесно связанные элементарные идеи, такие как векторы, экспоненциальные и тригонометрические функции и их производные. 92=-1$ и объединить эти объекты по обычным правилам алгебры. Мы отождествляем действительное число $x$ с точкой $(x,0)$, а комплексное число $x+0i$ также с точкой $(x,0)$, поэтому мы видим, что действительные числа на самом деле являются подмножеством комплексных чисел. Аналогичным образом отождествим комплексное число $i$ с точкой $(0,1)$.
Арифметика комплексных чисел
Прежде чем мы будем довольны тем, что эти «объекты» называются числами, мы должны увидеть, что их можно складывать, вычитать, умножать и делить и что они подчиняются правилам элементарной алгебры. 92}$$, который снова имеет вид [действительное число + $i\times$действительное число]. Например
$${{3+i}\over {1+2i}} = {{(3+i)(1-2i)}\over 5} = {5-5i \over 5} = 1-i. $$
$$
Комплексные числа как векторы
Правила сложения и вычитания комплексных чисел, а именно сложения или вычитания соответствующих компонентов, точно такие же, как правила сложения и вычитания векторов. Комплексные числа ведут себя точно так же, как двумерные векторы. Действительно, действительные числа — это одномерные векторы (на прямой), а комплексные числа — двумерные векторы (на плоскости).
Возникает естественный вопрос: «Могут ли существовать трехмерные числа, соответствующие трехмерным векторам, и могут ли существовать числа более высокой размерности?». Ответ — нет. Единственные наборы чисел, которые удовлетворяют всем обычным правилам элементарной алгебры (то есть удовлетворяют аксиомам поля), имеют размерность один или два. Мы можем определить деление комплексных чисел, но мы не можем определить
разделение трехмерных векторов. Не существует трехмерных или многомерных чисел, подчиняющихся всем правилам элементарной алгебры. Хотя существуют четырехмерные числа, называемые кватернионами, их умножение не является коммутативным, то есть для некоторых кватернионов $p$ и $q$ имеем $p q \neq q p$. 92+2x+5=0$ имеют решения $${-2\pm \sqrt -16 \over 2}= -1\pm 2i.$$ Более того, можно доказать красивую Фундаментальную теорему алгебры, которая утверждает что не только квадратные уравнения всегда имеют два корня, а кубические уравнения всегда имеют три корня, но и всякое полиномиальное уравнение степени
$n$ имеет ровно $n$ корней.
92+2x+5=0$ имеют решения $${-2\pm \sqrt -16 \over 2}= -1\pm 2i.$$ Более того, можно доказать красивую Фундаментальную теорему алгебры, которая утверждает что не только квадратные уравнения всегда имеют два корня, а кубические уравнения всегда имеют три корня, но и всякое полиномиальное уравнение степени
$n$ имеет ровно $n$ корней.
Модуль и аргумент комплексного числа
При определении тригонометрических функций $\sin\theta$ и $\cos\theta$ мы связываем значения этих функций с координатами точек на единичной окружности (окружность радиусом в одну единицу и центрировать начало координат). На этой окружности, если $P$ — точка, угол между осью $x-$ и $O P$ (измеренный против часовой стрелки) равен $\theta$, то координаты $P$
задаются $x=\cos\theta$ и $y=\sin\theta$. Когда луч $O P$ повернулся на угол 360 градусов или $2\pi$ радиан, он повторяет тот же путь и повторяет те же значения $\cos\theta$ и $\sin\theta$, показывая, что эти функции являются периодическими с периодом $2\pi$. 2)$$.
2)$$.
Если две точки $P$ и $Q$ равноудалены от начала координат, то есть если они обе лежат на окружности радиуса $r$ с центром в начале координат, то длина дуги этой окружности между $ P$ и $Q$ равно $r$, умноженной на разницу их аргументов, измеренную в радианах.
Комплексные числа и преобразования на плоскости
Функции комплексной переменной обеспечивают эффективный способ математической работы с преобразованиями на плоскости. Изометрии — это преобразования, сохраняющие углы и расстояния. Отражения, переводы, вращения и скользящие отражения являются изометриями. Все изометрии представляют собой комбинации отражений. Для ознакомления с этой идеей см. Mirror Mirror и . ..на стене. Чтобы продолжить идею о том, что все изометрии являются комбинациями отражений, и чтобы увидеть, как функции сложной переменной используются для работы с преобразованиями, см. Следы. |
Немного истории комплексных чисел
Исторически эти числа считались просто математическими инструментами, полезными для решения уравнений, и назывались мнимыми числами. {i\pi} = -1.$$
{i\pi} = -1.$$
Мы предполагаем, что читатель знаком с тем фактом, что производная от $\sin\theta$ по $\theta$ равна $\cos\theta$, а производная от $\cos\theta$ равна $-\ грех \тета$. Следовательно, производная от $\cos\theta + i\sin\theta$ равна $$-\sin\theta + i\cos\theta = i(\cos\theta + i\sin\theta)$$, так что $f (\theta)= \cos \theta + i \sin \theta$ удовлетворяет дифференциальному уравнению
$${\mathrm{d}f(\theta) \over \mathrm{d\theta}} = {i}f(\theta).\quad (1)$$ Показательная функция — это функция $g(x ) = \exp(x)$, которое удовлетворяет дифференциальному уравнению $${\mathrm{d}g(x)\over \mathrm{dx}} = g(x).$$ Отсюда следует, что если $g(\theta ) = \exp(i\theta)$, тогда $${dg(\theta) \over \mathrm{d\theta}} = i g(\theta).\quad (2)$$ но это точно такой же дифференциал уравнение как уравнение
(1) поэтому функции $f$ и $g$ могут отличаться только на константу, так как у них одна и та же производная. Полагая $\theta = 0$, мы видим, что $f(0)=g(0)=1$, так что эти две функции должны фактически быть идентичными. {i\pi} = -1.$$ Это доказательство использует дифференциал
уравнений, и это не просто упражнение в их решении.
{i\pi} = -1.$$ Это доказательство использует дифференциал
уравнений, и это не просто упражнение в их решении.
См. также статью Введение в комплексные числа.
3.1 Комплексные числа. Предварительное исчисление 2e
Цели обучения
В этом разделе вы:
- Выразите квадратные корни из отрицательных чисел кратными ii.
- Нанесение комплексных чисел на комплексную плоскость.
- Сложение и вычитание комплексных чисел.
- Умножать и делить комплексные числа.
Изучение математики постоянно саморазвивается. Отрицательные целые числа, например, заполняют пустоту, оставленную набором положительных целых чисел. Множество рациональных чисел, в свою очередь, заполняет пустоту, оставленную множеством целых чисел. Множество действительных чисел заполняет пустоту, оставленную множеством рациональных чисел. Неудивительно, что множество действительных чисел также имеет пустоты. Например, у нас до сих пор нет решения таких уравнений, как
x2+4=0x2+4=0
Наши лучшие предположения могут быть +2 или –2. Но если мы проверим +2 в этом уравнении, это не сработает. Если мы проверим -2, это не сработает. Если мы хотим получить решение этого уравнения, нам придется пойти дальше, чем мы до сих пор. В конце концов, до сих пор мы описывали квадратный корень из отрицательного числа как неопределенный. К счастью, есть другая система чисел, которая обеспечивает решение подобных проблем. В этом разделе мы рассмотрим эту систему счисления и то, как в ней работать.
Но если мы проверим +2 в этом уравнении, это не сработает. Если мы проверим -2, это не сработает. Если мы хотим получить решение этого уравнения, нам придется пойти дальше, чем мы до сих пор. В конце концов, до сих пор мы описывали квадратный корень из отрицательного числа как неопределенный. К счастью, есть другая система чисел, которая обеспечивает решение подобных проблем. В этом разделе мы рассмотрим эту систему счисления и то, как в ней работать.
Выражение квадратных корней из отрицательных чисел как кратных
iМы знаем, как найти квадратный корень из любого положительного действительного числа. Аналогичным образом мы можем найти квадратный корень из отрицательного числа. Отличие в том, что рут не настоящий. Если значение подкоренной черты отрицательное, корень называется мнимым числом . Мнимое число ii определяется как квадратный корень из минус 1.
−1=i−1=i
Итак, используя свойства радикалов,
i2=(−1)2=−1i2=(−1)2=−1
Квадратный корень любого отрицательного числа можно записать как кратное i. i. Возьмем квадратный корень из –25.
i. Возьмем квадратный корень из –25.
−25=25⋅(−1) =25−1 =5i−25=25⋅(−1) =25−1 =5i
Мы используем 5i5i, а не −5i−5i потому что главный корень числа 2525 является положительным корнем.
Комплексное число представляет собой сумму действительного числа и мнимого числа. Комплексное число выражается в стандартной форме: a+bia+bi, где aa — действительная часть, а bibi — мнимая часть. Например, 5+2i5+2i — комплексное число. Так же и 3+43i.3+43i.
Мнимые числа отличаются от действительных чисел, потому что возведение в квадрат мнимого числа дает отрицательное действительное число. Вспомните, когда возводится в квадрат положительное действительное число, результатом является положительное действительное число, а когда возводится в квадрат отрицательное действительное число, снова получается положительное действительное число. Комплексные числа представляют собой комбинацию действительных и мнимых чисел.
Мнимые и комплексные числа
Комплексное число — это число вида a+bia+bi, где
- аа — действительная часть комплексного номера.

- биби — мнимая часть комплексного числа.
Если b=0,b=0, то a+bia+bi — действительное число. Если a=0a=0 и bb не равно 0, комплексное число называется мнимым числом . Мнимое число – это четный корень из отрицательного числа.
Как
Дано мнимое число, представить его в стандартной форме.
- Запишите -a-a как a-1.a-1.
- Экспресс-1-1 как i.i.
- Напишите a⋅ia⋅i в простейшей форме.
Пример 1
Выражение мнимого числа в стандартной форме
Выражение −9−9 в стандартной форме.
Решение
−9=9−1=3i−9=9−1=3i
В стандартной форме это 0+3i.0+3i.
Попытайся #1
Express −24−24 в стандартной форме.
Нанесение комплексного числа на комплексную плоскость
Мы не можем нанести на числовую прямую комплексные числа, как настоящие числа. Однако мы все еще можем представить их графически. Чтобы представить комплексное число, нам нужно обратиться к двум компонентам числа. Мы используем комплексную плоскость, которая представляет собой систему координат, в которой горизонтальная ось представляет действительную составляющую, а вертикальная ось представляет мнимую составляющую. Комплексные числа — это точки на плоскости, выраженные в виде упорядоченных пар (a,b),(a,b), где aa представляет собой координату по горизонтальной оси, а bb представляет собой координату по вертикальной оси.
Однако мы все еще можем представить их графически. Чтобы представить комплексное число, нам нужно обратиться к двум компонентам числа. Мы используем комплексную плоскость, которая представляет собой систему координат, в которой горизонтальная ось представляет действительную составляющую, а вертикальная ось представляет мнимую составляющую. Комплексные числа — это точки на плоскости, выраженные в виде упорядоченных пар (a,b),(a,b), где aa представляет собой координату по горизонтальной оси, а bb представляет собой координату по вертикальной оси.
Рассмотрим число −2+3i.−2+3i. Действительная часть комплексного числа равна −2−2, а мнимая часть равна 3i.3i. Мы наносим упорядоченную пару (−2,3)(−2,3) для представления комплексного числа −2+3i−2+3i, как показано на рисунке 1 .
Рисунок 1
Сложный самолет
В комплексной плоскости горизонтальная ось является реальной осью, а вертикальная ось — мнимой осью, как показано на рисунке 2 .
Рисунок 2
907:50 КакДля заданного комплексного числа представить его компоненты на комплексной плоскости.
- Определите действительную и мнимую части комплексного числа.
- Перемещайтесь по горизонтальной оси, чтобы показать действительную часть числа.
- Перемещение параллельно вертикальной оси, чтобы показать мнимую часть числа.
- Поставьте точку.
Пример 2
Нанесение комплексного числа на комплексную плоскость
Нанесите комплексное число 3−4i3−4i на комплексную плоскость.
Решение
Действительная часть комплексного числа равна 3,3, а мнимая часть равна −4i.−4i. Наносим упорядоченную пару (3,−4)(3,−4), как показано на рисунке 3.
Рисунок 3
Попытайся #2
Нанесите комплексное число −4−i−4−i на комплексную плоскость.
Сложение и вычитание комплексных чисел
Как и с вещественными числами, мы можем выполнять арифметические операции над комплексными числами. Чтобы сложить или вычесть комплексные числа, мы объединяем действительные части и объединяем мнимые части.
Комплексные числа: сложение и вычитание
Сложение комплексных чисел:
(a+bi)+(c+di)=(a+c)+(b+d)i(a+bi)+(c+di)=(a+c)+ (b+d)i
Вычитание комплексных чисел:
(a+bi)−(c+di)=(a−c)+(b−d)i(a+bi)−(c+di)= (а-в)+(б-г)i
Как
Даны два комплексных числа, найдите их сумму или разность.
- Определите действительную и мнимую части каждого числа.
- Добавьте или вычтите действительные части.
- Сложите или вычтите мнимые части.
Пример 3
Добавление комплексных чисел
Добавьте 3-4i3-4i и 2+5i. 2+5i.
2+5i.
Решение
Складываем действительные части и складываем мнимые части.
(a+bi)+(c+di)=(a+c)+(b+d)i(3−4i)+(2+5i)=(3+2)+(−4+5) i =5+i(a+bi)+(c+di)=(a+c)+(b+d)i(3−4i)+(2+5i)=(3+2)+(−4 +5)i =5+i
Попытайся #3
Вычесть 2+5i2+5i из 3–4i.3–4i.
Умножение комплексных чисел
Умножение комплексных чисел очень похоже на умножение биномов. Основное отличие состоит в том, что мы работаем с реальной и мнимой частями отдельно.
Умножение комплексного числа на действительное число
Начнем с умножения комплексного числа на действительное число. Мы распределяем действительное число так же, как и биномиальное. Так, например,
Как
Даны комплексное число и действительное число, умножьте их, чтобы найти произведение.
- Используйте свойство дистрибутива.
- Упростить.
Пример 4
Умножение комплексного числа на действительное число
Найдите произведение 4(2+5i).4(2+5i).
Решение
Распределить 4.
4(2+5i)=(4⋅2)+(4⋅5i)=8+20i4(2+5i)=(4⋅2)+(4⋅5i)=8+20i
Попытайся #4
Найдите произведение −4(2+6i).−4(2+6i).
Умножение комплексных чисел
Теперь давайте перемножим два комплексных числа. Мы можем использовать либо распределительное свойство, либо метод FOIL. Напомним, что FOIL — это аббревиатура для умножения первого, внешнего, внутреннего и последнего членов вместе. Используя либо распределительное свойство, либо метод FOIL, мы получаем
(a+bi)(c+di)=ac+adi+bci+bdi2(a+bi)(c+di)=ac+adi+bci+bdi2
Поскольку i2=−1,i2=−1, у нас
(a+bi)(c+di)=ac+adi+bci−bd(a+bi)(c+di)=ac+adi+bci−bd
Для упрощения объединим действительные части, и мы соединить воображаемые части.
(a+bi)(c+di)=(ac−bd)+(ad+bc)i(a+bi)(c+di)=(ac−bd)+(ad+bc)i
Как
Даны два комплексных числа, умножьте их, чтобы найти произведение.
- Используйте свойство распределения или метод FOIL.
- Упростить.
Пример 5
Умножение комплексного числа на комплексное число
Умножение (4+3i)(2−5i).(4+3i)(2−5i).
Решение
Использование (a+bi)(c+di)=(ac−bd)+(ad+bc)i(a+bi)(c+di)=(ac−bd)+(ad+bc)i
(4+3i)(2−5i)=(4⋅2−3⋅(−5))+(4⋅(−5)+3⋅2)i = (8+15)+(−20+6) i =23−14i(4+3i)(2−5i)=(4⋅2−3⋅(−5))+(4⋅(−5)+3⋅2)i = (8+15)+( −20+6)i =23−14i
Попытайся #5
Умножить (3−4i)(2+3i).(3−4i)(2+3i).
Деление комплексных чисел
Деление двух комплексных чисел сложнее, чем сложение, вычитание и умножение, потому что мы не можем делить на мнимое число, а это означает, что у любой дроби должен быть действительный знаменатель. Нам нужно найти член, на который мы можем умножить числитель и знаменатель, который исключит мнимую часть знаменателя, чтобы мы получили действительное число в качестве знаменателя. Этот член называется комплексно-сопряженным знаменателем, который находится при изменении знака мнимой части комплексного числа. Другими словами, комплексное сопряжение a+bia+bi есть a−bi.a−bi.
Нам нужно найти член, на который мы можем умножить числитель и знаменатель, который исключит мнимую часть знаменателя, чтобы мы получили действительное число в качестве знаменателя. Этот член называется комплексно-сопряженным знаменателем, который находится при изменении знака мнимой части комплексного числа. Другими словами, комплексное сопряжение a+bia+bi есть a−bi.a−bi.
Обратите внимание, что комплексно-сопряженные числа имеют обратную связь: комплексно-сопряженное число a+bia+bi равно a-bi,a-bi, а комплексно-сопряженное число a-bia-bi равно a+bi.a+bi. Кроме того, когда квадратное уравнение с действительными коэффициентами имеет комплексные решения, решения всегда комплексно сопряжены друг другу.
Предположим, мы хотим разделить c+dic+di на a+bi,a+bi, где ни aa, ни bb не равны нулю. Сначала запишем деление в виде дроби, затем найдем комплексно-сопряженную часть знаменателя и умножим.
c+dia+bi где a≠0 и b≠0c+dia+bi где a≠0 и b≠0
Умножить числитель и знаменатель на комплексно-сопряженное число знаменателя.
(c+di)(a+bi)⋅(a−bi)(a−bi)=(c+di)(a−bi)(a+bi)(a−bi)(c+di)(a +bi)⋅(a−bi)(a−bi)=(c+di)(a−bi)(a+bi)(a−bi)
Применить распределительное свойство.
=ca-cbi+adi-bdi2a2-abi+abi-b2i2=ca-cbi+adi-bdi2a2-abi+abi-b2i2
Упростите, помня, что i2=-1.i2=-1.
=ca-cbi+adi-bd(-1)a2-abi+abi-b2(-1)=(ca+bd)+(ad-cb)ia2+b2=ca-cbi+adi-bd(- 1)a2-abi+abi-b2(-1)=(ca+bd)+(ad-cb)ia2+b2
Комплексное сопряжение
Комплексное сопряжение комплексного числа a+bia+bi равно a−bi.a−bi. Его находят изменением знака мнимой части комплексного числа. Действительная часть числа остается неизменной.
- Когда комплексное число умножается на его комплексно-сопряженное, результатом является действительное число.
- Когда комплексное число добавляется к его комплексно-сопряженному, результатом является действительное число.
Пример 6
Нахождение комплексно-сопряженных чисел
Нахождение комплексно-сопряженных чисел каждого числа.
- ⓐ 2+i52+i5
- ⓑ −12i−12i
Решение
- ⓐ Номер уже имеет форму a+bi.a+bi. Комплексно-сопряженным является a−bi,a−bi или 2−i5.2−i5.
- ⓑ Мы можем переписать это число в виде a+bia+bi как 0−12i.0−12i. Комплексно-сопряженное число равно a−bi,a−bi или 0+12i.0+12i. Это можно записать просто как 12i.12i.
Анализ
Хотя мы видели, что мы можем найти комплексно-сопряженные числа мнимого числа, на практике мы обычно находим комплексно-сопряженные только комплексные числа с вещественной и мнимой компонентами. Чтобы получить действительное число из мнимого числа, мы можем просто умножить на i.i.
Как
Даны два комплексных числа, разделите одно на другое.
- Запишите задачу деления в виде дроби.
- Определите комплексное сопряжение знаменателя.

- Умножьте числитель и знаменатель дроби на комплексно-сопряженную часть знаменателя.
- Упростить.
Пример 7
Деление комплексных чисел
Разделить (2+5i)(2+5i) на (4−i).(4−i).
Решение
Начнем с того, что запишем задачу в виде дроби.
(2+5i)(4−i)(2+5i)(4−i)
Затем умножаем числитель и знаменатель на комплексное сопряжение знаменателя.
(2+5i)(4−i)⋅(4+i)(4+i)(2+5i)(4−i)⋅(4+i)(4+i)
Чтобы умножить два сложных чисел, мы расширяем произведение так же, как и с многочленами (процесс, обычно называемый FOIL).
(2+5i)(4−i)⋅(4+i)(4+i)=8+2i+20i+5i216+4i−4i−i2 =8+2i+20i+5(−1)16 +4i−4i−(−1)Becausei2=−1 =3+22i17 =317+2217iРазделите действительную и мнимую части. 2i+20i+5i216+4i — 4i — I2 = 8+2i+20i+5 (−1) 16+4i — 4i — ( — 1), потому что 2 = −1 = 3+22i17 = 317+2217Iseparate реальные и воображаемые части.
Обратите внимание, что это выражает частное в стандартной форме.
Пример 8
Подстановка комплексного числа в полиномиальную функцию
Пусть f(x)=x2−5x+2.f(x)=x2−5x+2. Вычислите f(3+i).f(3+i).
Решение
Подставить x=3+ix=3+i в функцию f(x)=x2−5x+2f(x)=x2−5x+2 и упростить.
Анализ
Мы пишем f(3+i)=−5+i.f(3+i)=−5+i. Обратите внимание, что на входе 3+i3+i, а на выходе -5+i.-5+i.
Попытайся #6
Пусть f(x)=2×2−3x.f(x)=2×2−3x. Вычислите f(8−i).f(8−i).
Пример 9
Замена мнимого числа в рациональной функции
Пусть f(x)=2+xx+3.f(x)=2+xx+3. Вычислите f(10i).f(10i).
Решение
Подставьте x=10ix=10i и упростите.
2+10i10i+3Подставить 10i на x.2+10i3+10iПереписать знаменатель в стандартной форме. 2+10i3+10i⋅3–10i3–10iПодготовиться к умножению числителя и знаменателя i на комплексно-сопряженное число 9–1i0+30–20 знаменателя.6–30i+30i–100i2Умножьте, используя свойство распределения или метод FOIL.6–20i+30i–100(–1)9–30i+30i–100(–1)Замените –1 на i2.106+10i109Упростите.106109+10109iРазделите действительную и мнимую части.2+10i10i+3Подставить 10i вместо x.2+10i3+10iПереписать знаменатель в стандартной форме.2+10i3+10i⋅3–10i3–10iПодготовиться к умножению числителя и знаменателя на комплексно-сопряженное число знаменателя.6–20i 30i–100i29–30i+30i–100i2Умножьте, используя распределительное свойство или метод FOIL.6–20i+30i–100(–1)9–30i+30i–100(–1)Замените–1 на i2.106+10i109Упростите.106109+10109iРазделите действительную и мнимую части.
2+10i3+10i⋅3–10i3–10iПодготовиться к умножению числителя и знаменателя i на комплексно-сопряженное число 9–1i0+30–20 знаменателя.6–30i+30i–100i2Умножьте, используя свойство распределения или метод FOIL.6–20i+30i–100(–1)9–30i+30i–100(–1)Замените –1 на i2.106+10i109Упростите.106109+10109iРазделите действительную и мнимую части.2+10i10i+3Подставить 10i вместо x.2+10i3+10iПереписать знаменатель в стандартной форме.2+10i3+10i⋅3–10i3–10iПодготовиться к умножению числителя и знаменателя на комплексно-сопряженное число знаменателя.6–20i 30i–100i29–30i+30i–100i2Умножьте, используя распределительное свойство или метод FOIL.6–20i+30i–100(–1)9–30i+30i–100(–1)Замените–1 на i2.106+10i109Упростите.106109+10109iРазделите действительную и мнимую части.
Попытайся #7
Пусть f(x)=x+1x−4.f(x)=x+1x−4. Вычислите f(−i).f(−i).
Упрощающие степени
i Степени ii цикличны. Давайте посмотрим, что произойдет, если мы возведем ii в возрастающую степень.
i1=ii2=-1i3=i2⋅i=-1⋅i=-ii4=i3⋅i=-i⋅i=-i2=-(-1)=1i5=i4⋅i=1⋅i=ii1= ii2=-1i3=i2⋅i=-1⋅i=-ii4=i3⋅i=-i⋅i=-i2=-(-1)=1i5=i4⋅i=1⋅i=i
Мы можем видим, что когда мы добираемся до пятой степени i,i, оно равно первой степени. Продолжая умножать ii само на себя для увеличения степени, мы увидим цикл 4. Давайте рассмотрим следующие 4 степени i.i.
i6=i5⋅i=i⋅i=i2=−1i7=i6⋅i=i2⋅i=i3=−ii8=i7⋅i=i3⋅i=i4=1i9=i8⋅i=i4⋅i= i5=ii6=i5⋅i=i⋅i=i2=−1i7=i6⋅i=i2⋅i=i3=−ii8=i7⋅i=i3⋅i=i4=1i9=i8⋅i=i4⋅i= i5=i
Пример 10
Упрощение степеней II
Оценка i35.i35.
Решение
Так как i4=1,i4=1, мы можем упростить задачу, выделив как можно больше множителей i4i4. Для этого сначала определите, сколько раз 4 входит в число 35: 35=4⋅8+3,35=4⋅8+3.
i35=i4⋅8+3=i4⋅8⋅i3=(i4)8⋅i3=18⋅i3=i3=−ii35=i4⋅8+3=i4⋅8⋅i3=(i4)8⋅i3 =18⋅i3=i3=−i
вопросы и ответы
Можем ли мы написать i35i35 другими полезными способами?
Как мы видели в примере 10, мы уменьшили i35i35 до i3i3, разделив показатель степени на 4 и используя остаток, чтобы найти упрощенную форму. Но, возможно, другая факторизация i35i35 может оказаться более полезной. В таблице 1 показаны некоторые другие возможные факторизации.
Но, возможно, другая факторизация i35i35 может оказаться более полезной. В таблице 1 показаны некоторые другие возможные факторизации.
| Факторизация i35i35 | i34⋅ii34⋅i | i33⋅i2i33⋅i2 | i31⋅i4i31⋅i4 | i19⋅i16i19⋅i16 |
| Уменьшенная форма | (i2) 17⋅i(i2)17⋅i | i33⋅(−1)i33⋅(−1) | i31⋅1i31⋅1 | i19⋅(i4)4i19⋅(i4)4 |
| Упрощенная форма | (−1)17⋅i(−1)17⋅i | −i33−i33 | i31i31 | i19i19 |
Стол 1
Каждый из них в конечном итоге приведет к ответу, который мы получили выше, но может потребоваться несколько больше шагов, чем в нашем предыдущем методе.
3.1 Секционные упражнения
устно
1.
Объясните, как складывать комплексные числа.
2.
Каков основной принцип умножения комплексных чисел?
3.
Приведите пример, показывающий, что произведение двух мнимых чисел не всегда мнимое.
4.
Что является характеристикой графика действительного числа в комплексной плоскости?
Алгебраический
В следующих упражнениях оцените алгебраические выражения.
5.
Iff(x)=x2+x−4,Iff(x)=x2+x−4, вычислить f(2i).f(2i).
6.
Iff(x)=x3−2,Iff(x)=x3−2, вычислить f(i).f(i).
7.
Iff(x)=x2+3x+5,Iff(x)=x2+3x+5, оценить f(2+i). f(2+i).
f(2+i).
8.
Iff(x)=2×2+x−3,Iff(x)=2×2+x−3, вычислить f(2−3i).f(2−3i).
9.
Iff(x)=x+12−x,Iff(x)=x+12−x, вычислить f(5i).f(5i).
10.
Iff(x)=1+2xx+3,Iff(x)=1+2xx+3, вычислить f(4i).f(4i).
Графический
В следующих упражнениях определите количество действительных и недействительных решений для каждой показанной квадратичной функции.
11.
12.
Для следующих упражнений нанесите комплексные числа на комплексную плоскость.
13.
1-2i1-2i
14.
−2+3i−2+3i
15.
II
16.
−3−4i−3−4i
Цифровой
Для следующих упражнений выполните указанную операцию и выразите результат в виде упрощенного комплексного числа.
17.
(3+2i)+(5−3i)(3+2i)+(5−3i)
18.
(−2−4i)+(1+6i)(−2−4i)+(1+6i)
19.
(−5+3i)−(6−i)(−5+3i)−(6−i)
20.
(2−3i)−(3+2i)(2−3i)−(3+2i)
21.
(-4+4i)-(-6+9i)(-4+4i)-(-6+9i)
22.
(2+3i)(4i)(2+3i)(4i)
23.
(5−2i)(3i)(5−2i)(3i)
24.
(6−2i)(5)(6−2i)(5)
25.
(−2+4i)(8)(−2+4i)(8)
26.
(2+3i)(4−i)(2+3i)(4−i)
27.
(-1+2i)(-2+3i)(-1+2i)(-2+3i)
28.
(4−2i)(4+2i)(4−2i)(4+2i)
29.
(3+4i)(3−4i)(3+4i)(3−4i)
30.
3+4i23+4i2
31.
6-2i36-2i3
32.
−5+3i2i−5+3i2i
33.
6+4ii6+4ii
34.
2−3i4+3i2−3i4+3i
35.
3+4i2-i3+4i2-i
36.
2+3i2−3i2+3i2−3i
37.
−9+3−16−9+3−16
38.
−−4−4−25−4−4−25
39.
2+-1222+-122
40.
4+-2024+-202
41.
i8i8
42.
i15i15
43.
i22i22
Технология
В следующих упражнениях используйте калькулятор, чтобы ответить на вопросы.
44.
Вычислить (1+i)k(1+i)k для k=4, 8 и 12.k=4, 8 и 12. Предсказать значение, если k=16.k=16.
45.
Вычислить (1−i)k(1−i)k для k=2, 6 и 10.k=2, 6 и 10. Предсказать значение, если k=14.k=14.
46.
Вычислить (1+i)k−(1−i)k(1+i)k−(1−i)k для k=4, 8 и 12k=4, 8 и 12. Предсказать значение для к=16.к=16.
47.
Покажите, что решение x6+1=0x6+1=0 равно 32+12i.32+12i.
48.
Покажите, что решение x8−1=0x8−1=0 равно 22+22i.22+22i.
Расширения
В следующих упражнениях оцените выражения, записав результат в виде упрощенного комплексного числа.
49.
1i+4i31i+4i3
50.
1i11−1i211i11−1i21
51.
i7(1+i2)i7(1+i2)
52.
i-3+5i7i-3+5i7
53.
(2+i)(4−2i)(1+i)(2+i)(4−2i)(1+i)
54.
(1+3i)(2−4i)(1+2i)(1+3i)(2−4i)(1+2i)
55.
(3+i)2(1+2i)2(3+i)2(1+2i)2
56.
3+2i2+i+(4+3i)3+2i2+i+(4+3i)
57.
4+ii+3−4i1−i4+ii+3−4i1−i
58.
3+2i1+2i−2−3i3+i3+2i1+2i−2−3i3+i
Комплексные номера
Обзор
[Вернитесь к началу страницы]
Комплексные числа возникли потому, что математики хотели иметь возможность решать математические задачи, которые нельзя было решить, используя только действительные числа. В шестнадцатом веке нашей эры ряд математиков пытались найти способ решения различных типов полиномиальных уравнений, в том числе второй степени (квадратичных) уравнений и особенно третьей степени (кубических) уравнений. Им мешал тот факт, что такие уравнения были еще относительно плохо изучены. Сегодня мы знаем, что n полиномиальное уравнение степени будет иметь в общей сложности n корней (решений), включая корни, которые могут быть комплексными числами. Это знание воплощено в основной теореме алгебры . Однако эта теорема не могла появиться в какой-либо значимой форме до семнадцатого века нашей эры. Еще одна проблема заключалась в том, что многие математики по-прежнему не хотели признавать законность отрицательных чисел или допускать, что уравнения могут иметь отрицательные корни (что, конечно, они часто делают).
Им мешал тот факт, что такие уравнения были еще относительно плохо изучены. Сегодня мы знаем, что n полиномиальное уравнение степени будет иметь в общей сложности n корней (решений), включая корни, которые могут быть комплексными числами. Это знание воплощено в основной теореме алгебры . Однако эта теорема не могла появиться в какой-либо значимой форме до семнадцатого века нашей эры. Еще одна проблема заключалась в том, что многие математики по-прежнему не хотели признавать законность отрицательных чисел или допускать, что уравнения могут иметь отрицательные корни (что, конечно, они часто делают).
В авангарде поиска решений различных форм кубического полиномиального уравнения стояли итальянский математик и инженер Никколо Фонтана Тарталья (1499-1557) и итальянский математик Джероламо Кардано (1501-1576). Тарталья придумал общее решение, которое работало для всех форм кубического уравнения, которое он (несколько неохотно) передал Кардано при условии, что Кардано никому не раскроет решение, пока у Тартальи не будет возможности опубликовать свои выводы. . Хотя впоследствии он отказался от своего слова и опубликовал решение в своей книге по алгебре Ars Magna в 1545 году, он, по крайней мере, имел порядочность признать вклад Тартальи. Тем временем Кардано обнаружил нечто довольно странное, когда попытался решить следующее кубическое уравнение:
. Хотя впоследствии он отказался от своего слова и опубликовал решение в своей книге по алгебре Ars Magna в 1545 году, он, по крайней мере, имел порядочность признать вклад Тартальи. Тем временем Кардано обнаружил нечто довольно странное, когда попытался решить следующее кубическое уравнение:
x 3 = 15 x + 4
Выражение, к которому он пришел, применив решение Тартальи к этому уравнению, включало в качестве одного из членов квадратный корень из минус сто двадцать один (√-121). Это озадачило Кардано, потому что он знал, что квадратный корень из отрицательного числа не может быть выражен как действительное число. И все же он также знал, что это должно в конечном итоге привести к реальному решению, а именно 90 231 x 90 232 = 4. Сам Тарталья не мог пролить свет на этот вопрос. Впоследствии Кардано опубликовал решение подобных задач в своем Ars Magna , в котором каким-то образом ухитрился манипулировать такими терминами, но, по его собственному признанию, не до конца понимал собственные расчеты. По этой причине Кардано часто приписывают то, что он был первым математиком, использовавшим комплексные числа, но, скорее, он был первым, кто продемонстрировал, что такие вещи могут существовать. Однако он был первым математиком, придумавшим решения полиномиальных уравнений, которые были отрицательными числами (которые он назвал 9).0231 фиктивные номера ).
По этой причине Кардано часто приписывают то, что он был первым математиком, использовавшим комплексные числа, но, скорее, он был первым, кто продемонстрировал, что такие вещи могут существовать. Однако он был первым математиком, придумавшим решения полиномиальных уравнений, которые были отрицательными числами (которые он назвал 9).0231 фиктивные номера ).
Следующая глава в истории комплексных чисел касается итальянского математика Рафаэля Бомбелли (1526–1572). Бомбелли пересмотрел опубликованную Кардано формулу для решения кубических уравнений вида x 3 = cx + d , которая (используя современные обозначения) выглядит следующим образом:
x = 3 √( D / 2 +√ E )+ 3 √ ( D / 2 -√ E )
Переменная E здесь представляет выражение ( D / 2 ) 2 — ( C / 3 ) 3 . Бомбелли применил формулу Кардано к решению уравнения 90 231 x 90 232 91 405 3 91 406 = 15 90 231 x 90 232 + 4 (то же самое уравнение, которое ранее вызывало у Кардано такой ужас) и получил практически тот же результат, что и Кардано:
Бомбелли применил формулу Кардано к решению уравнения 90 231 x 90 232 91 405 3 91 406 = 15 90 231 x 90 232 + 4 (то же самое уравнение, которое ранее вызывало у Кардано такой ужас) и получил практически тот же результат, что и Кардано:
x = 3 √( 2 + √-121 ) + 3 √( 2 — √-121 )
Поэтому ему пришлось столкнуться с той же проблемой, что и у Кардано, а именно с наличием члена, представляющего собой квадратный корень из отрицательного числа. Неустрашимый Бомбелли продолжал манипулировать уравнением в надежде найти разумное решение. Хотя мы не будем воспроизводить различные этапы, через которые прошел Бомбелли, в конце концов он смог определить, что:
3 √( 2 + √-121 ) = 2 + √-1
а также
3 √( 2 — √-121 ) = 2 — √-1
Возможно, вы не сможете сразу увидеть, как Бомбелли пришел к этим результатам, но мы можем убедиться, что они верны. На самом деле, если у вас есть калькулятор, который может работать с комплексными числами, вы можете проверить это сами. В противном случае попробуйте ввести каждое из следующих выражений в Google:
9(1/3)
На самом деле, если у вас есть калькулятор, который может работать с комплексными числами, вы можете проверить это сами. В противном случае попробуйте ввести каждое из следующих выражений в Google:
9(1/3)
Эти выражения являются эквивалентом ASCII 3 √( 2 + √-121 ) и 3 √( 2 — √-121 ) соответственно. Они должны быть введены в этом формате, потому что встроенный калькулятор Google может принимать только символы ASCII в качестве входных данных, хотя он, очевидно, понимает значение i в этом контексте! Вывод будет 2 + 1 i для первого выражения и 2 — 1 i для второго (то, что перед и в обоих случаях совершенно лишний, и его можно игнорировать). Подставив упрощенные условия в исходное уравнение, Бомбелли получил следующее:
x = 2 + √-1 + 2 — √-1 = 4
То, что мы здесь рассматриваем, по сути является сложением двух комплексных чисел (2 + i и 2 — i ). Результатом махинаций Бомбелли является решение ( x = 4), которое, вероятно, можно было бы определить, просто взглянув на исходное уравнение. Тем не менее усилия Бомбелли выявили довольно неудобный факт, что решение полиномиальных уравнений неизбежно включало бы квадратные корни из отрицательных чисел. Это означало, что математики должны были найти способ справиться с ними. В своей книге «Алгебра », написанная в 1572 году, Бомбелли изложил концепцию комплексной системы счисления и установил набор правил для арифметических операций ( сложение , вычитание , умножение и деление ), включающих комплексные числа. Вероятно, нам следует указать здесь, что полиномиальное уравнение x 3 — 15 x — 4 = 0 на самом деле имеет три действительных корня, как можно увидеть, изучив график соответствующей функции, показанный ниже, хотя только один из этих корней ( х = 4) положительный.
Результатом махинаций Бомбелли является решение ( x = 4), которое, вероятно, можно было бы определить, просто взглянув на исходное уравнение. Тем не менее усилия Бомбелли выявили довольно неудобный факт, что решение полиномиальных уравнений неизбежно включало бы квадратные корни из отрицательных чисел. Это означало, что математики должны были найти способ справиться с ними. В своей книге «Алгебра », написанная в 1572 году, Бомбелли изложил концепцию комплексной системы счисления и установил набор правил для арифметических операций ( сложение , вычитание , умножение и деление ), включающих комплексные числа. Вероятно, нам следует указать здесь, что полиномиальное уравнение x 3 — 15 x — 4 = 0 на самом деле имеет три действительных корня, как можно увидеть, изучив график соответствующей функции, показанный ниже, хотя только один из этих корней ( х = 4) положительный.
График y = ƒ( x ) = x 3 — 15 x — 4
К концу восемнадцатого века комплексные числа стали рутинно использоваться при решении полиномиальных уравнений, но в некоторых кругах все еще существовало сопротивление идее, что их можно считать самостоятельными числами или что они существуют внутри числа. система, отличная от действительной системы счисления. Тем не менее, концепция комплексной системы счисления начала набирать поддержку. В 1799, немецкий математик и физик Иоганн Карл Фридрих Гаусс опубликовал статью, содержащую доказательство того, что полиномиальное уравнение n -й степени имеет n корней вида a + bi , в котором a и b — действительные числа, а i представляет мнимую единицу (√-1) — другими словами, корни любого многочлена можно выразить в виде комплексных чисел.
Комплексные числа также начали находить применение в других областях, особенно в упрощении вычислений с использованием тригонометрических функций. В 1806 году швейцарский математик-любитель Жан-Робер Арган (1768-1822) не только представил строгое доказательство фундаментальной теоремы алгебры, но и опубликовал эссе, в котором описывалось, как комплексные числа могут быть представлены в виде точек на двумерной плоскости, во многом таким же способ представления точек с использованием декартовых координат на двумерной геометрической плоскости. Идея представления комплексных чисел в виде точек на «комплексной плоскости» (как она стала известна) впервые была выдвинута норвежско-датским математиком и картографом 9.0231 Каспер Вессель (1745-1818). Гаусс также поддержал эту идею. Он опубликовал изложение комплексных чисел как точек на комплексной плоскости в 1831 году, в котором также установил большую часть обозначений и терминологии, используемых сегодня. Комплексные числа теперь находят применение в математике, физических науках, телекоммуникациях и почти во всех областях техники.
Комплексные числа теперь находят применение в математике, физических науках, телекоммуникациях и почти во всех областях техники.
Свойства комплексных чисел
[Вернитесь к началу страницы]
Комплексное число состоит из двух частей: реальной части и мнимой части (отсюда и название комплексное число ). Набор комплексных чисел обычно обозначается символом ℂ (двойная буква C). Если вы не знакомы с концепцией мнимых чисел, было бы неплохо прочитать страницу под названием «Воображаемые числа», прежде чем читать эту страницу. Комплексное число имеет вид:
a + bi
где a и b — действительные числа, а i — мнимая единица (√-1). Хотя a и b являются действительными числами, a называется «действительной» частью комплексного числа, а b считается «мнимой» частью, поскольку оно умножается на мнимую единицу. и . На самом деле не должно быть слишком сложно признать, что число может быть составлено из двух отдельных и отдельных числовых компонентов — в конце концов, мы все принимаем дроби и знакомы с ними, а каждая дробь состоит из числитель часть и знаменатель часть.
и . На самом деле не должно быть слишком сложно признать, что число может быть составлено из двух отдельных и отдельных числовых компонентов — в конце концов, мы все принимаем дроби и знакомы с ними, а каждая дробь состоит из числитель часть и знаменатель часть.
Комплексное число a + bi , мнимая часть которого равна нулю (т. е. b = 0), фактически является действительным числом a . Это означает, что каждое действительное число может быть представлено как комплексное число. Кроме того, для любого действительного числа n должно быть бесконечно много комплексных чисел, у которых n является их действительной частью, потому что мнимая часть комплексного числа также является действительным числом. Это означает, что, как и множество всех действительных чисел, множество комплексных чисел равно 9.0231 несчетно бесконечное . Комплексное число a + bi , действительная часть которого равна нулю (т. е. a = 0), фактически является мнимым числом bi . Мы называем такое число чисто мнимым числом .
е. a = 0), фактически является мнимым числом bi . Мы называем такое число чисто мнимым числом .
Математики склонны называть действительные числа полем , а не набором, потому что слово множество подразумевает нечто, что можно сосчитать. По той же причине они также называют набор комплексных чисел полем. В то время как реальные числа существуют в пределах упорядоченное поле , однако комплексных чисел нет. Для любых двух действительных чисел одно всегда должно быть больше или меньше другого. Однако, как вы увидите, когда мы посмотрим на комплексную плоскость, два различных комплексных числа могут иметь одинаковую величину. Таким образом, считается, что комплексные числа существуют в неупорядоченном поле (обратите внимание, однако, что два комплексных числа могут считаться одним и тем же комплексным числом только , если их действительные части 0231 и их мнимые части совпадают).
Сложная плоскость
[Вернитесь к началу страницы]
Поскольку комплексное число состоит из двух отдельных частей, мы можем представить его как точку в двумерной декартовой системе координат. Мы называем эту систему координат комплексной плоскостью . Мы идентифицируем каждую точку на комплексной плоскости, используя координаты x и y , точно так же, как мы идентифицируем точки на двумерной геометрической плоскости. Фактически, используя комплексную плоскость, мы находим ряд параллелей между изучением комплексных чисел и изучением геометрии. Эти сходства станут очевидными по мере нашего продвижения. По соглашению горизонталь 9Ось 0231 x комплексной плоскости используется для представления действительной части комплексного числа, а вертикальная ось y используется для представления мнимой части. Оси x и y иногда обозначаются как Re и Im соответственно, чтобы показать, что они представляют реальную и мнимую оси. Мы будем использовать это соглашение здесь. Комплексное число 5 + 4 i представлено на комплексной плоскости следующим образом:
Мы будем использовать это соглашение здесь. Комплексное число 5 + 4 i представлено на комплексной плоскости следующим образом:
Комплексное число 5+4 i в виде точки на комплексной плоскости
Этот вид визуального представления комплексных чисел иногда называют диаграммой Аргана , в честь Жана-Роберта Аргана , о котором мы упоминали ранее. Обратите внимание, что мы идентифицировали комплексное число на диаграмме, используя пару значений, разделенных запятыми, в скобках. Первое значение представляет действительную часть комплексного числа, а второе значение представляет мнимая часть . Говорят, что комплексное число, отображаемое в этом формате, имеет декартову , прямоугольную или алгебраическую форму . Пара действительных и мнимых координат описывает не только положение комплексного числа на комплексной плоскости, но и его смещение от начала координат (если вы хоть сколько-нибудь глубоко изучали векторы, вы, несомненно, знакомы с понятием векторов положения и векторы смещения). В комплексной плоскости расстояние между комплексным числом и началом координат известно как его по модулю и может быть представлен линией, соединяющей начало координат с точкой, представляющей комплексное число.
В комплексной плоскости расстояние между комплексным числом и началом координат известно как его по модулю и может быть представлен линией, соединяющей начало координат с точкой, представляющей комплексное число.
Стрелка представляет модуль комплексного числа 5 + 4 i
Модуль комплексного числа представляет его величину (абсолютное значение). Все точки комплексной плоскости, находящиеся на одинаковом расстоянии от начала координат, имеют одинаковый модуль и, следовательно, одно и то же абсолютное значение. Глядя на диаграмму, вы должны увидеть, что модуль комплексного числа (т. е. расстояние между ним и началом координат) будет равен по длине гипотенузе прямоугольного треугольника, в котором длина горизонтали и вертикальные ножки соответствуют значению действительной и мнимой частей комплексного числа соответственно. Таким образом, мы можем найти абсолютное значение комплексного числа, используя теорему Пифагора. Предположим, мы хотим найти абсолютное значение комплексного числа 9.0231 з . Требуемая формула:
Предположим, мы хотим найти абсолютное значение комплексного числа 9.0231 з . Требуемая формула:
| с | = √( x 2 + y 2 )
где x и y представляют действительные и мнимые координаты комплексного числа z в комплексной плоскости (обратите внимание, что вертикальные черты, окружающие переменную, используются для обозначения ее абсолютного значения). Применим эту формулу к комплексному числу 5 + 4 i , чтобы найти его модуль, r :
r = |5 + 4 i | = √(5 2 + 4 2 ) = √(41) = 6,403
Хотя многие точки на комплексной плоскости (фактически бесконечное число) могут иметь один и тот же модуль, каждая точка на комплексной плоскости однозначно идентифицируется с помощью комбинации ее модуля и угла между модулем и положительной действительной осью, измеренного против — по часовой стрелке от этой оси. Этот угол обычно обозначается строчной греческой буквой 9.0231 фи ( φ ), называется аргументом комплексного числа. Для комплексного числа z мы бы выразили аргумент этого комплексного числа как arg( z ). Модуль и аргумент комплексного числа вместе известны как его полярные координаты . Таким образом, есть два возможных способа указать положение комплексного числа в комплексной плоскости. Мы можем использовать либо его декартовы координаты, либо его полярные координаты.
Этот угол обычно обозначается строчной греческой буквой 9.0231 фи ( φ ), называется аргументом комплексного числа. Для комплексного числа z мы бы выразили аргумент этого комплексного числа как arg( z ). Модуль и аргумент комплексного числа вместе известны как его полярные координаты . Таким образом, есть два возможных способа указать положение комплексного числа в комплексной плоскости. Мы можем использовать либо его декартовы координаты, либо его полярные координаты.
Мы уже видели, как можно использовать теорему Пифагора для нахождения модуля комплексного числа, используя его значения координат x и y . Используя эти же координаты, мы можем использовать тригонометрию, чтобы найти его аргумент. Точная формула, используемая для нахождения аргумента φ комплексного числа, будет зависеть от знака координат x и y . Давайте сначала разберемся с некоторыми тривиальными случаями. Если комплексный номер z имеет абсолютное значение, равное нулю (т. е. z = 0 + 0 i ), тогда, очевидно, координаты x и y также будут равны нулю, а значение φ называется равным . не определено .
Если комплексный номер z имеет абсолютное значение, равное нулю (т. е. z = 0 + 0 i ), тогда, очевидно, координаты x и y также будут равны нулю, а значение φ называется равным . не определено .
Если только мнимая часть числа равна нулю, y также будет нулем, а значение φ будет зависеть от того, является ли x положительным или отрицательным. Для положительных значений x , φ будет иметь значение ноль градусов (0°). Для отрицательных значений x φ будет иметь значение сто восемьдесят градусов (180°). И наоборот, если только действительная часть числа равна нулю, х также будет нулем, а значение φ будет зависеть от того, является ли y положительным или отрицательным. Для положительных значений y , φ будет иметь значение девяносто градусов (90°). Для отрицательных значений x φ будет иметь значение двести семьдесят градусов (270°).
Для отрицательных значений x φ будет иметь значение двести семьдесят градусов (270°).
Это оставляет четыре возможных случая для комплексного числа z = x + yi . В первом случае, который мы рассматриваем, z имеет как положительную действительную часть , так и положительную мнимую часть. Он будет представлен точкой в пределах первого квадранта (верхний правый квадрант) комплексной плоскости. Таким образом, мы можем получить аргумент φ из z следующим образом:
φ = arg ( z ) = arctan ( y / x )
Мы уже получили модуль r (см. выше) для комплексного числа 5 + 4 i . Теперь найдем аргумент φ для этого комплексного числа:
φ = аргумент (5 + 4 i ) = arctan ( 4 / 5 ) = 38,66°
Ниже мы видим комплексное число 5 + 4 i , представленное в виде точки на комплексной плоскости, помеченной ее декартовыми координатами. Модуль и аргумент комплексного числа (то есть полярные координаты ) также показаны на диаграмме.
Модуль и аргумент комплексного числа (то есть полярные координаты ) также показаны на диаграмме.
Комплексное число 5 + 4 i в комплексной плоскости.
Если z имеет отрицательную действительную часть и положительную мнимую часть, то она будет представлена точкой, лежащей в пределах второго квадранта (верхнего левого квадранта) комплексной плоскости. В этом случае мы можем получить аргумент φ из z , используя:
φ = arg ( z ) = 180 + arctan ( y / x )
Найдем полярные координаты для комплексного числа -6 + 3 i , точечное представление которого попадает во второй квадрант комплексной плоскости. Расчет для нахождения модуля r будет таким же, как и раньше:
r = |-6 + 3 i | = √(-6 2 + 3 2 ) = √(45) = 6,708
Вот расчет для аргумента φ из -6 + 3 и :
φ = ARG (-6+3 I ) = 180+Arctan ( 3 / -6 ) = 180-26,57 = 153,43 °
Вот комплексное число -6 + 3 i , представленное в виде точки на комплексной плоскости вместе с ее декартовыми и полярными координатами:
Комплексное число -6 + 3 i в комплексной плоскости
Комплексное число z , представленное точкой в третьем квадранте (нижний левый квадрант) комплексной плоскости, имеет как отрицательную действительную часть , так и отрицательную мнимую часть. Здесь мы получаем аргумент φ из z , используя:
Здесь мы получаем аргумент φ из z , используя:
φ = arg ( z ) = -180 + arctan ( y / x )
На этот раз мы найдем полярные координаты для комплексного числа -4 — 2 i , точечное представление которого попадает в третий квадрант комплексной плоскости. Расчет для нахождения модуля r будет:
r = |-4 — 2 i | = √((-4) 2 + (-2) 2 ) = √(20) = 4,472
Вот расчет для аргумента φ из -4 — 2 и :
φ = arg (-4 — 2 i ) = -180 + arctan ( -2 / -4 ) = -180 + 26,57 = 3 °
Обратите внимание, что отрицательные углы измеряются 90 231 по часовой стрелке 90 232 от положительной вещественной оси. Результат, заданный как положительный угол (т.е. измеренный против часовой стрелки от положительной действительной оси), эквивалентен этому отрицательному углу плюс триста шестьдесят градусов. Чтобы выразить аргумент комплексного числа -4 — 2 i как положительный угол, поэтому мы могли бы написать следующее:
Результат, заданный как положительный угол (т.е. измеренный против часовой стрелки от положительной действительной оси), эквивалентен этому отрицательному углу плюс триста шестьдесят градусов. Чтобы выразить аргумент комплексного числа -4 — 2 i как положительный угол, поэтому мы могли бы написать следующее:
φ = 360° + (-153,43°) = 206,57°
Вот комплексное число -4 — 2 i , представленное в виде точки на комплексной плоскости вместе с ее декартовыми и полярными координатами:
Комплексный номер -4 — 2 и в комплексной плоскости
Точка в четвертом квадранте (нижний правый квадрант) комплексной плоскости представляет собой комплексное число z , имеющее положительную действительную часть и отрицательную мнимую часть. Аргумент φ числа z можно найти по формуле:
φ = arg ( z ) = arctan ( y / x )
Эта формула, вероятно, кажется вам знакомой, как и должно быть. Это та же самая формула, которую мы использовали для нахождения аргумента комплексного числа, представленного точкой в первом квадранте. Однако на этот раз арктангенс числа y / x даст отрицательный результат. Это означает, что угол снова будет измеряться 90 231 по часовой стрелке 90 232 от положительной вещественной оси. Найдем полярные координаты для комплексного числа 2 — 3 i , точечное представление которого попадает в четвертый квадрант комплексной плоскости. Расчет для нахождения модуля r будет:
Это та же самая формула, которую мы использовали для нахождения аргумента комплексного числа, представленного точкой в первом квадранте. Однако на этот раз арктангенс числа y / x даст отрицательный результат. Это означает, что угол снова будет измеряться 90 231 по часовой стрелке 90 232 от положительной вещественной оси. Найдем полярные координаты для комплексного числа 2 — 3 i , точечное представление которого попадает в четвертый квадрант комплексной плоскости. Расчет для нахождения модуля r будет:
r = |2 — 3 i | = √(2 2 + (-3) 2 ) = √(13) = 3,606
Вот расчет аргумента φ от 2 до 3 i :
φ = arg (2 — 3 i ) = Arctan ( -3 / 2 ) = -56,31° (или 303,69°)
Вот комплексное число 2 — 3 i , представленное в виде точки на комплексной плоскости вместе с ее декартовыми и полярными координатами:
Комплексный номер 2 — 3 и в комплексной плоскости
Как и следовало ожидать, существует ряд альтернативных формул для нахождения как полярных, так и декартовых координат точечного представления комплексного числа на комплексной плоскости. Формула, используемая в данной ситуации, будет полностью зависеть от того, какая информация доступна, и, конечно же, от результата, который мы пытаемся получить. Когда мы начнем рассматривать арифметические операции, которые можно выполнять над комплексными числами, мы будем рассматривать как алгебраические методы решения задач, так и методы, включающие тригонометрию. Запомните одну очень полезную формулу, которая позволяет нам получить значение комплексного числа 9.0231 z = x + yi из его полярных координат следующим образом:
Формула, используемая в данной ситуации, будет полностью зависеть от того, какая информация доступна, и, конечно же, от результата, который мы пытаемся получить. Когда мы начнем рассматривать арифметические операции, которые можно выполнять над комплексными числами, мы будем рассматривать как алгебраические методы решения задач, так и методы, включающие тригонометрию. Запомните одну очень полезную формулу, которая позволяет нам получить значение комплексного числа 9.0231 z = x + yi из его полярных координат следующим образом:
Z = x + YI = R (COS φ + I SIN φ ) = R (COS φ ) = R (COS φ ) = R (COS φ ) = R (COS ). я
Надеюсь, теперь вы лучше понимаете, что такое комплексные числа. По сути действительные числа существуют только на одномерной числовой прямой, представленной здесь действительной осью комплексной плоскости. Точно так же мнимых чисел также существуют только на одномерной числовой прямой, представленной здесь мнимой осью комплексной плоскости. Хотя и действительные, и мнимые числа полезны сами по себе, комплексная система счисления объединяет эти два типа чисел, позволяя нам создавать числа, существующие в двумерной плоскости, и тем самым давая нам мощный инструмент для решения сложных математических задач. .
Точно так же мнимых чисел также существуют только на одномерной числовой прямой, представленной здесь мнимой осью комплексной плоскости. Хотя и действительные, и мнимые числа полезны сами по себе, комплексная система счисления объединяет эти два типа чисел, позволяя нам создавать числа, существующие в двумерной плоскости, и тем самым давая нам мощный инструмент для решения сложных математических задач. .
Комплексное сопряжение
[Вернитесь к началу страницы]
Комплексное сопряжение комплексного числа — это число с равной действительной частью и мнимой частью, равной по величине, но противоположной по знаку . Так, например, комплексное сопряжение a + bi равно a — bi . Для получения комплексного сопряжения e (или просто сопряжено с ) комплексного числа, все, что вам нужно сделать, это изменить знак мнимой части комплексного числа. Сопряженное комплексное число z = x + yi может быть выражено, как показано ниже. Обратите внимание, что сопряжение комплексного числа обозначается размещением черты, обычно называемой над чертой (хотя формальный термин — vinculum ), над названием комплексного числа.
Сопряженное комплексное число z = x + yi может быть выражено, как показано ниже. Обратите внимание, что сопряжение комплексного числа обозначается размещением черты, обычно называемой над чертой (хотя формальный термин — vinculum ), над названием комплексного числа.
z = x — yi
Тот факт, что мы отрицаем мнимую часть комплексного числа, чтобы получить сопряженное число, имеет два следствия. Во-первых, если мнимая часть комплексного числа равна нулю , то сопряженным комплексным числом будет само комплексное число (которое фактически будет действительным числом). Во-вторых, точечное представление комплексно-сопряженного числа в комплексной плоскости будет отражением точечного представления комплексного числа в действительном ( x ) ось. На приведенном ниже рисунке показано комплексное число 3 + 2 i и его сопряженное число 3 — 2 i в виде точек на комплексной плоскости.
Комплексное сопряжение отрицает мнимую часть комплексного числа
Как видно из диаграммы, комплексное сопряжение находится путем отражения z поперек действительной оси. Комплексное сопряжение может быть весьма полезным в ряде ситуаций, как мы увидим в свое время. Его обычно используют, например, для упрощения формулы деления одного комплексного числа на другое или для нахождения обратное комплексного числа. Комплексно-сопряженные также полезны для нахождения корней многочленов. Согласно теореме о комплексно-сопряженном корне , если комплексное число является корнем многочлена от одной переменной с действительными коэффициентами (например, квадратное или кубическое уравнение), его сопряженное число также будет корнем этого многочлена.
Сложение и вычитание
[Вернитесь к началу страницы]
Сложить два комплексных числа вместе алгебраически совершенно просто. Все, что нам нужно сделать, это сложить действительную и мнимую части слагаемых (комплексные числа, которые мы хотим сложить). Предположим, у нас есть два комплексных числа: a + bi и c + di . Формула сложения этих комплексных чисел:
Все, что нам нужно сделать, это сложить действительную и мнимую части слагаемых (комплексные числа, которые мы хотим сложить). Предположим, у нас есть два комплексных числа: a + bi и c + di . Формула сложения этих комплексных чисел:
( a + bi ) + ( c + di ) = ( a + c ) + ( b + d ) i
Например, допустим, мы хотели сложить комплексные числа 4 + 9 i и 2 + 8 i . Применяя приведенную выше формулу, получаем:
(4 + 9 i ) + (2 + 8 i ) = (4 + 2) + (9 + 8) i = 6 + 17 i
Вычитание также довольно просто. Предположим, что на этот раз мы хотим вычесть комплексное число a + b i из комплексного числа c + d i . Формула, которую мы будем использовать, чтобы найти разность этих двух комплексных чисел:
(c + di) — (a + bi) = (c — a) + (d — b)i
Например, предположим, что мы хотим вычесть комплексное число 4 + 9 и из сложного числа 5 + 3 и . Применяя формулу вычитания, как показано на рисунке, мы получаем:
Применяя формулу вычитания, как показано на рисунке, мы получаем:
(5 + 3i) — (4 + 9i) = (5 — 4) + (3 — 9)i = 1 — 6i
Мы также можем выполнять сложение и вычитание графически, используя комплексную плоскость. Этот процесс по существу представляет собой сложение векторов, потому что мы складываем векторы смещения двух комплексных чисел. Одним из распространенных способов достижения этого является построение параллелограмма, в котором векторы смещения образуют две смежные стороны параллелограмма. Начало комплексной плоскости — одна вершина параллелограмма. Результатом сложения комплексных чисел является комплексное число, точка которого представлена на комплексной плоскости вершиной параллелограмма, лежащей напротив начала координат. На приведенной ниже диаграмме показано, как мы можем использовать такую конструкцию, чтобы найти результат сложения комплексных чисел 3 + 9.0231 и и 2 + 3 и . Результатом является точка с декартовыми координатами (5, 4), которая представляет собой комплексное число 5 + 4 i .
Сложение комплексных чисел в комплексной плоскости с использованием векторов смещения
Вычитание может быть выполнено с использованием того же метода. Хотя мы говорим о вычитании, мы все же можем думать об этом как о сложении. У нас есть два комплексных числа, одно из которых ( вычитаемое ) необходимо вычесть из другого ( вычитаемое ). Если мы отрицаем вычитаемое, мы можем просто добавить его к уменьшаемому. Чтобы инвертировать комплексное число, мы просто меняем знак как у действительной, так и у мнимой частей. Предположим, мы хотим отделить комплексное число 2 + 3 i (вычитаемое) от комплексного числа 6 + 2 i (уменьшаемое). Мы начинаем с отрицания 2 + 3 i , чтобы получить комплексное число -2 — 3 и . Теперь просто построим наш параллелограмм, как и раньше. На приведенной ниже диаграмме показан результат сложения комплексных чисел 6 + 2 i и -2 — 3 i . Результатом является точка с декартовыми координатами (4, -1), которая представляет собой комплексное число 4 — i .
Результатом является точка с декартовыми координатами (4, -1), которая представляет собой комплексное число 4 — i .
Векторы смещения также можно использовать для вычитания
Умножение
[Вернитесь к началу страницы]
Комплексное число можно умножить на действительное число, чтобы получить результат, являющийся другим комплексным числом. Все, что нам нужно сделать, это умножить действительную и мнимую части комплексного числа на действительное число. Чтобы умножить комплексное число a + b i на действительное число n , мы используем формулу:
( a + bi ) n = an + bni
Умножение комплексного числа на другое комплексное число немного сложнее, но все еще относительно просто. По сути, каждая часть первого комплексного числа умножается на каждую часть второго. Предположим, что у нас есть два комплексных числа, a + bi и c + di , для которых мы хотим найти произведение. Конечно, мы могли бы использовать стандартный метод FOIL ( Firsts , Outers , Внутренние , Lasts ) используются для умножения двух биномиальных выражений следующим образом:
Предположим, что у нас есть два комплексных числа, a + bi и c + di , для которых мы хотим найти произведение. Конечно, мы могли бы использовать стандартный метод FOIL ( Firsts , Outers , Внутренние , Lasts ) используются для умножения двух биномиальных выражений следующим образом:
( a + bi )( c + di ) = ac + adi + bci + bdi 2
Обратите внимание, однако, что член i 2 по определению равен минус единице (-1), поэтому мы можем несколько упростить формулу, чтобы получить следующее:
( A + BI ) ( C + DI ) = ( AC — BD )+( A + BC ) .
Имея в виду, что мнимое число — это просто комплексное число, действительная часть которого равна нулю, давайте посмотрим, что произойдет, если мы воспользуемся этим методом, чтобы найти квадрат мнимого числа i (мнимая единица, равная √ -1). Мы, конечно, должны добиться результата минус один — но как это получается? Вот расчет:
(0 + 1 i )(0 + 1 i ) = ((0)(0) — (1)(1)) + ((0)(1) + (1)(0)) i = -1
Таким образом, мы доказали, что так называемая воображаемая единица вовсе не воображаемая, а действительно существует — или, по крайней мере, существует, пока мы играем по правилам комплексной системы счисления.
Мы также можем перемножить полярные координаты двух комплексных чисел, чтобы получить алгебраическое выражение их произведения. Мы видели выше, что комплексное число z = x + yi можно выразить через его полярные координаты как:
z = r (cos φ + i sin φ )
Чтобы найти произведение двух комплексных чисел z 1 и z 2 , для которых у нас есть полярные координаты, мы можем использовать следующую формулу:
z 1 z 2 = r 1 r 2 (cos ( φ 1 + φ 2 ) + i sin ( φ 1 + φ 2 ))
где r 1 и φ 1 — соответственно модуль и аргумент комплексного числа z 1 и r 2 и φ 2 — модуль и аргумент комплексного числа z 2 .
Умножение комплексного числа z = a + bi на последовательные степени i дает интересные результаты. Вот что получается, когда мы умножаем х на степени х в диапазоне от х -4 до х 4 :
zi -4 = ( a + bi ) i -4 = a + bi
zi -3 = ( a + bi ) I -3 = — B + AI
ZI -2 = ( A + BI ).0231 a — bi
zi -1 = ( a + bi ) i -1 = b — ai
zi 0 = ( a + bi ) i 0 = a + bi
zi 1 = ( a + bi ) i 1 = — б + ai
zi 2 = ( a + bi ) i 2 = — a — bi
zi 3 = ( a + bi ) i 3 = b — ai
zi 4 = ( a + bi ) i 4 = a + bi
Если вы продолжите умножать z на последовательные отрицательные числа или степени i , результаты просто продолжат циклически повторяться через те же четыре значения комплексных чисел.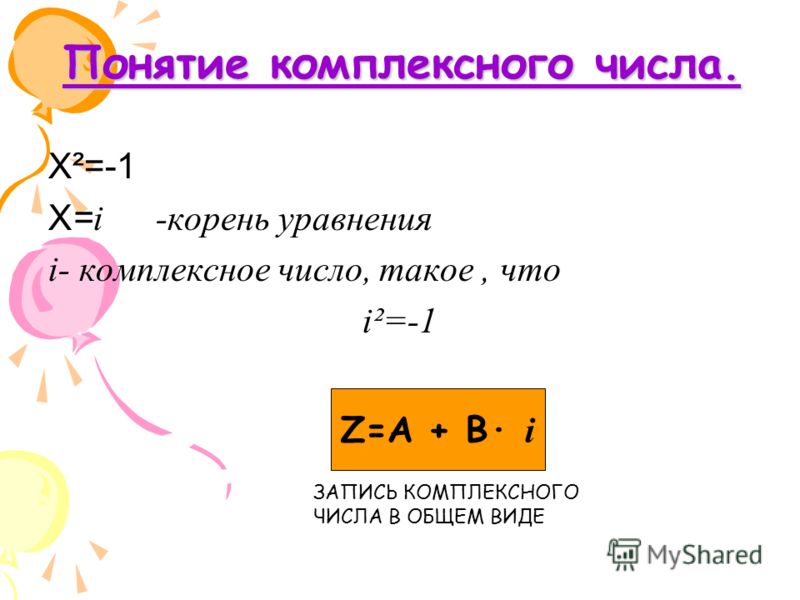 Если мы представим z как точку на комплексной плоскости, мы увидим, что умножение z на последовательные степени i приводит к вращению этой точки вокруг начала координат с шагом (90°). ). Для положительных степеней i вращение против часовой стрелки, а для отрицательных степеней i вращение по часовой стрелке. Если вы читали страницу о мнимых числах, то поняли, что такое циклическое поведение связано с тем, что i n = i ( n mod 4) . Ниже вы можете увидеть, что происходит, когда мы умножаем комплексное число 3 + 2 i на последовательные степени i . Результаты представлены в виде точек на комплексной плоскости.
Если мы представим z как точку на комплексной плоскости, мы увидим, что умножение z на последовательные степени i приводит к вращению этой точки вокруг начала координат с шагом (90°). ). Для положительных степеней i вращение против часовой стрелки, а для отрицательных степеней i вращение по часовой стрелке. Если вы читали страницу о мнимых числах, то поняли, что такое циклическое поведение связано с тем, что i n = i ( n mod 4) . Ниже вы можете увидеть, что происходит, когда мы умножаем комплексное число 3 + 2 i на последовательные степени i . Результаты представлены в виде точек на комплексной плоскости.
Умножение 3 + 2 i на последовательные степени i
Разделение
[Вернитесь к началу страницы]
Точно так же, как мы можем умножить комплексное число на действительное число, мы также можем разделить комплексное число на действительное число, чтобы получить в результате другое комплексное число. Все, что нам нужно сделать, это разделить и действительную, и мнимую части комплексного числа на действительное число. Чтобы разделить комплексное число a + bi на вещественное число n используем формулу:
Все, что нам нужно сделать, это разделить и действительную, и мнимую части комплексного числа на действительное число. Чтобы разделить комплексное число a + bi на вещественное число n используем формулу:
| a + bi | = | a | + | b | i |
| n | n | n |
Алгебраическая формула деления одного комплексного числа на другое комплексное число несколько сложнее, чем умножение двух комплексных чисел вместе. Предположим, мы хотим разделить комплексное число a + bi по комплексному номеру c + di . Вот формула, которую мы используем для этого:
| a + bi | = | ( ac + bd ) + (- ad + bc ) i |
| c + di | в 2 + d 2 |
Пример должен служить для демонстрации того, как это работает.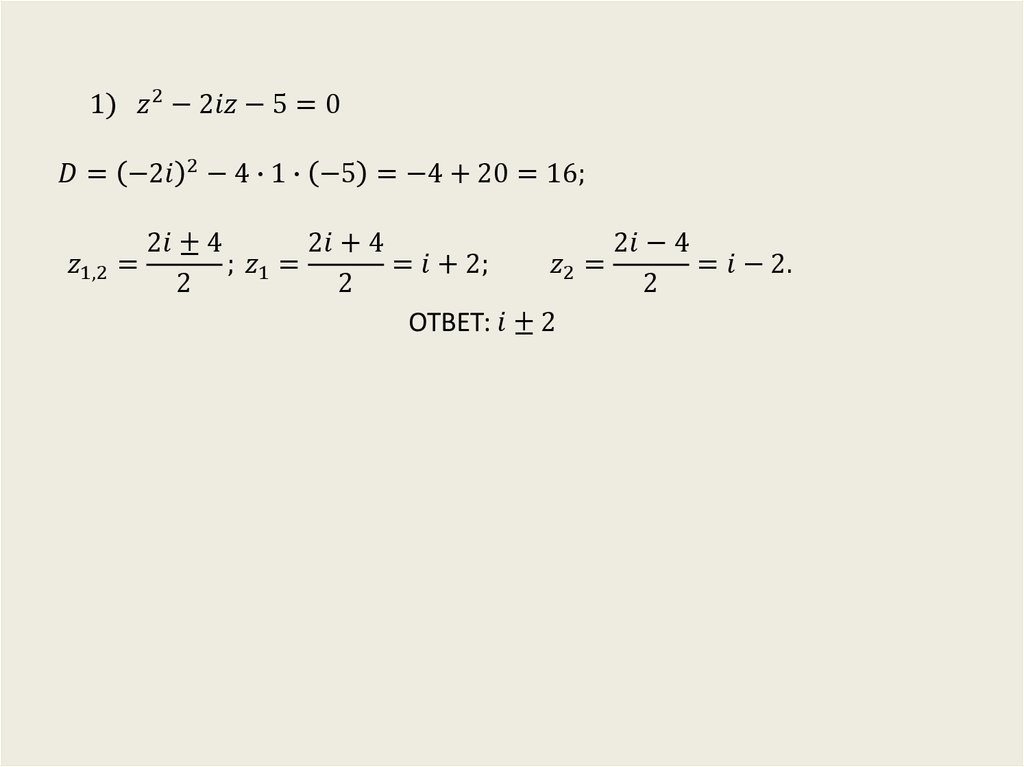 Предположим, мы хотим разделить комплексное число 2 + 3 i на комплексное число 4 — 5 i . Применяя приведенную выше формулу, получаем:
Предположим, мы хотим разделить комплексное число 2 + 3 i на комплексное число 4 — 5 i . Применяя приведенную выше формулу, получаем:
| 2 + 3 i | = | ((2)(4) + (3)(-5)) + (-(2)(-5) + (3)(4)) 9023 i | = | -7 | + | 22 | i | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 4 — 5 i | 4 2 + 5 2 | 41 | 41 | Мы можем несколько упростить эту формулу, используя комплексное сопряжение, которое мы видели выше. Мы можем получить тот же результат, умножив числитель (2 + 3 i ) и знаменатель (4 — 5 i ) на сопряженное знаменателю (4 + 5 i ). Если мы это сделаем, то получим:
Чтобы найти частное двух комплексных чисел z 1 и z 2 , для которых у нас есть полярные координаты, мы можем использовать следующую формулу:
где r 1 и φ 1 соответственно модуль и аргумент комплекса номера Z 1 (число) и R 2 2 2 2 (число) и R 2 2 (число) и R 2 2 (число) и R 2 2 (число) и R 2 (число) и R 2 (число). Полномочия комплексных чисел[Вернитесь к началу страницы] Когда комплексное число z возводится в степень положительного целого числа n , алгебраическая формула для вычисления значения z n по существу включает перемножение n экземпляров 2 z . Это может стать очень запутанным, поскольку значение n увеличивается. Чтобы проиллюстрировать это, вот формулы для z 2 , z 3 , z 4 и z 5 : z 2 = ( x 2 — y 2 ) + (2 xy ) i z 3 = ( x 3 — 3 xy 2 ) + (3 x 2 y — y 3 ) i z 4 = ( x 4 — 6 x 2 y 2 + y 4 ) + (4 x 3 y — 4 xy 3 ) i z 5 = ( x 5 — 10 x 3 y 2 + 5 xy 4 ) + (5 x 4 Y -10 x 2 Y 3 + Y 5 ) I I Y 5 ) I I I I Y 5 ) I Y 5 ) I Y 5 ) К счастью, есть гораздо более элегантный способ вычисления n -й степени комплексного числа с использованием полярных координат. z = r (cos φ + i sin φ ) Существует формула, иногда называемая формулой де Муавра или теоремой де Муавра в честь французского математика Абрахама де Муавра (1667-1754), которая утверждает, что для любого комплексного числа z и действительного значения n мы можно сказать: (cos з + i sin z ) n = cos ( nz ) + i sin ( nz ) Доказательство этой теоремы было предоставлено самим де Муавром для всех натуральных чисел. В 1749 году математик и физик из Зивса Леонард Эйлер (1707-1783) доказал, что формула работает для любого действительного значения n . z n = r n (cos nφ + 0 i sin 2 nφгде r и φ — соответственно модуль и аргумент (то есть полярные координаты) комплексного числа z . Конечно, использование этого метода требует сначала найти модуль и аргумент комплексного числа, но связанные с этим вычисления относительно тривиальны. Давайте попробуем пример. Предположим, мы хотим найти z 5 для комплексного номера z = 2 + 3 i . Сначала воспользуемся соответствующей алгебраической формулой: z 5 = ( x 5 — 10 x 3 y 2 + 5 xy 4 ) + (5 x 4 y — 10 x 2 г 3 + г 5 ) i z 5 = (32 — (10)(8)(9) + (5)(2)(81)) + ((5)(16) -(10) (4) (27)+243) I Z 5 = (32-720+810)+(240-1080+243) I Z 141405 5732 . Прежде чем использовать альтернативную формулу для нахождения z 5 , нам нужно найти полярные координаты (т.е. модуль r и аргумент φ ) числа z = 2 + 3 i : r = | с | = √ ( x 2 + y 2 ) = √ (4+9) = √13 = 3,606 φ = ARG ( Z ) = ARCCT ( 05 3 ( Z ) = ARCT ( 3905 ( Z ) = ARCT. ) = 56,310°Теперь мы можем использовать полярные координаты, чтобы найти z 5 : z 5 = R 5 (COS ((5) (56,310))+ I SIN (5) (56,310)) Z 5 1414141414141414141414141414141414141414145 9106))) (5) (56,310))))). 0,980 i ) = 122 — 597 i Обратите внимание, что мы привели результаты промежуточных вычислений, округленные до трех знаков после запятой. Корни комплексных чисел[Вернитесь к началу страницы] Найти n -й корень комплексного числа несколько сложнее, чем найти n -й корень действительного числа. Мы можем найти n -й корень положительного действительного числа достаточно легко, используя калькулятор. n -й корень отрицательного действительного числа также можно найти с помощью калькулятора. √ ( a + bi ) = ± ( γ + δi ) куда:
а также:
Обратите внимание, что функция sign() просто извлекает знак действительного числа (в данном случае b ). Как только мы начинаем говорить о n корнях комплексного числа, где n больше, чем два , все становится еще интереснее. Фактически, n -й корень комплексного числа z можно найти с помощью следующей формулы, в которой используются полярные координаты комплексного числа:
|

 Активизация деятельности.
Активизация деятельности.




 Небезынтересно отметить, что в том случае, когда все три корня уравнения были вещественными, формула Кардано приводила к комплексным числам, по которым можно было найти вещественные корни.{72} Таким образом, Кардано мог не придавать большого значения комплексным числам, но, поскольку он не знал, как извлекать из комплексных чисел кубический корень и, следовательно, как получать вещественные корни, ему так и не удалось преодолеть эту трудность. Вещественные корни Кардано находил другим способом.
Небезынтересно отметить, что в том случае, когда все три корня уравнения были вещественными, формула Кардано приводила к комплексным числам, по которым можно было найти вещественные корни.{72} Таким образом, Кардано мог не придавать большого значения комплексным числам, но, поскольку он не знал, как извлекать из комплексных чисел кубический корень и, следовательно, как получать вещественные корни, ему так и не удалось преодолеть эту трудность. Вещественные корни Кардано находил другим способом.
 Иначе говоря, задачи, которые не допускают решений, имеющих физический или геометрический смысл, должны иметь комплексные корни.
Иначе говоря, задачи, которые не допускают решений, имеющих физический или геометрический смысл, должны иметь комплексные корни. По существу, Валлис утверждал, что комплексные числа ничуть не более бессмысленны, чем отрицательные числа, а так как последние можно изобразить точками направленной прямой, то комплексные числа можно представить точками плоскости. Валлис предложил несовершенное представление комплексных чисел и способ, позволяющий геометрически построить корни уравнения ax2 + bx + c = 0 для случая вещественных и комплексных корней. Хотя работа Валлиса оказалась правильной, ее предали забвению, поскольку в то время, математики еще не могли по достоинству оценить применение комплексных чисел.
По существу, Валлис утверждал, что комплексные числа ничуть не более бессмысленны, чем отрицательные числа, а так как последние можно изобразить точками направленной прямой, то комплексные числа можно представить точками плоскости. Валлис предложил несовершенное представление комплексных чисел и способ, позволяющий геометрически построить корни уравнения ax2 + bx + c = 0 для случая вещественных и комплексных корней. Хотя работа Валлиса оказалась правильной, ее предали забвению, поскольку в то время, математики еще не могли по достоинству оценить применение комплексных чисел. 
 Как компании прогнозируют привычки и манипулируют ими
Как компании прогнозируют привычки и манипулируют ими д.
д. Поэтому естественно стремление сделать эти уравнения разрешимыми, что в свою очередь приводит к расширению понятия числа. Например, для того чтобы любое уравнение х+а = в имело корни, положительных чисел недостаточно и поэтому возникает потребность ввести отрицательные числа и нуль.
Поэтому естественно стремление сделать эти уравнения разрешимыми, что в свою очередь приводит к расширению понятия числа. Например, для того чтобы любое уравнение х+а = в имело корни, положительных чисел недостаточно и поэтому возникает потребность ввести отрицательные числа и нуль. Решение квадратного уравнения, например, х2 – 8х + 25 = 0, можно записать следующим образом: х = 4 = 4 = 4 = 4 3 = 4 3i.
Решение квадратного уравнения, например, х2 – 8х + 25 = 0, можно записать следующим образом: х = 4 = 4 = 4 = 4 3 = 4 3i. е. если выполняются равенства
е. если выполняются равенства Их справедливость следует из того, что сложение комплексных чисел по существу сводится к сложению действительных частей и коэффициентов мнимых частей, а они являются действительными числами, для которых справедливы указанные законы.
Их справедливость следует из того, что сложение комплексных чисел по существу сводится к сложению действительных частей и коэффициентов мнимых частей, а они являются действительными числами, для которых справедливы указанные законы. Для умножения комплексных чисел также справедливы переместительный и сочетательный законы, а также распределительный закон умножения по отношению к сложению.
Для умножения комплексных чисел также справедливы переместительный и сочетательный законы, а также распределительный закон умножения по отношению к сложению.
 ru Все права принадлежат авторам размещенных материалов. Обратная связь…
ru Все права принадлежат авторам размещенных материалов. Обратная связь…

 модуль и аргумент комплексного числа z 2 (знаменатель).
модуль и аргумент комплексного числа z 2 (знаменатель).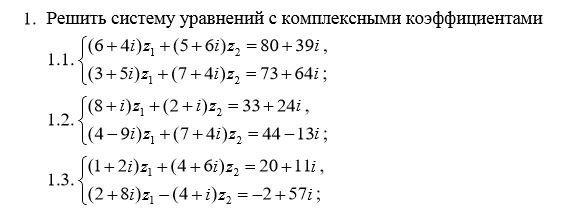 Выше мы видели, что комплексное число z = x + yi может быть выражено через его полярные координаты как:
Выше мы видели, что комплексное число z = x + yi может быть выражено через его полярные координаты как: Поэтому мы можем использовать обобщение теоремы де Муавра, чтобы вывести следующую формулу, которая позволяет нам найти n -я степень любого комплексного числа:
Поэтому мы можем использовать обобщение теоремы де Муавра, чтобы вывести следующую формулу, которая позволяет нам найти n -я степень любого комплексного числа: = 122 — 597 i
= 122 — 597 i  Чтобы получить точный результат при использовании калькулятора, мы предлагаем использовать эти промежуточные результаты без округления в большую или меньшую сторону. Для низких значений n , нахождение n -й степени комплексного числа с использованием полярных координат может потребовать такого же объема работы (или, может быть, немного больше), что и использование соответствующей алгебраической формулы. Однако для больших значений n использование полярных координат является более эффективным вариантом.
Чтобы получить точный результат при использовании калькулятора, мы предлагаем использовать эти промежуточные результаты без округления в большую или меньшую сторону. Для низких значений n , нахождение n -й степени комплексного числа с использованием полярных координат может потребовать такого же объема работы (или, может быть, немного больше), что и использование соответствующей алгебраической формулы. Однако для больших значений n использование полярных координат является более эффективным вариантом. Мы просто берем n -й корень соответствующего положительного числа и умножаем результат на мнимую единицу i . Однако n -й корень комплексного числа с ненулевой мнимой частью будет другим комплексным числом. Чтобы получить квадратный корень из комплексного числа a + bi (в котором b ≠ 0), мы можем использовать следующую алгебраическую формулу:
Мы просто берем n -й корень соответствующего положительного числа и умножаем результат на мнимую единицу i . Однако n -й корень комплексного числа с ненулевой мнимой частью будет другим комплексным числом. Чтобы получить квадратный корень из комплексного числа a + bi (в котором b ≠ 0), мы можем использовать следующую алгебраическую формулу: Используемые здесь греческие буквы: гамма ( γ ) и дельта 9.0232 ( δ ). Обратите также внимание, что √( a 2 + b 2 ) — это модуль (т. е. абсолютное значение) комплексного числа a + bi .
Используемые здесь греческие буквы: гамма ( γ ) и дельта 9.0232 ( δ ). Обратите также внимание, что √( a 2 + b 2 ) — это модуль (т. е. абсолютное значение) комплексного числа a + bi . В этой формуле k может быть любым положительным целым числом, большим или равным нулю и меньшим 9.0231 n , r модуль (абсолютное значение) z , а φ аргумент z . Из приведенного выше вы должны увидеть, что если мы ищем n -й корень (ненулевого) комплексного числа, будет n возможных решений, каждое из которых будет комплексным числом.
В этой формуле k может быть любым положительным целым числом, большим или равным нулю и меньшим 9.0231 n , r модуль (абсолютное значение) z , а φ аргумент z . Из приведенного выше вы должны увидеть, что если мы ищем n -й корень (ненулевого) комплексного числа, будет n возможных решений, каждое из которых будет комплексным числом. Однако, поскольку сумма действительной и мнимой частей этого нового комплексного числа равна одному (действительному числу), то мнимая часть должна быть равна нулю . Это, в свою очередь, означает, что действительная часть должна быть равна единице . Итак, теперь мы можем вывести следующие два уравнения:
Однако, поскольку сумма действительной и мнимой частей этого нового комплексного числа равна одному (действительному числу), то мнимая часть должна быть равна нулю . Это, в свою очередь, означает, что действительная часть должна быть равна единице . Итак, теперь мы можем вывести следующие два уравнения: а также
а также Многие культуры, даже некоторые современные, приписывают числам некоторые мистические свойства из-за их огромного значения в описании природы. Хотя математика и современная наука не подтверждают таких взглядов, значение теории чисел бесспорно.
Многие культуры, даже некоторые современные, приписывают числам некоторые мистические свойства из-за их огромного значения в описании природы. Хотя математика и современная наука не подтверждают таких взглядов, значение теории чисел бесспорно. $a+b\in \mathbb{N}$, $a\cdot b \in \mathbb{N}$ множество $\mathbb{N}$ замкнуто на сложение и умножение
$a+b\in \mathbb{N}$, $a\cdot b \in \mathbb{N}$ множество $\mathbb{N}$ замкнуто на сложение и умножение  ..$
..$ ..$
..$ {-1}$:
{-1}$:  2=a$, где $a$ — заданное рациональное число, а x — неизвестное число, не всегда имеет решение в пределах множества рациональных чисел и требует расширения множества чисел происходит снова. Эти числа называются иррациональными числами, и $\sqrt{2}$, $\sqrt{3}$, $\pi$… принадлежат этому множеству.
2=a$, где $a$ — заданное рациональное число, а x — неизвестное число, не всегда имеет решение в пределах множества рациональных чисел и требует расширения множества чисел происходит снова. Эти числа называются иррациональными числами, и $\sqrt{2}$, $\sqrt{3}$, $\pi$… принадлежат этому множеству.