Лучший ответ по мнению автора | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||
Посмотреть всех экспертов из раздела Учеба и наука > Математика
Решено
На плоскости отмечены 17 точек, не лежащих на одной прямой (т. е. найдутся хотя бы 3 точки, не лежащие на одной прямой). Через каждые две точки
е. найдутся хотя бы 3 точки, не лежащие на одной прямой). Через каждые две точки
МУЛЬТФИЛЬМ НАЧАЛСЯ В 15Ч12МИН А ЗАКОНЧИЛСЯЧЕРЕЗ ЧЕТВЕРТЬ ЧАСА.ПОСЛЕ МУТФИЛЬМАПОКАЗАЛИ ПЯТИМИНУТНЫЙ РЕКЛАМНЫЙ РОЛИК.В КОТОРОМ ЧАСУЗАКОНЧИЛСЯ МУТФИЛЬМ?В КОТОРОМ ЧАСУ ЗАКОНЧИЛСЯ РЕКЛАМНЫЙ РОЛИК.
рабочий за восьмичасовой рабочий день вытачивает 80 деталей,а его ученик работает 6 ч в день и вытачивает 42 такие детали.На сколько больше…
На плоскости отмечены 17 точек, не лежащих на одной прямой (т.е. найдутся хотя бы 3 точки, не лежащие на одной прямой). Через каждые две точки
3 снегоуборочные машины работая одновременно за 1 час могут очистить не более 17 км дороги шириной 10 м.Сколько может потребоваться машин для очистки…
Пользуйтесь нашим приложением
Глава 40. Нормальное уравнение плоскости. Расстояние от точки до плоскости
Нормальным уравнением плоскости называется ее уравнение, написанное в виде, (1)
где
,
,
— направляющие
косинусы нормали плоскоти, p —
расстояние от начала координат до плоскости. При
вычислении направляющих косинусов нормали
следует считать, что она направлена от начала
координат к плоскости (если же плоскость
проходит через начало координат, то выбор
положительного направления нормали
безразличен).
При
вычислении направляющих косинусов нормали
следует считать, что она направлена от начала
координат к плоскости (если же плоскость
проходит через начало координат, то выбор
положительного направления нормали
безразличен).
Пусть — какая угодно точка пространства, d — расстояние от нее до данной плоскости. Отклонением точки от данной плоскости называется число +d, если точка и начало координат лежат по разные стороны от данной плоскости, и число -d, если они лежат по одну сторону от данной плоскости (если лежит на самой плоскости, то отклонение равно нулю).
Если точка имеет координаты , , , а плоскость задана нормальным уравнением
,
то отклонение точки от этой плоскости дается формулой
.
Очевидно, .
Общее уравнение плоскости
приводится к нормальному виду (1) умножением на нормирущий множитель, определяемый формулой
;
знак нормирующего множителя берется
противоположным знаку свободного члена
нормируемого уравнения.
| 956 | Определить, какие из следующих уравнений плоскостей являются нормальными: | |
| 956.1 | ; | |
| 956.2 | ; | |
| 956.3 | ; | |
| 956.4 | ; | |
| 956.5 | ; | |
956.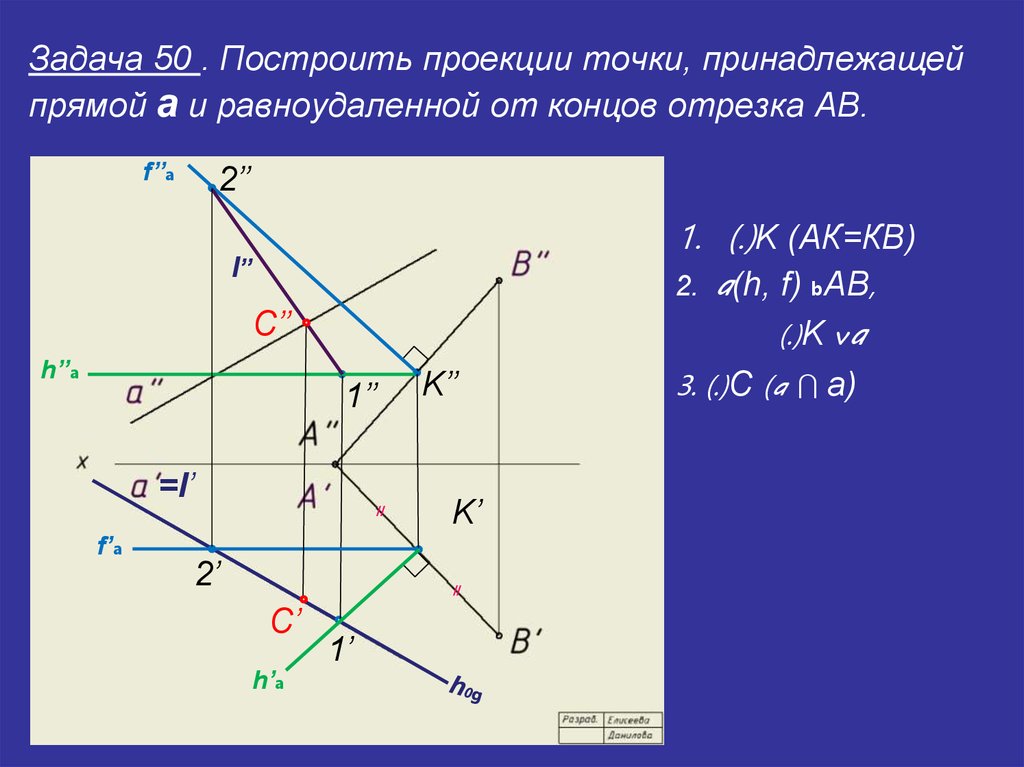 6 6 | ; | |
| 956.7 | ; | |
| 956.8 | ;. | |
| 956.9 | ; | |
| 956.10 | ; | |
| 956.11 | ; | |
| 956.12 | . | |
| 957 | Привести каждое из следующих уравнений плоскостей к нормальному виду: | |
957. 1 1 | ; | |
| 957.2 | ; | |
| 957.3 | ; | |
| ; | ||
| 957.5 | ; | |
| 957.6 | ; | |
| 957.7 | ; | |
| 957.8 | ; | |
957. 9 9 | ; | |
| 957.10 | . | |
| 958 | Для каждой из следующих плоскостей вычислить углы , , , образуемые нормальню с осями координат, и расстояние р от начала координат: | |
| 958.1 | ; | |
| 958.2 | ; | |
| 958.3 | ; | |
| 958.4 | ; | |
958.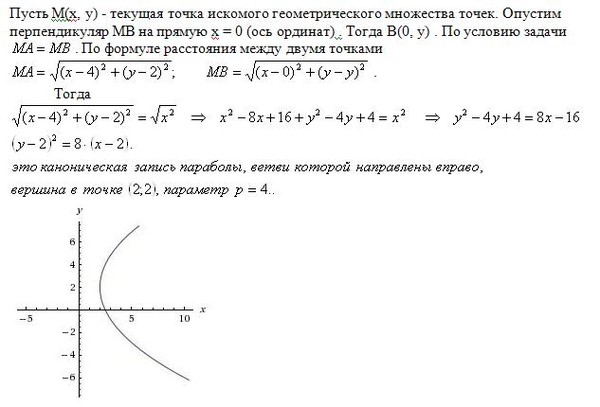 5 5 | ; | |
| 958.6 | ; | |
| 958.7 | ; | |
| 958.8 | ; | |
| 958.9 | ; | |
| 958.10 | . | |
| 959 | Вычислиь величину отклонения и расстояние d от точки до плоскости в каждом из следующих случаев:М2(2; -1; -1), ; | |
959. 1 1 | М1(-2; -4; 3), ; | |
| 959.2 | М3(1; 2; -3), ; | |
| 959.3 | М3(1; 2; -3), ; | |
| 959.4 | М4(3; -6; 7), ; | |
| 959.5 | М5(9; 2; -2), . | |
| 960 | Вычислить
расстояние d от точки Р(-1; 1; -2) до плоскости,
проходящей через точки М1(1; -1; 1),
М2(-2; 1; 3), М3(4;
-5; -2). | |
| 961 | Определить, лежит ли точка Q(2; -1; 1) и начало координат по одну или по разные стороны относительно каждой из следующих плоскостей: | |
| 961.1 | ; | |
| 961.2 | ; | |
| 961.3 | ; | |
| 961.4 | ; | |
| 961.5 | ; | |
961. 6 6 | . | |
| 962 | Доказать, что плоскость пересекает отрезок, ограниченный точками М1(3; -2; 1) и М2(-2; 5; 2). | |
| 963 | Доказать, что плоскость не пересекает отрезка, ограниченного точками М1(1; 4; -3) и М2(2; 5; 0). | |
| 964 | В каждом из следующих случаев вычислить расстояние между параллельными плоскостями: | |
| 964.1 | , ; | |
964. 2 2 | , ; | |
| 964.3 | , ; | |
| 964.4 | , ; | |
| 964.5 | , ; | |
| 964.6 | , . | |
| 965 | Две грани куба лежат на плоскостях , . Вычислить объем этого куба. | |
| 966 | На оси Оу найти
точку, отстоящую от плоскости на
расстояние d=4.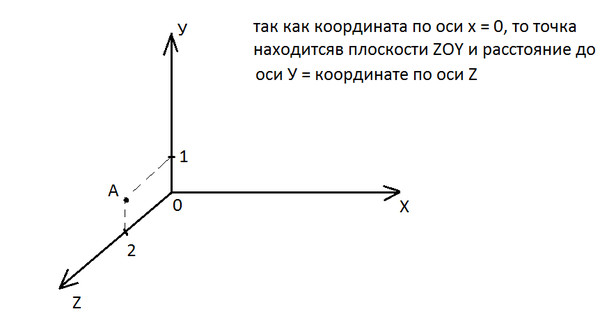 | |
| 967 | На оси Oz найти точку, равноудаленную от точки М(1; -2; 0) и от плоскости . | |
| 968 | На оси Ох найти точку, равноудаленную от двух плоскостей , . | |
| 969 | Вывести уравнение геометрического места точек, отклонение которых от плоскости равно 2. | |
| 970 | Вывести уравнение геометрического места точек, отклонение которых от плоскости равено –3. | |
| 971 | Составить
уравнения плоскостей, параллельных плоскости и отстоящих от нее на расстояние d=5. | |
| 972 | В каждом из следующих случаев составить уравнение геометрического места точек, равноудаленных от двух параллельных плоскостей: | |
| 972.1 | , ; | |
| 972.2 | , ; | |
| 972.3 | , . | |
| 973 | В каждом из следующих случаев составить уравнения плоскостей, которые делят пополам двугранные углы, образованные двумя пересекающимися плоскостями: | |
973. 1 1 | , ; | |
| 973.2 | , ; | |
| 973.3 | , . | |
| 974 | В каждом из следующих случаев определить, лежат ли точка М(2; -1; 3) и начало координат в одном, в смежных или вертикальных двугранных углах, образованных при пересечении двух плоскостей: | |
| 974.1 | , ; | |
| 974.2 | , ; | |
974. 3 3 | , . | |
| 975 | В каждом из следующих случаев определить, лежат ли точки М(2; -1; 1) и N(1; 2; -3) в одном, в смежных или вертикальных двугранных углах, образованных при пересечении двух плоскостей: | |
| 975.1 | , ; | |
| 975.2 | , . | |
| 976 | Определить, лежит ли начало координат внутри острого или тупого угла, образованного двумя плоскостями , . | |
| 977 | Определить, лежит
ли точка М(3; 2; -1) внутри острого или тупого угла,
образованного двумя плоскостями , . | |
| 978 | Составить уравнение плоскости, делящей пополам тот двугранный угол между двумя плоскостями , , в котором лежит начало координат. | |
| 979 | Составить уравнение плоскости, делящей пополам тот двугранный угол между двумя плоскостями , , в котором лежит точка М(1; 2; -3). | |
| 980 | Составить уравнение плоскости, которая делит пополам острый двугранный угол, образованный двумя плоскостями , . | |
| 981 | Составить
уравнение плоскости, которая делит пополам тупой
двугранный угол, образованный двумя плоскостями , .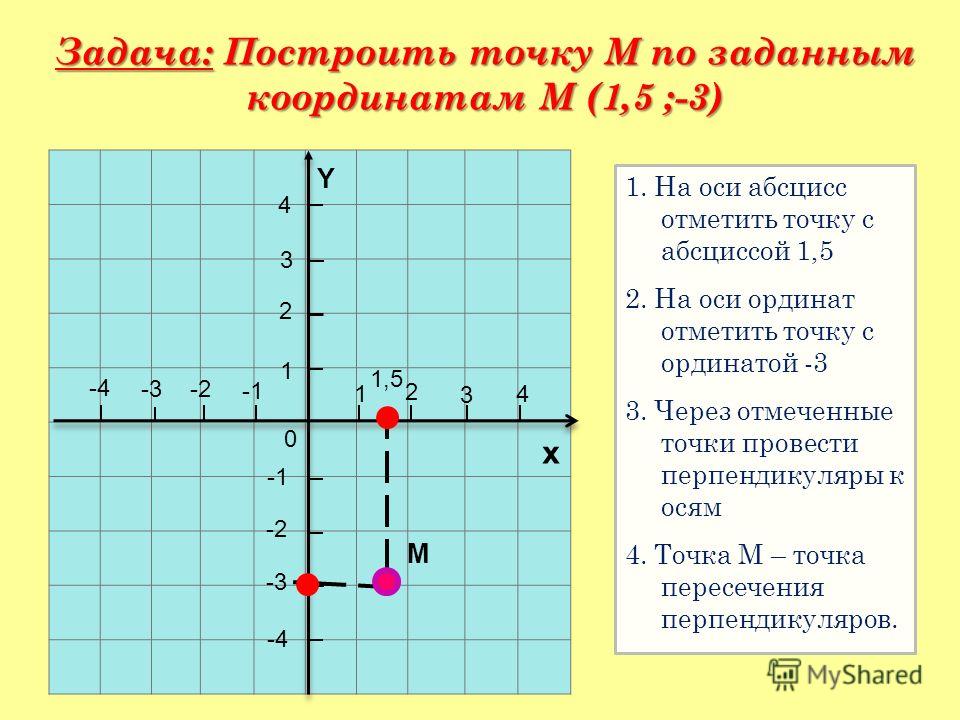 |
геометрия — Найдите точку, равноудаленную от двух точек и линии
Подход, который может быть полезен не только для предоставления решений, но и для обсуждения и понимания их существования, заключается в следующем. Имея две точки $P_1$ и $P_2$ и прямую, мы можем без ограничения общности задать плоскость $xy$, в которой ось $x$ совпадает с прямой, а неотрицательная часть $y$ -ось содержит $P_1$. Тогда координаты $P_1$ и $P_2$ можно записать как $(0,y_1)$ и $(x_2,y_2)$ соответственно (с $y_1 \geq 0\,$). Отрезок $P_1P_2$ имеет наклон $(y_2-y_1)/x_2$, а его средняя точка имеет координаты $(x_2/2,(y_1+y_2)/2)\,\,\,\,$. Таким образом, уравнение его геометрической оси равно 92}{2y_1}$$
Также обратите внимание, что для того, чтобы решения были действительными, $y_1y_2$ должно быть равно $\geq 0\,\,$. Поскольку $y_1$ предполагалось $\geq 0$ в исходных предположениях ($P_1$ находится на неотрицательной части оси $y$), это означает, что:
в случае $y_1 \neq y_2 \,$, если $y_1$ и $y_2$ оба равны $>0$ (т.
 е. $P_1$ находится на положительной оси $y$, а $P_2$ находится в первом или втором квадранте), мы имеем два разных реальные решения;
е. $P_1$ находится на положительной оси $y$, а $P_2$ находится в первом или втором квадранте), мы имеем два разных реальные решения;в случае $y_1 \neq y_2\,$, если $y_1=0$ или $y_2=0$ (т.е. один из $P_1$ и $P_2$ лежит на оси $x$) имеем единственное действительное решение;
в случае $y_1 \neq y_2\,$, если $y_1>0$ и $y_2<0$ (т. е. $P_1$ лежит на положительной оси $y$, а $P_2$ — на третьей или четвертый квадрант) у нас нет реальных решений;
наконец, в случае $y_1 = y_2\,$ у нас есть единственное действительное решение.
В качестве примера установим $P_1=(0,2) \,\,$ и $P_2=(2,4)\,\,$. В этом случае имеем $y_1=2\,$, $x_2=2\,\,$,$y_2=4\,\,$, а в случае $y_1 \neq y_2\,\,\ , $. Применяя формулы выше, получаем 92} \right) }=-2 \pm 4$$
Подставляя эти два возможных значения $X$ в уравнение, дающее $Y$, для случая $X=2\,\,$ получаем
$$ Y= \frac{2+4}{2} + \frac{2 (4-2)}{2(-2)}= 3-1=2$$
и для случая $X=-6 \ ,\,$ дает
$$ Y= \frac{2+4}{2} + \frac{2 (2 \cdot (-6)-2)}{2(-2)}= 3+7= 10$$
, что в итоге дает два решения $(2,2)\,$ и $(-6,10)\,$.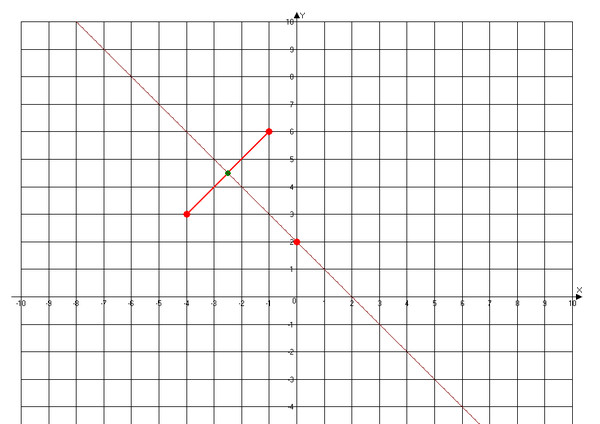 Соответственно расстояния $(2,2) \,$ от $P_1$, $P_2$ и оси $x$ равны $2$, а $(-6,10)\,$ все равны $10$. 92}{2 \cdot4}=\frac{13}{2}$$
Соответственно расстояния $(2,2) \,$ от $P_1$, $P_2$ и оси $x$ равны $2$, а $(-6,10)\,$ все равны $10$. 92}{2 \cdot4}=\frac{13}{2}$$
, что дает единственное решение $(6,13/2) \,\,$, расстояния которого от $P_1$, $P_2$ и все оси $x$ равны $13/2 \,$.
Найдите точку на оси Y, равноудаленную от точек (6, −6) и (3, 3).
Домашнее задание по предварительному исчислению
Кевин С.
спросил 16.09.18 Найдите точку на оси Y, равноудаленную от точек
(6, −6),
и
(3, 3).
Подписаться І 3
Подробнее
Отчет
2 ответа от опытных наставников
Лучший Новейшие Самый старыйАвтор: Лучшие новыеСамые старые
Марк М. ответил 16.09.18
Репетитор
4. 9
(918)
9
(918)
Репетитор по математике — уровни средней школы/колледжа
Об этом репетиторе ›
Об этом репетиторе ›
Множество точек, равноудаленных от двух данных точек, является серединным перпендикуляром к отрезку с данными точками в качестве его концов.
Пусть A = (6,-6) и B = (3,3)
Середина AB = (9/2, -3/2)
Наклон AB = 9/( -3) = -3
Биссектриса имеет наклон 1/3 и содержит точку (9/2, -3/2)
Уравнение перпендикулярного бисектора: y — (-3/2) = 1/3 (x — 9/2)
y + 3/2 = (1/3 ) x-3/2
y = (1/3) x-3 (y-intercept (0, -3))
(0, -3) находится на перпендикулярном бисекторе AB и находится на оси Y.
Голосовать за 0 Понизить
Подробнее
Отчет
Дэвид В.

 10.17
10.17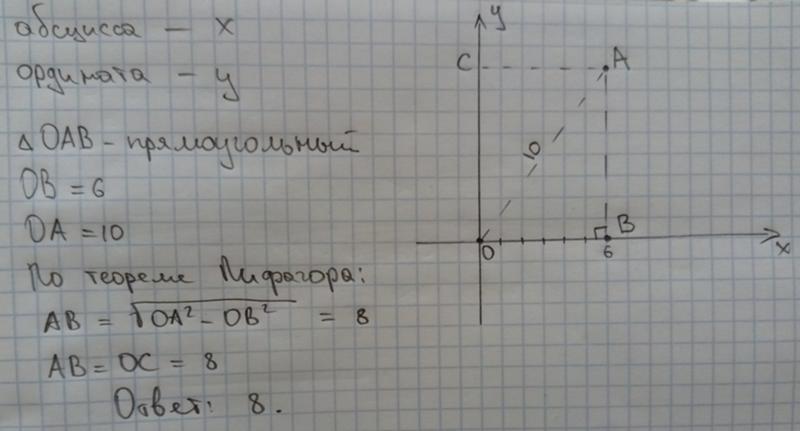 е. $P_1$ находится на положительной оси $y$, а $P_2$ находится в первом или втором квадранте), мы имеем два разных реальные решения;
е. $P_1$ находится на положительной оси $y$, а $P_2$ находится в первом или втором квадранте), мы имеем два разных реальные решения;