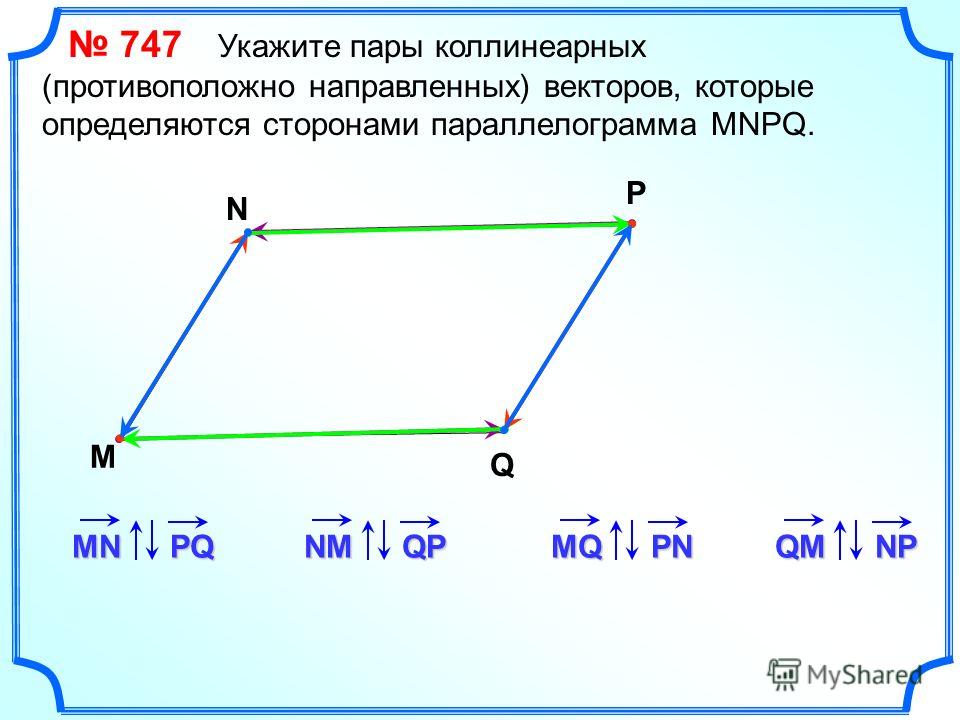
Кинематика в двух измерениях
Наш мир трехмерен. Для облегчения анализа многие движения можно упростить до двух измерений. Например, объект, запущенный в воздух, движется в вертикальной двухмерной плоскости; кроме того, горизонтальное движение над земной поверхностью на коротких расстояниях двумерно. Элементарная векторная алгебра необходима для изучения отношений между векторными величинами в двух измерениях.Сложение и вычитание векторов: геометрический метод
Вектор A , показанный на рисунке (a), представляет собой скорость 10 м/с к северо-востоку, а вектор B представляет скорость 20 м/с в точке 30 градусов к северу от востока. (Вектор обозначается буквой, набранной полужирным шрифтом , не курсивом , а его величина обозначается той же буквой обычным шрифтом , курсивом . Вы часто будете видеть векторы на рисунках в книге, которые представлены их величинами. в математических выражениях.
Рисунок 1
Графическое сложение векторов, A + B = C.
На рисунке (b) те же векторы расположены для геометрического сложения. Хвост одного вектора, в данном случае A , перемещается в начало другого вектора ( B ). Сумма векторов ( C ) — это вектор, простирающийся от конца одного вектора до начала другого. Чтобы найти величину C, измерьте вдоль его длины и используйте заданный масштаб для определения представленной скорости. Чтобы найти направление θ C, измерить угол с горизонтальной осью в конце C .
Рисунок (a) показывает, что A + B = B + A . Сумма векторов называется равнодействующей и является диагональю параллелограмма со сторонами А, и В.
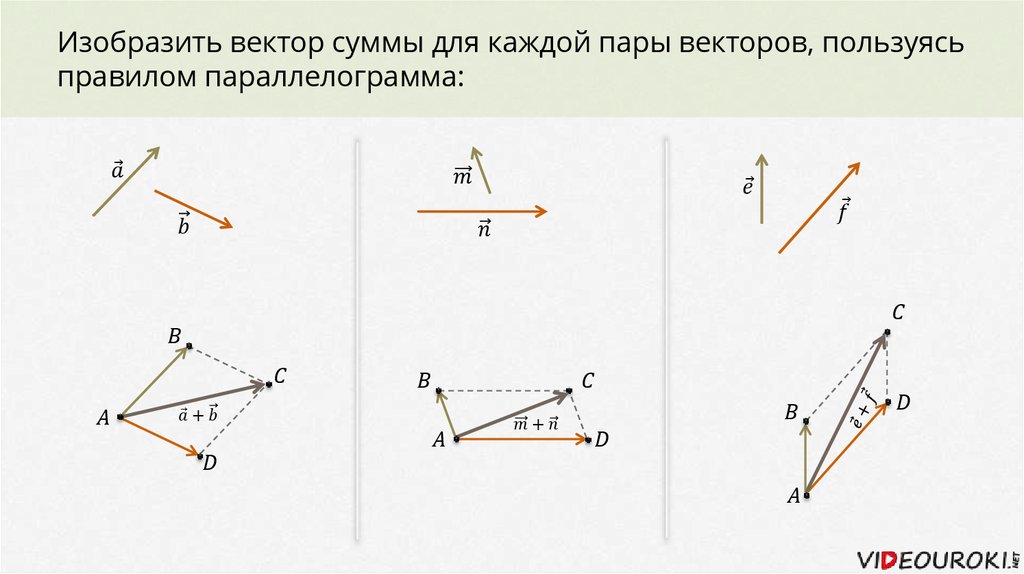
Рисунок (b) иллюстрирует построение для сложения четырех векторов.
Результирующий вектор — это вектор, из которого получается вектор, завершающий многоугольник.Рисунок 2
(a) A + B = B + A. (b) Графическое сложение нескольких векторов.
Чтобы вычесть векторы, сложите хвосты вместе. Разность двух векторов ( D ) — это вектор, который начинается с начала вычитаемого вектора ( B ) и идет к началу другого вектора ( A ). Альтернативный метод заключается в добавлении отрицательного значения вектора, который является вектором той же длины, но направленным в противоположном направлении. Второй способ показан на рисунке.
Рисунок 3
Графическое вычитание векторов, A − B = D.
Сложение и вычитание векторов: компонентный метод
Для точности сложения векторов требуется аналитический метод с использованием базовой тригонометрии, поскольку чертежи в масштабе не дают точных значений.
Рассмотрим вектор A в прямоугольной системе координат на рис. Вектор A можно представить как сумму двух векторов вдоль x и y оси, A = A x + A y , где A x и A y называются компонентами из A . Направление A x параллельно оси x , а направление A y параллельно оси y . Величины компонентов получаются из определений синуса и косинуса угла: cos θ = A x / A и sin θ = A y / A
илиРисунок 4
Компоненты вектора.
Чтобы сложить векторы численно, сначала найдите компоненты всех векторов. Знаки компонентов такие же, как знаки косинуса и синуса в данном квадранте. Затем просуммируйте компоненты в направлении x и просуммируйте компоненты в направлении y .
Как показано на рисунке, сумма 9Компоненты 0011 x и сумма компонентов y данных векторов ( A и B ) составляют компоненты x и y результирующего вектора ( C ).
Рисунок 5
Компонентный метод сложения векторов, A + B = C .
Эти равнодействующие составляющие образуют две стороны прямого угла с гипотенузой величины C ; таким образом, величина результирующей равна
Направление равнодействующей ( C ) вычисляется по касательной, поскольку тангенс θ = C x / C y . Чтобы найти угол θ, используйте θ = tan −1 ( C y / C x ).
Процедуру можно обобщить следующим образом:
1. Нарисуйте векторы в системе координат.
2. Найдите компоненты x и y всех векторов с соответствующими знаками.
3. Суммируйте компоненты в направлениях x и y .
4. Найдите модуль результирующего вектора по теореме Пифагора.
5. Найдите направление результирующего вектора с помощью функции касательной.
Выполните ту же процедуру для вычитания векторов путем вычисления соответствующей алгебраической суммы компонентов на шаге 3.
Умножение векторов
Скалярный продукт: Существует два разных способа перемножения двух векторов. Первый — это скалярное произведение, также называемое скалярным произведением, которое записывается как A · B . Это можно оценить двумя способами:
- А · B = A x B x + A y B y
- A · B = AB cos θ, где θ — угол между векторами, когда они установлены хвост к хвосту, а A и B — длины векторов.
Обратите внимание, что порядок векторов не имеет значения и что результатом скалярного произведения является скаляр, а не вектор. Обратите внимание, что если два вектора перпендикулярны, их скалярное произведение равно нулю в соответствии со вторым правилом выше.
Перемножение: Второй способ умножения векторов называется перекрестным произведением или векторным произведением . Пишется А · В . Его можно оценить двумя способами:
- A · B = ( A x B y − A y B x z , when the vectors A и B оба находятся в плоскости x–y . z указывает, что результатом является вектор, который указывает вдоль оси z . Как правило, вектор, полученный в результате векторного произведения, всегда перпендикулярен обоим векторам, умножаемым вместе.
Как правило, вектор, полученный в результате векторного произведения, всегда перпендикулярен обоим векторам, умножаемым вместе.- A · B = AB z sin θ, где θ — угол между векторами A и B , когда они расположены хвост к хвосту. Опять же, результатом является вектор, перпендикулярный A и B (и, следовательно, указывает вдоль оси z , если A и B находятся в плоскости x–y ).
Результат векторного произведения зависит от порядка векторов. Обратите внимание на первое правило, что A · B = −
Наконец, векторное произведение приводит к «правилу правой руки», которое позволяет легко определить направление результирующего вектора.
Для общего выражения A × B = C , укажите большим пальцем в направлении A. Теперь укажите указательным пальцем в направлении B ; при необходимости переверните руку. Вектор C указывает наружу от вашей ладони.
Векторы скорости и ускорения в двух измерениях
Для движения в двух измерениях более ранние уравнения кинематики должны быть выражены в векторной форме. Например, вектор средней скорости равен v = ( d f
− d o )/ t , where d o and d f are the initial and final displacement vectors and t — истекшее время. Как отмечалось ранее, векторы скорости и смещения показаны жирным шрифтом, а скаляр (t) — нет. Аналогичным образом средний вектор ускорения равен a = ( v F — V O )/ T , где V O и V F .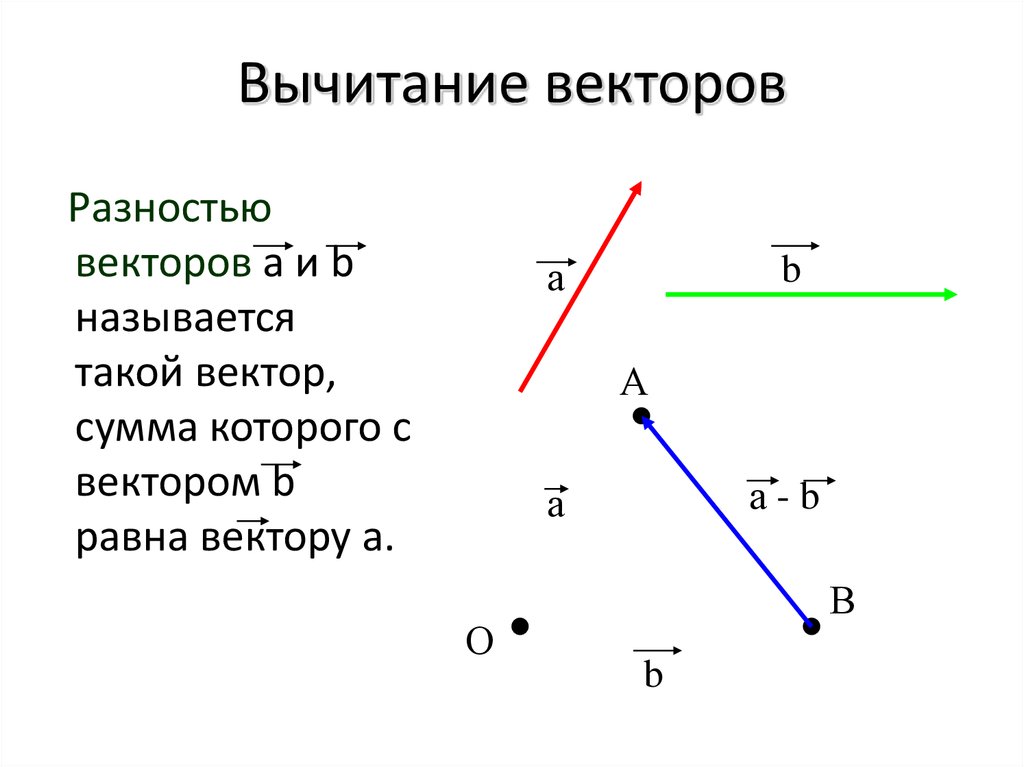
Важным моментом является то, что ускорение может возникать как от изменения величины скорости (скорости), так и от изменения направления скорости. Если объект движется по окружности с постоянной скоростью, возникает ускорение из-за изменения направления скорости, даже если величина скорости не меняется. Масса движется по горизонтальной окружности с постоянной скоростью на рис. Векторы скорости в положениях 1 и 2 вычитаются, чтобы найти среднее ускорение, которое направлено к центру окружности. (Обратите внимание, что средний вектор ускорения находится в середине пути в заданный интервал времени.)
Рисунок 6
Векторы скорости и ускорения объекта, движущегося по окружности
Следующее обсуждение обобщает четыре различных случая ускорения в плоскости:
- Вариант 1: Нулевое ускорение
- Случай 2: Ускорение из-за изменения направления, но не скорости
- Случай 3: Ускорение из-за изменения скорости, но не направления
- Случай 4: Ускорение из-за изменения скорости и направления.
Представьте себе шар, катящийся по горизонтальной поверхности, освещенной стробоскопическим светом. На рис. (а) показано положение мяча через равные промежутки времени вдоль пунктирной траектории. Случай 1 показан в позициях с 1 по 3; величина и направление скорости не меняются (картинки расположены равномерно и по прямой линии), а значит, и ускорения нет. Случай 2 указан для позиций с 3 по 5; мяч имеет постоянную скорость, но меняет направление, поэтому существует ускорение. Рисунок (b) иллюстрирует вычитание v 3 и v 4 и результирующее ускорение к центру дуги. Случай 3 происходит с позиций с 5 по 7; направление скорости постоянно, но величина меняется. Ускорение на этом участке пути соответствует направлению движения. Мяч изгибается из положения 7 в положение 9, показывая случай 4; скорость меняет как направление, так и величину. В этом случае ускорение направлено почти вверх между 7 и 8 и имеет составляющую к центру дуги из-за изменения направления скорости и составляющую вдоль траектории из-за изменения величины скорости.
Рисунок 7
(а) Путь мяча на столе. (b) Ускорение между точками 3 и 4.
Движение снаряда
Любой, кто наблюдал брошенный объект, например, бейсбольный мяч в полете, наблюдал движение снаряда . Для анализа этого распространенного типа движения делаются три основных предположения: (1) ускорение свободного падения постоянно и направлено вниз, (2) влияние сопротивления воздуха незначительно и (3) поверхность земли неподвижна. плоскости (то есть кривизна земной поверхности и вращение Земли пренебрежимо малы).
Для анализа движения разделите двухмерное движение на вертикальную и горизонтальную составляющие. Вертикально объект подвергается постоянному ускорению за счет силы тяжести. Горизонтально объект не испытывает ускорения и, следовательно, сохраняет постоянную скорость. Эта скорость показана на рисунке, где компоненты скорости изменяются в направлении y ; однако все они имеют одинаковую длину в направлении x (постоянная).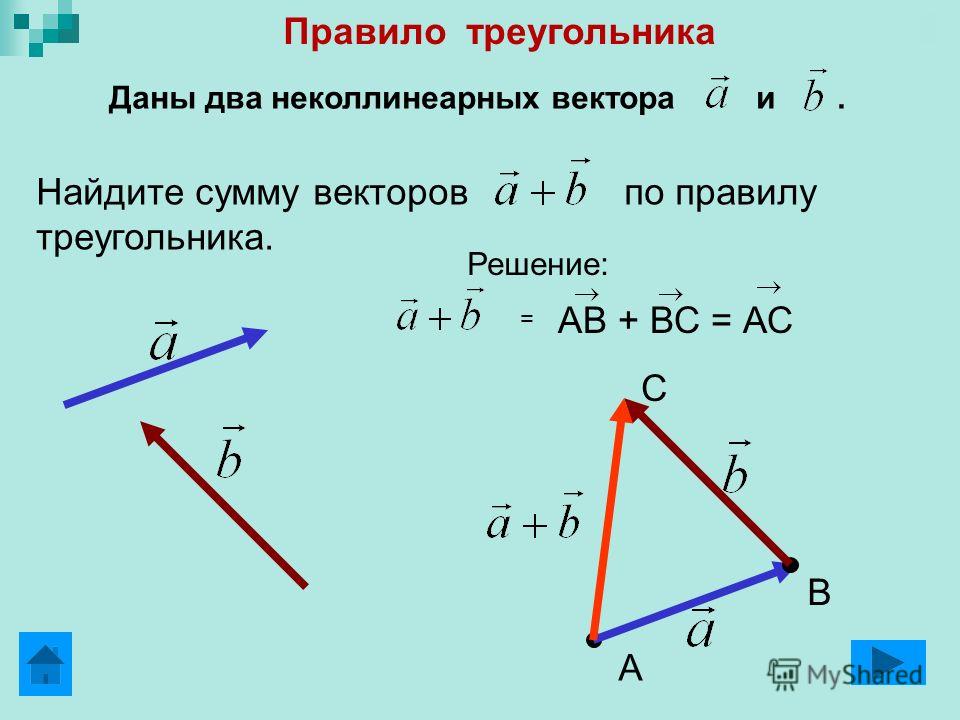
Обратите внимание, что вектор скорости изменяется со временем из-за того, что меняется вертикальная составляющая.
Рисунок 8
Движение снаряда.
В этом примере частица покидает начало координат с начальной скоростью ( v o ) вверх под углом θ o . The original x and y components of the velocity are given by v x0 = v o and v y0 = v o sin θ o .
Разделив движения на компоненты, можно проанализировать величины в направлениях x и y с помощью одномерных уравнений движения, индексированных для каждого направления: для горизонтального направления v x = v x0 и x = v x0 t ; for vertical direction, v y = v y0 − gt and y = v y0 − (1/2) gt 2 , where x и y представляют расстояния в горизонтальном и вертикальном направлениях соответственно, а ускорение свободного падения ( g ) равно 9,8 м/с 2 .
(Знак «минус» уже включен в уравнения.) Если объект выстреливается под углом, y составляющая начальной скорости отрицательна. Скорость снаряда в любой момент можно вычислить по составляющим в этот момент по теореме Пифагора, а направление найти по арктангенсу отношений составляющих:
Другая информация полезна при решении проблем со снарядами. Рассмотрим пример, показанный на рисунке, где снаряд выстреливается под углом к уровню земли и возвращается на тот же уровень. Время, за которое снаряд достигнет земли из высшей точки, равно времени падения свободно падающего предмета, падающего прямо вниз с той же высоты. Это равенство времени связано с тем, что горизонтальная составляющая начальной скорости снаряда влияет на то, как далеко снаряд перемещается по горизонтали, но не на время полета. Траектории снарядов параболические и, следовательно, симметричные. Также для этого случая объект достигает вершины своего подъема за половину общего времени (Т) рейса.
На вершине подъема вертикальная скорость равна нулю. (Ускорение всегда равно g даже в верхней точке полета.) Эти факты можно использовать для определения дальности полета снаряда или расстояния, пройденного по горизонтали. На максимальной высоте v y = 0 и t = T /2; поэтому уравнение скорости в вертикальном направлении принимает вид 0 = v o sin θ − g T /2 или решение для T , T = (2 v 0 sin θ)/ g .
Подстановка в уравнение горизонтального расстояния дает R = ( v o cos θ) T . Подставьте T в уравнение дальности и используйте тождество тригонометрии sin 2θ = 2 sin θ cos θ, чтобы получить выражение для дальности через начальную скорость и угол движения, R = ( v o 2 / g ) sin 2θ.
Как видно из этого выражения, максимальная дальность имеет место при θ = 45 градусов, потому что при этом значении θ максимальное значение sin 2θ равно 1. На рисунке показаны траектории снарядов, брошенных с одинаковой начальной скоростью под разными углами наклона.
Рисунок 9
Набор снарядов, выпущенных под разными углами.
Равномерное круговое движение
Для равномерного движения объекта по горизонтальному кругу радиусом (R) постоянная скорость определяется как одна революция. Время одного оборота (T) определяется как период . За один оборот головка вектора скорости описывает окружность 2π v за один период; таким образом, модуль ускорения равен a = 2π v / T . Объедините эти два уравнения, чтобы получить два дополнительных соотношения с другими переменными: a = v 2 / R и a = (4π 2 / T 10 2 )
Вектор смещения направлен наружу от центра круга движения.
Вектор скорости касается траектории. Вектор ускорения, направленный к центру окружности, называется центростремительное ускорение . На рисунке показаны векторы смещения, скорости и ускорения в различных положениях, когда масса движется по кругу на горизонтальной плоскости без трения.
Рисунок 10
Равномерное круговое движение.
Математика и наука были изобретены людьми для описания и
понимать окружающий мир.
Заметим, что существуют некоторые величины и процессы в
наш мир, который зависит от направление в котором
они происходят, и есть некоторые величины, которые не зависят
по направлению.
Математики и ученые называют количество
который зависит от направления векторной величины . Количество
которая не зависит от направления, называется скалярной величиной .
А
векторное количество
имеет две характеристики: величину и направление . На этом слайде мы описываем метод сложения двух векторов. Сложение векторов — это один из аспектов большой векторной алгебры, которую мы изучаем. , а не будут представлены на этом сайте. Добавление вектора представлено здесь, потому что это встречается довольно часто при изучении движения и потому что он демонстрирует некоторые фундаментальные различия между векторы и скаляры. Векторы обычно обозначаются на рисунках стрелкой.
Длина стрелки указывает величину и
кончик стрелки указывает направление. Вектор
помечены буквой в алфавитном порядке
буква с линией сверху, чтобы отличить ее от скаляра.
Величину вектора будем обозначать символом |а| . Направление
будет измеряться углом фи относительно координаты
оси х . Ось координат y перпендикулярна х . Примечание: Оси координат x и y сами по себе
векторы! Они имеют величину и направление. Если мы построим пунктирную линию от кончика вектор а идущий параллельно оси х, он пересекает ось у в том месте, где мы этикетка или . Точно так же линия от кончика вектора параллельно оси Y пересекает ось X на x . Величины x и x называются компоненты вектора, и оба являются скалярными квантитами. Чтобы добавить два вектора, a и b , мы сначала разбиваем каждый вектор на его компоненты, x и a , и bx и по , как показано на рисунке. Из правил, регулирующих равенство векторов, синий вектор b равен черному вектору b потому что он имеет одинаковую равную длину и одинаковое направление. Теперь, поскольку компоненты вектора и вектор b являются скалярами, мы можем добавить x-компонент для генерации x-компонент нового вектора c : сх = топор + Ьх Точно так же мы можем добавить y-компонентов : су = ау + по Новые компоненты cx и cy полностью определяют
новый вектор c , указав как величину, так и направление. |
Когда
сравнение
две векторные величины одного и того же типа, вы должны сравнить обе
величина и направление.
Сначала ты
столкнуться с осями координат, когда вы учитесь строить графики. Так что у тебя есть
использовал векторы в течение некоторого времени, даже не подозревая об этом! 