Справочник. Планиметрия
Планиметрия
Основные сведения из школьной геометрии
1. Признаки равенства треугольников.
1) Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то треугольники равны.
2) Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то треугольники равны.
3) Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то треугольники равны.
2. Основные свойства и признаки равнобедренного треугольника.
1) Углы при основании равнобедренного треугольника равны.
2) Медиана равнобедренного треугольника, проведенная к основанию, является биссектрисой и высотой.
3) Если два угла треугольника равны, то он равнобедренный.
4) Если медиана треугольника является его высотой, то треугольник
равнобедренный.
5) Если биссектриса треугольника является его высотой, то треугольник равнобедренный.
6) Если медиана треугольника является его биссектрисой, то треугольник равнобедренный.
3. Геометрическое место точек, равноудаленных от концов отрезка, есть прямая, перпендикулярная этому отрезку и проходящая через его середину (серединный перпендикуляр к отрезку).
4. Признаки и свойства параллельных прямых.
1) Аксиома параллельных. Через данную точку можно провести не более одной прямой, параллельной данной.
2) Если при пересечении двух прямых третьей образуются равные внутренние накрест лежащие углы, то прямые параллельны.
3) Если две прямые параллельны одной и той же прямой, то они параллельны между собой.
4) Две прямые, перпендикулярные одной и той же прямой, параллельны.
5) Если две параллельные прямые пересечь третьей, то образованные при этом внутренние накрест лежащие углы равны.
5. Теорема о сумме углов треугольника и следствия из нее.
1) Сумма внутренних углов треугольника равна 180◦.
2) Внешний угол треугольника равен сумме двух внутренних не смежных с ним углов.
3) Сумма внутренних углов выпуклого n-угольника равна 180◦(n−2).
4) Сумма внешних углов n-угольника равна 360◦.
5) Углы со взаимно перпендикулярными сторонами равны, если они оба острые или оба тупые.
6. Если биссектрисы углов B и C треугольника ABC пересекаются в точке M , то ∠BMC = 90◦+ ∠A/2.
7. Угол между биссектрисами смежных углов равен 90◦.
8. Биссектрисы внутренних односторонних углов при параллельных прямых и секущей перпендикулярны.
9. Признаки равенства прямоугольных треугольников.
1) По двум катетам.
2) По катету и гипотенузе.
3) По гипотенузе и острому углу.
4) По катету и острому углу.
10. Геометрическое место внутренних точек угла, равноудаленных от его сторон, есть биссектриса угла.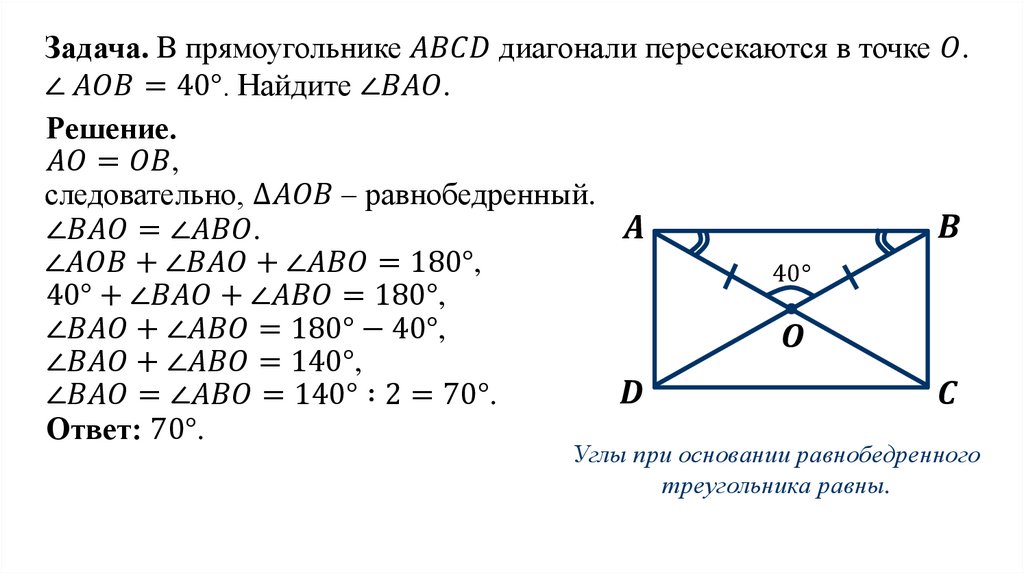
11. Катет прямоугольного треугольника, лежащий против угла в 30◦, равен половине гипотенузы.
12. Если катет прямоугольного треугольника равен половине гипотенузы, то угол, противолежащий этому катету, равен 30◦.
13. Неравенство треугольника. Сумма двух сторон треугольника больше третьей стороны.
14. Следствие из неравенства треугольника. Сумма звеньев ломаной больше отрезка, соединяющего начало первого звена с концом последнего.
15. Против большего угла треугольника лежит большая сторона.
16. Против большей стороны треугольника лежит больший угол.
17. Гипотенуза прямоугольного треугольника больше катета.
18. Если из одной точки проведены к прямой перпендикуляр и наклонные, то
1) перпендикуляр короче наклонных;
2) большей наклонной соответствует большая проекция и наоборот
19.
Параллелограмм. Параллелограммом называется четырехугольник, противоположные стороны которого попарно параллельны.
Свойства и признаки параллелограмма.
1) Диагональ разбивает параллелограмм на два равных треуголь-ника.
2) Противоположные стороны параллелограмма попарно равны.
3) Противоположные углы параллелограмма попарно равны.
4) Диагонали параллелограмма пересекаются и делятся точкой пересечения пополам.
5) Если противоположные стороны четырехугольника попарно равны, то этот четырехугольник — параллелограмм.
6) Если две противоположные стороны четырехугольника равны
и параллельны, то этот четырехугольник — параллелограмм.
7) Если диагонали четырехугольника делятся точкой пересечения пополам, то этот четырехугольник — параллелограмм.
20. Прямоугольник. Прямоугольником называется параллелограмм с прямым углом.
Свойства и признаки прямоугольника.
1) Диагонали прямоугольника равны.
2) Если диагонали параллелограмма равны, то этот параллелограмм — прямоугольник.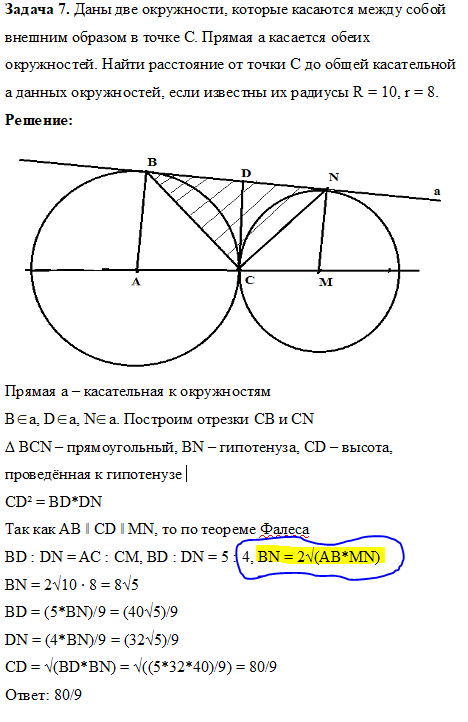
21. Ромб. Ромбом называется четырехугольник, все стороны которого равны.
Свойства и признаки ромба.
1) Диагонали ромба перпендикулярны.
2) Диагонали ромба делят его углы пополам.
3) Если диагонали параллелограмма перпендикулярны, то этот параллелограмм — ромб.
4) Если диагонали параллелограмма делят его углы пополам, то этот параллелограмм — ромб.
22. Квадрат. Квадратом называется прямоугольник, все стороны которого равны.
23. Геометрическое место точек, равноудаленных от данной прямой — две параллельные прямые.
24. Теорема Фалеса. Если на одной стороне угла отложить равные отрезки и через их концы провести параллельные прямые, пересекающие второю сторону угла, то на второй стороне угла отложатся также равные отрезки.
25. Средняя линия треугольника. Отрезок, соединяющий середины двух сторон треугольника называется средней линией треугольника.
Теорема о средней линии треугольника.
Средняя линия треугольника параллельна стороне треугольника и равна ее половине.
26. Свойство середин сторон четырехугольника. Середины сторон любого четырехугольника являются вершинами параллелограмма.
27. Теорема о медианах треугольника. Медианы треугольника пересекаются в одной точке и делятся ею в отношении 2 : 1, считая от вершины.
28. а) Если медиана треугольника равна половине стороны, к которой она проведена, то треугольник прямоугольный.
б) Медиана прямоугольного треугольника, проведенная из вершины прямого угла, равна половине гипотенузы.
29. Трапеция. Трапецией называется четырехугольник, у которого только две противоположные стороны (основания) параллельны. Средней линией трапеции называется отрезок, соединяющий середины непараллельных сторон (боковых сторон).
Теорема о средней линии трапеции. Средняя линия трапеции параллельна основаниям и равна их полусумме.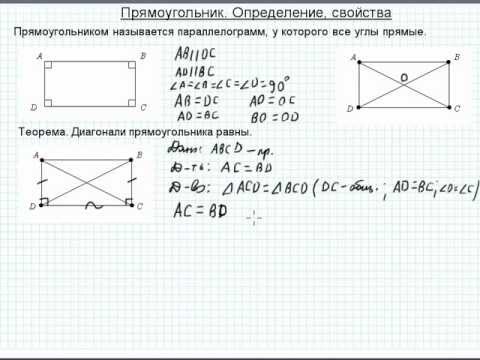
30. Отрезок, соединяющий середины диагоналей трапеции, равен полуразности оснований.
31. Трапеция называется равнобедренной, если ее боковые стороны равны.
Свойства и признаки равнобедренной трапеции.
1) Углы при основании равнобедренной трапеции равны.
2) Диагонали равнобедренной трапеции равны.
3) Если углы при основании трапеции равны, то она равнобедренная.
4) Если диагонали трапеции равны, то она равнобедренная.
5) Проекция боковой стороны равнобедренной трапеции на основание равна полуразности оснований, а проекция диагонали — полусумме оснований.
32. Окружность. Окружностью называется геометрическое место точек плоскости, удаленных от данной точки, называемой центром окружности, на одно и то же положительное расстояние.
Свойства окружности.
1) Диаметр, перпендикулярный хорде, делит ее пополам.
2) Диаметр, проходящий через середину хорды, не являющейся диаметром, перпендикулярен этой хорде.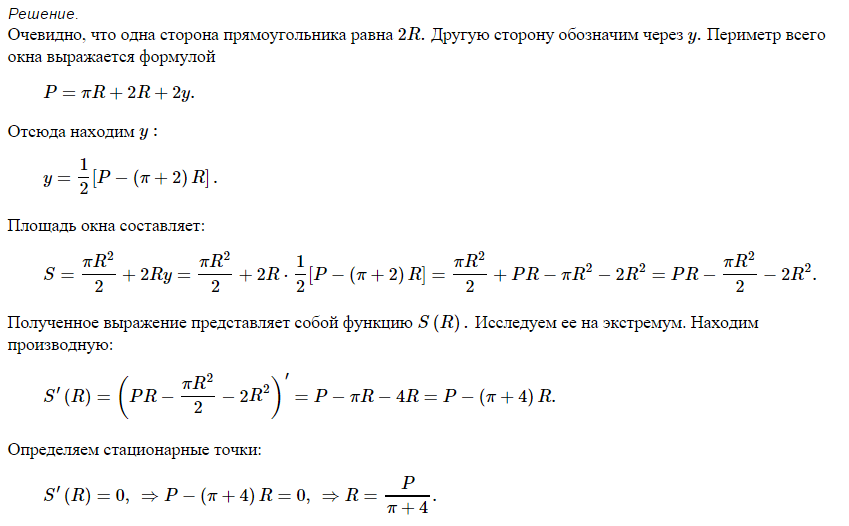
3) Серединный перпендикуляр к хорде проходит через центр окружности.
4) Равные хорды удалены от центра окружности на равные расстояния.
5) Хорды окружности, удаленные от центра на равные расстояния, равны.
6) Окружность симметрична относительно любого своего диаметра.
7) Дуги окружности, заключенные между параллельными хордами, равны.
8) Из двух хорд больше та, которая менее удалена от центра.
9) Диаметр есть наибольшая хорда окружности.
33. Замечательное свойство окружности. Геометрическое место точек M , из которых отрезок AB виден под прямым углом (∠AMB =90◦), есть окружность с диаметром AB без точек A и B.
34. Геометрическое место точек M , из которых отрезок AB виден под острым углом (∠AMB < 90◦) есть внешность круга с диаметром AB без точек прямой AB.
35. Геометрическое место точек M , из которых отрезок AB виден под тупым углом (∠AMB > 90◦), есть внутренность круга с диаметром AB без точек отрезка AB.
36. Свойство серединных перпендикуляров к сторонам треугольника. Серединные перпендикуляры к сторонам треугольника пересекаются в одной точке, которая является центром окружности, описанной около треугольника.
37. Линия центров двух пересекающихся окружностей перпендикулярна их общей хорде.
38. Центр окружности, описанной около прямоугольного треугольника — середина гипотенузы.
39. Теорема о высотах треугольника. Прямые, содержащие высоты треугольника, пересекаются в одной точке.
40. Касательная к окружности. Прямая, имеющая с окружностью единственную общую точку, называется касательной к окружности.
1) Касательная перпендикулярна радиусу, проведенному в точку касания.
2) Если прямая l, проходящая через точку на окружности, перпендикулярна радиусу, проведенному в эту точку, то прямая l — касательная к окружности.
3) Если прямые, проходящие через точку M , касаются окружности в точках A и B, то MA = MB.
4) Центр окружности, вписанной в угол, лежит на биссектрисе этого угла.
5) Теорема о биссектрисах треугольника. Биссектрисы треугольника пересекаются в одной точке, которая является центром окружности, вписанной в треугольник
41. Радиус окружности, вписанной в прямоугольный треугольник с катетами a, b и гипотенузой c, равен (a + b − c)/2.
42. Если M — точка касания со стороной AC окружности, вписанной в треугольник ABC, то AM = p − BC, где p — полупериметр треугольника.
43. Окружность касается стороны BC треугольника ABC и продолжений сторон AB и AC. Тогда расстояние от вершины A до точки касания окружности с прямой AB равно полупериметру треугольника ABC.
44. Окружность, вписанная в треугольник ABC, касается сторон AB, BC и AC соответственно в точках K, L и M . Если ∠BAC = α, то ∠KLM = 90◦− α/2.
45. Даны окружности радиусов r и R (R > r). Расстояние между их центрами равно a (a > R + r).
Тогда отрезки общих внешних и общих внутренних касательных, заключенные между точками касания, равны соответственно и
46. Если в четырехугольник можно вписать окружность, то суммы его противоположных сторон равны.
47. Касающиеся окружности. Говорят, что две окружности касаются, если они имеют единственную общую точку (точка касания).
1) Точка касания двух окружностей лежит на их линии центров.
2) Окружности радиусов r и R с центрами O1 и O2 касаются внешним образом тогда и только тогда, когда R + r = O1O2.
3) Окружности радиусов r и R (r < R) с центрами O1 и O2 касаются внутренним образом тогда и только тогда, когда R − r = O1O2.
4) Окружности с центрами O1 и O2 касаются внешним образом в точке K. Некоторая прямая касается этих окружностей в различных точках A и B и пересекается с общей касательной, проходящей через точку K, в точке C. Тогда ∠AKB = 90◦ и ∠O1CO2 = 90◦.
48. Углы, связанные с окружностью.
1) Угловая величина дуги окружности равна угловой величине центрального угла.
2) Вписанный угол равен половине угловой величины дуги, на которую он опирается.
3) Угол между пересекающимися хордами равен полусумме противоположных дуг, высекаемых хордами.
4) Угол между двумя секущими равен полуразности дуг, высекаемых секущими на окружности.
5) Угол между касательной и хордой равен половине угловой величины дуги, заключенной между ними.
49. Вписанные углы, опирающиеся на одну и ту же дугу, равны.
50. Геометрическое место точек, из которых данный отрезок виден под данным углом, есть две дуги равных окружностей (без концов этих дуг).
51. Если четырехугольник можно вписать в окружность, то сумма его противоположных углов равна 180◦.
52. Если сумма противоположных углов четырехугольника равна 180◦, то около него можно описать окружность.
53. Если в трапецию можно вписать окружность, то боковая сторона трапеции видна из центра окружности под прямым углом.
54. Если M — точка на отрезке AB, причем AM : BM = a : b, то AM : AB = a : (a + b), BM : AB = b : (a + b).
55. Теорема о пропорциональных отрезках. Параллельные прямые, пересекающие стороны угла, высекают на них пропорциональные отрезки.
56. Подобие. Признаки подобия треугольников.
1) Если две стороны одного треугольника соответственно пропорциональны двум сторонам другого, а углы, заключенные между этими сторонами, равны, то треугольники подобны.
2) Если два угла одного треугольника соответственно равны двум углам другого, то треугольники подобны.
3) Если три стороны одного треугольника соответственно пропорциональны трем сторонам другого, то треугольники подобны.
57. Отношение соответствующих линейных элементов подобных фигур равно коэффициенту подобия.
58. Замечательное свойство трапеции. Точка пересечения диагоналей трапеции, точка пересечения продолжений боковых сторон и середины оснований лежат на одной прямой.
59. Свойство биссектрисы треугольника. Биссектриса треугольника делит его сторону на отрезки, пропорциональные двум другим сторонам.
60. Произведение основания на высоту для данного треугольника постоянно.
61. Если BM и CN — высоты треугольника ABC (∠A 90◦), то треугольник AMN подобен треугольнику ABC, причем коэффициент подобия равен |cos ∠A|.
62. Произведения длин отрезков хорд AB и CD окружности, пересекающихся в точке E, равны, то есть |AE| · |EB| = |CE| · |ED|.
63. Теорема о касательной и секущей и следствие из нее.
1) Если из одной точки проведены к окружности касательная и секущая, то произведение всей секущей на ее внешнюю часть равно квадрату касательной
2) Произведение всей секущей на ее внешнюю часть для данной точки и данной окружности постоянно.
64. Тригонометрические соотношения в прямоугольном треугольнике.
1) Катет прямоугольного треугольника равен произведению гипотенузы на синус противолежащего или на косинус прилежащего к этому катету острого угла.
2) Катет прямоугольного треугольника равен другому катету, умноженному на тангенс противолежащего или котангенс прилежащего к этому катету острого угла.
65. Теорема Пифагора. Квадрат гипотенузы прямоугольного треугольника равен сумме квадратов катетов.
66. Теорема, обратная теореме Пифагора. Если квадрат стороны тре-угольника равен сумме квадратов двух других его сторон, то треугольник — прямоугольный.
67. Средние пропорциональные в прямоугольном треугольнике. Высота прямоугольного треугольника, проведенная из вершины прямого угла, есть среднее пропорциональное проекций катетов на гипотенузу, а каждый катет есть среднее пропорциональное гипотенузы и своей проекции на гипотенузу.
68. Если в трапецию можно вписать окружность, то радиус окружности есть среднее пропорциональное отрезков, на которые точка касания делит боковую сторону.
69. Отрезок общей внешней касательной к двум касающимся окружностям радиусов r и R равен отрезку общей внутренней касательной, заключенному между общими внешними.
Оба эти отрезка равны .
70. Метрические соотношения в треугольнике.
1) Теорема косинусов. Квадрат стороны треугольника равен сумме квадратов двух других сторон без удвоенного произведения этих сторон на косинус угла между ними.
2) Следствие из теоремы косинусов. Сумма квадратов диагоналей параллелограмма равна сумме квадратов всех его сторон.
3) Формула для медианы треугольника. Если m — медиана треугольника, проведенная к стороне c, то , где a и b —остальные стороны треугольника.
4) Теорема синусов. Стороны треугольника пропорциональны синусам противолежащих углов.
5) Обобщенная теорема синусов. Отношение стороны треугольника к синусу противолежащего угла равно диаметру окружности, описанной около треугольника.
71. Формулы площади треугольника.
1) Площадь треугольника равна половине произведения основания на высоту.
2) Площадь треугольника равна половине произведения двух его сторон на синус угла между ними.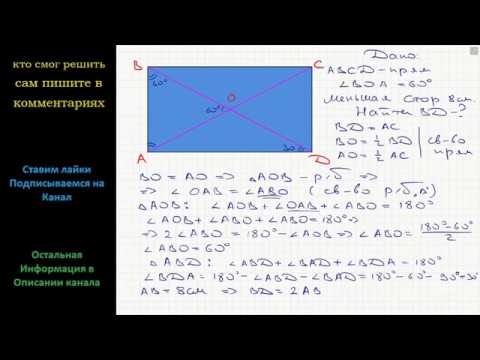
3) Площадь треугольника равна произведению его полупериметра на радиус вписанной окружности.
4) Площадь треугольника равна произведению трех его сторон, деленному на учетверенный радиус описанной окружности.
5) Формула Герона. , где — полупериметр треугольника.
72. Элементы равностороннего треугольника со стороной a. Пусть h, S, r, R — высота, площадь, радиусы описанной и вписанной окружности равностороннего треугольника со стороной a. Тогда
73. Формулы площади параллелограмма.
1) Площадь параллелограмма равна произведению основания на высоту.
2) Площадь параллелограмма равна произведению его соседних сторон на синус угла между ними.
3) Площадь прямоугольника равна произведению двух его соседних сторон.
4) Площадь ромба равна половине произведения его диагоналей.
74. Площадь трапеции равна произведению полусуммы оснований на высоту.
75.
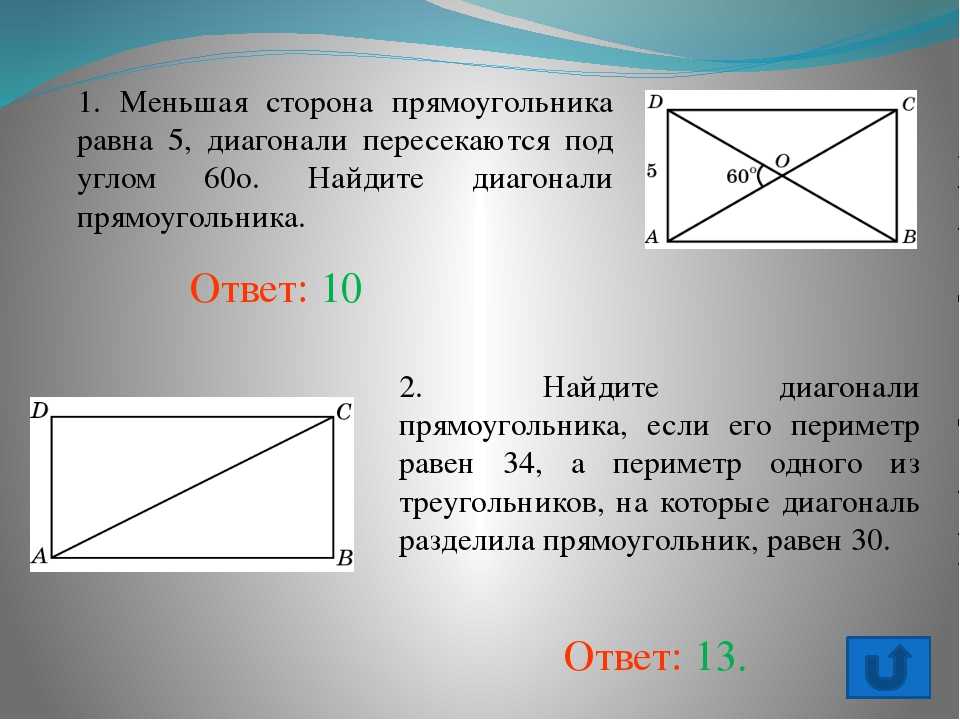Площадь четырехугольника равна половине произведения его диагоналей на синус угла между ними.
76. Отношение площадей подобных треугольников равно квадрату коэффициента подобия.
77. Если в многоугольник можно вписать окружность, то его площадь равна произведению полупериметра многоугольника на радиус этой окружности.
78. Если M — точка на стороне BC треугольника ABC, то
79. Если P и Q — точки на сторонах AB и AC (или на их продолжениях) треугольника ABC, то
80. Длина окружности радиуса R равна 2πR.
81. Площадь круга радиуса R равна πR2.
Литература: Гордин Р.К., «Это должен знать каждый матшкольник»
ФОС 5-9 класс по математике | Учебно-методическое пособие по алгебре (5, 6, 7, 8, 9 класс):
9 класс. Контрольная работа №1
Квадратный трехчлен. Квадратичная функция.
Вариант 1
1.Разложите на множители квадратный трехчлен:
1) х2 – 5х + 6; 2) 5у2 – 3у – 2.
2.Изобразите схематически график функции: у=3х2;
3.Постройте график функции у=х2 — 4х + 4. С помощью графика найдите:
1)значение у при х= -0,5;
2)значение х при у=2;
3)нули функции;
4)промежутки, в которых у
4.Сократите дробь:
5.Найдите область определения функции:
1)у=х2 – 8х; 2)у=; 3)у=.
Вариант 2
1.Разложите на множители квадратный трехчлен:
1) х2 + 10х — 11; 2) 3у2 – 4у + 1.
2.Изобразите схематически график функции: у=2х2;
3.Постройте график функции у=х2 — 2х + 1. С помощью графика найдите:
1)значение у при х= -0,5;
2)значение х при у= -2;
3)нули функции;
4)промежутки, в которых у
4.Сократите дробь :
5.Найдите область определения функции:
1)у=х2+ 9х; 2)у=; 3)у=.
Вариант 3
1.Разложите на множители квадратный трехчлен:
1) х2 – 8х + 7; 2) 5у2 – 8у + 3.
2.Изобразите схематически график функции: у =х2;
3.Постройте график функции у=х2 — 10х + 25. С помощью графика найдите:
1)значение у при х= 2,5;
2)значение х при у=1;
3)нули функции;
4)промежутки, в которых у
4.Сократите дробь :
5.Найдите область определения функции:
1)у=х2+ 12х; 2)у=; 3)у=.
Вариант 4
1.Разложите на множители квадратный трехчлен:
1) х2 + 5х + 4; 2) 4у2 – 3у – 7.
2.Изобразите схематически график функции: у= -3х2;
3.Постройте график функции у=х2 — 4х + 3. С помощью графика найдите:
1)значение у при х= -0,5;
2)значение х при у= — 1;
3)нули функции;
4)промежутки, в которых у
4.Сократите дробь :
5.Найдите область определения функции:
1)у=3х2 + 2х; 2)у=; 3)у=.
Вариант 5
1.Разложите на множители квадратный трехчлен:
1) х2 – 7х + 6; 2) 9у2 + 2у – 7.
2.Изобразите схематически график функции: у= — 2х2;
3.
Постройте график функции у=х2 + 4х — 5. С помощью графика найдите:
1)значение у при х= -0,5;
2)значение х при у=2;
3)нули функции;
4)промежутки, в которых у
4.Сократите дробь:
5.Найдите область определения функции:
1)у=х2+ 3х; 2)у=; 3)у=.
Вариант 6
1.Разложите на множители квадратный трехчлен:
1) х2 – 6х + 8; 2) 6у2 + 2у – 8.
2.Изобразите схематически график функции: у= 5х2;
3.Постройте график функции у=х2 + 4х + 4. С помощью графика найдите:
1)значение у при х= -0,5;
2)значение х при у=1;
3)нули функции;
4)промежутки, в которых у
4.Сократите дробь:
5.Найдите область определения функции:
1)у=х2 – 18х; 2)у=; 3)у=.
Нормы оценок: «3»- любые 3 задания, « 4» — 4 задания , «5» — 5 заданий.
Контрольная работа № 2
Системы уравнений с двумя переменными.
Вариант 1
1.Решите систему уравнений:
2.Площадь прямоугольного треугольника равна 15 дм2, а сумма его катетов равна 11дм.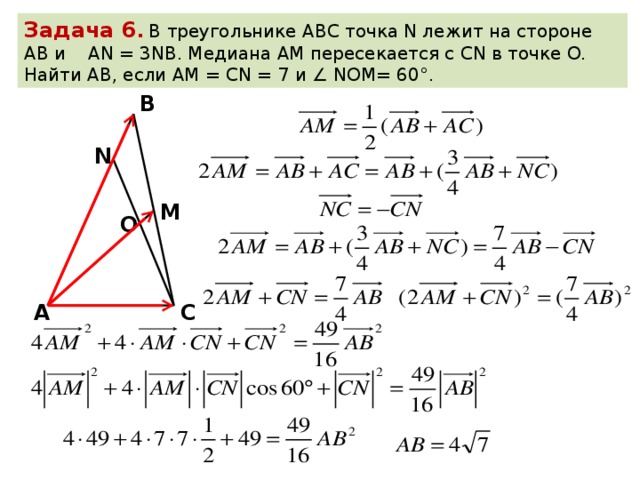
Найдите катеты.
3.Решите графически систему уравнений:
4.Не выполняя построения, найдите координаты точек пересечения окружности и прямой х+у= — 3.
5. Решите систему уравнений:
Вариант 2
1.Решите систему уравнений:
2.Площадь прямоугольника равна 12 дм2, а его периметр равен 14 дм. Найдите стороны прямоугольника.
3.Решите графически систему уравнений:
4.Не выполняя построения, найдите координаты точек пересечения окружности и прямой х+у= — 1.
5. Решите систему уравнений:
Вариант 3
1.Решите систему уравнений:
2.Площадь прямоугольного треугольника равна 5 дм2, а сумма его катетов равна 11 дм. Найдите катеты.
3.Решите графически систему уравнений:
4.Не выполняя построения, найдите координаты точек пересечения окружности и гиперболы ху= 8.
5. Решите систему уравнений:
Вариант 4
1.Решите систему уравнений:
2.Площадь прямоугольника равна 8 см2, а периметр равен 12 см.
Найдите стороны прямоугольника.
3.Решите графически систему уравнений:
4.Не выполняя построения, найдите координаты точек пересечения окружности и прямой х + у= 0.
5. Решите систему уравнений:
Вариант 5
1.Решите систему уравнений:
2.Площадь прямоугольного треугольника равна 12 см2, а сумма его катетов равна 10 см. Найдите катеты.
3.Решите графически систему уравнений:
4.Не выполняя построения, найдите координаты точек пересечения окружности и прямой х + у= — 3.
5. Решите систему уравнений:
Вариант 6
1.Решите систему уравнений:
2.Площадь прямоугольника равна 10 см2, а периметр равен 14 см. Найдите стороны прямоугольника.
3.Решите графически систему уравнений:
4.Не выполняя построения, найдите координаты точек пересечения параболы и прямой у — 2х= 1.
5. Решите систему уравнений:
Нормы оценок: «3»- любые 3задания, « 4» — 4 задания , «5» — 5 заданий.
Контрольная работа №3 по теме:
«Элементы комбинаторики и теории вероятностей»
Вариант 1
А1. Сколькими способами можно разместить 5 различных книг на полке?
А2. Сколько трехзначных чисел, в которых нет одинаковых цифр можно составить из цифр 1, 3, 5, 7, 9?
А3. В классе 20 учеников. Нужно выбрать 8 человек для участия в школьных конкурсах. Сколькими способами это можно сделать?
А4. Какова вероятность того, что при бросании игрального кубика выпадет менее 2 очков?
В1. Из 8 мальчиков и 5 девочек надо выделить для работы на пришкольном участке 3 мальчиков и 2 девочек. Сколькими способами это можно сделать?
Вариант 2
А1. Сколькими шестизначных чисел можно составить из цифр 1, 2, 3, 4, 5, 6 без повторения цифр?
А2. Сколько четырехзначных чисел, в которых нет одинаковых цифр можно составить из цифр 1, 2, 3, 5, 7, 9?
А3. В классе 15 учеников. Нужно выбрать 2 дежурных по классу. Сколькими способами это можно сделать?
А4.
Какова вероятность того, что при бросании игрального кубика выпадет 6 очков?
В1. Из 9 ручек и 6 карандашей надо выбрать 2 ручки и 3 карандаша. Сколькими способами можно сделать этот выбор?
Нормы оценок: «3»- любые 3А, « 4» — 4А, «5» — 4А + 1В.
Контрольная работа №4 Итоговая контрольная работа
Вариант 1
А1. Решите уравнение: .
А2. Вычислите:
А3. Решите систему уравнений:
А4. Найдите область определения функции
А5. Решите неравенство:
В1. Решите уравнение .
C1. Решите систему уравнений: .
Вариант 2
А1. Решите уравнение: .
А2. Упростите выражение:
А3. Решите систему уравнений:
А4. Найдите область определения функции
А5. Решите неравенство:
В1. Решите уравнение .
C1. Решите систему уравнений: .
Нормы оценок:
«3»- любые 3А, 4» — 3А + 1В, «5» — 5А + 1В или 3А + 1В + 1С.
Получение квадрата с помощью треугольника 3:4:5
Chace — универсальный магазин проектов по благоустройству дома
Компания по снабжению зданий Чейс
•
02 января 2022 г.
•
МИШЕЛЬ УОРРЕН — АВТОР ХРОНИКИ
Деловые новости
Компания по снабжению зданий Чейс • 04 мая, 2021 •
Опубликовано в разделе деловых новостей местной газеты Chace Building Supply
Информация о дверных петлях и грубом открытии
По снабжению здания Чейс • 29 мая, 2018 •
При заказе или продаже дверей важно, чтобы вы помогли покупателю приобрести подходящие петли. Петли на внутренних и внешних дверях определяются, когда вы тянете дверь на себя, с какой бы стороны ни была ручка. Например, когда дверь открывается перед вами, а ручка находится слева, это ЛЕВАЯ ДВЕРЬ. Когда ручка находится справа, это ПРАВАЯ ДВЕРЬ.
Наш обновленный веб-сайт
Маркетинговая группа CAM • 28 мая, 2018 •
Мы предприняли шаги по пересмотру и оптимизации нашего нового сайта в соответствии с современными потребностями. Предлагая многоэкранный дружественный дизайн и качество, которое вы ожидаете от Chace Building Supply.
Спасибо нашим бывшим и новым партнерам по разработке веб-сайтов, CAM Marketing Group из Бристоля, Коннектикут.
Вернуть крыльцо
Скотт Сидлер • 09 мая, 2016 •
Думаю, пора вернуть крыльцо. Слишком долго наши гаражи росли, а подъезды уменьшались. Мы изолируем себя и свои дома, чтобы внешний мир не проникал внутрь, а внутренний […] Читать далее Сообщение «Верните переднее крыльцо» впервые появилось в блоге The Craftsman.
Нет, Джоанна, это не шиплап
Скотт Сидлер • 25 апр, 2016 •
Мы с женой, как и большинство владельцев старых домов, в последнее время являемся поклонниками многих тематических шоу «Сделай сам», посвященных реставрации. Rehab Addict, Barnyard Builders, American Pickers и, конечно же, Fixer Upper. Их дизайн и стремление сохранить […] Читать далее Пост No Joanna, That’s Not Shiplap впервые появился в блоге The Craftsman.
Как сделать маленький дом большим
Скотт Сидлер
•
20 января 2014 г.
•
Старые дома часто намного меньше, чем их сегодняшние аналоги. Размер среднего американского дома значительно вырос за 20 век. От среднего размера около 1100 кв. футов в начале века до […] Читать далее Сообщение «Как сделать маленький дом большим» впервые появилось в блоге The Craftsman.
Контрольный список профилактического обслуживания
Скотт Сидлер • 20 мая 2013 г. •
Уход за старым домом иногда может показаться работой на полный рабочий день. Старые дома были построены из материалов и таким образом, что требовалось регулярное техническое обслуживание. Хотя это техническое обслуживание требует времени, в конечном итоге это более доступный вариант, чем […] Читать далее Пост «Контрольный список профилактического обслуживания» впервые появился в блоге The Craftsman.
Как ухаживать за паркетными полами
Скотт Сидлер • 04 мар, 2013 •
В Austin Historical мы часто ремонтируем паркетные полы, и клиенты часто спрашивают меня, как им следует ухаживать за недавно отремонтированными деревянными полами.
Существует конкретный график лечения и ухода […]
Читать далее
Сообщение «Как ухаживать за паркетными полами» впервые появилось в блоге The Craftsman.
Как открыть зависшие окна за 4 простых шага
Скотт Сидлер • 21 августа 2012 г. •
Если ваш дом достаточно старый, чтобы за всю свою жизнь нуждаться в новой покраске, то у вас может быть пара закрашенных окон. Если ваш дом такой же старый, как мой (1929 г.), вам повезет […] Читать далее Сообщение How To: Open Stuck Windows in 4 Easy Steps впервые появилось в блоге The Craftsman.
Оконные и дверные перегородки и решетки
Варианты дизайна изделия
Внешний вид нескольких отдельных оконных стекол в оконной раме популярен в самых разных архитектурных стилях — от исторических копий до современных фермерских домов. Для тех, кто ищет историческую достоверность, в аутентичных разделенных окнах используется множество отдельных стеклянных панелей в одном окне. Имитация разделенных стекол, доступная в различных стилях, имитирует внешний вид отдельных оконных стекол в оконной раме без ущерба для энергоэффективности отдельного стекла.
Authentic Divided Lite (ADL)
Отдельные куски стекла застеклены между решетчатыми перекладинами – таким же образом делались окна с самого начала, но с обновленным дизайном Marvin для повышения энергоэффективности.
Simulated Divided Lite (SDL)
Энергосберегающий способ создать внешний вид аутентичных разделенных lite, планки SDL постоянно приклеиваются к обеим сторонам стекла и доступны с прокладкой или без нее, установленной между стеклом для создания еще больше глубины, напоминающей ADL.
Имитация Divided Lite с разделительной планкой (SDLS)
В сочетании с планками SDL на внешней стороне стекла между стеклами устанавливается разделительная планка, что еще больше приближает внешний вид Authentic Divided Lite.
Решетки между стеклами (GBGs)
Решетки стационарно устанавливаются между стеклянными панелями, что обеспечивает простоту обслуживания, гладкий внешний вид и простоту очистки. Выберите один из 6 цветов кузова и 3 цветов салона.
Разделенные профили Lite
Накладные планки SDL и SDL предлагаются различной ширины в соответствии с профилем приклеивания створки или панели или штапика. Выберите стандартный вариант Ogee (используется в традиционных проектах) или дополнительный квадратный профиль с тремя стандартными ширинами стержней:
- 5 ⁄ 8 »
- 7 ⁄ 8 »
- 1 1 ⁄ 8 »
- 1 15 ⁄ 16 »
- 2 13 ⁄ 32 »
Marvin Signature
® UltimateВыберите один из вариантов разделенного облегченного стекла, аутентичного или имитационного, с прокладкой или решетками между стеклами или без них для получения гладкой поверхности и легкой очистки.
Что касается узоров, мы можем создать практически любой разделенный узор Lite, включая комбинации ширины, уникальные профили, прямоугольные или криволинейные вырезы и многое другое.
Выберите один из существующих облегченных разрезов, задайте индивидуальные разделенные разрезы в соответствии с новым дизайном или попросите наших специалистов по дизайну помочь в создании шаблона для вашего проекта.
Выбрано: 
*Это некоторые из наших наиболее часто запрашиваемых паттернов разделенного облегчения.
Marvin Signature
® ModernДобейтесь уникальной эстетики с разделенными литниками на любом окне или двери Modern. Выберите один из множества настраиваемых шаблонов, доступных как для продуктов с двойным, так и с тройным стеклом.
Имитированные разделенные рамы доступны шириной 7/8 дюйма и 1 1/8 дюйма, в дополнение к моделируемой раме шириной 2 7/8 дюйма.
Шаблоны
Имитация разделенных листов доступна в виде набора предварительно разработанных шаблонов.
Выбрано: 
Marvin Elevate
® Выберите одну из имитаций разделенных стекол или решеток между стеклами из заранее разработанных узоров, чтобы завершить внешний вид вашего проекта.