§ Нули функции
Прежде чем перейти к изучению темы «Нули функции»
внимательно изучите уроки
«Что такое функция в математике»
и
«Как решать задачи на функцию».
Запомните!
Нули функции — это
значения « x »
(аргумента функции),
при которых « y = 0 ».
В заданиях «Найдите нули функции» чаще всего сама функция задана через формулу (аналитически). Разберем алгоритм решения подобных задач.
Как найти нули функции, заданной формулой
Важно!
Чтобы найти нули функции, нужно:
- в формулу функции вместо
« у » (или « f(x) », « g(x) » и т.п.)
подставить «0»; - решить полученное уравнение
относительно « x »; - записать полученные решения уравнения для « x » в ответ.

По традиции разберемся на примере.
Разбор примера
Найдите нули функции:
f(x) = 0,2x + 3
Подставим вместо значения функции « f(x) » ноль.
0 = 0,2x + 3
Решаем полученное линейное уравнение
и записываем полученный ответ
для « x ».
0 = 0,2x + 3
Перенесем неизвестное « 0,2x » из правой части уравнения в левую с противоположным знаком.
−0,2x = 3 | · (−1)
0,2x = −3
Переведем десятичную дробь «0,2» в обыкновненную для упрощения дальнейших расчетов.
0,2x = −3
· x = −3 | · 10
· x · 10 = −3 · 10
| 2 · 10 |
| 10 |
· x = −30
2x = −30
x =
x = −15
Ответ: x = −15 является нулем
функции f(x) = 0,2x + 3
Разбор примера
Найдите нули функции:
f(x) = x 3 − 4x
Вместо « f(x) » подставим ноль.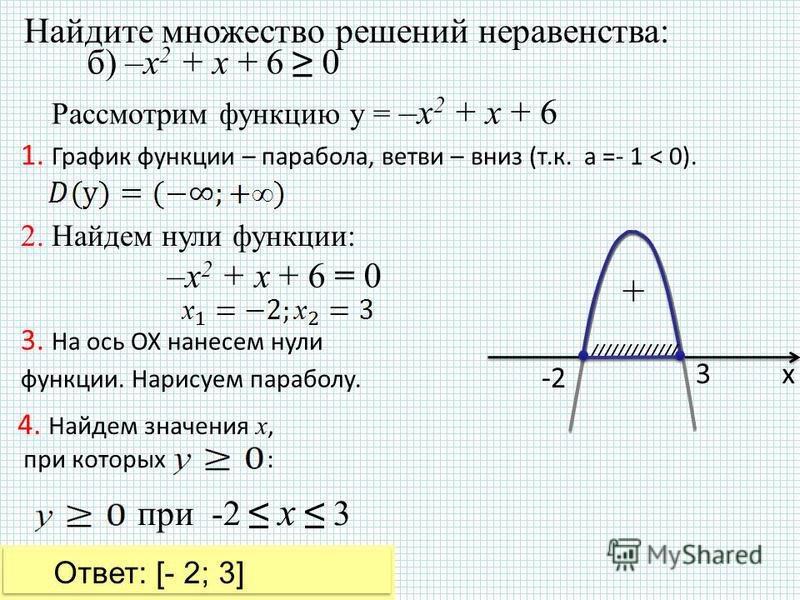
0 = x 3 − 4x
−x 3 + 4x = 0 | · (−1)
(−1) · (−x 3 + 4x) = 0 · (−1)
x 3 − 4x = 0
Вынесем общий множитель « x » за скобки.
x(x 2 − 4) = 0
В левой части полученного уравнения у нас два множителя:
« x »
и «(x 2 − 4)». Результат их умножения равен нулю.
Это возможно, когда любой из множителей равен нулю. Поэтому рассмотрим оба варианта: когда множитель « x » равен нулю и когда множитель «(x 2 − 4)» равен нулю.
1) x = 0
2) x 2 − 4 = 0
Решаем квадратное уравнение
«x 2 − 4 = 0».
Используем формулу
для решения квадратного уравнения с дискриминантом.
a · x 2 + b · x + c = 0
x1;2 =
| −b ± √b2 − 4ac |
| 2a |
x 2 − 4 = 0
x1;2 =
| 0 ± √02 − 4 · 1 · (−4) |
| 2 · 1 |
x1;2 =
| ± √16 |
| 2 |
x1;2 =
| x1 = | x2 = |
| x1 = 2 | x2 = −2 |
Запишем все полученные корни уравнений в ответ в порядке возрастания.
Ответ: x = −2; x = 0; x = 2 являются нулями функции f(x) = x 3 − 4x
Разбор примера
Найдите нули функции:
h(x) =
| x 2 − x − 6 |
| x + 3 |
Подставим вместо « h(x) » ноль.
0 =
| x 2 − x − 6 |
| x + 3 |
Перенесем правую часть
| x 2 − x − 6 |
| x + 3 |
в левую, изменив ее знак на минус.
− (
| x 2 − x − 6 |
| x + 3 |
) = 0 | · (−1)
| x 2 − x − 6 |
| x + 3 |
= 0
Единственный вариант, когда дробь будет равна нулю, только если
ее числитель
«x 2 − x − 6» будет равен нулю. Знаменатель
«x + 3» не может быть равен нулю, так как на ноль делить нельзя.
Знаменатель
«x + 3» не может быть равен нулю, так как на ноль делить нельзя.
x 2 − x − 6 = 0
Решим полученное квадратное уравнение через формулу с дискриминантом.
a · x 2 + b · x + c = 0
x1;2 =
| −b ± √b2 − 4ac |
| 2a |
x 2 − x − 6 = 0
x1;2 =
| −(−1) ± √(−1)2 − 4 · 1 · (−6) |
| 2 · 1 |
x1;2 =
| 1 ± √1 + 24 |
| 2 |
x1;2 =
| 1 ± √25 |
| 2 |
x1;2 =
| 1 ± 5 |
| 2 |
x1 =
| x2 =
| ||||
| x1 = | x2 = | ||||
| x1 = 3 | x2 = −2 |
Ответ: x = −2; x = 3 являются нулями функции h(x) =
| x 2 − x − 6 |
Разбор примера
Найдите нули функции:
f(x) = √x 2 − 4
Заменим «f(x)» на ноль.
√x 2 − 4 = 0
Единственное число, квадратный корень которого равен нулю — это сам ноль.
Поэтому, квадратный корень
«√ x 2 − 4 = 0 »
будет равен нулю, когда его подкоренное выражение
« x 2 − 4 »
будет равно нулю.
x 2 − 4 = 0
Осталось решить полученное квадратное уравнение, чтобы найти нули функции
«f(x) = √x 2 − 4».
x1;2 =
| −b ± √b2 − 4ac |
| 2a |
x 2 − 4 = 0
x1;2 =
| −(−0) ± √(−0) 2 − 4 · 1 · (−4) |
| 2 · 1 |
x1;2 =
| ± √16 |
| 2 |
x1;2 =
| x1 = | x2 = |
| x1 = 2 | x2 = −2 |
Ответ: x = −2; x = 2 являются нулями функции f(x) = √x 2 − 4
Как найти нули функции на графике функции
Важно!
Графически нули функции — это точки пересечения графика функции
с осью «Ox»
(осью абсцисс).
По определению
нули функции — это значения « x »,
при которых
« y = 0 ». Другими словами, у точек
графика функции, которые являются нулями функции,
Чтобы найти нули функции на графике нам остается, только найти, какая у них координата по оси « Ox ».
Рассмотрим на примере.
Разбор примера
На рисунке ниже изображен график функции « y = f(x) », определенной на множестве действительных чисел. Используя график, найдите нули функции.
Отметим на графике функции его точки пересечения с осью « Ox ».
Назовем полученные точки «(·)А» и «(·)B».
В точках «(·)А» и «(·)B» график функции пересекает
ось
« Ox » , то есть координаты точки «(·)А» и «(·)B»
по оси « Oy »
равны нулю.
Точки «(·)А» и «(·)B» — нули функции. Теперь определим, чему равны их координаты по оси « Ox ».
На графике видно, что у точки «(·)А» координата « x » равна
« 0 », а у точки «(·)B» координата « x » равна
« 2 ».
Запишем полученные значения координат « x » в ответ.
Ответ: x = 0; x = 2 являются нулями функции.
Как найти нули функции, заданной таблицей
В некоторых заданиях, где требуется найти нули функции, сама функция задана не вполне привычно с помощью формулы, а с помощью таблицы. Поиск нулей в таких примерах является легкой задачей.
Разбор примера
Найдите нули функции, заданной таблицей.
| x | −2 | −1 | 0 | 1 | 2 | 3 |
| y | −3 | −1,5 | 0 | 1 | 0 |
Вспомним определение нулей функции.
Запомните!
Нули функции — это
значения « x » в функции,
при которых « y = 0 ».
Согласно определению нулей функции нам достаточно найти значения « x » в таблице,
где
« y = 0 ». Выделим их цветом.
| x | −2 | −1 | 0 | 1 | 2 | 3 |
| y | −3 | −1,5 | 0 | 2 | 1 | 0 |
Остаётся только записать в ответ значения « x » из таблицы.
Ответ: x = 0; x = 3 являются нулями функции, заданной таблицей.
Калькулятор нулей
+ онлайн-решатель с бесплатными шагами
Калькулятор нулей — это онлайн-калькулятор для определения нулей любой функции, включая линейные, полиномиальные, квадратичные, тригонометрические функции и т. д. на заданном интервале.
Вычисленные нули могут быть действительными, комплексными или точными. Нули вещественных или комплексных функций — это числовые значения, при которых функция f(x) становится равной нулю, или, другими словами, может быть записана как:
f(x) = 0
такой, что x является нулем данной функции в указанной области.
Что такое калькулятор нулей?
Калькулятор нулей — это калькулятор, который может найти нули функций любого типа на любом заданном интервале, даже самых сложных.
Калькулятор нулей помогает определить нули различных функций на любом заданном интервале. Ниже приведен список различных функций, нули которых можно легко и быстро вычислить с помощью этого калькулятора нулей:
Ниже приведен список различных функций, нули которых можно легко и быстро вычислить с помощью этого калькулятора нулей:
- Линейные функции
- Квадратичные функции
- Кубические функции
- Полиномиалы
- Рациональные функции
- иррациональные функции
- . решать утомительные уравнения всего за несколько секунд. Калькулятор нулей находит нули заданной полиномиальной функции с некоторыми дополнительными функциями, включая график корней, сумму корней и произведение корней указанной функции.
Как использовать калькулятор нулей
Давайте обсудим, как использовать калькулятор нулей для нахождения нулей любой заданной функции.
Калькулятор нулей помогает легко найти нули любой функции. Найти нули любой функции можно и вручную, но это требует много времени и является очень длительной процедурой с точки зрения численных расчетов.

Рисунок-1 Методы поиска нулей
Таким образом, с помощью этого калькулятора вы можете шагнуть к желаемому результату с умом и сэкономить гораздо больше времени. Вам просто нужно выполнить эти простые шаги, чтобы найти нули любой функции.
Шаг 1:
Используйте калькулятор нуля , чтобы найти нули требуемой функции.
Шаг 2:
В калькуляторе есть вкладка выражения . Введите здесь функцию, для которой необходимо вычислить нули.
Шаг 3:
После того, как вы ввели функцию, для которой хотите найти нули, нажмите кнопку отправки , расположенную чуть ниже вкладки выражения.
Шаг 4:
После нажатия кнопки отправки перед вами появится новое окно с результатами. Калькулятор нулей находит нули заданной функции вместе с графиком корней, нулями, представленными на числовой прямой, суммой нулей и произведением нулей.
Шаг 5:
Наконец, для подробного и пошагового решения вам просто нужно нажать соответствующую кнопку, указанную для подробного решения, и вы можете просмотреть шаги.
 Если вы хотите найти корни любой другой функции, введите новое уравнение на вкладке выражения и выполните ту же процедуру, что и выше.
Если вы хотите найти корни любой другой функции, введите новое уравнение на вкладке выражения и выполните ту же процедуру, что и выше.Как работает нулевой калькулятор?
A Калькулятор нулей работает, устанавливая функцию, эквивалентную нулю, и вычисляя нули. Он работает, выделяя переменную x на одной стороне уравнения или изменяя указанное уравнение несколько раз, чтобы найти все нули функции. Давайте углубимся в концепцию нулей функций.
Нахождение корней или нулей функций любого типа вручную очень трудоемко и чревато ошибками. Может быть многочлен с большим количеством корней, который вам почти невозможно вычислить вручную, но этот онлайн-калькулятор нулей поможет вам. Вы можете вычислить нули быстро, просто введя в него нужную функцию.
Что такое ноль функции?
ноль функции — это точка, соответствующая значениям переменной функции, которые при помещении в функцию становятся нулевыми. Графически нуль функции — это точка, в которой она пересекает ось абсцисс.
 Другими словами, это также можно назвать x-пересечениями графика функции.
Другими словами, это также можно назвать x-пересечениями графика функции.Чтобы найти значение нуля для данной функции, установите функцию равной нулю, а затем вычислите значение переменной функции; соответствующие значения называются нулями. Чтобы еще больше упростить концепцию, ноль функции определяется как точка, в которой функция становится равной нулю или пересекает ось x графика функции.
Еще одна важная вещь, которую следует учитывать, это то, что функция может иметь более одного нуля в зависимости от степени многочлена или функции. степень функции определяется как наивысшая степень ее переменной. Следовательно, общее количество нулей любой функции зависит от степени функции.
Например, чтобы еще больше прояснить эту концепцию, Линейная функция является функцией степени 1. Следовательно, все линейные функции имеют только один нуль. Аналогично, Квадратичная функция является функцией второй степени, поэтому все квадратичные функции имеют два нуля или пересекают ось абсцисс графика функции в двух точках.

Что такое настоящий ноль?
Нуль называется Вещественным нулем , если он принадлежит множеству действительных чисел при условии, что функция значения становится равной нулю. Если f(x) = 0, где x $\in$ $\mathbb{R}$, то x называется действительным нулем функции.
В чем разница между нулем и корнем?
Основное различие между нулем и корнем заключается в том, что ноль связан с функцией, тогда как корень относится к уравнению. ноль функции — это значение, при котором функция становится равной нулю, поскольку х называется корнем функции f(x) тогда и только тогда, когда f(x) становится равным нулю.
Корень уравнения — это значение его переменной x, при котором уравнение удовлетворяется или обе части уравнения становятся равными. Полиномиальное уравнение также может иметь более одного корня в зависимости от степени полиномиального уравнения.
Возможности калькулятора нулей
A Калькулятор нулей — очень полезный инструмент, так как он не только предоставляет вам корни функции, но также имеет некоторые дополнительные функции, перечисленные ниже:
Рис.

Корневой график
Корневой график — это графическое представление всех корней функции. На нем изображен график функции с указанием x-отрезков, являющихся нулями функции.
Номер Строка Представление
Калькулятор нулей также представляет нули функции на числовой прямой. Числовая линия определяется как линия, на которой через различные интервалы отмечены различные точки.
Сумма корней
Калькулятор нулей также позволяет вычислить сумму всех корней функции.
Произведение корней
Наконец, он также вычисляет произведение всех корней функции.
Решенные примеры
Пример 1:
Найдите корни заданной функции с помощью калькулятора нулей. Нарисуйте корневую диаграмму и числовое представление нулей. Также найдите сумму и произведение корней функции. 92-8 \]
Введите данную функцию на вкладке выражения калькулятора нулей.
Он отобразит следующие результаты:
Корни функции задаются как:
\[ x = + 2 \sqrt{2} \]
\[ x = – 2 \sqrt{2} \]
Корневой график показан на рисунке 1:
Рисунок 3.
 Нули функции три
Нули функции триНули, представленные на числовой прямой, показаны на рисунке 2:
Рисунок 4. Нули функции четыре
Сумма всех корней:
сумма = 0
произведение = – 8
Пример 2:
Найдите нули следующей тригонометрической функции:
\[ \s f(x) = 2 qrt x +} ]
Используйте калькулятор, чтобы найти корни.
Введите заданную функцию на вкладке выражения калькулятора нулей, чтобы найти нули функции.
Он отобразит следующие результаты:
Корни функции даны как: 94 – 16 \]
Введите заданную функцию на вкладке выражения Калькулятора нулей, чтобы найти нули функции.
Эта полиномиальная функция имеет 4 корня (нули), так как это функция 4 степени. Он имеет два действительных корня и два комплексных корня
Результаты отобразятся в новом окне.
Корни функции задаются следующим образом:
x = + 2
x = – 2
x = + 2i
х = 902 + 8x + 35 \]Используйте калькулятор, чтобы найти корни.

Введите заданную функцию на вкладке выражения калькулятора нулей, чтобы найти нули функции.
Это полиномиальная функция степени 4. Следовательно, она имеет четыре корня.
Все корни лежат в комплексной плоскости.
Корни функции задаются следующим образом:
x = -2 – i
x = -2 + i
\[ x = 2 – \iota \sqrt{3} \]
\[ x = 2 + \iota\ \sqrt{3} \]
Предыдущее
< Список математических калькуляторов > СледующееВсе изображения созданы с помощью Geogebr Онлайн-заметки Пола
Главная / Алгебра / Полиномиальные функции / Нахождение нулей многочленовПоказать мобильное уведомление Показать все примечания Скрыть все примечания
Уведомление для мобильных устройств
Похоже, вы используете устройство с «узкой» шириной экрана ( т.
 е. вы, вероятно, используете мобильный телефон). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.
е. вы, вероятно, используете мобильный телефон). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.Раздел 5.4. Нахождение нулей многочленов
Мы говорили о нулях многочлена и зачем они нам сейчас в паре разделов. Мы, однако, толком не говорили о том, как на самом деле найти их для многочленов степени больше двух. Это тема этого раздела. Ну, это как раз тема этого раздела. Вообще, нахождение всех нулей любого многочлена — довольно сложный процесс. В этом разделе мы дадим процесс, который найдет все рациональные (, т.е. целых или дробных) нулей многочлена. Мы сможем использовать этот процесс для нахождения всех нулей полинома при условии, что все нули, кроме не более двух, рациональны.
 2} — 38x + 40 = \left( {x — 4} \right)\left( {3x — 2} \right )\влево( {4x + 5} \вправо)\]
2} — 38x + 40 = \left( {x — 4} \right)\left( {3x — 2} \right )\влево( {4x + 5} \вправо)\]Показать решение
Из факторизованной формы мы видим, что нули равны
\[x = 4 = \frac{4}{1}\hspace{0,25 дюйма}\,\,\,x = \frac{2}{3}\hspace{0,25 дюйма}x = — \frac{5} {4}\]
Обратите внимание, что мы записали целое число в виде дроби, чтобы оно соответствовало теореме. Кроме того, с отрицательным нулем мы можем поставить минус в числителе или знаменателе. Это не имеет значения.
Итак, согласно теореме о рациональном корне, все числители этих дробей (со знаком минус в третьем нуле или без него) должны быть множителями 40, а знаменатели должны быть множителями 12.
Вот несколько способов размножить 40 и 12.
\[\begin{align*}40 & = \left( 4 \right)\left( {10} \right) & \hspace{0.
 25in}40 & = \left( 2 \right)\left( {20} \right) & \hspace{0.25in}40 & = \left( 5 \right)\left( 8 \right)& \hspace{0.25in}40 & = \left( { — 5} \right)\left( { — 8} \right)\\ 12 & = \left( 1 \right)\left( {12} \right) & \hspace{0.25in} 12 & = \left( 3 \right)\left( 4 \ справа) & \hspace{0.25in}12 & = \left( { — 3} \right)\left( { — 4} \right) & & \end{align*}\]
25in}40 & = \left( 2 \right)\left( {20} \right) & \hspace{0.25in}40 & = \left( 5 \right)\left( 8 \right)& \hspace{0.25in}40 & = \left( { — 5} \right)\left( { — 8} \right)\\ 12 & = \left( 1 \right)\left( {12} \right) & \hspace{0.25in} 12 & = \left( 3 \right)\left( 4 \ справа) & \hspace{0.25in}12 & = \left( { — 3} \right)\left( { — 4} \right) & & \end{align*}\]Из них мы видим, что на самом деле все числители представляют собой множители 40, а знаменатели все множители 12. Также обратите внимание, что, как показано, мы можем поставить знак минус перед третьим нулем как в числителе, так и в знаменателе. и это все равно будет множитель соответствующего числа.
Чем же так полезна эта теорема? Ну, для начала это позволит нам записать список из возможных рациональных нулей для многочлена и, что более важно, любые рациональные нули многочлена БУДУТ в этом списке. 92} — 17x + 6\) Показать решение
Что же говорит теорема о рациональном корне? В нем говорится, что если \(x = \frac{b}{c}\) должно быть нулем \(P\left( x \right)\), то \(b\) должно быть множителем 6 и \ (c\) должен быть множителем 1.
 Кроме того, как мы видели в предыдущем примере, мы не можем забывать отрицательные множители.
Кроме того, как мы видели в предыдущем примере, мы не можем забывать отрицательные множители.Итак, первое, что нужно сделать, это составить список всех возможных множителей 1 и 6. Вот они.
\[\begin{align*}6 & : \pm 1,\,\, \pm 2,\,\, \pm 3,\,\, \pm 6\\ 1 & : \pm 1\end{align *}\]
Теперь, чтобы получить список возможных рациональных нулей многочлена, все, что нам нужно сделать, это записать все возможные дроби, которые мы можем составить из этих чисел, где числители должны быть делителями 6, а знаменатели должны быть делителями 1. На самом деле это проще, чем может показаться на первый взгляд.
Есть очень простой сокращенный способ сделать это. Давайте подробно рассмотрим первый, а остальные сделаем быстрее. Во-первых, возьмите первый множитель из списка числителя, включая \(\pm\), и разделите его на первый множитель (хорошо, в данном случае только множитель) из списка знаменателя, снова включая \(\pm \) .
 Это дает
Это дает\[\frac{{ \pm 1}}{{ \pm 1}}\]
Похоже на беспорядок, но не так уж и плохо. Здесь четыре дроби. Они есть,
\[\frac{{ + 1}}{{ + 1}} = 1\hspace{0,25 дюйма}\frac{{ + 1}}{{ — 1}} = — 1\hspace{0,25 дюйма}\frac{ { — 1}}{{ + 1}} = — 1\hspace{0,25 дюйма}\frac{{ — 1}}{{ — 1}} = 1\]
Однако обратите внимание, что все четыре дроби сводятся к двум возможным числам. Это всегда будет происходить с такими фракциями. Что мы будем делать с этого момента, так это формировать дробь, делать любые упрощения чисел, игнорируя \( \pm \), а затем отбрасывать один из \(\pm \).
Итак, список возможных рациональных нулей для этого полинома:
\[\frac{{ \pm 1}}{{ \pm 1}} = \pm 1\hspace{0,25 дюйма}\frac{{ \pm 2}}{{ \pm 1}} = \pm 2\hspace {0.25in}\frac{{ \pm 3}}{{ \pm 1}} = \pm 3\hspace{0.
 25in}\frac{{ \pm 6}}{{ \pm 1}} = \pm 6 \]
25in}\frac{{ \pm 6}}{{ \pm 1}} = \pm 6 \]Получается, что возможных рациональных нулей всего 8, и в данном случае все они целые. Заметим также, что любые рациональные нули этого многочлена БУДУТ находиться где-то в этом списке, хотя мы их еще не нашли. 92} + 3x — 9\) Показать решение
Мы не будем вдаваться в подробности. Сначала получите список всех делителей -9 и 2. Обратите внимание, что знак минус на 9 на самом деле не так уж важен, поскольку мы все равно получим \(\pm \) для каждого из факторов.
\[\begin{align*} — 9 & : \pm 1,\,\, \pm 3,\,\, \pm 9\\ 2 & : \pm 1,\,\, \pm 2\end{ выровнять*}\]
Теперь множители -9 — это все возможные числители, а множители 2 — все возможные знаменатели.
Вот список всех возможных рациональных нулей этого многочлена.
\[\begin{align*}\frac{{ \pm 1}}{{ \pm 1}} & = \pm 1 & \hspace{0.
 25in}\frac{{ \pm 3}}{{ \pm 1 }} & = \pm 3 & \hspace{0.25in}\frac{{ \pm 9}}{{ \pm 1}} & = \pm 9\\ & \\ \frac{{ \pm 1}}{ { \pm 2}} & = \pm \frac{1}{2} & \hspace{0,25in}\frac{{ \pm 3}}{{ \pm 2}} & = \pm \frac{3} {2} & \hspace{0,25 дюйма}\frac{{ \pm 9}}{{ \pm 2}} & = \pm \frac{9}{2}\конец{выравнивание*}\]
25in}\frac{{ \pm 3}}{{ \pm 1 }} & = \pm 3 & \hspace{0.25in}\frac{{ \pm 9}}{{ \pm 1}} & = \pm 9\\ & \\ \frac{{ \pm 1}}{ { \pm 2}} & = \pm \frac{1}{2} & \hspace{0,25in}\frac{{ \pm 3}}{{ \pm 2}} & = \pm \frac{3} {2} & \hspace{0,25 дюйма}\frac{{ \pm 9}}{{ \pm 2}} & = \pm \frac{9}{2}\конец{выравнивание*}\]Итак, всего у нас есть 12 возможных рациональных нулей, половина из них — целые числа, а половина — дроби.
Следующий факт также иногда будет полезен при нахождении нулей полинома.
Факт
Если \(P\left( x \right)\) является полиномом и мы знаем, что \(P\left( a \right) > 0\) и \(P\left( b \right) <0\), то где-то между \(a\) и \(b\) находится ноль \(P\left( x \right)\).
Этот факт говорит нам о том, что если мы оцениваем многочлен в двух точках и одна из оценок дает положительное значение ( т.е. точка выше оси \(х\)), а другая оценка дает отрицательное значение ( т.е. точка ниже оси \(х\)), то единственный способ получить из одного точка на другую должна пройти через ось \(x\).
 Или, другими словами, многочлен должен иметь нуль, поскольку мы знаем, что нули находятся там, где график касается или пересекает ось \(x\).
Или, другими словами, многочлен должен иметь нуль, поскольку мы знаем, что нули находятся там, где график касается или пересекает ось \(x\).Обратите внимание, что этот факт не говорит нам, что такое ноль, он только говорит нам, что единица будет существовать. Также обратите внимание, что если обе оценки положительные или обе оценки отрицательные, между ними может быть или не быть ноль.
Вот процесс определения всех рациональных нулей многочлена.
Процесс поиска рациональных нулей
- Используйте теорему о рациональных корнях для получения списка всех возможных рациональных нулей многочлена \(P\left( x \right)\).
- Вычисляем многочлен по числам с первого шага, пока не найдем ноль. Предположим, что ноль равен \(x = r\), тогда мы будем знать, что это ноль, потому что \(P\left( r \right) = 0\). После того, как было установлено, что это на самом деле нуль, запишите исходный многочлен как \[P\влево( x \вправо) = \влево( {x — r} \вправо)Q\влево( x \вправо)\]
- Повторите процесс, используя \(Q\left( x \right)\) на этот раз вместо \(P\left( x \right)\).
 Это повторение будет продолжаться до тех пор, пока мы не достигнем полинома второй степени. На данный момент мы можем решить это непосредственно для оставшихся нулей.
Это повторение будет продолжаться до тех пор, пока мы не достигнем полинома второй степени. На данный момент мы можем решить это непосредственно для оставшихся нулей.
Для упрощения второго шага воспользуемся синтетическим делением. Это значительно упростит нашу жизнь в нескольких отношениях. Во-первых, напомним, что последнее число в последней строке — это многочлен, оцененный в \(r\), и если мы получим ноль, оставшиеся числа в последней строке — это коэффициенты для \(Q\left( x \right)\ ), и поэтому нам не придется возвращаться и находить это. 92} — 17х + 6\).
Показать решение
В предыдущем примере мы нашли список всех возможных рациональных нулей. Они здесь.
\[ \pm 1,\,\, \pm 2,\,\, \pm 3,\,\, \pm 6\]
Теперь нам нужно начать вычисление многочлена для этих чисел. Мы можем начать с любого места в списке и будем продолжать, пока не найдем ноль.

Для оценки мы построим синтетическая таблица деления . В синтетической таблице деления выполняем умножение в уме и опускаем среднюю строку, просто записывая третью строку, и, поскольку мы будем проходить этот процесс несколько раз, мы помещаем все строки в таблицу.
Вот первая синтетическая таблица деления для этой задачи.
\[\begin{массив}{г|ррррл} {} & 1 & -7 & 17 & -17 & 6 \\ \hline -1 & 1 & -8 & 25 & -42 & 48=P\left(-1 \right)\ne 0 \\ 1 & 1 & -6 & 11 & -6 & 0=P\left( 1 \right)=0\,\,!\,\,! \конец{массив}\]
Итак, мы нашли ноль. Прежде чем перейти к этому, давайте повторим вычисления здесь, чтобы убедиться, что вы можете их выполнить.
Верхняя строка — это коэффициенты полинома, а первый столбец — это числа, по которым мы оцениваем полином.
Каждая строка (после первой) является третьей строкой процесса синтетического деления.
 Давайте быстро посмотрим на первую пару чисел во второй строке. Число во втором столбце — это первый опущенный коэффициент. Затем число в третьем столбце находится путем умножения -1 на 1 и прибавления к -7. Это дает -8. Ибо четвертое число — это -1, умноженное на -8, прибавленное к 17. Это 25, 9.2} + 11х — 6\). Итак, первое, что нужно сделать, это записать все возможные рациональные корни этого многочлена, и в этом случае нам повезло, что первое и последнее числа в этом многочлене совпадают с исходным многочленом, что обычно не будет случается, поэтому не всегда ожидайте этого. Вот список всех возможных рациональных нулей этого многочлена.
Давайте быстро посмотрим на первую пару чисел во второй строке. Число во втором столбце — это первый опущенный коэффициент. Затем число в третьем столбце находится путем умножения -1 на 1 и прибавления к -7. Это дает -8. Ибо четвертое число — это -1, умноженное на -8, прибавленное к 17. Это 25, 9.2} + 11х — 6\). Итак, первое, что нужно сделать, это записать все возможные рациональные корни этого многочлена, и в этом случае нам повезло, что первое и последнее числа в этом многочлене совпадают с исходным многочленом, что обычно не будет случается, поэтому не всегда ожидайте этого. Вот список всех возможных рациональных нулей этого многочлена.\[ \pm 1,\,\, \pm 2,\,\, \pm 3,\,\, \pm 6\]
Теперь, перед созданием новой синтетической таблицы деления, давайте вспомним, что мы ищем нули в \(P\left( x \right)\) и из нашей первой таблицы деления мы определили, что \(x = — 1\) равно НЕ является нулем \(P\left( x \right)\), и поэтому нет причин снова возиться с этим числом.

Это то, что мы всегда должны делать на этом этапе. Взгляните на список новых возможных рациональных нулей и спросите, есть ли такие, которые не могут быть рациональными нулями исходного многочлена. Если они есть, выбросьте их, так как мы уже знаем, что они не будут работать. Итак, сокращенный список чисел, которые можно попробовать здесь, 9.0005
\[1,\,\, \pm 2,\,\, \pm 3,\,\, \pm 6\]
Обратите внимание, что нам необходимо включить \(x = 1\) в список, поскольку ноль может встречаться более одного раза (, т.е. кратность больше единицы).
Вот синтетическая таблица деления этого многочлена.
\[\begin{массив}{r|rrrl} {} & 1 & -6 & 11 & -6 \\ \hline 1 & 1 & -5 & 6 & \,\,0=P\left( 1 \right)=0!! \\ \конец{массив}\] 92} — 5x + 6 = \left( {x — 2} \right)\left( {x — 3} \right) = 0\hspace{0.
 25in} \Rightarrow \hspace{0.25in}\,\,\ ,\,х = 2,\,\,х = 3\]
25in} \Rightarrow \hspace{0.25in}\,\,\ ,\,х = 2,\,\,х = 3\]Обратите внимание, что эти два числа находятся в списке возможных рациональных нулей.
Завершение этой задачи дает следующий список нулей для \(P\left( x \right)\).
\[\ begin{align*}& x = 1\hspace{0,25in}\left( {{\mbox{кратность 2}}} \right)\\ & x = 2\hspace{0,25in}\left({ {\mbox{кратность 1}}} \right)\\ & x = 3\hspace{0,25 дюйма}\left( {{\mbox{кратность 1}}} \right)\end{align*}\] 92} + 3х — 9\).
Показать решение
Из второго примера мы знаем, что список всех возможных рациональных нулей равен
. \[\begin{align*}\frac{{ \pm 1}}{{ \pm 1}} & = \pm 1 & \hspace{0.25in}\frac{{ \pm 3}}{{ \pm 1 }} & = \pm 3 & \hspace{0.25in}\frac{{ \pm 9}}{{ \pm 1}} & = \pm 9\\ & \\ \frac{{ \pm 1}}{ { \pm 2}} & = \pm \frac{1}{2} & \hspace{0,25in}\frac{{ \pm 3}}{{ \pm 2}} & = \pm \frac{3} {2} & \hspace{0,25 дюйма}\frac{{ \pm 9}}{{ \pm 2}} & = \pm \frac{9}{2}\end{align*}\]
Следующим шагом является создание синтетической таблицы деления.
 Когда у нас есть дроби, обычно лучше начинать с целых чисел и делать их в первую очередь. Кроме того, на этот раз мы начнем сначала с вычисления всех отрицательных целых чисел. Мы делаем это, чтобы указать, как мы можем использовать приведенный выше факт, чтобы помочь нам идентифицировать нули.
Когда у нас есть дроби, обычно лучше начинать с целых чисел и делать их в первую очередь. Кроме того, на этот раз мы начнем сначала с вычисления всех отрицательных целых чисел. Мы делаем это, чтобы указать, как мы можем использовать приведенный выше факт, чтобы помочь нам идентифицировать нули.\[\begin{массив}{г|ррррл} {} и 2 и 1 и 3 и 3 и -9\\ \hline -9 & 2 & -17 & 156 & -1401 & 12600=P\left(-9 \right)\ne 0 \\ -3 & 2 & -5 & 18 & -51 & 144=P\left(-3 \right)\ne 0 \\ -1 & 2 & -1 & 4 & -1 & -8=P\left(-1 \right)\ne 0 \\ \конец{массив}\]
Теперь мы еще не нашли ноль, однако заметим, что \(P\left( { — 3} \right) = 144 > 0\) и \(P\left( -1 \right)=- 8 \[\begin{массив}{г|ррррр} {} & 2 & \,\,1 & 3 & \,\,3 & -92} + 6х — 6\]
Теперь нам нужно повторить весь процесс с этим полиномом. Кроме того, в отличие от предыдущего примера, мы не можем просто повторно использовать исходный список, поскольку на этот раз последнее число отличается.
 Итак, вот коэффициенты -6 и 2.
Итак, вот коэффициенты -6 и 2.\[\begin{align*} — 6 & : \pm 1,\,\, \pm 2,\,\, \pm 3,\,\, \pm 6\\ 2 & : \pm 1,\, \, \pm 2\end{выравнивание*}\]
Вот список всех возможных рациональных нулей для \(Q\left( x \right)\).
\[\begin{align*}\frac{{ \pm 1}}{{ \pm 1}} & = \pm 1 & \hspace{0.25in}\frac{{ \pm 2}}{{ \pm 1 }} & = \pm 2 & \hspace{0.25in}\frac{{ \pm 3}}{{ \pm 1}} & = \pm 3 &\hspace{0.25in}\frac{{ \pm 6} }{{ \pm 1}} & = \pm 6\\ & \\ \frac{{ \pm 1}}{{ \pm 2}} & = \pm \frac{1}{2} & \hspace{ 0.25in}\frac{{ \pm 2}}{{ \pm 2}} & = \pm 1& \hspace{0.25in}\frac{{ \pm 3}}{{ \pm 2}} & = \pm \frac{3}{2} & \hspace{0,25 дюйма}\frac{{ \pm 6}}{{ \pm 2}} & = \pm 3\end{align*}\]
Обратите внимание, что некоторые числа появляются в обеих строках, поэтому мы можем сократить список, записав их только один раз.




 Если вы хотите найти корни любой другой функции, введите новое уравнение на вкладке выражения и выполните ту же процедуру, что и выше.
Если вы хотите найти корни любой другой функции, введите новое уравнение на вкладке выражения и выполните ту же процедуру, что и выше.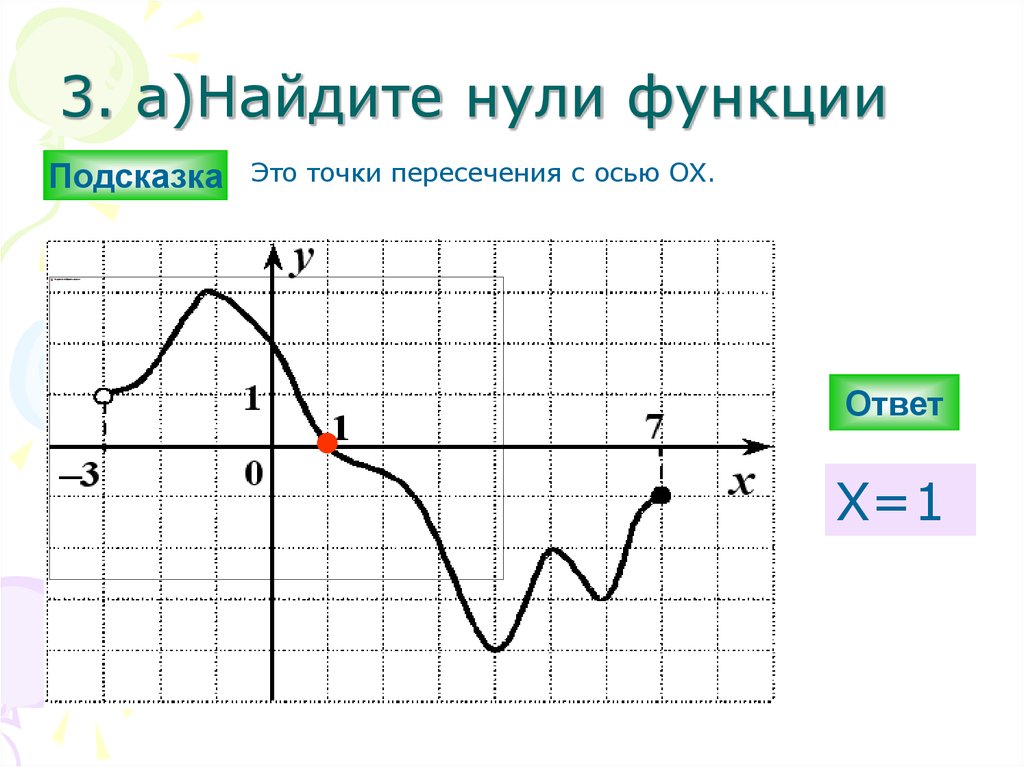 Другими словами, это также можно назвать x-пересечениями графика функции.
Другими словами, это также можно назвать x-пересечениями графика функции.

 Нули функции три
Нули функции три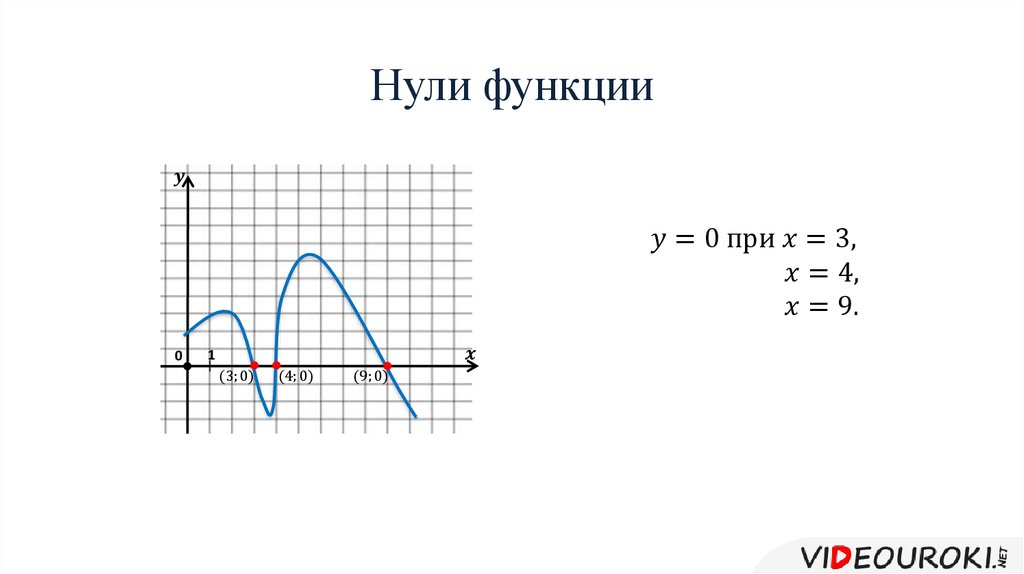
 е. вы, вероятно, используете мобильный телефон). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.
е. вы, вероятно, используете мобильный телефон). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана. 2} — 38x + 40 = \left( {x — 4} \right)\left( {3x — 2} \right )\влево( {4x + 5} \вправо)\]
2} — 38x + 40 = \left( {x — 4} \right)\left( {3x — 2} \right )\влево( {4x + 5} \вправо)\] 25in}40 & = \left( 2 \right)\left( {20} \right) & \hspace{0.25in}40 & = \left( 5 \right)\left( 8 \right)& \hspace{0.25in}40 & = \left( { — 5} \right)\left( { — 8} \right)\\ 12 & = \left( 1 \right)\left( {12} \right) & \hspace{0.25in} 12 & = \left( 3 \right)\left( 4 \ справа) & \hspace{0.25in}12 & = \left( { — 3} \right)\left( { — 4} \right) & & \end{align*}\]
25in}40 & = \left( 2 \right)\left( {20} \right) & \hspace{0.25in}40 & = \left( 5 \right)\left( 8 \right)& \hspace{0.25in}40 & = \left( { — 5} \right)\left( { — 8} \right)\\ 12 & = \left( 1 \right)\left( {12} \right) & \hspace{0.25in} 12 & = \left( 3 \right)\left( 4 \ справа) & \hspace{0.25in}12 & = \left( { — 3} \right)\left( { — 4} \right) & & \end{align*}\] Кроме того, как мы видели в предыдущем примере, мы не можем забывать отрицательные множители.
Кроме того, как мы видели в предыдущем примере, мы не можем забывать отрицательные множители. Это дает
Это дает 25in}\frac{{ \pm 6}}{{ \pm 1}} = \pm 6 \]
25in}\frac{{ \pm 6}}{{ \pm 1}} = \pm 6 \] 25in}\frac{{ \pm 3}}{{ \pm 1 }} & = \pm 3 & \hspace{0.25in}\frac{{ \pm 9}}{{ \pm 1}} & = \pm 9\\ & \\ \frac{{ \pm 1}}{ { \pm 2}} & = \pm \frac{1}{2} & \hspace{0,25in}\frac{{ \pm 3}}{{ \pm 2}} & = \pm \frac{3} {2} & \hspace{0,25 дюйма}\frac{{ \pm 9}}{{ \pm 2}} & = \pm \frac{9}{2}\конец{выравнивание*}\]
25in}\frac{{ \pm 3}}{{ \pm 1 }} & = \pm 3 & \hspace{0.25in}\frac{{ \pm 9}}{{ \pm 1}} & = \pm 9\\ & \\ \frac{{ \pm 1}}{ { \pm 2}} & = \pm \frac{1}{2} & \hspace{0,25in}\frac{{ \pm 3}}{{ \pm 2}} & = \pm \frac{3} {2} & \hspace{0,25 дюйма}\frac{{ \pm 9}}{{ \pm 2}} & = \pm \frac{9}{2}\конец{выравнивание*}\] Или, другими словами, многочлен должен иметь нуль, поскольку мы знаем, что нули находятся там, где график касается или пересекает ось \(x\).
Или, другими словами, многочлен должен иметь нуль, поскольку мы знаем, что нули находятся там, где график касается или пересекает ось \(x\). Это повторение будет продолжаться до тех пор, пока мы не достигнем полинома второй степени. На данный момент мы можем решить это непосредственно для оставшихся нулей.
Это повторение будет продолжаться до тех пор, пока мы не достигнем полинома второй степени. На данный момент мы можем решить это непосредственно для оставшихся нулей.
 Давайте быстро посмотрим на первую пару чисел во второй строке. Число во втором столбце — это первый опущенный коэффициент. Затем число в третьем столбце находится путем умножения -1 на 1 и прибавления к -7. Это дает -8. Ибо четвертое число — это -1, умноженное на -8, прибавленное к 17. Это 25, 9.2} + 11х — 6\). Итак, первое, что нужно сделать, это записать все возможные рациональные корни этого многочлена, и в этом случае нам повезло, что первое и последнее числа в этом многочлене совпадают с исходным многочленом, что обычно не будет случается, поэтому не всегда ожидайте этого. Вот список всех возможных рациональных нулей этого многочлена.
Давайте быстро посмотрим на первую пару чисел во второй строке. Число во втором столбце — это первый опущенный коэффициент. Затем число в третьем столбце находится путем умножения -1 на 1 и прибавления к -7. Это дает -8. Ибо четвертое число — это -1, умноженное на -8, прибавленное к 17. Это 25, 9.2} + 11х — 6\). Итак, первое, что нужно сделать, это записать все возможные рациональные корни этого многочлена, и в этом случае нам повезло, что первое и последнее числа в этом многочлене совпадают с исходным многочленом, что обычно не будет случается, поэтому не всегда ожидайте этого. Вот список всех возможных рациональных нулей этого многочлена.
 25in} \Rightarrow \hspace{0.25in}\,\,\ ,\,х = 2,\,\,х = 3\]
25in} \Rightarrow \hspace{0.25in}\,\,\ ,\,х = 2,\,\,х = 3\] Когда у нас есть дроби, обычно лучше начинать с целых чисел и делать их в первую очередь. Кроме того, на этот раз мы начнем сначала с вычисления всех отрицательных целых чисел. Мы делаем это, чтобы указать, как мы можем использовать приведенный выше факт, чтобы помочь нам идентифицировать нули.
Когда у нас есть дроби, обычно лучше начинать с целых чисел и делать их в первую очередь. Кроме того, на этот раз мы начнем сначала с вычисления всех отрицательных целых чисел. Мы делаем это, чтобы указать, как мы можем использовать приведенный выше факт, чтобы помочь нам идентифицировать нули. Итак, вот коэффициенты -6 и 2.
Итак, вот коэффициенты -6 и 2.