Площади геометрических фигур | matanu.net
Привет. Сегодня мы узнаем формулы площадей некоторых фигур.
При решении задач зачастую становится нужным нахождение площадей фигур как по условию задачи, так и в процессе нахождения других каких-то величин. Поэтому давайте сегодня поговорим о них. Начнем с треугольника и по возрастанию числа вершин. Для произвольного треугольника существует несколько формул нахождения площади и их применение зависит от ситуации, когда какую будет удобнее применить: которая через высоту, или которая через угол. Когда-то проблематично найти одно, а когда-то выгоднее использовать другое. Формулы следующие:
Площади треугольника.Однако, есть у нас особый случай — это прямоугольный треугольник. Его площадь можно найти легко, перемножив его катеты. По сути, этот случай использует обе формулы, поскольку за высоту в нем можно принять и катет, да и синус угла 90° это единица. Из чего и получаем данное соотношение:
Площадь прямоугольного треугольника.
Также стоит упомянуть ещё одну формулу площади треугольника. Хоть она и выглядит страшно и громоздко, однако иногда, когда не остаётся выхода, ее применить удобнее всего:
Формула Герона для нахождения площади произвольного треугольника.Идём далее: четырехугольники. Их большое множество, и для каждого из них есть свои формулы нахождения площади. Однако, есть и формулы, которые применимы для всех четырехугольников. Первая из них требует знание длин диагоналей этого четырехугольника, а также угла между ними, вторая же также, как и для треугольников, требует знание всех сторон для нахождения полупериметра:
Теперь же перейдем к «частным» случаям.
Параллелограмм — по сути, это два равных склеенных треугольника по одной из сторон, поэтому его площадь и равна удвоенной площади треугольника, то есть:
Опять же, если у нас углы в параллелограмме равны по 90°, то мы получаем прямоугольник, и его площадь будет равна длину умножить на ширину (также по сути удвоенная площадь прямоугольного треугольника):
Теперь, что если у нас все стороны в параллелограмме равны.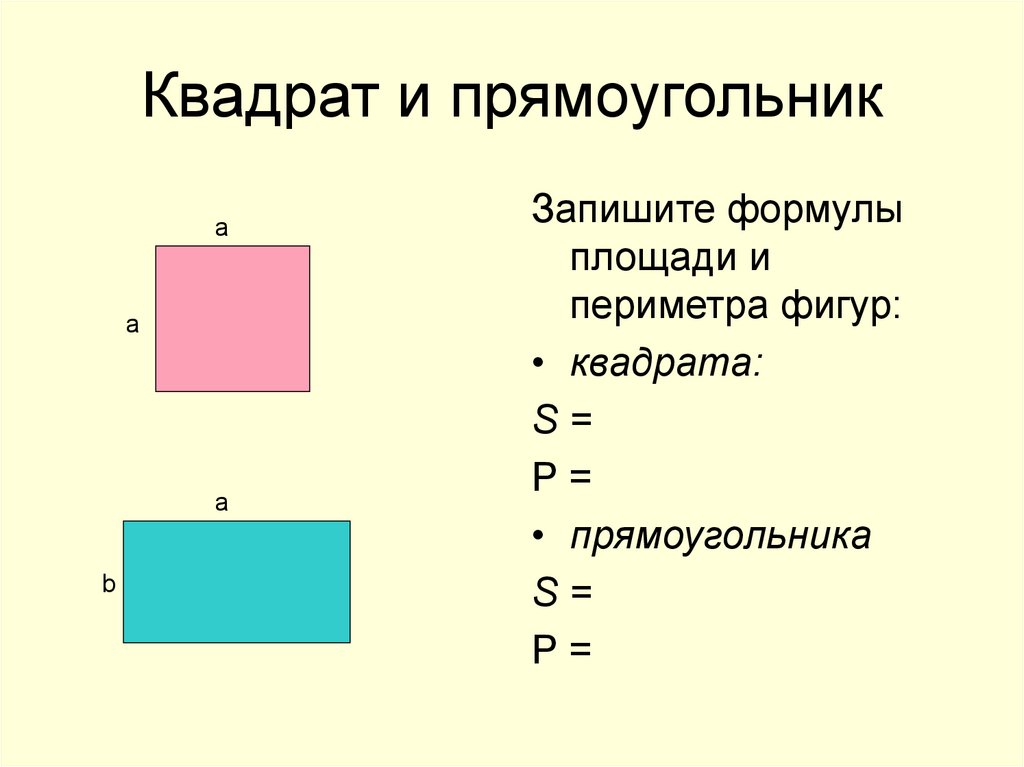 Получаем ромб, площадь которого ищется также, как и у параллелограмма. Однако, у ромба есть одно интересное свойство: его диагонали перпендикулярны. Поэтому, из формулы для произвольного четырехугольника следует ещё и следующая формула, по которой иногда тоже легко считается площадь:
Получаем ромб, площадь которого ищется также, как и у параллелограмма. Однако, у ромба есть одно интересное свойство: его диагонали перпендикулярны. Поэтому, из формулы для произвольного четырехугольника следует ещё и следующая формула, по которой иногда тоже легко считается площадь:
А что если у нас в параллелограмме и все стороны равны, и все углы по 90°? Получаем квадрат. Для него справедливы все формулы, написанные выше, которые даже упрощаются до квадрата стороны.
Далее, у нас идёт трапеция. Для нахождения ее площади формула следующая:
Можно заметить, что полусумма оснований, которая присутствует в этой формуле — это длина средней линии трапеции, вследствие чего получаем:
Перед тем, как идти далее в сторону увеличения вершин фигур, стоит упомянуть кое-что. Зачастую нахождение площадей произвольных фигур — довольно трудная задача. Поэтому часто делаются упрощения: данную фигуру разбивают на более мелкие, и находят их площади, после чего суммируют и получают площадь всей большой фигуры.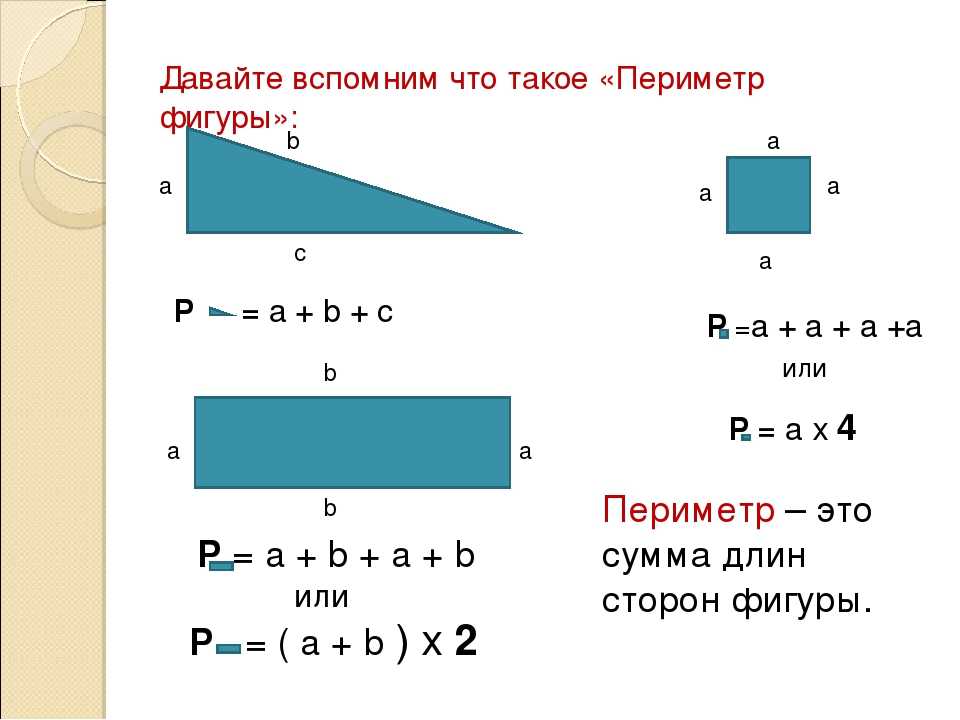 Однако, это не всегда удобно, поскольку для этого метода нужно знать стороны этих фигур, чтобы ним применить формулы, упомянутые выше. Поэтому далее будем рассматривать формулы площадей для правильных n-угольников — фигур, у которых все стороны и углы равны.
Однако, это не всегда удобно, поскольку для этого метода нужно знать стороны этих фигур, чтобы ним применить формулы, упомянутые выше. Поэтому далее будем рассматривать формулы площадей для правильных n-угольников — фигур, у которых все стороны и углы равны.
Есть формула, которая использует радиус вписанной окружности:
Кстати, эта формула применима и для некоторых неправильных фигур. Такие фигуры называются выпуклыми. К ним относят фигуры, в которых нет углов превышающих 180°. К ним также относятся треугольники и рассмотренные выше четырехугольники. Из этой формулы мы можем вывести соотношения для правильных фигур, которые уже разбирали. Так, для правильного треугольника мы получаем следующие соотношения. Для квадрата мы получаем точно такую же формулу, как и ранее — квадрат стороны. Далее идут шестиугольники. Для них формулы следующие. Все формулы приведены на рисунке ниже. Также там указано то, как найти их через радиус описанной окружности.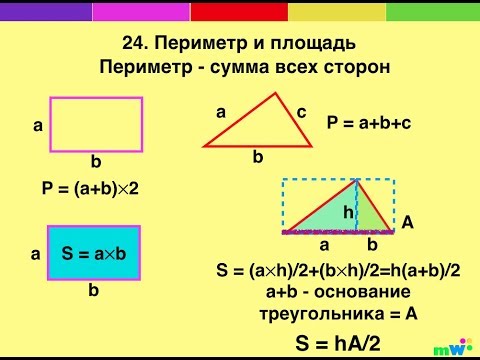
Далее, что если, у нас 0-угольник. Правильно — это круг, и его площадь ищется по следующей формуле:
Сегодня мы изучили формулы площадей разных плоских фигур. Подписывайтесь на канал, ставьте лайки, пишите свои комментарии. Также предлагайте темы для будущих разборов.
Пока.
школаобразованиеобразованиевроссииматематикаматан
Поделиться в социальных сетях
Вам может понравиться
Все формулы по нахождению площади. Вычисление площадей фигур, ограниченных заданными линиями
Площади геометрических фигур — численные значения, характеризующие их размер в двумерном пространстве. Эта величина может измеряться в системных и внесистемных единицах. Так, например, внесистемная единица площади — сотка, гектар. Это в том случае, если измеряемой поверхностью является участок земли. Системная же единица площади — квадрат длины. В системе СИ принято считать, что единица площади плоской поверхности — это квадратный метр.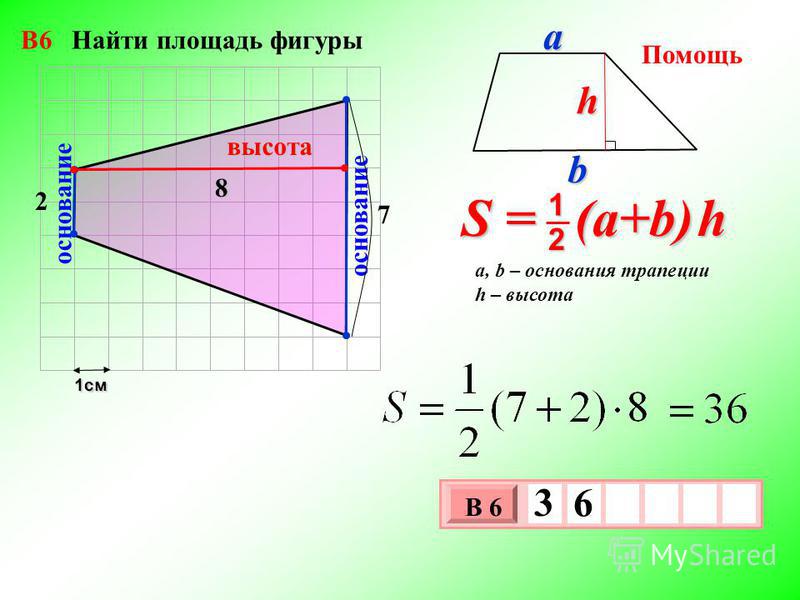 В СГС единица площади выражается через квадратный сантиметр.
В СГС единица площади выражается через квадратный сантиметр.
Геометрия и формулы площадей неразрывно связаны. Эта связь заключается в том, что вычисление площадей плоских фигур основывается именно на их применении. Для многих фигур выведены несколько вариантов, по которым вычисляются их квадратные размеры. Опираясь на данные из условия задачи, мы можем определить максимально простой способ для решения. Тем самым облегчить расчет и свести вероятность ошибки вычисления к минимуму. Для этого рассмотрим основные площади фигур в геометрии.
Формулы для нахождения площади любого треугольника представлены несколькими вариантами:
1) Площадь треугольника рассчитывается по основанию a и высоте h. Основанием считают сторону фигуры, на которую опущена высота. Тогда площадь треугольника:
2) Площадь прямоугольного треугольника рассчитывается точно также, если гипотенузу считать основанием. Если же за основание принять катет, то площадь прямоугольного треугольника будет равна уменьшенному вдвое произведению катетов.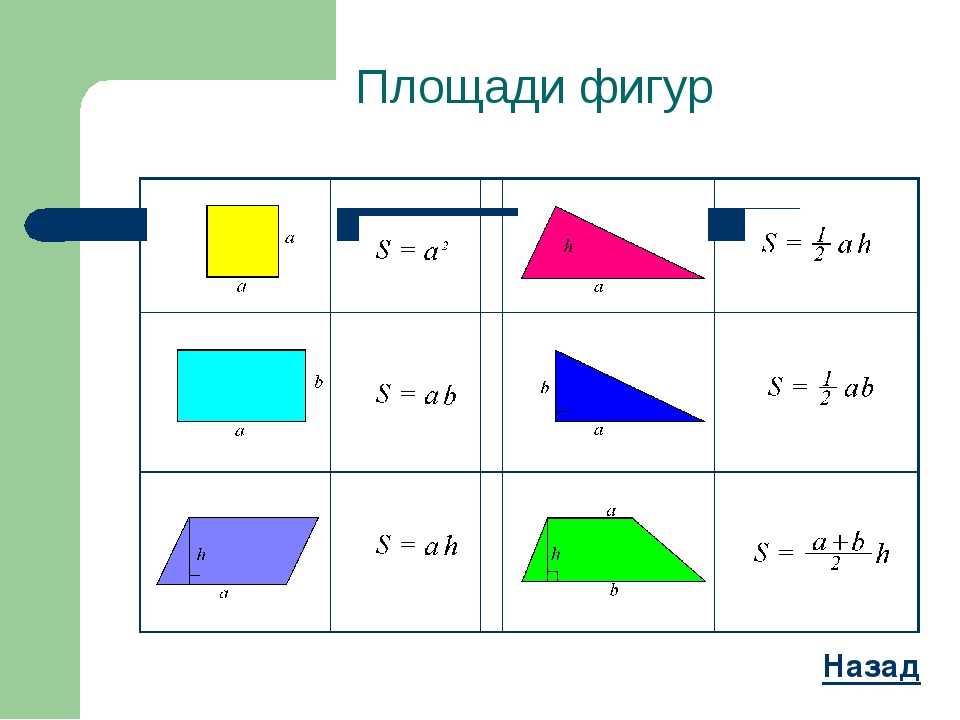
На этом формулы для вычисления площади любого треугольника не заканчиваются. Другое выражение содержит стороны a,b и синусоидальную функцию угла γ, заключенного между a и b. Значение синуса находится по таблицам. Также его можно узнать с помощью калькулятора. Тогда площадь треугольника:
По данному равенству тоже можно убедиться в том, что площадь прямоугольного треугольника определяется через длины катетов. Т.к. угол γ — прямой, поэтому площадь прямоугольного треугольника рассчитывается без умножения на функцию синуса.
3) Рассмотрим частный случай — правильный треугольник, у которого сторона a известна по условию или ее длина найдется при решении. О фигуре в задаче по геометрии больше ничего не известно. Тогда площадь как найти при этом условии? В этом случае применяется формула для площади правильного треугольника:
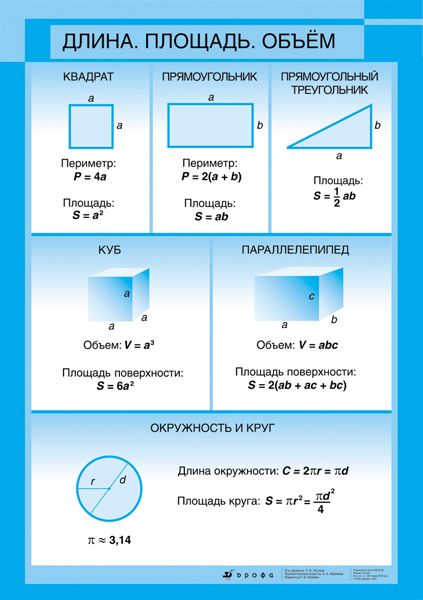
Прямоугольник
Как найти площадь прямоугольника и использовать при этом размеры сторон, имеющих общую вершину? Выражение для вычисления такое:
Если для вычисления площади прямоугольника требуется использовать длины диагоналей, то тогда понадобится функция синуса угла, образованного при их пересечении.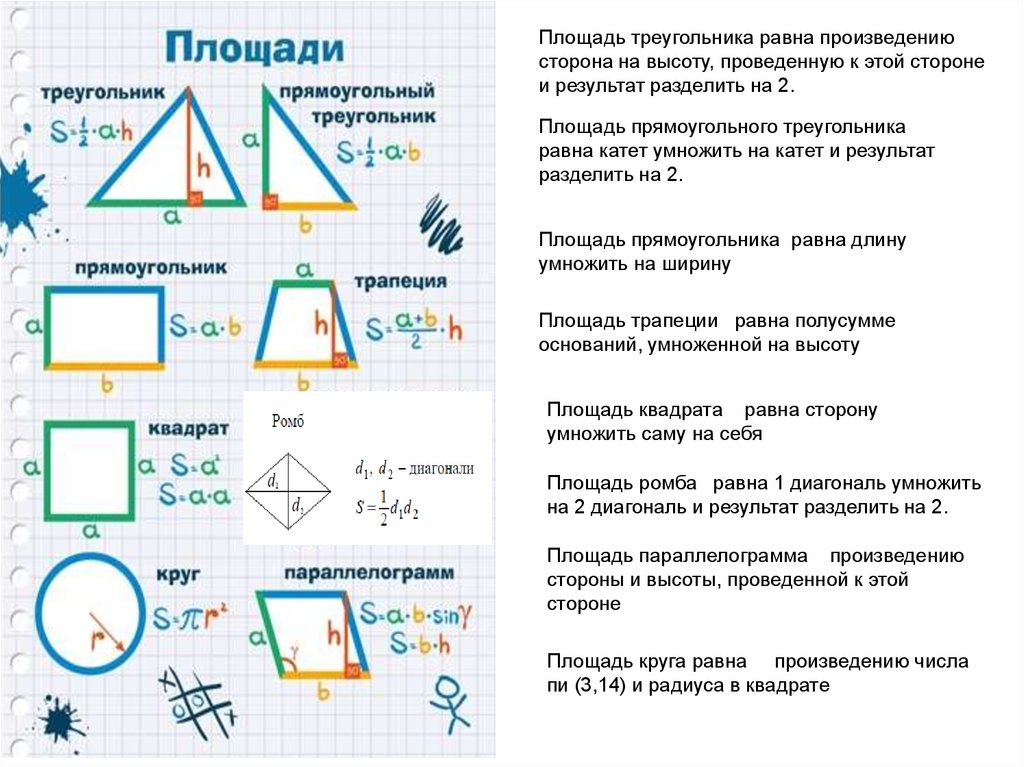
Квадрат
Площадь квадрата определяют как вторую степень длины стороны:
Доказательство вытекает из определения, согласно которому квадратом называют прямоугольник. У всех сторон, образующих квадрат, одинаковые размеры. Поэтому вычисление площади такого прямоугольника сводится к перемножению одной на другую, т. е. ко второй степени стороны. И формула для вычисления площади квадрата примет искомый вид.
Площадь квадрата можно найти другим способом, например, если использовать диагональ:
Как вычислить площадь фигуры, которая образована частью плоскости, ограниченной окружностью? Для расчета площади формулы такие:
Параллелограмм
Для параллелограмма формула содержит линейные размеры стороны, высоты и математическое действие — умножение. Если же высота неизвестна, то тогда как найти площадь параллелограмма? Есть еще один способ вычисления. Потребуется определенное значение, которое примет тригонометрическая функция угла, образованного смежными сторонами, а также их длины.
Формулы площади параллелограмма таковы:
Ромб
Как найти площадь четырехугольника, называемого ромбом? Площадь ромба определяется с помощью простых математических действий с диагоналями. Доказательство опирается на тот факт, что отрезки диагоналей в d1 и d2 пересекаются под прямым углом. По таблице синусов видно, что для прямого угла данная функция равна единице. Поэтому площадь ромба рассчитывается так:
Еще площадь ромба может быть найдена другим способом. Доказать это тоже нетрудно, если учесть, что стороны его одинаковы по длине. Затем подставить их произведение в похожее выражение для параллелограмма. Ведь частным случаем именно этой фигуры является ромб. Здесь γ — внутренний угол ромба. Площадь ромба определяют так:
Трапеция
Как найти площадь трапеции через основания (a и b), если в задаче указаны их длины? Здесь без известного значения длины высоты h вычислить площадь такой трапеции не удастся. Т.к. эту величину содержит выражение для вычисления:
Квадратный размер прямоугольной трапеции тоже можно вычислить таким же способом.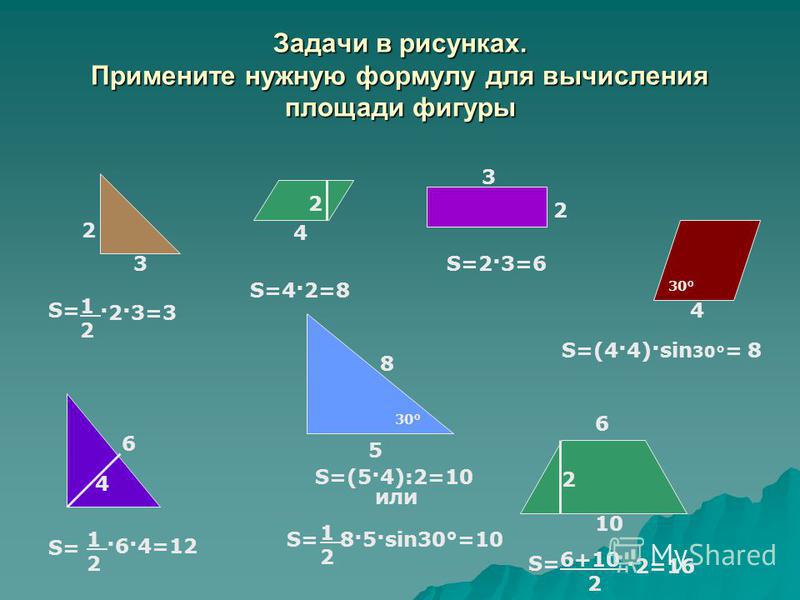 При этом учитывают, что в прямоугольной трапеции понятия высоты и боковой стороны объединены. Поэтому для прямоугольной трапеции нужно указывать вместо высоты длину боковой стороны.
При этом учитывают, что в прямоугольной трапеции понятия высоты и боковой стороны объединены. Поэтому для прямоугольной трапеции нужно указывать вместо высоты длину боковой стороны.
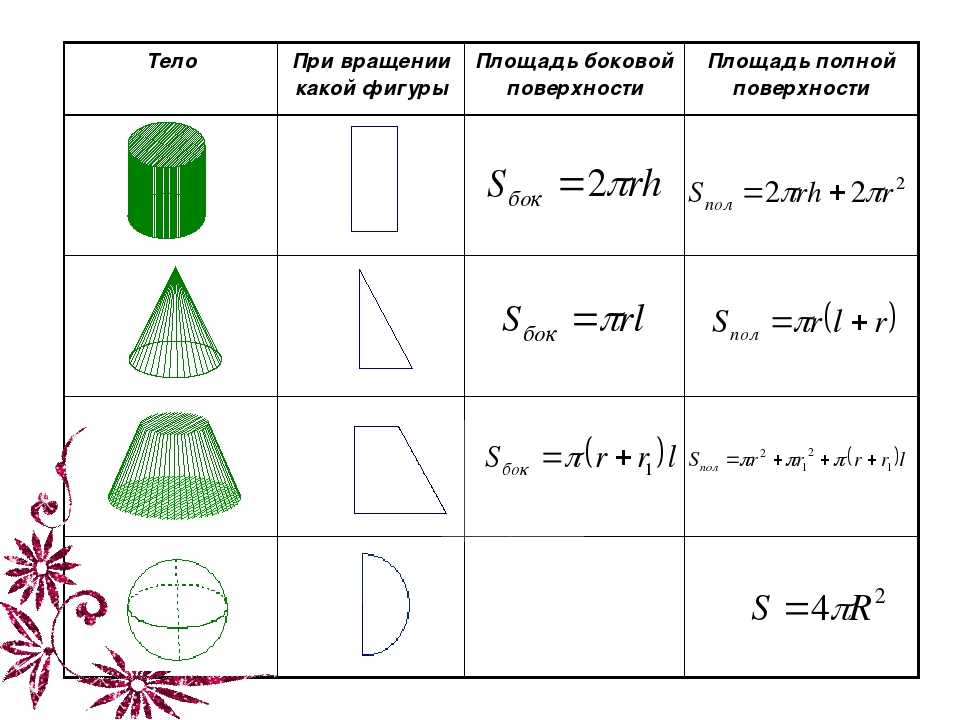
Цилиндр и параллелепипед
Рассмотрим что нужно, чтобы рассчитать поверхность всего цилиндра. Площадь данной фигуры составляет пара кругов, называемых основаниями, и боковая поверхность. Окружности, образующие круги имеют длины радиусов, равные r. Для площади цилиндра имеет место такое вычисление:
Как найти площадь параллелепипеда, который состоит из трех пар граней? Его измерения совпадают с конкретной парой. Грани, находящиеся противоположно, имеют одинаковые параметры. Сначала находят S(1), S(2), S(3) — квадратные размеры неравных граней. Затем уже площадь поверхности параллелепипеда:
Кольцо
Две окружности с общим центром образуют кольцо. Они же ограничивают площадь кольца. При этом обе расчетные формулы учитывают размеры каждой окружности. Первая из них, вычисляющая площадь кольца, содержит больший R и меньший r радиусы.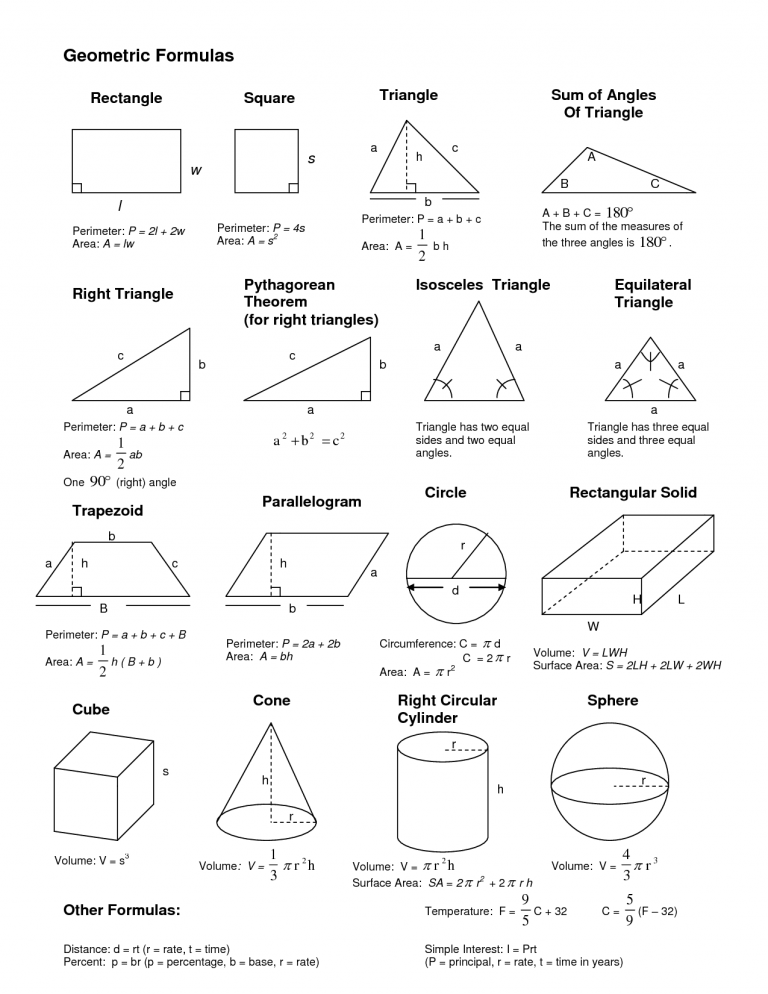 Чаще их называют внешним и внутренним. Во втором выражении площадь кольца рассчитывается через больший D и меньший d диаметры. Таким образом, площадь кольца по известным радиусам рассчитывают так:
Чаще их называют внешним и внутренним. Во втором выражении площадь кольца рассчитывается через больший D и меньший d диаметры. Таким образом, площадь кольца по известным радиусам рассчитывают так:
Площадь кольца, с использованием длин диаметров, определяют следующим образом:
Многоугольник
Как найти площадь многоугольника, форма которого не является правильной? Общей формулы для площади таких фигур нет. Но если она изображена на координатной плоскости, например, это может быть клетчатая бумага, тогда как найти площадь поверхности в этом случае? Тут применяют способ, который не требует приблизительно измерить фигуру. Поступают так: если нашли точки, которые попадают в уголок клетки или имеют целые координаты, то учитывают только их. Чтобы затем выяснить, чему равна площадь, используют формулу, доказанную Пиком. Необходимо сложить количество точек, расположенных внутри ломаной линии с половиной точек, лежащих на ней, и вычесть единицу, т. е. вычисляется это таким образом:
где В,Г — количество точек, расположенных внутри и на всей ломаной линии соответственно.
Вычисление площади фигуры – это, пожалуй, одна из наиболее сложных задач теории площадей. В школьной геометрии учат находить площади основных геометрических фигур таких как, например, треугольник, ромб, прямоугольник, трапеция, круг и т.п. Однако зачастую приходится сталкиваться с вычислением площадей более сложных фигур. Именно при решении таких задач очень удобно использовать интегральное исчисление.
Определение.
Криволинейной трапецией называют некоторую фигуру G, ограниченную линиями y = f(x), у = 0, х = а и х = b, причем функция f(x) непрерывна на отрезке [а; b] и не меняет на нем свой знак (рис. 1). Площадь криволинейной трапеции можно обозначить S(G).
Определенный интеграл ʃ а b f(x)dx для функции f(x), являющийся непрерывной и неотрицательной на отрезке [а; b], и есть площадь соответствующей криволинейной трапеции.
То есть, чтобы найти площадь фигуры G, ограниченной линиями y = f(x), у = 0, х = а и х = b, необходимо вычислить определенный интеграл ʃ а b f(x)dx.
Таким образом,
В случае, если функция y = f(x) не положительна на [а; b], то площадь криволинейной трапеции может быть найдена по формуле S(G) = -ʃ а b f(x)dx.
Пример 1.
Вычислить площадь фигуры, ограниченной линиями у = х 3 ; у = 1; х = 2.
Решение.
Заданные линии образуют фигуру АВС, которая показана штриховкой на рис. 2.
Искомая площадь равна разности между площадями криволинейной трапеции DACE и квадрата DABE.
Используя формулу S = ʃ а b f(x)dx = S(b) – S(a), найдем пределы интегрирования. Для этого решим систему двух уравнений:
{у = х 3 ,
{у = 1.
Таким образом, имеем х 1 = 1 – нижний предел и х = 2 – верхний предел.
Итак, S = S DACE – S DABE = ʃ 1 2 x 3 dx – 1 = x 4 /4| 1 2 – 1 = (16 – 1)/4 – 1 = 11/4 (кв. ед.).
Ответ: 11/4 кв. ед.
Пример 2.
Вычислить площадь фигуры, ограниченной линиями у = √х; у = 2; х = 9.
Решение.
Заданные линии образуют фигуру АВС, которая ограничена сверху графиком функции
у = √х, а снизу графиком функции у = 2. Полученная фигура показана штриховкой на рис. 3.
Искомая площадь равна S = ʃ а b (√x – 2). Найдем пределы интегрирования: b = 9, для нахождения а, решим систему двух уравнений:
{у = √х,
{у = 2.
Таким образом, имеем, что х = 4 = а – это нижний предел.
Итак, S = ∫ 4 9 (√x – 2)dx = ∫ 4 9 √x dx –∫ 4 9 2dx = 2/3 x√х| 4 9 – 2х| 4 9 = (18 – 16/3) – (18 – 8) = 2 2/3 (кв. ед.).
Ответ: S = 2 2/3 кв. ед.
Пример 3.
Вычислить площадь фигуры, ограниченной линиями у = х 3 – 4х; у = 0; х ≥ 0.
Решение.
Построим график функции у = х 3 – 4х при х ≥ 0. Для этого найдем производную у’:
y’ = 3x 2 – 4, y’ = 0 при х = ±2/√3 ≈ 1,1 – критические точки.
Если изобразить критические точки на числовой оси и расставить знаки производной, то получим, что функция убывает от нуля до 2/√3 и возрастает от 2/√3 до плюс бесконечности.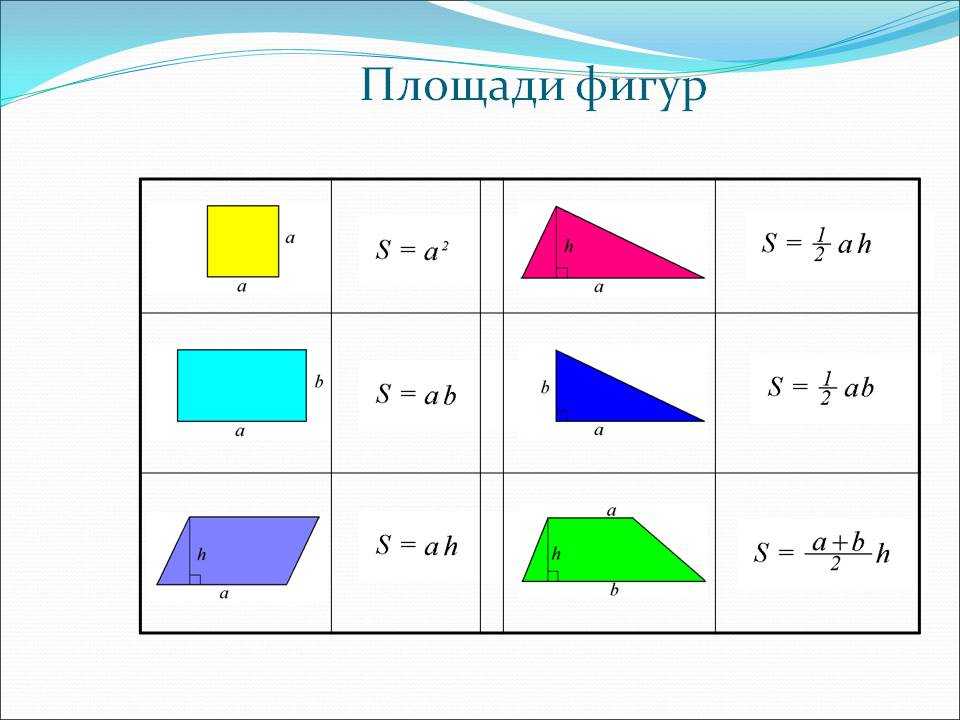 Тогда х = 2/√3 – точка минимума, минимальное значение функции у min = -16/(3√3) ≈ -3.
Тогда х = 2/√3 – точка минимума, минимальное значение функции у min = -16/(3√3) ≈ -3.
Определим точки пересечения графика с осями координат:
если х = 0, то у = 0, а значит, А(0; 0) – точка пересечения с осью Оу;
если у = 0, то х 3 – 4х = 0 или х(х 2 – 4) = 0, или х(х – 2)(х + 2) = 0, откуда х 1 = 0, х 2 = 2, х 3 = -2 (не подходит, т.к. х ≥ 0).
Точки А(0; 0) и В(2; 0) – точки пересечения графика с осью Ох.
Заданные линии образуют фигуру ОАВ, которая показана штриховкой на рис. 4.
Так как функция у = х 3 – 4х принимает на (0; 2) отрицательное значение, то
S = |ʃ 0 2 (x 3 – 4x)dx|.
Имеем: ʃ 0 2 (x 3 – 4х)dx =(x 4 /4 – 4х 2 /2)| 0 2 = -4, откуда S = 4 кв. ед.
Ответ: S = 4 кв. ед.
Пример 4.
Найти площадь фигуры, ограниченной параболой у = 2х 2 – 2х + 1, прямыми х = 0, у = 0 и касательной к данной параболе в точке с абсциссой х 0 = 2.
Решение.
Сначала составим уравнение касательной к параболе у = 2х 2 – 2х + 1 в точке с абсциссой х₀ = 2.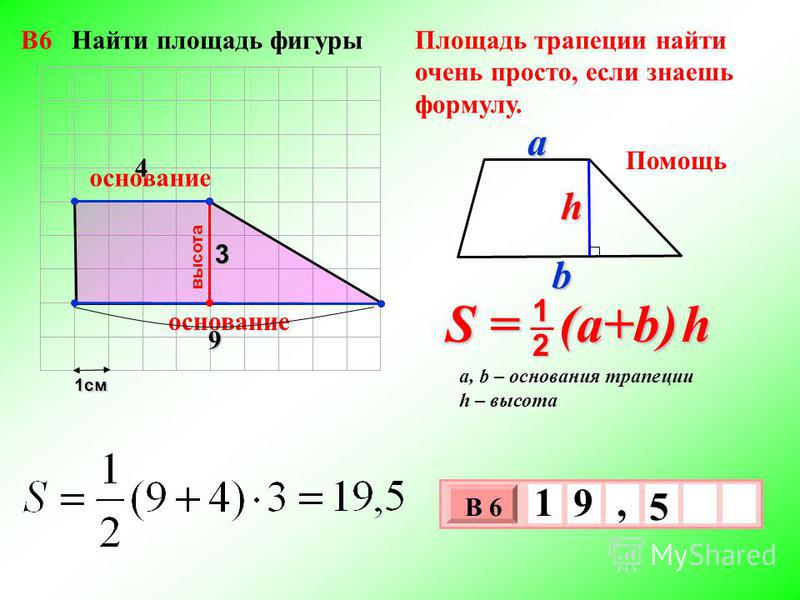
Так как производная y’ = 4x – 2, то при х 0 = 2 получим k = y’(2) = 6.
Найдем ординату точки касания: у 0 = 2 · 2 2 – 2 · 2 + 1 = 5.
Следовательно, уравнение касательной имеет вид: у – 5 = 6(х – 2) или у = 6х – 7.
Построим фигуру, ограниченную линиями:
у = 2х 2 – 2х + 1, у = 0, х = 0, у = 6х – 7.
Г у = 2х 2 – 2х + 1 – парабола. Точки пересечения с осями координат: А(0; 1) – с осью Оу; с осью Ох – нет точек пересечения, т.к. уравнение 2х 2 – 2х + 1 = 0 не имеет решений (D
x b = 2/4 = 1/2;
y b = 1/2, то есть вершина параболы точка В имеет координаты В(1/2; 1/2).
Итак, фигура, площадь которой требуется определить, показана штриховкой на рис. 5.
Имеем: S О A В D = S OABC – S ADBC .
Найдем координаты точки D из условия:
6х – 7 = 0, т.е. х = 7/6, значит DC = 2 – 7/6 = 5/6.
Площадь треугольника DBC найдем по формуле S ADBC = 1/2 · DC · BC. Таким образом,
S ADBC = 1/2 · 5/6 · 5 = 25/12 кв. ед.
S OABC = ʃ 0 2 (2x 2 – 2х + 1)dx = (2x 3 /3 – 2х 2 /2 + х)| 0 2 = 10/3 (кв. ед.).
ед.).
Окончательно получим: S О A В D = S OABC – S ADBC = 10/3 – 25/12 = 5/4 = 1 1/4 (кв. ед).
Ответ: S = 1 1/4 кв. ед.
Мы разобрали примеры нахождения площадей фигур, ограниченных заданными линиями . Для успешного решения подобных задач нужно уметь строить на плоскости линии и графики функций, находить точки пересечения линий, применять формулу для нахождения площади, что подразумевает наличие умений и навыков вычисления определенных интегралов.
сайт, при полном или частичном копировании материала ссылка на первоисточник обязательна.
Соблюдение Вашей конфиденциальности важно для нас. По этой причине, мы разработали Политику Конфиденциальности, которая описывает, как мы используем и храним Вашу информацию. Пожалуйста, ознакомьтесь с нашими правилами соблюдения конфиденциальности и сообщите нам, если у вас возникнут какие-либо вопросы.
Сбор и использование персональной информации
Под персональной информацией понимаются данные, которые могут быть использованы для идентификации определенного лица либо связи с ним.
От вас может быть запрошено предоставление вашей персональной информации в любой момент, когда вы связываетесь с нами.
Ниже приведены некоторые примеры типов персональной информации, которую мы можем собирать, и как мы можем использовать такую информацию.
Какую персональную информацию мы собираем:
- Когда вы оставляете заявку на сайте, мы можем собирать различную информацию, включая ваши имя, номер телефона, адрес электронной почты и т.д.
Как мы используем вашу персональную информацию:
- Собираемая нами персональная информация позволяет нам связываться с вами и сообщать об уникальных предложениях, акциях и других мероприятиях и ближайших событиях.
- Время от времени, мы можем использовать вашу персональную информацию для отправки важных уведомлений и сообщений.
- Мы также можем использовать персональную информацию для внутренних целей, таких как проведения аудита, анализа данных и различных исследований в целях улучшения услуг предоставляемых нами и предоставления Вам рекомендаций относительно наших услуг.

- Если вы принимаете участие в розыгрыше призов, конкурсе или сходном стимулирующем мероприятии, мы можем использовать предоставляемую вами информацию для управления такими программами.
Раскрытие информации третьим лицам
Мы не раскрываем полученную от Вас информацию третьим лицам.
Исключения:
- В случае если необходимо — в соответствии с законом, судебным порядком, в судебном разбирательстве, и/или на основании публичных запросов или запросов от государственных органов на территории РФ — раскрыть вашу персональную информацию. Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.
- В случае реорганизации, слияния или продажи мы можем передать собираемую нами персональную информацию соответствующему третьему лицу – правопреемнику.
Защита персональной информации
Мы предпринимаем меры предосторожности — включая административные, технические и физические — для защиты вашей персональной информации от утраты, кражи, и недобросовестного использования, а также от несанкционированного доступа, раскрытия, изменения и уничтожения.
Соблюдение вашей конфиденциальности на уровне компании
Для того чтобы убедиться, что ваша персональная информация находится в безопасности, мы доводим нормы соблюдения конфиденциальности и безопасности до наших сотрудников, и строго следим за исполнением мер соблюдения конфиденциальности.
Формула площади необходима для определения площадь фигуры, которая является вещественнозначной функцией, определённой на некотором классе фигур евклидовой плоскости и удовлетворяющая 4м условиям:
- Положительность — Площадь не может быть меньше нуля;
- Нормировка — квадрат со стороной единица имеет площадь 1;
- Конгруэнтность — конгруэнтные фигуры имеют равную площадь;
- Аддитивность — площадь объединения 2х фигур без общих внутренних точек равна сумме площадей этих фигур.
| Геометрическая фигура | Формула | Чертеж |
|---|---|---|
Результат сложения расстояний между серединами противоположных сторон выпуклого четырехугольника будут равна его полупериметру. | ||
Сектор круга. Площадь сектора круга равна произведению его дуги на половину радиуса. | ||
Сегмент круга. Чтобы получить площадь сегмента ASB, достаточно из площади сектора AOB вычесть площадь треугольника AOB. | S = 1 / 2 R(s — AС) | |
Площадь эллипса равна произведению длин большой и малой полуосей эллипса на число пи. | ||
Эллипс . Еще один вариант как вычислить площадь эллипса — через два его радиуса. | ||
Треугольник. Через основание и высоту. Формула площади круга через его радиус и диаметр. | ||
Квадрат . Через его сторону. Площадь квадрата равна квадрату длины его стороны. | ||
Квадрат. Площадь квадрата равна половине квадрата длины его диагонали. | ||
Правильный многоугольник . Для определения площади правильного многоугольника необходимо разбить его на равные треугольники, которые бы имели общую вершину в центре вписанной окружности. | S= r·p = 1/2 r·n·a |
Площадь геометрической фигуры — численная характеристика геометрической фигуры показывающая размер этой фигуры (части поверхности, ограниченной замкнутым контуром данной фигуры). Величина площади выражается числом заключающихся в нее квадратных единиц.
Формулы площади треугольника
- Формула площади треугольника по стороне и высоте
Площадь треугольника равна половине произведения длины стороны треугольника на длину проведенной к этой стороне высоты - Формула площади треугольника по трем сторонам и радиусу описанной окружности
- Формула площади треугольника по трем сторонам и радиусу вписанной окружности
Площадь треугольника равна произведения полупериметра треугольника на радиус вписанной окружности. где S — площадь треугольника,
где S — площадь треугольника,
— длины сторон треугольника,
— высота треугольника,
— угол между сторонами и,
— радиус вписанной окружности,
R — радиус описанной окружности,
Формулы площади квадрата
- Формула площади квадрата по длине стороны
Площадь квадрата равна квадрату длины его стороны. - Формула площади квадрата по длине диагонали
Площадь квадрата равна половине квадрата длины его диагонали.S = 1 2 2 где S — Площадь квадрата,
— длина стороны квадрата,
— длина диагонали квадрата.
Формула площади прямоугольника
- Площадь прямоугольника равна произведению длин двух его смежных сторон
где S — Площадь прямоугольника,
— длины сторон прямоугольника.
Формулы площади параллелограмма
- Формула площади параллелограмма по длине стороны и высоте
Площадь параллелограмма - Формула площади параллелограмма по двум сторонам и углу между ними
Площадь параллелограмма равна произведению длин его сторон умноженному на синус угла между ними.a · b · sin α
где S — Площадь параллелограмма,
— длины сторон параллелограмма,
— длина высоты параллелограмма,
— угол между сторонами параллелограмма.
Формулы площади ромба
- Формула площади ромба по длине стороны и высоте
Площадь ромба равна произведению длины его стороны и длины опущенной на эту сторону высоты. - Формула площади ромба по длине стороны и углу
Площадь ромба равна произведению квадрата длины его стороны и синуса угла между сторонами ромба. - Формула площади ромба по длинам его диагоналей
Площадь ромба равна половине произведению длин его диагоналей. где S — Площадь ромба,
где S — Площадь ромба,
— длина стороны ромба,
— длина высоты ромба,
— угол между сторонами ромба,
1 , 2 — длины диагоналей.
Формулы площади трапеции
- Формула Герона для трапеции
Где S — Площадь трапеции,
— длины основ трапеции,
— длины боковых сторон трапеции,
Математика, 6 класс, площадь поверхности и объем, базовые и составные числа
Обзор
Учащиеся используют свои знания о нахождении площадей простых фигур для нахождения площадей составных фигур.
Составная фигура — это фигура, которую можно разделить на две или более основных фигуры.
Площадь составной фигуры можно найти, разделив ее на базовые фигуры, площадь которых легко вычислить.
Для некоторых фигур площадь также можно найти, окружив фигуру базовой фигурой, создав другие базовые фигуры «между» исходной фигурой и окружающей фигурой. Затем площадь исходной фигуры можно найти, вычитая основную фигуру.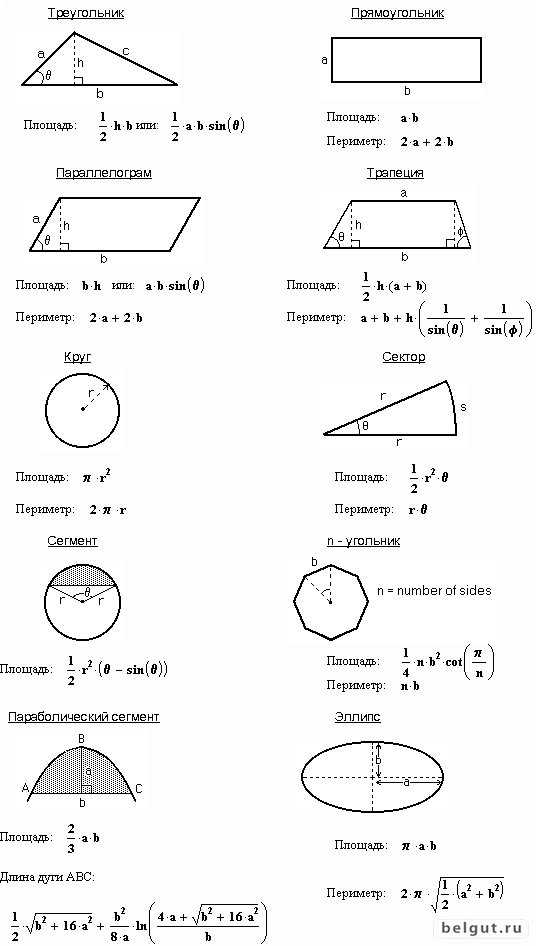
- Найдите площадь составных фигур, разложив и составив их на более простые фигуры.
Объясните, что эта фигура является частью парка, покрытого травой.
Партнеры должны обсудить способы нахождения площади этой фигуры.
ELL: при наблюдении за учащимися обращайте особое внимание на ELL, чтобы убедиться, что они выполняют задание и четко понимают, что необходимо сделать. Некоторые учащиеся могут не распознать стратегии нахождения областей составных фигур. Обеспечить прямой инструктаж учащимся, испытывающим затруднения.
Спросите:
- Как разбить фигуру на прямоугольники или треугольники, чтобы найти ее площадь?
- Можете ли вы придумать другую стратегию для поиска области?
Открытие
На этой фигуре изображена часть парка, покрытая травой. Обсудите следующие вопросы.
- Как фигура составлена из других фигур?
- Как можно разложить фигуру на другие фигуры?
- Как найти площадь этой фигуры?
Обсудить математическую миссию.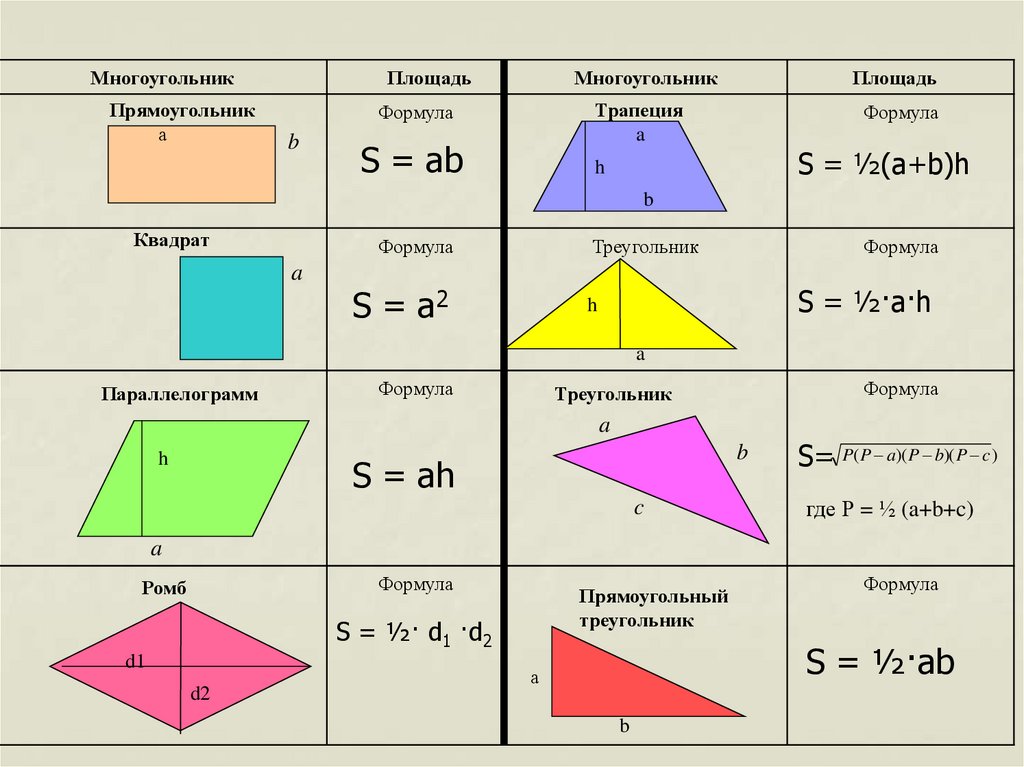 Учащиеся будут составлять и разлагать фигуры, чтобы найти их площади. Просмотрите определения компоновки и декомпозиции, если эти термины не знакомы учащимся.
Учащиеся будут составлять и разлагать фигуры, чтобы найти их площади. Просмотрите определения компоновки и декомпозиции, если эти термины не знакомы учащимся.
Открытие
Составьте и разложите фигуры, чтобы найти их площади.
Предложите учащимся составить и разложить фигуры, чтобы найти их площади.
Предложите учащимся несколько минут поработать над этими задачами в одиночку, а затем решить их вместе с партнером. Попросите партнеров подготовить презентацию вместе.
Во время работы учащиеся задают вопросы, например, следующего содержания:
- Какова ваша стратегия нахождения площади фигуры?
- Можно ли разбить фигуру другим способом, чтобы найти площадь?
SWD: Предложите учащимся перечислить ключевые фигуры, которые они видят в составной фигуре. Предложите учащимся выделить треугольники, параллелограммы, прямоугольники и трапеции, которые они узнают. Это поможет им найти общую площадь.
Математическая практика 5: Стратегически используйте соответствующие инструменты.
Учащиеся могут использовать линейку и карандаш, чтобы разделить фигуры. Некоторые учащиеся могут использовать ножницы, чтобы разрезать фигуру на части. Учащимся, которые разрезают фигуру, возможно, потребуется измерить ее длину, чтобы найти длину. Убедитесь, что они понимают, что 1 см на прямоугольнике равен 1 м в парке. Учащиеся должны измерить необходимые им длины с точностью до полсантиметра, чтобы найти площадь каждой части.
Математическая практика 1: Разбираться в задачах и упорно решать их.
Ищите учащихся, которые по-разному подходят к нахождению площадей составных фигур. Ищите учеников, которые разлагают одну и ту же фигуру по-разному, или тех, кто использует совершенно другой подход. Определите учащихся, которые борются с проблемой, но продолжают решать ее, пока не найдут решение.
Студенту трудно начать.
- Опишите задание своими словами своему партнеру.
- Как найти площади каких фигур вы уже знаете?
- Можете ли вы разбить эту фигуру на знакомые фигуры?
Студент не разбивает цифру на самые основные.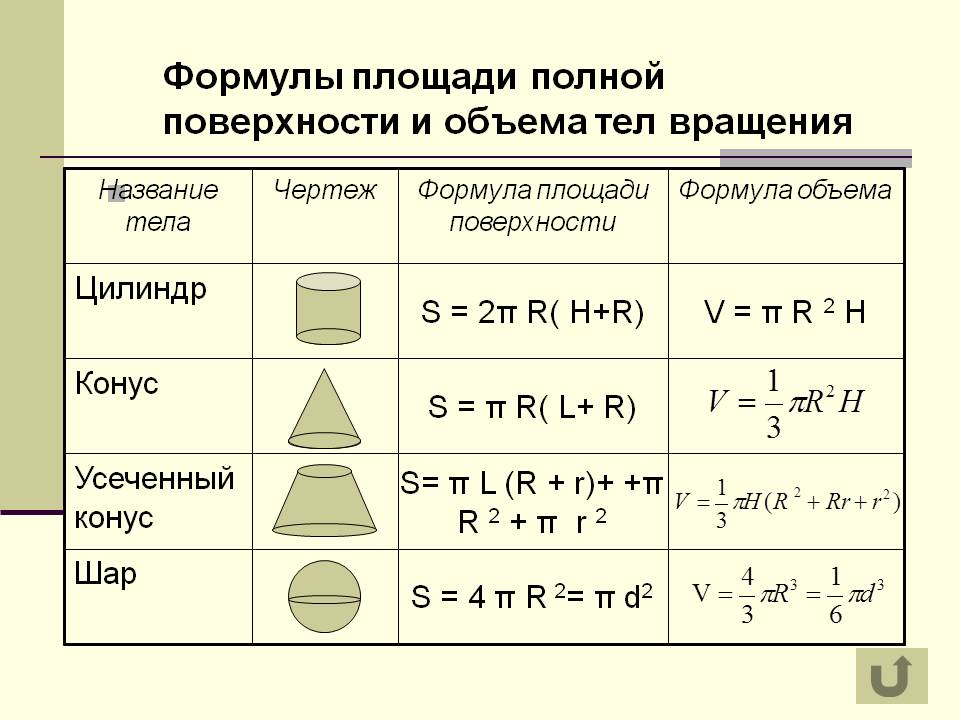
- Посмотрите на фигуры, на которые вы разделили составную фигуру. Все ли фигуры можно найти, площадь которых можно найти?
- Сможете ли вы найти площадь этой фигуры? Если нет, можете ли вы разбить его на знакомые цифры?
Ученик дал неверное решение.
- Как проверить свою работу?
- Учитывали ли вы площадь каждой части ровно один раз, когда вычисляли общую площадь?
- Что, если разбить фигуру другим способом? У вас такая же площадь?
У учащегося есть уникальный или интересный метод решения.
- Почему вы подошли к проблеме именно так?
- Объясните свою стратегию решения проблемы.
SWD: во время работы с партнером наблюдайте за обсуждениями учащихся и задавайте наводящие вопросы из интервенций, чтобы помочь учащимся увидеть математику и найти собственный путь к решению. Если студент борется с определенной концепцией, проведите индивидуальную конференцию. Если многие учащиеся борются с концепцией, соберите небольшую группу для обсуждения концепции.
Если многие учащиеся борются с концепцией, соберите небольшую группу для обсуждения концепции.
- Площадь фигуры 209 м 2 .
Рабочее время
Эта цифра является примером составной фигуры. Составная фигура — это фигура, которую можно разбить на две или более основных фигуры. Он состоит из базовых фигур и может быть разложен на базовые фигуры.
- Найдите площадь этой составной фигуры.
Подсказка:
- Можете ли вы разложить составную фигуру на основные фигуры, площади которых вы уже знаете?
- Или вы можете нарисовать знакомую фигуру вокруг составной фигуры и с помощью вычитания найти площадь составной фигуры?
Предложите учащимся составить и разложить фигуры, чтобы найти их площади.
Предложите учащимся несколько минут поработать над этими задачами в одиночку, а затем решить их вместе с партнером. Попросите партнеров подготовить презентацию вместе.
Пока учащиеся работают, задавайте вопросы, например, следующего содержания:
- Какова ваша стратегия нахождения площади фигуры?
- Можно ли разбить фигуру другим способом, чтобы найти площадь?
SWD: Предложите учащимся перечислить ключевые фигуры, которые они видят в составной фигуре. Предложите учащимся выделить треугольники, параллелограммы, прямоугольники и трапеции, которые они узнают. Это поможет им найти общую площадь.
Математическая практика 5: Стратегически используйте соответствующие инструменты.
Учащиеся могут использовать линейку и карандаш, чтобы разделить фигуры. Некоторые учащиеся могут использовать ножницы, чтобы разрезать фигуру на части. Учащимся, которые разрезают фигуру, возможно, потребуется измерить ее длину, чтобы найти длину. Убедитесь, что они понимают, что 1 см на прямоугольнике равен 1 м в парке. Учащиеся должны измерить необходимые им длины с точностью до полсантиметра, чтобы найти площадь каждой части.
Математическая практика 1: Разбираться в задачах и настойчиво решать их.
Ищите учащихся, которые по-разному подходят к нахождению площадей составных фигур. Ищите учеников, которые разлагают одну и ту же фигуру по-разному, или тех, кто использует совершенно другой подход. Определите учащихся, которые борются, но продолжайте решать проблему, пока они не найдут решение.
Студенту трудно начать.
- Опишите задание своими словами своему партнеру.
- Как найти площади каких фигур вы уже знаете?
- Сможете разбить эту фигуру на знакомые фигуры?
Студент не разбивает цифру на самые основные.
- Посмотрите на фигуры, на которые вы разделили составную фигуру. Все ли фигуры можно найти, площадь которых можно найти?
- Сможете ли вы найти площадь этой фигуры? Если нет, можете ли вы разбить его на знакомые цифры?
Ученик дал неверное решение.
- Как проверить свою работу?
- Учитывали ли вы площадь каждой части ровно один раз, когда вычисляли общую площадь?
- Что, если разбить фигуру другим способом? У вас такая же площадь?
У учащегося есть уникальный или интересный метод решения.
- Почему вы подошли к проблеме именно так?
- Объясните свою стратегию решения проблемы.
- Площадь фигуры 38 футов 2 .
Рабочее время
- Найдите площадь этой составной фигуры.
Подсказка:
- Можете ли вы разложить составную фигуру на основные фигуры, площади которых вы уже знаете?
- Или вы можете нарисовать знакомую фигуру вокруг составной фигуры и с помощью вычитания найти площадь составной фигуры?
Предложите учащимся составить и разложить фигуры на планшете, чтобы найти их площади.
Предложите учащимся несколько минут поработать над этими задачами в одиночку, а затем решить их вместе с партнером. Попросите партнеров подготовить презентацию вместе.
Попросите партнеров подготовить презентацию вместе.
Во время работы учащиеся задают вопросы, например, следующего содержания:
- Какова ваша стратегия нахождения площади фигуры?
- Можно ли разбить фигуру другим способом, чтобы найти площадь? SWD:
Предложите учащимся перечислить ключевые фигуры, которые они видят в составной фигуре. Предложите учащимся выделить треугольники, параллелограммы, прямоугольники и трапеции, которые они узнают. Это поможет им найти общую площадь.
Математическая практика 5: Стратегически используйте соответствующие инструменты.
Учащиеся могут использовать линейку и карандаш, чтобы разделить фигуры. Некоторые учащиеся могут использовать ножницы, чтобы разрезать фигуру на части. Учащимся, которые разрезают фигуру, возможно, потребуется измерить ее длину, чтобы найти длину. Убедитесь, что они понимают, что 1 см на прямоугольнике равен 1 м в парке. Учащиеся должны измерить необходимые им длины с точностью до полсантиметра, чтобы найти площадь каждой части.
Математическая практика 1: Разбираться в задачах и настойчиво решать их.
Ищите учащихся, которые по-разному подходят к нахождению площадей составных фигур. Ищите учеников, которые разлагают одну и ту же фигуру по-разному, или тех, кто использует совершенно другой подход. Определите учащихся, которые борются, но продолжайте решать проблему, пока они не найдут решение.
Студенту трудно начать.
- Опишите задание своими словами своему партнеру.
- Как найти площади каких фигур вы уже знаете?
- Сможете разбить эту фигуру на знакомые фигуры?
Студент не разбивает цифру на самые основные.
- Посмотрите на фигуры, на которые вы разделили составную фигуру. Все ли фигуры можно найти, площадь которых можно найти?
- Сможете ли вы найти площадь этой фигуры? Если нет, можете ли вы разбить его на знакомые цифры?
Ученик дал неверное решение.
- Как проверить свою работу?
- Учитывали ли вы площадь каждой части ровно один раз, когда вычисляли общую площадь?
- Что, если разбить фигуру другим способом? У вас такая же площадь?
У учащегося есть уникальный или интересный метод решения.
- Почему вы подошли к проблеме именно так?
- Объясните свою стратегию решения проблемы.
SWD: во время работы с партнером следите за обсуждениями учащихся и задавайте наводящие вопросы из интервенций, чтобы помочь учащимся увидеть математику и найти собственный путь к решению. Если студент борется с определенной концепцией, проведите индивидуальную конференцию. Если многие учащиеся борются с концепцией, соберите небольшую группу для обсуждения концепции.
- Площадь фигуры 0,165 фута 2 .
Рабочее время
- Найдите площадь этой составной фигуры.
Подсказка:
- Метка на двух сторонах означает, что они имеют одинаковую длину.

- Можете ли вы разложить составную фигуру на основные фигуры, площади которых вы уже знаете?
- Или вы можете нарисовать знакомую фигуру вокруг составной фигуры и с помощью вычитания найти площадь составной фигуры?
Определить учащихся с различными методами решения, которыми они могут поделиться во время Пути мышления:
- Учащиеся, которые разлагают исходную фигуру на различные базовые фигуры, а затем находят и складывают их площади
- Учащиеся, которые окружают исходную фигуру базовой фигурой, а затем вычитают из нее площадь базовой фигуры, образованная между окружающей фигурой и исходной фигурой
- [общая ошибка] Следите за учащимися, которые правильно разлагают фигуру, но допускают ошибку при объединении площадей. Учащиеся могут опустить площадь одной или нескольких основных фигур или посчитать площадь базовой фигуры дважды. Предложите учащимся написать выражение сложения для общей площади с добавлением для каждой базовой фигуры.
 Перед выполнением сложения учащиеся должны посчитать, чтобы количество слагаемых соответствовало количеству основных фигур.
Перед выполнением сложения учащиеся должны посчитать, чтобы количество слагаемых соответствовало количеству основных фигур.
ELL: Предложите учащимся использовать схемы, если это необходимо, чтобы объяснить, как они нашли эту область. Важно, чтобы вы создали среду, в которой все учащиеся чувствовали бы себя комфортно, делясь своими решениями.
SWD: Учащиеся должны чувствовать себя в достаточной безопасности, чтобы делиться своими идеями, стратегиями и, самое главное, ошибками. Большинство учащихся — и особенно учащиеся с ограниченными возможностями — не привыкли говорить о математике; тем не менее, на курсах более высокого уровня успех студента может зависеть от участия в учебных группах и способности студента делиться идеями.
Ответы
- Ответы будут разными. Проверьте фигуры и площади учащихся.
Рабочее время
- Объясните, как вы находите площади составных фигур. Используйте свою работу, чтобы поддержать свое объяснение.

- Нарисуйте составную фигуру и найдите ее площадь.
Предложите учащимся рассказать о том, как они разлагали фигуры и находили их площади.
Для первой фигуры есть много способов разложить ее на прямоугольники. Вот один из вариантов:
Другая стратегия состоит в том, чтобы нарисовать прямоугольник вокруг фигуры и вычесть площади белых прямоугольников ( A , B и C на рисунке ниже) из площади окружающего прямоугольника.
Спросите:
- Несмотря на то, что мы разбили фигуры по-разному, получили ли мы одинаковую площадь для каждой фигуры?
Математическая практика 3: Создание убедительных аргументов и критика рассуждений других.
Предложите учащимся критически оценить и сравнить различные методы, используемые классом для различных фигур, и обсудить, какие методы кажутся самыми простыми или более эффективными.
Performance Task
- Делайте заметки о подходах других одноклассников к поиску областей.
 Насколько подходы похожи на ваш подход? Насколько они разные?
Насколько подходы похожи на ваш подход? Насколько они разные?
Подсказка:
Пока ваши одноклассники присутствуют, задайте такие вопросы, как:
- Как вы разложили фигуру?
- Как вы нашли основание и высоту фигуры?
- Для какой фигуры вам было труднее всего найти площадь?
- Какую формулу вы использовали?
- Откуда вы узнали, что нужно использовать эту формулу?
Пусть пары тихо обсудят, как они могут использовать площадь треугольника и площадь прямоугольника для определения площади всех многоугольников. Пусть пары используют описанные методы для нахождения площади нескольких многоугольников, как правильных, так и неправильных.
Пока учащиеся работают вместе, прислушивайтесь к учащимся, у которых все еще могут быть неверные представления, чтобы вы могли обсудить их в ходе обсуждения в классе.
Через несколько минут обсудите резюме всем классом. Попросите добровольцев поделиться своими методами нахождения площадей многоугольников. Включите в примеры как правильные, так и неправильные многоугольники. Затем суммируйте следующие точки:
Включите в примеры как правильные, так и неправильные многоугольники. Затем суммируйте следующие точки:
- Вы можете найти площадь любого многоугольника, разбив его на треугольники и прямоугольники.
- Иногда вы можете окружить многоугольник прямоугольником или другой базовой фигурой и вычесть ее, чтобы найти площадь составной фигуры.
Формирующее оценивание
Прочитать и обсудить
- Зная формулы площади треугольника и площади прямоугольника, можно определить площади всех других многоугольников, правильных и неправильных.
- Площадь параллелограмма и трапеции можно найти, разложив многоугольник на комбинации прямоугольных треугольников и прямоугольников, а затем сложив площади составляющих фигур.
- Для других многоугольников хорошим методом является сначала построить любую диагональ многоугольника. Затем присоедините каждую из других вершин к диагонали перпендикулярными отрезками. Разложите любые трапеции, которые образуются в этом процессе, на прямоугольники и прямоугольные треугольники, а затем найдите площади составляющих фигур.

- Вы также можете нарисовать знакомую фигуру вокруг составной фигуры и использовать вычитание, чтобы найти площадь составной фигуры.
Подсказка:
Сможете ли вы:
- Найти площади составных фигур?
- Приведите примеры, иллюстрирующие ваши стратегии нахождения площадей составных фигур?
Пусть каждый учащийся напишет краткое размышление перед окончанием урока. Просмотрите размышления, чтобы узнать, что учащиеся узнали о нахождении площади составных фигур.
ELL: при написании размышления дайте ELL дополнительное время для обсуждения с партнером, прежде чем писать, чтобы помочь им организовать свои мысли. Разрешить ELL, говорящим на одном основном языке, обсуждать на этом языке, если они предпочитают, и использовать словарь.
Рабочее время
Напишите размышления об идеях, обсуждавшихся сегодня в классе. Используйте приведенный ниже образец предложения, если он окажется вам полезным.
Способ, которым я нашел площадь одной из составных фигур, был …
Нахождение площади составной фигуры
Составная фигура состоит из простых геометрических фигур.
Чтобы найти площадь составной фигуры или другой фигуры неправильной формы, разделите ее на простые непересекающиеся фигуры.
Найдите площадь каждой простой фигуры, а затем сложите площади, чтобы найти общую площадь составной фигуры.
Пример 1 :
Найдите площадь фигуры, приведенной ниже.
Решение:
Шаг 1 :
Разделите фигуру на более мелкие, знакомые фигуры: параллелограмм и трапецию.
Шаг 2 :
Найдите площадь параллелограмма.
Основание (b) = 10 см
Высота (h) = 1,5 см
Используйте формулу.
A = bh
A = 10 · 1,5
= 15
Площадь параллелограмма 15 квадратных см.
Шаг 3 :
Найдите площадь трапеции.
Основание 1 (б 1 ) = 7 см
Основание 2 (b 2 ) = 10 см
Высота (h) = 1,5 см
Используйте формулу.
A = (1/2)h(b 1 + b 2 )
= (1/2)(1,5)(7 + 10)
= (1/2)(1,5)(17 )
= 12,75
Площадь трапеции 12,75 квадратных см.
Шаг 4:
Добавьте площади, чтобы найти общую площадь.
A = 15 + 12,75
= 27,75
Итак, площадь данной составной фигуры равна 27,75.
Пример 2 :
Найдите площадь фигуры, приведенной ниже.
Решение :
Шаг 1 :
Разделите фигуру на более мелкие знакомые фигуры: два треугольника и прямоугольник.
Шаг 2 :
Найдите площадь первого треугольника.
Основание (b) = 3 фута
Высота (h) = 2 фута
Используйте формулу.
A = (1/2)bh
= (1/2)(3)(2)
= 3
Площадь первого треугольника равна 3 кв. фута.
Шаг 3 :
Найдите площадь прямоугольника.
Длина (l) = 8 + 3 = 11 футов
Высота (h) = 4 фута
Используйте формулу.
A = l x w
= 11 x 4
= 44
Площадь прямоугольника 44 квадратных фута.
Шаг 4:
Найдите площадь второго треугольника.
Основание (b) = 3 фута
Высота (h) = 3 фута
Используйте формулу.
A = (1/2)bh
= (1/2)(3)(3)
= 4,5
Площадь второго треугольника составляет 4,5 квадратных фута.
Шаг 5:
Сложите площади, чтобы найти общую площадь.
A = 3 + 44 + 4,5
= 51,5
Итак, площадь данной составной фигуры равна 51,5 квадратных фута.
Пример 3 :
Найдите площадь фигуры, приведенной ниже.
Решение:
Шаг 1:
Разделите фигуру на более мелкие, знакомые фигуры: квадрат и полукруг.
Шаг 2 :
Найдите площадь квадрата.
Длина каждой стороны = 10 м
Используйте формулу.
A = Сторона x Сторона
= 10 x 10
= 100
Площадь прямоугольника 100 квадратных метров.
Шаг 3 :
Найдите площадь полукруга.
Диаметр = 10 м
Радиус (r) = Диаметр/2
= 10/2
= 5 м
Используйте формулу.

 Через его диагонали .
Через его диагонали .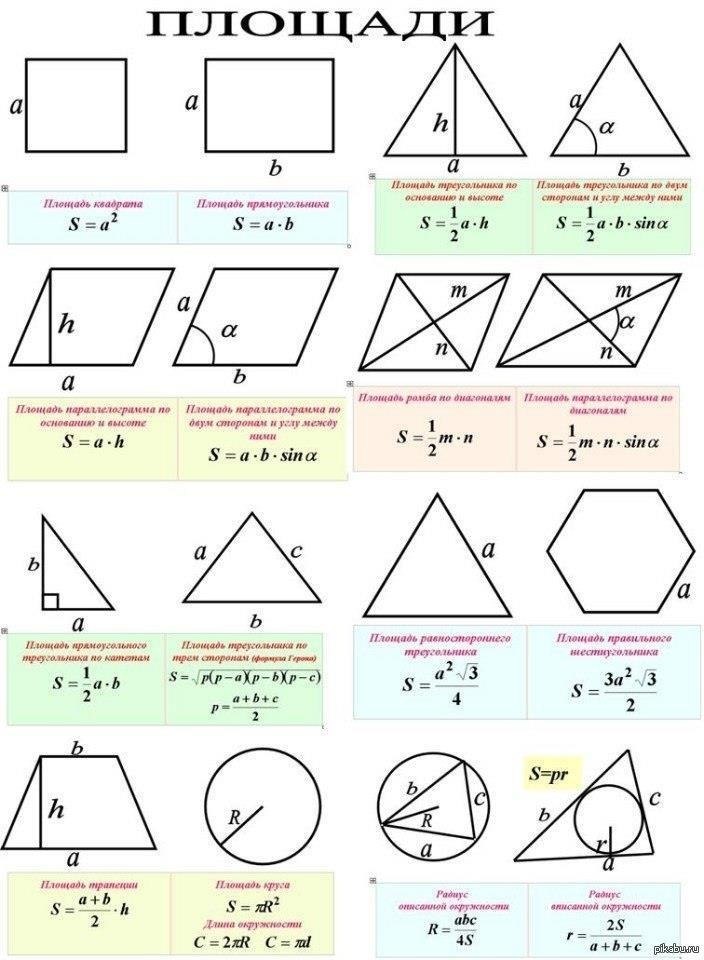


 Перед выполнением сложения учащиеся должны посчитать, чтобы количество слагаемых соответствовало количеству основных фигур.
Перед выполнением сложения учащиеся должны посчитать, чтобы количество слагаемых соответствовало количеству основных фигур.
 Насколько подходы похожи на ваш подход? Насколько они разные?
Насколько подходы похожи на ваш подход? Насколько они разные?