Скалярное произведение векторов 11 класс онлайн-подготовка на Ростелеком Лицей
Введение
Тема данного урока: «Скалярное произведение векторов». Для вас эти слова не должны быть новыми: в планиметрии мы уже говорили о скалярном произведении. Вспомним, что скалярным произведением двух векторов на плоскости называется число, равное произведению длин данных векторов на косинус угла между ними. Также мы выводили формулу для нахождения скалярного произведения векторов в координатах: , где ; .
Угол между векторами
Введем понятие угла между векторами – оно, как и многое на этом уроке, будет абсолютно аналогичным тому, что было на плоскости.
Пусть даны два вектора , . Отложим их от некоторой точки пространства: ; . Тогда угол между векторами – это угол . (См. Рис. 1.) Угол может быть прямым, тупым или острым.
Рис. 1. Угол между векторами
Если векторы сонаправлены, то будем считать, что угол между ними равен .
(См. Рис. 2.)
Рис. 2. Угол между сонаправленными векторами
Если угол между векторами равен , такие векторы называют перпендикулярными. (См. Рис. 3.)
Рис. 3. Перпендикулярные векторы
Если векторы направлены в разные стороны, тогда угол между ними . (См. Рис. 4.)
Рис. 4. Угол между противоположно направленными векторами
Скалярное произведение векторов
Скалярным произведением двух векторов называется произведение их длин на косинус угла между ними: .
Если угол между векторами острый и векторы ненулевые, то скалярное произведение положительно (т. к. ). (См. Рис. 5.)
Рис. 5. Случай, когда скалярное произведение положительно
Если угол между векторами тупой и векторы ненулевые, то скалярное произведение отрицательно (т. к. ). (См. Рис. 6.)
Рис. 6. Случай, когда скалярное произведение отрицательно
Если угол между векторами прямой, то скалярное произведение равно (т.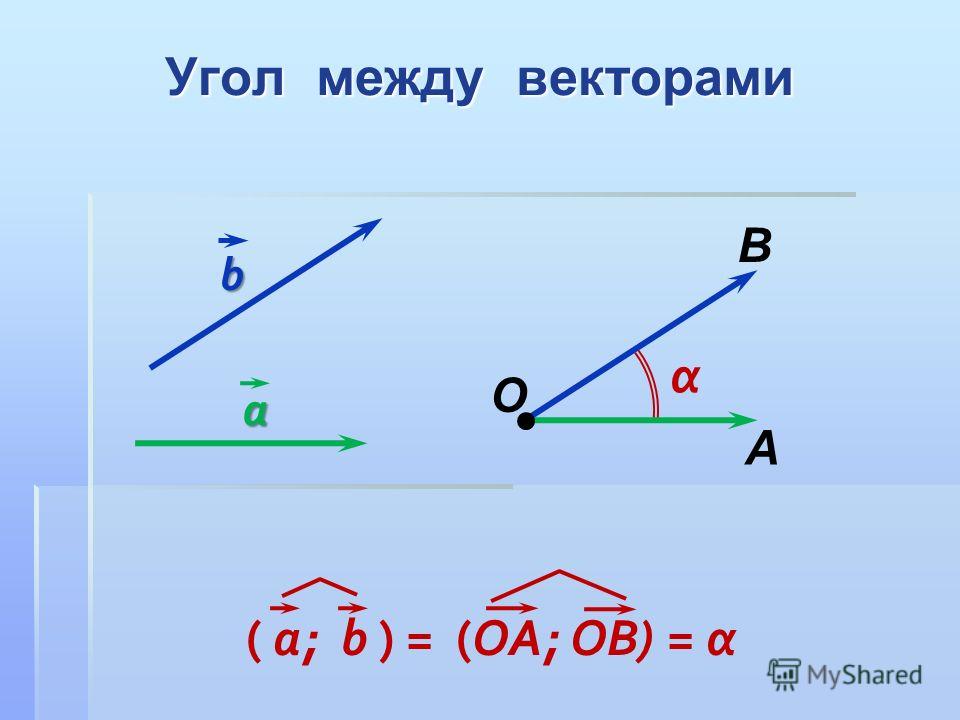
к. ). (См. Рис. 7.)
Рис. 7. Случай, когда скалярное произведение равно
Скалярное произведение через координаты векторов и нахождения косинуса угла между векторами
Важный момент: .
Произведение длин в координатах, мы уже искать умеем – знаменатель сможем преобразовать. А как преобразовать числитель?
Если ; , то . Формула аналогична плоскостной и доказывается точно так же.
Тогда формула для нахождения косинуса угла между векторами выглядит так:
.
И это очень важный момент. Теперь, если у нас даны две произвольные прямые, каждая задана двумя точками, мы можем найти соответствующие направляющие векторы этих прямых (см. Рис. 8) и посчитать косинус угла между ними по выведенной формуле.
Рис. 8. Угол между произвольными прямыми
Но не стоит забывать, что есть отличие между углом между векторами и углом между прямыми. Угол между прямыми может быть острым или прямым, а угол между векторами может быть еще и тупым.
Поэтому соответствующий косинус, который мы найдем у векторов, надо будет взять по модулю, чтобы при необходимости вместо тупого угла найти смежный с ним острый угол.
Свойства скалярного произведения
Остановимся на свойствах скалярного произведения; они абсолютно аналогичны тому, что было в планиметрии.
1. (причем )
2. .
3. (
4. , где – число, , – векторы.
Доказываются эти утверждения аналогично планиметрическим.
Примеры
Задача 1. Найти угол между векторами , .
Решение. Вспомним, что .
По формулам: ; .
Тогда .
Значит, .
Ответ: .
Задача 2. В единичном кубе найти угол между прямыми и . (См. Рис. 9.)
Рис. 9. Иллюстрация к условию
Решение. Сразу отметим, что требуется найти угол между прямыми, то есть угол между ними будет острым. Значит, если косинус получится отрицательным, то надо взять его по модулю, найдя смежный острый угол.
Способ 1. Введем систему координат. (См. Рис. 10.)
Рис. 10. Ввели систему координат
Найдем координаты интересующих нас точек: , , , .
Теперь найдем координаты векторов: , .
Тогда нужно найти косинус угла между данными векторами: . Тогда .
Значит,. Тогда эти векторы перпендикулярны, а тогда и угол между исходными прямыми – прямой, то есть .
Способ 2. Перенесем вектор параллельно так, чтобы точка совместилась с точкой , получим вектор , тогда найдем угол между и . (См. Рис. 11.)
Рис. 11. Иллюстрация ко второму способу решения
Способ 3. Используем теорему о трех перпендикулярах. Проекцией прямой на плоскость передней грани является прямая , которая перпендикулярна (как диагональ квадрата). (См. Рис. 12.) Значит, исходные прямые перпендикулярны.
Рис. 12. Прямая и ее проекция
Ответ: .
Пример
В правильной треугольной призме , все ребра которой равны , найдите косинус угла между прямыми и .
(См. Рис. 13.)
Рис. 13. Иллюстрация к задаче
Решение. 1. Введем систему координат. (См. Рис. 14.)
Рис. 14. Ввели систему координат
Если сделать выносной рисунок основания призмы, получим уже понятный плоскостной рисунок. (См. Рис. 15.) Тогда мы сможем найти координаты всех интересующих нас точек.
Рис. 15. Выносной рисунок основания призмы
Точка имеет координаты . Точка – . Точка – .
Тогда точка имеет координаты , а точка – .
2. Найдем координаты векторов и :
, .
3. Найдем длины векторов и :
.
.
4. Найдем скалярное произведение векторов и :
5. Найдем косинус угла между прямыми и :
, ,
Ответ: .
Заключение
На этом уроке мы ввели понятие скалярного произведения для пространства, выяснили, что скалярное произведение обладает теми же свойствами и соответствующими формулами, что и для плоскости. Разобрали формулу скалярного произведения через координаты, поняли, как искать угол между векторами через координаты и между прямыми через координаты, не забыв, что в определенных условиях возникает модуль.
То есть если косинус угла между векторами отрицателен, скалярное произведение векторов отрицательно (а мы ищем угол между прямыми), то соответствующий косинус, который тоже будет отрицателен, надо взять по модулю.
Список литературы
- Геометрия. Учебник для 10-11 классов. Атанасян Л.С. и др. 18-е изд. – М.: Просвещение, 2009. – 255 с.
- А.В. Погорелов. Геометрия 11 класс. – М.: Просвещение, 2002.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
- Yaklass.ru (Источник).
- Cleverstudents.ru (Источник).
- Mathematics.ru (Источник).
Домашнее задание
- Определите скалярное произведение векторов и .
- Даны векторы и . Определите, какой угол образован этими векторами.
- Определите косинус треугольника , если даны координаты вершин треугольника: , , .
Как вычислить углы между векторами? :: SYL.ru
При изучении геометрии немало вопросов возникает по теме векторов. Особенные трудности обучающийся испытывает при необходимости найти углы между векторами.
Основные термины
Перед тем как рассматривать углы между векторами, необходимо ознакомиться с определением вектора и понятием угла между векторами.
Вектором называют отрезок, имеющий направление, то есть отрезок, для которого определено его начало и конец.
Углом между двумя векторами на плоскости, имеющих общее начало, называют меньший из углов, на величину которого требуется переместить один из векторов вокруг общей точки, до положения, когда их направления совпадут.
Формула для решения
Поняв, что собой представляет вектор и как определяется его угол, можно вычислить угол между векторами. Формула решения для этого достаточно проста, и результатом её применения будет значение косинуса угла.
Согласно определению, он равен частному скалярного произведения векторов и произведения их длин.
Скалярное произведение векторов считается как сумма помноженных друг на друга соответствующих координат векторов-сомножителей. Длина вектора, или его модуль, вычисляется как квадратный корень из суммы квадратов его координат.
Получив значение косинуса угла, вычислить величину самого угла можно с помощью калькулятора или воспользовавшись тригонометрической таблицей.
Пример
После того как вы разберетесь с тем, как вычислить угол между векторами, решение соответствующей задачи станет простым и понятным. В качестве примера стоит рассмотреть несложную задачу о нахождении величины угла.
Первым делом удобнее будет вычислить необходимые для решения значения длин векторов и их скалярного произведения. Воспользовавшись описанием, представленным выше, получим:
Подставив полученные значения в формулу, вычислим значение косинуса искомого угла:
Это число не является одним из пяти распространённых значений косинуса, поэтому для получения величины угла, придётся воспользоваться калькулятором или тригонометрической таблицей Брадиса.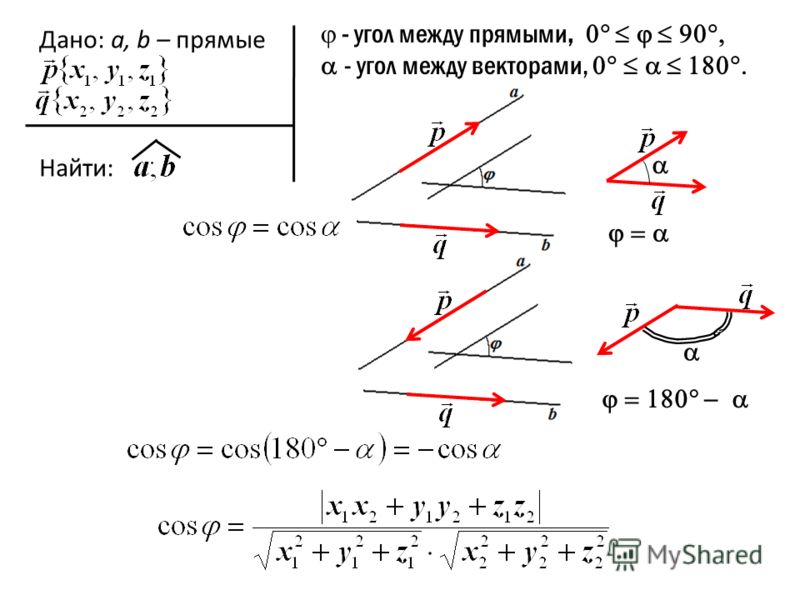
Но перед тем, как получить угол между векторами, формула может быть упрощена, чтобы избавиться от лишнего отрицательного знака:
Итоговый ответ для сохранения точности можно оставить в таком виде, а можно вычислить значение угла в градусах. По таблице Брадиса его величина составит примерно 116 градусов и 70 минут, а калькулятор покажет значение 116,57 градуса.
Вычисление угла в n-мерном пространстве
При рассмотрении двух векторов в трёхмерном пространстве, понять, о каком угле идёт речь гораздо сложнее, если они не лежат в одной плоскости. Для упрощения восприятия можно начертить два пересекающихся отрезка, которые образуют наименьший угол между ними, он и будет искомым. Несмотря на наличие третьей координаты в векторе, процесс того, как вычисляются углы между векторами, не изменится. Вычислите скалярное произведение и модули векторов, арккосинус их частного и будет являться ответом на данную задачу.
В геометрии нередко встречаются задачи и с пространствами, имеющими больше трёх измерений.
Но и для них алгоритм нахождения ответа выглядит аналогично.
Разница между 0 и 180 градусами
Одна из распространённых ошибок при написании ответа на задачу, рассчитанную на то чтобы вычислить угол между векторами, — решение записать, что векторы параллельны, то есть искомый угол получился равен 0 или 180 градусам. Этот ответ является неверным.
Получив по итогам решения значение угла 0 градусов, правильным ответом будет обозначение векторов как сонаправленных, то есть у векторов будет совпадать направление. В случае получения 180 градусов векторы будут носить характер противоположно направленных.
Специфические векторы
Найдя углы между векторами, можно встретить один из особых типов, помимо описанных выше сонаправленных и противоположно направленных.
- Несколько векторов параллельных одной плоскости называются компланарными.
- Векторы, одинаковые по длине и направлению, называются равными.
- Векторы, лежащие на одной прямой, независимо от направления, именуются коллинеарными.
- Если длина вектора равна нулю, то есть его начало и конец совпадают, то его называют нулевым, а если единице, то единичным.
между двумя векторами: формулы, вывод и примеры.
Мы знаем, что любая величина, имеющая не только направление, но и величину, называется вектором. Принимая во внимание, что скалярная величина имеет только величину, но не направление. Векторы могут быть представлены в двух формах, как в двух, так и в трех измерениях.
Угол между векторами равен углу между их хвостами. Этот угол можно найти с помощью точечного или векторного произведения. Единственное, что нужно учитывать, это то, что угол между двумя векторами всегда лежит между 0 и 180 градусами.
В этой статье по математике мы узнаем об угле между двумя векторами и его формуле с использованием перекрестного и скалярного произведений. Мы также решим некоторые связанные примеры для лучшего понимания концепции.
Угол между двумя векторами
Угол, образованный пересечением хвостов векторов, называется углом между двумя векторами.
В случае, если заданные векторы не соединены хвост в хвост, нам нужно сдвинуть один из векторов, чтобы они встретились в точке, используя параллельный сдвиг.
Давайте проверим это на нескольких примерах:
Случай 1: На первом рисунке вектор a не соединен с вектором b, поэтому угол не может быть найден, но когда мы сдвигаем вектор параллельным сдвигом, мы получаем угол \(\theta \) между ними.
Случай 2: Во втором случае показан угол между началом одного вектора и хвостом другого. Это также можно не называть углом между двумя векторами. Нам нужно продлить сдвиг, чтобы получить нужные векторы.
Случай 3: Подобно случаю 2, векторы не соединены хвост к хвосту, и нам нужно сдвинуть вектор b, чтобы получить угол между векторами.
Таким образом, мы можем сделать вывод, что векторы, которые не соединены хвост к хвосту, требуется сдвинуть либо в одном направлении, либо параллельно самому себе, чтобы хвосты встретились.
Формула угла между двумя векторами
Угол между двумя векторами можно найти с помощью двух разных формул: скалярного произведения и перекрестного произведения векторов. Однако чаще всего формула, используемая для нахождения угла между векторами, представляет собой скалярное произведение. 9{-1}\frac{|u\times v|}{|u||v|}\)
Здесь u.v — скалярное произведение, а \(u\times v \) — перекрестное произведение. Кроме того, из приведенной выше формулы мы можем сделать вывод, что перекрестное произведение включает в себя величину в числителе, а скалярное произведение — нет.
Угол между двумя векторами с использованием скалярного произведения
Мы знаем, по определению скалярного произведения \(u.v\ =\ \left|u\right|\left|v\right|\cos\theta\)
Решение этой for \(\cos\theta\)
Разделив обе части на \(\left|u\right|\left|v\right|\) 9{-1}\frac{\left(u.v\right)}{\left|u\right|\left|v\right|}\)
Угол между двумя векторами с помощью векторного произведения
Мы знаем по определению векторного произведения \(u\times v=\left|u\right|\left|v\right|\sin\theta\ \hat{n}\)
Чтобы найти \(\theta\), взять величину с обеих сторон:
\(\left|u\times v\right|=\left|u\right|\left|v\right|\sin\theta\ \left|\hat{n}\right |\)
Так как \(\left|\hat{n}\right|\) является единичным вектором, то величина \(\left|\hat{n}\right|\) равна 1,9{-1}\frac{\left|u\times v\right|}{\left|u\right|\left|v\right|}\)
Узнать о скалярном тройном произведении
Как найти углы между Два вектора
Давайте узнаем, как находить углы между двумя векторами, используя скалярное произведение и векторное произведение в 2D и 3D.
Углы между двумя векторами в двух измерениях
Пусть два вектора в двух измерениях равны a= <1,-2> и b= <-2,1>. Пусть угол между ними равен \(\theta\).
Использование перекрестного и скалярного произведения векторов для нахождения угла между заданными векторами: 9{-1}\frac{3}{5}\)
Мы можем использовать калькулятор, чтобы найти значение \(\theta\)
Итак, \(\theta\ приблизительно36,87\) или, 180 – 36,87.
У нас есть два ракурса, и мы не можем быть уверены, какой из них правильный. Итак, мы можем сделать вывод, что векторное произведение не всегда является правильным выбором для нахождения углов между двумя векторами.
Углы между двумя векторами в трехмерном пространстве
Чтобы найти угол между двумя векторами, рассмотрим пример в трехмерном пространстве. Пусть a = i + 2j + 3k и b = 3i – 2j + k. Давайте сначала вычислим скалярное произведение двух векторов: 9{-1}\frac{\left|a\times b\right|}{\left|a\right|\left|b\right|}\)
Угол между двумя векторами Решенные примеры
Que 1 : Найдите угол между 5i -j + k и i + j -k.
Решение 1:
Пусть вектор a = 5i -j + k и вектор b = i + j -k
Тогда скалярное произведение двух векторов будет определено как:
a.b = (5i -j + k).(i + j -k)
а.б = (5)(1) + (-1)(1) + (1)(-1)
а.б = 5 – 1 – 1 = 5 – 2 = 3 9{\circ}\)
Que 2: Если \(\theta\) угол между двумя векторами a и b такой, что |a · b| = \(|a \times b|\), то что такое \(\theta\)?
Решение 2:
Дано, что \( |a · b| = |a \times b|.\)
Используя определение скалярного и векторного произведения:
\(||a|| b|\cos\theta|=||a||b|\sin\theta\hat{\ n}|\)
Так как \(\hat{\ n}\) является единичным вектором, то его величина равна 1
\(|a||b|\cos\theta=|a||b|\sin\theta\) 9{\circ}\)
Мы надеемся, что приведенная выше статья поможет вам понять и подготовиться к экзамену. Оставайтесь с нами в приложении Testbook, чтобы получать больше обновлений по связанным с математикой темам и другим подобным предметам.