Найди все решения неравенства: ГДЗ учебник по математике 4 класс Петерсон. 1 урок. Решение неравенства Номер 7

ГДЗ Найдем все решения неравенства. Упр 737 параграф 42 Алгебра 10-11 класс Алимов – Рамблер/класс

ГДЗ Найдем все решения неравенства. Упр 737 параграф 42 Алгебра 10-11 класс Алимов – Рамблер/класс

Интересные вопросы

Школа

Подскажите, как бороться с грубым отношением одноклассников к моему ребенку?

Новости

Поделитесь, сколько вы потратили на подготовку ребенка к учебному году?

Школа

Объясните, это правда, что родители теперь будут информироваться о снижении успеваемости в школе?

Школа

Когда в 2018 году намечено проведение основного периода ЕГЭ?

Новости

Будет ли как-то улучшаться система проверки и организации итоговых сочинений?

Вузы

Подскажите, почему закрыли прием в Московский институт телевидения и радиовещания «Останкино»?

Кто-нибудь уже решал? Требуется найти все решения неравенства, принадлежащие промежутку (-π, 2π):

1) tg х ≥ 1;

3) tg х < -1;
4) tg х ≥ — √3.
 

ответы

Добрый) Вот, недавно разбирали)

ваш ответ

Можно ввести 4000 cимволов

отправить

дежурный

Нажимая кнопку «отправить», вы принимаете условия  пользовательского соглашения

похожие темы

ЕГЭ

9 класс

11 класс

Химия

похожие вопросы 5

Алгебра. 9 класс. Алимов Ш. А. Параграф 9. Упражнение №116. Провсти доказательство

Даровчики. Помощь нужна с алгеброй…никак решить не могу(((
Доказать, что —
(Подробнее…)

ГДЗАлгебраАлимов Ш.А.Школа9 класс

Когда скорость изменения функции будет наибольшей или наименьшей? Алгебра 10-11 класс Колмогоров Упр 308

 Совсем я в точных науках не сильна) Кто поможет?) Найдите значения аргумента из промежутка [-2; 5], при которых скорость изменения (Подробнее.

..)

ГДЗ11 классКолмогоров А.Н.Алгебра

Почему сейчас школьники такие агрессивные ?

Читали новость про 10 классника который растрелял ? как вы к этому относитесь 

Новости10 классБезопасность

ГДЗ Тема 21 Физика 7-9 класс А.В.Перышкин Задание №475 В обоих случаях поплавок плавает. В какую жидкость он погружается глубже?

Привет. Выручайте с ответом по физике…
Поплавок со свинцовым грузилом внизу опускают
сначала в воду, потом в масло. В обоих (Подробнее…)

ГДЗФизикаПерышкин А.В.Школа7 класс

ГДЗ Тема 21 Физика 7-9 класс А.В.Перышкин Задание №476 Изобразите силы, действующие на тело.

Привет всем! Нужен ваш совет, как отвечать…
Изобразите силы, действующие на тело, когда оно плавает на поверхности жидкости. (Подробнее…)

ГДЗФизикаПерышкин А.В.Школа7 класс

Конспект урока по математике «Решение неравенств» 3 класс

Математика

3 класс

Тема: Решение неравенств (Урок сообщения нового знания)

Цели: 1. Ввести понятие «решение неравенства».

2. Познакомиться со способом решения неравенств путём подбора значений переменной.

4. Осуществлять проверку вычислений на основе знания о взаимосвязи действий сложения и вычитания.

5. Решать на новом числовом концентре текстовые задачи изученного вида.

6. Систематизировать, повторять и закреплять ранее изученное.

7. Развивать умения решать занимательные и стохастические задачи.

Оборудование:

1. Учебник математики для 3 кл., авторы Демидова Т.Е., Козлова С.А., Тонких А.П.

2. Конверты с заданиями.

3. Карточки с домашним заданием.

4. Солнышка для рефлексии.

Тип урока: урок сообщения нового знания.

Этапы урока

Ход урока

Формирование УУД,

I. Актуализация знаний.

1. Организационный момент.

Психологический настрой детей на урок. 

-Сегодня чудесный день. Улыбнитесь! Скажите друг другу добрые слова!

Один мудрец однажды сказал: «Не для школы, а для жизни мы учимся!»

-А для чего вы изучаете такую сложную науку как математика?

Высказывания детей

— Сегодня мы продолжим исследовать и постигать тайны этой науки, такой сложной, но ужасно интересной.

— Каким Вы хотите видеть наш урок?

-А Вы поможете мне его провести?

-Ну, что ж, ребята, в добрый путь! Я жду от вас красивых мыслей!

Познавательные УУД

Развиваем умения:

1. Ориентироваться в своей системе знаний: самостоятельно предполагать, какая информация нужна для решения учебной задачи в один шаг.

II. Открытие нового знания (знакомимся…).

-Сегодня на уроке нам предстоит совершить открытие, выдвинуть гипотезу и постараться найти правильное решение.

Парно-групповая работа.

1. Задание

Цель работы:

– создание проблемной ситуации и выдвижение гипотез.

— Сегодня мы с вами ребята отправимся в путешествие. Но чтобы отправится нам нужны билеты. А билеты в конвертах с заданием, которые лежат у вас на столах. А в билете потайное слово ребята, это тема урока.Откройте и достаньте карточки.

— Обсудите в парах и скажите, что вы видите? (математические записи, выражения)

— Подумайте и разделите данные математические записи на две группы.

Неравенства Равенства

0

20 18 51 : х = 3 (х = 17)

7

х  х + 7 = 42 (х = 35)

— А что такое равенство? (Выражение со знаком =)

— А что такое неравенство? (Выражение со знаком )

— Посмотрите группу равенств и давайте найдем чему равны значения х в каждом выражении?

— Значит, что же такое равенство? (Выражение, при котором переменная х имеет только одно значение)

— А что же такое переменная? (Неизвестная)

— А теперь, посмотрите группу неравенств. Найдите лишнее неравенство (х

—Почему? (Содержит неизвестную переменную)

2. Задание

— А как вы думаете, мы можем найти, чему равна неизвестная переменная?

— Значит чем мы сегодня на уроке познакомимся? (Научимся решить неравенства)

— Цель нашего урока: научиться решить неравенства.

— Для этого что мы должны сделать

— Давайте откроем тетради и напишем сегодняшнее число и тему урока.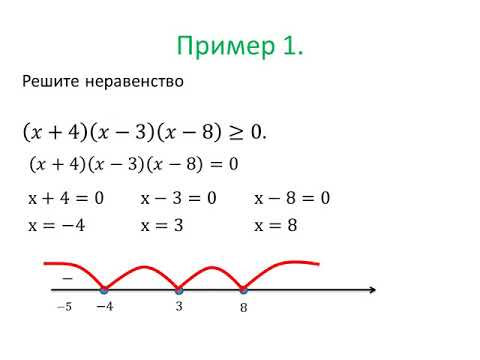

— Вот и нашли ребята тему нашего урока, значит билет у нас есть можем идти дальше.

— И I наша станция «Станция юных натуралистов»

3. Задание.

— На поляне выросло 6 грибов. Маша собралась идти в лес за грибами.

— Могла ли Маша не найти ни одного гриба? (Да)

— А могла ли Маша найти больше 6 грибов, например, 7? (Нет, так как на поляне всего 6 грибов выросло).

— А сколько грибов может оказаться в Машиной корзине? (0,1,2,3,4,5,6)

— Как вы думаете, чем являются эти значения для нашего неравенства. (Решением)

— А теперь давайте посмотрим наше неравенство х

— Как вы думаете, какое число можно подставить вместо х, чтобы неравенство было верным. (0, 1, 2, 3, 4, 5)

— Что мы нашли? (нашли решение неравенств)

— Как нашли? (методом подбора)

— Данное неравенство сколько решений имеет? (6)

— Давайте сами попробуем сформулировать правило, что же называется решением неравенства?

Значение переменной, при котором неравенство будет верным, называют его решением. Например: 0, 1, 2, 3, 4, 5 – это решение неравенства х

— А если вместо переменной х подставить число 6, наше неравенство будет верным? (Нет)

— Значит число 6 и все числа больше 6 решениями этого неравенства не являются.

— Решение неравенства х

Задание.

Дано числовое множество от 0 до 10.

Посмотрите на экран, сколько решений имеет следующее неравенства?

х

х

— А если, х (только одно решение, х = 0)

— А теперь попробуйте сами назовите неравенство, при котором переменная не имеет решения? (х

— Значит, что же такое решить неравенство? Давайте попробуем сформулировать правило.

Решение неравенств с переменной – значит найти все его решения (множество решений) или доказать, что их нет.

2. — отбирать необходимые для решения учебной задачи источники информации среди предложенных учителем словарей, энциклопедий, справочников.

3. добывать новые знания: извлекать информацию, представленную в разных формах (текст, таблица, схема, иллюстрация и др. ).

4. перерабатывать полученную информацию: сравнивать и группировать математические факты и объекты.

5. делать выводы на основе обобщения умозаключений.

III. Физкультминутка.

IV. Первичное закрепление.

Парно-групповая работа.

Задание № 1, с. 68. Задача на экране.

А далее у нас ребята II станция «Станция океанарий»

— Сколько фотографий сделали мальчики? (Несколько, т.е. неизвестно)

— А что нам известно? (то, что в альбоме из 16 листов остались свободные места)

— Т.е. фотографий было больше 16 или меньше 16?

— Лика нам уже составила неравенство х

— При каких значениях переменной х это неравенство будет верным?

— А при каких будет неверным?

— Как вы думаете, какие значения переменной будут решениями этого неравенства?

— Попробуйте теперь сами сформулировать правило, что значит решить неравенство, подставив значения переменной х из данного задания.

— Откроем учебники на стр. 68 и проверим.

— Дома это правило еще раз прочитаете и запомните.

6 — преобразовывать информацию из одной формы в другую:

— представлять информацию в виде текста, таблицы, схемы.

7 – переходить от условно-схематических моделей к тексту.

Регулятивные УУД:

Развиваем умения:

1 – самостоятельно формули-ровать цели урока после

предварительного обсуждения;

V. Закрепление изученного

III станция «Станция планетарий»

1. Самостоятельная работа.

79, 42, 18, 8, 23

Даны неравенства, а ключи к этим неравенствам скрылись у наших звездочек. Напишите рядом с неравенством только решения неравенства.

— А теперь, давайте поменяемся листочками и сделаем проверку. Если все 5 заданий правильно ставим оценку 5, если 4 правильных ставим оценку 4, если 3 правильных ставим 3, ну уж если меньше 3 то тут вам уж надо еще раз постараться.

2. Задание № 2, с. 68

— Напишите только те числа, которые являются решениями данного неравенства.

Задание № 3, стр. 68

3. Задание. Составление задач.

— Например, у меня на руках 9 конфет. Сколько конфет я могла съесть? (0, 1, 2, 3, 4, 5, 6, 7, 8, 9)

— А теперь сами попробуйте составить задачу.

4. Решение задач.

А теперь давайте еще раз отправимся на поляну. Но на этот раз грибы нам уже собрали и отправили с заданиями. Посмотрите задания. Обсудите в парах и давайте попробуем их решить.

1. Напишите все значения переменной х при котором неравенство будет верным: х

2. Подберите и напишите 3 решения неравенства у 134.

2 – совместно с учителем обнаруживать и формулировать учебную проблему;

3 – составлять план решения отдельной учебной задачи

совместно с классом;

4 – работая по плану, сверять

свои действия с целью и, при необходимости, исправлять ошибки с помощью класса;

5 – в диалоге с учителем и другими учащимися учиться вырабатывать критерии оценки и определять степень успешности выполнения своей работы и работы всех, исходя из имеющихся критериев.

ТОУУ

Коммуникативные УУД

Развиваем умения:

1.- доносить свою позицию до других: оформлять свои мысли в устной и письменной речи (выражение решения учебной задачи в общепринятых формах) с учётом своих учебных речевых ситуаций;

2 – доносить свою позицию до других: высказывать свою точку зрения и пытаться её обосновать, приводя аргументы;

3 – слушать других, пытаться принимать другую точку зре-ния, быть готовым изменить

свою точку зрения;

ТОУУ

4 – читать про себя тексты учебников и при этом: ставить

вопросы к тексту и искать ответы; проверять себя;

отделять новое от известного;

выделять главное; составлять план;

5 – договариваться с людьми: выполняя различные роли в группе, сотрудничать в совместном решении проблемы (задачи).

Личностные результаты:

1 – придерживаться этических норм общения и сотрудничества при совместной работе над учебной задачей;

VI. Итог урока.

— Ну что ж ребята, вот мы и вернулись с путешествия. С каким же настроением вы вернулись?

— Что нового вы узнали сегодня на уроке?

— Чему научились?

— Что у вас получилось лучше всего?

— Что вызвало затруднение?

— Над чем ещё надо поработать?

— Вот у нас скоро весна ребята, солнышко светит все ярче и ярче и у вас на столах лежат солнышка, дорисуйте пожалуйста ротик солнышка с каким настроением вы уходите от данного урока.

2. – в созданных совместно с педагогом на уроке ситуациях общения и сотрудничества, опираясь на общие для всех простые правила поведения, делать выбор, как себя вести.

VII. Рефлексия

VIII. Домашнее задание.

1. Выпишите только те неравенства, одним из решений которых будет число 634.

1. х 15

2. y

3. z 634

4. 965 k

5. 254 n

6. m

1. Стр. 69 № 4

2. Составьте неравенство и подберите 3 решения этого неравенства.

Предварительное вычисление алгебры — Поиск всех решений уравнения неравенства

спросил 9 лет, 4 месяца назад

Изменено 9 лет, 4 месяца назад

Просмотрено 1к раз

$\begingroup$

У меня есть следующее неравенство, для которого мне нужно найти все решения: 92-8x+20=0$). Используя факторную теорему, вы можете угадать решение с коэффициентом $20$, а затем использовать длинное деление для нахождения двух других корней. Но как узнать, больше ли неравенство корня (т. е. $>$) или меньше корня (т. е. $<$)? Это то, что вам нужно просто угадать и проверить? Или есть другой способ?

• алгебра-предварительное исчисление

$\endgroup$

1

$\begingroup$

Обратите внимание, что обе стороны делят:

$$2x(x-2)(x+2)>5(x-2)(x+2)$$

что приводит к неравенству:

$$( 2x-5)(x-2)(x+2)>0$$

Таким образом, корни равны $-2,2,$ и $\frac{5}{2}$.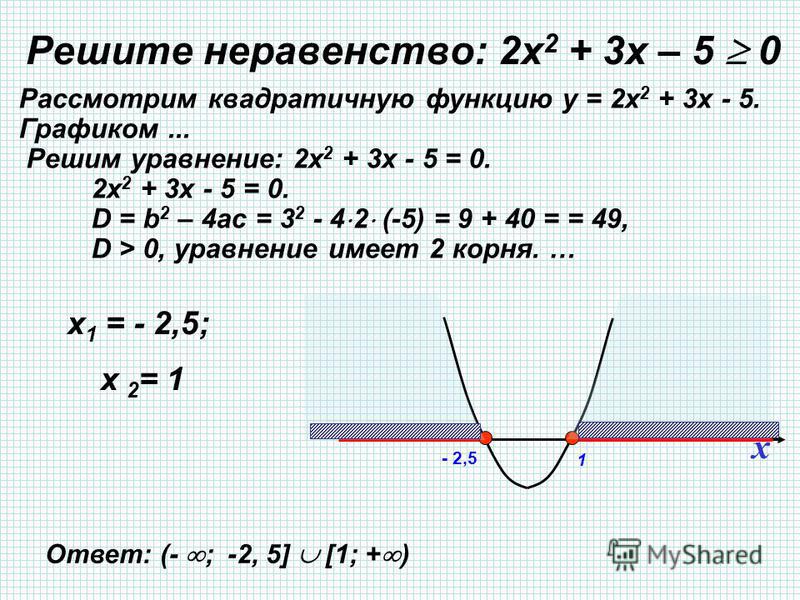 Поскольку это положительная кубическая, мы знаем, что она стремится к бесконечности, когда $x$ становится большим, поэтому мы должны иметь $x>\frac{5}{2}$ в качестве возможных решений. Далее заметьте, что ни один из корней не является двойным, поэтому полином будет менять знак в каждом из них. Это означает, что оно отрицательно в диапазоне $(2,\frac{5}{2})$, положительно в диапазоне $(-2,2)$ и отрицательно в диапазоне $(-\infty,-2). )$. Итак, ответ:

$$(-2,2)\cup(\frac{5}{2},\infty)$$

Заметьте, я сделал примерно то, что вы рекомендовали, за исключением того, что разложение на множители упростило поиск корней, и я не нужно было проверять какие-либо точки из-за формы кубического многочлена без двойных корней.

$\endgroup$

$\begingroup$

Как только вы нашли корни многочлена, вы можете записать неравенство в виде: $$(x-a)(x-b)(x-c)>0,$$ с $a\leq b \leq c$. Реальная линия разделена на 4 интервала следующим образом: $$\mathbb R=(-\infty,a] \cup (a,b]\cup (b,c]\cup (c,+\infty). $$ Теперь все, что вам нужно сделать, это проверить знак полинома в этих четырех областях.0005

$\endgroup$

3

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя электронную почту и пароль

Опубликовать как гость

Электронная почта

Требуется, но никогда не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie

.

Уравнения и неравенства — Решение неравенств

Решая уравнения, мы нашли все значения переменной, которые делают уравнение верным. Точно так же мы можем решить неравенства, чтобы найти все значения переменной, которые делают неравенство верным. Идея состоит в том, чтобы получить переменную саму по себе по одну сторону от знака неравенства, чтобы мы могли легко увидеть решения неравенства.

Если вам нужно, вы всегда можете переманить его с помощью горячих крыльев. Почему-то они любят  тех.

Чтобы изолировать переменную, мы делаем почти то же самое, что и для решения уравнений. Во-первых, если мы добавим или вычтем одну и ту же константу из обеих частей неравенства, мы получим эквивалентное неравенство. Мы также можем добавить или вычесть одинаковое количество копий переменной с обеих сторон неравенства. Все эти вещи кажутся устрашающе знакомыми, верно? Добро пожаловать в Панксатони.

Пример задачи

Каковы решения неравенства x + 2 < 2?

Чтобы решить эту проблему, мы вычтем 2 из обеих частей неравенства.

x + 2 < 2
x < 2 – 2
x < 0

Это дает нам x < 0 как решение неравенства. Решения во множественном числе , помните, потому что x может быть любым отрицательным. Как твой постоянно ворчливый дядя Мелвин. Какова его сделка?

Мы также можем представить решения, нарисовав изображение числовой линии, которое представляет неравенство x < 0.

Пример задачи

Каковы решения задачи 3 x < 9?

Забавный факт: мы также можем умножить или разделить обе части неравенства на одно и то же положительное число. Вы нас знаете — мы сделаем все, потому что можем. В этом случае давайте разделим обе стороны на 3, чтобы получить x .

3 x ÷ 3 < 9 ÷ 3
x < 3

Таким образом, наш набор решений равен x < 3: все, что меньше 3, подойдет.

Будьте осторожны: Мы можем умножить или разделить обе части неравенства на одно и то же положительное число. Однако, если мы умножим обе части неравенства на отрицательное число , произойдут странные вещи, которые мы вам сейчас продемонстрируем. Здесь вот-вот начнется какой-то паранормальный бизнес.

Вот пример с числами вместо переменных, который более наглядно иллюстрирует происходящее. Выберите свое любимое неравенство между двумя последовательными целыми числами. Мы будем использовать 5 < 6.

Мы знаем, что 5 меньше 6, потому что 5 находится слева от 6 на числовой прямой. Вы также знаете эту информацию, потому что до вашего дня рождения осталось всего 5 месяцев вместо 6. Почти здесь. Ура!

Обратите внимание, что 5 ближе к 0, чем 6. Поскольку и 5, и 6 находятся на положительной стороне числовой прямой, то число, которое ближе к 0, меньше. Если мы умножаем каждое из чисел 5 и 6 на -1, мы отражаем их через 0 на числовой прямой, поэтому 5 отправляется в -5, а 6 отправляется в -6. Перелет включен, все расходы оплачены. Тоже хорошо. Им действительно нужно было уйти.

Обратите внимание, что -5 все еще ближе к 0, чем -6. Поскольку сейчас мы смотрим на два числа на отрицательной стороне числовой прямой, то число, которое ближе к 0, на

больше . Когда мы сравниваем -5 и -6, мы видим, что -5 > -6. Судя по всему, -5 съел больше, чем -6 во время этого их небольшого отдыха.

Мораль этой истории такова: если мы умножаем обе части неравенства на отрицательное число, нам также нужно поменять направление знака неравенства. Это достаточно важно, чтобы сказать еще раз: если мы умножаем или делим обе части неравенства на отрицательное число, нам также нужно изменить направление знака неравенства. На самом деле достаточно важно сказать в третий раз, но мы чувствуем, что теряем тебя, поэтому остановимся.

Еще проще понять, что происходит, если одно число отрицательное, а другое положительное. Мы знаем, что -2 < 1. Если мы умножим обе части этого неравенства на -2, мы отправим -2 в 4, а 1 в -2.

Умножение значения на отрицательное число отражает это значение через 0 на числовой прямой. Следовательно, нам также необходимо изменить направление неравенства. Вот так.

-2 < 1
-2(-2) < 1(-2)
4 > -2

Видите, как мы заменили этот символ «<" на ">«? В результате получается неравенство 4 > -2.

Теперь, когда у нас есть представление о том, что происходит, мы вернем переменные и попробуем.

Пример задачи

Решите неравенство — x < 3.

Путь рок-звезды:

Умножьте обе части неравенства на -1 и измените направление неравенства.

x > -3

Путь поклонницы (также известный как Неправильный путь):

Если мы умножим обе части неравенства на -1, но забудем поменять направление неравенства, вот что мы получим получить:

x < -3

По внешнему виду мы должны понять, что здесь что-то не так. Если все значения меньше -3 являются решениями, то -4 должно быть решением.