Скалярное произведение векторов | После уроков
Урок геометрии в 9 классе
Столяренко Е.М., учитель математики КГУ ОШ№66, г.Алматы, Республика Казахстан
Цели урока:
— знать формулы для определения координат вектора, длины вектора;
— уметь применять формулы к решению задач;
— понять способ нахождения скалярного произведения векторов и его назначение;
— охватить вниманием всех учащихся, оценить работу каждого ученика.
Форма организации: индивидуальная, коллективная, самостоятельная, работа в парах.
Дидактическое обеспечение: презентация, учебник, раздаточный материал.
Ход урока:
I. Организационный момент.
Психологический настрой учащихся.
II.
Деление учащихся на группы: учащиеся 1-го варианта проводят устную разминку. На интерактивной доске задание: закончить предложение или ответить на вопрос:
1) Скаляр — это…
2) Вектор — это…
3) Модуль вектора — это…
4) Равные векторы — это…
5) Сумму векторов можно найти…
6) Произведение вектора на число — это…
7) Ортогональные векторы — это…
8) Сонаправленные векторы — это…
9) Равны ли векторы, если их длины равны?
10) Какая теорема позволяет найти длину вектора?
Учащиеся 2-го варианта выполняют задание самостоятельно, проверяем правильность решения через интерактивную доску взаимопроверкой.
Карточка №1: Найдите координаты вектора АВ, если А(12;5) и В(6;1).
Трое учащихся работают у доски по карточкам №2, №3, №4.
Карточка№2: Векторы АВ и СD равны, причём А(-15;9), В(6;-4), D(0;-1). Найдите координаты начала вектора СD.
Карточка №3
: ОА1(1;2) и А1А2(-2;3). Найдите координаты точкиА2. Как называется вектор ОА1?
Найдите координаты точкиА2. Как называется вектор ОА1?Карточка №4: Найдите абсолютную величину вектора АВ, координаты векторов 4АВ и -6АВ, если А(7;-3), В(4;9).
Таким образом, каждый ученик получает первую оценку по 5-бальной шкале (за устный ответ, индивидуальное решение или решение в тетради задачи).
Проверку знаний учащихся завершает мини-тест на два варианта. Проверку проводят учащиеся с помощью взаимоконтроля и критериев оценивания, которые показываются через интерактивную доску.
Мини-тест
Запиши решение и обведи ответ. Ф.И.——————————————
Вариант 1
| №1. Дано: А(5;1) , В(4;-9) Найдите координаты вектора АВ | Ответы: |
| а) (9;-8) б) (-1;10) в) (6;-8) г) (-1;10) | |
| №2. Найдите длину вектора АВ, если А(5;1) , В(4;-9) | Ответы: |
| Решение: | а) 1 б) 100 в) 10 г) -5 |
№3.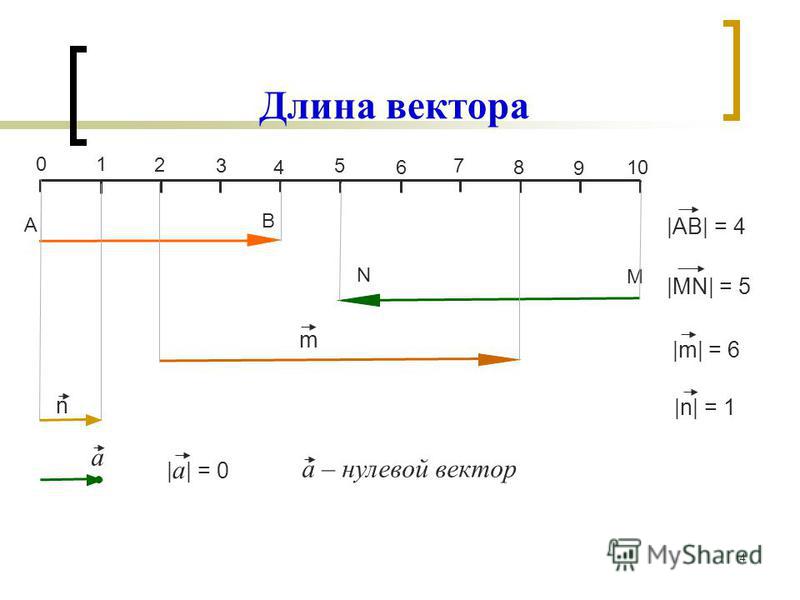 Если а(2;-7), в(-5;4), то -3а+4в=? Если а(2;-7), в(-5;4), то -3а+4в=? | Ответы: |
| Решение: | а) (-3;3) б)(-26;37) в) (17;-11) г) (-1;6) |
Мини-тест
Запиши решение и обведи ответ. Ф.И.——————————————
Вариант 2
| №1. Дано: С(7;-5) , D(1;3) Найдите координаты вектора CD | Ответы: |
| Решение: | а) (-6;8) б) (8;-2) в) (2;4) г) (6;-8) |
| №2. Найдите длину вектор CD , если C(7;-5) ,D(1;3) | Ответы: |
| Решение: | а) 1 б) 100 в) 10 г) -5 |
| №3. Если а(-3;5), b(2;1) , то -3а+4в=? | Ответы: |
| Решение: | а) (-3;3) б)(-26;37) в) (17;-11) г) (-1;6) |
III. Формирование новых знаний
Учащиеся получают карточку-консультацию по вариантам и по образцу выполняют предложенное задание. Затем обмениваются полученными знаниями и делают выводы.
Затем обмениваются полученными знаниями и делают выводы.
Скалярное произведение векторов
Скалярное произведение векторов — это число, равное сумме произведений соответственных координат. Если а(а1;а2) и b(b1;b2), то а b= a1b1+a2b2. Запомни эту формулу!
Пример:
Дано: а=(8;4) b=(1;5) Найти: а b.
Решение: а ∙ b = a
Найди сам скалярное произведение векторов а(2;4) и b(5;3). Решение запиши в тетрадь.
IV. Домашнее задание: №168, 171, 175(3;4), повторить значения тригонометрических функций некоторых углов (30˚,45˚,60˚,90˚), знать формулы нахождения скалярного произведения векторов, уметь находить угол между векторами.
V. Итог урока.
Источник: конспекты-уроков. рф
рф
Дидактический материал по геометрии 9 класс | Материал для подготовки к ЕГЭ (ГИА) по геометрии (9 класс) на тему:
Дидактический материал по геометрии 9 класс
Составила
учитель математики
МБОУ СОШ №3
станицы Березанской
Выселковского района
Коломиец С.В.
Декабрь 2015
1.Скалярное произведение векторов.
2.Простейшие задачи в координатах
3. Геометрические задачи
Скалярное произведение векторов.
- Вычислите скалярное произведение векторов а и в, если а = 5, в = 4, а угол
между ними 120°.
- (самостоятельно). Вычислите скалярное произведение векторов а и в, если а = 7,
в = 5, а угол между ними 135°.
3. Вычислите скалярное произведение векторов m {3; -2} , n{-2; 3}
4. (самостоятельно). Вычислите скалярное произведение векторов а {-4; 5},
в{-5; 4}.
5. Найдите угол между ненулевыми векторами а{ х; у} и в{ –у; х} .
6. (самостоятельно). Найдите угол между ненулевыми векторами а {х; -у} и
в{у; х}.
7. Вычислите косинус угла между векторами p и q , если p {3; -4} и q{ 15; 8}.
8. (самостоятельно). Вычислите косинус угла между векторами а и в,
если а{ -12; 5} в{3; 4}.
9. Даны вектора p {2; -3} q{х; -4 }при каких значениях х векторы
перпендикулярны?
10. (самостоятельно). Даны вектора а{3; у} и в {2; -6}, При каких значениях у
векторы перпендикулярны?
11. Дан прямоугольный треугольник АВС, где угол С = 90° , тангенс угла В равен
¾.Известно, что ВС = 8см. Найдите АВ?
12. (самостоятельно). Дан прямоугольный треугольник АВС, где угол С = 90°,
косинус угла В равен 4/5. Известно, что АВ = 10см. Найдите АС?
Простейшие задачи в координатах
Вариант 1.
1.Найдите координаты середины отрезка АВ, если А (-2;3), В(6;-3).
2.Найдите длину отрезка ЕН, если Е (-3;8), Н (2:-4).
3.Найдите длину вектора с, равного a + в, если а{6; 0}, в{0;-8}.
4. Найдите длину вектора а{-12;5}.
5.Найти координаты вектора АВ, если А(2;5),В(-3;4)
6.Принадлежит ли точка А (-6; 2) графику функции y = — 0,5x?
7.Функция задана уравнением у = 2х – 3. Какая линия служит графиком этой функции?
8. На окружности радиуса 7 см даны точки А и В, расстояние между которыми равно
13см. Лежит ли центр окружности на прямой АВ?
9. Вершины треугольника АВС имеют следующие координаты: А(8;- 3), В(5;1),
С(12;0). Докажите, что
9 класс. Вариант 2.
1.Найдите координаты середины отрезка СД, если С (3; -4), Д(-3; 6).
2.Найдите длину отрезка КВ, если К (-6; -3), В(2; 3).
3.Найдите длину вектора с, равного а + в, если а{-12; 0}, в{0;5}.
4. Найдите расстояние между двумя точками А(-1;3) и В(2;-1)
5. Принадлежит ли точка В (2; -8) графику функции у = — 4х?
6. Функция задана уравнением у = 5 – х. Какая линия служит графиком этой
функции?
7. Какой фигурой является множество точек, равноудалённых от данной точки?
8. Найдите координаты вектора СД, если С(-1;6), Д(3; -2)
9. Вершины четырёхугольника АВСД имеют следующие координаты: А(-3; -1),
В(1; 2), С(5; -1), Д(1; — 4). Докажите, что этот четырёхугольник — ромб.
Геометрические задачи
Вариант № 1
- Лежит ли точка А (2; -1) на окружности, заданной уравнением (х – 2)2 + (у — 3)2 = 25?
- Длина вектора а равна 2, а вектор . Найдите скалярное произведение
а∙в, если векторы одинаково направленные.
3. В параллелограмме ABCD сторона , . Найдите площадь
параллелограмма, если диагональ .
- В равнобедренной трапеции средняя линия равна 4, а диагональ – 5.
 Найдите высоту
Найдите высоту
трапеции.
- Один из катетов прямоугольного треугольника равен , другой в 3 раза
меньше гипотенузы. Найдите гипотенузу треугольника.
5. В трапеции АВСД боковые стороны АВ и СД равны.
а) Постройте отрезок СА1, на который отображается сторона АВ
при параллельном переносе на вектор ВС.
б) Найдите площадь треугольника А1СД, если АД = 10см, ВС = 4см, АВ = 6см.
Вариант № 2.
1. Лежит ли точка А (2; -1) на прямой, заданной уравнением 2х – 3у =7?
2. Длина вектора а равна 3, а вектор . Найдите скалярное
произведение а∙в , если векторы противоположно направленные.
3. В параллелограмме ABCD сторона , . Найдите площадь
параллелограмма, если диагональ .
4.В равнобедренной трапеции средняя линия равна 12, а диагональ – 13. Найдите высоту трапеции.
5. В прямоугольном треугольнике гипотенуза равна , а один из катетов в
2 раза больше другого. Найдите наибольший катет треугольника.
Найдите наибольший катет треугольника.
6. Точка М – середина стороны АС треугольника АВС.
а) постройте отрезок МВ1, на который отображается сторона АВ при
параллельном переносе на вектор АМ.
б) Найдите периметр треугольника МДС, Д – точка пересечения
отрезков ВС и МВ1,если периметр треугольника АВС равен 12см.
Нахождение величины и угла вектора равнодействующей силы — Криста Кинг Математика
Шаги для нахождения величины и угла равнодействующей силы
Когда нам даны два вектора с одинаковой начальной точкой, разной длины и направленные в разные стороны, мы можем рассматривать каждый из них как силу. Чем длиннее вектор, тем большую силу он притягивает в своем направлении.
Часто нам нужно найти суммарную силу двух векторов, которая будет третьим вектором, уравновешивающим силу и направление двух других. Думайте о результирующем векторе как о величине силы и направлении, в котором вам придется тянуть, чтобы нейтрализовать силу двух других векторов.
Привет! Я Криста.
Я создаю онлайн-курсы, чтобы помочь вам в учебе по математике. Прочитайте больше.
Чтобы определить этот третий вектор, нам нужно найти
его величину (его длину), которая будет силой в Ньютонах Н, и
его угол , от положительного направления ??? х???-ось.
Чтобы найти модуль и угол равнодействующей силы, мы
создаем векторных уравнений для каждой из заданных сил 9\circ-\arctan{\frac{|y|}{|x|}}???
Нахождение модуля и угла результирующего вектора силы по двум векторам силы
Пройти курс
Хотите узнать больше об исчислении 3? У меня есть пошаговый курс для этого. 🙂
Учить больше
Векторы сил в первом и втором квадрантах
Пример 9\circ}\ \жирный j???
???F_2=-193,19\ \жирный i+51,76\ \жирный j???
???F_2=\langle-193. 19,\ 51.76\rangle???
19,\ 51.76\rangle???
Чем длиннее вектор, тем большую силу он притягивает в своем направлении.
Сложим наши силы, чтобы найти векторное уравнение равнодействующей силы.
???F_R=F_1+F_2???
???F_R=38,82\ \жирный i+144,89\ \жирный j-193,19\ \жирный i+51,76\ \жирный j???
???F_R=-154,37\ \жирный i+196,65\ \жирный j??? 9\ круг???.
Обратите внимание, как мы построили векторные уравнения для ???F_1??? и ???F_2??? в этом последнем примере.
Когда мы измеряем угол вектора, мы всегда измеряем его от горизонтальной оси, что означает, что мы будем измерять углы векторов в первом и четвертом квадрантах от положительного направления горизонтальной оси, но измерять углы векторы во втором и третьем квадрантах от отрицательного направления горизонтальной оси. 9\ круг???.
И мы всегда будем рассматривать угол между вектором и горизонтальной осью как положительный угол. \circ} \\жирный j???.
\circ} \\жирный j???.
Получите доступ к полному курсу Calculus 3
Начать
Изучайте математикуКриста Кинг математика, учитесь онлайн, онлайн-курс, онлайн-математика, исчисление 3, исчисление 3, исчисление 3, исчисление iii, векторное исчисление, сила, векторы силы, многомерное исчисление, многомерное исчисление, многомерное исчисление, многомерный расчет, векторный расчет, величина, величина равнодействующей силы, угол равнодействующей силы
r — Разбить вектор на подвекторы с постоянной длиной и постоянным перекрытием
Я хочу разбить вектор на набор подвекторов так, чтобы выполнялись следующие условия:
все подвекторы должны иметь постоянную длину
все подвекторы должны перекрываться с постоянной длиной перекрытия
Мне нужна модификация:
########Функция блокировки#######################
блоки <- функция (len, ov, n) {
начинает <- уникальный(sort(c(seq(1, n, len), seq(len-ov+1, n, len))))
концы <- pmin(начала + len - 1, n)
# обрезать начинается и заканчивается до первых элементов num
число <- соответствует (n, заканчивается)
голова (data. frame (начало, конец), число)
}
########Перемещение блока#############
vec = 1:17 # список или вектор
len = 8 # длина подвектора
ov = потолок(len/2) # длина перекрытия
b <- блоки (len, ov, length (vec))
with (b, Map (функция (i, j) vec [i: j], начинается, заканчивается))
frame (начало, конец), число)
}
########Перемещение блока#############
vec = 1:17 # список или вектор
len = 8 # длина подвектора
ov = потолок(len/2) # длина перекрытия
b <- блоки (len, ov, length (vec))
with (b, Map (функция (i, j) vec [i: j], начинается, заканчивается))
, который производит это:
[1] 1 2 3 4 5 6 7 8 # подвектор 1
[2] 5 6 7 8 9 10 11 12 # подвектор 2
[3] 9 10 11 12 13 14 15 16 # подвектор 3
[4] 13 14 15 16 17 # подвектор 4: необходимо изменить перекрытие для достижения постоянной длины
Что я хочу
Я хочу, чтобы последний подвектор, который не достигает указанной длины, имел такое перекрытие:
новое_перекрытие = старое_перекрытие + (старая_длина - новая_длина)
новое_перекрытие — длина перекрытия последнего подвектора, длина которого меньше установленной длины.


 Найдите высоту
Найдите высоту 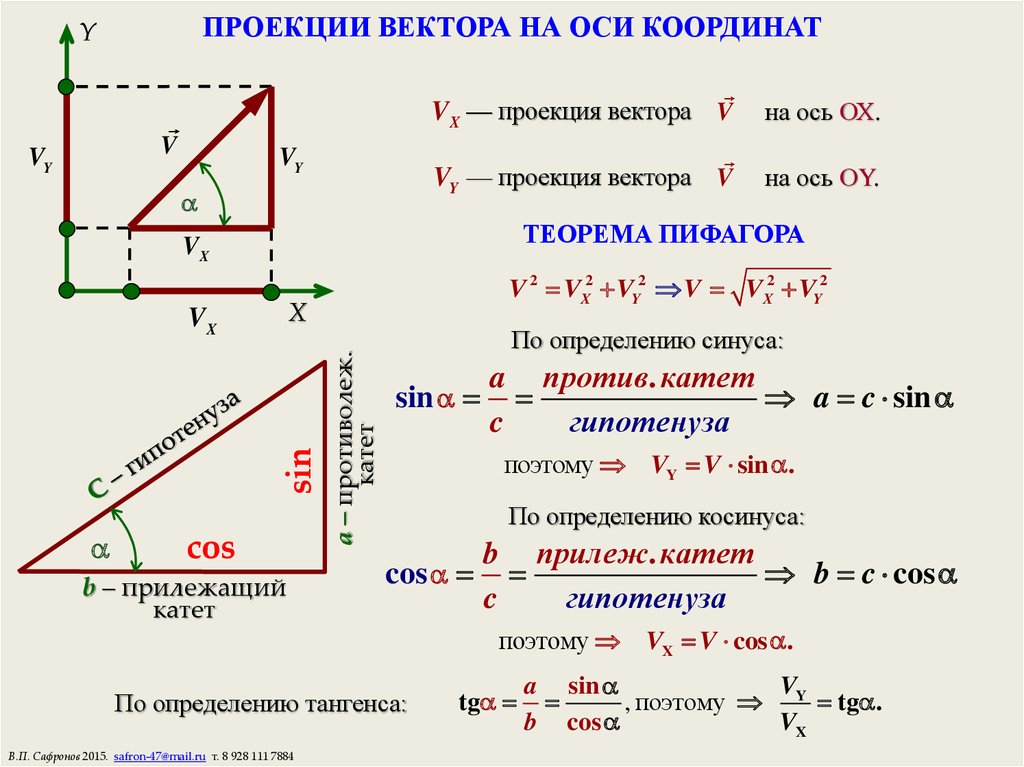 frame (начало, конец), число)
}
########Перемещение блока#############
vec = 1:17 # список или вектор
len = 8 # длина подвектора
ov = потолок(len/2) # длина перекрытия
b <- блоки (len, ov, length (vec))
with (b, Map (функция (i, j) vec [i: j], начинается, заканчивается))
frame (начало, конец), число)
}
########Перемещение блока#############
vec = 1:17 # список или вектор
len = 8 # длина подвектора
ov = потолок(len/2) # длина перекрытия
b <- блоки (len, ov, length (vec))
with (b, Map (функция (i, j) vec [i: j], начинается, заканчивается))
