Как узнать длину дуги окружности: Найти длину дуги окружности радиус окружности 3 см градусная мера этой дуги 120

12. Вычисление длины дуги параллели

Параллель на эллипсоиде вращения является окружностью, поэтому вычисление дуги параллели сводится к определению дуги окружности с центральным углом, равным разности долгот конечных точек дуги.

Радиус параллели r определяется по формуле (9.9), которая имеет вид:

. (12.1)

Длина дуги параллели s΄, имеющей широту В и разность долгот конечных точек дуги l, очевидно, дается формулой:

. (12.2)

Отсюда легко получаем разность долгот двух точек параллели под широтой В, расположенных на расстоянии s’,

l» = [2]s’ sec B (12. 3)

В табл. 3 приводятся для справок длины дуг параллелей для широт от 30 до 70° на эллипсоиде Красовского.

Таблица 3

В	Длина дуги параллели (м)
	в один градус	в одну минуту	в одну секунду
30° 40° 50° 60° 70°	96 489,9 85 395,3 71 696,9 55 800,9 38 187,2	1608,1 1423,3 1194,9 930,0 636,5	26,8 23,7 19,9 15,5 10,6

П р и м е р. Вычислить длину дуги параллели между точками, лежащими на одной параллели, если даны долготы этих точек и широта параллели.

L₂= 64°53’17»,358 L₁= 62°45’14»,812 B = 55°48’12»,382

L2 L1 l = L2 — L1 l»

64°53’17»,358 lg l» 62°45’14»,812 lg cosB 2°08’02»,546 доп lg[2] 7682″,546 lg s s

3. 8855 0517 9.7497 6238 1.4912 7268 5.1265 4023 133 825,912 м

Вычисление площади съемочной трапеции или листа карты сводится к определению части поверхности эллипсоида, ограниченной линиями меридианов и параллелей.

Возьмем на эллипсоиде (рис. 13.1) два бесконечно близко расположенных меридиана РВАР₁ и PCDP₁ с долготами l и 1 + dl и две бесконечно близко расположенные параллели TBCR и QADS с широтами В и B+dB, пересечения которых образуют бесконечно малую трапецию АВС

D.

Рис. 13.1

Стороны этой трапеции как элементы дуг меридианов и параллелей будут равны:

AB= CD = М dB,

AD = ВС = NcosBdl.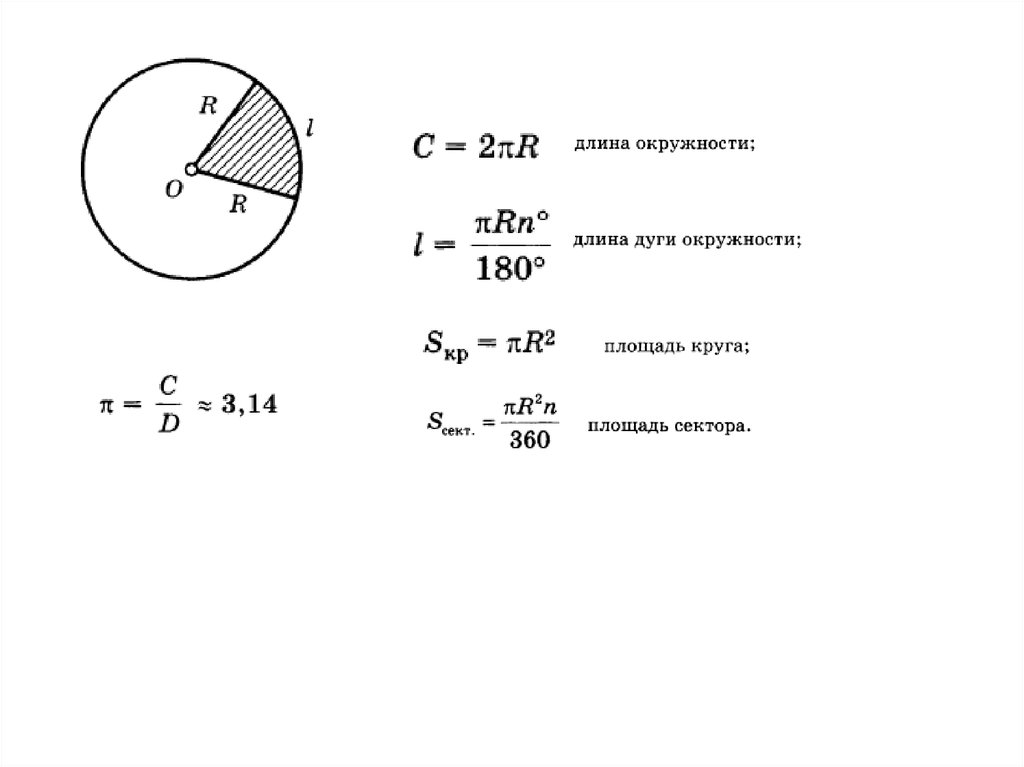

Площадь элементарной трапеции ABCD выразится формулой:

dТ = MNcos BdB dl. (13.1)

Площадь dZ всего пояса, ограниченного указанными параллелями, получится, если в формуле для dT

величину dl заменить через 2π, т. е

dZ = 2π MN cos BdB = 2π R² cos BdB,

или

. (13.2)

Площадь поверхности пояса эллипсоида, расположенного между параллелями с широтами B₁ и В₂, будет:

. (13.3)

Для вычисления интеграла (13.3) разложим подинтегральную функцию в ряд по биному Ньютона (интеграл берется и в конечном виде, однако получаемое при этом выражение мало пригодно для вычислений):

(13.5)

Для приведения этой формулы к виду, удобному для практического применения, воспользуемся формулами, дающими выражения синусов нечетных степеней в функции синусов кратных дуг(эти формулы получаются на основе общей формулы:

(13.6)

Заменяя в формуле (13.5) синусы нечетных степеней согласно выражениям (13.6) и подставляя пределы интегрирования, будем иметь:

(13.7)

Заменяя разности синусов по известным формулам тригонометрии, получим:

При разложении выражения (13. 4) в ряд члены с

е⁶, е⁸ и т. д. не были приняты во внимание. Более точная формула для площади пояса, с учетом членов с е⁶, е⁸, будет иметь следующий вид:

Для эллипсоида Красовского эти коэффициенты имеют следующие численные значения:

1g А’ = 0.001 45834

1g В’ = 7.050 7767_-10

1g C’ =4.230 14_-10

1g D’ = 1.428_-10

(13.9)

Формула (13.8) выражает площадь пояса эллипсоида, ограниченного параллелями с широтами

В₁ и В₂. Чтобы получить формулы для вычисления площадей трапеций данного масштаба и номенклатуры, берут разность широт северной и южной рамок трапеций B₂ — B₁ и определяют, какую долю площади всего пояса составляет площадь трапеции данного масштаба, причем, очевидно, эта доля определится в зависимости от разности долгот меридианов западной и восточной рамок трапеции.

Например, для государственной карты масштаба 1: 1 000 000 B₂ — B₁= 4°; разность долгот восточной и западной рамок карты Δl = 6°, т. е. равна 1: 60 от полной окружности пояса. Поэтому рабочая формула для вычисления площадей трапеции масштаба 1: 1 000 000 будет:

(13.10)

Положив в формуле (13.7) B₁= 0, B₂ = 90° и удвоив полученное выражение, получим формулу для вычисления площади ∑ всей поверхности эллипсоида с удержанием любого числа членов, так как закон построения членов ряда совершенно ясен:

(13. 11)

Рассмотрим пример на вычисление площади трапеции масштаба 1: 100 000.

П р и м е р. Вычислить площадь трапеции карты масштаба 1:100 000 N-36-14.

Для площади трапеции карты этого масштаба формула будет иметь следующий вид:

Имеем:

B₂ = 55°40΄; В₁ = 55°20΄; В_m = 55°30΄.

Вычисления производим по следующей схеме:

1g А‘ lg sin 10° lg cos Вm lg I I

4583 7. 463 7255-10 9.753 1280-10 7.218 3118-10 +0,001 653148

1g B’ lg sin 30° lg cos 3Вm lg II II

7.05 078-10 7.94 084-10 9.98 783n -10 4.97 945n -10 -0,000009538

1g C’ lg sin 50° lg cos 5Вm lg III III

4. 23-10 8.16-10 9.12-10 1.51-10 +0,00000003

I -II +III k	+0,001653148 +0,000009538 +0,000000003	lg π 2 lg b доп. lg 180	0.497 1499 7.606 4857 7.744 7275-10	lg Q lg k	5. 848 3631 7.220 8110-10
	+0,001662689	lg Q	5.848 3631	Lg P	3.069 1741

Р = 1172,666 кв. км.

Как найти длину дуги окружности зная радиус и градусную меру?

Как найти длину дуги окружности зная радиус и градусную меру?

Длина дуги окружностиЗа 1° дуги принимают 1/360 часть окружности. Необходимо понимать, что величина центрального угла никак не зависит от дины души. Так как длина окружности равна 2 pi r , то развернутому углу будет соответствовать длина дуги pi r. Тогда длина дуги центрального угла 1° будет равна {pi r} / {180^0}.

Как найти длину дуги окружности Если известен угол?

Если угол измеряется в градусах, этим методом пользоваться нельзя. Умножьте радиус на центральный угол (измеренный в радианах). Получится длина дуги. Таким образом, если радиус окружности равен 10 см, а центральный угол равен 2,36 радиан, длина дуги приблизительно равна 23,6 см.

Как измерить радиус дуги окружности?

Ну а дальше все просто: измеряем расстояние от пересечения дуг до начала (или конца) рассматриваемой дуги, а затем расстояние от пересечения дуг до точки, соответствующей высоте сегмента.

Как узнать радиус полукруга?

Полукруг — это половина круга. Для вычисления площади полукруга необходимо найти площадь полного круга, а затем разделить ее на два….Вот как это делается:

1. Площадь = (πr2)/2.
2. Площадь = (π x 5 см x 5 см)/2.
3. Площадь = (π x 25 см2)/2.
4. Площадь = (3,14 x 25 см2)/2.
5. Площадь = 39,25 см

Как правильно рассчитать радиус арки?

Важно! Формула для вычисления радиуса окружности арки: R = (L2 + h3)/ 2H, где R – радиус окружности арки, H – высота подъема арки, L – половина хорды дуги (длина арочного просвета).

Как определить радиус сектора?

Площадь кругового сектора круга радиуса равна S α = π R 2 ⋅ α 360 , где – градусная мера дуги сектора.

Как найти дугу сектора?

Формулы для нахождения длины дуги сектора Длина (L) дуги сектора равняется числу π, умноженному на радиус круга (r), умноженному на центральный угол в градусах (α°), деленному на 180°. Примечание: в расчетах используется число π, приблизительно равное 3,14.

Как найти площадь круга сектора?

Площадь сектора круга – это часть S всей плоской фигуры, ограниченной окружностью с радиусом r. Площадь круга равна произведению квадрата радиуса на число «пи». Площадь сектора может быть выражена формулой S = π х r² х α/360. В ином виде при указании угла сектора α не в градусах, а в радианах, S = (α/2) х r².

Что такое полукруг?

Полукруг — сегмент круга, хордой которого является диаметр этого круга, и дуга окружности, лежащая между концами диаметра. Площадь полукруга составляет одну вторую (1/2) от площади круга с таким же диаметром.

Как называется четверть круга?

Квадрант плоскости — любая из 4 областей (углов), на которые плоскость делится двумя взаимно перпендикулярными прямыми, принятыми в качестве осей координат Квадрант круга — сектор с центральным углом в 90°, четверть круга

Как правильно написать слово полукругом?

Слова, начинающиеся с полу-, всегда пишутся слитно, например: в полуверсте от города, полустанок, полукруг.

Объяснение урока: Длины дуг | Nagwa

В этом объяснителе мы узнаем, как найти длину дуги и периметр окружности. сектора, используя радианы, и решать проблемы, в том числе в реальных жизненных ситуациях.

Напомним, что дуга окружности – это часть ее окружности между двумя радиусами. Если мы знать, какую часть окружности составляет дуга, то мы можем использовать длину длину окружности, чтобы определить длину дуги. Например, рассмотрим дугу четверти окружности радиуса 1,

Во-первых, вспомним, что круг радиуса 𝑟 имеет длину окружности 2𝜋𝑟. Это означает, что длина окружности этого круга 2𝜋(1)=2𝜋.

Далее, мы знаем, что длина дуги равна 14 длины окружности. Итак, длина 𝑙 дуги равна 𝑙=14(2𝜋)=𝜋2.

Мы видим, что эта дуга представляет собой четверть круга, но это хорошая практика, чтобы понять, почему это так. Полный оборот — это угол 2𝜋 рад, поэтому угол 𝜋2 рад равен 2𝜋=14 окружности. Следовательно, дуга будет стягивать угол 𝜋2, и деление этого значения на 2𝜋 даст скажите нам пропорцию круга, который является дугой.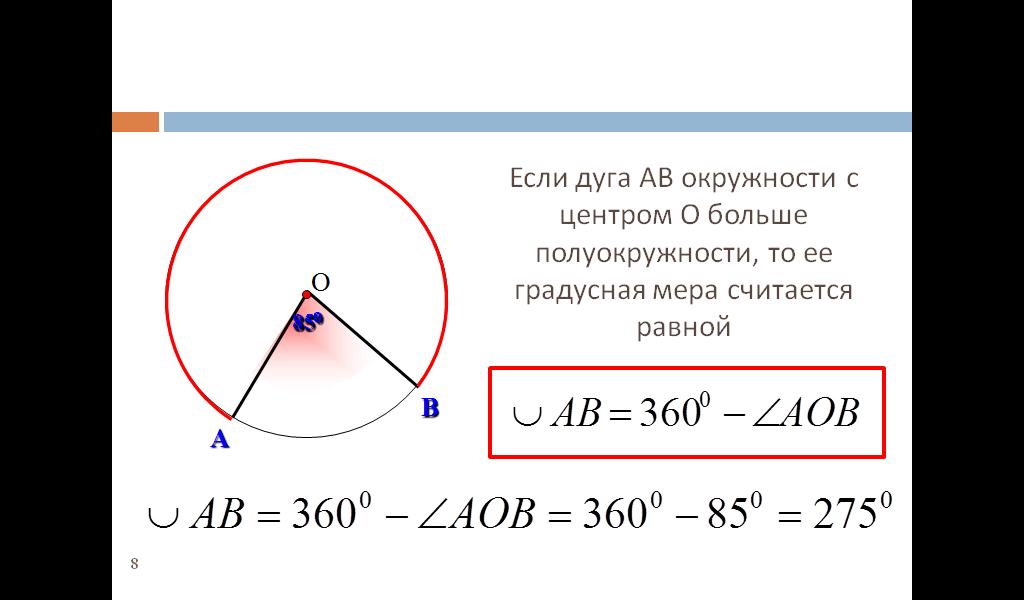

Следовательно, длина дуги равна четверти длины окружности: 𝑙=×=2𝜋×(2𝜋)=14(2𝜋)=𝜋2.пропорционально окружности

В общем, если дуга образует угол 𝜃 рад, то пропорция круга, которая дуга 𝜃2𝜋 а длина окружности равна 2𝜋𝑟.

Следовательно, 𝑙=×=𝜃2𝜋×(2𝜋𝑟)=𝜃2𝜋×2𝜋𝑟=𝑟𝜃.proportioncircumference

Мы показали следующий результат.

Свойство: Длина дуги

Длина 𝑙 дуги окружности радиуса 𝑟, стягивающий угол 𝜃 рад определяется выражением 𝑙=𝑟𝜃.

В нашем первом примере мы будем использовать формулу длины дуги, чтобы определить длину дуги кругового сектора по его радиусу и центральному углу.

Пример 1. Определение длины дуги сегмента

Дуга имеет меру 2𝜋3 радиана и радиусом 9. Вычислить длину дуги, давая ваш ответ с точки зрения 𝜋 в его простейшей форме.

Ответ

Сначала напомним, что если дуга имеет меру 2𝜋3 радиана, это то же самое, что сказать, что стягивает этот угол.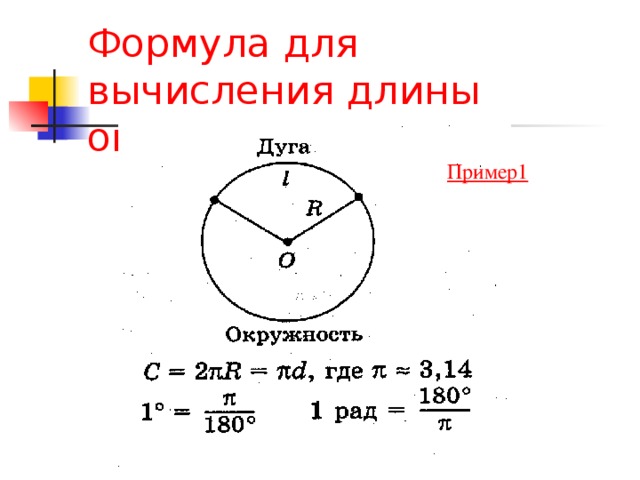 Мы можем сделать набросок информация, предоставленная для лучшего понимания вопрос. Имеем сектор окружности радиуса 9 с центральным углом 2𝜋3 рад.

Мы хотим определить длину дуги этого сектора. Мы можем сделать это, вспомнив, что длина дуги окружности радиуса 𝑟 стягивающий угол 𝜃 рад определяется выражением 𝑟𝜃.

Замена 𝑟=9 и 𝜃=2𝜋3 в формулу дает нам длина дуги=𝑟𝜃=9×2𝜋3.

Отмена общего коэффициента 3 дает 9×2𝜋3=3×2𝜋=6𝜋.

Дальнейшее упрощение невозможно. Следовательно, длина дуги 6𝜋.

В нашем следующем примере мы будем использовать длину дуги окружности и радиус окружности для определить угол, образуемый дугой, в радианах.

Пример 2. Нахождение меры угла дуги по ее дуге Длина и радиус

Дуга окружности радиусом 5 см имеет длина 3,5см. Найдите угол, образуемый дугой в радианах.

Ответ

Сначала вспомним эту длину 𝑙 дуги окружности радиуса 𝑟, опирающейся на угол 𝜃 рад дается 𝑙=𝑟𝜃. Нам говорят, что 𝑟=5 и что 𝑙=3,5. Мы можем заменить эти значения в уравнение, чтобы получить 3,5=5𝜃.

Мы можем найти 𝜃, разделив обе части уравнения на 5. Мы получим 𝜃=3,55=0,7 рад

В нашем следующем примере мы найдем радиус дуги, используя длину дуга и мера угла, образуемого дугой.

Пример 3. Определение радиуса дуги по заданной длине дуги и Измерение угла

Дуга окружности имеет длину 2,7 см. и стягивается под углом 0,3 рад. Найдите радиус круга.

Ответ

Сначала вспомним, что длина 𝑙 дуги окружность с радиусом 𝑟, образующая угол 𝜃 рад дается 𝑙=𝑟𝜃. Нам говорят, что 𝑙=2,7 см и что 𝜃=0,3 рад. Мы можем подставьте эти значения в уравнение, чтобы получить 2,7=𝑟0,3.

Затем мы можем разделить обе части уравнения на 0,3, чтобы найти 𝑟. Мы получили 𝑟=2,70,3=9 см

В нашем следующем примере мы будем использовать формулу длины дуги для определения периметра.

Пример 4. Нахождение периметра фигуры с использованием длин дуг

Найдите периметр 𝐴𝐵𝐶𝐷 на следующей диаграмме.

Ответ

Начнем с выделения 𝐴𝐵𝐶𝐷 на диаграмме, чтобы мы могли видеть фигуру, нас просят вычислить периметр.

Мы видим, что 𝐴𝐵𝐶𝐷 состоит из двух строк отрезки и две дуги окружности. Мы знаем это периметр фигуры будет равен сумме длин отрезки линии 𝐴𝐵 и 𝐶𝐷 и дуги 𝐴𝐷 и 𝐵𝐶.

Нам дано, что 𝐴𝐵=4см, и мы можем найти 𝐶𝐷, заметив, что 𝑂𝐶 — это радиус окружности длина 7 см и что 𝑂𝐷 является радиусом окружности длиной 3 см. Следовательно, 𝐶𝐷=7−3=4.см

Мы можем определить длину дуг, вспомнив эту длину 𝑙 дуги окружности радиуса 𝑟, стягивающий угол 𝜃 рад дается 𝑙=𝑟𝜃. Мы можем найти длину дуга 𝐴𝐷, отметив сектор 𝐴𝑂𝐷 имеет радиус 3 см и образует угол 1,6 рад.

Следовательно, мы можем заменить 𝑟=3см и 𝜃=1,6 рад в формулу длины дуги, чтобы получить 𝐴𝐷=3×1. 6=4.8.см

Аналогично можно заметить, что дуга 𝐵𝐶 это дуга окружности радиусом 7 см который образует угол измерения 1,6 рад.

Таким образом, мы можем заменить 𝑟=7см и 𝜃=1,6 рад в формулу длины дуги, чтобы получить 𝐵𝐶=7×1,6=11,2 см

Наконец, сумма этих четырех длин дает нам периметр 𝐴𝐵𝐶𝐷.

У нас есть 4+11,2+4+4,8=24 см

Следовательно, периметр 𝐴𝐵𝐶𝐷 имеет периметр 24 см.

В двух последних примерах мы будем использовать длины дуг для решения реальных задач.

Пример 5. Использование длины дуги для решения реальной задачи

Форма основания бутылки состоит из отрезка длиной 5 см то есть соединяется с дугой окружности радиусом 3 см, как показано на рисунке.

Найдите длину дуги окружности с точностью до одного десятичного знака.

Ответ

Для определения длины дуги окружности воспользуемся формула 𝑙=𝑟𝜃, где 𝑙 — длина дуги, 𝑟 — радиус окружности, а 𝜃 — угол, образуемый дугой. дуга в радианах. Нам известно, что радиус окружности равен 3 см. Однако нам не известен угол, образуемый дугой.

Мы можем определить один из углов в центре круга, заметив, что у нас есть треугольник с тремя известными длинами сторон.

Мы можем применить правило косинуса, чтобы определить угол при 𝑂. Правило косинусов говорит нам, что 𝑎=𝑏+𝑐−2𝑏𝑐𝐴.cos

Мы хотим определить угол при 𝑂; мы можем назвать это 𝐴 на диаграмме и обозначить сторону длины 𝑎, 𝑏 и 𝑐, как показано.

Затем подставляем 𝑎=5см, 𝑏=3см, и 𝑐=3 см в теорему косинусов, чтобы получить 5=3+3−2(3)(3)𝐴.cos

Вычисляя и упрощая, имеем 25=9+9−18𝐴25=18−18𝐴.coscos

Затем мы можем вычесть 18 из обеих частей уравнения, чтобы получить 7=−18𝐴.cos

Затем мы делим обе части уравнения на −18, что дает нам −718=𝐴.cos

Мы можем найти значение 𝐴, взяв арккосинус обе части уравнения, где важно убедиться, что наш калькулятор настроен на режим радианов. Это дает нам 𝐴=−718=1,97….cosrad

Мы можем добавить этот угол на исходную диаграмму.

Теперь мы можем определить длину дуги этого круга двумя разными способами.

Первый метод, который мы можем использовать, это найти угол, образуемый дугой заметив, что два угла при 𝑂 в сумме дают 2𝜋.

Таким образом, cos−718+𝜃=2𝜋.

Мы используем точное значение cos−718, чтобы избежать ошибок округления. Мы можем переставить и решить для 𝜃: 𝜃=2𝜋−−718=4,31….cosrad

Теперь мы можем определить длину дуги, подставив 𝑟=3 см и 𝜃=4,31… рад в формула длины дуги. Мы получили 𝑙=3×(4,31…)=12,93….cm

Опять же, важно использовать точное значение для 𝜃 чтобы избежать слишком раннего округления. Мы можем теперь округлите это до одного десятичного знака, чтобы получить наше решение 𝑙 = 12,9 см.

Теперь рассмотрим второй метод. В этом методе найдем длину дуги под углом 1,97… рад.

Подставляем 𝑟=3см и 𝜃=−718cosrad в формулу длины дуги, чтобы получить 𝑙=3−718=5,91….коссм

Длину окружности можно найти по формуле 𝑐=2𝜋𝑟. Таким образом, 𝑐=2𝜋(3)=6𝜋см

Тогда длина большой дуги в этом круге равна длине окружности минус длина малая дуга. Мы нашли 6𝜋−(5,91…)=12,93….см

Мы используем точные значения в этих расчетах, чтобы избежать ошибок округления.

Еще раз находим, что длина дуги на схеме равна 12,9 см. до одного десятичного знака.

Пример 6. Использование длины дуги для решения реальной проблемы

В футболе игроки соперника должны стоять на расстоянии 10 ярдов от мяча во время штрафного удара и ворота шириной 8 ярдов. Штрафной удар выполняется таким образом, что мяч находится на расстоянии 25 ярдов. подальше от цель с углами и точками, как показано на диаграмме. Точка 𝐹 — это место, где лежит мяч, точки 𝐶 и 𝐷 отмечают края ворот, а точки 𝐴 и 𝐵 отмечают точки на 𝐹𝐶 и 𝐹𝐷, которые составляют 10 ярдов от 𝐹.

Учитывая, что 𝐹𝐴𝐵 является сектором, найдите периметр заштрихованного области до ближайшего двора.

Ответ

Начнем с того, что заштрихованная область ограничена тремя отрезками и дуга окружности, поэтому периметр регионов равен сумме длин этих линий отрезки и длину дуги.

Нам даны длины двух отрезков в вопросе и диаграмма. Мы можем найти длину дуги окружности, вспомнив эту длину 𝑙 дуги окружности радиуса 𝑟 образующий угол 𝜃 рад, определяется как 𝑙=𝑟𝜃. Мы видим, что радиус окружности 10 ярдов и дуга стягивается угол 0,3 рад. Подставив эти значения в длину дуги формула дает 𝑙=10(0,3)=3,ярд

Чтобы определить длину конечной стороны области, мы можем отметить, что она является частью треугольник с двумя известными длинами сторон и известным углом.

Длину недостающей стороны треугольника можно найти по теореме косинусов: 𝑐=𝑎+𝑏−2𝑎𝑏𝐶. cos

Имеем 𝐶=1,67 рад, 𝑎=25 ярдов, и 𝑏=8ярдов. Подставляя эти значения в косинус правило дает нам 𝑐=25+8−2(25)(8)(1,67).cos

Оценка дает нам 𝑐=625+64−400(1,67).cos

Теперь мы можем извлечь квадратные корни из обеих частей уравнения, учитывая, что 𝑎 должен быть положительным, получить 𝑐=√625+64−400(1,67)≈26,99….cos

Это длина всей стороны треугольника. Вычитание 10 ярдов от этого дает 16.99… ярдов. Теперь мы можем добавить длины к диаграмме.

Сложение всех этих длин дает нам периметр области: периметрyd=3+15+8+16,99…≈43.

Давайте закончим повторением некоторых важных моментов из этого объяснения.

Ключевые точки

• Дуга окружности радиуса 𝑟, образующая угол 𝜃 измеряется в радианах имеет длину 𝑟𝜃.
• Периметр 𝑃 кругового сектора, образующего угол 𝜃измеряется в радианах равно 𝑃=2𝑟+𝑟𝜃.

Формула длины дуги | Как найти длину дуги (видео + примеры)

Что такое длина дуги?

Длина дуги — это мера расстояния по окружности окружности, образующей дугу. Чтобы найти меру длины дуги окружности, помните, что на самом деле вы находите дробную часть всего круга, представленного этой дугой. Зная меру центрального угла либо в градусах, либо в радианах и всю окружность, можно найти точную длину дуги.

1. Длина дуги окружности
2. Окружность и длина дуги
3. Формулы длины дуги

• Градусов
• радиан

Как найти длину дуги

Примеры длины дуги

Что нужно знать

Окружность имеет измеримое расстояние вокруг своей внешней стороны, окружность . Круги также имеют диаметров , отрезков линии от круга через центр к кругу на другой стороне. Круги имеют радиусов или радиусов , которые являются половиной диаметра (от окружности к центру). Любая часть окружности, например, образованная двумя радиусами, отстоящими друг от друга на несколько известных центральных углов, представляет собой дугу .

Длина дуги окружности

Углы в окружностях могут быть измерены в градусах (360°) или радианах . Радианы — это метрическая мера углов. Один радиан — это угол, образованный дугой окружности, длина которой равна радиусу этой окружности. Это означает, что любой круг имеет длину окружности 2π радиан. Один радиан примерно равен 57,29.6°, хотя такое преобразование обычно бесполезно.

Завершите всю свою работу в градусах или радианах. Старайтесь избегать прыжков между юнитами.

Градусные меры окружности обозначаются курсивной буквой m (для меры), за которой следуют две конечные точки дуги на окружности, с крошечной дугой, проведенной над двумя заглавными буквами. Таким образом, в круге ниже дуга AB⌢ имеет угловую меру 36 °. Обозначение будет mAB⌢.

Окружность и длина дуги

Окружность имеет особое числовое соотношение между длиной окружности и либо диаметром, либо радиусом.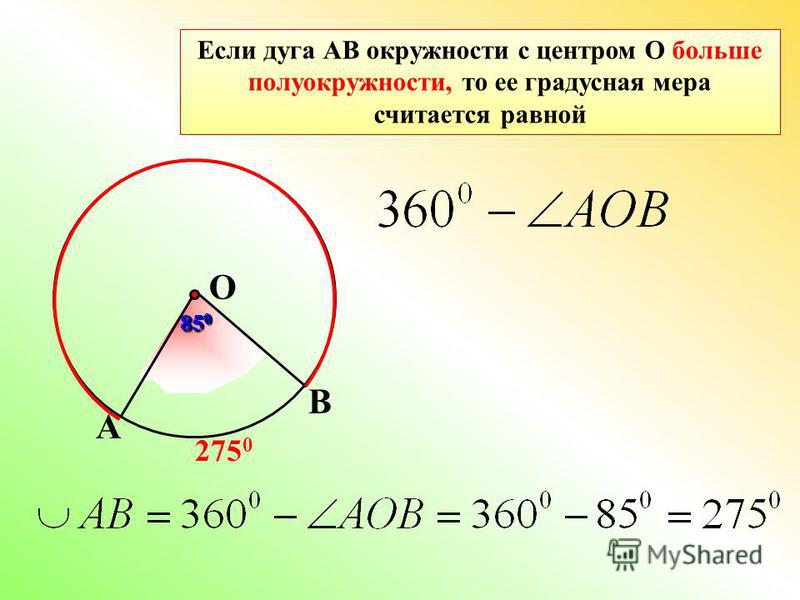 Если вы знаете радиус r, вы можете использовать его для нахождения длины окружности C по формуле C = 2πr . Если вы знаете диаметр d, то:

C = πd

Мы используем 3,14159 в качестве приближения значения π, которое, как вы, вероятно, помните, является неповторяющимся и неконечным числом. Калькуляторы с клавишами π гораздо более точны, но десятичное число, выраженное до 100 000, также очень точно.

Формулы длины дуги

Для определения длины дуги можно использовать формулу для градусов или радианов. Давайте рассмотрим каждое уравнение длины дуги шаг за шагом.

Формула длины дуги для градусов

Длина дуги определяется путем вычисления отношения дуги ко всей окружности, а затем умножения на формулу длины окружности, 2πr или πd, например:

Длина дуги AB⌢ = mAB⌢360° 2πr

Или, если у вас есть диаметр:

Длина дуги AB⌢ = mAB⌢360° πd

Формула длины дуги в радианах

При работе с радианами формула еще проще, где θ (тета) — центральный угол в радианах, а r — радиус:

Дуга length = θr

Как найти длину дуги

Определение длины дуги с помощью градусов

Еще раз взгляните на окружность выше, где ∠ACB измеряется как 36°, а радиус равен 30 см. Если вы подставите этот угол (36°) и этот радиус (30 см) в формулу длины дуги, используемую для градусов, вы получите следующее:

Начало с нашей формулы:

ДЛЯ ДЕЛЕЙ ДЛЯ ДЕЛЕВА = MAB⌢360 ° 2πr

Подключите то, что мы знаем:

= 36 ° 360 ° 2 · π · 30

. Умножьте 2πr Times 110, используя 3,14159 в качестве очень близкого приближения π, если у вас нет калькулятора с π -ключом:

= 110 · 2 · π · 30

= 110 · 60 0009

= 6π

≈ 18.84954 см

Поскольку 36° составляет 110 от 360°, длина дуги AB⌢ составляет 110 длины окружности.

Определение длины дуги в радианах

Использование формулы в радианах еще проще. Для того же круга угол в радианах равен 0,628319 рад, поэтому мы используем его вместо градусов:

. Начнем с нашей формулы:

. число, которое мы можем использовать:

     = 0,628319 · 30

     = 18,84957 см

Обратите внимание на два измерения: они отличаются всего на 0,00003 см из-за ошибок округления.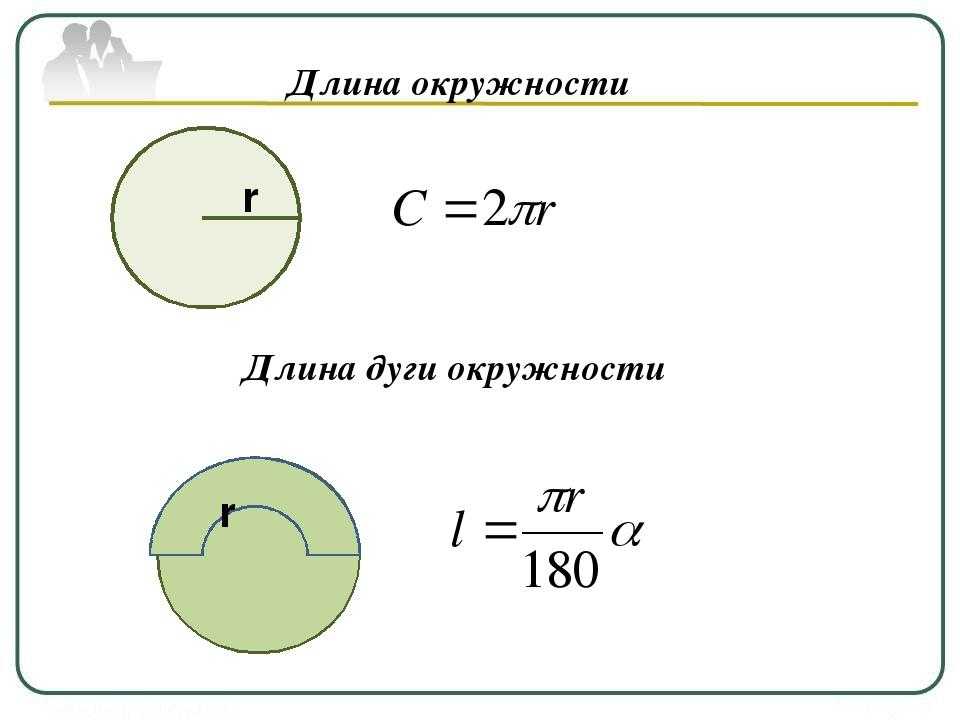 Калькулятор с π был бы еще точнее.

Давайте проверим нашу работу

Мы можем проверить оба этих измерения, потому что мы установили центральный угол ∠ACB как удобную часть нашего круга. Мы сделали это 36°, или 110-е место. Это означает, что мы можем проверить дробную часть длины окружности, используя 2πr, чтобы найти длину окружности, а затем взять 110-ю: ·30

Окружность = 188,4954 см

110 Окружности = 18,84954 см

Проверено!

Примеры длины дуги

Вот еще две задачи для определения длины дуги, одна с центральным углом, измеряемым в градусах, и другая, измеряемая в радианах. Помните, что вы можете рассчитать длину дуги, только если знаете этот центральный угол.

Задача о длине дуги № 1

[вставьте чертеж окружности A с точками W и Y на окружности, создающей радиусы AW и AY и центральный угол 22,5° {1/16 часть окружности} и отмеченный радиус 5 ярдов]

Найдите минутку, чтобы записать важные факты, затем отойдите и сделайте свои расчеты. Получив ответы, посмотрите, соответствует ли ваша работа этой работе.

ARC LEANDWY⌢ = MWY⌢360 ° 2πr

= 22,5 ° 360 ° 2 · π · 5

= 116 · 10π

— или —

= 0,0625 · 10 0009

9000 3

9000 3 9000 3

9000 3

9000 3 9000 3 9000 3 9000 3

9000 3 9000 3 9000 3

9000 3

9000 3 9000 3

= 0,0625. дробная часть круга в виде дроби или десятичной дроби. В любом случае вы получите один и тот же ответ:

      = 1,96349 ярдов

Задача №2 о длине дуги

[вставьте рисунок окружности E с точками Y и 2 на окружности, образующей радиусы EY и ES, и центральным углом, обозначенным 1,0472 рад {угол 60°, 1/6th круга} и помеченный радиус 3 метра]

Нам нужно использовать формулу для радиан:

Длина дуги = θr

= 1,0472 RAD · 3

= 3,1416 метра

Следующий урок:

119

= 3,1416 метра

.