Найдите f x для f x: f(x) = 3x найти первообразную

как решать, правила вычисления, объяснение

Одна из операций дифференцирования- нахождение производной (дифференциала) и применении к исследованию функций.

Не менее важной является обратная задача. Если известно поведение функции в окрестностях каждой точки ее определения, то как восстановить функцию в целом, т.е. во всей области ее определения. Эта задача составляет предмет изучения так называемого интегрального исчисления.

Интегрированием называется действие обратное дифференцированию. Или восстановление функции f(х) по данной производной f`(х). Латинское слово “integro” означает – восстановление.

Пример №1 .

Пусть (f(х))’ = 3х 2 . Найдем f(х).

Решение:

Опираясь на правило дифференцирования, нетрудно догадаться, что f(х)=х 3 , ибо

(х 3)’ = 3х 2 Однако, легко можно заметить, что f(х) находится неоднозначно. В качестве f(х) можно взять f(х)= х 3 +1 f(х)= х 3 +2 f(х)= х 3 -3 и др.

Т.к. производная каждой из них равно 3х 2 .

(Производная постоянной равна 0). Все эти функции отличаются друг от друга постоянным слагаемым. Поэтому общее решение задачи можно записать в виде f(х)= х 3 +С, где С — любое постоянное действительное число.

Любую из найденных функций f(х) называют первообразной для функции F`(х)= 3х 2

Определение.

Функция F(х) называется первообразной для функции f(х) на заданном промежутке J, если для всех х из этого промежутка F`(х)= f(х). Так функция F(х)=х 3 первообразная для f(х)=3х 2 на (- ∞ ; ∞). Так как, для всех х ~R справедливо равенство: F`(х)=(х 3)`=3х 2

Как мы уже заметили, данная функция имеет бесконечное множество первообразных.

Пример №2.

Функция есть первообразная для всех на промежутке (0; +∞), т.к. для всех ч из этого промежутка, выполняется равенство.

Задача интегрирования состоит в том, чтобы для заданной функции найти все ее первообразные. При решении этой задачи важную роль играет следующее утверждение:

Признак постоянства функции. Если F»(х) = 0 на некотором промежутке I, то функция F — постоянная на этом промежутке.

Доказательство.

Зафиксируем некоторое x 0 из промежутка I. Тогда для любого числа х из такого промежутка в силу формулы Лагранжа можно указать такое число c, заключенное между х и x 0 , что

F(x) — F(x 0) = F»(c)(x-x 0).

По условию F’ (с) = 0, так как с ∈1, следовательно,

F(x) — F(x 0) = 0.

Итак, для всех х из промежутка I

т е. функция F сохраняет постоянное значение.

Все первообразные функции f можно записать с помощью одной формулы, которую называютобщим видом первообразных для функции f. Справедлива следующая теорема (основное свойство первообразных ):

Теорема. Любая первообразная для функции f на промежутке I может быть записана в виде

F(x) + C, (1) где F (х) — одна из первообразных для функции f (x) на промежутке I, а С — произвольная постоянная.

Поясним это утверждение, в котором кратко сформулированы два свойства первообразной:

1. какое бы число ни поставить в выражение (1) вместо С, получим первообразную для f на промежутке I;
2. какую бы первообразную Ф для f на промежутке I ни взять, можно подобрать такое число С, что для всех х из промежутка I будет выполнено равенство

Доказательство.

1. По условию функция F — первообразная для f на промежутке I. Следовательно, F»(х)= f (х) для любого х∈1, поэтому (F(x) + C)» = F»(x) + C»=f(x)+0=f(x), т. е. F(x) + C — первообразная для функции f.
2. Пусть Ф (х) — одна из первообразных для функции f на том же промежутке I, т. е. Ф»(x) = f (х) для всех x∈I.

Тогда (Ф(x) — F (x))» = Ф»(х)-F’ (х) = f(x)-f(x)=0.

Отсюда следует в. силу признака постоянства функции, что разность Ф(х) — F(х) есть функция, принимающая некоторое постоянное значение С на промежутке I.

Таким образом, для всех х из промежутка I справедливо равенство Ф(х) — F(x)=С, что и требовалось доказать. Основному свойству первообразной можно придать геометрический смысл: графики любых двух первообразных для функции f получаются друг из друга параллельным переносом вдоль оси Оу

Вопросы к конспектам

Функция F(x) является первообразной для функции f(x). Найдите F(1), если f(x)=9×2 — 6x + 1 и F(-1) = 2.

Найдите все первообразные для функции

Для функции (x) = cos2 * sin2x, найдите первообразную F(x), если F(0) = 0.

Для функции найдите первообразную, график которой проходит через точку

Первообразная.

Первообразную легко понять на примере.

Возьмем функцию у = х 3 . Как мы знаем из предыдущих разделов, производной от

х 3 является 3х 2:

(х 3)» = 3х 2 .

Следовательно, из функции у = х 3 мы получаем новую функцию: у = 3х 2 .
Образно говоря, функция у = х 3 произвела функцию у = 3х 2 и является ее «родителем». В математике нет слова «родитель», а есть родственное ему понятие: первообразная.

То есть: функция у = х 3 является первообразной для функции у = 3х 2 .

Определение первообразной:

В нашем примере (х 3)» = 3х 2 , следовательно у = х 3 – первообразная для у = 3х 2 .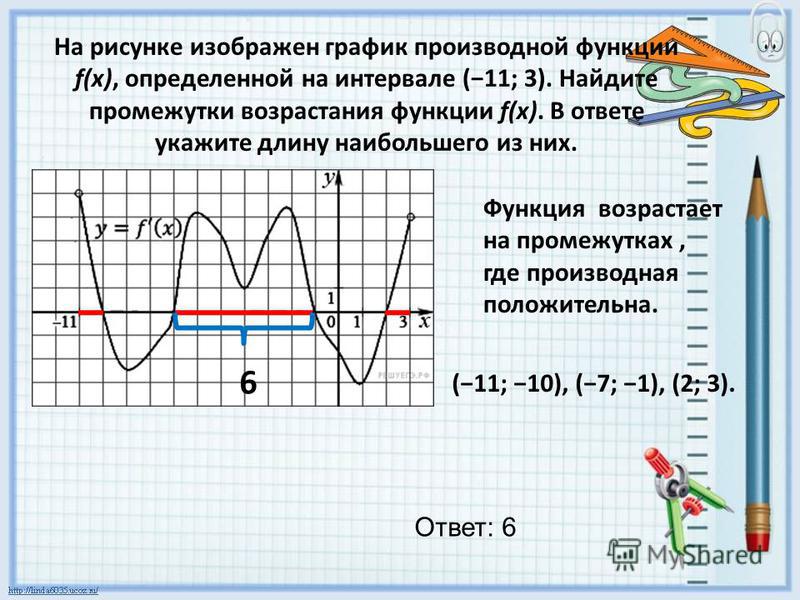

Интегрирование.

Как вы знаете, процесс нахождения производной по заданной функции называется дифференцированием. А обратная операция называется интегрированием.

Пример-пояснение :

у = 3х 2 + sin x .

Решение :

Мы знаем, что первообразной для 3х 2 является х 3 .

Первообразной для sin x является –cos x .

Складываем два первообразных и получаем первообразную для заданной функции:

у = х 3 + (–cos x ),

у = х 3 – cos x .

Ответ :
для функции у = 3х 2 + sin x у = х 3 – cos x .

Пример-пояснение :

Найдем первообразную для функции у = 2 sin x .

Решение :

Замечаем, что k = 2. Первообразной для sin x является –cos x .

Следовательно, для функции у = 2 sin x первообразной является функция у = –2 cos x .
Коэффициент 2 в функции у = 2 sin x соответствует коэффициенту первообразной, от которой эта функция образовалась.

Пример-пояснение :

Найдем первообразную для функции y = sin 2x .

Решение :

Замечаем, что k = 2. Первообразной для sin x является –cos x .

Применяем нашу формулу при нахождении первообразной для функции y = cos 2x :

1
y = — · (–cos 2x ),
2

cos 2x
y = – —-
2

cos 2x
Ответ : для функции y = sin 2x первообразной является функция y = – —-
2

(4)

Пример-пояснение .

Возьмем функцию из предыдущего примера: y = sin 2x .

Для этой функции все первообразные имеют вид:

cos 2x
y = – —- + C .
2

Пояснение .

Возьмем первую строчку. Читается она так: если функция y = f(x )равна 0, то первообразной для для нее является 1. Почему? Потому что производная единицы равна нулю: 1″ = 0.

В таком же порядке читаются и остальные строчки.

Как выписывать данные из таблицы? Возьмем восьмую строчку:

(-cos x )» = sin x

Пишем вторую часть со знаком производной, затем знак равенства и производную.

Читаем: первообразной для функции sin x является функция -cos x .

Или: функция -cos x является первообразной для функции sin x .

Первообразная функция и неопределённый интеграл

Факт 1. Интегрирование — действие, обратное дифференцированию, а именно, восстановление функции по известной производной этой функции. Восстановленная таким образом функция F (x ) называется первообразной для функции f (x ).

Определение 1. Функция F (x f (x ) на некотором промежутке X , если для всех значений x из этого промежутка выполняется равенство F «(x )=f (x ), то есть данная функция

f (x ) является производной от первообразной функции F (x ). .

Например, функция F (x ) = sin x является первообразной для функции f (x ) = cos x на всей числовой прямой, так как при любом значении икса (sin x )» = (cos x ) .

Определение 2. Неопределённым интегралом функции f (x ) называется совокупность всех её первообразных . При этом употребляется запись

∫

f (x )dx

,

где знак ∫ называется знаком интеграла, функция f (x ) – подынтегральной функцией, а f (x )dx – подынтегральным выражением.

Таким образом, если F (x ) – какая-нибудь первообразная для f (x

) , то

∫

f (x )dx = F (x ) +C

где C — произвольная постоянная (константа).

Для понимания смысла множества первообразных функции как неопределённого интеграла уместна следующая аналогия. Пусть есть дверь (традиционная деревянная дверь). Её функция — «быть дверью». А из чего сделана дверь? Из дерева. Значит, множеством первообразных подынтегральной функции «быть дверью», то есть её неопределённым интегралом, является функция «быть деревом + С», где С — константа, которая в данном контексте может обозначать, например, породу дерева. Подобно тому, как дверь сделана из дерева при помощи некоторых инструментов, производная функции «сделана» из первообразной функции при помощи формулы, которую мы узнали, изучая производную .

Тогда таблица функций распространённых предметов и соответствующих им первообразных («быть дверью» — «быть деревом», «быть ложкой» — «быть металлом» и др.) аналогична таблице основных неопределённых интегралов, которая будет приведена чуть ниже. В таблице неопределённых интегралов перечисляются распространённые функции с указанием первообразных, из которых «сделаны» эти функции. В части задач на нахождение неопределённого интеграла даны такие подынтегральные функции, которые без особых услилий могут быть проинтегрированы непосредственно, то есть по таблице неопределённых интегралов.

В задачах посложнее подынтегральную функцию нужно предварительно преобразовать так, чтобы можно было использовать табличные интегралы.

Факт 2. Восстанавливая функцию как первообразную, мы должны учитывать произвольную постоянную (константу) C , а чтобы не писать список первообразной с различными константами от 1 до бесконечности, нужно записывать множество первообразных с произвольной константой C , например, так: 5x ³+С . Итак, произвольная постоянная (константа) входит в выражение первообразной, поскольку первообразная может быть функцией, например, 5x ³+4 или 5x ³+3 и при дифференцировании 4 или 3, или любая другая константа обращаются в нуль.

Поставим задачу интегрирования: для данной функции f (x ) найти такую функцию F (x ), производная которой равна f (x ).

Пример 1. Найти множество первообразных функции

Решение. Для данной функции первообразной является функция

Функция F (x ) называется первообразной для функции f (x ), если производная F (x ) равна f (x ), или, что одно и то же, дифференциал F (x ) равен f (x ) dx , т. е.

(2)

Следовательно, функция — первообразная для функции . Однако она не является единственной первообразной для . Ими служат также функции

где С – произвольная постоянная. В этом можно убедиться дифференцированием.

Таким образом, если для функции существует одна первообразная, то для неё существует бесконечное множество первообразных, отличающихся на постоянное слагаемое. Все первообразные для функции записываются в приведённом выше виде. Это вытекает из следующей теоремы.

Теорема (формальное изложение факта 2). Если F (x ) – первообразная для функции f (x ) на некотором промежутке Х , то любая другая первообразная для f (x ) на том же промежутке может быть представлена в виде F (x ) + C , где С – произвольная постоянная.

В следующем примере уже обращаемся к таблице интегралов, которая будет дана в параграфе 3, после свойств неопределённого интеграла. Делаем это до ознакомления со всей таблицей, чтобы была понятна суть вышеизложенного. А после таблицы и свойств будем пользоваться ими при интегрировании во всей полносте.

Пример 2. Найти множества первообразных функций:

Решение. Находим множества первообразных функций, из которых «сделаны» данные функции. При упоминании формул из таблицы интегралов пока просто примите, что там есть такие формулы, а полностью саму таблицу неопределённых интегралов мы изучим чуть дальше.

1) Применяя формулу (7) из таблицы интегралов при n = 3, получим

2) Используя формулу (10) из таблицы интегралов при n = 1/3, имеем

3) Так как

то по формуле (7) при n = -1/4 найдём

Под знаком интеграла пишут не саму функцию f , а её произведение на дифференциал dx . Это делается прежде всего для того, чтобы указать, по какой переменной ищется первообразная. Например,

, ;

здесь в обоих случаях подынтегральная функция равна , но её неопределённые интегралы в рассмотренных случаях оказываются различными. В первом случае эта функция рассматривается как функция от переменной x , а во втором — как функция от z .

Процесс нахождения неопределённого интеграла функции называется интегрированием этой функции.

Геометрический смысл неопределённого интеграла

Пусть требуется найти кривую y=F(x) и мы уже знаем,что тангенс угла наклона касательной в каждой её точке есть заданная функция f(x) абсциссы этой точки.

Согласно геометрическому смыслу производной, тангенс угла наклона касательной в данной точке кривой y=F(x) равен значению производной F»(x) . Значит, нужно найти такую функцию F(x) , для которой F»(x)=f(x) . Требуемая в задаче функция F(x) является первообразной от f(x) . Условию задачи удовлетворяет не одна кривая, а семейство кривых. y=F(x) — одна из таких кривых, а всякая другая кривая может быть получена из неё параллельным переносом вдоль оси Oy .

Назовём график первообразной функции от f(x) интегральной кривой. Если F»(x)=f(x) , то график функции y=F(x) есть интегральная кривая.

Факт 3. Неопределённый интеграл геометрически представлен семеством всех интегральных кривых , как на рисунке ниже. Удалённость каждой кривой от начала координат определяется произвольной постоянной (константой) интегрирования C .

Свойства неопределённого интеграла

Факт 4. Теорема 1. Производная неопределённого интеграла равна подынтегральной функции, а его дифференциал – подынтегральному выражению.

Факт 5. Теорема 2. Неопределённый интеграл от дифференциала функции f (x ) равен функции f (x ) с точностью до постоянного слагаемого , т.е.

(3)

Теоремы 1 и 2 показывают, что дифференцирование и интегрирование являются взаимно-обратными операциями.

Факт 6. Теорема 3. Постоянный множитель в подынтегральном выражении можно выносить за знак неопределённого интеграла , т.е.

Решение интегралов — задача легкая, но только для избранных. Эта статья для тех, кто хочет научиться понимать интегралы, но не знает о них ничего или почти ничего. Интеграл… Зачем он нужен? Как его вычислять? Что такое определенный и неопределенный интегралы? Если единственное известное вам применение интеграла – доставать крючком в форме значка интеграла что-то полезное из труднодоступных мест, тогда добро пожаловать! Узнайте, как решать интегралы и почему без этого никак нельзя обойтись.

Изучаем понятие «интеграл»

Интегрирование было известно еще в Древнем Египте. Конечно, не в современном виде, но все же. С тех пор математики написали очень много книг по этой теме. Особенно отличились Ньютон и Лейбниц , но суть вещей не изменилась. Как понять интегралы с нуля? Никак! Для понимания этой темы все равно понадобятся базовые знания основ математического анализа. Именно эти фундаментальные сведения о Вы найдете у нас в блоге.

Неопределенный интеграл

Пусть у нас есть какая-то функция f(x) .

Неопределенным интегралом функции f(x) называется такая функция F(x) , производная которой равна функции f(x) .

Другими словами интеграл – это производная наоборот или первообразная. Кстати, о том, как читайте в нашей статье.

Первообразная существует для всех непрерывных функций. Также к первообразной часто прибавляют знак константы, так как производные функций, различающихся на константу, совпадают. Процесс нахождения интеграла называется интегрированием.

Простой пример:

Чтобы постоянно не высчитывать первообразные элементарных функций, их удобно свести в таблицу и пользоваться уже готовыми значениями:

Определенный интеграл

Имея дело с понятием интеграла, мы имеем дело с бесконечно малыми величинами. Интеграл поможет вычислить площадь фигуры, массу неоднородного тела, пройденный при неравномерном движении путь и многое другое. Следует помнить, что интеграл – это сумма бесконечно большого количества бесконечно малых слагаемых.

В качестве примера представим себе график какой-нибудь функции. Как найти площадь фигуры, ограниченной графиком функции?

С помощью интеграла! Разобьем криволинейную трапецию, ограниченную осями координат и графиком функции, на бесконечно малые отрезки. Таким образом фигура окажется разделена на тонкие столбики. Сумма площадей столбиков и будет составлять площадь трапеции. Но помните, что такое вычисление даст примерный результат. Однако чем меньше и уже будут отрезки, тем точнее будет вычисление. Если мы уменьшим их до такой степени, что длина будет стремиться к нулю, то сумма площадей отрезков будет стремиться к площади фигуры. Это и есть определенный интеграл, который записывается так:

Точки а и b называются пределами интегрирования.

Бари Алибасов и группа «Интеграл»

Кстати! Для наших читателей сейчас действует скидка 10% на

Правила вычисления интегралов для чайников

Свойства неопределенного интеграла

Как решать неопределенный интеграл? Здесь мы рассмотрим свойства неопределенного интеграла, которые пригодятся при решении примеров.

• Производная от интеграла равна подынтегральной функции:

• Константу можно выносить из-под знака интеграла:

• Интеграл от суммы равен сумме интегралов. Верно также для разности:

Свойства определенного интеграла

• Линейность:

• Знак интеграла изменяется, если поменять местами пределы интегрирования:

• При любых точках a , b и с :

Мы уже выяснили, что определенный интеграл — это предел суммы. Но как получить конкретное значение при решении примера? Для этого существует формула Ньютона-Лейбница:

Примеры решения интегралов

Ниже рассмотрим несколько примеров нахождения неопределенных интегралов. Предлагаем Вам самостоятельно разобраться в тонкостях решения, а если что-то непонятно, задавайте вопросы в комментариях.

Для закрепления материала посмотрите видео о том, как решаются интегралы на практике. Не отчаиваетесь, если интеграл не дается сразу. Спросите , и они расскажут вам о вычислении интегралов все, что знают сами. С нашей помощью любой тройной или криволинейный интеграл по замкнутой поверхности станет вам по силам.

Определение первообразной.

Первообразной функции f(x) на промежутке (a; b) называется такая функция F(x) , что выполняется равенство для любого х из заданного промежутка.

Если принять во внимание тот факт, что производная от константы С равна нулю, то справедливо равенство . Таким образом, функция f(x) имеет множество первообразных F(x)+C , для произвольной константы С , причем эти первообразные отличаются друг от друга на произвольную постоянную величину.

Определение неопределенного интеграла.

Все множество первообразных функции f(x) называется неопределенным интегралом этой функции и обозначается .

Выражение называют подынтегральным выражением , а f(x) – подынтегральной функцией . Подынтегральное выражение представляет собой дифференциал функции f(x) .

Действие нахождения неизвестной функции по заданному ее дифференциалу называется неопределенным интегрированием, потому что результатом интегрирования является не одна функция F(x) , а множество ее первообразных F(x)+C .

На основании свойств производной можно сформулировать и доказать свойства неопределенного интеграла (свойства первообразной).

Промежуточные равенства первого и второго свойств неопределенного интеграла приведены для пояснения.

Для доказательства третьего и четвертого свойств достаточно найти производные от правых частей равенств:

Эти производные равны подынтегральным функциям, что и является доказательством в силу первого свойства. Оно же используется в последних переходах.

Таким образом, задача интегрирования является обратной задаче дифференцирования, причем между этими задачами очень тесная связь:

• первое свойство позволяет проводить проверку интегрирования. Чтобы проверить правильность выполненного интегрирования достаточно вычислить производную полученного результата. Если полученная в результате дифференцирования функция окажется равной подынтегральной функции, то это будет означать, что интегрирование проведено верно;
• второе свойство неопределенного интеграла позволяет по известному дифференциалу функции найти ее первообразную. На этом свойстве основано непосредственное вычисление неопределенных интегралов.

Рассмотрим пример.

Пример.

Найти первообразную функции , значение которой равно единице при х = 1 .

Решение.

Мы знаем из дифференциального исчисления, что (достаточно заглянуть в таблицу производных основных элементарных функций). Таким образом, . По второму свойству . То есть, имеем множество первообразных . При х = 1 получим значение . По условию, это значение должно быть равно единице, следовательно, С = 1 . Искомая первообразная примет вид .

Пример.

Найти неопределенный интеграл и результат проверить дифференцированием.

Решение.

По формуле синуса двойного угла из тригонометрии , поэтому

Работа в IT-индустрии, свежие вакансии и резюме, поиск работы — Хабр Карьера

СпециалистамРаботодателям

Помогаем

работу в IT

Найди работу по душе

В базе Хабр Карьеры актуальные вакансии по всем ведущим специализациям IT-индустрии

• Senior React разработчик c опытом в блокчейн

  от 3 500 до 5 500 €

• Middle Frontend Developer

  от 2 000 до 4 000 $

• ReactJs разработчик, Middle+ (удаленно)

  от 1 500 до 2 500 $

• Frontend-разработчик

  До 250 000 ₽

• Frontend developer (React) / Middle, Middle+

  от 150 000 ₽

• Frontend Developer

  от 180 000 до 220 000 ₽

• Python/Django-разработчик (Middle+) в стартап Athena AI

  от 100 000 до 160 000 ₽

• Frontend-разработчик (Middle) на Vue/Nuxt

  от 150 000 ₽

Больше вакансий

• Middle QA-engineer (manual)

  от 120 000 до 200 000 ₽

• QA-engineer (manual)

  от 80 000 до 110 000 ₽

• QA engineer / Тестировщик (тестирование web-проектов)

  от 60 000 до 100 000 ₽

• QA Engineer (удалённо)

  от 3 500 $

• QA engineer/Тестировщик

  от 170 000 до 300 000 ₽

• Тестировщик

  от 60 000 до 80 000 ₽

• Тестировщик

  от 60 000 до 90 000 ₽

• Тестировщик

  от 50 000 до 65 000 ₽

Больше вакансий

• Технический эксперт

  от 120 000 до 220 000 ₽

• Middle/Senior Linux System Administrator (Infrastructure)

  от 2 500 €

• DevOps engineer (Nginx, Kubernetes, Teamcity)

  До 300 000 ₽

• DevOps Engineer (Kubernetes Platform)

  от 2 500 €

• Middle/Senior Linux Administrator (Ops)

  от 2 500 €

• Support/SRE engineer

  от 100 000 до 140 000 ₽

• DevOps инженер

  от 200 000 до 270 000 ₽

• Middle/Senior DevOps Engineer

  До 3 500 $

Больше вакансий

• Project Manager (web-разработка)

  от 130 000 ₽

• Руководитель проекта

  от 200 000 ₽

• Middle+ IT Project Manager

  от 140 000 до 180 000 ₽

• Product Manager / Consultant

  от 150 000 до 190 000 ₽

• Менеджер проектов 💘

  от 90 000 до 160 000 ₽

• Product Manager

  от 120 000 ₽

• Project Manager

  от 200 000 до 300 000 ₽

• IT Project Manager

  от 120 000 до 200 000 ₽

Больше вакансий

• Продуктовый дизайнер мобильного приложения

  от 120 000 ₽

• Product designer 🔥

  от 2 500 до 4 000 $

• UI/UX дизайнер

  от 120 000 ₽

• Графический / веб-дизайнер

  от 80 000 ₽

• Lead mobile games analyst

  До 5 000 $

• Графический дизайнер

  от 70 000 до 85 000 ₽

Больше вакансий

• Data Scientist

  от 170 000 до 300 000 ₽

• Бизнес/системный аналитик в команду машинного обучения (ML)

  от 250 000 ₽

• Системный аналитик

  от 200 000 до 250 000 ₽

• Бизнес-аналитик / Business Analyst

  от 200 000 до 350 000 ₽

• Data Scientist

  от 150 000 до 250 000 ₽

• Системный аналитик

  от 200 000 до 250 000 ₽

• Бизнес-аналитик

  от 123 000 ₽

• Data Scientist

  от 120 000 до 200 000 ₽

Больше вакансий

• Трафик-менеджер (тимлид)

  от 100 000 до 150 000 ₽

• SEO специалист

  от 70 000 до 125 000 ₽

• SEO-specialist

  от 2 000 €

• SEO специалист

  от 150 000 ₽

• Директолог

  от 40 000 ₽

• Маркетолог / Интернет-маркетолог

  от 90 000 до 160 000 ₽

Больше вакансий

• Developer

  1672 вакансии

• Software Engineer

  1672 вакансии

• Инженер разработчик

  1213 вакансий

• Инженер программист 2 категории

  1170 вакансий

• Веб разработчик

  1004 вакансии

• Технолог разработчик

  826 вакансий

• Backend разработчик

  813 вакансий

• Инженер программист 3 категории

  771 вакансия

• Аналитик

  652 вакансии

• Тестировщик

  586 вакансий

• Инженер технолог программист

  569 вакансий

• Удалённая работа

  2271 вакансия

Больше вакансий

Изучи будущее место работы

Нам доверяют лучшие компании, которые регулярно размещают вакансии для IT-специалистов у нас

• Code the lifestyle

  • Современные технологии

    4. 77

  • Интересные задачи

    4.77

  • Профессиональный рост

    4.73

• Ведущая глобальная компания, оказывающая услуги по формированию digital стратегии и разработке программного обеспечения

  • Профессиональный рост

    4.62

  • Социальный пакет

    4.57

  • Комфортные условия труда

    4.56

• Делаем жизнь 15 миллионов клиентов проще и удобнее каждый день

  • Компания делает мир лучше

    4.74

  • Современные технологии

    4.7

  • Интересные задачи

    4.57

• Место встречи лучших

  • Комфортные условия труда

    4.76

  • Социальный пакет

    4.64

  • Профессиональный рост

    4.55

• Разработка системы деловых коммуникаций и электронного документооборота с >1 млн. компаний-пользователей

  • Комфортные условия труда

    4.71

  • Компания делает мир лучше

    4. 49

  • Отношения с коллегами

    4.45

• Digital-подразделение Альфа-Банка

  • Отношения с коллегами

    4.63

  • Компания делает мир лучше

    4.48

  • Карьерный рост

    4.43

• Многопрофильная группа ИТ-компаний, лидер российской отрасли информационных технологий

  • Отношения с коллегами

    4.59

  • Компания делает мир лучше

    4.53

  • Профессиональный рост

    4.44

• Компания, которая развивает самую популярную в России поисковую систему и десятки других сервисов

  • Комфортные условия труда

    4.78

  • Социальный пакет

    4.72

  • Компания делает мир лучше

    4.6

• Компания с гибким подходом к работе, инновационными проектами, технологичными решениями и яркой корпоративной культурой

  • Отношения с коллегами

    4.45

  • Комфортные условия труда

    4. 4

  • Современные технологии

    4.4

• Крупнейший оптовый поставщик товаров народного потребления в России

  • Карьерный рост

    4.82

  • Современные технологии

    4.64

  • Профессиональный рост

    4.55

• IT-компания и основной цифровой партнер торговых сетей и бизнесов X5 Group

• Группа компаний, которые оказывают профессиональные услуги в области информационных и цифровых технологий

  • Социальный пакет

    4.42

  • Компания делает мир лучше

    4.39

  • Отношения с коллегами

    4.37

• The online collaborative whiteboarding platform

  • Компания делает мир лучше

    4.99

  • Социальный пакет

    4.99

  • Профессиональный рост

    4.94

• Аутсорсинговая компания, ориентированная на разработку ПО

  • Комфортные условия труда

    4.87

  • Профессиональный рост

    4. 86

  • Современные технологии

    4.84

• Технологии — это просто, понятно и удобно

  • Компания делает мир лучше

    4.9

  • Профессиональный рост

    4.9

  • Грамотность менеджмента

    4.85

• Делаем эффективные инструменты для разработчиков

  • Компания делает мир лучше

    5.0

  • Связь с топ-менеджментом

    5.0

  • Карьерный рост

    5.0

• Лизинговая компания

  • Компания делает мир лучше

    5.0

  • Связь с топ-менеджментом

    4.9

  • Социальный пакет

    4.9

• Международный сервис пассажирских и грузовых перевозок со штаб-квартирой в Маунтин-Вью, Калифорния

  • Компания делает мир лучше

    5.0

  • Профессиональный рост

    4.91

  • Комфортные условия труда

    4.91

• Американская компания со штаб-квартирой в Калифорнии, разрабатывающая одноимённый продукт для управления проектами

  • Комфортные условия труда

    4. 92

  • Социальный пакет

    4.85

  • Отношения с коллегами

    4.77

• Ведущий платёжный сервис в России и странах СНГ

  • Комфортные условия труда

    4.92

  • Профессиональный рост

    4.83

  • Современные технологии

    4.83

• Одна из крупнейших российских ИТ-компаний

  • Интересные задачи

    4.86

  • Компания делает мир лучше

    4.79

  • Комфортные условия труда

    4.79

• Global Money App

• Один из лидеров российской индустрии медиа и развлечений

  • Комфортные условия труда

    4.85

  • Отношения с коллегами

    4.74

  • Современные технологии

    4.67

• Международная компания, специализирующаяся на консалтинге, технологических услугах и аутсорсинге

Рейтинг компаний

03

Создай профессиональное резюме

Из профиля на Хабр Карьере можно получить исчерпывающую информацию о твоих достижениях. Просто отправь работодателю ссылку на свой профиль.

и расскажи о себе больше

Создать профиль

Следи за актуальными зарплатами

Сервис позволяет узнать текущую зарплату по любой специальности ИТ-отрасли. Ежедневно мы обновляем данные о зарплате

Больше данных

Качай свой скилл

На Хабр Карьере собраны образовательные курсы от 100 лучших школ дополнительного образования в IT

• Разработка игр на Unity

  61 900 ₽

• Офлайн-курс JavaScript-разработчик

  29 900 ₽

• Углубленный курс по Python

  45 000 ₽

• 1C-разработчик trial

  100 087 ₽

• Архитектура и шаблоны проектирования

  45 000 ₽

• PRO версия курса GAMEDEV

  151 500 ₽

• Hyper Casual

  67 500 ₽

• Разработка игр в Unreal Engine на C++

  67 500 ₽

Больше курсов

• Офлайн-курс инженер по тестированию

  29 900 ₽

• Нагрузочное тестирование

  70 000 ₽

• Тестировщик

  177 503 ₽

• Профессия Тестировщик на Python

  129 600 ₽

• Тестировщик ПО

  80 925 ₽

• Инженер по тестированию

  20 050 ₽

• Тестировщик ПО

  82 500 ₽

• Автоматизированное тестирование веб-приложений на JavaScript

  48 000 ₽

Больше курсов

• DevOps практики и инструменты

  100 000 ₽

• Профессия Системный администратор

  113 400 ₽

• DevOps-инженер PRO

  180 000 ₽

• Факультет DevOps

  270 000 ₽

• DevOps-инженер с нуля

  161 100 ₽

• Инфраструктурная платформа на основе Kubernetes

  85 000 ₽

• Administrator Linux. Professional

  85 000 ₽

• DevOps-инженер

  111 600 ₽

Больше курсов

• Менеджмент игровых проектов

  61 900 ₽

• Офлайн-курс Тайм-менеджмент

  9900 ₽

• Управление разработкой продукта

  59 502 ₽

• Product Manager IT-проектов

  70 000 ₽

• Быстрое погружение в продакт-менеджмент

  29 000 ₽

• Agile: от основ до скрам-мастера

  96 200 ₽

• Методологии Agile в управлении проектами

  10 900 ₽

• Продюсирование Игр

  79 200 ₽

Больше курсов

• 3D-художник по оружию

  146 200 ₽

• 3D-художник по персонажам

  132 900 ₽

• Моушен-дизайнер

  72 600 ₽

• Анатомия игровых персонажей

  16 300 ₽

• Текстурный трип

  45 900 ₽

• Пиксель-арт

  45 800 ₽

• Houdini FX

  61 900 ₽

• 3D-Аниматор

  139 800 ₽

Больше курсов

• Офлайн-курс Data Science

  59 900 ₽

• Excel + Google Таблицы с нуля до PRO

  31 597 ₽

• Компьютерное зрение

  70 000 ₽

• Мастер Google-таблиц

  24 833 ₽

• Аналитик данных

  30 200 ₽

• SQL и получение данных

  36 050 ₽

• Офлайн-курс Power BI

  19 900 ₽

• Power BI PRO

  53 820 ₽

Больше курсов

Читай полезные статьи

Мы регулярно публикуем полезные статьи для карьеры: исследования, дайджесты событий, рейтинги работодателей и многое другое.

• Активность найма

  7 апреля

  Активность найма на IT-рынке в марте 2023

• Мероприятия

  28 марта

  Дайджест событий для HR и рекрутеров в IT в апреле 2023

• Кем работать

  21 марта

  Кем работать в IT в 2023: Системный аналитик

• Спецпроекты

  13 марта

  Неделю фронтенда 2023 объявляем открытой

• Кем работать

  9 марта

  Кем работать в IT: scrum-мастер

• Активность найма

  7 марта

  Активность найма на IT-рынке в феврале 2023

• Мероприятия

  2 марта

  Дайджест событий для эйчаров и рекрутеров в IT в марте 2023

• Зарплаты

  1 марта

  Зарплаты разработчиков во второй половине 2022: языки и квалификации

• Зарплаты

  22 февраля

  Сколько тратят в IT: сеньор бэкендер

• Спецпроекты

  22 февраля

  Карьерная неделя с победителями рейтинга работодателей Хабр Карьеры — 27 февраля

• Активность найма

  6 февраля

  Активность найма на IT-рынке в январе 2023

• Зарплаты

  2 февраля

  Зарплаты айтишников во втором полугодии 2022: +7% за счет регионов

Больше статей

f(x+h)-f(x)/h — Формула, Вывод | Коэффициент разности

LearnPracticeDownload

f(x+h)-f(x)/h — это формула, являющаяся частью предельного определения производной (основные принципы). Предельное определение производной функции f(x) таково: f'(x) = lim ₕ → ₀ [f(x + h) — f(x)] / h. Но какая связь между производной и формулой f(x+h)-f(x)/h? Покажи нам.

Давайте узнаем больше о f(x+h)-f(x)/h, а также о его значении, выводе и примерах.

1.	Что такое F(x+h) — F(x)/h?
2.	F(x+h) — F(x)/h Вывод
3.	Как найти F(x+h)-F(x)/h?
4.	Часто задаваемые вопросы по F(x+h)-F(x)/h

Что такое F(x+h) — F(x)/h?

f(x+h)-f(x)/h называется разностным отношением функции f(x). Что такое разностный коэффициент функции? Здесь слова «разность» и «частное» дают представление о доле разности координат и, следовательно, представляют наклон линии, проходящей через две точки кривой. Линия, пересекающая кривую в двух точках, называется секущей. Следовательно, f(x+h)-f(x)/h представляет собой наклон секущей.

F(x+h)-F(x)/h Формулы

Вот некоторые формулы, связанные с f(x+h)-f(x)/h:

• f(x+h) )-f(x)/h называется разностным отношением функции f(x).
• f(x+h)-f(x)/h — наклон секущей функции f(x), проходящей через две точки (x, f(x)) и (x + h, f(x + час)).
• f(x+h)-f(x)/h — среднее значение изменения функции f(x) на интервале [x, x + h].
• lim ₕ → ₀ f(x+h)-f(x)/h дает производную функции f(x) и обозначается f ‘(x).

F(x+h) — F(x)/h Вывод

Рассмотрим приведенный выше рисунок, где y = f(x) — кривая с двумя точками A (x, f(x)) и B (x + h, f(x + h)) на ней. Найдем наклон секущей АВ по формуле наклона. Для этого предположим, что A (x, f(x)) = (x₁, y₁) и B (x + h, f(x + h)) = (x₂, y₂). Тогда наклон секущей AB равен

(y₂ — y₁) / (x₂ — x₁)

= (f (x + h) — f(x)) / (x + h — x)

= f(x+h)-f(x)/h

Отсюда формула.

Как F(x+h) — F(x)/h связано с производной?

Мы знаем, что производная функции f(x) есть не что иное, как наклон касательной. На приведенном выше рисунке, если точка B приближается к A (т. е. если B приблизительно совпадает с A), то секущая AB становится касательной в точке A. Для этого расстояние по горизонтали между двумя точками A и B должно быть примерно равно 0 , т. е. секущая становится касательной, если h → 0, т. е.

Наклон касательной = lim ₕ → ₀ f(x+h)-f(x)/h

(или)

f ‘(x) = lim ₕ → ₀ f( х+ч)-f(х)/ч

Как найти F(x+h)-F(x)/h?

Вот шаги для вычисления f(x+h)-f(x)/h для заданной функции f(x). Шаги объясняются на примере f(x) = x ² + 2x.

• Шаг — 1: Вычислите f(x + h), подставив x = x + h с обеих сторон f(x).
  Тогда f(x + h) = (x + h) ² + 2(x + h)
  = x ² + 2xh + h ² + 2x + 2h
• Шаг — 2: Вычислите разницу f(x + h) — f(x).
  f(x + h) — f(x) = [x ² + 2xh + h ² + 2x + 2h] — [x ² + 2x]
  = х ² + 2хч + ч ² + 2х + 2ч — х ² — 2х
  = 2хч + ч ² + 2ч
• Шаг — 3: Разделить разницу от Шаг — 2 по h.
  [f(x + h) — f(x)]/h = (2xh + h ² + 2h) / h
  = ч (2х + ч + 2) / ч
  = 2х + ч + 2

Важные моменты по F(x+h)-F(x)/h:

• f(x+h)-f(x)/h называется формулой разностного отношения.
• f(x+h)-f(x)/h дает среднюю скорость изменения функции f(x) на интервале [x, x + h].
• f(x+h)-f(x)/h при стремлении h к 0 дает производную от f(x).
• f(a+h)-f(a)/h при стремлении h к 0 дает наклон касательной кривой y = f(x) в точке x = a.
• f(x+h)-f(x)/h для любой строки f(x) = mx + b равно m.
• f(x+h)-f(x)/h для любой постоянной функции f(x) = c равно 0,

Связанные темы:

• f(x+h)-f(x)/h Калькулятор
• Калькулятор производных
• Калькулятор касательной
• Калькулятор антипроизводных

 

Примеры F(x+h)-F(x)/h

1. Пример 1: Вычислить f(x+h)-f(x)/h, когда f(x) = 2x — 7.

   Решение:

   Дано, что f(x) = 2x + 7

   Тогда f(x+h) = 2(x+h) + 7 = 2x + 2h + 7

   Теперь f(x+h)-f(x)/h = [2x + 2h + 7 — 2x — 7] / ч

   = 2ч/ч

   = 2

   Ответ: f(x+h)-f(x)/h = 2.

2. Пример 2: Найти разностное частное функции f(x) = x ³ — 4.

   Решение:

   Дано, что f(x) = x ³ — 4.

   Тогда f(x +h) = (x+h) ³ — 4 = x ³ + 3x ² h + 3xh ² + h ³ — 4

   Разностное частное y = f(x) равно :

   f(x+h)-f(x)/h = [x ³ + 3x ² h + 3xh ² + h ³ — 4 — x ³ + 4] / h

   = [3x ² H + 3XH ² + H ³ ] / H

   = H [3x ² + 3XH + H ² ] / H

   = 3x ² + 3XH 3x 3x 3x 3x 3x 3x 3xhh 3x 3xhh 3xhh 3xhh 3 ] / ч ^{= 3x 2 . + h 2}

   Ответ: Частное разности равно 3x ² + 3xh + h ² .

3. Пример 3: Найдите среднюю скорость изменения функции f(x) = e ^x на интервале [x, x + h].

   Решение:

   Дано, что f(x) = e ^x .

   Тогда f(x+h) = e ^{(x + h)} .

   Средняя скорость изменения функции f(x):

   f(x+h)-f(x)/h = [e ^{(x + h)} — e ^x ]/h

   Ответ: х [е ^ч — 1] /ч.

перейти к слайду перейти к слайду перейти к слайду

Отличное обучение в старшей школе с использованием простых подсказок

Увлекаясь зубрежкой, вы, скорее всего, забудете понятия. С Cuemath вы будете учиться визуально и будете удивлены результатами.

Записаться на бесплатный пробный урок

Практические вопросы по F(x+h)-F(x)/h

 

перейти к слайдуперейти к слайду

Часто задаваемые вопросы по F(x+h)-F(x)/h

Что такое F(x+h)-F(x)/h?

f(x+h)-f(x)/h называется коэффициентом разности и представляет наклон секущей кривой y = f(x).

Как найти F(x+h)-F(x)/h?

Чтобы найти f(x+h)-f(x)/h для заданной функции y = f(x):

• Найдите f(x+h), заменив x на x + h в f(x ).
• Найдите разность f(x+h)-f(x).
• Разделите вышеуказанную разницу на h.

Какое другое название для F(x+h)-F(x)/h?

f(x+h)-f(x)/h считается равным:

• наклон секущей
• коэффициент разности
• средняя скорость изменения

Каков предел F(x+h)-F(x)/h, когда h стремится к 0?

f(x+h)-f(x)/h — наклон секущей, проходящей через точки (x, f(x)) и (x+h, f(x+h)) на кривой у = f (х). Когда h стремится к нулю, секущая линия становится касательной, и в этом случае f(x+h)-f(x)/h представляет наклон касательной и, следовательно, также представляет производную f'(x).

Как F(x+h)-F(x)/h связано с производной от F(x)?

f(x+h)-f(x)/h участвует в предельном определении производной. Для любой функции f(x) ее производная равна f'(x) = lim ₕ → ₀ f(x+h)-f(x)/h.

Является ли F(x+h)-F(x)/h наклоном касательной?

Нет, f(x+h)-f(x)/h — наклон секущей. Он представляет собой наклон касательной только тогда, когда h стремится к 0.2, найти fx(2,1) и fy(2,1)?

Выберите область веб-сайта для поиска

Искать на этом сайте

Цитата страницы Начать эссе значок-вопрос Задайте вопрос

Начать бесплатную пробную версию

Скачать PDF PDF Цитата страницы Цитировать Поделиться ссылкой Делиться 92 -4 года

Замените на (2,1)

==> fy(2,1) = 3(4)(1) -4(1) = 12-4= 8

См. eNotes без рекламы

Начните с 48-часовой бесплатной пробной версией , чтобы получить доступ к более чем 30 000 дополнительных руководств и более чем 350 000 вопросов помощи при выполнении домашних заданий, на которые наши эксперты ответили.

Получите 48 часов бесплатного доступа

Уже зарегистрирован? Войдите здесь.

Утверждено редакцией eNotes

Задайте вопрос

Похожие вопросы

Просмотреть все

Математика

Последний ответ опубликован 07 сентября 2010 г. в 12:47:25.

Что означают буквы R, Q, N и Z в математике?

14 ответов воспитателя

математика

Последний ответ опубликован 07 октября 2013 г. в 20:13:27.

Как определить, является ли это уравнение линейной или нелинейной функцией?

84 Ответы воспитателя

Математика

Последний ответ опубликован 25 февраля 2016 г.