558. Найдите координаты точки пересечения графиков функций. Макарычев алгебра 8 класс – Рамблер/класс
558. Найдите координаты точки пересечения графиков функций. Макарычев алгебра 8 класс – Рамблер/классИнтересные вопросы
Школа
Подскажите, как бороться с грубым отношением одноклассников к моему ребенку?Новости
Поделитесь, сколько вы потратили на подготовку ребенка к учебному году?Школа
Объясните, это правда, что родители теперь будут информироваться о снижении успеваемости в школе?Школа
Когда в 2018 году намечено проведение основного периода ЕГЭ?Новости
Будет ли как-то улучшаться система проверки и организации итоговых сочинений?Вузы
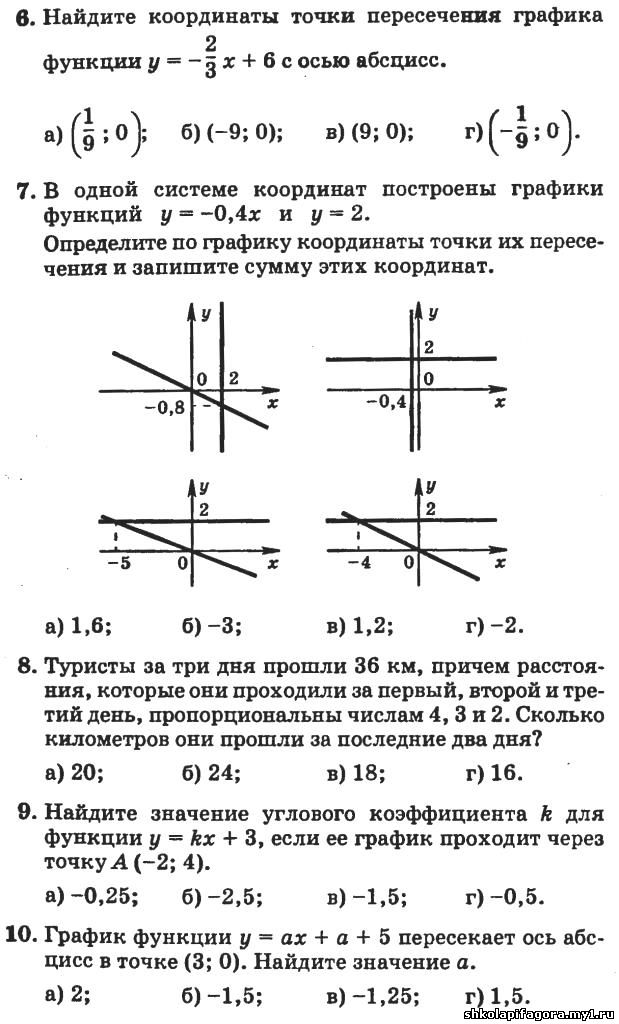
Подскажите, почему закрыли прием в Московский институт телевидения и радиовещания «Останкино»?558. Не выполняя построения, найдите координаты точки пересече-
ния графиков линейных функций:
а) у =7х −1 и у = 2х; в) у = 5х + 8 и у = 3х + 2;
б) у = 3х − 11 и у = 4; г) у = 4 − х и у = 3х.
ответы
решаем алгебраически
ваш ответ
Можно ввести 4000 cимволов
отправить
дежурный
Нажимая кнопку «отправить», вы принимаете условия пользовательского соглашения
похожие темы
ПсихологияЕГЭ10 класс9 класспохожие вопросы 5
150 Алгебра 9 класс Макарычев Помогите решить графическиРешите графически уравнение:
а) х3 = 2; б) х3 = 4; в) х3 = -5.
ЭкзаменыАлгебра9 классМакарычев Ю.Н.ГДЗ
Когда скорость изменения функции будет наибольшей или наименьшей? Алгебра 10-11 класс Колмогоров Упр 308Совсем я в точных науках не сильна) Кто поможет?) Найдите значения аргумента из промежутка [-2; 5], при которых скорость изменения (Подробнее…)
ГДЗ11 классКолмогоров А.Н.Алгебра
Приготовление раствора сахара и расчёт его массовой доли в растворе. Химия. 8 класс. Габриелян. ГДЗ. Хим. практикум № 1. Практ. работа № 5.Попробуйте провести следующий опыт. Приготовление раствора
сахара и расчёт его массовой доли в растворе.
Отмерьте мерным (Подробнее…)
ГДЗШкола8 классХимияГабриелян О.С.
16. Расставьте все знаки препинания: укажите цифру(-ы), на месте которой(-ых)… Цыбулько И. П. Русский язык ЕГЭ-2017 ГДЗ. Вариант 13.16.
Расставьте все знаки препинания: укажите цифру(-ы), на месте которой(-ых)
в предложении должна(-ы) стоять запятая(-ые). (Подробнее…)
ГДЗЕГЭРусский языкЦыбулько И.П.
ЕГЭ-2017 Цыбулько И. П. Русский язык ГДЗ. Вариант 13. 18. Расставьте все знаки препинания: укажите цифру(-ы), на месте которой(-ых)…18.
Расставьте все знаки препинания: укажите цифру(-ы), на месте которой(-ых)
в предложении должна(-ы) стоять запятая(-ые). (Подробнее…)
ГДЗЕГЭРусский языкЦыбулько И.П.
Функции: графики и пересечения
Горячая математика Предполагать
ф
(
Икс
)
и
г
(
Икс
)
две функции, которые принимают на вход действительное число и выводят действительное число.
Тогда точки пересечения ф ( Икс ) и г ( Икс ) это те числа Икс для которого ф ( Икс ) «=» г ( Икс ) .
Иногда точные значения можно легко найти, решив уравнение ф ( Икс ) «=» г ( Икс ) алгебраически.
Пример 1:
Каковы точки пересечения функций ф ( Икс ) и г ( Икс ) если ф ( Икс ) «=» Икс + 6 и г ( Икс ) «=» − Икс ?
Точки пересечения
ф
(
Икс
)
и
г
(
Икс
)
это те числа
Икс
для которого
ф
(
Икс
)
«=»
г
(
Икс
)
.
То есть, Икс + 6 «=» − Икс .
Решить для Икс .
Икс + 6 «=» − Икс 2 Икс + 6 «=» 0 2 Икс «=» − 6 Икс «=» − 3
Теперь вы можете использовать значение Икс найти соответствующий у -координата точки пересечения.
Подставьте значение Икс в любой из двух функций.
г ( − 3 ) «=» − ( − 3 ) «=» 3
Уравнения также можно решить графически, нанеся две функции на координатную плоскость и указав точку их пересечения.
В других случаях точные значения найти сложно. Возможно, вам придется использовать технологию для их оценки.
Пример 2:
Найдите точку (точки) пересечения двух функций.
ф ( Икс ) «=» | Икс − 5 | г ( Икс ) «=» бревно Икс
Здесь решить алгебраически не так просто. Решения уравнения | Икс − 5 | «=» бревно Икс не являются красивыми рациональными числами.
График функций на координатная плоскость .
Вы можете использовать графическую утилиту, чтобы найти, что координаты точек пересечения приблизительно
(
4,36
,
0,64
)
и
(
5,76
,
0,76
)
.
3.2: Перекрестки — Mathematics LibreTexts
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 63370
Во многих задачах интегрального исчисления вы будете находить площадь, заключенную между несколькими функциями или между ними. В рамках нахождения площади вам нужно будет определить, где функции пересекаются друг с другом, то есть пары координат \((x,y)\), где пересекаются кривые. точки пересечения двух функций, \(f(x)\) и \(g(x)\), являются парами координат \((x,y)\), для которых вход, \(x\) , приводит к одинаковому выходному значению обеих функций. В этом разделе мы рассмотрим три различных метода нахождения точек пересечения двух графиков.
Первые два метода, которые мы обсудим, в значительной степени зависят от навыков, которые вы приобрели в предыдущем разделе, где узнали, как находить переменные.
Обратите внимание, что, хотя мы в основном использовали обозначение функции, такое как \(f(x)\), здесь мы часто будем указывать вывод функции как \(y\). Одна из причин, по которой мы используем \(y\) здесь, заключается в том, что некоторые из наших функций будут определены
3.2.1 Замена
Замена чаще всего используется, когда одна или обе функции определены неявно или когда обе функции имеют общий термин. С помощью этого метода мы решим одно уравнение для одной из переменных, а затем подставим решение во второе уравнение и решим для оставшейся переменной.
В этом курсе нас интересуют только решения действительных чисел. Здесь это вопрос личных предпочтений при выборе, с какой функцией работать изначально и для какой переменной решать. Однако мы рекомендуем начать с уравнения, которое является «более простым»; если одно уравнение линейное, а другое квадратичное, обычно проще начать с линейной функции. Давайте посмотрим на пример. 92=4\) квадратично как по \(x\), так и по \(y\), но второе уравнение \(y-1=2(x-1)\) линейно по обоим \(x\) и в \(у\). Поэтому мы начнем нашу работу со второго уравнения.
Кроме того, во втором уравнении \(y\) уже почти изолировано, поэтому мы сначала изолируем \(y\) в этом уравнении.
\[\begin{align}\begin{align}\begin{split} y-1 & = 2(x-1) \\ y & = 2(x-1)+1 \\ & = 2x-2 +1 \\ & = 2x-1 \end{split}\end{align}\end{align}\]
92-4(8)(-3)}}{2(8)} \\[6pt] & = \frac{4 \pm \sqrt{16+96}}{16} \\[6pt] & = \ frac{4\pm \sqrt{112}}{16} \\[6pt] & = \frac{4 \pm 4 \sqrt{7}}{16} \\[6pt] & = \frac{1 + \ sqrt{7}}{4}, \frac{1 — \sqrt{7}}{4} \end{split}\end{aligned}\end{align}\] Это дает нам только \(x \) координаты; нам также нужны координаты \(y\).
Чтобы получить соответствующие координаты \(y\), мы будем использовать линейное уравнение, где мы уже решили для \(y\) через \(x\). Мы могли бы использовать более раннюю форму этого уравнения или даже квадратное уравнение, но любое из них потребовало бы дополнительной работы. Первая координата \(y\):
\[\begin{align}\begin{align} y&=2x-1 \\ &=2\left(\frac{1+\sqrt{7}}{4}\right)-1 \\ &= \frac{1+\sqrt{7}}{2}-\frac{2}{2} \\ &=\frac{-1+\sqrt{7}}{2}\end{выровнено}\end{ align}\]
Вторая координата \(y\): \[\begin{align}\begin{aligned}\begin{split} y & = 2x -1 \\ & = 2\Bigg(\frac{ 1 — \sqrt{7}}{4}\Bigg) -1 \\[6pt] & =\frac{1 — \sqrt{7}}{2} — \frac{2}{2} \\[6pt ] & = \frac{-1 — \sqrt{7}}{2} \end{split}\end{aligned}\end{align}\]
Теперь у нас есть обе точки пересечения:
\[\left(\frac{1+\sqrt{7}}{4},\frac{-1+\sqrt{7}}{2}\right)\text{ и }\left(\frac {1-\sqrt{7}}{4},\frac{-1-\sqrt{7}}{2}\right)\]
Иногда мы можем проявить творческий подход к использованию замены.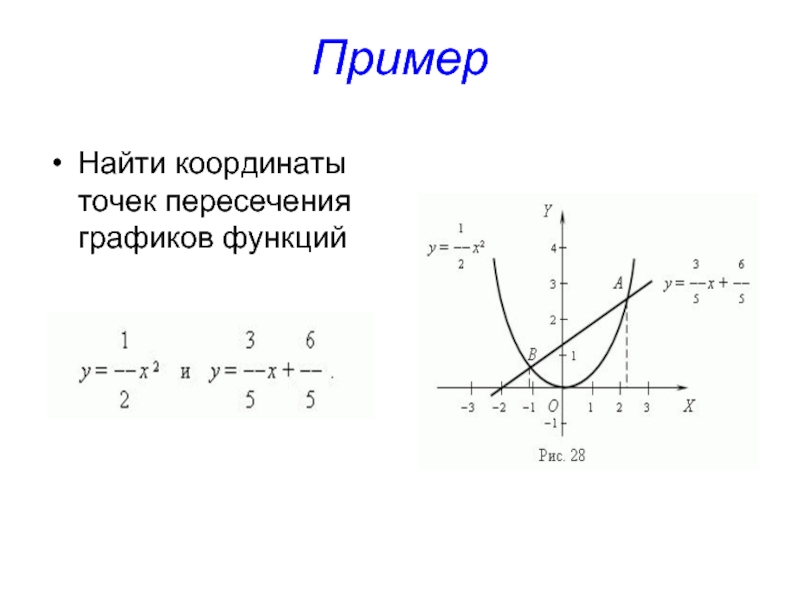
В зависимости от уравнений, с которыми вы работаете, иногда может быть быстрее решить , а не для переменной полностью, а скорее для члена, который появляется в обоих уравнениях. Давайте посмотрим на пример.
Пример \(\PageIndex{2}\): точки пересечения: замена 92\). Здесь это дает нам воображаемый ответ для \(y\), так что мы не получаем дополнительную точку пересечения. Единственной точкой пересечения этих уравнений является
\[(4,0)\]
3.2.2 Приравнивание функций
Следующий метод, который мы обсудим, хорошо работает, когда обе функции явные или заданы в виде функций. Для этого метода мы сначала решим каждое уравнение для одной и той же переменной, установим два равными для каждого и решим.
Пример \(\PageIndex{3}\): Точки пересечения: равенство 92 -x &= 0 \\ x(x-1)&=0 \\ x&= 0,1 \end{split}\end{aligned}\end{align}\]
Теперь осталось найти координаты \(у\). Для этого мы можем использовать \(f(x)\) или \(g(x)\); \(g(x)\) проще, поэтому мы будем использовать его.
Получаем, что \(g(0) = 1\) и \(g(1)=2\). Таким образом, у нас есть две точки пересечения:
\[(0,1)\text{ и }(1,2)\]
3.2.3 Исключение
Третий метод, который мы обсудим, немного отличается от первого. другие методы, которые мы видели. Этот метод также требует сильных навыков алгебры. Основное преимущество этого метода не будет очевидным до следующего раздела этой книги, потому что он наиболее полезен, когда у нас есть система из двух или более линейных уравнений. Здесь мы покажем, как использовать его только с двумя переменными, но идея расширяется (это означает, что этот метод легко адаптировать к другим, более сложным ситуациям). Для исключения мы возьмем каждое уравнение, умножим все уравнение на константу и сложим уравнения вместе таким образом, чтобы исключить одну переменную.
Пример \(\PageIndex{4}\): Точки пересечения: Исключение
Найти все точки пересечения \(2x+3y=2\) и \(-x+y=4\).
Решение
Сначала попробуем исключить \(x\) из обоих уравнений.
Первое уравнение имеет \(2x\), а второе имеет \(-x\). Если мы умножим второе уравнение на \(2\) и добавим его к первому, члены \(x\) сократятся:
\[\begin{align}\begin{align}2x+3y&=2 \ \ +2(-x+y&=4)\end{выровнено}\end{выровнено}\]
или:
\[\begin{align}\begin{aligned}2x+3y&=2 \\ +(-2x+2y&=8) \\ \hline 5y&=10\end{align}\end{align }\]
Обратите внимание, что мы выровняли наши переменные и обработали это как большую задачу сложения. Упорядочивание переменных упрощает нашу работу.
Теперь мы можем взять результат и легко найти \(y\), получив \(y=2\). Теперь мы можем использовать \(y\), чтобы найти \(x\). Подойдет любое уравнение, но мы будем использовать второе: \(-x+(2) = 4\) или \(x=-2\). Это дает использование одной точки пересечения на
\[(-2,2)\]
Исключение — особенно гибкий метод. Чтобы проиллюстрировать это, мы снова решим задачу, но на этот раз сначала исключим \(y\).
Пример \(\PageIndex{5}\): Точки пересечения: Исключение
Найти все точки пересечения \(2x+3y=2\) и \(-x+y=4\).
Решение
Первое уравнение имеет \(3y\), а второе имеет \(y\). Умножим первое уравнение на \(-\frac{1}{3}\) и добавим его ко второму уравнению:
\[\begin{align}\begin{aligned}-\frac{1}{3}(2x+3y&=2) \\ +\quad (-x+y&=4) \\ \hline -\frac {5}{3}x&=\frac{10}{3}\end{aligned}\end{align}\]
Решение \(-\frac{5}{3}x = \frac{10}{ 3}\) дает нам \(x=-2\), а подстановка в любое уравнение дает нам \(y=2\). Мы получаем ту же точку пересечения:
\[(-2,2)\]
Кроме того, мы могли бы умножить второе уравнение, \(-x+y=4\), на \(3\) и вычесть из первого, чтобы исключить \(y\) первым. При исключении лучше немного спланировать, чтобы выяснить, какую переменную проще всего исключить в первую очередь и какие комбинации сохранят числа простыми.
3.2.4 Графики
Теперь мы кратко обсудим распространенный метод, используемый студентами: построение графиков. Хотя построение графика — отличный способ определить, сколько существует точек пересечения и их приблизительные координаты, он не даст вам точного набора координат, если только вы не воспользуетесь калькулятором или компьютером.