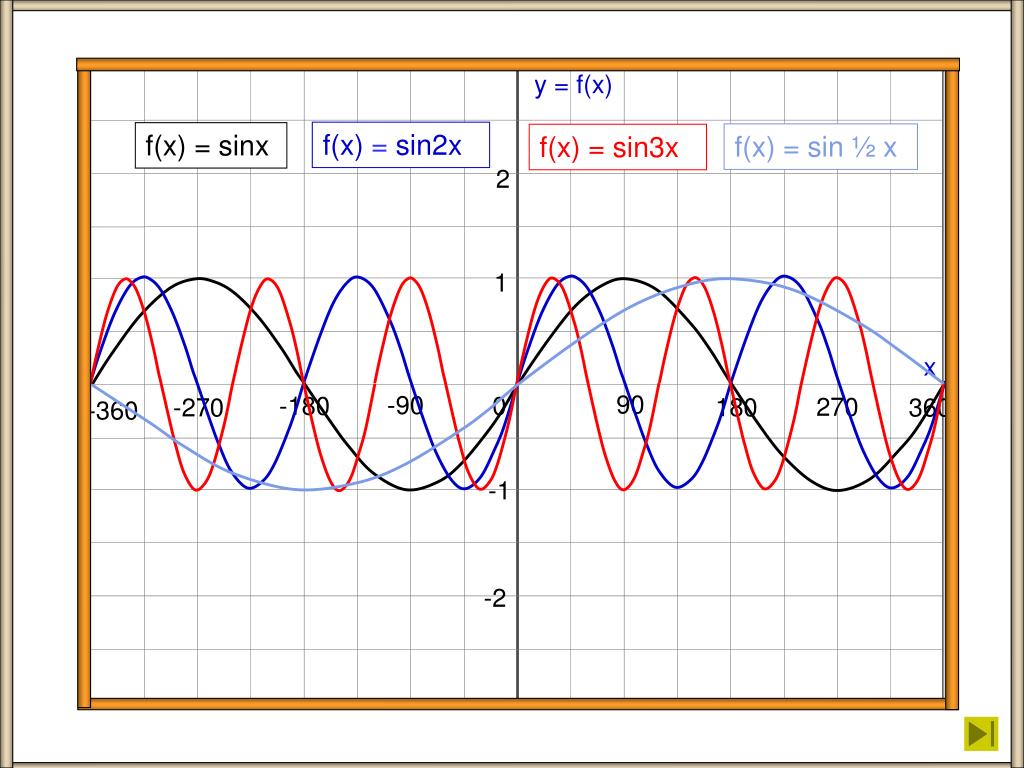
График функции y sin 2x. График функции y=sin x
«Построение графика функции с модулем» — Y = lnx. Закрепили знания на ранее изученных функциях. Построение графиков функций. Вопрос классу. Y = x2 – 2x – 3. Проектная деятельность. Урок обобщения и систематизации знаний. График функции. Актуализация знаний о графиках функций. Обобщение. Попробуйте самостоятельно построить графики. Y = f(x).
««Графики функций» 9 класс» — Цели урока. Большему значению аргумента соответствует большее значение функции. Нули функции. Определение. Заполните пропуски. Установите соответствие между функцией и вершиной. Тренажер. Выберите уравнение, с помощью которого задана линейная функция. Установите соответствие. Выберите уравнение. Обратная пропорциональность.
«Графики функций с модулями» — Найдём вершину функции. Кубическая функция. Отрицательная сторона. Графики функций. Квадратичная функция. Сложная функция. Функция с модулем. Графики функций надо обязательно уметь строить.
«Уравнение касательной к графику функции» — Производная в точке. Правила дифференцирования. График функции. Алгоритм нахождения уравнения. Ответьте на вопросы. Геометрический смысл производной. Номера из учебника. Уравнение касательной к графику функции. Определение. Касательная к графику функции. Основные формулы дифференцирования. Провести касательную.
«Построение графиков функций» — Построение графика функции y = sinx. Линия тангенсов. Алгебра. Тема: Построение графиков функций. График функции y = sinx. Выполнила: Филиппова Наталья Васильевна учитель математики Белоярская средняя общеобразовательная школа №1. Построить график функции y=sin(x) +cos(x).
«График обратной пропорциональности» — Применение гиперболы. Гипербола. Монотонность функции. Чётность, нечётность. Функция «Обратная пропорциональность». График. Построение графика обратной пропорциональности. Гипербола и космические спутники. Однополостной гиперболоид.
С нами легко в режиме онлайн строить графики различной сложности. Построение производится мгновенно. Сервис востребован для нахождения точек пересечения функций, для изображения графиков для дальнейшего их перемещения в Word документ в качестве иллюстраций при решении задач, для анализа поведенческих особенностей графиков функций. Оптимальным браузером для работы с графиками на данной странице сайта является Google Chrome. При использовании других браузеров корректность работы не гарантируется.
Дополнительные материалы
Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания! Все материалы проверены антивирусной программой.
Пособия и тренажеры в интернет-магазине «Интеграл» для 10 класса от 1С
Решаем задачи по геометрии. Интерактивные задания на построение для 7-10 классов
Программная среда «1С: Математический конструктор 6.1»
Что будем изучать:
- Свойства функции Y=sin(X).
- График функции.
- Как строить график и его масштаб.
- Примеры.
Свойства синуса. Y=sin(X)
Ребята, мы уже познакомились с тригонометрическими функциями числового аргумента. Вы помните их?
Давайте познакомимся поближе с функцией Y=sin(X)
Запишем некоторые свойства этой функции:
1) Область определения – множество действительных чисел.
3) Функция Y=sin(X) возрастает на отрезке и убывает на отрезке [π/2; π].
Когда мы движемся по первой четверти (против часовой стрелки), ордината увеличивается, а при движении по второй четверти она уменьшается.4) Функция Y=sin(X) ограничена снизу и сверху. Данное свойство следует из того, что
-1 ≤ sin(X) ≤ 1
5) Наименьшее значение функции равно -1 (при х = — π/2+ πk). Наибольшее значение функции равно 1 (при х = π/2+ πk).
Давайте, воспользовавшись свойствами 1-5, построим график функции Y=sin(X). Будем строить наш график последовательно, применяя наши свойства. Начнем строить график на отрезке .
Построение графика функции синус х, y=sin(x)
Посчитаем значения функции на нашем отрезке:
Построим график по нашим точкам, с учетом третьего свойства.
Таблица преобразований для формул привидения
Воспользуемся вторым свойством, которое говорит, что наша функция нечетная, а это значит, что ее можно отразить симметрично относительно начало координат:
Мы знаем, что sin(x+ 2π) = sin(x).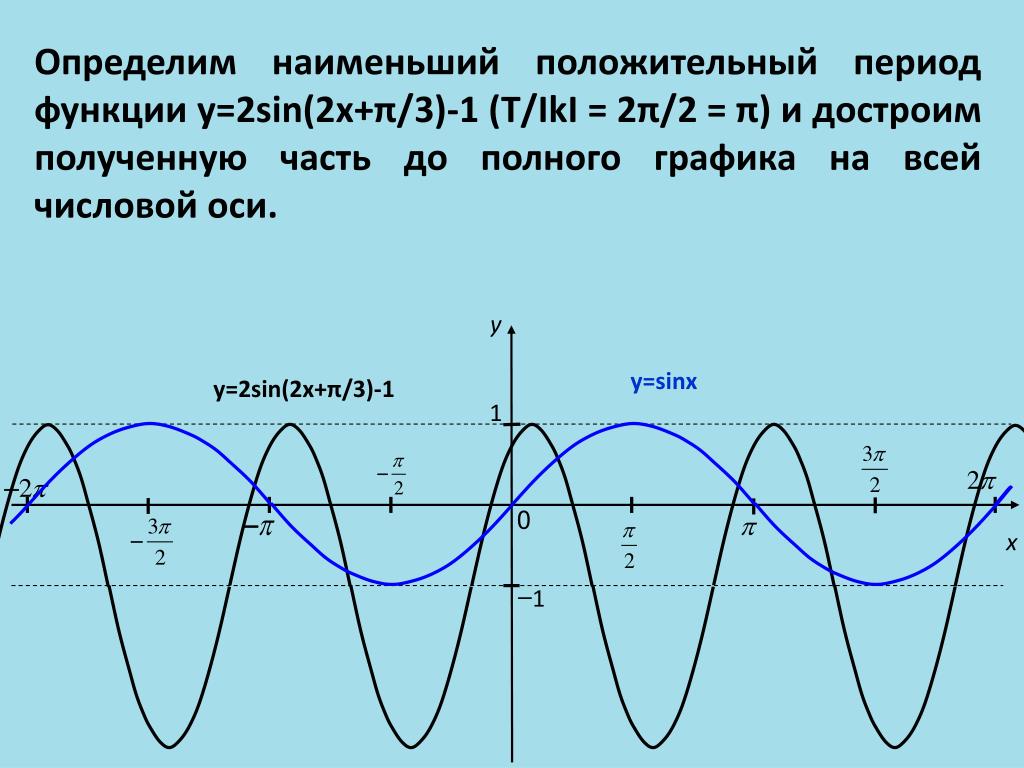
Это значит, что на отрезке [- π; π] график выглядит так же, как на отрезке [π; 3π] или или [-3π; — π] и так далее. Нам остается аккуратно перерисовать график на предыдущем рисунке на всю ось абсцисс.
График функции Y=sin(X) называют — синусоидой.
Напишем еще несколько свойств согласно построенному графику:
6) Функция Y=sin(X) возрастает на любом отрезке вида: [- π/2+ 2πk; π/2+ 2πk], k – целое число и убывает на любом отрезке вида: [π/2+ 2πk; 3π/2+ 2πk], k – целое число.
8) Область значений: отрезок [- 1; 1]. Это также хорошо видно из графика функции.
9) Функция Y=sin(X) — периодическая функция. Посмотрим опять на график и увидим, что функция принимает одни и те же значения, через некоторые промежутки.
Примеры задач с синусом
1. Решить уравнение sin(x)= x-π
Решение: Построим 2 графика функции: y=sin(x) и y=x-π (см.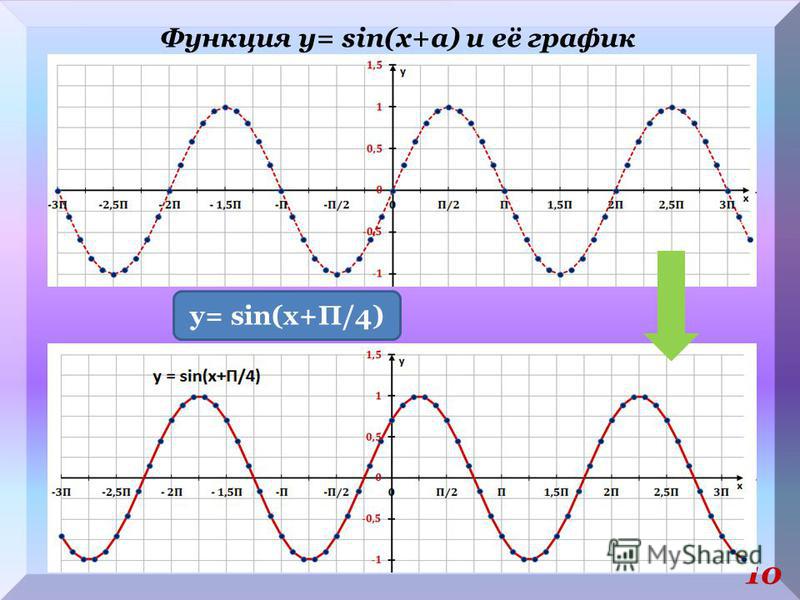
рисунок).
Наши графики пересекаются в одной точке А(π;0), это и есть ответ: x = π
2. Построить график функции y=sin(π/6+x)-1
Решение: Искомый график получится путем переноса графика функции y=sin(x) на π/6 единиц влево и 1 единицу вниз.
Решение: Построим график функции и рассмотрим наш отрезок [π/2; 5π/4].
На графике функции видно, что наибольшие и наименьшие значения достигаются на концах отрезка, в точках π/2 и 5π/4 соответственно.
Ответ: sin(π/2) = 1 – наибольшее значение, sin(5π/4) = наименьшее значение.
Задачи на синус для самостоятельного решения
- Решите уравнение: sin(x)= x+3π, sin(x)= x-5π
- Построить график функции y=sin(π/3+x)-2
- Построить график функции y=sin(-2π/3+x)+1
- Найти наибольшее и наименьшее значение функции y=sin(x) на отрезке
- Найти наибольшее и наименьшее значение функции y=sin(x) на отрезке [- π/3; 5π/6]
Как построить график функции y=sin x? Для начала рассмотрим график синуса на промежутке .
Единичный отрезок берём длиной 2 клеточки тетради. На оси Oy отмечаем единицу.
Для удобства число π/2 округляем до 1,5 (а не до 1,6, как требуется по правилам округления). В этом случае отрезку длиной π/2 соответствуют 3 клеточки.
На оси Ox отмечаем не единичные отрезки, а отрезки длиной π/2 (через каждые 3 клеточки). Соответственно, отрезку длиной π соответствует 6 клеточек, отрезку длиной π/6 — 1 клеточка.
При таком выборе единичного отрезка график, изображённый на листе тетради в клеточку, максимально соответствует графику функции y=sin x.
Составим таблицу значений синуса на промежутке :
Полученные точки отметим на координатной плоскости:
Так как y=sin x — нечётная функция, график синуса симметричен относительно начала отсчёта — точки O(0;0). С учётом этого факта продолжим построение графика влево, то точки -π:
Функция y=sin x — периодическая с периодом T=2π. Поэтому график функции, взятый на на промежутке [-π;π], повторяется бесконечное число раз вправо и влево.
Как построить график \\[y = \\sin 2x\\]?
Подсказка: Нам нужно построить график данной функции.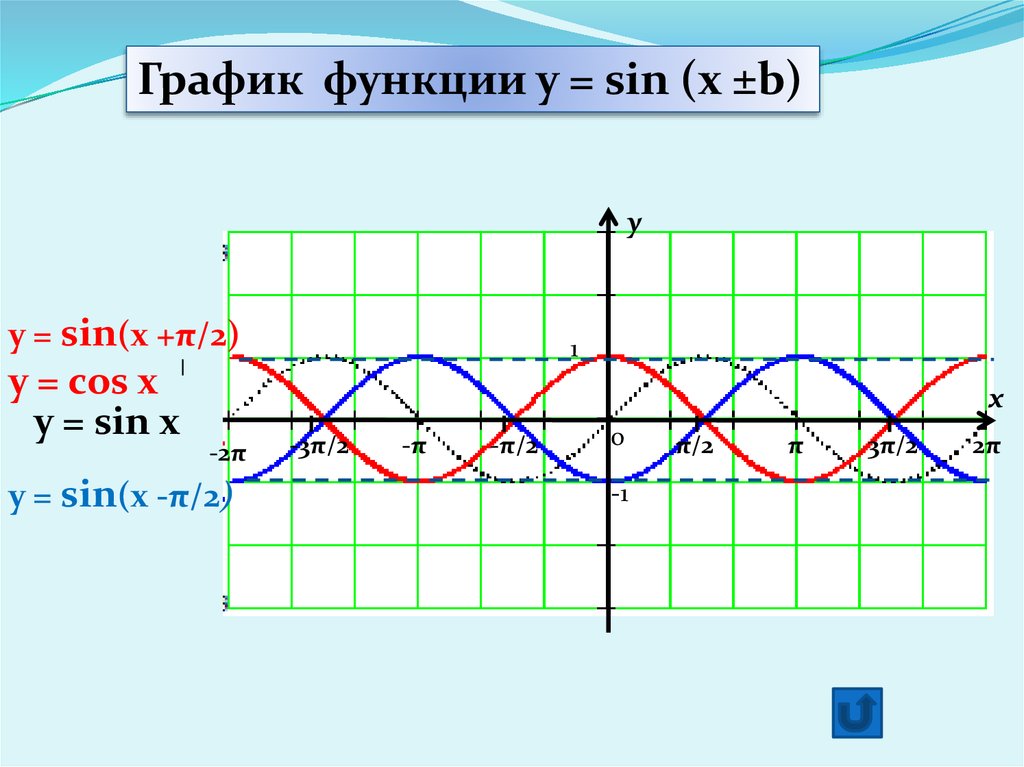
Мы будем использовать домен и некоторые значения \[x\], лежащие между \[ — \pi \] и \[\pi \], чтобы найти некоторые значения \[y\]. Затем по значениям \[y\] найдем координаты точек, лежащих на искомом графике, и по полученным координатам построим график функции.
Полное пошаговое решение:
Область определения всех синусоидальных функций — это множество всех действительных чисел.
Таким образом, область определения функции \[y = \sin 2x\] задается выражением \[\left\{ {x:x \in R} \right\}\]. Это означает, что функция \[y = \sin 2x\] существует для всех значений \[x\] и является непрерывной функцией.
Теперь мы найдем некоторые значения \[y\] для некоторых значений \[x\], лежащих между \[ — \pi \] и \[\pi \].
\[\begin{array}{l}y = \sin \left( {2\left( { — \pi } \right)} \right)\\ \Стрелка вправо y = \sin \left( { — 2\pi } \right)\end{массив}\]
Синус угла \[ — x\] можно записать как \[\sin \left( { — x} \right) = — \sin x\].
Упрощая выражение, получаем
\[\begin{array}{l} \Rightarrow y = — \sin \left( {2\pi } \right)\\ \Rightarrow y = 0\end{array}\]
Подставляя \[x = — \dfrac{{3\pi }}{4}\] в функцию \[y = \sin 2x\], получаем
\[\begin{array}{l} \Rightarrow y = \sin \left( {2\left( { — \dfrac{{3\pi }}{4}} \right)} \right)\\ \Rightarrow y = \sin \left( { — \dfrac{{ 3\pi }}{2}} \right)\end{массив}\]
Поскольку функция синуса является нечетной функцией, мы можем записать приведенное выше уравнение в виде
значение угла, получаем
\[ \Rightarrow y = 1\]
Подставив \[x = — \dfrac{\pi }{2}\] в функцию \[y = \sin 2x\], получим get
\[\begin{array}{l} \Rightarrow y = \sin \left( {2\left( { — \dfrac{\pi} {2}} \right)} \right)\\ \Rightarrow y = \sin \left( { — \pi } \right)\end{array}\]
Поскольку функция синуса является нечетной функцией, мы можем записать приведенное выше уравнение как
\[\begin{array}{l} \Rightarrow y = — \sin \left( \pi \right)\\ \Rightarrow y = 0\end{array}\]
Замена \[x = — \dfrac{ \pi }{4}\] в функции \[y = \sin 2x\] получаем
\[\begin{array}{l} \Rightarrow y = \sin \left( {2\left( { — \dfrac{\pi }{4}} \right)} \right)\\ \Rightarrow y = \sin \left( { — \dfrac{\pi }{2}} \right)\end{array}\]
Подставляя значение угла, получаем
\[ \Rightarrow y = — 1\]
Подставляя \[x = 0\] в функцию \[y = \sin 2x\], получаем
\[\begin{array}{l} \Стрелка вправо y = \sin \left( {2\left( 0 \right)} \right)\\ \Стрелка вправо y = \sin \left( 0 \right)\end {array}\]
Подставляя значение угла, получаем
\[ \Rightarrow y = 0\]
Подставляя \[x = \dfrac{\pi }{4}\] в функцию \[y = \ sin 2x\], получаем
\[\begin{array}{l} \Rightarrow y = \sin \left( {2\left( {\dfrac{\pi }{4}} \right)} \right) \\ \Rightarrow y = \sin \left( {\dfrac{\pi }{2}} \right)\end{array}\]
Подставляя значение угла, получаем
\[ \Rightarrow y = 1\]
Подставляя \[x = \dfrac{\pi }{2}\] в функцию \[y = \sin 2x\], получаем
\[\begin{array} {l} \Rightarrow y = \sin \left( {2\left( {\dfrac{\pi} {2}} \right)} \right)\\ \Rightarrow y = \sin \left(\pi \right )\end{array}\]
Подставляя значение угла, получаем
\[ \Rightarrow y = 0\]
Подставляя \[x = \dfrac{{3\pi }}{4}\] в функция \[y = \sin 2x\], мы получаем
\[\begin{array}{l} \Rightarrow y = \sin \left( {2\left( {\dfrac{{3\pi}}}{4 }} \right)} \right)\\ \Rightarrow y = \sin \left( {\dfrac{{3\pi}}{2}} \right)\end{array}\]
Подставляя значение угла, получаем
\[ \Rightarrow y = — 1\]
Подставляя \[x = \pi \] в функцию \[y = \sin 2x\], получаем
\[\ begin{array}{l} \Стрелка вправо y = \sin \left( {2\left( \pi \right)} \right)\\ \Стрелка вправо y = \sin \left( {2\pi } \right)\ end{array}\]
Подставляя значение угла, получаем
\[ \Rightarrow y = 0\]
Располагая значения \[x\] и \[y\] в таблице и записывая координаты, получаем
| \[x\] | \[y\] | \[\left( {x,y} \right)\] |
| \[ — \pi \] | \[0\] | \[\left( { — \pi ,0} \right)\] |
| \[ — \dfrac{{3\pi }}{4}\] | \[1\] | \ [\left( { — \dfrac{{3\pi}}{4},1} \right)\] |
| \[ — \dfrac{\pi }{2}\] | \[0\ ] | \[\left( { — \dfrac{\pi }{2},0} \right)\] |
| \[ — \dfrac{\pi }{4}\] | \[ — 1\] | \[\left( { — \dfrac{\pi }{4}, — 1} \right)\] |
| \[0\] | \[0\] | \[\left( {0,0} \right)\] |
| \[\dfrac{\pi }{4}\] | \[1\] | \[\left( {\dfrac{\pi }{4 },1} \right)\] |
| \[\dfrac{\pi }{2}\] | \[0\] | \[\left( {\dfrac{\pi }{2} ,0} \right)\] |
| \[\dfrac{{3\pi}}{4}\] | \[ — 1\] | \[\left( {\dfrac{{3\ пи }}{4}, — 1} \справа)\] |
| \[\pi \] | \[0\] | \[\left( {\pi ,0} \right)\] |
Теперь воспользуемся координатами точек для построения нужного графика.